Параллелограмма авсд: У параллелограмма ABCD ∠A = 30°. Чему равны углы B, C, D? Объясните ответ.

Как найти площадь параллелограмма abcd: формула через стороны, диагонали

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение площади параллелограмма: формула и примеры

Параллелограмм – это геометрическая фигура; четырехугольник, у которого противоположные стороны равны и параллельны.

Формула вычисления площади
- По длине стороны и высоте
- По двум сторонам и углу между ними
- По двум диагоналям и углу между ними
Примеры задач

Формула вычисления площади

По длине стороны и высоте

Площадь параллелограмма (S) равняется произведению длины его стороны и высоты, проведенной к ней:

S = a ⋅ h

По двум сторонам и углу между ними

Площадь параллелограмма находится путем умножения длин его обеих сторон и синуса угла между ними:

S = a ⋅ b ⋅ sin α

По двум диагоналям и углу между ними

Площадь параллелограмма равна одной второй произведения длин его диагоналей, умноженного на синус угла между ними:

S = ¹/₂ ⋅ d₁ ⋅ d₂ ⋅ sin α

Примеры задач

Задание 1
Найдите площадь параллелограмма, если длина его стороны равняется 7 см, а высоты – 4 см.

Решение:
Используем первую формулу, в которой задействованы известные нам по условиям задания значения: S = 4 см * 7 см = 28 см

Задание 2
Найдите площадь параллелограмма, если его стороны равны 6 и 8 см, а угол между ними – 30°.

Решение:
Применим вторую формулу, рассмотренную выше: S = 6 см * 8 см * sin 30° = 24 см².

Задание 3
Найдите площадь параллелограмма с диагоналями, равными 4 и 6 см. Угол между ними составляет 90°.

Решение:
Воспользуемся формулой, в которой фигурируют диагонали: S = 1/2 * 4 см * 6 см * sin 90° = 12 см².

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Вершины А и D параллелограмма ABCD лежат в плоскости а, а две другие.

.. 10 класс Геометрия Зив Б.Г. Самостоятельная работа 9. Вариант 5 Вершины А и D параллелограмма ABCD лежат в плоскости а, а две другие… 10 класс Геометрия Зив Б.Г. Самостоятельная работа 9. Вариант 5 – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Вершины А и D параллелограмма ABCD лежат в плоскости а, а две другие — вне этой плоскости, АВ = 15 см, ВС = 19 см.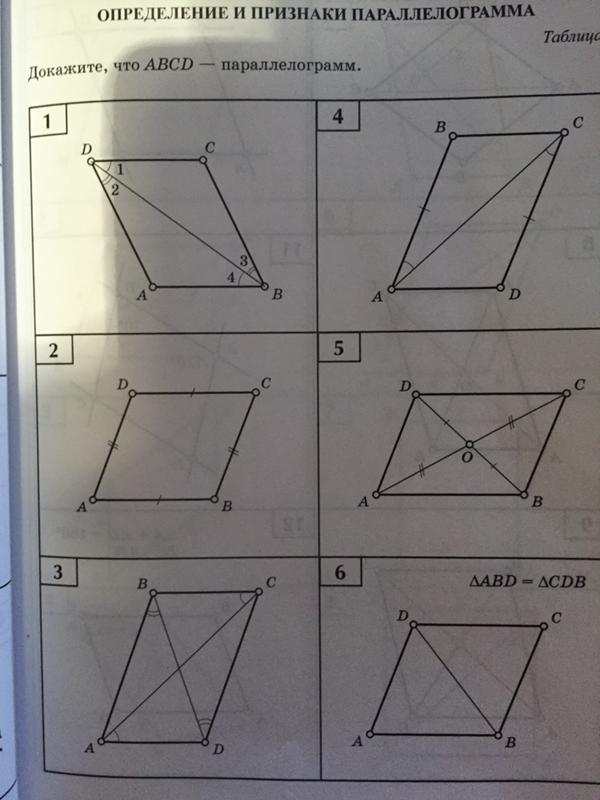

Проекции диагоналей параллелограмма на плоскость а равны 20 и 22 см. Найдите расстояние от стороны ВС до плоскости а.

ответы

ответ

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Досуг

Химия

похожие вопросы 5

В основании прямой призмы АВСА1В1С1 лежит прямоугольный треугольник… 10 класс Зив Б.Г. Геометрия. Самостоятельная работа 14. Вариант 2

(Подробнее…)

ГДЗГеометрияЗив Б. Г.10 класс

1. На гранях двугранного угла взяты две точки, удаленные от ребра… 10 класс Зив Б.Г. Геометрия. Самостоятельная работа 11. Вариант 3

1. На гранях двугранного угла взяты две точки, удаленные от ребра двугранного угла на 6 и 10 см.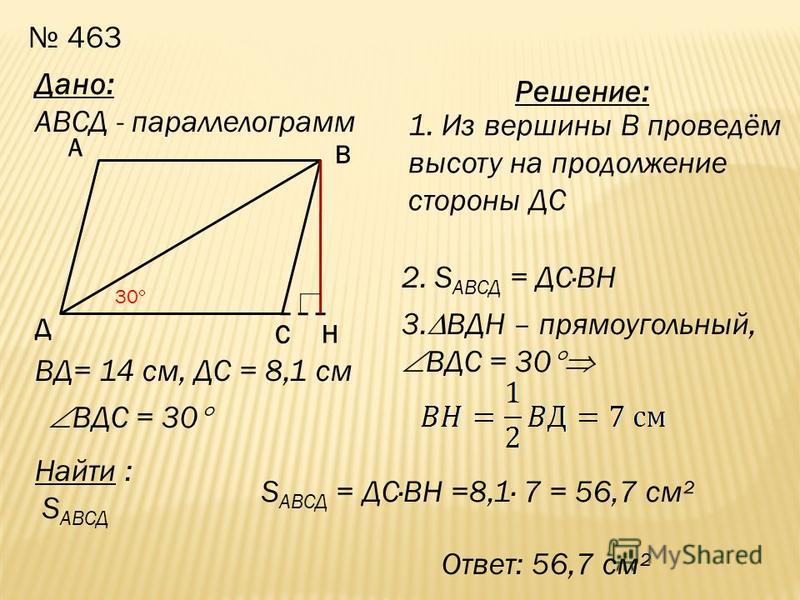 Известно, что одна из этих точек (Подробнее…)

ГДЗГеометрияЗив Б. Г.10 класс

АНГЛИЙСКИЙ ЯЗЫК. Past Simple/Present Perfect/Past Perfect — Correct the errors if necessary (Исправьте ошибки, если это необходимо)

1. His grandmother had lived in a village when he was a child.
2. Ken began to wave at me before I looked across the (Подробнее…)

ЭкзаменыГДЗ

Привет! Помогите завершить диалоги. Unit 2. Section 2. № 64. ГДЗ Английский язык Enjoy English 9 класс Биболетова.

Work in pairs. Look at the pictures of Steve’s journey. Complete the dialogues with your own words. Then act out one of the (Подробнее…)

ГДЗАнглийский язык9 классБиболетова М. З.

1. Основанием пирамиды служит ромб, сторона которого равна а, а острый… 10 класс Зив Б.Г. Геометрия. Самостоятельная работа 17. Вариант 4

1. Основанием пирамиды служит ромб, сторона которого равна а, а острый угол равен 60°.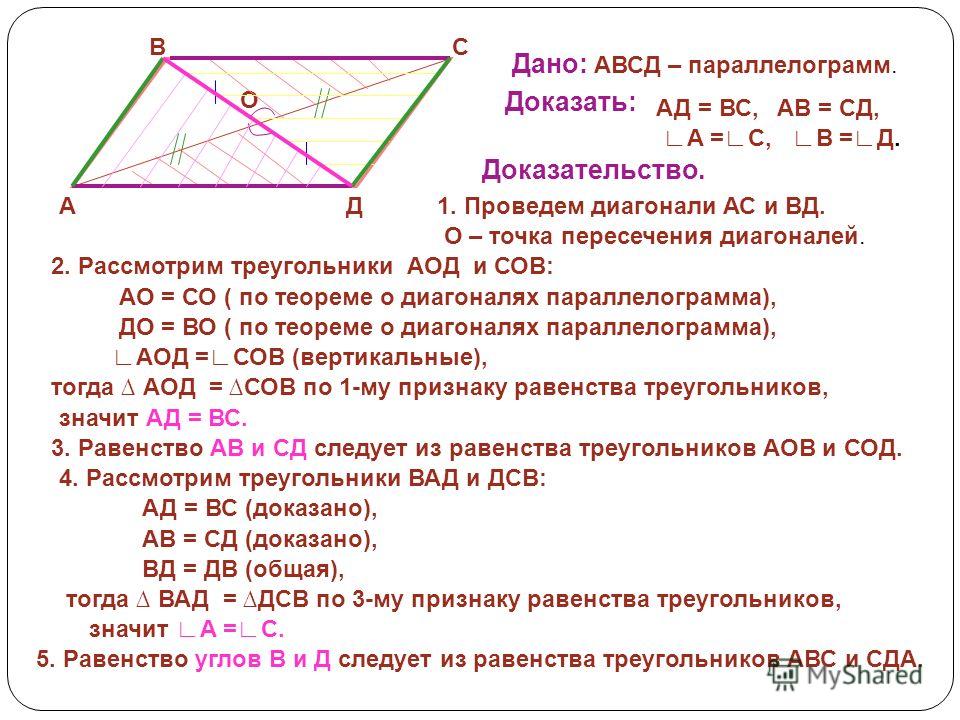 Боковые грани наклонены к основанию под углом (Подробнее…)

ГДЗГеометрияЗив Б. Г.10 класс

Q1 Дан параллелограмм ABCD. Дополните каждое утверждение вместе с используемым определением или свойством i A…

Перейти к

Упражнение 3.1
Упражнение 3.2
Упражнение 3.3

Упражнение 3.4

Рациональное число
Линейные уравнения с одной переменной
Понимание четырехугольников
Практическая геометрия

Обработка данных
Квадраты и квадратные корни
Кубы и кубические корни
Сравнение количеств

Алгебраические выражения и тождества
Визуализация твердых фигур
Измерение
Показатели и силы
Прямые и обратные пропорции
Факторизация
Введение в графики
Игра с числами

Главная > Решения НЦЭРТ Класс 8 Математика > Глава 3. Понимание четырехугольников > Упражнение 3.3 > Вопрос 24

Вопрос 24 Упражнение 3.3

Q1)

Дан параллелограмм ABCD. Заполните каждый оператор

вместе с используемым определением или свойством.

(i) AD = …… (ii) ∠ DCB = ……

(iii) OC = …… (iv) m ∠DAB + m ∠CDA = . …..

Ответ:

Решение 1 :

(i): AD=BC (В параллелограмме противоположные равные длины

(ii): \угол DCB=\угол DAB (Противоположные углы равны в параллелограмме )

(iii): OC=OA (в параллелограмме диагонали делят друг друга пополам)

(iv): m\угол DAB\ +m\угол CDA=180 (дополнительная теория угла)

Связанные вопросы

**Рассмотрите следующий параллелограмм. Найдите значения неизвестных x, y, z**

** Дан параллелограмм ABCD. Дополните каждое утверждение вместе с используемым определением или свойством. ***…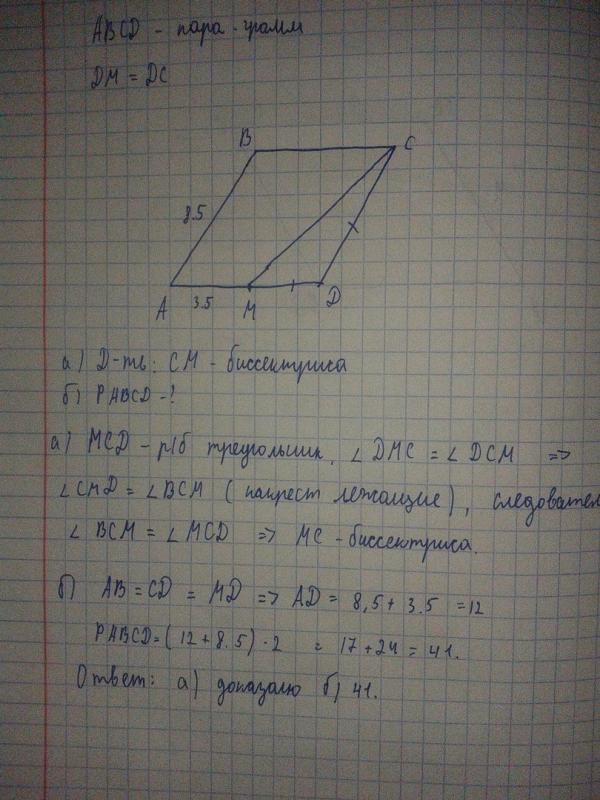

**Рассмотрите следующий параллелограмм. Найдите значения неизвестных x, y, z**

**На приведенном рисунке и РИСК, и ПОДСКАЗКА являются параллелограммами. Найдите значение x.**

**Может ли четырехугольник ABCD быть параллелограммом, если ∠A = 70° и ∠C = 65°?**

**Может ли четырехугольник ABCD быть параллелограммом, если AB = DC = 8 см, AD = 4 см и BC = 4,4 см?**

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Упражнения

Упражнение 3. 1

Упражнение 3.2

Упражнение 3.3

Упражнение 3.4

Главы

Рациональные числа

Linear Equations in One Variable

Understanding Quadrilaterals

Practical Geometry

Data Handling

Squares and Square Roots

Cubes and Cube Roots

Comparing Quantities

Algebraic Expressions and Identities

Visualising Solid Shapes

Mensuration

Показатели и степени

Прямые и обратные пропорции

Факторизация

Введение в графики

Игра с числами

Курсы

Быстрые ссылки

Условия и политика

Параллелограммы и трапеции — Бесплатная помощь по математике

Параллелограмм – это четырехугольник, у которого обе пары противоположных сторон параллельны. Между мерами последовательных углов, противоположных углов и противоположных сторон параллелограмма существуют особые отношения. Квадрат — самый простой параллелограмм, потому что он имеет 2 набора параллельных сторон. Естественно, все его углы и стороны совпадают по длине или размеру.

Факты о параллелограмме

(1) Градусная мера четырех углов параллелограмма в сумме составляет 360 градусов. Помните, что все четырехугольники (четырехсторонние фигуры) имеют углы, сумма которых составляет 360 градусов. Вот пример:

Тогда: a + b + c + d = 360 градусов

(2) Градусная мера любых двух последовательных углов в сумме составляет 180 градусов. В параллелограмме ABCD:

угол a + угол b = 180 градусов
угол b + угол c = 180 градусов
угол c + угол d = 180 градусов
угол a + угол d = 180 градусов

(3) Противоположные углы имеют одинаковую меру в градусах.

В параллелограмме ABCD:

угол a = угол c
угол b = угол d

Стороны параллелограмма

В параллелограмме ABCD:

(1) Противоположные стороны параллельны:

сторона AD || сторона ВС
сторона АВ || боковой CD

ПРИМЕЧАНИЕ: Символ || значит параллельно.

(2) Противоположные стороны имеют одинаковую длину:

сторона AD = сторона BC
сторона AB = сторона CD

Диагонали параллелограмма

Диагонали параллелограмма делят параллелограмм на два расположенных рядом треугольника. Как показано на рисунке ниже, диагональ AC образует равные чередующиеся внутренние углы с каждой парой параллельных сторон. Мы также можем видеть, что на картинке ниже есть два треугольника. Треугольник 1 конгруэнтен треугольнику 2 по методу ASA (угол-сторона-угол).

Откуда взялись два треугольника? Они были образованы диагональю AC.

Следует также отметить, что диагонали параллелограмма делят друг друга пополам, как показано на рисунке ниже.

АЕ = ЕС
Германия = ЕВ
где Е — середина ОБЕИХ диагоналей.

Пример:

В параллелограмме WXYZ угол X = 4a — 40, а угол Z = 2a — 8. Найдите величину угла W?

Решение:

(1) Найдите значение a.

Поскольку углы X и Z являются противоположными углами параллелограмма WXYZ, они имеют одинаковую меру.