Правильная пирамида
Правильная пирамида — частный случай пирамиды.
Определение 1. Пирамида называется правильной, если её основанием является правильный многоугольник, при этом вершина такой пирамиды проецируется в центр ее основания.
Определение 2. Пирамида называется правильной, если ее основание – правильный многоугольник, а высота проходит через центр основания.
Элементы правильной пирамиды
- Высота боковой грани, проведенная из ее вершины называется апофема. На рисунке обозначена как отрезок ON
- Точка, соединяющая боковые рёбра и не лежащая в плоскости основания, называется вершиной пирамиды (О)
- Треугольники, имеющие общую сторону с основанием и одну из вершин, совпадающую с вершиной, называются боковыми гранями (AOD, DOC, COB, AOB)
- Отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания называется высотой пирамиды (ОК)
- Диагональное сечение пирамиды — это сечение, проходящее через вершину и диагональ основания (AOC, BOD)
- Многоугольник, которому не принадлежит вершина пирамиды, называется основанием пирамиды (ABCD)
Если в основании правильной пирамиды лежит треугольник, четырехугольник и т. д. то она называется правильной треугольной, четырехугольной и т.д.
д. то она называется правильной треугольной, четырехугольной и т.д.
Треугольная пирамида есть четырехгранник — тетраэдр.
- боковые ребра равны между собой
- апофемы равны
- боковые грани равны между собой (при этом, соответственно, равны их площади, боковые стороны и основания), то есть они являются равными треугольниками
- все боковые грани являются равными равнобедренными треугольниками
- в любую правильную пирамиду можно как вписать, так и описать около неё сферу
- если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна π, а каждый из них соответственно π/n, где n — количество сторон многоугольника основания
- площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему
- около основания правильной пирамиды можно описать окружность (см.
 также радиус описанной окружности треугольника)
также радиус описанной окружности треугольника) - все боковые грани образуют с плоскостью основания правильной пирамиды равные углы
- все высоты боковых граней равны между собой
- Расстояние между основаниями усеченной пирамиды называется высотой усеченной пирамиды
- Все грани правильной усеченной пирамиды являются равнобокими (равнобедренными) трапециями
- Для правильной треугольной пирамиды
- Ознакомьтесь со справочными материалами
- Выясните, по условию задачи, о какой именно правильной пирамиде идет речь
- После этого в дереве знаний справа, найдите подходящий урок с данной фигурой (см.
 решение задач про правильную пирамиду с треугольником в основании, с четырехугольником в основании). Если нужного решения не нашлось, попробуйте ознакомиться с содержанием соседних уроков, возможно, решение подобной задачи есть именно там
решение задач про правильную пирамиду с треугольником в основании, с четырехугольником в основании). Если нужного решения не нашлось, попробуйте ознакомиться с содержанием соседних уроков, возможно, решение подобной задачи есть именно там - Если Вы просмотрели весь раздел, но аналогичной задачи не нашлось, напишите о своей проблеме на форуме «раздел для школьников» в соответствующей теме. Обязательно ознакомьтесь предварительно с правилами форума.
- Апофема правильной пирамиды
- Объем правильной усеченной пирамиды
- Правильная пирамида с четырехугольником в основании
- Правильная пирамида с четырехугольником в основании
- Нахождение боковой поверхности и высоты правильной пирамиды с четырехугольником в основании
- Правильная пирамида с четырехугольником в основании (часть 3)
- Нахождение углов пирамиды
- Нахождение величины наклона боковых граней правильной прамиды
- Нахождение расстояний в правильной четырехугольной пирамиде
- algebra
- expression of a variable from the formula
- arithmetic
- square root
- solid geometry
- pyramid
- planimetrics
- right triangle
- triangle
- goniometry и тригонометрия
- синус
- косинус
- тангенс
- арктангенс
- Совместное преобразование
- Длина
- Угол
- Пирамида
Пирамида имеет основание a = 3 см и высоту v = 15 см. а) вычислить угол между плоскостью ABV и базовой плоскостью б) вычислить угол между противоположными боковыми гранями.
а) вычислить угол между плоскостью ABV и базовой плоскостью б) вычислить угол между противоположными боковыми гранями. - Четырехугольная пирамида
Рассчитайте площадь поверхности и объем правильной четырехугольной пирамиды: стороны оснований (низ, верх): а1 = 18 см, а2 = 6 см угол α = 60° (угол α угол между боковой стенкой и базовая плоскость.) S =? , В =? - Угол двух прямых
Имеется правильная четырехугольная пирамида ABCDV; | АБ | = 4 см; высота v = 6 см. Определить углы прямых AD и BV. - Пирамида — угол
Рассчитайте поверхность правильной четырехугольной пирамиды, длина ребра основания которой равна 6 см, а отклонение от плоскости боковой стенки основания составляет 50 градусов. - Четырехгранная пирамида
Рассчитайте объем и поверхность правильной четырехугольной пирамиды, если длина ребра основания равна 4 см, а высота пирамиды 7 см. - Четырехугольная пирамида
Дана правильная четырехугольная пирамида с квадратным основанием. Высота тела 30 см, объем V = 1000 см³. Вычислите его сторону и площадь поверхности.
Высота тела 30 см, объем V = 1000 см³. Вычислите его сторону и площадь поверхности. - Пятиугольная пирамида
Вычислите объем правильной 5-гранной (пентапризмы) пирамиды ABCDEV; если |АВ| = 7,7 см и плоскость ABV, угол ABC 37 градусов. - Четырехугольная пирамида
Правильная четырехугольная пирамида имеет длину основания 6 см и длину бокового ребра 9 сантиметров. Вычислите его объем и площадь поверхности. - Четырехгранная призма
Рассчитайте объем и площадь поверхности правильной четырехугольной призмы, высота которой равна 28,6 см, а диагональное тело образует с плоскостью основания угол 50 градусов. - Пирамида 8
Вычислите объем и площадь поверхности правильной четырехугольной пирамиды со стороной основания 9см, а боковая стенка с основанием составляет угол 75°. - Четырехгранная пирамида 8
Пусть все боковые ребра четырехгранной пирамиды ABCDV имеют одинаковую длину, а ее основание пусть будет прямоугольником. Найдите его объем, если известны отклонения A=40° B=70° между плоскостями соседних боковин и плоскостью основания. Высота пирамиды h
Высота пирамиды h - Четырехугольник 8120
Включите длину боковой грани правильной четырехугольной пирамиды, если высота пирамиды 4 см, а площадь основания 16 см². - Высота стены
Рассчитайте площадь и объем правильной четырехугольной пирамиды, если сторона a = 6 см, а высота стены v = 0,8 дм. - Крыша 7
Крыша представляет собой правильную четырехугольную пирамиду с ребром основания 12 м и высотой 4 м. Сколько процентов составляет фальц и отходы, если в строительстве было израсходовано 181,4м² плиты? - Вычислить 8354
В правильной пирамиде, у которой ребро основания | АБ | = 4см; высота = 6 см, рассчитайте угол линий AV и CV, V = вершина. - Четырехугольная пирамида
Высота правильной четырехугольной пирамиды равна 6,5 см, а угол между основанием и боковой стенкой равен 42°. Вычислите площадь поверхности и объем тела, округлив результаты до 1 знака после запятой. - Четырехугольник 28491
Рассчитайте вес правильной четырехугольной пирамиды с длиной основания 4 см и высотой корпуса 6 см, если она изготовлена из материала плотностью 8 г/см³.
- Общая площадь поверхности (TSA)
- Площадь боковой поверхности (LSA)
- основание, которое является квадратом.
- 4 боковые грани, каждая из которых представляет собой треугольник.
- а = длина основания квадратной пирамиды
- l = наклонная высота или высота каждой боковой поверхности
- h = высота квадратной пирамиды
- Сложите все площади вместе, чтобы получить общую площадь поверхности квадратной пирамиды, а площадь четырех треугольных граней дает боковую площадь квадратной пирамиды.
- Таким образом, площадь поверхности квадратной пирамиды равна 2 + 2al, а площадь боковой поверхности равна 2al в квадратных единицах.
Пример 1: Найдите площадь поверхности квадратной пирамиды с наклонной высотой 15 единиц и длиной основания 12 единиц.
Решение
Длина основания квадратной пирамиды а = 12 единиц.
Наклонная высота l = 15 ед.
Площадь поверхности = a 2 +2al = 12 2 +2 (12) (15) = 504 шт.
 2
2 Ответ: Площадь поверхности данной квадратной пирамиды составляет 504 единицы 2 .
Пример 2: Высота квадратной пирамиды составляет 25 единиц, а площадь основания квадратной пирамиды составляет 256 квадратных единиц. Найдите площадь его поверхности.
Решение
Пусть сторона основания (квадрата) равна а единиц.
Тогда а 2 = 256 ⇒ а = 16 единиц.
Высота данной квадратной пирамиды h = 25 единиц. 9{2}}\) ≈ 1095,96 квадратных единиц.
Ответ: Площадь поверхности данной квадратной пирамиды = 1095,96 квадратных единиц.
Свойства правильной пирамиды
Для решения задач необходимо знать свойства отдельных элементов, которые в условии обычно опускаются, так как считается, что ученик должен это знать изначально.
Указания к решению задач. Свойства, перечисленные выше, должны помочь в практическом решении. Если требуется найти углы наклона граней, их поверхность и т. д., то общая методика сводится к разбиению всей объемной фигуры на отдельные плоские фигуры и применение их свойств для нахождения отдельных элементов пирамиды, поскольку многие элементы являются общими для нескольких фигур.
Необходимо разбить всю объемную фигуру на отдельные элементы — треугольники, квадраты, отрезки. Далее, к отдельным элементам применить знания из курса планиметрии, что существенно упрощает нахождение ответа.
Формулы для правильной пирамиды
Формулы для нахождения объема и площади боковой поверхности:
Обозначения:
V — объем пирамиды
S — площадь основания
h — высота пирамиды
Sb — площадь боковой поверхности
a — апофема (не путать с α)
P — периметр основания
n — число сторон основания
b — длина бокового ребра
α — плоский угол при вершине пирамиды
Данная формула нахождения объема может применяться только для правильной пирамиды:
, где
V — объем правильной пирамиды
n — число сторон правильного многоугольника, который является основанием для правильной пирамиды
a — длина стороны правильного многоугольника
Правильная усеченная пирамида
Если провести сечение, параллельное основанию пирамиды, то тело, заключённое между этими плоскостями и боковой поверхностью, называется усеченной пирамидой. Это сечение для усеченной пирамиды является одним из её оснований.
Это сечение для усеченной пирамиды является одним из её оснований.
Высота боковой грани (которая является равнобокой трапецией), называется — апофема правильной усеченной пирамиды
Усечённая пирамида называется правильной, если пирамида, из которой она была получена – правильная.
Примечания
См. также: частные случаи (формулы) для правильной пирамиды:
Как воспользоваться приведенными здесь теоретическими материалами для решения своей задачи:
Содержание главы:
0
Пирамида и вписанный конус | Описание курса | Апофема правильной пирамиды
Правильная четырехугольная пирамида
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2013-01-08
Продолжаем рассматривать задачи входящие в ЕГЭ по математике.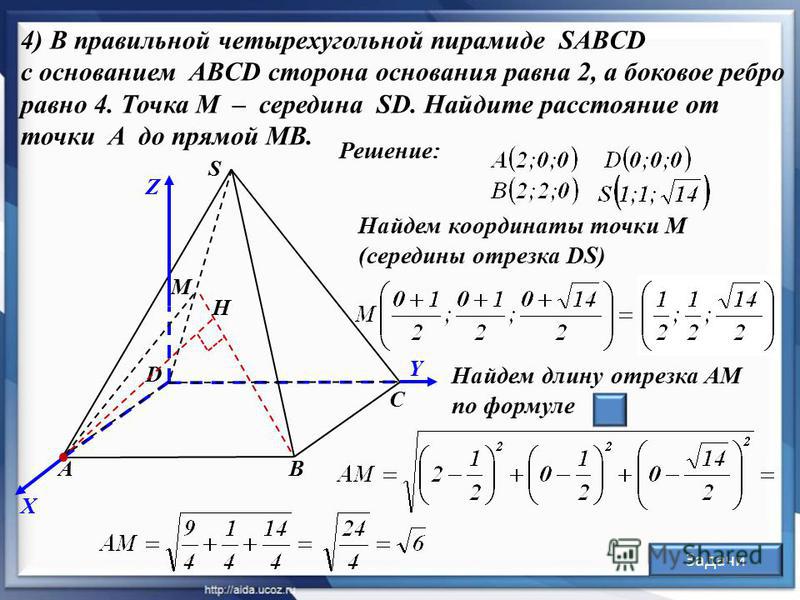 Мы уже исследовали задачи, где в условии дан составной многогранник и требуется найти расстояние между двумя данными точками либо угол.
Мы уже исследовали задачи, где в условии дан составной многогранник и требуется найти расстояние между двумя данными точками либо угол.
Пирамида — это многогранник, основание которого является многоугольником, остальные грани — треугольники, при чём они имеют общую вершину.
Правильная пирамида — это пирамида в основании которой лежит правильный многоугольник, а его вершина проецируется в центр основания.
Правильная четырехугольная пирамида — снованием является квадрат.Вершина пирамиды проектируется в точку пересечения диагоналей основания (квадрата).
ML — апофема
∠MLO — двугранный угол при основании пирамиды
∠MCO — угол между боковым ребром и плоскостью основания пирамиды
В этой статье мы с вами рассмотрим задачи на решение правильной пирамиды. Требуется найти какой-либо элемент, площадь боковой поверхности, объём, высоту. Разумеется, необходимо знать теорему Пифагора, формулу площади боковой поверхности пирамиды, формулу для нахождения объёма пирамиды.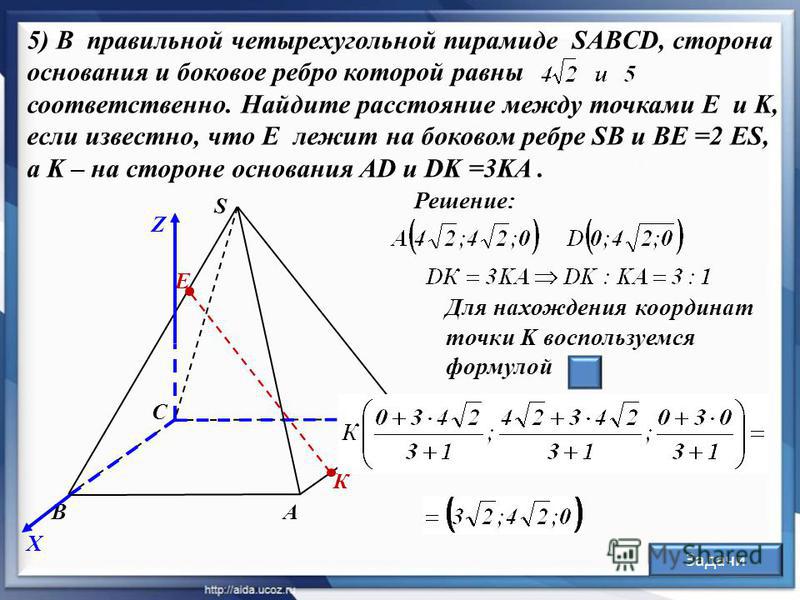
В статье «Общий обзор. Формулы стереометрии!» представлены формулы, которые необходимы для решения задач по стереометрии. Итак, задачи:
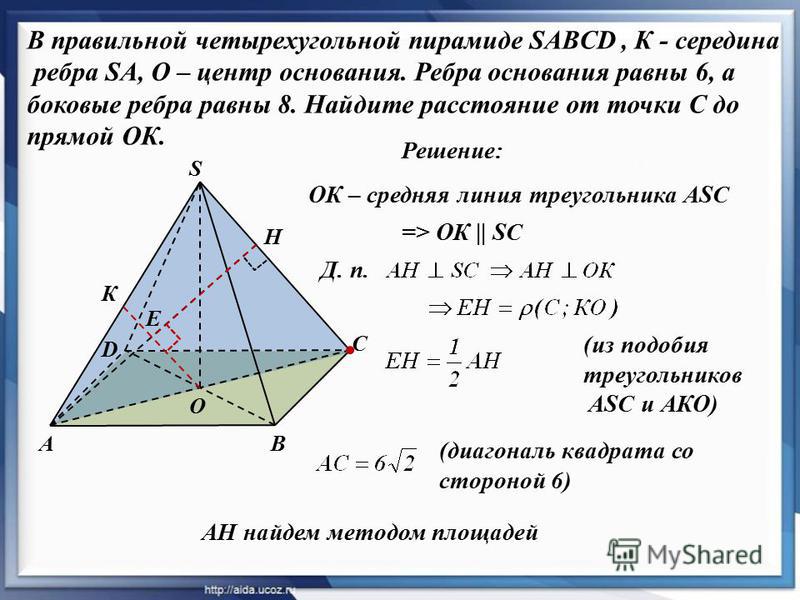
В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO = 51, AC = 136. Найдите боковое ребро SC.
В данном случае в основании лежит квадрат. Это означает, что диагонали AC и BD равны, они пересекаются и точкой пересечения делятся пополам. Отметим, что в правильной пирамиде высота опущенная из её вершины проходит через центр основания пирамиды. Таким образом, SO является высотой, а треугольник SOC прямоугольный. Тогда по теореме Пифагора:
Как извлекать корень из большого числа описано здесь.
Ответ: 85
Решите самостоятельно:
В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO = 4, AC = 6. Найдите боковое ребро SC.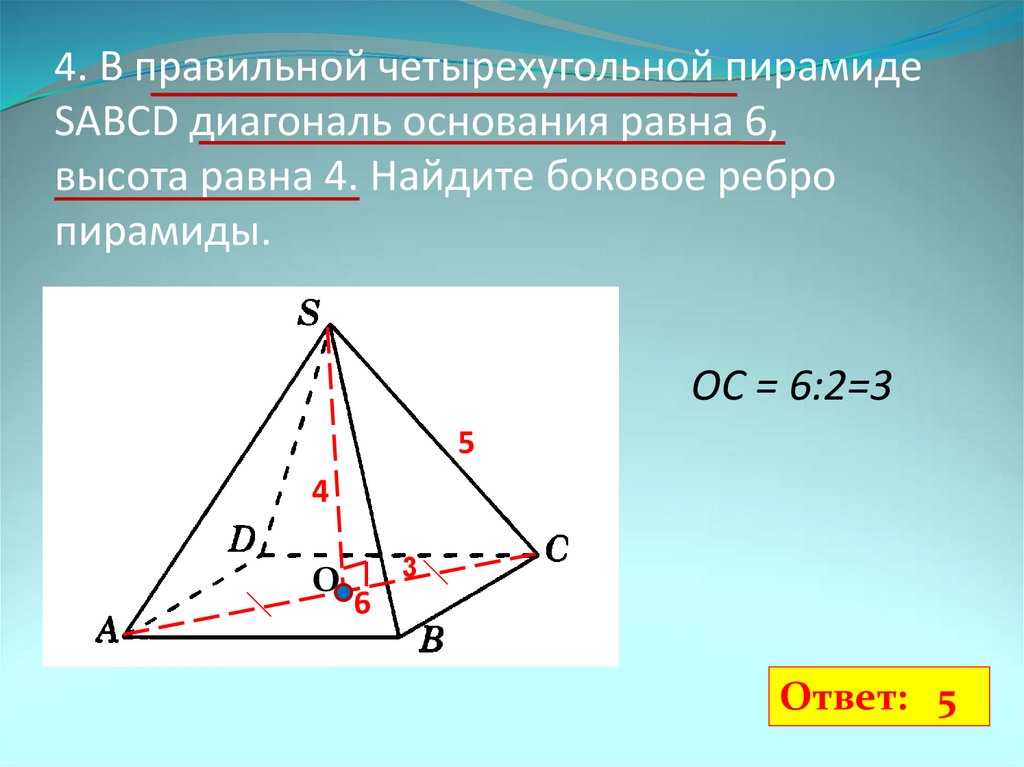
Посмотреть решение
В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SC = 5, AC = 6. Найдите длину отрезка SO.
Посмотреть решение
В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO = 4, SC = 5. Найдите длину отрезка AC.
Посмотреть решение
В правильной треугольной пирамиде SABC R — середина ребра BC, S — вершина. Известно, что AB = 7, а SR = 16. Найдите площадь боковой поверхности.
Площадь боковой поверхности правильной треугольной пирамиды равна половине произведения периметра основания на апофему (апофема это высота боковой грани правильной пирамиды, проведённая из её вершины):
Или можно сказать так: площадь боковой поверхности пирамиды равна сумме площадей трёх боковых граней. Боковыми гранями в правильной треугольной пирамиде являются равные по площади треугольники.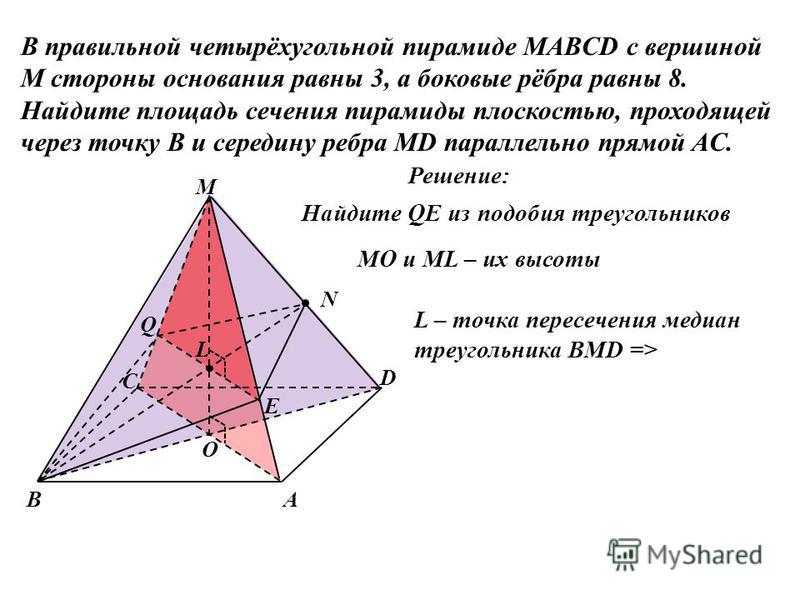 В данном случае:
В данном случае:
Ответ: 168
Решите самостоятельно:
В правильной треугольной пирамиде SABC R — середина ребра BC, S — вершина. Известно, что AB = 1, а SR = 2. Найдите площадь боковой поверхности.
Посмотреть решение
В правильной треугольной пирамиде SABC R — середина ребра BC, S — вершина. Известно, что AB = 1, а площадь боковой поверхности равна 3. Найдите длину отрезка SR.
Посмотреть решение
В правильной треугольной пирамиде SABC L — середина ребра BC, S — вершина. Известно, что SL = 2, а площадь боковой поверхности равна 3. Найдите длину отрезка AB.
Посмотреть решение
В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 25, объем пирамиды равен 100. Найдите длину отрезка MS.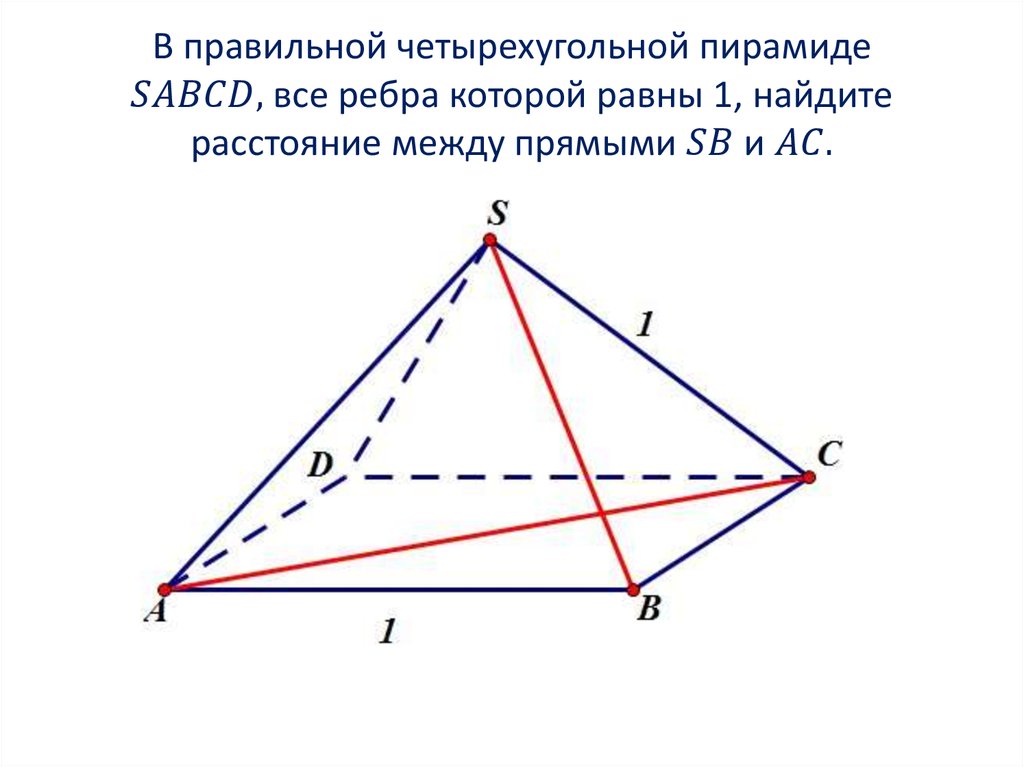
Основание пирамиды — равносторонний треугольник. Поэтому M является центром основания, а MS — высотой правильной пирамиды SABC. Объем пирамиды SABC равен:
Ответ: 12
Решите самостоятельно:
В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, объем пирамиды равен 1. Найдите длину отрезка MS.
Посмотреть решение
В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, MS = 1. Найдите объем пирамиды.
Посмотреть решение
В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Объем пирамиды равен 1, MS = 1. Найдите площадь треугольника ABC.
Посмотреть решение
На этом закончим. Как видите, задачи решаются в одно-два действия. В будущем рассмотрим с вами другие задачи из данной части, где даны тела вращения, не пропустите!
В будущем рассмотрим с вами другие задачи из данной части, где даны тела вращения, не пропустите!
Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Стереометрия ПИРАМИДЫ | ЕГЭ-№2
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Математическая задача: Правильная четырехугольная пирамида
Высота правильной четырехугольной пирамиды 6 см, а длина основания 4 см. Чему равен угол между плоскостями ABV и BCV?
Правильный ответ:
x = 36,8699 °Пошаговое объяснение:
h=6 см a=4 см s1=a/2=4/2=2 см s2=s12+h3
=22+62
=2 10
см≐6,3246 см тангенс x/2 = с1/ч x1= арктангенс (с1/ч) = арктангенс (2/6) ≐ 0,3218 рад x2 =x1→ °=x1⋅ π180 °=0,3218⋅ π180 °=18,43495 ° x=2⋅ x2=2⋅ 18,4349=36,8699∘=36°52′12″
Нашли ошибку или неточность? Не стесняйтесь
, напишите нам . Спасибо!
Спасибо!
Советы по теме онлайн калькуляторы
Вы хотите преобразовать единицы длины
См. также наш калькулятор прямоугольного треугольника
См. также наш калькулятор тригонометрического треугольника
Попробуйте перевести единицы измерения угла градусы, минуты, секунды, радианы, грады
Вам нужно знать следующие знания, чтобы решить эту математическую задачу слова:
Единицы физических величин:
Серка математическая задача: видео1
Площадь поверхности квадратной пирамиды
В этом разделе мы узнаем о площади поверхности квадратной пирамиды. Пирамида — это трехмерный объект, все боковые грани которого представляют собой конгруэнтные треугольники, а его основанием может быть любой многоугольник. Одна сторона каждого из этих треугольников совпадает с одной стороной базового многоугольника. Квадратная пирамида — это пирамида, основание которой — квадрат. Пирамиды названы в соответствии с формой их оснований. Как и другие трехмерные фигуры, квадратная пирамида также имеет два типа областей.
Давайте узнаем о площади поверхности квадратной пирамиды вместе с формулой и несколькими решенными примерами здесь. В конце вы найдете несколько практических вопросов.
| 1. | Какова площадь поверхности квадратной пирамиды? |
2. | |
| 3. | Как рассчитать площадь поверхности квадратной пирамиды? |
| 4. | Часто задаваемые вопросы о площади поверхности квадратной пирамиды |
Какова площадь поверхности квадратной пирамиды?
Слово «поверхность» означает «внешняя или внешняя часть предмета или тела». Итак, площадь полной поверхности квадратной пирамиды равна сумме площадей ее боковых граней и основания. Мы знаем, что квадратная пирамида имеет:
Все эти треугольники равнобедренные и конгруэнтные, каждый из которых имеет сторону, совпадающую со стороной основания (квадрата).
Итак, площадь поверхности квадратной пирамиды равна сумме площадей четырех ее треугольных боковых граней и площади основания, которая является квадратной.
Формула площади поверхности квадратной пирамиды
Рассмотрим квадратную пирамиду, у которой длина основания (длина стороны квадрата) равна «a», а высота каждой боковой грани (треугольника) равна «l» (это также известно как наклонная высота). т. е. основание и высота каждой из 4 треугольных граней равны «a» и «l» соответственно. Таким образом, площадь основания пирамиды, являющейся квадратом, равна a × a = a 2 , а площадь каждой такой треугольной грани равна 1/2 × a × l. Таким образом, сумма площадей всех 4-х треугольных граней равна 4 (½ ар) = 2 ар. Давайте теперь разберемся с формулами для расчета боковой и общей площади поверхности квадратной пирамиды с использованием высоты и наклонной высоты.
Общая площадь поверхности квадратной пирамиды с использованием наклонной высоты
Общая площадь поверхности квадратной пирамиды — это общая площадь, покрытая четырьмя треугольными гранями и квадратным основанием. Общая площадь поверхности квадратной пирамиды с учетом наклонной высоты может быть определена по формуле 9{2}}\)
где
Как рассчитать площадь поверхности квадратной пирамиды?
Площадь поверхности квадратной пирамиды можно рассчитать, представив трехмерную фигуру в двумерную сеть.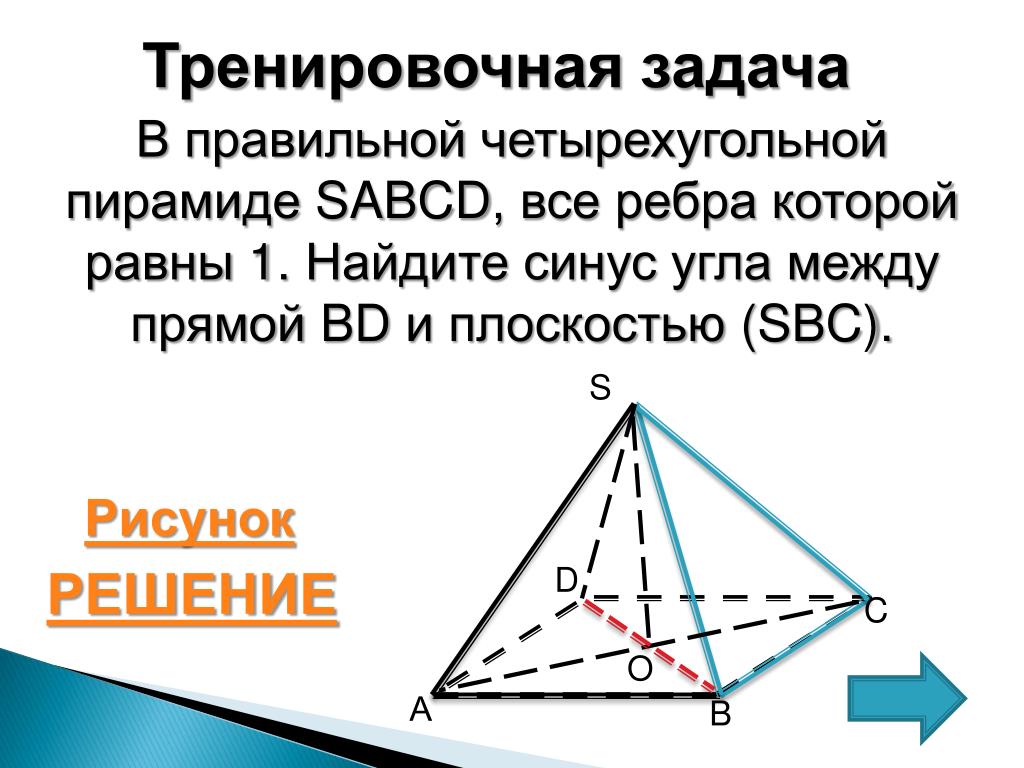 После расширения трехмерной фигуры в двухмерную сеть мы получим один квадрат и четыре треугольника.
После расширения трехмерной фигуры в двухмерную сеть мы получим один квадрат и четыре треугольника.
Теперь, когда мы увидели формулу и метод расчета площади поверхности квадратной пирамиды, давайте взглянем на несколько решенных примеров, чтобы лучше понять это.
Примеры площади поверхности квадратной пирамиды
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Запишитесь на бесплатный пробный урок
Практические вопросы по площади поверхности квадратной пирамиды
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о площади поверхности квадратной пирамиды
Какова площадь поверхности квадратной пирамиды?
Площадь поверхности квадратной пирамиды равна сумме площадей всех ее 4-х треугольных боковых граней с площадью основания квадратной пирамиды.

 также радиус описанной окружности треугольника)
также радиус описанной окружности треугольника) решение задач про правильную пирамиду с треугольником в основании, с четырехугольником в основании). Если нужного решения не нашлось, попробуйте ознакомиться с содержанием соседних уроков, возможно, решение подобной задачи есть именно там
решение задач про правильную пирамиду с треугольником в основании, с четырехугольником в основании). Если нужного решения не нашлось, попробуйте ознакомиться с содержанием соседних уроков, возможно, решение подобной задачи есть именно там а) вычислить угол между плоскостью ABV и базовой плоскостью б) вычислить угол между противоположными боковыми гранями.
а) вычислить угол между плоскостью ABV и базовой плоскостью б) вычислить угол между противоположными боковыми гранями. Высота тела 30 см, объем V = 1000 см³. Вычислите его сторону и площадь поверхности.
Высота тела 30 см, объем V = 1000 см³. Вычислите его сторону и площадь поверхности. Высота пирамиды h
Высота пирамиды h
 2
2
Leave A Comment