Средняя скорость на протяжении всего пути. Как вычислить среднюю скорость.
- Альфашкола
- Статьи
- Вычисление средней скорости
Давайте разберем как вычислить среднюю скорость
Для этого надо сделать три шага:
- вычислить весь путь;
- вычислить время, за которое прошел объект весь путь;
- путь разделить на время;
Пример 1. Саша прошел за 3 часа 9 км, а Сергей за 2 часа 6 км. Найдите их среднюю скорость.
Решение:
\(v_{ср}=\frac{9+6}{3+2}=\frac{15}{5}=3\) км/час
Ответ: 3 км/час.
Пример 2. Пешеход прошел за 4 часа 10 км, а велосипедист за 3 часа 11 км.
Решение:
\(v_{ср}=\frac{10+11}{4+3}=\frac{21}{7}=3\) км/час
Ответ: 3 км/час.
Пример 3. Пароход проплыл за 2 часа со скоростью 20 км/ч и 3 часа со скоростью 30 км/ч. Вычислите среднюю скорость парохода.
Решение:
- \(2*20 + 3*30 = 40 +90 =130 \) (км) — весь путь .
- \(2+3=5 \) (час) — все время.
- \(130:5 =26 \) (км/час) — средняя скорость .
Ответ : 26 км/час.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Светлана Михайловна Радова
Репетитор по математике
Стаж (лет)
Образование:
Тираспольский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Андрей Алексеевич Тарасов
Репетитор по математике
Стаж (лет)
Образование:
Новосибирский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Оксана Александровна Латтеган
Репетитор по математике
Стаж (лет)
Образование:
Новосибирский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Предметы
- Математика
- Репетитор по физике
- Репетитор по химии
- Репетитор по русскому языку
- Репетитор по английскому языку
- Репетитор по обществознанию
- Репетитор по истории России
- Репетитор по биологии
- Репетитор по географии
- Репетитор по информатике
Специализации
- Репетитор по геометрии
- Репетитор по грамматике русского языка
- Репетитор по английскому языку для подготовки к ЕГЭ
- Подготовка к олимпиадам по английскому языку
- Репетитор для подготовки к ЕГЭ по истории
- ВПР по математике
- Репетитор для подготовки к ВПР по русскому языку
- ВПР по физике
- Репетитор по информатике для подготовки к ОГЭ
- Программирование Pascal
Похожие статьи
- Что такое процент?
- Геологический факультет МГУ: вступительные экзамены
- Обратно пропорциональная зависимость
- НИУ ВШЭ (Программная инженерия): проходной балл, отзывы
- Иррациональные уравнения: примеры с решениями
- ЕГЭ по математике, базовый уровень.
 Задачи на координатной решетке
Задачи на координатной решетке - ЕГЭ по математике, базовый уровень. Задачи на координатной решетке
- Самые необычные животные на планете
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Текст с ошибкой:
Расскажите, что не так
разные методологии и проблемы —
Средняя скорость — одна из основных функций, определяемых в движении. В этой статье мы узнаем, как найти среднюю скорость.
Основной метод определения средней скорости — это отношение суммы изменения положения объекта к общему времени, затраченному этим объектом на завершение своего движения. Поскольку это векторная физическая величина, направление объекта также имеет важное значение при вычислении средней скорости.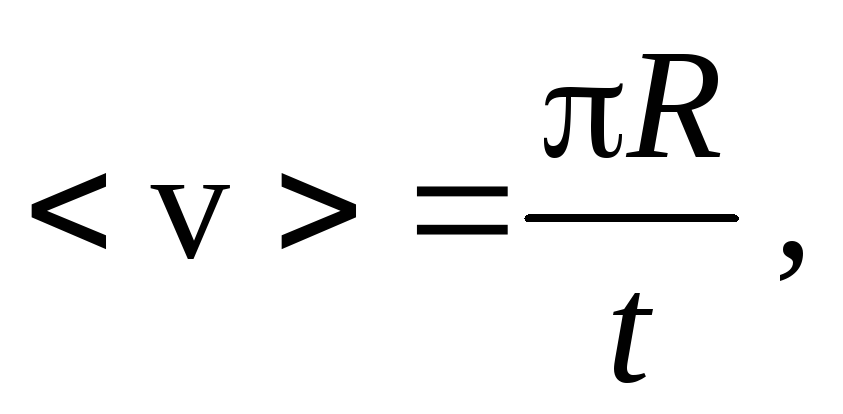
Далее мы изучим больше методов, как найти среднюю скорость, так как это основная цель поста.
Какая формула для средней скоростиОсновная формула, используемая для расчета Vсредний включает как смещение во времени.
Общая используемая формула имеет следующий вид:
Он используется при решении основных задач, связанных со средней скоростью.
В = Сf — Si / т2 — т1
V = Δs / Δt
Где,
Δs = смещение
Δt = затраченное время
Теперь давайте посмотрим, как найти среднюю скорость с помощью расстояния и времени.
Как найти среднюю скорость в зависимости от расстояния и времениРасстояние и время — основные термины, без которых невозможно определить среднюю скорость.
Прежде всего, мы должны рассчитать общую длину пути, по которому прошел объект, а затем мы должны проверить продолжительность времени, необходимого для достижения пункта назначения. Позже, чтобы найти среднюю скорость этого движения, нам нужно использовать ранее рассчитанные расстояние и время с помощью формулы.
Позже, чтобы найти среднюю скорость этого движения, нам нужно использовать ранее рассчитанные расстояние и время с помощью формулы.
Теперь давайте продолжим изучение, чтобы узнать больше подходов к нахождению средней скорости.
Как найти среднюю скорость за интервалУвидев важность расстояния и времени при вычислении средней скорости. Теперь давайте, как рассчитать это за интервал.
- Если вы вычисляете среднюю скорость на графике, вам следует рассмотреть любые два интервала времени и расстояния, а затем найти значения расстояния и времени и подставить их в формулу средней скорости.
В = Сf — Si / т2 — т1
- В другом методе, если вы собираетесь напрямую использовать формулу, вы должны знать начальную и конечную точки, чтобы вам было легко вычислить Vсредний, вы даже можете рассмотреть некоторую часть интервала, чтобы найти Vсредний Это происходит путем деления общего расстояния на общее время.

V = общее расстояние / общее время или
В = (Вf + Vi) / 2
Теперь давайте посмотрим, как рассчитать Vсредний между двумя точками.
Средняя скорость между двумя точкамиСреднюю скорость между двумя точками можно найти по простой формуле.
В общем, мы знаем, что Vavg тела равно среднему арифметическому начальных и конечных точек, приведенному ниже.
Vavg = [Начальная скорость (i) + Конечная скорость (v)] / 2
Пора узнать, как найти Vсредний на графике.
Как найти среднюю скорость на графикеМы можем найти среднюю скорость с помощью графика смещения-времени.
- Здесь смещение будет по оси y, а время по оси x.
- Постройте точки в соответствии с осью и соедините их, чтобы создать область на графике.

- Затем найдите общую площадь на графике, взяв два интервала времени и расстояния.
- Измерьте его по линии графика и рассчитайте по формуле
Vсредний = (Vi+Vf) / 2.
Переменные, взятые на графике, имеют характерную природу, все факторы, такие как изменение положения (между начальной и конечной точками), характер графика, т. Е. Является ли он линейным или нет, имеет значение.
При таком подходе мы можем рассчитать среднюю скорость по графику.
Как найти среднюю скорость на линейном графикеЛинейный график иногда называют прямолинейным графиком.
Если мы хотим узнать среднюю скорость на линейном графике, тогда мы должны взять как начальную, так и конечную скорости и разделить ее на число 2. Это похоже на среднее значение, которое мы используем в математике для решения определенных задач.
Теперь давайте узнаем условие вычисления средней скорости на нелинейном графике.
Как найти среднюю скорость на нелинейном графикеНелинейный граф также можно рассматривать как искривленный граф.
В нелинейном графике, что мы можем сделать, чтобы вычислить Vсредний мы можем рассмотреть область под графиком, которая состоит из смещения (интегрировать его), а затем разделить на время.
Таким образом мы можем вычислить Vсредний в нелинейном графике.
Пример задачи средней скоростиПриведенное ниже — одна из основных проблем, которую можно решить, используя подходы к вычислению средней скорости.
Пример 1Представьте, что человек едет на своей машине в какой-то пункт назначения, но в течение первых 15 секунд положение машины меняется с x1 = 80 м до x2= 100 м. Какова средняя скорость автомобиля?
Решение: учитывая исходное положение x1= 80m
Точно так же конечная позиция x2 = 100m
Изменение водоизмещения автомобиля рассчитывается следующим образом:
Δx = х2 — Икс1 = 100 м — 80 м = 20 м
Δt = 15 с
По формуле мы имеем
v = Δx / Δt
v = 20/15
v = 1. 33 м / с
33 м / с
Таким образом, средняя скорость автомобиля составляет 1.33 м / с.
Из поставленной выше задачи мы узнали еще об одном подходе к нахождению средней скорости
Часто задаваемые вопросы | FAQsЧто такое средняя скорость?Средняя скорость — заметное явление в физике.
Это векторная величина, определяемая как деление ∆x на ∆t. Где ∆x обозначает смещение, а ∆t обозначает общее время, затрачиваемое телом на завершение движения. Иногда может быть положительным или отрицательным, все зависит от направления смещения. Обозначается с помощью единицы СИ м / с.
Чем средняя скорость отличается от других скоростей?Есть два основных типа скоростей, с которыми мы обычно сталкиваемся в физике.
Два основных типа скоростей — средние и мгновенные скорости. Как следует из их названия, среднее означает сумму скоростей каждого интервала, рассчитанную за общее время. Напротив, мгновенная скорость будет вычислением скорости в конкретный период движения.
Напротив, мгновенная скорость будет вычислением скорости в конкретный период движения.
Если мы возьмем конкретный временной интервал, тогда будет разница в измерении средней и мгновенной скорости.
Основное различие заключается в том, что для определенного периода интервала мгновенная скорость измеряется смещением и временем в определенной точке (s, t), а средняя скорость считается общим изменением положения во времени в определенном временном интервале.
Сохраняется ли средняя скорость в движении?Скорость не остается неизменной в конкретном движении, она продолжает изменяться.
Мы выяснили, что скорость является переменной, зависящей от многих факторов. Он не остается постоянным, но продолжает изменять свое значение с помощью перемещения и времени этого объекта. Исходя из этого, мы можем сказать, что средняя скорость движения не остается неизменной.
Есть много приложений, с помощью которых мы можем легко измерить среднюю скорость.
Первый метод — найти среднюю скорость, взяв первую и конечную точки движения, вычтя ее, а затем разделив весь член на 2.
Второй метод основан на использовании формулы, известной как уравнение средней скорости.
Уравнение средней скорости = В = (Вf + Vi) / 2
- V = средняя скорость.
- Vf = конечная скорость.
- Vi = начальная скорость
Это простое уравнение для измерения средней скорости.
Как найти смещение со средней скоростью?Есть много способов найти смещение в кинематике.
Один из них — найти смещение с помощью формулы средней скорости, которая состоит из изменения положения / смещения. Меняя местами члены формулы, мы можем использовать ее для расчета смещения.
Меняя местами члены формулы, мы можем использовать ее для расчета смещения.
Оба термина означают совершенно разные друг от друга, когда мы изучаем их в физике.
Здесь мы знаем, что скорость — это скаляр, а скорость — вектор, тогда основное различие заключается в физических величинах, которые измеряют важность того, как их можно измерить.
Разница между средней скоростью и средней скоростьюОсновные различия между этими двумя величинами приведены ниже:
- Средняя скорость говорит только о положении движущегося тела, здесь мы должны заметить, что величина будет разной для каждого положения, и определение скорости на любом временном интервале на длине курса осуществляется с помощью средней скорости.
- Средняя скорость говорит о сохранении скорости на всем пути движения. Это общая скорость, рассчитанная с учетом общей длины пути и времени, и, поскольку это скаляр, мы не можем определить направление пути.

Как найти среднюю скорость (формула и примеры)
, написанный
Малкольм Маккинси
Проверка по фактам
Пол Маццола
Средняя скорость
Средняя скорость объединяет. два слова: среднее значение, означающее среднее значение, полученное из множества отдельных точек данных, и скорость, означающая изменение положения. Вы можете рассчитать среднюю скорость для любого типа движения, если можете рассчитать время движения и измерить расстояние.
Формула средней скорости
Средняя скорость это общее расстояние, пройденное для рассматриваемого объекта, деленное на общее время, затраченное на преодоление расстояния, общий период времени. Формула средней скорости:
Определение средней скорости и формулаСредняя скорость отличается от мгновенной скорости.
Мгновенная скорость
Средняя скорость учитывает совокупность событий, таких как ускорение автомобиля с места, ускорение, движение некоторое время, затем замедление на желтый сигнал светофора и, наконец, остановка.
Автомобиль движется с разной скоростью. В любой момент автомобиль не едет со скоростью 55 миль в час (миль в час). Это может быть 0 миль в час, затем 7 миль в час, затем 53 мили в час, затем 61 миля в час и, наконец, 3 мили в час, прежде чем вернуться к 0 милям в час.
Чтобы упростить измерения и добиться прогресса в решении задачи по физике или математике, вы берете среднюю скорость всех дискретных событий, говоря, что автомобиль проехал 5,5 миль за 6 минут :
Все эти другие измерения в определенные моменты времени в путешествии мгновенные скорости . В большинстве случаев вам нужно , а не знать формулу мгновенной скорости, v , нахождение предела по мере того, как изменение во времени («момент») приближается к 0:
Мгновенные скорости колеблются в течение хронометрируемого события. Найти среднюю скорость far проще и, как правило, гораздо полезнее, чем вычислить мгновенную скорость.
Скалярные и векторные величины
Скорость есть скалярная величина . У него нет направления. Он имеет только размер, то есть величину или масштаб. Скалярные величины могут изменяться от 0 (без скорости) до бесконечно быстрой.
У него нет направления. Он имеет только размер, то есть величину или масштаб. Скалярные величины могут изменяться от 0 (без скорости) до бесконечно быстрой.
Векторная величина имеет размер и направление, как и движение самолета в небе. Скорость является векторной величиной.
Скорость, будучи скалярной величиной, никогда не может быть меньше 0. Средняя и мгновенная скорости всегда являются скалярными величинами, что означает, что вы всегда можете измерить их числом. Расстояние и время также являются скалярными величинами и также могут быть измерены числами.
Как рассчитать среднюю скорость
Чтобы рассчитать среднюю скорость объекта, вы должны знать общее расстояние, которое проходит объект, и общее время, затраченное на весь его путь.
Треугольник расстояние/скорость/время удобен для расчета этой и двух других скалярных величин (расстояние и время):
Скорость расстояние время треугольник и формулыТри части треугольника математически расставлены в правильном положении:
Чтобы получить среднюю скорость, s , разделите общее расстояние на прошедшее время: Dt\frac{D}{t}tD
Чтобы получить пройденное время, t , разделите общее расстояние на скорость: Ds\frac{D }{s}sD
Чтобы получить расстояние, D , умножьте скорость на количество времени: s×ts\times ts×t
Допустим, вы хотите найти среднюю скорость Тихоокеанская афалина. Вам говорят, что он может пройти расстояние 89,7 км за 3 часа.
Вам говорят, что он может пройти расстояние 89,7 км за 3 часа.
Подставьте эти два заданных числа в треугольник в их двух углах, чтобы получить:
Как рассчитать среднюю скоростьЕсли вы знаете две из трех переменных, расстояние, время и скорость, то вы можете использовать алгебру, чтобы найти то, что вы повторно отсутствует.
Если вам нужно общее время, вы должны иметь расстояние и скорость. Вы подставляете эти две скалярные величины в соответствующие части треугольника, чтобы получить:
Вычисление общего времени по средней скорости и расстояниюЕсли вам нужно общее расстояние, вы должны знать скорость и время:
Расчет общего расстояния по средней скорости и времениСредняя скорость особенно полезна, поскольку она учитывает реальность события, а не предполагает, что что-то или кто-то движется с постоянной скоростью.
Морская свинья могла начать медленно, ускориться, сделать паузу, чтобы поиграть, и продолжить. Этот трехпалый ленивец, возможно, остановился на мгновение, чтобы отдышаться, прежде чем поспешить дальше.
Возможно, вам придется делать многочисленные остановки при выгуле собаки, но во всех трех случаях вы можете легко рассчитать среднюю скорость, разделив общее пройденное расстояние на общее затраченное время.
Предостережение
Средняя скорость часто выводится из единиц расстояния или времени, которые должны быть преобразованы в другие единицы для окончательного ответа. Соблюдайте осторожность при этом.
Обычными преобразованиями являются умножение единиц в секунду на 60 или 3600, чтобы получить единицы в минуту и единицы в час. Просто убедитесь, что ваш ответ дан в правильной единице времени.
Преобразование единиц измерения средней скоростиЕсли изменяется только одна единица измерения, вам нужно будет выполнить только одну математическую операцию (например, умножить секунды, чтобы получить минуты или часы). Если изменить две единицы (футы в секунду на мили в час), вы должны умножить и разделить (или умножить на десятичное значение).
Проблемы средней скорости
Тарпон (разновидность рыбы) может путешествовать 105 миль за 3 часа .
 Какова его средняя скорость?
Какова его средняя скорость?Синий тунец может проплыть и преодолеть 286 миль за обычный учебный день 6,5 часов . Какова его средняя скорость, пока вы проводите свой день в классе?
Мировой рекорд по скорости бега назад (во время жонглирования!) принадлежит Джо Солтеру, который проехал 5280 футов дюйма 457 секунд . Какова была его средняя скорость в милях за час ? (умножить на 3600 и затем разделить на 5280 ; или умножить на 0,681818 )
Гепард может пройти 0,6 мили за 3 секунд. Какова средняя скорость гепарда в милях за секунду ? Как насчет скорости в милях за час ? (умножить на 3600 )
Косатка может двигаться со средней крейсерской скоростью 8 миль в час. Большая белая акула может преодолеть расстояние 35 миль за семь часов. Какова скорость большой белой акулы и какое животное плывет быстрее?
Самый быстрый человек в воде преодолел 22,9 метра за 10 секунд.
 Кальмар Гумбольдта может пройти 399,6 метра за 60 секунд . Вам нужно рассчитать среднюю скорость самого быстрого человека и кальмара Гумбольдта, чтобы узнать, кто кого может обогнать.
Кальмар Гумбольдта может пройти 399,6 метра за 60 секунд . Вам нужно рассчитать среднюю скорость самого быстрого человека и кальмара Гумбольдта, чтобы узнать, кто кого может обогнать.
Мы знаем, что вы сначала сделаете работу, прежде чем проверять эти ответы, верно?
Рассчитайте среднюю скорость тарпона следующим образом: s=105miles3hourss=\frac{105miles}{3hours}s=3hours105miles, что означает, что рыба может двигаться со средней скоростью 35 миль в час .
Формула голубого тунца будет выглядеть так: s = 286 миль 6,5 часов = \ frac {286 миль {6,5 часов} s = 6,5 часов 286 миль, поэтому средняя скорость рыбы составляет 44 мили в час.
Joe Salter’s Cover 5,280 футов в 457 секунд , S = 5,280FEET457Seconds = \ frac {\ mathrm {5,280} футов} {457S {\ sepers {5,280} футов} {457S {\ sepends useeled weeelds {\ seture {5,280}}. . Мы умножаем это на 3600 (количество секунд в часе), а затем делим на 5280 (футы в миле), чтобы получить среднюю скорость 7,87745 миль в час .

Формула для средней скорости гепарда будет:0021 0,01666 (повторяющееся десятичное число, поэтому мы аппроксимируем 0,01666 ) в милях за секунду , которые можно умножить на 3600 , чтобы получить среднюю скорость 60 миль/ч .
Косатка может двигаться со средней крейсерской скоростью 8 миль/ч , в то время как средняя скорость большой белой акулы s=35mi.7hours=5mph=\frac{35mi.}{7hours}=5mph=7hours35mi. =5 миль в час. Косатка плавает быстрее.
Самый быстрый человек в воде плавал 22,9 метра в 10 секунд , поэтому средняя скорость s=22,9м10секунд=2,29метра/секунды=\frac{22,9м}{10секунд}=2,29метра/секунды=10секунд22,9м=2,29метра/секунду. Кальмар Гумбольдта может пройти 399,6 метров за 60 секунд , поэтому s=399,6м60секунд=6,67м/сс=\frac{399,6м}{60секунд}=6,67м/сс=60секунд399,6м=6,67м/с , значительно быстрее, чем самый быстрый пловец-человек. Будем надеяться, что вас никогда не преследовал кальмар Гумбольдта!
Формула средней скорости — Что такое формула для средней скорости? Примеры
Средняя скорость — это среднее значение скорости тела за определенный период времени. Формула для средней скорости необходима, поскольку скорость движущегося тела непостоянна и меняется с течением времени. Даже при различной скорости можно использовать значения общего времени и общего пройденного расстояния, а с помощью формулы для средней скорости мы можем найти одно значение для представления всего движения.
Формула для средней скорости необходима, поскольку скорость движущегося тела непостоянна и меняется с течением времени. Даже при различной скорости можно использовать значения общего времени и общего пройденного расстояния, а с помощью формулы для средней скорости мы можем найти одно значение для представления всего движения.
Что такое формула средней скорости?
Средняя скорость тела равна общему пройденному расстоянию, деленному на общее время. Формула для средней скорости задается как:
Формула средней скорости:
Средняя скорость = общее пройденное расстояние ÷ общее затраченное время
Особые случаи формулы средней скорости
Случай 1: время \( t_1 \) и скорость \(s_2 \) за время \( t_2 \), формула для средней скорости приведена в приведенном ниже выражении. Произведение \(s_1 \times t_1 \) и \(s_2 \times t_2 \) дает расстояния, пройденные за интервалы времени \(t_1 \) и \(t_2 \) соответственно.
Формула средней скорости \(= \frac{s_1 \times t_1 + s_2 \times t_2}{t_1 + t_2}\)
Случай 2: Аналогично, когда ‘n’ различных скоростей, \(s_{1} , s_{2}, s_{3},.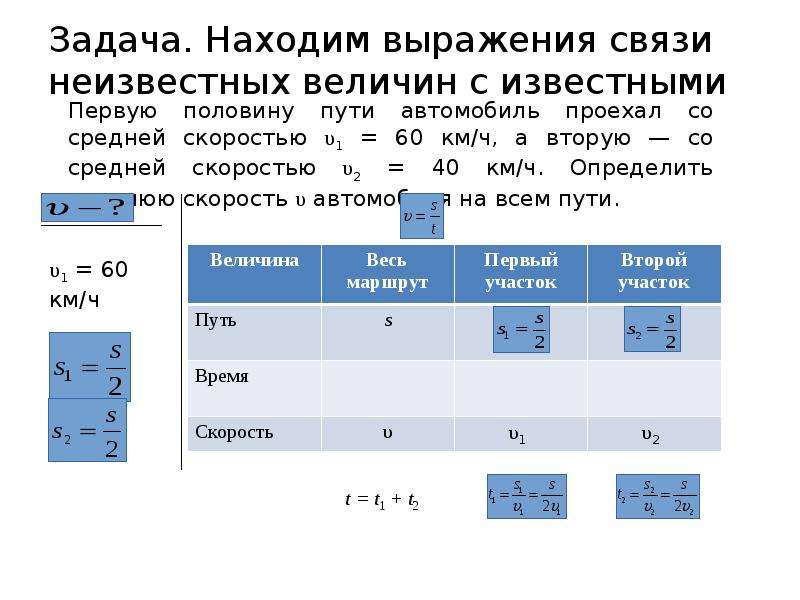 .. s_{n}\), даны для ‘n’ соответствующих отдельных интервалов времени, \(t_{1}, t_{2}, t_{3},. .. t_{n}\) соответственно, формула средней скорости задается как:
.. s_{n}\), даны для ‘n’ соответствующих отдельных интервалов времени, \(t_{1}, t_{2}, t_{3},. .. t_{n}\) соответственно, формула средней скорости задается как:
Формула средней скорости \(= \frac{s_1 t_1 + s_2 t_2 + … + s_n t_n}{t_1 + t_2 +… + t_n}\)
Случай 3: Средняя скорость при прохождении разных расстояний \(d_{1}, d_{2}, d_{3},… d_{n}\) за разные интервалы времени, \(t_{1}, t_{2}, t_{3},… t_{n}\) соответственно задается как:
Формула средней скорости \(S_{avg}\) \(= \frac{d_1 + d_2 + d_3 +…+ d_n} {t_1 + t_2 + t_3 +….+ t_n}\)
Случай 4: Средняя скорость, когда разные скорости, \(s_{1}, s_{2}, s_{3},… s_{n}\), даны для разных расстояний, \(d_{1}, d_{2}, d_{3},… d_{n}\) соответственно задается как:
Формула средней скорости \(S_{avg}\) \(= \frac{d_1 + d_2 + d_3 +. ..+ d_n} {\dfrac{d_1}{s_1} + \dfrac{d_2}{s_2} + \dfrac{d_3}{s_3} +….+ \dfrac{d_n}{s_n}}\)
Корпус 5: Формула средней скорости, когда заданы две или более скоростей (\(s_{1}, s_{2}, s_{3},. .. s_{n}\)) так, что эти скорости были пройдены за одинаковое количество времени (\(t_{1} = t_{2} = t_{3} =… t_{n} = t)\) задается как:
.. s_{n}\)) так, что эти скорости были пройдены за одинаковое количество времени (\(t_{1} = t_{2} = t_{3} =… t_{n} = t)\) задается как:
Формула средней скорости, \(S_{avg}\) \( = \frac{s_{1} t + s_{2} t +…+ s_{n} t} {t\times n} = \frac{s_{1} + s_{2} +…+ s_{n}} {n} \)
Случай 6: Средняя скорость при заданных разных скоростях (\(s_{1}, s_{2}, s_{3},… s_{n})\ ) для того же расстояния (\(d_{1} = d_{2} = d_{3} =… d_{n} = d)\) задается как:
Формула средней скорости \(S_{avg}\) \(= \frac{ n \times d} { d \times \left[ \dfrac{1}{s_1} + \dfrac{1}{s_2} + \ dfrac{1}{s_3} +….+ \dfrac{1}{s_n}\right]} = \frac{n} {\left[\dfrac{1}{s_1} + \dfrac{1}{ s_2} + \dfrac{1}{s_3} +….+ \dfrac{1}{s_n}\right]}\)
Cuemath — одна из ведущих мировых платформ для обучения математике, которая предлагает LIVE 1-к- 1 онлайн-урок по математике для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
Закажите бесплатный пробный урок
Примеры формулы средней скорости
Давайте рассмотрим несколько примеров, чтобы лучше понять формулу средней скорости.
Пример 1: Используя формулу средней скорости, найдите среднюю скорость Сэма, который проходит первые 200 километров за 4 часа, а следующие 160 километров еще за 4 часа.
Решение:
Чтобы найти среднюю скорость, нам нужно общее расстояние и общее время.
Общее расстояние, пройденное Сэмом = 200 км + 160 км = 360 км
Общее время, затраченное Сэмом = 4 часа + 4 часа = 8 часов
Средняя скорость = общее пройденное расстояние ÷ общее затраченное время
Средняя скорость = 360 ÷ 8 = 45 км/ч
Ответ: Средняя скорость Сэма составляет 45 км/ч.
Пример 2: Поезд движется со скоростью 80 миль в час в течение первых 4 часов и со скоростью 110 миль в час в течение следующих 3 часов. Найдите среднюю скорость поезда по формуле средней скорости.
Решение:
Известно, что первые 4 часа поезд движется со скоростью 80 миль в час.
Здесь \(S_1\) = 80 и \(T_1\) = 4.
И поезд движется со скоростью 110 миль в час следующие 3 часа.
Следовательно \(S_2\) = 110 и \(T_2\) = 3,
Формула средней скорости = \(\frac{S_1 \times T_1 + S_2 \times T_2}{T_1 + T_2}\)
Средняя скорость = (80 × 4 + 110 × 3) ÷ (4 + 3) 90 335
= (650) ÷ (7) = 92,86 мили/час
Ответ: Средняя скорость поезда 92,86 мили/час.
Пример 3: Автомобиль движется со скоростью 45 км/ч в течение 5 часов, а затем решает снизить скорость до 40 км/ч в течение следующих 2 часов. Рассчитайте среднюю скорость, используя формулу средней скорости.
Решение:
Расстояние I = 45 × 5 = 225 миль
Расстояние II = 40 × 2 = 80 миль
Общее расстояние = расстояние 1 + расстояние 2 90 335
D = 225 + 80 = 305 миль
Используя формулу средней скорости = Общее пройденное расстояние ÷ Общее затраченное время
Средняя скорость = 305 ÷ 7 = 43,57 м/с.
Ответ: Средняя скорость автомобиля 43,57 м/с.
Часто задаваемые вопросы о формуле средней скорости
Как рассчитать расстояние с помощью формулы средней скорости?
Общая формула для средней скорости задается как [Средняя скорость = Пройденное расстояние ÷ Общее затраченное время]
Чтобы рассчитать расстояние, формулу средней скорости можно представить в виде [Расстояние = Средняя скорость × Время].
Как рассчитать время, используя формулу средней скорости?
Формула общей средней скорости задается как [Средняя скорость = Расстояние ÷ Время]
Для расчета времени формула средней скорости будет иметь вид [Время = Пройденное расстояние ÷ Средняя скорость].
Как использовать формулу для средней скорости?
Чтобы понять, как использовать формулу для средней скорости, рассмотрим пример.
Пример. Бегун пробегает 100 м за 40 сек. После финиша первого круга он вернулся к исходной точке. Вычислите среднюю скорость бегуна.

 Задачи на координатной решетке
Задачи на координатной решетке


 Какова его средняя скорость?
Какова его средняя скорость? Кальмар Гумбольдта может пройти 399,6 метра за 60 секунд . Вам нужно рассчитать среднюю скорость самого быстрого человека и кальмара Гумбольдта, чтобы узнать, кто кого может обогнать.
Кальмар Гумбольдта может пройти 399,6 метра за 60 секунд . Вам нужно рассчитать среднюю скорость самого быстрого человека и кальмара Гумбольдта, чтобы узнать, кто кого может обогнать.
Leave A Comment