Олимпиада физического факультета МГУ 10 класс
Задачи первого этапа олимпиады физического факультета МГУ имени М. В. Ломоносова
Задача 1
Маленький шарик падает без начальной скорости с некоторой высоты H на систему из двух закрепленных клиньев, верхние грани которых образуют угол «альфа» с горизонтом (см. рис).
Место падения находится на расстоянии l по горизонтали от линии касания клиньев.
Испытав три абсолютно упругих удара о клинья, шарик вновь поднимается на ту же высоту.
Укажите возможные виды траекторий движения шарика и рассчитайте высоту H в наиболее простом случае.
Задача 2
Из тонкой стальной ленты изготовлена трубка диаметром d = 10 мм.
Какое внутреннее давление она может выдержать, если при приложении продольного усилия F = 2000 кГ трубка рвется?
Считать, что шов на трубке имеет такую же прочность на разрыв, что и материал трубки.
Задача 3
Зависимость приведенной температуры T/T0 гелия от приведенного давления p/p0 имеет вид окружности,
центр которой находится в точке (1;1), причем минимальная приведенная температура гелия в этом процессе равна «тау».
Найти отношение минимальной и максимальной концентраций атомов гелия при таком процессе.
Задача 4
К точкам 1, 2, 3 электрической цепи, изображенной на рисунке,
длинными тонкими проводниками подсоединили изначально незаряженные
металлические шары с радиусами r, р и r соответственно.
Найти заряды, установившиеся на каждом из шаров.
Сопротивлением и емкостью проводников пренебречь.
Считать, что расстояние между шарами много больше их размеров,
заряд на самой электрической цепи пренебрежимо мал, а внутреннее сопротивление источника тока равно нулю.
Задача 5
Мэр одного городка начал получать жалобы на большую автомобильную пробку перед светофором на главной улице.
Скорость машин при движении составляла 6 м/c, а средняя скорость продвижения по пробке — всего 1,5 м/с.
При этом время свечения светофора зеленым светом было равно времени свечения красным,
время свечения желтым светом мало.
Мэр распорядился увеличить время свечения светофора зеленым светом в два раза,
а время свечения красным светом оставить прежним.
Чему станет равна средняя скорость продвижения машин по пробке?
Считать, что скорость машин при движении не изменилась.
Учесть, что при включении зеленого света автомобили начинают двигаться не одновременно.
Олимпиада физического факультета МГУ 10 класс. вариант 2.
Задача 1
Оцените отношение силы сопротивления воздуха к силе тяжести для пули, вылетевшей из ствола пистолета.
Скорость пули u = 500 м/с , ее диаметр d = 7 мм, масса пули m = 9 г.
Плотность воздуха составляет 1.3 кг/м3.
Задача 2
Платформа, установленная на вертикальной невесомой пружине, совершает установившиеся колебания.
В тот момент, когда платформа проходит через положение своего равновесия, о нее абсолютно упруго ударяется маленький шарик, падающий с некоторой высоты, причем после соударения скорости платформы и шарика, оставаясь неизменными по модулю, изменяют свои направления на противоположные.
Считая известными амплитуду установившихся колебаний платформы A и период ее свободных колебаний T,
найти отношение масс шарика и платформы.
Задача 3
Над одним молем идеального одноатомного газа совершают процесс 1-2-3-4-1 (см. рис),
Какое количество теплоты будет получать газ за один цикл,
если совершать над ним процесс 2-3-4-A-B-C-2?
Известно, что T3 = 16T1, T2 = T4, B — точка пересечения изотермы T = T2 с прямой 1-3,
проходящей через начало координат pV-диаграммы.
Ответ выразить через Q.
Задача 4
Частица с зарядом q и массой m влетает со скоростью v в плоский незаряженный конденсатор емкостью C параллельно его пластинам.
В этот момент в схеме, изображенной на рисунке, замыкают ключ К.
Как зависит ускорение частицы a от времени?
Считать, что время пролета частицы через конденсатор много меньше RC,
Расстояние между пластинами конденсатора равно d, краевыми эффектами можно пренебречь.
Задача 5
Рентгеновский аппарат состоит из точечных источника «И» и приемника «П», жестко закрепленных на станине.
Между источником и приемником перемещают цилиндрический толстостенный баллон
(см. рис.1).
При этом интенсивность A рентгеновского излучения, регистрируемого приемником, зависит от координаты «x» так,
как показано на рис. 2.
Есть ли внутри баллона содержимое, поглощающее рентгеновские лучи?
Олимпиады по физике 10 класс Школьный этап всероссийской олимпиады -10 класс
Задачи по кинематике для подготовки к олимпиаде по физике
Здесь представлено 20 задач по кинематике для подготовки к олимпиадам по физике из методического пособия В. Грабцевича. Задачи имеют ответы, но предлагаются без готовых решений.
1. Из двух портов, расстояние между которыми l, одновременно выходят два катера со скоростями v1 и v2, направленными соответственно под углами α и β к прямой, соединяющей порты. Каково минимальное расстояние между ними?
| [ rmin = | l (v2 sin β − v1 sin α) | |
| √(v12 + v22 + 2v1v2cos(α + β)) |
2. С поверхности Земли бросили вертикально вверх кусочек пластилина со скоростью vo. Одновременно такой же кусочек пластилина начал падать без начальной скорости с высоты H. При столкновении кусочки слиплись. Через какое время после начала бросания и с какой скоростью слипшийся комок упадет на Землю?
С поверхности Земли бросили вертикально вверх кусочек пластилина со скоростью vo. Одновременно такой же кусочек пластилина начал падать без начальной скорости с высоты H. При столкновении кусочки слиплись. Через какое время после начала бросания и с какой скоростью слипшийся комок упадет на Землю?
| [ t = | vo + √(vo2 | ] |
| 2g |
| [ v = | √(vo2 + 4gH) | ] |
| 2 |
3. С подводной лодки, погружающейся равномерно, испускаются звуковые импульсы длительностью 30,1 c. Длительность импульса, принятого на лодке после его отражения от дна, равна 29,9 c. Определите скорость погружения лодки. Скорость звука в воде 1500 м/с.
| [ v = vЗ | t1 − t2 | = 5 м/с ] |
| t1 + t2 |
4.
| [ α = | t2 | = | 5 | ] |
| √(t22 − t12) | 3 |
5.
 Сопротивлением воздуха пренебречь.
Сопротивлением воздуха пренебречь.| [ Smax = | 3vo2 | ≈ 0,94 м. ] |
| 8g |
6. Вдоль железной дороги через каждые 100 м расставлены столбики с номерами 1, 2,…, 10, 1, 2,…, 10,…. Через 2 минуты после того, как кабина машиниста равномерно движущегося поезда проехала столбик с цифрой «1», машинист увидел в окне столбик с цифрой «2». Через какое время после проезда этого столбика кабина машиниста может проехать мимо ближайшего столбика с цифрой «3»? Скорость поезда меньше 100 км/ч.
| [ t1 = 120 с, t2 = 10,9 с, t3 = 5,7 с, t4 = 3,9 с ] |
7. У мальчика, сидящего на вращающейся с угловой скоростью
 На каком расстоянии друг от друга ударятся о землю эти камушки, если высота, с которой они упали, равна h?
На каком расстоянии друг от друга ударятся о землю эти камушки, если высота, с которой они упали, равна h?| [ ΔL = 2R • |sin | wt | | • √(1 + | 2hw2 | ) ] |
| 2 | g |
8. Первый вагон тронувшегося с места поезда прошел мимо неподвижного наблюдателя, стоявшего у начала этого вагона, за время t1, последний вагон — за t
| Ответ: t = | t12 + t22 | , |
| 2t2 |
если исходные данные таковы, что:
| ( | t12 + t22 | )2 — целое число, |
| 2t1t2 |
то искомое время:
| t = | t12 + t2 | ; |
| 2t2 |
если:
| ( | t12 + t22 | )2 — не является целым числом, |
| 2t1t2 |
то задача решения не имеет.
9. На пол кабины лифта, движущегося вертикально вверх с постоянной скоростью, падает вертикально вниз упругий шарик. Определить скорость лифта, если после каждого удара шарик, не касаясь потолка, удаляется от пола лифта на максимальное расстояние за время
| [ u = √(g(L − gt2)). |
Из этого выражения следует, что задача имеет решение, если исходные данные удовлетворяют условию:
| L > gt2. |
При невыполнении этого условия в рамках сделанных предположений задача не имеет решения.]
10. Эскалатор метро движется со скоростью v. Пассажир заходит на эскалатор и начинает идти по его ступеням следующим образом: делает шаг на одну ступеньку вперёд и два шага по ступенькам назад. При этом он добирается до другого конца эскалатора за время
 Через какое время пассажир добрался бы до конца эскалатора, если бы шёл другим способом: делал два шага вперёд и один шаг назад? Скорость пассажира относительно эскалатора при движении вперёд и назад одинакова и равна u. Считайте, что размеры ступеньки много меньше длины эскалатора.
Через какое время пассажир добрался бы до конца эскалатора, если бы шёл другим способом: делал два шага вперёд и один шаг назад? Скорость пассажира относительно эскалатора при движении вперёд и назад одинакова и равна u. Считайте, что размеры ступеньки много меньше длины эскалатора.| [ t1 = | (3v − u)t | ] |
| 3v + u |
11. На полу около стены стоит гладкий клин. На его плоскости, образующей с горизонтом угол φ, лежит груз, удерживаемый невесомой нерастяжимой нитью. Один конец нити прикреплен к стене так, что участок нити между стеной и клином горизонтален. Остальная часть нити лежит на наклонной плоскости (рисунок). Найдите зависимость от времени t скорости движения груза относительно пола после начала движения клина от стены с ускорением a, параллельным горизонтальному участку нити.
| [ vгр(t) = 2at sin ( | φ | ). ] ] |
| 2 |
12. Стержень длиной l = 0,85 м движется в горизонтальной плоскости. В некоторый момент времени скорости концов стержня равны v1 = 1 м/с и v2 = 1,5 м/с, причем скорость первого из них направлена под углом α = 30° к стержню. Какова угловая скорость w вращения стержня вокруг его центра?
| [ w = | 1 | (v1 sin α + √(v22 − v12cos2α)) ≈ 2 рад/с. ] |
| l |
13. Маленький шарик падает без начальной скорости с некоторой высоты H на наклонную плоскость (рисунок). После удара он попадает на вторую плоскость. Точка первого удара находится на расстоянии L от линии соприкосновения плоскостей. С какой высоты H упал шарик, если после двух упругих ударов он снова поднялся на ту же высоту? Угол наклона плоскостей к горизонту равен α, причем α < π/4.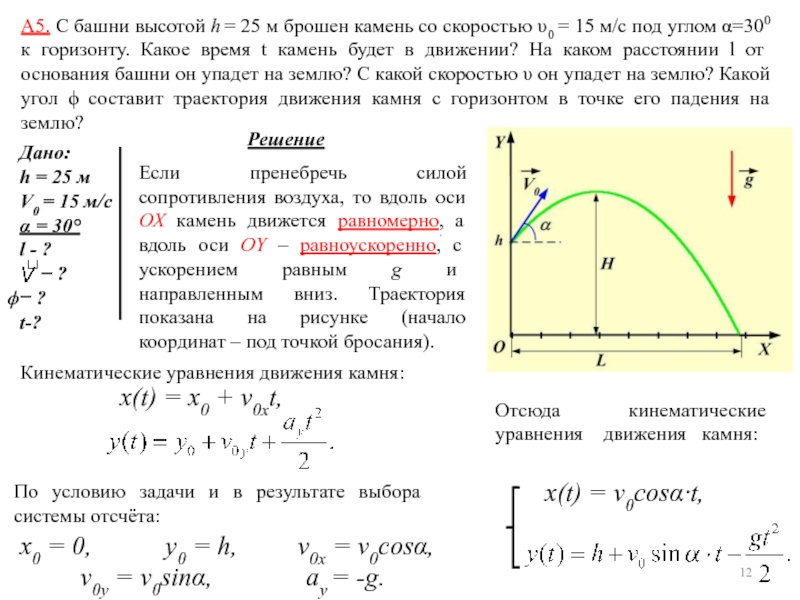
| [ H = | L | . ] |
| sin 4α |
14. Дымовая шашка падает вертикально с высоты Ho с нулевой начальной скоростью. Дым сносится ветром, который дует горизонтально на всех высотах с постоянной скоростью vo. На сколько будет снесен относительно вертикальной траектории шашки на высоте h над поверхностью Земли в момент падения шашки на земли? Ускорение свободного падения g.
| [ x = vo√( | 2ho | )(1 − √(1 − | h | )). ] |
| g | Ho |
15. Колесо катится без проскальзывания с постоянной скоростью v. С верхней точки обода колеса срывается камешек. Через какое время колесо наедет на этот камешек? Радиус колеса R, ускорение свободного падения g.
| [ T = 4√( | R | ). ] ] |
| g |
16. Зал для зимнего футбола имеет высоту h = 8 м и длину L = 100 м. Найти скорость мяча, при которой он пролетит от ворот до ворот, почти коснувшись потолка. Ускорение свободного падения g =10 м/с2. Сопротивлением воздуха и размером мяча пренебречь.
| [ v = 1,312√(gL) = 41,5 м/с] |
17. В коридоре длиной 11 м и с высотой потолка 3 м у самого начала ударяют о пол мяч со скоростью 10 м/с под углом 60° к горизонту. На какой высоте от пола ударяется мяч о торцевую стенку коридора?
[h = 2,03 м]
18. Трактор «Беларусь» поворачивает так, что частота вращения одного из задних колес равна n1 = 1,5 об/с, а другого — n2 = 1,4 об/с. Расстояние между колесами равно l = 1,9 м. Определите радиус разворота трактора.
[R = 27,6 м]
19. Орудие, установленное на горе высотой h = 2000 м, посылает горизонтально снаряд со скоростью v1 = 800 м/с. Через промежуток времени τ = 5 c из этой же точки выпускается другой снаряд. Какой скоростью v2 он должен обладать и как его надо выпустить, чтобы оба снаряда одновременно упали в одну точку поверхности Земли?
Через промежуток времени τ = 5 c из этой же точки выпускается другой снаряд. Какой скоростью v2 он должен обладать и как его надо выпустить, чтобы оба снаряда одновременно упали в одну точку поверхности Земли?
| [ v2 = | l | = 1,07 км/с, |
| (1 − τ)cos α |
| α = arctg 0.055 = − 3°12′. ] |
20. На длинном шоссе на расстоянии 1 км друг от друга установлены светофоры. Красный сигнал каждого светофора горит в течение 30 секунд, зелёный – в течение следующих 30 секунд. При этом все автомобили, движущиеся со скоростью 40 км/ч, проехав один из светофоров на зелёный свет, проезжают без остановки, то есть тоже на зелёный свет, и все следующие светофоры. С какими другими скоростями могут двигаться автомобили, чтобы, проехав один светофор на зелёный свет, далее нигде не останавливаться?
| [ vn = | 1 км | = | 1 км × 3600 | = | 120 | км | = 120 км/ч, 40 км/ч, 24 км/ч . ..] ..] | |
| (30 + 60n) c | (30 + 60n) час | 2n + 1 | ч |
Вы читате материалы из пособия для подготовки к олимпиадам по физике. Далее: задачи по динамике без решений (с ответами).
Шар массой m падает без начальной скорости с высоты h над поверхностью Земли. Найти приращение вектора углового момента мяча, полученного за время падения (относительно точки О системы отсчета, движущейся поступательно в горизонтальном направлении со скоростью V). Мяч начинает падать из точки О. Сопротивлением воздуха пренебрегаем.
Вопрос
Вопрос
И.Е. ИРОДОВ, Л.А. СЕНА, С.С. КРОТОВ-ФИЗИЧЕСКИЕ ОСНОВЫ МЕХАНИКИ-Законы сохранения энергии, импульса и углового момента
20 видеоРЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!
Обновлено: 27 июня 2022 г.
Текст Решение
Решение
В течение времени свободного падения t=τ=√2hg опорная точка O перемещается в горизонтальном направлении (скажем, вправо) на расстояние Vτ . В переводящей системе координат как →M(O)=0, поэтому
В переводящей системе координат как →M(O)=0, поэтому
Δ→M=→Mf=→r
=(−Vτ→i+h→j)×m[>au→j−V→j]
= −mVgτ2→h+mVh(+→k)
=-mVg(2hg)→k+mVh(+→k)=−mVh→k
Отсюда ∣∣Δ→M∣∣=mVh
Ответ
Пошаговое решение от экспертов, которое поможет вам в устранении сомнений и отличные оценки на экзаменах.
Видео по теме
Стальной шарик массой m падает в вязкую жидкость с конечной скоростью v, тогда стальной шарик массой 8m падает в ту же жидкость с конечной скоростью
10964950
с постоянной скоростью u сталкивается с гладкой горизонтальной поверхностью в точке O, как показано на рис. Силой тяжести и трением пренебречь. Ось y проведена перпендикулярно горизонтальной поверхности в точке удара O, а ось x горизонтальна, как показано. Около какой точки будет сохраняться угловой момент мяча?
11301561
Брусок массы m движется по горизонтальной шероховатой поверхности с начальной скоростью v. Центр масс бруска находится на высоте h от поверхности. Рассмотрим точку А на поверхности.
Центр масс бруска находится на высоте h от поверхности. Рассмотрим точку А на поверхности.
12229820
Камень без начальной скорости падает с высоты h на поверхность Земли. Предполагается, что сопротивление воздуха пренебрежимо мало, камень падает на землю со скоростью v_0=sqrt(2gh) относительно Земли. Получите ту же формулу в терминах системы отсчета, «падающей» на Землю с постоянной скоростью v_0.
12305972
Текст Решение
Мяч массой m брошен под углом α к горизонту с начальной скоростью v0. Найти зависимость от времени модуля вектора углового момента мяча относительно точки, из которой мяч был брошен. Найти угловой момент M в высшей точке траектории, если m=130g, α=45∘ и v0=25м/с. Сопротивлением воздуха следует пренебречь.
12305994
Диск A массы m, скользящий по гладкой горизонтальной поверхности со скоростью v, испытывает абсолютно упругий удар о гладкую неподвижную стенку в точке O (рисунок). Угол между направлением движения диска и нормалью к стенке равен α.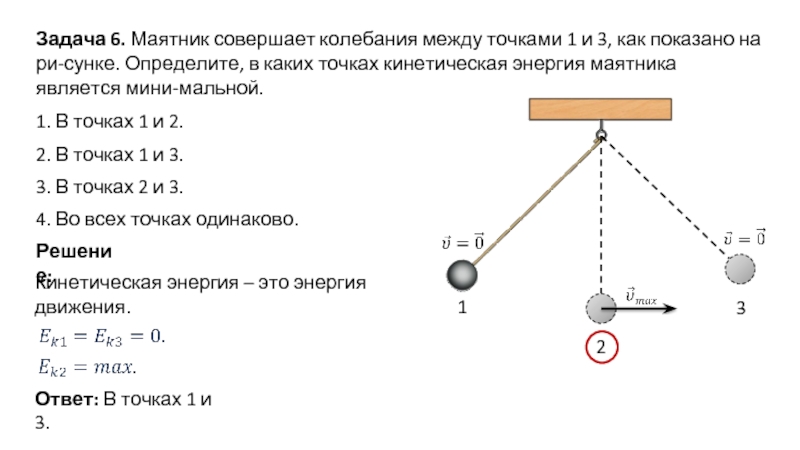 Найти:
Найти:
(а) точки, относительно которых угловой момент M диска остается постоянным при этом,
(б) величина приращения вектора углового момента диска относительно точки O′, находящейся в плоскость движения диска на расстоянии l от точки O.
12305995
Маленький шарик массы m, подвешенный к потолку в точке O на нити длиной l, движется по горизонтальной окружности с постоянной угловой скоростью омега. Относительно каких точек момент количества движения М мяча остается постоянным? Найти величину приращения вектора углового момента мяча относительно точки О, взятой за пол-оборота.
12305996
Мяч падает с высоты h. Через 1 с из точки, находящейся на 25 м ниже точки падения первого мяча, свободно падает другой мяч. Оба они достигают земли одновременно. Значение h равно
13396154
Утверждение:- Боулер бросает мяч так, что он движется в воздухе с постоянной угловой скоростью (без учета сопротивления воздуха) Причина:- Угловой момент вращения мяча не зависит от системы отсчета
14626456
Треугольный клин массы M движется с равномерной скоростью v_(0) по гладкой горизонтальной поверхности влево. Частица массы m падает из состояния покоя с высоты h на наклонную грань, упруго сталкиваясь с ней. Найти скорость мяча и клина после удара, приняв М = 2м.
Частица массы m падает из состояния покоя с высоты h на наклонную грань, упруго сталкиваясь с ней. Найти скорость мяча и клина после удара, приняв М = 2м.
462815613
Текст Решение
Небольшой шарик массой m падает с очень большой высоты, после падения на 10м он достигает критической скорости и затем падает с той же скоростью. Найти работу, совершенную при первом падении тела с высоты 100 м за счет истирания воздуха.
505786117
Два мяча одновременно выпущены с определенной высоты, один свободно падает, а другой брошен с некоторой горизонтальной скоростью. В любой момент падения скорость мяча будет одинаковой?
642937065
Стальной шарик массой m падает в вязкую жидкость с конечной скоростью v, тогда стальной шарик массой 8m падает в эту же жидкость с конечной скоростью u сталкивается с гладкой горизонтальной поверхностью в точке O, как показано на рис. Силой тяжести и трением пренебречь. Ось y проведена перпендикулярно горизонтальной поверхности в точке удара O, а ось x горизонтальна, как показано.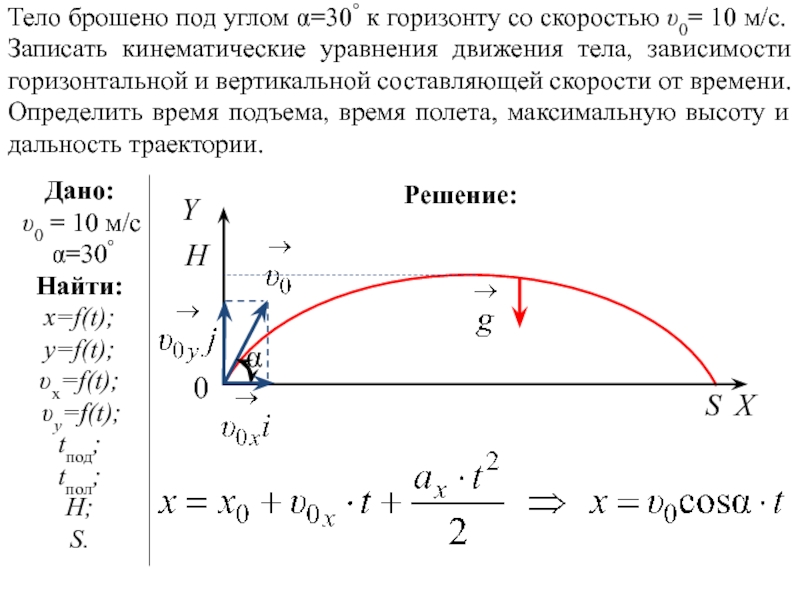 Около какой точки будет сохраняться угловой момент мяча?
Около какой точки будет сохраняться угловой момент мяча?
644102733
Мяч массой m брошен под углом α к вертикали с начальной скоростью u. В любой момент времени t модуль вектора углового момента мяча относительно точки, из которой мяч брошен, равен
644161157
Text Solution
Honors Physics: Free Fall
Фон
Изучение свободно падающих тел восходит к временам Аристотеля. В то время Аристотель считал, что более массивные предметы падают быстрее, чем менее массивные. Он верил в это во многом благодаря тому, что при рассмотрении камня и пера, падающих с одной высоты, видно, что камень первым ударяется о землю. При дальнейшем рассмотрении становится ясно, что Аристотель был неверен в своей гипотезе.
В качестве доказательства возьмите баскетбольный мяч и лист бумаги. Бросьте их одновременно с одной и той же высоты… они приземлятся одновременно? Возможно нет. Теперь возьмите этот лист бумаги, скомкайте его в плотный шар и повторите эксперимент. Теперь, что вы видите происходит? Вы должны увидеть, что и мяч, и бумага приземляются одновременно. Следовательно, вы можете сделать вывод, что предсказания Аристотеля не учитывали влияние сопротивления воздуха. В рамках данного курса такими силами сопротивления, как сопротивление воздуха, пренебрегают.
Теперь, что вы видите происходит? Вы должны увидеть, что и мяч, и бумага приземляются одновременно. Следовательно, вы можете сделать вывод, что предсказания Аристотеля не учитывали влияние сопротивления воздуха. В рамках данного курса такими силами сопротивления, как сопротивление воздуха, пренебрегают.
В 17 веке Галилео Галилей начал новое исследование движения падающих тел. Галилей, признав, что сопротивление воздуха влияет на движение падающего тела, провел свой знаменитый мысленный эксперимент, в котором он постоянно задавался вопросом, что произойдет, если устранить эффект сопротивления воздуха. Командир корабля «Аполлон-15» Дэвид Скотт провел этот эксперимент на Луне. Он одновременно уронил молоток и перо и заметил, что они упали на землю одновременно.
После экспериментов Галилея ученые лучше поняли, как гравитационное притяжение Земли ускоряет свободно падающие тела. Экспериментально было установлено, что локальная напряженность гравитационного поля (г) на поверхности Земли составляет 9,8 Н/кг, что также указывает на то, что все объекты в свободном падении (без учета сопротивления воздуха) испытывают эквивалентное ускорение 9,8 м. /с 2 по направлению к центру Земли.
/с 2 по направлению к центру Земли.
(ПРИМЕЧАНИЕ: если вы удаляетесь от поверхности Земли, локальная напряженность гравитационного поля и, следовательно, ускорение свободного падения изменяется.)
Вы можете рассматривать свободно падающие тела как объекты, падающие с некоторой высоты или брошенные вертикально вверх. В этом экзамене вы будете анализировать движение каждого состояния.
Объекты, падающие из состояния покоя
Объекты, выходящие из состояния покоя, имеют начальную скорость, равную нулю, что дает вам первую кинематическую величину, необходимую для решения задачи. Кроме того, если вы назовете направление начального движения (вниз) положительным, объект будет иметь положительное ускорение и скорость при падении.
Важным первым шагом в анализе объектов в свободном падении является решение, какое направление вдоль оси Y вы собираетесь назвать положительным, а какое направление, следовательно, будет отрицательным. Хотя вы можете установить положительное направление любым удобным для вас способом и получить правильный ответ, следуя приведенным ниже советам, вы сможете упростить свою работу, чтобы постоянно получать правильный ответ.
Хотя вы можете установить положительное направление любым удобным для вас способом и получить правильный ответ, следуя приведенным ниже советам, вы сможете упростить свою работу, чтобы постоянно получать правильный ответ.
- Определите направление начального движения объекта и назначьте его как положительное направление. В случае падения объекта положительное направление Y будет указывать на нижнюю часть бумаги.
- Теперь, когда ось идентифицирована, вы можете идентифицировать и записать заданную кинематическую информацию. Не забывайте, что у брошенного объекта начальная скорость равна нулю.
- v 0 =0
- v=?
- Δy=?
- а=9,8 м/с 2
- т=?
- Обратите внимание на направление векторных стрелок — если скорость и ускорение указывают в одном направлении, объект ускоряется. Если они указывают в противоположных направлениях, объект замедляется.

КЛЮЧЕВАЯ КОНЦЕПЦИЯ: Величина ускорения свободного падения (g) является постоянной величиной 9,81 м/с 2 на поверхности Земли.
Вопрос: Какова скорость груза массой 2,5 кг после свободного падения из состояния покоя с высоты 12 метров?
Переменная Значение v 0 0 против НАЙТИ Δy 12 м и 9,8 м/с 2 т ? Ответ: Вертикальная задача: объявить положительное направление вниз.
Это означает, что ускорение, которое также направлено вниз, является положительной величиной.
Объекты, запущенные вверх
Изучение движения объекта, запущенного вертикально вверх, выполняется почти так же, как вы изучали движение объекта, падающего из состояния покоя. Основное отличие состоит в том, что вы должны смотреть на два сегмента его движения вместо одного: и вверх, и вниз.
Прежде чем приступить к созданию системы отсчета и работе с количественным анализом, вы должны получить четкое концептуальное представление о том, что происходит, когда мяч находится в воздухе. Представьте, что мяч подбрасывается вертикально вверх, как показано на рисунке.
Чтобы мяч двигался вверх, его начальная скорость должна быть больше нуля. Когда мяч поднимается, его скорость уменьшается, пока он не достигнет максимальной высоты, где он остановится, а затем начнет падать. Когда мяч падает, его скорость увеличивается.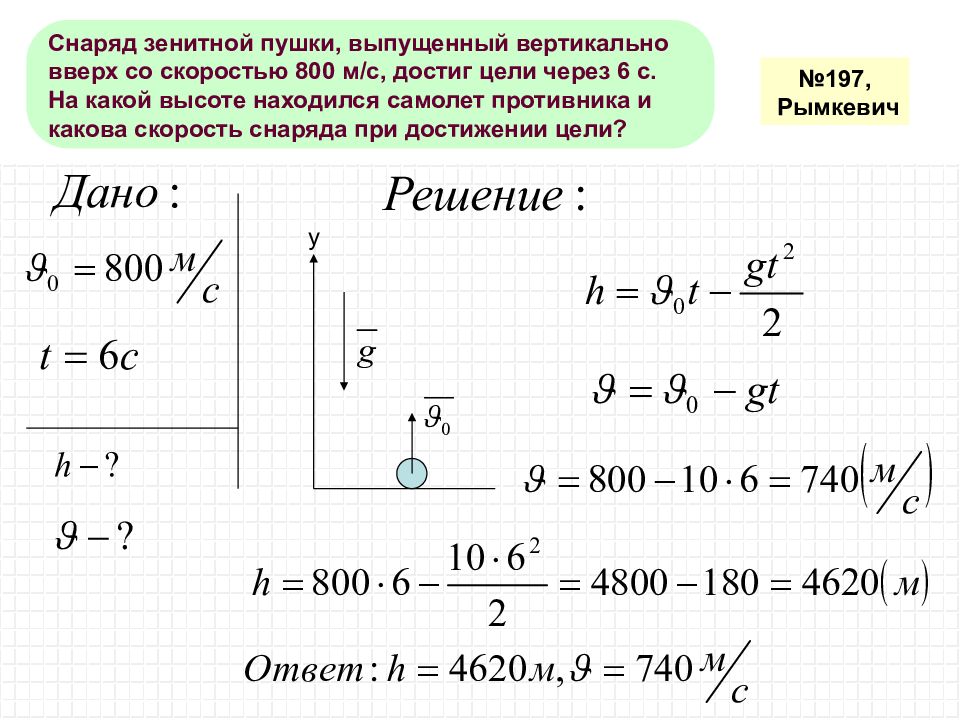 Другими словами, мяч ускоряется все время, пока он находится в воздухе, как на пути вверх, так и в момент остановки в высшей точке, и на пути вниз.
Другими словами, мяч ускоряется все время, пока он находится в воздухе, как на пути вверх, так и в момент остановки в высшей точке, и на пути вниз.
Причиной ускорения мяча является гравитация. Все время, пока мяч находится в воздухе, его ускорение равно 90,8 м/с 2 вниз при условии, что это происходит на поверхности Земли. Обратите внимание, что ускорение может быть равно 9,8 м/с 2 или -9,8 м/с 2 . Знак ускорения зависит от направления, которое вы назвали положительным, но во всех случаях направление ускорения силы тяжести направлено вниз, к центру Земли.
Вы уже установили ускорение мяча за все время нахождения в воздухе 9,8 м/с 2 вниз. Это ускорение заставляет скорость мяча уменьшаться с постоянной скоростью, пока он не достигнет максимальной высоты, после чего он разворачивается и начинает падать. Чтобы повернуться, скорость мяча должна пройти через ноль. Следовательно, на максимальной высоте скорость мяча должна быть равна нулю.
Вопрос: Мяч, брошенный вертикально вверх, достигает максимальной высоты 30 метров над поверхностью Земли. На максимальной высоте скорость мяча:
Ответ: 0 м/с. Мгновенная скорость любого снаряда на максимальной высоте равна нулю.
Поскольку гравитация придает мячу такое же ускорение как на пути вверх (замедляя его падение), так и на пути вниз (ускоряя его), время достижения максимальной высоты равно времени возврата в исходное положение. Точно так же начальная скорость мяча на пути вверх будет равна скорости мяча в момент, когда он достигнет точки, из которой он был брошен на пути вниз. Иными словами, время подъема равно времени опускания, а начальная скорость подъема равна конечной скорости опускания (при условии, что объект начинается и заканчивается на одной высоте над землей).
Теперь, когда вы получили концептуальное представление о движении мяча, вы можете работать над количественным решением. Следуя эмпирическому правилу, установленному ранее, вы можете начать с определения направления, в котором мяч начинает двигаться, как положительного. Помните, что назначение положительных и отрицательных направлений совершенно произвольно. У вас есть свобода назначать их так, как вы считаете нужным. Однако, как только вы их назначите, не изменяйте их.
Следуя эмпирическому правилу, установленному ранее, вы можете начать с определения направления, в котором мяч начинает двигаться, как положительного. Помните, что назначение положительных и отрицательных направлений совершенно произвольно. У вас есть свобода назначать их так, как вы считаете нужным. Однако, как только вы их назначите, не изменяйте их.
Как только это положительное опорное направление установлено, все остальные скорости и перемещения назначаются соответствующим образом. Например, если вверх является положительным направлением, ускорение свободного падения будет отрицательным, потому что ускорение свободного падения направлено вниз, к центру Земли. В своей высшей точке мяч будет иметь положительное смещение и будет иметь нулевое смещение, когда вернется в исходную точку. Если мяч не пойман, но продолжает движение к Земле за пределы начальной точки, он будет иметь отрицательное смещение.
«Уловка» для решения задач свободного падения включает симметрию. Время, за которое объект достигает своей высшей точки, равно времени, которое требуется ему, чтобы вернуться в то же вертикальное положение. Скорость, с которой снаряд начинает свой путь вверх, равна скорости снаряда, когда он возвращается на ту же высоту (хотя, конечно, его скорость и в обратном направлении). Если вы хотите упростить задачу, по вертикали в самой высокой точке вертикальная скорость равна 0. Эта дополнительная информация может помочь вам в заполнении таблицы вертикального движения. Если вы сократите движение объекта вдвое, вы сможете упростить решение задачи, но не забывайте, что если вы хотите получить общее время в воздухе, вы должны удвоить время, которое требуется объекту, чтобы подняться в самую высокую точку.
Скорость, с которой снаряд начинает свой путь вверх, равна скорости снаряда, когда он возвращается на ту же высоту (хотя, конечно, его скорость и в обратном направлении). Если вы хотите упростить задачу, по вертикали в самой высокой точке вертикальная скорость равна 0. Эта дополнительная информация может помочь вам в заполнении таблицы вертикального движения. Если вы сократите движение объекта вдвое, вы сможете упростить решение задачи, но не забывайте, что если вы хотите получить общее время в воздухе, вы должны удвоить время, которое требуется объекту, чтобы подняться в самую высокую точку.
Вопрос: Баскетболист подпрыгнул, чтобы отбить мяч. Если она находилась в воздухе 0,80 секунды, на какую высоту она прыгнула?
Переменная Значение v 0 ? против 0 м/с Δy НАЙТИ и -9,8 м/с 2 т 0,40 с Ответ: Определить вверх как положительное направление Y.


 Это означает, что ускорение, которое также направлено вниз, является положительной величиной.
Это означает, что ускорение, которое также направлено вниз, является положительной величиной.
Leave A Comment