Многогранники и Объем многогранников
Многоугольники относятся к плоским геометрическим фигурам. К объемным (трехмерным) геометрическим фигурам относятся многогранники.
Определение. Многогранник — это геометрическое пространственное тело, ограниченное со всех сторон конечным числом плоских многоугольников (граней).
Прямоугольный параллелепипед является многогранником. Простейший прямоугольный параллелепипед — это куб. У него все грани равны
.
У прямоугольного параллелепипеда каждая грань — прямоугольник, который имеет с соседней гранью общую сторону и две общие вершины.
У параллелепипеда 8 вершин, 4 боковых прямоугольника и 2 прямоугольника в основаниях. У куба все б граней — равные квадраты. У прямоугольного параллелепипеда боковые фигуры и основания — прямоугольники. Эти прямоугольники попарно равны (равны прямоугольники оснований и две пары противолежащих прямоугольников, составляющих боковые грани). Следовательно, грани прямоугольного параллелепипеда являются прямоугольниками трех типов, различающихся размерами.
Три прямоугольника с разными размерами имеют
одну общую точку — вершину параллелепипеда.
У каждой вершины параллелепипед имеет общую точку для трех отрезков, которые называются измерениями параллелепипеда (длина, ширина и высота). Три измерения на верхнем рисунке параллелепипеда выделены жирной линией.
Объем — это то количество жидкости или сыпучего материала, которое можно поместить внутрь фигуры (между граничными плоскостями).
Объем — это одна из характеристик трехмерных геометрических фигур.
Объем обозначается большой латинской буквой V
Правило. Объем прямоугольного параллелепипеда равен произведению трех его измерений.
Единицами измерения объема служат:
Формула для расчета объема прямоугольного параллелепипеда:
V = a * b * c
где а — длина, Ь — ширина, с — высота.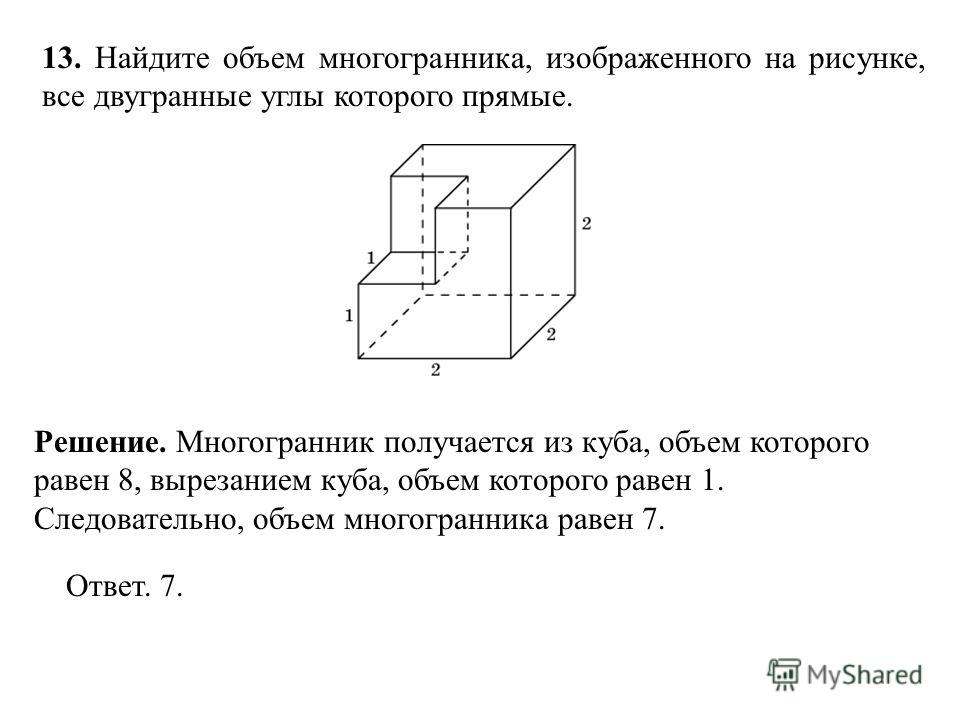
Так как у куба все измерения равны (а = Ь = с), то формула для вычисления объема куба V = а3.
Примеры
-
Вычислить объем прямоугольного параллелепипеда длиной 6 м, шириной 4 м и высотой 8 м.
Решение. Так как длина, ширина и высота измеряются одной и той же единицей длины (м), то подставим их в формулу V=а*Ь*с и вычислим объем:
V = 6 * 4 * 8 = 192 (м3)
Ответ: 192 м3. -
Вычислите объем куба со стороной основания 10 см.
Решение. Подставим численное значение стороны куба в формулу вычисления объема V=а3 и вычислим:
V = 10 * 10 * 10 = 103 = 1 000 (см3) — 1 л.Ответ: 1 000 см3, или 1 л.
Запись опубликована в рубрике Математика с метками многогранник, объем. Добавьте в закладки постоянную ссылку.
Формулы объема и площади поверхности многогранников: призма, пирамида, куб, параллелепипед
youtube.com/embed/gOuxtPsqXCQ» frameborder=»0″ allowfullscreen=»»>Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:
- Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
- Элементарная логика.
Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.
| | диагональ | |
| Параллелепипед | высота | |
| Прямоугольный параллелепипед | | |
| Призма | ||
| Пирамида |
Проще всего найти объём куба — это куб его стороны.
Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.
Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.
Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.
Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.
Задача 1.Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
Решение:
Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб 🙂
Очевидно, их 6, поскольку у куба 6 граней.
Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.
А дальше — читайте о приемах решения задач по стереометрии.
Разберем задачи, где требуется найти площадь поверхности многогранника.
Мы рассмотрим призмы и пирамиды. Начнем с призмы.
Площадь полной поверхности призмы можно найти как сумму площадей всех ее граней. А это площади верхнего и нижнего оснований плюс площадь боковой поверхности.
Площадь боковой поверхности призмы – это сумма площадей боковых граней, которые являются прямоугольниками. Она равна периметру основания, умноженному на высоту призмы.
Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Многогранник на рисунке – это прямая призма с высотой 12.
Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:
(больший квадрат), (маленький прямоугольник),
Подставим все данные в формулу: и найдем площадь поверхности многогранника:
Ответ: 424.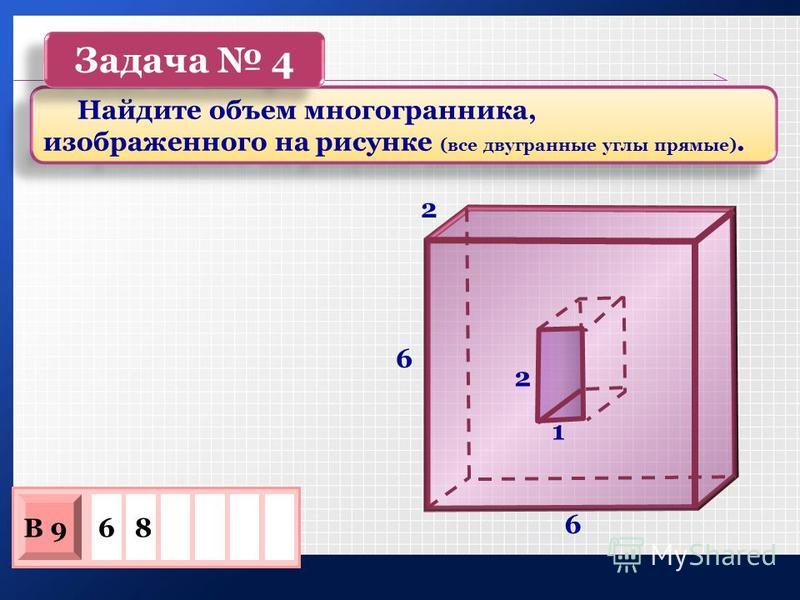
Задача 3. Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).
Решение.
Перевернем многогранник так, чтобы получилась прямая призма с высотой 1.
Площадь поверхности этой призмы находится по формуле:
Найдем площадь основания. Для этого разделим его на два прямоугольника и посчитаем площадь каждого:
(большой прямоугольник), (маленький прямоугольник).
Найдем площадь полной поверхности:
Ответ: 54
Задача 4.Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
Покажем еще один способ решения задачи.
Посмотрим, как получился такой многогранник. Можно сказать, что к «кирпичику», то есть прямоугольному параллелепипеду со сторонами 4, 1 и 3, сверху приклеен «кубик», все стороны которого равны 1.
И значит, площадь поверхности данного многогранника равна сумме площадей поверхностей прямоугольного параллелепипеда со сторонами 4,1,3 и
Почему мы вычитаем удвоенную площадь квадрата? Представьте себе, что нам надо покрасить это объемное тело.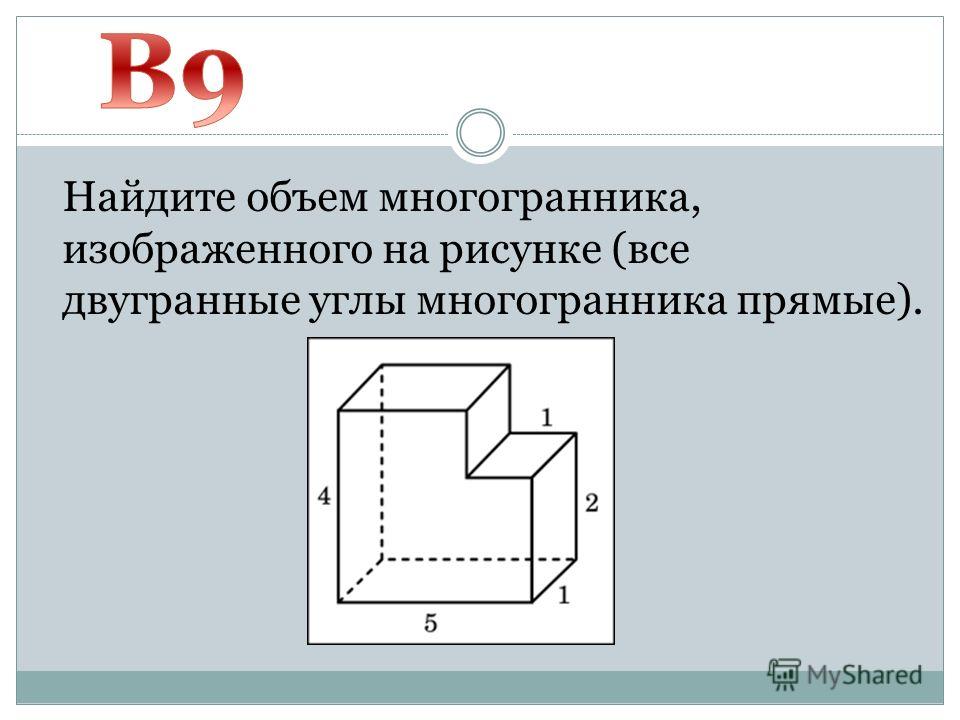 Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.
Мы красим все грани параллелепипеда, кроме квадрата на верхней его грани, где на него поставлен кубик. И у куба мы покрасим все грани, кроме этого квадрата.
Ответ: 42
Задача 5. . Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 120° между ними. Наибольшая из площадей боковых граней равна 35 см². Найдите площадь боковой поверхности призмы.
Решение.
Пусть АВ = 5 см, ВС = 3 см, тогда
Из по теореме косинусов найдем ребро АС:
Отрезок АС – большая сторона , следовательно, большая боковая грань призмы.
Поэтому или откуда
Ответ: 75
Теперь две задачи на площадь боковой поверхности пирамиды.
Задача 6. Основанием пирамиды DАВС является треугольник АВС, у которого АВ = АС = 13, ВС = 10; ребро АD перпендикулярно к плоскости основания и равно 9. Найдите площадь боковой поверхности пирамиды.
Решение.
Площадь боковой поверхности пирамиды – это сумма площадей всех ее боковых граней.
Проведем , тогда (по теореме о 3-х перпендикулярах), то есть DК – высота треугольника DВС.
– равнобедренный (по условию АВ = АС), то высота АК, проведенная к основанию ВС, является и медианой, то есть ВК = КС = 5.
Из прямоугольного получим:
Из прямоугольного имеем:
(по двум катетам), тогда следовательно
Ответ: 192
Задача 8. Стороны основания правильной четырехугольной пирамиды равны 24, боковые ребра равны 37. Найдите площадь поверхности пирамиды.
Решение:
Так как четырехугольная пирамида правильная, то в основании лежит квадрат, а все боковые грани — равные равнобедренные треугольники.
Площадь поверхности пирамиды равна
где р – полупериметр основания, h — апофема (высота боковой грани правильной пирамиды), a – сторона основания.
Значит, полупериметр основания .
Апофему найдем по теореме Пифагора:
Ответ: 2256
Как решать задачи на нахождение объема многогранника сложной формы?
Покажем два способа.
Первый способ
1.Составной многогранник достроить до полного параллелепипеда или куба.
2.Найти объем параллелепипеда.
3.Найти объем лишней части фигуры.
4.Вычесть из объема параллелепипеда объем лишней части.
Второй способ.
1.Разделить составной многогранник на несколько параллелепипедов.
2.Найти объем каждого параллелепипеда.
3.Сложить объемы.
Задача 9. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Решение.
1) Достроим составной многогранник до параллелепипеда.
2) Найдем объем параллелепипеда – для этого перемножим его длину, ширину и высоту:
3) Найдем объем лишней части, то есть маленького параллелепипеда.
Его длина равна 9 – 4 = 5, ширина 4, высота 7, тогда его объем
4) Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:
Ответ: 220.
Задача 10. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.
Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 7, боковое ребро равно 6. Найдите объем призмы.
Объем призмы равен , а так как призма прямая, то ее боковое ребро является и высотой, то есть
Основанием призмы является прямоугольный треугольник c катетами 6 и 7, тогда площадь основания
Ответ: 126
Задача 11. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 324 см. На какой высоте будет находиться уровень воды, если ее перелить в другой сосуд, у которого сторона в 9 раз больше, чем у первого? Ответ выразите в сантиметрах.
Решение.
Объем призмы равен
Воду перелили в другой такой же сосуд. Это значит, что другой сосуд также имеет форму правильной треугольной призмы, но все стороны основания второго сосуда в 9 раз больше, чем у первого.
Основанием второго сосуда также является правильный треугольник. Он подобен правильному треугольнику в основании первого сосуда.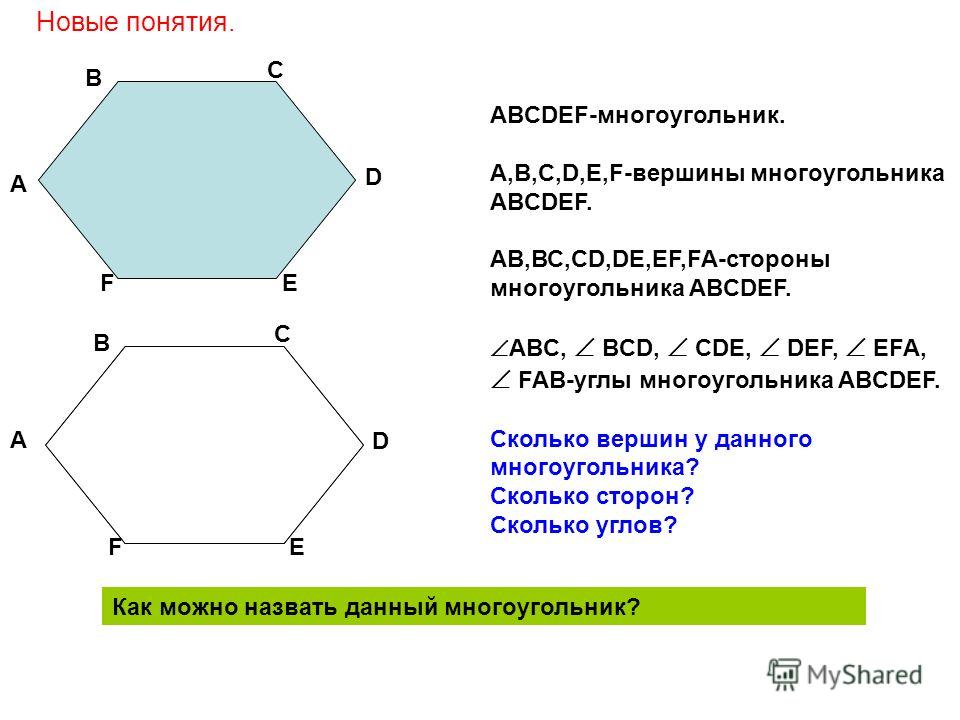 Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Отношение площадей подобных фигур равно квадрату коэффициента подобия.
Если все стороны треугольника увеличить в 9 раз, его площадь увеличится в раз. Мы получили, что площадь основания второго сосуда в 81 раз больше, чем у первого.
Объем воды не изменился, Так как высота воды должна быть в 81 раз меньше, чем Она равна (см).
Ответ: 4
Задача 12. Объем параллелепипеда Найдите объем треугольной пирамиды
Решение.
Опустим из вершины высоту Н на основание
Диагональ основания делит его на два равных треугольника, следовательно,
Имеем:
Ответ: 3,5
Задача 13. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 8, а высота равна
Решение.
По формуле объема пирамиды, .
В основании пирамиды лежит правильный треугольник. Его площадь равна
Объем пирамиды
Ответ: 96
Задача 14. Через середины сторон двух соседних ребер основания правильной четырехугольной призмы проведена плоскость, параллельная боковому ребру.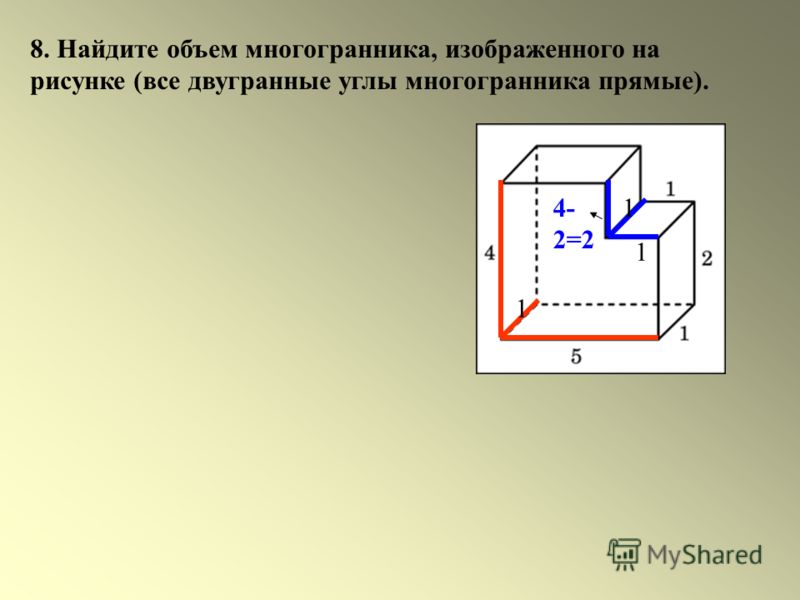 Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.
Найдите объем меньшей из частей, на которые эта плоскость делит призму, если объем призмы равен 32.
Решение.
По условию, призма правильная, значит, в ее основании лежит квадрат, а высота равна боковому ребру.
Пусть тогда
Так как точки М и К – середины АD и DС соответственно, то
Площадь треугольника MDK, лежащего в основании новой призмы, составляет часть площади квадрата в основании исходной призмы.
Высоты обеих призм одинаковые. Согласно формуле объема призмы: , и значит, объем маленькой призмы в 8 раз меньше объема большой призмы. Он равен
Ответ: 4
Докажем полезную теорему.
Теорема: Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.
Доказательство:
Плоскость перпендикулярного сечения призмы перпендикулярна к боковым ребрам, поэтому стороны перпендикулярного сечения призмы являются высотами параллелограммов.
Больше задач на формулы объема и площади поверхности здесь.
Спасибо за то, что пользуйтесь нашими материалами. Информация на странице «Формулы объёма и площади поверхности. Многогранники.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена: 09.03.2023
Polygon Volume (3D Analyst)—ArcGIS Pro
В этом разделе
- Сводка
- Использование
- Параметры
- Окружающая среда
- Лицензионная информация
5
Сводка
Вычисляет объем и площадь поверхности между многоугольником постоянной высоты и поверхностью.
Usage
Сначала каждый полигон будет пересекать поверхность.
 Затем будут произведены расчеты объема и поверхности для всех треугольников поверхности и частей треугольников, попадающих в пересекаемый полигон. Если расчеты на основе экстента подходят для ваших нужд, вы можете использовать инструмент Surface Volume для получения более быстрых результатов.
Затем будут произведены расчеты объема и поверхности для всех треугольников поверхности и частей треугольников, попадающих в пересекаемый полигон. Если расчеты на основе экстента подходят для ваших нужд, вы можете использовать инструмент Surface Volume для получения более быстрых результатов.Площадь поверхности представляет части поверхности, находящиеся выше или ниже высоты полигональных объектов. Объем представляет собой область между поверхностью и пространством выше или ниже высоты полигонального объекта. Когда расчеты выполняются над плоскостью, объем представляет собой область между плоскостью и нижней стороной поверхности. Когда расчеты выполняются ниже плоскости, объем представляет собой область между плоскостью и верхней стороной поверхности.
Входная поверхность оценивается как нерегулярная триангулированная сеть (TIN). Набор данных LAS обрабатывается как поверхность путем построения TIN из набора данных LAS.
 Поскольку наборы данных LAS обычно содержат большое количество точек, построение промежуточной поверхности, которая используется для анализа, может занять значительное время обработки, когда входной полигон охватывает большое количество точек. В этом случае вы можете экспортировать прореженный TIN из набора данных LAS с помощью инструмента Набор данных LAS в TIN.
Поскольку наборы данных LAS обычно содержат большое количество точек, построение промежуточной поверхности, которая используется для анализа, может занять значительное время обработки, когда входной полигон охватывает большое количество точек. В этом случае вы можете экспортировать прореженный TIN из набора данных LAS с помощью инструмента Набор данных LAS в TIN.
Параметры
Метка Объяснение Тип данных Входная поверхность
.
Уровень набора данных LAS; Слой местности; Слой TIN Входные полигоны
Полигональные объекты, определяющие обрабатываемую область.
Уровень объектов Поле высоты
Поле в таблице атрибутов полигона, определяющее высоту опорной плоскости, которая будет использоваться при определении объемных вычислений.

Строка Базовая плоскость
(дополнительно)
Указывает направление от базовой плоскости, в которой будут вычисляться объем и площадь поверхности.
- Рассчитать над плоскостью — объем и площадь поверхности будут рассчитываться над высотой опорной плоскости полигонов.
- Рассчитать ниже плоскости — объем и площадь поверхности будут рассчитываться ниже высоты опорной плоскости многоугольников. Это значение по умолчанию.
- Рассчитать выше и ниже плоскости — объем и площадь поверхности будут рассчитываться выше и ниже высоты опорной плоскости многоугольников.
Строка Поле объема
(необязательно)
Имя поля, которое будет содержать расчеты объема.
 По умолчанию — Громкость.
По умолчанию — Громкость.Строка Поле площади поверхности
(необязательно)
Имя поля, которое будет содержать расчеты площади поверхности. По умолчанию используется SArea.
Строка Разрешение уровня пирамиды
(необязательно)
Допуск по оси z или разрешение размера окна уровня пирамиды ландшафта, который будет использоваться. По умолчанию 0 или полное разрешение.
Двойной Поле объема
(необязательно)
Имя поля, которое будет содержать объем, рассчитанный выше высоты полигона.
 Значение по умолчанию — Above_Vol.
Значение по умолчанию — Above_Vol.Строка Поле объема
(необязательно)
Имя поля, которое будет содержать объем, рассчитанный ниже высоты полигона. Значение по умолчанию — Lower_Vol.
Строка Площадь поверхности над полем
(необязательно)
Имя поля, которое будет содержать площадь поверхности, рассчитанную над высотой многоугольника. Значение по умолчанию — Above_SA.
Строка Площадь поверхности ниже поля
(необязательно)
Имя поля, которое будет содержать площадь поверхности, рассчитанную ниже высоты многоугольника.
 Значение по умолчанию — Below_SA.
Значение по умолчанию — Below_SA.Строка Производные выходные данные
Метка Объяснение Тип данных Выходные объекты, которые будут обновлены - 8
Feature Layer arcpy.ddd.PolygonVolume(in_surface, in_feature_class, in_height_field, {reference_plane}, {out_volume_field}, {surface_area_field}, {pyramid_level_resolution}, {out_volume_above_field}, {out_volume_below_field}, {surface_area_above_field}, { поверхность_область_ниже_поля})Имя Объяснение Тип данных Уровень набора данных LAS; Слой местности; Слой TIN in_feature_class
Полигональные объекты, определяющие обрабатываемую область.

Слой признаков in_height_field
Поле в таблице атрибутов полигона, определяющее высоту опорной плоскости, которая будет использоваться при определении объемных вычислений.
Строка reference_plane
(Необязательно)
Указывает направление от базовой плоскости, в которой будут вычисляться объем и площадь поверхности.
- ВЫШЕ—объем и площадь поверхности будут рассчитываться выше высоты опорной плоскости полигонов.
- НИЖЕ — объем и площадь поверхности будут рассчитываться ниже высоты опорной плоскости полигонов. Это значение по умолчанию.

- BOTH — объем и площадь поверхности будут рассчитываться выше и ниже высоты опорной плоскости полигонов.
Строка out_volume_field
(Необязательно)
Имя поля, которое будет содержать объемные расчеты. По умолчанию — Громкость.
Строка surface_area_field
(Необязательно)
Имя поля, которое будет содержать расчеты площади поверхности. По умолчанию используется SArea.
Строка пирамида_уровня_разрешения
(Необязательно)
Допуск по оси z или разрешение размера окна уровня пирамиды ландшафта, который будет использоваться.
 По умолчанию 0 или полное разрешение.
По умолчанию 0 или полное разрешение.Двойной out_volume_above_field
(Необязательно)
Имя поля, которое будет содержать объем, рассчитанный над высотой полигона. Значение по умолчанию — Above_Vol.
Строка out_volume_below_field
(Необязательно)
Имя поля, которое будет содержать объем, рассчитанный ниже высоты полигона. Значение по умолчанию — Lower_Vol.
Строка surface_area_above_field
(Необязательно)
Имя поля, которое будет содержать площадь поверхности, рассчитанную над высотой полигона.
 Значение по умолчанию — Above_SA.
Значение по умолчанию — Above_SA.Строка surface_area_below_field
(Необязательно)
Имя поля, которое будет содержать площадь поверхности, рассчитанную ниже высоты полигона. Значение по умолчанию — Below_SA.
Строка Полученная выход
Имя Объяснение Тип данных upture_feature_class .
Feature Layer Пример кода
PolygonVolume, пример 1 (окно Python)В следующем примере демонстрируется использование этого средства в окне Python.
arcpy.env.workspace = "C:/данные" arcpy.ddd.PolygonVolume("sample.gdb/featuredataset/terrain", "cut_off_plane.Пример 2 PolygonVolume (автономный скрипт) shp",
in_height_field="Z", reference_plane="ВЫШЕ",
пирамида_уровень_разрешение="5")
shp",
in_height_field="Z", reference_plane="ВЫШЕ",
пирамида_уровень_разрешение="5") В следующем примере демонстрируется использование этого средства в автономном скрипте Python.
'''****************************************************** ********************************** Имя: Пример PolygonVolume Описание: Этот сценарий демонстрирует, как использовать Инструмент Объем многоугольника. ******************************************************* ****************************''' # Импорт системных модулей импортировать аркпи из окружения импорта arcpy # Установить параметры среды env.workspace = "C:/данные" # Установить локальные переменные inSurface = "sample.gdb/featuredataset/terrain" inPoly = "пойма_100.shp" zField = "Высота" refPlane = "НИЖЕ" volFld = "Громкость" sAreaFld = "SArea" #Выполнение многоугольника arcpy.ddd.PolygonVolume(inSurface, inPoly, zField, refPlane, volFld, sAreaFld)Окружающая среда
Текущая рабочая область, географические преобразования, протяженность, использование памяти местности
Информация о лицензировании
- Основная: Требуется 3D аналитик
- Стандарт: Требуется 3D -аналитик
- Advanced: Tress 3d 9
.

Отзыв по этой теме?
Объем призмы | Объем призмы Формула
9{3}$ и т. д.Давайте узнаем, как найти объем призмы и его формулу .
Каков объем призмы?
Объем призмы — это объем пространства, которое призма занимает в трехмерном пространстве. Призма — это твердое трехмерное тело, имеющее две одинаковые многоугольные грани и другие боковые грани, являющиеся параллелограммами. Призма представляет собой многогранник, и различные типы призм называются в соответствии с формой их оснований, например,
.- треугольная призма (треугольное основание)
- квадратная призма (квадратное основание)
- прямоугольная призма (прямоугольное основание)
- пятиугольная призма (пятиугольная основа)
- шестигранная призма (шестиугольное основание)
- восьмиугольная призма (восьмиугольное основание)
В общем случае объем призмы рассчитывается по формуле $\text{Площадь основания} \times \text{Высота призмы}$ .

Общая формула для нахождения площади $n$-стороннего многоугольника имеет вид 9{\circ}}$
Примечание:
- Приведенные выше формулы применимы только в том случае, если основания представляют собой правильные многоугольники.
- Если основания представляют собой неправильные многоугольники, то сначала найдите площадь основания и умножьте ее на высоту призмы, чтобы найти объем.
Примеры
Пример 1: Найдите объем следующей треугольной призмы.
Основанием призмы является прямоугольный треугольник со стороной $6 м$. 9{3}$.
Типы систем координатПризма – трехмерная твердотельная форма
Призма является важным членом семейства многогранников, имеющих конгруэнтные многоугольники в основании и на вершине.
 Остальные грани призмы — параллелограммы, называются боковыми гранями. Это означает, что призма не имеет криволинейной грани. Призма имеет одинаковое поперечное сечение по всей своей длине. Призмы называются в зависимости от их поперечного сечения. Наиболее распространенным примером призмы является металлическая гайка.
Остальные грани призмы — параллелограммы, называются боковыми гранями. Это означает, что призма не имеет криволинейной грани. Призма имеет одинаковое поперечное сечение по всей своей длине. Призмы называются в зависимости от их поперечного сечения. Наиболее распространенным примером призмы является металлическая гайка.СКАЧАТЬ БЕСПЛАТНО КАРТОЧКИ ПО МАТЕМАТИКЕ:
Красиво оформленные карточки для печати, которые помогут вам запомнить все важные математические понятия и формулы.
Типы призм
Призмы классифицируются в зависимости от следующих факторов:
- Призмы по типу многоугольника, основания
- Призмы на основе совмещения одинаковых оснований
- Призмы по форме оснований
Призма по типу многоугольника основания может быть следующих двух типов.
- Обычная призма: Если основание призмы имеет форму правильного многоугольника, призма является правильной призмой.

- Неправильная призма: Если основание призмы имеет форму неправильного многоугольника, призма является неправильной призмой.
Призма на основе совмещения одинаковых оснований может быть следующих двух типов
- Правая призма: Правая призма имеет два плоских конца, идеально выровненных со всеми боковыми гранями в форме прямоугольников.
- Наклонная призма: Наклонная призма кажется наклоненной, два плоских конца не выровнены, а боковые грани представляют собой параллелограммы.
Призму называют на основе формы, получаемой поперечным сечением призмы, и она может быть любого из следующих типов
- Треугольная призма: Призма, основания которой имеют треугольную форму, считается треугольной призмой.
- Квадратная призма: Призма, основания которой имеют квадратную форму, считается квадратной призмой. (прямоугольная призма кубической формы)
- Прямоугольная призма: Призма, основания которой имеют прямоугольную форму, считается прямоугольной призмой (прямоугольная призма имеет кубическую форму).

- Трапециевидная призма: Призма, основания которой имеют форму трапеции, считается трапециевидной призмой.
- Пятиугольная призма: Призма, основания которой имеют пятиугольную форму, считается пятиугольной призмой.
- Шестиугольная призма: Призма, основания которой имеют форму шестиугольника, считается шестиугольной призмой. 9{3} и др.
Какая формула объема призмы?
Формула объема призмы получается путем нахождения произведения площади основания и высоты призмы. Объем призмы определяется как $\text{V} = \text{B} \times \text{H}$, где $\text{V}$ — объем призмы, $\text{B} $ — площадь основания призмы, $\text{H}$ — высота призмы.
Как изменится объем призмы при изменении типа призмы?
Объем призмы зависит от площади основания призмы. При изменении типа призмы меняется основание призмы, что приводит к изменению площади основания призмы. Это изменение площади основания призмы изменяет объем призмы.


 Затем будут произведены расчеты объема и поверхности для всех треугольников поверхности и частей треугольников, попадающих в пересекаемый полигон. Если расчеты на основе экстента подходят для ваших нужд, вы можете использовать инструмент Surface Volume для получения более быстрых результатов.
Затем будут произведены расчеты объема и поверхности для всех треугольников поверхности и частей треугольников, попадающих в пересекаемый полигон. Если расчеты на основе экстента подходят для ваших нужд, вы можете использовать инструмент Surface Volume для получения более быстрых результатов. Поскольку наборы данных LAS обычно содержат большое количество точек, построение промежуточной поверхности, которая используется для анализа, может занять значительное время обработки, когда входной полигон охватывает большое количество точек. В этом случае вы можете экспортировать прореженный TIN из набора данных LAS с помощью инструмента Набор данных LAS в TIN.
Поскольку наборы данных LAS обычно содержат большое количество точек, построение промежуточной поверхности, которая используется для анализа, может занять значительное время обработки, когда входной полигон охватывает большое количество точек. В этом случае вы можете экспортировать прореженный TIN из набора данных LAS с помощью инструмента Набор данных LAS в TIN.
 По умолчанию — Громкость.
По умолчанию — Громкость. Значение по умолчанию — Above_Vol.
Значение по умолчанию — Above_Vol. Значение по умолчанию — Below_SA.
Значение по умолчанию — Below_SA.
 По умолчанию 0 или полное разрешение.
По умолчанию 0 или полное разрешение. Значение по умолчанию — Above_SA.
Значение по умолчанию — Above_SA.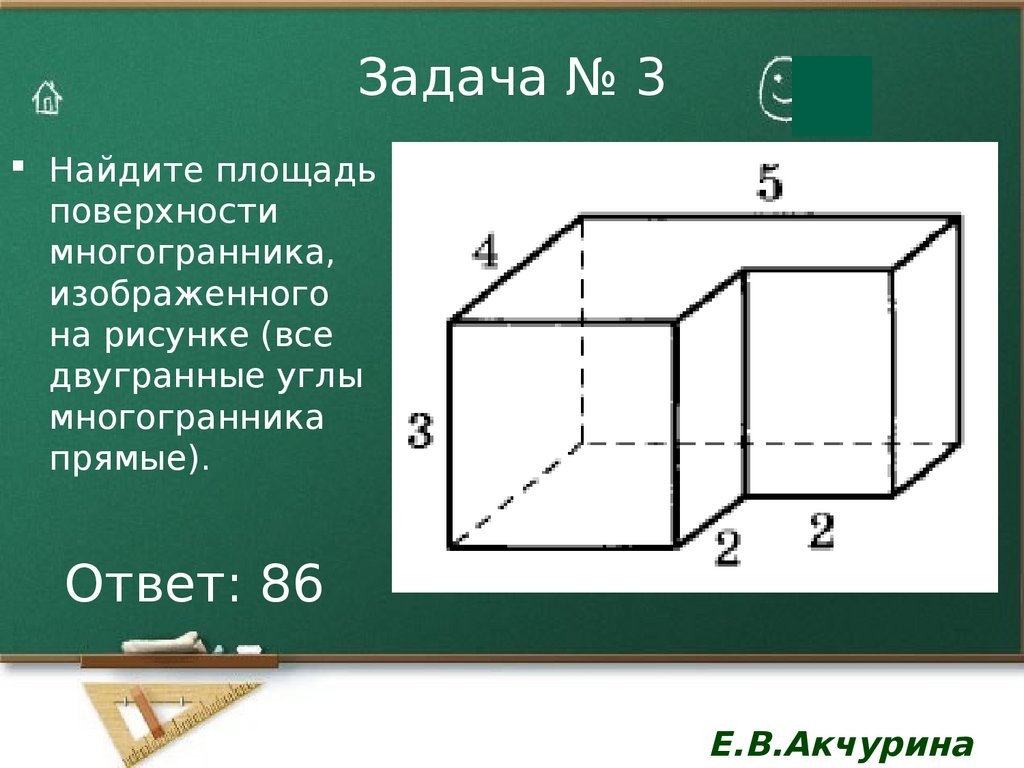 shp",
in_height_field="Z", reference_plane="ВЫШЕ",
пирамида_уровень_разрешение="5")
shp",
in_height_field="Z", reference_plane="ВЫШЕ",
пирамида_уровень_разрешение="5") 
 Остальные грани призмы — параллелограммы, называются боковыми гранями. Это означает, что призма не имеет криволинейной грани. Призма имеет одинаковое поперечное сечение по всей своей длине. Призмы называются в зависимости от их поперечного сечения. Наиболее распространенным примером призмы является металлическая гайка.
Остальные грани призмы — параллелограммы, называются боковыми гранями. Это означает, что призма не имеет криволинейной грани. Призма имеет одинаковое поперечное сечение по всей своей длине. Призмы называются в зависимости от их поперечного сечения. Наиболее распространенным примером призмы является металлическая гайка.

Leave A Comment