Задание 6 ЕГЭ по математике (профиль)
Открытый банк заданий mathege.ru — тренажер задания 6 профильного ЕГЭ по математике-2022 (с ответами). Все прототипы задания 6 на исследование функций. Это задание на использование свойств производной при анализе функций, либо на геометрический смысл производной, либо на физический смысл производной, либо на первообразную функции. Номер заданий соответствует номеру заданий в базе mathege.ru.
27487 На рисунке изображен график функции y = f(x), определенной на интервале (-6; 8). Определите количество целых точек, в которых производная функции положительна.
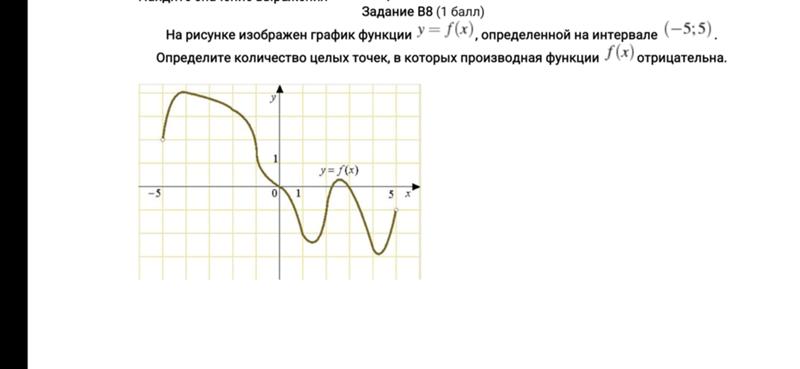
27488. На рисунке изображён график функции y = f(x), определенной на интервале (-5;5). Определите количество целых точек, в которых производная функции отрицательна.
27490. На рисунке изображен график функции y = f(x), определенной на интервале (-2; 12). Найдите сумму точек экстремума функции f(x).
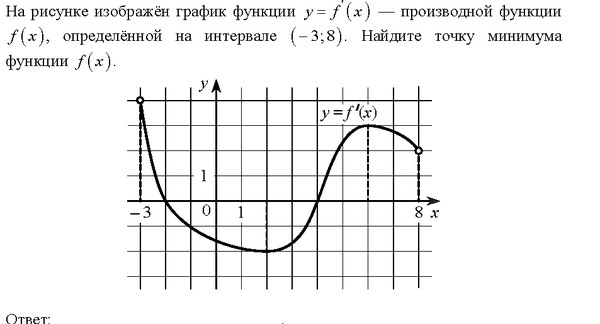
27491. На рисунке изображён график y = f'(x) — производной функции f(x), определенной на интервале (-8; 3). В какой точке отрезка [-3; 2] функция f(x) принимает наибольшее значение?
27492. На рисунке изображён график y = f'(x) — производной функции f(x), определенной на интервале (-8; 4). В какой точке отрезка [-7;-3] функция f(x) принимает наименьшее значение?
27494. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-7; 14). Найдите количество точек максимума функции f(x), принадлежащих отрезку [-6;9].
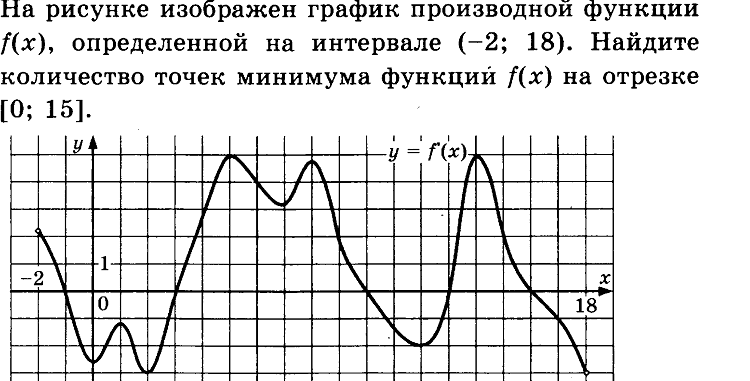
27495. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-18; 6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [-13;1].
27496. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-11; 11).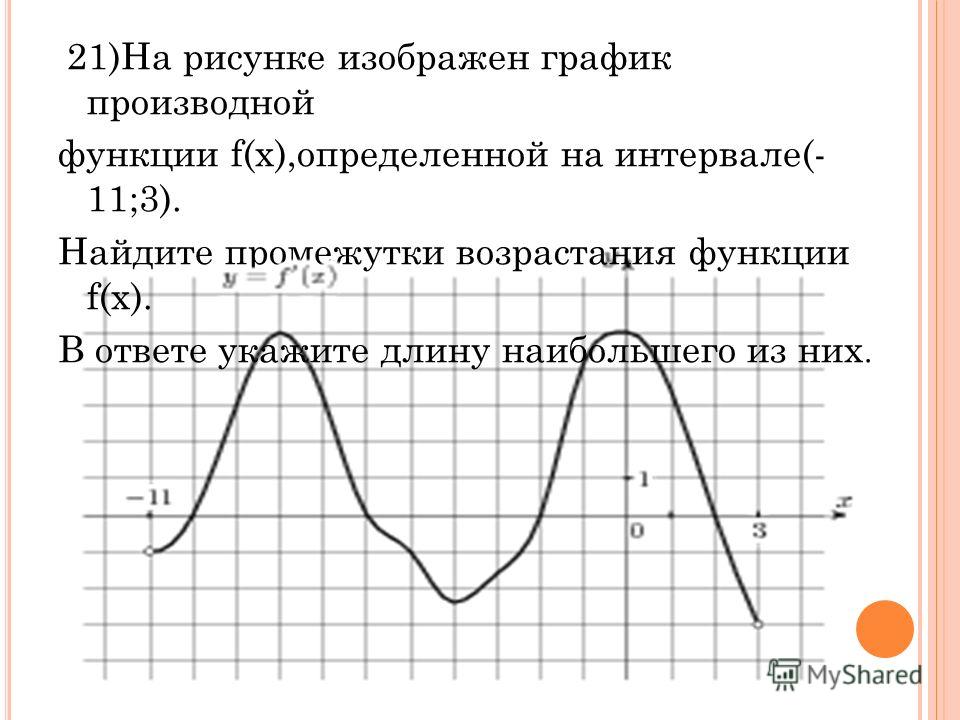 Найдите количество точек экстремума функции f(x), принадлежащих отрезку [-10;10].
Найдите количество точек экстремума функции f(x), принадлежащих отрезку [-10;10].
27497. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
27498. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-5; 7). Найдите промежутки убывания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
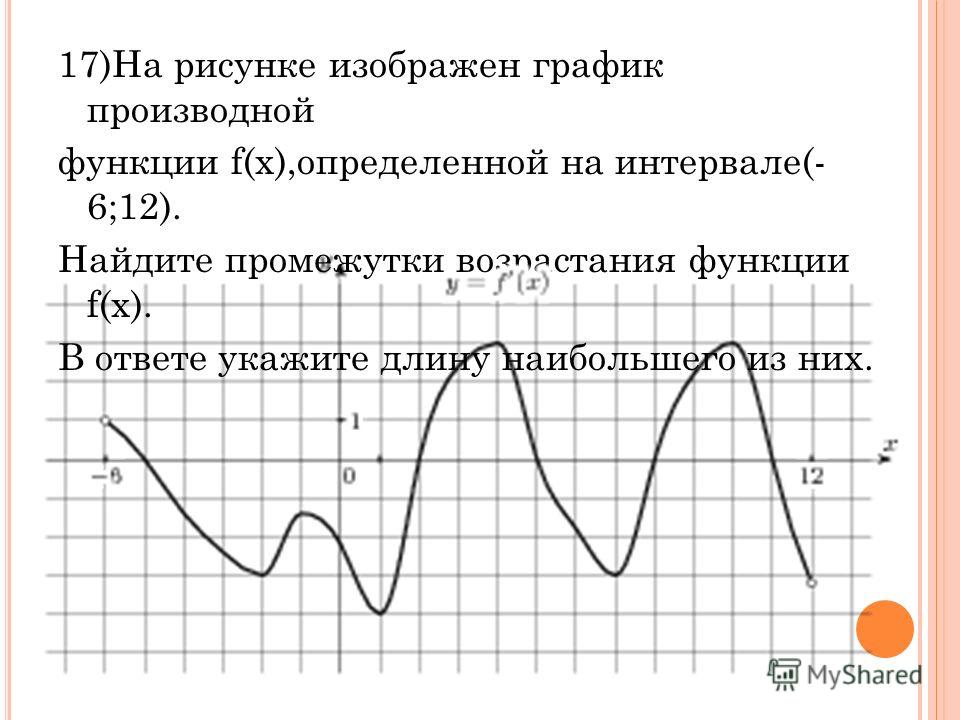
27499. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-11; 3). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
27500. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-2; 12). Найдите промежутки убывания функции f(x).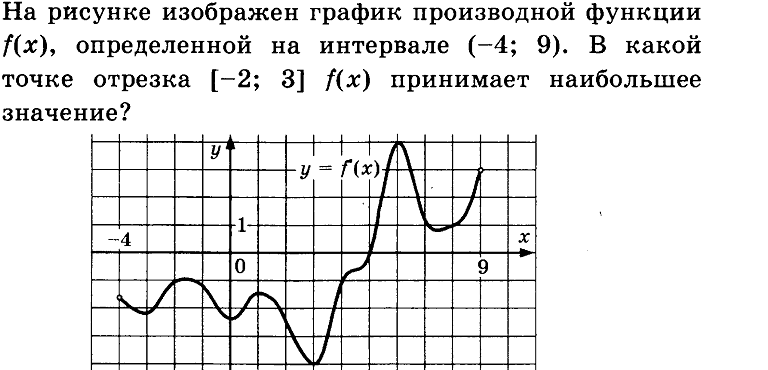
27502. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-4; 8). Найдите точку экстремума функции f(x), принадлежащую отрезку [-2; 6 ].
119971. На рисунке изображен график функции f(x), определенной на интервале (-5;5). Найдите количество точек, в которых производная функции f(x) равна 0.
317539. На рисунке изображён график функции y = f(x) и восемь точек на оси абсцисс: x
317540. На рисунке изображён график функции y = f(x) и двенадцать точек на оси абсцисс: x1, x2, x3, x4, x5, x6, x7, x8, x9, x10, x11, x12.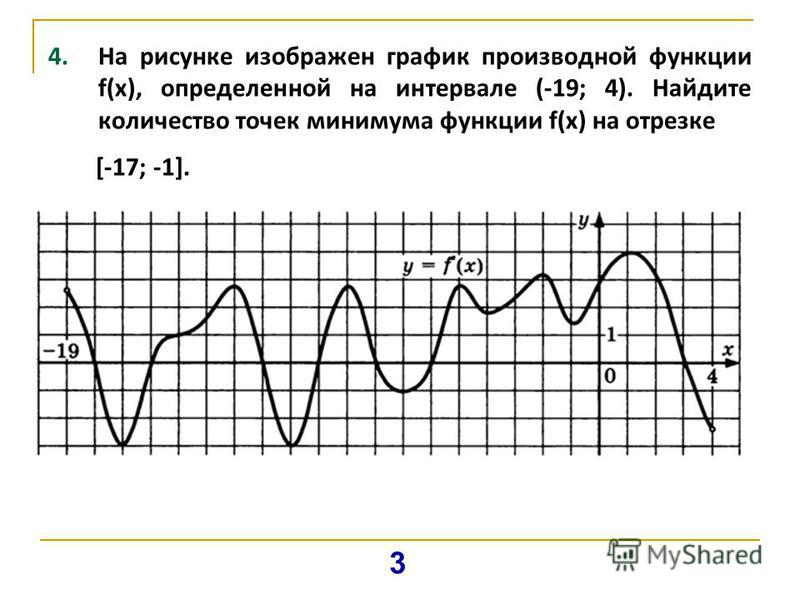 В скольких из этих точек производная функции f(x) отрицательна?
В скольких из этих точек производная функции f(x) отрицательна?
317541. На рисунке изображён график y = f'(x) — производной функции f(x). На оси абсцисс отмечены восемь точек: x
317542. На рисунке изображён график y = f'(x) — производной функции f(x). На оси абсцисс отмечены восемь точек: x1, x2, x3, x4, x5, x6, x7, x8. Сколько из этих точек лежит на промежутках убывания функции f(x)?
27485. Прямая y = 7x — 5 параллельна касательной к графику функции y = x2 + 6x — 8. Найдите абсциссу точки касания.
27486. Прямая y = -4x — 11 является касательной к графику функции y = x3 + 7x2 + 7x — 6. Найдите абсциссу точки касания.
Найдите абсциссу точки касания.
27489. На рисунке изображен график функции y = f(x), определенной на интервале (-5;5). Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.
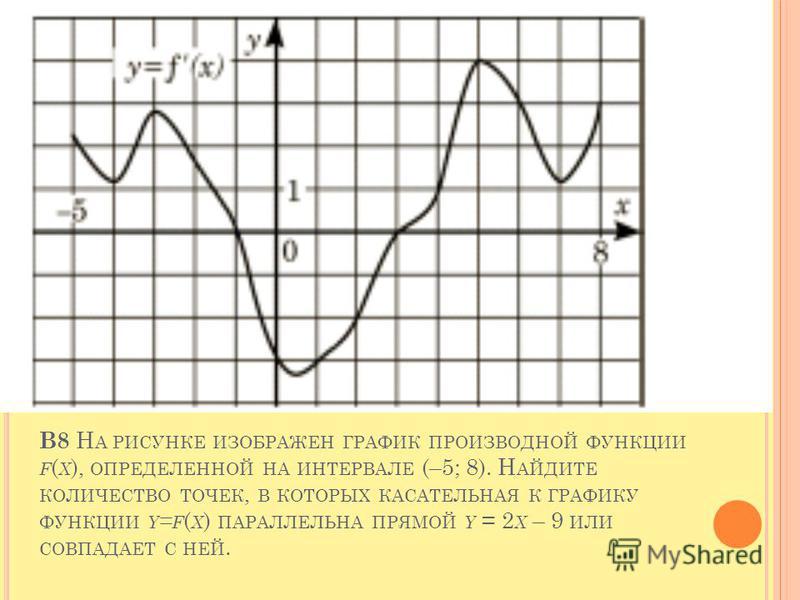
27501. На рисунке изображен график y = f'(x) — производной функции f(x), определенной на интервале (-10; 2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой y = -2x -11 или совпадает с ней.
27503. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
27504. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
27505.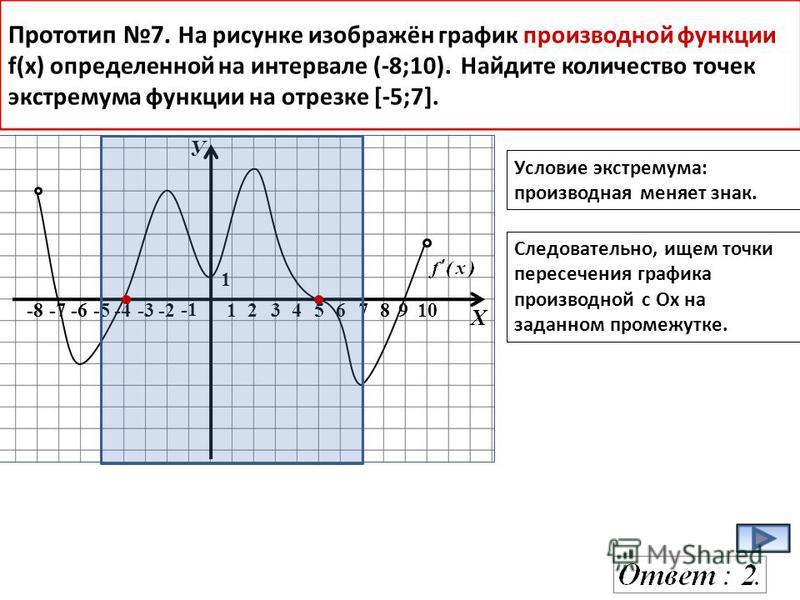 На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x
27506. На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
40130. На рисунке изображен график y = f'(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 2x — 2 или совпадает с ней.
40131. На рисунке изображен график y = f'(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна оси абсцисс или совпадает с ней.
119972. Прямая y = 3x +1 является касательной к графику функции ax2 + 2x + 3. Найдите a.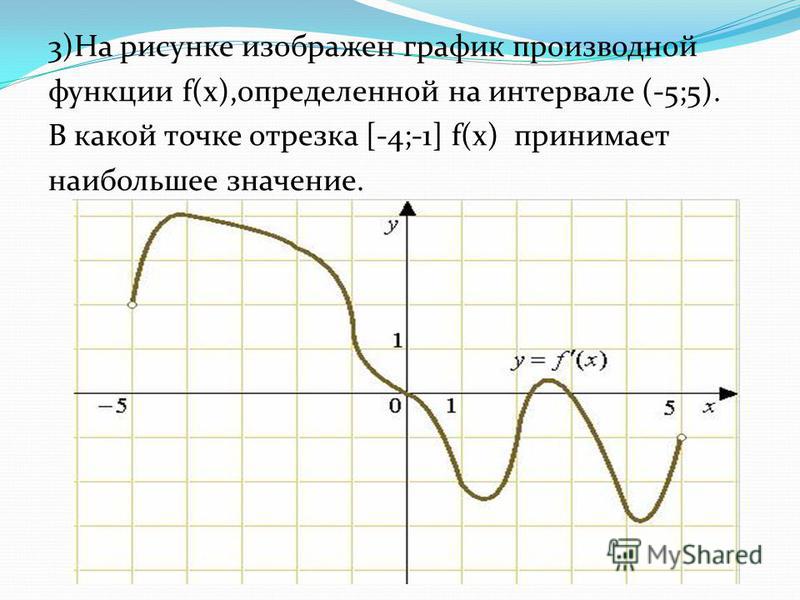
119973. Прямая y = -5x + 8 является касательной к графику функции 28x2 + bx + 15. Найдите b, учитывая, что абсцисса точки касания больше 0.
119974. Прямая y = 3x + 4 является касательной к графику функции 3x2 — 3x + c. Найдите c.
317543. На рисунке изображён график функции y = f(x). На оси абсцисс отмечены точки −2, −1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
317544. На рисунке изображён график функции y = f(x). На оси абсцисс отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
[s60u_expand more_text=»Ответ» less_text=»Свернуть» height=»1″ hide_less=»no» text_color=»#333333″ link_color=»#0088FF» link_style=»default» link_align=»left» more_icon=»» less_icon=»» class=»»]
4
[/su_expand]
119975.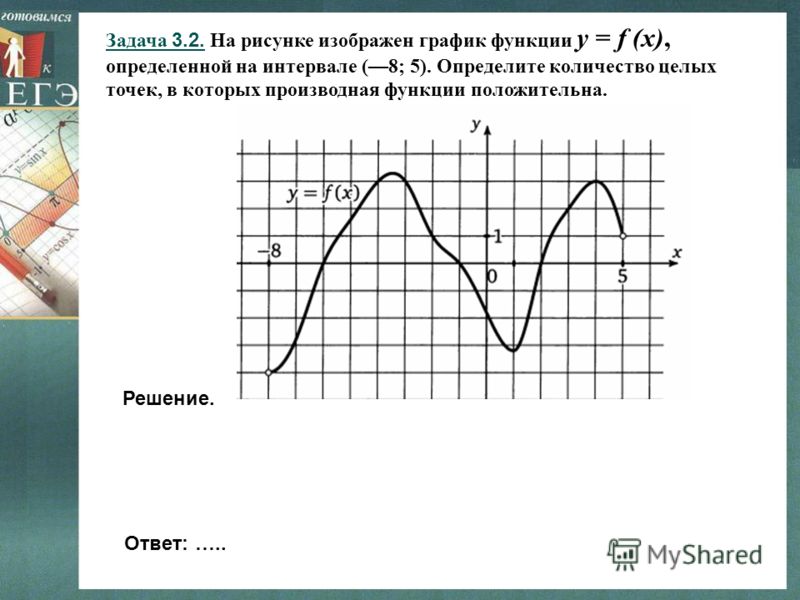
119976. Материальная точка движется прямолинейно по закону x(t) = 1/2t3 — 3t2 + 2t, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 6 с.
119977. Материальная точка движется прямолинейно по закону x(t) = -t4 + 6t
119978. Материальная точка движется прямолинейно по закону x(t) = t2 -13t +23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 3 м/с?
В какой момент времени (в секундах) ее скорость была равна 3 м/с?
119979. Материальная точка движется прямолинейно по закону x(t) = 1/3t3 — 3t2 — 5t + 3, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 2 м/с?
323077. На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (-3;5). Найдите количество решений уравнения f(x) = 0 на отрезке [-2;4].
323078. На рисунке изображён график функции y = f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(8) — F(2), где F(x) — одна из первообразных функции f(x).
323079. На рисунке изображён график некоторой функции y = f(x). Функция F(x) = x3 + 30x2 + 302x — 15/8 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Найдите площадь закрашенной фигуры.
323080. На рисунке изображён график некоторой функции y = f(x). Функция F(x)= -x3 — 27x2 — 240x — 8 — одна из первообразных функции f(x). Найдите площадь закрашенной фигуры.
Понравилось это:
Нравится Загрузка…
Решутест. Продвинутый тренажёр тестов
Решутест. Продвинутый тренажёр тестов- Главная
- ЕГЭ
- Математика профильная
- Анализ функций
- Визуальная связь производной и функции
Решил заданий
Не решил заданий
Осталось заданий
История решения
7350 — не приступал 2319 — не приступал 2067 — не приступал 7251 — не приступал 2256 — не приступал 3530 — не приступал 8106 — не приступал 3945 — не приступал 1140 — не приступал 2635 — не приступал 9363 — не приступал 2258 — не приступал 4263 — не приступал 4855 — не приступал 5257 — не приступал 7178 — не приступал 4862 — не приступал 5154 — не приступалФормат ответа: цифра или несколько цифр, слово или несколько слов.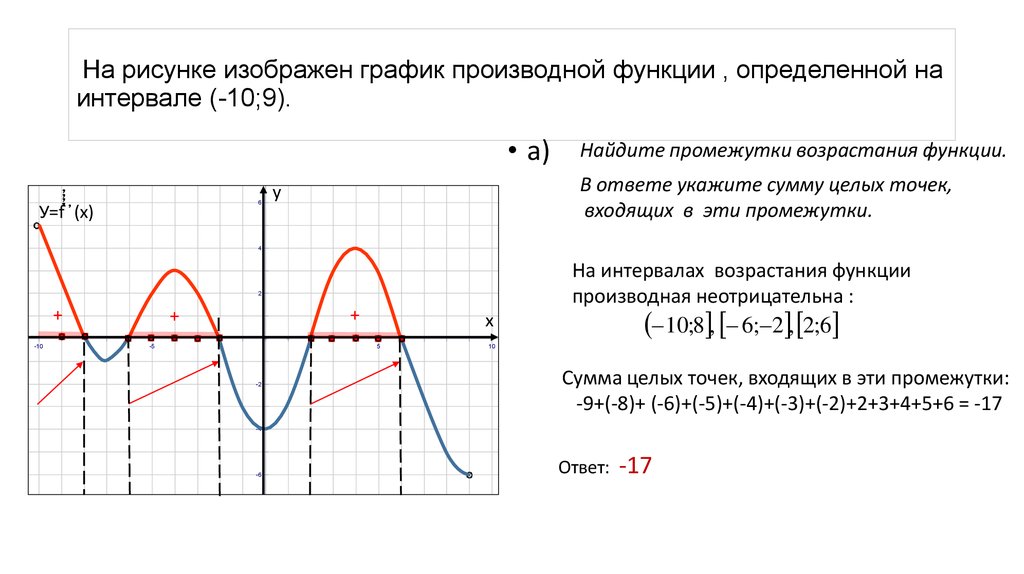 Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.
Вопросы на соответствие «буква» — «цифра» должны записываться как несколько цифр. Между словами и цифрами не должно быть пробелов или других знаков.
Примеры ответов: 7 или здесьисейчас или 3514
Раскрыть Скрыть
№1На рисунке изображен график производной функции f (x), определенной на интервале (–8; 3). В какой точке отрезка [–3; 2] функция f (x) принимает наибольшее значение?
№2На рисунке изображен график функции y = f (x) и отмечены точки −2, −1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
№3На рисунке изображён график y = f′ (x) производной функции f (x) и восемь точек на оси абсцисс: x1, x2, x3, …, xS.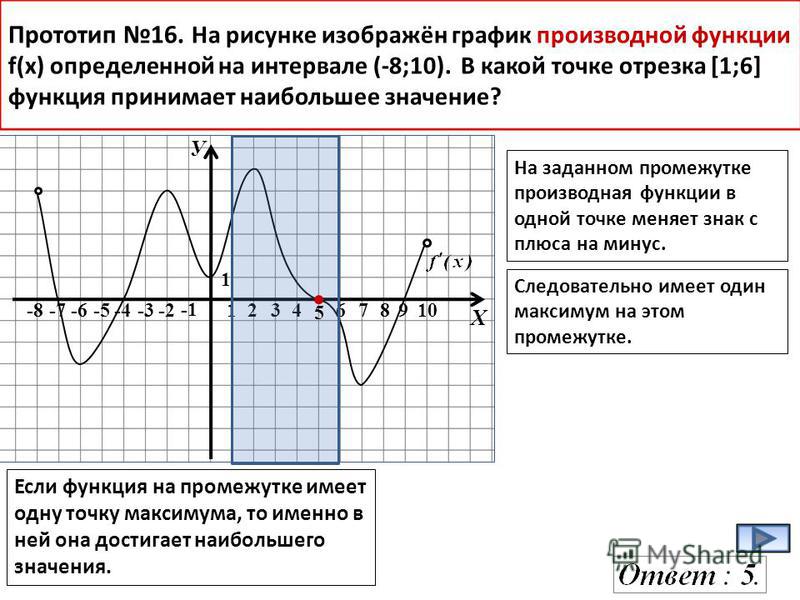 В скольких из этих точек функция f (x) убывает?
В скольких из этих точек функция f (x) убывает?
На рисунке изображен график производной функции f (x), определенной на интервале (−2; 12). Найдите промежутки убывания функции f (x). В ответе укажите длину наибольшего из них.
№5На рисунке изображен график производной функции f (x), определенной на интервале (−5; 7). Найдите промежутки убывания функции f (x). В ответе укажите сумму целых точек, входящих в эти промежутки.
№6На рисунке изображен график производной функции f (x), определенной на интервале (–18; 6). Найдите абсциссу точки минимума функции f (x) на отрезке [–13; 1].
№7На рисунке изображен график производной функции f (x), определенной на интервале (−7; 14). Найдите абсциссу точки максимума функции f (x) на отрезке [−6; 9].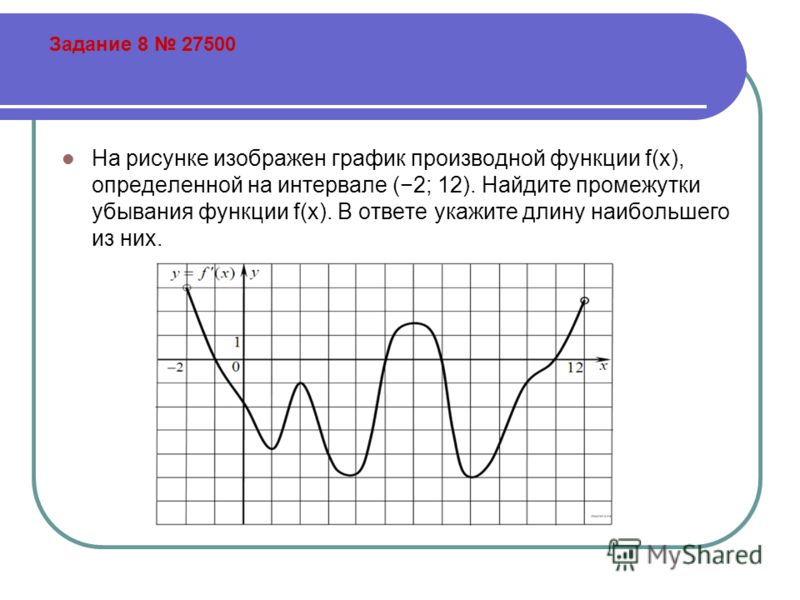
На рисунке изображен график производной функции f (x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции f (x). В ответе укажите сумму целых точек, входящих в эти промежутки.
№9На рисунке изображён график функции y = f (x) и восемь точек на оси абсцисс: x1, x2, x3, …, xS. В скольких из этих точек производная функции f (x) положительна?
№10На рисунке изображен график функции y = f (x) и отмечены точки −2, −1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
№11На рисунке изображен график производной функции f (x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f (x) на отрезке [−10; 10].
На рисунке изображен график производной функции f (x), определенной на интервале (–8; 4). В какой точке отрезка [–7; –3]
f (x) принимает наименьшее значение.
№13На рисунке изображен график производной функции f (x), определенной на интервале (−4; 8). Найдите точку экстремума функции f (x) на отрезке [−2; 6].
№14На рисунке изображен график функции f (x), определенной на интервале (−5; 5). Найдите количество точек, в которых производная функции f (x) равна 0.
№15На рисунке изображён график функции y = F(x) — одной из первообразных некоторой функции f (x), определённой на интервале (−3; 5). Пользуясь рисунком, определите количество решений уравнения f (x) = 0 на отрезке [−2; 4].
№16На рисунке изображен график функции y = f(x), определенный на интервале (-2;12).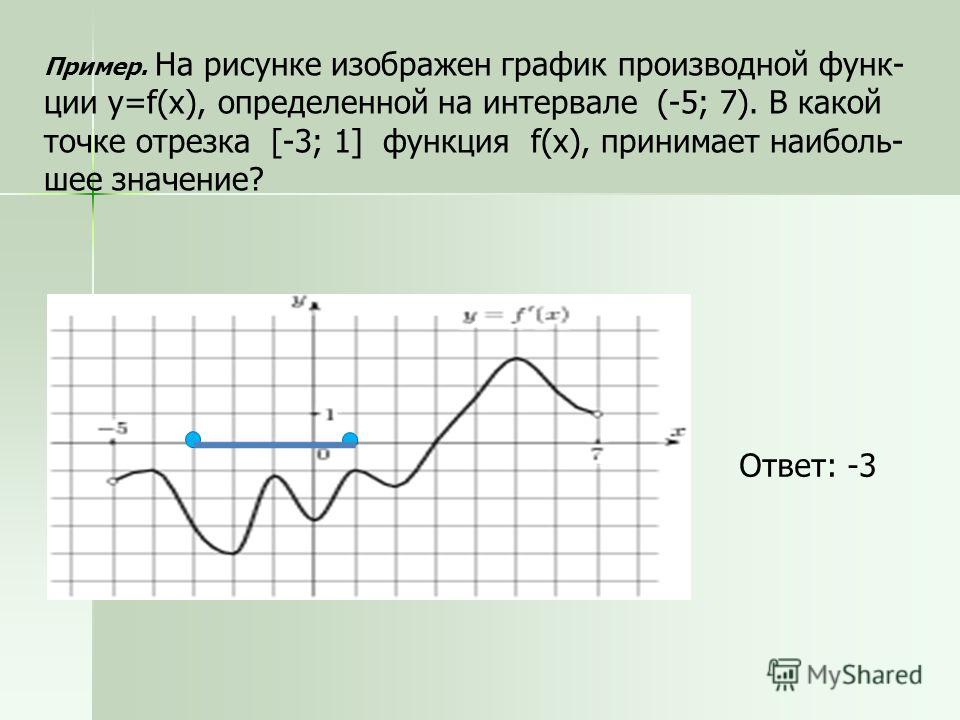 Найдите сумму точек экстремума функции f(x).
Найдите сумму точек экстремума функции f(x).
На рисунке изображен график y = f’(x) — производной функции f(x), определенный на интервале (-8;3). В какой точке отрезка [-3;2] функция f(x) принимает наибольшее значение?
№18На рисунке изображен график y = f’(x) — производной функции f(x) и восемь точек на оси абсцисс: х1, х2, х3… х8. В скольких из этих точек функция f(x) возрастает?
Так твой прогресс будет сохраняться.
Регистрация
Мы отправили код на:
ИзменитьПолучить код повторно через 00:00
Я прочитал(-а) Политику конфиденциальности и согласен(-на) с правилами использования моих персональных данных
Ништяк!
Решено верно
Браво!
Решено верно
Крутяк!
Решено верно
Зачёт!
Решено верно
Чётко!
Решено верно
Бомбезно!
Решено верно
Огонь!
Решено верно
Юхууу!
Решено верно
Отпад!
Решено верно
Шикарно!
Решено верно
Блестяще!
Решено верно
Волшебно!
Решено верно
3.
 2: Производная как функция
2: Производная как функция- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2491
- Гилберт Странг и Эдвин «Джед» Герман
- OpenStax
Цели обучения
- Определить производную функцию заданной функции.
- График производной функции по графику заданной функции.
- Укажите связь между производными и непрерывностью.
- Опишите три условия, при которых функция не имеет производной.
- Объясните значение производной высшего порядка.
Как мы видели, производная функции в данной точке дает нам скорость изменения или наклон касательной к функции в этой точке. Если мы продифференцируем функцию положения в данный момент времени, мы получим скорость в этот момент. Кажется разумным заключить, что знание производной функции в каждой точке даст ценную информацию о поведении функции. Однако процесс нахождения производной даже при нескольких значениях с использованием методов из предыдущего раздела быстро стал бы довольно утомительным. В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения.
Если мы продифференцируем функцию положения в данный момент времени, мы получим скорость в этот момент. Кажется разумным заключить, что знание производной функции в каждой точке даст ценную информацию о поведении функции. Однако процесс нахождения производной даже при нескольких значениях с использованием методов из предыдущего раздела быстро стал бы довольно утомительным. В этом разделе мы определяем производную функцию и изучаем процесс ее нахождения.
Производные функции
Функция производной дает производную функции в каждой точке области определения исходной функции, для которой определена производная. Мы можем формально определить производную функцию следующим образом.
Определение: производная функция
Пусть \(f\) — функция. Производная функция , обозначаемая \(f’\), является функцией, область определения которой состоит из таких значений \(x\), что существует следующий предел:
\[f'(x)=\lim_{h→0}\frac{f(x+h)−f(x)}{h}.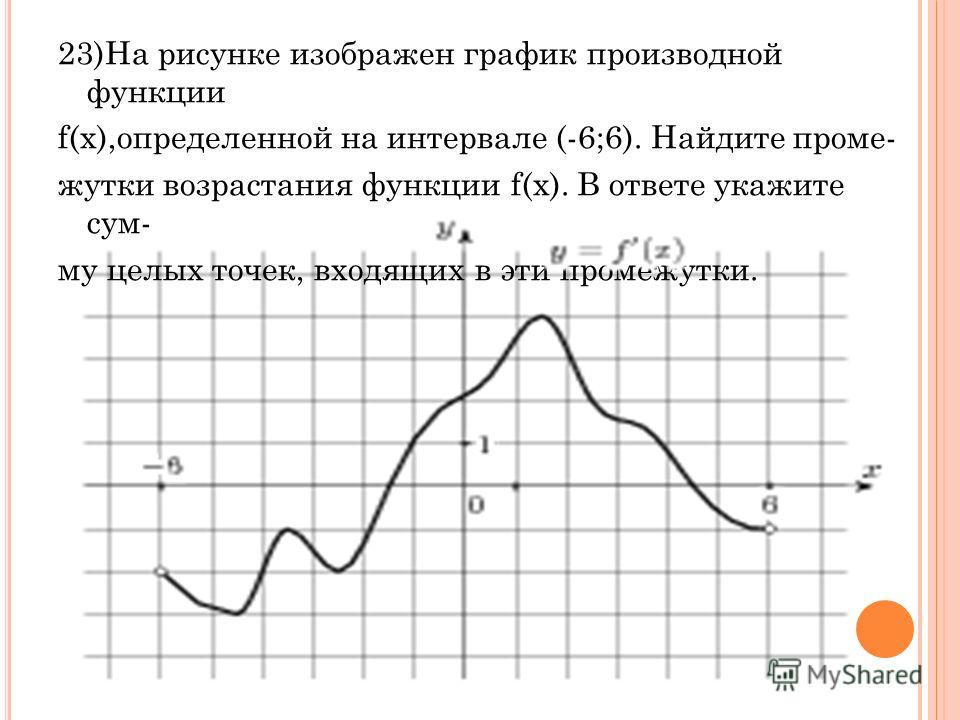 \label{derdef} \]
\label{derdef} \]
Функция \(f(x)\) называется дифференцируемой в \(a\), если \(f'(a)\) существует. В более общем смысле функция называется дифференцируемой на \(S\), если она дифференцируема в каждой точке открытого множества \(S\), а дифференцируемой функцией является функция, в которой \(f'( x)\) существует в своей области определения.
В следующих нескольких примерах мы используем уравнение \ref{derdef} для нахождения производной функции.
Пример \(\PageIndex{1}\): нахождение производной функции квадратного корня
Найдите производную \(f(x)=\sqrt{x}\).
Решение
Начните непосредственно с определения функции производной.
Замените \(f(x+h)=\sqrt{x+h}\) и \(f(x)=\sqrt{x}\) на \(f'(x)= \displaystyle \lim_{ h→0}\frac{f(x+h)−f(x)}{h}\).
| \(f'(x)=\displaystyle \lim_{h→0}\frac{\sqrt{x+h}−\sqrt{x}}{h}\) | ||
| \(=\displaystyle\lim_{h→0}\frac{\sqrt{x+h}−\sqrt{x}}{h}⋅\frac{\sqrt{x+h}+\sqrt{ х}}{\sqrt{х+ч}+\sqrt{х}}\) | Умножить числитель и знаменатель на \(\sqrt{x+h}+\sqrt{x}\) без распределения в знаменателе.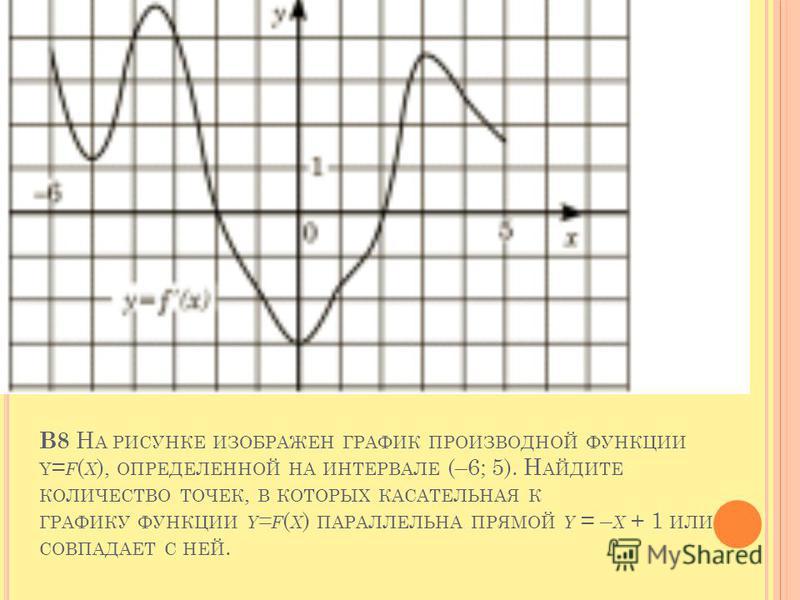 2\). 92−2x\справа)=2x−2\). Таким образом, для функции \(y=f(x)\) каждое из следующих обозначений представляет собой производную от \(f(x)\): 2\). 92−2x\справа)=2x−2\). Таким образом, для функции \(y=f(x)\) каждое из следующих обозначений представляет собой производную от \(f(x)\):\(f'(x), \quad \dfrac{dy }{dx}, \quad y′,\quad \dfrac{d}{dx}\big(f(x)\big)\). Вместо \(f'(a)\) мы также можем использовать \(\dfrac{dy}{dx}\Big|_{x=a}\). Использование нотации \(\dfrac{dy}{dx}\) (называемой нотацией Лейбница) довольно распространено в технике и физике. Чтобы лучше понять это обозначение, вспомним, что производная функции в точке — это предел наклона секущих по мере приближения секущих к касательной. Наклоны этих секущих часто выражаются в виде \(\dfrac{Δy}{Δx}\), где \(Δy\) — разность значений \(y\), соответствующая разнице в \(x \) значения, которые выражаются как \(Δx\) (рисунок \(\PageIndex{1}\)). Таким образом, производная, которую можно рассматривать как мгновенную скорость изменения \(у\) по отношению к \(х\), выражается как \(\displaystyle \frac{dy}{dx}= \lim_{Δx→0}\frac{Δy}{Δx}\). Рисунок \(\PageIndex{1}\): производная выражается как \(\dfrac{dy}{dx}=\displaystyle\lim_{Δx→0}\frac{Δy}{Δx}\).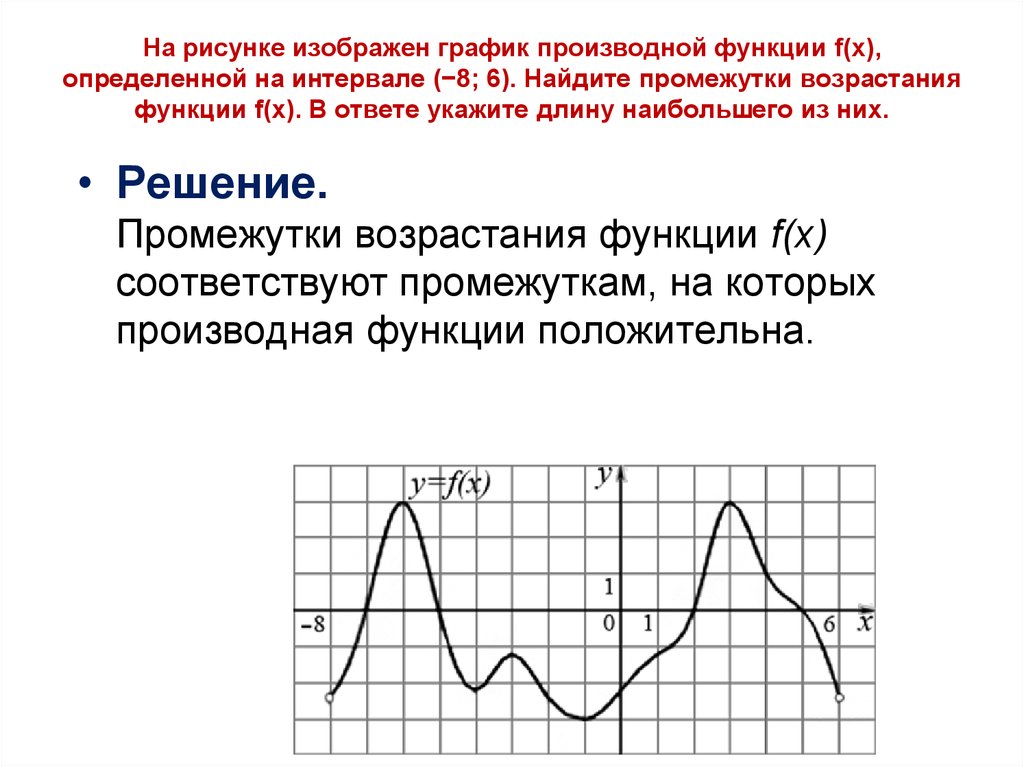 Построение графика производнойМы уже обсуждали, как построить график функции, поэтому, имея уравнение функции или уравнение функции производной, мы можем построить ее график. Учитывая оба, мы ожидаем увидеть соответствие между графиками этих двух функций, поскольку \(f'(x)\) дает скорость изменения функции \(f(x)\) (или наклон касательной строка к \(f(x)\)). В примере \(\PageIndex{1}\) мы обнаружили, что для \(f(x)=\sqrt{x}\), \(f'(x)=\frac{1}{2\sqrt {Икс}}\). Если мы изобразим эти функции на тех же осях, как на рисунке \(\PageIndex{2}\), мы сможем использовать графики, чтобы понять связь между этими двумя функциями. Во-первых, мы замечаем, что \(f(x)\) возрастает по всей своей области, а это означает, что наклоны ее касательных во всех точках положительны. Следовательно, мы ожидаем \(f'(x)>0\) для всех значений x в его области определения. Кроме того, по мере увеличения \(x\) наклоны касательных линий к \(f(x)\) уменьшаются, и мы ожидаем увидеть соответствующее уменьшение \(f'(x)\). Пример \(\PageIndex{3}\): набросок производной с помощью функцииИспользуйте следующий график \(f(x)\) для построения графика \(f'(x)\). Решение Решение показано на следующем графике. Заметим, что \(f(x)\) возрастает и \(f'(x)>0\) на \((–2,3)\). Кроме того, \(f(x)\) убывает и \(f'(x)<0\) на \((−∞,−2)\) и на \((3,+∞)\). Также обратите внимание, что \(f(x)\) имеет горизонтальные касательные в точках \(-2\) и \(3\), а \(f'(-2)=0\) и \(f'(3)= 0\).
Производные и непрерывностьТеперь, когда мы можем изобразить производную, давайте рассмотрим поведение графиков. Сначала рассмотрим связь между дифференцируемостью и непрерывностью. Мы увидим, что если функция дифференцируема в точке, она должна быть там непрерывной; однако функция, непрерывная в точке, не обязательно должна быть дифференцируемой в этой точке. На самом деле функция может быть непрерывной в точке и не быть дифференцируемой в этой точке по одной из нескольких причин. Дифференцируемость подразумевает непрерывность Пусть \(f(x)\) — функция и \(a\) находится в ее области определения. Если \(f(x)\) дифференцируема в \(а\), то \(f\) непрерывна в \(а\). ДоказательствоЕсли \(f(x)\) дифференцируема в \(a\), то \(f'(a)\) существует и, если положить \(h = x — a\), мы имеют \( x = a + h \), и поскольку \(h=x-a\to 0\), мы можем видеть, что \(x\to a\). Тогда \[ f'(a) = \lim_{h\to 0}\frac{f(a+h)-f(a)}{h}\nonumber \] можно переписать как \(f'(a)=\displaystyle \lim_{x→a}\frac{f(x)−f(a)}{x−a}\). Мы хотим показать, что \(f(x)\) непрерывно в \(a\), показав, что \(\displaystyle \lim_{x→a}f(x)=f(a).\) Таким образом , \(\begin{align*} \displaystyle \lim_{x→a}f(x) &=\lim_{x→a}\;\big(f(x)−f(a)+f( a)\big)\\[4pt] Следовательно, поскольку \(f(a)\) определено и \(\displaystyle \lim_{x→a}f(x)=f(a)\), мы заключаем, что \(f\) непрерывна в \(a\). □ Мы только что доказали, что дифференцируемость влечет непрерывность, но теперь мы рассмотрим, влечет ли непрерывность дифференцируемость. Чтобы определить ответ на этот вопрос, мы исследуем функцию \(f(x)=|x|\). Эта функция всюду непрерывна; однако \(f'(0)\) не определено. Это наблюдение приводит нас к мысли, что непрерывность не влечет дифференцируемости. Давайте исследовать дальше. Для \(f(x)=|x|\), 92}}=+∞\). Таким образом, \(f'(0)\) не существует. Беглый взгляд на график \(f(x)=\sqrt[3]{x}\) проясняет ситуацию. Функция имеет вертикальную касательную в точке \(0\) (рисунок \(\PageIndex{5}\)). Рисунок \(\PageIndex{5}\): функция \(f(x)=\sqrt[3]{x}\) имеет вертикальную касательную в точке \(x=0\). Он непрерывен в точке \(0\), но не дифференцируем в точке \(0\). Функция \(f(x)=\begin{cases} x\sin\left(\frac{1}{x}\right), & & \text{ if } x≠0\\0, & & \ text{ if } x=0\end{cases}\) также имеет производную, которая демонстрирует интересное поведение при \(0\). Мы видим, что \(f'(0)=\displaystyle \lim_{x→0}\frac{x\sin\left(1/x\right)−0}{x−0}= \lim_ {x→0}\sin\left(\frac{1}{x}\right)\). Этого предела не существует, в основном потому, что наклон секущих постоянно меняет направление по мере приближения к нулю (рис. \(\PageIndex{6}\)). Рисунок \(\PageIndex{6}\): функция \(f(x)=\begin{cases} x\sin\left(\frac{1}{x}\right), & & \text{, если } x≠0\\0, & & \text{ если } x=0\end{cases}\) не дифференцируемо в \(0\).Итого:
Пример \(\PageIndex{4}\): кусочная функция, которая является непрерывной и дифференцируемой 92+bx+c, & & \text{, если }x<−10\\−\frac{1}{4}x+\frac{5}{2}, & & \text{, если } x≥−10\ end{cases}\), где \(x\) и \(f(x)\) указаны в дюймах. Для плавного движения автомобиля по трассе функция \(f(x)\) должна быть одновременно непрерывной и дифференцируемой в точке \(−10\). Найдите значения \(b\) и \(c\), которые делают \(f(x)\) одновременно непрерывным и дифференцируемым. Рисунок \(\PageIndex{7}\): Чтобы автомобиль двигался плавно по трассе, функция должна быть одновременно непрерывной и дифференцируемой.92−10b+c=10−10b+c\) и \(f(−10)=5\), мы должны иметь \(10−10b+c=5\).
Производные высшего порядкаПроизводная функции сама по себе является функцией, поэтому мы можем найти производную производной. Например, производная функции положения — это скорость изменения положения или скорость. Производная скорости — это скорость изменения скорости, то есть ускорение. Новая функция, полученная дифференцированием производной, называется второй производной. Кроме того, мы можем продолжать брать производные, чтобы получить третью производную, четвертую производную и так далее. В совокупности они обозначаются как 92−3h}{ч}\) | Упростите числитель. |
| \(=\displaystyle \lim_{h→0}(4x+2h−3)\) | Вынесите \(h\) в числителе и сократите с \(h\) в знаменателе.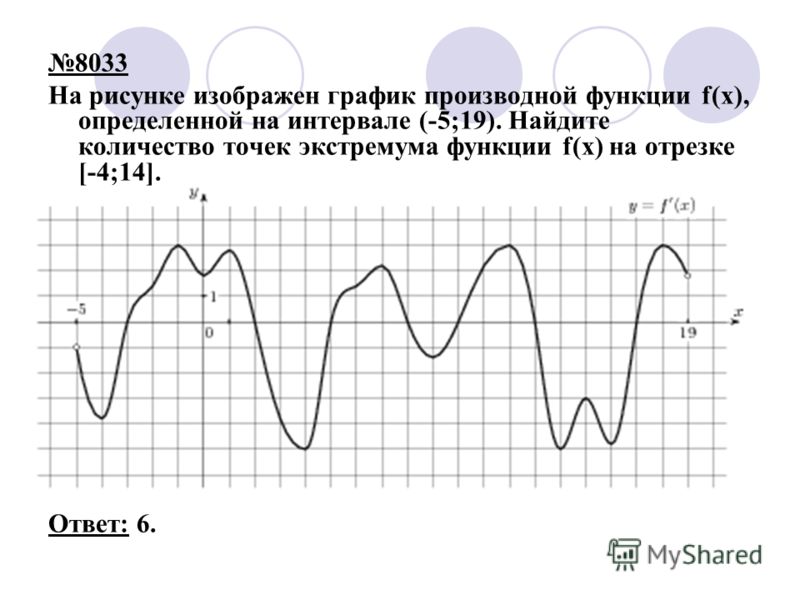 | |
| \(=4x−3\) | Возьмите предел. |
Затем найдите \(f»(x)\), взяв производную от \(f'(x)=4x−3.\)
\), найти \(a(t).\)- Подсказка
Используйте пример \(\PageIndex{6}\) в качестве руководства.
- Ответить
\(а(т)=6т\)
Основные понятия
- Производной функции \(f(x)\) называется функция, значение которой в точке \(x\) равно \(f'(x)\).

- График производной функции \(f(x)\) связан с графиком функции \(f(x)\). Где \(f(x)\) имеет касательную с положительным наклоном, \(f'(x)>0\). Где \(f(x)\) имеет касательную с отрицательным наклоном, \(f'(x)<0\). Где \(f(x)\) имеет горизонтальную касательную, \(f'(x)=0.\) 9{\text{th}}\) производная.
Ключевые уравнения
- Производная функция
\(f'(x)=\displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}\)
Глоссарий
- производная функция
- дает производную функции в каждой точке области определения исходной функции, для которой определена производная
- дифференцируемый по \(а\)
- функция, для которой \(f'(a)\) существует, дифференцируема в точке \(a\) 9{\text{th}}\) производная, называется производной высшего порядка
Авторы и авторство
Эта страница под названием 3. 2: Производная как функция распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
2: Производная как функция распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Гилбертом Стрэнгом и Эдвином «Джедом» Херманом (OpenStax) через исходный контент, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Вернуться к началу
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- ОпенСтакс
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
- Показать страницу TOC
- нет
- Теги
- автор @ Эдвин «Джед» Герман
- автор@Гилберт Странг
- производная функция
- Дифференцируемая функция
- дифференцируемый на S
- производная высшего порядка
- источник@https://openstax.
 org/details/books/calculus-volume-1
org/details/books/calculus-volume-1
Как найти увеличивающиеся интервалы с помощью графических функций
Все ресурсы по исчислению 1
10 Диагностические тесты 438 практических тестов Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 3 Следующая →
Исчисление 1 Помощь » Функции » Графические функции » Интервалы » Увеличение интервалов » Как найти возрастающие интервалы с помощью графических функций
На каких интервалах увеличивается f(x) = (1/3)x 3 + 2,5x 2 – 14x + 25?
Возможные ответы:
(–∞, –7)
(–∞, –7) и (2, ∞)
(–∞, –7), (–7, 2), и (2, ∞)
(2, ∞)
(–7, 2) и (2, ∞)
Правильный ответ:
(–∞, –7) и (2, ∞)
Объяснение:
Мы будем использовать наклон касательной, чтобы определить увеличение/уменьшение f(x). С этой целью начнем с первой производной от f(x):
С этой целью начнем с первой производной от f(x):
f'(x) = x 2 + 5x – 14
Найдите потенциальные относительные максимумы и минимумы, установив f'(x ) на 0 и решить:
x 2 + 5х – 14 = 0; (x – 2)(x + 7) = 0
Возможные относительные максимумы/минимумы: x = 2, x = –7
Мы должны проверить следующие интервалы: (–∞, –7), (–7, 2 ), (2, ∞)
f'(–10) = 100 – 50 – 14 = 36
f'(0) = –14
f'(10) = 100 + 50 – 14 = 136
Следовательно, уравнение возрастает на (–∞, –7) и (2, ∞)
Сообщить об ошибке
Найдите интервал(ы), на которых следующая функция возрастает. График, чтобы перепроверить свой ответ.
Возможные ответы:
Никогда
Всегда
Правильный ответ:
Объяснение: Чтобы определить, когда функция возрастает, вы должны сначала взять производную, затем приравнять ее к 0, а затем найти, между какими нулевыми значениями функция положительна.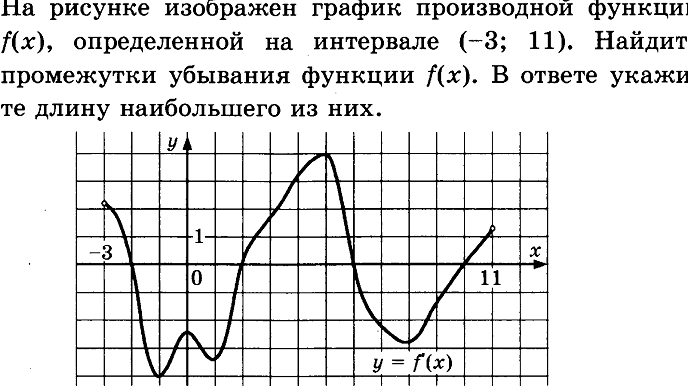
Сначала возьмем производную:
Приравняем к 0 и решим:
Теперь проверьте значения со всех сторон, чтобы определить, когда функция положительна и, следовательно, увеличивается. Я проверю значения -6, 0 и 2.
Поскольку значения положительные, когда x = -6 и 2, интервал увеличивается на интервалах, которые включают эти значения. . Таким образом, наш ответ:
Сообщить об ошибке
Найдите интервал(ы), где следующая функция возрастает. График, чтобы перепроверить свой ответ.
Возможные ответы:
Никогда
Всегда
Правильный ответ:
Объяснение: Чтобы определить, когда функция возрастает, вы должны сначала взять производную, затем приравнять ее к 0, а затем найти, между какими нулевыми значениями функция положительна.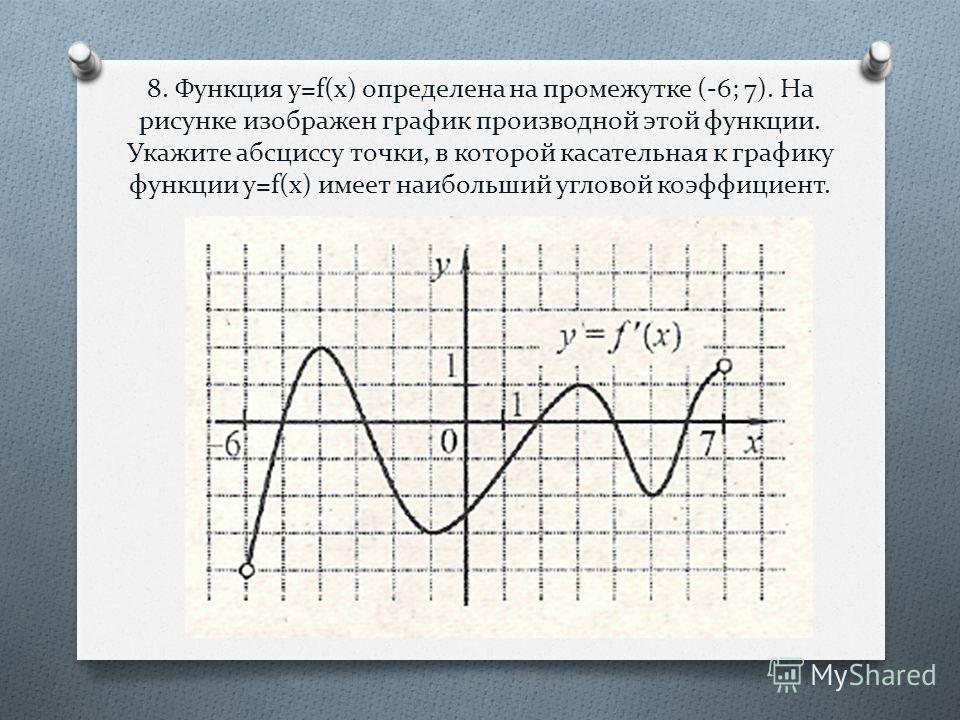
Сначала возьмем производную:
Приравняем к 0 и решим:
Теперь проверьте значения со всех сторон, чтобы определить, когда функция положительна и, следовательно, увеличивается. Я проверю значения 0, 2 и 10.
Поскольку значение является положительным, когда x = 0 и 10, интервал увеличивается в обоих этих интервалах. Поэтому наш ответ:
Сообщить об ошибке
Увеличивается или уменьшается на интервале ?
Возможные ответы:
По убыванию. на интервале.
Увеличение. на интервале.
Увеличение. на интервале.
Невозможно определить на основании предоставленной информации
Уменьшается. на интервале.
Правильный ответ:
Возрастание. на интервале.
Объяснение:
Чтобы найти возрастающие и убывающие интервалы, нам нужно найти, где наша первая производная больше или меньше нуля.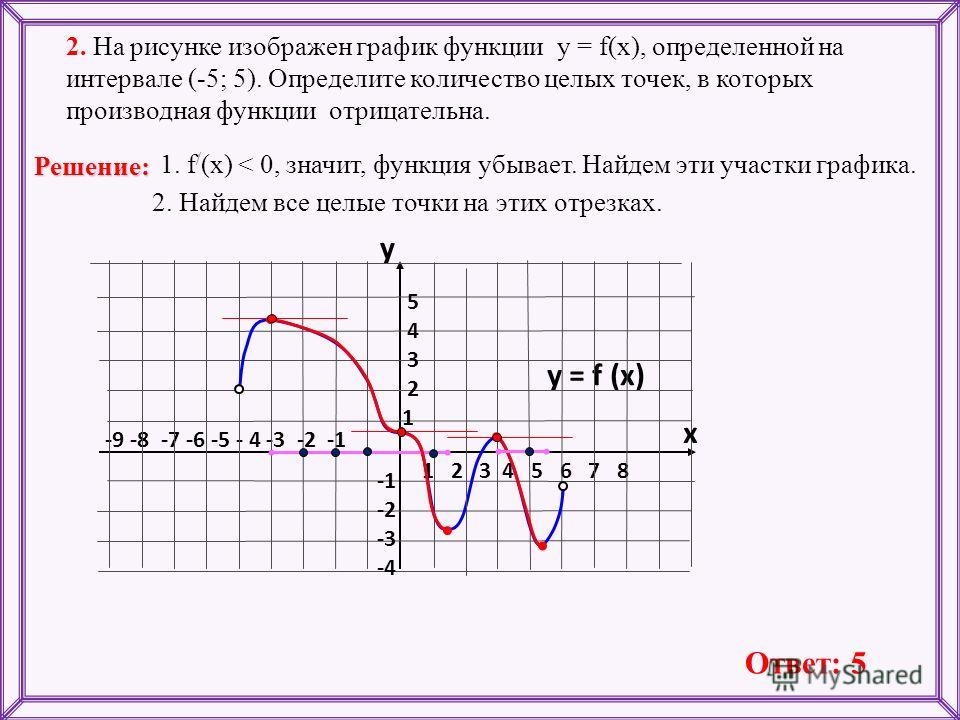 Если наша первая производная положительна, наша исходная функция возрастает, а если g'(x) отрицательна, g(x) убывает.
Если наша первая производная положительна, наша исходная функция возрастает, а если g'(x) отрицательна, g(x) убывает.
Начните с:
Если мы подставим любое число от 3 до 6, мы получим положительное число для g'(x). Таким образом, эта функция должна возрастать на интервале {3,6 }, так как g'(x) положительна.
Сообщить об ошибке
Увеличивается или уменьшается на интервале?
Возможные ответы:
Уменьшение, так как положительно.
Возрастание, поскольку положительно.
Уменьшение, поскольку отрицательно.
Возрастает, потому что отрицательное значение.
не увеличивается и не уменьшается на заданном интервале.
Правильный ответ:
Возрастает, потому что положительно.
Объяснение:
Чтобы узнать, является ли функция возрастающей или убывающей, нам нужно определить, положительна или отрицательна первая производная на заданном интервале.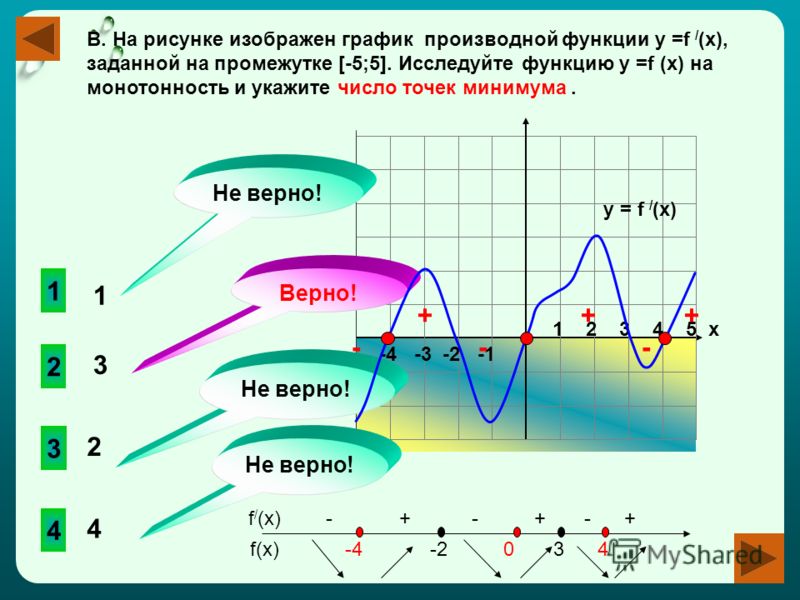
Таким образом, начиная с:
, мы получаем:
используя степенное правило .
Найдите функцию на каждом конце интервала.
Итак, первая производная положительна на всем интервале, поэтому g(t) возрастает на интервале.
Сообщить об ошибке
Является ли следующая функция возрастающей или убывающей на интервале?
Возможные ответы:
По убыванию, так как на данном интервале отрицательно.
Возрастание, так как на данном интервале положительно.
Функция не возрастает и не убывает на интервале.
Возрастание, поскольку отрицательно на заданном интервале.
Уменьшение, так как на данном интервале положительно.
Правильный ответ:
Возрастание, т.к. положительно на данном интервале.
Объяснение:
Функция возрастает на интервале, если для каждой точки этого интервала первая производная положительна.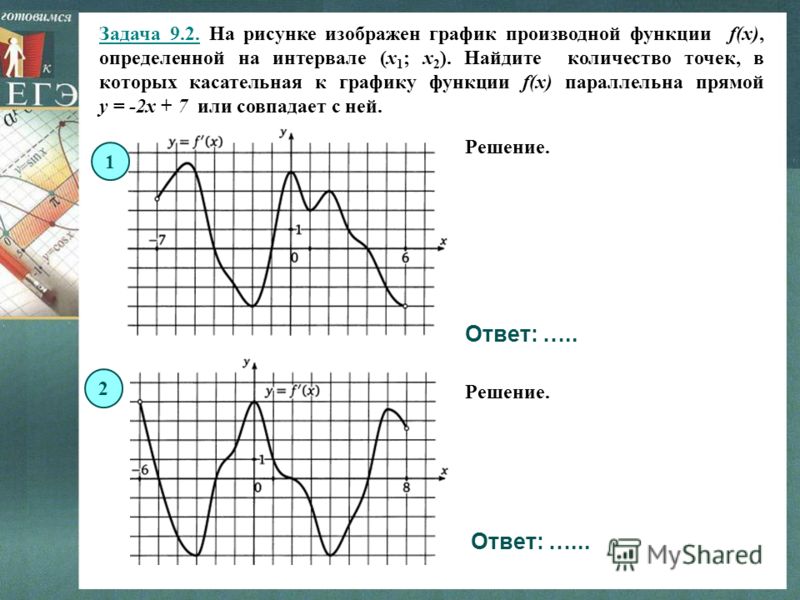
Итак, нам нужно найти первую производную, а затем подставить конечные точки нашего интервала.
Найдите первую производную с помощью степенного правила
Подставьте конечные точки и оцените функцию.
Оба положительны, поэтому наша функция возрастает на данном интервале.
Сообщить об ошибке
С какими интервалами увеличивается следующая функция?
Возможные ответы:
Правильный ответ:
Пояснение:
Первый шаг — найти первую производную.
Помните, что производная от
Далее найдите критические точки, которые являются точками, где или не определены. Чтобы найти точки, установите числитель на , чтобы найти неопределенные точки, установите знаменатель на . Критические точки – это и
. Последний шаг – попробовать точки во всех регионах, чтобы увидеть, какой диапазон дает положительное значение для .
Если мы подставим число из первого диапазона, т.е. получим отрицательное число.
Из второго диапазона мы получаем положительное число.
Из третьего диапазона мы получаем отрицательное число.
Из последнего диапазона мы получаем положительное число.
Таким образом, второй и последний диапазоны — это те, где увеличивается.
Сообщить об ошибке
Ниже приведен полный график . На каком интервале(ах) происходит увеличение?
Возможные ответы:
Правильный ответ:
Объяснение:
увеличивается, когда является положительным (над осью). Это происходит на интервалах .
Report an Error
Function A
Function B
Function C
Функция D
Функция E
5 Графики различных функций.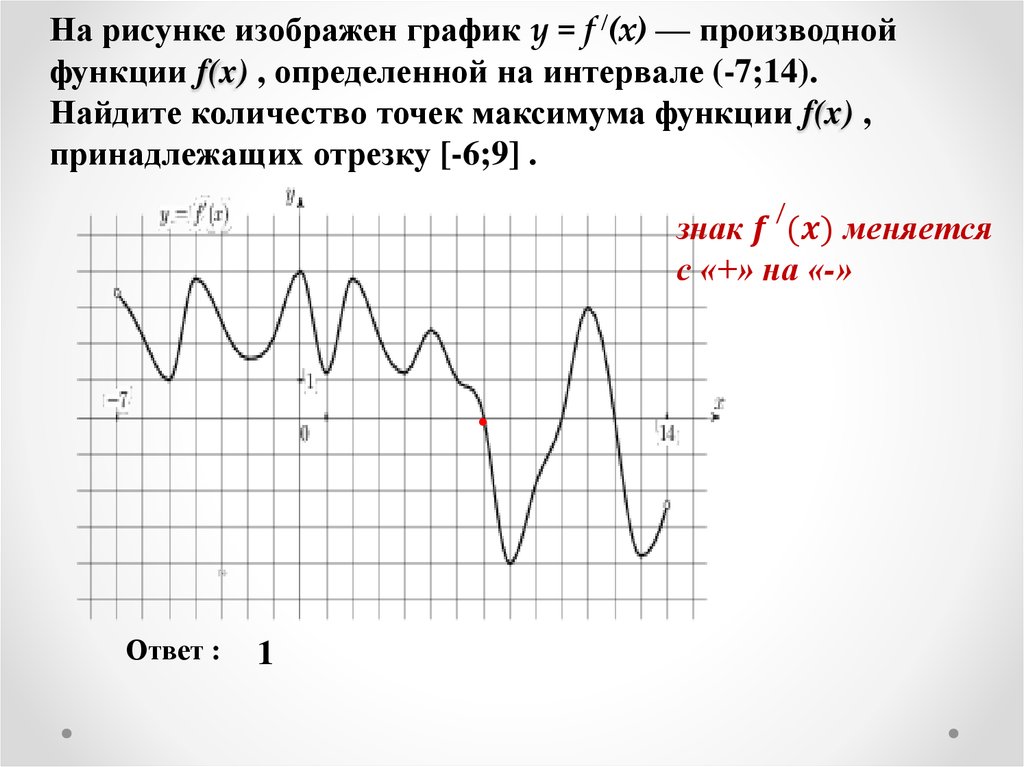 На каком графике показана возрастающая/неубывающая функция ?
На каком графике показана возрастающая/неубывающая функция ?
Возможные ответы:
Функция A
Функция E
Функция B
Функция C
Функция D
5 Правильный ответ:
0046
Функция E
Объяснение:
Функция возрастает, если для любого , (т. е. наклон всегда больше или равен нулю)
Функция E – единственная функция, обладающая этим свойством. Обратите внимание, что функция E является возрастающей, но не строго возрастающей
Сообщить об ошибке
Найдите возрастающие интервалы следующей функции на интервале:
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти возрастающие интервалы заданной функции, нужно определить интервалы, на которых функция имеет положительную первую производную.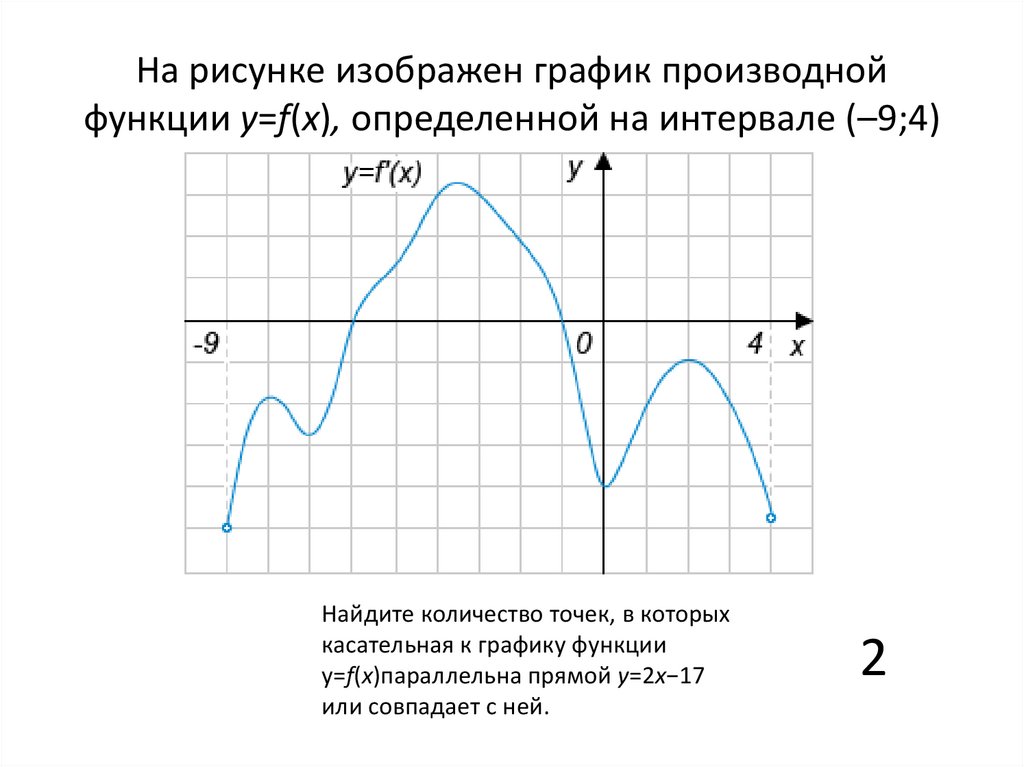
| \(f»(x)= \displaystyle \lim_{h→0}\frac{f'(x+h)−f'(x)}{h}\) | Используйте \(f'(x)=\displaystyle \lim_{h→0}\frac{f(x+h)−f(x)}{h}\) с \(f ‘(x)\) в место \(f(x).\) |
| \(=\displaystyle \lim_{h→0}\frac{(4(x+h)−3)−(4x−3)}{h}\) | Замените \(f'(x+h)=4(x+h)−3\) и \(f'(x)=4x−3.\) |
| \(=\displaystyle \lim_{h→0}4\) | Упростить. |
| \(=4\) | Возьмите предел. |

 +}f'(x)=+∞\), что соответствует вертикальной касательной к \(f( х)\) в \(0\). 92−2x,\; f'(x)=2x−2\). Графики этих функций показаны на рисунке \(\PageIndex{3}\). Обратите внимание, что \(f(x)\) убывает при \(x<1\). Для этих же значений \(x\), \(f'(x)<0\). Для значений \(x>1\) \(f(x)\) возрастает и \(f'(x)>0\). Кроме того, \(f(x)\) имеет горизонтальную касательную в точках \(x=1\) и \(f'(1)=0\).
+}f'(x)=+∞\), что соответствует вертикальной касательной к \(f( х)\) в \(0\). 92−2x,\; f'(x)=2x−2\). Графики этих функций показаны на рисунке \(\PageIndex{3}\). Обратите внимание, что \(f(x)\) убывает при \(x<1\). Для этих же значений \(x\), \(f'(x)<0\). Для значений \(x>1\) \(f(x)\) возрастает и \(f'(x)>0\). Кроме того, \(f(x)\) имеет горизонтальную касательную в точках \(x=1\) и \(f'(1)=0\).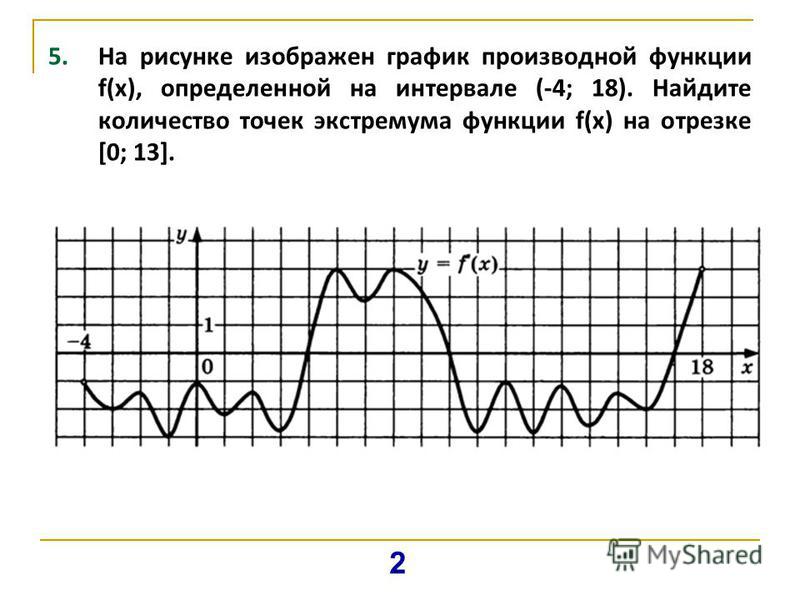 92−4\). На каком интервале находится график \(f'(x)\) над осью \(x\)?
92−4\). На каком интервале находится график \(f'(x)\) над осью \(x\)?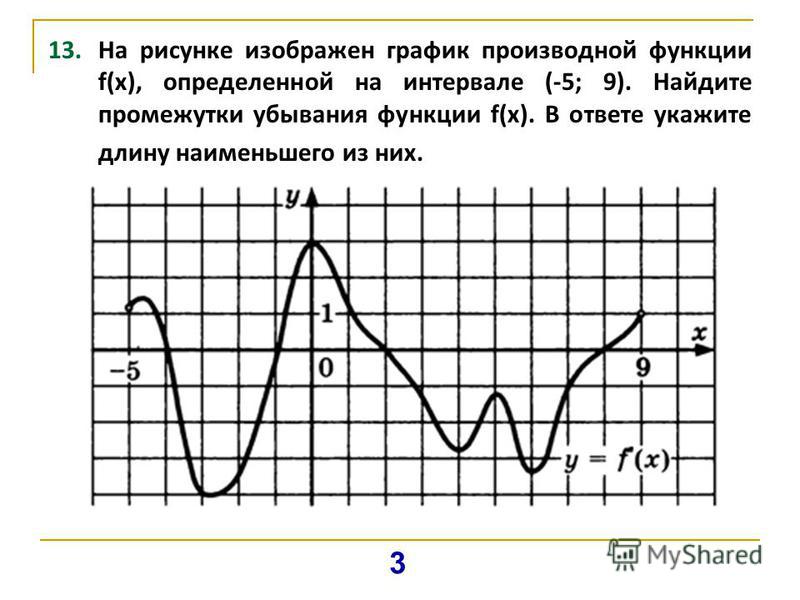

 2+bx+c−5}{x+10}\\[4pt] 92, & & \text{ если } x≥3\end{cases}\) как непрерывны, так и дифференцируемы в \(3\).
2+bx+c−5}{x+10}\\[4pt] 92, & & \text{ если } x≥3\end{cases}\) как непрерывны, так и дифференцируемы в \(3\).
 org/details/books/calculus-volume-1
org/details/books/calculus-volume-1
Leave A Comment