Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Справочник по математикеГеометрия (Планиметрия)Четырехугольники

      Определение 1. Окружностью, вписанной в четырёхугольник, называют окружность, которая касается касается каждой из сторон четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, описанным около окружности или описанным четырёхугольником.

Рис.1

      Замечание. В настоящем разделе мы рассматриваем только выпуклые четырёхугольники.

      Теорема 1. Если четырёхугольник описан около окружности, то суммы длин его противоположных сторон равны.

      Доказательство. Рассмотрим четырёхугольник ABCD, описанный около окружности, и обозначим буквами E, F, G, H – точки касания сторон четырёхугольника с окружностью (рис. 2).

Рис.2

      В силу теоремы об отрезках касательных, проведённых к окружности из одной точки, справедливы равенства

AH = AE,       BF = BE,       CF = CG,       DH = DG,

      Складывая эти равенства, получим:

AH + BF + CF + DH =
= AE + BE + CG + DG,

      Поскольку

AH + BF + CF + DH =
= AD + BC,      
AE + BE + CG + DG =
= AB + CD,

то справедливо равенство

AD + BC = AB + CD,

что и требовалось доказать.

      Теорема 2 (обратная теорема к теореме 1). Если у четырёхугольника суммы длин противоположных сторон равны, то в этот четырёхугольник можно вписать окружность.

      Доказательство. Рассмотрим четырёхугольник ABCD, длины сторон которого удовлетворяют равенству

AD +BC = AB + CD,

и проведём биссектрисы углов BAD и CDA.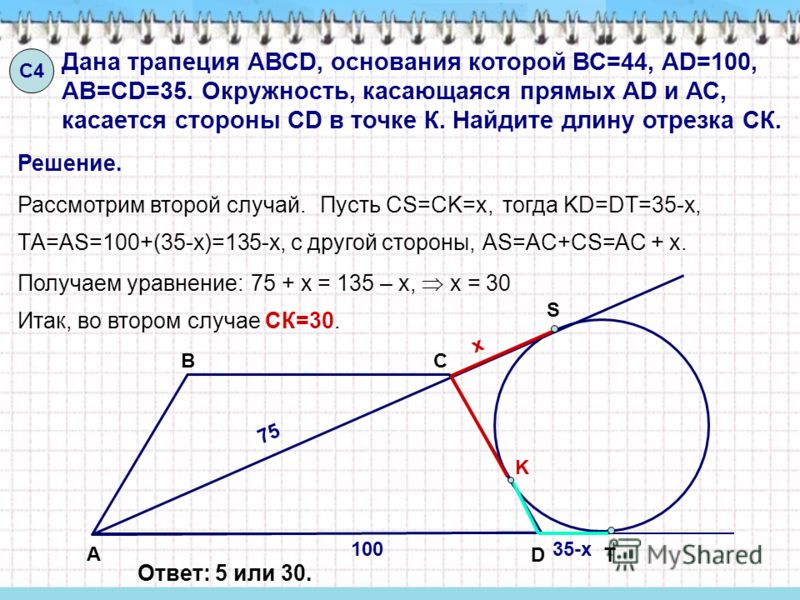 Обозначим точку пересечения этих биссектрис буквой O, и опустим из точки O перпендикуляры OH, OE и OG на стороны AD, AB и CD соответственно (рис.3).

Рис.3

      Поскольку точка O лежит на биссектрисе угла BAD, то справедливо равенство

OH = OE,

      Поскольку точка O лежит на биссектрисе угла ADC, то справедливо равенство

OH = OG,

      Следовательно, справедливы равенства

OH = OE = OG,

из которых вытекает, что точки H, E и G лежат на окружности с центром в точке O и радиусом OH, касающейся сторон четырёхугольника AD, AB и CD в точках H, E и G соответственно. При этом возможны два случая:

  1. Окружность касается касается стороны BC (рис.4).

    Рис.4

          В этом случае четырёхугольник ABCD описан около окружности, и теорема доказана.

  2. Окружность не касается стороны BC.

    В этом случае касательная, проведенная к окружности из точки B, пересекает прямую DC в точке K, и возможны два случая:

    1. Точка K лежит между точками C и D (рис.5)

      2. Рис.5

    2. Точка C лежит между точками K и D (рис.6)

      3. Рис.6

      Рассмотрим случай 2а и приведём его к противоречию. В этом случае в силу того, что четырёхугольник ABKD является описанным, а также по условию теоремы справедливы равенства:

      Последнее равенство утверждает, что в треугольнике BKC сумма двух сторон равна третьей стороне, что противоречит неравенству треугольниканеравенству треугольниканеравенству треугольника. Полученное противоречие доказывает, что случай 2а невозможен.

      Совершенно аналогичные рассуждения позволяют заключить, что случай 2b также невозможен.

      Итак, возможен и реализуется лишь случай 1.

      Теорема доказана.

      Из доказательства теоремы 2 непосредственно вытекает

      Теорема 3. Биссектрисы всех внутренних углов описанного четырёхугольника пересекаются в одной точке – центре вписанной окружности.

      В следующей таблице приводятся примеры четырёхугольников, в которые можно вписать окружность. Доказательства утверждений непосредственно вытекают из теорем 1 и 2 и предоставляются читателю в качестве несложных упражнений.

      Примеры описанных четырёхугольников

ФигураРисунокУтверждение
РомбВ любой ромб можно вписать окружность
КвадратВ любой квадрат можно вписать окружность
ПрямоугольникВ прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом
ПараллелограммВ параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом
ДельтоидВ любой дельтоид можно вписать окружность
ТрапецияВ трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон рана сумме длин оснований
Ромб

В любой ромб можно вписать окружность

Квадрат

В любой квадрат можно вписать окружность

Прямоугольник

В прямоугольник можно вписать окружность тогда и только тогда, когда он является квадратом

Параллелограмм

В параллелограмм можно вписать окружность тогда и только тогда, когда он является ромбом

Дельтоид

В любой дельтоид можно вписать окружность

Трапеция

В трапецию можно вписать окружность тогда и только тогда, когда у трапеции сумма длин боковых сторон рана сумме длин оснований

      На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Репетитор по математике и физике в Отрадном 8(915)389-73-44 представляет материалы для изучающих математику и для подготовки к ЕГЭ

Опубликовано вт, 10/04/2016 — 21:38 пользователем DmitryM

1

За­да­ние 16 № 505176. На диа­го­на­ли па­рал­ле­ло­грам­ма взяли точку, от­лич­ную от её се­ре­ди­ны. Из неё на все сто­ро­ны па­рал­ле­ло­грам­ма (или их про­дол­же­ния) опу­сти­ли пер­пен­ди­ку­ля­ры.

а) До­ка­жи­те, что четырёхуголь­ник, об­ра­зо­ван­ный ос­но­ва­ни­я­ми этих пер­пен­ди­ку­ля­ров, яв­ля­ет­ся тра­пе­ци­ей.

б) Най­ди­те пло­щадь по­лу­чен­ной тра­пе­ции, если пло­щадь па­рал­ле­ло­грам­ма равна 24, а один из его углов равен 45°.

 

Аналоги к заданию № 505176: 511398

За­да­ние 16 № 505155. На диа­го­на­ли па­рал­ле­ло­грам­ма взяли точку, от­лич­ную от её се­ре­ди­ны.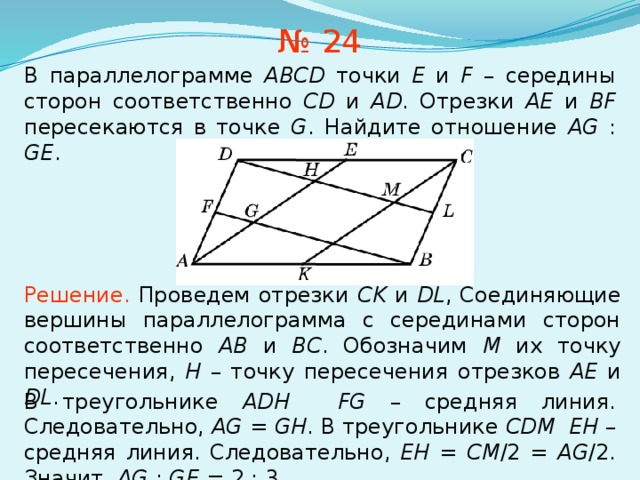 Из неё на все сто­ро­ны па­рал­ле­ло­грам­ма (или их про­дол­же­ния) опу­сти­ли пер­пен­ди­ку­ля­ры.

а) До­ка­жи­те, что четырёхуголь­ник, об­ра­зо­ван­ный ос­но­ва­ни­я­ми этих пер­пен­ди­ку­ля­ров, яв­ля­ет­ся тра­пе­ци­ей.

б) Най­ди­те пло­щадь по­лу­чен­ной тра­пе­ции, если пло­щадь па­рал­ле­ло­грам­ма равна 16, а один из его углов равен 60°.

 

2

За­да­ние 16 № 505239. В рав­но­бед­рен­ном тре­уголь­ни­ке ABC с углом 120° при вер­ши­не A про­ве­де­на бис­сек­три­са BD. В тре­уголь­ник ABC впи­сан пря­мо­уголь­ник DEFH так, что сто­ро­на FH лежит на от­рез­ке BC, а вер­ши­на E —  на от­рез­ке AB.

а) До­ка­жи­те, что

FH = 2DH.

б) Най­ди­те пло­щадь пря­мо­уголь­ни­ка DEFH, если AB = 4.

 

Аналоги к заданию № 505239: 511400

 

Источник: ЕГЭ по ма­те­ма­ти­ке 08.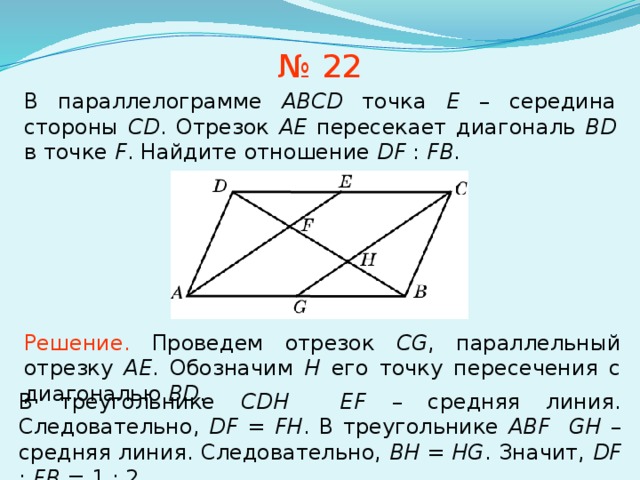 05.2014. До­сроч­ная волна, ре­зерв­ный день. Ва­ри­ант 1.

 

3

Окруж­ность, по­стро­ен­ная на ме­ди­а­не BM рав­но­бед­рен­но­го тре­уголь­ни­ка ABC как на диа­мет­ре, вто­рой раз пе­ре­се­ка­ет ос­но­ва­ние BC в точке K.

а) До­ка­жи­те, что от­ре­зок

BK боль­ше от­рез­ка CK.

б) Пусть ука­зан­ная окруж­ность пе­ре­се­ка­ет сто­ро­ну AB в точке N. Най­ди­те AB, если BK = 18 и BN = 17.

 

За­да­ние 16 № 509823

 

Аналоги к заданию № 509823: 511600

 

Источник: ЕГЭ по математике — 2015. До­сроч­ная волна, ре­зерв­ный день (часть С).

Вневписанная окружность:

Пря­мые, со­дер­жа­щие ка­те­ты AC и CB пря­мо­уголь­но­го тре­уголь­ни­ка АСВ, яв­ля­ют­ся об­щи­ми внут­рен­ни­ми ка­са­тель­ны­ми к окруж­но­стям ра­ди­у­сов 2 и 4.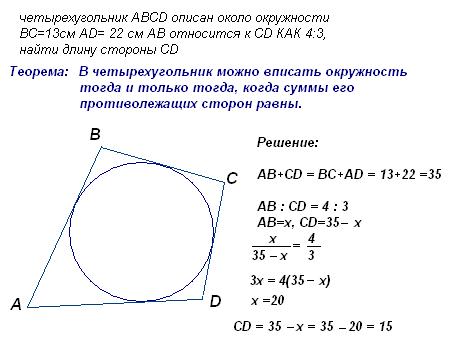

Пря­мая, со­дер­жа­щая ги­по­те­ну­зу АВ, яв­ля­ет­ся их общей внеш­ней ка­са­тель­ной.

а) До­ка­жи­те, что длина от­рез­ка внут­рен­ней ка­са­тель­ной, про­ве­ден­ной из вер­ши­ны остро­го угла тре­уголь­ни­ка до одной из окруж­но­стей, равна по­ло­ви­не пе­ри­мет­ра тре­уголь­ни­ка АСВ.

б) Най­ди­те пло­щадь тре­уголь­ни­ка АСВ.

 

За­да­ние 16 № 505568

 

Аналоги к заданию № 505568: 511412

Основные формулы о вписанной и вневписанной окружности

Внев­пи­сан­ной окруж­но­стью тре­уголь­ни­ка на­зы­ва­ет­ся окруж­ность, ка­са­ю­ща­я­ся одной сто­ро­ны тре­уголь­ни­ка и про­дол­же­ний двух дру­гих его сто­рон. Ра­ди­у­сы двух внев­пи­сан­ных окруж­но­стей пря­мо­уголь­но­го тре­уголь­ни­ка равны 7 и 17. Най­ди­те рас­сто­я­ние между их цен­тра­ми.

 

За­да­ние 16 № 500964

 

Аналоги к заданию № 500964: 511349

Угол C тре­уголь­ни­ка ABC равен 60°, D — от­лич­ная от A точка пе­ре­се­че­ния окруж­но­стей, по­стро­ен­ных на сто­ро­нах AB и AC как на диа­мет­рах.

Из­вест­но, что DB : DC = 1 : 3. Най­ди­те угол A.

 

За­да­ние 16 № 500410

 

Аналоги к заданию № 500410: 502025 502056 503323 503363 511343

В пря­мо­уголь­ной траеп­ции ABCD с пря­мым углом при вер­ши­не A рас­по­ло­же­ны две окруж­но­сти. Одна из них ка­са­ет­ся бо­ко­вых сто­рон и боль­ше­го ос­но­ва­ния AD, вто­рая — бо­ко­вых сто­рон, мень­ше­го ос­но­ва­ния BC и пер­вой окруж­но­сти.

а) Пря­мая, про­хо­дя­щая через цен­тры окруж­но­стей, пе­ре­се­ка­ет ос­но­ва­неи AD в точке

P. До­ка­жи­те, что

б) Най­ди­те пло­щадь тра­пе­ции, если ра­ди­у­сы окруж­но­стей равны 3 и 1.

 

За­да­ние 16 № 514373

 

 

Источник: За­да­ния 16 (С4) ЕГЭ 2015

Показать решение
 

 

24

Диа­го­на­ли AC и BD четырёхуголь­ни­ка ABCD, впи­сан­но­го в окруж­ность, пе­ре­се­ка­ет­ся в точке P, причём BC = CD.

а) До­ка­жи­те, что

б) Най­ди­те пло­щадь тре­уголь­ни­ка COD, где O — центр окруж­но­сти, впи­сан­ной в тре­уголь­ник

ABD, если до­пол­ни­тель­но из­вест­но, что BD — диа­метр опи­сан­ной около четырёхуголь­ни­ка ABCD окруж­но­сти, AB = 6, а

 

За­да­ние 16 № 514374

 

 

Источник: За­да­ния 16 (С4) ЕГЭ 2015

Пло­щадь тра­пе­ции ABCD равна 810. Диа­го­на­ли пе­ре­се­ка­ют­ся в точке O. От­рез­ки, со­еди­ня­ю­щие се­ре­ди­ну P ос­но­ва­ния AD с вер­ши­на­ми B и C, пе­ре­се­ка­ют­ся с диа­го­на­ля­ми тра­пе­ции в точ­ках M и N. Най­ди­те пло­щадь тре­уголь­ни­ка

MON, если одно из ос­но­ва­ний тра­пе­ции вдвое боль­ше дру­го­го.

За­да­ние 16 № 486002

 

Аналоги к заданию № 486002: 507369 511422 507358

 

Источник: МИОО: Ди­а­гно­сти­че­ская ра­бо­та по ма­те­ма­ти­ке 01. 03.2012 ва­ри­ант 2. (Часть С)

 

Показать решение

Пря­мая, про­хо­дя­щая через вер­ши­ну В, пря­мо­уголь­ни­ка ABCD, пер­пен­ди­ку­ляр­ная диа­го­на­ли АС и пе­ре­се­ка­ет сто­ро­ну 

АD в точке M, рав­но­уда­лен­ной от вер­шин В и D. 

а) До­ка­жи­те, что ∠ABM = ∠DBC = ∠MBD.

б) Най­ди­те рас­сто­я­ние от точки О, точки пе­ре­се­че­ния диа­го­на­лей, до от­рез­ка СМ, если BC = 42.

 

За­да­ние 16 № 513915

 

 

Источник: ЕГЭ по ма­те­ма­ти­ке — 2016. До­сроч­ная волна, ре­зерв­ный день (часть С).

Показать решение
 

 

51

Пря­мая, про­хо­дя­щая через вер­ши­ну В, пря­мо­уголь­ни­ка ABCD, пер­пен­ди­ку­ляр­ная диа­го­на­ли АС и пе­ре­се­ка­ет сто­ро­ну АD в точке 

M, рав­но­уда­лен­ной от вер­шин В и D.  

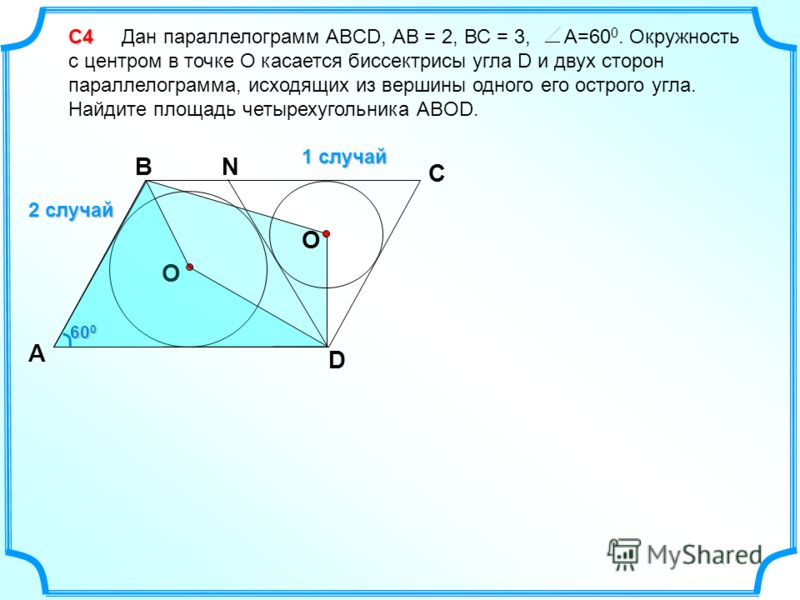
а) До­ка­жи­те, что BM и ВD делят угол В на три рав­ных угла.

б) Най­ди­те рас­сто­я­ние от точки пе­ре­се­че­ния диа­го­на­лей пря­мо­уголь­ни­ка ABCD до пря­мой СМ, если

 

За­да­ние 16 № 513922

 

 

Источник: ЕГЭ по ма­те­ма­ти­ке — 2016. До­сроч­ная волна, ре­зерв­ный день, вариант А. Ларина (часть С).

Показать решение

Формула длины медианы

 

Ме­ди­а­ны АА1 и ВВ

1 и CC1 тре­уголь­ни­ка ABC пе­ре­се­ка­ют­ся в точке М. Точки А2, В2 и С2 — се­ре­ди­ны от­рез­ков MA, MB и МС со­от­вет­ствен­но.

а) До­ка­жи­те, что пло­щадь ше­сти­уголь­ни­ка A1B2C1A2B1C2 вдвое мень­ше пло­ща­ди тре­уголь­ни­ка ABC.

б) Най­ди­те сумму квад­ра­тов всех сто­рон этого ше­сти­уголь­ни­ка, если из­вест­но, что АВ = 4, ВС = 7 и АС = 8.

 

За­да­ние 16 № 507204

 

Аналоги к заданию № 507204: 511416

Ме­ди­а­ны AA1, BB1 и CC1 тре­уголь­ни­ка ABC пе­ре­се­ка­ют­ся в точке M. Точки A2, B2 и C2 — се­ре­ди­ны от­рез­ков MA, MB и MC со­от­вет­ствен­но.

а) До­ка­жи­те, что пло­щадь ше­сти­уголь­ни­ка A1B2C1A2B1C2 вдвое мень­ше пло­ща­ди тре­уголь­ни­ка ABC.

б) Най­ди­те сумму квад­ра­тов всех сто­рон этого ше­сти­уголь­ни­ка, если из­вест­но, что AB = 5, BC = 8 и AC = 10.

 

За­да­ние 16 № 507510

 

Аналоги к заданию № 507510: 511440

 

Источник: МИОО: Ди­а­гно­сти­че­ская ра­бо­та по ма­те­ма­ти­ке 12. 12.2013 с решениями: ва­ри­ант МА10301 (Часть С).

Ме­ди­а­ны AA1, BB1 и CC1 тре­уголь­ни­ка ABC пе­ре­се­ка­ют­ся в точке M. Из­вест­но, что AC = 3MB.

а) До­ка­жи­те, что тре­уголь­ник ABC пря­мо­уголь­ный.

б) Най­ди­те сумму квад­ра­тов ме­ди­ан AA1 и CC1, если из­вест­но, что AC = 12.

За­да­ние 16 № 508974

 

 

Источник: СтатГрад: Ди­а­гно­сти­че­ская ра­бо­та по ма­те­ма­ти­ке 05.03.2015 ва­ри­ант МА10309.

Ме­ди­а­ны AA1, BB1 и CC1 тре­уголь­ни­ка ABC пе­ре­се­ка­ют­ся в точке M. Из­вест­но, что AC = 3MB.

а) До­ка­жи­те, что тре­уголь­ник ABC пря­мо­уголь­ный.

б) Най­ди­те сумму квад­ра­тов ме­ди­ан AA1 и CC1, если из­вест­но, что AC = 10.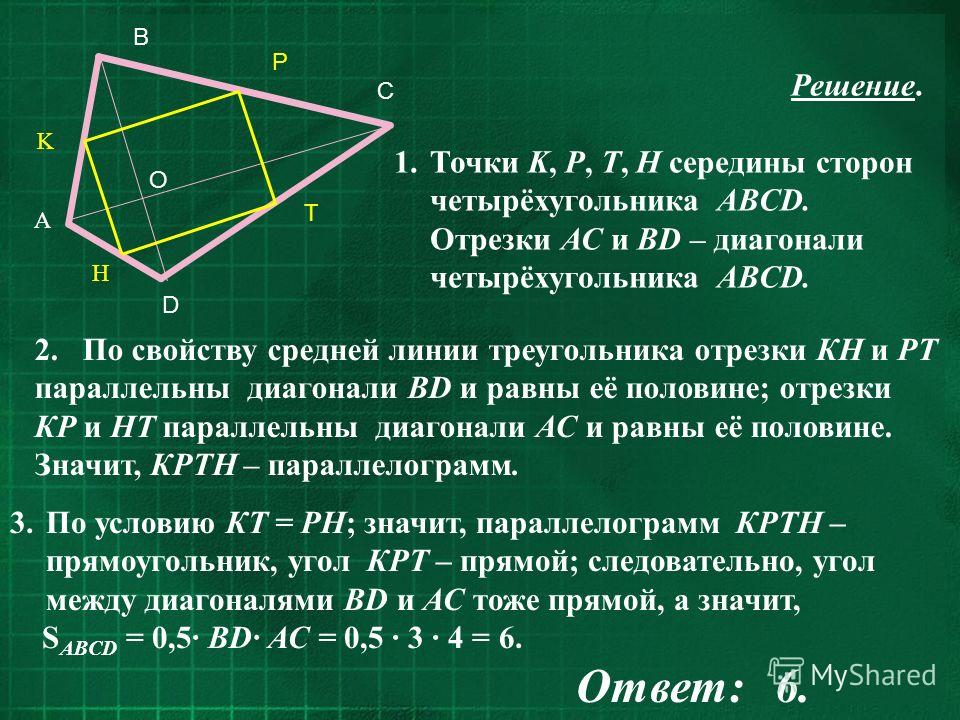

 

За­да­ние 16 № 509003

 

 

Источник: СтатГрад: Ди­а­гно­сти­че­ская ра­бо­та по ма­те­ма­ти­ке 05.03.2015 ва­ри­ант МА10310.

Теорема о сумме противопложных углов вписанного четырехугольника, теорема синусов

На ги­по­те­ну­зу AB пря­мо­уголь­но­го тре­уголь­ни­ка ABC опу­сти­ли вы­со­ту CH . Из точки H на ка­те­ты опу­сти­ли пер­пен­ди­ку­ля­ры HK и HE.

а) До­ка­жи­те, что точки A, B, K и E лежат на одной окруж­но­сти.

б) Най­ди­те ра­ди­ус этой окруж­но­сти, если AB = 24, CH = 7.

 

За­да­ние 16 № 504567

 

 

Источник: МИОО: Ди­а­гно­сти­че­ская ра­бо­та по ма­те­ма­ти­ке 13.03.2014 ва­ри­ант МА10506.

 

На ги­по­те­ну­зу AB пря­мо­уголь­но­го тре­уголь­ни­ка ABC опу­сти­ли вы­со­ту CH . Из точки H на ка­те­ты опу­сти­ли пер­пен­ди­ку­ля­ры HK и HE.

а) До­ка­жи­те, что точки A, B, K и E лежат на одной окруж­но­сти.

б) Най­ди­те ра­ди­ус этой окруж­но­сти, если AB = 12, CH = 5.

 

За­да­ние 16 № 504546

 

Аналоги к заданию № 504546: 511390

 

Источник: МИОО: Ди­а­гно­сти­че­ская ра­бо­та по ма­те­ма­ти­ке 13.03.2014 ва­ри­ант МА10505

Теорема об угле между касательной и хордой

Сто­ро­ны KN и LM тра­пе­ции KLMN па­рал­лель­ны, пря­мые LM и MN — ка­са­тель­ные к окруж­но­сти, опи­сан­ной около тре­уголь­ни­ка KLN.

а) До­ка­жи­те, что тре­уголь­ни­ки LMN и KLN по­доб­ны.

б) Най­ди­те пло­щадь тре­уголь­ни­ка KLN, если из­вест­но, что KN = 3, а ∠LMN = 120°.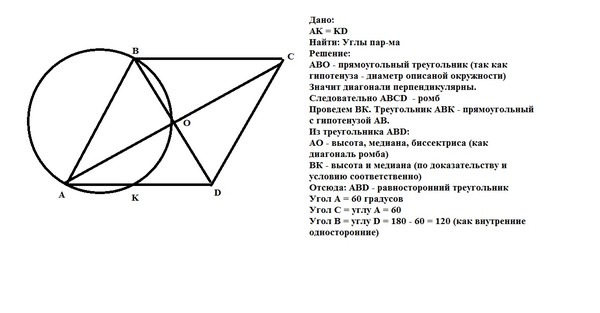

 

За­да­ние 16 № 513430

 

Аналоги к заданию № 513430: 513449 514189 513627

 

 

ABCD — прямоугольник. Окружность, проходящая через вершину C, касается сторон AB и AD в точках M и N соответственно. Если расстояние линии MN от вершины C равно P единицам, то площадь прямоугольника ABCD равна

CENGAGE ENGLISH-CONIC SECTIONS-All Questions

20 видео

РЕКЛАМА

Ab Padhai karo bina ads ke

Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!

Ответить

Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.

Похожие видео

ABCD — прямоугольник. Окружность, проходящая через вершину C, касается сторон AB и AD в точках M и N соответственно. Если расстояние от линии MN до вершины C равно P единиц, то площадь прямоугольника ABCD is

Окружность проходит через вершину P и касается QR и RS в точках A и B прямоугольника PQRS. Если длина перпендикуляра из P на AB равна √7, то площадь прямоугольника PQRS равна.

ABCD — прямоугольник со сторонами AB=p,BC=q. Если AB и AD принять за отрицательные направления осей координат, то уравнение окружности, описывающей прямоугольник, равно

8133813

ABCD — прямоугольник со сторонами AB=p,BC=q. Если AB и AD взяты как отрицательные направления координатных осей, то уравнение окружности, описывающей прямоугольник, будет

8187967

. и касаясь стороны компакт-диска. Нарисована другая окружность, проходящая через В и С и касающаяся стороны AD. Пусть r1 и r2 будут радиусами этих двух окружностей соответственно.
r1r2 равно

14948769

Пусть ABCD – прямоугольник с AB=a и BC=b, и нарисована окружность, проходящая через A и B и касающаяся стороны CD. Нарисована другая окружность, проходящая через точки B и C и касающаяся стороны AD. Пусть r1 и r2 будут радиусами этих двух окружностей соответственно.
Минимальное значение (r1+r2 равно

14948771

Текст Решение

Окружность, проходящая через вершину C прямоугольника ABCD и касающаяся его сторон AB и AD в точках M и N соответственно.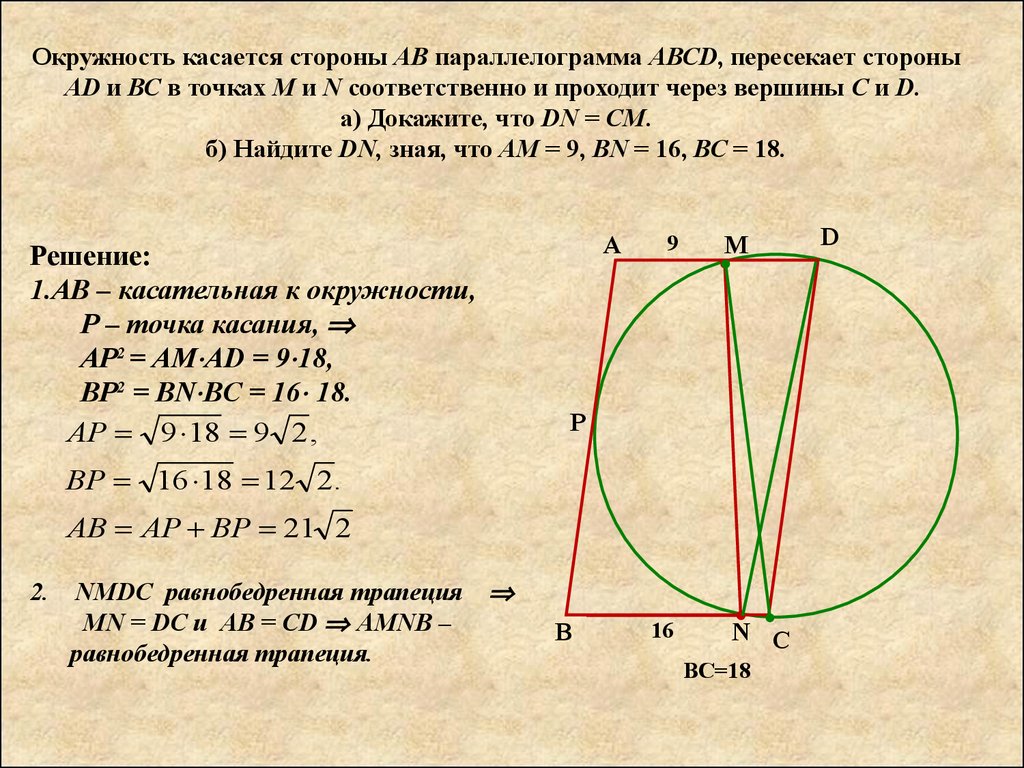 Если расстояние от C до отрезок MN равен 5 единицам, то найдите площадь прямоугольника ABCD.

51725423

Текст Решение

Окружность касается прямоугольника ABCD со сторонами 2a и 2b в точках M и N по сторонам AB и AD соответственно, она также проходит через точку C. Если перпендикулярное расстояние прямой MN от точек C составляет 6 см. Тогда значение AB равно ____

2801

Текстовое решение

एक आयत abcd की भुजा ab, रेखा y = x के सम सम एक है तथ तथ शी शी शी a, b तथा d क्रमशः ा y = 1, x = 2 तथ x तथ तथ प तथ तथ तथ तथ तथ प क कшить ेख ेख ेख है है है तथ शी शी तथ क g क Как स्थित है। तब, शीर्ष C का बिन्दुपथ है

400485775

Текст Решение

Окружность, проходящая через вершину C прямоугольника ABCD и касающаяся его сторон AB и AD в точках M и N соответственно. Если расстояние от C до отрезка MN равно 5 единицам, то найдите площадь прямоугольника ABCD.

642548518

एक वृत्त, आयत abcd की भुजाओं ab तथा ad को क्रमशः p तथा q पर सшить क क है औшить शी तथ से गुजшком स स गुज गुज स गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज गुज से गुज गुज से से से से से से से से से से से से गुज से से प प गुज प प गुज गुज प प यदि जीवा PQ से C की दूरी 5 इकाई है, तो आयत का क्षेत्रफल है —

643176214

Текст Решение

ABCD — прямоугольник.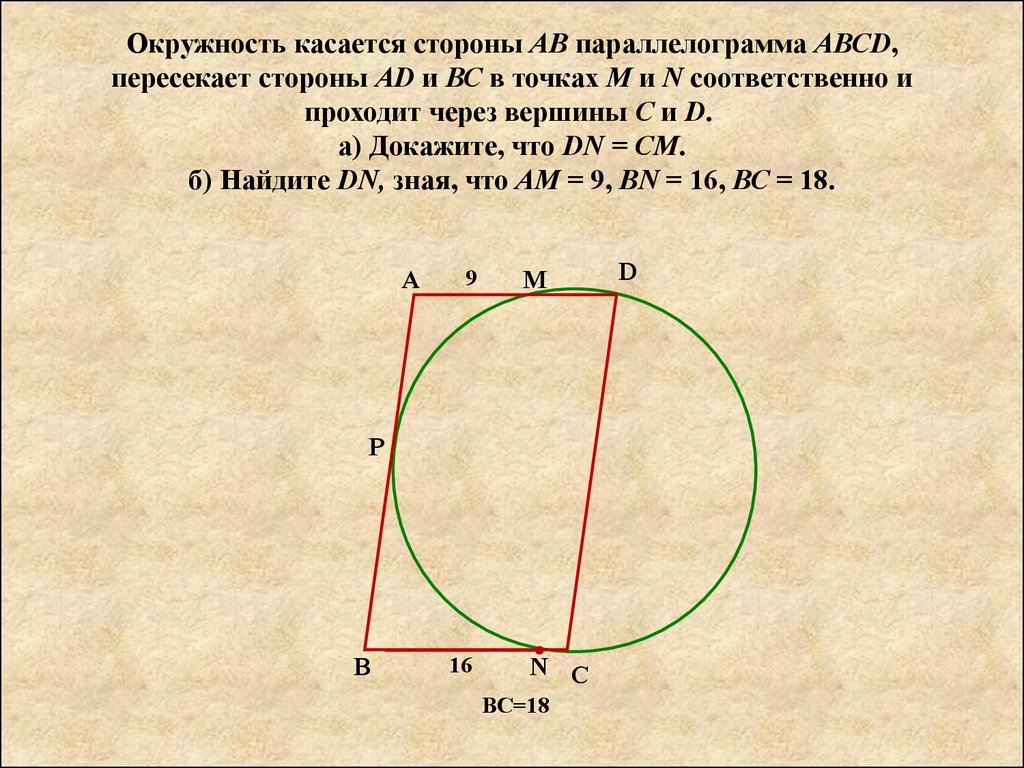 Окружность, проходящая через вершину C, касается сторон AB и AD в точках M и N соответственно. Если расстояние линии MN от вершины C равно P единицам, то площадь прямоугольника ABCD равна

645276369

ABCD. Окружность, проходящая через вершину C, касается сторон AB и AD в точках M и N соответственно. Если расстояние l линии MN от вершины C равно P единицам, то площадь прямоугольника ABCD равна

646276086

На данном рисунке в прямоугольнике ABCD есть полуокружность. Между вершиной B и полуокружностью проведена окружность. Каково будет отношение площадей круга и полукруга?

646465270

Пусть ABCD – прямоугольник с AB=a и BC=b, и нарисована окружность, проходящая через A и B и касающаяся стороны CD. Нарисована другая окружность, проходящая через В и С и касающаяся стороны AD. Пусть r1 и r2 будут радиусами этих двух окружностей соответственно.
r1r2 равно

646687849

Математические задачи: Построить — вопрос № 5974, задачи на построение по геометрии

Построить ромб ABCD, если длина диагонали AC равна 6 см, а диагонали BD 8 см.

Правильный ответ:

Вы нашли ошибку или неточность? Не стесняйтесь

написать нам

. Спасибо!

Советы по использованию связанных онлайн-калькуляторов

См. также наш калькулятор прямоугольного треугольника.
См. также наш калькулятор тригонометрического треугольника.

You need to know the following knowledge to solve this word math problem:

  • planimetrics
  • Pythagorean theorem
  • right triangle
  • triangle
  • rhombus
  • diagonal
Themes, topics:
  • задачи на построение геометрии
Уровень задачи:
  • практика для 13-летних
  • практика для 14-летних

 

Рекомендуем посмотреть это обучающее видео по этой математической задаче: video1   video2   video3

  • Построить 5333
    Построить ромб ABCD, если AB = 5 см, BD = 6 см и AC = 3 см
  • Построить ромб 30 Построить ромб ABCD по длине диагонали | переменный ток | = 8 см, радиус вписанной окружности r = 1,5 см
  • Постройте 10921
    Постройте ромб ABCD так, чтобы его диагональ BD была равна 8 см, а расстояние от вершины В до линии AD было равно 5 см. Указать все варианты
  • Ромб
    Вычислите длину диагонали AC ромба ABCD, если его периметр равен 84 дм, а другая диагональ BD имеет длину 20 дм.
  • Четырехугольник 27693
    Постройте четырехугольник ABCD с диагоналями AC = e 7 см, BD = f = 6,2 см, d = 4,3 см, a = 5,3 см и β = 125 °
  • Построение ромба
    Постройте ромб ABCD, если его диагональ AC= 9 см, а сторона АВ = 6 см. Впишите в него окружность, касаясь всех сторон.
  • Диагонали ромба
    Найдите длину диагонали AC ромба ABCD, если его периметр P = 112 дм, а вторая диагональ BD имеет длину 36 дм.
  • Постройте 11511
    Постройте ромб ABCD так, чтобы его диагональ BD была равна 8 см, а расстояние от вершины В до линии AD было равно 5 см. Укажите все опции
  • Построение ромба
    Построение параллелограмма (ромба) ABCD, | АБ | = 4 см альфа = 30° и | БД | = 5 см.
  • Построить 80719
    Построить прямоугольник ABCD, если a = 8 см, а длина диагонали AC равна 13 см. Измерьте длину сторон прямоугольника.
  • Четырехугольник 3262
    Постройте четырехугольник ABCD с размерами AB, BC, AC, BD и углом d = CDA.
  • Диагонали 2
    Диагонали AC и BD прямоугольника ABCD пересекаются в точке O. Если OA=4см, найдите AC и BD.
  • Окружность 16933
    В ромбе ABCD угол BAD равен 60°; длина диагонали BD равна 7 см. Вычислите окружность алмаза.
  • Диагонали
    Диагонали в ромбе ABCD имеют длину 6 см и 8 см. Каков периметр этого алмаза?
  • Вычислить 2556
    Вычислить размер плеча b трапеции ABCD, если a = 12 см, c = 4 см, d (AC) = d (BC) и площадь S (треугольник ABC) = 9см кв.
  • Построение 30121
    Точка B является вершиной прямоугольника ABCD. Диагональ BD этого прямоугольника лежит на прямой p. Точка X — внутренняя точка стороны AD прямоугольника ABCD, а точка Y — внутренняя точка стороны CD. Постройте недостающие вершины D, A и C прямоугольника AB
  • Диагонали трапеции
    Дана трапеция ABCD с основаниями | АБ | = 12 см, |CD| = 8 см.