Три тела одинаковой массы по 3 кг каждое совершали движения уравнения: Три тела одинаковой массы по 2 кг каждое совершали движения. Уравнения проекции перемещения представлены в таблице. На каком графике представлена зависимость проекции силы от времени, действующей на каждое тело?

Контрольно-измерительные материалы по физике по разделу «Механика» (10 класс, 1 курс на базе 9 класса)

КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ МАТЕРИАЛЫ

по дисциплине «Физика» (I семестр)

Разработаны преподавателем Моисеевой А.Ф.

Октябрьский 2014 г.

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

1. Назначение заданий

Контрольно–измерительные материалы по дисциплине «Физика» для студентов I курса специальности для всех специальностей среднего профессионального образования.

2. Вид контроля – текущий (контрольный срез) по разделу «Механика»

3. Документы, определяющие содержание заданий.

Содержание заданий соответствует государственным требованиям к минимуму содержания и уровню подготовки по дисциплине «Физика» по разделу «Механика».

4. Система оценивания выполнения отдельных заданий и работы в целом.

Блок	Количество баллов за одно задание	Количество заданий	Максимальное количество баллов
Часть А (1-8)	1	8	8
Часть В (В1)	3	1	3
Часть С (С1,С2)	2	2	4
Общее число баллов			15

Критерии оценки работ

Оценка

Количество набранных баллов

менее 8

8 — 11

12-13

более 14

5. Инструкция по выполнению работы.

На выполнение работы по отводится 45 минут.

Работа состоит из трех блоков:

часть А — 8 тестовых вопросов с выбором одного правильного ответа,

часть В — задача на сопоставление,

часть С — 2 задачи С1, С2

Всего в работе 11 заданий.

При выполнении работы будьте внимательны, выполняйте задания в том порядке, в котором они даны. Для экономии времени пропускайте задание, которое не удается выполнить сразу, и переходите к следующему. К пропущенному заданию вы сможете вернуться после выполнения всей работы, если останется время.

Баллы, полученные вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.

6. Оформление работы.

При выполнении работы учащиеся вносят ответы на вопросы части А,В в таблицу для ответов; решение задач частей С приводят в полном объеме.

Часть А

Часть В

А	Б	В

Часть С

Оформить и решить задачу.

7. Таблица верных ответов:

№ задания	1вариант	2вариант	3вариант	4 вариант
А1	1	3	2	4
А 2	1	3	3	3
А 3	2	2	1	3
А 4	3	2	1	4
А 5	1	2	3	3
А 6	2	2	4	3
А 7	2	3	1	4
А8	2	1	4	3
В 1	324	234	423	321
С 1	5с, 50м	4с, 64м	5с, 37,5м	3с, 18м
С 2	30 м/с	2,5 м/с	20 м/с	0

Контрольно–измерительные материалы по дисциплине «Физика» для студентов

I курса

Оценка заданий и работы в целом производится по баллам.

Инструкция по выполнению работы.

На выполнение работы по отводится 45 минут.

Работа состоит из трех блоков:

часть А — 8 тестовых вопросов с выбором одного правильного ответа,

часть В — задача на сопоставление,

часть С — 2 задачи С1, С2

Всего в работе 11 заданий.

Блок	Количество баллов за одно задание	Количество заданий	Максимальное количество баллов
Часть А (1-8)	1	8	8
Часть В (В1)	3	1	3
Часть С (С1,С2)	2	2	4
Общее число баллов			15

Критерии оценки работ

Оценка

Количество набранных баллов

менее 8

8- 11

12-13

более 14

Баллы, полученные вами за выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов

1вариант

Часть А

А1. Плот равномерно плывет по реке со скоростью 6 км/ч. Человек движется поперек плота со скоростью 8 км/ч. Чему равна скорость человека в системе отсчета, связанной с берегом?

1) 10 км/ч2) 7 км/ч3) 14 км/ч4) 2 км/ч

А2. На рисунке представлен график зависимости скорости υ автомобиля от времени t. Найдите путь, пройденный автомобилем за 1 с.

1) 5 м 2) 20 м 3) 10 м 4) 35 м

А3. Зависимость пути от времени для прямолинейно движущегося тела имеет вид:

s(t)=2t+t², где все величины выражены в СИ. Ускорение тела равно

1) 1м/c²2) 2м/c²3) 3м/c²4) 6м/c²

А4. На тело массой 2кг действует сила 6Н. Чему равно ускорение тела?

1) 1м/c²2) 2м/c²3) 3м/c²4) 6м/c²

А5. Жесткость пружины 500Н/м. К пружине подвесили груз 2кг. На сколько удлинилась пружина?(g=10м/с²)

1) 0,04 м 2) 0,08 м 3) 0,1 м 4) 0,5 м

А6. Тело массой 10кг поднимают на высоту 5м. Чему равна работа этой силы?

1) 250 Дж 2) 500 Дж 3) 100 Дж 4) 1000 Дж

А7. На рисунке показан график колебаний струны. Согласно этому графику амплитуда колебаний равна

1) 0,1 см 2)0,2 см 3)0,4см 4)4см

А, см

0,2

0,1

1 2 3 4 5

-0,1

-0,2

А8. Импульс тела в системе СИ имеет размерность

1) кг · м² /с 2) кг · м /с 3) кг · м /с² 4) кг · м² /с²

Часть В.

Используя условие задачи, установите соответствия уравнений из левого столбца таблицы с их графиками в правом столбце.

В1

Три тела одинаковой массы по 3 кг каждое совершали движения. Уравнения проекции перемещения представлены в таблице. На каком графике представлена зависимость проекции силы от времени, действующей на каждое тело?

Часть С

Решите и оформите задачи

С1. Зависимость скорости от времени при торможении автомобиля задается формулой n(t)= 20-4t (величины выражены в СИ). Рассчитайте время, через которое остановится автомобиль, и путь, пройденный за время торможения.

С2. С какой скоростью должна лететь хоккейная шайба массой 160г, чтобы её импульс был равен импульсу пули массой 8г, летящей со скоростью 600 м/с.

2 вариант

Часть А

А1. По прямому шоссе в одном направлении движутся два автомобиля со скоростями

30 м/с и 40 м/с. Их относительная скорость по модулю равна

1) 0 м/с 2) 10 м/с 3) 50 м/с 4) 70 м/с

А2. На рисунке представлен график зависимости скорости υ автомобиля от времени t. Найдите путь, пройденный автомобилем с 1-2 с.

1) 5 м 2) 20 м 3) 10 м 4) 35 м

А3. Зависимость пути от времени для прямолинейно движущегося тела имеет вид:

s(t)=3t-t², где все величины выражены в СИ. Модуль ускорения тела равен

1) 1 м/c²2) 2 м/c²3) 3 м/c²4) 6 м/c²

А4. На тело массой 3кг действует сила 6Н. Чему равно ускорение тела?

1) 1м/c²2) 2м/c²3) 3м/c²4) 6м/c²

А5. Жесткость пружины 500Н/м. К пружине подвесили груз 4кг. На сколько удлинилась пружина?(g=10м/с²)

1)0,04м 2)0,08м 3) 0,1м 4)0,5м

А6. Тело массой 1кг поднимают на высоту 50м. Чему равна работа этой силы?

1) 250 Дж 2) 500 Дж 3) 100 Дж 4) 1000 Дж

А7. На рисунке показан график колебаний струны. Согласно этому графику амплитуда колебаний равна

1) 0,1 см 2)0,2 см 3)0,4см 4)0,8см

А, см

0,4

0,2

1 2 3 4 5

-0,2

-0,4

А8. Механическая работа в системе СИ имеет размерность

1) Дж 2) кг · м /с 3) Вт 4) Н

Часть В.

В1

Три тела одинаковой массы по 2 кг каждое совершали движения. Уравнения проекции перемещения представлены в таблице. На каком графике представлена зависимость проекции силы от времени, действующей на каждое тело?

Часть С

Решите и оформите задачи

С1. Зависимость скорости от времени при торможении автомобиля задается формулой n(t)= 32-8t (величины выражены в СИ). Рассчитайте время, через которое остановится автомобиль, и путь, пройденный за время торможения.

С2. С лодки массой 200 кг, движущейся со скоростью 3 м/с, прыгает мальчик массой 50 кг в горизонтальном направлении с носа по ходу движения со скоростью 5 м/с относительно лодки. Какова скорость лодки после прыжка мальчика?

3вариант

Часть А

А1. По прямому шоссе в одном направлении движутся два автомобиля со скоростями

30 м/с и 50 м/с. Их относительная скорость по модулю равна

1) 0 м/с 2) 20 м/с 3) 40 м/с 4) 80 м/с

А2. На рисунке представлен график зависимости скорости υ автомобиля от времени t. Найдите путь, пройденный автомобилем со 2-3 с.

1) 5 м 2) 20 м 3) 10 м 4) 35 м

А3. Зависимость пути от времени для прямолинейно движущегося тела имеет вид:

s(t)=3t+0,5t², где все величины выражены в СИ. Ускорение тела равно

1) 1 м/c²2) 2 м/c²3) 3 м/c²4) 6 м/c²

А4. На тело массой 6кг действует сила 6Н. Чему равно ускорение тела?

1) 1м/c²2) 2м/c²3) 3м/c²4) 36м/c²

А5. Жесткость пружины 500Н/м. К пружине подвесили груз 5кг. На сколько удлинилась пружина?(g=10м/с²)

1) 0,04м 2)0,08м 3) 0,1м 4)0,5м

А6. Тело массой 5кг поднимают на высоту 30м. Чему равна работа этой силы?

1) 150 Дж 2) 500 Дж 3) 100 Дж 4) 1500 Дж

А7. На рисунке показан график колебаний струны. Согласно этому графику амплитуда колебаний равна

1) 0,1 см 2)0,2 см 3)0,4см 4)4см

А, см

0,1

0,05

1 2 3 4 5

-0,05

-0,1

А8. Сила в системе СИ имеет размерность

1) Дж 2) кг · м /с 3) Вт 4) Н

Часть В.

В1

Три тела одинаковой массы по 4 кг каждое совершали движения. Уравнения проекции перемещения представлены в таблице. На каком графике представлена зависимость проекции силы от времени, действующей на каждое тело?

Часть С

Решите и оформите задачи

С1. Зависимость скорости от времени при торможении автомобиля задается формулой n(t)= 15-3t (величины выражены в СИ). Рассчитайте время, через которое остановится автомобиль, и путь, пройденный за время торможения.

С2. С какой скоростью должна лететь хоккейная шайба массой 240г, чтобы её импульс был равен импульсу пули массой 8г, летящей со скоростью 600 м/с.

4 вариант

Часть А

А1. По прямому шоссе навстречу друг другу движутся два автомобиля со скоростями

30 м/с и 40 м/с. Их относительная скорость по модулю равна

1) 0 м/с 2) 10 м/с 3) 50 м/с 4) 70 м/с

А2. На рисунке представлен график зависимости скорости υ автомобиля от времени t. Найдите путь, пройденный автомобилем с3-5с.

1) 5 м 2) 20 м 3) 10 м 4) 35 м

А3. Зависимость пути от времени для прямолинейно движущегося тела имеет вид:

s(t)=8t-2t², где все величины выражены в СИ. Модуль ускорения тела равен

1) 1 м/c²2) 2 м/c²3) 4 м/c²4) 8 м/c²

А4. На тело массой 1кг действует сила 6Н. Чему равно ускорение тела?

1)1м/c²2) 2м/c²3) 3м/c²4) 6м/c²

А5. Жесткость пружины 500Н/м. К пружине подвесили груз 10кг. На сколько удлинилась пружина?(g=10м/с²)

1) 0,04м 2) 0,08м 3) 0,2м 4) 0,5м

А6. Тело массой 100 кг поднимают на высоту 5м. Чему равна работа этой силы?

1) 250 Дж 2) 500 Дж 3) 5000 Дж 4) 1000 Дж

А7. На рисунке показан график колебаний струны. Согласно этому графику амплитуда колебаний равна

1) 0,1 см 2)0,2 см 3)0,4см 4)0,8см

А, см

0,8

0,4

1 2 3 4 5

-0,4

-0,8

А8. Мощность в системе СИ имеет размерность

1) Дж 2) кг · м /с 3) Вт 4) Н

Часть В.

В1

Часть С

Решите и оформите задачи

С1. Зависимость скорости от времени при торможении автомобиля задается формулой n(t)= 12-4t (величины выражены в СИ). Рассчитайте время, через которое остановится автомобиль, и путь, пройденный за время торможения.

С2. Два шара массами m₁=1кг и m₂=2 кг скользят по гладкой горизонтальной поверхности навстречу друг другу со скоростями v₁= 4 м/с и v₂=2 м/с соответственно. Определить скорость шаров после неупругого соударения.

Три тела одинаковой массы по 2 кг каждое совершали движения. Уравнения проекции перемещения представлены в таблице.

На каком графике представлена зависимость проекции силы от времени, действующей на каждое тело?

Последние вопросы

Информатика
3 минуты назад
«Оаоланч, но аа» значение выражения, скажите пожалуйста
Українська мова
3 минуты назад
Поможіть прошу умаляю
Обществознание
3 минуты назад
в каких случаях идентификация с ролью и статусом и дистанцирование от роли и статуса приносит личности пользу, а в каком — вред? заполнить таблицу, добавить примеры
Литература
3 минуты назад
1. про що писали Ліна Костенко і Василь Симоненко
Українська мова
3 минуты назад
Скласти 4 речення, використовуючи різні за значенням прикметники (якісні,відносні,присвійні). Даю 50 балів. Я вже заливала це питання, але мені не відповіли.
Биология
3 минуты назад
Архегоній у мохлподібних :
Биология
3 минуты назад
Доповніть реченняКолір очей визначають…,які містяться в …Допоможіть будь ласка дам 50 балів . Дуже потрібно.
Математика
3 минуты назад
знайти ответ на этот пример 7. 7*5\7=
Литература
8 минут назад
Литература, помогите пожалуйста
Литература
8 минут назад
Литература Кр спасибо)
Обществознание
8 минут назад
Что из перечисленного можно отнести к земле как фактору производства?
Физика
8 минут назад
Вычислить недостающие данные переменного тока
Обществознание
8 минут назад
Выберите все верные суждения о государственной политике РФ в сфере занятости.
Информатика
8 минут назад
Помогите с задачей по информатике!
Математика
8 минут назад
сколько будет 18 разделить на 0,45 в столбик

Все предметы

Выберите язык и регион

English

United States

Polski

Polska

Português

Brasil

English

India

Türkçe

Türkiye

English

Philippines

Español

España

Bahasa Indonesia

Indonesia

Русский

Россия

How much to ban the user?

1 hour 1 day 100 years

Моделирование задачи трех тел в классической механике с помощью Python | by Gaurav Deshmukh

Обзор основ гравитации, решатель odeint в Scipy и трехмерное построение в Matplotlib автор Лю Цисинь.

В нем он описывает вымышленную инопланетную цивилизацию, живущую на планете Трисолярис, окруженной тремя звездами. Как вы думаете, насколько их существование будет отличаться от нашего из-за наличия трех звезд? Слепящее солнце? Постоянное лето? Как оказалось, нечто гораздо худшее.

Нам повезло, что мы живем в солнечной системе только с одной крупной звездой, поскольку это делает орбиту звезды (нашего Солнца) предсказуемой. Увеличьте количество звезд до двух, и система по-прежнему останется стабильной. У него есть то, что мы называем аналитическим решением — то есть мы можем решить описывающие его уравнения и получить функцию, которая дает время эволюции системы с точностью от 1 секунды до миллиона лет.

Однако, когда вы добавляете третье тело, происходит нечто экстраординарное. Система становится хаотичной и крайне непредсказуемой. Он не имеет аналитического решения (за исключением нескольких особых случаев), а его уравнения можно решить только численно на компьютере. Они могут резко переходить из стабильного состояния в нестабильное и наоборот. Трисолярианцы, живущие в таком хаотичном мире, развили способность «обезвоживать» себя и впадать в спячку в «хаотические эпохи» и просыпаться и мирно жить в «стабильные эпохи».

Интригующая визуализация звездной системы в книге вдохновила меня на то, чтобы прочитать о задачах класса n тел в гравитации и о численных методах, используемых для их решения. Эта статья затрагивает несколько основных концепций гравитации, необходимых для понимания проблемы, и численных методов, необходимых для решения уравнений, описывающих системы.

В этой статье вы узнаете о реализации следующих инструментов и концепций:

Решение дифференциальных уравнений в Python с использованием 9Функция 0011 odeint в модуле Scipy .
Обезразмеривание уравнения
Создание трехмерных графиков в Matplotlib

2.1 Закон всемирного тяготения Ньютона

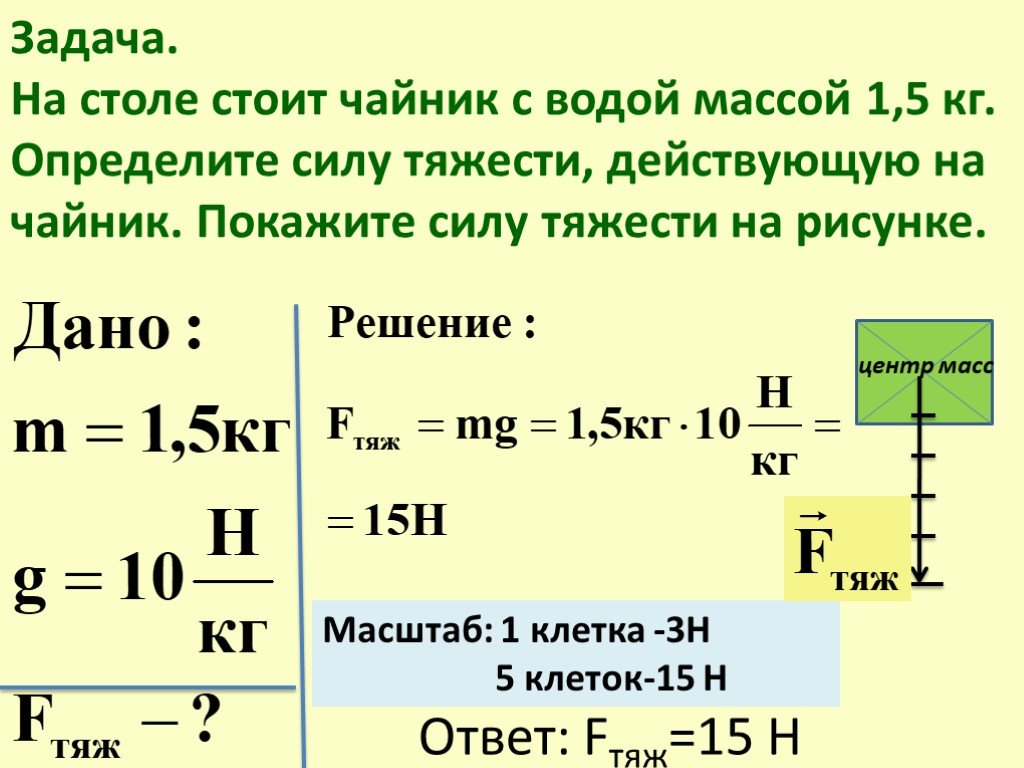
Закон тяготения Ньютона гласит, что между любыми двумя точечными массами существует сила притяжения (называемая силой гравитации), величина которого прямо пропорциональна произведению их масс и обратно пропорционально квадрату расстояния между ними. Приведенное ниже уравнение представляет этот закон в векторной форме.

Здесь G — универсальная гравитационная постоянная, m₁ и m₂ — массы двух объектов, а r — расстояние между ними. Единичный вектор направлен от тела м₁ к м₂ , и сила действует в том же направлении.

2.2 Уравнение движения

Согласно второму закону движения Ньютона результирующая сила, действующая на объект, вызывает результирующее изменение импульса объекта — проще говоря, сила равна массе, умноженной на ускорение . Итак, применяя приведенное выше уравнение к телу массой м₁ , мы получаем следующее дифференциальное уравнение движения тела.

Обратите внимание, что мы разложили единичный вектор как вектор r , разделенный на его величину |r| , таким образом увеличивая степень члена r в знаменателе до 3.

Теперь у нас есть дифференциальное уравнение второго порядка , которое описывает взаимодействие между двумя телами под действием силы тяжести. Чтобы упростить его решение, мы можем разбить его на два дифференциальных уравнения первого порядка.

Ускорение объекта — это изменение скорости объекта во времени, поэтому дифференциал второго порядка положения можно заменить дифференциалом первого порядка скорости . Точно так же скорость может быть выражена как дифференциал положения первого порядка.

Индекс i предназначен для тела, положение и скорость которого должны быть рассчитаны, тогда как индекс j для другого тела, которое взаимодействует с телом i . Таким образом, для системы двух тел мы будем решать два набора этих двух уравнений.

2.3 Центр масс

Еще одно полезное понятие, о котором следует помнить, это центр масс системы. Центр масс — это точка, в которой сумма всех моментов масс системы равна нулю — проще говоря, вы можете представить ее как точку, в которой вся масса системы уравновешена.

Существует простая формула для нахождения центра масс системы и ее скорости. Он включает взвешивание средних значений векторов положения и скорости.

Прежде чем моделировать систему из трех тел, давайте сначала смоделируем систему из двух тел, понаблюдаем за ее поведением, а затем расширим код для работы с тремя телами.

3.1 Звездная система Альфа Центавра

Известным реальным примером системы из двух тел является, пожалуй, звездная система Альфа Центавра . Он содержит три звезды — Альфа Центавра A, Альфа Центавра B и Альфа Центавра C (обычно называемая Проксима Центавра). Однако, поскольку масса Проксимы Центавра пренебрежимо мала по сравнению с двумя другими звездами, Альфа Центавра считается двойной звездной системой . Здесь важно отметить, что все тела, рассматриваемые в системе из n тел, имеют одинаковые массы. Итак, Солнце-Земля-Луна не является системой трех тел, так как они не имеют эквивалентных масс, а Земля и Луна не оказывают существенного влияния на путь Солнца.

Двойная звездная система Альфа Центавра, полученная Джоном Колозимо из обсерватории Параналь в Чили

3.2 Обезразмеривание

Прежде чем мы начнем решать эти уравнения, мы должны сначала обезразмерить их. Что это значит? Мы преобразуем все величины в уравнении (например, положение , скорость, масса и т. д.), которые имеют размеры (например, м, м/с, кг соответственно) в безразмерные величины, имеющие величины, близкие к единице. Причины для этого:

В дифференциальном уравнении разные члены могут иметь разный порядок величины (от 0,1 до 10³⁰). Такое огромное расхождение может привести к медленной сходимости численных методов.
Если величина всех слагаемых станет близкой к единице, все расчеты станут вычислительно дешевле, чем если бы величины были асимметрично большими или малыми.
Вы получите точку отсчета относительно шкалы . Например, если я дам вам количество, скажем, 4×10³⁰ кг, вы, возможно, не сможете понять, мало оно или велико в космическом масштабе. Однако, если я скажу, что в 2 раза больше массы Солнца, вы легко сможете понять значение этой величины.

Чтобы обезразмерить уравнения, разделите каждую величину на фиксированную ссылочную величину . Например, разделите массовые члены на массу Солнца, положения (или расстояния) на расстояние между двумя звездами в системе Альфа Центавра, временные члены на период обращения Альфы Центавра и скоростной член на относительную скорость земля вокруг солнца.

При делении каждого члена на исходную величину вам также потребуется умножить его, чтобы избежать изменения уравнения. Все эти термины вместе с G можно превратить в константу, скажем, K₁ для уравнения 1 и K₂ для уравнения 2. Таким образом, безразмерные уравнения выглядят следующим образом:

термины безразмерны. Итак, это окончательные уравнения, которые мы будем использовать в нашем моделировании.

3.3 Код

Начнем с импорта всех необходимых модулей для моделирования.

 #Import scipy 
 import scipy as sci#Import matplotlib и связанные модули для 3D и анимации 
 импортировать matplotlib.pyplot как plt 
 из mpl_toolkits.mplot3d импортировать Axes3D 
 из matplotlib импортировать анимацию

Далее определим константы и эталонные величины, которые используются для обезразмеривания уравнений, а также чистые константы K₁ и К₂ .

 #Определить постоянную всемирного тяготения 
 G=6.67408e-11 #Н-м2/кг2#Эталонные величины 
 m_nd=1.989e+30 #kg #масса солнца 
 r_nd=5.326e+12 #m #расстояние между звездами в Альфе Центавра 
 v_nd=30000 #м/с #относительная скорость Земли вокруг Солнца 
 t_nd=79.91*365*24*3600*0.51 #с #период обращения Альфы Центавра#Константы сети 
 K1=G*t_nd*m_nd/(r_nd **2*v_nd) 
 K2=v_nd*t_nd/r_nd

Пришло время определить некоторые параметры, которые определяют две звезды, которые мы пытаемся смоделировать — их масс , начальных положений и начальных скоростей . Обратите внимание, что эти параметры являются безразмерными, поэтому масса Альфы Центавра A определяется как 1,1 (что указывает на 1,1-кратную массу Солнца, которая является нашей эталонной величиной). Скорости определяются произвольно таким образом, что ни одно из тел не избегает гравитационного притяжения друг друга.

 #Определить массы 
 m1=1.1 #Альфа Центавра A 
 m2=0.907 #Альфа Центавра B#Определить векторы начального положения 
 r1=[-0.5,0,0] #m 
 r2=[0.5,0,0] # m#Преобразование векторов позиций в массивы 
 r1=sci.array(r1,dtype="float64") 
 r2=sci.array(r2,dtype="float64")#Найти центр масс 
 r_com=(m1*r1+ m2*r2)/(m1+m2)#Определить начальные скорости 
 v1=[0.01,0.01,0] #м/с 
 v2=[-0.05,0,-0.1] #м/с#Преобразовать векторы скорости в массивы 
 v1=sci.array(v1,dtype="float64") 
 v2=sci.array(v2,dtype="float64")#Найти скорость COM 
 v_com=(m1*v1+m2*v2)/(m1+m2)

Теперь мы определили большинство основных величин, необходимых для моделирования. Теперь мы можем перейти к подготовке решателя odeint в scipy для решения нашей системы уравнений.

Чтобы решить любое ОДУ, вам потребуются уравнений (конечно!), набор начальных условий и временной интервал , для которого уравнения должны быть решены. Решатель odeint также требует этих трех основных вещей. Уравнения определяются через функцию. Функция принимает массив, содержащий все зависимые переменные (здесь положение и скорость), и массив, содержащий все независимые переменные (здесь время) в указанном порядке. Он возвращает значения всех дифференциалов в массиве.

 # Функция, определяющая уравнения движения 
 def TwoBodyEquations(w,t,G,m1,m2): 
 r1=w[:3] 
 r2=w[3:6] 
 v1=w[6:9 ] 
 v2=w[9:12] r=sci.linalg.norm(r2-r1) # Вычислить модуль или норму вектора dv1bydt=K1*m2*(r2-r1)/r**3 
 dv2bydt=K1* m1*(r1-r2)/r**3 
 dr1bydt=K2*v1 
 dr2bydt=K2*v2 r_derivs=sci. concatenate((dr1bydt,dr2bydt)) 
 derivs=sci.concatenate((r_derivs,dv1bydt,dv2bydt) ) 
 return derivs

Из фрагмента кода вы можете довольно легко идентифицировать дифференциальные уравнения. Каковы другие шансы и концы? Помните, что мы решаем уравнение для 3-х измерений, поэтому каждый вектор положения и скорости будет иметь 3 компонента. Теперь, если вы рассмотрите два векторных дифференциальных уравнения, приведенных в предыдущем разделе, их нужно решить для всех трех компонентов векторов. Итак, для одного тела нужно решить 6 скалярных дифференциальных уравнений. Для двух тел, вы поняли, 12 скалярных дифференциальных уравнений. Итак, мы делаем массив w размером 12, в котором хранятся координаты положения и скорости двух рассматриваемых тел.

В конце функции мы конкатенируем или соединяем все различные производные и возвращаем массив производных размера 12.

Трудная работа сделана! Остается только ввести функцию, начальные условия и интервал времени в функцию odeint .

 # Начальные параметры пакета 
 init_params=sci.array([r1,r2,v1,v2]) #создать массив начальных параметров 
 init_params=init_params.flatten() # сгладить массив, чтобы сделать его одномерным 
 time_span=sci.linspace(0,8,500) #8 орбитальных периодов и 500 точек#Запустить решатель ОДУ TwoBodyEquations,init_params,time_span,args=(G,m1,m2))

Переменная two_body_sol содержит всю информацию о системе двух тел, включая векторы положения и скорости. Для создания наших графиков и анимации нам нужны только векторы положения, поэтому давайте извлечем их в две разные переменные.

 r1_sol=two_body_sol[:,:3] 
 r2_sol=two_body_sol[:,3:6]

Пришло время строить планы! Здесь мы будем использовать возможности 3D-графики Matplotlib.

 #Создать фигуру 
 fig=plt.figure(figsize=(15,15))#Создать трехмерные оси 
 ax=fig.add_subplot(111,projection="3d")#Построить орбиты 
 ax.plot(r1_sol[ :,0],r1_sol[:,1],r1_sol[:,2],color="darkblue") 
 ax. plot(r2_sol[:,0],r2_sol[:,1],r2_sol[:,2] ,color="tab:red")#Нанесите конечные положения звезд 
 ax.scatter(r1_sol[-1,0],r1_sol[-1,1],r1_sol[-1,2],color="darkblue ",marker="o",s=100,label="Альфа Центавра А") 
 ax.scatter(r2_sol[-1,0],r2_sol[-1,1],r2_sol[-1,2],color="tab:red",marker="o",s=100,label=" Alpha Centauri B")#Добавить еще несколько наворотов 
 ax.set_xlabel("x-coordinate",fontsize=14) 
 ax.set_ylabel("y-coordinate",fontsize=14) 
 ax.set_zlabel("z -coordinate",fontsize=14) 
 ax.set_title("Визуализация орбит звезд в системе двух тел\n",fontsize=14) 
 ax.legend(loc="upper left",fontsize=14)

Окончательный график ясно показывает, что орбиты следуют предсказуемой схеме, как и ожидается от решения задачи двух тел.

График Matplotlib, показывающий эволюцию во времени орбит двух звезд

Вот анимация, показывающая пошаговую эволюцию орбит.

Анимация, сделанная в Matplotlib, которая показывает пошаговую эволюцию во времени (код в статье не указан)

Есть еще одна визуализация, которую мы можем сделать, и это из системы отсчета центра масс. Вышеупомянутая визуализация сделана из какой-то произвольной стационарной точки в пространстве, но если мы будем наблюдать за движением двух тел из центра масс системы, мы увидим еще более наглядную картину.

Итак, сначала давайте найдем положение центра масс на каждом временном шаге, а затем вычтем этот вектор из векторов положения двух тел, чтобы найти их положение относительно центра масс.

 #Найти местоположение COM 
 rcom_sol=(m1*r1_sol+m2*r2_sol)/(m1+m2)#Найти местоположение Alpha Centauri A по COM 
 r1com_sol=r1_sol-rcom_sol#Найти местоположение Alpha Centauri B на COM 
 r2com_sol=r2_sol-rcom_sol

Наконец, мы можем использовать код, использованный для построения предыдущего изображения с изменением переменных, для построения следующего изображения.

График Matplotlib, показывающий эволюцию во времени орбит двух звезд, как видно из COM

Если бы вы сидели за COM и наблюдали за двумя телами, вы бы увидели указанные выше орбиты. Это неясно из этой симуляции, поскольку шкала времени очень мала, но даже эти орбиты продолжают слегка вращаться.

Теперь совершенно ясно, что они следуют очень предсказуемыми путями и что вы можете использовать функцию — возможно, уравнение эллипсоида — для описания их движения в пространстве, как и ожидается от системы из двух тел.

4.1 Код

Теперь, чтобы расширить наш предыдущий код на систему из трех тел, мы должны сделать несколько дополнений к параметрам — добавить векторы массы, положения и скорости третьего тела. Будем считать, что Третья Звезда имеет массу, равную массе Солнца.

 #Масса Третьей Звезды 
 m3=1.0 #Третья Звезда#Положение Третьей Звезды 
 r3=[0,1,0] #m 
 r3=sci.array(r3,dtype="float64")#Скорость Третьей звезды 
 v3=[0,-0.01,0] 
 v3=sci.array(v3,dtype="float64")

Нам нужно обновить формулы центра масс и скорости центра масс в коде.

 #Обновить формулу COM 
 r_com=(m1*r1+m2*r2+m3*r3)/(m1+m2+m3)#Обновить скорость формулы COM 
 v_com=(m1*v1+m2*v2+m3* v3)/(m1+m2+m3)

Для системы из трех тел нам потребуется изменить уравнения движения, чтобы включить дополнительную гравитационную силу, создаваемую присутствием другого тела. Таким образом, нам нужно добавить силовой член в правую сторону для каждого другого тела, оказывающего силу на рассматриваемое тело. В случае системы из трех тел на одно тело будут воздействовать силы двух остальных тел, и, следовательно, на RHS появятся два принудительных условия. Это может быть представлено математически как.

Чтобы отразить эти изменения в коде, нам нужно создать новую функцию для решателя odeint .

 def ThreeBodyEquations(w,t,G,m1,m2,m3): 
 r1=w[:3] 
 r2=w[3:6] 
 r3=w[6:9] 
 v1=w[9 :12] 
 v2=w[12:15] 
 v3=w[15:18] r12=sci.linalg.norm(r2-r1) 
 r13=sci.linalg.norm(r3-r1) 
 r23=sci .linalg.norm(r3-r2)  dv1bydt=K1*m2*(r2-r1)/r12**3+K1*m3*(r3-r1)/r13**3 
 dv2bydt=K1*m1*(r1-r2)/r12**3+K1*m3*(r3-r2)/r23**3 
 dv3bydt=K1*m1*(r1-r3)/r13**3+ K1*m2*(r2-r3)/r23**3 
 dr1bydt=K2*v1 
 dr2bydt=K2*v2 
 dr3bydt=K2*v3 r12_derivs=sci.concatenate((dr1bydt,dr2bydt)) 
 r_derivs=sci. concatenate ((r12_derivs,dr3bydt)) 
 v12_derivs=sci.concatenate((dv1bydt,dv2bydt)) 
 v_derivs=sci.concatenate((v12_derivs,dv3bydt)) 
 derivs=sci.concatenate((r_derivs,v_derivs))

0 return05s

Наконец, нам нужно позвонить в odeint и задайте для нее вышеуказанную функцию, а также начальные условия.

#Исходные параметры пакета
init_params=sci.array([r1,r2,r3,v1,v2,v3]) #Начальные параметры
init_params=init_params.flatten() #Свести для создания одномерного массива
time_span=sci.linspace (0,20,500) #20 орбитальных периодов и 500 точек#Запустите решатель ОДУ
при моделировании двух тел нам нужно извлечь координаты положения всех трех тел для построения графика.

 r1_sol=three_body_sol[:,:3] 
 r2_sol=three_body_sol[:,3:6] 
 r3_sol=three_body_sol[:,6:9]

Окончательный график можно построить, используя код, приведенный в предыдущем разделе, с несколько изменений. Орбиты не имеют предсказуемой закономерности, как вы можете видеть из беспорядка на графике ниже.

График Matplotlib, показывающий эволюцию во времени орбит трех звезд

Анимация облегчит понимание беспорядочного сюжета.

Анимация, сделанная в Matplotlib, пошагово показывающая временную эволюцию (код в статье не приводится)

Вот решение для другой исходной конфигурации, в которой вы можете заметить, что решение сначала кажется стабильным, но затем резко становится нестабильным.

Анимация, сделанная в Matplotlib и пошагово показывающая временную эволюцию (код в статье не приводится)

Вы можете попробовать поиграть с начальными условиями, чтобы увидеть различные решения. В последние годы благодаря доступности больших вычислительных мощностей было обнаружено много интересных решений задачи трех тел, некоторые из которых кажутся периодическими — например, решение в виде восьмерки, в котором все три тела движутся по плоской фигуре. -8 путь.

Некоторые ссылки для дальнейшего чтения:

Небольшой очерк по математическому описанию задачи трех тел.
Диссертация по исследованию плоских ограниченных решений задачи трех тел (включает рисунок-8 и решения Хилла).

Я не включил код анимации в эту статью. Если вы хотите узнать больше, вы можете написать мне по электронной почте или связаться со мной в Twitter.

Второй закон движения Ньютона

Первый закон движения Ньютона предсказывает поведение объектов, для которых все существующие силы уравновешены. Первый закон, иногда называемый законом инерции, гласит, что если силы, действующие на объект, уравновешены, то ускорение этого объекта будет равно 0 м/с/с. Объекты на равновесие (состояние, при котором все силы уравновешены) не будет ускоряться. Согласно Ньютону, объект будет ускоряться только в том случае, если на него действует чистая или неуравновешенная сила. Наличие неуравновешенной силы ускоряет объект, изменяя его скорость, направление или и скорость, и направление.

Второй закон движения Ньютона относится к поведению объектов, для которых все существующие силы не уравновешены. Второй закон гласит, что ускорение объекта зависит от двух переменных — общей силы, действующей на объект, и массы объекта. Ускорение объекта напрямую зависит от чистой силы, действующей на объект, и обратно пропорционально массе объекта. Когда сила, действующая на объект, увеличивается, ускорение объекта увеличивается. По мере увеличения массы объекта ускорение объекта уменьшается.

БОЛЬШОЕ Уравнение

Второй закон движения Ньютона можно формально сформулировать следующим образом:

Ускорение объекта, создаваемое результирующей силой, прямо пропорционально величине результирующей силы в том же направлении, что и результирующая сила, и обратно пропорционально массе объекта.

Это словесное утверждение может быть выражено в виде уравнения следующим образом:

a = F _net / m

Приведенное выше уравнение часто преобразуется в более знакомую форму, как показано ниже. Чистая сила равна произведению массы на ускорение.

F _net = m • a

Во всем этом обсуждении акцент делался на net force . Ускорение прямо пропорционально чистой силе ; результирующая сила равна массе, умноженной на ускорение; ускорение в том же направлении, что и чистая сила ; ускорение производится чистой силой . ЧИСТАЯ СИЛА. Важно помнить об этом различии. Не используйте значение просто «любой «старой силы» в приведенном выше уравнении. Это чистая сила, связанная с ускорением. Как обсуждалось в предыдущем уроке, результирующая сила представляет собой векторную сумму всех сил. Если известны все отдельные силы, действующие на объект, то можно определить результирующую силу. При необходимости повторите этот принцип, вернувшись к практическим вопросам урока 2.

В соответствии с приведенным выше уравнением единица силы равна единице массы, умноженной на единицу ускорения. Подставив стандартные метрические единицы силы, массы и ускорения в приведенное выше уравнение, можно записать следующую единицу эквивалентности.

1 Ньютон = 1 кг • м/с ²

Стандартная метрическая единица силы определяется приведенным выше уравнением. Один ньютон определяется как количество силы, необходимой для придания массе 1 кг ускорения 1 м/с/с.

Ваша очередь практиковаться

Сеть F = m • уравнение часто используется при решении алгебраических задач. Приведенную ниже таблицу можно заполнить, подставив в уравнение и найдя неизвестную величину. Попробуйте сами, а затем используйте кнопки для просмотра ответов.

	Чистая сила (Н)	Масса (кг)	Ускорение (м/с/с)
1.	10	2
2.	20	2
3.	20	4
4.		2	5
5.	10		10

Второй закон Ньютона как руководство к размышлению

Числовая информация в приведенной выше таблице демонстрирует некоторые важные качественные соотношения между силой, массой и ускорением. Сравнивая значения в строках 1 и 2, можно увидеть, что удвоение чистой силы приводит к удвоению ускорения (если масса сохраняется постоянной). Аналогичным образом, сравнение значений в строках 2 и 4 показывает, что деление вдвое чистой силы приводит к уменьшение вдвое ускорения (если масса остается постоянной). Ускорение прямо пропорционально чистой силе.

Кроме того, качественную связь между массой и ускорением можно увидеть путем сравнения числовых значений в приведенной выше таблице. Заметьте из строк 2 и 3, что удвоение массы приводит к уменьшению вдвое ускорения (если сила сохраняется постоянной). Точно так же строки 4 и 5 показывают, что уменьшение массы на вдвое на приводит к удвоению ускорения (если сила сохраняется постоянной). Ускорение обратно пропорционально массе.

Анализ данных таблицы показывает, что такое уравнение, как F _net = m*a, может служить руководством к размышлению о том, как изменение одной величины может повлиять на другую величину. Каково бы ни было изменение результирующей силы, такое же изменение произойдет с ускорением. Удвойте, утройте или учетверите результирующую силу, и ускорение будет таким же. С другой стороны, какое бы изменение ни производилось в массе, противоположное или обратное изменение будет происходить с ускорением. Удвойте, утройте или учетверите массу, и ускорение составит половину, треть или четверть первоначального значения.

Направление чистой силы и ускорения

Как указано выше, направление чистой силы совпадает с направлением ускорения. Таким образом, если известно направление ускорения, то известно и направление результирующей силы. Рассмотрим две диаграммы падения масла ниже для ускорения автомобиля. По диаграмме определите направление чистой силы, действующей на автомобиль. Затем нажмите кнопки, чтобы просмотреть ответы. (При необходимости просмотрите ускорение по сравнению с предыдущим блоком. )

В заключение, второй закон Ньютона дает объяснение поведения объектов, на которые силы не уравновешиваются. Закон гласит, что неуравновешенные силы заставляют объекты ускоряться с ускорением, которое прямо пропорционально результирующей силе и обратно пропорционально массе.

Мы хотели бы предложить ...

Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего Force Interactive. Вы можете найти его в разделе Physics Interactives на нашем сайте. Force Interactive позволяет учащимся исследовать влияние изменений приложенной силы, результирующей силы, массы и трения на ускорение объекта.

Посетите: Force

Ракетостроение!

Ракеты НАСА (и другие) ускоряются вверх от стартовой площадки, сжигая огромное количество топлива. По мере того, как топливо сгорает и расходуется для приведения ракеты в движение, масса ракеты изменяется. Таким образом, одна и та же движущая сила может привести к увеличению значений ускорения с течением времени. Используйте Rocket Science ниже, чтобы изучить этот эффект.

	Ракетостроение

Проверьте свое понимание

1. Определите ускорения, возникающие при приложении чистой силы 12 Н к объекту массой 3 кг, а затем к объекту массой 6 кг.

2. На энциклопедию действует результирующая сила 15 Н, заставляющая ее ускоряться со скоростью 5 м/с ² . Определите массу энциклопедии.

3. Предположим, что сани разгоняются со скоростью 2 м/с ² .

Контрольно-измерительные материалы по физике по разделу «Механика» (10 класс, 1 курс на базе 9 класса)

Три тела одинаковой массы по 2 кг каждое совершали движения. Уравнения проекции перемещения представлены в таблице.

Моделирование задачи трех тел в классической механике с помощью Python | by Gaurav Deshmukh

Обзор основ гравитации, решатель odeint в Scipy и трехмерное построение в Matplotlib автор Лю Цисинь.

2.1 Закон всемирного тяготения Ньютона

2.2 Уравнение движения

2.3 Центр масс

3.1 Звездная система Альфа Центавра

3.2 Обезразмеривание

3.3 Код

4.1 Код

Второй закон движения Ньютона

Насморк при прорезывании зубов у детей: причины, симптомы и лечение

Как развивать ребенка в 10 месяцев: игры и занятия для малыша

Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования

УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов

Когда и как вводить прикорм грудному ребенку: рекомендации педиатров

Leave A Comment Отменить ответ

Контрольно-измерительные материалы по физике по разделу «Механика» (10 класс, 1 курс на базе 9 класса)

Три тела одинаковой массы по 2 кг каждое совершали движения. Уравнения проекции перемещения представлены в таблице.

Моделирование задачи трех тел в классической механике с помощью Python | by Gaurav Deshmukh

Обзор основ гравитации, решатель odeint в Scipy и трехмерное построение в Matplotlib автор Лю Цисинь.

2.1 Закон всемирного тяготения Ньютона

2.2 Уравнение движения

2.3 Центр масс

3.1 Звездная система Альфа Центавра

3.2 Обезразмеривание

3.3 Код

4.1 Код

Второй закон движения Ньютона

Share This Story, Choose Your Platform!

Related Posts

Насморк при прорезывании зубов у детей: причины, симптомы и лечение

Как развивать ребенка в 10 месяцев: игры и занятия для малыша

Во сколько месяцев можно ставить мальчиков в ходунки: оптимальный возраст и безопасность использования

УЗИ брюшной полости у детей: подготовка, проведение и расшифровка результатов

Когда и как вводить прикорм грудному ребенку: рекомендации педиатров

Leave A Comment Отменить ответ