Определите № 1566 ГДЗ Физика 7-9 класс Перышкин А.В. – Рамблер/класс
Определите № 1566 ГДЗ Физика 7-9 класс Перышкин А.В. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Через неподвижный блок перекинута нить, к концам которой подвешены два груза в 120 г и 125 г.
ответы
Держи:
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г.Я.
Досуг
Химия
похожие вопросы 5
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №475 В обоих случаях поплавок плавает. В какую жидкость он погружается глубже?
Привет. Выручайте с ответом по физике…
Поплавок со свинцовым грузилом внизу опускают
ГДЗФизикаПерышкин А.В.Школа7 класс
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.
Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)
(Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
Ребята нужны ответы на пересдачу по математике 9 класс 11 регион. Срочно!
ГИА9 класс
11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.
11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 12. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Блоки, нити, грузы и перегрузки | Простая физика
Задача 1. К телу массой кг подвешено на веревке тело массой кг. Масса веревки кг. Вся система движется ускоренно вверх под действием силы Н, приложенной к верхнему телу (рис.1). Найти натяжение веревки в ее центре и в точках крепления тел и .
Масса веревки кг. Вся система движется ускоренно вверх под действием силы Н, приложенной к верхнему телу (рис.1). Найти натяжение веревки в ее центре и в точках крепления тел и .
Рисунок 1
Представим всю систему единым телом массой . Будем действовать на эту систему с силой . Тогда по второму закону Ньютона
Откуда найдем ускорение системы:
Теперь вернемся к первому рисунку и запишем уравнения по второму закону Ньютона для верхнего и нижнего грузов:
Откуда
Очевидно, что посередине веревки сила ее натяжения будет средним арифметическим найденных двух сил:
Ответ: Н, Н, Н.
Задача 2. Маляр массой кг работает в подвесном кресле. Ему понадобилось срочно подняться вверх. Он начинает тянуть веревку с такой силой, что сила давления на кресло уменьшается до Н. Масса кресла кг. Чему равно ускорение маляра? Чему равна нагрузка на блок?
Рисунок 2
Расставим силы. Отметим все силы, действующие не маляра, и силы, действующие на люльку:
Отметим все силы, действующие не маляра, и силы, действующие на люльку:
Теперь можно написать уравнения:
Вычитаем уравнения:
Ответ: м/с.
Задача 3.
Через легкий неподвижный блок перекинута невесомая нерастяжимая нить с двумя грузами на концах, массы которых и , . Система приходит в движение, причем нить не проскальзывает относительно блока. Определить ускорение грузов, силу натяжения нити и силу давления на ось блока.
Рисунок 3
Понятно, что больший груз перетянет и начнет двигаться вниз, а меньший – подниматься. Запишем для них уравнение по второму закону:
Сложим уравнения:
Откуда
Теперь можно найти и силу натяжения нити:
Сила давления на блок равна :
Ответ: , ,
.
Задача 4.
Через блок перекинута нить, на концах которой висят два груза с одинаковыми массами . Одновременно на каждый из грузов кладут по перегрузку: справа массой , слева (рис.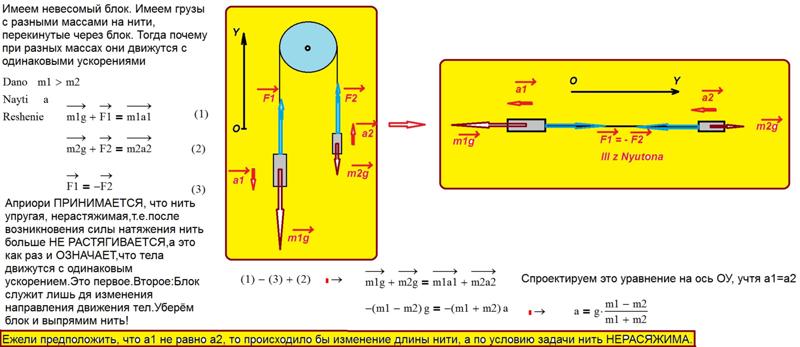 2). Определить ускорение системы, силу натяжения нити и силу давления перегрузков на основные грузы.
2). Определить ускорение системы, силу натяжения нити и силу давления перегрузков на основные грузы.
Рисунок 4
Запишем уравнение по второму закону Ньютона для обоих грузов с учетом массы перегрузков:
Сложение уравнений даст нам
Сила натяжения нити найдется подстановкой найденного ускорения в любое уравнение системы:
Определим силу давления меньшего перегрузка массой на груз :
Для большего перегрузка
Ответ: , , , .
Задача 5.
Через неподвижный блок перекинута нить, к которой подвешены три одинаковых груза массой кг каждый (рис. 3). Найти ускорение системы и силу натяжения нити между грузами 1 и 2. Какой путь пройдут грузы за первые с движения? Трением пренебречь.
Рисунок 5
Сначала мысленно объединим два груза слева в один и запишем уравнение по второму закону:
Для правого грузика
Складываем уравнения:
Определим силу натяжения нити между грузиками. Обозначим ее . Тогда для самого нижнего грузика слева:
Обозначим ее . Тогда для самого нижнего грузика слева:
Определяем путь грузиков за 4 с:
Ответ: м/с, Н, м.
Задача 6.
Определить ускорение грузов и силы натяжения всех нитей в системе, изображенной на рисунке. Масса каждого груза , массой блока пренебречь.
Рисунок 6
Сначала определяем ускорение. Для этого записываем уравнение по второму закону для грузиков справа и слева, пока не вспоминая о том, что их там несколько. Для нас сейчас это груз массой справа и слева. Силу натяжения основной нити обозначим :
Складываем уравнения:
Тогда
Рассмотрим теперь грузы, висящие справа. Обозначим натяжение нити между ними . Для нижнего груза справа
Осталось определить и . Для верхнего грузика слева
Откуда
А для нижнего грузика слева
Ответ: , , , , .
Задача 7.
Два груза массами г и г соединены нерастяжимой нитью, перекинутой через невесомый блок (рис. ). Грузы прижимаются друг к другу с постоянными силами Н. Коэффициент трения между ними . Найти ускорение, с которым движутся грузы.
). Грузы прижимаются друг к другу с постоянными силами Н. Коэффициент трения между ними . Найти ускорение, с которым движутся грузы.
Рисунок 7
Записываем уравнение по второму закону:
Тогда
Ответ: .
Задача 8.
Невесомая нить, перекинутая через неподвижный блок, пропущена через щель (рис.). При движении нити на нее действует постоянная сила трения . На концах нити подвешены грузы, массы которых и . Определить ускорение грузов.
Рисунок 8
Давайте предположим, что . Тогда левый груз начинает движение вверх, правый – вниз. Записываем для них уравнение по второму закону с учетом наличия силы трения:
Складывая уравнения, имеем:
Откуда
Но, если бы , тогда
Тогда, чтобы учесть обе возможности, запишем ответ так:
Ответ: .
Задача 9.
Через невесомый блок перекинута легкая нерастяжимая нить, к одному концу которой привязан груз массой г, а по другому
скользит кольцо массой г (рис. ). С каким ускорением движется кольцо, если груз неподвижен?
). С каким ускорением движется кольцо, если груз неподвижен?
Рисунок 9
Сила трения кольца в данном случае и порождает силу натяжения нити, то есть это одна и та же сила. Поэтому для неподвижного груза
А для кольца
Ответ: 6 м/с.
Блок соединен с таким же блоком через невесомый блок невесомой нерастяжимой нитью длиной 2l (рис.). Левый брусок кладут на стол на расстоянии l от его края, а правый брусок держат на том же уровне, чтобы нить не натягивалась и не провисала, а затем отпускают. Что произойдет раньше: левый брусок достигнет края стола (и коснется шкива) или правый брусок ударится о стол?
И.Э. ИРОДОВ, Л.А. СЕНА и С.С. КРОТОВ-МЕХАНИКА-Задачи механики
20 видеоРЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Про и дехо сари видео бина киси объявление ки рукаават ке!
Ответить
Пошаговое решение, разработанное экспертами, чтобы помочь вам в решении вопросов и получении отличных оценок на экзаменах.
Похожие видео
Блок массой 4 кг лежит на гладком горизонтальном столе. Блок соединен со вторым блоком массой 1 кг безмассовым гибким натянутым шнуром, пропущенным через шкив без трения. Блок массой 1 кг находится на высоте 1 м от пола. Два блока выводятся из состояния покоя. С какой скоростью падает на землю брусок массой 1 кг? .
10956187
Два бруска массами m1 и m2, соединенные невесомой пружиной жесткости k, покоятся на гладкой горизонтальной плоскости, как показано на рис. Блок 2 сдвинут на небольшое расстояние x влево и затем отпущен. Найти скорость центра масс системы после отрыва блока 1 от стенки.
11300567
Текст Решение
Как показано на рисунке, левый блок лежит на столе на расстоянии l от края, а правый блок держится на том же уровне, чтобы нить не растянулась и не перекосилась, а затем отпускается . Что произойдет в первую очередь?
15220107
Брусок массы m подвешен вертикально на упругой нити с постоянной силы mg/a. Первоначально нить имела свою естественную длину, и блок мог свободно падать. Kinetic energy of the block when it passes through the equilibrium position will be
Первоначально нить имела свою естественную длину, и блок мог свободно падать. Kinetic energy of the block when it passes through the equilibrium position will be
17458593
प्रकश के किसी अवरोधक के किनारो से मुड़ने की घटना को कहते है-
110484503
Two blocks and a pulley are connected by inextensible cords as shown . Относительная скорость блока А относительно блока В составляет 0,8 м/с влево в момент времени t = 0 и 0,4 м/сек влево при t = 0,25 с. Зная, что угловое ускорение шкива постоянно, относительное ускорение блока А по отношению к блоку В равно?
460908328
দুটি ব্লক একটি সুতোর সাহায্যে যুক্ত এবং সুতোটি একটি ভারহীন ও ঘর্ষণহীন ওপর দিয়ে গেছে [চিত্র 1.82] ।ব্লক ত্বরণ এবং সুতোর টান করো করো।। ধরে নাও, সুতোটি ভরহীন।
498170189
Четыре одинаковых блока длиной L расположены друг над другом, как показано на рисунке. Максимальное расстояние самого верхнего блока от края самого нижнего блока равно x, при котором ни один блок не падает. Тогда x равно
Тогда x равно
642674813
Четыре одинаковых блока длины L расположены друг над другом, как показано на рисунке. Максимальное расстояние самого верхнего блока от края самого нижнего блока равно x, при котором ни один блок не падает. Тогда х равно:
642707975
Текст Решение
Брусок массой 4 кг лежит на гладком горизонтальном столе. Блок соединен со вторым блоком массой 1 кг безмассовым гибким натянутым шнуром, пропущенным через шкив без трения. Блок массой 1 кг находится на высоте 1 м от пола. Два блока выводятся из состояния покоя. С какой скоростью падает на землю брусок массой 1 кг? .
643181589
Брусок массы m подвешен вертикально на упругой нити с постоянной силы mg//a . Первоначально нить имела свою естественную длину, и блок мог свободно падать. Кинетическая энергия бруска при прохождении им положения равновесия будет равна
643186533
Нерастяжимая нить прикреплена к шкиву. На нити подвешен брусок массой m_2 = 100 г. Нить тянет за собой брусок массы m_1 = 200 г, который держится на гладком столе. Найдите натяжение нити и ускорение блоков.
Нить тянет за собой брусок массы m_1 = 200 г, который держится на гладком столе. Найдите натяжение нити и ускорение блоков.
643965354
Блок A массы m_1 лежит на горизонтальном столе. Связанная с ним легкая нить проходит по блоку без трения у края стола, а к другому ее концу подвешен другой брусок B массы m_(2). Коэффициент трения между блоком и столом равен mu_(k) . Когда блок А скользит по столу, натяжение нити равно.
6439
Два бруска массами m_(1) и m_(2) , соединенные невесомой пружиной жесткости k, покоятся на гладкой горизонтальной плоскости, как показано на рис. Блок 2 сдвинут на небольшое расстояние x влево и потом выпустили. Найти скорость центра масс системы после отрыва блока 1 от стенки.
644101885
Два блока соединены длинной нерастяжимой нитью, проходящей через идеальный шкив, как показано на рисунке. Если систему вывести из состояния покоя, то общая скорость блоков при перемещении блока m_2 на расстояние I будет равна
644384208
Динамика прямолинейного движения связанных тел.
 Решение задач по динамике
Решение задач по динамикеЦель занятия:
Тип урока: вместе взятых.
План урока: 1. Вступительная часть 1-2 мин.
2. Опрос 15 мин.
3. Объяснение 25 мин.
4. Домашнее задание 2-3 мин.
II. Обзор фундаментальный: Движение под действием силы трения.
Задания:
1. Каким должен быть минимальный коэффициент трения между шинами двух задних ведущих колес и поверхностью наклонной дороги с уклоном 30 0 , чтобы автомобиль мог двигаться по ней с ускорение 0,6 м/с 2? Нагрузка на колеса распределяется равномерно. Не обращайте внимания на габариты автомобиля.
2. Брусок массы m из состояния покоя под действием силы F, направленной вдоль горизонтального стола, начинает двигаться по его поверхности. Через время Δt 1 действие силы F прекращается, а через время Δt 2 после этого останавливается брусок. Какова сила трения, действующая на брусок при движении? На какое расстояние продвинется брусок за все время своего движения?
Какова сила трения, действующая на брусок при движении? На какое расстояние продвинется брусок за все время своего движения?
3. Два шара одинакового диаметра, имеющие массы 1 кг и 2 кг, связаны между собой легкой и длинной нерастяжимой нитью. Мяч был сброшен с достаточно большой высоты над Землей. Найдите натяжение нити при равномерном падении шариков.
Вопросы:
- Чем объяснить, что при пробуксовке колес тепловоза или вагона сила тяги значительно падает?
- Равно ли время подъема камня, брошенного вертикально, времени его падения?
- Можно ли измерить среднюю скорость ветра, бросив легкий предмет с определенной высоты. Например, кусок ваты?
- Если локомотив не может двинуть тяжеловесный поезд, то машинист применяет следующий прием: он дает задний ход и, немного толкая состав назад, затем дает вперед. Объяснять.
- Скрип дверных петель и пение скрипки объясняется тем, что максимальная сила трения покоя больше силы трения скольжения.

- Почему скорость капель дождя не зависит от высоты облаков и сильно зависит от размера капель?
- Скорость падения капель одного душа может различаться в 10 раз. Почему?
- Почему самолеты всегда взлетают и садятся против ветра?
- Камень брошен вертикально вверх. В каких точках траектории камень будет иметь максимальное ускорение, если сопротивление воздуха увеличивается с увеличением скорости камня? Как изменится скорость камня?
III . Объясните примерами задач, решаемых учителем.
Задания:
1. С каким ускорением движется брусок по наклонной плоскости с углом наклона 30 o при коэффициенте трения 0,2? При каком условии штанга будет скользить (tg
2. Устройство, показанное на рис. 1, в котором два груза поддерживаются блоком, называется машиной Этвуда. Считая, что брусок не имеет ни массы, ни трения, вычислить: а) ускорение системы; б) натяжение нити. Проверка справедливости второго закона Ньютона и измерение ускорения свободного падения с помощью машины Этвуда.
Проверка справедливости второго закона Ньютона и измерение ускорения свободного падения с помощью машины Этвуда.
Основной задачей динамики при рассмотрении движения связанных тел в различных системах отсчета является объяснение причин, определяющих характер движения. В этом случае возникает необходимость понять, при каких условиях системы тел движутся прямолинейно, в каком случае их траектория является кривой, в результате чего тела движутся равномерно, ускоренно или замедленно.
При изучении поведения систем связанных тел со скоростями, много меньшими скорости света, используются классические законы Ньютона:
Если тела не взаимодействуют с другими телами или действие других тел скомпенсировано, то скорость системы не меняется ни по модулю, ни по направлению. Система движется равномерно и прямолинейно.
Сила ($\overline(F)$), вызывающая ускорение системы тел ($\overline(a)$), в инерциальной системе отсчета пропорциональна массе ($m$) тел , умноженное на его ускорение:
\[\overline(F)=m\overline(a)\left(1\right). \]
\]
Силы взаимодействия тел равны по величине, направлены вдоль одной прямой и имеют противоположные направления.
Если не указано иное, связи, обычно нити, считаются нерастяжимыми и невесомыми. В этом случае при рассмотрении движения связанных тел необходимо помнить, что ускорение движения тел в системе одинаково (результат действия связей). Сила натяжения нитей считается равной по всей длине нити.
В некоторых случаях можно выбирать разные системы координат при рассмотрении движения разных тел системы.
Схема решения типовой задачи о движении связанных тел
- Графически изобразите ситуацию, описанную в задаче. Рисуем рисунок, изображаем силы, скорости движения тел, ускорения. Выбор и изображение систем отсчета.
- Запишем основной закон динамики поступательного движения (второй закон Ньютона) в векторной форме, необходимые кинематические уравнения движения, другие необходимые законы и формулы, например, основной закон динамики вращательного движения, формулу для силы трения и др.

- Проецируем векторные уравнения на оси систем координат.
- Решаем уравнения.
- Проводим необходимые расчеты, предварительно убедившись, что все величины записаны в единой системе единиц.
Примеры задач с решением
Пример 1
Упражнение. Тележка массой $M$ стоит на горизонтальной поверхности. К нему привязана невесомая, нерастяжимая нить. Нить переброшена через невесомый блок. Ко второму концу нити прикреплен груз массой $m$ (рис. 1). С каким ускорением будет двигаться тележка? Силы трения не учитываются.
Раствор. Изобразим силы, действующие на тележку и груз на рис.1. и ускорение движения тел системы. Помните, что сил трения нет. Заметим, что ускорения связанных тел (тележки и груза) будут одинаковыми, за исключением того, что силы натяжения нити ($\overline(N)$), действующие на тележку и груз, равны по величине (невесомый блок), но имеют разные направления (рис. 1). Запишем второй закон Ньютона для тележки:
\[(\overline(F))_R+M\overline(g)+\overline(N)=M\overline(a)\left(1. 1\right).\]
1\right).\]
Основной закон динамики для нагрузка имеет вид:
Соединим систему отсчета с Землей, запишем проекции уравнения (1.1) на оси координат:
\[\left\( \begin(array)(c) X:N =Ma \\ Y:Mg=F_R \end(array) \right.\left(1.3\right).\]
В проекциях на те же оси координат уравнение (1.2) даст одно скалярное уравнение:
\ [\left\( \begin(массив)(c) X:mg-N=ma \\ Y:0 \end(массив) \right.\left(1.4\right).\]
Из первого уравнения системы (1.3) и уравнения (1.4) имеем:
Выразим из (1.5) искомое ускорение:
Ответ. $a=\frac(m)(M+m)$
Пример 2
Упражнение. Два груза массами $m_1\ и\ m_2$, связанные невесомой нитью, скользят по гладкой поверхности. На груз массой $m_1\$ действует сила F, направленная горизонтально (рис.2). Каково ускорение грузов? Каково будет натяжение нити, связывающей эти грузы? Сила трения грузов о поверхность не учитывается. \текстит()
Раствор. На рис. 2 изобразим силы, действующие на груз массой $m_1$ (рис. 2).
2).
В соответствии со вторым законом Ньютона запишем:
Соединим систему отсчета с Землей, выберем направления осей координат (рис. 2).
Для решения задачи нам потребуется проекция уравнения (2.1) только на ось Y:
В уравнении (2.2) есть две неизвестные величины: сила натяжения нити ($T$) и ускорение тела ($а$). Чтобы найти ускорение, с которым движется первое тело и вся система связанных тел, выясним, какие силы действуют на систему, если оба тела считать одним. Тогда на систему с массой $m_1+m_2$ действует одна сила $\overline(F)$. В этом случае второй закон Ньютона принимает вид:
\[\влево(m_1+m_2\вправо)\над чертой(a)=\над чертой(F)+\влево(m_1+m_2\вправо)\над чертой(g)+\над чертой(N)\влево(2.3\ справа) .\]
В проекции на ось Y формулы (2.3) получаем:
\[\left(m_1+m_2\right)a=F\ \left(2.4\right).\]
Из (2.4) ускорение тел равно:
Из (2.2) и (2.5) получаем силу натяжения нити, равную:
Ответ. $\ 1)a=\frac(F)(m_1+m_2). $ 2) $T=F\left(1-\frac(m_1)(m_1+m_2)\right)$
$ 2) $T=F\left(1-\frac(m_1)(m_1+m_2)\right)$
Урок решения задач «Движение связанных тел»
10 класс
Учитель Смирнова С.Г.
Саранск, МОУ «Луховский лицей»
Вид урока : Урок-практика.
Цель урока: Воспитывать умение применять законы Ньютона при решении комбинированных задач расчета
Цели урока:
Образовательные: повторять законы Ньютона, прививать умение определять равнодействующую сил при движении по наклонной плоскости. При движении соединенных тел.
Проявление: развивать внимание и речь, совершенствовать навыки самостоятельной и парной работы.
Образовательный формировать целостное представление учащихся об окружающем мире (природе, обществе и самом себе), о роли и месте физики в системе наук.
Оборудование: учительский компьютер, мультимедийный проектор, Физика 7-11 Библиотека электронных наглядных пособий. «Кирилл и Мефодий».
«Кирилл и Мефодий».
Во время занятий
1. Организационный момент
2. Организация внимания учащихся
Тема нашего занятия: Решение задачи «Движение связанных тел»
3. Актуализация базовых знаний
Прежде чем перейти к решению задач, предлагаю проверка степени вашей готовности к этому
Фронтальный опрос:
Сформулировать законы Ньютона
Начертить наклонную плоскость, показать все силы, действующие на тело при вытягивании тела вверх
Определить проекции этих сил на выбранные координатные оси
3. Решение проблем.
Вт черт 1. Лежащий на столе груз массой 1 кг связан легкой нерастяжимой нитью, накинутой на идеальный брусок весом 0,25 кг. На первую нагрузку действует горизонтальная постоянная сила F, равная по модулю 1 Н (см. рисунок). При этом второй груз движется с ускорением 0,8 м/с2, направленным вниз. Чему равен коэффициент трения скольжения первого груза по поверхности стола?
Решение.
Два груза соединены нерастяжимой нитью через блок. Сила, действующая на первый груз Н, и сила трения, направленная в сторону, противоположную движению груза. На вторую нагрузку действует только сила тяжести, равная Н. Равнодействующая этих тел равна силе, которая заставляет систему двух масс двигаться с ускорением. Тогда по второму закону Ньютона можно написать:
Где массы первого и второго груза соответственно. Отсюда находим силу трения:
и коэффициент трения
.
Ответ: 0,05.
Задача 2. Грузы массами М = 1 кг и m соединены легкой нерастяжимой нитью, накинутой на брусок, по которому нить может скользить без трения (см. рисунок). Груз массой М находится на шероховатой наклонной плоскости (угол наклона плоскости к горизонту α = 30°, коэффициент трения µ = 0,3). При каком максимальном значении массы m система масс еще не выходит из начального состояния покоя?
Решение.
1. Если масса m достаточно велика, но грузы еще покоятся, то сила трения покоя, действующая на груз массой M, направлена вниз по наклонной плоскости (см. рисунок).
Если масса m достаточно велика, но грузы еще покоятся, то сила трения покоя, действующая на груз массой M, направлена вниз по наклонной плоскости (см. рисунок).
2. Будем считать систему отсчета, связанную с наклонной плоскостью, инерциальной. Запишем второй закон Ньютона для каждого из покоящихся тел в проекциях на оси введенной системы координат:
Учтем, что Т1 = Т2 = Т (нить легкая, трения между бруском и нитью нет), (сила трения покоя). Тогда Т = мг, , и приходим к неравенству с решением. Таким образом,
кг.
Задача 3. В показанной на рисунке установке груз А соединен нитью, перекинутой через блок, со стержнем В, лежащим на горизонтальной поверхности трибометра, закрепленного на столе. Вес отводят в сторону, поднимая его на высоту h, и отпускают. Длина висящей части нити равна L. Какую величину должен превысить вес гири, чтобы стержень сдвинулся со своего места в момент прохождения гирей нижней точки траектории? Масса бруска M, коэффициент трения бруска о поверхность µ. Трением в блоке, а также размерами блока пренебречь.
Трением в блоке, а также размерами блока пренебречь.
Брусок сдвинется со своего места при условии, что сила, действующая на него со стороны резьбы, станет больше максимальной силы трения покоя:, . Второй закон Ньютона для веса в нижнем положении:
. (1)
Закон сохранения механической энергии:
, . (2)
В этой задаче необходимо найти отношение силы натяжения к
Рис. 3. Решение задачи 1 ()
Натянутая нить в этой системе действует на стержень 2, заставляя его двигаться вперед, но она же действует и на стержень 1, пытаясь воспрепятствовать его движению. Эти две силы натяжения равны по величине, и нам просто нужно найти эту силу натяжения. В таких задачах необходимо упростить решение следующим образом: считаем, что сила является единственной внешней силой, которая заставляет двигаться систему из трех одинаковых стержней, а ускорение остается неизменным, то есть сила заставляет двигаться все три стержня с тем же ускорением. Тогда напряжение всегда перемещается только на один стержень и по второму закону Ньютона будет равно ma. будет равна удвоенному произведению массы на ускорение, так как третий стержень лежит на втором и натяжная нить уже должна перемещаться на два стержня. В этом случае отношение к будет равно 2. Правильный ответ – первый.
Тогда напряжение всегда перемещается только на один стержень и по второму закону Ньютона будет равно ma. будет равна удвоенному произведению массы на ускорение, так как третий стержень лежит на втором и натяжная нить уже должна перемещаться на два стержня. В этом случае отношение к будет равно 2. Правильный ответ – первый.
Два тела, имеющие массу и соединенные невесомой нерастяжимой нитью, могут без трения скользить по гладкой горизонтальной поверхности под действием постоянной силы (рис. 4). Каково отношение сил натяжения нити в случаях а и б?
Вариант ответа: 1. 2/3; 2.1; 3,3/2; 4,9/4.
Рис. 4. Иллюстрация к заданию 2 ()
Рис. 5. Решение задачи 2 ()
На бруски действует одна и та же сила, только в разные стороны, поэтому ускорение в случае «а» и случае «б» будет одинаковым, так как одна и та же сила вызывает ускорение двух массы. Но в случае «а» эта сила натяжения заставляет двигаться и стержень 2, а в случае «б» — стержень 1. Тогда отношение этих сил будет равно отношению их масс и мы получим ответ — 1. 5. Это третий ответ.
5. Это третий ответ.
На столе лежит брусок массой 1 кг, к которому привязана нить, перекинутая через неподвижный блок. Ко второму концу нити подвешен груз массой 0,5 кг (рис. 6). Определите ускорение, с которым движется брусок, если коэффициент трения бруска о стол равен 0,35.
Рис. 6. Иллюстрация к заданию 3 ()
Запишем краткое условие задачи:
Рис. 7. Решение задачи 3 ()
Необходимо помнить, что силы натяжения и как векторы различны, но величины этих сил одинаковы и равны. Точно так же мы будем иметь одинаковые ускорения этих тел, так как они связаны нерастяжимой нитью, хотя и направлены в разные стороны: — горизонтально, — вертикально. Соответственно, выбираем свои оси для каждого из тел. Запишем уравнения второго закона Ньютона для каждого из этих тел, при сложении силы внутреннего натяжения будут уменьшаться, и получим обычное уравнение, подставив в него данные, получим, что ускорение равно .
Для решения таких задач можно использовать метод, который использовался еще в прошлом веке: движущей силой в данном случае является равнодействующая внешних сил, приложенных к телу. Сила тяжести второго тела заставляет эту систему двигаться, но движению мешает сила трения бруска о стол, в этом случае:
Сила тяжести второго тела заставляет эту систему двигаться, но движению мешает сила трения бруска о стол, в этом случае:
Поскольку движутся оба тела, движущая масса будет равна сумма масс, то ускорение будет равно отношению движущей силы к движущей массе Так что можно сразу приходить к ответу.
В верхней части двух наклонных плоскостей, образующих углы с горизонтом и , закреплен блок. По поверхности плоскостей при коэффициенте трения 0,2 стержни кг и перемещаются, соединенные нитью, перекинутой через блок (рис. 8). Найдите силу давления на ось бруска.
Рис. 8. Иллюстрация к заданию 4 ()
Сделаем краткую запись условия задачи и пояснительный рисунок (рис. 9):
Рис. 9. Решение задачи 4 ()
Помним, что если одна плоскость составляет с горизонтом угол 60 0 , а вторая плоскость составляет с горизонтом угол 30 0 , то угол при вершине будет 90 0 , это обычный прямоугольный треугольник. Через блок перекинута нить, к которой подвешены стержни, они тянут вниз с одинаковой силой, а действие сил натяжения F н1 и F н2 приводит к тому, что их результирующая сила действует на брусок. Но между собой эти силы натяжения будут равны, они составляют между собой прямой угол, поэтому при сложении этих сил вместо обычного параллелограмма получается квадрат. Искомая сила F d является диагональю квадрата. Мы видим, что для результата нам нужно найти натяжение нити. Проанализируем: в каком направлении движется система из двух соединенных стержней? Более массивный блок, конечно, потянет за собой более легкий, блок 1 скатится вниз, а блок 2 сдвинется вверх по склону, тогда уравнение второго закона Ньютона для каждого из брусков будет иметь вид:
Но между собой эти силы натяжения будут равны, они составляют между собой прямой угол, поэтому при сложении этих сил вместо обычного параллелограмма получается квадрат. Искомая сила F d является диагональю квадрата. Мы видим, что для результата нам нужно найти натяжение нити. Проанализируем: в каком направлении движется система из двух соединенных стержней? Более массивный блок, конечно, потянет за собой более легкий, блок 1 скатится вниз, а блок 2 сдвинется вверх по склону, тогда уравнение второго закона Ньютона для каждого из брусков будет иметь вид:
Решение системы уравнений для связанных тел выполняется методом сложения, затем преобразуем и находим ускорение:
Это значение ускорения необходимо подставить в формулы для силы натяжения и силы давления на ось блок необходимо найти:
Мы выяснили, что сила давления на ось блока составляет примерно 16 Н.
Мы рассмотрели различные способы решения задач, которые пригодятся многим из вас в будущем, чтобы понимать принципы устройства и работы тех машин и механизмов, с которыми вам придется иметь дело на производстве, в армии и в быту.
Список литературы
- Тихомирова С.А., Яворский Б.М. Физика (базовый уровень) — М.: Мнемозина, 2012.
- Генденштейн Л.Е., Дик Ю.И. Физика 10 класс. — М.: Мнемозина, 2014.
- Кикоин И.К., Кикоин А.К. Физика-9. — М.: Просвещение, 1990. .
Домашнее задание
- Какой закон мы используем при написании уравнений?
- Какие величины одинаковы для тел, соединенных нерастяжимой нитью?
- Интернет-портал Bambookes.ru ( ).
- Интернет-портал 10класс.ру ().
- Интернет-портал Festival.1september.ru ().
Найти ускорение груза массой $3m$ в системе, состоящей из неподвижного и подвижного блоков. Массами блоков и трением в их осях пренебречь. Нить, накинутая на блоки, невесома и нерастяжима. Ускорение свободного падения $g$.
Решение
Мы выбираем систему отсчета, связанную с фиксированным блоком. Выбираем систему координат, как показано на рисунке (ось координат $Oy$ выделена красным цветом). Это инерциальная система отсчета, поскольку она неподвижна по отношению к Земле. Он подчиняется законам Ньютона.
Это инерциальная система отсчета, поскольку она неподвижна по отношению к Земле. Он подчиняется законам Ньютона.
1) Изобразим силы, действующие на тело массой $m$ (отмечено на рисунке синим цветом): $m\vec(g_())$ — сила тяжести, всегда направленная вертикально вниз; $\vec(T_())$ — сила натяжения нити, направленная вдоль нити от тела.
2) Изобразим силы, действующие на систему, состоящую из тела массой $3m$ и подвижного блока (обозначен на рисунке зеленым): $3m\vec(g_())$ — сила тяжести; $\vec(T_())$ — сила натяжения нити, направленная вдоль нити от тела.
Предположим, что грузы перемещаются, как показано на рисунке. Обозначим ускорение груза массой $3m$ $\vec(a_1)$, а ускорение груза массой $m$ — $\vec(a_2)$.
3) По второму закону Ньютона для тела массой $m$: $\,\vec(R_2)=m\vec(a_2)$, т.е. $m\vec(g_())+\vec(T_ ( ) )= m\vec(a_2)$.
В проекции на ось $Oy$:
$T-mg=ma_2\,\, (1). $
4) Согласно второму закону Ньютона для тела массой $3m$: $\,\vec(R_1)=3m\vec(a_1)$, т.



Leave A Comment