Как представлено число 83 10 в двоичной системе счисления решение: Перевод 83 из десятичной в двоичную систему счисления

Системы счисления (часть 2): Продвинутый уровень — Статьи

Дата публикации: 2012-09-05 19:16:00
Темы: ЕГЭ по информатике,Часть А, Знания о системах счисления и двоичном представлении информации в памяти компьютера, Решения

 

В этой статье я постараюсь описать вам некоторые закономерности, которые помогут вам быстрее решать определенные задания, связанные с двоичной системой счисления в ЕГЭ по информатике. Кроме того, мы разберем несколько типичных заданий, встречающихся в ЕГЭ.

В прошлой статье («Системы счисления: Первое знакомство») я познакомил вас с основными правилами работы с системами счисления, а также правилами «быстрого» перевода. В случае, если вы не читали предыдущую статью, то вам сюда: http://egedb.ru/article/41.

1. Числа, в двоичной системе счисления, которые делятся на 2ⁿ, оканчиваются на n нулей.

Пример 1: Четное число в двоичной системе счисления оканчивается на 0, нечетное – на 1.

Пример 2: Число, делящееся на 8 (2³), оканчивается на «000» (три нуля).

Следствие 1: Числа вида 2ⁿ записываются как 1 (единица) и n нулей. (Пример: 128₁₀=10000000₂)

Следствие 2: Числа вида 2ⁿ-1 записываются как n единиц. (Пример: 63₁₀ = 111111₂)

Следствие 3: Запись числа 2*N – это запись числа N с нулем в конце. (Пример: N=52₁₀=11100₂ => 2*N=104₁₀=111000₂)

 

2. Число

k в двоичной системе счисления содержит ровно n цифр, если оно находится в промежутке от 2^n-1 до 2ⁿ (2^n-1 <= k <= 2ⁿ).

Пример 1: Число 1100111₂ содержит 7 цифр, следовательно его десятичное значение находится в пределах от 64 (2⁶) до 128 (2⁷).

 

3. Отрицательные числа записываются в виде дополнительного кода.

Алгоритм перевода отрицательного числа (-x, x>0) в дополнительный код:

1.      Вычесть из числа единицу (x = x – 1).

2.      Перевести получившееся число в двоичную систему счисления.

3.      Инвертировать биты – это означает, что каждую цифру «1» в числе нужно заменить на «0», а «0» соответственно на «1».

1. Дано: a=70₁₀, b=40₁₆. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству b<C<a?

1) 1000000₂            2)  1000110₂            3)  1000101₂     4) 1000111₂

Решение: Переведем числа a и b в двоичную систему счисления: a = 70₁₀ = 64₁₀ + 4₁₀ + 2₁₀ = 1000000

2 + 100₂ + 10₂ = 1000110₂ (пользуясь следствием 1 первой закономерности), b = 40₁₆ = 1000000₂ (пользуюясь «быстрым» переводом при помощи тетрад). Теперь сравним каждый из возможных вариантов и выберем нужный. Если C=1000000₂, то C=b. Если C=1000110₂, то C=a. Если C=1000101₂, то b < C < a – то, что нужно, следовательно ответ: 3.

2. Как представлено число 83₁₀ в двоичной системе счисления?

1)  1001011₂     2) 1100101

2       3) 1010011₂      4) 101001₂

Решение: Здесь достаточно просто перевести число. Можно просто столбиком, как я описывал в предыдущей статье, но проще конечно пользуясь следствием 1: 83₁₀ = 64₁₀ + 16₁₀ + 2₁₀ + 1₁₀ = 1000000₂ + 10000₂ + 10₂ + 1₂ = 1010011₂. Отсюда ответ: 3.

3. Сколько единиц в двоичной записи числа 173?

            1)  7                   2) 5                    3) 6                   4) 4

Решение: По большому счету, здесь не обязательно даже переводить число, достаточно разложить на степени двойки и подсчитать количество слагаемых (следствие 1 вам в помощь).

173₁₀ = 128₁₀ + 32₁₀ + 8₁₀ + 4₁₀ + 1₁₀. Всего 5 слагаемых (128, 32, 8, 4 и 1), значит и единиц будет 5. Ответ: 2.

4. Как записывается число A87₁₆ в восьмеричной системе счисления?

1)  435₈             2) 1577₈             3) 5207₈                        4) 6400₈

Решение: Вместо того, чтобы идти напролом и переводить число в десятичную систему счисления, а из нее в восьмиричную предлагаю воспользоваться «быстрыми» переводами и перевести, пользуясь тетрадами в двоичную систему счисления, а из нее уже, пользуясь триадами в восьмиричную. Итак, A87

16 = 101010000111₂ = 5207₈. Ответ: 3.

5. Для хранения целого числа со знаком используется один байт. Сколько единиц содержит внутреннее представление числа (-128)?

1) 1            2)  2                                    3)  3        4) 4

Решение: Внутреннее представление числа – двоичная система счисления + допонительный код для отрицательных чисел. Следовательно нам нужно узнать, как же будет выглядеть число -128 в допонительном коде. Действуем по алгоритму: 1. 128-1 = 127, 2. 127

10 = 1111111₂ (по следствию 2). Так как отводится 1 байт (=8 бит) значит инвертировать нужно не 1111111, а 01111111. После инвертирования получается: 10000000₂ – двоичное представление числа (-128). Ответ: 1.

6. Сколько значащих нулей в двоичной записи числа 254?

1) 1                   2)  2                   3)  4                  4) 8

Решение: Значащие нули – дословно – нули, которые имеют значение. Ведь число 624 можно представить и в виде 0000000624 – значение то не изменится, то эти нули не значимые, значит считать их не нужно. 254

10 = 255₁₀ – 1₁₀ = 11111111₂ – 1₂ = 11111110₂. Здесь я использовал другой прием «быстрого» перевода: я представлял не в виде суммы, а в виде разности числа 255 (256-1 = 2⁸-1) и 1 (2⁰). Оба эти числа очень просто переводятся и в уме, благодаря следствию 2.

Итак, в этих двух статьях мы рассмотрели основные правила для работы с системами счисления, правила «быстрого» перевода и основные типы задания А1.Считаю тему на этом закрытой. Если у вас есть предложения как улучшить эти статьи, или если вы считаете что данного материала не хватает для решения заданий ЕГЭ, связанных с системами счисления – пишите в комментариях к этой статье, буду рад услышать отзывы.

Также даю ссылку на первую статью с основами из этой серии, если кому интересно:

• Системы счисления: Первое знакомство

 

Надеюсь, что тебе, читателю эта статья помогла, и ты узнал что-либо новое.

Если тебе ещё предстоит сдать ЕГЭ, то желаю тебе получить МАКСИМУМ баллов,

Никита Евстигнеев,

aka Hack.Nick.

 

Похожие статьи: Шкала для переводов первичных баллов в 100-бальную шкалу по информатике, Системы счисления: Первое знакомство, Системы счисления: Первое знакомство, Системы счисления: Первое знакомство

Задание 2

Для хранения целого числа со знаком используется один байт. Сколько единиц содержит внутреннее представление числа (-78)?

1) 3 2) 4 3) 5 4) 6

Решение (вариант 1, классический):

1. переводим число 78 в двоичную систему счисления:

78 = 64 + 8 + 4 + 2 = 2⁶ + 2³ + 2² + 2¹ = 1001110₂

2. по условию число занимает в памяти 1 байт = 8 бит, поэтому нужно представить число с помощью 8 разрядов

3. чтобы получилось всего 8 разрядов (бит), добавляем впереди один ноль:

78 = 01001110₂

4. делаем инверсию битов (заменяем везде 0 на 1 и 1 на 0):

01001110₂ → 10110001₂

5. добавляем к результату единицу

10110001₂ + 1 = 10110010₂

это и есть число (-78) в двоичном дополнительно коде

6. в записи этого числа 4 единицы

7. таким образом, верный ответ – 2 .

Возможные проблемы:

Решение (вариант 1, неклассический):

1. переводим число 78 – 1=77 в двоичную систему счисления:

77 = 64 + 8 + 4 + 2 = 2⁶ + 2³ + 2² + 2⁰ = 1001101₂

2. по условию число занимает в памяти 1 байт = 8 бит, поэтому нужно представить число с помощью 8 разрядов

3. чтобы получилось всего 8 разрядов (бит), добавляем впереди один ноль:

77 = 01001101₂

4. делаем инверсию битов (заменяем везде 0 на 1 и 1 на 0):

01001101₂ → 10110010₂

это и есть число (-78) в двоичном дополнительно коде

5. в записи этого числа 4 единицы

6. таким образом, верный ответ – 2 .

Возможные проблемы: нужно помнить, что в этом способе в двоичную систему переводится не число a, а число a-1; именно этот прием позволяет избежать добавления единицы в конце (легче вычесть в десятичной системе, чем добавить в двоичной)

1. Как представлено число 83₁₀ в двоичной системе счисления?

1) 1001011₂ 2) 1100101₂ 3) 1010011₂ 4) 101001₂

2. Сколько единиц в двоичной записи числа 195?

1) 5 2) 2 3) 3 4) 4

3. Сколько единиц в двоичной записи числа 173?

1) 7 2) 5 3) 6 4) 4

4. Как представлено число 25 в двоичной системе счисления?

1) 1001₂ 2) 11001₂ 3) 10011₂ 4) 11010₂

5. Как представлено число 82 в двоичной системе счисления?

1) 1010010₂ 2) 1010011₂ 3) 100101₂ 4) 1000100₂

6. Как представлено число 263 в восьмеричной системе счисления?

1) 301₈ 2) 650₈ 3) 407₈ 4) 777₈

7. Как записывается число 567₈ в двоичной системе счисления?

1) 1011101₂ 2) 100110111₂ 3) 101110111₂ 4) 11110111₂

8. Как записывается число A87₁₆ в восьмеричной системе счисления?

1) 435₈ 2) 1577₈ 3) 5207₈ 4) 6400₈

9. Как записывается число 754₈ в шестнадцатеричной системе счисления?

1) 738₁₆ 2) 1A4₁₆ 3) 1EC₁₆ 4) A56₁₆

10. Для хранения целого числа со знаком используется один байт. Сколько единиц содержит внутреннее представление числа (-128)?

1) 1 2) 2 3) 3 4) 4

11. Для хранения целого числа со знаком используется один байт. Сколько единиц содержит внутреннее представление числа (-35)?

1) 3 2) 4 3) 5 4) 6

12. Дано: ,. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству?

1) 10011010 2) 10011110 3) 10011111 4) 11011110

13. Дано: ,. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству?

1) 11111001 2) 11011000 3) 11110111 4) 11111000

14. Дано: ,. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству?

1) 11011010 2) 11111110 3) 11011110 4) 11011111

15. Дано: ,. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству?

1) 11101010 2) 11101110 3) 11101011 4) 11101100

16. Дано: ,. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству?

1) 11101010 2) 11101000 3) 11101011 4) 11101100

17. Дано: ,. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству?

1) 11010011 2) 11001110 3) 11001010 4) 11001100

18. Дано: ,. Какое из чисел С, записанных в двоичной системе счисления, удовлетворяет неравенству?

1) 10011010 2) 10011110 3) 10011111 4) 11011110

19. Сколько единиц в двоичной записи числа 64?

1) 1 2) 2 3) 4 4) 6

20. Сколько единиц в двоичной записи числа 127?

1) 1 2) 2 3) 6 4) 7

21. Сколько значащих нулей в двоичной записи числа 48?

1) 1 2) 2 3) 4 4) 6

22. Сколько значащих нулей в двоичной записи числа 254?

1) 1 2) 2 3) 4 4) 8

23. Какое из чисел является наименьшим?

1) E6₁₆ 2) 347₈ 3) 11100101₂ 4) 232

24. Какое из чисел является наибольшим?

1) 9B₁₆ 2) 234₈ 3) 10011010₂ 4) 153

Ответы

	A1
	3
	4
	2
	2
	1
	3
	3
	3
	3
	1
	4
	2
	4
	3
	3
	2
	1
	2
	1
	4
	3
	1
	3
	2

83 в двоичном формате — Как преобразовать 83 из десятичного в двоичный?

83 в двоичном формате равно 1010011. В отличие от десятичной системы счисления, где мы используем цифры от 0 до 9 для представления числа, в двоичной системе мы используем только 2 цифры, которые равны 0 и 1 (биты). Мы использовали 7 бит для представления 83 в двоичном виде. В этой статье давайте узнаем, как преобразовать десятичное число 83 в двоичное.

Как преобразовать 83 в двоичный код?

Шаг 1: Разделите 83 на 2. Используйте целое частное, полученное на этом шаге, в качестве делимого для следующего шага. Повторяйте процесс, пока частное не станет равным 0,9.0005

Дивиденд	Остаток
83/2 = 41	1
41/2 = 20	1
20/2 = 10	0
10/2 = 5	0
5/2 = 2	1
2/2 = 1	0
1/2 = 0	1

Шаг 2: Запишите остаток снизу вверх, т. е. в обратном хронологическом порядке. Это даст двоичный эквивалент 83.

Следовательно, двоичный эквивалент десятичного числа 83 равен 1010011.

Давайте посмотрим на значение десятичного числа 83 в различных системах счисления.

• 83 в двоичном формате: 83₁₀ = 1010011₂
• 83 в восьмеричном: 83₁₀ = 123₈
• 83 в шестнадцатеричном формате: 83₁₀ = 53₁₆
• 1010011₂ в десятичном формате: 83₁₀

Формулировки задач:

☛Связанные темы

• Калькулятор преобразования десятичных чисел в двоичные
• Двоично-десятичный калькулятор
• Двоичный код в десятичный
• 113 в двоичном формате — 1110001
• 101 в двоичном формате — 1100101
• 141 в двоичном формате — 10001101
• 157 в двоичном формате — 10011101
• 175 в двоичном формате — 10101111
• 31 в двоичном формате — 11111
• 17 в двоичном формате — 10001

Часто задаваемые вопросы о 83 в двоичном формате

Что такое 83 в двоичном формате?

83 в двоичном формате равно 1010011. Чтобы найти десятичный эквивалент в двоичном, разделите 83 последовательно на 2, пока частное не станет равным 0. Двоичный эквивалент можно получить, записывая остаток на каждом шаге деления снизу вверх.

Найдите значение 6 × 83 в двоичной форме.

Мы знаем, что 83 в двоичном формате равно 1010011, а 6 равно 110. Используя правила двоичного умножения (0 × 0 = 0; 0 × 1 = 0, 1 × 0 = 0 и 1 × 1 = 1), мы можем умножить 1010011 × 110 = 111110010, что равно 498 в десятичной системе счисления. [83 × 6 = 498]

Как преобразовать 83 в двоичный эквивалент?

Мы можем разделить 83 на 2 и продолжать деление, пока не получим 0. Записывайте остаток на каждом шаге.

• 83 mod 2 = 1 — LSB (младший значащий бит)
• 41 модуль 2 = 1
• 20 мод 2 = 0
• 10 мод 2 = 0
• 5 мод 2 = 1
• 2 мод 2 = 0
• 1 mod 2 = 1 — MSB (старший бит)

Записать остатки от MSB до LSB. Следовательно, десятичное число 83 в двоичном виде можно представить как 1010011.

Что такое двоичный эквивалент числа 83 + 37?

83 в двоичной системе счисления равно 1010011, а 37 равно 100101. Мы можем сложить двоичный эквивалент 83 и 37, используя правила двоичного сложения [0 + 0 = 0, 0 + 1 = 1, 1 + 1 = 10, обратите внимание, что 1 равно перенос на следующий бит]. Следовательно, (1010011)₂ + (100101)₂ = (1111000)₂, что равно 120,9.0005

Сколько бит имеет число 83 в двоичном формате?

Мы можем подсчитать количество нулей и единиц, чтобы увидеть, сколько битов используется для представления 83 в двоичном формате, то есть 1010011. Таким образом, мы использовали 7 бит для представления 83 в двоичном формате.

Рабочие листы по математике и визуальный учебный план


Двоичная система счисления

Двоичное число состоит только из 0 с и 1 с.

110100

Пример двоичного числа

В двоичном формате нет 2, 3, 4, 5, 6, 7, 8 или 9!

Двоичные числа широко используются в математике и не только.


На самом деле в цифровом мире используются двоичные числа.

Как считать с помощью двоичного кода?

Это похоже на десятичный счет, за исключением того, что мы достигаем 10 гораздо раньше.

Двоичный
0		Начнем с 0
1		Затем 1
???		Но тогда нет символа 2… что делать?

 

Ну как считать в десятичной системе?
	0		Начать с 0
	…		Сосчитайте 1,2,3,4,5,6,7,8, а затем…
	9		Это последняя цифра в десятичном формате
	10		Итак, мы снова начинаем с 0, но добавляем 1 слева

То же самое делается в двоичном коде. ..

	Двоичный
	0		Начать с 0
•	1		Затем 1
••	10		Теперь снова начните с 0, но добавьте 1 слева
•••	11		еще 1
••••	???		Но что СЕЙЧАС… ?

 

Что происходит в Decimal?
	99		Когда у нас заканчиваются цифры, мы…
	100		… снова начать с 0, но добавить 1 слева

И это то, что мы делаем в двоичном формате . ..

	Двоичный
	0		Начать с 0
•	1		Затем 1
••	10		Снова начать с 0, но добавить 1 слева
•••	11
••••	100		снова начать с 0 и добавить единицу к числу слева… … но это число уже равно 1, поэтому оно также возвращается к 0… … и 1 добавляется к следующей позиции слева
•••••	101
••••••	110
•••••••	111
••••••••	1000		Снова начать с 0 (для всех 3 цифр), добавить 1 слева
•••••••••	1001		И так далее!

 

Посмотрите, как это делается в этой небольшой демонстрации (нажмите кнопку воспроизведения):

Десятичный против двоичного

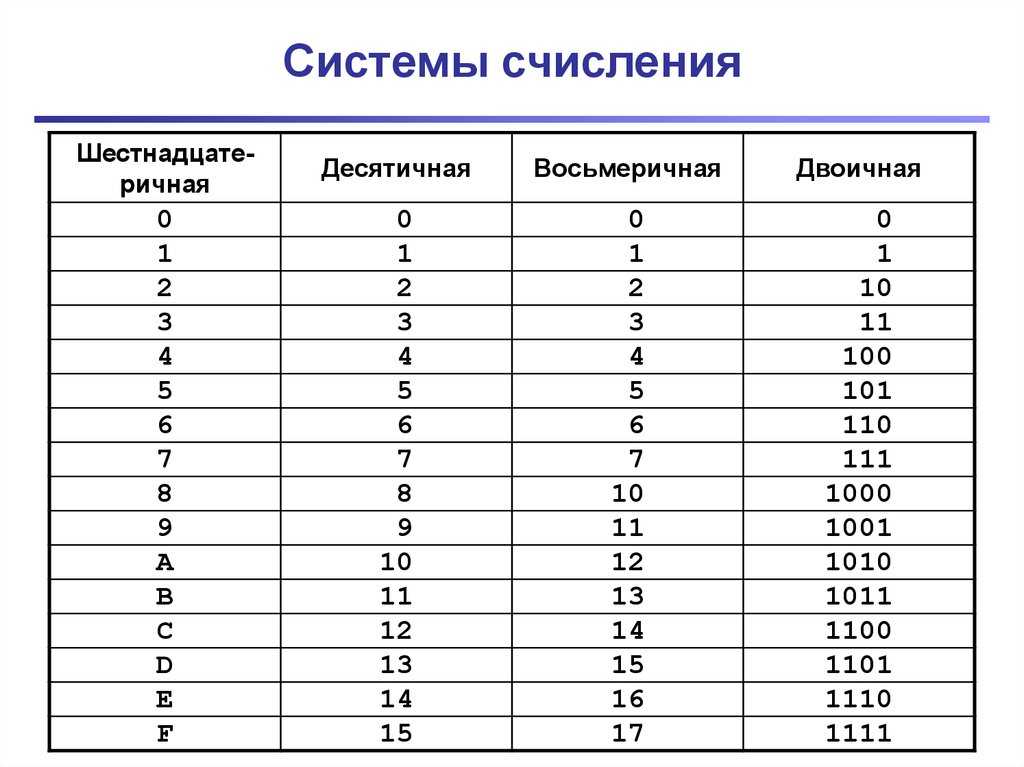
Вот некоторые эквивалентные значения:

Десятичный:	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Двоичный:	0	1	10	11	100	101	110	111	1000	1001	1010	1011	1100	1101	1110	1111

Симметрия

Двоичные числа также имеют красивый и элегантный узор:

Вот несколько больших значений:

Десятичный:	20	25	30	40	50	100	200	500
Двоичный:	10100	11001	11110	101000	110010	1100100	11001000	111110100

«Двоичный код так же прост, как 1, 10, 11. »

Теперь посмотрите, как использовать двоичный код, чтобы считать на пальцах больше 1000:

Деятельность: Бинарные пальцы

 

Позиция

В десятичной системе есть единицы, десятки, сотни и т. д.

В Двоичный есть Единицы, Двойки, Четверки и т. д., например:

Это 1×8 + 1×4 + 0×2 + 1 + 1×(1/2) + 0×(1/4) + 1×(1/8)
= 13,625 в десятичной системе счисления

 

Цифры можно размещать слева или справа от точки, чтобы показать значения больше единицы и меньше одного.

10,1
	Число слева от точки целое число (например, 10)
По мере того, как мы двигаемся дальше влево, каждый числовой разряд получает 2 раз больше .
	Первая цифра справа означает половинки (1/2).
	По мере того, как мы двигаемся дальше вправо, каждый числовой разряд получает в 2 раза меньше (в два раза больше).

Пример: 10.1

• «10» означает 2 в десятичной системе,
• «.1» означает половину,
• Таким образом, «10,1» в двоичном формате равно 2,5 в десятичном виде

Вы можете выполнять преобразования в Конвертер двоичных и десятичных чисел в шестнадцатеричные.

Слов

Слово двоичное происходит от «Би-», что означает два. Мы видим «би-» в таких словах, как «велосипед» (два колеса) или «бинокль» (два глаза).

Когда вы произносите двоичное число, произносите каждую цифру (например, двоичное число «101» произносится как «один ноль один» , или иногда «один-о-один» ). Таким образом, люди не путаются с десятичным числом.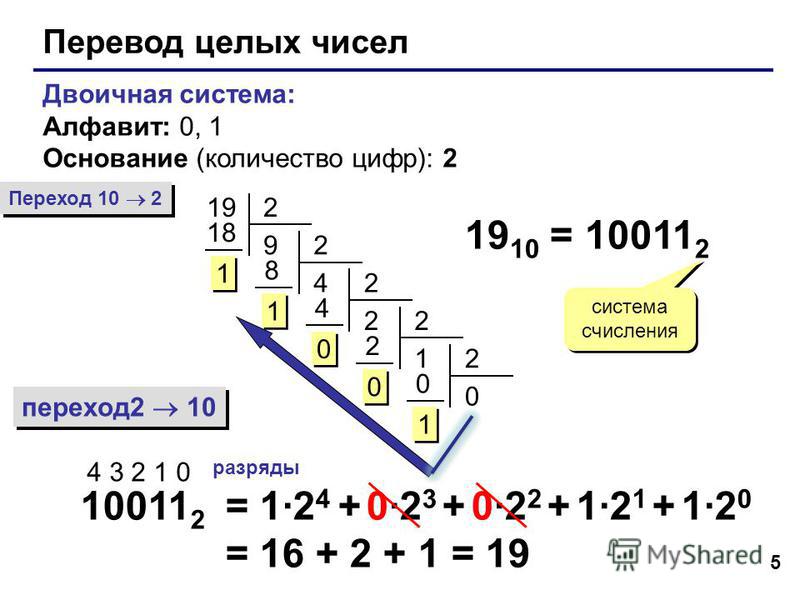

Одна двоичная цифра (например, «0» или «1») называется «бит».

Например, 11010 имеет длину пять бит.

Слово бит составлено из слов « b inary dig it »

Как показать, что число является двоичным

Чтобы показать, что число является двоичным числом , добавьте к нему маленькую двойку, например: 101 ₂

Таким образом, люди не будут думать, что это десятичное число «101» (сто один).

Примеры

Пример: Что такое 1111

₂ в десятичном формате?
• «1» слева находится в позиции «2×2×2», что означает 1×2×2×2 (=8)
• Следующая «1» находится в позиции «2×2», так что это означает 1×2×2 (=4)
• Следующая «1» находится в позиции «2», так что это означает 1×2 (=2)
• Последняя «1» стоит в позиции единиц, значит 1
• Ответ: 1111 = 8+4+2+1 = 15 в десятичной дроби

Пример: Что такое 1001

₂ в десятичном формате?
• «1» слева находится в позиции «2×2×2», что означает 1×2×2×2 (=8)
• «0» стоит в позиции «2×2», значит, это означает 0×2×2 (=0)
• Следующий «0» находится в позиции «2», что означает 0×2 (=0)
• Последняя «1» стоит в позиции единиц, значит 1
• Ответ: 1001 = 8+0+0+1 = 9 в десятичной системе счисления

Пример: Что такое 1.