В трапеции проведены диагонали (рис. 60.3). Укажите пары равновеликих треугольников.

Другие предметы, 17.04.2019 03:40, PHVRVOH

В трапеции проведены диагонали (рис. 60.3). Укажите пары равновеликих треугольников.

Посмотреть ответы

Другие вопросы по: Другие предметы

Найдите геометрическое место вершин треугольников, равновеликих данному треугольнику и имеющих с ним одну общую сторону….

Опубликовано: 17.04.2019 03:40

Ответов: 2

Докажите, что медианы треугольника делят его на шесть равновеликих треугольников….

Опубликовано: 17.04.2019 03:40

Ответов: 3

В трапеции проведены диагонали. Площади двух треугольников, прилежащих к основаниям трапеции, равны 4 и 9. Найдите площадь трапеции….

Опубликовано: 17.04.2019 03:40

Ответов: 1

Знаешь правильный ответ?

В трапеции проведены диагонали (рис. 60.3). Укажите пары равновеликих треугольников….

Популярные вопросы

.(Аня движется относительно люды, которая, в свою очередь, движется относительно кати, может ли аня находиться в покое относительно кати? обоснуйте ответ)….

Опубликовано: 26.02.2019 20:30

Ответов: 1

Скласти план до оповідання «якого кольору слова? «…

Опубликовано: 02.03.2019 14:00

Ответов: 2

Лабораторная работа. экспериментальная часть. влияние ph среды на характервосстановление перманганата калия.1)kmno4+h3so4+kno2=mnso4+kno3 +k2so4+h3o. 2)kmno4+h3o+kno2=mno21+kno3+ko…

Опубликовано: 02.03.2019 18:00

Ответов: 1

Проверь, все ли равентва верны. исправь неверные равенства, поствив скобки. 9*3+45/9=72 9*3+45/9=32 9*3+45/9=8 6*16-8*2=80 6*16-8*2=96 6*16-8*2=176…

Опубликовано: 03.03.2019 12:40

Ответов: 2

Каковы размеры средне-сибирского плоскогорья.

..

Опубликовано: 03.03.2019 19:50

Ответов: 3

Разберити слово по составу корень суффекс приставка окончание слова учительница читательница зубчатый…

Опубликовано: 04.03.2019 03:10

Ответов: 2

Масса ящика с лимонами 34 кг. когда половину лимонов продали, масса ящика с оставшимися лимонами оказалось равной 19 кг. найди массу пустого ящика….

Опубликовано: 04.03.2019 04:20

Ответов: 1

Расположите фамилии лиц в хронологическом порядке их деятельности. запишите буквы, которыми обозначены фамилии, в правильной последовательности. а) ф. ф. ушаков б) в. шуйский в) а…

Опубликовано: 04.03.2019 09:30

Ответов: 1

Найдите производную функции f(x)1,5cos2x-5sin3x…

Опубликовано: 04.03.2019 09:50

Ответов: 1

1. найти площадь треугольника, если его основание равно 8 см, а высота равна 3 см 2. два угла треугольника имеют величину по 30 градусов. определить величину третьего угла…

Опубликовано: 06.03.2019 20:00

Ответов: 3

Больше вопросов по предмету: Другие предметы Случайные вопросы

Популярные вопросы

Презентация. Площадь трапеции. Решение задач. 8 класс

ПЛОЩАДЬ

ТРАПЕЦИИ

8 класс

МБОУ «Большаковская СОШ» Яковлева Ирина Владимировна

Теорема. Площадь трапеции равна произведению полусуммы оснований на высоту.

В режиме слайдов ответы появляются после кликанья мышкой

Следствие 1. Площадь трапеции равна произведению средней линии на высоту.

№ 1

Основания трапеции равны 10 см и 35 см, площадь равна 225 см 2 . Найдите ее высоту.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 10 см.

№ 2

Докажите, что прямая, проходящая через середину средней линии трапеции и пересекающая основания, делит эту трапецию на две равновеликие части.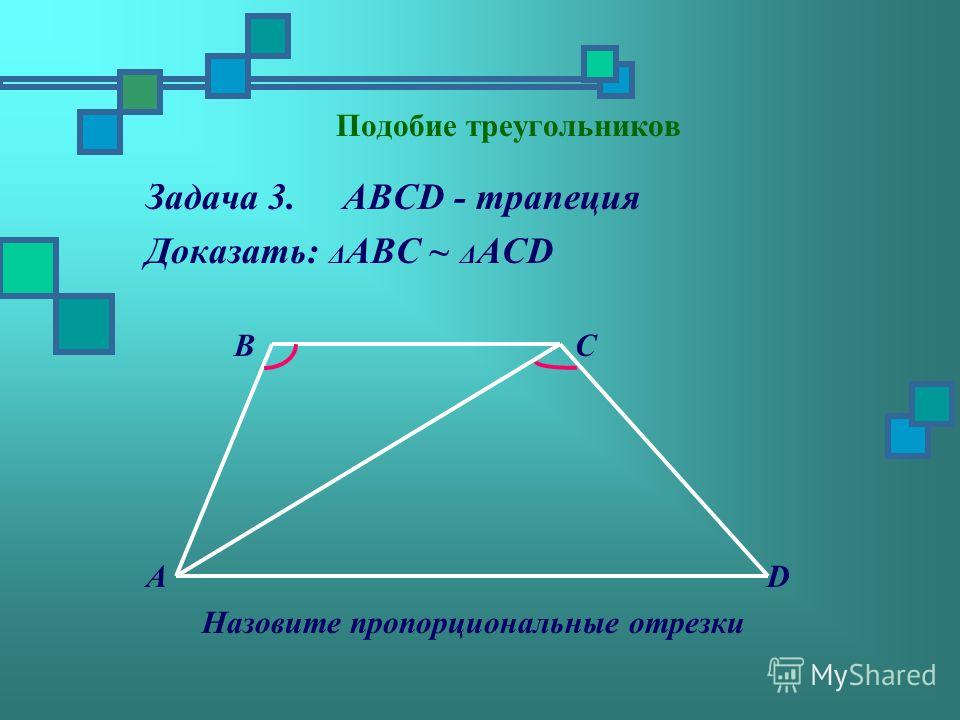

Доказательство: Пусть ABCD – трапеция ( AB || CD ), EF – средняя линия, MN – прямая, проходящая через середину G средней линии и пересекающая основания в точках M и N . Трапеции AMND и MBCN имеют равные средние линии и высоты. Следовательно, площади этих трапеций равны, т.е. они равновелики.

В режиме слайдов ответы появляются после кликанья мышкой

№ 3

Найдите площадь трапеции, изображенной на клетчатой бумаге, клетками которой являются единичные квадраты.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 6 .

№ 4

Найдите площадь трапеции, изображенной на клетчатой бумаге, клетками которой являются единичные квадраты.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 7,5 .

№ 5

Найдите площадь трапеции, изображенной на клетчатой бумаге, клетками которой являются единичные квадраты.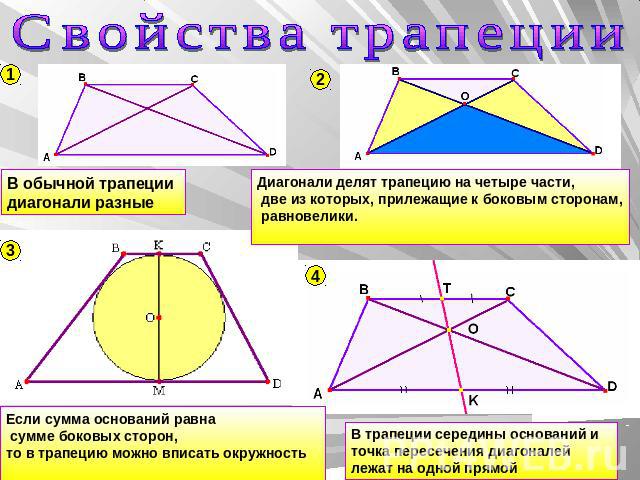

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 5 .

№ 6

Найдите площадь трапеции, изображенной на клетчатой бумаге, клетками которой являются единичные квадраты.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 6 .

№ 7

Найдите площадь трапеции, изображенной на клетчатой бумаге, клетками которой являются единичные квадраты.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 7,5 .

№ 8

Найдите площадь трапеции, основания которой 12 см и 16 см, а высота 15 см.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 210 см 2 .

№ 9

Основания трапеции равны 36 см и 12 см, боковая сторона, равная 7 см, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 84 см 2 .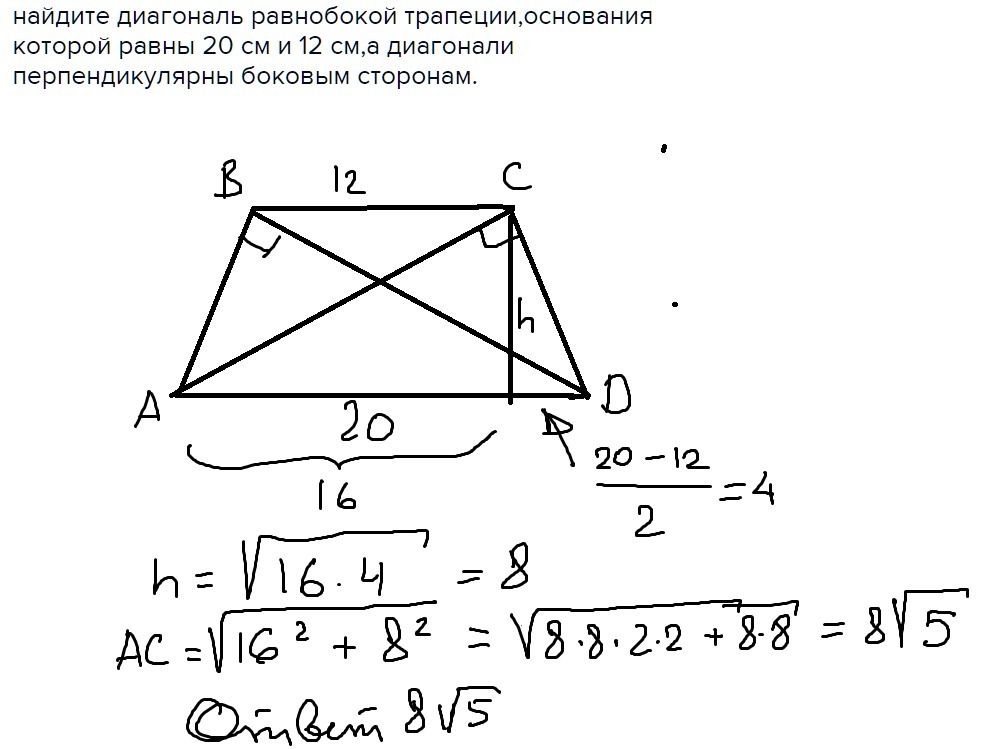

№ 10

Основание трапеции равно 26 см, высота 10 см, а площадь 200 см 2 . Найдите второе основание трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 14 см.

№ 11

Высота трапеции равна 20 см, площадь — 400 см 2 . Найдите среднюю линию трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 20 см.

№ 12

Площадь трапеции равна 36 см 2 , высота равна 2 см. Найдите основания трапеции, если они относятся как 4:5.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 16 см и 20 см.

№ 13

Найдите площадь прямоугольной трапеции, основания которой равны 3 см и 1 см, большая боковая сторона составляет с основанием угол 45 о .

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 4 см 2 .

№ 14

Найдите площадь трапеции, у которой средняя линия равна 10 см, боковая сторона – 6 см и составляет с одним из оснований угол 150 о .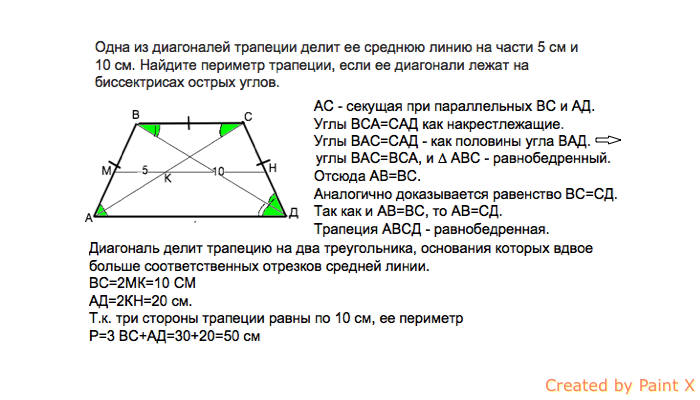

Ответ: 30 см 2 .

В режиме слайдов ответы появляются после кликанья мышкой

№ 15

Тупой угол равнобедренной трапеции равен 135 о , а высота, проведенная из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 4,76 см 2 .

№ 16

В трапеции проведены диагонали. Укажите пары равновеликих треугольников.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: ABD и ABC , ACD и BCD , AOD и BOC .

№ 17*

Трапеция разбита диагоналями на четыре треугольника. Найдите ее площадь, если площади треугольников, прилегающих к основаниям трапеции, равны S 1 и S 2 .

В режиме слайдов ответы появляются после кликанья мышкой

Ответ:

19

Использованы ресурсы:

\circ \cdot i}n \end{align*}$$

Для следующего (то есть $(i+1)$th) треугольника $\triangle P_0P_{i+1}P_{i+2}$ отразите $P_{i} $ по диагонали $P_0P_{i+1}$, чтобы получить $P_{i}’$.

$P_{i}’$ может быть снаружи, внутри или на краю многоугольника, но случаи аналогичны.

Примеры $i=1$ и $i=5$ в правильном многоугольнике:

В обоих случаях стратегия доказательства такова:

  1. Рассмотрим внутренний угол многоугольника $\angle P_iP_{i+1 }P_{i+2}$ и три угла, имеющие общую вершину: $\angle P_iP_{i+1}P_0$, $\angle P_0P_{i+1}P_i’$ и $\angle P_i’P_{i+ 1}P_{i+2}$;
  2. Используйте предположение индукции для решения $\angle P_i’P_{i+1}P_{i+2}$;
  3. Рассмотрим равнобедренный треугольник $\triangle P_i’P_{i+1}P_{i+2}$ и решите его углы при основании $\angle P_{i+1}P_i’P_{i+2}$ и $\ угол P_i’P_{i+2}P_{i+1}$;
  4. Покажите, что $P_0$, $P_i’$ и $P_{i+2}$ лежат на одной прямой, используя первый угол при основании;
  5. Докажите утверждение индукции для $i+1$.

Если $P_{i}’$ находится внутри многоугольника, т.е. $i=1$ выше, рассмотрим треугольники при $P_{i+1}$: $\triangle P_0P_iP_{i+1}$, $\triangle P_0P_i’P_{i+1}$ и $\triangle P_i’P_ {i+1}P_{i+2}$. 9\circ}n$ для $i = 1, 2, \ldots , n-2$.

Какие бывают четырехугольники?

Четырехугольники являются многоугольниками. Они являются частью плоскости, окруженной четырьмя сторонами (quad означает четыре, а lateral означает сторону). Все четырехугольники имеют ровно четыре стороны и четыре угла. Их можно разделить на определенные группы в зависимости от длины их сторон или углов.

Четырехугольники включают квадрат, прямоугольник, трапецию, ромб, параллелограмм и воздушный змей (также называемый касательным четырехугольником). Пока четыре стороны соединяются прямыми линиями, это четырехугольник. Он не должен образовывать узнаваемую форму. 9{\circ}$.

Диагонали — это линии, соединяющие противоположные углы.

Деление четырехугольников по перпендикулярности диагоналей и параллельности сторон:

Разносторонний четырехугольник

Первая группа четырехугольников — это разносторонний четырехугольник . Разносторонний четырехугольник — это четырехугольник, не обладающий какими-либо особыми свойствами. Стороны и углы имеют разную длину и размеры.


Трапеции

Четырехугольники, имеющие одну пару параллельных сторон, называются трапециями . Параллельные стороны называются основаниями трапеции, а непараллельные называются катетами .

Равнобедренная трапеция

Трапеции, катеты которых имеют одинаковую длину, называются равнобедренными трапециями .

Диагонали равнобедренных трапеций равны.

Высота или Высота трапеции — это длина прямой, перпендикулярной основанию и проходящей через противоположную вершину. Высота трапеции будет одинакова независимо от того, из какой вершины мы ее проводим. Если мы рисуем высоту от большего основания, мы просто удлиняем более короткое основание.

Теорема

Если $\alpha$ угол в вершине $A$, $\beta$ в вершине $B$, $\gamma$ в вершине $C$ и $\delta$ в вершине $D$ в трапеции $ABCD$, то верно:

$\alpha + \delta = 180^{\circ}$ 9{\circ}$.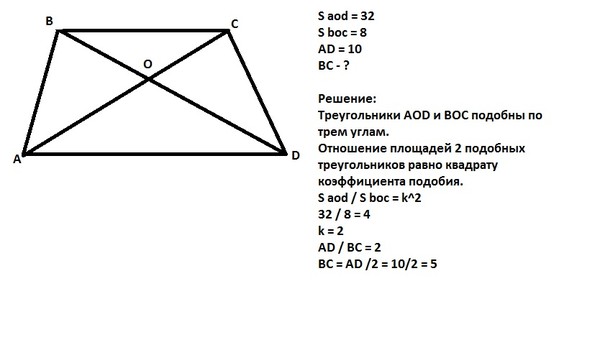 {\circ} $. 9{\circ}$.

 

Параллелограмм

Параллелограмм — это четырехугольник, противоположные стороны которого равны и параллельны.

Высота или  высота параллелограмма в метке $h$ — это отрезок, соединяющий вершину с противоположной стороной и перпендикулярный этой стороне.

Помимо того, что параллелограммы являются четырехугольниками, существуют определенные формы, которые являются параллелограммами так же, как и четырехугольниками. Это квадрат, прямоугольник и ромб. 9{\circ}.$$

Отсюда следует $\beta = \delta$ и $\alpha = \gamma$.

 

Теорема

Следующие утверждения эквивалентны друг другу:

1) Четырехугольник $ABCD$ является параллелограммом

2) Существуют две противоположные стороны четырехугольника $ABCD$, которые равны и параллельны

3) Каждые две противоположные стороны четырехугольника $ABCD$ равны

4) Диагонали четырехугольника $ABCD$ делят друг друга пополам

5) Обе пары противоположных углов четырехугольника $ABCD$ равны

Каждое из приведенных выше утверждений может быть альтернативным определением параллелограмма. Остальные утверждения нам нужно доказать.

Доказательство.

$1) \Rightarrow 2)$

Пусть $ABCD$ — параллелограмм. Затем $\overline{AB} \| \overline{CD}$ и $\overline{AD} \| \overline{BC}$.

 

 

Так как прямая $AC$ является ходом параллельных прямых $AB$ и $CD$ , то $\angle{ACD} =\angle{CAB}$. Прямая $AC$ также является обходом параллельных прямых $BC$ и $AD$, то есть $\angle{ACB}=\angle{DAC}$.

$\overline{AC}$ также является общей стороной треугольников $ABC$ и $CDA$. По теореме А-С-А о конгруэнтности треугольников треугольники $ABC$ и $CDA$ конгруэнтны. Отсюда следует, что $|AB| = |CD]$ и $|AD| = |BC|$.

$2) \Rightarrow 3)$

В четырехугольнике  $ABCD$ пусть будет $AB \| CD$ и $|AB| = |CD|$.

Так как $AC$ является ходом параллельных прямых $AB$ и $CD$, то $\angle{ACD} =\angle{CAB}$. Сторона $\overline{AC}$ является общей стороной треугольников $ABC$ и $CDB$. По теореме S-A-S о конгруэнтности треугольников треугольники $ABC$ и $CDB$ конгруэнтны.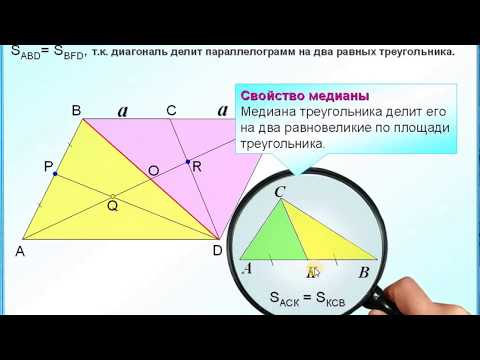 Отсюда следует, что $|BC| = |CD|.$

 

$3) \Rightarrow 4)$

В четырехугольнике $ABCD$ пусть $|AB|=|CD|$ и $|BC| = |CD|$, а точка $S$ является пересечением диагоналей $\overline{AC}$ и $\overline{BD}$.

 

Сначала рассмотрим треугольники $ABC$ и $CDB$. По теореме С-С-С о конгруэнтности треугольников треугольники $ABC$ и $CDB$ конгруэнтны. Отсюда следует, что $\angle{ACB} = \angle {CAD}$.

Углы $ASD$ и $BSC$ являются вертикальными углами. Если теперь рассмотреть треугольники $ASD$ и $BSD$, то следует, что $\angle{ADS} = \angle{CBS}$. Поскольку $|BC|= |AD|$, треугольники $ASD$ и $BSC$ конгруэнтны по теореме A-S-A о конгруэнтности треугольников. Отсюда следует, что $|AS| = |SC|$ и $|BS| = |SD|$, что означает, что точка $S$ является средней точкой $\overline{AC}$ и $\overline{BD}$.

$4) \Rightarrow 5)$

В четырехугольнике $ABCD$ точка $S$ будет серединой диагоналей $\overline{AC}$ и $\overline{AD}$: $|AS|=|CS |$ и $|BS|=|DS|$.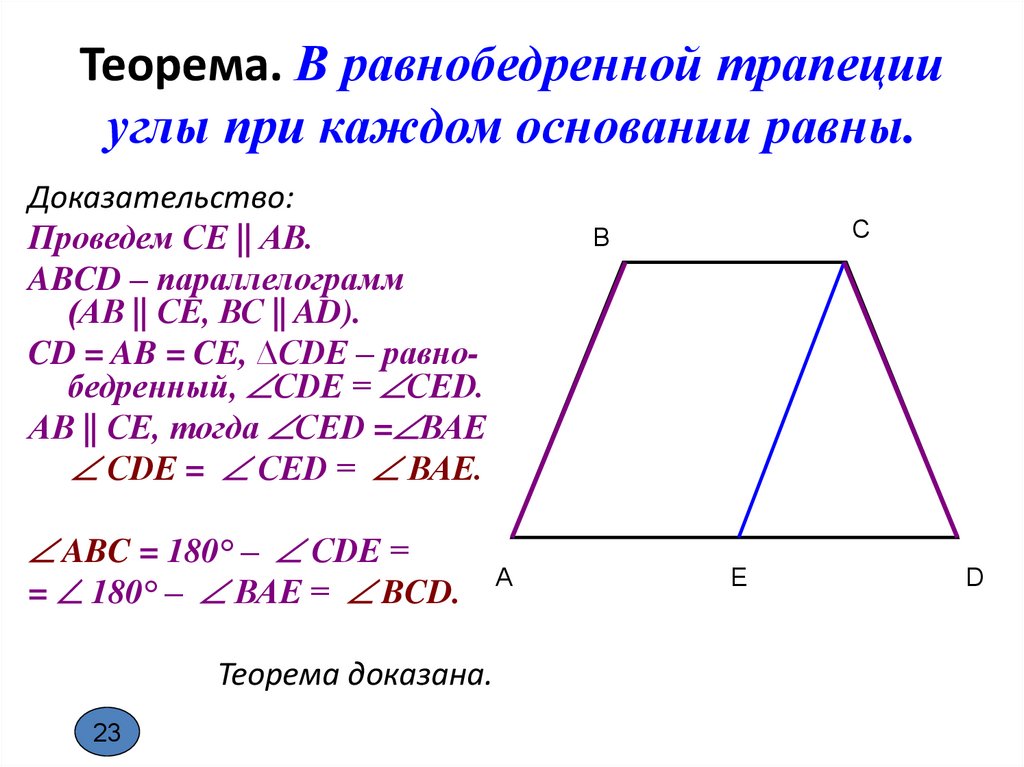

Рассмотрим треугольники $BCS$ и $ADS$. По теореме S-A-S они конгруэнтны ($|CS| = |AS|$ – $\angle{BSC}=\angle{ASB}$ (вертикальные углы) – $|BS|=|DS|$). Отсюда следует, что $\angle{BCS}=\angle{DAS}$ и $\angle{CBS}=\angle{ADS}$.

Треугольники $ABS$ и $CDS$ также конгруэнтны по теореме S-A-S ($|AS|=|CS|$ – $\angle{ASB}=\angle{CSD}$ (вертикальные углы)  – $|BS|= |ДС|$). Отсюда следует, что $\angle{BAS}=\angle{DCS}$ и $\angle{ABS}=\angle{CDS}$. 9{\circ}$, что также является противоречием.

Отсюда следует, что $AB \| AC$.

Аналогично доказывается, что $BC \| AD$.

Ромб

Ромб  – это параллелограмм, у которого хотя бы одна пара смежных сторон имеет одинаковую длину.

Противоположные углы равновелики: $\alpha = \gamma$, $\beta = \delta$ и что смежные углы являются дополнительными.

Диагонали ромба равны и перпендикулярны.

 

Касательный четырехугольник

Воздушный змей — это четырехугольник, характеризующий две пары сторон равной длины, смежных друг с другом. Диагонали воздушного змея перпендикулярны, и по крайней мере одна диагональ является линией симметрии. Воздушный змей также является касательным четырехугольником.

Прямоугольник

Прямоугольник  – это параллелограмм, у которого хотя бы один внутренний угол прямой.

Диагонали прямоугольников равны. 92$

 

Площадь четырехугольника

Площадь квадрата равна квадрату длины его стороны.

Далее идет площадь прямоугольника. Площадь прямоугольника равна произведению длин смежных сторон.

Площадь ромба равна произведению длины его стороны на высоту.

Это верно, потому что из рисунка: Если мы перенесём высоту $\overline{BE}$ в точку $A$ и продолжим сторону $ED$ над вершиной $D$, мы получим треугольник $E’DA$, который совпадает с треугольником $ECB$. Если «перевести» треугольник $ECB$ на треугольник $E’DA$, то получится прямоугольник с одной стороной $a$ и другой $h$.

То же, что и для ромба, работает на параллелограмме , площадь параллелограмма является произведением его одной стороны и высоты на этой стороне.

Площадь трапеции равна половине произведения суммы ее оснований и высоты.

Эта формула является результатом деления трапеции на два треугольника $AED$ и $BCF$ и прямоугольник $EFCD$.

Теперь мы можем записать нашу площадь в виде суммы меньших площадей: $ A_{(ABCD)} = A_{(AED)} + A_{(FBC)} + A_{(EFCD)}$.

Мы знаем, что $ A_{(EFCD)} =h \cdot c$.
Теперь нам нужно найти $A_{(AED)}$ и $A_{(FBC)}$. Если мы перенесем сторону $b$ рядом с $AED$, то получим треугольник $AHD$.

Высота треугольника $AHD$ равна высоте трапеции $ABCD$.

А сторона, на которой задана эта высота, равна $a – c$. Это приводит к выводу, что:

$\ A_ {(AHD)} = h \cdot \frac{a – c}{2}$.

Это означает, что:

$$A_ {(ABCD)} = A_ {(AHD)} + A_ {(HBCD)} =$$

$$=\frac{h \cdot (a – c)}{2} + c\cdot h= \frac{a \cdot h – h\cdot c + 2h \cdot c}{2} = \frac {ч \cdot a + h \cdot c}{2} =$$

$$=\frac{h \cdot (a + c)}{2}$$.

 

Что такое четырехугольник?

Четырехугольник — это многоугольник с четырьмя сторонами.

Четырёхугольники какой формы?

Четырехугольники: квадрат, прямоугольник, трапеция, ромб.

Как определить четырехугольник?

Четырехугольник представляет собой плоскую фигуру с четырьмя соединяющимися сторонами. Квадрат означает четыре. Боковая значит боковая. Все линии должны быть соединены. Это также плоская форма, 2-мерная. Одни четырехугольники образуют идентифицируемые формы, другие нет.

Какие 7 четырехугольников?

Четырехугольников семь. К ним относятся: квадрат, прямоугольник, ромб, трапеция, равнобедренная трапеция, параллелограмм, касательный четырехугольник (также известный как воздушный змей из-за его формы воздушного змея).

Какие есть 4 типа четырехугольников?

Четырехугольники можно разделить на четыре типа. Это параллелограмм, ромб, квадрат и прямоугольник. Кроме того, ромбы, квадраты, прямоугольники — все это параллелограммы.