Подготовка школьников к ЕГЭ и ОГЭ Справочник по математике — Планиметрия
| Справочник по математике | Геометрия (Планиметрия) | Средние линии |
| Средние линии треугольника |
| Средняя линия трапеции |
| Средние линии четырехугольников. Теорема Вариньона |
| Средние линии тетраэдра |
Средние линии треугольника
Определение. Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника (рис. 1).
Рис.1
На рисунке 1 средней линией является отрезок DE.
Утверждение 1. Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.
Доказательство. Рассмотрим произвольный треугольник ABC и обозначим буквой D середину стороны AB (рис. 2). Проведем через точку D до пересечения с прямой BC прямую, параллельную прямой AC . Обозначим буквой E точку пересечения прямых DE и BC .
Рассмотрим произвольный треугольник ABC и обозначим буквой D середину стороны AB (рис. 2). Проведем через точку D до пересечения с прямой BC прямую, параллельную прямой AC . Обозначим буквой E точку пересечения прямых DE и BC .
Рис.2
Поскольку AD = DB , а прямые AC и DE параллельны, то выполнены все условия теоремы Фалеса, и можно заключить, что выполнено равенство: CE = EB . Отсюда вытекает, что точка E является серединой стороны CB , а отрезок DE является средней линией треугольника.
Первую часть утверждения 1 мы доказали.
Для того, чтобы доказать вторую часть утверждения 1, заметим, что в любом треугольнике можно провести три средних линии – отрезки DE , EF и FD (рис.3).
Рис.3
Поскольку
DE | | FC , DF | | EC ,
то четырёхугольник DECF – параллелограммчетырёхугольник DECF – параллелограмм, следовательно, DE = FC .
Поскольку
DE | | AF , AD | | FE ,
то четырёхугольник DEFA – параллелограммчетырёхугольник DEFA – параллелограмм, следовательно, DE = AF .
Но поскольку AF = FC , то отсюда вытекает равенство
что и требуется доказать.
Доказательство утверждения 1 закончено.
Следствие.
- Три средних линии делят треугольник на 4 равных треугольника ADF , DBE , ECF , DEF (рис. 4).
- Каждый из четырёх треугольников ADF , DBE , ECF , DEF подобен треугольнику ABC с коэффициентом подобия 0,5.
Рис.4
Средняя линия трапеции
Напомним, что трапециейтрапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны.
Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции.
Отрезки, соединяющие противоположные вершины трапеции, называют диагоналями трапеции.
Определение. Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции (рис. 5).
Рис.5
На рисунке 5 средней линией трапеции является отрезок EF .
Утверждение 2. Средняя линия трапеции параллельна основаниям трапеции и равна половине суммы этих оснований.
Рис.6
Доказательство. Проведем через вершину B и середину боковой стороны F трапеции прямую линию (рис. 6). Обозначим точку пересечения прямых BF и AD буквой G . Рассмотрим треугольники BCF и FDG . У этих треугольников стороны CF и FD равны, поскольку точка F – середина стороны CD . Углы BCF и FDG равны, поскольку они являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых BC и AD с секущей CD . Углы BFC и DFG равны, поскольку они являются вертикальными. Тем самым выполнены все условия признака равенства треугольников «По стороне и прилежащим к ней углам», и можно заключить, что треугольники BCF и FDG равны. Из равенства треугольников BCF и FDG следует равенство отрезков BF и FG , откуда вытекает, что отрезок EF является средней линией треугольника ABG . Поэтому
Углы BCF и FDG равны, поскольку они являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых BC и AD с секущей CD . Углы BFC и DFG равны, поскольку они являются вертикальными. Тем самым выполнены все условия признака равенства треугольников «По стороне и прилежащим к ней углам», и можно заключить, что треугольники BCF и FDG равны. Из равенства треугольников BCF и FDG следует равенство отрезков BF и FG , откуда вытекает, что отрезок EF является средней линией треугольника ABG . Поэтому
что и требовалось доказать.
Задача 1. Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции.
Рис.7
Решение. Пусть ABCD – трапеция, EF – её средняя линия, LM – указанный отрезок (рис.7). Поскольку AE = EB , то, в силу теоремы Фалеса, выполнено равенство: LN = NM , что и требовалось доказать.
Задача 2. Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции.
Рис.8
Решение. Пусть ABCD – трапеция, EF – её средняя линия, KL – указанный отрезок (рис.8). В соответствии с задачей 1 можем заключить, что точка K – середина отрезка AC , а точка L – середина отрезка BD . Поэтому отрезок EK – средняя линия треугольника BAC , а отрезок EL – средняя линия треугольника ABD . В силу утверждения 1 выполнены равенства:
Следовательно,
что и требовалось доказать.
Утверждение 3. Прямая, проходящая через середины оснований трапеции, проходит через точку пересечения боковых сторон трапеции.
Рис.9
Доказательство. Пусть K и L – середины оснований BC и AD трапеции ABCD соответственно (рис.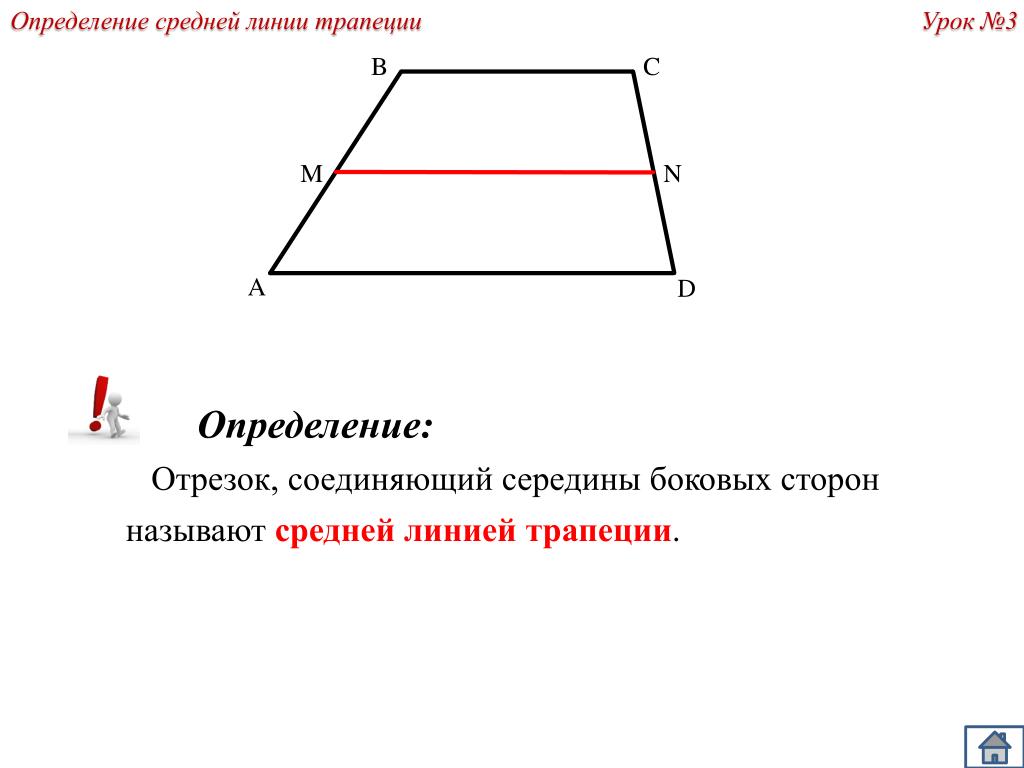 9). Обозначим буквой M точку пересечения боковых сторон AB и CD . Проведем через точки M и K прямую и обозначим точку пересечения этой прямой с основанием AD символом N . Докажем, что точки N и L совпадают. Для этого заметим, что треугольник BMK подобен треугольнику AMN . Следовательно, выполнено равенство:
9). Обозначим буквой M точку пересечения боковых сторон AB и CD . Проведем через точки M и K прямую и обозначим точку пересечения этой прямой с основанием AD символом N . Докажем, что точки N и L совпадают. Для этого заметим, что треугольник BMK подобен треугольнику AMN . Следовательно, выполнено равенство:
Заметим также, что треугольник KMC подобен треугольнику NMD . Поэтому
Из этих соотношений получаем:
откуда вытекает, что точки N и L совпадают. Доказательство завершено.
Почти те же рассуждения позволяют доказать следующий факт, который мы предоставляем читателю в качестве упражнения.
Утверждение 4. Прямая, проходящая через точку пересечения диагоналей и середину одного из оснований трапеции, проходит через середину другого основания трапеции.
Следствие.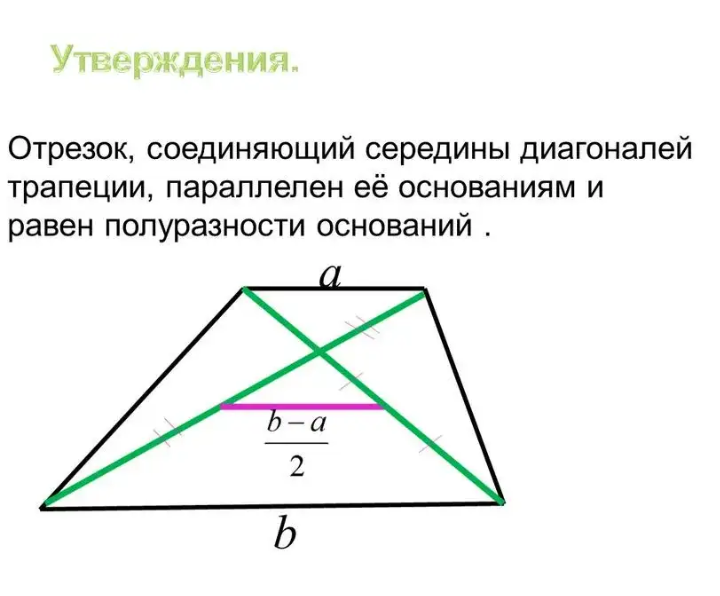 Точка пересечения диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой.
Точка пересечения диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой.
Средние линии четырехугольника. Теорема Вариньона
Определение. Средней линией четырехугольника называют отрезок, соединяющий середины непересекающихся сторон четырёхугольника.
Поскольку у каждого четырехугольника имеются две пары непересекающихся сторон, то у каждого четырехугольника имеются две средних линии (рис.10).
Рис.10
На рисунке 10 средние линии – это отрезки EF и GH .
Замечание 1. Приведенное определение средней линии относится не только к плоским четырехугольникам, но и к «пространственным четырехугольникам» (рис.11). «Пространственным четырехугольником» мы называем замкнутую ломаную линию из 4 звеньев без самопересечений, не лежащую в одной плоскости.
Рис.11
На рисунке 11 изображен «пространственный четырёхугольник» ABCD , средними линиями которого являются отрезки EF и GH .
Замечание 2. Несмотря на то, что трапеция является четырехугольником, принято средней линией трапеции называть только отрезок, соединяющий середины её боковых сторон.
Замечание 3. В данном разделе справочника не рассматриваются невыпуклые четырёхугольники и четырёхугольники с самопересечениями.
Теорема Вариньона. Середины сторон произвольного плоского или «пространственного» четырёхугольника являются вершинами параллелограммапараллелограмма.
Доказательство. Рассмотрим плоский четырёхугольник ABCD , изображенный на рисунке 12. Точки E, G, F, H – середины сторон, отрезок AC – диагональ четырёхугольника.
Рис.12
Поскольку отрезок EG – средняя линия треугольника ABC , то отрезок EG параллелен диагонали AC и равен её половине. Поскольку отрезок FH – средняя линия треугольника CDA , то отрезок FH параллелен диагонали AC и равен её половине. Таким образом, в четырёхугольнике EGFH противоположные стороны EG и FH равны и параллельны. В силу признака параллелограммапризнака параллелограммапризнака параллелограмма отсюда вытекает, что четырёхугольник EGFH – параллелограмм, что и требовалось доказать.
Замечание 4 . В случае «пространственного четырёхугольника» ABCD доказательство остаётся тем же (рис. 13).
Рис.13
Поскольку диагонали параллелограмма в точке пересечения делятся пополамдиагонали параллелограмма в точке пересечения делятся пополамдиагонали параллелограмма в точке пересечения делятся пополам, то справедливо следующее утверждение, непосредственно вытекающее из теоремы Вариньона.
Утверждение 5. Средние линии произвольного четырёхугольника пересекаются и в точке пересечения делятся пополам (рис. 14).
Рис.14
Утверждение 6. Рассмотрим произвольный плоский или «пространственный» четырёхугольник ABCD , у которого отрезок EF является одной из средних линий (рис. 15). Тогда будет выполнено векторное равенство:
Рис.15
Доказательство. Рассмотрим в пространстве или на плоскости произвольную декартову систему координат с началом в некоторой точке O (рис. 16).
Рис.16
В соответствии со свойствами векторов справедливы следующие равенства:
что и требовалось доказать.
Следствие. Средняя линия четырёхугольника меньше или равна половине суммы не пересекающих её сторон четырёхугольника, причём равенство достигается лишь в том случае, когда указанные стороны четырёхугольника параллельны.
Другими словами, средняя линия четырёхугольника равна половине суммы не пересекающих её сторон четырёхугольника лишь в том случае, когда этот четырехугольник является трапециейтрапецией, а не пересекающие среднюю линию стороны четырёхугольника – основания трапеции.
Средние линии тетраэдра
Тетраэдром называют произвольную треугольную пирамиду (рис.17).
Рис.17
У каждого тетраэдра имеется 4 вершины, 4 грани и 6 рёбер, причем все рёбра делятся на 3 пары непересекающихся рёбер. На рисунке 17 каждая пара непересекающихся рёбер выделена отдельным цветом. Каждые два непересекающихся ребра тетраэдра лежат на скрещивающихся прямых скрещивающихся прямых.
Определение. Средней линией (бимедианой) тетраэдра называют отрезок, соединяющий середины двух непересекающихся рёбер тетраэдра.
Рис.18
У каждого тетраэдра имеется 3 средних линии. Изображённый на рисунке 18 отрезок EF является одной из средних линий тетраэдра.
Утверждение 7. Все средние линии тетраэдра пересекаются в одной точке и делятся этой точкой пополам.
Доказательство. Выберем какую-нибудь среднюю линию тетраэдра, например, EF и докажем, что любая другая средняя линия тетраэдра проходит через середину отрезка EF . Для этого рассмотрим, например, среднюю линию GH , соединяющую середины рёбер AC и BD , и соединим отрезками точки E, H, F, G (рис.19).
Рис.19
Заметим, что отрезок EH является средней линией треугольника ADB , поэтому
Отрезок GF является средней линией треугольника ACB , поэтому
Отсюда вытекает, что отрезки EH и GF равны и параллельны, следовательно, четырёхугольник EHFG – параллелограммследовательно, четырёхугольник EHFG – параллелограммследовательно, четырёхугольник EHFG – параллелограмм. Поскольку средние линии тетраэдра EF и GH являются диагоналями этого параллелограмма, то в точке пересечения они делятся пополамв точке пересечения они делятся пополамв точке пересечения они делятся пополам, что и требовалось доказать.
Поскольку средние линии тетраэдра EF и GH являются диагоналями этого параллелограмма, то в точке пересечения они делятся пополамв точке пересечения они делятся пополамв точке пересечения они делятся пополам, что и требовалось доказать.
Определение. Точку пересечения средних линий тетраэдра называют центроидом тетраэдра.
Утверждение 8. Рассмотрим в пространстве декартову систему координат с началом в точке O и произвольный тетраэдр ABCD . Если обозначить буквой M центроид этого тетраэдра (рис. 20), то будет выполнено векторное равенство:
Рис.20
Доказательство. По свойствам векторов
что и требовалось доказать.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Доказать, что отрезок, соединяющий середины оснований трапеции, делит её на две равные по площади части.
 — вопрос №1878249 — Учеба и наука
— вопрос №1878249 — Учеба и наукагеометрия
математика
планиметрия
трапеция
отрезок
доказать
Лучший ответ по мнению автора | |||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
Средний сегмент трапеции Калькулятор
Создано Luciano Mino
Отзыв от Davide Borchia
Последнее обновление: 02 февраля 2023 г.
- Что такое медиана трапеции?
- Средняя часть трапеции формула
- Как найти среднюю часть трапеции?
- Другие полезные инструменты
- Часто задаваемые вопросы
Калькулятор среднего сегмента трапеции позволяет получить длину среднего сегмента или медианы трапеции. Медиана трапеции — это прямая, параллельная основаниям, расположенным посередине между ними. С помощью этого инструмента вы узнаете формулу средней части трапеции и узнаете, как найти среднюю часть любой трапеции.
Что такое медиана трапеции?
Медиана или середина трапеции — это линия, параллельная основаниям трапеции, которая проходит через середину между ними. Он простирается от одной непараллельной стороны к другой.
Трапеция с abcd сторонами.
Зная длину одного основания, вы можете использовать средний отрезок, чтобы найти длину другого. Давайте посмотрим на средний сегмент формулы трапеции, чтобы узнать, как это сделать.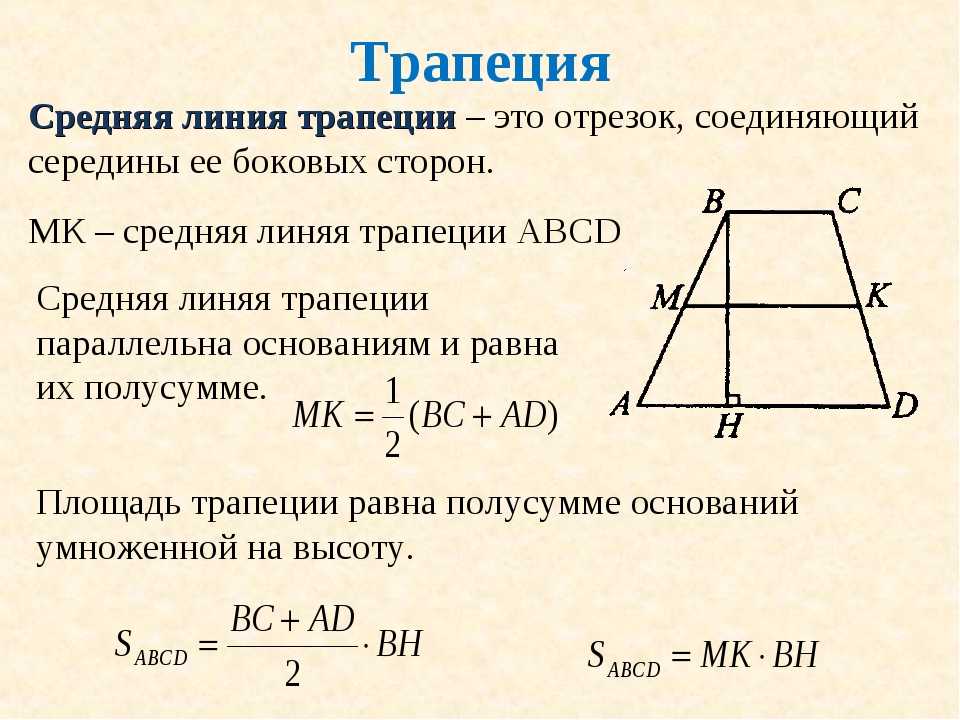
Средняя часть трапеции формулы
Медиана или средний отрезок формулы трапеции ABCD является прямой. Нам просто нужна длина каждого из оснований (ABABAB и CDCDCD), складываем их, а затем делим результат на два:
Midsegment=AB+CD2\text{Midsegment} = \frac{AB+CD}{2} Midsegment=2AB+CD
Это то же самое, что и нахождение медианы или среднего значения между основаниями, отсюда и название. Если вы найдете какие-либо две переменные, вы можете легко получить другую, заменив значения в приведенном выше уравнении, или просто использовать средний сегмент калькулятора трапеций, и он сделает всю работу за вас 😉.
Как найти среднюю часть трапеции?
Чтобы найти среднюю часть трапеции:
- Измерьте и запишите длину двух параллельных оснований.
- Добавьте два числа.
- Разделите результат на два. Это длина среднего сегмента.
Вы можете проверить результат с помощью среднего отрезка калькулятора трапеций или взглянуть на наш калькулятор трапеций, чтобы узнать больше.
Другие полезные инструменты
В этом тексте мы рассмотрели:
- Определение медианы трапеции;
- Медиана формулы трапеции; и
- Как найти середину трапеции.
Не стесняйтесь прочитать раздел часто задаваемых вопросов или попробовать другие полезные инструменты, похожие на средний сегмент калькулятора трапеций:
- Калькулятор трапеций
- Калькулятор площади трапеции
- Калькулятор периметра трапеции
- Калькулятор угла трапеции
- Калькулятор высоты трапеции
- Калькулятор равнобедренной трапеции
- Калькулятор площади равнобедренной трапеции
- Калькулятор правой трапеции
- Калькулятор площади правой трапеции
- Калькулятор площади неправильной трапеции
Часто задаваемые вопросы
Сколько средних сегментов у трапеции?
Трапеция имеет только один средний сегмент. Срединный отрезок — это линия, проходящая от одной непараллельной стороны к другой, параллельная основаниям и проходящая посередине между ними.
Срединный отрезок — это линия, проходящая от одной непараллельной стороны к другой, параллельная основаниям и проходящая посередине между ними.
Какой длины средний отрезок трапеции с основанием 2 см?
Средняя часть трапеции с основаниями 2 см равна 2 см . Формула для среднего отрезка равна (AB + CD) / 2 , и, поскольку AB и CD идентичны, результат и длины оснований равны по количеству.
Лучано Миньо
Середина сегмента
Посмотреть 23 похожих калькулятора 2D-геометрии 📏
ПлощадьПлощадь прямоугольникаПлощадь полумесяца… 20 еще
Видео-урок: Теоремы о средней линии треугольника
Стенограмма видео
В этом видео мы научимся использовать теорему о середине треугольника, чтобы доказать, что прямые параллельны или найти недостающая длина стороны в конкретном сценарии треугольника.
Начнем с первого
теоремы о середине треугольника.
Эта теорема говорит нам, что этот отрезок 𝐵𝐸, который проходит от середины одной из сторон треугольника, параллельного другой стороне, является биссектрисой третьей стороны. Эквивалентно это означает, что это точка 𝐸 должна быть серединой отрезка 𝐴𝐶. Давайте теперь посмотрим, как эта теорема может быть доказанным.
Начнем с того же треугольника
𝐴𝐶𝐷, и у нас есть отрезок 𝐵𝐸, проведенный из середины 𝐵, т. е.
параллельно отрезку 𝐶𝐷. Поскольку мы пытаемся доказать
теоремы, то мы еще ничего не знаем о третьей стороне отрезка
𝐴𝐶. Мы можем построить линию 𝐴𝑦 такую
что 𝐴𝑦 параллельно отрезкам 𝐵𝐸 и 𝐷𝐶. Причина, по которой мы это делаем, будет
ясно скоро. Если мы рассмотрим отрезки 𝐴𝐷
и 𝐴𝐶, это обе трансверсали трех параллельных прямых.
е.
параллельно отрезку 𝐶𝐷. Поскольку мы пытаемся доказать
теоремы, то мы еще ничего не знаем о третьей стороне отрезка
𝐴𝐶. Мы можем построить линию 𝐴𝑦 такую
что 𝐴𝑦 параллельно отрезкам 𝐵𝐸 и 𝐷𝐶. Причина, по которой мы это делаем, будет
ясно скоро. Если мы рассмотрим отрезки 𝐴𝐷
и 𝐴𝐶, это обе трансверсали трех параллельных прямых.
Напомним, что если набор параллельных прямых делит секущую на отрезки одинаковой длины, то это множество делит любую другую секущую на отрезки одинаковой длины. Итак, поскольку отрезок 𝐴𝐷 был разделить на две равные части, мы знаем, что отрезок 𝐴𝐶 будет такой же. Он также будет разделен на два конгруэнтные куски. Другими словами, эта третья сторона треугольник был разделен пополам, что доказывает теорему о середине треугольника.
Теперь обратная теорема
также соответствует действительности. Мы можем сформулировать это как строку
отрезок, соединяющий середины двух сторон треугольника, параллелен его третьей
сторона. Итак, на этот раз, если мы возьмем треугольник
𝐴𝐶𝐷 и соединить середины 𝐵 и 𝐸 отрезков 𝐴𝐷 и 𝐴𝐶,
соответственно, то по обращению к первой теореме о середине треугольника прямая
отрезки 𝐵𝐸 и 𝐷𝐶 параллельны. Теперь мы увидим последний треугольник
теорема о срединном отрезке. Вторая часть треугольника
Теорема о середине отрезка касается длин двух важных отрезков.
Мы можем сформулировать это как строку
отрезок, соединяющий середины двух сторон треугольника, параллелен его третьей
сторона. Итак, на этот раз, если мы возьмем треугольник
𝐴𝐶𝐷 и соединить середины 𝐵 и 𝐸 отрезков 𝐴𝐷 и 𝐴𝐶,
соответственно, то по обращению к первой теореме о середине треугольника прямая
отрезки 𝐵𝐸 и 𝐷𝐶 параллельны. Теперь мы увидим последний треугольник
теорема о срединном отрезке. Вторая часть треугольника
Теорема о середине отрезка касается длин двух важных отрезков.
Прежде чем сформулировать эту теорему, давайте
сделать некоторые исследования, чтобы подтвердить результат. Мы можем взять этот треугольник 𝑃𝑄𝑅
и нарисуйте отрезок 𝑆𝑇, где 𝑆 — середина отрезка 𝑃𝑅 и 𝑇
является серединой отрезка 𝑃𝑄. Мы постараемся разработать
соотношение между длинами отрезков 𝑆𝑇 и 𝑅𝑄. Для этого добавим луч 𝑆𝑦
такой, что отрезок 𝑆𝑦 параллелен отрезку 𝑃𝑄. Теперь мы уже видели
свойство, состоящее в том, что отрезок, соединяющий середины двух сторон треугольника,
параллельно третьей стороне; это была противоположность первой части
теорема. Следовательно, отрезок 𝑆𝑇 есть
параллельно отрезку 𝑅𝑄.
Теперь мы уже видели
свойство, состоящее в том, что отрезок, соединяющий середины двух сторон треугольника,
параллельно третьей стороне; это была противоположность первой части
теорема. Следовательно, отрезок 𝑆𝑇 есть
параллельно отрезку 𝑅𝑄.
Тогда, поскольку мы построили линию
отрезок 𝑆𝑦, параллельный отрезку 𝑃𝑄, мы можем применить первый треугольник
теорема о срединном отрезке. Отрезок прямой, проходящий через
середина одной стороны треугольника, параллельная другой стороне треугольника
треугольник делит третью сторону треугольника пополам. 𝑆𝑦 — это отрезок от
середина 𝑆 параллельна отрезку 𝑃𝑄. А это значит, что отрезок
𝑅𝑄 делится пополам. Это может быть немного сложнее
визуализировать сначала, но это также иллюстрирует тот момент, что нам не всегда нужно
параллельные стороны горизонтальны, а стороны, разделенные пополам, направлены вверх от этого. А это значит, что теперь мы знаем
что каждый из отрезков 𝑅𝑦 и 𝑦𝑄 будет равен половине длины
весь отрезок 𝑅𝑄.
А это значит, что теперь мы знаем
что каждый из отрезков 𝑅𝑦 и 𝑦𝑄 будет равен половине длины
весь отрезок 𝑅𝑄.
Давайте сделаем еще один шаг к посмотрим, как мы можем определить длину отрезка 𝑆𝑇. Обратите внимание, что внутри этого треугольника у нас есть четырехугольник 𝑆𝑇𝑄𝑦. 𝑆𝑇𝑄𝑦 имеет две пары параллельных сторон, а значит, по определению это параллелограмм. Параллелограммы имеют противоположные стороны конгруэнтный. Следовательно, длина линии отрезок 𝑆𝑇 также будет половиной 𝑅𝑄. Важно, что это дает нам соотношение, согласно которому длина отрезка 𝑆𝑇 составляет половину длины отрезка 𝑅𝑄. Теперь мы можем формально определить вторая часть теоремы о середине треугольника. Длина сегмента линии Соединяющая середины двух сторон треугольника равна половине его длины. третья сторона.
Прежде чем мы рассмотрим некоторые вопросы,
мы можем заметить, что иногда то, что мы видели как обратную часть первой и второй части
теоремы о середине треугольника объединены в одну теорему. На это часто ссылаются
в совокупности как теорема о середине треугольника, сформулированная как отрезок прямой
Соединяющая середины двух сторон треугольника параллельна третьей стороне
и составляет половину его длины. Теперь мы увидим вопрос, в котором мы
применить теорему о середине треугольника, чтобы найти периметр фигуры.
На это часто ссылаются
в совокупности как теорема о середине треугольника, сформулированная как отрезок прямой
Соединяющая середины двух сторон треугольника параллельна третьей стороне
и составляет половину его длины. Теперь мы увидим вопрос, в котором мы
применить теорему о середине треугольника, чтобы найти периметр фигуры.
Учитывая, что 𝐷 и 𝐸 являются середины отрезков 𝐴𝐵 и 𝐴𝐶 соответственно, 𝐴𝐷 равно 32 сантиметров, 𝐴𝐸 равно 19 сантиметрам, а 𝐷𝐸 равно 39 сантиметрам, найдите периметр 𝐷𝐵𝐶𝐸.
Начнем с заполнения
дана информация о длине по фигуре 32 сантиметра для 𝐴𝐷, 19
сантиметры для 𝐴𝐸 и 39 сантиметров для 𝐷𝐸. Мы также можем идентифицировать
информация о том, что 𝐷 и 𝐸 являются серединами соответствующих отрезков. Итак, 𝐸𝐶 также имеет длину
19сантиметров, а 𝐷𝐵 имеет длину 32 сантиметра. Мы знаем, что нам нужно работать
вне периметра этого четырехугольника 𝐷𝐵𝐶𝐸. Мы разработали три из них
четыре стороны, так что нам еще нужно определить длину отрезка
𝐶𝐵. Для этого воспользуемся
теорема о середине треугольника.
Мы знаем, что нам нужно работать
вне периметра этого четырехугольника 𝐷𝐵𝐶𝐸. Мы разработали три из них
четыре стороны, так что нам еще нужно определить длину отрезка
𝐶𝐵. Для этого воспользуемся
теорема о середине треугольника.
Эта теорема утверждает, что Отрезок, соединяющий середины двух сторон треугольника, параллелен третью сторону и составляет половину его длины. Это означает, что мы можем распознать что отрезок 𝐶𝐵 должен быть параллелен отрезку 𝐷𝐸, и мы знаем кое-что о длине отрезка 𝐶𝐵. Поскольку 𝐷𝐸 составляет половину длины из 𝐶𝐵, мы также можем написать, что 𝐶𝐵 равно удвоенному 𝐷𝐸. Нам дали, что 𝐷𝐸 равно 39сантиметров, поэтому, удвоив это, мы можем вычислить, что 𝐶𝐵 равно 78 сантиметрам.
Итак, теперь у нас достаточно
информация для расчета периметра 𝐷𝐵𝐶𝐸. Напомним, что периметр
расстояние вокруг внешнего края фигуры. Это означает, что нам нужно добавить
четыре длины 39, 32, 78 и 19 сантиметров, что дает нам окончательный
Ответьте, что периметр 𝐷𝐵𝐶𝐸 равен 168 сантиметрам.
Это означает, что нам нужно добавить
четыре длины 39, 32, 78 и 19 сантиметров, что дает нам окончательный
Ответьте, что периметр 𝐷𝐵𝐶𝐸 равен 168 сантиметрам.
В следующем примере мы применим теорему о середине треугольника несколько раз на одном и том же рисунке. И когда мы работаем через проблема, как это, может быть очень полезно выделить определенные сегменты линии так что мы можем легко определить ключевые части, с которыми мы работаем.
На рисунке 𝐸, 𝐹, и 𝐷 — середины отрезков 𝐵𝐶, 𝐴𝐵 и 𝐴𝐶, соответственно. Найдите периметр треугольника 𝐸𝐹𝐷.
Следует отметить, что из
информация нам дана и маркировка на схеме, что у нас три
середины отрезков здесь. 𝐸, 𝐹 и 𝐷 делят свои
соответствующие отрезки линии. Итак, для того, чтобы найти
периметр треугольника 𝐸𝐹𝐷, это расстояние вокруг внешнего края, мы будем
нужно вычислить длины трех отрезков 𝐹𝐷, 𝐷𝐸 и
𝐸𝐹.
Так как мы знаем, что там являются серединами линий, что может заставить нас задаться вопросом, не могли бы мы применить одну из теорем о середине треугольника. Напомним, что длина отрезка, соединяющего середины двух сторон треугольника, равна половину длины третьей стороны. Смотрим на отрезок 𝐹𝐷. Отрезок 𝐹𝐷 — это прямая отрезок, соединяющий середины двух сторон треугольника. Следовательно, его длина будет быть половиной длины третьей стороны, которая является отрезком прямой 𝐵𝐶. Длина 𝐵𝐶 определяется как 4,6 сантиметра, так что половина этого составляет 2,3 сантиметра.
Теперь посмотрим, сможем ли мы сделать
то же самое, чтобы вычислить длины двух других сторон в треугольнике 𝐸𝐹𝐷. Мы можем рассмотреть линию
сегмент 𝐷𝐸 следующий. Отрезок 𝐷𝐸 соединяет
середины двух сторон треугольника, потому что он соединяется с 𝐷, серединой линии
отрезок 𝐴𝐶, а 𝐸 — середина отрезка 𝐵𝐶. Поэтому мы знаем, что он должен
быть половиной длины отрезка 𝐴𝐵, который является третьей стороной
треугольник. Половина 5,5 см это 2,75
сантиметры. И мы можем сделать то же самое для
длина отрезка 𝐸𝐹. Он соединяет середины 𝐸 и
𝐹. Итак, длина 𝐸𝐹 будет
половина отрезка 𝐴𝐶; половина 6,2 сантиметра равна 3,1 сантиметра.
Поэтому мы знаем, что он должен
быть половиной длины отрезка 𝐴𝐵, который является третьей стороной
треугольник. Половина 5,5 см это 2,75
сантиметры. И мы можем сделать то же самое для
длина отрезка 𝐸𝐹. Он соединяет середины 𝐸 и
𝐹. Итак, длина 𝐸𝐹 будет
половина отрезка 𝐴𝐶; половина 6,2 сантиметра равна 3,1 сантиметра.
А теперь найдем периметр треугольника 𝐸𝐹𝐷, мы складываем эти три рассчитанные длины вместе. 2,3 плюс 2,75 плюс 3,1 равно до 8,15 см. И так, применяя теорему о середине треугольника три раза, мы определили, что периметр треугольника 𝐸𝐹𝐷 равна 8,15 см.
Давайте теперь посмотрим, как мы можем применить обратная теорема о середине треугольника для определения неизвестной длины.
Периметр квадрата
𝐴𝐵𝐶𝐷 равно 352. Найдите 𝐴𝐹.
Найдите 𝐴𝐹.
В этом вопросе нам нужно найдите длину отрезка 𝐴𝐹, который является частью отрезка 𝐴𝐵 на одной из сторон площади. Нам не дана длина информацию на диаграмме, но нам говорят, что периметр квадрата 352 единицы длины.
Теперь, учитывая, что периметр это расстояние вокруг внешнего края фигуры, и мы знаем, что форма является квадратом, то мы можем вычислить длину одной из сторон. Потому что в четыре раза длиннее одной стороны дало бы нам периметр квадрата, чтобы вычислить длину одной стороны этого квадрата, мы делим периметр 352 на четыре. Это дает нам длину 88 единицы измерения. Итак, все стороны квадрата будет иметь длину 88 единиц длины.
Теперь, учитывая, что мы хотим найти
длину 𝐴𝐹, мы могли бы попытаться угадать в этот момент, но важно
применять наши знания геометрии в таких вопросах, чтобы мы могли доказать нашу
рассчитанная длина верна. Итак, давайте подумаем, что мы
знать геометрию квадрата. В частности, мы можем вспомнить
что в квадрате диагонали делят друг друга пополам. Итак, диагонали прямой
отрезки 𝐴𝐶 и 𝐷𝐵 делятся пополам в точке 𝑀. Но давайте сосредоточимся на линейном сегменте
𝐴𝐶.
Итак, давайте подумаем, что мы
знать геометрию квадрата. В частности, мы можем вспомнить
что в квадрате диагонали делят друг друга пополам. Итак, диагонали прямой
отрезки 𝐴𝐶 и 𝐷𝐵 делятся пополам в точке 𝑀. Но давайте сосредоточимся на линейном сегменте
𝐴𝐶.
Используя треугольник 𝐴𝐵𝐶,
заметим, что здесь можно применить одну из теорем о средней линии треугольника. Эта теорема утверждает, что
отрезок, проходящий через середину одной из сторон треугольника, также
параллельна другой стороне треугольника, делит пополам третью сторону
треугольник. Здесь у нас есть линия
отрезок 𝑀𝐹, проходящий через середину одной из сторон треугольника, потому что мы
известно, что 𝑀 является серединой отрезка 𝐴𝐶. Мы также знаем, что это самое
Отрезок 𝑀𝐹 параллелен другой стороне треугольника, так как
отметки на схеме. И так, это означает, что
третья сторона треугольника должна быть разделена пополам.
И так, это означает, что
третья сторона треугольника должна быть разделена пополам.
Отрезок 𝐴𝐵, который мы расчетная имеет длину 88 единиц длины, разделена на две равные части. И 88 разделить на два равно 44. Итак, применяя это теореме о середине треугольника, мы нашли, что длина отрезка 𝐴𝐹 составляет 44 единицы длины.
Теперь мы можем суммировать ключевые моменты этого видео. Мы видели и доказали первую часть теоремы о середине треугольника. Отрезок прямой, проходящий через середина одной стороны треугольника, параллельная другой стороне треугольника треугольник делит третью сторону треугольника пополам.
Обратная первая теорема
также верно. То есть отрезок, соединяющий
середины двух сторон треугольника параллельны третьей стороне. Мы также видели, что длина
Отрезок, соединяющий середины двух сторон треугольника, равен половине
длина третьей стороны.

 03.16
03.16
Leave A Comment