Площадь сечения конуса
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2014-12-10
Площадь сечения конуса. Для вас представлена очередная статья с конусами. На момент написания этой статьи на блоге решены все примеры (прототипы) заданий с конусами, которые возможны на экзамене. Процесс решения несложен (1-2 действия), при определённой практике решаются устно. Нужно знать понятие образующей, об этом информация в этой статье. Так же необходимо понимать как образуются сечения конуса.
1. Если плоскость проходит через вершину конуса, то сечением является треугольник.
*Если плоскость проходит через ось конуса, то сечением является равнобедренный треугольник, высота которого равна высоте конуса, а основание на которое опущена эта высота равна диаметру основания конуса.
2. Если плоскость проходит перпендикулярно оси конуса, то сечением является круг.
Особенностью данных заданий является то, что применяется формула площади треугольника, здесь она первая.
Формулы периодически повторяйте. Рассмотрим задачи:
324453. Площадь основания конуса равна 16Пи, высота равна 6. Найдите площадь осевого сечения конуса.
Осевым сечением конуса является треугольник с основанием равным диаметру основания конуса и высотой равной высоте конуса. Обозначим диаметр как D, высоту как Н, запишем формулу площади треугольника:
Высота известна, вычислим диаметр. Используем формулу площади круга:
Значит диаметр будет равен 8. Вычисляем площадь сечения:
Ответ: 24
324454. Площадь основания конуса равна 18. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 3 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.
Сечением является круг. Необходимо найти площадь этого круга.
Построим осевое сечение:
Рассмотрим треугольники AKL и AOC – они подобны. Известно, что в подобных фигурах отношения соответствующих элементов равны.
Мы рассмотрим отношения высот и катетов (радиусов):
OC это радиус основания, его можно найти:
Значит
Теперь можем вычислить площадь сечения:
*Это алгебраический способ вычисления без использования свойства подобных тел, касающегося их площади. Можно было рассудить так:
Два конуса (исходный и отсечённый) подобны, значит пощади их оснований являются подобными фигурами. Для площадей подобных фигур существует зависимость:
Коэффициент подобия в данном случае равен 1/3 (высота исходного конуса равна 9, отсечённого 3), 3/9=1/3.
Таким образом, площадь основания полученного конуса равна:
Ответ: 2
323455. Высота конуса равна 8, а длина образующей — 10. Найдите площадь осевого сечения этого конуса.
Пусть образующая это L, высота это H, радиус основания это R.
Найдём диаметр основания и используя формулу площади треугольника вычислим площадь. По теореме Пифагора:
Вычисляем площадь сечения:
Ответ: 48
Диаметр основания конуса равен 40, а длина образующей — 25.
Найдите площадь осевого сечения этого конуса.
Пусть образующая это L, высота это H, радиус основания это R.
Радиус основания равен половине диаметра, то есть 20.
Вычислим высоту и далее используя формулу площади треугольника найдём искомую площадь. По теореме Пифагора:
Вычисляем площадь сечения:
Ответ: 300
На этом всё. Успеха вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Стереометрия КОНУС ЦИЛИНДР | ЕГЭ-№2Площадь
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
10.21
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Боря купил 4 книги.
Все книги без первой стоят 42 р., без второй — 40 р., без третьей — 38 р., без четвёртой — 36 р. Сколько стоит каждая книга?
Решено
В трапеции MNPQ основание MQ в 5 раз больше основания NP. На стороне MQ отмечена точка X так, что MX=5/8MQ. Вырази векторы PX, XQ и NP
Решено
Дан куб ABCDA1B1C1D1 Найдите угол между прямыми AD1 и BM, где М-середина ребра DD1
В коробке находятся белые,чёрные и…
Найдите углы прямоугольной трапеции, если один из углов равен 20 градусов
Пользуйтесь нашим приложением
Как найти площадь осевого сечения конуса 🚩 площадь осевого сечения конуса формула 🚩 Математика
Как найти площадь осевого сечения конуса 🚩 площадь осевого сечения конуса формула 🚩 Математика Пожалуйста, включите JavaScript для получения наилучших результатов.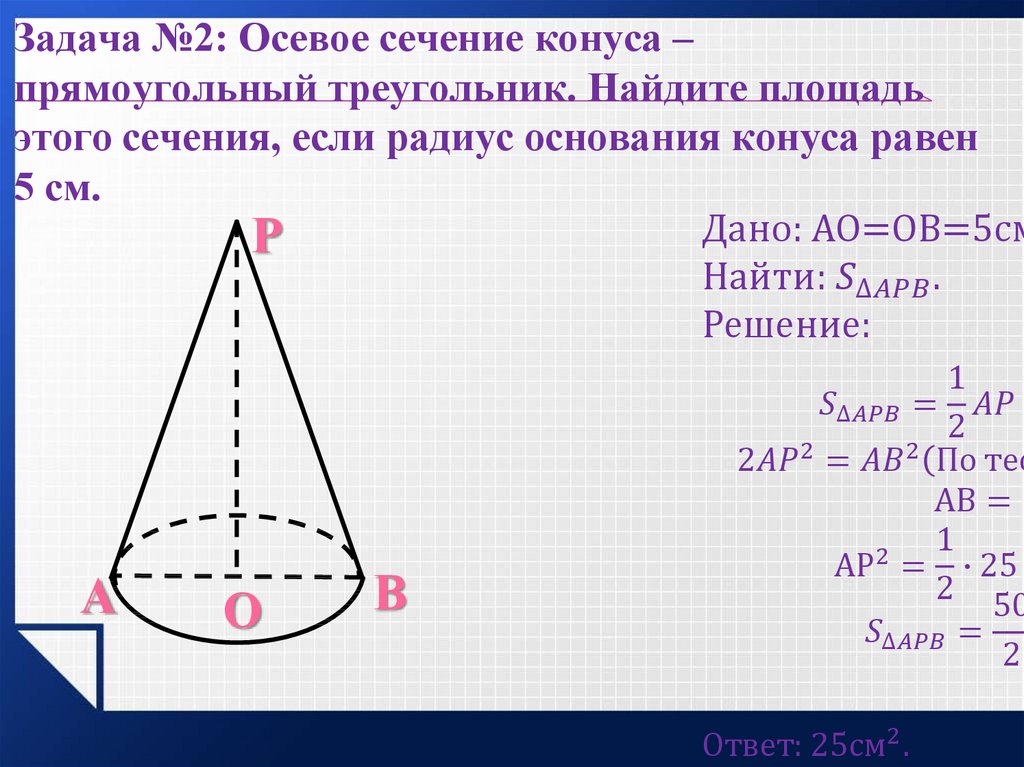
база, на эту базу. Прямой конус, который обычно встречается в школьном курсе геометрии, можно представить, как твердое тело образуется при вращении прямоугольного треугольника вокруг одного из катетов. Перпендикулярное сечение конуса – это плоскость, проходящая через его вершину перпендикулярно основанию.
Потребуется
- Рисование конуса с заданными параметрами
- Линия
- Карандаш
- Математические формулы и определения треугольника
Инструкция
Начертить конус с заданными параметрами. Отметьте центр круга как О, а вершину конуса — как Р. Вам нужно знать радиус основания и высоту конуса. Обобщить свойства высоты конуса. Это перпендикуляр, проведенный из вершины конуса к его основанию. Точка пересечения высоты конуса с плоскостью основания в прямом конусе совпадает с центром кругового основания. Постройте осевое сечение конуса. Он образован диаметром основания и образует конус, проходящий через точку пересечения диаметра с окружностью.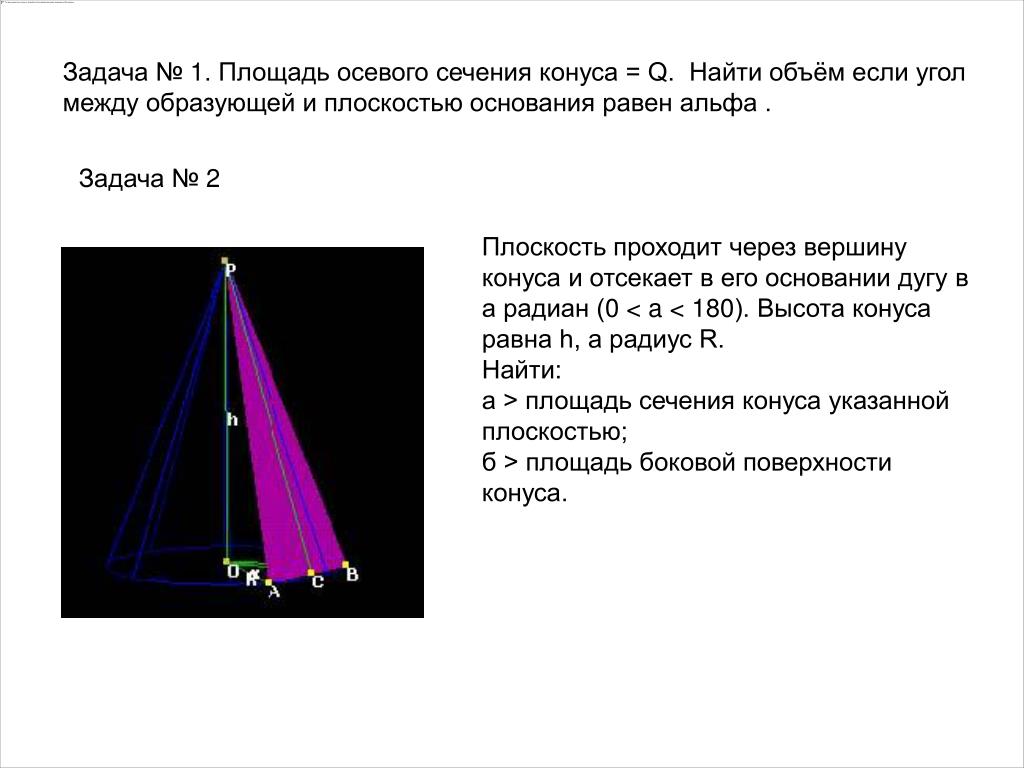
Обозначим полученные точки как A и B.
Осевой разрез образован двумя прямоугольными треугольниками, лежащими в одной плоскости и имеющими одну общую сторону. Вычислить площадь осевого сечения можно двумя способами. Первый способ заключается в том, чтобы найти площади получившихся треугольников и сложить их вместе. Это самый очевидный способ, но по сути он ничем не отличается от классического расчета площади равнобедренного треугольника. Итак, у вас есть 2 прямоугольных треугольника, общая сторона которых равна высоте конуса h, вторые катеты — это радиусы основания окружности R, а гипотенуза — образующая конуса. Так как все три стороны этих треугольников равны, то и треугольники получились равными, по третьему свойству треугольников равенства. Площадь прямоугольного треугольника равна половине произведения двух других сторон, то есть S=1/2Rh. Площадь двух треугольников соответственно будет равна произведению радиуса круглого основания на высоту, S=Rh.
Осевое сечение часто рассматривают как равнобедренный треугольник, высота которого равна высоте конуса.
В этом случае треугольник ст, основание которого равно диаметру окружности основания конуса D, а высота равна высоте конуса h. Его площадь вычисляется по классической формуле площади треугольника, то есть в итоге получается та же формула S = 1/2Dh = Rh, где S — площадь равнобедренного треугольника, R — радиус кругового основания h — высота треугольника и высота конуса.
Полезный совет
Площадь осевого сечения конуса вычисляется по формуле площади трапеции. При этом необходимо знать и радиус оснований, и высоту, и биссектрису.
Совет полезен?
Площадь поверхности конуса
Горячая математикаплощадь боковой поверхности конуса – это площадь только боковой или боковой поверхности.
Поскольку конус тесно связан с
пирамида
, формулы для их площадей связаны.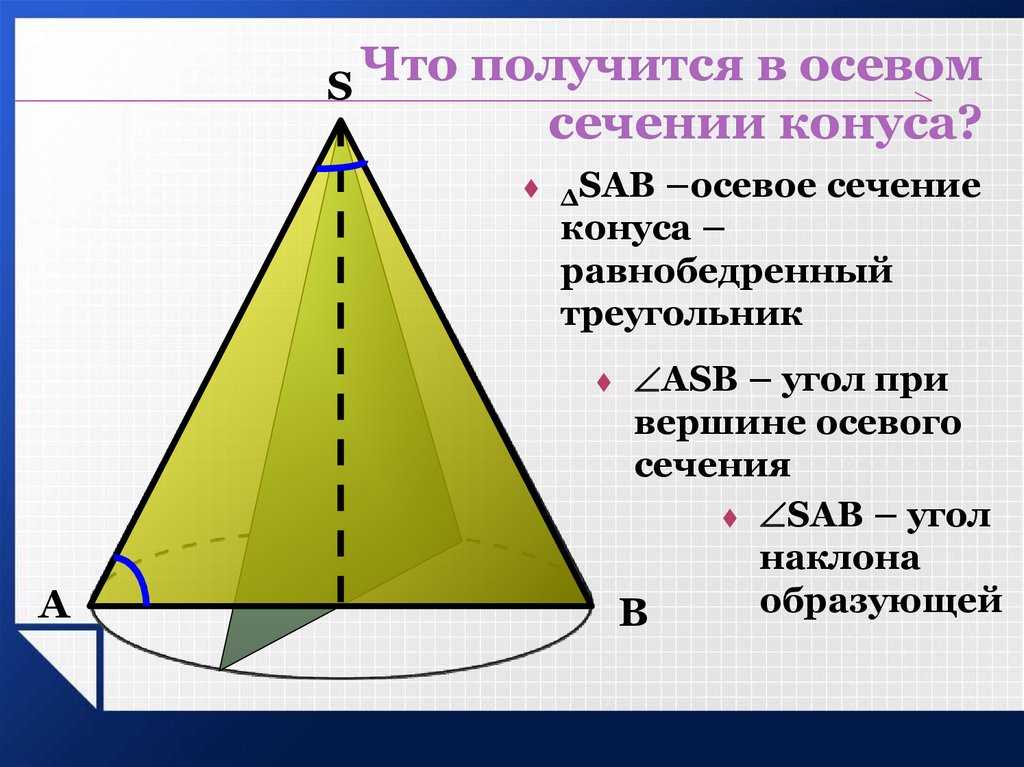
Помните, формула площади боковой поверхности пирамиды 1 2 п л а общая площадь поверхности 1 2 п л + Б .
Поскольку основанием конуса является круг, подставляем 2 π р для п и π р 2 для Б где р это радиус основания цилиндра.
Итак, формула для площадь боковой поверхности прямого конуса
л
.
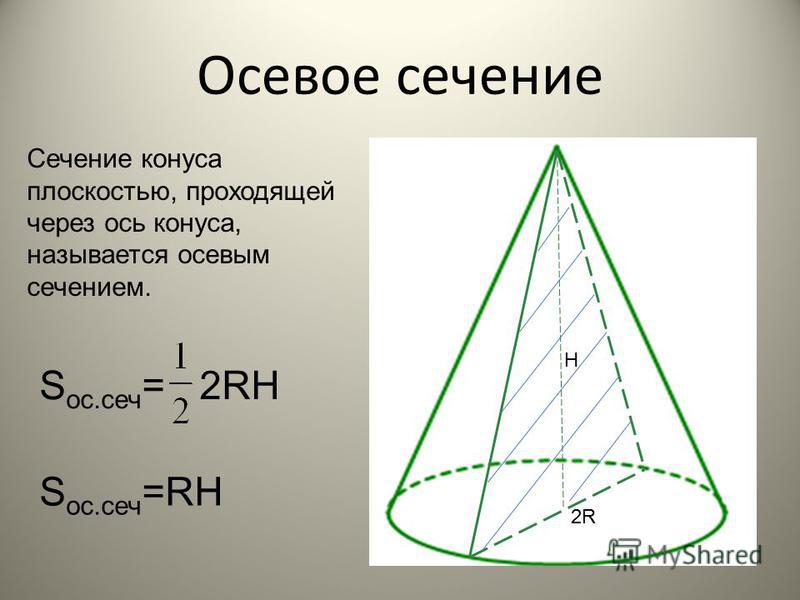С
.
А
«=»
π
р
л
, где
л
— наклонная высота конуса .
Пример 1:
Найдите площадь боковой поверхности прямого конуса, если радиус 4 см, а наклонная высота 5 см.
л . С . А «=» π ( 4 ) ( 5 ) «=» 20 π ≈ 62,82 см 2
Формула для общая площадь поверхности прямого конуса
Т
.
Leave A Comment