Первый сосуд налили m литров жидкости во второй на 7 литров меньше чем в 1 of 3 сосуд на 10 литров больше чем во второй 3 сосуде оказалось только жидкости сколько в первом и втором сосудах вместе — Школьные Знания.net

  • Все предметы

  • Математика

  • Литература

  • Алгебра

  • Русский язык

  • Геометрия

  • Английский язык

  • Физика

  • Биология

  • Другие предметы

  • История

  • Обществознание

  • Окружающий мир

  • География

  • Українська мова

  • Информатика

  • Українська література

  • Қазақ тiлi

  • Экономика

  • Музыка

  • Беларуская мова

  • Французский язык

  • Немецкий язык

  • Психология

  • Оʻzbek tili

  • Кыргыз тили

  • Астрономия

  • Физкультура и спорт

Ответ дан

rjkzgjkbyf

m-7 — налиили во второй сосуд    (m-7)+10 — налили в третий сосуд
Уравнение:
m+m-7=m-7+10
m=10 — в 1 сосуде
10-7=3 л во 2 сосуде
3+10=13 л — в 3 сосуде
надеюсь помогла)

Решение задач на смеси и сплавы при подготовке к ОГЭ по математике.

Методические рекомендации.

Муниципальное общеобразовательное учреждение

«Еловская средняя общеобразовательная школа»

Решение задач на растворы, смеси и сплавы при подготовке к ОГЭ по математике

Меренкова

Татьяна Владиславовна,

учитель математики

МОУ «Еловская СОШ»,

соответствие занимаемой

должности

с. Елово

2017

В математике есть ряд текстовых задач, которые вызывают затруднение у учащихся при их решении. К таким задачам можно отнести задачи на растворы, смеси и сплавы. Практическое значение этих задач огромно. Встречаются они при изучении смежных дисциплин, например, химии. Самостоятельно справиться с ними могут немногие. Вместе с этим они являются хорошим средством развития мышления учащихся.

Трудности при решении этих задач могут возникать на различных этапах:

  • составления математической модели (уравнения, системы уравнений, неравенства и т. п.;

  • решения полученной модели;

  • анализа математической модели (по причине кажущейся ее неполноты: не хватает уравнения в системе и пр.).

Все сложности преодолимы при тщательном анализе задачи. Основными компонентами в этих задачах являются:

При решении большинства задач этого вида, удобнее использовать таблицу, которая нагляднее и короче обычной записи с пояснениями. Зрительное восприятие определенного расположения величин в таблице дает дополнительную информацию, облегчающую процесс решения задачи и её проверки.

Этапы решения задачи:

1. Знакомство учащихся с текстом задач и выделение основных компонентов в них. Заполнение таблицы.

Таблица для решения задач имеет следующий вид:

Наименование веществ, растворов, смесей, сплавов

Масса раствора (смеси, сплава)

М

% содержание вещества (доля содержания вещества)

m / M * 100%

Масса вещества

m

 

 

 

2. Составление уравнения и его решение.

3. Анализ полученных данных, ответ на вопрос задачи.

Рассмотрим решение задач с применением таблицы.

Задача 1. В сосуд содержащий 2 кг 80 % -го водного раствора уксуса добавили 3 кг воды. Найдите концентрацию получившегося раствора уксусной кислоты.

Решение:

Наименование веществ, смесей

Масса раствора (смеси, сплава)

М, кг

% содержание вещества (доля содержания вещества)

m / M * 100%

Масса вещества

m, кг

Исходный раствор

2

80 % = 0,8

0,8·2

Вода

3

—

—

Новый раствор

5

х % = 0,01х

0,01х·5

Масса уксусной кислоты не изменилась, тогда получаем уравнение:

0,01х·5 = 0,8·2; 0,05х = 1,6; х = 1,6:0,05; х = 32.

Ответ: 32 %.

Задача 2. Сколько нужно добавить воды в сосуд, содержащий 200 г 70 % -го раствора уксусной кислоты, чтобы получить 8 % раствор уксусной кислоты?

Решение:

Наименование веществ, смесей

Масса раствора (смеси, сплава)

М, г

% содержание вещества (доля содержания вещества)

m / M * 100%

Масса вещества

m, г

Исходный раствор

200

70 %

0,7·200

Вода

х

—

—

Новый раствор

200 + х

8 %

0,08(200 + х)

Анализируя таблицу, составляем уравнение :

0,08(200 + х) = 0,7·200; 16 + 0,08х = 140; 0,08х = 124; х = 1550.

Ответ :1,55 кг воды.

Задача 3. Смешали некоторое количество 12% раствора соляной кислоты с таким же количеством 20 % раствора этой же кислоты. Найти концентрацию получившейся соляной кислоты.

Решение:

Наименование веществ, смесей

Масса раствора (смеси, сплава)

М, г

% содержание вещества (доля содержания вещества)

m / M * 100%

Масса вещества

m, г

I раствор

х

12 %

0,12х

II раствор

х

20 %

0,2х

Смесь

2х

0,32х/2х * 100%

0,12х+ 0,2 х = 0,32х

Анализируя таблицу, получаем :

0,32х/2х * 100% = 16 %

Ответ : 16 %.

Задача 4. Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?

Решение:

Наименование веществ, растворов, смесей, сплавов

Масса раствора (смеси, сплава)

М

% содержание вещества (доля содержания вещества)

m / M * 100%

Масса вещества

m

Первый сплав

х

60%

0,6 х

Второй сплав

у

45%

0,45 у

Новый сплав

х + у

55%

0,6 х + 0,45у

Пусть первый сплав взят в количестве x кг, тогда он будет содержать 0,6x кг меди, а второй сплав взят в количестве y кг, тогда он будет содержать 0,45y кг меди. Соединив два этих сплава, получим сплав меди массой x + y, по условию задачи он должен содержать 0,55(x + y) меди. Следовательно, можно составить уравнение: 0,55(x + y) = 0,6 х + 0,45у;

0,55 х + 0,55 у = 0,6 х+ 0,45 у; 0,05 х = 0,1 у . Выразим x через y: х = 2 у.

Следовательно, отношение, в котором нужно взять сплавы 1:2.

Ответ: 1:2

Задача 5. Пер­вый сплав со­дер­жит 5% меди, вто­рой — 13% меди. Масса вто­ро­го спла­ва боль­ше массы пер­во­го на 4 кг. Из этих двух спла­вов по­лу­чи­ли тре­тий сплав, со­дер­жа­щий 10% меди. Най­ди­те массу тре­тье­го спла­ва.

Ре­ше­ние:

Наименование веществ, растворов, смесей, сплавов

Масса раствора (смеси, сплава)

М

% содержание вещества (доля содержания вещества)

m / M * 100%

Масса вещества

m

Первый сплав

х

5%

0, 05 х

Второй сплав

х + 4

13%

0,13(х +4)

Новый сплав

2х + 4

10%

0, 05 х + 0,13(х +4)=0,18 х + 0,52

Пусть масса пер­во­го спла­ва x кг. Тогда масса вто­ро­го спла­ва (x + 4) кг, а тре­тье­го — (2x + 4) кг. В пер­вом спла­ве со­дер­жит­ся 0,05x кг меди, а во вто­ром — 0,13(x + 4) кг. По­сколь­ку в тре­тьем спла­ве со­дер­жит­ся 0,1(2x + 4) кг меди, со­ста­вим и решим урав­не­ние: 0,1(2x + 4) = 0,18 х + 0,52; 0,02 х = 0,12; х = 6.

От­ку­да масса тре­тье­го спла­ва равна 16 кг.

 

Ответ:16 кг.

Задача 6. Сме­ша­ли не­ко­то­рое ко­ли­че­ство 10 % рас­тво­ра­ не­ко­то­ро­го ве­ще­ства с таким же ко­ли­че­ством 12 % рас­тво­ра ­это­го же ве­ще­ства. Сколь­ко про­цен­тов со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

Ре­ше­ние:

Наименование веществ, растворов, смесей, сплавов

Масса раствора (смеси, сплава)

М

% содержание вещества (доля содержания вещества)

m / M * 100%

Масса вещества

m

1

х

10%

0, 1 х

2

х

12%

0,12 х

3

2х

(0, 22 х / 2х)* 100 %

0, 1 х + 0,12х =

0,22 х

Пусть взяли х г 10-про­цент­но­го рас­тво­ра, тогда взяли и х г 12-про­цент­но­го рас­тво­ра. Кон­цен­тра­ция рас­тво­ра — масса ве­ще­ства, раз­делённая на массу всего рас­тво­ра.  Кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра равна 0, 22 х / 2х или 11%.

 Ответ: 11%.

Задача 7. Име­ют­ся два со­су­да, со­дер­жа­щие 4 кг и 16 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чит­ся рас­твор, со­дер­жа­щий 57% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 60% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся в пер­вом рас­тво­ре?

Ре­ше­ние:

Наименование веществ, растворов, смесей, сплавов

Масса раствора (смеси, сплава)

М, кг

% содержание вещества (доля содержания вещества)

m / M * 100%

Масса вещества

M, кг

Первый раствор

4

х %

0,04 х

Второй раствор

16

у %

0,16 у

Смесь 1

20

57%

0,04 х + 0,16у

Смесь 2

4+4 =8

60 %

0,04х + 0,04 у

Пусть кон­цен­тра­ция пер­во­го рас­тво­ра – х %, кон­цен­тра­ция вто­ро­го рас­тво­ра – y %. Со­ста­вим си­сте­му урав­не­ний со­глас­но усло­вию за­да­чи:


0,57 * 20 = 0,04 х + 0,16у, х = 65,

0,6 * 8 = 0,04х + 0,04 у; у = 55.

Таким об­ра­зом, в пер­вом рас­тво­ре со­дер­жит­ся 0,65 * 4 = 2,6 ки­ло­грам­ма кис­ло­ты

 Ответ: 2,6

Задача 8.  Сме­шав 60% и 30% рас­тво­ры кис­ло­ты и, до­ба­вив 5 кг чи­стой воды, по­лу­чи­ли 20% рас­твор кис­ло­ты. Если бы вме­сто 5 кг воды до­ба­ви­ли 5 кг 90% рас­тво­ра той же кис­ло­ты, то по­лу­чи­ли бы 70% рас­твор кис­ло­ты. Сколь­ко ки­ло­грам­мов 60% рас­тво­ра ис­поль­зо­ва­ли для по­лу­че­ния смеси?

Ре­ше­ние:

Наименование веществ, растворов, смесей, сплавов

Масса раствора (смеси, сплава)

М, кг

% содержание вещества (доля содержания вещества)

m / M * 100%

Масса вещества

M, кг

Первый раствор

х

60 %

0,6 х

Второй раствор

у

30 %

03 у

Смесь 1

х + у +5

20 %

0,6 х + 0,3у

Третий раствор

5

90 %

0,9* 5 = 4,5

Смесь 2

х + у +5

70 %

0,6х + 0,3 у + 4,5

Пусть х кг и у кг — массы пер­во­го и вто­ро­го рас­тво­ров, взя­тые при сме­ши­ва­нии. Тогда (х + у +5) кг — масса по­лу­чен­но­го рас­тво­ра, со­дер­жа­ще­го (0,6 х + 0,3у) кг кис­ло­ты. Кон­цен­тра­ция кис­ло­ты в по­лу­чен­ном рас­тво­ре 20 %, значит 0,2(х + у +5) %. Концентрация кислоты во втором растворе 70 %, значит 0,7 ( х + у + 5) = 0,6х + 0,3 у + 4,5. Решим си­сте­му двух по­лу­чен­ных урав­не­ний:

0,2(х + у +5) = 0,6 х + 0,3у,

0,7 ( х + у + 5) = 0,6х + 0,3 у + 4,5;

0,4 х + 0,1 у = 1, х =2,

0,1 х + 0,4 у = 1; у = 2.

Ответ: 2 кг.

Задача 9. Имеется два сплава. Первый содержит 10% никеля, второй — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава меньше массы второго?

Решение:

Наименование веществ, растворов, смесей, сплавов

Масса раствора (смеси, сплава)

М

% содержание вещества (доля содержания вещества)

m / M * 100%

Масса вещества

m

Первый сплав

х

10%

0, 1 х

Второй сплав

200-х

30%

0,3(200-х)

Новый сплав

200

25%

0, 1 х + 0,3(200-х )= 0,25*200

Решим уравнение: 0, 1 х + 0,3(200-х )= 0,25*200; х = 50.

Масса второго сплава 150 кг.

Ответ: на 100 кг.

 Задача 10. Имеется два куска слитка олова и свинца, содержащие 40% и 60% олова. По сколько граммов от каждого куска надо взять, чтобы получить 600 граммов сплава, содержащего 45% олова?

Решение:

Наименование веществ, растворов, смесей, сплавов

Масса раствора (смеси, сплава)

М

% содержание вещества (доля содержания вещества)

m / M * 100%

Масса вещества

m

Первый кусок

х

40%

0, 4 х

Второй кусок

600-х

60%

0,6 (600-х)

Новый сплав

600

45%

0, 4 х + 0,6(600-х )= 0,45*600

Решим уравнение: 0, 4 х + 0,6(600-х )= 0,45*600; х = 450.

Ответ:450 кг и 150 кг.

Задача 11.  Кусок сплава меди и цинка массой 36 кг, содержит 45% меди. Сколько килограммов меди нужно добавить к этому куску, чтобы получить новый сплав, содержащий 60% меди?

Решение:

Наименование веществ, растворов, смесей, сплавов

Масса раствора (смеси, сплава)

М, кг

% содержание вещества (доля содержания вещества)

m / M * 100%

Масса вещества

M, кг

Первый кусок

36

45%

0, 45 *36 = 16,2

Медь

х

100%

х

Новый сплав

36 + х

60 %

16,2 +х=0,6(36 + х)

Получаем уравнение: 0, 45 х +х=0,6(36 + х), х = 13,5

Ответ: 13,5 кг

Задача 12. Имеется три сосуда. В первый сосуд налили 4 кг 70 % сахарного сиропа, а во второй – 6 кг 40 % сахарного сиропа. Если содержимое первого сосуда смешать с содержимым третьего сосуда, то получим в смеси 55 % содержание сахара, а если содержимое второго сосуда смешать с третьим, то получим 35 % содержание сахара. Найдите массу сахарного в третьем сосуде сиропа и концентрацию сахара в нем.

Решение:

Наименование веществ, смесей

Масса раствора (смеси, сплава)

М, кг

% содержание вещества (доля содержания вещества)

m / M * 100%

Масса вещества

M, кг

I сосуд

4

70 %

0,7·4=2,8

II сосуд

6

40 %

0,4·6 = 2,4

III сосуд

х

у %

0,01ху

I и III сосуды

4+х

55 %

0,55(4+х)

=

2,8+0,01ху

II и III сосуды

6+х

35 %

0,35(6+х)

=

2,4+0,01ху

Итак, получаем систему уравнений :

Ответ :1,5 кг сахарного сиропа 15 % концентрации.

Задачи для самостоятельного решения:

13. Име­ют­ся два со­су­да, со­дер­жа­щие 10 кг и 16 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чит­ся рас­твор, со­дер­жа­щий 55% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 61% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся в пер­вом рас­тво­ре?

Ответ: 8,7

14. Име­ют­ся два со­су­да, со­дер­жа­щие 40 кг и 30 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чим рас­твор, со­дер­жа­щий 73% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 72% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся во вто­ром рас­тво­ре?

 Ответ: 19,5

15. Име­ют­ся два со­су­да, со­дер­жа­щие 40 кг и 20 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чит­ся рас­твор, со­дер­жа­щий 33% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 47% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся в пер­вом рас­тво­ре?

Ответ: 2.

16. Име­ют­ся два со­су­да, со­дер­жа­щие 24 кг и 26 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чит­ся рас­твор, со­дер­жа­щий 39% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 40% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся в пер­вом рас­тво­ре?

 

Ответ: 15,6

17. Име­ют­ся два со­су­да, со­дер­жа­щие 30 кг и 20 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чим рас­твор, со­дер­жа­щий 81% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 83% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся во вто­ром рас­тво­ре?

 

Ответ: 18,6

18. Име­ют­ся два со­су­да, со­дер­жа­щие 22 кг и 18 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чит­ся рас­твор, со­дер­жа­щий 32% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 30% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся в пер­вом рас­тво­ре?

Ответ: 11

19. Име­ют­ся два со­су­да, со­дер­жа­щие 30 кг и 42 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чим рас­твор, со­дер­жа­щий 40% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 37% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся во вто­ром рас­тво­ре?

20. Име­ют­ся два со­су­да, со­дер­жа­щие 48 кг и 42 кг рас­тво­ра кис­ло­ты раз­лич­ной кон­цен­тра­ции. Если их слить вме­сте, то по­лу­чим рас­твор, со­дер­жа­щий 42% кис­ло­ты. Если же слить рав­ные массы этих рас­тво­ров, то по­лу­чен­ный рас­твор будет со­дер­жать 40% кис­ло­ты. Сколь­ко ки­ло­грам­мов кис­ло­ты со­дер­жит­ся во вто­ром рас­тво­ре?

21. Сме­ша­ли не­ко­то­рое ко­ли­че­ство 21-про­цент­но­го рас­тво­ра­ не­ко­то­ро­го ве­ще­ства с таким же ко­ли­че­ством 95-про­цент­но­го рас­тво­ра ­это­го же ве­ще­ства. Сколь­ко про­цен­тов со­став­ля­ет кон­цен­тра­ция по­лу­чив­ше­го­ся рас­тво­ра?

 Ответ: 58.

Заключение

В задачах этого типа прослеживается системный подход к решению задач. Происходит успешная отработка и закрепление интеллектуальных умений (анализ, синтез, аналогия, обобщение. конкретизация и т.д.). Данная система задач на смеси, растворы и сплавы была апробирована в ходе КПВ по математике в 8 классе в 2016-17 учебном году. Опыт показал, что учащиеся не знавшие вначале, как подойти к решению этих задач, в конце темы успешно заполняли таблицу и получали верный ответ.

Литература:

1.Открытый банк заданий ОГЭ http://www.fipi.ru/content/otkrytyy-bank-zadaniy-oge;

2. https://oge.sdamgia.ru Каталог заданий. Задачи на проценты, сплавы и смеси

Математическая задача: Емкости для воды — вопрос № 19753, алгебра, уравнение

В три одинаковых сосуда наливается разное количество воды. В первом сосуде вода заполняет 30 % своего объема, а во втором — 40 % своего объема. Третий контейнер содержит 19 литров воды. Если бы мы распределили воду из всех сосудов поровну, то вода в каждом сосуде заполнила бы две пятых его объема.

Каков объем одного контейнера?

Правильный ответ:

x =  38 l

Пошаговое объяснение:

0,30x + 0,40x+19 = 2/5·3·x

0,30·x + 0,40·x+19 = 2/5·3· x

2,5x = 95

x = 95/2,5 = 38

x = 38

Наш простой калькулятор вычисляет это уравнение.


Нашли ошибку или неточность? Не стесняйтесь

пишите нам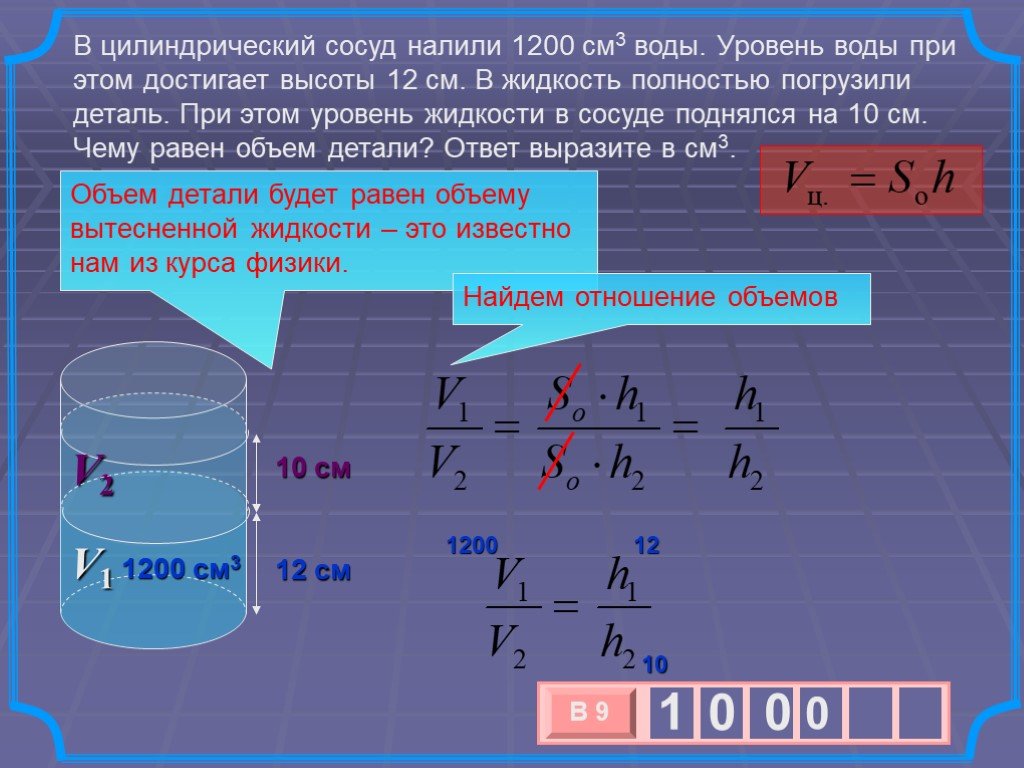

. Спасибо!

Советы по связанным онлайн-калькуляторам

Наш процентный калькулятор поможет вам быстро рассчитать различные типовые задачи с процентами.
У вас есть линейное уравнение или система уравнений и вы ищете ее решение? Или у вас есть квадратное уравнение?
Совет: конвертер единиц объема поможет вам преобразовать единицы объема.

You need to know the following knowledge to solve this word math problem:

  • algebra
  • equation
  • basic functions
  • percentages
Units of physical quantities:
  • volume
Уровень сложности слова:
  • практика для 13-летних
  • практика для 14-летних
  • Фармацевт
    У фармацевта был 12-литровый сосуд с травяным лосьоном, который содержал 30% активного ингредиента. Ее помощник налил в контейнер 18 литров травяного лосьона, содержащего 45% активного ингредиента. Какой процент травяного лосьона был произведен?
  • Контейнер для воды
    Контейнер кубической формы заполнен на две трети своей высоты. Если мы нальем 18 литров, то он будет заполнен на три пятых высоты. Каков объем всей емкости?
  • Бутылка
    Бутыль содержит 1,5 литра минеральной воды. Вылейте всю воду из бутылки в пустые чашки объемом 1/3 л. Мы наполним все, кроме одного, до краев. Какая часть объема последней чашки заполнена водой?
  • Температура 36991
    Хонза залил 2 литра горячей воды температурой 90°С из нагревателя в пятилитровую емкость. Какой температуры должна быть вода, которую наполняет сосуд, с температурой смеси 42 °С?
  • Живей
    Живей хочет разделить 19 литров воды поровну на шесть горшков. Найдите объем воды в каждом горшке.
  • Емкость с водой
    Емкость в форме куба наполовину заполнена водой. Если мы добавим 20 литров воды, компания заполнит контейнер на три четверти его высоты. Каков объем всей емкости?
  • Идентичный 73194
    Три одинаковых насоса закачивают в бак 50 400 литров дизельного топлива за 7 часов. Насколько больше (меньше) солярки они перекачают, если мы добавим еще два насоса, и все они будут работать 4 часа?
  • Процент 3501
    Сначала налили 0,25 воды из полной емкости, затем 0,2 оставшейся воды. Какой процент контейнера остался полным?
  • Три насоса
    Наполняем бассейн. Бассейн наполнит первый насос за 12 часов, а второй за 15 часов. Если бы все три насоса работали одновременно, они наполнили бы бассейн за 4 часа. Как долго бассейн будет наполняться только третьим насосом?
  • Меньший 4657
    В бассейн выходят две трубы подачи, и меньшая труба наполняет бассейн за 40 часов. Пустой бассейн наполнится через 16 часов, если мы откроем обе трубы подачи. Сколько времени потребовалось бы для заполнения, если бы была открыта только вторая, более крупная впускная труба?
  • Ава налила
    Ава наполнила 3 ​​чашки разным количеством воды. Количество составляло 225 мл, 370 мл и 435 мл воды. Что из следующего является общим количеством воды в литрах, которое Ава использовала, чтобы наполнить 3 чашки?
  • Идентичен 15863
    Бутылка содержит 2 литра молока. Сколько одинаковых стаканов вы наполните из этой бутылки, если в стакан поместится 1/3 литра молока?
  • Воронка
    Воронка имеет форму равностороннего конуса. Вычислите смачиваемую водой поверхность, если мы налили в воронку 7,1 л воды.
  • Второй 5586
    Первый насос наполняет бассейн за 12 часов. Второй насос наполняет его за 15 часов. Если все три насоса работают, бассейн наполнится за 4 часа. За какое время бассейн наполнится только третьим насосом?
  • Полусферическое углубление
    Полусферическое углубление сосуда заполнено водой на высоту 10 см =. Сколько литров воды находится внутри, если внутренний диаметр полости d = 28 см?
  • Насосы
    Первый насос подает в бассейн 16 литров в секунду, второй насос на 75% меньше первого, а третий насос наполовину больше, чем второй. За какое время одновременно всеми тремя насосами наполнится бассейн объемом 15 м³ (куб. метров)?
  • Молоко
    В трех контейнерах было 22 литра молока. В первой таре было на 6 литров больше, чем во второй. После переливания 5 литров из первой емкости в третью емкость, во второй и третьей емкостях

находится одинаковое количество молока, в первой содержится 500 мл спирта, а во второй 500 мл воды. Три стакана спирта из первой тары вынимаются и составляют

.
  • # Институт последипломного медицинского образования им. Джавахарлала Исследовательский институт MBBS
  • #IBPS РРБ Помощник офиса
  • # Всеиндийский институт медицинских наук MBBS
  • #Вакансии
  • #IBPS Офицерская шкала RRB 1
  • Клерк #IBPS
  • # Аллигатор и смесь
  • # Государственный банк Индии Клерк
  • #RRB Группа D (RRB Уровень 1)
  • # ИБПС ПО
  • # Государственный банк Индии PO
  • #RRB Помощник пилота локомотива
  • Помощник #RBI
  • # Количественные способности

Есть две емкости: первая содержит 500 мл спирта, а вторая — 500 мл воды.