Диагональ треугольника – формула
4.7
Средняя оценка: 4.7
Всего получено оценок: 76.
4.7
Средняя оценка: 4.7
Всего получено оценок: 76.
Очень часто в начале изучения фигуры ученики путают значение диагонали прямоугольника и треугольника. Поэтому, чтобы не путаться в обозначениях, лучше разобраться в тематике раз и навсегда.
Треугольник
Треугольник – это фигура, состоящая из трех сторон и трех углов. Треугольник имеет три характеризующих отрезка:
- Высота;
- Медиана;
- Биссектриса.
Треугольник не может иметь диагональ в принципе. Дело в том, что диагонали могут быть проведены только в многоугольниках, количество сторон которых больше 3.
Почему так? Потому что диагональ это отрезок, соединяющий противоположные вершины. В треугольнике противоположных вершин нет и быть не может. Существует сторона, противоположная вершине, но сами по себе вершины всегда смежные, т.е. соединенные одной стороной.
Прямоугольник
Прямоугольник – это первая фигура школьного курса математики, которая имеет диагональ. Так же, как диагональ имеет и квадрат.
Диагональ прямоугольника или квадрата всегда:
- Делит фигуру на две равных прямоугольных треугольника.
- В полученных треугольниках диагональ будет являться гипотенузой
- Диагональ будет равняться корню квадратному из суммы квадратов катетов согласно теореме Пифагора
Диагоналей в любом четырехугольнике 2, а в квадрате и прямоугольнике обе диагонали равны между собой.
При этом правило не касается других четырехугольников. Например, диагонали параллелограмма всегда неравны между собой. Запомните, если перед вами произвольный четырехугольник использовать утверждение о равенстве диагоналей без доказательства нельзя. Любое утверждение в геометрии, кроме аксиом должно быть доказано.
Кроме прямоугольника и квадрата равными диагоналями обладает ромб.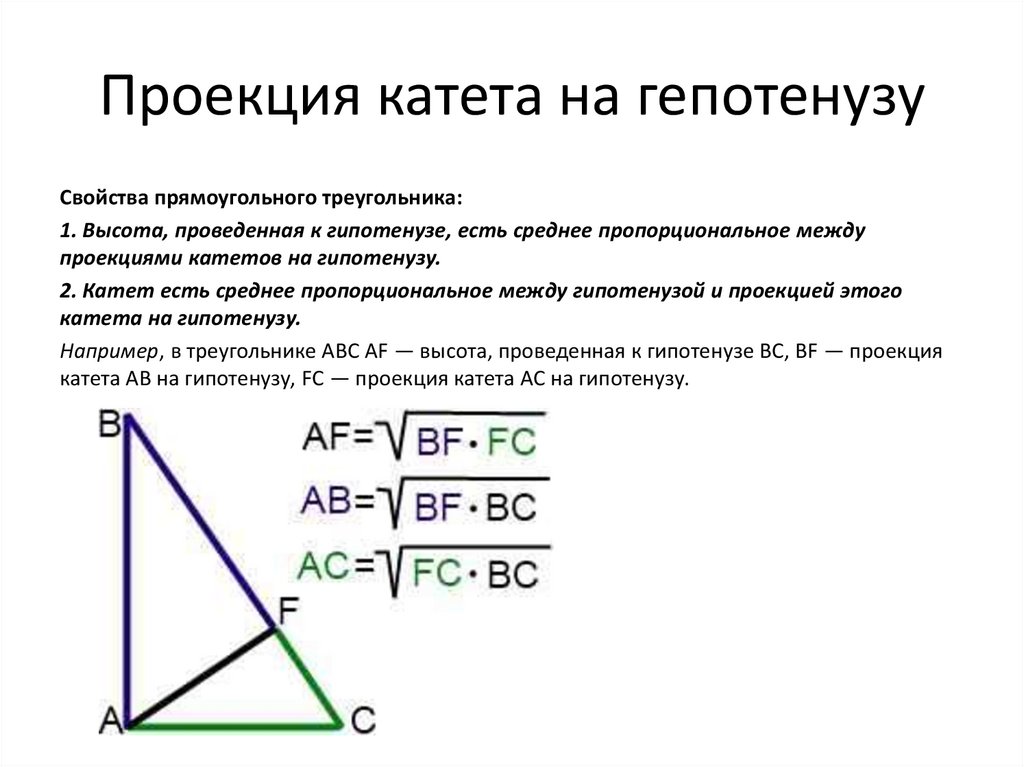 При этом диагонали ромба перпендикулярны друг другу и, так же, как и диагонали квадрата и прямоугольника, точкой пересечения делятся пополам.
При этом диагонали ромба перпендикулярны друг другу и, так же, как и диагонали квадрата и прямоугольника, точкой пересечения делятся пополам.
Многоугольник
На самом деле, многоугольником может называться любая фигура с количеством углов, больше 2. По факту, любая фигура может называться многоугольником, поскольку 2 угла у замкнутой фигуры быть не может.
Рассмотрим многоугольники с количеством углов больше 4, поскольку четырехугольники мы уже рассмотрели.
Рис. 2. Диагонали многоугольника.В многоугольнике, если он не является правильным, не получится решить задачу нахождения диагонали без дополнительных построений. В правильном многоугольнике все диагонали равны между собой и точкой пересечения делятся пополам.
Правильным многоугольником зовется фигура, все стороны и углы которой соответственно равны между собой.
Количество диагоналей можно посчитать, прикинув количество смежных и несмежных вершин. Смежными зовутся вершины, соединенные одним отрезком.
Например, в четырехугольнике у любой вершины есть две смежные вершины. Значит, для каждой вершины есть только одна диагональ. Диагональ соединяет две противоположные вершины, всего вершин 4, значит 4:2=2 – в любом четырехугольнике 2 диагонали.
Но этот способ не подойдет, если в задаче требуется подсчитать количество диагоналей у многоугольника с 5989 сторонами. Такая фигура вполне возможна в теории. На практике начертить ее весьма утомительно, как и подсчитать диагонали на чертеже. Поэтому была выведена формула числа диагоналей многоугольника:
$P={n(n-3)\over{2}}$ – где n это число сторон многоугольника.
Проверим для квадрата:
$P={4(4-3)\over{2}}={4\over2}=2$ – все верно.
Рис. 3. Диагонали квадрата.Что мы узнали?
Мы узнали, почему не существует формулы диагонали треугольника. Поговорили о том, что диагонали в принципе нет, и не может быть в многоугольниках с количеством сторон, меньше 3. Обсудили различные свойства диагоналей в различных фигурах.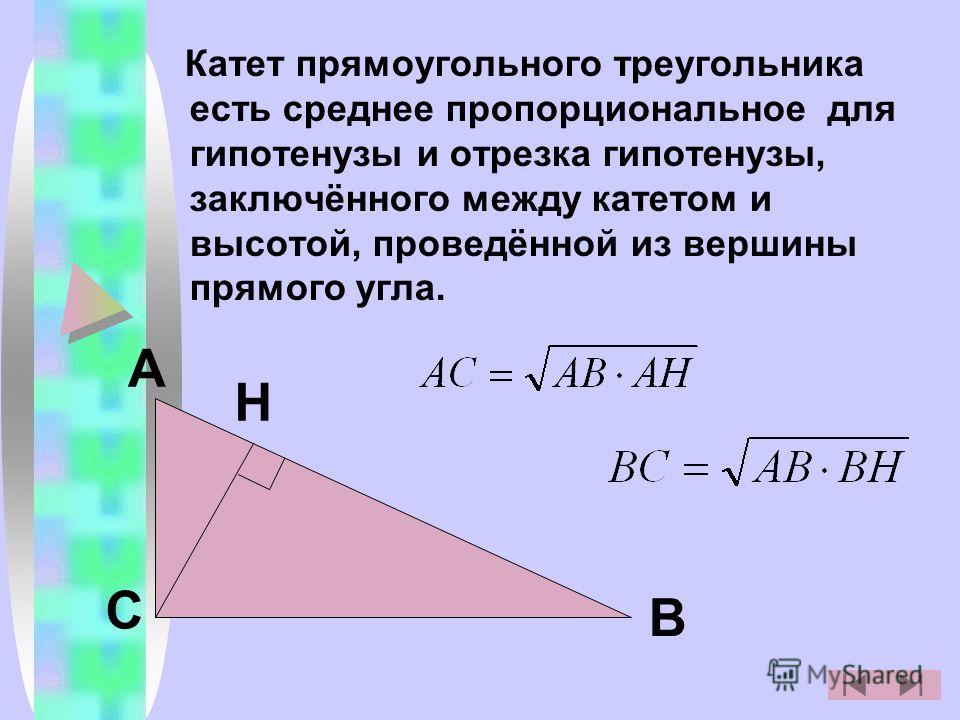
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Алексей Касюгин
4/5
Оценка статьи
4.7
Средняя оценка: 4.7
Всего получено оценок: 76.
А какая ваша оценка?
Вычислить диагональ прямоугольника онлайн, способы и формулы
Одна из основных фигур курса математики – прямоугольник.
Впервые о нем заговорили еще в Древнем Египте, а позже и в
Древней Греции. Именно свойства его диагоналей помогают
решить многие задания учебного курса. Подход, который
сейчас используется в геометрии разработал Евклид. Формулы,
представленные в данной статье, пригодятся как при решении
домашних упражнений, так и на ЕГЭ. Именно такие задачки
помогают набрать недостающие баллы, поэтому ими не стоит пренебрегать.
- Диагональ прямоугольника через его стороны
- Диагональ прямоугольника через площадь и известную сторону
- Диагональ прямоугольника через периметр и сторону
- Диагональ прямоугольника через диаметр описанной окружности
- Диагональ прямоугольника через радиус описанной окружности
- Диагональ прямоугольника через площадь и острый угол между диагоналями
- Диагональ прямоугольника через угол прилегающей диагонали и длину стороны прилегающей к этому углу
- Что такое диагональ прямоугольника, когда требуется ее вычисление
Диагональ прямоугольника через его стороны
Если заданы хотя бы 2 стороны, то вычислить линию, соединяющую противоположные вершины, будет довольно просто. Применяется классическая теорема Пифагора. Достаточно подставить приведенные в дано числовые параметры в виде суммы квадратов под корнем:
Применяется классическая теорема Пифагора. Достаточно подставить приведенные в дано числовые параметры в виде суммы квадратов под корнем:
Где a, b – это стороны, а d – прямая, которую мы ищем.
Сторона (a)
ммсмдмм
Сторона (b)
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Диагональ прямоугольника через площадь и известную сторону
Когда в дано есть S и одна сторона, то узнать искомое значение можно используя следующее равенство:
Где D – это прямая, которую необходимо найти, a и b – любая заданная сторона, а S – площадь.
Площадь (S):
мм²см²дм²м²
Сторона (b):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Диагональ прямоугольника через периметр и сторону
Когда задан периметр (сумма сторон) и, хотя бы одна сторона, отрезок, соединяющий несмежные точки высчитывают так:
Где P – сумма сторон, a и b – любая заданная сторона.
Рассчитать искомый отрезок можно и через соотношение сторон и площадь.
Периметр (P):
ммсмдмм
Сторона (a):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Диагональ прямоугольника через диаметр описанной окружности
Поиск отрезка через описанную окружность еще более прост, здесь даже не придется проводить расчеты: D = d
Где d – это обозначенный диаметр.
Различить вписанную/описанную окружность легко. Когда геометрическое тело вписано куда-то, то оно всегда будет находиться в другой фигуре. Когда окружность описана, то она находится снаружи, она как бы описывает другое геометрическое тело. Описанные фигуры задевают собой точки, а вписанные – касаются сторон.
Диаметр (d):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
Диагональ прямоугольника через радиус описанной окружности
Для расчета искомого отрезка через описанную окружность нужно провести вычисления, где: D = 2R
Где R – это заданный радиус.
Радиус (R):
ммсмдмм
Цифр после запятой:
012345678910Результат в: ммсмдмм
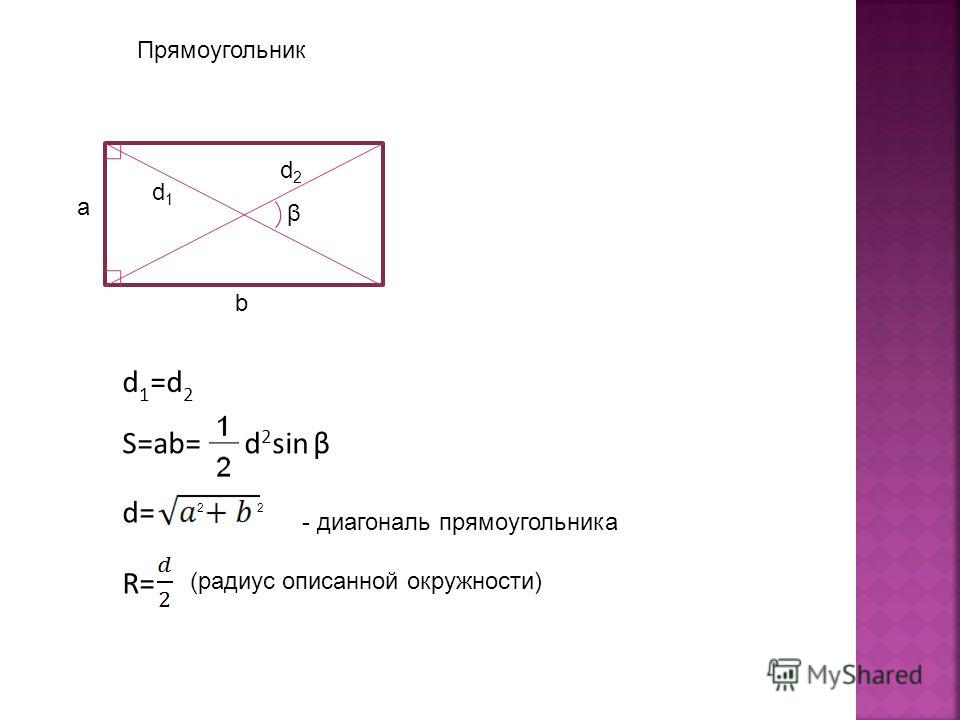
Диагональ прямоугольника через площадь и острый угол между диагоналями
Если необходимо узнать прямую, соединяющую вершины 4-хугольника, это можно осуществить с помощью двух диагоналей. Для получения ответа к задаче понадобится sin β между ними и S (произведение длины и ширины). Расчет проводится с равенством:
Где соответственно S – это площадь, а sin β – это острый угол, расположенный внутри фигуры (меж пересекающимися прямыми).
Если в 4-хугольнике расчертить 2 отрезка, объединяющие несмежные вершины, то они будут равны меж собой (все 4 отрезка), а точка пересечения разделит их пополам.
Пересечение всегда происходит в геометрическом центре самой фигурки. Этот же центр является центром описанной окружности.
Площадь (S):
мм²см²дм²м²
Угол (α):
градусырадианыsin
Цифр после запятой:
012345678910Результат в: ммсмдмм
Диагональ прямоугольника через угол прилегающей диагонали и длину стороны прилегающей к этому углу
Когда одна из сторон 4-хугольника прилегает к углу, то просчитать отрезок, соединяющий вершины тоже возможно:
Где b – это сторона, прилегающая к углу, а cos a – это тот самый угол.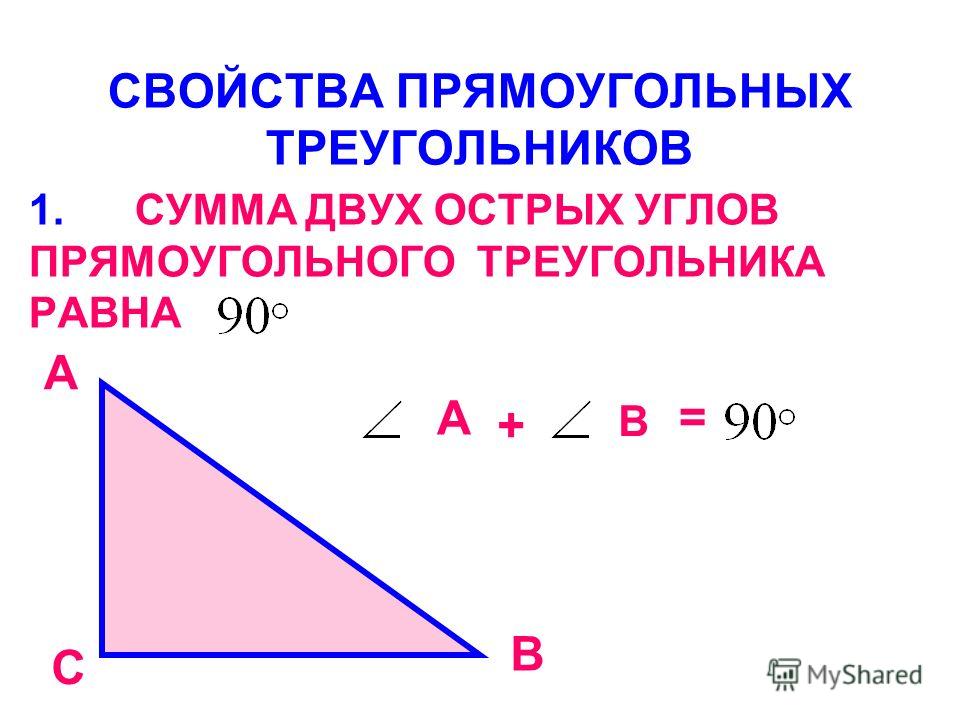
Косинус угла в треугольнике с прямым углом рассчитывается по формуле – длина соседней стороны, разделенная на гипотенузу. Синус – это противолежащий катет, разделенный на гипотенузу. Либо можно поступить еще проще, подсмотрев в таблицу Брадиса.
Сторона (b):
ммсмдмм
Угол (α):
градусырадианыcos
Цифр после запятой:
012345678910Результат в: ммсмдмм
Диагональ прямоугольника через угол прилегающей диагонали и длину стороны противоположной этому углу
Чтобы найти нужный отрезок внутри четырехугольника, должен быть задан угол, прилегающий к искомому отрезку и сторона, противоположная углу:
Где a – это сторона четырехугольника, а sin a – это прилегающий угол.
Длинная сторона 4-хугольника– это длина, а короткая – его ширина. Помните, что каждая сторона одновременно является высотой.
Сторона (a):
ммсмдмм
Угол (α):
градусырадианыsin
Цифр после запятой:
012345678910Результат в: ммсмдмм
Прямоугольник – это частный случай параллелограмма.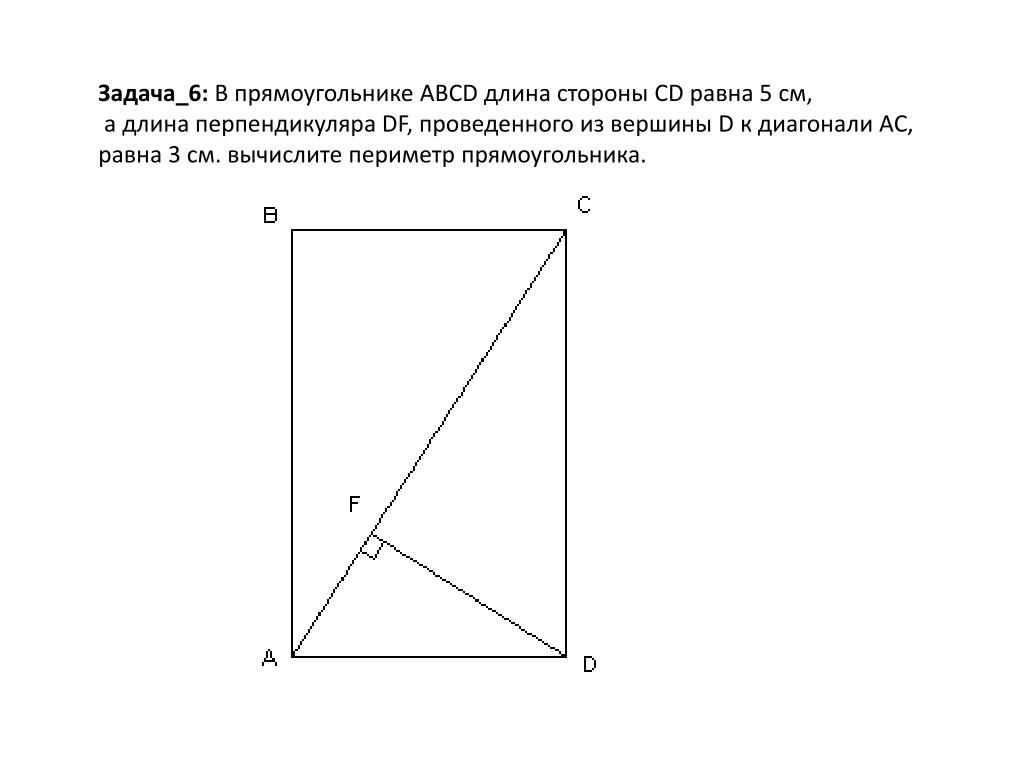 Иначе 4-хугольник с попарно равными сторонами, параллельными друг другу, а также равными прямыми углами по 90⁰. Сумма углов четырехугольника составляет 360⁰.
Иначе 4-хугольник с попарно равными сторонами, параллельными друг другу, а также равными прямыми углами по 90⁰. Сумма углов четырехугольника составляет 360⁰.
Диагональ разделяет фигуру на два новых элемента – треугольники с прямым углом. Это прямая, объединяющая противоположные вершины. Имея 2 прямоугольных треугольника, отрезок уже можно рассчитать по теореме Пифагора. По теореме гипотенуза – это квадрат из суммы катетов (обозначенных сторон треугольника), возведенных в квадрат.
Линии, соединяющие противоположные точки в четырехугольнике всегда пересекаются друг с другом.
Отрезок обозначают как d или D. Если названы все точки, то его можно называть в соответствии с ними – AC или BD.
Знания о линии, проходящей через несмежные точки 4-хугольника может понадобиться в легких геометрических упражнениях, так и в более сложных многоуровневых задачках, которые появляются на ЕГЭ. Свойства данного отрезка помогают находить важные параметры прямоугольника. Зная данные обеих линий, соединяющих противоположные углы, можно рассчитать S геометрического тела.
Зная данные обеих линий, соединяющих противоположные углы, можно рассчитать S геометрического тела.
Перед решением любой геометрической задачки рекомендуется сделать чертеж и обозначить всю заданную информацию. Так будет значительно проще сосредоточиться на искомом значении.
Если регулярно решать тесты по геометрии, то формулы легче запомнятся, а их применение будет доведено до автоматизма.
Как вычислить диагональ треугольника
••• doraartem/iStock/GettyImages
Обновлено 16 ноября 2020 г. вам ценная информация. Эта фраза говорит вам, что вы имеете дело с прямоугольным треугольником, две стороны которого перпендикулярны друг другу (или, говоря иначе, они образуют прямоугольный треугольник), и только одна сторона остается «диагональной» по отношению к другим. . Эта диагональ называется гипотенузой, и вы можете найти ее длину, используя теорему Пифагора.
TL;DR (слишком длинно, не читал)
Чтобы найти длину диагонали (или гипотенузы) прямоугольного треугольника, подставьте длины двух перпендикулярных сторон в формулу a 2 + b 2 = c 2 , где a и b длины перпендикулярных сторон и c гипотенуза.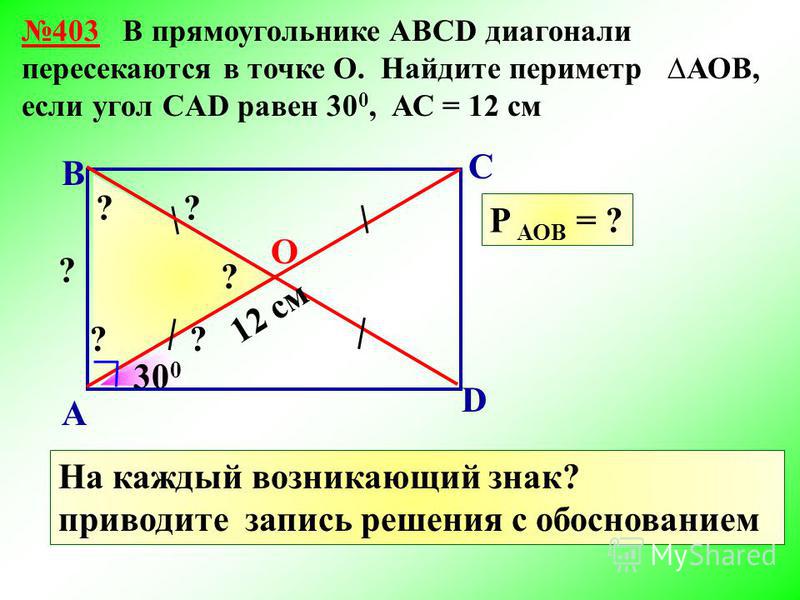 Затем найдите c .
Затем найдите c .
Теорема Пифагора 92
В реальном мире это означает, что если вы знаете длину любых двух сторон прямоугольного треугольника, вы можете использовать эту информацию, чтобы узнать длину недостающей стороны. Обратите внимание, что это работает только для прямоугольных треугольников.
Решение для гипотенузы
Предполагая, что вы знаете длины двух недиагональных сторон треугольника, вы можете подставить эту информацию в теорему Пифагора, а затем найти c.
Что, если вы знаете длину диагонали треугольника и длины одной другой стороны? Вы можете использовать ту же формулу, чтобы найти длину неизвестной стороны.
 Просто подставьте длины сторон, которые вы знаете, изолируйте оставшуюся буквенную переменную с одной стороны от знака равенства, а затем найдите эту букву, которая представляет длину неизвестной стороны.
Просто подставьте длины сторон, которые вы знаете, изолируйте оставшуюся буквенную переменную с одной стороны от знака равенства, а затем найдите эту букву, которая представляет длину неизвестной стороны.
Подставить известные значения 92 = 25
Возьмите квадратный корень из обеих частей, последний шаг в решении для c . Это дает вам:
c = \sqrt{25}= 5
Итак, длина диагонали или гипотенузы этого треугольника равна 5 единицам.
Связанные статьи
Ссылки
- Purple Math: Теорема Пифагора
- Математика — это весело: Pythagoras Theoorem
- Encyclopaedia Britannica: Pythagoras
- , Artanile
, 9008, 9008, 9008, 9008,
, 9008, 9008, 9008,
- , а Энцикл. Анкоридже, и провел несколько лет, обучая старшеклассников и студентов университетов страшным, но веселым! — математические предметы, такие как алгебра и исчисление.
Формула прямоугольного треугольника — Что такое формула прямоугольного треугольника? Примеры
Треугольник – это замкнутая фигура или фигура с 3 сторонами, 3 углами и 3 вершинами. Для формул прямоугольного треугольника свойства должны быть более конкретными. Если какой-либо из углов треугольника является прямым углом (составляет 90º), треугольник называется прямоугольным треугольником или просто прямоугольным треугольником.
 Формулы прямоугольного треугольника помогут вам выполнять различные вычисления, связанные с периметром, площадью и т. д. прямоугольного треугольника.
Формулы прямоугольного треугольника помогут вам выполнять различные вычисления, связанные с периметром, площадью и т. д. прямоугольного треугольника.Что такое формулы прямоугольного треугольника?
Прямоугольный треугольник — это треугольник, один из внутренних углов которого равен 90 градусов. Формулы прямоугольного треугольника используются для вычисления периметра, площади, высоты и т. д. прямоугольного треугольника с использованием трех его сторон.
Формула прямоугольного треугольника
Различные формулы, связанные с прямоугольным треугольником:
- Теорема Пифагора — Формула
Определение теоремы Пифагора показывает отношение между тремя сторонами прямоугольного треугольника. Квадрат гипотенузы равен сумме квадратов двух других катетов.
(Гипотенуза) 2 = (Перпендикуляр) 2 + (Основание) 2
- Формула площади прямоугольного треугольника
Формула для вычисления площади прямоугольного треугольника задается следующим образом:
Площадь = 1/2 × Основание × Высота = 1/2 × b × h
, где высота,h равна длине перпендикуляра сторона треугольника.

- Формула периметра прямоугольного треугольника
Формула для расчета площади прямоугольного треугольника задается как:
Периметр = a + b + c
, где a, b и c — три стороны треугольника.
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Забронировать бесплатный пробный урок
Примеры использования формул прямоугольного треугольника
Пример 1: Длина основания и перпендикуляра прямоугольного треугольника составляет 6 дюймов и 8 дюймов соответственно. Найти:
- Длина гипотенузы
- Периметр треугольника
- Площадь треугольника
Решение:
Чтобы найти:
Дано: длина основания = 6 дюймов, длина перпендикуляра = 8 дюймов 2 + (Перпендикуляр) 2
(Гипотенуза) 2 = 6 2 + 8 2 = 100
Гипотенуза = √100 = 10 из
ii) Используя формулу периметра прямоугольного треугольника,
Периметр = сумма всех сторон
Периметр = 6 + 8 + 10 = 24 из
2 iii) Используя формулу
3 формула площади треугольника,
Площадь = (1/2) × b × h
= (1/2) × 6 × 8
= 24 в 2
Ответ: Гипотенуза прямоугольного треугольника = 10 дм, периметр прямоугольного треугольника = 24 дм, а площадь прямоугольного треугольника = 24 дм 2 .

Пример 2: Высота и гипотенуза прямоугольного треугольника равны 12 и 13 дюймов соответственно. Найдите его площадь.
Решение:
Чтобы найти: площадь прямоугольного треугольника
Дано: высота = 12 дюймов, гипотенуза = 13 в
Используя теорему Пифагора,
(13) 2 + (12) 2
(база) 2 = (13) 2 — (12) 2 = 25
Основание = √25 = 5 в
Используя формулу площади треугольника,
Площадь = (1/2) × b × h
Площадь = (1/2) × 5 × 12
Площадь = 30 в 2
Ответ: Площадь прямоугольного треугольника = 30 в 2
30 единиц, высота 12 единиц, гипотенуза 13 единиц
Решение:
Чтобы найти: Площадь прямоугольного треугольника
Дано: периметр = 30 единиц, гипотенуза = 13 единиц, высота = 12 единиц
Мы знаем, что периметр = основание + гипотенуза + высота
30 единиц = 13 + 12 + основание
Следовательно, основание = 30 — 25 = 5 единиц
Площадь = 1/2bh = 1/2 (5 × 12) = 30 квадратных единиц.

Ответ: Площадь прямоугольного треугольника = 30 ед.0037
Что такое формула прямоугольного треугольника в геометрии?
В геометрии формулы прямоугольного треугольника — это формулы прямоугольного треугольника, которые используются для вычисления периметра, площади, высоты и т. д. треугольника с использованием трех его сторон — основания, высоты и гипотенузы. Эти формулы задаются следующим образом:
- Теорема Пифагора — Формула: (Гипотенуза) 2 = (Перпендикуляр) 2 + (Основание) 2
- Формула площади прямоугольного треугольника: Площадь = 1/2 × Основание × Высота
- Формула периметра прямоугольного треугольника = Сумма длин трех сторон
Каковы применения формулы прямоугольного треугольника?
Существует множество применений прямоугольного треугольника в реальной жизни, наиболее распространенным является его использование в области тригонометрии, поскольку отношение между его углами и сторонами составляет основу тригонометрии.


 Просто подставьте длины сторон, которые вы знаете, изолируйте оставшуюся буквенную переменную с одной стороны от знака равенства, а затем найдите эту букву, которая представляет длину неизвестной стороны.
Просто подставьте длины сторон, которые вы знаете, изолируйте оставшуюся буквенную переменную с одной стороны от знака равенства, а затем найдите эту букву, которая представляет длину неизвестной стороны. Формулы прямоугольного треугольника помогут вам выполнять различные вычисления, связанные с периметром, площадью и т. д. прямоугольного треугольника.
Формулы прямоугольного треугольника помогут вам выполнять различные вычисления, связанные с периметром, площадью и т. д. прямоугольного треугольника.


Leave A Comment