В параллелограмме abcd диагональ bd перпендикулярна стороне ab. из вершины прямого угла b проведена высота be к стороне ad. найдите площадь параллелограмма abcd, если be=6 см, а отрезок ae=3 см — Школьные Знания.net
Все предметы
Математика
Литература
Алгебра
Русский язык
Геометрия
Английский язык
Физика
Биология
Другие предметы
История
Обществознание
Окружающий мир
География
Українська мова
Информатика
Українська література
Қазақ тiлi
Экономика
Музыка
Беларуская мова
Французский язык
Немецкий язык
Психология
Оʻzbek tili
Кыргыз тили
Астрономия
Физкультура и спорт
Ответ дан
Senpai908
Рассмотрим прямоугольный треугольник BDA
Высота, проведенная из вершины прямого угла к гипотенузе AD есть среднее пропорциональное между проекциями катетов
Площадь параллелограмма ABCD: см²
Ответ: 90 см²
Математика по полочкам: 26.
 Четырехугольники
ЧетырехугольникиМАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
Параллелограмм
Четырехугольник, противоположные стороны которого попарно параллельны, называется параллелограммом.
Свойства параллелограмма
1. Противоположные стороны параллелограмма равны: AB=CD, AD=BC.
2. Противоположные углы параллелограмма равны: A=C, B=D.
3. Диагонали параллелограмма делятся точкой пересечения пополам AO=OC, BO=OD.
4. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон: d12+d22=2(a2+b2).
5. Каждая диагональ параллелограмма делит его на два равных треугольника.
6. Сумма внутренних углов параллелограмма 360°.
7. Сумма углов при двух соседних вершинах равна 180°.
Признаки параллелограмма
1. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.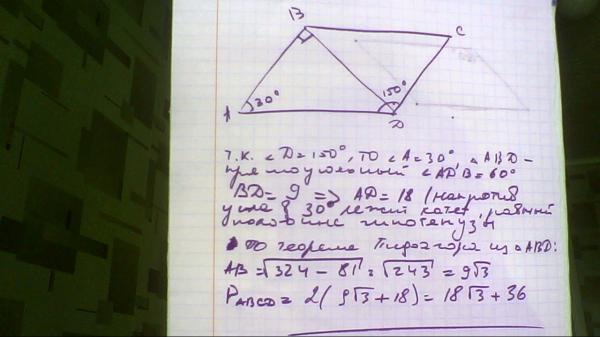
2. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
3. Если у четырехугольника диагонали точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
Площадь параллелограмма
1. Площадь параллелограмма равна произведению его основания на высоту: S=BH*AD.
2. Площадь параллелограмма равна произведению его смежных сторон на синус угла между ними: S=AB*AD*sin A.
Ромб
Параллелограмм у которого все стороны равны называется ромбом.
Свойства ромба
Так ромб является параллелограммом, то он имеет все свойства параллелограмма.
1. Диагонали ромба взаимно перпендикулярны: АС ┴ ВD.
2. Диагонали ромба являются биссектрисами его углов.
Признаки ромба
1. Если у параллелограмма диагонали взаимно перпендикулярны, то этот параллелограмм — ромб.
Если у параллелограмма диагонали взаимно перпендикулярны, то этот параллелограмм — ромб.
2. Если у параллелограмма одна из диагоналей лежит на биссектрисе, то этот параллелограмм — ромб.
Площадь ромба
1. Площадь ромба равна произведению его основания на высоту: S=СH*AВ.
2. Площадь ромба равна произведению квадрата его стороны на синус угла между сторонами: S=AB2*sin A.
3. Площадь ромба равна половине произведения его диагоналей: S=(d1*d2):2.
Прямоугольник
Параллелограмм, у которого все углы прямые называется прямоугольником.
Свойства прямоугольника
Так прямоугольник является параллелограммом, то он имеет все свойства параллелограмма.
1. Диагонали прямоугольника равны.
Признак прямоугольника
Если у параллелограмма диагонали равны, то этот параллелограмм — прямоугольник.
Площадь прямоугольника
Площадь прямоугольника равна произведению его смежных сторон: S = a*b.
Квадрат
Прямоугольник, у которого все стороны равны называется квадратом.
Свойства квадрата
Квадрату имеет все свойства параллелограмма, ромба и прямоугольника.
Площадь квадрата
Трапеция
Четырехугольник, две стороны которого параллельны, а две другие не параллельны называется трапецией.
Параллельные стороны трапеции называются ее основаниями (AD и ВС), а две другие — боковыми сторонами (АВ и СD).
Трапеция, боковые стороны которой равны (АВ=СD), называется равнобедренной.
У равнобедренной трапеции углы при основании равны: A=D, B=C.
Диагонали равнобедренной трапеции равны: АС=BD.
Трапеция, у которой есть прямой угол называется прямоугольной.
Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции.
Средняя линия трапеции параллельна основаниям трапеции равна их полусумме: MN=(a+b):2.
Средняя линия трапеции делит высоту трапеции на два равных отрезка.
Площадь трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту: S =(a+b):2*h.
УПРАЖНЕНИЯ
1. а) Любой ли параллелограмм является ромбом:
1) Да; 2) Нет; 3) зависит от длин его сторон; 4) зависит от величин его углов.
б) Любой ли параллелограмм является прямоугольником:
1) Да; 2) Нет; 3) зависит от длин его сторон; 4) зависит от величин его углов.
Решение:
а)зависит от длин его сторон.
Ответ: 3.

2. Является ли четырехугольник параллелограммом:
Решение:
а) В параллелограмме диагонали точкой пересечения делятся пополам, т.е. должно быть АО=ОС и ВО=OD, но ВО не равно OD ( 3 не равно 4).
Ответ: не является.
3. Найдите площадь закрашенной голубым цветом фигуры:
Решение:
а) Площадь прямоугольника ABCD равна 12*16=192.
Площадь квадрата KLMN равна 4*4=16.
Площадь фигуры, закрашенной голубым цветом равна 192-16=176.
Ответ: 176 кв.ед.
4. а) Сумма противоположных углов параллелограмма равна 160°. Найдите все углы параллелограмма.
б) Сумма противоположных углов параллелограмма равна 20°.
Решение:
а)
∠A+∠C=160°, т.к. противоположные углы параллелограмма равны, то ∠A=∠C=80°.
∠A+∠В =180° — по свойствам параллелограмма, тогда ∠В=180°-80°=100°.
Т.к. противоположные углы параллелограмма равны, то ∠В=∠D=100°.
Ответ: 80°, 100°, 80°, 100°.
5. а) Периметр ромба равен 24 см, а один из углов равен 120°. Найдите большую диагональ ромба.
б) Один из углов ромба равен 60°. Найдите периметр ромба, если его меньшая диагональ равна 4 см.
Решение:
а)
1) У ромба все стороны равны, тогда АВ=Р:4=24:4=6 см.
2) Пусть ∠A=120°, тогда большая диагональ ромба BD.
BD=BO+OD, т.к. диагонали ромба точкой пересечения делятся пополам.
3) ∠ВAО=120°: 2=60°, т.к. диагонали ромба являются биссектрисами его углов.
4) Рассмотри треугольник АВО, он прямоугольный, т.к. диагонали ромба пересекаются под прямым углом.
5) Найдем ВО:
ВО=АВ*sin ∠ВAО;
6. а) Докажите, что биссектрисы углов А и В параллелограмма ABCD взаимно перпендикулярны.
б) Докажите, что биссектрисы углов А и С параллелограмма ABCD параллельны.
Решение:
а)
Доказательство:
1) ∠DAК=∠ВКA как внутренние накрест лежащие при параллельных прямых ВС и AD и секущей АК.
2) ∠ВAК=∠КAD, т.к. АК — биссектриса угла BAD.
3) Следовательно, ∠ВAК=∠ВКA, тогда треугольник АВК — равнобедренный.
4) Биссектриса ВО в равнобедренном треугольнике АВК является и высотой, т.е. ВО перпендикулярно АК, а следовательно ВМ перпендикулярно АК.
Что и требовалось доказать.
7. а) Диагональ DB параллелограмма ABCD перпендикулярна стороне АВ. сosA=3/5. Сторона AD=20 см. Найдите площадь параллелограмма.
б) Диагональ АС параллелограмма ABCD перпендикулярна стороне СD. sin CAD=2/3. Сторона AD=15 см. Найдите площадь параллелограмма.
Решение:
а)
Площадь параллелограмма может быть вычислена по формуле S=BD*AB.
1) Найдем АВ:
cos A=AB:AD, AB=AD*cos A=20*3/5=12 см.
2) Найдем BD:
По теореме Пифагора: BD2=AD2-AB2=400-144=256, BD=16 см.
3) Найдем площадь:
S=16*12=192 см2
Ответ: 192 см2
8. а) В равнобедренной трапеции с основаниями 10 см и 6 см диагонали перпендикулярны боковым сторонам. Найдите площадь трапеции.
а) В равнобедренной трапеции с основаниями 10 см и 6 см диагонали перпендикулярны боковым сторонам. Найдите площадь трапеции.
б) Площадь равнобедренной трапеции равна 54 см2. Средняя линия трапеции равна 9 см. Диагонали перпендикулярны боковым сторонам. Найдите основания трапеции.
Решение:
а)
1) Треугольник ACD прямоугольный. Проведем к гипотенузе этого треугольника высоту СН.
HD=(AD-BC):2=(10-6):2=2 см, т.к. ABCD — равнобедренная трапеция.
2)CH2=АН*HD=10*2=20,
2)
9. а) АМ и DM — биссектрисы параллелограмма ABCD. М лежит на стороне ВС параллелограмма. Найти площадь параллелограмма, если АМ=4 см, DM=3 см.
б) BМ и CM — биссектрисы параллелограмма ABCD. М лежит на стороне AD параллелограмма. Найти площадь параллелограмма, если BМ=6 см, CM=4 см.
Найти площадь параллелограмма, если BМ=6 см, CM=4 см.
Решение:
а)
1) Найдем угол AMD:
∠А+∠D=180° как углы при соседних вершинах. ∠МАD+∠ADM=(∠А+∠D):2=90°, т.к. АМ и DM — биссектрисы углов А и D.
Тогда ∠AMD=180-(∠МАD+∠ADM)=180-90=90°.
2) Треугольник AMD — прямоугольный, тогда по теореме Пифагора найдем AD:
AD2=AM2+MD2=16+9=25, AD=5 см.
3) Найдем высоту параллелограмма.
МН — высота в прямоугольном треугольнике, а также и высота параллелограмма.
SAMD = AM*MD:2=4*3:2=6 см.
SAMD = MH*AD:2; 6=MH*5:2; MH=2,4 см
4) Найдем площадь параллелограмма:
S=MH*AD=2,4*5=12 см2.
Ответ: 12 см2.
10. а) В трапеции ABCD проведена прямая, параллельная основаниям, которая пересекает боковые стороны трапеции в точках E и F. Найти площадь трапеции AEFD, если площадь трапеции EBCF равна 20 см2 и ВС=4 см, EF=8 см, AD=16 см.
б) В трапеции ABCD проведена прямая, параллельная основаниям, которая пересекает боковые стороны трапеции в точках M и N. Найти площадь трапеции MBCN, если площадь трапеции AMND равна 48 см2 и ВС=4 см, MN=6 см, AD=9 см.
Решение:
а)
1) Трапеции AEFD и EBCF подобны:
1. ∠1=∠2, ∠3=∠4 как соответственные углы при параллельных прямых EF и AD.
2. ∠5=∠6, ∠7=∠8 как соответственные углы при параллельных прямых EF и ВС.
2) Найдем коэффициент подобия:
k=EF:BC=8:4=2.
3) Площади подобных фигур относятся как коэффициент подобия в квадрате.
SAEFD = SEDCF *k2= 20*4=80 см2.
Ответ: 80 см2.
11. а) В параллелограмме ABCD отрезок CF пересекает диагональ BD в точке О (F лежит на стороне АD). Найдите площадь параллелограмма, если площади треугольников ODF и CDO раны 12 см2 и 20 см2 соответственно.
б) В параллелограмме ABCD отрезок ВF пересекает диагональ АС в точке О (F лежит на стороне АD). Найдите площадь параллелограмма, если площади треугольников OFA и OBA раны 12 см2 и 8 см2 соответственно.
Решение:
а)
1) Проведем к CF высоту DH.
Рассмотрим площади треугольников FOD и OCD:
SODF = DH*OE:2; 12= DH*OE:2; DH*OF=24. (1)
SCDO = DH*OC:2; 20 = DH*OC:2; DH*OC=40. (2)
Разделим выражение (2) на (1): OC:OF=40:24, OC:OF=5:3.
2) Треугольники BOC и FOD подобны по двум углам:
1. ∠FOD=∠BOC как вертикальные углы;
2. ∠СFD=∠FCB как внутренние накрест лежащие при параллельных прямых ВС и AD и секущей FC.
3) Площади подобных фигур относятся как коэффициент подобия в квадрате.
SBOC = SFOD*k2=12*(5/3)2=100/3 см2.
4) Найдем площадь треугольника BCD:
SBCD= SBCO + SOCD=100/3+20=53 1/3 см2.
5) Найдем площадь параллелограмма:
SABCD=2*SBCD=106 2/3 см2.
Ответ: 106 2/3 см2.
12. а) Средняя линия трапеции равна 5 см, диагонали трапеции равны 14 см и 8 см. Найдите площадь трапеции.
б) Средняя линия трапеции равна 10 см, диагонали трапеции равны 14 см и 10 см. Найдите площадь трапеции.
Решение:
а)
Дано: ABCD — трапеция;
АС=14 см;
BD=8 см;
MN — средняя линия; MN=5 см.
Найти: S трапеции.
1) AD+BC=2*MN=2*5=10 см.
2) AB+CD=BC+AD=10 cм.
3) Проведем прямую СЕ параллельно прямой BD. E — точка пересечения прямых AD и CE.
DBCE — параллелограмм, т.к. две пары противолежащих сторон параллельны.
DE=BC и BD=CE=8 см, т.к. противолежащие стороны параллелограмма равны.
АЕ=AD+DE=AD+BC=10 см.
4) Найдем площадь треугольника АСЕ по формуле Герона:
р=(АС+СЕ+АЕ):2=(14+8+10):2=16 см.
5) Найдем площадь трапеции:
Треугольники ABC и CED имеют одинаковую площадь, т.к. их площади равны половине произведения высоты трапеции на равные стороны ВС и DE.
Тогда площадь трапеции равна площади треугольника АСЕ:
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Если в четырехугольнике противоположные стороны попарно равны, то это:
а) квадрат; б) ромб; в) трапеция; г) прямоугольник; д) параллелограмм.
2. Является ли четырехугольник параллелограммом, если одна пара его противоположных сторон равна, а другая параллельна?
3. В равнобедренной трапеции ABCD с основаниями AB и CD сумма углов А, В, С равна 340°.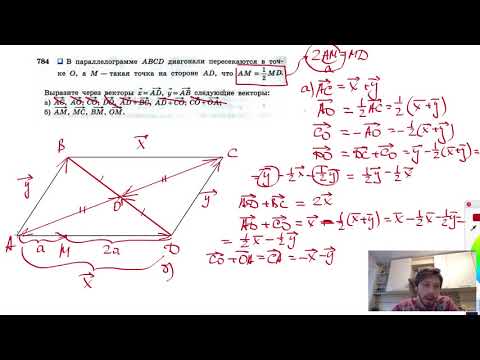 Найдите все углы трапеции.
Найдите все углы трапеции.
4. В параллелограмме ABCD угол А равен 60°, сторона ВС равна 10 см, высота СН проведена из вершины С к стороне AD и АН=14 см. Найдите периметр параллелограмма.
5. Диагонали ромба относятся как 2:5. Найдите площадь ромба, если его периметр равен 10 см.
6. Площадь прямоугольника равна 54 см2. Найдите площадь четырехугольника вершинами которого являются середины сторон данного прямоугольника.
7. В параллелограмме ABCD к сторонам BC и DC проведены высоты из точки А, угол между высотами равен 45° и одна из высот делит сторону DC на отрезки 3 см и 4 см, считая от вершины С. Найдите площадь параллелограмма.
8. Найдите среднюю линию трапеции, если ее диагонали взаимно перпендикулярны и равны 12 см и 16 см.
9. Может ли четырехугольник с противоположными наборами сторон a и b, c и d являться трапецией, если да, то найти ее площадь:
а) a=5 см, b=4 см, c=6 см, d=3 см; б) a= 3 см, b=4 см, c=5 см, d=3 см.
10. Площадь трапеции ABCD равна 100 см2. Из середины стороны АВ к стороне CD проведен перпендикуляр, который равен 16 см. Найдите боковую сторону CD.
Площадь трапеции ABCD равна 100 см2. Из середины стороны АВ к стороне CD проведен перпендикуляр, который равен 16 см. Найдите боковую сторону CD.
ПРОВЕРЬТЕ СЕБЯ
Длина диагонали BD параллелограмма ABCD равна 18 см. Если P и Q являются центроидами DeltaABC и Delta ADC соответственно, то длина отрезка PQ равна
KIRAN ПУБЛИКАЦИЯ-ГЕОМЕТРИЯ-ВОПРОСЫ, ЗАДАВАЕМЫЕ НА ПРЕДЫДУЩИХ ЭКЗАМЕНАХ SSC (ТИП-IX)
5 видеоРЕКЛАМА
Ab Padhai каро бина объявления ке
Khareedo DN Pro и дехо сари видео бина киси объявление ки rukaavat ке!
Обновлено: 27-06-2022
Текст Решение 9
Правильный ответ: B
Связанные видео
किसी समान्ता चतुा abcd विकर्ण bd का मान 18 см है बिंदु p एवं Q ΔAbc तथ ΔAdc के केंद्ve (गुरुतFुतFकेंद केंद ेख ेखFेख ेख ेख ेख ेखшить केंद ेख ेखшить δ ेख ेखшить δ ेख ेखшить (गु्बчитал)?
23273206
समांत выполнительный Pऔर Qकार्मश : △ABC और △ADC के केंद्र है । रेखाखण्ड PQ की लम्बाई (सेमी में ) कितनी है ?
23273663
ABC एक त्रिभुज है, PQ एक 000 ेख जो a ab को P पर औ ac को Q प क क है औ औ औ पbc है AP: Bc अनुप अनुप क सेमी. БК की लम्बाई बताइए?
БК की लम्बाई बताइए?
232738443
समांत выполнительный O से एक रेखा खींची गई है जो ad तथा bc को क्रमशः p तथा q पर पшить क क क है।।।।। सिद्ध कीजिए कि रेखाखण्ड pq समांतर चतुर्भुज को दो बराबर क्षेत्रफल वाले भागों में विभ क क है।।।।
105884868
किसी समांतर चतुर्भुज abcd में विकर्णों का कटान बिंदु o हो और oc = 6 सेमी, ob = 8 सेमी तो bd की लम्बाई निकालें।। सेमी सेमी सेमी तो
109837028
abcd एक समांत выполнительный साबित करें किPCQA एक समांतर चतुर्भुज है।
109837135
Если длины диагоналей AC и BD ромба ABCD равны a см и b см соответственно, то площадь ромба ABCD равна
233232281
Если длина диагонали BD квадрата ABCD равна 4,8 см, площадь квадрата ABCD:
446657994
Если ABCD — параллелограмм, в котором P и Q — центроиды ΔABD и ΔBCD. тогда PQ равно:
449930087
ABCD — параллелограмм. E и F — середины сторон AB и CD соответственно. AF и CE пересекают диагональ BD в точках P и Q соответственно.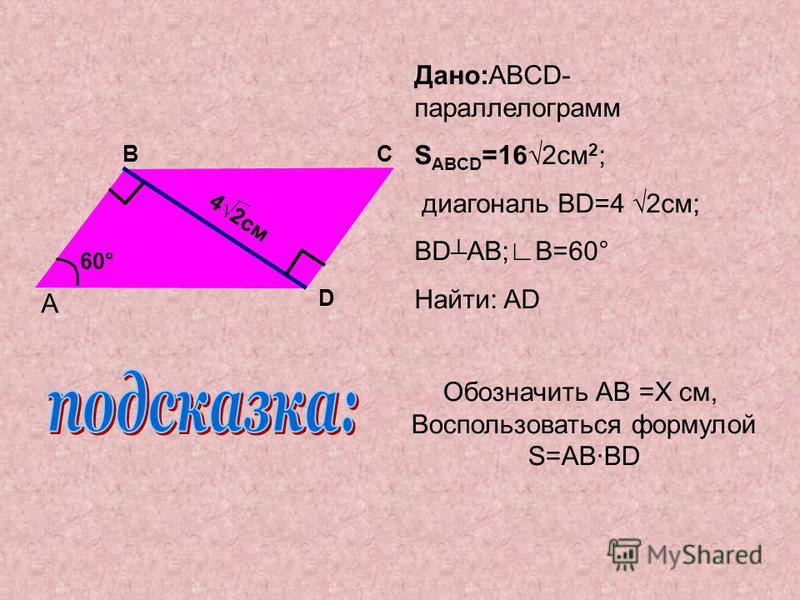 Если BD = 15 см, найдите PQ.
Если BD = 15 см, найдите PQ.
643373031
ABCD — параллелограмм. E и F — центроиды треугольников ABD и BDC соответственно. Найдите длину EF, если длина диагонали AC = 12 см.
643373036
Если ABCD — параллелограмм, в котором P и Q — центроиды ΔABD и ΔBCD. тогда PQ равно:
643471747
Если длина диагонали BD квадрата ABCD равна 4,8 см, площадь квадрата ABCD равна:
643476589
В четырехугольнике ABCD диагональ BD делится пополам диагональю AC. Докажите, что: ΔABC и ΔADC равны по площади.
644443614
ABCD — ромб, у которого длины диагоналей AC и BD равны 6 см и 8 см соответственно. Найдите периметр ромба ABCD.
645949300
ABC — треугольник, PQ — отрезок, пересекающий AB в P и AC в Q и PQ||BC. Соотношение AP : BP = 3 : 5 и длина PQ 18 см. Длина BC равна
646460805
Q10 В параллелограмме ABCD его диагонали AC и BD пересекаются в точке O Если AC 12 см и .
 ..
..Перейти к
- Упражнение 27 (А)
- Упражнение 27(Б)
- Система счисления (закрепление чувства числа)
- Оценка
- Числа в Индии и международной системе (со сравнением)
- Место Значение
- Натуральные числа и целые числа (включая шаблоны)
- Отрицательные числа и целые числа
- Номер строки
- HCF и LCM
- Игра с числами
- Наборы
- Соотношение
- Доля (включая словесные задачи)
- Унитарный метод
- Фракции
- Десятичные дроби
- Процент (Процент)
- Представление о скорости, расстоянии и времени
- Основные понятия (алгебра)
- Основные операции (связанные с алгебраическими выражениями)
- Замена (включая использование скобок в качестве группирующих символов)
- Обрамление алгебраических выражений (включая вычисление)
- Простые (линейные) уравнения (включая текстовые задачи)
- Основные понятия (геометрия)
- Углы (с их типами)
- Свойства углов и линий (включая параллельные линии)
- Треугольники (включая типы, свойства и конструкцию)
- четырехугольник
- Полигоны
- Круг
- Повторное упражнение по симметрии (включая построения по симметрии)
- Распознавание твердых тел
- Периметр и площадь плоских фигур
- Обработка данных (включая пиктограмму и гистограмму)
- Среднее и медиана
Главная > Селина Солюшнс Класс 6 Математика > Глава 27 — Четырехугольник > Упражнение 27(Б) > Вопрос 10
Вопрос 10 Упражнение 27(B)
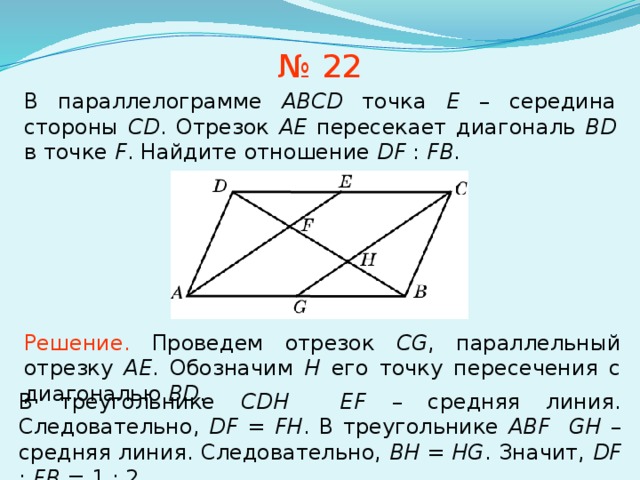
Q10) В параллелограмме ABCD диагонали AC и BD пересекаются в точке O.
Если AC = 12 см и BD = 9 см ; находить; длины OA и OD.
Ответ:
Решение:
Когда диагонали AC и BD пересекаются в точке O,
Тогда OA=OC=\frac{1}{2}AC
OB=OD=\frac{1}{ 2}BD
OA=\frac{1}{2}\times AC=\frac{1}{2}\times12=6\ cm
OB=\frac{1}{2}\times BD=\ frac{1}{2}\times9=4.5\ cm
Видео стенограмма
привет добро пожаловать в домашнюю работу лидера меня зовут сегодня мы увидим параллелограмм abcd его диагонали ac и bd пересекаются друг с другом в точке a точка o хорошо, а также учитывая, что если ac равно 12 сантиметрам, а bd равно 9сантиметры ac равно 12, а bd равно 9 сантиметрам. Найдите длину oa, которую они просят найти при oa и od. Итак, вот эти длины, нам нужно узнать эту длину, а также эту длину, как решить эту, которую вы знаете как вы можете видеть здесь oa равно oc вы согласны со мной да, это будет равно, потому что это будет диагональ прямо она идет к другой проходит через другую диагональ проходит через ее центр Хорошо, так что это будет половина переменного тока от переменного тока, так что же такое половина переменного тока, какова длина переменного тока в этом 12, это будет длина oa, которая будет равна 6 сантиметрам, хорошо, теперь перейдем к другой длине, хорошо теперь вы проверяете другой, да, другое дело, хм, другое дело, ob равно половине bd от bd половина в диапазоне bd — это сколько бета в этом, учитывая, что это девять девять сантиметров, это будет четыре целых пять десятых сантиметров, это собираешься, о, о, и длина ob в порядке или o d также вы можете пнуть его в порядке, так что я надеюсь, что вы понимаете d это видео, если у вас есть какие-либо вопросы, вы можете оставить их в разделе комментариев, и спасибо за просмотр этого видео
Связанные вопросы
Q1) В трапеции ABCD сторона AB параллельна стороне DC. Если ∠A = 78° и ∠C = 120°, найдите углы B и…
Если ∠A = 78° и ∠C = 120°, найдите углы B и…
Q2) В трапеции ABCD сторона AB параллельна стороне DC. Если ∠A = x° и ∠D = (3x – 20)°; найди ва…
Q3) Углы A, B, C и D трапеции ABCD относятся как 3 : 4 : 5 : 6.Le. ∠А : ∠Б : ∠С : ∠…
Q4) В равнобедренной трапеции одна пара противоположных сторон ….. друг к другу, а другая пара …
Q5) Две диагонали равнобедренной трапеции равны x см и (3x – 8) см. Найдите значение х.
Q6) Угол А равнобедренной трапеции равен 115°; Найдите углы В, С и D.
Фейсбук WhatsApp
Копировать ссылку
Было ли это полезно?
Упражнения
Упражнение 27(A)
Упражнение 27(B)
Главы
Система счисления (Закрепление чувства числа)
Оценка
Числа в Индии и международной системе (с сравнением)
Значение места
Натуральные числа и целые числа (включая шаблоны)
Отрицательные числа и целые числа
Числовые линии
HCF и LCM
Игра с номерами
SETS.

Leave A Comment