17.2. Параллелограмм (Задачи ОГЭ) — Uchus.Online
Сайт подготовки к экзаменам Uchus.online
Задачи ОГЭ
№2481
Сложность:
22 %
!
Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 21°. Ответ дайте в градусах.
Подпишись на ютуб канал
Подписаться
№2491
Сложность:
22 %
!
Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 8°. Ответ дайте в градусах.
Подпишись на ютуб канал
Подписаться
№2820
Сложность:
23 %
!
Найдите величину острого угла параллелограмма \(ABCD\), если биссектриса угла \(A\) образует со стороной \(BC\) угол, равный 21°. {\circ}\). Ответ дайте в градусах.
{\circ}\). Ответ дайте в градусах.
Подпишись на ютуб канал
Подписаться
№2102
Сложность:
23 %
!
Найдите острый угол параллелограмма \(ABCD\), если биссектриса угла \(A\) образует с его стороной \(BC\) угол, равный 15°. Ответ дайте в градусах.
Подпишись на ютуб канал
Подписаться
№4013
Сложность:
23 %
!
Найдите величину острого угла параллелограмма \(ABCD\), если биссектриса угла \(A\) образует со стороной \(BC\) угол, равный 13°. Ответ дайте в градусах.
Подпишись на ютуб канал
Подписаться
№4620
Сложность:
25 %
!
Диагональ \(AC\) параллелограмма \(ABCD\) образует с его сторонами углы, равные 30° и 45°.
Подпишись на ютуб канал
Подписаться
№4796
Сложность:
25 %
!
Найдите площадь параллелограмма, изображенного на рисунке.
Подпишись на ютуб канал
Подписаться
№2050
Сложность:
26 %
!
Диагональ \(BD\) параллелограмма \(ABCD\) образует с его сторонами углы, равные 25° и 110°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.
Подпишись на ютуб канал
Подписаться
Загрузка…
2023 ©, ИП Иванов Дмитрий Михайлович- ВК
- Почта
Используйте ваш ВК для того, чтобы войти в систему
Пользуясь сайтом вы автоматически принимаете пользовательское соглашение.
Чтобы выслать код сброса пароля, пожалуйста, введите ваш адрес электронной почты.
ВНИМАНИЕ: НЕ задавайте здесь вопросы! Для этого есть форум. Задать вопрос на форуме
Опишите ошибку
Всего задач в тесте: 0
Вы ответили верно на: 0 (0 %)
Вы ответили неверно на: 0
ВИДЕОКУРС по задачам 20-22 ОГЭ:
Открыть
Загрузка. ..
..
Многоугольники. Задание 15. Ч.4
Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 15°. Ответ дайте в градусах.
Решение
Параллелограмм – это четырехугольник у которого противоположные стороны параллельны.
Биссектриса – это луч, выходящий из вершины угла и делящий этот угол на две равные части.
Если две прямые параллельны ( BC || AD), то накрест лежащие углы равны (<BKA=<KAD).
Ответ: 30
Теория
Тренажер
Нажмите здесь, чтобы открыть тренажер
Решение
Трапеция – это четырехугольник с двумя параллельными сторонами (основаниями) и двумя не параллельными сторонами (боковыми сторонами).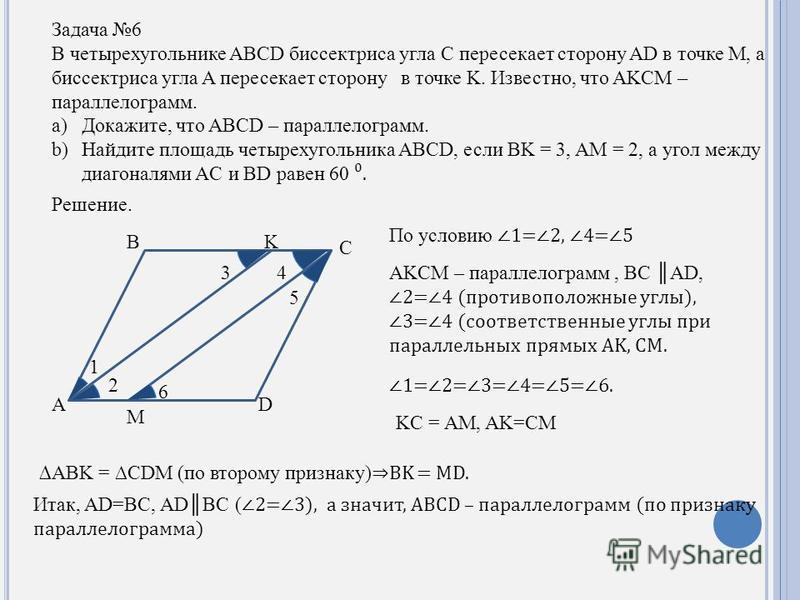
В равнобедренной трапеции боковые стороны равны и углы при основаниях равны,
Ответ: 7
Теория
Тренажер
Нажмите здесь, чтобы открыть тренажер
В остроугольном треугольнике ABC проведена высота BH, <BAC=37°. Найдите угол.
Решение
Т.к. треугольник ABH – прямоугольный (BH – высота), то сумма острых углов треугольника равна 90 градусов:
Ответ: 53
Теория
Тренажер
Нажмите здесь, чтобы открыть тренажер
В треугольнике ABC угол С равен 142°. Найдите внешний угол при вершине С. Ответ дайте в градусах.
Решение
т.к. один из углов треугольника равен 142 градуса, значит он тупоугольный.
Угол называется тупым, если его градусная мера больше 90 градусов.
Треугольник называется тупоугольным если имеет тупой угол.
Внешний угол треугольника – это угол треугольника смежный с внутренним углом при той же вершине.
Смежные углы треугольника в сумме дают 180 градусов:
Ответ: 38
Теория
Тренажер
Нажмите здесь, чтобы открыть тренажер
Один из углов равнобедренной трапеции равен 66°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение
Угол, градусная мера которого меньше 90 градусов называется острым.
В равнобедренной трапеции углы при основании равны: <A=<D, <B=<C.
Угол в 66 градусов – острый угол, трапеция равнобедренная, следовательно в нашей трапеции это углы А и D.
Трапеция – это четырехугольник у которого две противоположные стороны параллельны, а две другие нет.
Поэтому рассмотрим один из признаков параллельности прямых (отрезков): если две прямые параллельны, то односторонние углы в сумме составляют 180 градусов.
Углы A и B – односторонние, BC параллельно AD, значит:
Ответ: 114
Теория
Тренажер
Нажмите здесь, чтобы открыть тренажер
Один из углов прямоугольной трапеции равен 64°. Найдите больший угол этой трапеции. Ответ дайте в градусах.
Решение
Трапеция называется прямоугольной, если у нее два угла прямые.
Угол, градусная мера которого меньше 90 градусов называется острым.
Угол в 64 градуса – острый угол, трапеция прямоугольная, следовательно в нашей трапеции это угол D.
Трапеция – это четырехугольник у которого две противоположные стороны параллельны, а две другие нет.
Поэтому рассмотрим один из признаков параллельности прямых (отрезков): если две прямые параллельны, то односторонние углы в сумме составляют 180 градусов.
Углы C и D – односторонние, BC параллельно AD, значит:
Ответ: 116
Теория
Тренажер
Нажмите здесь, чтобы открыть тренажер
Один из углов параллелограмма равен 41°. Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
Найдите больший угол этого параллелограмма. Ответ дайте в градусах.
Решение
В параллелограмме противоположные углы равны: <A=<C, <B=<D.
Угол, градусная мера которого меньше 90 градусов называется острым.
Угол в 41 градус – острый угол, следовательно это углы A и D.
Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны.
Поэтому рассмотрим один из признаков параллельности прямых (отрезков): если две прямые параллельны, то односторонние углы в сумме составляют 180 градусов.
Углы A и B – односторонние, BC параллельно AD, значит:
Ответ: 139
Теория
Тренажер
Нажмите здесь, чтобы открыть тренажер
Один из углов ромба равен 43°. Найдите больший угол этого ромба. Ответ дайте в градусах.
Решение
В ромбе противоположные углы равны: <A=<C, <B=<D.
Угол, градусная мера которого меньше 90 градусов называется острым.
Угол в 43 градуса – острый угол, следовательно в нашем ромбе это углы A и C.
Ромб – это параллелограмм с равными сторонами. Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны.
Поэтому рассмотрим один из признаков параллельности прямых (отрезков): если две прямые параллельны, то односторонние углы в сумме составляют 180 градусов.
Углы A и B – односторонние, BC параллельно AD, значит:
Ответ: 137
Теория
Тренажер
Нажмите здесь, чтобы открыть тренажер
Геометрия— Как мне доказать, что этот метод определения знака биссектрисы острого или тупого угла в формуле биссектрисы угла работает?
У меня есть аналитическое доказательство. Это не особенно красиво, но, похоже, работает.
Пусть ${L}_{1} , {L}_{2}$ — две прямые, а $\binom{{x}_{0}}{{y}_{0}}$ — их пересечение.
Используя ${x’} = x-{x}_{0}$ и ${y’} = y-{y}_{0}$ вместо
$x$ и $y$, можно предположить, что $\boxed{c = r = 0}$. {2} = 1}$. Уравнения ${L}_{1}$ и ${L}_{2}$
теперь $a x+b y = 0$ и $p x+q y = 0$.
{2} = 1}$. Уравнения ${L}_{1}$ и ${L}_{2}$
теперь $a x+b y = 0$ и $p x+q y = 0$.
Точка $M = \binom{a+p}{b+q}$ лежит на биссектрисе ${L}_{1} , {L}_{2}$. На самом деле его координаты удовлетворяют $a x+b y = 1+a p+b q = p x+q y$, что является примером случая $+$ в вашей формуле. Мы хотим вычислить угол ${\alpha}$ между ${L}_{1}$ и линией $O M$.
Пусть ${M}_{1}$ — ортогональная проекция $M$ на ${L}_{1}$. Его координаты равны $t \binom{{-b}}{a}$ для некоторого $t \in \mathbb{R}$. Мы найти $t$ по условию, что вектор $\binom{a+p}{b+q}-t \binom{{-b}}{a}$ пропорциональна $\binom{a}{b}$. В результате получается $t = a q-b p$. 9{2} = 2 \left(1+a p+b q\right)$. Наконец, $\left|{M}_{1}\right| = \влево|t\вправо|$. Отсюда следует, что
$$\left|\cos \left({\alpha}\right)\right| = \frac{{M}_{1} \cdot M}{\left|M\right| \left|{M}_{1}\right|} = \frac{\sqrt{2}}{2} \frac{\left|t\right|}{\sqrt{1+a p+b q}} $$
Если $a p+b q \geqslant 0$, то $\left|t\right| \leqslant 1 \leqslant \sqrt{1+a p+b q}$ и отсюда следует
что $\left|\cos \left({\alpha}\right)\right| \leqslant \frac{\sqrt{2}}{2}$. Отсюда имеем ${\alpha} \in \left[\frac{{\pi}}{4} , \frac{{\pi}}{2}\right]$, что означает, что $2 {\alpha} \ в \left[\frac{{\pi}}{2} , {\pi}\right]$ и точка
$M$ лежит на тупой биссектрисе.
Отсюда имеем ${\alpha} \in \left[\frac{{\pi}}{4} , \frac{{\pi}}{2}\right]$, что означает, что $2 {\alpha} \ в \left[\frac{{\pi}}{2} , {\pi}\right]$ и точка
$M$ лежит на тупой биссектрисе.
Это доказывает заявление вашей книги. Для изучения отрицательного знака можно использовать точку ${M’} = \binom{a-p}{b-q}$ на второй биссектрисе.
Обратите внимание, что знаки $c$ и $r$ в доказательстве вообще не используются. Ты можно безопасно вывести их из состояния.
Изменить : теперь мне кажется, что доказательство можно еще больше сократить, не вычисляя ортогональную проекцию $M_1$. Можно использовать $\binom{-b}{a}$ напрямую для вычисления угла.
Редактировать 2: Лучшее доказательство 9{2}}$$
Пусть теперь наши единичные векторы нормалей равны ${n}_{1} = \binom{a}{b}$ и ${n}_{2} = \binom{p}{q}$. Предположим, что ${n}_{1} \cdot {n}_{2} = a p+b q \geqslant 0$. Определим
$${\theta} = \arctan \left(\frac{a q-b p}{1+a p+b q}\right)$$
Из леммы следует, что $\cos \left( 2 {\theta}\right) = a p+b q = {n}_{1} \cdot {n}_{2}$ и
$\sin\left(2 {\theta}\right) = a qb p$. Надо
${\ theta} \in \left[{-\frac{{\pi}}{4}} , \frac{{\pi}}{4}\right]$, потому что $\cos \left(2 {\ theta}\right) \geqslant 0$.
Мы гарантируем, что ${\theta} \neq 0$, требуя, чтобы ${n}_{1}$ и ${n}_{2}$
не пропорциональны. Определим векторы
Надо
${\ theta} \in \left[{-\frac{{\pi}}{4}} , \frac{{\pi}}{4}\right]$, потому что $\cos \left(2 {\ theta}\right) \geqslant 0$.
Мы гарантируем, что ${\theta} \neq 0$, требуя, чтобы ${n}_{1}$ и ${n}_{2}$
не пропорциональны. Определим векторы
$${e}_{1} = \frac{1}{2 \sin\left({\theta}\right)} \left({n}_{1}-{n}_{2} \right) \quad \text{ и } \quad {e}_{2} = \frac{1}{2 \cos \left({\theta}\right)} \left({n}_{1} +{n}_{2}\right)$$
Исчисление легко показывает, что $\left({e}_{1} , {e}_{2}\right)$ являются прямым ортонормированным базисом и что
$${n}_{1} =\sin \left({\theta}\right) {e}_{1}+\cos \left({\theta}\right) {e}_{2 } \quad \text{ и } \quad {n}_{2} = -\sin \left({\theta}\right) {e}_{1}+\cos \left({\theta}\right ) {е}_{2}$$
Отсюда следует, что уравнения ${L}_{1}$ и ${L}_{2}$ в базисе $\left({e}_{1} , {e}_{2}\ right)$ равны соответственно $y = -\tan \left({\theta}\right) x$ и $y =\tan \left({\theta}\right) x$, которые
означает, что ${L}_{1} , {L}_{2}$ — прямые линии с наклонами $-\tan \left({\theta}\right)$
и ${\tan} \left({\theta}\right)$.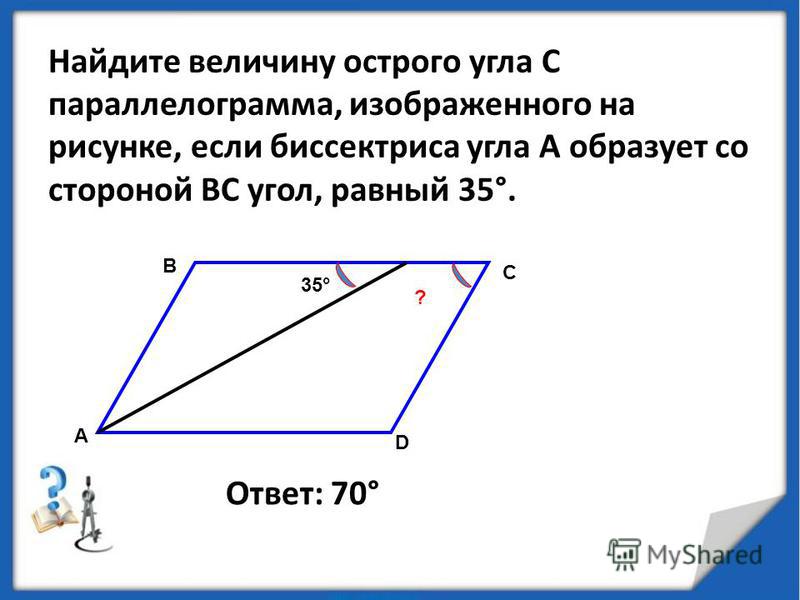

Leave A Comment