Максимум и минимум функции: понятие
Время чтения: 2 минуты
469
Исследование функции в математическом анализе предполагает нахождение экстремумов, которые представляют собой максимальное и минимальное значение на заданном множестве. Для того чтобы определить минимум функции, необходимо произвести несколько простых операций с ее производной. Сначала следует приравнять функцию к нулю и найти значения переменной, а затем, используя их, разбить координатную плоскость и определить, какие отрезки будут положительными или отрицательными.
Определение максимума и минимума функции
Минимумом заданной функции \[y=f(x)\] принято называть одну некоторую точку, если в ее окрестности соблюдается неравенство \[y=f(x) \geq f\left(x_{0}\right)\].
Таким образом \[x_{0}\] – это и есть минимум.
\[x_{0}\] можно назвать максимумом \[y=f(x)\], если в некоторой ее окрестности будет выполняться следующее неравенство \[y=f(x) \leq f\left(x_{0}\right)\].
- максимум, при условии, что \[0>a\];
- минимум, при условии \[a>0\].
Экстремум на всей области определения будет совпадать с вершиной параболы. Это показано на рисунке:
Экстремумы в математическом анализе делятся на два вида:
- глобальный;
- локальный.
К локальному применимо общее определение экстремума. Глобальный вид – это набольшее и наименьшее значение функции на определенном участке.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Достижение глобальных экстремумов возможно на обоих концах отрезка, а также в местах нахождения локального экстремума. Для определения их необходимого условия используется следующая теорема:
Теорема 1 — 3
Если экстремум \[y=f(x)\] находится в некоторой точке \[x_{0}\], то производная \[f^{\prime}(x)\] в той же точке будет равна нулю, либо вовсе не будет существовать. {2}+12 x\] представлен на рисунке:
{2}+12 x\] представлен на рисунке:
Рассмотренные примеры наглядно показывают, как должно осуществляться исследование функции в математическом анализе. Однако следует учитывать, что в процессе выполнения любого задания нужно также обращать внимание на точки разрыва и интервалы, которые входят в непосредственную область определения. Бывают такие случаи, когда производная находится именно на этих участках.
Оценить статью (79 оценок):
Поделиться
Александр Летов — Магистр физико-математических наук
Популярные статьи
Выполнение любых работ по математике
Возрастание и убывание функции — как найти?
Поможем понять и полюбить математику
Начать учиться
Сегодня мы поговорим о возрастании и убывании функции. Как вы знаете, эта тема достаточно важна, потому что встречается на ЕГЭ, во вступительных экзаменах. А еще ее подробно разбирают на уроках в школе. Сложная ли она? И да, и нет. Мы бы сказали, что она не трудная, а скорее комплексная — в теме много нюансов и моментов, которые тянутся к ней с начальной школы. Но не беспокойтесь, сегодня мы обязательно во всем разберемся!
Сложная ли она? И да, и нет. Мы бы сказали, что она не трудная, а скорее комплексная — в теме много нюансов и моментов, которые тянутся к ней с начальной школы. Но не беспокойтесь, сегодня мы обязательно во всем разберемся!
Что такое функция
Как обычно, начнем мы с самого начала: с определения слова «функция».
Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой.
Под функцией понимают правило, формулу, уравнение, которое описывает зависимость одной переменной от другой (например, у от х). Если изучить функцию, мы поймем:
как изменится одна переменная, если другая увеличится;
что произойдет с аргументом, если мы уменьшим функцию;
что будет, если мы отобразим эту зависимость графически.
Спойлер: если изобразить зависимость в координатной системе, мы получим график! Давайте рассмотрим некоторые виды функций и графики, которые им соответствуют.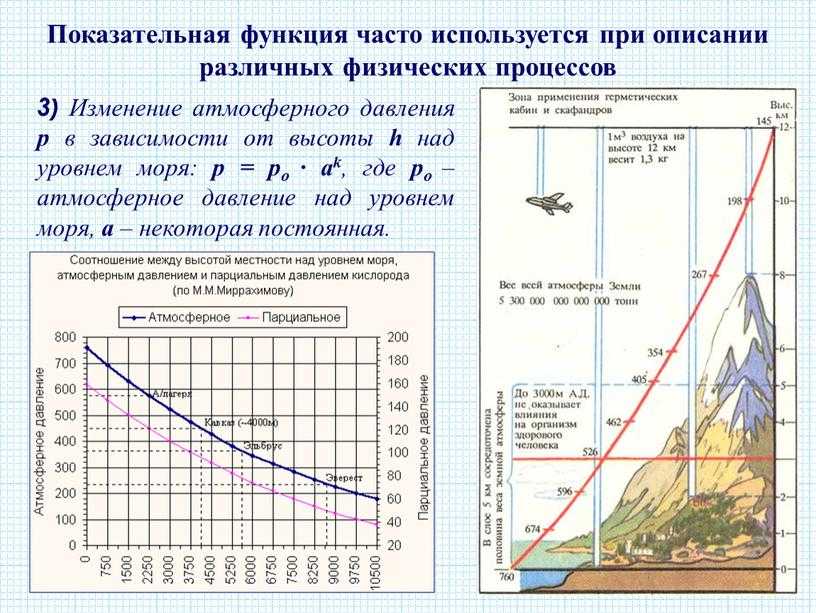
Важное напоминание: функция — это зависимая переменная величина (чаще у), аргумент — независимая переменная (чаще х).
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Возрастание и убывание функции
В исследовании функции особое значение уделяют ее поведению в системе координат — монотонности функции. Функции бывают монотонными, немонотонными и постоянными.
Монотонная функция — функция, которая возрастает или убывает на всем промежутке области определения.
Функцию считают немонотонной, если на промежутке области своего определения она чередует возрастание и убывание.
Постоянная функция, как ясно из названия, постоянна на всем промежутке и представляет собой прямую, параллельную оси x.
Теперь к теме раздела: приведем определение возрастающей и убывающей функции.
Функция называется возрастающей, когда при увеличении аргумента увеличивается и сама функция.
Проще говоря, здесь работает правило «чем больше, тем больше»: чем больше значение х, тем больше и значение у.
Функция считается убывающей, когда при увеличении аргумента функция уменьшается: чем больше х, тем меньше у.
Теперь вы знаете, как понять, что функция возрастает или убывает. Давайте решим пару задач, чтобы разобраться во всем наглядно.
Задача 1
Определите, возрастающая или убывающая функция y = 2x + 3.
1) Найдем область определения функции: х ∈ R.
2) Найдем координаты нескольких точек, которые ей принадлежат.
х | 0 | 1 | 2 | 3 |
3 | 6 | 7 | 9 |
Как вы уже заметили, значения х и у одновременно увеличиваются — функция возрастает на всем промежутке.
Задача 2
Определите, возрастающая или убывающая функция y = 1/2х.
1) Найдем область определения функции: х ≠ 0.
2) Найдем координаты нескольких точек, которые ей принадлежат.
х | 1 | 2 | 3 | 4 |
у | ½ | ¼ | ⅙ | ⅛ |
х | -1 | -2 | -3 | -4 |
у | -½ | -¼ | -⅙ | -⅛ |
Мы видим, что функция убывает при любом значении х ≠ 0.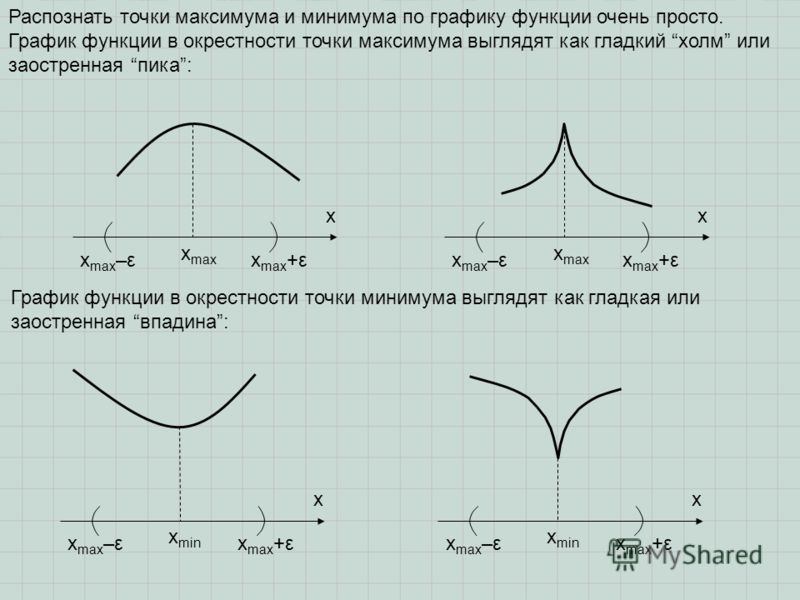 Это можно записать так: функция убывает при х∈ (– ∞ ;0) ∪ (0; + ∞). Подытожим эту информацию небольшой схемой.
Это можно записать так: функция убывает при х∈ (– ∞ ;0) ∪ (0; + ∞). Подытожим эту информацию небольшой схемой.
Возрастание и убывание функции на интервале
Мы еще не закончили с возрастающими и убывающими функциями — эх, если бы все было так просто! Дело в том, что нас, математиков, интересуют вот какие вопросы:
Как найти промежутки возрастания и убывания функции по графику?
Что делать, если просят определить характер на числовом промежутке?
Как определить поведение функции без построения?
Давайте разбираться! Сначала узнаем, как определить характер функции на промежутке:
Подставим значение х из промежутка в функцию.
Проанализируем полученные значения у.
Если при увеличении х увеличивается и у — это промежуток возрастания функции.

Если у уменьшается при увеличении х — это промежуток убывания функции.
Достаточно просто, правда? 🙂
Пример
Возьмем функцию y = 4x – 6 и определим ее характер на промежутке [0;2]. Подставим числа из промежутка вместо х в функцию:
Мы видим, что при возрастании х возрастает и значение у, т. е. на этом промежутке функция возрастает.
Точки экстремума, экстремумы функции
Не пугайтесь этих страшных слов! Сейчас разберем их подробнее — это проще, чем кажется.
Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве.
На графике выше y min — минимальное значение функции, 
Точка минимума — это значение переменной х, при которой функция минимальна.
На том же графике y мах — максимальное значение функции, точка максимума.
Точка максимума — это значение переменной х, при которой функция максимальна.
Иначе точки минимума и максимума в математике принято называть точками экстремума, а значения функции, которые соответствуют точкам экстремума — экстремумами функции.
В точках экстремума функция меняет свой характер. Обратите внимание на рисунок ниже: функция стремительно возрастала до точки максимума, но после нее начала также стремительно уменьшаться. И наоборот, после прохождения точки минимума функция снова начинает возрастать.
Здесь вам может стать интересно: наибольшее/наименьшее значение функции на промежутке — это то же самое или нет.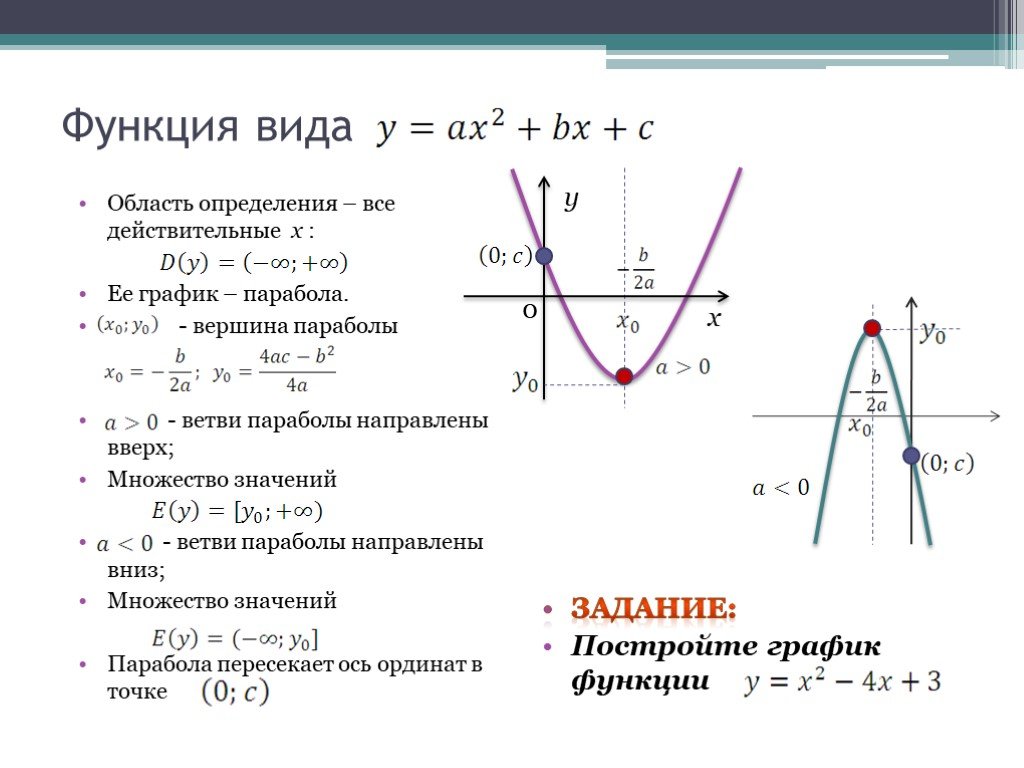 Отвечаем: к сожалению, нет. Эти значения иногда могут совпадать, но часто определяются разными точками.
Отвечаем: к сожалению, нет. Эти значения иногда могут совпадать, но часто определяются разными точками.
Достаточные условия возрастания и убывания функции
У нас есть две новости: хорошая и не очень. Начнем с первой: если использовать достаточные условия возрастания/убывания, можно определить промежутки монотонности функции. И для этого даже не придется строить график! Но здесь нам пригодится производная.
Производная функции — это отношение приращения функции к приращению аргумента при бесконечно малом приращении аргумента.
Иначе говоря, производная функции показывает, как быстро увеличивается функция при бесконечно малом увеличении х.
К сожалению, в рамках этой статьи мы не будем долго останавливаться на производных. Как это сделать с помощью таблицы и правил дифференцирования, мы уже разбирали в статье «Таблица производных функций». Советуем почитать!
Достаточные признаки возрастания и убывания функции на интервале:
если производная функции y = f(x) положительна для любого x из интервала, то функция возрастает на этом интервале;
если производная функции y = f(x) отрицательна для любого x из интервала, то функция убывает на этом интервале.

Составим алгоритм действий, который поможет найти интервалы возрастания и убывания функции:
Найдем область определения функции.
Найдем производную функции.
Решим неравенства ƒ`(x) > 0 и ƒ`(x) < 0 на области определения.
К полученным промежуткам добавим граничные точки, в которых функция определена и непрерывна.
Проверим достаточные признаки возрастания и убывания функции, подставив значения из промежутков.
Задача 3
Укажите промежутки возрастания и убывания функции у = х2 + 5х + 6
Решение
Область определения функции: х ∈ R
Найдем производную функции: y’ = 2х + 5
Решим неравенство: 2х + 5 > 0
2х+5 >0 2x>-5 x> –2,5 Исследуем знаки производной с помощью числовой прямой.

Ответ: Функция убывает при х∈ (– ∞; –2,5], возрастает при х∈ [–2,5; +∞)
Задача 4
Определите интервалы возрастания и убывания функции у = х3 – 18х.
Решение
Область определения функции: х ∈ R.
Найдем производную функции: y’ = 3x2 + (–18).
Решим неравенство:
3x2 + (–18) > 0 3 (x2–9) > 0 3(x – 3)(x + 3) > 0 Исследуем знаки производной с помощью числовой прямой. Чтобы определить знак на каждом промежутке, подставим произвольное значение из этого промежутка в выражение для производной.
Ответ: Функция убывает при х∈ [–3;3], возрастает при х∈ (–∞;—3] ∪ [3; +∞).
Первое достаточное условие экстремума
Пусть для функции у = f(x) определены следующие условия:
Функция непрерывна в окрестности точки x0 (нет разрыва).
ƒ′(x0) = 0 или ƒ′(x0) не существует;
Производная ƒ′(x) при переходе через точку x0 меняет свой знак.
Тогда в точке x = x0 функция y = f(x) имеет экстремум, причем это минимум, если при переходе через точку x0 производная меняет свой знак с минуса на плюс; максимум, если при переходе через точку x0 производная меняет свой знак с плюса на минус.
Если производная в точке x0 не меняет свой знак, то в этой точке нет экстремума.
Итак, точки 1 и 4 — точки максимума, точка 3 — точка минимума. В точке 2 экстремума нет.
Алгоритм для нахождения точек экстремума
Теперь разберемся, как найти точки экстремума функции. Для этого пройдем по этим шагам:
Для этого пройдем по этим шагам:
Найдем область определения функции.
Найдем производную функции на этой области.
Определим нули и точки, где функция не существует.
Определим знак производной на интервалах.
Выберем точки, где функция меняет знак.
Найдем точки минимума/максимума и экстремумы функции.
Задача 5
Найдите экстремумы функции у = –x2 + 8x – 7.
Решение
Область определения функции: х ∈ R.
Производная функции: y’ = –2x + 8
Решим неравенство:
–2x + 8 > 0 –2x > –8 x < 4 Определим знак производной на числовой прямой.
 Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
В точке х = 4 функция меняет свой знак с «+» на «–», значит, точка х = 4 — это точка максимума.
Ответ: у(4) = 9 — экстремум функции.
Задача 6
Найдите экстремумы функции у = ⅓ x3 + 2x2 – 12x + 6.
Решение
Область определения функции: х ∈ R.
Производная функции: y’ = x2 + 4x – 12.
Решим неравенство:
x2 + 4x – 12 > 0 (x – 2)(x + 6) > 0 Определим знак производной на числовой прямой.
 Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
Так на интервале (–∞; –6) и (2; +∞) производная положительна — на них функция возрастает. На интервале (–6;2) производная отрицательна — функция убывает.
Ответ: x = 2 — точка минимума, у(2) = –7 ⅓ — экстремум функции; х = –6 — точка максимума, у(–6) = 78 — экстремум функции.
Как можно запомнить переход знаков для точек максимум или минимум:
Когда функция возрастает, а потом убывает, мы будто поднимались на вершину горы — значит, посетили точку максимума.
Когда функция убывает, а потом возрастает, мы будто спускались в овраг и выбрались из него — а значит, были в точке минимума.
Второе достаточное условие экстремума
x0 — это точка экстремума функции f(x), если вторая производная функции в этой точке не равна нулю (f »(x) ≠ 0).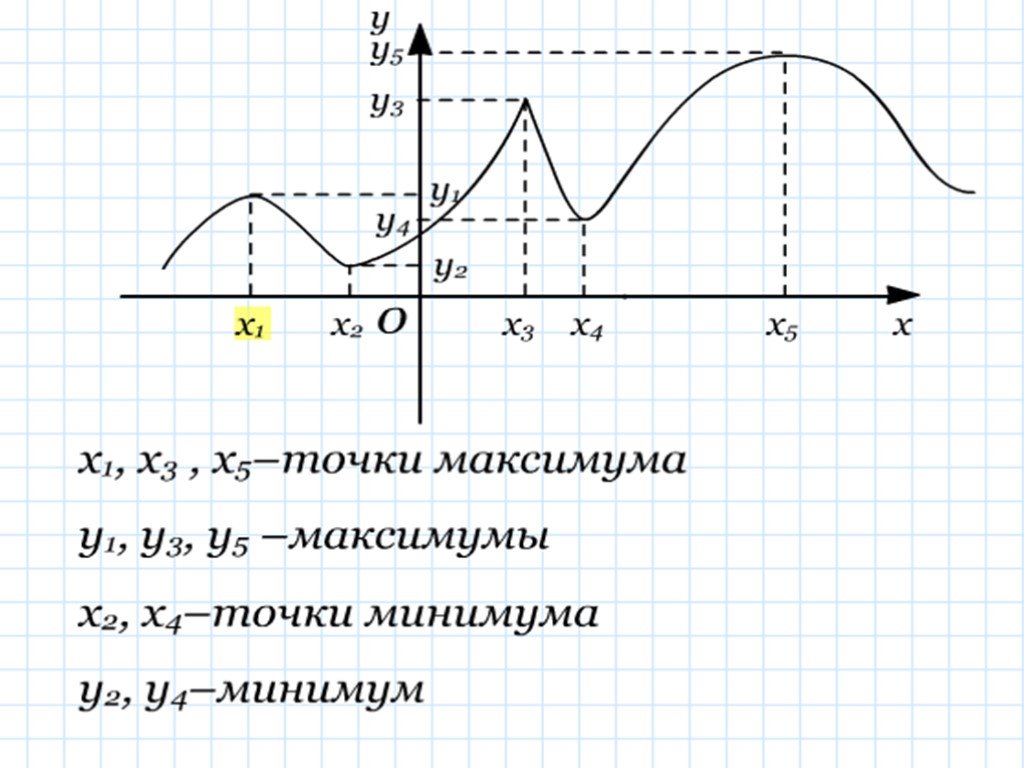 Причем, если вторая производная больше нуля (f »(x) > 0), то точкой минимума, а если вторая производная меньше нуля (f »(x) < 0), то точкой максимума.
Причем, если вторая производная больше нуля (f »(x) > 0), то точкой минимума, а если вторая производная меньше нуля (f »(x) < 0), то точкой максимума.
Рассмотрим это условие экстремума на примере из задачи 6 — функции у = ⅓ x3 + 2x2 – 12x + 6:
Ее первая производная равна y’= x2 + 4x – 12.
Определим нули производной — значение х, при котором производная обращается в ноль: x2 + 4x – 12 = 0 при х = 2 и х = –6.
Возьмем вторую производную функции y’’= 2х + 4.
Подставим значения х = 2 и х = –6 во вторую производную и определим, являются ли эти точки максимумом или минимумом:
y’’(2) = 8, y’’ > 0, значит, х = 2 является точкой минимума, y’’(–6) = –8, y’’ < 0, значит, х = –6 является точкой максимум. 
В этом условии есть два важных замечания:
Если в точке x0 и первая, и вторая производные обращаются в ноль, то в этом случае нужно воспользоваться первым достаточным признаком экстремума функции, по второму признаку нельзя судить о наличии или отсутствии экстремумов.
Второй достаточный признак нельзя применять, когда в стационарной точке (нуле производной) первая производная не существует. Ведь тогда не существует и вторая производная.
Третье достаточное условие экстремума
Это условие не используется в школьной программе, так как требует большого количества вычислений и логических размышлений. Мы все равно познакомим вас с ним — возможно, вам захочется изучить это усaловие самостоятельно и блеснуть знаниями перед учителем. Что ж, мы только за!
Пусть функция y=f(x) имеет производные до n-ого порядка в ε-окрестности точки x0 и производные до n+1-го порядка в самой точке x0. Пусть
ƒ′(x0) = ƒn(x0) = ƒm(x0) = … = ƒ(n)(x0) = 0 и ƒ(n+1)(x0) ≠ 0.
Пусть
ƒ′(x0) = ƒn(x0) = ƒm(x0) = … = ƒ(n)(x0) = 0 и ƒ(n+1)(x0) ≠ 0.
Тогда,
если n – четное, то x0 — точка перегиба;
если n – нечетное, то x0 — точка экстремума, причем
если ƒ(n+1)(x0) > 0, то x0 — точка минимума;
если ƒ(n+1)(x0) < 0, то x0 — точка максимума.
Думаем, вы убедились, что тема «Возрастание и убывание функции» достаточно интересна. В то же время, она требует умения исследовать графики, находить первую и вторую производную функции, определять знаки по числовым прямым. Получить практический опыт решения таких заданий можно на курсах по профильной математике в школе Skysmart! Там мы сможем закрепить полученные знания, подготовиться к контрольным работам и даже к ОГЭ! Заинтригованы? Тогда мы ждем вас на занятиях!
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Дарья Вишнякова
К предыдущей статье
Разложение чисел на простые множители
К следующей статье
Плоскость
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
минимум – определение, значение и синонимы
минимум; минимумы
Минимум — это наименьшая или наименьшая сумма, возможная или приемлемая. Если вы выполняете минимум объемов работы на своей работе, вас могут не уволить, но вы определенно не получите повышения.
Если вы выполняете минимум объемов работы на своей работе, вас могут не уволить, но вы определенно не получите повышения.
Минимум на латыни означает «наименьший», так что очевидно, что носители английского языка сделали меньше минимального количества возни со значением этого слова. Очевидно, что максимум наоборот. Как минимум, вы должны знать, что это слово означает наименьший предел чего-либо. Самое большее, вы должны быть в состоянии говорить о его латинских корнях.
Определения минимума
существительное
минимально возможное количество
- синонимы: Нижний предел
существительное
точка на кривой, где касательная меняется с отрицательной слева на положительную справа
прилагательное
наименее возможный
« минимальная заработная плата »
- синонимы: минимальный
- пограничный, маргинальный
сомнительного или минимального качества
- незначительный
настолько мал, что не имеет смысла; незначительный
- номинальный, символический, символический
незначительно мелкий; только вопрос формы («символический» неформален)
- раздетый, раздетый
имеющие только основные или минимальные характеристики
- пограничный, маргинальный
ОТКАЗ ОТ ОТВЕТСТВЕННОСТИ: Эти примеры предложений появляются в различных источниках новостей и книгах, чтобы отразить использование слова «минимум» . Мнения, выраженные в примерах, не отражают мнение Vocabulary.com или его редакции.
Отправьте нам отзыв
Мнения, выраженные в примерах, не отражают мнение Vocabulary.com или его редакции.
Отправьте нам отзыв
ВЫБОР РЕДАКТОРА
Посмотрите
минимум в последний разЗакройте пробелы в словарном запасе с помощью персонализированного обучения, которое фокусируется на обучении слова, которые нужно знать.
Начните изучение словарного запаса
Независимо от того, являетесь ли вы учителем или учеником, Vocabulary.com может направить вас или ваш класс на путь систематического улучшения словарного запаса.
НачатьМинимальное определение и значение | Dictionary.com
- Основные определения
- Викторина
- Связанный контент
- Подробнее о минимуме
- Примеры
- Британский
- Научный
.
[мин-эм-мум]
/ ˈmɪn ə məm /
Сохранить это слово!
См. синонимы слова «минимум» на сайте Thesaurus.com
Показывает уровень обучения в зависимости от сложности слова.
существительное во множественном числе min·i·mums, min·i·ma [min-uh-muh]. /ˈmɪn ə mə/.
наименьшее количество или сумма, возможная, назначаемая, допустимая и т.п.
минимальная разрешенная скорость на шоссе.
наименьшее количество, значение или степень, достигнутая или зарегистрированная.
Произвольная сумма, установленная рестораном, ночным клубом и т. д. как наименьшая сумма, взимаемая с каждого человека за еду и напитки. Сравните плату за покрытие.
Математика.
- Также называется относительным минимумом, локальным минимумом. значение функции в некоторой точке ее области определения, которое меньше или равно значениям во всех других точках в непосредственной близости от точки.
 Сравните абсолютный минимум.
Сравните абсолютный минимум. - точка в области, в которой происходит минимум.
прилагательное
отмечая или указывая минимум.
наименее возможный: минимальный риск.
самый низкий: минимальная ставка.
, относящийся к минимуму или минимумам.
ВИКТОРИНА
ВСЕ ЗА(U)R ЭТОГО БРИТАНСКОГО ПРОТИВ. ВИКТОРИНА ПО АМЕРИКАНСКОМУ АНГЛИЙСКОМУ
Существует огромная разница между тем, как люди говорят по-английски в США и Великобритании. Способны ли ваши языковые навыки определить разницу? Давай выясним!
Вопрос 1 из 7
Правда или ложь? Британский английский и американский английский различаются только сленговыми словами.
Происхождение минимума
Впервые зафиксировано в 1655–1665 гг.; от латинского neuter of minimus «наименьший, наименьший»; см. минор
СЛОВА, КОТОРЫЕ МОЖНО СПУТАТЬ С минимум
минимум, минимумСлова рядом минимум
минимальный термометр, минимальная обработка почвы
Dictionary. com Полный текст
На основе Random House Unabridged Dictionary, © Random House, Inc., 2023
com Полный текст
На основе Random House Unabridged Dictionary, © Random House, Inc., 2023
ПОДРОБНЕЕ О MINIMUM
Что означает
минимум ?Минимум означает наименьшее количество или уровень чего-либо.
Минимум может быть существительным или прилагательным, и у него есть несколько более конкретных значений, каждое из которых так или иначе связано с его основным значением. Когда минимум используется как существительное, его множественное число может быть 9.0071 минимумы или, реже, минимумы .
Пример: Выньте пирог из духовки и дайте ему остыть не менее 30 минут перед подачей на стол.
Откуда
минимум ?Первые записи минимум относятся к середине 1600-х годов. Оно происходит от латинского слова minimus , что означает «наименьший» или «наименьший».
В общем, минимум часто относится к наименьшему возможному количеству чего-то, что может удовлетворить требование, как в Чтобы претендовать на эту вакансию, требуется не менее 10 лет опыта . Это также может относиться к наименьшему количеству, которое наблюдалось, и используется в математике соответствующим образом.
Это также может относиться к наименьшему количеству, которое наблюдалось, и используется в математике соответствующим образом.
Минимум также используется в более конкретных целях. С точки зрения ограничения скорости, минимум — это самая низкая скорость, разрешенная на определенной дороге, особенно на шоссе, где ехать медленнее было бы опасно. Некоторые рестораны и клубы устанавливают минимум на деньги, взимаемые с каждого клиента, а это означает, что вы должны потратить как минимум эту сумму. Точно так же многие магазины устанавливают минимальная сумма , которую вы должны потратить, чтобы использовать кредитную карту. Минимальная заработная плата рабочих зарабатывают наименьшую сумму, разрешенную законом или каким-либо другим соглашением.
Минимум часто используется во фразах голый минимум , что означает «абсолютный минимум», и как минимум , что означает «по крайней мере», как в Как минимум, нам нужно сделать еще пять до конца дня.
Знаете ли вы…?
Какие другие формы относятся к минимуму ?
- минимумы (множественное число)
- минимум (множественное число)
Какие есть синонимы для минимум ?
- минимальный
- самый низкий
- самый маленький
Какие слова имеют общий корень или элемент слова с минимум ?
- минимальный
- свернуть
Какие слова часто используются при обсуждении минимум ?
- низкий
- уровень
- предел
- сумма
- измерить
- данные
- заработная плата
Как
минимум используется в реальной жизни? Минимум — это обычное слово, которое используется во всех смыслах. Это всегда относится к наименьшей сумме, которая может быть отрицательной или положительной в зависимости от контекста.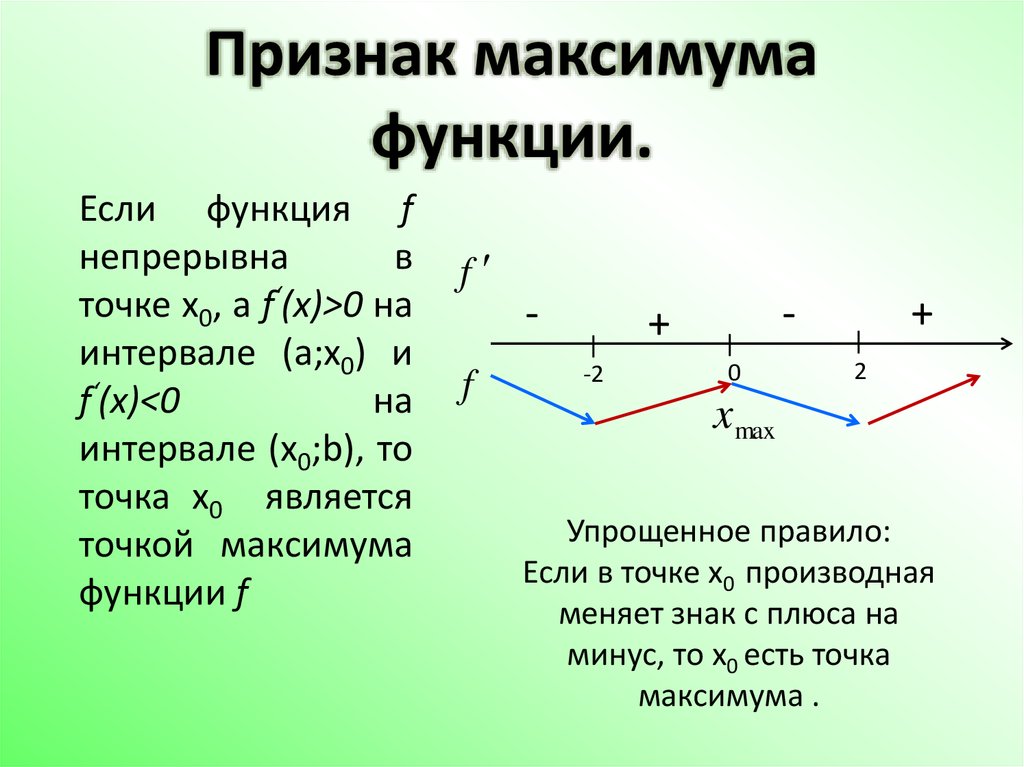
С гордостью сообщаю, что сегодня я сделал абсолютный минимум
— Деббириан (@DebbyRyan) 11 марта 2019 г.
ТротуарамНью-Йорка нужны полосы движения и ограничение минимальной скорости.
— Брэндон / Джинкс / Большой Джинкс (@brandonjinx) 20 мая 2015 г.
они платят минимальную заработную плату, а затем взимают арендную плату более чем в 3 раза больше, чем она должна быть, а затем говорят вам, что в стране все хорошо с экономической точки зрения
— Ши Серрано (@SheaSerrano) 10 января 2020 г.0072 !
Какое из следующих слов НЕ является синонимом минимум ?
A. самый
B. самый низкий
C. самый маленький
D. самый маленькийСлова, относящиеся к слову минимум минимальная, минимальная, молекула, надир, частица, копейки, точка, мерцание
Как использовать минимум в предложении
Минимальное количество персонала, необходимое для безопасного проведения мероприятия, также будет присутствовать, а всех остальных спросят работать удаленно.
Открытый чемпионат Австралии запрещает болельщикам из-за блокировки из-за коронавируса|Кендалл Бейкер|12 февраля 2021 г.|Axios
Как минимум, вы можете выполнить поиск по запросу «винтажный стакан Crate & Barrel».
Замена столовых приборов или фарфоровой посуды может оказаться непростой задачей. Вот как их отследить.|Laura Daily|11 февраля 2021 г.|Washington Post
Google требует, чтобы в вашей кампании было не менее 15 конверсий за 30 дней при использовании целевой рентабельности инвестиций в рекламу для оптимизации поисковых объявлений, а также существуют другие минимальные требования. для других типов объявлений.
Умное назначение ставок: пять способов, которыми машинное обучение улучшает контекстную рекламу|Габриэль Садех|10 февраля 2021 г.|Наблюдение за поисковыми системами
Этот процесс уже начался с некоторыми командами, например, в Новом Орлеане, где Дрю Брис спас Святых примерно на 24 доллара. миллионов, уменьшив свою зарплату до минимума лиги перед ожидаемым выходом на пенсию.
10 самых важных вопросов о составе в НФЛ в начале межсезонья|Джон Клейтон|9 февраля 2021 г.|Washington Post
Майкл Райх, известный эксперт по минимальной заработной плате в Калифорнийском университете в Беркли, чью работу цитирует CBO, оспорил более пессимистичные оценки отчета.
В отчете CBO говорится, что минимальная заработная плата в размере 15 долларов будет стоить рабочих мест, но снизит уровень бедности|Эли Розенберг|8 февраля 2021|Washington Post
С ним обращались как с иммигрантом, работающим за минимальную заработную плату, скучающим по семье и вынужденным двигаться дальше из его музыкальной карьеры.
Кубинский хип-хоп родился в Аламаре|Дэниел Левин|26 декабря 2014 г.|DAILY BEAST
Выньте жаркое из формы и дайте постоять не менее 15 минут.
Приготовьте жареную свиную вырезку Карлы Холл с клюквой|Карла Холл|24 декабря 2014|DAILY BEAST
Одаренный маркетолог, он разослал образцы шляп торговцам по всему Западу с просьбой сделать минимальный заказ в дюжину .
Мое любовное письмо Стетсону|Марк Маккиннон|24 декабря 2014 г.|DAILY BEAST
Чтобы работать в Rizzoli, нужно было свободно владеть несколькими языками: минимум три, когда я начинал.
Книжный магазин, который очаровал Мика Джаггера, Джона Леннона и Грету Гарбо|Феличе Пикано|16 декабря 2014|DAILY BEAST
В результате неопытные люди могут получать намного меньше минимальной заработной платы или подвергаться насилию со стороны закулисных работодателей. .
Туркеры Amazon запускают первую краудсорсинговую гильдию труда|Кевин Заваки|3 декабря 2014 г.|DAILY BEAST
Закон о минимальной заработной плате должен так или иначе стать частью кодекса каждого сообщества.
Неразгаданная загадка социальной справедливости|Стивен Ликок
Это можно сделать, как и в случае с минимальной заработной платой, частично с помощью позитивного законодательства и частично коллективными действиями.
Неразгаданная загадка социальной справедливости|Стивен Ликок
Это даст нам шестнадцать долларов и восемьдесят центов за перевозку машины минимум за двадцать четыре тысячи.
Scattergood Baines|Clarence Budington Kelland
До сих пор он не понес никаких убытков и может свести свои убытки к минимуму, ограничив кредит определенной цифрой.
Третий класс индийских железных дорог|Махатма Ганди
Гидравлическими испытаниями было доказано, что хорошая работа каменщиков может выполняться при последнем минимуме.
Encyclopaedia Britannica, 11th Edition, том 4, часть 3 | Различные
Определения британского словаря для минимума
Минимум
/ (ˈmɪnɪməm) /
Noun Plural -mums или -ma)
955555555555555555555555555555559559559555595559559555595595595595955955955955955955959559559559559 наименьшее возможное количество, степень или количествонаименьшее количество, зарегистрированное, разрешенное или достигнутоеминимум в нашей температурной записи за этот месяц был 50°
(модификатор) является наименьшим возможным, зарегистрированным, разрешенным и т.



 Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной. Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
Чтобы это сделать, на каждом промежутке подставим произвольное значение из этого промежутка в выражение для производной.
 Сравните абсолютный минимум.
Сравните абсолютный минимум.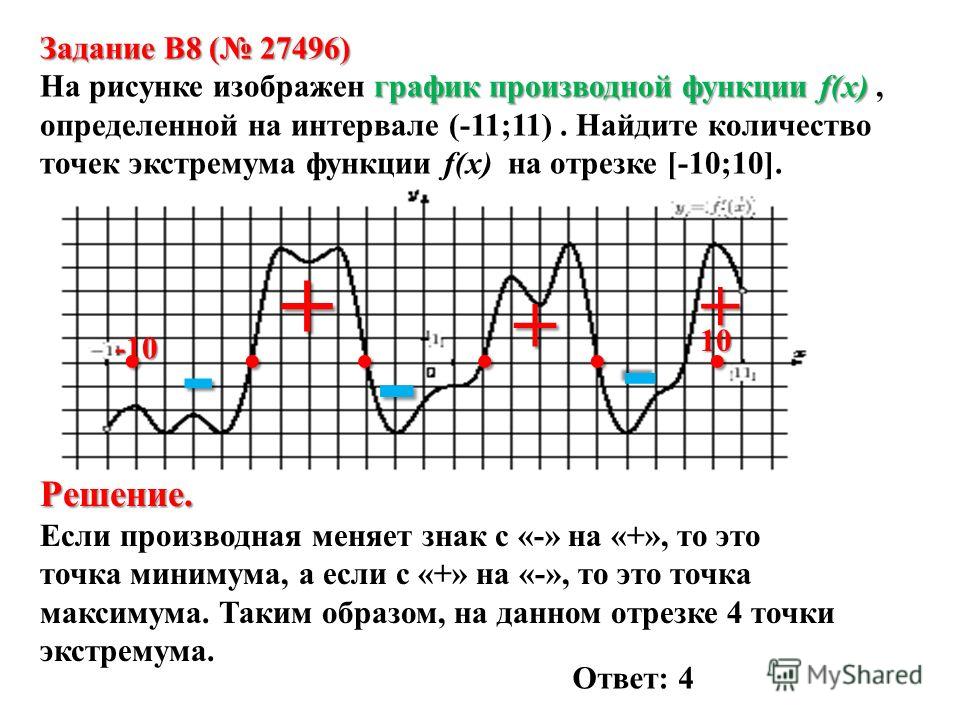


Leave A Comment