Найдите значение выражения корень из 42 минус 5 в квадрате: Найдите значения выражения: (√42-2)² — ответ на Uchi.ru

2

Что такое квадратный корень? Формулы и Примеры

Вот несколько примеров извлечения корней, чтобы научиться пользоваться таблицей:

• 1. Извлеките квадратный корень:

Ищем в таблице число 289, двигаемся от него влево и вверх, чтобы определить цифры, образующие нужное нам число.

Влево — 1, вверх — 7.

Ответ: .

• 2. Извлеките квадратный корень:

Ищем в таблице число 3025.
Влево — 5, вверх —  5.

Ответ: .

• 3. Извлеките квадратный корень:

Ищем в таблице число 7396.

Влево — 8, вверх — 6.

Ответ: .

• 4. Извлеките корень:

Ищем в таблице число 9025.

Влево — 9, вверх — 5.

Ответ: .

• 5. Извлеките корень

Ищем в таблице число 1600.

Влево — 4, вверх — 0.

Ответ: .

Извлечением корня называется нахождение его значение.

Свойства арифметического квадратного корня

У арифметического квадратного корня есть 3 свойства — их нужно запомнить, чтобы проще решать примеры.

• Корень произведения равен произведению корней

• Извлечь корень из дроби — это извлечь корень из числителя и из знаменателя

• Чтобы возвести корень в степень, нужно возвести в степень значение под корнем

Давайте потренируемся и порешаем примеры на все три операции с корнями.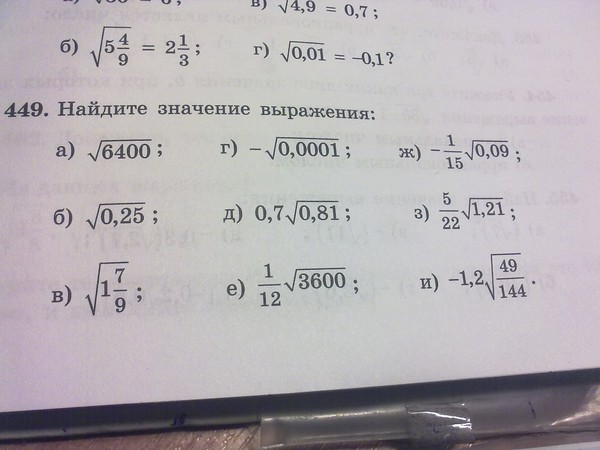 Не забывайте обращаться к таблице квадратов. Попробуйте решить примеры самостоятельно, а для проверки обращайтесь к ответам.

Умножение арифметических корней

Для умножения арифметических корней используйте формулу:

Примеры:

1. Ответ:

2. Ответ:

Внимательно посмотрите на второе выражение и запомните, как записываются такие примеры.

Если нет возможности извлечь корни из чисел, то поступаем так:

 

3. Ответ:

4. Ответ:

5. Если множителей больше двух, то решается примерно точно так, как и с двумя множителями:

   Ответ:

Добрая напоминалочка

Чтобы решать примеры быстрее, не забывайте пользоваться таблицей квадратов.

6. Ответ:

Деление арифметических корней

Для деления арифметических корней используйте формулу:

Примеры:

1. Ответ: смешанную дробь превращаем в неправильную (16 * 3) + 1 = 49

2. Ответ:

5. Ответ:

Выполняя деление, не забывайте сокращать множители. При делении арифметических корней, используйте правила преобразования обыкновенных дробей.

Возведение арифметических корней в степень

Для возведения арифметического корня в степень используйте формулу:

Примеры:

2. Ответ: , т.

   к.

3. Ответ: , т.к. .

Эти две формулы нужно запомнить:

4. Ответ:

5. Ответ:

Повторите свойства степеней или запишитесь на курсы по математике, чтобы без труда решать такие примеры.

Внесение множителя под знак корня

Вы уже умеете по-всякому крутить и вертеть квадратными корнями: умножать, делить, возводить в степень. Богатый арсенал, не правда ли? Осталось овладеть еще парой приемов и можно без страха браться за любую задачку.

А теперь давайте разберемся, как вносить множитель под знак корня.

Дано выражение:

Число семь умножено на квадратный корень из числа девять. 

Извлечем квадратный корень и умножим его на 7.

.

В данном выражение число 7 — множитель. Давайте внесем его под знак корня. 

Запомните, что вносить множитель под знак корня обязательно нужно так, чтобы значение исходного выражения осталось неизменным. Иными словами, после наших манипуляций с корнем, значение выражения должно по-прежнему оставаться 21.

Вы помните, что

Тогда число 7 должно быть возведено во вторую степень. В этом случае значение выражения останется тем же.

Формула внесения множителя под знак корня:

Запоминаем:

Нельзя вносить отрицательные числа под знак корня.

Потренируемся вносить множители. Попробуйте решить примеры самостоятельно, сверяясь с ответами.

 

1. Ответ:




2. Ответ:




3. Ответ:

Вынесение множителя из-под знака корня 

С тем, как вносить множитель под корень мы, кажется, разобрались. Но алгебра — такая алгебра, поэтому теперь неплохо бы и вынести множитель из-под знака корня.

Дано выражение в виде квадратного корня из произведения.

Вы уже наверняка без труда извлекаете квадратный корень из чего угодно, поэтому знаете, что делать.

Извлекаем корень из всех имеющихся множителей.

В данном выражении квадратный корень мы можем извлечь только из 4, поэтому:

Таким образом множитель выносится из-под знака корня.

Давайте разберем примеры. Попробуйте вынести множители из-под знака корня самостоятельно, сверяясь с ответами.

1. Раскладываем подкоренное выражение на множители 28 = 7*4.

   Извлекаем корень из 4. Множитель 7 оставляем под знаком корня.

   Ответ:

2. Ответ: по правилу извлечения квадратного корня из произведения,

   .

   Так как вынесенный множитель должен стоять перед подкоренным знаком, то меняем их местами.

   .

3. Вынесите множитель из-под знака корня в выражении:

   Ответ: Раскладываем выражение под корнем на множители 24 = 6 * 4.

4. Упростите выражение: .

   Представим в виде

   Представим в виде

   Тогда

   Вынесем в двух последних выражения множитель из-под знака корня.

   Умножаем . Все остальное выражение записываем в неизменном виде.

   Мы видим, что во всем выражении есть один общий множитель — .

   Выносим общий множитель за скобки:

   Далее вычисляем все, что в скобках:

Сравнение квадратных корней

Мы почти досконально разобрали арифметический квадратный корень, научились умножать, делить и возводить его в степень. Теперь вы без труда можете вносить множители под знак корня и выносить их оттуда. Осталось научиться сравнивать корни и стать непобедимым теоретиком.

Итак, чтобы понять, как сравнить два квадратных корня, нужно запомнить пару правил.

Если:

• , то

• , то

Давайте разберем на примере.

Сравните два выражения: и

Первым делом преобразуем второе выражение: .

.

Это значит, что .

Запоминаем

Чем больше число под знаком корня, тем больше сам корень.

Потренируйтесь в сравнении корней. Сверяете свои результаты с ответами.

1. Сравните два выражения: и

   Ответ: преобразовываем выражение .

   Это значит, что .

2. Сравните два выражения: и

   Ответ: преобразовываем выражение .

   Это значит, что .

3. Сравните два выражения: и

   Ответ: преобразовываем выражение .

   Это значит, что .

Как видите, ничего сложного в сравнении арифметических квадратных корней нет. 

Самое главное — выучить формулы и сверяться с таблицей квадратов, если значения корня слишком большие для легкого вычисления в уме.

Не бойтесь пользоваться вспомогательными материалами. Математика просто создана для того, чтобы окружить себя подсказками и намеками.

Когда вы почувствуете, что уже достаточно натренировались в решении примеров с квадратными корнями, можете позволить себе время от времени прибегать к помощи онлайн-калькуляторов. Они помогут решать примеры быстрее и быть эффективнее.  

Таких калькуляторов в интернете много, вот один из них.

Извлечение квадратного корня из большого числа

Вы уже наверняка познакомились и подружились с таблицей квадратов. Она — ваша правая рука. С ее помощью вы реактивно решаете примеры и, возможно, даже подумываете запомнить ее наизусть.

Но, как вы можете заметить, таблица заканчивается на числе 9801. А это, согласитесь, не самое крупное число из тех, что могут вам попасться в примере.

Чтобы извлечь корень из большого числа, которое отсутствует в таблице квадратов, нужно:

1. Определить «сотни», между которыми оно стоит.

2. Определить «десятки», между которыми оно стоит.

3. Определить последнюю цифру в этом числе.

Извлечь корень из большого числа можно разными способами — вот один из них.

Извлечем корень из .

Наша задача в том, чтобы определить между какими десятками стоит число 2116.

10² = 100

20² = 400

30² = 900

40² = 1600

50² = 2500 

Мы видим что, 2116 больше 1600, но меньше 2500.

Это значит, что число 2116 находится между 40²и 50².

41, 42, 43, 44, 45, 46, 47, 48, 49.

Запомните лайфхак по вычислению всего на свете, что нужно возвести в квадрат.

Не секрет, что на последнем месте в любом числе может стоять только одна цифра от 1 до 0.

Как пользоваться таблицей

1² = 1

2² = 4

3² = 9

4² = 16 ⇒ 6

5² = 25 ⇒ 5

6² = 36 ⇒ 6

7² = 49 ⇒ 9

8² = 64 ⇒ 4

9² = 81 ⇒ 1

Мы знаем, что число 41, возведенное в квадрат, даст число, на конце которого — цифра 1.

Число, 42, возведенное в квадрат, даст число, на конце которого — цифра 4.

Число 43, возведенное в квадрат, даст число, на конце которого — 9.

Такая закономерность позволяет нам без записи «перебрать» все возможные варианты, исключая те, которые не дают нужную нам цифру 6 на конце.

Таким образом, у нас остаются два варианта: 44² и 46².

Далее вычисляем: 44 * 44 = 1936.

46 * 46 = 2116.

Ответ:

Если такой способ показался не до конца понятным — можно потратить чуть больше времени и разложить число на множители. Если решить все правильно, получим такой же результат. 

Еще пример. Извлечем корень из числа

Разложим число 11664 на множители: 

11664 : 4 = 2916

2916 : 4 = 729

729 : 3 = 243

243 : 3 = 81

11664	4
2916	4
729	3
243	3
81	81

Запишем выражение в следующем виде:

Ответ:

Извлечь квадратный корень из большого числа гораздо проще с помощью калькулятора. Но знать парочку таких способов «на экстренный случай» точно не повредит. Например, для контрольной или ЕГЭ.

Чтобы закрепить все теоретические знания, давайте ещё немного поупражняемся в решении примеров на арифметические квадратные корни.
 

• 1. Вычислите значение квадратного корня:

  Как решаем:

  Ответ: 6.

• 2. Вычислите значение квадратного корня:

  Как решаем:

  Ответ: .

• 3. Вычислите значение квадратного корня:

  Как решаем:

  Ответ: .

• 4. Вычислите значение квадратного корня:

  Как решаем:

  Ответ: .

• 5. Вычислите значение квадратного корня:

  Как решаем:

  Ответ: .

• 6. Вычислите значение выражения:

  Как решаем:

  Ответ: .

• 7. Вычислите значение выражения:

  Как решаем:

  Ответ: .

• 8. Вычислите значение выражения:

  Как решаем:

  Ответ: .

• 9. Вычислите значение квадратного корня:

  Как решаем:

  Ответ:

• 10. Вычислите значение квадратного уравнения:

  Как решаем:

  Ответ: .

• 11. Вычислите значение квадратного уравнения:

  Как решаем:

  Ответ: .

• 12. Извлеките квадратный корень из числа удобным вам способом

  Как решаем:

  7056	4
  1764	4
  441	3
  147	3
  49	7
  7	7
  1

  Ответ:

• 13. Вычислите значение квадратного корня

  Ответ:

• 14. Вычислите значение квадратного корня:

  Как решаем:

• 15. Вычислите значение выражения:

  Как решаем:

  Ответ: .

• 16. Вычислите значение выражения:

  Как решаем:

  Ответ: .

• 17. Вычислите значение выражения:

  Как решаем:

• 18. Вычислите значение выражения:

  Как решаем:

  Ответ: .

• 19. Вычислите значение выражения:

  Как решаем:

  Ответ: .

• 20. Вычислите значение выражения:

  Как решаем:

  Ответ: .

• 21. Вынесите множитель из-под знака корень:

  Как решаем:

  Ответ: .

• 22. Вынесите множитель из-под знака корень:

  Как решаем:

  Ответ: .

• 23. Внесите множитель под знак корня:

  Как решаем:

  Ответ: .

• 24. Внесите множитель под знак корня:

  Как решаем:

  Ответ: .

• 25. Внесите множитель под знак корня:

  Как решаем:

  Ответ: .

• 26. Упростите выражение:

  Как решаем:

  Ответ: .

• 27. Вычислите значение выражения:

  Как решаем:

  Ответ: .

• 28. Вычислите значение квадратного корня:

  Как решаем:

  Ответ: .

• 29. Вычислите значение квадратного корня:

  Как решаем:

  Ответ: .

• 30. Найдите значение выражения:

  Как решаем:

  Ответ: .

Квадратный корень из 42 — Как найти квадратный корень из 42?

LearnPracticeDownload

Число 42 — это число с тремя простыми делителями 2, 3 и 7. Итак, его простая факторизация. Квадратный корень из числа бывает как положительным, так и отрицательным. Теперь мы вычислим квадратный корень из 42, используя различные методы, а также узнаем несколько интересных фактов и вопросов.

• Квадратный корень из 42: 6,48074
• Квадрат 42: 1764
  

1.	Что такое квадратный корень из 42?
2.	Является ли квадратный корень из 42 рациональным или иррациональным?
3.	Как найти квадратный корень из 42?
4.	Часто задаваемые вопросы о квадратном корне из 42
5.	Важные замечания по квадратному корню из 42

Чему равен квадратный корень из 42?

• Квадратный корень числа подразумевает число, произведение которого на себя дает начальное число.
• Квадратный корень из 42 равен 6,4807.
• Квадратный корень из 42 записывается как √42 в радикальной форме, и его нельзя уменьшить дальше.
• Квадратный корень из 42 можно записать как (42) ^1/2 в экспоненциальной форме.
  

Является ли квадратный корень из 42 рациональным или иррациональным?

Рациональное число — это число, которое может быть выражено в виде p/q, где q ≠ 0,
И квадратный корень из 42 не может быть выражен в виде p/q.
Итак, квадратный корень из 42 — иррациональное число.

Как найти квадратный корень из 42?

Теперь мы вычислим квадратный корень из 42, используя следующие методы:

Квадратный корень из 42, используя метод приближения

• Найдите два последовательных полных квадрата, между которыми лежит число 42. Два числа: 36 (6 ² ) и 49 (7 ² ).
  Таким образом, целая числовая часть квадратного корня из 42 будет равна 6,9. 0010
• Теперь для десятичной части мы будем использовать формулу:
  (Заданное число – меньший правильный квадрат) / (Большой правильный квадрат – меньший правильный квадрат)
  = (42 — 36)/(49 — 36) = 6/13 = 0,461
• Итак, расчетный квадратный корень из 42 по методу аппроксимации равен 6,461.

Квадратный корень из 42 методом деления в длину

Теперь мы вычислим квадратный корень из 42 методом деления в длину.

• Начните соединять цифры с правой стороны, поставив на них черту. В этом случае у нас есть только одна пара (42).
• Теперь найдите число (z), такое что z × z ≤ 42. Таким образом, z будет равно 6, так как 6 × 6 = 36 ≤ 42.
• Мы получаем и частное, и остаток как 6. Теперь мы сложим делитель z с самим собой и получим новый делитель (12).
• Поставьте запятую в делимом и частном после 6 одновременно. Также поставьте 3 пары нулей в делимой части после запятой.
• Сбить одну пару нулей. Следовательно, наше делимое становится равным 600. Найдите число (m) такое, что 12m × m ≤ 600. Число m будет равно 4, так как 124 × 4 = 49.6 ≤ 600.
• Теперь повторите вышеуказанный шаг для оставшихся двух пар нулей.

Итак, мы получаем квадратный корень из √42 = 6,480 методом деления в большую сторону.

Исследуйте квадратные корни с помощью иллюстраций и интерактивных примеров.

• Квадратный корень из 44
• Квадратный корень из 72
• Квадратный корень из 22
• Квадратный корень из 85
• Квадратный корень из 64

Важные примечания:

• Число 42 не является идеальным квадратом.
• Квадратный корень из -42 является мнимым числом.
• Квадратный корень из 42 — иррациональное число.

 

 

1. Пример 1: Алекс едет на своей машине со скоростью √42 м/с. На сколько она должна увеличить свою скорость, чтобы пройти 1 км за 100 секунд?

   Решение:
   Требуемая скорость = 1000/100 = 10 м/с
   Ее текущая скорость = √42 м/с
   Следовательно, ей придется увеличить свою скорость на = 10 — √42 = 10 — 6,48 = 3,52 м/с

2.  

   Пример 2: Какое наименьшее число, кратное 42, является полным квадратом?

   Решение:
   Полный квадрат — это число, делители которого являются квадратом числа.
   Простая факторизация 42: 2 × 3 × 7
   Чтобы сделать его идеальным квадратом, мы должны составить пары 2, 3 и 7.
   Таким образом, кратное 42, которое является полным квадратом, будет 42 × 2 × 3 × 7 9.0014 Это квадрат 42 = 1764,

   .

перейти к слайдуперейти к слайду

 

Как ваш ребенок может освоить математические понятия?

Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу Cuemath.

Записаться на бесплатный пробный урок

 

перейти к слайдуперейти к слайдуперейти к слайду

 

Часто задаваемые вопросы о квадратных корнях из 42

Чему равен отрицательный квадратный корень из 42?

Отрицательный квадратный корень из 42 равен -6,4807.

Чему равен квадрат 42?

Квадрат 42 равен (42) ² = 1764.

Можем ли мы найти квадратный корень из 42, используя форму простой факторизации?

Нет, мы не можем найти квадратный корень из 42 методом простой факторизации, так как его нельзя уменьшить дальше.
Потому что число 42 имеет три простых делителя 2, 3 и 7.

Можем ли мы вычислить квадратный корень из 42, используя метод повторного вычитания?

Нет, мы не можем найти квадратный корень из 42, используя метод повторного вычитания.
Потому что этот метод можно использовать только для целых чисел с квадратным корнем.

Является ли число 42 полным квадратом?

Нет, число 42 не является полным квадратом
Потому что квадратный корень из 42 — это бесконечное и неповторяющееся число.

Рабочие листы по математике и визуальная программа

Бесплатный калькулятор квадратного корня | Математические вкусности

Форма поиска

Поиск

Работа с квадратными корнями — захватывающая тема для студентов-математиков, но они могут оказаться сложными. Начинающие математики часто полагаются на предположения, например, ошибочно принимают квадрат 3 за 6 только потому, что 6 кажется 3, считая дважды. Но возведение в квадрат подразумевает умножение, а не сложение. Когда мы возводим 3 в квадрат (или умножаем 3 само на себя), мы получаем 9 — квадратный корень из 9 равен 3.  

Квадратные корни не обязательно должны быть сложным вопросом. На самом деле легко запомнить таблицу идеальных квадратов и произвести впечатление на учителя. Но работа с несовершенными квадратами — или теми числами, квадратные корни которых содержат дроби или десятичные дроби — не всегда может быть такой простой. Вот тут-то и пригодится наш бесплатный онлайн-калькулятор квадратного корня. 

Как пользоваться нашим бесплатным онлайн-калькулятором квадратного корня

Как и некоторые другие наши калькуляторы, этот бесплатный онлайн-калькулятор квадратного корня чрезвычайно прост в использовании. В калькуляторе всего четыре части:

• Числовое поле
• Кнопка расчета
• Кнопка очистки
• Поле квадратного корня

Чтобы найти квадратный корень с помощью нашего бесплатного онлайн-калькулятора квадратного корня:  

1. Нажмите ОЧИСТИТЬ, чтобы обновить калькулятор.
2. Введите значение, квадратный корень которого вы хотите найти, в числовое поле.
3. Щелкните ВЫЧИСЛИТЬ.
4. Ваш ответ появится в поле квадратного корня.
5. Нажмите ОЧИСТИТЬ, чтобы начать заново и найти другое значение.

Номер:
Квадратный корень:

Другие калькуляторы

Что такое квадратный корень?

Квадратный корень относится к любому числу, которое дает вам исходное число как произведение при умножении на себя. Квадратные корни, выраженные символом «√», принадлежат к семейству показателей степени. Квадраты и корни являются специальными показателями. Любой квадрат x — это просто x, возведенный в степень ½, или x1/2.

Пример

Например, когда вас спрашивают о квадратном корне из 16, вы ищете число, которое даст вам произведение 16 при умножении на себя. Это число равно 4, потому что 4, умноженное на 4 — или возведенное в степень 2 (математически выраженное как 42), — равно 16. 16 1/2 равно 4, 9.0003

Работа с совершенными квадратами

Совершенные квадраты — это положительные числа, квадратные корни которых — целые числа. Ниже приведены наиболее распространенные способы нахождения квадратных корней из этих идеальных квадратов.

Повторное вычитание

Вычитание последовательных нечетных чисел (1, 3, 5, 7 и т. д.), начиная с 1, из числа, квадратный корень которого вы пытаетесь найти, пока не получите 0. 

Например: 

1. 9 — 1 = 8
2. 8 — 3 = 5
3. 5 — 5 = 0

Вы выполнили 3 вычитания из 0. Квадратный корень из 9 равен 3.

Факторизация простых чисел

Этот метод состоит из четырех шагов. Давайте пройдемся по каждому из них, чтобы найти квадратный корень из 144.