Определение координаты движущегося тела 9 класс онлайн-подготовка на Ростелеком Лицей
Введение
Представьте: вы изо всей силы бросили мяч. Как определить, где он будет находиться через две секунды? Можно подождать две секунды и просто посмотреть, где он. Но, даже не глядя, вы приблизительно можете предсказать, где будет мяч: бросок был сильнее обычного, направлен под большим углом к горизонту, значит, полетит высоко, но недалеко… Используя законы физики, можно будет точно определить положение нашего мяча.
Определить положение движущегося тела в любой момент времени – это и есть основная задача кинематики.
Система отсчета
Начнем с того, что у нас есть тело: как определить его положение, как объяснить кому-то, где оно находится? Об автомобиле мы скажем: он на дороге за 150 метров перед светофором или на 100 метров за перекрестком (см. рис. 1).
Рис. 1. Определение местоположения машины
Или на трассе за 30 км к югу от Москвы. О телефоне на столе скажем: он сантиметров на 30 правее клавиатуры или рядом с дальним углом стола (см. рис. 2).
О телефоне на столе скажем: он сантиметров на 30 правее клавиатуры или рядом с дальним углом стола (см. рис. 2).
Рис. 2. Положение телефона на столе
Заметьте: мы не сможем определить положение автомобиля, не упомянув другие объекты, не привязавшись к ним: светофор, город, клавиатуру. Мы определяем положение, или координаты, всегда относительно чего-то.
Координаты – это набор данных, по которому определяется положение того или иного объекта, его адрес.
Примеры упорядоченных и неупорядоченных имен
Координата тела – это его адрес, по которому мы его можем найти. Он упорядоченный. Например, зная ряд и место, мы точно определяем, где находится наше место в зале кинотеатра (см. рис. 3).
Рис. 3. Зал кинотеатра
Буквой и цифрой, например e2, точно задается положение фигуры на шахматной доске (см. рис. 4).
Рис. 4. Положение фигуры на доске
Зная адрес дома, например улица Солнечная 14, мы будем искать его на этой улице, на четной стороне, между домами 12 и 16 (см. рис. 5).
рис. 5).
Рис. 5. Поиск дома
Названия улиц не упорядочены, мы не будем искать Солнечную улицу по алфавиту между улицами Розовой и Тургенева. Также не упорядочены номера телефонов, номерные знаки автомобилей (см. рис. 6).
Рис. 6. Неупорядоченные имена
Эти номера, идущие подряд, – это лишь совпадение, не означающее соседства.
Мы можем задать положение тела в разных системах координат, как нам удобно. Для того же автомобиля, можно задать точные географические координаты (широту и долготу) (см. рис. 7).
Рис. 7. Долгота и широта местности
Можно выбрать любую точку в городе и считать, сколько километров нужно проехать на юг и сколько на восток, чтобы найти автомобиль (см. рис. 8).
Рис. 8. Местоположение относительно точки
Причем если мы выберем разные такие точки, то получим разные координаты, хотя они будут задавать положение одного и того же автомобиля.
Итак, положение тела относительно разных тел в разных системах координат будет разным. А что такое движение? Движение – это изменение положения тела со временем. Поэтому описывать движение мы будем в разных системах отсчета по-разному, и нет смысла рассматривать движение тела без системы отсчета.
А что такое движение? Движение – это изменение положения тела со временем. Поэтому описывать движение мы будем в разных системах отсчета по-разному, и нет смысла рассматривать движение тела без системы отсчета.
Например, как движется стакан с чаем на столе в поезде, если сам поезд едет? Смотря относительно чего. Относительно стола или пассажира, сидящего рядом на сидении, стакан покоится (см. рис. 9).
Рис. 9. Движение стакана относительно пассажира
Относительно дерева около железной дороги стакан движется вместе с поездом (см. рис. 10).
Рис. 10. Движение стакана вместе с поездом относительно дерева
Относительно земной оси стакан и поезд вместе со всеми точками земной поверхности будут еще и двигаться по окружности (см. рис. 11).
Рис. 11. Движение стакана с вращением Земли относительно земной оси
Поэтому нет смысла говорить о движении вообще, движение рассматривается в привязке к системе отсчета.
Наблюдение и вычисление
Всё, что мы знаем о движении тела, можно разделить на наблюдаемое и вычисляемое. Вспомним пример с мячом, который мы бросили. Наблюдаемое – это его положение в выбранной системе координат, когда мы его только бросаем (см. рис. 12).
Вспомним пример с мячом, который мы бросили. Наблюдаемое – это его положение в выбранной системе координат, когда мы его только бросаем (см. рис. 12).
Рис. 12. Наблюдение
Это момент времени, когда мы его бросили; время, которое прошло после броска. Пусть на мяче нет спидометра, который показал бы скорость мяча, но ее модуль, как и направление, тоже можно узнать, используя, например, замедленную съемку.
С помощью наблюдаемых данных мы можем предсказать, например, что мяч через 5 секунд упадет за 20 м от места броска или через 3 секунды попадет в верхушку дерева. Положение мяча в любой момент времени – это в нашем случае вычисляемые данные.
Что определяет каждое новое положение движущегося тела? Его определяет перемещение, потому что перемещение – это вектор, характеризующий изменение положения. Если начало вектора совместить с начальным положением тела, то конец вектора укажет на новое положение переместившегося тела (см. рис. 13).
Рис. 13. Вектор перемещения
13. Вектор перемещения
Нахождение координаты тела по перемещению
Рассмотрим несколько примеров на определение координаты движущегося тела по его перемещению.
Пусть тело двигалось прямолинейно из точки 1 в точку 2. Построим вектор перемещения и обозначим его (см. рис. 14).
Рис. 14. Перемещение тела
Тело двигалось вдоль одной прямой, значит, нам будет достаточно одной оси координат, направленной вдоль перемещения тела. Допустим, мы наблюдаем за движением со стороны, совместим начало отсчета с наблюдателем.
Перемещение – вектор, удобнее работать с проекциями векторов на оси координат (у нас она одна). – проекция вектора (см. рис. 15).
Рис. 15. Проекция вектора
Как определить координату начальной точки, точки 1? Опускаем перпендикуляр из точки 1 на ось координат. Этот перпендикуляр пересечет ось и отметит на оси координату точки 1. Так же определяем координату точки 2 (см. рис. 16).
Рис. 16. Опускаем перпендикуляры на ось ОХ
16. Опускаем перпендикуляры на ось ОХ
Проекция перемещения равна:
При таком направлении оси и перемещения будет по модулю равна самому перемещению .
Зная начальную координату и перемещение, найти конечную координату тела – дело математики:
Уравнение
Уравнение – это равенство, содержащее неизвестный член. В чем его смысл?
Любая задача заключается в том, что что-то нам известно, а что-то – нет, и неизвестное нужно найти. Например, тело из некоторой точки переместилось на 6 м в направлении оси координат и оказалось в точке с координатой 9 (см. рис. 17).
Рис. 17. Начальное положение точки
Как найти, из какой точки тело начало движение?
У нас есть закономерность: проекция перемещения – это разность конечной и начальной координат:
Смысл уравнения будет в том, что перемещение и конечную координату мы знаем () и можем подставить эти значения, а начальную координату не знаем, она будет неизвестным в этом уравнении:
И уже решая уравнение, мы получим ответ: начальная координата .
Перемещение и направление оси не совпадают по направлению
Рассмотрим другой случай: перемещение направлено в сторону, противоположную направлению оси координат.
Координаты начальной и конечной точек определяются так же, как и раньше, – опускаются перпендикуляры на ось (см. рис. 18).
Рис. 18. Ось направлена в другую сторону
Проекция перемещения (ничего не меняется) равна:
Обратите внимание, что больше, чем , и проекция перемещения , когда она направлена против оси координат, будет отрицательной.
Конечная координата тела из уравнения для проекции перемещения равна:
Как видим, ничего не меняется: в проекции на ось координат конечное положение равно начальному положению плюс проекция перемещения. В зависимости от того, в какую сторону тело переместилось, проекция перемещения будет положительной или отрицательной в данной системе координат.
Перемещение и ось координат находятся под углом друг к другу
Рассмотрим случай, когда перемещение и ось координат направлены под углом друг к другу. Теперь одной оси координат нам недостаточно, нужна вторая ось (см. рис. 19).
Теперь одной оси координат нам недостаточно, нужна вторая ось (см. рис. 19).
Рис. 19. Ось направлена в другую сторону
Теперь перемещение будет иметь ненулевую проекцию на каждую ось координат. Эти проекции перемещения будут определяться, как и раньше:
Заметьте, модуль каждой из проекций в этом случае меньше модуля перемещения. Модуль перемещения можем легко найти, используя теорему Пифагора. Видно, что если построить прямоугольный треугольник (см. рис. 20), то его катеты будут равны и , а гипотенуза равна модулю перемещения или, как часто записывают, просто .
Рис. 20. Треугольник Пифагора
Тогда по теореме Пифагора запишем:
Задача
Автомобиль находится в 4 км к востоку от гаража. Воспользуйтесь одной осью координат, направленной на восток, с началом отсчета в гараже. Укажите координату автомобиля в заданной системе через 3 минуты, если автомобиль этим временем ехал со скоростью 0,5 км/мин на запад.
В задаче ничего не сказано о том, что автомобиль поворачивал или изменял скорость, поэтому считаем движение равномерным прямолинейным.
Изобразим систему координат: начало координат у гаража, ось х направлена на восток (см. рис. 21).
Рис. 21. Направление оси Ох
Автомобиль изначально был в точке и двигался по условию задачи на запад (см. рис. 22).
Рис. 22. Движение автомобиля на запад
Проекция перемещения, как мы неоднократно писали, равна:
Мы знаем, что автомобиль проезжал по 0,5 км каждую минуту, значит, чтобы найти суммарное перемещение, нужно скорость умножить на количество минут :
На этом физика закончилась, осталось математически выразить искомую координату. Выразим ее из первого уравнения:
Подставим перемещение:
Осталось подставить числа и получить ответ. Не забывайте, что автомобиль двигался на запад против направления оси х, это значит, что проекция скорости отрицательна: .
Задача решена.
Итоги
Главное, чем мы сегодня пользовались для определения координаты, – выражение для проекции перемещения:
И из него мы уже выражали координату:
При этом сама проекция перемещения может быть задана, может вычисляться как , как в было в задаче о равномерном прямолинейном движении, может вычисляться сложнее, что нам еще предстоит изучить, но в любом случае координату движущегося тела (где тело оказалось) можно определить по начальной координате (где тело было) и по проекции перемещения (куда переместилось).
На этом наш урок окончен, до свидания!
Список литературы
- Соколович Ю.А., Богданова Г.С Физика: Справочник с примерами решения задач. – 2-е издание, передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
- Перышкин А.В., Гутник Е.М. Физика: 9 класс. Учебник для общеобразовательных учреждений. – 14-е изд. – М.: Дрофа, 2009.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «Class-fizika.narod.ru» (Источник)
- Интернет-портал «Av-physics.narod.ru» (Источник)
- Интернет-портал «Class-fizika.narod.ru» (Источник)
Домашнее задание
- Что такое перемещение, путь, траектория?
- Как можно определить координаты тела?
- Запишите формулу для определения проекции перемещения.
- Как будет определяться модуль перемещения, если перемещение имеет проекции на две оси координат?
Кинематика. Практика 9 класс онлайн-подготовка на Ростелеком Лицей
Введение
При решении задач необходимо придерживаться схемы решения, которую можно применить к любой физической задаче.
- Проанализировать условие. Определить, какие процессы происходят.
- Определить закономерности, которым подчиняются происходящие процессы, записать эти закономерности в виде уравнений.
 Посмотреть на величины, входящие в эти формулы: определить, какие из них даны в условии, а какие нужно дополнительно выразить. При необходимости перевести величины в СИ.
Посмотреть на величины, входящие в эти формулы: определить, какие из них даны в условии, а какие нужно дополнительно выразить. При необходимости перевести величины в СИ. - Математическая часть: решить полученную систему уравнений. Получить ответ, подставив численные значения переменных.
Задача 1
Пассажир зашел в автобус через задние двери, а на следующей остановке вышел через передние. Одинаковое ли перемещение относительно дороги совершили между остановками автобус и пассажир?
Анализ условия. В задаче описано движение автобуса и пассажира в системе отсчета, связанной с дорогой. К пассажиру можно применить модель материальной точки, отметим ее буквой П (рис. 1). Если автобус движется прямолинейно и поступательно, перемещение всех его точек одинаково. Поэтому можно рассматривать движение автобуса как движение какой-то одной его точки. Выберем для удобства точку около задней двери, чтобы в начале движения она совпадала с пассажиром, обозначим эту точку А (рис.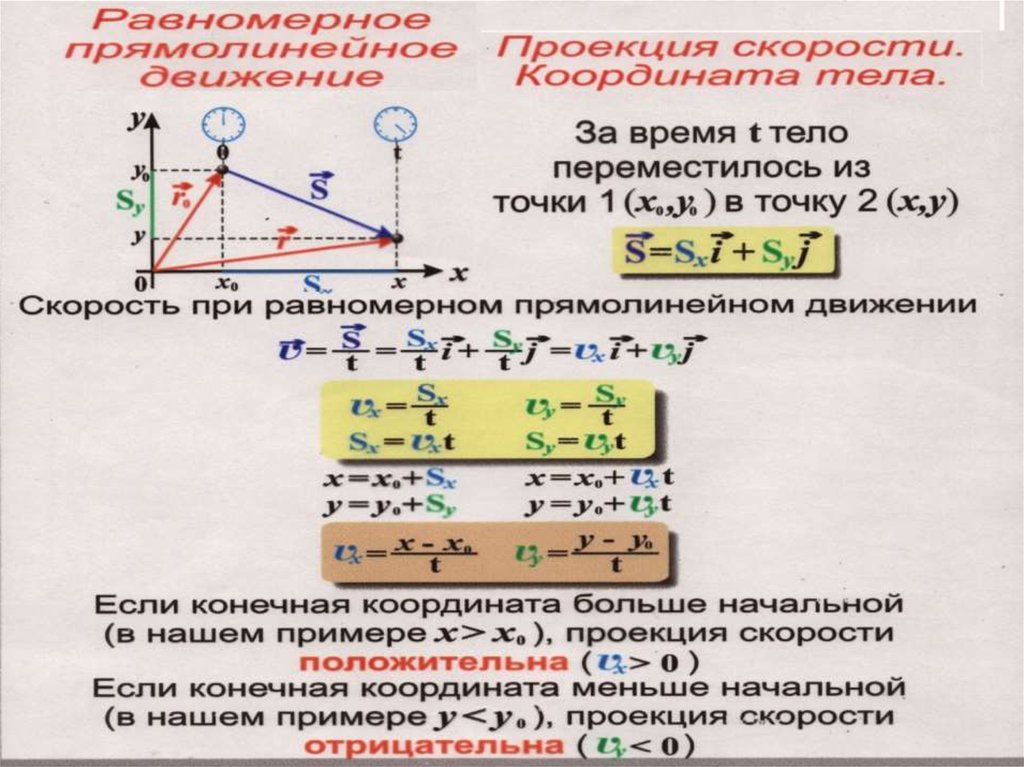 1).
1).
Рис. 1. Обозначения автобуса и пассажира
Физическая часть решения. Сравниваем перемещения двух материальных точек А и П (автобус и пассажир). В начальный момент времени они находились в одной точке. На следующей остановке, то есть в конце движения, точка А будет находиться в другой точке (рис. 2), а точка П (если А – это задняя дверь) – возле передней двери.
И если начертить векторы перемещения и , то видно, что они не совпадают, перемещение пассажира получилось по модулю больше.
Рис. 2. Векторы перемещения пассажира и автобуса
Сложение перемещений и скоростей
Можно заметить, что, даже если автобус движется не прямолинейно, общее перемещение пассажира относительно Земли равно векторной сумме перемещения автобуса и перемещения пассажира относительно автобуса.
Если тело движется в подвижной системе отсчета, то ее абсолютное перемещение (относительно Земли) равно его относительному перемещению (относительно системы отсчета) плюс перемещению самой системы отсчета.
Мы записывали закон сложения скоростей, для нахождения скорости тела, которое движется в подвижной системе отсчета. Эти перемещения совершались одновременно, на протяжении одного и того же времени . Разделим обе части на это время :
И получим тот самый закон сложения скоростей:
Задача 2
Два автомобиля одновременно выехали из города А в город В. Первый автомобиль первую половину времени ехал со скоростью , а вторую – с меньшей скоростью . Второй автомобиль первую половину пути ехал со скоростью , а вторую – со скоростью . Какой из автомобилей доехал до города В раньше?
Рис. 3. Задача 2
Анализ условия. В задаче описано движение автомобилей, скорость которых по ходу движения изменялась. Нас интересует общее время, затраченное на весь путь, а эти величины удобно описать понятием средней скорости:
где – длина всего пути, – все время, которое понадобилось для его преодоления.
У какого автомобиля средняя скорость больше, тот и доедет до города В раньше при одном и том же .
Физическая часть решения. Найдем среднюю скорость первого автомобиля (рис. 4). За первую половину времени , которую он ехал со скоростью , он проехал путь , а за вторую половину времени он проехал путь .
Рис. 4. Средняя скорость первого автомобиля
Средняя скорость – это весь путь, деленный на все время. Так и запишем:
где – это две половины времени, а и – это два разных участка пути.
Запишем среднюю скорость для второго автомобиля (рис. 5). У него два участка пути – это две половины пути, каждая по .
Рис. 5. Средняя скорость второго автомобиля
Двигаясь на них с разными скоростями, он на одну половину пути потратил время , а на вторую – . Запишем:
На каждом участке пути движение можно считать равномерным, скорость и перемещение на них связаны простым уравнением:
Математическая часть решения задачи 2
Рассмотрим среднюю скорость первого автомобиля.
Известны скорости автомобиля на этих участках.
Для первого и второго участка запишем (на каждый участок затрачена половина времени ):
Отсюда:
Подставим:
Выразили скорость через известные скорости и .
Теперь найдем .
Здесь нам не известны интервалы времени и . Выразим их тоже через скорости на двух равных участках пути:
Отсюда выразим время:
Подставим:
Осталось сравнить полученные средние скорости. Найдем их разность:
Получили положительную разность , это значит, что больше, чем , и первый автомобиль приедет к городу В раньше, чем второй.
Задача 3
Паровая турбина имеет ротор и рабочее колесо, которые вращаются. Ротор делает 1200 оборотов в минуту, а частота вращения колеса в 40 раз меньше, чем частота вращения ротора. Определите частоту вращения и период колебания рабочего колеса турбины.
Анализ условия. В задаче описано вращение ротора и рабочего колеса турбины (рис. 6).
В задаче описано вращение ротора и рабочего колеса турбины (рис. 6).
Рис. 6. Модель паровой турбины
Есть удобная модель для описания такого движения: равномерное движение по окружности.
По условию, за время , или в СИ , ротор делает 1200 оборотов – обозначим это количество . Частоту обозначим буквой , можно записать характеристики колеса с индексом 2, и тогда .
Физическая часть решения задачи.
Частота – количество оборотов, совершаемое за единицу времени. Если оборотов совершается за секунд, то за одну секунду:
Частота и период – взаимно обратные величины, запишем для колеса, т. к. о нем спрашивается в условии:
Вместе с отношением из условия получили простую систему уравнений, из которой осталось найти частоту и период вращения колеса.
Математическая часть решения.
Подставим из первого уравнения в третье:
Найдем из второго уравнения период:
Задача решена.
Задача 4
С какой скоростью должен лететь самолет над экватором Земли, чтобы для пассажиров самолета Солнце не изменяло своего положения на небосводе?
Анализ условия. Солнце меняет положение на небосводе из-за суточного вращения Земли вокруг своей оси. Чтобы положение Солнца относительно самолета не менялось, он должен быть как бы неподвижен относительно Солнца, хотя Земля под ним вращается вокруг своей оси. Получается, что относительно поверхности Земли самолет должен лететь в направлении, противоположном вращению Земли, со скоростью, по модулю равной линейной скорости движения поверхности Земли относительно ее оси (рис. 7).
Рис. 7. Задача 4
Вычислим эту скорость.
Физическая часть решения задачи. Применим модель равномерного движения по окружности.
Радиус Земли можно узнать из справочника, он равен приблизительно 6400 км. Самолеты летают на высоте нескольких километров, поэтому радиус окружности, по которой движется самолет, будем считать приблизительно равным радиусу Земли. Период вращения Земли – 24 часа. Можно даже не переводить в СИ и найти скорость в км/ч.
Период вращения Земли – 24 часа. Можно даже не переводить в СИ и найти скорость в км/ч.
Зная период вращения и радиус траектории, линейную скорость можно вычислить по формуле:
Математическая часть. Остается подставить значения и получить скорость:
Задача решена. Для сравнения, самолеты-истребители движутся со скоростями порядка 2500 км/ч, так что полученная скорость реально достижима.
Задача 5
Тело двигалось равноускорено продолжительное время. На рисунке подан график зависимости для этого тела начиная с некоторого момента времени (рис. 8).
Рис. 8. График зависимости
Определите время, когда тело изменило направление скорости своего движения.
Анализ условия. Задан график , по нему можно определить проекцию скорости тела в разные моменты времени, в данном случае от 0 до 6 секунд. Направление движения обозначается знаком проекции , а при равноускоренном движении скорость меняет знак, когда прямая ее графика пересекает ось (рис.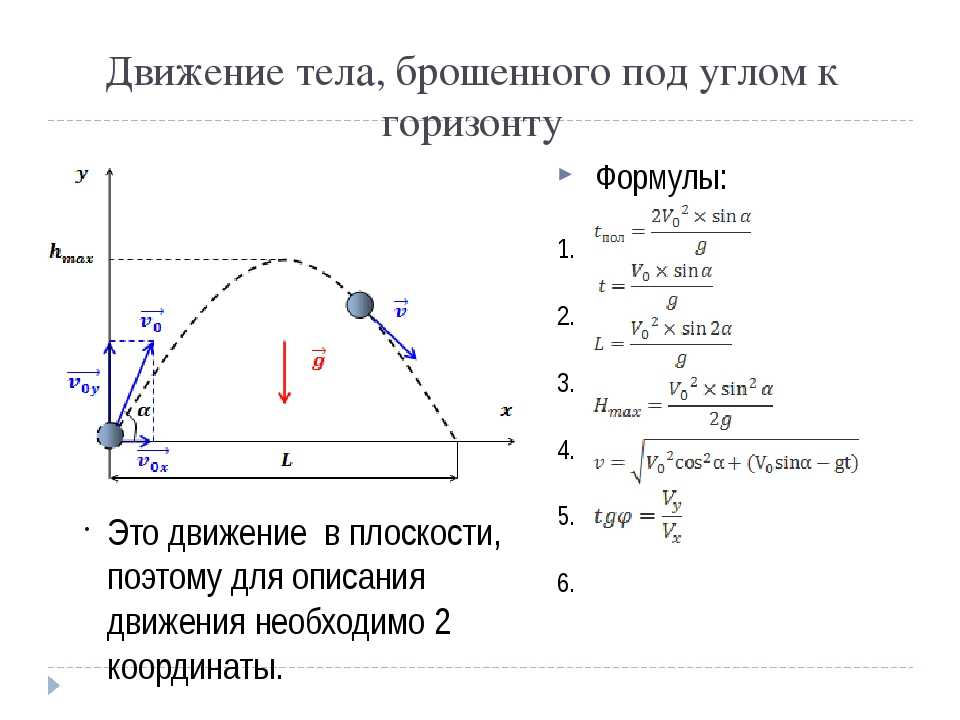 9). Допустим, скорость уменьшается. Тогда она в точке пересечения становится равна нулю и дальше продолжает уменьшаться, приобретая отрицательные значения: тело останавливается и начинает разгоняться в противоположном направлении.
9). Допустим, скорость уменьшается. Тогда она в точке пересечения становится равна нулю и дальше продолжает уменьшаться, приобретая отрицательные значения: тело останавливается и начинает разгоняться в противоположном направлении.
Рис. 9. Равноускоренное движение
Надо найти момент, когда скорость равна нулю.
Физическая часть решения. Запишем уравнение для скорости при равноускоренном движении:
Оно связывает любой момент времени со скоростью в этот момент . Скорость в момент найдем из графика, . Не хватает только ускорения.
Ускорение по определению равно:
Ускорение постоянно, поэтому выберем на графике любой удобный интервал, на котором сможем определить начальную и конечную скорость и длительность интервала. Например, от момента до момента . В эти моменты скорости равны , и .
Математическая часть решения. Подставим ускорение, которое мы практически вычислили, в уравнение для скорости:
Нам нужно найти момент времени , когда . Так и запишем в уравнении, что скорость в этот момент равна 0:
Так и запишем в уравнении, что скорость в этот момент равна 0:
В это уравнении, кроме искомого , все известно, осталось выразить :
Внесем минус под знак дроби:
Знаком плюс или минус мы обозначаем направление, в котором движемся: по направлению или против направления оси. – это момент начала наблюдения. Когда мы говорим о моментах позже некоторого момента, мы прибавляем время, а когда говорим о моментах раньше – отнимаем. Момент означает момент за 4 секунды до начала наблюдения.
Задача 6
По прямолинейному участку дороги идет пешеход с постоянной скоростью . Его догоняет мотоциклист, который увеличивает скорость, двигаясь с ускорением . Через какое время мотоцикл обгонит пешехода, если на момент начала отсчета времени расстояние между ними составляло , а мотоцикл двигался со скоростью ? Какой путь пройдет мотоциклист за это время?
Анализ условия. В задаче описано прямолинейное движение: равноускоренное для мотоциклиста и равномерное для пешехода. Выберем систему координат и будем описывать эти движения математически.
Выберем систему координат и будем описывать эти движения математически.
Физическая часть решения задачи. Выберем систему отсчета. Удобно направить ось х в направлении движения пешехода и мотоциклиста. Начало координат для удобства поместим в точку, из которой начинает движение мотоцикл: левее него у нас ничего не будет.
Нас интересует момент, когда мотоциклист и пешеход встретятся, то есть будут находиться одновременно в одной координате. Запишем уравнение для координаты тела в любой момент времени:
Запишем это уравнение для наших тел. Для мотоцикла в нашей системе отсчета , начальная скорость задана, , .
Для пешехода начальная координата на расстоянии 300 м от мотоцикла в направлении оси , то есть . Начальная скорость равна , и она постоянная, так как ускорение .
В момент обгона мотоциклист и пешеход находятся в одной точке, их координаты равны, запишем это:
Или:
Математическая часть решения задачи 6
Решим квадратное уравнение:
Что означает момент времени ? Даже если мотоциклист и пешеход так же двигались все это время, то нас интересует не этот момент, а момент обгона после начала наблюдения. Поэтому оставляем одно решение: .
Поэтому оставляем одно решение: .
Зная уравнение движения мотоцикла, найдем его координату в момент встречи :
Эту же точку можно было найти и из уравнения движения пешехода, все равно они в этот момент находятся в одной точке: .
Так вот, перемещение мотоциклиста, по определению, равно:
А так как мотоциклист все это время двигался в одном направлении вдоль одной прямой, то его путь будет равен тем же 320 метрам.
Задача решена.
Задача 7
На рисунке дан график проекции скорости движения некоторого тела (рис. 10).
Рис. 10. График проекции скорости движения тела
Определите путь и перемещение тела на протяжении после начала отсчета времени. Запишите уравнение координаты, если в момент времени тело было в точке с координатой .
Анализ условия. На графике видно, что скорость изменяется линейно, значит, описано равноускоренное движение, будем использовать уравнения для равноускоренного движения. Найти координату и перемещение легко из уравнения для координаты . Обратите внимание на график: тело двигалось сначала в направлении оси координат, потом остановилось и начало двигаться в обратном направлении. Это значит, что путь не будет равен перемещению (рис. 11), нужно найти путь до и после остановки.
Найти координату и перемещение легко из уравнения для координаты . Обратите внимание на график: тело двигалось сначала в направлении оси координат, потом остановилось и начало двигаться в обратном направлении. Это значит, что путь не будет равен перемещению (рис. 11), нужно найти путь до и после остановки.
Рис. 11. Перемещение тела
Физическая часть решения. Запишем уравнение для координаты:
Начальная координата дана в условии: . Это скорость в момент времени , . Ускорение по определению равно:
Его можно найти на графике. Выберем интервал времени от 0 до 2 с. Скорость за эти 2 с изменилась от 20 до 0 м/с:
Математическая часть решения. Часть расчетов уже выполнена, получено уравнение для координаты:
Координата тела в момент времени равна:
Найдем перемещение:
В момент времени перемещение равно:
На графике видно, что тело остановилось в момент времени . Найдем координату тела в этот момент:
Теперь понятно: тело начало движение из точки , затем оказалось в точке , то есть прошло путь . Затем развернулось и из точки попало в точку , то есть прошло еще . В сумме путь составил .
Затем развернулось и из точки попало в точку , то есть прошло еще . В сумме путь составил .
Задача решена.
Задача 8
Воздушный шар равномерно поднимается со скоростью . На высоте от земли с него упало небольшое тело. Через какой интервал времени это тело упадет на землю? Какой будет скорость движения тела в момент падения? Падение тела считайте свободным.
Анализ условия. В задаче описано свободное падение тела с воздушного шара. Свободное падение – это равноускоренное движение с ускорением . Так как это тело упало с шара, который поднимался со скоростью , это будет начальной скоростью этого тела.
Физическая часть решения. Выберем систему отсчета. Направим ось координат вертикально вниз, куда будет падать тело. А начало координат поместим в точку, откуда оно падает, то есть на высоту 7 м над поверхностью (рис. 12).
Рис. 12. Система отсчета
В задаче рассматривается падение тела на землю, то есть координата тела будет в нашей системе равна 7 м. Запишем уравнения для координаты и скорости:
Запишем уравнения для координаты и скорости:
В данной системе координат начальная координата равна нулю: . Проекция скорости направлена против оси координат, поэтому равна заданной по условию скорости со знаком минус, , ускорение свободного падения положительно, для простоты расчетов округлим его до десяти: .
Уравнения принимают вид:
Математическая часть решения задачи 8
Мы ищем время, за которое тело упадет на землю, то есть его координата в этот момент времени равна . Подставим все известные значения в уравнение для координаты:
Решим уравнение:
Решение отбрасываем, так как за секунду до падения тело еще поднималось на шаре. А момент – это и есть наше решение.
Из уравнения для скорости найдем скорость тела в момент падения :
Задача решена.
Список литературы
- Соколович Ю.А., Богданова Г.С. Физика: справочник с примерами решения задач.

- Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений / А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-сайт «Внеклассный урок» (Источник)
- Интернет-сайт «Внеклассный урок» (Источник)
- Интернет-сайт «Класс!ная физика» (Источник)
Домашнее задание
- Лифт в течение первых 3 c поднимается равноускоренно и достигает скорости 3 м/с, с которой продолжает равномерный подъем в течение 6 c. Затем движется с прежним по модулю ускорением до полной остановки. Построить график зависимости скорости подъема лифта от времени и определить высоту подъема.
- Тело начало двигаться вдоль оси x с постоянной скоростью 6 м/с из точки, имеющей координату −7 м. Через сколько секунд координата тела окажется равной 5 м?
- Шкив диаметром 1 метр делает 500 оборотов за 300 секунд.
 Определить угловую и линейную скорости точки на ободе шкива, период вращения шкива.
Определить угловую и линейную скорости точки на ободе шкива, период вращения шкива.
4.3 Движение снарядов — University Physics Volume 1
Цели обучения
К концу этого раздела вы сможете:
- Используйте одномерное движение в перпендикулярных направлениях для анализа движения снаряда.
- Рассчитайте дальность, время полета и максимальную высоту снаряда, который запускается и поражает плоскую горизонтальную поверхность.
- Найдите время полета и скорость удара снаряда, который приземляется на высоте, отличной от высоты запуска.
- Рассчитать траекторию снаряда.
Снарядное движение — это движение объекта, брошенного или отброшенного в воздух, с ускорением только под действием силы тяжести. Применения движения снаряда в физике и технике многочисленны. Некоторые примеры включают метеоры, когда они входят в атмосферу Земли, фейерверки и движение любого мяча в спорте.
Наиболее важным фактом, который следует помнить, является то, что движений вдоль перпендикулярных осей являются независимыми и поэтому могут быть проанализированы отдельно. Мы обсуждали этот факт в разделе «Векторы смещения и скорости», где увидели, что вертикальное и горизонтальное движения независимы. Ключом к анализу двумерного движения снаряда является разбиение его на два движения: одно по горизонтальной оси, а другое по вертикальной. (Этот выбор осей является наиболее разумным, потому что ускорение, вызванное силой тяжести, является вертикальным; таким образом, нет никакого ускорения вдоль горизонтальной оси, когда сопротивление воздуха незначительно.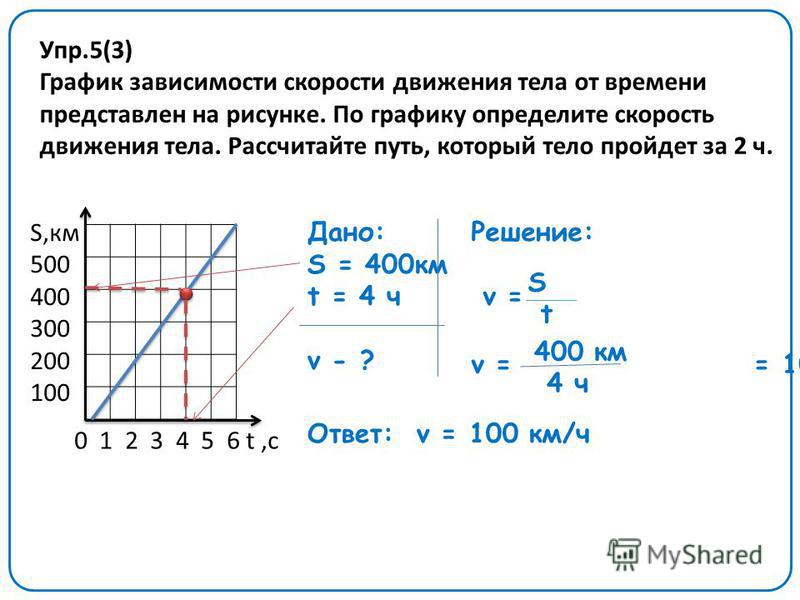
Рисунок
4.11
Полное перемещение с футбольного мяча в точке на его пути. Вектор s→s→ имеет компоненты x→x→ и y→y→ вдоль горизонтальной и вертикальной осей. Его величина составляет
Чтобы полностью описать движение снаряда, мы должны включить скорость и ускорение, а также перемещение. Мы должны найти их компоненты по х- и и -оси. Предположим, что все силы, кроме гравитации (такие, например, как сопротивление воздуха и трение), пренебрежимо малы. Определив положительное направление как восходящее, компоненты ускорения получаются очень простыми:
Мы должны найти их компоненты по х- и и -оси. Предположим, что все силы, кроме гравитации (такие, например, как сопротивление воздуха и трение), пренебрежимо малы. Определив положительное направление как восходящее, компоненты ускорения получаются очень простыми:
с2).
Поскольку гравитация вертикальна, ax=0.ax=0. Если ax=0,ax=0, это означает, что начальная скорость в направлении
Горизонтальное движение
v0x=vx,x=x0+vxtv0x=vx,x=x0+vxt
4.
Вертикальное движение
y=y0+12(v0y+vy)ty=y0+12(v0y+ vy)t
4.20
vy=v0y−gtvy=v0y−gt
4.21
y=y0+v0yt−12gt2y=y0+v0yt−12gt2
4.22
vy2=v0y2−2g(y−y0) vy2=v0y2−2g(y−y0)
4,23
Используя эту систему уравнений, мы можем анализировать движение снаряда, учитывая некоторые важные моменты.
Стратегия решения проблем
Движение снаряда
- Разделите движение на горизонтальную и вертикальную составляющие вдоль осей
 12.
12. - Рассматривайте движение как два независимых одномерных движения: одно по горизонтали, а другое по вертикали. Используйте кинематические уравнения для горизонтального и вертикального движения, представленные ранее.
- Найдите неизвестные в двух отдельных движениях: горизонтальном и вертикальном. Обратите внимание, что единственной общей переменной между движениями является время t . Процедуры решения задач здесь такие же, как и для одномерной кинематики, и проиллюстрированы в следующих решенных примерах.
- Рекомбинируйте величины в горизонтальном и вертикальном направлениях, чтобы найти полное перемещение s→s→ и скорость v→.v→. Найдите величину и направление смещения и скорости, используя
s=x2+y2,Φ=tan−1(y/x),v=vx2+vy2,s=x2+y2,Φ=tan−1(y/ x),v=vx2+vy2,
, где Φ — направление перемещения s→.s→.
Рисунок
4.12
(а) Мы анализируем двумерное движение снаряда, разбивая его на два независимых одномерных движения вдоль вертикальной и горизонтальной осей.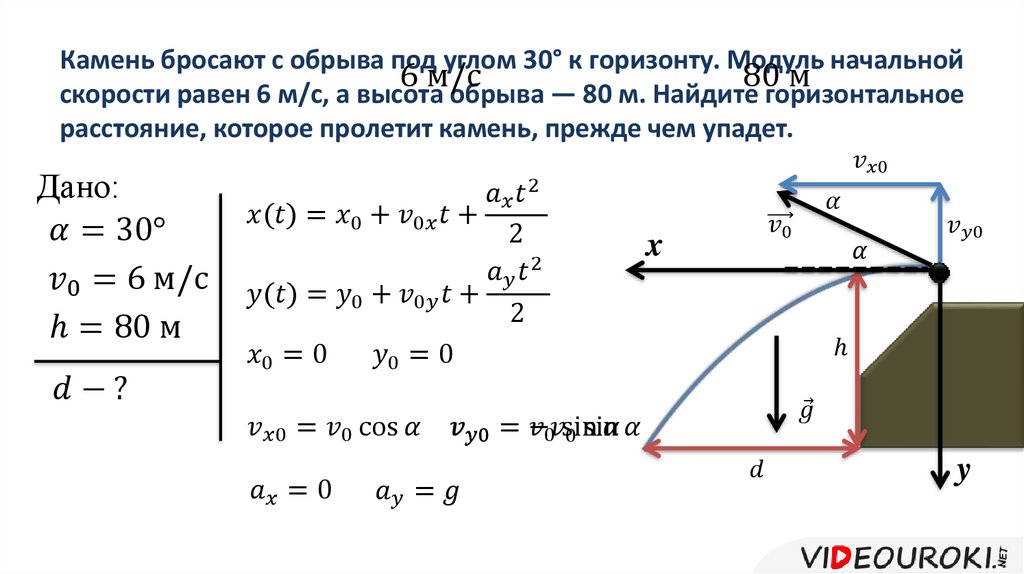 (b) Горизонтальное движение простое, потому что ax=0ax=0, а vxvx — константа. (в) Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта. В высшей точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает направление, противоположное начальной вертикальной скорости. (г) x и y движений рекомбинируются для получения общей скорости в любой заданной точке траектории.
(b) Горизонтальное движение простое, потому что ax=0ax=0, а vxvx — константа. (в) Скорость в вертикальном направлении начинает уменьшаться по мере подъема объекта. В высшей точке вертикальная скорость равна нулю. Когда объект снова падает на Землю, вертикальная скорость снова увеличивается по величине, но указывает направление, противоположное начальной вертикальной скорости. (г) x и y движений рекомбинируются для получения общей скорости в любой заданной точке траектории.
Пример 4.7
Снаряд фейерверка взрывается высоко и прочь
Во время фейерверка снаряд взлетает в воздух с начальной скоростью 70,0 м/с под углом 75,0°75,0° над горизонтом, как показано на рис. 4.13. Взрыватель рассчитан на воспламенение снаряда, когда он достигает своей высшей точки над землей. а) Вычислите высоту взрыва снаряда. б) Сколько времени проходит между запуском снаряда и взрывом? в) Чему равно горизонтальное перемещение снаряда при взрыве? г) Чему равно полное перемещение от точки запуска до высшей точки?
Рисунок
4. 13
Траектория снаряда фейерверка. Взрыватель предназначен для подрыва снаряда в высшей точке его траектории, которая находится на высоте 233 м и на расстоянии 125 м по горизонтали.
13
Траектория снаряда фейерверка. Взрыватель предназначен для подрыва снаряда в высшей точке его траектории, которая находится на высоте 233 м и на расстоянии 125 м по горизонтали.
Стратегия
Движение можно разбить на горизонтальное и вертикальное движения, в которых ax=0ax=0 и ay=-g.ay=-g. Затем мы можем определить x0x0 и y0y0 равными нулю и найти нужные величины.
Раствор
(а) Под «высотой» мы подразумеваем высоту или вертикальное положение y выше начальной точки. Высшая точка любой траектории, называемая вершиной , достигается, когда vy=0.vy=0. Поскольку мы знаем начальную и конечную скорости, а также начальное положение, мы используем следующее уравнение, чтобы найти y :
vy2=v0y2−2g(y−y0).vy2=v0y2−2g(y−y0).
Поскольку y0y0 и vyvy равны нулю, уравнение упрощается до
0=v0y2−2gy.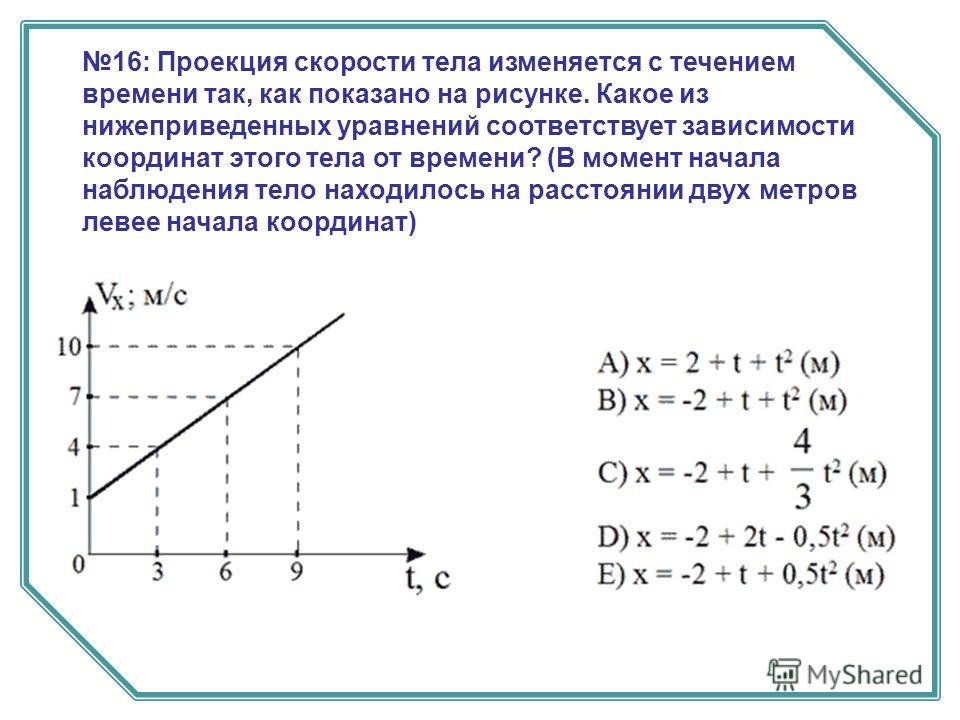 0=v0y2−2gy.
0=v0y2−2gy.
Решение для y дает
y=v0y22g.y=v0y22g.
Теперь мы должны найти v0y,v0y, составляющую начальной скорости в направлении y . Она определяется как v0y=v0sinθ0,v0y=v0sinθ0, где v0v0 — начальная скорость 70,0 м/с, а θ0=75°θ0=75° — начальный угол. Таким образом,
v0y=v0sinθ=(70,0 м/с)sin75°=67,6 м/sv0y=v0sinθ=(70,0 м/с)sin75°=67,6 м/с
и y равно
y=(67,6 м/с)22(9,80 м/с2).y=(67,6 м/с)22(9,80 м/с2).
Таким образом, имеем
y=233m.y=233m.
Обратите внимание, что, поскольку значение up положительно, начальная вертикальная скорость положительна, как и максимальная высота, но ускорение от силы тяжести отрицательно. Отметим также, что максимальная высота зависит только от вертикальной составляющей начальной скорости, так что любой снаряд с начальной вертикальной составляющей скорости 67,6 м/с достигает максимальной высоты 233 м (без учета сопротивления воздуха).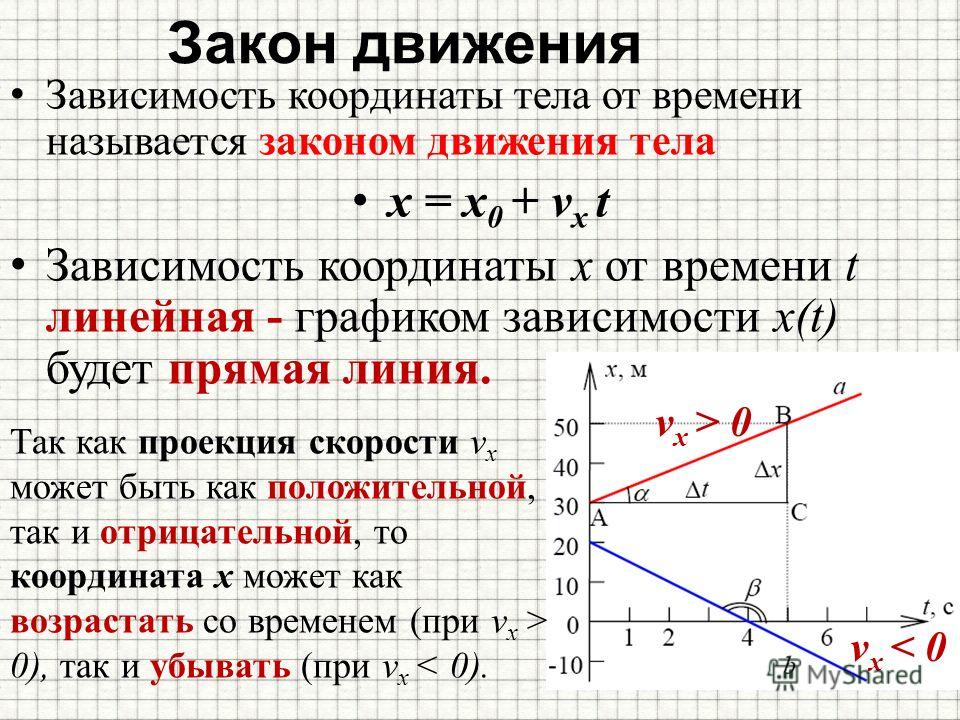 Числа в этом примере разумны для больших фейерверков, снаряды которых действительно достигают такой высоты перед взрывом. На практике сопротивлением воздуха нельзя полностью пренебречь, поэтому начальная скорость должна быть несколько больше заданной, чтобы достичь той же высоты.
Числа в этом примере разумны для больших фейерверков, снаряды которых действительно достигают такой высоты перед взрывом. На практике сопротивлением воздуха нельзя полностью пренебречь, поэтому начальная скорость должна быть несколько больше заданной, чтобы достичь той же высоты.
(b) Как и во многих физических задачах, существует более одного способа решения для времени, когда снаряд достигает своей высшей точки. В этом случае проще всего использовать vy=v0y-gt.vy=v0y-gt. Поскольку vy=0vy=0 на вершине, это уравнение сводится к простому виду м/с9,80 м/с2=6,90 с.
Это время подходит и для больших фейерверков. Если вы можете увидеть запуск фейерверка, обратите внимание, что проходит несколько секунд, прежде чем снаряд взорвется. Другой способ найти время — использовать y=y0+12(v0y+vy)t.y=y0+12(v0y+vy)t. Это оставлено вам в качестве упражнения для выполнения.
(c) Поскольку сопротивлением воздуха можно пренебречь, ax=0ax=0, а горизонтальная скорость постоянна, как обсуждалось ранее. Горизонтальное смещение представляет собой произведение горизонтальной скорости на время по формуле x=x0+vxt,x=x0+vxt, где x0x0 равно нулю. Таким образом,
Горизонтальное смещение представляет собой произведение горизонтальной скорости на время по формуле x=x0+vxt,x=x0+vxt, где x0x0 равно нулю. Таким образом,
x=vxt,x=vxt,
, где vxvx — x -компонент скорости, которая определяется выражением
vx=v0cosθ=(70,0 м/с)cos75°=18,1 м/с .vx=v0cosθ=(70,0 м/с)cos75°=18,1 м/с.
Время t для обоих движений одинаково, поэтому x равно
x=(18,1 м/с)6,90 с=125 м.x=(18,1 м/с)6,90 с=125 м.
Горизонтальное движение с постоянной скоростью при отсутствии сопротивления воздуха. Найденное здесь горизонтальное смещение может быть полезно для предотвращения падения фрагментов фейерверка на зрителей. Когда снаряд взрывается, большое влияние оказывает сопротивление воздуха, и многие осколки приземляются прямо под ним.
(d) Горизонтальная и вертикальная составляющие смещения были только что рассчитаны, поэтому все, что здесь нужно, это найти величину и направление смещения в самой высокой точке: 9
|с→|=1252+2332=264м|с→|=1252+2332=264м
Φ=tan−1(233125)=61,8°.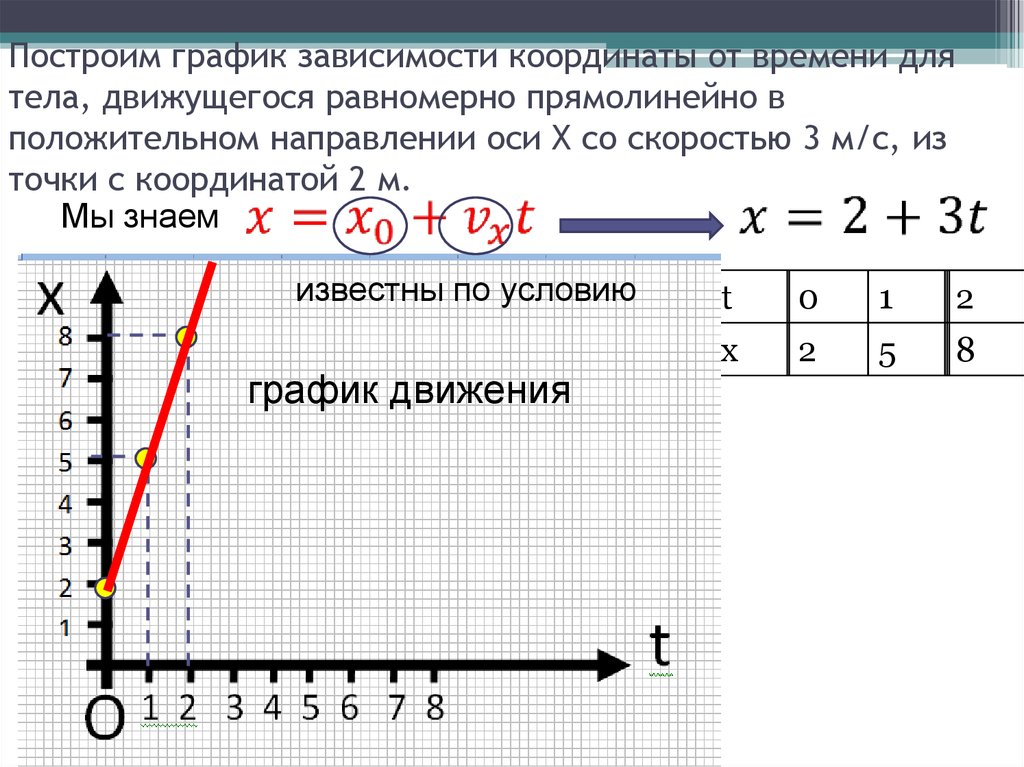 Φ=tan−1(233125)=61,8°.
Φ=tan−1(233125)=61,8°.
Обратите внимание, что угол вектора смещения меньше начального угла запуска. Чтобы понять, почему это так, просмотрите рисунок 4.11, на котором показана кривизна траектории по направлению к уровню земли.
При решении примера 4.7(а) выражение, которое мы нашли для y , справедливо для любого движения снаряда, когда сопротивлением воздуха можно пренебречь. Назовите максимальную высоту г = ч . Тогда
ч=v0y22g.h=v0y22g.
Это уравнение определяет максимальную высоту снаряда над точкой старта и зависит только от вертикальной составляющей начальной скорости.
Проверьте свое понимание 4.3
Камень брошен горизонтально со скалы высотой 100,0 м 100,0 м со скоростью 15,0 м/с. (a) Определите начало системы координат. б) Какое уравнение описывает горизонтальное движение? в) Какие уравнения описывают вертикальное движение? г) Какова скорость камня в момент удара?
Пример 4,8
Расчет движения снаряда: теннисист
Теннисист выиграл матч на стадионе имени Артура Эша и ударил мячом по трибунам со скоростью 30 м/с и под углом 45°45° над горизонтом (рис. 4.14). На пути вниз мяч ловится зрителем на высоте 10 м над точкой удара по мячу. а) Вычислите время, за которое теннисный мяч достигнет зрителя. б) Каковы модуль и направление скорости мяча в момент удара?
4.14). На пути вниз мяч ловится зрителем на высоте 10 м над точкой удара по мячу. а) Вычислите время, за которое теннисный мяч достигнет зрителя. б) Каковы модуль и направление скорости мяча в момент удара?
Рисунок 4.14 Траектория попадания теннисного мяча в трибуны.
Стратегия
Опять же, разложение этого двумерного движения на два независимых одномерных движения позволяет нам найти нужные величины. Время нахождения снаряда в воздухе определяется только его вертикальным движением. Таким образом, мы сначала решим для t . Пока мяч поднимается и падает вертикально, горизонтальное движение продолжается с постоянной скоростью. В этом примере запрашивается конечная скорость. Таким образом, мы рекомбинируем результаты по вертикали и горизонтали, чтобы получить v→v→ в последний момент времени t , определенные в первой части примера.
Раствор
(a) Пока мяч находится в воздухе, он поднимается, а затем падает в конечное положение на 10,0 м выше начальной высоты.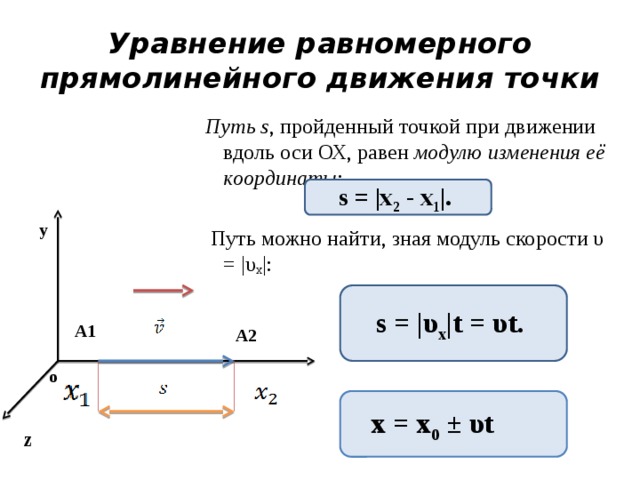 Мы можем найти время для этого, используя уравнение 4.22:
Мы можем найти время для этого, используя уравнение 4.22:
y=y0+v0yt−12gt2.y=y0+v0yt−12gt2.
Если принять начальное положение y0y0 равным нулю, то конечное положение будет y = 10 м. Начальная вертикальная скорость – это вертикальная составляющая начальной скорости:
v0y=v0sinθ0=(30,0 м/с)sin45°=21,2 м/с.v0y=v0sinθ0=(30,0 м/с)sin45°=21,2 м/с.
Подстановка в уравнение 4.22 вместо y дает нам
10,0 м=(21,2 м/с)t−(4,90 м/с2)t2,10,0 м=(21,2 м/с)t−(4,90 м/с2) т2.
Перестановка членов дает квадратное уравнение в t :
(4,90 м/с2)t2−(21,2 м/с)t+10,0 м=0,(4,90 м/с2)t2−(21,2 м/с) т+10,0м=0.
Использование квадратичной формулы дает t = 3,79 с и t = 0,54 с. Поскольку мяч находится на высоте 10 м два раза на протяжении своей траектории — один раз по пути вверх и один раз по пути вниз — мы принимаем более длинное решение для времени, которое требуется мячу, чтобы достичь зрителя:
t=3,79 с. t=3,79 с.
t=3,79 с.
Время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, имеющий начальную вертикальную скорость 21,2 м/с и приземлившийся на 10,0 м выше начальной высоты, находится в воздухе 3,79 с.
(б) Мы можем найти конечные горизонтальную и вертикальную скорости vxvx и vyvy, используя результат (а). Затем мы можем объединить их, чтобы найти модуль полного вектора скорости v→v→ и угол θθ, который он образует с горизонтом. Поскольку vxvx является постоянным, мы можем найти его в любом горизонтальном положении. Мы выбираем начальную точку, потому что знаем и начальную скорость, и начальный угол. Следовательно,
vx=v0cosθ0=(30 м/с)cos45°=21,2 м/с.vx=v0cosθ0=(30 м/с)cos45°=21,2 м/с.
Конечная вертикальная скорость определяется уравнением 4.21:
vy=v0y-gt.vy=v0y-gt.
Поскольку v0yv0y было найдено в части (a) равным 21,2 м/с, мы имеем
vy=21,2 м/с−9,8 м/с2(3,79 с)=−15,9 м/с.vy=21,2 м/с −9,8 м/с2(3,79 с)=−15,9 м/с.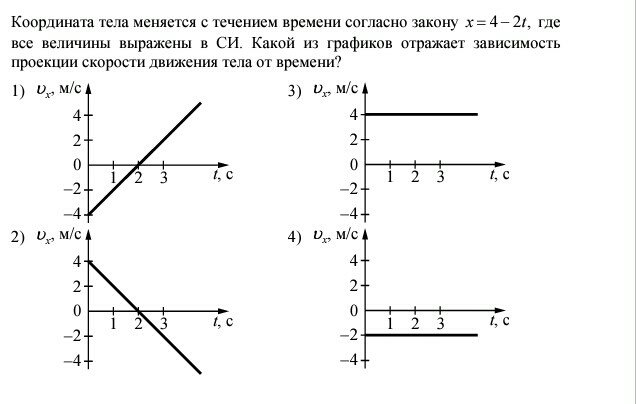
Величина конечной скорости v→v→ равна
v=vx2+vy2=(21,2м/с)2+(−15,9м/с)2=26,5м/с.v=vx2+vy2=(21,2м /с)2+(−15,9 м/с)2=26,5 м/с.
Направление θvθv находится с помощью арктангенса:
θv=tan-1(vyvx)=tan-1(-15,921,2)=36,9° ниже горизонта. θv=tan-1(vyvx)=tan-1(-15,921,2)=36,9° ниже горизонт.
Значение
(a) Как упоминалось ранее, время движения снаряда полностью определяется вертикальным движением. Таким образом, любой снаряд, имеющий начальную вертикальную скорость 21,2 м/с и приземлившийся на 10,0 м выше начальной высоты, находится в воздухе 3,79 с. (b) Отрицательный угол означает, что скорость на 36,9°36,9° ниже горизонтали в точке удара. Этот результат согласуется с тем фактом, что мяч ударяется в точку по другую сторону от вершины траектории и, следовательно, имеет отрицательное значение 9.0019 y составляющая скорости. Величина скорости меньше, чем величина начальной скорости, которую мы ожидаем, поскольку она воздействует на высоту 10,0 м над уровнем запуска.
Время полета, траектория и дальность
Интерес представляют время полета, траектория и дальность полета снаряда, запущенного на плоской горизонтальной поверхности и упавшего на эту же поверхность. В этом случае кинематические уравнения дают полезные выражения для этих величин, которые выводятся в следующих разделах.
Время полета
Мы можем определить время полета снаряда, который одновременно запускается и ударяется о плоскую горизонтальную поверхность, выполняя некоторые манипуляции с кинематическими уравнениями. Заметим, что положение и перемещение в y должны быть равны нулю при запуске и при ударе о ровную поверхность. Таким образом, приравняем смещение в y к нулю и найдем
y−y0=v0yt−12gt2=(v0sinθ0)t−12gt2=0.y−y0=v0yt−12gt2=(v0sinθ0)t−12gt2=0.
Факторинг, у нас
t(v0sinθ0−gt2)=0.t(v0sinθ0−gt2)=0.
Решение для t дает нам
Ttof=2(v0sinθ0)g. Ttof=2(v0sinθ0)g.
Ttof=2(v0sinθ0)g.
4,24
Это время полета снаряда, выпущенного с ударом о плоскую горизонтальную поверхность. Уравнение 4.24 неприменимо, когда снаряд приземляется на другой высоте, чем он был запущен, как мы видели в примере 4.8, где теннисист отбивает мяч в трибуны. Другое решение, t = 0, соответствует моменту запуска. Время полета линейно пропорционально начальной скорости в y направление и обратно пропорционально g . Таким образом, на Луне, где гравитация составляет одну шестую от земной, снаряд, запущенный с той же скоростью, что и на Земле, будет находиться в воздухе в шесть раз дольше.
Траектория
Траекторию снаряда можно найти, исключив переменную времени t из кинематических уравнений для произвольных t и решив y ( x ). Мы берем x0=y0=0x0=y0=0, поэтому снаряд запускается из начала координат. Кинематическое уравнение для х дает
Мы берем x0=y0=0x0=y0=0, поэтому снаряд запускается из начала координат. Кинематическое уравнение для х дает
х=v0xt⇒t=xv0x=xv0cosθ0.x=v0xt⇒t=xv0x=xv0cosθ0.
Подстановка выражения для t в уравнение для положения y=(v0sinθ0)t−12gt2y=(v0sinθ0)t−12gt2 дает
y=(v0sinθ0)(xv0cosθ0)−12g(xv0cosθ0)2.y=(v0sinθ0)(xv0cosθ0)−12g(xv0cosθ0)2.
Переставляем члены, имеем
y=(tanθ0)x−[g2(v0cosθ0)2]x2.y=(tanθ0)x−[g2(v0cosθ0)2]x2.
4,25
Это уравнение траектории имеет вид y=ax+bx2,y=ax+bx2, которое представляет собой уравнение параболы с коэффициентами
a=tanθ0,b=−g2(v0cosθ0)2.a=tanθ0,b=−g2(v0cosθ0)2.
Диапазон
Из уравнения траектории мы также можем найти дальность или горизонтальное расстояние, пройденное снарядом. Факторинг Уравнение 4.25, мы имеем
y=x[tanθ0−g2(v0cosθ0)2x].y=x[tanθ0−g2(v0cosθ0)2x].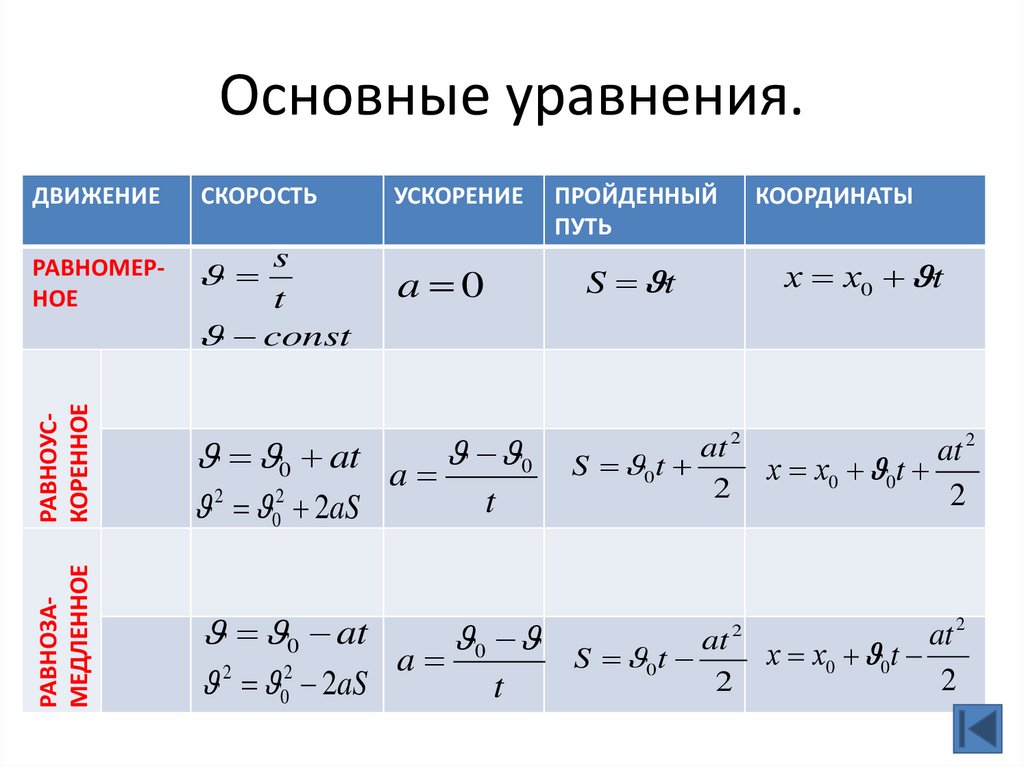
Позиция y равна нулю как для точки запуска, так и для точки удара, так как мы снова рассматриваем только плоскую горизонтальную поверхность. Установка y = 0 в этом уравнении дает решения х = 0, что соответствует точке запуска, и
х=2v02sinθ0cosθ0g,x=2v02sinθ0cosθ0g,
, соответствующий точке удара. Используя тригонометрическое тождество 2sinθcosθ=sin2θ2sinθcosθ=sin2θ и установив для диапазона x = R , мы находим
R=v02sin2θ0g.R=v02sin2θ0g.
4,26
Обратите внимание, что уравнение 4.26 справедливо только для запуска и удара о горизонтальную поверхность. Мы видим, что размах прямо пропорционален квадрату начальной скорости v0v0 и sin2θ0sin2θ0 и обратно пропорционален ускорению свободного падения. Таким образом, на Луне дальность была бы в шесть раз больше, чем на Земле, при той же начальной скорости. Кроме того, из коэффициента sin2θ0sin2θ0 мы видим, что диапазон максимален при 45°.45°. Эти результаты показаны на рис. 4.15. В (а) мы видим, что чем больше начальная скорость, тем больше радиус действия. На (b) мы видим, что диапазон максимален при 45°.45°. Это верно только для условий, в которых не учитывается сопротивление воздуха. Если учитывать сопротивление воздуха, максимальный угол несколько меньше. Интересно, что один и тот же диапазон найден для двух начальных углов запуска, которые в сумме составляют 90°.90°. Снаряд, запущенный с меньшим углом, имеет более низкую вершину, чем больший угол, но оба они имеют одинаковую дальность.
Кроме того, из коэффициента sin2θ0sin2θ0 мы видим, что диапазон максимален при 45°.45°. Эти результаты показаны на рис. 4.15. В (а) мы видим, что чем больше начальная скорость, тем больше радиус действия. На (b) мы видим, что диапазон максимален при 45°.45°. Это верно только для условий, в которых не учитывается сопротивление воздуха. Если учитывать сопротивление воздуха, максимальный угол несколько меньше. Интересно, что один и тот же диапазон найден для двух начальных углов запуска, которые в сумме составляют 90°.90°. Снаряд, запущенный с меньшим углом, имеет более низкую вершину, чем больший угол, но оба они имеют одинаковую дальность.
Рисунок
4.15
Траектории снарядов на ровной местности. (а) Чем больше начальная скорость v0,v0, тем больше диапазон для данного начального угла. (б) Влияние начального угла θ0θ0 на дальность полета снаряда с заданной начальной скоростью. Обратите внимание, что диапазон одинаковый для начальных углов 15°15° и 75°,75°, хотя максимальная высота этих путей различна.
Пример 4.9
Сравнение ударов по гольфу
Игрок в гольф оказывается в двух разных ситуациях на разных лунках. На второй лунке он находится в 120 м от грина и хочет отбить мяч на 90 м и дать ему вылететь на грин. Он направляет удар низко к земле под углом 30 ° 30 ° к горизонтали, чтобы мяч мог катиться после удара. На четвертой лунке он находится в 90 м от грина и хочет, чтобы мяч упал с минимальным количеством качения после удара. Здесь он направляет выстрел под углом 70°70° к горизонтали, чтобы свести к минимуму качение после удара. Оба выстрела попали в ровную поверхность.
а) Какова начальная скорость мяча у второй лунки?
(б) Какова начальная скорость мяча у четвертой лунки?
(c) Напишите уравнение траектории для обоих случаев.
(d) Нарисуйте траектории.
Стратегия
Мы видим, что уравнение дальности имеет начальную скорость и угол, поэтому мы можем найти начальную скорость как для (а), так и для (б).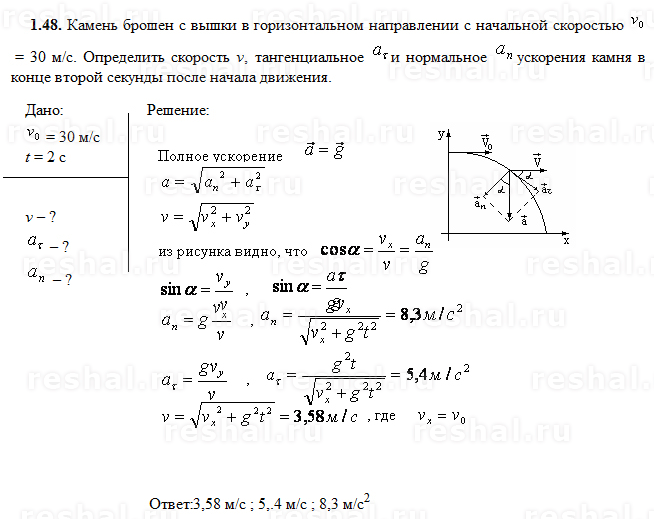 Когда у нас есть начальная скорость, мы можем использовать это значение для записи уравнения траектории.
Когда у нас есть начальная скорость, мы можем использовать это значение для записи уравнения траектории.
Раствор
(а) R=v02sin2θ0g⇒v0=Rgsin2θ0=90,0 м(9,8 м/с2)sin(2(30°))=31,9 м/сR=v02sin2θ0g⇒v0=Rgsin2θ0=90,0 м(9,8 м/с2)sin(2(30° ))=31,9 м/с
(б) R=v02sin2θ0g⇒v0=Rgsin2θ0=90,0 м(9,8 м/с2)sin(2(70°))=37,0 м/сR=v02sin2θ0g⇒v0=Rgsin2θ0=90,0 м(9,8 м/с2)sin(2(70° ))=37,0 м/с
(c)
y=x[tanθ0−g2(v0cosθ0)2x]Второе отверстие: y=x[tan30°−9,8 м/с22[(31,9 м/с)(cos30°) ]2x]=0,58x−0,0064×2Четвертое отверстие:y=x[tan70°−9,8 м/с22[(37,0 м/с)(cos70°)]2x]=2,75x−0,0306x2y=x[tanθ0−g2(v0cosθ0 )2x]Второе отверстие:y=x[tan30°−90,8 м/с22[(31,9 м/с)(cos30°)]2x]=0,58x−0,0064×2Четвертое отверстие:y=x[tan70°−9,8 м/с22[(37,0 м/с)(cos70°)]2x ]=2,75x−0,0306×2
(d) Используя графическую утилиту, мы можем сравнить две траектории, показанные на рис. 4.16.
Рисунок
4.16
Две траектории мяча для гольфа с дальностью 90 м. Точки удара обоих находятся на том же уровне, что и точка запуска.
Точки удара обоих находятся на том же уровне, что и точка запуска.
Значение
Начальная скорость выстрела под углом 70°70° больше, чем начальная скорость выстрела под углом 30°.30°. Обратите внимание на рис. 4.16, что если бы два снаряда были запущены с одинаковой скоростью, но под разными углами, снаряды имели бы одинаковую дальность, пока углы были бы меньше 90°.90°. Углы запуска в этом примере складываются, чтобы получить число больше 90°,90°. Таким образом, выстрел под углом 70°70° должен иметь большую стартовую скорость, чтобы достичь 90 м, иначе он попадет на более короткое расстояние.
Проверьте свое понимание 4.4
Если бы два удара для гольфа в примере 4.9 были произведены с одинаковой скоростью, какой удар имел бы наибольшую дальность?
Когда мы говорим о дальности полета снаряда на ровной поверхности, мы предполагаем, что R очень мала по сравнению с окружностью Земли.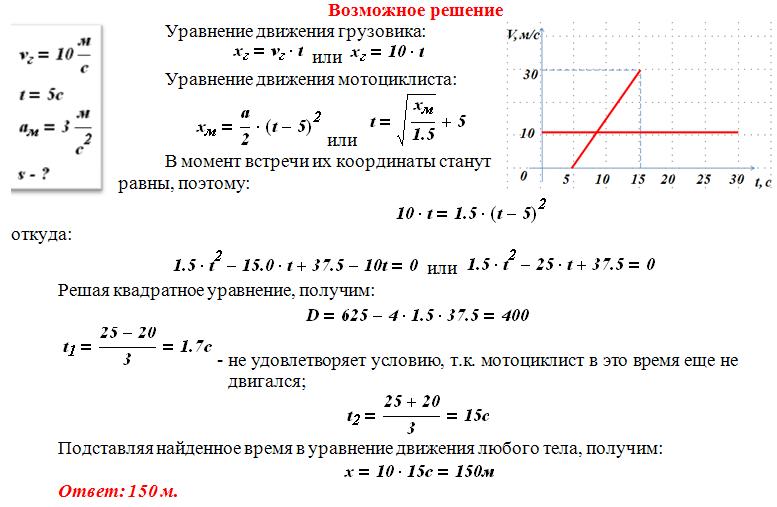 Однако, если диапазон большой, Земля изгибается ниже снаряда, и ускорение, возникающее в результате силы тяжести, меняет направление вдоль траектории. Дальность больше, чем предсказывается уравнением дальности, приведенным ранее, потому что снаряд должен упасть дальше, чем на ровной поверхности, как показано на рис. 4.17, основанном на рисунке Ньютона.0019 Принципы. Если начальная скорость достаточно велика, снаряд выходит на орбиту. Поверхность Земли опускается на 5 м каждые 8000 м. За 1 с тело без сопротивления воздуха падает с высоты 5 м. Таким образом, если объекту придать горизонтальную скорость 8000 м/с (или 18 000 миль/ч) вблизи поверхности Земли, он выйдет на орбиту вокруг планеты, потому что поверхность непрерывно отклоняется от объекта. Это примерно скорость космического корабля «Шаттл» на низкой околоземной орбите, когда он работал, или любого спутника на низкой околоземной орбите. Эти и другие аспекты орбитального движения, такие как вращение Земли, более подробно рассматриваются в «Гравитации».
Однако, если диапазон большой, Земля изгибается ниже снаряда, и ускорение, возникающее в результате силы тяжести, меняет направление вдоль траектории. Дальность больше, чем предсказывается уравнением дальности, приведенным ранее, потому что снаряд должен упасть дальше, чем на ровной поверхности, как показано на рис. 4.17, основанном на рисунке Ньютона.0019 Принципы. Если начальная скорость достаточно велика, снаряд выходит на орбиту. Поверхность Земли опускается на 5 м каждые 8000 м. За 1 с тело без сопротивления воздуха падает с высоты 5 м. Таким образом, если объекту придать горизонтальную скорость 8000 м/с (или 18 000 миль/ч) вблизи поверхности Земли, он выйдет на орбиту вокруг планеты, потому что поверхность непрерывно отклоняется от объекта. Это примерно скорость космического корабля «Шаттл» на низкой околоземной орбите, когда он работал, или любого спутника на низкой околоземной орбите. Эти и другие аспекты орбитального движения, такие как вращение Земли, более подробно рассматриваются в «Гравитации».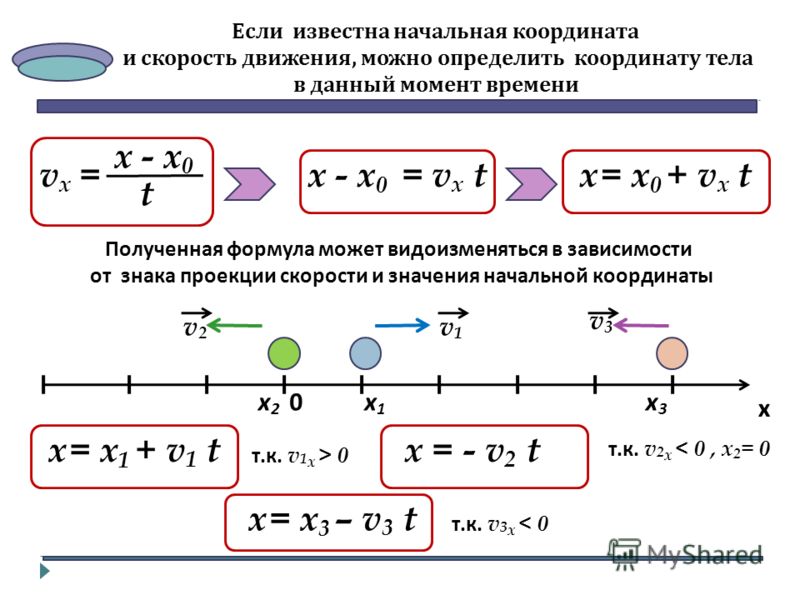
Рисунок 4.17 Снаряд к спутнику. В каждом показанном здесь случае снаряд запускается с очень высокой башни, чтобы избежать сопротивления воздуха. С увеличением начальной скорости диапазон увеличивается и становится длиннее, чем он был бы на ровной поверхности, потому что Земля изгибается под его траекторией. При скорости 8000 м/с достигается орбита.
4.1 Векторы смещения и скорости
Цели обучения
К концу этого раздела вы сможете:
- Расчет векторов положения в многомерной задаче смещения.
- Решите для смещения в двух или трех измерениях.
- Вычислить вектор скорости по заданному вектору положения как функцию времени.
- Вычислить среднюю скорость в нескольких измерениях.
Перемещение и скорость в двух или трех измерениях являются прямым расширением одномерных определений. Однако теперь они являются векторными величинами, поэтому вычисления с ними должны следовать правилам векторной алгебры, а не скалярной алгебры.
Вектор смещения
Чтобы описать движение в двух и трех измерениях, мы должны сначала установить систему координат и соглашение для осей. Обычно мы используем координаты x , y и z , чтобы найти частицу в точке P ( x , y , z ) в трех измерениях. Если частица движется, переменные x , y и z являются функциями времени ( t ):
[латекс] x=x(t)\quad y=y(t)\quad z=z(t). [/latex]
Вектор положения от начала системы координат до точки P равен [латекс] \overset{\to}{r}(t). [/latex] В записи единичного вектора, представленной в книге «Системы координат и компоненты вектора», [латекс] \overset{\to }{r}(t) [/latex] равно
[латекс] \overset{\to} {r}(t)=x(t)\шляпа{i}+y(t)\шляпа{j}+z(t)\шляпа{k}. [/latex]
(рисунок) показывает систему координат и вектор к точке P , где частица может находиться в определенное время t . Обратите внимание на ориентацию осей x , y и z . Эта ориентация называется правой системой координат (Системы координат и компоненты вектора) и используется на протяжении всей главы.
Обратите внимание на ориентацию осей x , y и z . Эта ориентация называется правой системой координат (Системы координат и компоненты вектора) и используется на протяжении всей главы.
Рисунок 4.2 Трехмерная система координат с частицей в положении P(x(t), y(t), z(t)).
С нашим определением положения частицы в трехмерном пространстве мы можем сформулировать трехмерное смещение. (Рисунок) показывает частицу в момент времени [латекс] {t}_{1} [/латекс], расположенную в [латекс] {P}_{1} [/латекс] с вектором положения [латекс] \overset{\to } {г}({т}_{1}). [/latex] В более позднее время [latex] {t}_{2}, [/latex] частица находится в [latex] {P}_{2} [/latex] с вектором положения [latex] \overset {\ to} {r} ({t} _ {2}) [/ латекс]. вектор смещения [латекс] \text{Δ}\overset{\to }{r} [/latex] находится путем вычитания [латекс] \overset{\to }{r}({t}_{1}) [/латекс] из [латекс] \overset{\to }{r}({t}_{2})\text{ }: [/latex]
[латекс] \text{Δ}\overset{\to {r} = \ overset {\ to {r} ({t} _ {2}) — \ overset {\ to {r} ({t} _ {1}). [/latex]
[/latex]
Добавление вектора обсуждается в разделе Векторы. Обратите внимание, что это та же самая операция, которую мы проделали в одном измерении, но теперь векторы находятся в трехмерном пространстве.
Рисунок 4.3 Смещение [латекс] \text{Δ}\overset{\to }{r}=\overset{\to }{r}({t}_{2})-\overset{\to }{r}( {t}_{1}) [/latex] — это вектор из [latex] {P}_{1} [/latex] в [latex] {P}_{2} [/latex].
Следующие примеры иллюстрируют концепцию смещения в нескольких измерениях.
Пример
Спутник на полярной орбите
Спутник находится на круговой полярной орбите вокруг Земли на высоте 400 км, т. е. проходит прямо над головой на Северном и Южном полюсах. Каковы величина и направление вектора смещения от момента, когда он находится прямо над Северным полюсом, до момента, когда он находится на широте [latex] -45\text{°} [/latex]?
Стратегия
Мы создаем картину проблемы, чтобы визуализировать решение графически. Это поможет нам понять смещение. Затем мы используем единичные векторы для решения смещения.
Затем мы используем единичные векторы для решения смещения.
Решение
Показать ответ
В представлении единичного вектора векторы положения равны
[латекс] \begin{array}{cc} \overset{\to }{r}({t}_{1})=6770.\,\text{ км}\шляпа{j}\hfill\\\overset{\to }{r}({t}_{2})=6770.\,\text{км}\,(\text{cos}\,45 \text{°})\шляпа{i}+6770.\,\text{км}\,(\text{sin}(-45\text{°}))\шляпа{j}.\end{массив} [/латекс]
Вычисляя синус и косинус, мы имеем
[латекс] \begin{array}{cc} \hfill \overset{\to }{r}({t}_{1})& =\hfill & 6770. \шляпа{j}\hfill \\ \hfill \overset{\to }{r}({t}_{2})& =\hfill & 4787\шляпа{i}-4787\шляпа{j}.\hfill \end{array} [/latex]
Теперь мы можем найти [latex] \text{Δ}\overset{\to }{r} [/latex], смещение спутника:
[latex] \text {Δ} \ overset {\ to {r} = \ overset {\ to {r} ({t} _ {2}) — \ overset {\ to {r} ({t} _ {1}) = 4787 \ шляпа {i} — 11 557 \ шляпа {j}. [/латекс] 9{-1}(\frac{-11 557}{4787})=-67,5\text{°}. [/latex]
[/latex]
Значимость
Построение графика смещения дает информацию и значение для решения задачи в виде единичного вектора. При построении графика смещения нам необходимо включить его компоненты, а также его величину и угол, который он образует с выбранной осью — в данном случае с осью x ((Рисунок)).
Рисунок 4.5 Вектор смещения с компонентами, углом и величиной.
Обратите внимание, что в этом примере спутник прошел криволинейный путь вдоль своей круговой орбиты, чтобы добраться из начального положения в конечное. Он также мог пройти 4787 км на восток, затем 11 557 км на юг, чтобы достичь того же места. Оба этих пути длиннее, чем длина вектора смещения. Фактически вектор смещения задает кратчайший путь между двумя точками в одном, двух или трех измерениях.
Многие приложения в физике могут иметь серию перемещений, как обсуждалось в предыдущей главе. Общее смещение — это сумма индивидуальных смещений, только на этот раз нам нужно быть осторожными, потому что мы добавляем векторы. Проиллюстрируем это понятие на примере броуновского движения.
Проиллюстрируем это понятие на примере броуновского движения.
Пример
Броуновское движение
Броуновское движение — хаотическое беспорядочное движение взвешенных в жидкости частиц, возникающее в результате столкновений с молекулами жидкости. Это движение трехмерно. Смещения в числовом порядке частицы, совершающей броуновское движение, могут выглядеть следующим образом в микрометрах ((рисунок)):
[латекс] \begin{array}{cc} \hfill \text{Δ}{\overset{\to }{r}}_{1}& =\hfill & 2.0\шляпа{i}+\шляпа{ j} +3,0 \ шляпа {k} \ hfill \\ \ hfill \ text {Δ} {\ overset {\ to {r}} _ {2} & = \ hfill & \ text {−} \ hat {i} +3,0 \ шляпа {k} \ hfill \\ \ hfill \ text {Δ} {\ overset {\ to {r}} _ {3} & = \ hfill & 4,0 \ hat {i} -2,0 \ hat {j }+\шляпа{k}\hfill \\ \hfill \text{Δ}{\overset{\to}}{r}}_{4}& =\hfill & -3.0\шляпа{i}+\шляпа{j }+2.0\hat{k}.\hfill \end{array} [/latex]
Каково полное смещение частицы от начала координат?
Рис. 4.6 Траектория частицы, совершающей случайные смещения броуновского движения. Общее смещение показано красным.
4.6 Траектория частицы, совершающей случайные смещения броуновского движения. Общее смещение показано красным.
Решение
Показать ответ
Значение
Из рисунка видно, что величина полного смещения меньше суммы величин отдельных перемещений.
Вектор скорости
В предыдущей главе мы нашли мгновенную скорость, вычислив производную функции положения по времени. Мы можем сделать ту же операцию в двух и трех измерениях, но мы используем векторы. Мгновенное вектор скорости теперь равен
[латекс] \overset{\to }{v}(t)=\underset{\text{Δ}t\to 0}{\text{lim}}\frac{\overset{ \ to {r} (t + \ text {Δ} t) — \ overset {\ to {r} (t)} {\ text {Δ} t} = \ frac {d \ overset {\ to} {r }}{дт}. [/latex]
Давайте посмотрим на относительную ориентацию вектора положения и вектора скорости графически. На (рис.) показаны векторы [латекс] \overset{\to }{r}(t) [/latex] и [латекс] \overset{\to }{r}(t+\text{Δ}t), [/latex], которые дают положение частицы, движущейся по пути, представленному серой линией.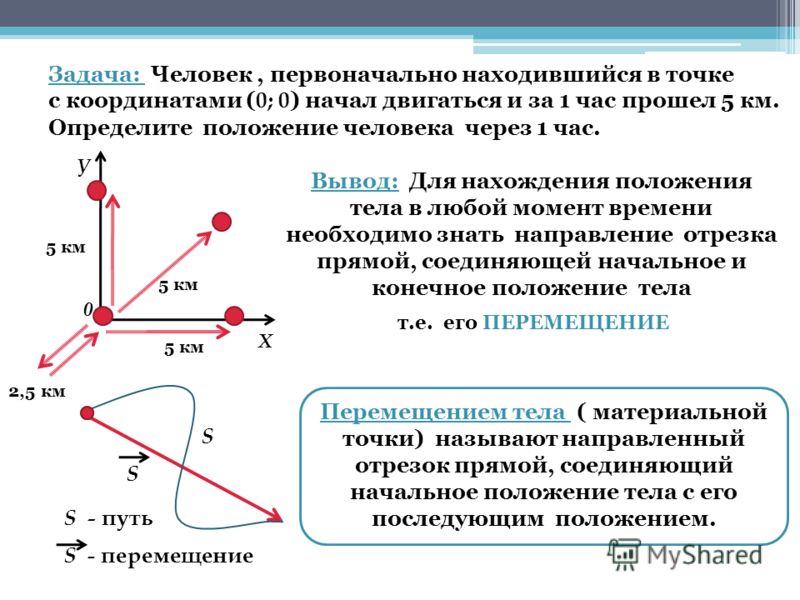 Когда [latex] \text{Δ}t [/latex] стремится к нулю, вектор скорости, заданный (рис.), становится касательным к пути частицы в момент времени т .
Когда [latex] \text{Δ}t [/latex] стремится к нулю, вектор скорости, заданный (рис.), становится касательным к пути частицы в момент времени т .
Рис. 4.7 Частица движется по пути, обозначенному серой линией. В пределе, когда [latex] \text{Δ}t [/latex] стремится к нулю, вектор скорости становится касательным к пути частицы.
(уравнение) также можно записать в терминах компонентов [латекс] \overset{\to }{v}(t). [/латекс] Так как
[латекс] \overset{\to}}{r}(t)=x(t)\шляпа{i}+y(t)\шляпа{j}+z(t)\шляпа{ k}, [/latex]
мы можем написать
[латекс] \overset{\to }{v}(t)={v}_{x}(t)\hat{i}+{v}_ {y}(t)\шляпа{j}+{v}_{z}(t)\шляпа{k} [/латекс]
, где
[латекс] {v}_{x}(t)=\frac{dx(t)}{dt},\quad {v}_{y}(t)=\frac{dy(t) )}{dt},\quad {v}_{z}(t)=\frac{dz(t)}{dt}. [/latex]
Если речь идет только о средней скорости, мы имеем векторный эквивалент одномерной средней скорости для двух и трех измерений:
[латекс] {\overset{\to}}{v}}_ {\ text {среднее}} = \ frac {\ overset {\ to {r} ({t} _ {2}) — \ overset {\ to {r} ({t} _ {1})} { {т}_{2}-{т}_{1}}. [/latex]
[/latex]
Пример
Расчет вектора скорости 9{2}\шляпа{i}+(2,0+3,0t)\шляпа{j}+5,0t\шляпа{k}\текст{m}. [/latex] (а) Чему равны мгновенная скорость и скорость
t = 2,0 с? б) Какова средняя скорость между 1,0 и 3,0 с?Решение
Используя (Рисунок) и (Рисунок) и взяв производную функции положения по времени, находим
Показать ответ
(b) От (Рисунок),
Показать ответ
Значимость
Мы видим, что средняя скорость такая же, как мгновенная скорость в 9{3}\шляпа{i}+4.0\шляпа{j}. [/latex] (а) Чему равна мгновенная скорость t = 3 с? (b) Равна ли средняя скорость между 2 и 4 с мгновенной скорости в t = 3 с?
Показать решение
Независимость перпендикулярных движений
Когда мы смотрим на трехмерные уравнения для положения и скорости, записанные в виде единичного вектора (Рисунок) и (Рисунок), мы видим, что компоненты этих уравнений являются отдельными и уникальными функциями времени которые не зависят друг от друга.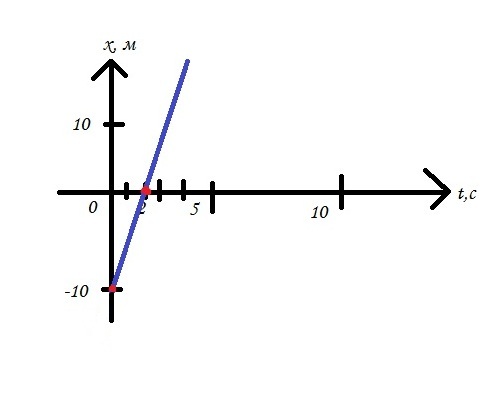 Движение по 9Направление 0473 x не имеет части своего движения по направлениям y и z , и аналогично для двух других осей координат. Таким образом, движение объекта в двух или трех измерениях можно разделить на отдельные независимые движения вдоль перпендикулярных осей той системы координат, в которой происходит движение.
Движение по 9Направление 0473 x не имеет части своего движения по направлениям y и z , и аналогично для двух других осей координат. Таким образом, движение объекта в двух или трех измерениях можно разделить на отдельные независимые движения вдоль перпендикулярных осей той системы координат, в которой происходит движение.
Чтобы проиллюстрировать эту концепцию относительно смещения, рассмотрим женщину, идущую от точки A до точки B в городе с квадратными кварталами. Женщина, идущая по пути из A — B может пройти столько-то блоков на восток, а затем на север (два перпендикулярных направления) еще один набор блоков, чтобы достичь B . Насколько далеко она пойдет на восток, зависит только от ее движения на восток. Точно так же на то, как далеко она пойдет на север, влияет только ее движение на север.
Независимость движения
В кинематическом описании движения мы можем рассматривать горизонтальную и вертикальную составляющие движения отдельно. Во многих случаях движение в горизонтальном направлении не влияет на движение в вертикальном направлении, и наоборот.
Во многих случаях движение в горизонтальном направлении не влияет на движение в вертикальном направлении, и наоборот.
Примером, иллюстрирующим независимость вертикального и горизонтального движений, являются два бейсбольных мяча. Один бейсбольный мяч выпадает из состояния покоя. В тот же момент с той же высоты горизонтально брошен другой снаряд, летящий по криволинейной траектории. Стробоскоп фиксирует положение шаров через фиксированные промежутки времени по мере их падения ((Рисунок)).
Рис. 4.8 Схема движения двух одинаковых шаров: один падает из состояния покоя, а другой имеет начальную горизонтальную скорость. Каждая последующая позиция представляет собой равный интервал времени. Стрелки представляют горизонтальную и вертикальную скорости в каждой позиции. Мяч справа имеет начальную горизонтальную скорость, тогда как мяч слева не имеет горизонтальной скорости. Несмотря на разницу в горизонтальных скоростях, вертикальные скорости и положения обоих шаров одинаковы, что показывает, что вертикальное и горизонтальное движения независимы.
Примечательно, что при каждой вспышке стробоскопа вертикальное положение двух шаров одинаково. Это сходство подразумевает, что вертикальное движение не зависит от того, движется ли мяч горизонтально. (Если предположить отсутствие сопротивления воздуха, вертикальное движение падающего объекта зависит только от силы тяжести, а не от каких-либо горизонтальных сил.) Тщательное изучение мяча, брошенного горизонтально, показывает, что он проходит такое же расстояние по горизонтали между вспышками. Это связано с тем, что после броска на мяч в горизонтальном направлении не действуют дополнительные силы. Этот результат означает, что горизонтальная скорость постоянна и не зависит ни от вертикального движения, ни от гравитации (которая является вертикальной). Обратите внимание, что этот случай верен только для идеальных условий. В реальном мире сопротивление воздуха влияет на скорость мячей в обоих направлениях.
Двумерная кривая траектория горизонтально брошенного мяча состоит из двух независимых одномерных движений (горизонтального и вертикального). Ключ к анализу такого движения, называемого движением снаряда , состоит в том, чтобы разложить его на движения вдоль перпендикулярных направлений. Разложение двумерного движения на перпендикулярные компоненты возможно, поскольку компоненты независимы.
Ключ к анализу такого движения, называемого движением снаряда , состоит в том, чтобы разложить его на движения вдоль перпендикулярных направлений. Разложение двумерного движения на перпендикулярные компоненты возможно, поскольку компоненты независимы.
Резюме
- Функция положения [латекс] \overset{\to }{r}(t) [/латекс] дает положение как функцию времени частицы, движущейся в двух или трех измерениях. Графически это вектор от начала выбранной системы координат до точки, в которой находится частица в определенное время.
- Вектор смещения [латекс] \text{Δ}\overset{\to }{r} [/латекс] дает кратчайшее расстояние между любыми двумя точками на траектории частицы в двух или трех измерениях.
- Мгновенная скорость дает скорость и направление движения частицы в определенный момент времени на ее траектории в двух или трех измерениях и представляет собой вектор в двух и трех измерениях.
- Вектор скорости касается траектории частицы.
- Перемещение [латекс] \overset{\to }{r}(t) [/latex] можно представить в виде векторной суммы одномерных перемещений [латекс] \overset{\to }{x}(t), \overset{\to}{y}(t),\overset{\to}{z}(t) [/latex] вдоль x , y и z направлений.

- Скорость [латекс] \overset{\to }{v}(t) [/латекс] может быть записана как векторная сумма одномерных скоростей [латекс] {v}_{x}(t),{v }_{y}(t),{v}_{z}(t) [/latex] вдоль направлений x , y и z .
- Движение в любом заданном направлении не зависит от движения в перпендикулярном направлении.
Концептуальные вопросы
Какую форму имеет траектория частицы, если расстояние от любой точки A до точки B равно величине смещения от A до B ?
Показать решение
Приведите пример траектории в двух или трех измерениях, вызванной независимыми перпендикулярными движениями.
Если мгновенная скорость равна нулю, что можно сказать о наклоне функции положения?
Показать решение
Задачи
Координаты частицы в прямоугольной системе координат (1.0, –4.0, 6.0). Каков вектор положения частицы?
Показать решение
Положение частицы меняется с [латекс] {\overset{\to }{r}}_{1}=(2. 0\text{}\шляпа{i}+3.0\шляпа{j})\текст {см} [/ латекс] до [латекс] {\ overset {\ to} {r}} _ {2} = (-4,0 \ шляпа {i} + 3,0 \ шляпа {j}) \, \ текст {см} . [/latex] Каково смещение частицы?
0\text{}\шляпа{i}+3.0\шляпа{j})\текст {см} [/ латекс] до [латекс] {\ overset {\ to} {r}} _ {2} = (-4,0 \ шляпа {i} + 3,0 \ шляпа {j}) \, \ текст {см} . [/latex] Каково смещение частицы?
18-я лунка на поле для гольфа Pebble Beach представляет собой изгиб влево длиной 496,0 м. Фарватер от ти принимается за направление x . Игрок в гольф наносит удар с ти с расстояния 300,0 м, что соответствует смещению [латекс] \text{Δ}{\overset{\to }{r}}_{1}=300,0\,\text{m}\hat {i}, [/latex] и наносит второй удар 189.0 м при водоизмещении [латекс] \text{Δ}{\overset{\to }{r}}_{2}=172,0\,\text{м}\шляпа{i}+80,3\,\text{ м}\шляпа{j}. [/latex] Каково окончательное смещение мяча для гольфа с площадки-ти?
Показать решение
Птица летит прямо на северо-восток на расстояние 95,0 км за 3,0 часа. С осью x строго на восток и осью y строго на север, каково смещение в представлении единичного вектора для птицы? Какова средняя скорость в пути?
Велосипедист проезжает 5,0 км строго на восток, затем 10,0 км [латекс] 20\text{°} [/латекс] западнее севера.


 Посмотреть на величины, входящие в эти формулы: определить, какие из них даны в условии, а какие нужно дополнительно выразить. При необходимости перевести величины в СИ.
Посмотреть на величины, входящие в эти формулы: определить, какие из них даны в условии, а какие нужно дополнительно выразить. При необходимости перевести величины в СИ.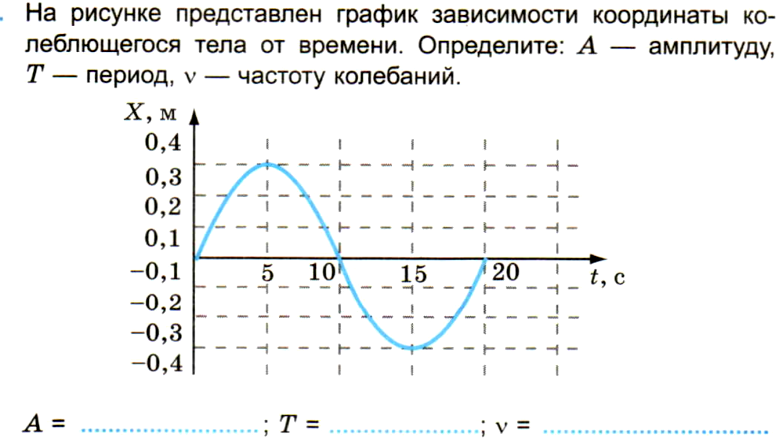
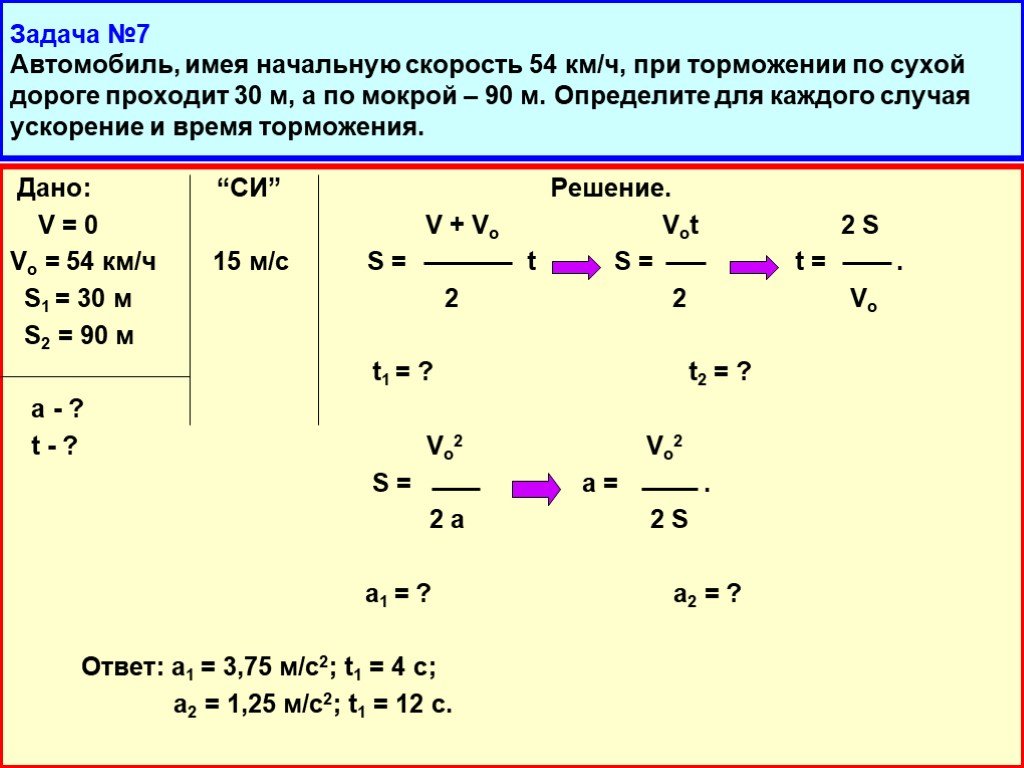 Определить угловую и линейную скорости точки на ободе шкива, период вращения шкива.
Определить угловую и линейную скорости точки на ободе шкива, период вращения шкива. 12.
12.
Leave A Comment