Скорость материальной точки.
| Пусть при движении
по криволинейной траектории материальная
точка в некоторый момент времени t1 занимала
положение A с
радиус-вектором |
Средней векторной скоростью материальной точки называют отношение приращения радиус-вектора точки к тому промежутку времени, за которые это приращение произошло:
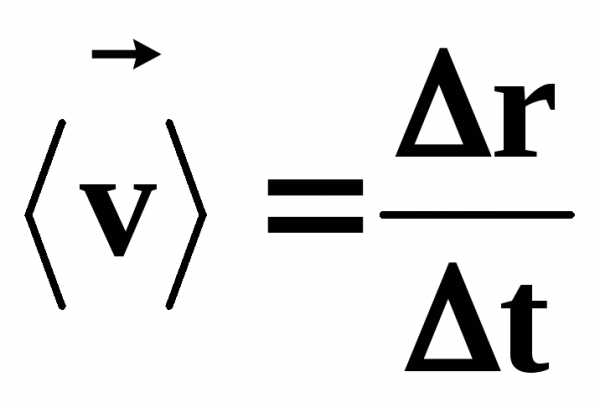 (1)
(1)
Средняя путевая скорость:
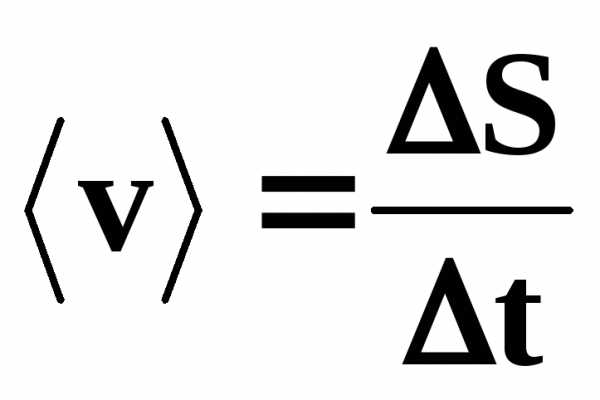
В Международной системе (СИ) единицей расстояния является метр, единицей времени – секунда, поэтому скорость выражается в метрах в секунду:
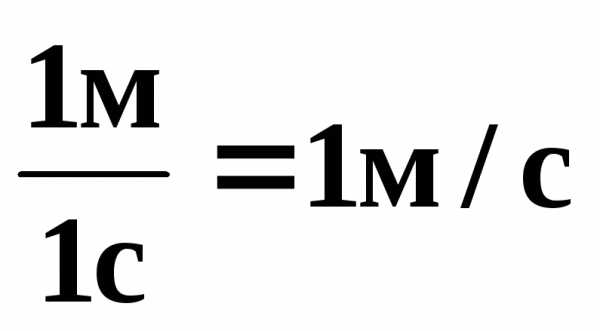
Если 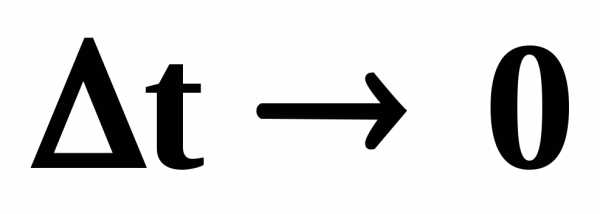 ,
то отношение
,
то отношение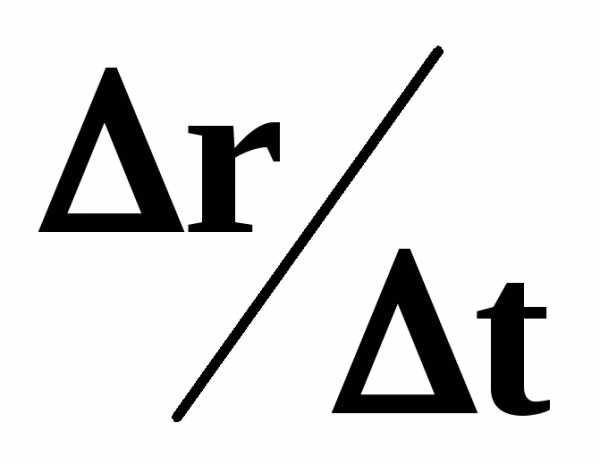 стремится к некоторому пределу,
называемому скоростью материальной
точки в момент времениt или мгновенной скоростью
стремится к некоторому пределу,
называемому скоростью материальной
точки в момент времениt или мгновенной скоростью  :
:
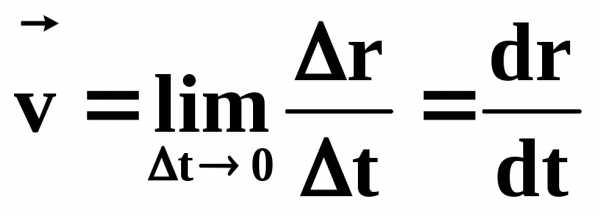
Мгновенной
скоростью точки называют вектор, численно равный
первой производной по времени от
радиус-вектора, определяющего положение
этой точки в данный момент времени.
Вектор  направлен по касательной к траектории
в этой точке, т.е.:
направлен по касательной к траектории
в этой точке, т.е.:
(3)
 — единичный вектор
касательной к траектории в данной точке;
— единичный вектор
касательной к траектории в данной точке;
.
Движение с постоянной по модулю и направлению скоростью называется прямолинейным равномерным движением.
При прямолинейном движении (по модулю):
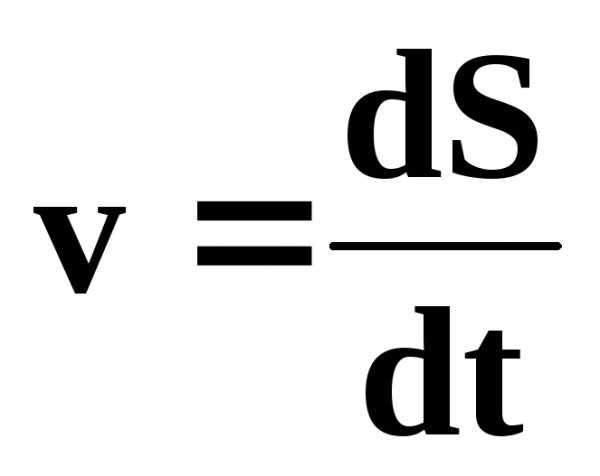
В реальных условиях движение любого тела никогда не бывает строго равномерным и прямолинейным. Движение, при котором тело за равные промежутки времени совершает неодинаковые перемещения, называют
Ускорение материальной точки.
Ускорение  характеризует быстроту изменения
скорости и по направлению и по величине.
характеризует быстроту изменения
скорости и по направлению и по величине.
Средним ускорением точки называют вектор, равный отношению приращения скорости к тому промежутку времени, за который это приращение произошло:
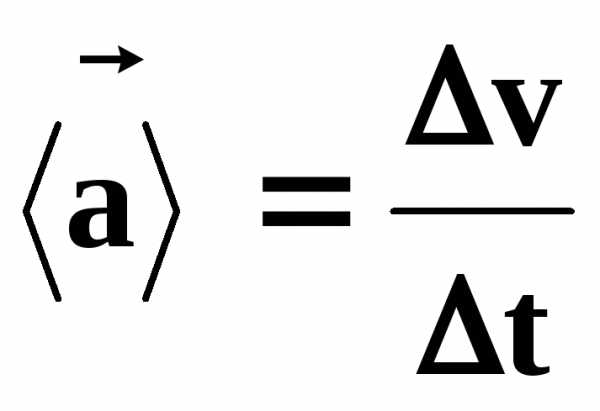 (4)
(4)
Вектор
(5)
— называется мгновенным ускорением точки или ускорением в данный момент времени.
Без учета направления:
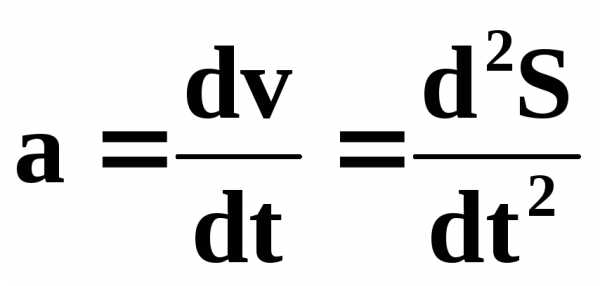 .
.
Тангенциальное и нормальное ускорение.
При криволинейном
движении происходит изменение скорости,
как по величине, так и по направлению.
Принимая во внимание, что 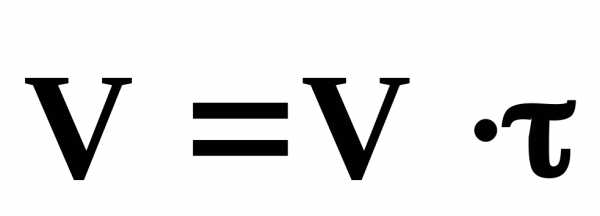 ,
представим
,
представим в виде суммы двух векторов:
в виде суммы двух векторов:
(6)
Первое слагаемое характеризует изменение скорости по величине и называется тангенциальным ускорением:
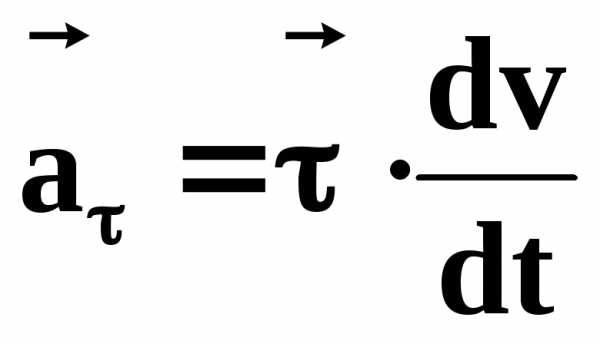 (7)
(7)
Численное значение
тангенциального ускорения равно 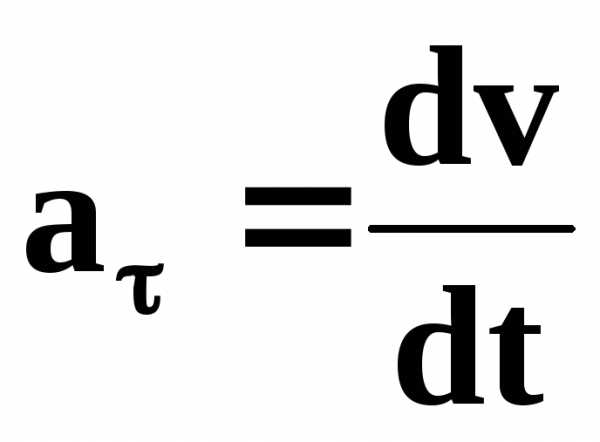 ,
а направление совпадает с направлением
касательной к траектории движения.
,
а направление совпадает с направлением
касательной к траектории движения.
Второе слагаемое
характеризует изменение скорости по
направлению и называется
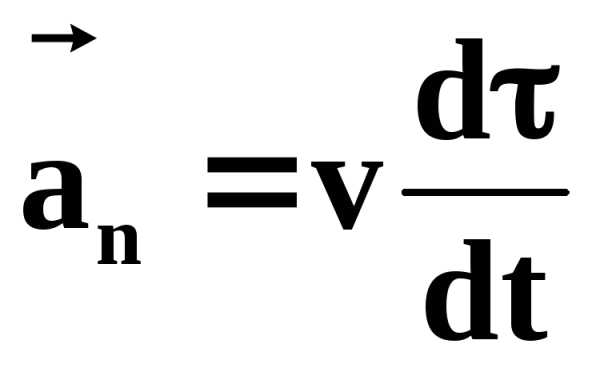 (8)
(8)
Численное значение нормального ускорения равно:
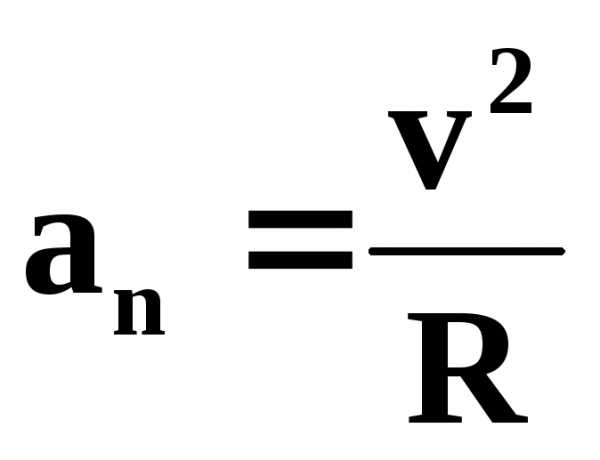 (9)
(9)
R – радиус
кривизны траектории в точке, где
определяется ускорение. Направление
совпадает с нормалью 
Разложение
ускорения на тангенциальное и нормальное
поясним рисунком. Представим вектор  в виде суммы двух векторов, для чего
вдоль направления
в виде суммы двух векторов, для чего
вдоль направления отложим длинуAL вектора
отложим длинуAL вектора  и соединим точкиD и L.
Из рисунка видно, что
,
причем вектор
и соединим точкиD и L.
Из рисунка видно, что
,
причем вектор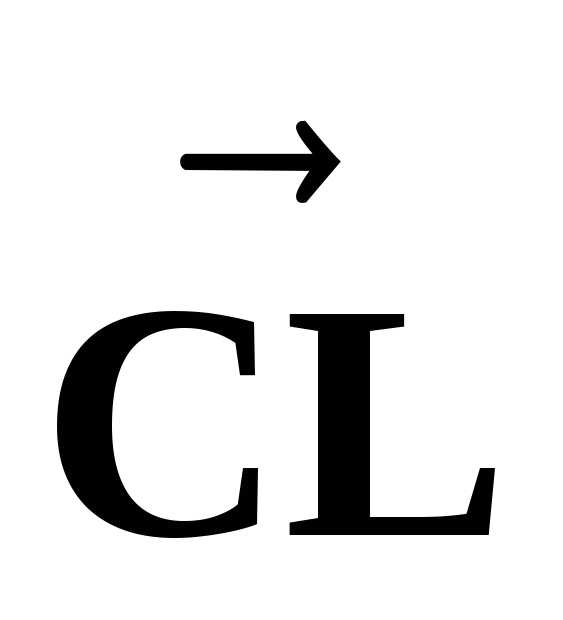 дает изменение скорости по величине
дает изменение скорости по величине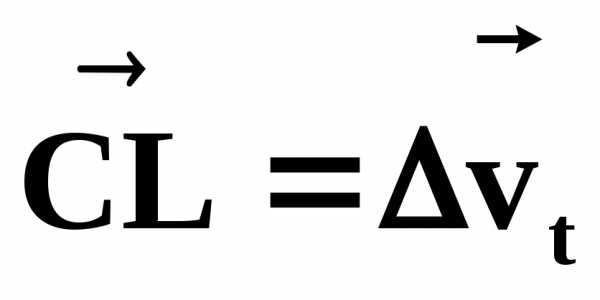
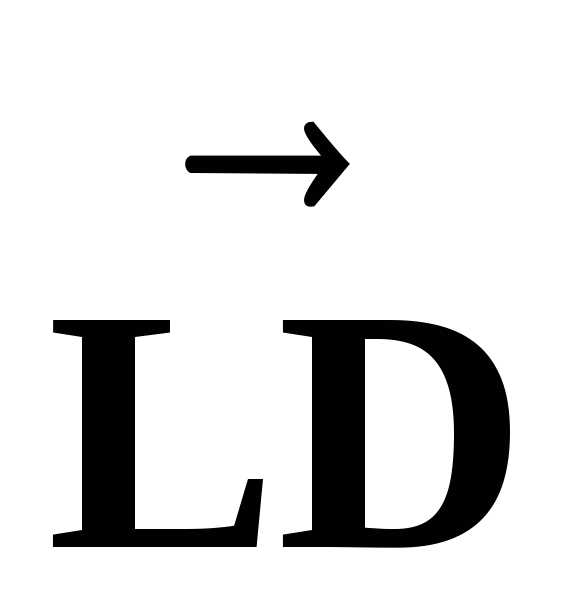 — по направлению
— по направлению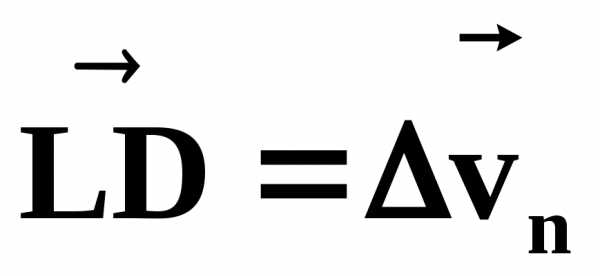 .
Тогда.
Разделим почленно наt
и перейдем к пределу t0:
.
Тогда.
Разделим почленно наt
и перейдем к пределу t0:тогда получим, что полное ускорение точки равно:
(10)
| По модулю полное ускорение равно: Направление определяется углом : |
Самый простой вид неравномерного движения – равноускоренное движение. Равноускоренным называется движение с постоянным по модулю и направлению ускорением.
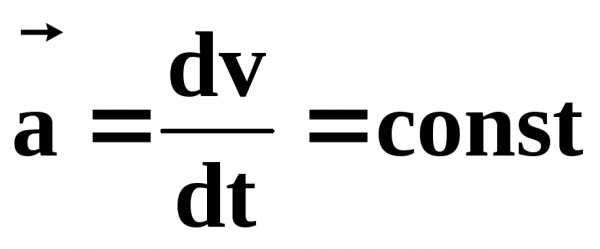
При равноускоренном
движении с начальной скоростью 
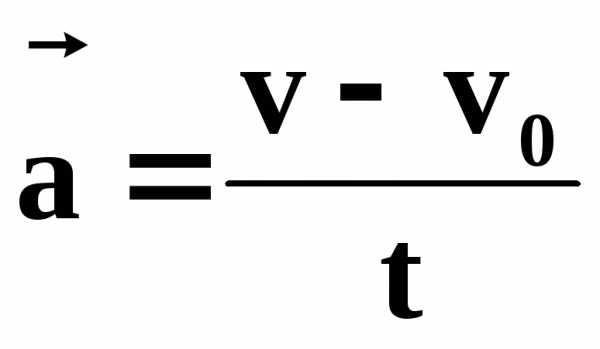
где  — скорость в момент времени t.
— скорость в момент времени t.
Отсюда скорость равноускоренного движения:
studfiles.net
Кинематика материальной точки
Основные формулы кинематики материальной точки
Приведем основные формулы кинематики материальной точки. После чего дадим их вывод и изложение теории.
Радиус-вектор материальной точки M в прямоугольной системе координат Oxyz:
,
где – единичные векторы (орты) в направлении осей x, y, z.
Скорость точки:
;
.
.
Единичный вектор в направлении касательной к траектории точки:
.
Ускорение точки:
;
;
;
; ;
Тангенциальное (касательное) ускорение:
;
;
.
Нормальное ускорение:
;
;
.
Единичный вектор, направленный к центру кривизны траектории точки (вдоль главной нормали):
.
Радиус кривизны траектории:
.
Далее приводится вывод этих формул и изложение теории кинематики материальной точки.
Радиус-вектор и траектория точки
Рассмотрим движение материальной точки M. Выберем неподвижную прямоугольную систему координат Oxyz с центром в некоторой неподвижной точке O. Тогда положение точки M однозначно определяются ее координатами (x, y, z). Эти координаты являются компонентами радиус-вектора материальной точки.
Радиус-вектор точки M – это вектор , проведенный из начала неподвижной системы координат O в точку M.
,
где – единичные векторы в направлении осей x, y, z.
При движении точки, координаты изменяются со временем . То есть они являются функциями от времени . Тогда систему уравнений
(1)
можно рассматривать как уравнение кривой, заданной параметрическими уравнениями. Такая кривая является траекторией точки.
Траектория материальной точки – это линия, вдоль которой происходит движение точки.
Если движение точки происходит в плоскости, то можно выбрать оси и системы координат так, чтобы они лежали в этой плоскости. Тогда траектория определяется двумя уравнениями
В некоторых случаях, из этих уравнений можно исключить время . Тогда уравнение траектории будет иметь зависимость вида:
,
где – некоторая функция. Эта зависимость содержит только переменные и . Она не содержит параметр .
Скорость материальной точки
Скорость материальной точки – это производная ее радиус-вектора по времени.
Согласно определению скорости и определению производной:
Производные по времени, в механике, обозначают точкой над символом. Подставим сюда выражение для радиус-вектора:
,
где мы явно обозначили зависимость координат от времени. Получаем:
,
где
,
,
– проекции скорости на оси координат. Они получаются дифференцированием по времени компонент радиус-вектора
.
Таким образом
.
Модуль скорости:
.
Касательная к траектории
С математической точки зрения, систему уравнений (1) можно рассматривать как уравнение линии (кривой), заданной параметрическими уравнениями. Время , при таком рассмотрении, играет роль параметра. Из курса математического анализа известно, что направляющий вектор для касательной к этой кривой имеет компоненты:
.
Но это есть компоненты вектора скорости точки. То есть скорость материальной точки направлена по касательной к траектории.
Касательная к траектории точки
Все это можно продемонстрировать непосредственно. Пусть в момент времени точка находится в положении с радиус-вектором (см. рисунок). А в момент времени – в положении с радиус-вектором . Через точки и проведем прямую . По определению, касательная – это такая прямая , к которой стремится прямая при .
Введем обозначения:
;
;
.
Тогда вектор направлен вдоль прямой .
При стремлении , прямая стремится к касательной , а вектор – к скорости точки в момент времени :
.
Поскольку вектор направлен вдоль прямой , а прямая при , то вектор скорости направлен вдоль касательной .
То есть вектор скорости материальной точки направлен вдоль касательной к траектории.
Введем направляющий вектор касательной единичной длины:
.
Покажем, что длина этого вектора равна единице. Действительно, поскольку
, то:
.
Тогда вектор скорости точки можно представить в виде:
.
Далее мы считаем, что если над буквой векторной величины не стоит стрелка, то это обозначает модуль вектора.
Ускорение материальной точки
Ускорение материальной точки – это производная ее скорости по времени.
Аналогично предыдущему, получаем компоненты ускорения (проекции ускорения на оси координат):
;
;
;
.
Модуль ускорения:
.
Тангенциальное (касательное) и нормальное ускорения
Теперь рассмотрим вопрос о направлении вектора ускорения по отношению к траектории. Для этого применим формулу:
.
Дифференцируем ее по времени, применяя правило дифференцирования произведения:
.
Вектор направлен по касательной к траектории. В какую сторону направлена его производная по времени ?
Чтобы ответить на этот вопрос, воспользуемся тем, что длина вектора постоянна и равна единице. Тогда квадрат его длины тоже равен единице:
.
Здесь и далее, два вектора в круглых скобках обозначают скалярное произведение векторов. Продифференцируем последнее уравнение по времени:
;
;
.
Поскольку скалярное произведение векторов и равно нулю, то эти векторы перпендикулярны друг другу. Так как вектор направлен по касательной к траектории, то вектор перпендикулярен к касательной.
Первую компоненту называют тангенциальным или касательным ускорением:
.
Вторую компоненту называют нормальным ускорением:
.
Тогда полное ускорение:
(2) .
Эта формула представляет собой разложение ускорения на две взаимно перпендикулярные компоненты – касательную к траектории и перпендикулярную к касательной.
Поскольку , то
(3) .
Тангенциальное (касательное) ускорение
Умножим обе части уравнения (2) скалярно на :
.
Поскольку , то . Тогда
;
.
Здесь мы положили:
.
Отсюда видно, что тангенциальное ускорение равно проекции полного ускорения на направление касательной к траектории или, что тоже самое, на направление скорости точки.
Тангенциальное (касательное) ускорение материальной точки – это проекция ее полного ускорения на направление касательной к траектории (или на направление скорости).
Символом мы обозначаем вектор тангенциального ускорения, направленный вдоль касательной к траектории. Тогда – это скалярная величина, равная проекции полного ускорения на направление касательной. Она может быть как положительной, так и отрицательной.
Подставив , имеем:
.
Подставим в формулу:
.
Тогда:
.
То есть тангенциальное ускорение равно производной по времени от модуля скорости точки. Таким образом, тангенциальное ускорение приводит к изменению абсолютной величины скорости точки. При увеличении скорости, тангенциальное ускорение положительно (или направлено вдоль скорости). При уменьшении скорости, тангенциальное ускорение отрицательно (или направлено противоположно скорости).
Радиус кривизны траектории
Теперь исследуем вектор .
Радиус кривизны траектории
Рассмотрим единичный вектор касательной к траектории . Поместим его начало в начало системы координат. Тогда конец вектора будет находиться на сфере единичного радиуса. При движении материальной точки, конец вектора будет перемещаться по этой сфере. То есть он будет вращаться вокруг своего начала. Пусть – мгновенная угловая скорость вращения вектора в момент времени . Тогда его производная – это скорость движения конца вектора. Она направлена перпендикулярно вектору . Применим формулу для вращающегося движения. Модуль вектора:
.
Теперь рассмотрим положение точки для двух близких моментов времени. Пусть в момент времени точка находится в положении , а в момент времени – в положении . Пусть и – единичные векторы, направленные по касательной к траектории в этих точках. Через точки и проведем плоскости, перпендикулярные векторам и . Пусть – это прямая, образованная пересечением этих плоскостей. Из точки опустим перпендикуляр на прямую . Если положения точек и достаточно близки, то движение точки можно рассматривать как вращение по окружности радиуса вокруг оси , которая будет мгновенной осью вращения материальной точки. Поскольку векторы и перпендикулярны плоскостям и , то угол между этими плоскостями равен углу между векторами и . Тогда мгновенная скорость вращения точки вокруг оси равна мгновенной скорости вращения вектора :
.
Здесь – расстояние между точками и .
Таким образом мы нашли модуль производной по времени вектора :
.
Как мы указали ранее, вектор перпендикулярен вектору . Из приведенных рассуждений видно, что он направлен в сторону мгновенного центра кривизны траектории. Такое направление называется главной нормалью.
Нормальное ускорение
Нормальное ускорение
направлено вдоль вектора . Как мы выяснили, этот вектор направлен перпендикулярно касательной, в сторону мгновенного центра кривизны траектории.
Пусть – единичный вектор, направленный от материальной точки к мгновенному центру кривизны траектории (вдоль главной нормали). Тогда
;
.
Поскольку оба вектора и имеют одинаковое направление – к центру кривизны траектории, то
.
Из формулы (2) имеем:
(4) .
Из формулы (3) находим модуль нормального ускорения:
.
Умножим обе части уравнения (2) скалярно на :
(2) .
.
Поскольку , то . Тогда
;
.
Отсюда видно, что модуль нормального ускорения равен проекции полного ускорения на направление главной нормали.
Нормальное ускорение материальной точки – это проекция ее полного ускорения на направление, перпендикулярное к касательной к траектории.
Подставим . Тогда
.
То есть нормальное ускорение вызывает изменение направления скорости точки, и оно связано с радиусом кривизны траектории.
Отсюда можно найти радиус кривизны траектории:
.
И в заключении заметим, что формулу (4) можно переписать в следующем виде:
.
Здесь мы применили формулу для векторного произведения трех векторов:
,
в которую подставили
.
Итак, мы получили:
;
.
Приравняем модули левой и правой частей:
.
Но векторы и взаимно перпендикулярны. Поэтому
.
Тогда
.
Это известная формула из дифференциальной геометрии для кривизны кривой.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Кинематика материальной точки (средняя школа)
Кинематика материальной точки
Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения. Скорость равномерного движения определяется по формуле:
|
Рис. 1. Перемещение, скорость и ускорение при равномерном прямолинейном движении |
|
Рис. 2. Перемещение, скорость и ускорение при равноускоренном прямолинейном движении |
Равноускоренным прямолинейным движением называется движение, при котором скорость и ускорение направлены вдоль одной прямой и ускорение остается неизменным по модулю. В этом случае модуль ускорения определяется по формуле:
Перемещение, в свою очередь, равно:
где x0 – значение перемещения в момент времени t = 0.
Также используется формула:Примером равноускоренного движения является свободное падение тела с небольшой (по сравнению с радиусом Земли) высоты h в безвоздушном пространстве. Ускорение свободного падения тела не зависит от самого тела и всегда направлено вертикально вниз. Высота тела при этом определяется формулой (при условии, что начальная скорость равна нулю). Время падения с высоты h равно
При равномерном движении со скоростью υ по окружности радиуса R ускорение (центростремительное ускорение) постоянно по модулю:
|
Рис. 3. Равномерное движение по окружности |
Период обращения T – это промежуток времени, в течение которого материальная точка совершает один оборот при равномерном движении по окружности. Модуль скорости движения тела при этом можно записать как:
Частота обращения ν – это число оборотов, совершаемых материальной точкой при равномерном движении по окружности за единицу времени:
Часто используется понятие круговой (или циклической) частоты:
В этом случае центростремительное ускорение записывается в виде:Если модуль скорости движения материальной точки при движении по окружности изменяется, то помимо центростремительного появляется тангенциальное (касательное) ускорение aτ. Оно направлено по касательной к окружности и равно по модулю Полное ускорение в этом случае будет равно:
|
Рис. 4. Нормальное и тангенциальное ускорение |
files.school-collection.edu.ru
Найти вектор скорости и ускорения точки, примеры решений
В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.
Траектория движения материальной точки через радиус-вектор
Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора — вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.
Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами — единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):
Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? «Наверное какой-то жуткий», подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:
Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:
В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.
Вектор скорости материальной точки
Всем известно, что скорость материальной точки — это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.
Пример нахождения вектора скорости
Имеем закон перемещения материальной точки:
Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:
Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.
Как найти вектор ускорения материальной точки
Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:
Модуль вектора скорости точки
Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора — это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:
Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.
Модуль вектора ускорения
Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:
Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.
Еще примеры решений задачи нахождения вектора скорости и ускорения
А вот тут вы можете найти примеры решения и других задач по физике на тему «механика твердых тел». А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.
Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.
artsybashev.ru
Модуль ускорения определяется выражением
. (2.21)
Выше
было отмечено, что вектор  ускорения
материальной точки характеризует
изменение скорости
ускорения
материальной точки характеризует
изменение скорости  по модулю и направлению. Оказывается,
что вектор
по модулю и направлению. Оказывается,
что вектор можно разложить на две составляющие,
одна из которых характеризует изменение
только модуля скорости, а другая — только
его направления. Такое разложение
возможно при любом виде движения
материальной точки. В качестве примера
покажем это для случая плоского движения
точки по произвольной криволинейной
траектории.
можно разложить на две составляющие,
одна из которых характеризует изменение
только модуля скорости, а другая — только
его направления. Такое разложение
возможно при любом виде движения
материальной точки. В качестве примера
покажем это для случая плоского движения
точки по произвольной криволинейной
траектории.
Пусть
материальная точка M совершает
неравномерное плоское движение по
криволинейной траектории
(рис.
2.6).
Проведем в точке М два
взаимно перпендикулярных единичных
вектора (орта)  и
и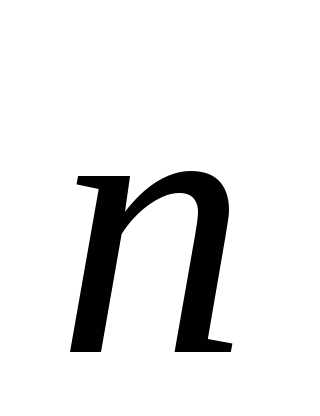 лежащих в плоскости траектории. Вектор
лежащих в плоскости траектории. Вектор направлен по касательной к траектории
в сторону движения материальной точки,
то есть в направлении ее скорости
направлен по касательной к траектории
в сторону движения материальной точки,
то есть в направлении ее скорости .
Вектор
.
Вектор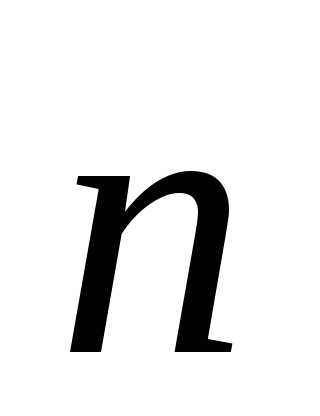 , проведен
в сторону вогнутости траектории по
линии, соединяющей точку M с
центром О кривизны
траектории для данной ее точки.
, проведен
в сторону вогнутости траектории по
линии, соединяющей точку M с
центром О кривизны
траектории для данной ее точки.
В
этих условиях ускорение  может быть разложено на две следующие
составляющие:
может быть разложено на две следующие
составляющие:
. (2.22)
В
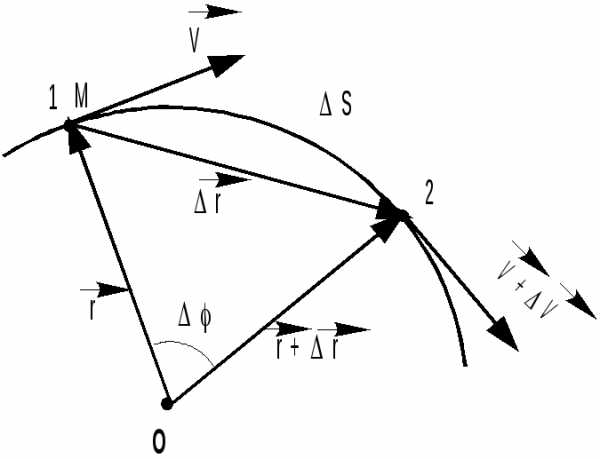
Рис. 2.7
качестве примера рассмотрим неравномерное движение точки М по окружности (рис 2.7). В момент времени t точка М находится в положении 1 и имеет скорость .
Через малый промежуток времениt
точка переместится в положение 2 и будет
иметь скорость
.
Через малый промежуток времениt
точка переместится в положение 2 и будет
иметь скорость 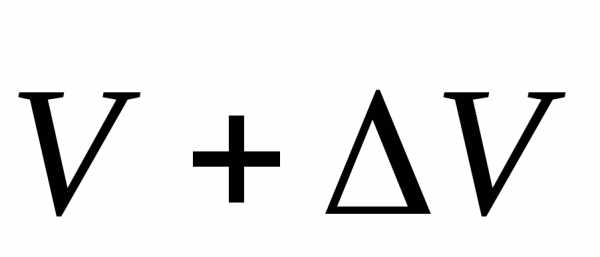 .
Найдем приращение вектора скорости
.
Найдем приращение вектора скорости за времяt.
Для этого перенесем вектор
за времяt.
Для этого перенесем вектор 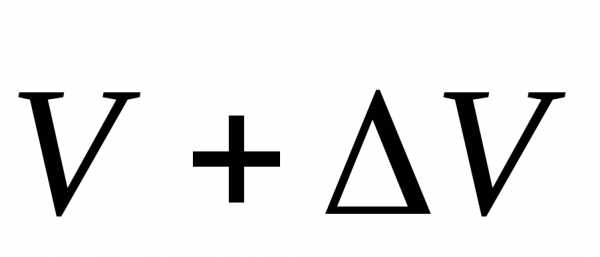 без изменения его направления так, чтобы
его начало совпало с началом вектора
без изменения его направления так, чтобы
его начало совпало с началом вектора (рис. 2.8). Вектор
(рис. 2.8). Вектор изображен направленным отрезком,
проведенным из конца вектора
изображен направленным отрезком,
проведенным из конца вектора в конец вектора
в конец вектора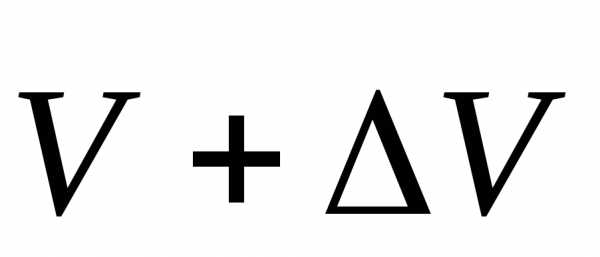 .
Разложим вектор
.
Разложим вектор на
две составляющие
на
две составляющие n и
n и  .
Составляющую
.
Составляющую  n выберем так, чтобы расстояние от точки
1 до конца вектора
n выберем так, чтобы расстояние от точки
1 до конца вектора  было равно
было равно .
При таком выборе
.
При таком выборе n,
составляющая
n,
составляющая  будет иметь модуль равный приращению
модуля (величины) скорости за время t,
то есть
будет иметь модуль равный приращению
модуля (величины) скорости за время t,
то есть | |=|
|=| |.
(2.27)
|.
(2.27)
Введем
единичный вектор 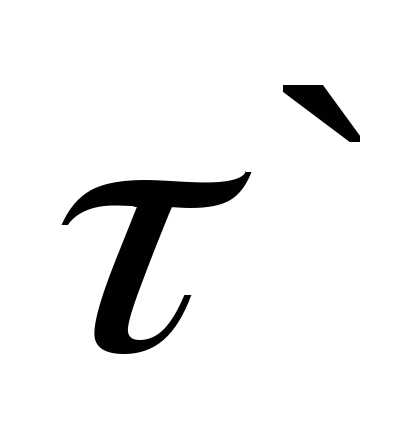 ,
совпадающий по направлению с вектором,
тогда его можно будет представить в
виде
,
совпадающий по направлению с вектором,
тогда его можно будет представить в
виде
 =
=
 .
(2.28)
.
(2.28)
Вектор  n также можно представить в виде произведения
его модуля на единичный вектор
n также можно представить в виде произведения
его модуля на единичный вектор 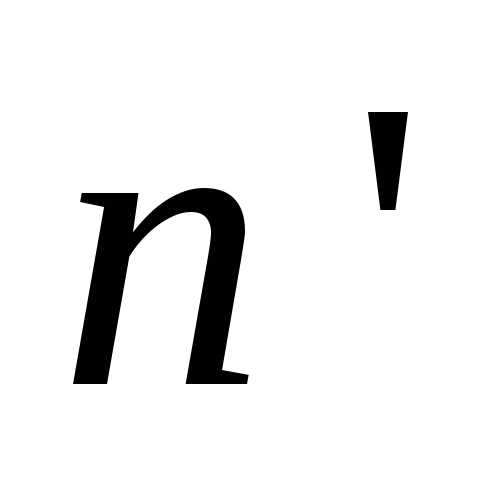 ,
задающий его направление
,
задающий его направление
 n =|
n =| n |
n |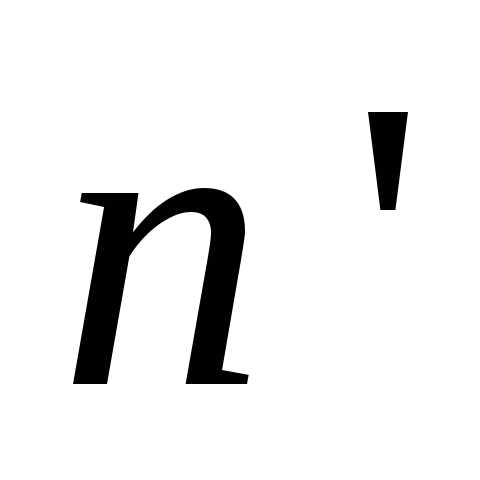 .(2.29)
.(2.29)
Угол
между векторами  и (
и (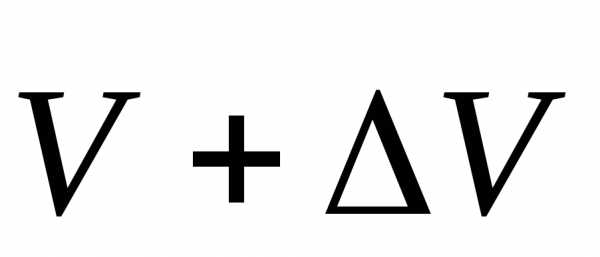 )
равен,
то есть углу между векторами
)
равен,
то есть углу между векторами 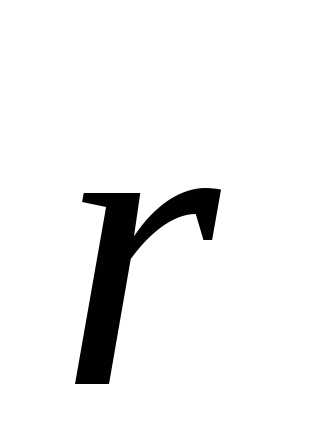 и (
и (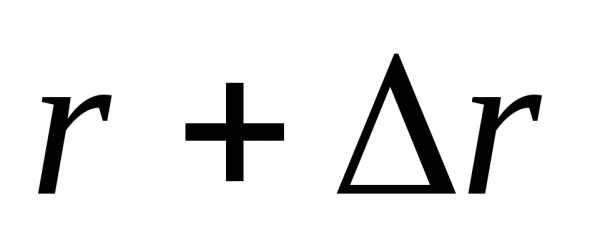 )
(рис 2.7 и 2.8). При малыхt
модуль вектора
)
(рис 2.7 и 2.8). При малыхt
модуль вектора  n можно приближенно заменить дугой
окружности радиуса |
n можно приближенно заменить дугой
окружности радиуса | |
(рис. 2.8):
|
(рис. 2.8):
 n
n .
(2.30)
.
(2.30)
Угол можно выразить через радиус окружности и пройденный точкой М путь S за время t (рис. 2.7) с помощью известного из геометрии соотношения
=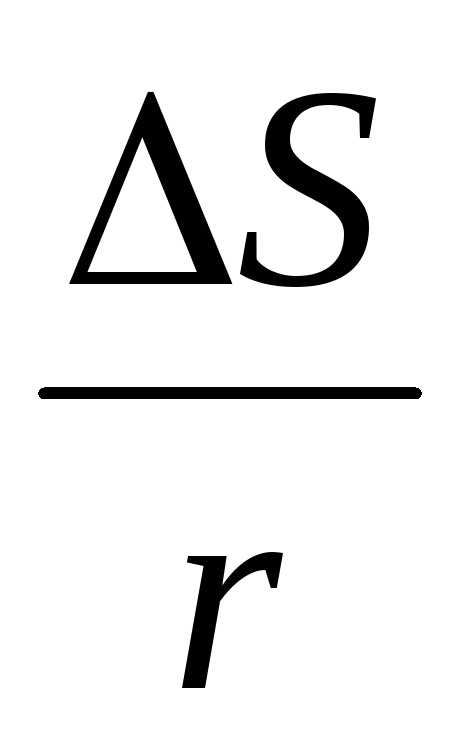 . (2.31)
. (2.31)
С учетом (2.31) формула (2.30) принимает вид:
 n
n 
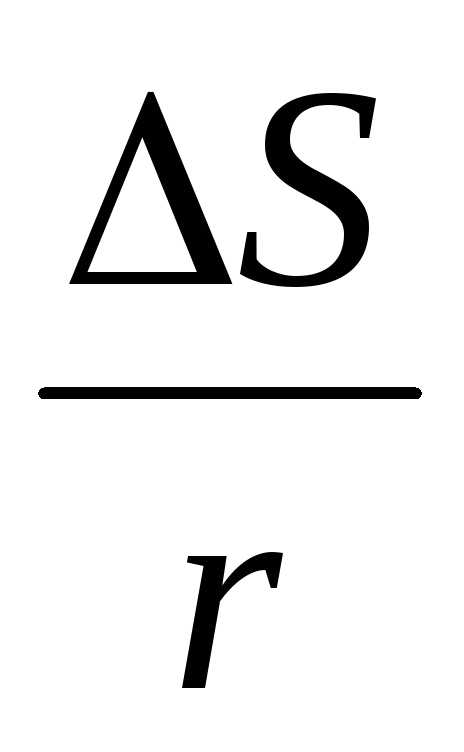
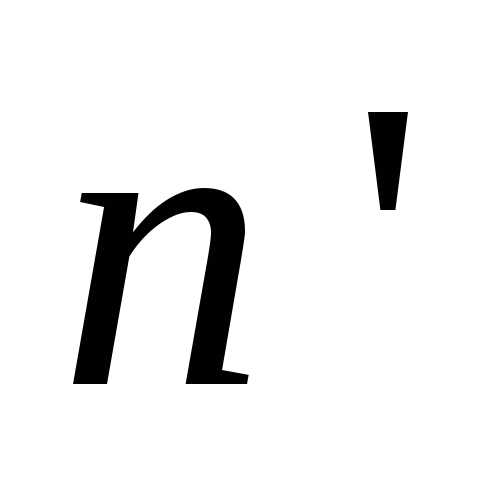 .
(2.32)
.
(2.32)
Найдем
ускорение точки М в положении 1 (рис.
2.7). Для этого учтем, что  =
= n +
n + ,
и воспользуемся формулой (2.21)
,
и воспользуемся формулой (2.21)
(2.33)
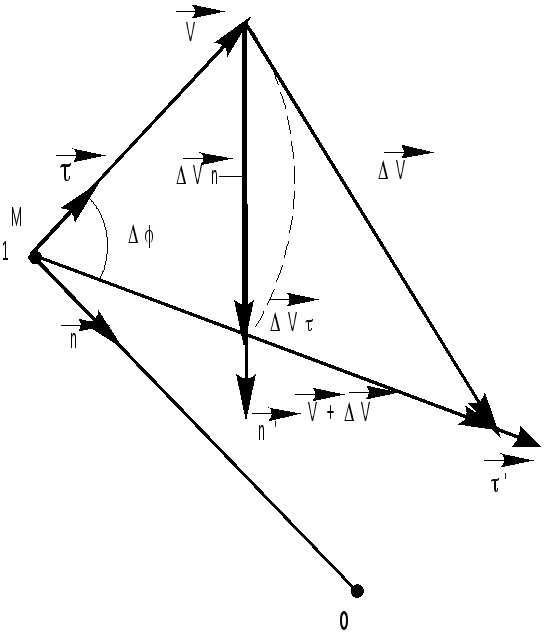
Рис 2.8
С учетом выражения (2.32) первый предел справа принимает вид:. (2.34)
В
точке 1 траектории V и 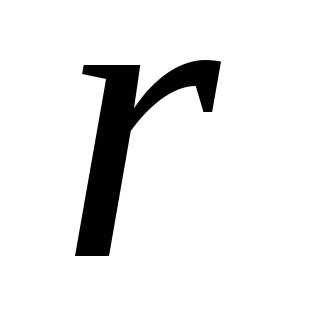 имеют фиксированные значения, а
имеют фиксированные значения, а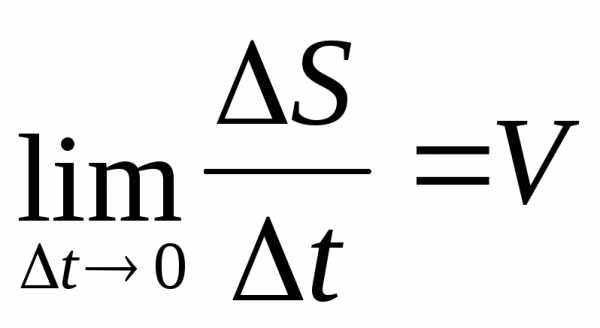 .
Кроме того, приt0
вектор
.
Кроме того, приt0
вектор 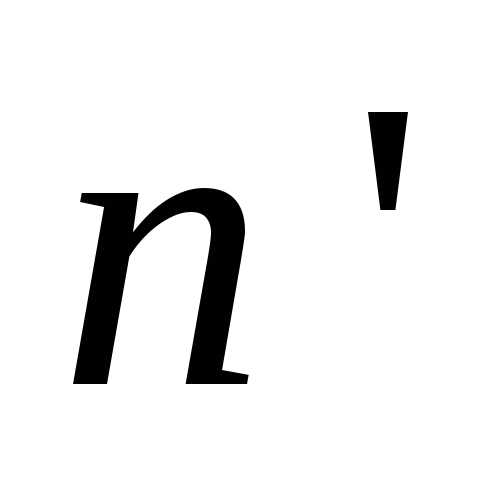 переходит в вектор
переходит в вектор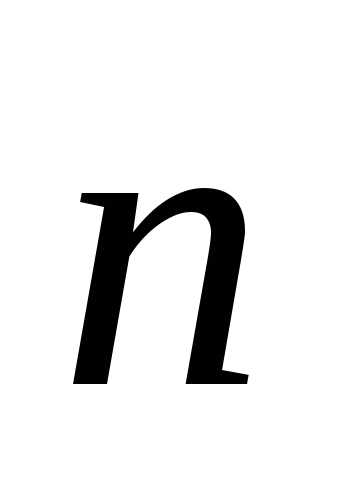 —
вектор главной нормали к траектории в
точке 1 (рис. 2.8). Таким образом, вычисляя
предел в (2.34) и обозначая его через
—
вектор главной нормали к траектории в
точке 1 (рис. 2.8). Таким образом, вычисляя
предел в (2.34) и обозначая его через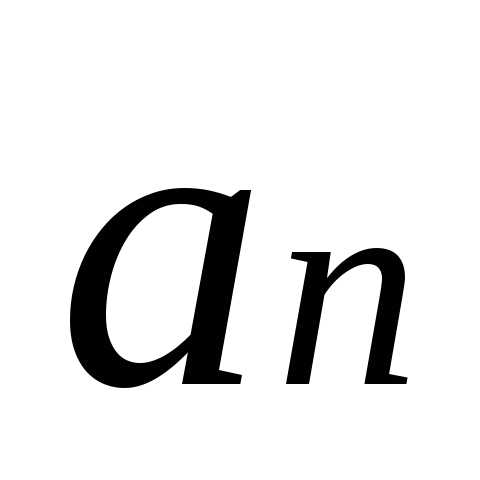 ,
получим
,
получим
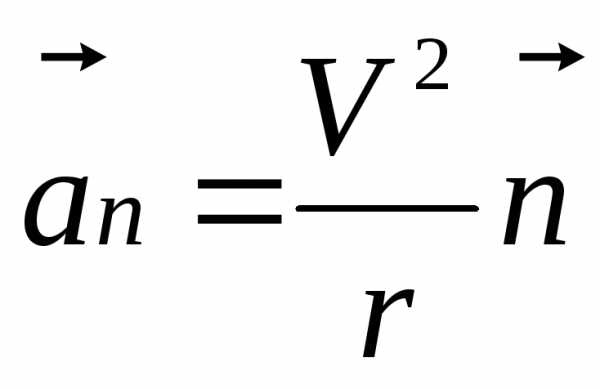 . (2.35)
. (2.35)
Второй
предел в выражении (2.33) обозначим через 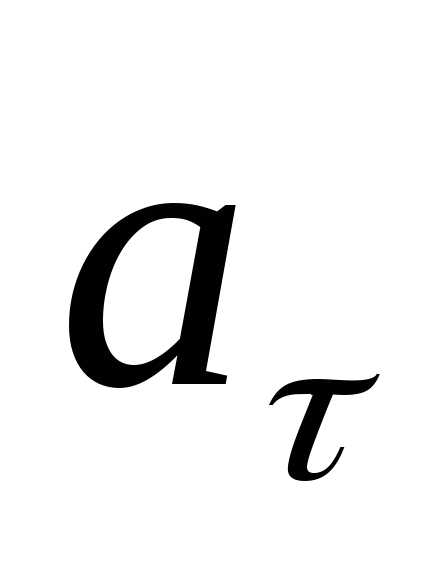 и учтем выражение (2.28), тогда можем
записать:
и учтем выражение (2.28), тогда можем
записать:
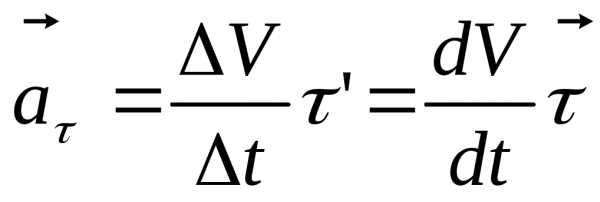 . (2.36)
. (2.36)
При
вычислении предела в (2.36) учтено, что
при t0 вектор  переходит в вектор
переходит в вектор —
единичный вектор касательной к траектории
в точке 1 (рис. 2.8).
—
единичный вектор касательной к траектории
в точке 1 (рис. 2.8).
Таким образом, вектор ускорения точки в любой момент времени может быть представлен в виде суммы двух векторов:
. (2.37)
Вектор 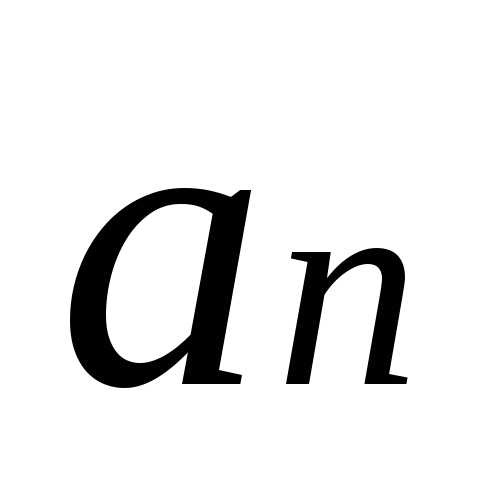 —
называется нормальным ускорением и
характеризует изменение скорости по
направлению.
—
называется нормальным ускорением и
характеризует изменение скорости по
направлению.
Вектор 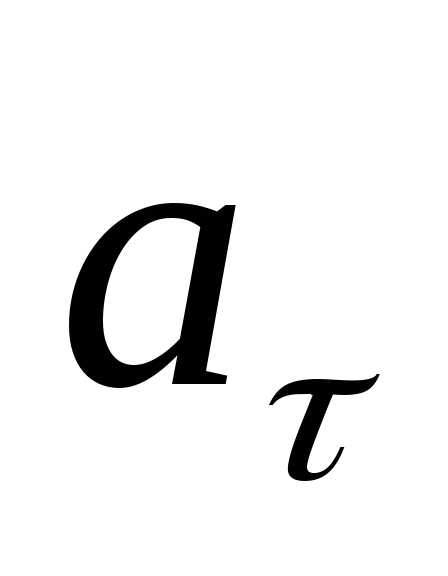 —
называется тангенциальным (касательным)
ускорением и характеризует изменение
скорости по величине.
—
называется тангенциальным (касательным)
ускорением и характеризует изменение
скорости по величине.
Модуль полного ускорения в соответствии с выражениями (2.35), (2.36) и (2.37) равен:
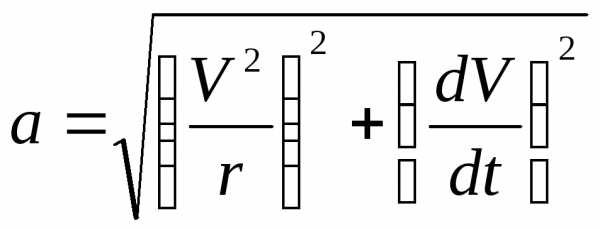 . (2.38)
. (2.38)
Если
траектория не окружность, а произвольная
кривая, то в формуле (2.38) 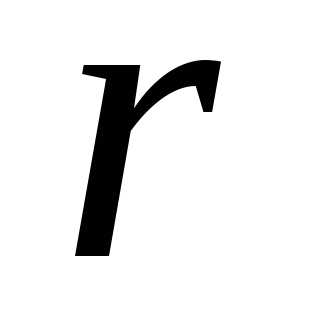 представляет собой радиус кривизны
траектории в точке, для которой
определяется полное ускорение.
представляет собой радиус кривизны
траектории в точке, для которой
определяется полное ускорение.
studfiles.net
Формула ускорения в физике
Определение и формула ускорения
ОпределениеУскорением (мгновенным ускорением) называют вектор, который определяет быстроту, с которой изменяется скорость перемещающейся материальной точки.
Обычно ускорение обозначают . В теоретической механике встречается обозначение ускорения: . Математическим определением мгновенного ускорения являются выражения:
где – скорость движения материальной точки
или
где – радиус – вектор, который определяет положение материальной точки в пространстве.
Вектор ускорения располагается в плоскости соприкосновения, в которой находится главная нормаль и касательная к траектории, при этом он имеет направление в сторону вогнутости траектории.
Единицы измерения ускорения
Основными единицами измерения ускорения в системе СИ является: [a]=м/с2
в СГС: [a]=см/с2
Виды ускорения
Если построить соприкасающуюся плоскость, в любой точке траектории, то вектор разложим на две взаимно перпендикулярные составляющие:
где — вектор, направленный по главной нормали к центру кривизны траектории материальной точки – это нормальное ускорение; — вектор, направленный по касательной к траектории – это касательное ускорение. При этом выполняются равенства:
где – модуль вектора скорости, R – радиус кривизны траектории, an – проекция вектора на направление единичного вектора главной нормали , aт – проекция вектора на направление единичного вектора касательной . Величина an определяет быстроту изменения направления скорости, а величина aт — быстроту изменения модуля скорости.
Если , то такое движение называют равномерным. Приa_ движение является равнопеременным (при равнозамедленным, при равноускоренным).
Средним ускорением материальной точки на отрезке времени от до называется векторная величина, равная отношению:
При в пределе среднее ускорение совпадает с мгновенным ускорением:
Формула ускорения в разных системах координат
В декартовых координатах проекции ускорения (ax,ay,az) на оси (X,Y,Z)можно представить как:
Соответственно, имеем:
где – единичные орты по осям X,Y.Z. При этом модуль ускорения равен:
В цилиндрической системе координат имеем:
В сферической системе координат модуль ускорения можно найти как:
Примеры решения задач
ПримерЗадание. Материальная точка движется по окружности (рис.1), которая имеет радиус R=2м, уравнение движения: , гдеtв секундах, а S в метрах. Каков модуль ускорения данной точки при t=3 c?
Решение. В качестве основы для решения задачи используем формулу:
Используя заданное уравнение движения, найдем модуль скорости материальной точки:
Продифференцировав уравнение для модуля скорости (1.2) по времени получим тангенциальную составляющую ускорения:
м/с2
Для вычисления нормальной составляющей скорости движения нашей материальной точки следует, используя выражение (1.2) найти:
м/с2
Используя выражение (1.1) вычислим искомое ускорение:
м/с2
Ответ. м/с2
ПримерЗадание. Какова зависимость ускорения материальной точки от времени (a(t)), если частица перемещается по оси Xи ее скорость изменяется в соответствии с уравнением: , где – постоянная большая нуля? В начальный момент времени (при t=0 с) материальная точка находилась в начале координат (x=0 м). Нарисуйте график a(t).
Решение. Из условий задачи можно записать, что:
Используя формулу (2.1) найдем зависимость координаты xот времени (x(t) ):
где постоянную интегрирования найдем из начального условия задачи. Мы знаем, что x(0)=0, значит C=0. Имеем:
Используя формулу для нахождения ускорениядля нашего случая (движение по оси X):
получим искомое выражение для a(t):
Ответ. ускорение от времени не зависит, значит, график a(t) принимает вид (рис.2).
Читать дальше: Формула давления.
www.webmath.ru
1.Кинематическое описание движения. Перемещение, скорость. Вычисление пройденного пути. Ускорение.
Кинематика изучает движение без выявления причин, вызывающих это движение. Кинематика является разделом механики. Главной задачей кинематики является математическое определение положения и характеристик движения точек или тел во времени.
Основные кинематические величины:
— Перемещение() –вектор, соединяющий начальную и конечную точки.
r – радиус-вектор, определяет положение МТ в пространстве.
— Скорость – отношение пути ко времени.
— Путь – множество точек через которое прошло тело.
— Ускорение – скорость изменения скорости, то есть первая производная от скорости.
2.Ускорение при криволинейном движении: нормальное и тангенциальное ускорение. Плоское вращение. Угловая скорость, ускорение.
Криволинейное движение – это движение, траектория которого представляет собой кривую линию. Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д.
Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости.
Изменение величины скорости за единицу времени – это тангенциальное ускорение:
Где ?τ, ?0 – величины скоростей в момент времени t0 + Δt и t0 соответственно. Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.
Нормальное ускорение — это изменение скорости по направлению за единицу времени:
Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.
Полное ускорение при равнопеременном криволинейном движении тела равно:
—угловая скорость показывает, на какой угол поворачивается точка при равномерном движении по окружности за единицу времени. Единица измерения в СИ — рад/с.
Плоское вращение – это вращение всех векторов скоростей точек тела в одной плоскости.
3.Связь между векторами скорости и угловой скорости материальной точки. Нормальное, тангенциальное и полное ускорение.
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Нормальное (центростремительное) ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n. Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
studfiles.net

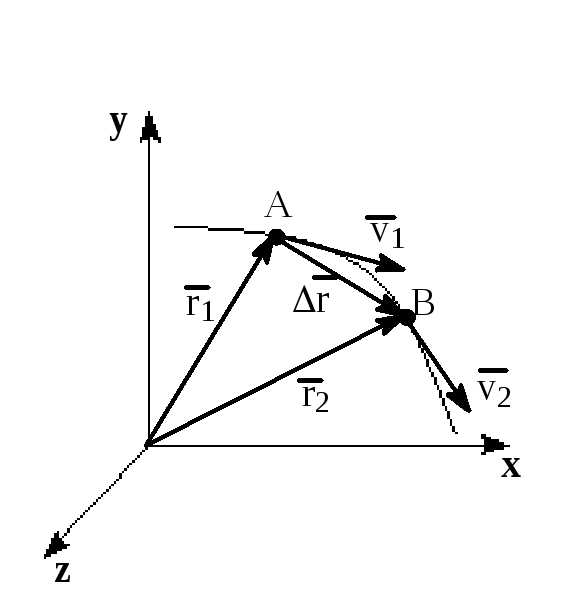
 ,
а в момент времениt2=t1+t – положение B с радиус-вектором
,
а в момент времениt2=t1+t – положение B с радиус-вектором 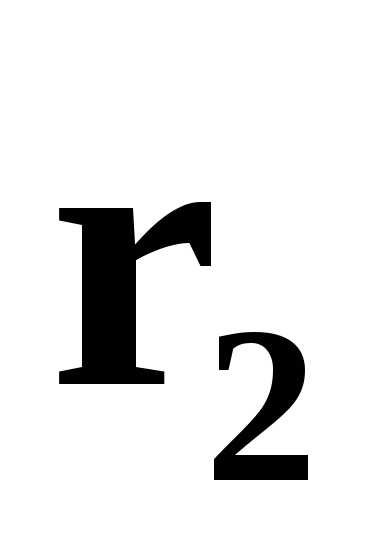 .
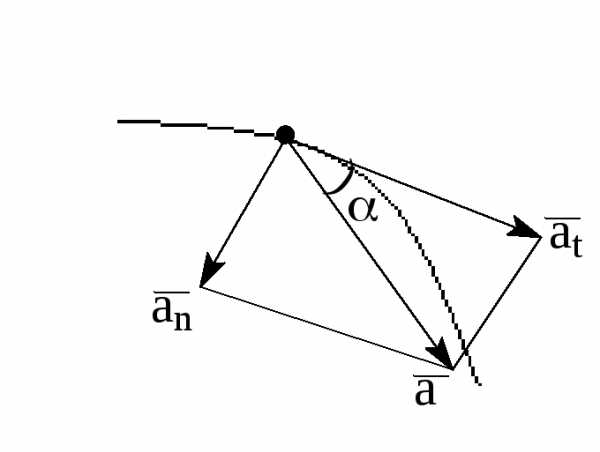
За времяt=t2—t1 радиус-вектор получил приращение
.
.
За времяt=t2—t1 радиус-вектор получил приращение
.
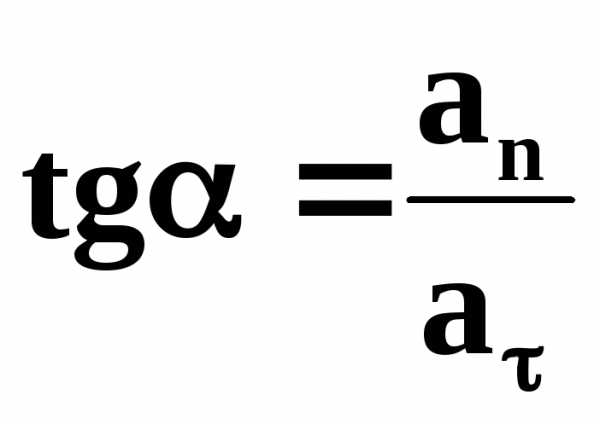
Leave A Comment