Вертикально расположенный замкнутый цилиндрический сосуд разделен на две части подвижным поршнем. В обеих частях сосуда содержится один и тот же идеальный газ. Расстояние между поршнем и дном сосуда см. Сосуд переворачивают так, что дном становится его верхняя плоскость. В новом положении расстояние между дном сосуда и поршнем составляет см. Найти отношение массы газа, содержавшегося в той части сосуда, которая первоначально находилась вверху, к массе газа, содержавшегося в другой части сосуда. Высота сосуда см. Температуру считать постоянной, толщиной поршня пренебречь.
Решение Обозначим через , и , массы и давления газа, содержащегося соответственно в нижней и верхней частях сосуда в его начальном положении. По условию
или
Из уравнений состояния газов в нижней и верхней частях сосуда следует, что
Когда сосуд переворачивают вверх дном, в нижней его части оказывается газ массой
под давлением , а в верхней части — газ массой под давлением , причем
Из условия равновесия поршня вытекает соотношение:
Подставляя сюда найденные выше давления, получаем равенство:
Ответ: .
Ответ
.
gitun.com
Горизонтально расположенный закрытый цилиндрический сосуд
Условие задачи:
Горизонтально расположенный закрытый цилиндрический сосуд с гладкими стенками разделен тонким подвижным теплопроводящим поршнем на две части, в которых находятся равные массы различных идеальных газов: в одной части газ с молярной массой \(\mu_1\), в другой — с молярной массой \(\mu_2\). Какую часть объема сосуда занимает газ с молярной массой \(\mu_1\) при равновесном положении поршня?
Задача №4.3.41 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m\), \(\mu_1\), \(\mu_2\), \(\frac{V_1}{V}-?\)
Решение задачи:
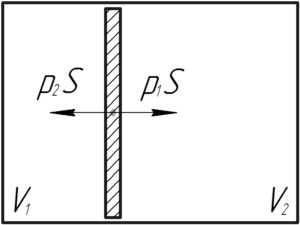 Для решения этой задачи приведем простейший рисунок.
Для решения этой задачи приведем простейший рисунок.
Во-первых, поскольку поршень находится в равновесном положении, и стенки сосуда гладкие, то согласно первому закону Ньютона имеем:
\[{p_1}S = {p_2}S\]
\[{p_1} = {p_2} = {p}\]
Также, так как поршень является теплопроводящим, то при равновесии поршня температуры левой и правой части будут равны:
\[{T_1} = {T_2} = T\]
А теперь запишем уравнение Клапейрона-Менделеева для обоих газов, учитывая, что равны их давления и температуры, исходя из наших рассуждений выше:
\[\left\{ \begin{gathered}
p{V_1} = \frac{m}{{{\mu _1}}}RT \hfill \\
p{V_2} = \frac{m}{{{\mu _2}}}RT \hfill \\
\end{gathered} \right.\]
Сложим оба уравнения:
\[p\left( {{V_1} + {V_2}} \right) = \left( {\frac{m}{{{\mu _1}}} + \frac{m}{{{\mu _2}}}} \right)RT\]
Обозначим общий объем сосуда \(V\), тогда \(V=V_1+V_2\), значит:
\[pV = \left( {\frac{m}{{{\mu _1}}} + \frac{m}{{{\mu _2}}}} \right)RT\]
Чтобы найти искомое отношение \(\frac{V_1}{V}\), поделим первое уравнение Клапейрона-Менделеева на полученное нами выражение:
\[\frac{{{V_1}}}{V} = \frac{{\frac{m}{{{\mu _1}}}}}{{\frac{m}{{{\mu _1}}} + \frac{m}{{{\mu _2}}}}}\]
\[\frac{{{V_1}}}{V} = \frac{{\frac{1}{{{\mu _1}}}}}{{\frac{{{\mu _1} + {\mu _2}}}{{{\mu _1}{\mu _2}}}}} = \frac{{{\mu _1}{\mu _2}}}{{{\mu _1}\left( {{\mu _1} + {\mu _2}} \right)}} = \frac{{{\mu _2}}}{{{\mu _1} + {\mu _2}}}\]
Ответ: \(\frac{{{\mu _2}}}{{{\mu _1} + {\mu _2}}}\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.
Горизонтально расположенный закрытый цилиндрический сосуд длины
Условие задачи:
Горизонтально расположенный закрытый цилиндрический сосуд длины 0,6 м с гладкими стенками, разделенный на две части легким теплонепроницаемым поршнем, заполнен идеальным газом. В начальный момент объем левой части сосуда вдвое больше объема правой, а температура газа в обеих частях одинакова. На сколько переместится поршень, если температуру газа в правой части увеличить вдвое, а в левой поддерживать постоянной?
Задача №4.3.45 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(L=0,6\) м, \(V_1=2V_2\), \(T_1=T_2\), \(T_2^*=2T_2\), \(T_1^*=T_1\), \(\Delta l-?\)
Решение задачи:
Приведем рисунок для решения задачи, причем условимся писать все величины, соответствующие начальному моменту времени, писать без «звездочки», а конечному — со «звездочкой».
Так как поршень и в начальный, и в конечный момент времени будет находится в равновесии, то можно записать первый закон Ньютона и два уравнения Клапейрона-Менделеева.
\[\left\{ \begin{gathered}
{p_1}S = {p_2}S \hfill \\
{p_1}{V_1} = {\nu _1}R{T_1} \hfill \\
{p_2}{V_2} = {\nu _2}R{T_2} \hfill \\
\end{gathered} \right.\]
Из первой строки системы видно, что давления газов равны, т.е. \(p_1=p_2=p\). Зная, что по условию \(V_1=2V_2\) и \(T_1=T_2=T\), получим:
\[\left\{ \begin{gathered}
2p{V_2} = {\nu _1}RT \hfill \\
p{V_2} = {\nu _2}RT \hfill \\
\end{gathered} \right.\]
Поделив верхнее выражение на нижнее, имеем:
\[\frac{{{\nu _1}}}{{{\nu _2}}} = 2\]
Отлично, мы нашли отношение количества молей газов в левой и правой части сосуда.
Теперь повторим то же самое и для конечного момента времени, т.е. опять запишем первый закон Ньютона и два уравнения Клапейрона-Менделеева:
\[\left\{ \begin{gathered}
p_1^*S = p_2^*S \hfill \\
p_1^*V_1^* = {\nu _1}RT_1^* \hfill \\
p_2^*V_2^* = {\nu _2}RT_2^* \hfill \\
\end{gathered} \right.\]
Опять видно, что \(p_1^*=p_2^*=p^*\).
Теперь разберемся с температурами. Так как \(T_2^*=2T_2=2T\) и \(T_1^*=T_1=T\), то очевидно, что их отношение равно \(\frac{T_2^*}{T_1^*}=2\). Тогда:
\[\left\{ \begin{gathered}
{p^*}V_1^* = {\nu _1}RT \hfill \\
{p^*}V_2^* = 2{\nu _2}RT \hfill \\
\end{gathered} \right.\]
Поделим нижнее выражение на верхнее:
\[\frac{{V_2^*}}{{V_1^*}} = 2\frac{{{\nu _2}}}{{{\nu _1}}} = 2 \cdot \frac{1}{2} = 1\]
Значит поршень в конце разделит сосуд на две равные части.
Для того, чтобы узнать на сколько сместиться поршень, следует заметить такой факт:
\[\frac{L}{{{l_1}}} = \frac{V}{{{V_1}}}\]
В задаче считается, что поршень имеет нулевую толщину. В этой формуле \(V\) — это общий объем сосуда, равный \(V=V_1+V_2\), тогда:
\[\frac{L}{{{l_1}}} = \frac{V}{{{V_1}}} = \frac{{{V_1} + {V_2}}}{{{V_1}}} = 1 + \frac{{{V_2}}}{{{V_1}}} = 1 + \frac{1}{2} = \frac{3}{2} \Rightarrow {l_1} = \frac{2}{3}L\]
Проделаем такие же действия для конечного момента:
\[\frac{L}{{l_1^*}} = \frac{V}{{V_1^*}} = \frac{{V_1^* + V_2^*}}{{V_1^*}} = 1 + \frac{{V_2^*}}{{V_1^*}} = 1 + 1 = 2 \Rightarrow l_1^* = \frac{1}{2}L\]
Перемещение поршня можно найти по формуле:
\[\Delta l = {l_1} — l_1^* = \frac{2}{3}L — \frac{1}{2}L = \frac{1}{6}L\]
\[\Delta l = \frac{{0,6}}{6} = 0,1\; м \]
Ответ: 0,1 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.
easyfizika.ru
Цилиндрический сосуд делится невесомым поршнем на две части. В одну часть сосуда
Условие задачи:
Цилиндрический сосуд делится невесомым поршнем на две части. В одну часть сосуда поместили кислород, а в другую — такую же массу водорода. Общая длина сосуда 85 см. Какую часть длины цилиндра будет занимать кислород?
Задача №4.2.90 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m_1=m_2=m\), \(L=85\) см, \(\frac{l_1}{L}-?\)
Решение задачи:
Так как поршень невесомый, то ориентация сосуда (горизонтально или вертикально) роли не играет.
Давления газов будут одинаковы, поскольку в противном случае поршень будет двигаться, причём до тех пор, пока давление не станет одинаковым в обеих частях сосуда. Температуры газов также одинаковы, поскольку не сказано, что поршень теплоизолированный.
Запишем уравнение Клапейрона-Менделеева для кислорода и водорода. Объем, занимаемый газами, запишем в виде произведения площади сечения сосуда на длину части сосуда, который занимает каждый газ.
\[\left\{ \begin{gathered}
pS{l_1} = \frac{m}{{{M_1}}}RT \hfill \\
pS{l_2} = \frac{m}{{{M_2}}}RT \hfill \\
\end{gathered} \right.\]
Молярная масса кислорода \(M_1\) равна 0,032 кг/моль, водорода \(M_2\) — 0,002 кг/моль.
Поделим нижнее уравнение на верхнее:
\[\frac{{{l_2}}}{{{l_1}}} = \frac{{{M_1}}}{{{M_2}}}\]
\[{l_2} = {l_1}\frac{{{M_1}}}{{{M_2}}}\;\;\;\;(1)\]
Сумма длин частей сосуда (\(l_1\) и \(l_2\)), который занимает каждый газ, равна общей длине сосуда \(L\).
\[{l_1} + {l_2} = L\]
Принимая во внимание выражение (1), получим:
\[{l_1} + {l_1}\frac{{{M_1}}}{{{M_2}}} = L\]
В левой части приведём под общий знаменатель:
\[{l_1}\frac{{\left( {{M_1} + {M_2}} \right)}}{{{M_2}}} = L\]
В итоге имеем такую конечную формулу:
\[\frac{{{l_1}}}{L} = \frac{{{M_2}}}{{{M_1} + {M_2}}}\]
Произведём вычисления:
\[\frac{{{l_1}}}{L} = \frac{{0,002}}{{0,032 + 0,002}} = 0,06\]
Ответ: 0,06.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Если Вам понравилась задача и ее решение, то Вы можете поделиться ею с друзьями с помощью этих кнопок.
easyfizika.ru
В цилиндрическом сосуде, разделенном свободно перемещающимся поршнем на две части
20(322). В цилиндрическом сосуде, разделенном свободно перемещающимся поршнем на две части, в каждой части находится по одному молю идеального одноатомного газа (рис.). Температура газа в левой части сосуда поддерживается постоянной. Найдите теплоемкость газа в правой части сосуда при таком положении поршня, когда он делит сосуд пополам. Поршень тепла не проводит.
Решение.
Состояние 1 моля идеального газа в правой части сосуда в начальный момент описывается уравнением Менделеева − Клапейрона:
p1V1 = RT1.
Здесь и в дальнейшем индекс «1» будет относиться к параметрам газа в правой части сосуда, а «2» − в левой.
Когда мы подведем к правой части сосуда небольшое количество теплоты ΔQ, параметры газа изменятся, но по-прежнему будут удовлетворять уравнению состояния:
(p1 + Δp1)(V1 + ΔV1) = R(T1 + ΔT1).
Вычитая почленно одно равенство из другого, получим:
p1ΔV1 + V1Δp1 + Δp1ΔV1 = RΔT1.
Как обычно, предполагая, что в проводимом нами процессе все параметры газа изменяются на малую величину
ΔT1 << T1, Δp1 << p1, ΔV1 << V1,
мы можем пренебречь малым членом Δp1ΔV1 по сравнению с другими и записать:
p1ΔV1 + V1Δp1 = RΔT1. (1)
Аналогичное выражение мы можем получить и для 1 моля газа в левой части сосуда:
p2ΔV2 + V2Δp2 = 0. (2)
По определению теплоемкость
C = ΔQ/ΔT.
Используя первое начало термодинамики, для газа в правой части сосуда можно записать:
ΔQ = CΔT1 = ΔU1 + p1ΔV1
или
CΔT1 = (3/2)RΔT1 + p1ΔV1.
Поскольку давления в обеих частях сосуда все время остаются равными:
p1 = p2 = p и Δp1 = Δp2 = Δp,
а изменения объемов связаны очевидным соотношением
ΔV1 = −ΔV2
из равенств (1) и (2) легко получить, что
p1ΔV1 = RΔT1/(1 + V1/V2),
и, следовательно.
C = (3/2)R + R/(1 + V1/V2).
В момент, когда поршень делит сосуд пополам, V1 = V2, откуда
C = (3/2)R + R/2 = 2R.
Еще одина задача по физике.Срочно!!!
p = nkT n — число молекул в единице объема k — постоянная Бользмана T — температура в Кельвинах Масса газов одинакова, а масса одной молекулы Н2 и О2 — разная — значит и число молекул Н2 и О2 разные молярная масса кислорода — 32 г/моль, водорода — 2 г/моль Значит число молей (количество молекул) Н2 и О2 отличаются в 16 раз N(h3)/N(O2) = 16 Из контекста задачи следует, что температура в обоих частях цилиндра одинакова. Тогда чтобы давление были одинаковы надо обеспечить одинаковую величину n. Для этого требуется, чтобы V(h3) / V(O2) = 16 или L(h3) /L(O2) = 16 по условию задачи L(h3) + L(O2) = 85 рещаем систему
Нужно объём газов расчитать . Объём газа равен масса делить на плотность
Задача. Горизонтально расположенный цилиндрический теплоизолированный сосуд объема Решение. После подведения тепла Q газ в левой части сосуда расширяется, совершая работу A. Эта работа целиком идет на увеличение энергии газа в правой части сосуда. Таким образом, , (1) Условие равновесия поршня до нагревания р1 = р2 = р , (2) где V1 + V2 = V0. После нагревания, когда поршень уже не будет двигаться, давления в левой и правой частях уравниваются. Обозначим увеличение давления в сосуде p, тогда (3) , (4) После простых преобразований получаем: , (5) С учетом формулы (1) соотношение (5) можно переписать в виде: , (6) Из формулы (6) получаем ответ к задаче: ≈ 667 Па. (7) ©Web-Tutor: Качественное и быстрое решение задач любой сложности: |

Leave A Comment