Прямоугольная трапеция
См. также: трапеция и ее свойства.
Прямоугольная трапеция — это трапеция, у которой хотя бы один из углов прямой (классическое определение)
Примечание. На самом деле, у прямоугольной трапеции, как минимум, два прямых угла (см. ниже — свойства)
Другие определения:
- Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям
- Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.
Формулы для прямоугольной трапеции
Обозначения формул даны на чертеже выше.
Соответственно:
a и b — основания трапеции
с — боковая сторона прямоугольной трапеции, перпендикулярная основаниям
d — боковая сторона трапеции, не являющаяся перпендикулярной основаниям
α — острый угол при большем основании трапеции
m — средняя линия трапеции
Интерпретация формул:
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна высоте трапеции (Формула 1)
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна произведению синуса острого угла при большем основании на длину второй боковой стороны. (Треугольник CKD — прямоугольный, соответственно h/d=sinα согласно свойствам синуса, а c=h) (Формула 2)
(Треугольник CKD — прямоугольный, соответственно h/d=sinα согласно свойствам синуса, а c=h) (Формула 2)
Боковая сторона, перпендикулярная основаниям,
Боковая сторона, которая не перпендикулярна основаниям, равна частному разности оснований к косинусу острого угла при большем основании или частному высоты трапеции и синуса острого угла при большем основании. (разность оснований равна KD. В прямоугольном треугольнике CKD по определению косинуса cos α = KD / d, откуда и проистекает искомая формула) (Формула 4)
Боковая сторона прямоугольной трапеции, которая  (Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, далее — следствие из теоремы Пифагора — из квадрата гипотенузы вычитаем квадрат катета и извлекая из полученного выражения квадратный корень, находим искомый катет) (Формула 5)
(Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, далее — следствие из теоремы Пифагора — из квадрата гипотенузы вычитаем квадрат катета и извлекая из полученного выражения квадратный корень, находим искомый катет) (Формула 5)
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна корню квадратному из суммы квадрата второй боковой стороны и квадрата разности оснований
Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна частному от деления двойной площади трапеции на сумму ее оснований. (Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 7)
Боковая сторона прямоугольной трапеции, которая не перпендикулярна основаниям, равна частному от деления двойной площади трапеции на произведение суммы ее оснований и синуса острого угла при основании. (Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а выразив высоту через вторую боковую сторону и подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 8)
(Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а выразив высоту через вторую боковую сторону и подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 8)
Так как прямоугольная трапеция
Свойства прямоугольной трапеции
- У прямоугольной трапеции два угла обязательно прямые
- Оба прямых угла прямоугольной трапеции обязательно принадлежат смежным вершинам
- Оба прямых угла в прямоугольной трапеции обязательно прилежат к одной и той же боковой стороне
- Диагонали прямоугольной трапеции образуют с одной из боковых сторон прямоугольный треугольник
- Длина боковой стороны трапеции, перпендикулярной основаниям равна ее высоте
- У прямоугольной трапеции основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям
- У прямоугольной трапеции два угла прямые, а два других – острый и тупой
Задача
В прямоугольной трапеции большая боковая сторона равна сумме оснований, высота равна 12 см.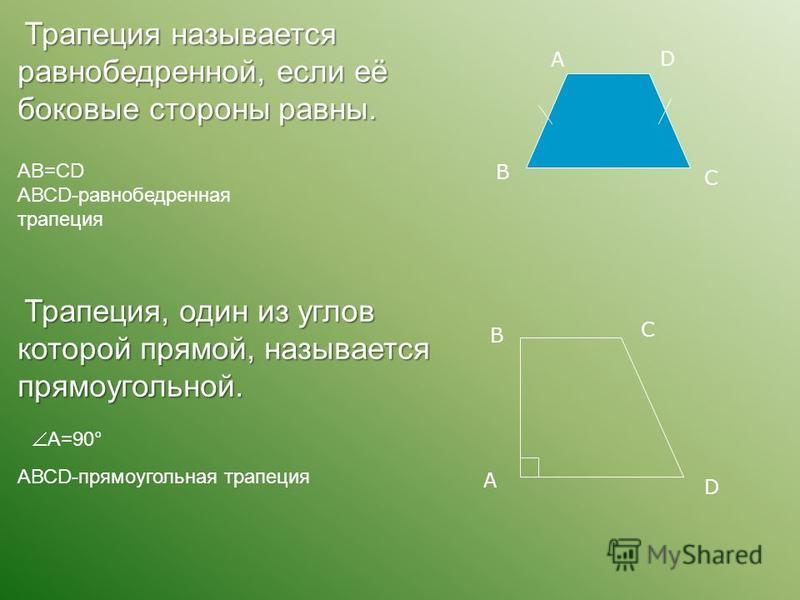 Найдите площадь прямоугольника, стороны которого равны основаниям трапеции.
Найдите площадь прямоугольника, стороны которого равны основаниям трапеции.
Решение.
Обозначим трапецию как ABCD. Обозначим длины оснований трапеции как a (большее основание AD) и b (меньшее основание BC). Пусть прямым углом будет ∠A.
S = ab
Из вершины C верхнего основания трапеции ABCD опустим на нижнее основание высоту CK. Высота трапеции известна по условию задачи. Тогда, по теореме Пифагора
CK2 + KD2 = CD2
Поскольку большая боковая сторона трапеции по условию равна сумме оснований, то CD = a + b
Поскольку трапеция прямоугольная, то высота, проведенная из верхнего основания трапеции разбивает нижнее основание на два отрезка AD = AK + KD. Величина первого отрезка равна меньшему основанию трапеции, так как высота образовала прямоугольник ABCK, то есть BC = AK = b, следовательно, KD будет равен разности длин оснований прямоугольной трапеции KD = a — b.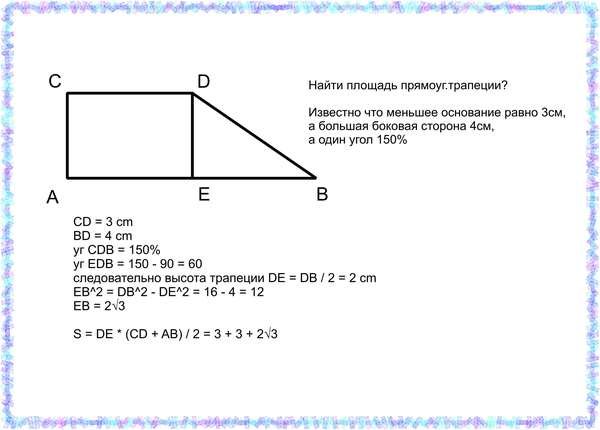
то есть
122 + (a — b)2 = (a + b)2
откуда
144 + a2 — 2ab + b2 = a2 + 2ab + b2
144 = 4ab
Поскольку площадь прямоугольника S = ab (см. выше), то
144 = 4S
S = 144 / 4 = 36
Ответ: 36 см2 .
0
все формулы и примеры задач. Видео «Площадь трапеции»
Задачи с трапецией не кажутся сложными в ряде фигур, которые изучены ранее. Как частный случай рассматривается прямоугольная трапеция. А при поиске ее площади иногда бывает удобнее разбить ее на две уже знакомые: прямоугольник и треугольник. Стоит только немного подумать, и решение обязательно найдется.
Определение прямоугольной трапеции и ее свойства
У произвольной трапеции основания параллельны, а боковые стороны могут иметь произвольное значение углов к ним. Если рассматривается прямоугольная трапеция, то в ней одна из сторон всегда перпендикулярна основаниям. То есть два угла в ней будут равны 90 градусам. Причем они всегда принадлежат смежным вершинам или, другими словами, одной боковой стороне.
То есть два угла в ней будут равны 90 градусам. Причем они всегда принадлежат смежным вершинам или, другими словами, одной боковой стороне.
Другие углы в прямоугольной трапеции − это всегда острый и тупой. Причем их сумма всегда будет равна 180 градусам.
Каждая диагональ образует с ее меньшей боковой стороной прямоугольный треугольник. А высота, которая проведена из вершины с тупым углом, делит фигуру на две. Одна из них прямоугольник, а другая − прямоугольный треугольник. Кстати, эта сторона всегда равна высоте трапеции.
Какие обозначения приняты в представленных формулах?
Все величины, используемые в разных выражениях, которые описывают трапецию, удобно сразу оговорить и представить в таблице:
Формулы, которые описывают элементы прямоугольной трапеции
Самая простая из них связывает высоту и меньшую боковую сторону:
Еще несколько формул для этой стороны прямоугольной трапеции:
с = d *sinα;
c = (a — b) * tg α;
c = √ (d 2 — (a — b) 2).
Первая вытекает из прямоугольного треугольника. И говорит о том, что катет к гипотенузе дает синус противолежащего угла.
В том же треугольнике второй катет равен разности двух оснований. Поэтому справедливо утверждение, которое приравнивает тангенс угла к отношению катетов.
Из того же треугольника можно вывести формулу, основываясь на знании теоремы Пифагора. Это третье записанное выражение.
Можно записать формулы для другой боковой стороны. Их тоже три:
d = (a — b) /cosα;
d = c / sin α;
d = √ (c 2 + (а — b) 2).
Первые две опять получаются из соотношения сторон в том же прямоугольном треугольнике, а вторая выводится из теоремы Пифагора.
Какой формулой можно воспользоваться для расчета площади?
Той, что дана для произвольной трапеции. Только нужно учесть, что высотой является сторона, перпендикулярная к основаниям.
S = (a + b) * h / 2.
Эти величины не всегда даны явно.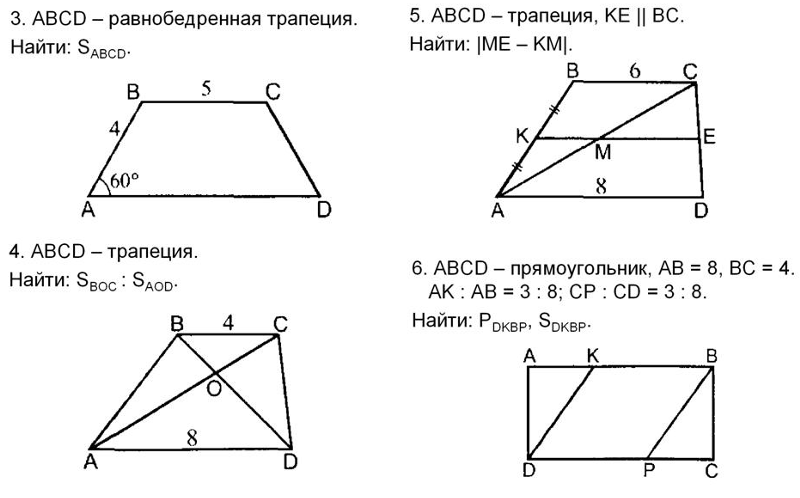 Поэтому чтобы вычислить площадь прямоугольной трапеции, потребуется выполнить некоторые математические выкладки.
Поэтому чтобы вычислить площадь прямоугольной трапеции, потребуется выполнить некоторые математические выкладки.
Как быть, если нужно вычислить диагонали?
В этом случае нужно увидеть, что они образуют два прямоугольных треугольника. Значит, всегда можно воспользоваться теоремой Пифагора. Тогда первая диагональ будет выражаться так:
d1 = √ (с 2 + b 2)
или по-другому, заменив «с» на «h»:
d1 = √ (h 2 + b 2).
Аналогичным образом получаются формулы для второй диагонали:
d2 = √ (с 2 + b 2) или d 2 = √ (h 2 + а 2).
Задача №1
Условие . Площадь прямоугольной трапеции известна и равна 120 дм 2 . Ее высота имеет длину 8 дм. Необходимо вычислить все стороны трапеции. Дополнительным условием является то, что одно основание меньше другого на 6 дм.
Решение. Поскольку дана прямоугольная трапеция, в которой известна высота, то сразу же можно сказать о том, что одна из сторон равна 8 дм, то есть меньшая боковая сторона.
Теперь можно сосчитать другую: d = √ (с 2 + (а — b) 2). Причем здесь сразу даны и сторона с, и разность оснований. Последнее равно 6 дм, это известно из условия. Тогда d будет равняться квадратному корню из (64 + 36), то есть из 100. Так найдена еще одна боковая сторона, равная 10 дм.
Сумму оснований можно найти из формулы для площади. Она будет равна удвоенному значению площади, разделенному на высоту. Если считать, то получается 240 / 8. Значит, сумма оснований — это 30 дм. С другой стороны, их разность равна 6 дм. Объединив эти уравнения, можно сосчитать оба основания:
а + b = 30 и а — b = 6.
Можно выразить а как (b + 6), подставить его в первое равенство. Тогда получится, что 2b будет равняться 24. Поэтому просто b окажется 12 дм.
Тогда последняя сторона а равна 18 дм.
Ответ. Стороны прямоугольной трапеции: а = 18 дм, b = 12 дм, с = 8 дм, d = 10 дм.
Задача №2
Условие. Дана прямоугольная трапеция. Ее большая боковая сторона равняется сумме оснований. Ее высота имеет длину 12 см. Построен прямоугольник, стороны которого равны основаниям трапеции. Необходимо вычислить площадь этого прямоугольника.
Ее высота имеет длину 12 см. Построен прямоугольник, стороны которого равны основаниям трапеции. Необходимо вычислить площадь этого прямоугольника.
Решение. Начать нужно с искомого. Нужная площадь определится как произведение a и b. Обе эти величины не известны.
Потребуется использовать дополнительные равенства. Одно из них построено на утверждении из условия: d = а + b. Необходимо воспользоваться третьей формулой для этой стороны, которая дана выше. Получится: d 2 = с 2 + (a — b) 2 или (a + b) 2 = с 2 + (a — b) 2 .
Необходимо сделать преобразования, подставив вместо с его значение из условия — 12. После раскрытия скобок и приведения подобных слагаемых получается, что 144 = 4 ab.
В начале решения шла речь о том, что а*b дает искомую площадь. Поэтому в последнем выражении можно заменить это произведение на S. Простой расчет даст значение площади. S = 36 см 2 .
Ответ. Искомая площадь 36 см 2 .
Задача №3
Условие. Площадь прямоугольной трапеции 150√3 см². Острый угол равняется 60 градусам. Такое же значение имеет угол между маленьким основанием и меньшей диагональю. Нужно вычислить меньшую диагональ.
Острый угол равняется 60 градусам. Такое же значение имеет угол между маленьким основанием и меньшей диагональю. Нужно вычислить меньшую диагональ.
Решение. Из свойства углов трапеции получается, что ее тупой угол равен 120º. Тогда диагональ делит его на равные, потому что одна его часть уже 60 градусов. Тогда и угол между этой диагональю и вторым основанием тоже 60 градусов. То есть треугольник, образованный большим основанием, наклонной боковой стороной и меньшей диагональю, является равносторонним. Таким образом, искомая диагональ будет равна а, как и боковая сторона d = а.
Теперь нужно рассмотреть прямоугольный треугольник. В нем третий угол равен 30 градусам. Значит катет, лежащий против него, равен половине гипотенузы. То есть меньшее основание трапеции равно половине искомой диагонали: b = a/2. Из него же нужно найти высоту, равную боковой стороне, перпендикулярной основаниям. Сторона с здесь катет. Из теоремы Пифагора:
с = (a/2) * √3.
Теперь осталось только подставить все величины в формулу площади:
150√3 = (a + a/2) * (a/2 * √3) / 2.
Решение этого уравнения дает корень 20
Ответ. Меньшая диагональ имеет длину 20 см.
Добрый день, дорогие друзья! Сегодня у нас тема — трапеция решение задач по геометрии.
Прежде чем начинать разбирать задачи, давайте вспомним, что такое трапеция, и какие у неё есть элементы.
Трапеция — выпуклый четырёхугольник, у которого две стороны параллельны, а две другие — не параллельны.
Параллельные стороны называют основаниями, а непараллельные — боковыми сторонами.
Трапеции бывают прямоугольные, равнобедренные и простые.
В прямоугольных трапециях есть 2 прямых угла.
В равнобедренных трапециях, как в равнобедренных треугольниках, углы при основаниях равны, равны так же и боковые стороны.
В трапеции имеется средняя линия, которая соединяет середины боковых сторон.
А теперь задачи.
Острый угол равнобедренной трапеции равен 60°. Доказать, что основание ВС = AD — AB.
Доказательство.
Опустим из вершин трапеции высоты BM и CN на нижнее основание AD.
Получим два прямоугольных треугольника ABM и DCN, а также прямоугольник BCNM.
Поскольку в прямоугольных треугольниках один угол равен 60°, то второй, согласно следствию из теоремы о сумме внутренних углов треугольника,
равен 30°.
А мы знаем, что катет, лежащий против угла в 30°, равен половине гипотенузы.
Т.е. АМ= с/2.
То же самое и в правом треугольнике — ND = с/2.
Получается, что нижнее основание можно представить в виде суммы трёх отрезков, а именно AM, MN, ND, где AM=ND=c/2.
MN=BC, или верхнему основанию.
Отсюда можно написать MN=BC=AD — AM — ND = AD — c/2 — c/2 = AD — AB.
Мы доказали, что верхнее основание равно разности нижнего основания и боковой стороны.
Основания трапеции равны AD и BC. Найти длину отрезка KP, который соединяет середины диагоналей трапеции.
Решение:
На основании теоремы Фалеса отрезок KP принадлежит большему отрезку MN, который является средней линией трапеции.
Средняя линия трапеции
, как мы знаем, равна полу-сумме оснований трапеции
, или (AD+BC)/2.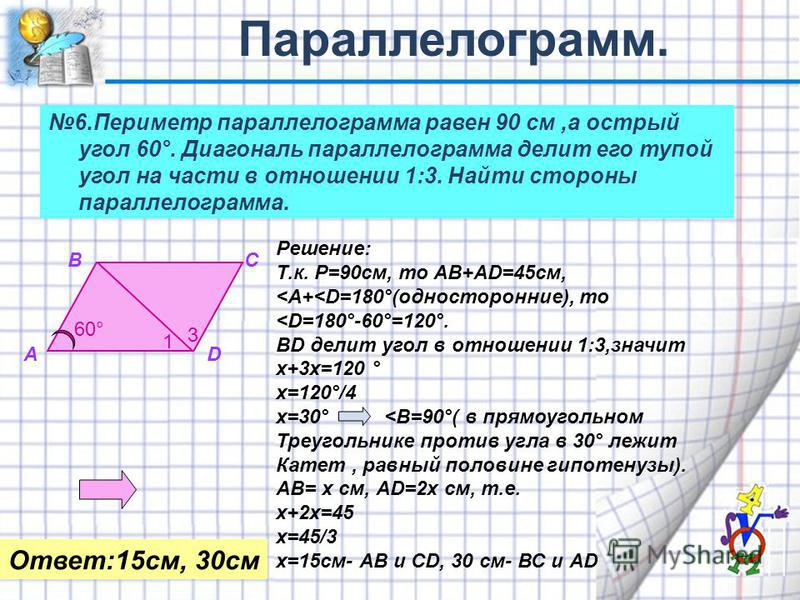
В то же время, рассматривая треугольник ACD и его среднюю линию KN, можно понять, что KN=AD/2.
Рассматривая другой треугольник BCD и его среднюю линию PN, можно увидеть, что PN=BC/2.
Отсюда, KP=KN-PN = AD/2 — BC/2 = (AD-BC)/2.
Мы доказали, что отрезок, который соединяет середины диагоналей трапеции, равен полу-разности оснований данной трапеции
.
Задача 3.
Найти меньшее основание ВС равнобедренной трапеции, если высота СK, проведённая из конца C меньшего основания, делит большее основание на отрезки AK и KD, разность которых равна 8 см.
Решение:
Сделаем дополнительное построение. Проведём высоту ВМ.
Рассмотрим треугольники ABM и DCK. Они равны по гипотенузе и катету
— AB=CD, как боковые стороны равнобедренной трапеции.
Высоты трапеции BM и CK тоже равны, как перпендикуляры, расположенные между двумя параллельными прямыми
.
Следовательно, AM=KD. Получается, что разность между AK и KD равна разности между AK и AM.
А это есть отрезок MK. Но MK равен ВС, поскольку BCKM — прямоугольник.
Отсюда меньшее основание трапеции равно 8 см.
Задача 4.
Найти отношение оснований трапеции, если её средняя линия делится диагоналями на 3 равные части.
Решение:
Поскольку MN — средняя линия трапеции, то она параллельна основаниям и делит боковые стороны пополам
.
По теореме Фалеса MN делит также и стороны AC и BD пополам.
Рассматривая треугольник АВС можно видеть, что MO в нём — средняя линия. А средняя линия треугольника параллельна основанию и равна его половине
. Т.е. если MO=Х, то ВС=2Х.
Из треугольника ACD имеем ON — средняя линия.
Она тоже параллельна основанию и равна его половине.
Но, поскольку OP+PN= Х+Х=2Х, тогда AD=4Х.
Получается, что верхнее основание трапеции равно 2Х, а нижнее — 4Х.
Ответ: отношение оснований трапеции равно 1:2.
В этой статье для вас сделана очередная подборка задач с трапецией. Условия так или иначе связаны с её средней линией. Типы заданий взяты из открытого банка типовых задач. Если есть желание, то можете освежить свои теоретические знания . На блоге уже рассмотрены задачи условия которых связаны с , а также . Кратко о средней линии:
На блоге уже рассмотрены задачи условия которых связаны с , а также . Кратко о средней линии:
Средняя линия трапеции соединяет середины боковых сторон. Она параллельна основаниям и равна их полусумме.
Перед решением задач давайте рассмотрим теоретический пример.
Дана трапеция ABCD. Диагональ АС пересекаясь со средней линией образует точку К, диагональ BD точку L. Доказать, что отрезок KL равен половине разности оснований.
Давайте сначала отметим тот факт, что средняя линия трапеции делит пополам любой отрезок концы которого лежат на её основаниях. Этот вывод напрашивается сам собой. Представьте отрезок соединяющий две точки оснований, он разобьёт данную трапецию на две других. Получится, что отрезок параллельный основаниям трапеции и проходящий через середину боковой стороны на другой боковой стороне пройдёт через её середину.
Так же это основывается на теореме Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
То есть в данном случае К середина АС и L середина BD. Следовательно EK есть средняя линия треугольника АВС, LF есть средняя линия треугольника DCB. По свойству средней линии треугольника:
Можем теперь выразить отрезок KL через основания:
Доказано!
Данный пример приведён не просто так. В задачах для самостоятельного решения имеется именно такая задача. Только в ней не сказано, что отрезок соединяющий середины диагоналей лежит на средней линии. Рассмотрим задачи:
27819. Найдите среднюю линию трапеции, если ее основания равны 30 и 16.
Вычисляем по формуле:
27820. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.
Выразим большее основание:
Таким образом:
27836. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.
Для того, чтобы найти среднюю линию необходимо знать основания. Основание АВ найти просто: 10+4=14. Найдём DC.
Построим второй перпендикуляр DF:
Отрезки AF, FE и EB будут равны соответственно 4, 6 и 4. Почему?
В равнобедренной трапеции перпендикуляры опущенные к большему основанию разбивают его на три отрезка. Два из них, являющиеся катетами отсекаемых прямоугольных треугольников, равны друг другу. Третий отрезок равен меньшему основанию, так как при построении указанных высот образуется прямоугольник, а в прямоугольнике противолежащие стороны равны. В данной задаче:
Таким образом DC=6. Вычисляем:
27839. Основания трапеции относятся 2:3, а средняя линия равна 5. Найдите меньшее основание.
Введём коэффициент пропорциональности х. Тогда АВ=3х, DC=2х. Можем записать:
Следовательно меньшее основание равно 2∙2=4.
27840. Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите боковую сторону трапеции.
Найдите боковую сторону трапеции.
Исходя из условия можем записать:
Если обозначить среднюю линию через величину х, то получится:
Второе уравнение уже можно записать в виде:
27841. Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.
Обозначим меньшее основание (DC) как х, тогда большее (AB) будет равно х+4. Можем записать
Получили, что меньшее основание рано пяти, значит большее равно 9.
27842. Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разность которых равна 2. Найдите большее основание трапеции.
Большее основание трапеции мы без труда найдём если вычислим отрезок ЕО. Он является средней линией в треугольнике ADB, и АВ=2∙ЕО.
Что имеем? Сказано что средняя линия равна 12 и разность отрезков ЕО и ОF равна 2. Можем записать два уравнения и решить систему:
Понятно, что в данном случае подобрать пару чисел можно без вычислений, это 5 и 7. Но, всё-таки, решим систему:
Но, всё-таки, решим систему:
Значит ЕО=12–5=7. Таким образом, большее основание равно АВ=2∙ЕО=14.
27844. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
Сразу отметим, что высота проведённая через точку пересечения диагоналей в равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.
Казалось бы, для вычисления средней линии мы должны найти основания. Тут небольшой тупик возникает… Как зная высоту, в данном случае, вычислить основания? А ни как! Таких трапеций с фиксированной высотой и диагоналями пересекающимися по углом 90 градусов можно построить множество. Как быть?
Посмотрите на формулу средней линии трапеции. Ведь нам необязательно знать сами основания, достаточно узнать их сумму (или полусумму). Это мы сделать можем.
Так как диагонали пересекаются под прямым углом, то высотой EF образуются равнобедренные прямоугольные треугольники:
Из выше сказанного следует, что FO=DF=FC, а OE=AE=EB. Теперь запишем чему равна высота выраженная через отрезки DF и AE:
Теперь запишем чему равна высота выраженная через отрезки DF и AE:
Таким образом, средняя линия равна 12.
*Вообще это задачка, как вы поняли, для устного счёта. Но, уверен, представленное подробное объяснение необходимо. А так… Если взглянуть на рисунок (при условии, что при построении соблюдён угол между диагоналями), сразу в глаза бросается равенство FO=DF=FC, а OE=AE=EB.
В составе прототипов имеется ещё типы заданий с трапециями. Построена она на листе в клетку и требуется найти среднюю линию, сторона клетки обычно равна 1, но может быть другая величина.
27848. Найдите среднюю линию трапеции ABCD , если стороны квадратных клеток равны 1.
Всё просто, вычисляем основания по клеткам и используем формулу: (2+4)/2=3
Если же основания построены под углом к клеточной сетке, то есть два способа. Например!
Всем выпускникам, которые готовятся к сдаче ЕГЭ по математике, будет полезно освежить в памяти тему «Произвольная трапеция».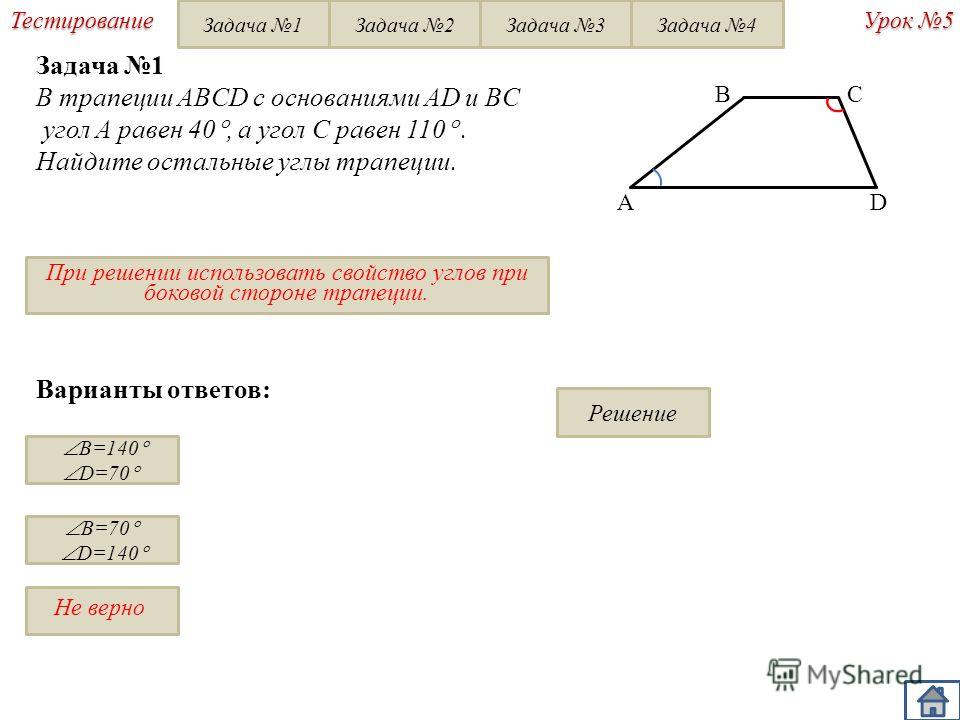 Как показывает многолетняя практика, планиметрические задачи из этого раздела вызывают у многих старшеклассников определенные сложности. При этом решить задачи ЕГЭ на тему «Произвольная трапеция» требуется при прохождении и базового, и профильного уровня аттестационного испытания. Следовательно, уметь справляться с подобными упражнениями должны все выпускники.
Как показывает многолетняя практика, планиметрические задачи из этого раздела вызывают у многих старшеклассников определенные сложности. При этом решить задачи ЕГЭ на тему «Произвольная трапеция» требуется при прохождении и базового, и профильного уровня аттестационного испытания. Следовательно, уметь справляться с подобными упражнениями должны все выпускники.
Как подготовиться к экзамену?
Большинство планиметрических задач решаются путем классических построений. Если в задаче ЕГЭ требуется найти, к примеру, площадь трапеции, изображенной на рисунке, стоит отметить на чертеже все известные параметры. После этого вспомните основные теоремы, относящиеся к ним. Применив их, вы сможете найти правильный ответ.
Чтобы подготовка к экзамену была действительно эффективной, обратитесь к образовательному порталу «Школково». Здесь вы найдете весь базовый материал по темам «Произвольная трапеция или который поможет вам успешно сдать ЕГЭ. Основные свойства фигуры, формулы и теоремы собраны в разделе «Теоретическая справка».
«Прокачать» навыки решения задач выпускники смогут также на нашем математическом портале. В разделе «Каталог» представлена большая подборка соответствующих упражнений разного уровня сложности. Перечень заданий наши специалисты регулярно обновляют и дополняют.
Последовательно выполнять упражнения учащиеся из Москвы и других городов могут в режиме онлайн. При необходимости любое задание можно сохранить в разделе «Избранное» и в дальнейшем вернуться к нему, чтобы обсудить с преподавателем.
Математическая задача: Прямоугольная трапеция — вопрос № 7289, геометрия
Прямоугольная трапеция ABCD с основаниями AB и CD разделена диагональю AC на два равносторонних прямоугольных треугольника. Длина диагонали АС равна 62 см. Вычислите площадь трапеции в квадратных см и вычислите, сколько различных периметров треугольников ABC и ACD в сантиметрах.
Правильный ответ:
S = 2883 см 2x = 62 см
Пошаговое объяснение:
u=62 см a=u2+u2
=622+622
=62 2
см≐87,6812 см c2 + c2 = 2 900/03
=62/2
=31 2
см≐43,8406 см S=2a+c⋅ c=287,6812+43,8406⋅ 43,8406=2883 см2
⋅⋅⋅⋅1 o1 43,8406+62≐149,6812 см o2=2⋅ u+a=2⋅ 62+87,6812≐211,6812 см x=o2−o1=211,6812−149,6812=62 см
Нашли ошибку или неточность? Не стесняйтесь
пишите нам . Спасибо!
Спасибо!
Советы по использованию связанных онлайн-калькуляторов
См. также наш калькулятор прямоугольного треугольника.
Вы хотите преобразовать единицы длины?
Расчет равнобедренного треугольника.
Расчет равностороннего треугольника.
См. также наш калькулятор тригонометрического треугольника.
Для решения этой задачи по математике необходимо знать следующие знания:
- геометрия
- подобие треугольников
- алгебра
- expression of a variable from the formula
- planimetrics
- Pythagorean theorem
- right triangle
- area of a shape
- perimeter
- triangle
- trapezoid
Units of physical quantities:
- length
- угол
Уровень задачи:
- практика для 14-летних
- старшая школа
Мы рекомендуем вам посмотреть это учебное видео по этой математической задаче: видео1 видео2
- Диагональное пересечение
Равнобедренная трапеция ABCD с длинами оснований | АБ | = 6 см, CD | = 4 см делится на четыре треугольника диагоналями, пересекающимися в точке S. Какую часть площади трапеции составляют треугольники ABS и CDS?
Какую часть площади трапеции составляют треугольники ABS и CDS? - Диагональ
Прямоугольная трапеция ABCD, плечо AD которой перпендикулярно основаниям AB и CD, имеет площадь 15 кв.см. Основания имеют длину AB = 6 см, CD = 4 см. Вычислите длину диагонали АС. - Диагонали трапеций
Дана трапеция ABCD с основаниями | АБ | = 12 см, |CD| = 8 см. Точка S — это пересечение диагоналей, для которых |AS| имеет длину 6 см. Вычислите длину полной диагонали АС. - трапеция 3428
Дана трапеция ABCD с основаниями AB, CD. Пусть K — середина стороны AB, а точка L — середина стороны CD. Площадь треугольника ALB равна 15 см 2 , а площадь треугольника DKC равна 10 см². Вычислите площадь трапеции ABCD. - Трапеция RT
Участок имеет форму прямоугольной трапеции ABCD, где ABIICD с прямым углом при вершине B. Сторона AB имеет длину 36 м. Длины сторон АВ и ВС относятся как 12:7. Длины сторон AB и CD относятся как 3:2. Вычислить con - Трапеция ABCD
На рисунке показано, что ABDC является трапецией, в которой AB || CD. Отрезки RN и LM проведены параллельно AB так, что AJ=JK=KP. Если AB=0,5 м и AP=BQ=1,8 м, найдите длины AC, BD, RN и LM. угол D=угол C=60
Отрезки RN и LM проведены параллельно AB так, что AJ=JK=KP. Если AB=0,5 м и AP=BQ=1,8 м, найдите длины AC, BD, RN и LM. угол D=угол C=60 - Трапециевидная призма
Рассчитайте поверхность четырехугольной призмы ABCDA’B’C’D’ с трапециевидным основанием ABCD. Высота призмы 12 см; Данные трапеции ABCD: длина основания AB 8 см, длина основания CD 3 см, длина плеча BC 4 см, длина диагонали АС 7 см. L - Трапеция ABCD
ABDC — это трапеция, в которой AB и CD — параллельные стороны, равные 6 и 9 соответственно. Углы ABC и BCD прямые. Найдите длину отрезка BD. - Одна трапеция
Одна трапеция имеет длинные стороны AB=24M, BC=36M, CD=80M, DA=80M. Найдите площадь. - Вычислить 2556
Вычислить размер плеча b трапеции ABCD, если a = 12 см, c = 4 см, d (AC) = d (BC) и площадь S (треугольник ABC) = 9 см кв. - Трапеция 2
Трапеция имеет площадь 24 квадратных см. Сколько различных трапеций можно составить? - Плавательный бассейн
Плавательный бассейн длиной 30 м наполнен водой на глубину 1 м в мелкой части и 5 м в глубокой части, а по вертикали бассейн имеет форму трапеции с площадь определяется как S (abcd) = 1/2 (ab + cd) x ad. Что такое
Что такое - Равносторонний 4301
Треугольник ABC равносторонний со стороной 8 см. Точки D, E и F являются серединами сторон AB, BC и AC. Вычислите площадь треугольника DEF. В каком отношении находится площадь треугольника ABC к площади треугольника DEF? - Трапеция ABCD v2
Трапеция ABCD имеет длину оснований в соотношении 3:10. Площадь треугольника ACD равна 825 дм². Чему равна площадь трапеции ABCD? - Трети трапеции
Трапеция ABCD имеет параллельные стороны AB и CD. Точка Е лежит на стороне АВ. Отрезок DE делит трапецию на две части одинаковой площади. Найдите длину отрезка AE. - Прямоугольная трапеция
Прямоугольная трапеция ABCD: /AB/ = /BC/ = /AC/. Длина медианы 6 см. Вычислите длину окружности и площадь трапеции. - Вычислить 2416
В прямоугольнике ABCD длина стороны AB = 16 см, а диагональ AC = 20 см. Вычислите его периметр и площадь.
Математическая задача: прямоугольная трапеция — вопрос № 4626, геометрия
Прямоугольная трапеция ABCD: /AB/ = /BC/ = /AC/. Длина медианы 6 см. Вычислите длину окружности и площадь трапеции.
Длина медианы 6 см. Вычислите длину окружности и площадь трапеции.
Правильный ответ:
o = 26,9282 смS = 41,5692 см 2
Пошаговое объяснение:
s=6 s=2 c/(a +c) = (a+a/2)/2 a=12/(1+1/2)=8 b=a=8 c=a/2=8/2=4 d=a2−(a/2)2
=82−(8/2)2
=4 3
≐6,9282 o=a+a+c+d=8+8+4+6,9282=26,9282 см
S=d⋅ s= 6,9282⋅ 6=24 3
=41,5692 см2
Нашли ошибку или неточность? Смело звоните по номеру
пишите нам. Спасибо!
Советы по использованию связанных онлайн-калькуляторов
См. также наш калькулятор прямоугольного треугольника.
Вы хотите преобразовать единицы длины?
См. также наш калькулятор тригонометрического треугольника.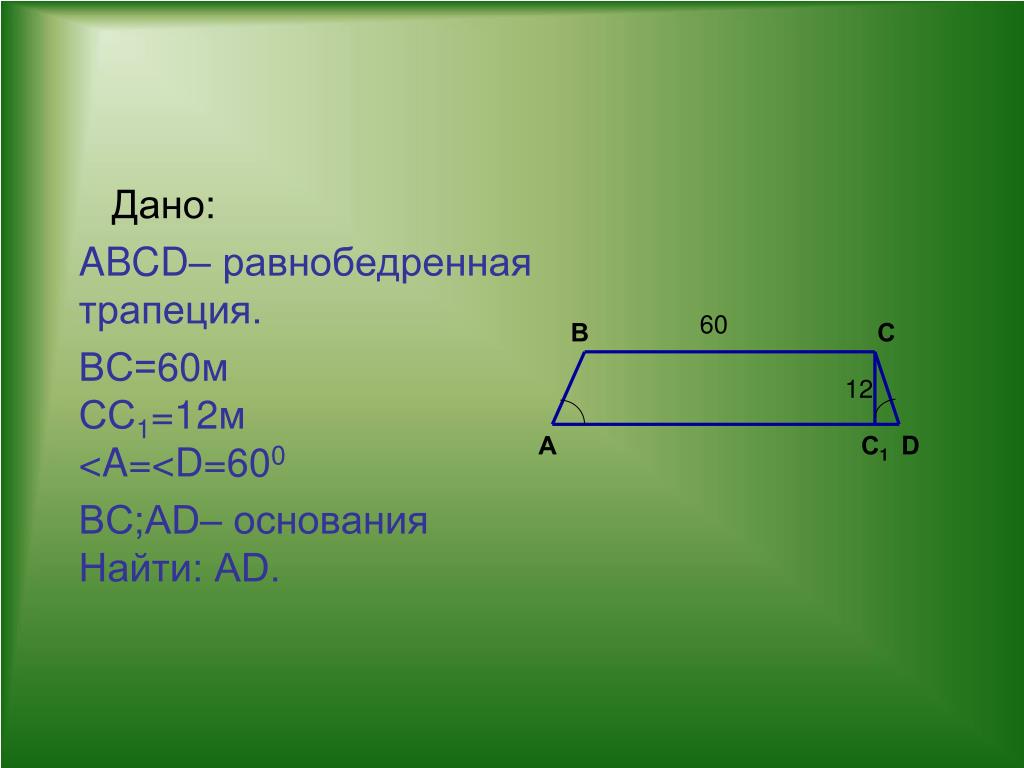
Вам необходимо знать следующие знания для решения этой задачи по математике:
- Геометрия
- Сегмент линий
- Algebra
- Экспрессия переменной из Formula
- 9 9 9 9 9 69 9 69 9 9 9 9 9 9 69 69 69
- .0007
- Pythagorean Теорема
- Правой треугольник
- Площадь формы
- Периметр
- .
- практика для 13-летних
- практика для 14-летних
- старшая школа
Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: видео1 видео2
- Диагональ
Прямоугольная трапеция ABCD, плечо AD которой перпендикулярно основаниям AB и CD, имеет площадь 15 кв.см. Основания имеют длину AB = 6 см, CD = 4 см. Вычислите длину диагонали АС. - Трапециевидная призма
Рассчитайте поверхность четырехугольной призмы ABCDA’B’C’D’ с трапециевидным основанием ABCD. Высота призмы 12 см; Данные трапеции ABCD: длина основания AB 8 см, длина основания CD 3 см, длина плеча BC 4 см, длина диагонали АС 7 см. Л
Высота призмы 12 см; Данные трапеции ABCD: длина основания AB 8 см, длина основания CD 3 см, длина плеча BC 4 см, длина диагонали АС 7 см. Л - Рассчитайте 2556
Рассчитайте длину плеча b трапеции ABCD, если a = 12 см, c = 4 см, d (AC) = d (BC) и площадь S (треугольник ABC) = 9 см2. - Диагонали трапеций
Дана трапеция ABCD с основаниями | АБ | = 12 см, |CD| = 8 см. Точка S — это пересечение диагоналей, для которых |AS| имеет длину 6 см. Вычислите длину полной диагонали АС. - Прямоугольная трапеция
Вычислите площадь прямоугольной трапеции с прямым углом в точке A и если |AC| = 4 см, |ВС| = 3 см, а диагональ АС перпендикулярна стороне ВС. - Трапеция: 18703
В трапеции ABCD: | ОБЪЯВЛЕНИЕ | = | компакт-диск | = | Британская Колумбия | а | АБ | = | переменный ток |. Определить размер угла дельты. - Прямоугольная трапеция
Прямоугольная трапеция ABCD с основаниями AB и CD разделена диагональю AC на два равносторонних прямоугольных треугольника. Длина диагонали АС равна 62 см. Вычислить площадь трапеции в квадратных см и количество различных периметров
Длина диагонали АС равна 62 см. Вычислить площадь трапеции в квадратных см и количество различных периметров - Трапеция IV
В трапеции ABCD (AB||CD) |AB| = 15см |CD| = 7 см, |AC| = 12 см, АС перпендикулярна ВС. Какую площадь имеет трапеция ABCD? - Параллелограмм ABCD
Имеем параллелограмм ABCD, где AB равен 6,2 см BC равен 5,4 см AC равен 4,8 см вычислить высоту на стороне AB и угол DAB - Трапеция
Прямоугольная трапеция ABCD с прямым углом при вершине A имеет стороны a, b, c и d. Вычислить длину окружности и площадь трапеции, если даны: a = 25 см, c = 10 см, d = 8 см - Трапеция 70454
Построить трапецию ABCD (AB // CD): | АБ | = 7см | Британская Колумбия | = 3,5 см | компакт-диск | = 4см Величина угла ABC = 60° - Вычислить 2416
В прямоугольнике ABCD длина стороны AB = 16 см, а диагональ AC = 20 см. Вычислите его периметр и площадь. - Трапеция RT
Участок имеет форму прямоугольной трапеции ABCD, где ABIICD с прямым углом при вершине B.


 Какую часть площади трапеции составляют треугольники ABS и CDS?
Какую часть площади трапеции составляют треугольники ABS и CDS? Отрезки RN и LM проведены параллельно AB так, что AJ=JK=KP. Если AB=0,5 м и AP=BQ=1,8 м, найдите длины AC, BD, RN и LM. угол D=угол C=60
Отрезки RN и LM проведены параллельно AB так, что AJ=JK=KP. Если AB=0,5 м и AP=BQ=1,8 м, найдите длины AC, BD, RN и LM. угол D=угол C=60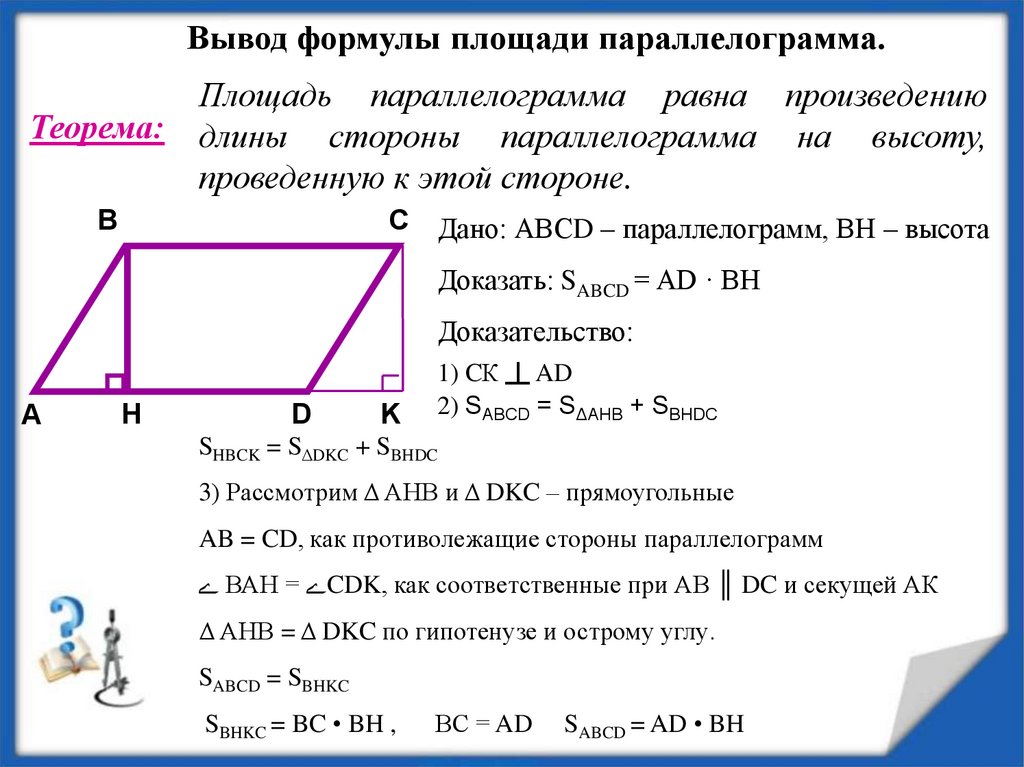 Что такое
Что такое Высота призмы 12 см; Данные трапеции ABCD: длина основания AB 8 см, длина основания CD 3 см, длина плеча BC 4 см, длина диагонали АС 7 см. Л
Высота призмы 12 см; Данные трапеции ABCD: длина основания AB 8 см, длина основания CD 3 см, длина плеча BC 4 см, длина диагонали АС 7 см. Л Длина диагонали АС равна 62 см. Вычислить площадь трапеции в квадратных см и количество различных периметров
Длина диагонали АС равна 62 см. Вычислить площадь трапеции в квадратных см и количество различных периметров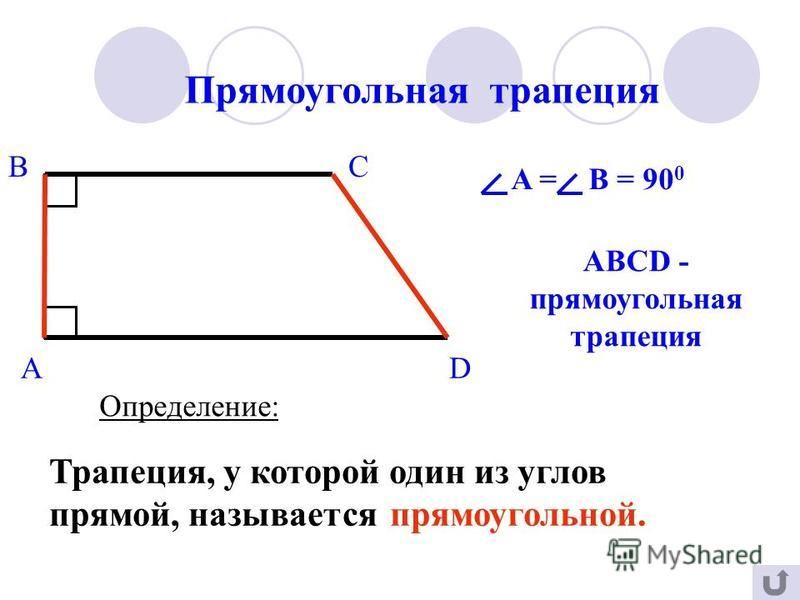
Leave A Comment