Параллелограмм – свойства, признаки, определение
Научим решать сложные задачи о параллелограммах
Начать учиться
390.4K
Геометрические фигуры изучают не только восьмиклассники и технари, но и представители творческих специальностей. Нестандартные четырехугольные формы можно встретить как в дизайне обуви, так и в современных зданиях. В этой статье расскажем о параллелограмме и его отличительных особенностях.
Определение параллелограмма
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны и равны. Как выглядит параллелограмм:
Частные случаи параллелограмма: ромб, прямоугольник, квадрат.
Диагонали — отрезки, которые соединяют противоположные вершины.
Свойства диагоналей параллелограмма:
- В параллелограмме точка пересечения диагоналей делит их пополам.

- Любая диагональ параллелограмма делит его на два равных треугольника.
- Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон.
Биссектриса угла параллелограмма — это отрезок, который соединяет вершину с точкой на одной из двух противоположных сторон и делит угол при вершине пополам.
Свойства биссектрисы параллелограмма:
- Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
- Биссектрисы углов, прилежащих к одной стороне параллелограмма пересекаются под прямым углом.
- Отрезки биссектрис противоположных углов равны и параллельны.
Как найти площадь параллелограмма:
- S = a × h, где a — сторона, h — высота.

- S = a × b × sinα, где a и b — две стороны, sinα — синус угла между ними. Для ромба формула примет вид S = a2 × sinα.
- Для ромба: S = 0,5 × (d1 × d2), где d1 и d2 — две диагонали.
Для параллелограмма: S = 0,5 × (d1 × d2) × sinβ, где β — угол между диагоналями.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
У нас есть отличные дополнительные курсы по математике для учеников с 1 по 11 классы!
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Свойства параллелограмма
Геометрическая фигура — это любое множество точек. У каждой фигуры есть свои свойства, которые отличают их между собой и помогают решать задачи по геометрии в 8 классе.
Рассмотрим основные свойства диагоналей и углов параллелограмма, узнаем чему равна сумма углов параллелограмма и другие особенности этой фигуры. Вот они:
Вот они:
- Противоположные стороны параллелограмма равны.
- Противоположные углы параллелограмма равны.
ABCD — параллелограмм, значит, ∠A = ∠C, ∠B = ∠D. - Диагонали параллелограмма точкой пересечения делятся пополам.
ABCD — параллелограмм, AC и BD — диагонали, AC∩BD=O, значит, BO = OD, AO = OC. - Диагональ делит параллелограмм на два равных треугольника.
ABCD — параллелограмм, AC — диагональ, значит, △ABC = △CDA. - Сумма углов в параллелограмме, прилежащих к одной стороне, равна 180 градусам.
ABCD — параллелограмм, значит, ∠A + ∠D = 180°. - В параллелограмме диагонали d1, d2 и стороны a, b связаны следующим соотношением: d12 + d22 = 2 × (a2 + b2 ).

А сейчас докажем теорему, которая основана на первых двух свойствах.
Теорема 1. В параллелограмме противоположные стороны и противоположные углы равны.
В любом выпуклом четырехугольнике диагонали пересекаются. Все, что мы знаем о точке их пересечения — это то, что она лежит внутри четырехугольника.
- AB = CD как противоположные стороны параллелограмма.
- ∠1 = ∠2 как накрест лежащие углы при пересечении секущей AC параллельных прямых AB и CD; ∠3 = ∠4 как накрест лежащие углы при пересечении секущей BD параллельных прямых AB и CD.
- Следовательно, треугольник AOB равен треугольнику COD по второму признаку равенства треугольников, то есть по стороне и прилежащим к ней углам, из чего следует:
- CO = AO
- BO = DO
Теорема доказана. Наше предположение верно.
Наше предположение верно.
Признаки параллелограмма
Признаки параллелограмма помогают распознать эту фигуру среди других четырехугольников. Сформулируем три основных признака.
Первый признак параллелограмма. Если в четырехугольнике две противолежащие стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Докажем 1 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
- AB || CD
- AB = CD
Чтобы назвать этот четырехугольник параллелограммом, нужно внимательно рассмотреть его стороны.
Сейчас мы видим одну пару параллельных сторон. Нужно доказать, что вторая пара сторон тоже параллельна.
Шаг 2. Проведем диагональ. Получились два треугольника ABC и CDA, которые равны по первому признаку равенства, то есть по по двум сторонам и углу между ними:
- AC — общая сторона;
- По условию AB = CD;
- ∠1 = ∠2 как внутренние накрест лежащие углы при пересечении параллельных прямых AB и CD секущей АС.

Шаг 3. Из равенства треугольников также следует:
- ∠3 = ∠4
Эти углы тоже являются внутренними накрест лежащими для прямых CB и AD. А это как раз и есть признак параллельности прямых. Значит, CB || AD и ABCD — параллелограмм.
Вот так быстро мы доказали первый признак.
Второй признак параллелограмма.
Докажем 2 признак параллелограмма:
Шаг 1. Пусть в четырехугольнике ABCD:
- AB = CD
- BC = AD
Шаг 2. Проведем диагональ AC и рассмотрим треугольники ABC и CDA:
- AC — общая сторона;
- AB = CD по условию;
- BC = AD по условию.

Из этого следует, что треугольники ABC и CDA равны по третьему признаку, а именно по трем сторонам.
Шаг 3. Из равенства треугольников следует:
- ∠ DCA = ∠BAC
А так как эти углы — накрест лежащие при сторонах BC и AD и диагонали AC, значит, стороны BC и AD параллельны.
- ∠DAC = ∠BCA
Эти углы — накрест лежащие при сторонах AB и CD и секущей AC. Поэтому стороны AB и CD тоже параллельны. Значит, четырехугольник ABCD — параллелограмм, ЧТД.
Доказали второй признак.
Третий признак параллелограмма.
Докажем 3 признак параллелограмма:
Шаг 1. Если диагонали четырехугольника ABCD делятся пополам точкой O, то треугольник AOB равен треугольнику COD по двум сторонам и углу между ними:
- CO = OA;
- DO = BO;
- углы между ними равны, как вертикальные, то есть угол AOB равен углу COD.

Эти стороны параллельны CD || AB, по равенству накрест лежащих углов: ∠1 = ∠2 (следует из равенства треугольников AOB и COD).
Значит, ABCD является параллелограммом по первому признаку, который мы доказали ранее. Что и требовалось доказать.
Теперь мы знаем свойства параллелограмма и то, что выделяет его среди других четырехугольников — признаки. Так как они совпадают, эти формулировки можно использовать для определения параллелограмма. Но самое распространенное определение все-таки связано с параллельностью противоположных сторон.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
398.2K
Натуральные числа
К следующей статье
281. 5K
5K
Обыкновенные дроби
Получите план обучения, который поможет понять и полюбить геометрию
ПремиумНа вводном уроке с методистом
Проверим знание геометрии и других разделов математики, выявим пробелы
Подберём курс
Познакомим с интерактивной платформой
Программа к зачету по теме «Параллелограмм» (8 класс) | Методическая разработка по геометрии (8 класс):
Программа к зачёту по теме «Параллелограмм» (8 класс)
Разработала учитель математики МБОУ Поваровской СОШ Морозова Н.С.
Учащиеся должны знать:
- определение параллелограмма;
- его основные свойства и признаки.
Учащиеся должны уметь решать основные задачи на применение свойств и признаков параллелограмма.
Теоретические вопросы.
- Свойства параллелограмма:
На « 3»: 1.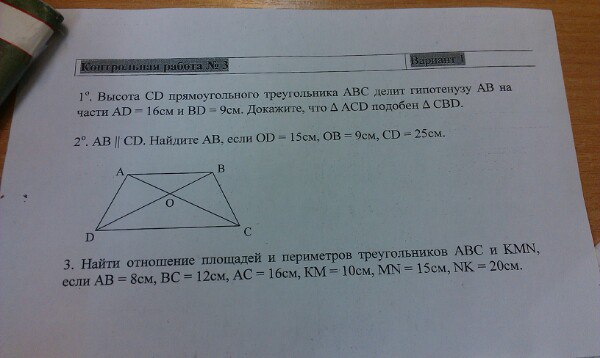 Диагональ параллелограмма разбивает его на два равных
Диагональ параллелограмма разбивает его на два равных
треугольника.
2. Диагонали параллелограмма делятся точкой пересечения
пополам.
3. В параллелограмме противолежащие стороны и углы равны.
4. Сумма величин углов, прилежащих к одной стороне
параллелограмма, равна 180о.
5. Биссектриса любого угла параллелограмма отсекает от него
равнобедренный треугольник.
На « 4-5»: 6. Сумма расстояний от любой точки, лежащей внутри
параллелограмма до прямых, на которых лежат его стороны, —
величина постоянная для данного параллелограмма.
7. Прямая, проходящая через точку пересечения диагоналей
параллелограмма, разбивает его на 2 равных четырёхугольника.
8. Биссектрисы двух противолежащих углов параллелограмма
Биссектрисы двух противолежащих углов параллелограмма
параллельны.
9. В параллелограмме биссектрисы углов, прилегающих к одной
стороне, взаимно перпендикулярны.
10. Докажите, что в параллелограмме против большего угла
лежит большая диагональ.
11. Докажите, что противоположные параллельные стороны
параллелограмма отсекают на прямой, не пересекающей
параллелограмм, параллельной его диагонали, равные отрезки.
12. Докажите, что в параллелограмме угол между высотами,
проведёнными из вершины его тупого угла, равен острому
углу параллелограмма.
- Признаки параллелограмма:
На «3» : 1. Если в четырёхугольнике диагонали в точке пересечения
делятся пополам, то этот четырёхугольник параллелограмм.
2. Если в четырёхугольнике противоположные стороны равны и
параллельны, то этот четырёхугольник параллелограмм.
3. Если в четырёхугольнике противолежащие стороны попарно
равны, то этот четырёхугольник параллелограмм.
На «4-5»: 4. Если в четырёхугольнике каждая диагональ делит его на два
равных треугольника, то этот четырёхугольник параллелограмм.
5.Если в четырёхугольнике противолежащие углы равны, то этот
четырёхугольник параллелограмм.
Практические задачи.
На « 3» :
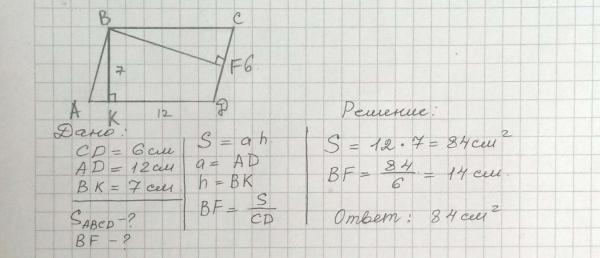
1. Расстояния от точки пересечения диагоналей параллелограмма до двух его вершин равны 3 и 4 см. Чему равны расстояния от неё до двух других вершин? Объясните ответ.
2. АВСД – параллелограмм, О – точка пересечения диагоналей.
а) Диагональ АС=12см. Чему равен отрезок АО? б) отрезок ВО= 3см. Чему равна диагональ ВД?
Чему равна диагональ ВД?
3. В параллелограмме АВСД АВ=10см, ВС=15см. Чему равны стороны АД и СД? Объясните ответ.
4. Докажите, что сумма углов параллелограмма равна 360о.
5. Может ли один угол параллелограмма быть прямым?
6. Может ли один угол параллелограмма быть равным 40о, а другой 50о.
7. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, лежит на противоположной стороне. Какому условию удовлетворяют стороны параллелограмма?
8. Дан треугольник АВС. Из вершин В и С проведены прямые,
параллельные сторонам АС и АВ и пересекающиеся в точке Д. Докажите, что четырёхугольник АВСД – параллелограмм.
9. Через точку С, лежащую во внутренней области угла MAN, проведены прямые, параллельные сторонам угла и пересекающие их в точках В и Д. Докажите, АВСД – параллелограмм.
10. ВМ — медиана треугольника АВС. На её продолжении за точку М отложен отрезок МД, равный ВМ. Докажите, что четырёхугольник АВСД – параллелограмм.
11. Стороны ВО и ОА треугольника АВО продолжены за точку О так, что АО=ОС, ВО=ОД. Докажите, что АВСД параллелограмм.
12. Две стороны четырёхугольника параллельны, а две другие равны. Можно ли утверждать, что этот четырёхугольник – параллелограмм.
На «4» :
1. В параллелограмме АВСД перпендикуляр, опущенный из вершины В на сторону АД , делит её пополам. Докажите, что: а) треугольник АВД – равнобедренный; б) треугольник ВДС – равнобедренный.
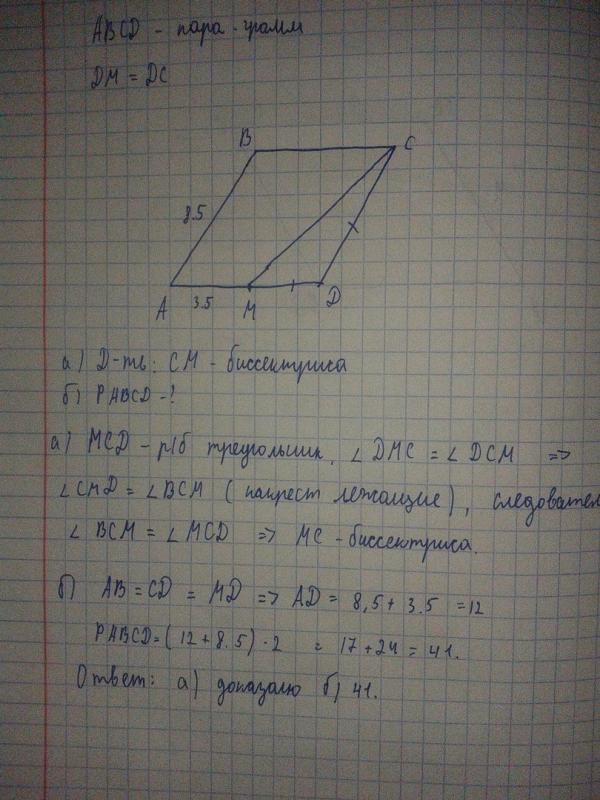
2. Сторона АВ параллелограмма АВСД равна 7 см, диагонали АС и ВД равны 6 и 10 см, О – точка пересечения диагоналей. Определить периметр треугольника АОВ.
3. В параллелограмме АВСД диагонали пересекаются в точке О. Докажите, что треугольники АОВ и СОД равны
4. АВСД – параллелограмм. Диагонали АС и ВД пересекаются в точке О. Докажите, что отрезок ВО является медианой треугольника АВС.
5. Стороны параллелограмма равны 3 и 6 см. Чему равен периметр параллелограмма.
6. Периметр параллелограмма равен 18 см. Чему равна сумма двух соседних сторон?
Чему равна сумма двух соседних сторон?
7. Периметр параллелограмма АВСД равен 48 см. Найдите стороны параллелограмма, если: а) одна сторона равна 10см; б) одна сторона на 3см больше другой; в) разность двух сторон равна 7 см: г) две стороны относятся как 3:5.
8. Могут ли углы треугольника быть равными каким-либо трём углам параллелограмма?
9. Найдите углы параллелограмма АВСД, если: а) ∟А=84о; б) ∟А-∟В=55о; в) ∟С+∟А=142о; г) ∟А=2∟В; д) ∟САД=16о, ∟АСВ=37о; е) углы, прилежащие к одной стороне параллелограмма, относятся как 4:5.
10. Диагональ параллелограмма образует с двумя его сторонами углы 25о и 35о. Найдите углы параллелограмма.
11. В параллелограмме проведена биссектриса угла А, которая пересекает сторону ВС в точке Е. а) Чему равны отрезки ВЕ и ЕС, если АВ=9см, АД=15см; б) Найти периметр параллелограмма, если ВЕ=7см, ЕС=14см.
12. Докажите, что если в четырёхугольнике АВСД ∟А+∟Д=180о и ВС//АД, то этот четырёхугольник – параллелограмм.
13. В четырёхугольнике АВСД диагональ АС разбивает углы А и С так, что ∟ВАС=∟АСД, ∟САД=∟АСВ. Докажите, АВСД – параллелограмм.
Докажите, АВСД – параллелограмм.
14. В параллелограмме АВСД BF//EД, FсАД, ЕсВС. Докажите, что ВFДE – параллелограмм.
15. В параллелограмме АВСД ВF┴АС, ДЕ┴АС. FсАД, ЕсВС. Докажите, что BFДЕ – параллелограмм.
16. АС и ВД – диаметры двух окружностей с общим центром О. Докажите, что АВСД – параллелограмм.
17. Диагонали параллелограмма АВСД пересекаются в т. О. Докажите, что четырёхугольник А1В1С1Д1 , вершинами которого являются середины отрезков ОА, ОВ, ОС, ОД – параллелограмм.
18. На диагонали ВД параллелограмма АВСД отмечены две точки P и Q так, что PВ=QД. Доказать, что четырёхугольник APCQ – параллелограмм.
19. На сторонах АД и ВС параллелограмма АВСД отложены равные отрезки АЕ и CF. Докажите, что четырёхугольник AFCE – параллелограмм.
20. В параллелограмме АВСД точка Е – середина стороны ВС, а т.F – середина стороны АД. Докажите, что AFCE – параллелограмм.
21. В параллелограмме АВСД продолжили сторону АВ за точку В на отрезок ВЕ=АВ, сторону СД – за точку Д на отрезок ДF=СД и провели отрезки ЕС и АF. Докажите, что АЕСF – параллелограмм.
Докажите, что АЕСF – параллелограмм.
22. В параллелограмме АВСД продолжили сторону АВ за точку В на отрезок ВЕ=АВ и провели отрезки ЕС и ВД. Докажите, что ВЕСД – параллелограмм.
23. Четырёхугольник АВСД – параллелограмм. АМ = 1/4АВ; BN = 1/4ВС; СР=1/4СД; ДК = 1/АД. Докажите, что MNPК – параллелограмм.
На «5» :
1. Четырёхугольник АВСД делится диагональю АС на 2 равных треугольников. Будет ли АВСД всегда параллелограммом?
2. Через точку пересечения диагоналей параллелограмма проведена прямая. Докажите, что отрезок прямой, заключённый между параллельными сторонами, делится этой точкой пополам.
3. В параллелограмме АВСД через точку пересечения диагоналей проведена прямая, которая отсекает на сторонах ВС и АД отрезки: ВЕ=2см (ЕcВС) и АF=2,8см (FсАД). Найдите стороны ВС и АД.
4. Через произвольную точку основания равнобедренного треугольника проведены прямые, параллельные боковым сторонам треугольника. а) Докажите, что периметр получившегося четырёхугольника равен сумме боковых сторон данного треугольника; б) Найти периметр получившегося четырёхугольника, если боковая сторона равнобедренного треугольника 5м.
5. Найдите углы параллелограмма, если : а) сумма двух из них равна: 100о; 160о; 180о; б) разность двух из них равна :70о; 110о; 140о.
6. Стороны параллелограмма равны 10 и 3см.Биссектрисы двух углов, прилежащих к большей стороне, делят противоположную сторону на 3 отрезка. Найдите эти отрезки.
7. Периметр параллелограмма равен 46см; АВ=14см. Какую сторону параллелограмма АВСД пересекает биссектриса ∟А. Найдите отрезки, которые образуются при этом пересечении.
8. Середины (точки E и F) параллельных сторон ВС и АД параллелограмма АВСД соединены с вершинами Д и В. Докажите, что полученные отрезки BF и ДЕ делят диагональ АС на 3 равные части.
9. В параллелограмме АВСД перпендикуляр, опущенный из вершины В на сторону АД, делит её пополам. Найти диагональ ВД, если известно, что периметр параллелограмма равен 3,8м, а периметр треугольника АВД равен 3м.
10. В параллелограмме АВСД проведен перпендикуляр ВК к прямой АД. Найти стороны и углы параллелограмма, если известно, что АК=3см, КД=5см, ∟АВК=30о.




Leave A Comment