Радиус описанной окружности | Треугольники

Удобно, когда все формулы, по которым можно найти радиус описанной окружности для треугольника, квадрата, многоугольника размещены на одной странице.

Радиус описанной окружности для произвольного треугольника

Формулы для нахождения радиуса описанной окружности треугольника (верны для треугольника любого вида):

   

   

где a, b, c — длины сторон треугольника, α, β, γ — противолежащие этим сторонам углы, S — площадь треугольника.

Центр описанной окружности лежит:

у остроугольного треугольника — внутри треугольника;

у прямоугольного — на середине гипотенузы;

у тупоугольного — вне треугольника, напротив тупого угла.

Радиус описанной окружности для прямоугольного треугольника

Радиус описанной около прямоугольного треугольника окружности равен половине гипотенузы:

   

 

 

Окружность, описанная около многоугольника

Если около многоугольника можно описать окружность, ее центр является точкой пересечения серединных перпендикуляров к сторонам многоугольника.

Радиус описанной около многоугольника окружности  находят как радиус окружности, описанной около треугольника. Для этого берут любые три вершины многоугольника.

Например, для пятиугольника ABCDE можно взять любой из треугольников ABC, ABD, ABE, BCD, BCE, CDE, ACD, ACE, ADE, BDE.

 

Радиус окружности, описанной около правильного многоугольника

Формула радиуса описанной окружности для правильного многоугольника

   

где a — длина стороны многоугольника, n — количество его сторон.

Частные случаи — правильный треугольник, правильный четырехугольник (то есть квадрат), правильный шестиугольник.

Радиус описанной окружности правильного треугольника

Формула радиуса описанной окружности для правильного треугольника

   

Если без иррациональности в знаменателе —

   

У правильного треугольника радиус описанной окружности в два раза больше радиуса вписанной окружности:

   

 

Радиус описанной окружности квадрата

Формула радиуса описанной окружности для квадрата

   

Если без иррациональности в знаменателе —

   

 

Радиус описанной окружности правильного шестиугольника

Формула радиуса описанной окружности для правильного шестиугольника

   

www.treugolniki.ru

Радиус описанной около треугольника окружности

Радиус описанной около треугольника окружности можно найти по одной из двух общих формул.

Кроме того, для правильного и прямоугольного треугольников существуют дополнительные формулы.

Радиус описанной около произвольного треугольника окружности

Формула I (следствие из теоремы синусов)

   

 

То есть радиус описанной окружности равен отношению длины стороны треугольника к удвоенному синусу противолежащего этой стороне угла.

В общем виде эту формулу записывают так:

   

 

Формула II.

   

в общем виде —

   

То есть чтобы найти радиус описанной около треугольника окружности, надо произведения длин сторон треугольника разделить на четыре площади треугольника.

Если площадь треугольника находить по формуле Герона

   

где p — полупериметр,

   

то получим формулу радиуса описанной около треугольника окружности через длины сторон:

   

Обе эти формулы можно применить к треугольнику любого вида. Следует только учесть положение центра.

Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника, напротив тупого угла.

 

Радиус окружности, описанной около прямоугольного треугольника

Формула:

   

То есть в прямоугольном треугольнике радиус описанной окружности равен половине гипотенузы.

Обычно гипотенузу обозначают через c (AB=c) и формулу записывают так:

   

 

Радиус окружности, описанной около правильного треугольника

Формула:

   

Если без иррациональности в знаменателе, то

   

В равностороннем треугольнике радиус описанной окружности в два раза больше радиуса вписанной окружности:

   

www.treugolniki.ru

Радиус описанной окружности равностороннего треугольника

 

— сторона треугольника

— высота

— радиус описанной окружности

 

 

Формула радиуса  описанной  окружности  равностороннего  треугольника через его сторону:

Калькулятор — вычислить, найти радиус описанной окружности равностороннего треугольника по стороне

 

 

Формула радиуса  описанной  окружности  равностороннего  треугольника через высоту:

 

Калькулятор — вычислить, найти радиус описанной окружности равностороннего треугольника по стороне

 

 

Подробности
Автор: Administrator

www-formula.ru

Радиус вписанной и описанной окружности: полезные формулы. Задание С4

В этой статье я хочу привести несколько полезных формул, которые помогают легко найти радиус вписанной и описанной окружности, и показать решение задачи из задания С4 с использованием этих формул.

1. Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности:

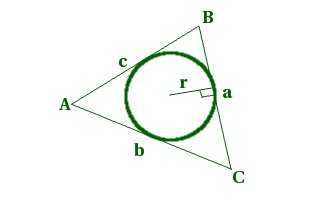 . где , r — радиус вписанной окружности.

Отсюда: 

То есть

радиус вписанной окружности равен отношению площади треугольника к его полупериметру.

Для прямоугольного треугольника , , тогда

где и — катеты треугольника, а — гипотенуза.

2. Площадь треугольника равна отношению произведения его сторон к учетверенному радиусу описанной окружности:

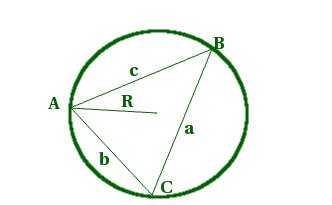
Отсюда:

Радиус  окружности, описанной около треугольника, равен отношению произведения сторон треугольника к его учетверенной площади.

3. По теореме синусов, отношение стороны треугольника к синусу противолежащего угла равно двум радиусам описанной окружности:

Отсюда:

Радиус  окружности, описанной около треугольника, равен отношению стороны треугольника к удвоенному синусу противолежащего угла.

Предлагаю вам посмотреть ВИДЕОРЕШЕНИЕ задачи:

Угол при основании равнобедренного треугольника  равен . Найдите отношение радиуса вписанной в этот треугольник окружности к радиусу описанной окружности:

 

 

И.В. Фельдман, репетитор по математике.

ege-ok.ru

Как найти радиус окружности описанной около треугольника

Предоставленные формулы помогут Вам разобраться, как найти радиус окружности, описанной около треугольника.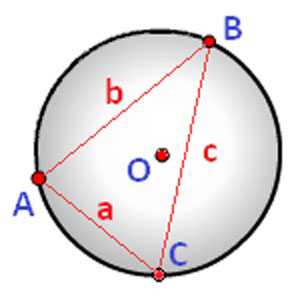

Первая формула. В формуле используются длины всех трех сторон, а также их полупериметр (то есть периметр треугольника, разделенный на 2). Полупериметр находится по формуле:

   

Запишем формулу радиуса описанной окружности:

   

Вторая формула.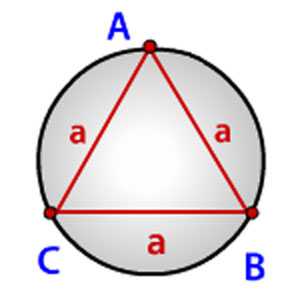


Радиус окружности, описанной вокруг треугольника с равными сторонами, можно найти лишь с помощью длины стороны этого треугольника:

   

Третья формула.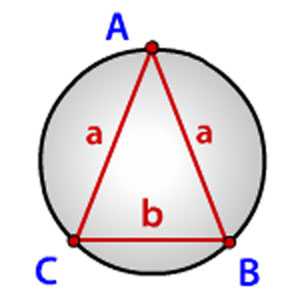

Радиус описанной вокруг равнобедренного треугольника окружности можно найти через длину боковой стороны и основания этого треугольника:

   

Четвертая формула.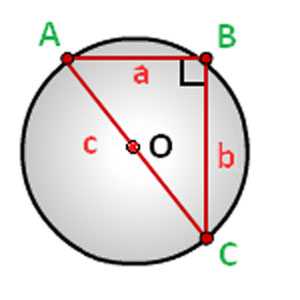

Радиус описанной вокруг прямоугольного треугольника окружности рассчитывается через катеты:

   

Шестая формула.
Радиус описанной вокруг прямоугольного треугольника окружности рассчитывается через гипотенузу:

   

Предоставленные формулы помогут найти радиус описанной окружности для любого вида треугольников.

ru.solverbook.com

Окружность, описанная около правильного треугольника

Окружность, описанная около правильного треугольника, обладает всеми свойствами описанной около произвольного треугольника окружности и, кроме того, имеет свои собственные свойства.

1) Центр описанной около треугольника окружности — точка пересечения серединных перпендикуляров к его сторонам.

Поскольку в равностороннем треугольнике медианы, высоты и биссектрисы совпадают, центр описанной около правильного треугольника окружности лежит в точке пересечения его медиан, высот и биссектрис.

Например, в правильном треугольнике ABC AB=BC=AC=a

точка O — центр описанной окружности.

AK, BF и CD — медианы, высоты и биссектрисы треугольника ABC.

   

   

2) Расстояние от центра описанной окружности до вершин треугольника равно радиусу. Так как центр описанной около равностороннего треугольника окружности лежит на пересечении его медиан, а медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то радиус описанной окружности составляет две трети от длины медианы:

   

   

Таким образом, формула радиуса описанной около правильного треугольника окружности —

   

И обратно, сторона равностороннего треугольника через радиус описанной окружности —

   

3) Формула для нахождения площади правильного треугольника по его стороне —

   

Отсюда можем найти площадь через радиус описанной окружности:

   

Таким образом, формула площади площади правильного треугольника через радиус описанной окружности —

   

4) Центр описанной около правильного треугольника окружности совпадает с центром вписанной в него окружности.

5) Радиус описанной около равностороннего треугольника окружности в два раза больше радиуса вписанной окружности:

   

www.treugolniki.ru

Радиус окружности, описанной около правильного треугольника

Определение и формулы окружности, описанной около правильного треугольника

Радиус описанной окружности для любого треугольника вычисляется по формуле

   

где – стороны треугольника, а – его площадь.

Рассмотрим правильный треугольник, у которого все стороны равны между собой. Тогда радиус окружности, описанной около этого треугольника, будет равен

   

или

   

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com