Средняя линия. Средняя линия в трапеции. Равносторонний треугольник

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Средняя линия. Средняя
линия в трапеции.
Равносторонний
треугольник.
№15,17.
План
›
›
›
›
Средняя линия треугольника
Средняя линия трапеции
Правильный треугольник
Формула высоты, медианы и биссектрисы правильного
треугольника
› Формула радиуса вписанной окружности правильного
треугольника
› Формула радиуса описанной окружности правильного

треугольника
› Свойство медиан
СРЕДНЯЯ ЛИНИЯ
ТРЕУГОЛЬНИК
СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА
› Треугольник — фигура, состоящая из трёх точек, не
лежащих на одной прямой, и трёх отрезков,
соединённых последовательно.
› Средняя линия треугольника – отрезок,
соединяющий середины двух сторон.
Свойства средней линии:
1. MN II AC – параллельна основанию
1
2. MN = 2AC – равна половине основания
1
1
3. SBMN = 4SABC – отсекает от треугольника 4 часть
4. 3 средние линии треугольника делят его на 4 равных
треугольника
ЗАДАНИЕ №15 ИЗ ОГЭ
ЗАДАНИЕ №1
Дан треугольник ABC. На
сторонах AB и BC взяты точки
M и N, которые являются
серединами сторон AB и BC.
Найдите длину MN, если
известно, что сторона AB
равна 10, сторона AC равна 12,
сторона BC равна 14.
Решение:
ЗАДАНИЕ №1
Дан треугольник ABC. На
сторонах AB и BC взяты точки
M и N, которые являются
серединами сторон AB и BC.
Найдите длину MN, если
известно, что сторона AB
равна 10, сторона AC равна 12,
сторона BC равна 14.
Решение:
MN – средняя линия.
Средняя линия параллельна основанию
и равна её половине.
ЗАДАНИЕ №1
Дан треугольник ABC. На
сторонах AB и BC взяты точки
M и N, которые являются
серединами сторон AB и BC.
Найдите длину MN, если
известно, что сторона AB
равна 10, сторона AC равна 12,
сторона BC равна 14.
Решение:
MN – средняя линия.
Средняя линия параллельна основанию
и равна её половине.
1
MN = ⋅ 12
2
MN = 6
Ответ: 6
ЗАДАНИЕ №2
Дан треугольник ABC, DE –
средняя линяя треугольника.
Площадь треугольника CDE
равна 15. Найдите площадь
треугольника ABC.
Решение:
ЗАДАНИЕ №2
Дан треугольник ABC, DE –
средняя линяя треугольника.
Площадь треугольника CDE
равна 15. Найдите площадь
треугольника ABC.
Решение:
Площадь маленького треугольника =
1
площади большого треугольника.
4
ЗАДАНИЕ №2
Дан треугольник ABC, DE –
средняя линяя треугольника.
Площадь треугольника CDE
равна 15. Найдите площадь
треугольника ABC.
Решение:
Площадь маленького треугольника =
1
площади большого треугольника.
4
SCDE = 15
SABC = ?
SCDE = 15
SABC = x
ЗАДАНИЕ №2
Дан треугольник ABC, DE –
средняя линяя треугольника.
Площадь треугольника CDE
равна 15. Найдите площадь
треугольника ABC.
Решение:
1

English     Русский Правила

Задание 3. — Студопедия

Поделись с друзьями: 

1. На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром 1 см 1 см изоб­ра­жен тре­уголь­ник (см. ри­су­нок). Най­ди­те его пло­щадь в квад­рат­ных сан­ти­мет­рах.

2. На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром 1 см 1 см изоб­ра­жен тре­уголь­ник (см. ри­су­нок). Най­ди­те его пло­щадь в квад­рат­ных сан­ти­мет­рах.

3. Пло­щадь пря­мо­уголь­но­го тре­уголь­ни­ка равна 16. Один из его ка­те­тов равен 4. Най­ди­те дру­гой катет.

4. Пло­щадь тре­уголь­ни­ка ABC равна 4. DE —сред­няя линия. Най­ди­те пло­щадь тре­уголь­ни­ка CDE.

5. В тре­уголь­ни­ке угол равен , . Най­ди­те угол . Ответ дайте в гра­ду­сах.

6. В тре­уголь­ни­ке – бис­сек­три­са, угол равен , угол равен . Най­ди­те угол . Ответ дайте в гра­ду­сах.

7. В пря­мо­уголь­ном тре­уголь­ни­ке угол между вы­со­той и бис­сек­три­сой, про­ве­ден­ны­ми из вер­ши­ны пря­мо­го угла, равен . Най­ди­те мень­ший угол дан­но­го тре­уголь­ни­ка. Ответ дайте в гра­ду­сах.

8. Най­ди­те пло­щадь пря­мо­уголь­ни­ка ABCD, счи­тая сто­ро­ны квад­рат­ных кле­ток рав­ны­ми 1.

9. Най­ди­те сто­ро­ну квад­ра­та, пло­щадь ко­то­ро­го равна пло­ща­ди пря­мо­уголь­ни­ка со сто­ро­на­ми 4 и 9.

10. Две сто­ро­ны пря­мо­уголь­ни­ка равны 6 и 8. Най­ди­те ска­ляр­ное про­из­ве­де­ние век­то­ров и .

11. Две сто­ро­ны пря­мо­уголь­ни­ка равны 6 и 8. Диа­го­на­ли пе­ре­се­ка­ют­ся в точке . Най­ди­те длину раз­но­сти век­то­ров и .

12. Две сто­ро­ны па­рал­ле­ло­грам­ма от­но­сят­ся как , а пе­ри­метр его равен 70. Най­ди­те боль­шую сто­ро­ну па­рал­ле­ло­грам­ма.

13. Пло­щадь тре­уголь­ни­ка ABC равна 12. DE ― сред­няя линия этого тре­уголь­ни­ка, па­рал­лель­ная сто­ро­не

AB. Най­ди­те пло­щадь тра­пе­ции ABDE.

14. Най­ди­те пло­щадь ромба, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

15. На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром 1 см 1 см изоб­ра­же­на тра­пе­ция (см. ри­су­нок). Най­ди­те ее пло­щадь в квад­рат­ных сан­ти­мет­рах.

16. Най­ди­те пло­щадь тра­пе­ции, изоб­ра­жен­ной на ри­сун­ке.

17. На клет­ча­той бу­ма­ге с клет­ка­ми раз­ме­ром 1 см 1 см изоб­ра­же­на фи­гу­ра (см. ри­су­нок).

Най­ди­те ее пло­щадь в квад­рат­ных сан­ти­мет­рах.

18. Най­ди­те тан­генс угла .

19. Най­ди­те тан­генс угла .

20. Най­ди­те (в см2) пло­щадь S за­кра­шен­ной фи­гу­ры, изоб­ра­жен­ной на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). В от­ве­те за­пи­ши­те .

21. Най­ди­те пло­щадь круга, длина окруж­но­сти ко­то­ро­го равна .

22. Най­ди­те пло­щадь коль­ца, огра­ни­чен­но­го кон­цен­три­че­ски­ми окруж­но­стя­ми, ра­ди­у­сы ко­то­рых равны и .

23. Ги­по­те­ну­за пря­мо­уголь­но­го тре­уголь­ни­ка равна 12. Най­ди­те ра­ди­ус опи­сан­ной окруж­но­сти этого тре­уголь­ни­ка.

24. Около тра­пе­ции опи­са­на окруж­ность. Пе­ри­метр тра­пе­ции равен 22, сред­няя линия равна 5. Най­ди­те бо­ко­вую сто­ро­ну тра­пе­ции.

25. На клет­ча­той бу­ма­ге на­ри­со­ва­но два круга. Пло­щадь внут­рен­не­го круга равна 1. Най­ди­те пло­щадь за­штри­хо­ван­ной фи­гу­ры.

26. Из круга с ра­ди­у­сом 7 вы­ре­зан сек­тор, пло­щадь ко­то­ро­го равна 35. Най­ди­те длину дуги сек­то­ра.

27. Бо­ко­вые сто­ро­ны тра­пе­ции, опи­сан­ной около окруж­но­сти, равны 3 и 5. Най­ди­те сред­нюю линию тра­пе­ции.

28. В че­ты­рех­уголь­ник впи­са­на окруж­ность, , . Най­ди­те пе­ри­метр че­ты­рех­уголь­ни­ка.

29. Най­ди­те длину век­то­ра (6; 8).

30. Век­тор с на­ча­лом в точке (2; 4) имеет ко­ор­ди­на­ты (6; 2). Най­ди­те абс­цис­су точки .

31. Най­ди­те квад­рат длины век­то­ра + .

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:  



‘pasagot naman po yung maayos. Оценка Выберите букву правильного ответа. Напишите свои ответы на отдельном листе бумаги; Для пунктов 1-2 треугольник ABC прямоугольный в B.

Если 2C= 426 и b= 18,5 см, какова длина стороны a? А11,75 см Б. 13,75 см 15,75 см Г. 17,75 см 2. Какова мера A ? 4. 480 Б. 520 560 Д. 620 17см бз 13 см 3. Какова длина стороны а? А 10,25 см Б. 10,65 см В. 10,95 см Д. 11,15 см Что является мерой ЛА? 432.120 Б. 36.160 С.38.120 Д. 40.120 5. Что такое mcasure LB? А.490,880 Б. 46,380 С.42.580 Д. 40.120 Для элементов 6-7 треугольник ACB прямоугольный в точке C. Если /B = 470 и a = 21 см, 6. Какова длина стороны c? 4 21,92 см Б. 28,69 см В. 30,79 см Г. 34,12 см 7.Как долго i5 tc сторона b? А 20,52 см Б 21,52 см С. 22,52 см Д. 23,52 см’

Вопрос

‘pasagot naman po yung maayos. Оценка Dtrectlons: Выберите букву правильного ответа. Напишите свои ответы на отдельном листе бумаги; Для пунктов 1-2 треугольник ABC прямоугольный в B. Если 2C= 426 и b= 18,5 см, какова длина стороны a? А11,75 см Б. 13,75 см 15,75 см Г. 17,75 см 2. Какова мера A ? 4. 480 Б. 520 560 Д. 620 Для пунктов 3-5 укажите свой ответ в данном прямоугольном треугольнике ниже: 17см бз 13 см 3. Какова длина стороны а? А 10,25 см Б. 10,65 см С 10,95 см Д. 11,15 см Что является мерой ЛА? 432.120 Б. 36.160 С.38.120 Д. 40.120 5. Что такое mcasure LB? А.49.880 Б.46.380 С.42.580 Д. 40.120 Для элементов 6-7 треугольник ACB прямоугольный в точке C. Если /B = 470 и a = 21 см, 6. Какова длина стороны c? 4 21,92 см Б. 28,69 см В. 30,79 см Г. 34,12 см 7.Как долго i5 tc сторона b? А 20,52 см Б 21,52 см С. 22,52 см Д. 23,52 см’

Мгновенное решение:

Шаг 1/5
Шаг 1: Начертите прямоугольный треугольник АВС. Длина стороны А равна 10,25 см.

Шаг 2/5
Шаг 2: Поскольку прямоугольный треугольник ABC прямоугольный в точке B, длина стороны BC также равна углу между BC и AB. Следовательно, длина стороны ВС равна 10,65 см.

Шаг 3/5
Шаг 3: Поскольку прямоугольный треугольник ABC прямоугольный в точке C, длина стороны CA также равна углу между CA и AB. Следовательно, длина стороны СА равна 10,95 см.

Рекомендация видео лучшего совпадения: 9*) Четверть 3 — Модуль 5: Trangle Mdllne Theoren Указания: Выберите один из вариантов правильного ответа: Запишите свой ответ на бланке для ответов. Как вы называете сегмент, который берет начало в середине двух сторон треугольника? Основание Средняя линия C: Середина D. Гипотенуза Что (теорема stales lhat; «Отрезок (hat соединяет середины двух сторон треугольника Параллелен t0 третьей стороне и вдвое короче»? Теорема о чередующихся внутренних углах Треугольник о средней линии Теорема Пифагора) Теорема D. Теорема подобия Какой длины средняя линия треугольника, если третья сторона, параллельная ей, равна 32 см? A. 8 см B. 10 см C. 14 см D. 16 см Найдите длину третьей стороны треугольника. (кольцо, если его средняя линия измеряет 24 м. A, 24 м B, 38 м C, 40 м D, 48 м 5, Учитывая ADOG со средней линией ME, найдите значение x A 10 B. 11 C 12 D.13 Какая теорема утверждает, что это; «Отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и вдвое короче» Теорема подобия C.

Теорема Пифагора B. Теорема о средней линии треугольника Теорема о альтернативных внутренних углах Найдите длину третьей стороны треугольника, если ее средняя линия меры 45 см? A. 45 см B, 50 см C.90 см Д. 100 см Размер третьей стороны треугольника (8x-5) см. Чему равен х, если длина средней линии 14 м? Б.9 В.10 Г.11 А.8 9. Учитывая ACAT со средней линией NG; найти значение x A. 4 B. 3 C.2 18 см и ЭН-(32-х) 10. В АЭАХ; M — середина EA, а T — середина HA: если MT-(2x-9) см см, каково значение x? C.12 D. 13 A. 10 B 11′

Рекомендуемые видео

Стенограмма

Нам нужно ответить на это. Итак, как называется отрезок, соединяющий две стороны треугольника? Это не может быть новостью о хип-хопе и не может быть базой, поскольку она соединяет две средние точки. Это средняя линия или средний сегмент. Отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне. Треугольник он такой. Линия была нулевой. Какова длина середины треугольника? Размер третьей стороны равен 32. Половина стороны параллельна средней линии. Это будет 16. Нам нужно узнать длину третьей стороны треугольника. Я думаю, что 18 умножить на два равно трем X. Это равно трем X плюс шесть. Перемещаем шестерку. Три Х равно 30. Так Х. Равно 10. Нужно найти средний отрезок. Я делаю пять из них. Вот этот. Вернемся к числу четыре. Найдите длину третьей стороны треугольника. Если он измеряет 24. Если вы хотите пойти на противоположную сторону, вы должны удвоить среднюю линию. Будет 48. Итак, вопрос шестой. Отрезок, соединяющий середины двух сторон треугольника, параллелен третьей стороне и равен половине его длины. Это треугольник. Теорема о средней линии связана. Если его средняя линия равна 45, нам нужно найти длину третьей стороны. Вы удваиваете его, когда мы идем от средней линии к противоположной стороне. Так что 90. Третья сторона треугольника равна трем Х 5. Если средняя линия равна 14, что это? Чтобы сделать третью сторону, нужно две линии. Это равно три х минус пять. Пять добавлены к другой стороне.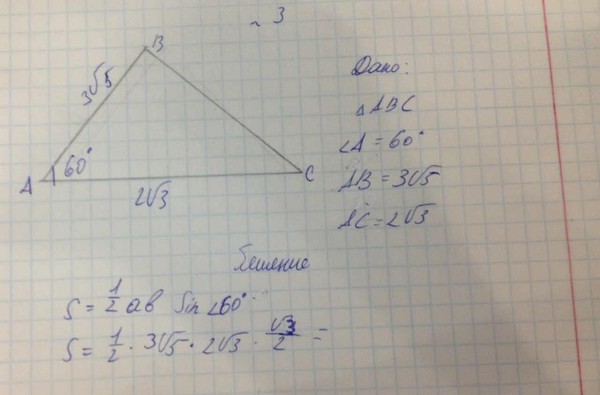 28 плюс пять равно 33. Это равно 11. Тогда у нас есть вопрос №9. Ценность действий — это то, что нам нужно найти. Требуется 23 X плюс шесть, чтобы получить 18, и еще два, чтобы получить большую единицу. Под двумя я подразумеваю. У нас есть три Х. Шесть равно девяти. Перемещаем шестерку. Это три X. Это равно трем. Это так X. У меня есть место для работы, потому что наш последний позволил мне участвовать в гонках. В последнем говорится, что если середина пути — это E. A. N. T. Какова картина? Без фото сложно сказать. Середина E.A.H. Это M, это H.A., это T. Мы знаем, что они параллельны, потому что у меня эта картинка сбоку. Мне нужно больше места, потому что потребуется два MT, чтобы равняться одному H.E. 2 х -9равен H.E. Четыре минус 18 равно 32 минус X. X нужно передвинуть. Это равно 30, чтобы переместить 18. 32 плюс 18 будет 50. Число 10 равно X.

Поделиться вопросом

Добавить в плейлист

Хммм, кажется, у вас нет плейлистов. Пожалуйста, добавьте свой первый плейлист.

`

глава 8 викторина 1 форма g ответы0005

[PDF] Тест по главе 8 1

www.anderson.k12.ky.us › Downloads › Обзор главы 8

Тест по главе 8 1. Форма G. Уроки с 8-1 по 8-3. Ты знаешь как? Найдите значение х. Выразите ответ в простейшей радикальной форме. 1.

[PDF] Глава 8 Геометрия Форма 1 Ответ Pdf

fotografiados.fmdos.cl › pdf › публикация › глава-8-геометрия-для…

Прямо здесь, у нас есть бесчисленное количество электронных книг Глава 8 Геометрия Форма 1 Ответ PDF и коллекции для проверки. Мы дополнительно даем варианты типов и в дополнение к.

Форма теста 1 главы 8

форма-теста главы 8-1.hammer-unternehmerinnen.de

Форма теста главы 8 1 ключ ответа By gr dr pv gi kk Приведенные ниже советы помогут вам заполнить главу 8 Test… Заключительный тест главы 1 12 форма g ответы геометрия.

[PDF] Prentice Hall Gold Geometry Form G Answers (PDF)

content. consello.com › trackid › FileName=Prentice Hall Gold Geome…

SOLUTIONS to HWK WORKBOOK 2.1-2.4 ADV GEO.pdf. Параллельные прямые и треугольники. Глава 8 Викторина 1 — anderson.k12.ky.us. Имя Класс Дата 7-1 — hart.k12.ky.us.

[PDF] Форма теста по главам G

portal.mywccc.org › Математика › Ресурсы

Тест по главам. Форма Г. Глава 8. Даны длины трех сторон треугольника. Опишите каждый треугольник как остроугольный, прямоугольный или тупоугольный. 1. 5, 6, 10.

Ответ на викторину 1 по главе 4 по геометрии — YB Pferdetransporte

nplqmc.yb-pferdetransporte.de › викторина по главе 4-1-a…

Викторина 1 Форма G Форма теста главы геометрии g, глава 8, викторина 1, глава 11, ресурсы, мастера, решение математических задач, название, дата, период 8, глава 8, форма теста 1 …

[PDF] Geometry Chapter 8 Test Answer Key Read Pdf Free — emotive

cms.uat.bluesphere.emotiveagency.com › читатель › анимация › FileNa. ..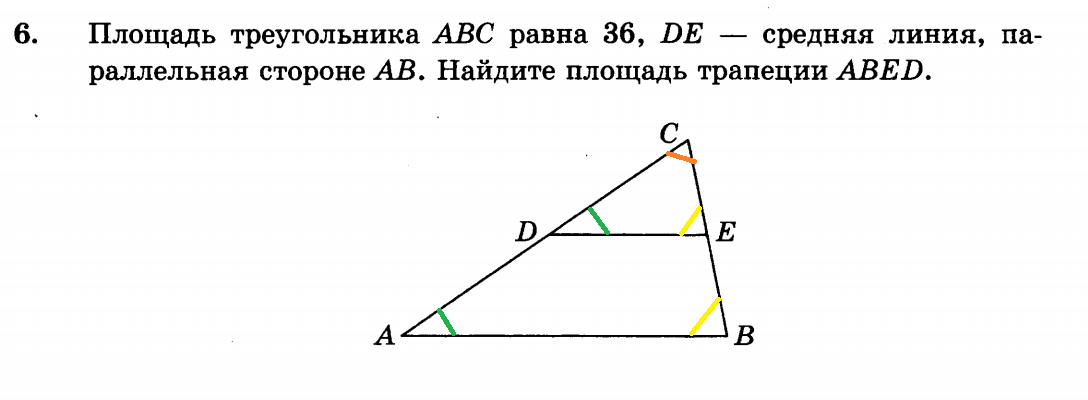

геометрия глава 5 тест ответы скачать бесплатно pdf треугольники глава 5 … викторина по главе 8 1 20 декабря 2021 г. веб-форма теста по главе 8 g знаете ли вы, как найти …

[PDF] Глава 8 Геометрия Форма 1 Ответ — SapnaOnline

clickanalytics.sapnaonline.com › fulldisplay › FileName=Глава 8 Ge…

28.05.2021 · Геометрия Глава 8 Тест Ответы Форма Г…8 Тест, Форма 1 БАЛЛ. PT3 Математика Форма 1 Глава 8 Прямые и углы Часть 1 PT3 Математика F1.

[PDF] Quiz Geometry 8 Form K Answers

mar.naturaeco.com › static › source=Quiz-Geometry-8-Form-K-Answ…

одна глава 8 викторина 1 веб-викторина глава 8 1 форма g уроки 8 с 1 по 8 3 знаете ли вы, как найти значение x выразить свой ответ в простейшей радикальной форме 1 …

[PDF] Глава 8 Форма K Test — CliqueiMudei

sentry.cliqueimudei.com › fulldisplay › FileName=Chapter 8 Form K …

08.01.2023 · Геометрия Chapter 8 Test Answers.