Геометрия 7-9 класс. Площадь параллелограмма и ромба — math200.ru
Skip to contentГеометрия 7-9 класс. Площадь параллелограмма и ромбаadmin2022-12-20T16:36:51+03:00
Скачать файл в формате pdf.
Геометрия 7-9 класс. Площадь параллелограмма и ромба
Параллелограмм. Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.
Свойства и признаки параллелограмма
- Диагональ разбивает параллелограмм на два равных треугольника.
- Противоположные стороны параллелограмма попарно равны.
- Противоположные углы параллелограмма попарно равны.
- Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
- Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.
- Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.

- Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник — параллелограмм.
Формулы площади параллелограмма
- Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне, т.е. \(S = a\,h\).
- Площадь параллелограмма равна произведению двух смежных сторон на синус угла между ними, т.е. \(S = ab\sin \alpha \).
- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними, т.е. \(S = \frac{1}{2}\,\,{d_1}\,{d_2}\,\sin \,{\rm{\varphi }}\).
Ромб. Ромбом называется четырёхугольник, все стороны которого равны.
Свойства и признаки ромба
- Диагонали ромба делят его углы пополам.
- Если диагонали параллелограмма перпендикулярны, то этот параллелограмм — ромб.
- Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм — ромб.
 2}\sin \alpha \).
2}\sin \alpha \). - Площадь ромба равна половине произведения диагоналей, т.е. \(S = \frac{1}{2}{d_1}{d_2}\).
| Задача 1. Найдите площадь параллелограмма ABCD, если DC = 7, а высота DH проведенная к стороне Ответ ОТВЕТ: 35. | |
| Задача 2. По данным на рисунке найдите площадь параллелограмма ABCD. Ответ ОТВЕТ: 156. | |
| Задача 3. По данным на рисунке найдите площадь ромба ABCD. Ответ ОТВЕТ: 32. | |
| Задача 4. По данным на рисунке найдите площадь параллелограмма ABCD. Ответ ОТВЕТ: 126. | |
| Задача 5. По данным на рисунке найдите площадь ромба ABCD, если его периметр равен 36. Ответ ОТВЕТ: 40,5. | |
| Задача 6. По данным на рисунке найдите площадь параллелограмма ABCD. Ответ ОТВЕТ: 40. | |
| Задача 7. По данным на рисунке найдите площадь параллелограмма ABCD. Ответ ОТВЕТ: 768. | |
| Задача 8. По данным на рисунке найдите площадь параллелограмма ABCD. Ответ ОТВЕТ: 480,5. | |
| Задача 9. По данным на рисунке найдите площадь параллелограмма Ответ ОТВЕТ: 48. | |
| Задача 10. По данным на рисунке найдите площадь параллелограмма ABCD, если его периметр равен 54. Ответ ОТВЕТ: 120. | |
Задача 11. По данным на рисунке найдите площадь параллелограмма ABCD, если его периметр равен 50. \circ }30′.\) Найдите площадь ромба, если его высота равна 10. \circ }30′.\) Найдите площадь ромба, если его высота равна 10.Ответ ОТВЕТ: 200. | |
Реклама
Поддержать нас
Задачи 1 ЕГЭ профильная математика, сортировка по темам
MATHM >> ЕГЭ >> ЕГЭ профиль >>
Задача 1
ЗАДАЧА 1
сортировка
по сложности
ЗАДАЧА 1
сортировка
по темам
СПИСОК ТЕМ
Тема 1: Прямоугольный треугольник
Тема 2: Равнобедренный треугольник
Тема 3: Треугольник общего вида
Тема 5: Трапеция
Тема 6: Квадрат, прямоугольник
Тема 7: Окружность – углы, касательные, секущие, хорды
Тема 8: Вписанные и описанные окружности
Тема 9: Прочие фигуры
Задачи разделены на темы.
 Задачи из любой темы вполне реально встретить на настоящем экзамене ЕГЭ. Внутри каждой темы задачи
мы постарались расположить по возрастанию сложности.
Задачи из любой темы вполне реально встретить на настоящем экзамене ЕГЭ. Внутри каждой темы задачи
мы постарались расположить по возрастанию сложности.Тема 1: Прямоугольный треугольник
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
Тема 2: Равнобедренный треугольник
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
Тема 3: Треугольник общего вида
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
Тема 4: Параллелограмм, ромб
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
Тема 5: Трапеция
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
Тема 6: Квадрат, прямоугольник
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
Тема 7: Окружность – углы, касательные, секущие, хорды
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
Тема 8: Вписанные и описанные окружности
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
Тема 9: Прочие фигуры
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
посмотреть ответ
Как найти площадь ромба (формула и видео)
ромб это плоская фигура, поэтому она двухмерна. Это замкнутая фигура с прямыми (линейными) сторонами, один из многих четырехугольников (четырехугольников). Это частный случай параллелограмма. Все четыре стороны имеют одинаковую длину, и обе пары противоположных сторон параллельны. Противоположные углы тоже равны. Вот и все!
Это замкнутая фигура с прямыми (линейными) сторонами, один из многих четырехугольников (четырехугольников). Это частный случай параллелограмма. Все четыре стороны имеют одинаковую длину, и обе пары противоположных сторон параллельны. Противоположные углы тоже равны. Вот и все!
Ромб также может называться ромбом, ромбом или ромбом. Квадрат – это ромб с четырьмя равными (прямыми) углами.
Свойства ромбаИногда вы видите ромб с двумя горизонтальными сторонами, как будто автобус наехал на квадрат и перевернул его (это удобная мнемоника, чтобы запомнить его название: бег, автобус; ромб). В этом представлении высоту (высоту) ромба можно очень легко увидеть.
Иногда ромб рисуется так, что одна из его двух диагоналей (линий, соединяющих противоположные вершины) является горизонтальной, что делает форму ромба более очевидной.
Одним из необычных свойств ромба является то, что его диагонали всегда перпендикулярны друг другу, независимо от углов четырех вершин ромба. {2}\sin \влево(\угол B\вправо)площадь=s2sin(∠A)=s2sin(∠B)
{2}\sin \влево(\угол B\вправо)площадь=s2sin(∠A)=s2sin(∠B)
Если известны длины диагоналей, формула будет следующей: площадь=(d1×d2)2площадь=\frac{({d}_{1}\times {d}_{2})}{2} area=2(d1×d2)
Как найти площадь ромба
Построим ромб со сторонами ss и четырьмя вершинами с внутренними углами A , B , C 9, и D . Мы можем соединить противоположные углы диагоналями d1{d}_{1}d1 и d2{d}_{2}d2. Соединение одной стороны с другой перпендикулярной линией дает высоту или высоту. У нашего ромба:
Площадь РомбаЧетыре равной длины: AB , до н.э. , CD и DA
Четыре внутренних ракурса с противоположными равенствами: ряд = ° С. и и и . ∠b=∠d
Две диагонали: d1{d}_{1}d1 и d2{d}_{2}d2; только в квадрате это будут диагонали одинаковой длины
Высота или высота – Когда ромб расположен двумя сторонами горизонтально (плоско),0089 h — расстояние от одной стороны до противоположной; отрезок прямой, перпендикулярный одной стороне, соединяющий с противоположной стороной
Поскольку четыре стороны равны, если вы знаете длину любой стороны ss, вы знаете длину всех четырех сторон.
Поскольку противоположные углы равны, а четыре угла в сумме составляют 360° , если известен один угол, можно найти все углы. Поскольку противоположные стороны параллельны, смежные углы ромба в сумме дают 180° .
Чтобы найти площадь, вам нужно знать высоту или высоту h ромба.
Помните, что высота не равна длине стороны.
Формула с использованием высоты и стороны
Если у вас есть мысленная картина ромба, являющегося наклонным квадратом, этот первый метод будет иметь большой смысл.
Если бы ромб был квадратом, его площадь в квадратных единицах была бы равна стороне на сторону, верно? Что ж, когда ромб наклонен, вы можете представить, что отрезали треугольную часть на одной стороне ромба и сдвинули ее на соответствующую другую сторону, восстановив форму до ее прямоугольности.
Вы не можете разрезать каждый встречный ромб, поэтому подумайте, что на самом деле представляет собой построенная перпендикулярная сторона: высота или высота ромба.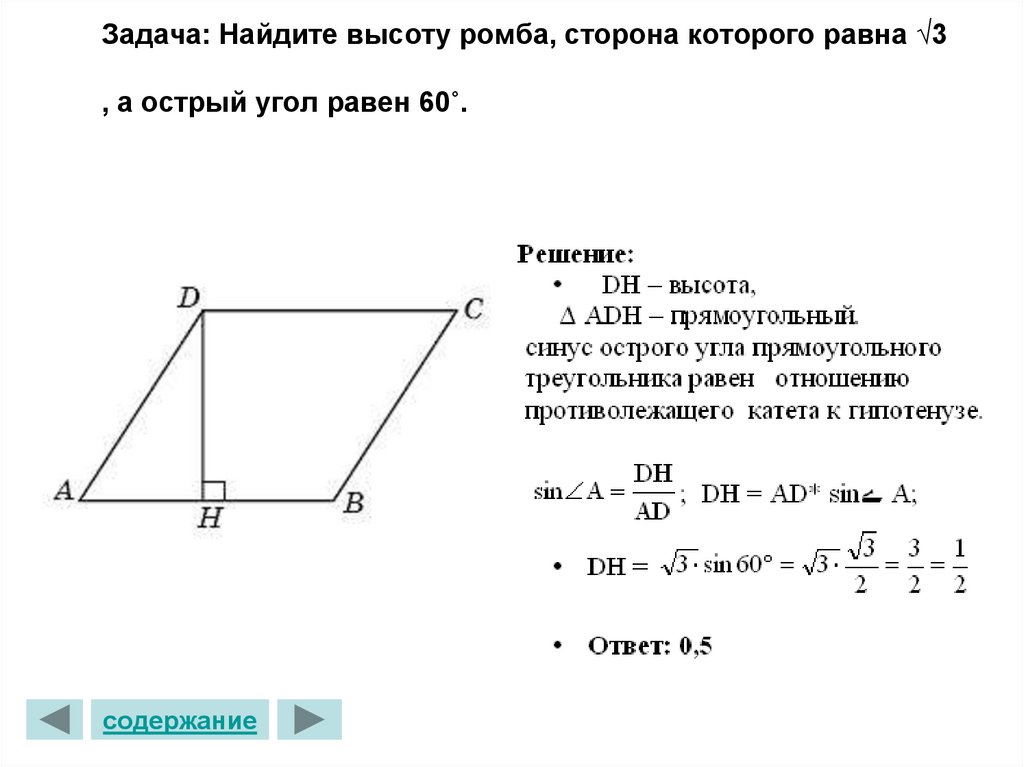
Итак, первый и, пожалуй, самый простой способ найти площадь ромба — найти длину одной стороны и высоту ромба. Умножьте их, и вы получите площадь в квадратных единицах:
Пример:
Итак, если у вас есть ромб, высота которого равна 3 дюймам, а стороны равны 5 дюймам, то площадь этого ромба равна:
Найдите площадь ромба, примерДругой пример: сторона s равна 15 футов , а высота 11 футов . Площадь этого ромба равна:
Формула с использованием стороны и угла
Второй способ найти площадь ромба — это знать длину стороны s и величину одного угла ( ∠A или ∠B ). Здесь нужно найти синус угла, но формула по-прежнему проста:
Вы можете видеть, что эти две формулы дают один и тот же результат, поэтому это означает:
Пример:
Найдите площадь ромба — боковой угол пример В ромбе с сторонами по 10 ярдов и внутренними смежными углами 60 ° и 120° тогда, чтобы найти площадь этого ромба, мы подставим это в нашу формулу площади, используя сторону и угол.
Что также равно:
Затем мы умножаем эти два числа вместе:
Тогда мы получаем ответ:
Помните, что для этого метода не имеет значения выбранный вами угол. Формула одинакова для обоих углов; вам просто нужно выбрать один.
Синус 60° и 120° один и тот же, 0,866
Формула с использованием диагоналей
Помните, что диагонали ромба всегда пересекаются пополам под прямым углом и друг друга. Это означает, что две диагонали образуют две стороны квадрата, который в два раза больше ромба.
Вы можете найти площадь ромба в квадратных единицах, умножив длины двух диагоналей (d1{d}_{1}d1 и d2{d}_{2}d2) и разделив на два.
Если бы у нашего ромба были размеры только диагоналей, мы бы использовали эту формулу.
Пример:
Если бы диагонали нашего ромба были равны 24 и 18 метров в длину, то чтобы найти площадь этого ромба, мы подставили бы числа в нашу формулу.
Площадь диагонали ромба формулаПеремножаем две диагонали:
Тогда получаем ответ:
Итог урока
Вы рассмотрели, что такое ромб, как он вписывается в семейство четырехугольников, каковы его различные части и как найти его площадь .
Объяснение урока: Площадь ромба
В этом объяснителе мы научимся находить площадь ромба с помощью длины его диагоналей.
Напомним, что ромбом называется любой четырехугольник, у которого все четыре стороны равны длина. Поскольку ромб также является параллелограммом, его площадь можно вычислить из длину его основания и высоту перпендикуляра по формуле площадь=𝑏ℎ.
Альтернативная формула площади ромба, которую мы здесь выводим, вместо этого использует длины его диагоналей. Диагонали любого параллелограмма делят единицу пополам. другое, но дополнительное свойство диагоналей ромба состоит в том, что они перпендикулярны, как показано на рисунке ниже.
Рассмотрим диагональ 𝐵𝐷, которая делит ромб на конгруэнтные
треугольники 𝐴𝐵𝐷 и 𝐶𝐵𝐷. Поскольку треугольники равны, каждая их площадь равна
половина площади ромба. Эквивалентно, мы можем утверждать, что
площадь ромбаплощадьтреугольника𝐴𝐵𝐶𝐷=2×𝐴𝐵𝐷.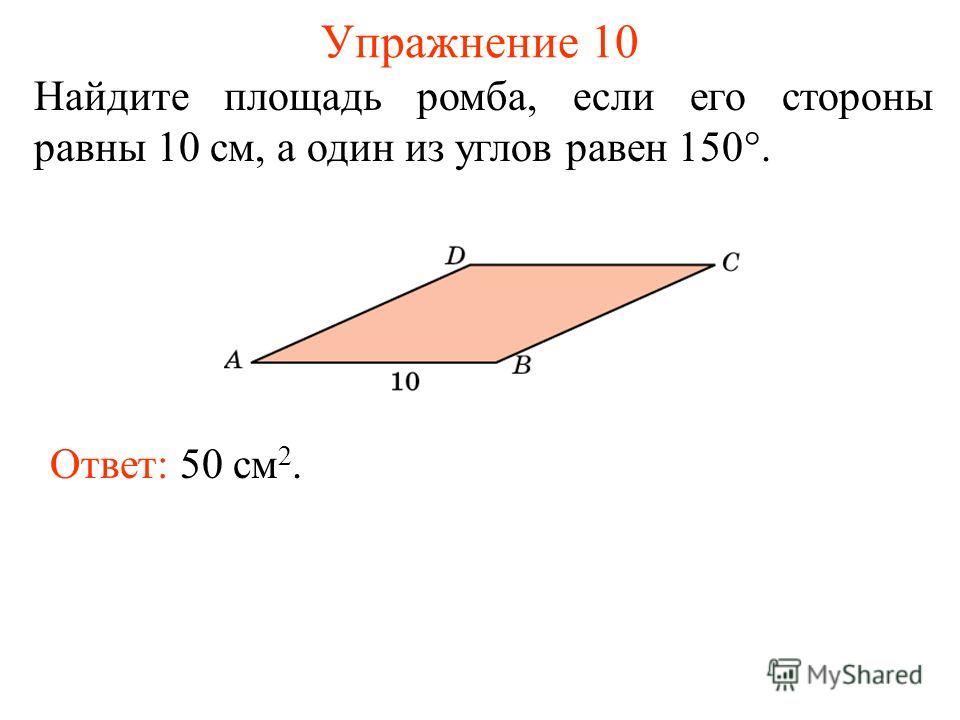
Предположим также, что длины диагоналей равны 𝑑 и 𝑑 единиц, как показано на рисунке ниже.
Площадь треугольника 𝐴𝐵𝐷 можно рассчитать по формуле площадьтреугольника=12𝑏ℎ, где 𝑏 представляет основание треугольника и ℎ представляет перпендикулярную высоту. Из рисунка мы определить, что основание этого треугольника равно 𝐵𝐷, длина которого 𝑑 единицы измерения. Перпендикулярная высота этого треугольника равна 𝐴𝐸. Вспоминая еще раз, что диагонали ромб делит друг друга пополам, мы известно, что 𝐴𝐸 составляет половину длины диагональ 𝐴𝐶 и поэтому имеет длину 𝑑2 ед. Следовательно, площадь треугольниковквадрата единиц𝐴𝐵𝐷=12×𝑑×𝑑2=𝑑𝑑4.
Следовательно, площадь ромба равна площадь ромбаквадрата единиц𝐴𝐵𝐶𝐷=2×𝑑𝑑4=𝑑𝑑2.
Формула: Площадь ромба
Площадь ромба равна половине произведения длин его
диагонали. Для ромба с диагоналями длины 𝑑 и
𝑑 единиц,
площадь ромбаквадрата единиц = 𝑑𝑑2.
В нашем первом примере мы применим эту формулу для вычисления площади ромб, нарисованный внутри прямоугольника.
Пример 1. Нахождение площади ромба внутри прямоугольника
На рисунке изображен ромб внутри прямоугольника. Найдите площадь ромба на два десятичных знака.
Ответ
При рассмотрении диаграммы мы видим, что каждая вершина ромба 𝑋𝑇𝑍𝑌 находится в середине одной из сторон прямоугольника. Например, вершина 𝑋 находится на середине стороны 𝐴𝐷. Мы знаем это, потому что 𝐴𝑋 и 𝑋𝐷 есть равной длины. Отсюда можно сделать вывод, что диагональ ромба 𝑋𝑍 параллелен 𝐴𝐵 и 𝐷𝐶, а диагональ 𝑌𝑇 параллелен 𝐴𝐷 и 𝐵𝐶.
Из этого также следует, что 𝑋𝑍=𝐴𝐵=𝐷𝐶 и 𝑌𝑇=𝐴𝐷=𝐵𝐶.
Размеры прямоугольника указаны в вопросе и, следовательно, 𝑋𝑍=15,8см и 𝑌𝑇=30,3см.
Теперь вспомним, что площадь ромба равна половине произведения
длины его диагоналей:
площадь ромба=𝑑𝑑2,
где 𝑑 и 𝑑 — длины
диагонали. В этой задаче длины диагоналей равны
30,3 см и
15,8 см,
так что у нас есть
площадьсм𝑋𝑇𝑍𝑌=30,3×15,82=478,742=239.37.
В этой задаче длины диагоналей равны
30,3 см и
15,8 см,
так что у нас есть
площадьсм𝑋𝑇𝑍𝑌=30,3×15,82=478,742=239.37.
Кратко отметим связь между ромбом 𝑋𝑇𝑍𝑌 и прямоугольник 𝐴𝐵𝐶𝐷 в предыдущем примере. Площадь любого прямоугольника равна произведению его длины на ширину, или, другими словами, произведение его размеров. В этой задаче длины диагоналей ромба равны размерам прямоугольник, а так как площадь ромба равна половине произведения его диагоналей, это эквивалентно половине произведения размеры прямоугольника. Это свидетельствует о том, что площадь ромб, нарисованный внутри прямоугольника так, что каждая вершина ромба находится в середине одной из сторон прямоугольника, составляет половину площади окружающего его прямоугольника.
Теперь мы рассмотрели один пример того, как вычислить площадь заданного ромба.
длины двух его диагоналей. Так же возможна работа в др. направление: если нам дана площадь ромба и длина одного из
его диагоналей, мы можем вычислить длину другой диагонали, составив
и решение уравнения. Зная площадь ромба, мы также можем вычислить
длину одной или обеих диагоналей, если мы явно не знаем
длина любого из них, но мы знаем соотношение между их длинами,
как мы увидим в нашем следующем примере.
направление: если нам дана площадь ромба и длина одного из
его диагоналей, мы можем вычислить длину другой диагонали, составив
и решение уравнения. Зная площадь ромба, мы также можем вычислить
длину одной или обеих диагоналей, если мы явно не знаем
длина любого из них, но мы знаем соотношение между их длинами,
как мы увидим в нашем следующем примере.
Пример 2. Расчет длины диагонали ромба по его площади
Одна диагональ ромба в два раза длиннее другой диагонали. Если площадь ромба 81 квадратный миллиметр, какова длина диагоналей?
Ответ
Напомним, что площадь ромба равна половине произведения длин его его диагонали 𝑑 и 𝑑: area=𝑑𝑑2.
Пусть длина меньшей диагонали равна 𝑑. Так как другая диагональ
в два раза больше первой, имеем 𝑑=2𝑑. Таким образом, мы можем сформировать
уравнение, подставив 𝑑=2𝑑 в приведенную выше формулу и установив это
выражение, равное известной площади:
𝑑×(2𝑑)2=81.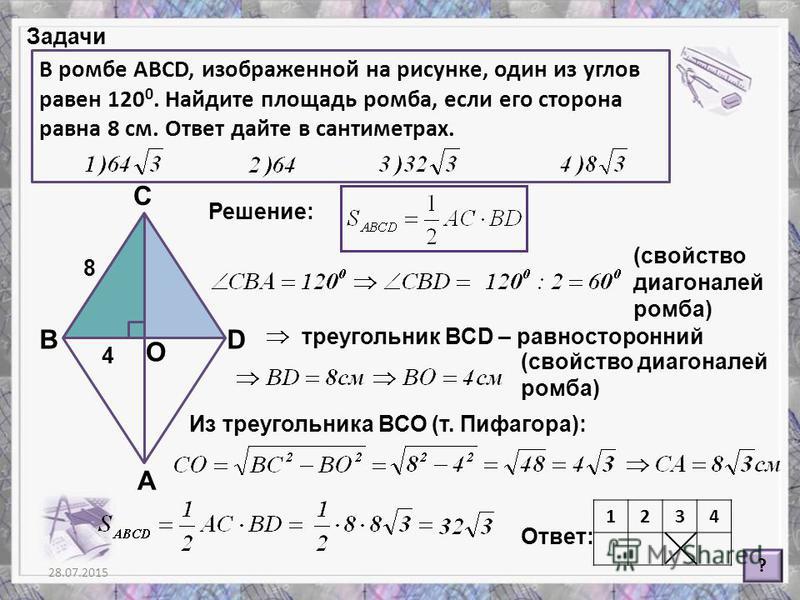
Упрощение выражения в левой части за счет сокращения коэффициента 2 дает 𝑑=81.
Мы находим 𝑑 путем извлечения квадратного корня из каждой части уравнения, принимая только положительное значение, поскольку 𝑑 представляет длину: 𝑑=√81=9.мм
Мы нашли длину меньшей диагонали 𝑑 быть 9 мм. Вторая диагональ в два раза длиннее, поэтому имеем 𝑑=2𝑑=2×9=18.мм
Длины диагоналей данного ромба равны 9мм и 18 мм.
В нашем следующем примере мы решим задачу с ромбом и квадратом которые имеют одинаковую площадь. Зная периметр квадрата и длину одной диагонали ромба вычислим длину другая диагональ ромба.
Пример 3. Нахождение длины диагонали ромба по длине другой диагонали и фигуре с одинаковой площадью
Ромб и квадрат имеют одинаковую площадь. Если периметр квадрата 44 и одна из диагоналей ромба равна 10, какой длины другая диагональ, до двух знаков после запятой?
Ответ
Чтобы связать две фигуры, нам нужно найти значение или
выражение для каждой из их областей, которые, как нам говорят, равны. Позволять
Начнем с рассмотрения квадрата.
Позволять
Начнем с рассмотрения квадрата.
Нам дано, что периметр квадрата равен 44 единицам. Мы помним, что периметр фигуры — это расстояние вокруг ее края. В случае квадрат, у которого четыре равные стороны по 𝑠 единиц длины, периметр равен равно 4𝑠. Установка этого выражения равным 44 дает уравнение, которое можно решить, чтобы определить длину стороны квадрата: 4𝑠=44𝑠=11.единиц
Площадь квадрата можно рассчитать по длине его стороны с помощью формула площадь квадрата=𝑠. Замена 𝑠=11 дает площадь квадратовквадратных единиц = 11 = 121.
Теперь мы знаем, что площадь ромба также равна 121 кв. Напомним, что площадь одного ромб равен половине произведения длин его диагоналей 𝑑 и 𝑑: площадь ромба=𝑑𝑑2.
Нам дано, что одна диагональ имеет длину 10 единиц, поэтому мы можем составить уравнение: 10×𝑑2=121.
Чтобы решить это уравнение для 𝑑, мы сначала упростим
в левой части, уменьшив коэффициент 2:
5𝑑=121.
Затем мы делим каждую часть уравнения на 5, чтобы получить 𝑑=1215=24,2.
С точностью до двух знаков после запятой длина другой диагонали ромба равна 24,20 ед.
В предыдущем примере мы использовали наши знания о том, как вычислить площадь квадрат по длине его стороны. Однако квадрат на самом деле является особым типом ромба, у которого две диагонали имеют одинаковую длину. Предположим, что каждая диагональ квадрата имеет длину 𝑑 единиц. Используя формулу площади ромба, площадь квадрата равна половине произведения длин его диагонали, ведущие к площадь квадрата=𝑑×𝑑2=𝑑2.
Формула: площадь квадрата
Площадь квадрата равна половине квадрата длины его диагонали. Для квадрата с диагональю длины 𝑑 единиц, areaofsquasquareunits=𝑑2.
В нашем следующем примере мы рассмотрим, как найти длину диагонали
шахматной доске, сначала рассмотрев взаимосвязь между площадью и
диагонали меньших квадратов, из которых состоит шахматная доска.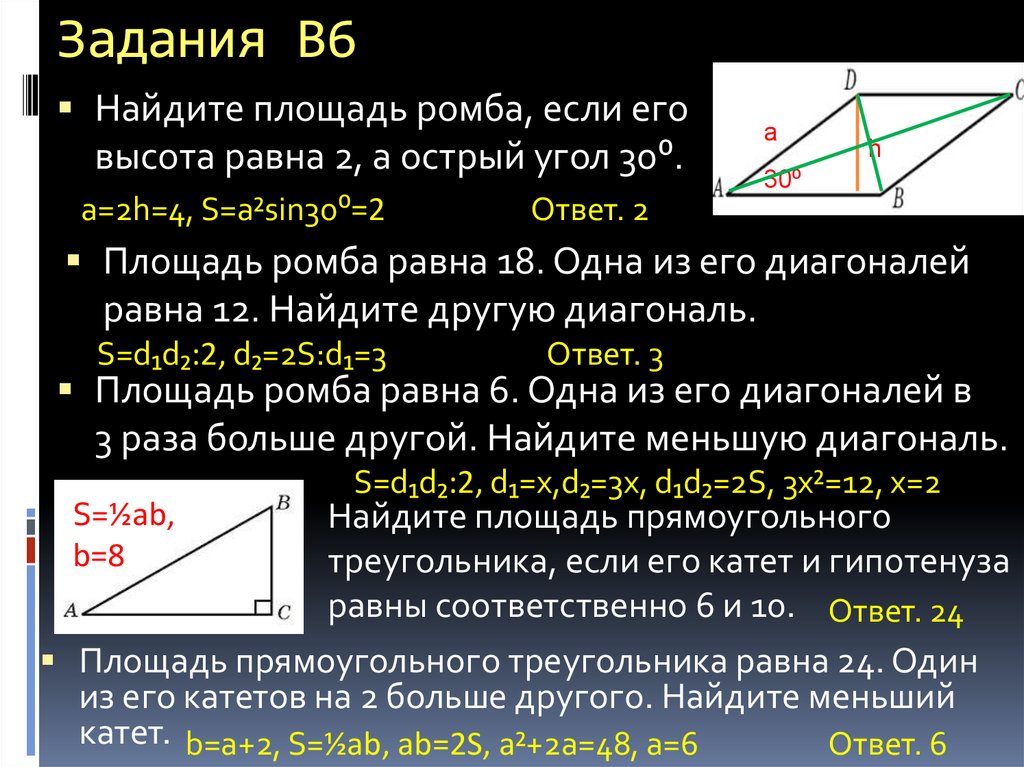
Пример 4. Нахождение длины диагонали квадрата по его площади
Учитывая, что площадь каждой клетки на шахматной доске равна 81 см 2 , найдите длину диагонали шахматной доски.
Ответ
Шахматная доска состоит из 64 равных квадратов, расположенных в 8 рядов. из 8. Заметим, что длина диагонали шахматной доски, которую мы будет обозначать 𝐷, равно 8-кратной длине диагонали каждого отдельного квадрата, который мы будем обозначать через 𝑑: 𝐷=8𝑑.
Нам известно, что площадь каждой клетки на шахматной доске равна 81 см 2 . Мы вспоминаем и что площадь квадрата можно вычислить по длине его диагональ 𝑑 по формуле areaofsquare=𝑑2.
Следовательно, мы имеем 𝑑2=81.
Чтобы найти 𝑑, мы начнем с умножения каждой стороны этого уравнение на 2, что приводит к 𝑑=162.
Затем извлекаем квадратный корень и упрощаем радикал, что дает
𝑑=√162=√81×2=√81×√2=9√2.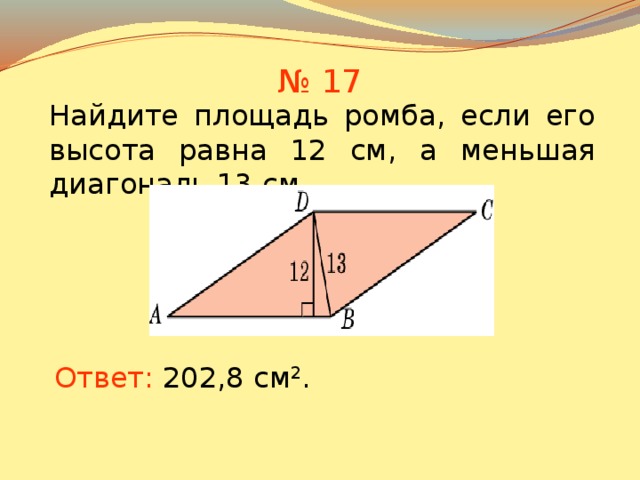 cm
cm
Наконец, мы можем вычислить длину диагонали шахматную доску (𝐷), вспомнив, что 𝐷=8𝑑. Следовательно, 𝐷=8×9√2=72√2.cm
В предыдущем примере альтернативный подход состоял бы в том, чтобы
- вычислить длину стороны каждого из меньших квадратов, вспомнив, что areaofsquare=𝑠,
- вычислить длину диагонали каждой из меньших квадратов по теореме Пифагора,
- умножьте это на 8, чтобы получить длину диагонали шахматная доска.
Несмотря на то, что это совершенно правильный метод, он включает такое же количество шагов к методу, который мы представили, поэтому он не более или менее эффективен.
В нашем последнем примере мы найдем разницу между площадями квадрат и ромб, каждый из которых рассчитывается с использованием длин их диагоналей.
Пример 5. Нахождение площадей квадрата и ромба по диагоналям
Определить разность площадей квадрата с диагональю
10 см и ромб
с диагоналями 2см
и 12 см.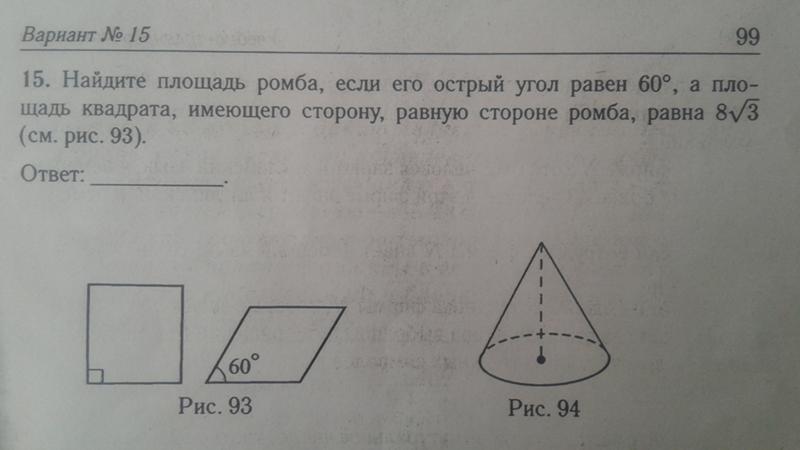


 2}\sin \alpha \).
2}\sin \alpha \).
Leave A Comment