Высота конуса равна 57 а диаметр основания 152 найдите образующую конуса: Высота конуса равна 57, а диаметр основания — 152. Найдите образующую конуса. · Issue #400 · nickkolok/chas-ege · GitHub

Дидактический материал — Блог Хидирова Ирина Мухадзировна

Самостоятельная работа. Геометрия 11 класс 

Вариант 1. База задание 13    

1.Длина окружности основания конуса равна 3, образующая равна 2. Найдите площадь боковой поверхности конуса.

2. Высота конуса равна 36, образующая равна 45. Найдите площадь его полной поверхности, деленную на .

3. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 11 раз?

4. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 10 раз?

5. Высота конуса равна 48, а диаметр основания — 72. Найдите образующую конус

6.Высота конуса равна 60, а длина образующей — 87. Найдите диаметр основания конуса.

7. Диаметр основания конуса равен 126, а длина образующей — 87. Найдите высоту конуса.

Проф. Задание 8

1.Площадь боковой поверхности конуса в два раза больше площади основания.

Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.

2.Площадь основания конуса равна , высота — 15. Найдите площадь осевого сечения конуса.

3. Высота конуса равна 40, а длина образующей — 50. Найдите площадь осевого сечения этого конуса.

   

Вариант 2 База задание 13    

1.Длина окружности основания конуса равна 6, образующая равна 2. Найдите площадь боковой поверхности конуса.

2. Высота конуса равна 21, образующая равна 35. Найдите площадь его полной поверхности, деленную на .

3. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 9 раз?

4. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 2 раза?

5. Высота конуса равна 30, а диаметр основания — 32. Найдите образующую конуса.

6. Высота конуса равна 48, а длина образующей — 52. Найдите диаметр основания конуса.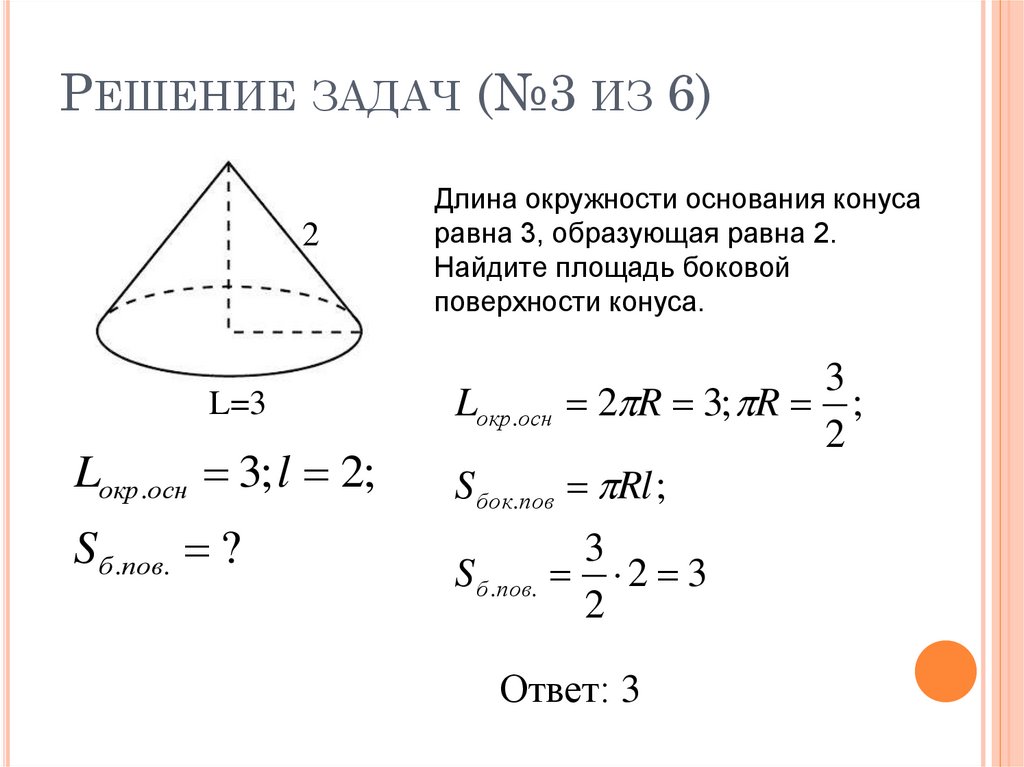

7. Диаметр основания конуса равен 40, а длина образующей — 52. Найдите высоту конуса.

Проф. Задание 8

 1.Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.

2.Площадь основания конуса равна , высота — 9. Найдите площадь осевого сечения конуса.

3.Высота конуса равна 32, а длина образующей — 40. Найдите площадь осевого сечения этого конуса.

     

Вариант 3 База задание 13    

1.Длина окружности основания конуса равна 5, образующая равна 8. Найдите площадь боковой поверхности конуса.

2. Высота конуса равна 24, образующая равна 26. Найдите площадь его полной поверхности, деленную на .

3. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 22 раза?

4. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 40 раз?

5. Высота ко­ну­са равна 12, а диа­метр основания – 10. Най­ди­те образующую конуса.

6. Высота конуса равна 30, а длина образующей — 34. Найдите диаметр основания конуса.

7. Диаметр основания конуса равен 120, а длина образующей — 65. Найдите высоту конуса.

Проф. Задание 8

1. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.

2. Площадь основания конуса равна 36π, высота — 3. Найдите площадь осевого сечения конуса.

3.Высота конуса равна 24, а длина образующей — 25. Найдите площадь осевого сечения этого конуса.

 

Вариант 4 База задание 13    

1.Длина окружности основания конуса равна 7, образующая равна 8. Найдите площадь боковой поверхности конуса.

2. Высота конуса равна 40, образующая равна 50. Найдите площадь его полной поверхности, деленную на .

3. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 35 раз?

4. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 28 раз?

5. Высота ко­ну­са равна 6, а диа­метр основания – 16. Най­ди­те образующую конуса.

6. Высота конуса равна 64, а длина образующей — 80. Найдите диаметр основания конуса

7. Диаметр основания конуса равен 96, а длина образующей — 80. Найдите высоту конуса.

Проф. Задание 8

1.Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.

2.Площадь основания конуса равна , высота — 10. Найдите площадь осевого сечения конуса.

3.Высота конуса равна 16, а длина образующей — 20. Найдите площадь осевого сечения этого конуса.

         

Вариант 5 База задание 13    

1. Длина окружности основания конуса равна 2, образующая равна 5. Найдите площадь боковой поверхности конуса.

2. Высота конуса равна 28, образующая равна 35. Найдите площадь его полной поверхности, деленную на .

3. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 40 раз?

4. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 15 раз?

5. Высота ко­ну­са равна 15, а диа­метр основания – 16. Най­ди­те образующую конуса.

6. Высота конуса равна 96, а длина образующей — 100. Найдите диаметр основания конуса.

7. Диаметр основания конуса равен 56, а длина образующей — 100. Найдите высоту конуса.

Проф. Задание 8

1. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.

2.Площадь основания конуса равна , высота — 2. Найдите площадь осевого сечения конуса.

3. Высота конуса равна 36, а длина образующей — 39. Найдите площадь осевого сечения этого конуса.

   

Вариант 6 База задание 13    

1.Длина окружности основания конуса равна 3, образующая равна 8. Найдите площадь боковой поверхности конуса.

2. Высота конуса равна 15, образующая равна 17. Найдите площадь его полной поверхности, деленную на .

3. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 20 раз?

4. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 19 раз?

5. Высота ко­ну­са равна 5, а диа­метр основания – 24. Най­ди­те образующую конуса.

6. Высота конуса равна 57, а длина образующей — 95. Найдите диаметр основания конуса.

7. Диаметр основания конуса равен 152, а длина образующей — 95. Найдите высоту конуса.

Проф. Задание 8

 1.Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.

2. Площадь основания конуса равна , высота — 8. Найдите площадь осевого сечения конуса.

3.Высота конуса равна 28, а длина образующей — 35. Найдите площадь осевого сечения этого конуса.

       

Домашняя работа.  База задание 13    

1.Длина окружности основания конуса равна 4, образующая равна 6. Найдите площадь боковой поверхности конуса.

2. Высота конуса равна 20, образующая равна 25. Найдите площадь его полной поверхности, деленную на .

3. Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 36 раз?

4. Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 8 раз?

5. Высота ко­ну­са равна 8, а диа­метр основания — 30.

Най­ди­те образующую конуса.

6. Высота конуса равна 21, а длина образующей — 75. Найдите диаметр основания конуса.

7. Диаметр основания конуса равен 144, а длина образующей — 75. Найдите высоту конуса.

Самостоятельная работа геометрия 11 класс цилиндр конус

№ 1 (Прототип: 284358)

1) Высота конуса равна 21, а диаметр основания — 144. Найдите образующую конуса.

2) Высота конуса равна 57, а диаметр основания — 152. Найдите образующую конуса.

3) Высота конуса равна 96, а диаметр основания — 56. Найдите образующую конуса.

4) Высота конуса равна 64, а диаметр основания — 96. Найдите образующую конуса.

5) Высота конуса равна 30, а диаметр основания — 32. Найдите образующую конуса.

№ 2 (Прототип: 284359)

1) Высота конуса равна 21, а длина образующей — 75 . Найдите диаметр основания конуса.

2) Высота конуса равна 57, а длина образующей — 95 . Найдите диаметр основания конуса.

3) Высота конуса равна 96, а длина образующей — 100 . Найдите диаметр основания конуса.

4) Высота конуса равна 64, а длина образующей — 80 . Найдите диаметр основания конуса.

5) Высота конуса равна 30, а длина образующей — 34 . Найдите диаметр основания конуса.

№ 3 (Прототип:284360)

1) Диаметр основания конуса равен 144, а длина образующей — 75 . Найдите высоту конуса.

2)  Диаметр основания конуса равен 152, а длина образующей — 95 . Найдите высоту конуса.

3) Диаметр основания конуса равен 56, а длина образующей — 100 . Найдите высоту конуса.

4) Диаметр основания конуса равен 96, а длина образующей — 80 . Найдите высоту конуса.

5) Диаметр основания конуса равен 32, а длина образующей — 34 . Найдите высоту конуса.

№ 4 (Прототип:284361)

1) Площадь боковой поверхности цилиндра равна , а диаметр основания — 8. Найдите высоту цилиндра.

2)Площадь боковой поверхности цилиндра равна , а диаметр основания — 9. Найдите высоту цилиндра.

3) Площадь боковой поверхности цилиндра равна , а диаметр основания — 5. Найдите высоту цилиндра.

4) Площадь боковой поверхности цилиндра равна , а диаметр основания — 8. Найдите высоту цилиндра.

 5) Площадь боковой поверхности цилиндра равна , а диаметр основания — 5. Найдите высоту цилиндра.

№ 5 (Прототип:284362)

1) Площадь боковой поверхности цилиндра равна , а высота — 2 . Найдите диаметр основания.

2) Площадь боковой поверхности цилиндра равна , а высота — 8 . Найдите диаметр основания.

3) Площадь боковой поверхности цилиндра равна , а высота — 4 . Найдите диаметр основания.

4) Площадь боковой поверхности цилиндра равна , а высота — 7 . Найдите диаметр основания.

5) Площадь боковой поверхности цилиндра равна , а высота — 8 . Найдите диаметр основания.

№ 6 (Прототип:27135)

1) Длина окружности основания конуса равна 7, образующая равна 2. Найдите площадь боковой поверхности конуса.

2) Длина окружности основания конуса равна 8, образующая равна 8. Найдите площадь боковой поверхности конуса.

3) Длина окружности основания конуса равна 5, образующая равна 8. Найдите площадь боковой поверхности конуса.

 4) Длина окружности основания конуса равна 8, образующая равна 4. Найдите площадь боковой поверхности конуса.

5) Длина окружности основания конуса равна 7, образующая равна 8. Найдите площадь боковой поверхности конуса.

№ 7 (Прототип:27136)

1) Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 36 раз?

2) Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 11 раз?

3) Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 9 раз?

4) Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 22 раза?

5) Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 35 раз?

№ 8 (Прототип:27137)

1) Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 8 раз?

2) Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 19 раз?

3) Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 15 раз?

4) Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 28 раз?

5) Во сколько раз уменьшится площадь боковой поверхности конуса, если радиус его основания уменьшить в 40 раз?

№ 9 (Прототип:27159)

1) Высота конуса равна 20, образующая равна 25.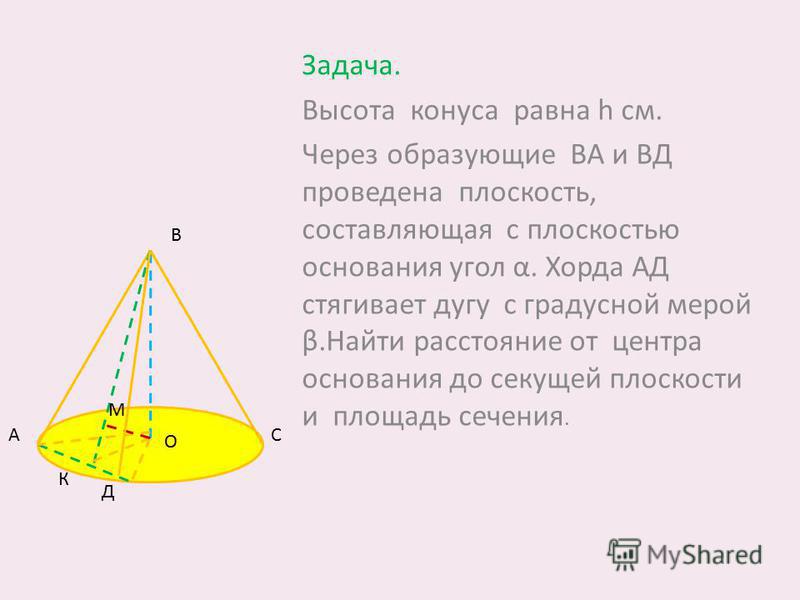 Найдите площадь его полной поверхности, деленную на пи .

2) Высота конуса равна 36, образующая равна 45. Найдите площадь его полной поверхности, деленную на пи .

3) Высота конуса равна 21, образующая равна 35. Найдите площадь его полной поверхности, деленную на пи .

4) Высота конуса равна 24, образующая равна 26. Найдите площадь его полной поверхности, деленную на пи .

5) Высота конуса равна 40, образующая равна 50. Найдите площадь его полной поверхности, деленную на пи.

№ 10 (Прототип:27161)

1) Площадь полной полной поверхности конуса равна 108. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной полной поверхности отсеченного конуса.

2) Площадь полной поверхности конуса равна 84. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.

3) Площадь полной поверхности конуса равна 148. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.

4) Площадь полной поверхности конуса равна 36. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.

5) Площадь полной поверхности конуса равна 100. Параллельно основанию конуса проведено сечение, делящее высоту пополам. Найдите площадь полной поверхности отсеченного конуса.                 

№ 11 (Прототип:27167)

1) Радиус основания конуса равен 12, высота равна 16. Найдите площадь полной поверхности конуса, деленную на пи.

2) Радиус основания конуса равен 28, высота равна 21. Найдите площадь полной поверхности конуса, деленную на пи.

3) Радиус основания конуса равен 16, высота равна 12. Найдите площадь полной поверхности конуса, деленную на пи.

4) Радиус основания конуса равен 72, высота равна 21. Найдите площадь полной поверхности конуса, деленную на пи.

5) Радиус основания конуса равен 24, высота равна 18. Найдите площадь полной поверхности конуса, деленную на пи.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Урок 22. Самостоятельная работа.                                            11 класс

Л.С.Атанасян

 

Самостоятельная работа по теме:

 «Цилиндр. Конус».

 

1 вариант

 

1. Радиус цилиндра равен 10 см. Сечение параллельное оси цилиндра и удалённое от неё на 8 см, имеет форму квадрата. Найдите площадь сечения.

2. Диагональ осевого сечения цилиндра равна дм и образует с плоскостью основания цилиндра угол 45°. Найдите площадь полной поверхности цилиндра.

3. Радиусы оснований усечённого конуса равны 3 см и 6 см, а высота равна

4 см. Найдите площадь осевого сечения и боковой поверхности конуса.

 

 

 

 

 

—————————————————————————————————-

 

 

 

 

Самостоятельная работа по теме:

 «Цилиндр. Конус».

 

2 вариант

 

1. Высота цилиндра равна 16 см. На расстоянии 6 см от оси цилиндра проведено сечение, параллельное оси цилиндра и имеющее форму квадрата. Найдите радиус цилиндра.

2. Диагональ осевого сечения цилиндра равна 8 дм и составляет с образующей угол 60°. Найдите площадь полной поверхности цилиндра.

3. Радиус большего основания, образующая и высота усечённого конуса равны 7 см, 5 см и 3 см соответственно.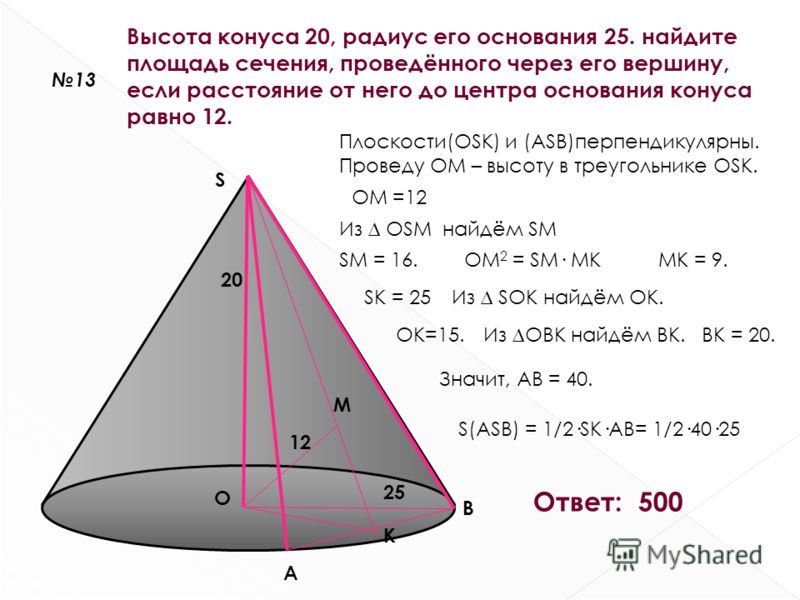 Найдите площадь осевого сечения и боковой поверхности конуса.

 

 

Урок 22. Самостоятельная работа.                                            11 класс

Л.С.Атанасян

 

Самостоятельная работа по теме:

 «Цилиндр. Конус».

 

3 вариант

 

1. Прямоугольник вращается вокруг одной из своих сторон, равной 5 см. Площадь боковой поверхности цилиндра, полученного при вращении, равна 100π см². Найдите площадь прямоугольника.

2. Хорда нижнего основания цилиндра отсекает от окружности основания дугу в 120°. Отрезок, соединяющий центр верхнего основания с серединой данной хорды, равен  см и образует с плоскостью основания угол 45°. Найдите площадь осевого сечения цилиндра.

3. Диагональ осевого сечения усечённого конуса равна 40 см и перпендикулярна к образующей конуса, равной 30 см. Найдите площадь сечения и полной поверхности конуса.

 

 

 

—————————————————————————————————-

 

 

 

Самостоятельная работа по теме:

 «Цилиндр. Конус».

 

4 вариант

 

1. Прямоугольник, одна из сторон которого равна 5 см, вращается вокруг неизвестной стороны. Найдите площадь прямоугольника, если площадь боковой поверхности цилиндра, полученного при вращении, равна 60π см².

2. Хорда нижнего основания цилиндра удалена от центра нижнего основания на см и отсекает от окружности основания дугу в 60°. Отрезок, соединяющий центр верхнего основания с одним из концов данной хорды, образует с осью цилиндра угол 45°. Найдите площадь осевого сечения цилиндра.

3. Радиусы оснований усечённого конуса равны

1 дм и 7 дм, а диагонали осевого сечения взаимно перпендикулярны. Найдите площадь осевого сечения и полной поверхности конуса.

 

Калькулятор высоты конуса

Создано Luciano Mino

Отзыв от Davide Borchia

Последнее обновление: 02 февраля 2023 г.

Содержание:

• Определение конуса
• Формула высоты конуса10 90 конуса, не зная его объема?
• Как найти высоту конуса, зная его объем?
• Примеры использования калькулятора высоты конуса
• Другие аналогичные инструменты
• Часто задаваемые вопросы

Калькулятор высоты конуса поможет вам найти высоту любого конуса по двум параметрам .

Здесь вы узнаете:

• Как найти высоту конуса, зная его объем и радиус .
• Как найти высоту конуса без его объема, зная его радиус и наклонную высоту .

Пропорционален ли радиус конуса его высоте? Продолжайте читать, чтобы узнать ответ на этот вопрос, и прочитайте несколько примеров высоты конуса!

Определение конуса

Конус представляет собой трехмерную форму с круглым основанием и единственной вершиной, называемой вершиной . Это самый интуитивно понятный конус для воображения (например, дорожные конусы или мороженое).

Калькулятор высоты конуса работает с конусами, вершина которых расположена непосредственно над центром его основания. Они называются правильными круговыми конусами . Конусы с вершиной не выше центра основания называются косыми конусами 9{2}}h=π×r23×V​

Посмотрим, когда применять каждое следующее.

Как найти высоту конуса, не зная его объема?

Чтобы найти высоту конуса, не зная его объема:

1. Запишите радиус и наклонную высоту размеры.
2. Введите их в формулу высоты конуса: h = √(l² - r²) где:
   • l — высота наклона;
   • р — радиус; и
   • h – результирующая высота.
3. Вот так !

Как найти высоту конуса, зная его объем?

Чтобы найти высоту конуса, зная его радиус и объем:

1. Запишите радиус и объем .
2. Введите их в высоту конуса формула объема: h = 3 × V/(π × r²) где:
   • V — объем конуса;
   • r — радиус; и
   • h – результирующая высота.
3. Это так просто !

Примеры с использованием калькулятора высоты конуса

Пример 1. Нахождение высоты по радиусу и наклонной высоте

Допустим, мы хотим найти высоту конуса с радиусом r=5 cmr = 5\ \text{cm} r=5 см и наклонная высота l=8 смl = 8\ \text{см}l=8 см.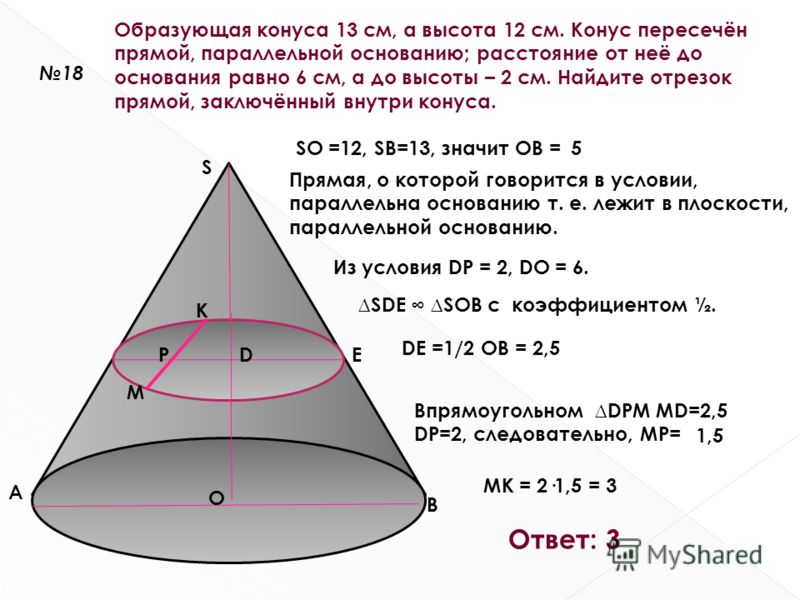 {2}} \\\\ ч & ≈ 2,39\ \текст{см} \end{align*}hh​=π×(20 cm)23×1000 cm³​≈2,39 cm​

Другие подобные инструменты

Обязательно ознакомьтесь с другими нашими калькуляторами, похожими на калькулятор высоты конуса!

• Правый круговой конус
• Радиус конуса
• Боковая часть конуса
• Наклонная высота конуса, а
• Диаметр конуса.

Часто задаваемые вопросы

Пропорционален ли радиус конуса его высоте?

№ . Радиус конуса и высота конуса не зависят друг от друга, если нет фиксированных переменных (например, объема конуса). Однако высота конуса и радиус прямо пропорциональны размеру его наклонной высоты.

Какова высота конуса с радиусом 10 см и высотой наклона 15 см?

5√5 = 11,18 . Чтобы найти высоту конуса 10 см радиуса и 15 см высоты наклона, вам нужно ввести эти параметры в формулу высоты конуса h = √(l² - r²) , где:

• l — высота наклона конуса; и
• r это радиус.

Лучано Миньо

Радиус (r)

Наклонная высота (l)

Объем (V)

Высота (h)

Посмотреть 23 похожих калькулятора 3d геометрии 📦

Площадь полушарияCubeCube Рассчитать: найти v, a, d… еще 20

Диаметр конуса Калькулятор

1 Понимание 90 свойства конуса могут быть трудными в лучшие времена, и именно здесь этот диаметр калькулятора конуса вступает в свои права! Неважно, какие переменные у вас есть — высота, площадь поверхности, объем конуса — ваш диаметр не за горами. Мы также объясняем 92}d=2×l2−h3

​

где:

• lll — Наклонная высота;
• чхх — Высота; и
• ddd — Диаметр.

Этот довольно просто запомнить, так как он опирается на , используя теорему Пифагора , чтобы найти радиус основания, а затем удвоить его. Наша следующая формула состоит в том, чтобы найти диаметр конуса по его объему и высоте :

d = 2 × 3 × Vπ × hd = 2 \times \sqrt{\frac{3 \times V}{\pi \times h}}d=2×π×h4×V​

​

где:

• ВВВ — Объем.

Как видите, хотя эту формулу не так уж сложно запомнить, довольно сложно точно вычислить из-за того, что требуются как π\piπ, так и квадратный корень. Вот почему мы сделали калькулятор диаметра конуса! Теперь мы подошли к нескольким вопросам, касающимся площади. Во-первых, мы используем боковую площадь и наклонную высоту конуса:

d=2×ALπ×ld = 2 \times \frac{A_L}{\pi \times l}d=2×π×lAL​​

где:

• ALA_LAL​ — Боковая область.

Затем мы используем площадь основания конуса , чтобы найти диаметр:

d=2×ABπd = 2 \times \sqrt{\frac{A_B}{\pi}}d=2×πAB​​

​

где:

• ALA_LAL​ — Базовая площадь.

Теперь, если у нас есть только площадь всей поверхности конуса и его наклонная высота , мы можем найти его диаметр, хотя мы должны решить следующее квадратное уравнение:

92 + \pi l r — A0=πr2+πlr−A

где:

• r — радиус; и
• А — Площадь поверхности.

Затем вы должны взять положительный корень и дать ответ d=2rd = 2rd=2r. Это много работы, так что просто используйте наш калькулятор диаметра конуса!

Как найти диаметр конуса?

Чтобы использовать высоту и объем конуса , чтобы найти диаметр:

1. Умножьте объем конуса на 3.
2. Разделите полученное число на число пи, умноженное на высоту.
3. Найдите квадратный корень из результата предыдущего деления.
4. Удвойте результат шага 3, чтобы получить диаметр .

Другие наши конусные калькуляторы.

При этом калькулятор диаметра конуса отвечает «Как рассчитать диаметр конуса?» полностью, возможно, вы захотите изучить другие темы, связанные с этой темой. В этом случае ознакомьтесь с другими нашими подходящими инструментами:

• Правый круглый конус;
• Вычислитель высоты конуса;
• Расчет радиуса конуса;
• Вычислитель площади бокового конуса; и
• Расчет высоты наклона конуса.