Прямоугольник. Его свойства и признаки.
Прямоугольник.
Приступаем к изучению разных видов параллелограмма.
Определение. Прямоугольником называется параллелограмм, у которого все углы прямые.
— прямоугольник
Поскольку прямоугольник – это параллелограмм, то он обладаем теми же свойствами, что и параллелограмм. Кроме того, у него есть ещё свои, особые свойства.
Рассмотрим эти свойства.
ТЕОРЕМА (СВОЙСТВО I). У прямоугольника диагонали равны.
Дано: – прямоугольник,
и – диагонали.
Доказать:
Доказательство.
1. Рассмотрим и .
по признаку равенства прямоугольных треугольников (или по I признаку равенства треугольников) все соответствующие стороны и углы у этих треугольников равны, т.е. , ч.т.д.
ТЕОРЕМА (СВОЙСТВО II). У прямоугольника каждая диагональ делит его на два равных прямоугольных треугольника.
Дано: – прямоугольник,
– диагональ.
Доказать:
Доказательство.
Рассмотрим и .
по III признаку равенства треугольников. по определению прямоугольника. Значит, треугольники и – равные и прямоугольные, ч.т.д.
Итак, прямоугольник обладает следующими свойствами:
1. У
прямоугольника противолежащие стороны и углы равны.
У
прямоугольника противолежащие стороны и углы равны.
2. У прямоугольника диагонали пересекаются и точкой пересечения делятся пополам.
3. У прямоугольника диагонали равны.
4. У прямоугольника каждая диагональ делит его на два равных прямоугольных треугольника.
5. Стороны прямоугольника являются его высотами.
Выясним теперь, по каким признакам можно утверждать, что геометрическая фигура является прямоугольником.
ТЕОРЕМА (ПРИЗНАК I). Если у четырёхугольника три угла прямые, то такой четырёхугольник является прямоугольником.
Дано:
Доказать: – прямоугольник.
Доказательство.
Данный четырёхугольник будет прямоугольником, если мы докажем, что четвёртый угол также равен .
1. Так как , то . Так как , то .
2. по признаку параллельности прямых.
3. по признаку параллельности прямых.
4. Значит, – параллелограмм (по определению). По свойству углов параллелограмма,
5. Итак, – параллелограмм, у которого все углы прямые. По определению, такой параллелограмм является прямоугольником, ч.т.д.
ТЕОРЕМА (ПРИЗНАК II). Если у параллелограмма диагонали равны, то такой параллелограмм является прямоугольником.
Дано: – параллелограмм,
– диагонали.
Доказать: – прямоугольник.
Доказательство.
Данный параллелограмм будет прямоугольником, если мы докажем, что у него все углы равны .
1. Рассмотрим и .
по III признаку равенства прямоугольных треугольников, следовательно, .
2. Так как – параллелограмм, то у него стороны попарно параллельны, т.е. . и – внутренние односторонние при параллельных прямых, значит, по свойству параллельных прямых, . Учитывая доказанное равенство этих углов, получаем, что .
3. По свойству углов параллелограмма, и .
4. Итак, у параллелограмма все углы прямые, значит, он является прямоугольником (по определению), ч.т.д.
ТЕОРЕМА
(ПРИЗНАК III). Если
у параллелограмма один угол прямой, то такой параллелограмм является
прямоугольником.
Если
у параллелограмма один угол прямой, то такой параллелограмм является
прямоугольником.
Дано: – параллелограмм,
.
Доказать: – прямоугольник.
Доказательство.
Данный параллелограмм будет прямоугольником, если мы докажем, что у него все углы равны
1. Т.к. – параллелограмм, то по определению, т.е. и .
По свойству углов параллелограмма, .
2. и – внутренние односторонние при параллельных прямых, значит, по свойству параллельных прямых, .
3. Т.к. , то .
4. Итак, , значит, по определению, параллелограмм является прямоугольником, ч.т.д.
1. Периметр прямоугольника
равен см, а одна из его сторон
меньше другой на см. Найдите меньшую сторону
прямоугольника.
Периметр прямоугольника
равен см, а одна из его сторон
меньше другой на см. Найдите меньшую сторону
прямоугольника.
2. В прямоугольнике один из углов, образованных диагоналями, равен . Меньшая сторона прямоугольника равна см. Найдите диагональ прямоугольника.
3. В прямоугольнике перпендикуляры, проведённые из точки пересечения диагоналей к его сторонам, равны соответственно см и см. Найдите периметр прямоугольника.
4.
В прямоугольнике диагональ составляет со стороной угол, равный . Найдите больший угол между диагоналями прямоугольника.
5. В прямоугольнике один из углов, образованных диагоналями, равен . Диагонали прямоугольника равны см. Найдите меньшую сторону прямоугольника.
6. В прямоугольнике диагонали пересекаются в точке . Точка – середина стороны . Найдите .
7. В прямоугольнике диагонали пересекаются в
точке .
8. В параллелограмме с острым углом диагонали пересекаются в точке . На отрезках и взяты точки и соответственно, . Докажите, что четырёхугольник является прямоугольником.
9. В прямоугольнике – точка пересечения диагоналей, и – высоты треугольников и соответственно, см. Найдите .
10. В четырёхугольнике диагонали пересекаются в точке . Найдите .
11. В прямоугольнике – точка пересечения диагоналей, и – перпендикуляры, проведённые из вершин и к прямой . Известно, что . Найдите .
12. В четырёхугольнике диагонали пересекаются в точке , . Найдите .
13. В прямоугольнике точки и – середины сторон и соответственно. На прямой взята точка , на прямой – точка . Известно, что . Найдите отношение сторон .
14. На основании равнобедренного треугольника взята точка , а на сторонах и – соответственно точки и , . Найдите .
15. В прямоугольнике – точка пересечения
диагоналей. Точки и – середины сторон и соответственно. Точка делит отрезок в отношении , считая от точки Найдите отношение .
Точки и – середины сторон и соответственно. Точка делит отрезок в отношении , считая от точки Найдите отношение .
16. Некая прямая, параллельная основанию равнобедренного треугольника , пересекает стороны и в отношении , считая от точки . Найдите .
17. На диагонали прямоугольника взята точка . Известно, что . Докажите, что .
18. Дан параллелограмм с острым углом . На отрезке , как на диаметре построена окружность, которая пересекает луч в точке , лежащей вне параллелограмма. . Найдите расстояние между прямыми и , если см.
19. На отрезках и в прямоугольнике взяты точки и соответственно, . Докажите, что .
20. Дан параллелограмм с тупым углом . На диагонали , как на диаметре, построена окружность, пересекающая отрезок в точке – перпендикуляр к прямой . Найдите , если см.
21. Биссектриса одного из
углов прямоугольника делит пересекаемую ею сторону на отрезки равной длины.
Найдите периметр этого прямоугольника, если длина меньшей стороны
прямоугольника равна см.
22. Периметр прямоугольника равен см. Найдите сумму расстояний от произвольной внутренней точки прямоугольника до его сторон.
23. Постройте прямоугольник:
а) по двум сторонам, имеющим общую вершину;
б) по стороне и диагонали;
в) по диагонали и углу между диагоналями;
г) по диагонали и сумме прилежащих сторон.
24. Диагональ прямоугольника равна см. Найдите медиану треугольника , проведённую к его большей стороне.
25. Найдите острый угол между диагоналями прямоугольника, если одна из них делит угол при вершине прямоугольника в отношении .
26. Периметр прямоугольника равен см. Найдите стороны прямоугольника, если одна из них в раз больше другой.
27. Периметр прямоугольника равен см. Найдите его стороны, если одна из них на см меньше другой.
28. Диагонали прямоугольника пересекаются в точке . Найдите угол между диагоналями, если .
29. В прямоугольнике проведена диагональ . Известно, что в 2 раза больше, чем .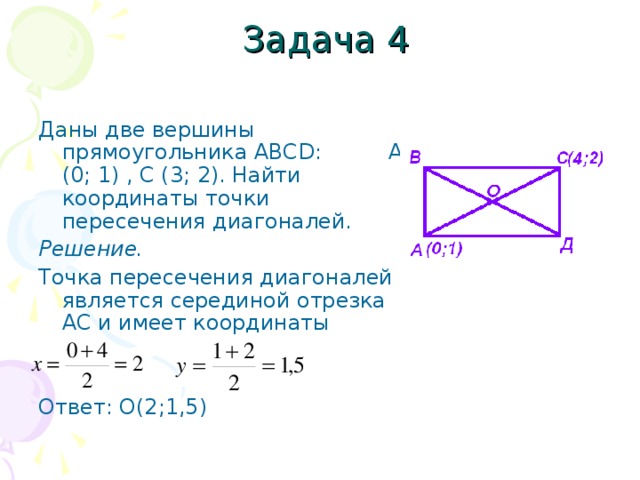 Чему равны эти углы?
Чему равны эти углы?
30. Одна из сторон прямоугольника на см больше другой. Найдите стороны прямоугольника, если его периметр равен см.
31. Меньшая сторона прямоугольника см, угол между диагоналями равен . Найдите диагонали прямоугольника.
32. Дан прямоугольник – точка пересечения его диагоналей. Докажите, что и – равные равнобедренные треугольники.
33. Найдите диагонали прямоугольника, если его периметр равен см, а периметр одного из треугольников, на которые диагональ разделила прямоугольник, равен см.
34. Докажите, что отрезок, соединяющий точку пересечения диагоналей прямоугольника с серединой стороны, перпендикулярен этой стороне.
35. В прямоугольнике диагональ в раз больше стороны . Периметр треугольника равен см ( – точка пересечения диагоналей). Найдите длину диагонали .
36. Из точки , взятой на стороне прямоугольника , опущен перпендикуляр на сторону . Докажите, что четырёхугольник – прямоугольник.
37. Диагонали
прямоугольника пересекаются в точке , его диагональ равна см. Найдите длины отрезков и
.
Найдите длины отрезков и
.
38. Диагонали прямоугольника пересекаются в точке . Докажите, что .
39. Диагонали прямоугольника пересекаются в точке . Найдите стороны прямоугольника, если его периметр равен см, а периметры треугольников и равны см и см соответственно.
40. Дан прямоугольник – точка пересечения его диагоналей. Найдите периметр треугольника , если
41. Диагонали прямоугольника пересекаются в точке . Найдите периметр треугольника , если .
42. Диагонали прямоугольника пересекаются в точке . Найдите периметр треугольника , если .
43. Диагонали прямоугольника пересекаются в точке . Найдите периметр треугольника , если .
44. Диагонали прямоугольника пересекаются в точке , сторона равна см, диагональ равна см. Определите вид треугольника (ответ обоснуйте) и найдите его периметр.
45. В прямоугольнике биссектриса угла пересекает сторону в точке . Докажите, что треугольник – равнобедренный.
46. В прямоугольнике диагональ делит угол в отношении . Найдите углы треугольника ( – точка пересечения
диагоналей).
Найдите углы треугольника ( – точка пересечения
диагоналей).
47. Найдите диагональ прямоугольника, если его периметр равен см, а периметр одного из треугольников, на которые диагональ делит прямоугольник, равен см.
48.
В прямоугольнике проведена биссектриса угла . Найдите периметр прямоугольника, если см, см.
49. Расстояния от точки пересечения диагоналей прямоугольника до его сторон равны см и см. Найдите большую сторону данного прямоугольника.
50. Диагонали прямоугольника пересекаются под углом . Найдите угол между диагональю прямоугольника и его меньшей стороной.
51. В прямоугольнике диагональ в два раза больше стороны . Найдите периметр треугольника , если расстояние от точки пересечения диагоналей прямоугольника до стороны равно см.
52. Диагонали
прямоугольника пересекаются в точке , образуя тупой угол . Определите, какое расстояние
больше: от точки до стороны или от точки до стороны .
Определите, какое расстояние
больше: от точки до стороны или от точки до стороны .
53.
В прямоугольном треугольнике ( – прямой) через точку , лежащую на гипотенузе, проведены прямые и , параллельные катетам и соответственно. Периметр треугольника равен см, а периметр треугольника равен см. Найдите периметр треугольника .
54. На стороне равностороннего треугольника взята точка так, что сумма расстояний от неё до сторон и равна см. Найдите высоту треугольника, проведённую из вершины .
55. Периметр прямоугольника равен см, а его диагональ равна см. Найдите периметр треугольника .
56.
Найдите периметр прямоугольника , если биссектрисы и углов и делят сторону на три отрезка, длина каждого
из которых равна см.
57. Точка пересечения диагоналей прямоугольника отстоит от его сторон на расстояниях см и см. Найдите меньшую сторону данного прямоугольника.
58. В прямоугольнике диагональ в два раза больше стороны . Найдите острый угол между диагоналями прямоугольника.
59. Меньшая сторона прямоугольника равна см. Угол между его диагоналями равен . Вычислите длину диагонали прямоугольника.
60. Диагонали прямоугольника пересекаются в точке . Определите, какое расстояние больше: от точки до стороны или от точки до стороны , если сторона больше стороны .
61.
В прямоугольнике через точку проведены прямая , параллельная сторонам и , и прямая , параллельная сторонами и . Периметр прямоугольника равен см, а периметр прямоугольника равен см. Найдите периметр прямоугольника .
62. На продолжении стороны равностороннего треугольника взята точка так, что разность расстояний
от неё до сторон и равна см. Найдите высоту
треугольника, проведённую из вершины .
Найдите высоту
треугольника, проведённую из вершины .
63. Диагонали прямоугольника пересекаются в точке . Периметр треугольника равен см, а периметр треугольника равен см. Найдите периметр треугольника , если диагональ прямоугольника равна см.
64.
Найдите периметр прямоугольника , если биссектрисы и углов и делят сторону на три отрезка, длина каждого из которых равна см.
65. Сумма расстояний от точки пересечения диагоналей прямоугольника до всех его вершин равна см. Найдите диагональ данного прямоугольника.
66. Диагональ прямоугольника образует угол с одной из его сторон. Найдите острый угол между диагоналями прямоугольника.
67. Диагональ прямоугольника равна см. Угол между его диагоналями равен . Вычислите длину меньшей стороны прямоугольника.
68. Диагонали
прямоугольника пересекаются в точке , образуя острый угол . Определите, какое расстояние
больше: от точки до стороны или от точки до стороны .
Определите, какое расстояние
больше: от точки до стороны или от точки до стороны .
69.
В прямоугольном равнобедренном треугольнике ( – прямой) через точки и , лежащие на гипотенузе, проведены прямые и , параллельные катету , и прямые и , параллельные катету . Сравните периметры четырёхугольников и .
70. На основании равнобедренного треугольника взята точка так, что сумма расстояний от неё до сторон и равна см. Найдите высоту треугольника, проведённую из вершины .
71. Диагонали прямоугольника пересекаются в точке . Периметр треугольника равен см, а сторона равна см. Найдите периметр треугольника .
72.
Биссектрисы углов и прямоугольника пересекаются на стороне в точке . Найдите периметр прямоугольника,
если длина равна см.
Найдите периметр прямоугольника,
если длина равна см.
73. Сумма расстояний от точки пересечения диагоналей прямоугольника до всех его сторон равна см. Найдите периметр данного прямоугольника.
74. Угол между диагоналями прямоугольника равен . Найдите угол .
75. В прямоугольнике сторона в два раза меньше диагонали . Найдите расстояние от точки пересечения диагоналей прямоугольника до стороны , если периметр треугольника равен см.
76. Диагонали прямоугольника пересекаются в точке . Определите, какое расстояние больше: от точки до стороны или от точки до стороны , если сторона меньше стороны .
77.
В прямоугольном равнобедренном треугольнике ( – прямой) через точку , лежащую на гипотенузе,
проведены прямые и , параллельные катетам и соответственно. Найдите
периметр прямоугольника , если катет треугольника равен см.
78. На продолжении основания равнобедренного треугольника взята точка так, что разность расстояний от неё до сторон и равна см. Найдите высоту треугольника, проведённую из вершины .
79. В прямоугольнике проведена диагональ . Перпендикуляр к диагонали составляет со стороной угол, равный и отсекает от диагонали отрезок , равный см. Найдите периметр прямоугольника, если сторона см.
80. Дан прямоугольник со стороной . К диагонали проведён перпендикуляр . Найдите периметр прямоугольника, если диагональ составляет со стороной угол, равный .
81.
В прямоугольнике – точка пересечения его диагоналей. Из точки к серединам сторон и проведены отрезки и соответственно. Найдите периметр прямоугольника.
82.
Биссектриса угла прямоугольника отсекает от стороны отрезки и .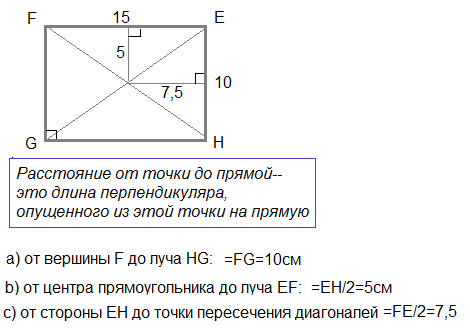 Найдите периметр
прямоугольника.
Найдите периметр
прямоугольника.
83. В прямоугольнике проведена биссектриса угла . Найдите .
84. В прямоугольнике диагональ составляет с его меньшей стороной угол . Найдите углы и .
85. В прямоугольнике диагонали пересекаются в точке . Найдите и меньший угол между диагоналями, если известно, что .
86.
Диагонали прямоугольника пересекаются в точке . Меньший угол между диагоналями равен . Найдите углы треугольника , если известно, что .
87. В прямоугольнике диагонали пересекаются в точке . Известно, что . Найдите эти углы.
88. В прямоугольнике . Найдите стороны прямоугольника, если его периметр равен .
89. В прямоугольнике из угла проведён луч, который
пересекает сторону в точке так, что и . Найдите стороны прямоугольника,
если известно, что периметр его равен .
Найдите стороны прямоугольника,
если известно, что периметр его равен .
90. Диагональ прямоугольника составляет со стороной угол, равный . Перпендикуляр, опущенный из вершины на эту диагональ отсекает от неё отрезок . Периметр данного прямоугольника равен . Найдите стороны
прямоугольника.
91.
Из вершины прямоугольника , с периметром , проведён луч, который пересекает сторону под углом . Разность отсекаемых отрезков равна . Найдите стороны прямоугольника.
8 класс.
 Геометрия. Четырехугольники. Прямоугольник, ромб и квадрат. — Обзор теории о четырехугольниках. Решение задач.Комментарии преподавателя
Геометрия. Четырехугольники. Прямоугольник, ромб и квадрат. — Обзор теории о четырехугольниках. Решение задач.Комментарии преподавателяПовторение теории и решение задач
Ранее мы уже познакомились с такими видами четырехугольников, как параллелограмм и трапеция, и их частными случаями – прямоугольником, ромбом и квадратом. Мы изучили их основные свойства и признаки. Сегодня мы повторим и обобщим все полученные нами знания по этой теме.
Повторим основной теоретический материал.
Трапеция – это четырехугольник, у которого две противоположные стороны параллельны, а две другие не параллельны (см. Рис. 1).
Рис. 1. Трапеция
Выделяют два отдельных типа трапеций: равнобедренную и прямоугольную.
Равнобедренная трапеция – это трапеция, в которой боковые стороны равны (см.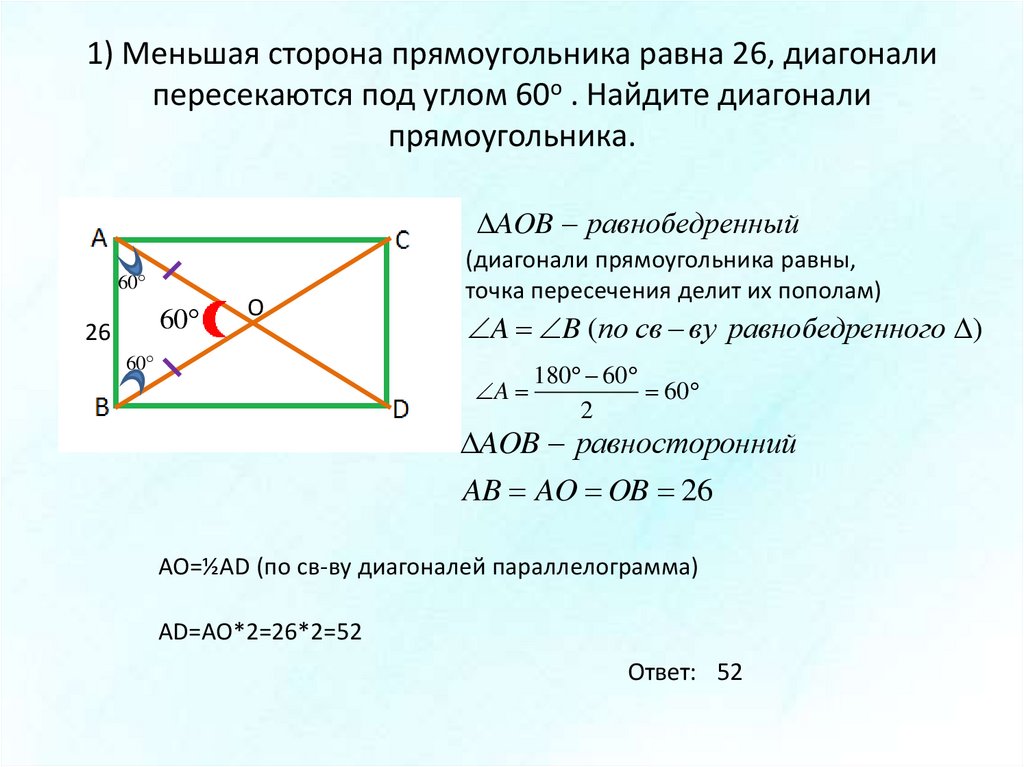 Рис. 2).
Рис. 2).
Рис. 2. Равнобедренная трапеция
Прямоугольная трапеция – это трапеция, в которой одна из боковых сторон перпендикулярна основанию (см. Рис. 3).
Рис. 3. Прямоугольная трапеция
Отдельно стоит вспомнить такой важный элемент трапеции, как ее средняя линия.
Средняя линия трапеции – это отрезок, соединяющий середины боковых сторон трапеции (см. Рис. 4).
Рис. 4. Средняя линия трапеции
Основные свойства средней линии трапеции:
1. – параллельна основаниям трапеции;
2. – равна их полусумме.
Параллелограмм – четырехугольник, у которого каждые две противоположные стороны параллельны (см. Рис. 5).
Рис. 5. Параллелограмм
Основные свойства параллелограмма:
Чтобы иметь возможность при решении задач пользоваться указанными свойствами, нам необходимо понимать, является ли указанный четырехугольник параллелограммом или нет. Для этого необходимо знать признаки параллелограмма.
Для этого необходимо знать признаки параллелограмма.
Теорема. Первый признак параллелограмма. Если в четырехугольнике две противоположные стороны равны и параллельны (см. Рис. 6), то этот четырехугольник – параллелограмм. параллелограмм.
Рис. 6. Первый признак параллелограмма
Теорема. Второй признак параллелограмма. Если в четырехугольнике каждые две противоположные стороны равны (см. Рис. 7), то этот четырехугольник – параллелограмм. параллелограмм.
Рис. 7. Второй признак параллелограмма
Теорема. Третий признак параллелограмма. Если в четырехугольнике диагонали точкой пересечения делятся пополам (см. Рис. 8), то этот четырехугольник – параллелограмм. параллелограмм.
Рис. 8. Третий признак параллелограмма
Теперь повторим частные случаи параллелограмма.
Прямоугольником называют параллелограмм, у которого все углы прямые (см. Рис. 9).
Рис. 9. Прямоугольник
Замечание. Очевидным эквивалентным определением прямоугольника (иногда его именуют признаком прямоугольника) можно назвать следующее. Прямоугольник – это параллелограмм с одним углом . Это утверждение практически очевидно, и мы оставим его без доказательства, пользуясь далее как определением.
Т.к. прямоугольник, как это видно из определения, является частным случаем параллелограмма, то ему присущи все ранее описанные свойства параллелограмма, однако у него имеются и свои специфические свойства, которые мы сейчас рассмотрим.
Теорема. Свойство прямоугольника. Диагонали прямоугольника равны (см. Рис. 10).
.
Рис. 10. Свойство прямоугольника
Теорема. Признак прямоугольника. Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник (см. Рис. 11).
Признак прямоугольника. Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник (см. Рис. 11).
Рис. 11. Признак прямоугольника
Ромб – параллелограмм, у которого все стороны равны (см. Рис. 12).
Рис. 12. Ромб
Замечание. Для определения ромба достаточно указывать даже более короткое утверждение, что это параллелограмм, у которого равны две смежные стороны .
Ромб обладает всеми свойствами параллелограмма, т.к. является его частным случаем, но имеет и свое специфическое свойство.
Теорема. Свойство ромба. Диагонали ромба перпендикулярны и делят углы ромба пополам (см. Рис. 13).
Рис. 13. Свойство ромба
Квадрат – 1) прямоугольник, у которого стороны равны; 2) ромб, у которого углы прямые (см. Рис. 14). Указанные определения эквивалентны и применяются в любой удобной форме.
Рис. 14. Квадрат
Квадрату присущи свойства тех фигур, частным случаем которых он является (параллелограмм, прямоугольник, ромб). Перечислим их.
Основные свойства квадрата (см. Рис. 15):
1. Все углы прямые.
2. Диагонали равны.
3. Диагонали перпендикулярны.
4. Точка пересечения делит диагонали пополам.
5. Диагонали делят углы квадрата пополам.
Рис. 15. Свойства квадрата
Теперь, когда мы перечислили и вспомнили основные свойства основных изученных четырехугольников, мы можем закрепить эти знания на примере решения задач.
Пример 1. (Обобщенная задача на трапецию и параллелограмм). Дана трапеция или параллелограмм (см. Рис. 16). биссектрисы углов при боковой стороне трапеции (параллелограмма). Найти угол между биссектрисами .
Найти угол между биссектрисами .
Решение. Это пример задачи, демонстрирующий схожесть некоторых свойств параллелограмма и трапеции, в нем не важно, какая конкретно из этих двух фигур задана. Изобразим рисунок.
Рис. 16
– биссектрисы, они делят соответствующие углы пополам, обозначим их и .
По свойству трапеции (параллелограмма) .
Рассмотрим : .
Ответ: .
Вспомним формулировку теоремы Фалеса.
Теорема Фалеса. Если параллельные прямые, которые пересекают стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне (см. Рис. 17).
Рис. 17. Теорема Фалеса
Рассмотрим задачу на трапецию с применением теоремы Фалеса.
Пример 2. Боковая сторона трапеции разделена на три равные части, и из точек деления проведены к другой стороне отрезки, параллельные основаниям. Найдите длину этих отрезков, если основания трапеции равны 2 м и 5 м.
Найдите длину этих отрезков, если основания трапеции равны 2 м и 5 м.
Решение. Изобразим Рис. 18 со всеми элементами, которые пригодятся нам в процессе решения. Известно, что . Найти длины .
Рис. 18
Для того, чтобы воспользоваться теоремой Фалеса относительно угла , проведем прямые .
Сначала рассмотрим параллелограмм , в нем по свойству .
Вернемся к проведенным параллельным прямым, по теореме Фалеса: . . Поскольку отрезок разделен на три равные части, то .
Теперь, если внимательно посмотреть на параллелограммы, образованные пересечениями линий с проведенными нами прямыми , можно легко определить длины отрезков : , .
Ответ. .
Пример 3. Основания трапеции относятся как 2:3. Средняя линия равна 5 м. Найдите основания.
Решение. Изобразим Рис. 19 и укажем, что нам дано: . Найти и .
Рис. 19
Поскольку известно, что , то выразим основания трапеции через условные части : .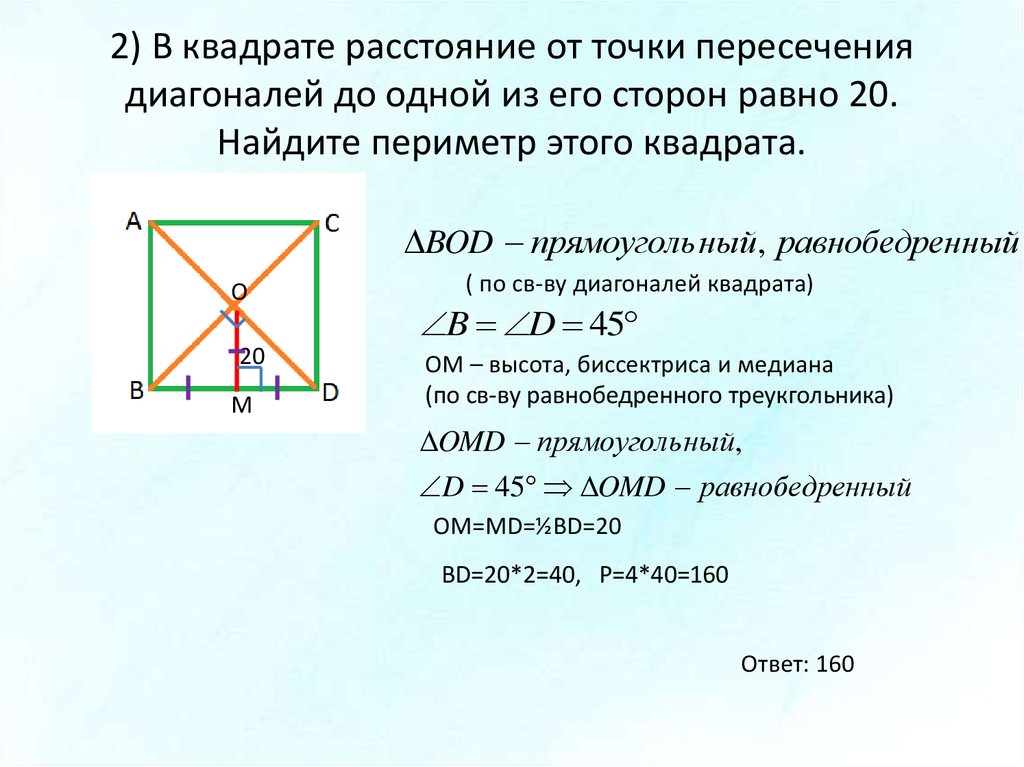 Запишем свойство средней линии трапеции:
Запишем свойство средней линии трапеции:
.
Ответ. .
Пример 4. Через данную точку внутри угла проведите прямую, отрезок которой, заключенный внутри этого угла, делился бы данной точкой пополам.
Решение. Внутри угла с вершиной дана точка . Изобразим это на Рис. 20 со всеми элементами, которые понадобятся нам для решения задачи.
Рис. 20
Отложим отрезок из точки через точку так, чтобы , затем проведем отрезки , получим точки пересечения со сторонами угла и соответственно. Соединим эти точки прямой, она и будет искомой. Докажем это.
Построенная фигура является параллелограммом, т.к. по построению имеет параллельные противоположные стороны, отрезки являются диагоналями параллелограмма, следовательно, по его свойству точкой пересечения () делятся пополам и , что и требовалось по условию задачи.
Ответ. Искомая прямая – .
Искомая прямая – .
Пример 5. В прямоугольнике точка пересечения диагоналей отстоит от меньшей стороны на 4 см дальше, чем от большей стороны. Периметр прямоугольника равен 56 см. Найдите стороны прямоугольника.
Решение. Изобразим Рис. 21.
Рис. 21
Опустим из точки пересечения диагоналей перпендикуляры на стороны, длины которых и будут расстояниями от точки пересечения диагоналей до сторон прямоугольника. Обозначим отрезок , тогда по условию . Поскольку получаем, что . Подставим это в формулу периметра прямоугольника:
.
Ответ: .
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/8-klass/chyotyrehugolniki/povtorenie-teorii-i-reshenie-zadach
http://www.youtube.com/watch?v=axMe7L_01j0
http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/83-test-po-geometrii-8-klass-tema-pryamougolnik-romb-kvadrat-variant-1. html
html
http://metodbook.ru/index.php/matematika/13-testy-po-geometrii-8-klass/84-test-po-geometrii-8-klass-tema-pryamougolnik-romb-kvadrat-variant-2.html
http://festival.1september.ru/articles/416997/
Как найти длину диагонали прямоугольника
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 4 Следующая →
Справка по основам геометрии » Плоская геометрия » Четырехугольники » Прямоугольники » Как найти длину диагонали прямоугольника
Длина прямоугольника 12 дюймов, а ширина 5 дюймов. Чему равна диагональ прямоугольника?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти диагональ, воспользуемся теоремой Пифагора:
где = гипотенуза
или
Сообщить об ошибке
Одна сторона прямоугольника равна 7 дюймам, а другая — 9 дюймам. Сколько сантиметров длина диагонали прямоугольника?
Сколько сантиметров длина диагонали прямоугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Вы можете найти диагональ прямоугольника, если у вас есть ширина и высота. Диагональ равна квадратному корню из квадрата ширины плюс квадрат высоты.
Сообщить об ошибке
Найдите длину диагонали.
Возможные ответы:
Правильный ответ:
Пояснение:
Прямоугольник можно разрезать на два равных прямоугольных треугольника, гипотенуза которых является диагональю прямоугольника.
Используйте теорему Пифагора, чтобы найти гипотенузу:
, где A и B — ноги, а C — гипотенуза
. Сообщение о ошибке
Сообщение о ошибке
А. Стандартный баскетбольный двор. 84 фута в длину и 50 футов в ширину. Во время тренировки тренер К. заставляет Кайри бежать из одного правого угла на одном конце площадки в левый угол на другом конце площадки. С точностью до фута, сколько пробежал Кирие?
Возможные ответы:
Правильный ответ:
Пояснение:
Рисунок очень помогает решить эту задачу, поэтому мы начнем с прямоугольной баскетбольной площадки.
Заметим, что расстояние, пройденное Кирие (отмечено красным), является диагональю нашего прямоугольника, который мы назовем . Нам также не следует, что эта диагональ делит наш прямоугольник на два конгруэнтных прямоугольных треугольника. Поэтому мы можем найти длину нашей диагонали, сосредоточившись на одном из этих треугольников и определив гипотенузу. Это можно сделать с помощью теоремы Пифагора, которая дает нам:
Извлечение квадратного корня дает
Округление до ближайшего фута дает ответ 98.
Сообщить об ошибке
Прямоугольник имеет высоту . Какова длина его диагонали, округленная до десятых?
Возможные ответы:
Правильный ответ:
Объяснение:
1. Используйте теорему Пифагора с и .
2. Решите для , длина диагонали:
Это округляется до сотни.
Сообщить об ошибке
Стороны прямоугольника ABCD равны 4 дюймам и 13 дюймам.
Какова длина диагонали прямоугольника ABCD?
Возможные ответы:
Правильный ответ:
Объяснение:
Диагональ прямоугольника делит прямоугольник на 2 прямоугольных треугольника со сторонами, равными сторонам прямоугольника, и с гипотенузой, являющейся диагональю. Все, что вам нужно сделать, это использовать теорему Пифагора:
Все, что вам нужно сделать, это использовать теорему Пифагора:
где a и b — стороны прямоугольника, а c — длина диагонали.
Сообщить об ошибке
Найдите длину диагонали прямоугольника, имеющего длину и ширину .
Возможные ответы:
Правильный ответ:
Пояснение:
Диагональ прямоугольника также является гипотенузой прямоугольного треугольника, катетами которого являются длина и ширина прямоугольника.
Затем мы можем использовать теорему Пифгора, чтобы найти диагональ.
Для заданного прямоугольника
Сообщить об ошибке
Найдите длину диагонали прямоугольника, имеющего длину и ширину .
Возможные ответы:
Правильный ответ:
Пояснение:
Диагональ прямоугольника также является гипотенузой прямоугольного треугольника, катетами которого являются длина и ширина прямоугольника.
Затем мы можем использовать теорему Пифгора, чтобы найти диагональ.
Для заданного прямоугольника
Сообщить об ошибке
Найдите длину диагонали прямоугольника, имеющего длину и ширину .
Возможные ответы:
Правильный ответ:
Пояснение:
Диагональ прямоугольника также является гипотенузой прямоугольного треугольника, катетами которого являются длина и ширина прямоугольника.
Затем мы можем использовать теорему Пифгора, чтобы найти диагональ.
Для заданного прямоугольника
Сообщить об ошибке
Найдите длину диагонали прямоугольника, имеющего длину и ширину .
Возможные ответы:
Правильный ответ:
Пояснение:
Диагональ прямоугольника также является гипотенузой прямоугольного треугольника, катетами которого являются длина и ширина прямоугольника.
Затем мы можем использовать теорему Пифгора, чтобы найти диагональ.
Для заданного прямоугольника
Сообщить об ошибке
← Предыдущий 1 2 3 4 Далее →
Уведомление об авторских правах
Все ресурсы по базовой геометрии
9 Диагностические тесты 164 практических теста Вопрос дня Карточки Learn by Concept
геометрия — Деление прямоугольника на 4 части в соотношении 1:2:3:4, всего 2 линиями
Существует однопараметрическое бесконечное семейство решений. Ниже приведен алгоритм, чтобы найти их все. В качестве спойлера сразу укажу, что этот алгоритм одинаково хорошо работает и для 92$ — не только конкретный рассматриваемый прямоугольник 5 на 6.
Для начала обозначим области в рассеченном прямоугольнике цифрами 1,2,3,4 в соответствии с их долей площади. Если мы посмотрим на порядок четырех областей, когда мы движемся по часовой стрелке вокруг точки пересечения двух линий, начиная с области 1, есть 6 возможностей: (1,2,3,4), (1,2,4, 3), (1,3,2,4), (1,3,4,2), (1,4,2,3), (1,4,3,2). На рисунке ниже показан пример, где n,p,q — любая перестановка 2,3,4.
На рисунке ниже показан пример, где n,p,q — любая перестановка 2,3,4.
Шаг 1 алгоритма: Выберите расположение регионов из 6 возможных.
Давайте теперь посмотрим, что произойдет, если мы выберем конкретную ориентацию для линии $l$ (как указано, например, единичным вектором или углом относительно некоторой опорной линии), которая проходит вдоль против часовой стрелки стороны области 1, как показано на рисунке выше. Пусть $n$ будет номером области, которая является соседней по часовой стрелке области 1. Затем мы хотим, чтобы $l$ разделил прямоугольник на две области, одна с долей $\frac{1+n}{10}$ Общая площадь. Если представить, что $l$ заметают по прямоугольнику, мы видим, что вся площадь перемещается от одной стороны линии к другой монотонным образом. По теореме о промежуточном значении существует единственная линия $l$, выполняющая эту работу.
Шаг 2 алгоритма: Выберите ориентацию для линии $l$. Согласно приведенным выше замечаниям, это полностью определяет строку.
Теперь я утверждаю, что положение второй строки $l’$ однозначно определяется уже сделанным нами выбором. Это следует из трех наблюдений:
- Для любой точки пересечения двух прямых существует уникальная ориентация второй прямой $l’$, при которой соотношение площадей 1 и $n$ становится правильным. Это снова следует из теоремы о промежуточном значении.
- Найденная в точке (1) ориентация монотонно меняется в зависимости от положения точки пересечения вдоль прямой $l$.
- Если точка пересечения находится в конце прямой $l$, то выбор $l’$, как указано выше, приведет к тому, что одна из областей $m$, $q$ на другой стороне будет иметь нулевую площадь. Итак, снова по теореме о промежуточном значении существует единственное положение точки пересечения вдоль $l$, при котором отношение оставшихся двух областей оказывается правильным.
Резюме: Разделение прямоугольника может быть задано двумя способами: расположением (1,n,p,q) и ориентацией линии $l$. 92$, этот алгоритм отлично работает и для соотношений, отличных от 1:2:3:4.
92$, этот алгоритм отлично работает и для соотношений, отличных от 1:2:3:4.
Уравнения для линий в этом случае имеют вид $y = \frac{5}{6} x$ для $l’$ (диагональ прямоугольника) и $x = \frac{6(\sqrt{ 2}+1)}{5} — \frac{12(\sqrt{2}-1)}{25} y$ для $l$.

Leave A Comment