Радиус вписанной окружности в ромб

Ромб – это параллелограмм, у которого все стороны равны. Следовательно, он наследует все свойства параллелограмма. А именно:


  • Диагонали ромба взаимно перпендикулярны.
  • Диагонали ромба являются биссектрисами его внутренних углов.

Окружность можно вписать в четырехугольник тогда и только тогда, когда суммы противоположных сторон равны.
Следовательно, в любой ромб можно вписать окружность. Центр вписанной окружности совпадает с центром пересечения диагоналей ромба.
Радиус вписанной окружности в ромб можно выразить несколькими способами

1 способ. Радиуса вписанной окружности в ромб через высоту

Высота ромба равна диаметру вписанной окружности. Это следует из свойства прямоугольника, который образуют диаметр вписанной окружности и высота ромба – у прямоугольника противолежащие стороны равны.

Следовательно формула радиуса вписанной окружности в ромб через высоту:

2 способ.

Радиус вписанной окружности в ромб через диагонали

Площадь ромба можно выразить через радиус вписанной окружности
, где Р– периметр ромба. Зная, что периметр это сумма всех сторон четырехугольника имеем P=4×а. Тогда
Но площадь ромба  также равна половине произведения его диагоналей
Прировняв правые части формул площади, имеем следующее равенство
В результате получаем формулу, позволяющую вычислить радиус вписанной окружности в ромб чрез диагонали

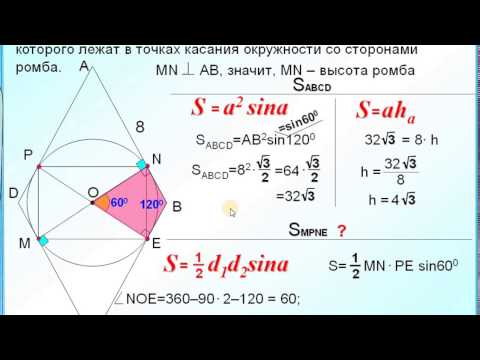
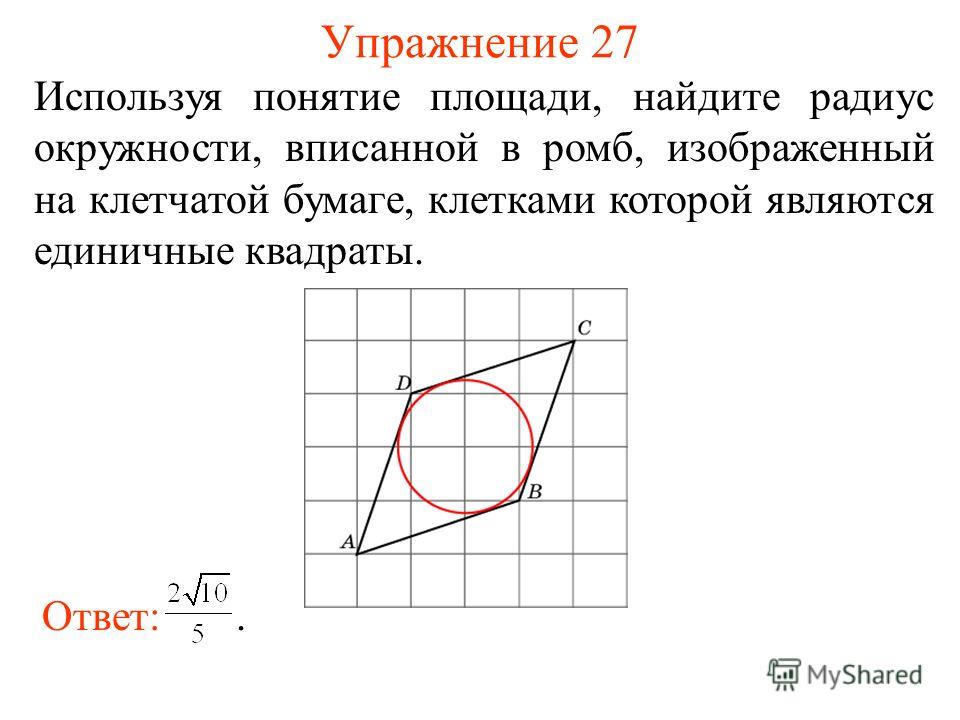
Пример расчета радиуса окружности вписанной в ромб, если известны диагонали
Найти радиус окружности вписанной в ромб, если известно, что длина диагоналей 30 см и 40 см
Пусть ABCD-ромб, тогда AC и BD его диагонали. AC=30 см, BD=40 см
Пусть точка О – это центр вписанной в ромб ABCD окружности, тогда она будет также являться и точкой пересечения его диагоналей, делящих их пополам.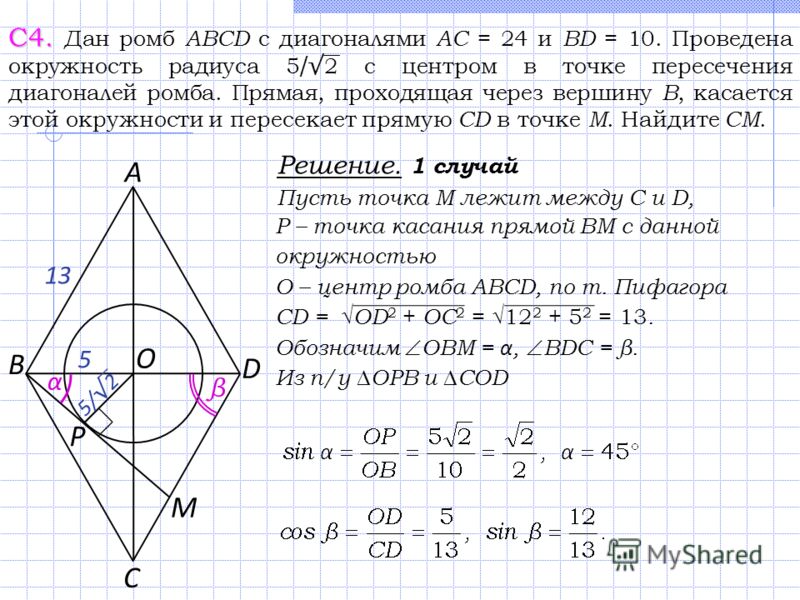


т.к диагонали ромба пересекаются под прямым углом, то треугольник AOB прямоугольный. Тогда по теореме Пифагора
, подставляем в формулу ранее полученные значения

AB = 25 см
Применив ранее выведенную формулу для радиуса описанной окружности в ромб, получаем

3 способ. Радиус вписанной окружности в ромб через отрезки m и n

Точка F – точка касания окружности со стороной ромба, которая делит ее на отрезки AF и BF. Пусть AF=m, BF=n.
Точка O – центр пересечения диагоналей ромба и центр вписанной в него окружности.
Треугольник AOB – прямоугольный, так как диагонали ромба пересекаются под прямым углом.
, т.к. является радиусом, проведенным в точку касания окружности . Следовательно OF – высота треугольника AOB к гипотенузе. Тогда AF и BF – проекции катетов на гипотенузу.
Высота в прямоугольном треугольнике, опущенная на гипотенузу есть среднее пропорциональное между проекциями катетов на гипотенузу.

Формула радиуса вписанной окружности в ромб через отрезки равна корню квадратному из произведения этих отрезков, на которые делит сторону ромба точка касания окружности

Пример расчета радиуса окружности вписанной в ромб, если известны отрезки m и n
Найдите радиус описанной окружности в ромб, если точка касания делит сторону ромба на 9 и 4
Пусть ABCD-ромб, тогда AC и BD его диагонали.
Пусть точка O – это центр вписанной в ромб ABCD окружности.
Пусть точка F – точка касания окружности со стороной ромбаAB. Тогда. AF=9, BF=4
Применив ранее полученную формулу, получаем

формула, как найти площадь и диагональ

Содержание:

  • Окружность, вписанная в ромб
    • Свойства ромба и вписанной окружности
  • Как найти радиус, основные способы
    • Радиус вписанной окружности, если известны диагонали и сторона
    • Если известны только диагонали ромба
    • Если известны сторона и угол
    • Если известна высота ромба
    • Если известны площадь ромба и его сторона
  • Вычисление радиуса через отрезки m и n
  • Задачи с решениями

Содержание

  • Окружность, вписанная в ромб
    • Свойства ромба и вписанной окружности
  • Как найти радиус, основные способы
    • Радиус вписанной окружности, если известны диагонали и сторона
    • Если известны только диагонали ромба
    • Если известны сторона и угол
    • Если известна высота ромба
    • Если известны площадь ромба и его сторона
  • Вычисление радиуса через отрезки m и n
  • Задачи с решениями

Окружность, вписанная в ромб

Ромб — это параллелограмм с четырьмя равными сторонами.

Квадрат — частный случай ромба; это ромб, все углы которого прямые.

Вписанная в ромб окружность — это окружность, которая лежит внутри ромба и касается всех его сторон.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Окружность можно вписать в многоугольник, у которого равны суммы противолежащих сторон. Ромб соответствует этому условию, поэтому в ромб можно вписать окружность.

Свойства ромба и вписанной окружности
  • в любой ромб можно вписать окружность;
  • точка пересечения диагоналей ромба является центром окружности, вписанной в ромб.

Как найти радиус, основные способы

Радиус вписанной окружности, если известны диагонали и сторона

Радиус r вписанной в ромб окружности равен произведению его диагоналей, деленному на периметр или на сторону, умноженную на 4. 2}}\).

Если известны сторона и угол

Радиус окружности, вписанной в ромб, равен половине произведения его стороны и синуса любого внутреннего угла ромба.

Формула 3

\(r=\frac{a\cdot\sin\alpha}2=\frac{a\cdot\sin\beta}2\)

где r — радиус вписанной окружности,

α и β — внутренние углы ромба,

a — сторона ромба.

Если известна высота ромба

Радиус вписанной в ромб окружности равен половине его высоты.

Формула 4

\(r=\frac h3\)

где r — радиус вписанной окружности,

h — высота ромба.

Из этой формулы следует, что высота ромба равна диаметру вписанной в него окружности.

Если известны площадь ромба и его сторона

Формула 5

\(r=\frac S{2a}=\frac Sр\)

где r — радиус вписанной окружности,

S — площадь ромба,

a — сторона ромба,

р — полупериметр ромба.

Вычисление радиуса через отрезки m и n

Вписанная окружность касается стороны ромба. Точка касания делит сторону ромба на два отрезка. Пусть это будут отрезки m и n

.

Диагонали ромба взаимно перпендикулярны, ΔАОD — прямоугольный. Высота ΔАОD к стороне АD равна радиусу вписанной в ромб АВСD окружности.

По свойству высоты прямоугольного треугольника, проведенной к гипотенузе, \(ОК=\sqrt{АК\cdot КD}\).

Следовательно, радиус вписанной в ромб окружности равен среднему пропорциональному между отрезками, на которые делит сторону ромба точка касания.

Формула 6

\(r=\sqrt{m\cdot n}\)

где r — радиус вписанной окружности,

m и n — отрезки, на которые делит сторону ромба точка касания.

Задачи с решениями

Задача 1

Дано: ромб с диагоналями 6 см и 8 см.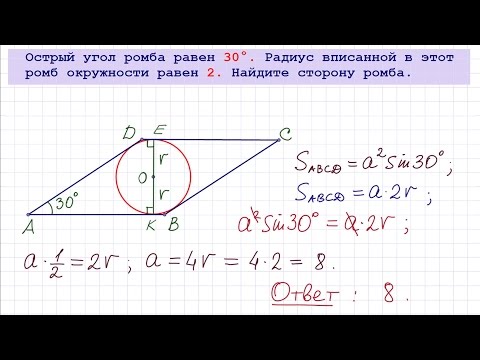 2}}=2,4 (см).\)

Ответ: радиус вписанной в ромб окружности равен 2,4 см.

Задача 2

Дано: ромб, сторона которого равна 16 см, а острый угол ромба — 30°.

Найти: радиус вписанной в ромб окружности.

Решение: применим формулу \(r=\frac{a\cdot\sin\alpha}2.\)

\(r=\frac{16\cdot0,5}2=\frac82=4 (см).\)

 Ответ: радиус вписанной в ромб окружности равен 4 см.

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 1)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Урок Окружность, вписанная в ромб

Этот Урок (Окружность, вписанная в ромб) создана пользователем ikleyn(47640)   : Просмотр исходного кода, Показать
О ikleyn :

0 Этот урок посвящен одной проблеме.

Задача

По заданному ромбу построить окружность, вписанную в ромб .

Чтобы решить эту проблему, мы разделим ее на более мелкие подзадачи.

Проблема 1
Где расположен центр окружности, вписанной в ромб?


Раствор
— Мммм… Находится в центре ромба.

— ОК. Тогда где находится центр ромба?

— Мммм… На пересечении его диагоналей.

— ОК. Это верно. Теперь ответьте на вопрос: почему центр
вписанной окружности расположен на пересечении диагоналей ромба?

— Мммм…
   Оооо!!! У меня есть идея!



     Рисунок 1 . К проблеме 1

Если окружность вписана в ромб, она вписана в каждый из четырех внутренних углов ромба.

Следовательно, центр вписанной окружности расположен на биссектрисе внутренних углов ромба. А биссектриса ромба — это его диагональ.
Значит, центр вписанной окружности лежит в точке пересечения диагоналей ромба.

— Очень хорошо. У вас есть основная идея решить эту строительную проблему.

В завершение этой части урока я хотел бы привести ссылки на уроки, на которых были доказаны соответствующие геометрические факты.

То, что центр окружности, вписанной в угол, находится на биссектрисе угла, было доказано в уроке Свойства биссектрисы угла по теме
Треугольники раздела Геометрия на этом сайте.
То, что в ромбе диагонали являются биссектрисами углов, было доказано в уроке Диагонали ромба делят его углы пополам в теме Параллелограммы
раздела Геометрия на этом сайте.

Проблема 2
Построить радиус окружности, вписанной в данный ромб.


Раствор
Если окружность вписана в ромб, то сторона ромба равна                          
касательной к окружности. Визуально это видно из Рисунок 2 .
Теперь примем это без формального доказательства.
(Это будет доказано позже на одном из следующих уроков).

Следовательно, для построения радиуса вписанной окружности
надо построить перпендикуляр из центра окружности
к стороне ромба. Неважно, к какой из четырех сторон
ромба. Любому.



     Рисунок 2 . К Задаче 2

Другими словами, мы должны построить перпендикуляр из центра ромба, являющегося точкой пересечения диагоналей, на сторону ромба.

Алгоритм построения перпендикуляра из точки вне прямой к прямой с помощью линейки и циркуля был описан в уроке
Как разделить отрезок пополам с помощью циркуля и линейки. Этот урок относится к теме Треугольники раздела Геометрия на этом сайте.

Таким образом, у вас есть алгоритм построения радиуса вписанной окружности до ромба.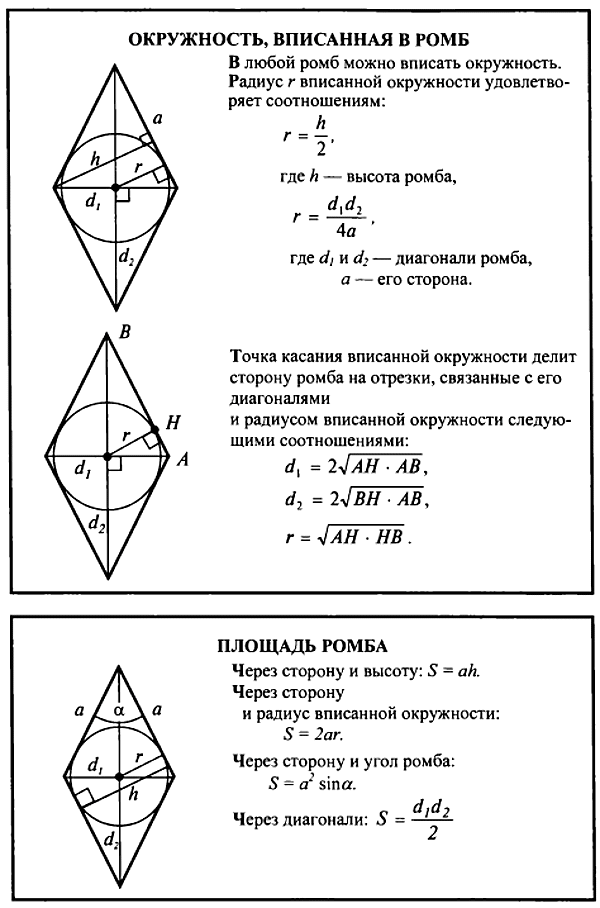
Конструкция Задача 2 решена.

В качестве последнего шага в этом уроке я хочу, чтобы вы решили следующее

Задача 3
Вычислите радиус окружности, вписанной в данный ромб.
Ромб задается мерой стороны и мерой диагонали и .


Решение
Как мы договорились выше при решении задачи 2 , радиус                             
окружности, вписанной в данный ромб, равен перпендикуляру, проведенному
из центра окружности (точки пересечения диагоналей)
в сторону ромб в точке касания.

Диагонали ромба перпендикулярны и делят друг друга пополам.
Это было доказано на уроках Диагонали ромба перпендикулярны
и Свойства диагоналей параллелограммов по теме
Параллелограммы раздела Геометрия на этом сайте.
Следовательно, диагонали ромба делят его на четыре конгруэнтных



     Рисунок 3 . К Задаче 3

прямоугольных треугольников, и нам нужно найти длину высоты любого из четырех прямоугольных треугольников, проведенных из вершины прямого угла к гипотенузе.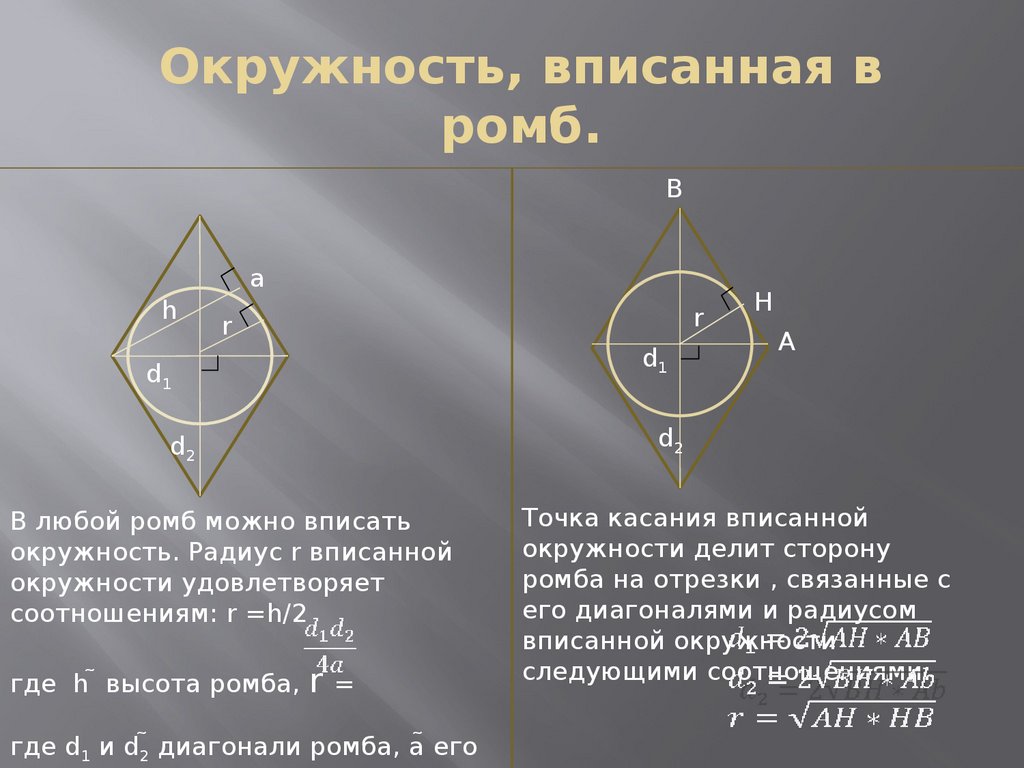

Итак, наша исходная задача сводится к следующей:

найти высоту прямоугольного треугольника, проведенного из вершины прямого угла к гипотенузе .

Параметрами этого прямоугольного треугольника являются его стороны a и b и мера гипотенузы c ( рис. 4 ), связанные с параметрами исходного ромба равенствами


, , .

Пусть x и y будут мерами отрезков, которые пересекает высота                                 
гипотенузы. Пусть z будет длиной высоты, проведенной к гипотенузе
( рис. 4 ).

Мы хотим получить формулу, выражающую z через a , b и c .

Существует несколько способов получения такой формулы.

8


Рисунок 4 . Высота прямоугольного треугольника

Например, можно записать равенство площади треугольника как

и вывести из него, что

.

Но я не предполагаю, что в этом уроке вы знакомы с понятием площади треугольников.

Действуя иначе, можно заметить, что треугольник ACD подобен треугольнику ABC ( Рисунок 4 ), то для получения пропорции из этого факта

и, наконец, получить ту же формулу из пропорции

.

Но я не предполагаю, что в этом уроке вы знакомы с понятием подобия треугольников.

Что я действительно хочу сделать в этом уроке, так это получить формулу для z из «первых принципов».


Этими «первыми принципами» являются следующие три уравнения для x , y и z :

          (1)    (формула Пифагора для прямоугольного треугольника ADC ),
          (2)    (формула Пифагора для прямоугольного треугольника BDC ), и
  (             (очевидно).

Возведем уравнение (3) в квадрат (обе части). Мы получаем
. (4)



Рисунок 5 . Высота прямоугольного треугольника

Сложим уравнения (1) и (2) (обе части). Мы получаем
,
или
(5),

потому что

по теореме Пифагора для прямоугольного треугольника ABC .

Сравнивая уравнения (4) и (5), получаем
. (6)

Возведите в квадрат обе части уравнения (6). Вы получаете
. (7)

Подставить выражения
и

в уравнение (7). (Обратите внимание, что эти выражения представляют собой переписанные уравнения (1) и (2)). Вы получаете
.

Раскройте скобки и сократите подобные условия. Вы получаете
,

или
.

Теперь извлеките квадратный корень из обеих частей. Вы получаете
,

, который является нашей целью.

Теперь, возвращаясь к нашему исходному ромбу, формула радиуса вписанной окружности выглядит так:

.

Сводка
На этом уроке вы узнали, что центр окружности, вписанной в ромб, лежит на пересечении его диагоналей.
Вы научились определять радиус вписанной окружности с помощью линейки и циркуля.
Вы научились вычислять радиус окружности, вписанной в ромб.
Вы узнали, что есть разные способы получить целевую формулу, и узнали, как получить эту формулу из «первых принципов».

По пути вы научились вычислять высоту прямоугольного треугольника, проведенного к гипотенузе через катеты и меры гипотенузы.

Ниже приведены несколько примеров, которые показывают, как работает формула.

Пример 1
Диагональ ромба 40 см и 30 см.
Найдите радиус окружности, вписанной в ромб.

Раствор
Сначала найдем длину стороны ромба.

Обратите внимание, что диагонали ромба перпендикулярны и делят друг друга пополам. Итак, диагонали ромба делят его на четыре равных прямоугольных треугольника
с мерами катетов и , где и — меры диагоналей ромба.

Найдите меру стороны ромба как длину гипотенузы прямоугольного треугольника с катетами 40/2 = 20 см и 30/2 = 15 см:
.

Получается длина стороны 25 см.

Или можно сразу применить формулу из урока Длина диагоналей ромба, который находится в текущей теме Геометрия раздела Словесные задачи на этом сайте:
,

где и — меры диагоналей ромба и — длина его стороны.

Подставить полученные данные для диагоналей ромба в эту формулу
,

и вы получите те же 25 см длины стороны ромба.

Итак, теперь вы знаете, что диагонали ромба равны 40 см и 30 см, а длина стороны 25 см.

Хорошо, очень хорошо.
Теперь используйте формулу Теоремы в этом уроке, чтобы вычислить радиус окружности, вписанной в ромб:
.

Получаем 12 см радиуса окружности, вписанной в ромб.

Ответить . Радиус окружности, вписанной в ромб, равен 12 см.

Пример 2
Ромб имеет длину одной диагонали 18 см и периметр 60 см.
Найдите радиус окружности, вписанной в ромб.

Раствор
Сначала найдем длину стороны ромба.
Равен одной четверти периметра, то есть 60/4 = 15 см.

Обратите внимание, что диагонали ромба перпендикулярны и делят друг друга пополам. Итак, диагонали ромба делят его на четыре равных прямоугольных треугольника. Для этих треугольников вы знаете длину гипотенузы, которая равна стороне ромба, равной 15 см, и меру катета, которая составляет половину известной длины диагонали 18/2 = 9.см.

Найдите неизвестную длину катета одного из этих прямоугольных треугольников, применив формулу Пифагора к треугольнику с гипотенузой 15 см и катетом 9 см:
.

Получается длина второй стороны прямоугольного треугольника 12 см.
Поскольку это половина диагонали ромба, вся диагональ равна 2*12 см = 24 см.

Или можно применить формулу, полученную в уроке Длина диагоналей ромба, который находится в текущей теме Геометрия раздела Задачи Word на этом сайте:
,

где — заданная и — неизвестная мера диагоналей ромба и — длина его стороны.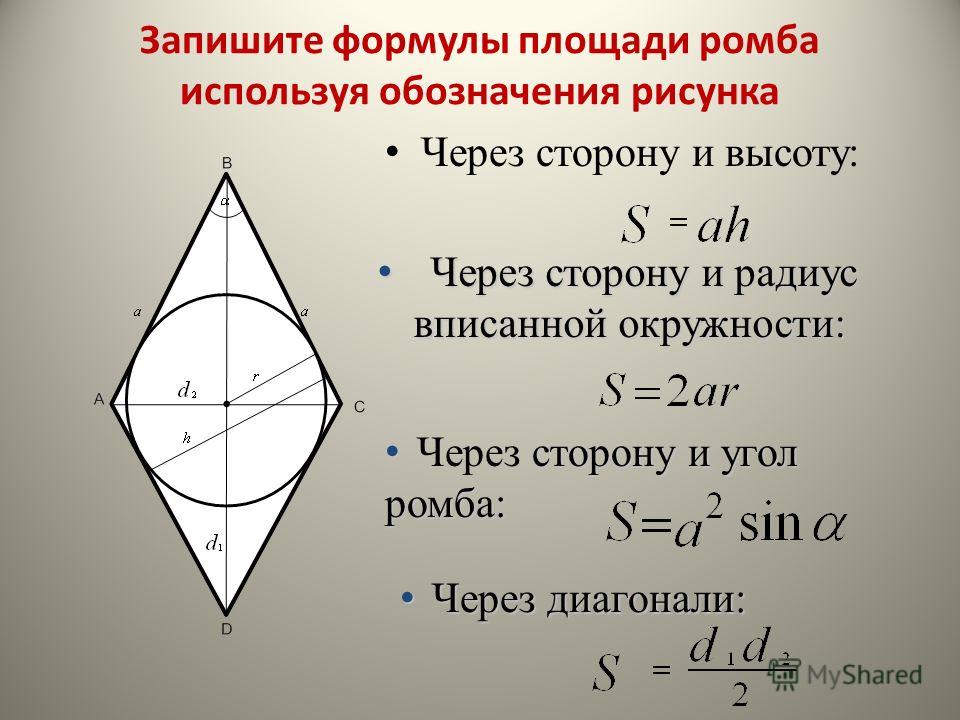

Подставить данные для ромба в эту формулу
,

и вы получите те же 24 см длины второй диагонали ромба.

Итак, теперь вы знаете, что диагонали ромба равны 18 см и 24 см, а длина стороны 15 см.

Хорошо, очень хорошо.
Теперь используйте формулу Теоремы в этом уроке, чтобы вычислить радиус окружности, вписанной в ромб:
.

Получаем 7,2 см радиуса окружности, вписанной в ромб.

Ответить . Радиус окружности, вписанной в ромб, равен 7,2 см.

Другие мои уроки по ромбам на этом сайте
    — Диагонали ромба перпендикулярны
    — Диагонали ромба делят его углы пополам
    — Длина диагоналей ромба
    — КАК РЕШАТЬ задачи на стороны ромба и меры диагоналей — Примеры,
    — Длина диагоналей ромба
    — СВОЙСТВА РОМБИСОВ

Для навигации по всем темам/урокам онлайн-учебника по геометрии используйте этот файл/ссылку  ГЕОМЕТРИЯ — ВАШ ОНЛАЙН-УЧЕБНИК.

[Решено] В ромб с диагоналями 12 см вписана окружность

  1. \(\frac{{\;2\pi }}{{15}}\)
  2. \(\frac{{\;3\pi}}{{25}}\)
  3. \(\frac{{\;6\pi}}{{25}}\)
  4. \(\frac {{\;5\pi}}{{18}}\)

Вариант 3: \(\frac{{\;6\pi}}{{25}}\)

Бесплатно

Понимание прочитанного Том 1

13 тыс.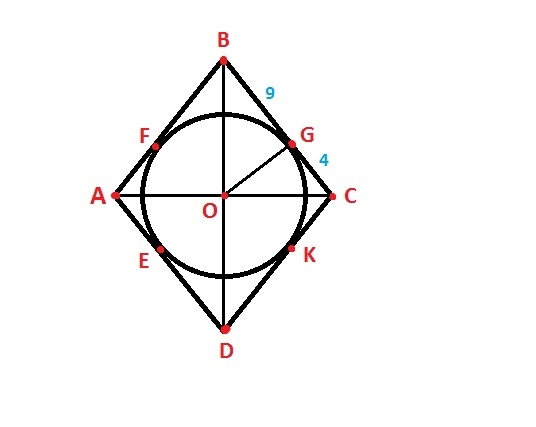 пользователей

12 вопросов

36 баллов

20 минут

Расчет:

Ромб и вписанный круг можно изобразить в соответствии со следующим рисунком:

ABCD — ромб с диагоналями 16 см и 12 см в длину.

Центр окружности находится в точке O, а радиус равен r.

Итак, получаем:

AO = OC = 16/2 = 8 см

И DO = OB = 12/2 = 6 см

Применяя теорему Пифагора к ΔADO, получаем:

(AD) 2 = (AO) 2 + (OD) 2

⇒ (AD)2 = 82 + 62

⇒ AD = 10 см

способы:

Использование гипотенузы AD в качестве основания или Использование OD в качестве основания. Площадь останется прежней. Итак,

(1/2) × АО × OD = (1/2) × r × AD

⇒ r = (8 × 6)/10 = 4,8 см

Итак, площадь круга = π × 4,8 2  = 23,04π см        —-(i)

А площадь ромба = (1/2) × 12 × 16 = 96 см2​      —-(ii)


9

∴ отношение площади круга к площади ромба = 23,04π/96 = 6π/25 см2​

Дополнительная информация

Площадь ромба = (1/2) × (произведение длин диагоналей)

Диагонали ромба пересекаются под прямым углом

Площадь прямоугольного треугольника = (1/2) × (произведение сторон, отличных от гипотенузы)

Теорема Пифагора.