Точки минимума и максимума на графике функции: Найдите точку максимума и точку минимума функции y=f(x),если известно ,что f'(x)=x^2-5x+6

Исследование графика функции. Минимум и максимум

На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:

• область определения функции;
• область значений функции;
• нули функции;
• промежутки возрастания и убывания;
• точки максимума и минимума;
• наибольшее и наименьшее значение функции на отрезке.

Уточним терминологию:

Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось X.
Ось ординат — вертикальная ось, или ось Y.

Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается x.
Другими словами, мы сами выбираем x, подставляем в формулу функции и получаем y.

Область определения функции — множество тех (и только тех) значений аргумента x, при которых функция существует.

Обозначается: D(f) или D(y).

На нашем рисунке область определения функции  — это отрезок . Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.

Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок  — от самого нижнего до самого верхнего значения .

Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки и .

Значения функции положительны там, где . На нашем рисунке это промежутки и .
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от до .

Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества  можно взять отрезок , интервал , объединение промежутков или всю числовую прямую.

Функция возрастает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .

Иными словами, чем больше , тем больше , то есть график идет вправо и вверх.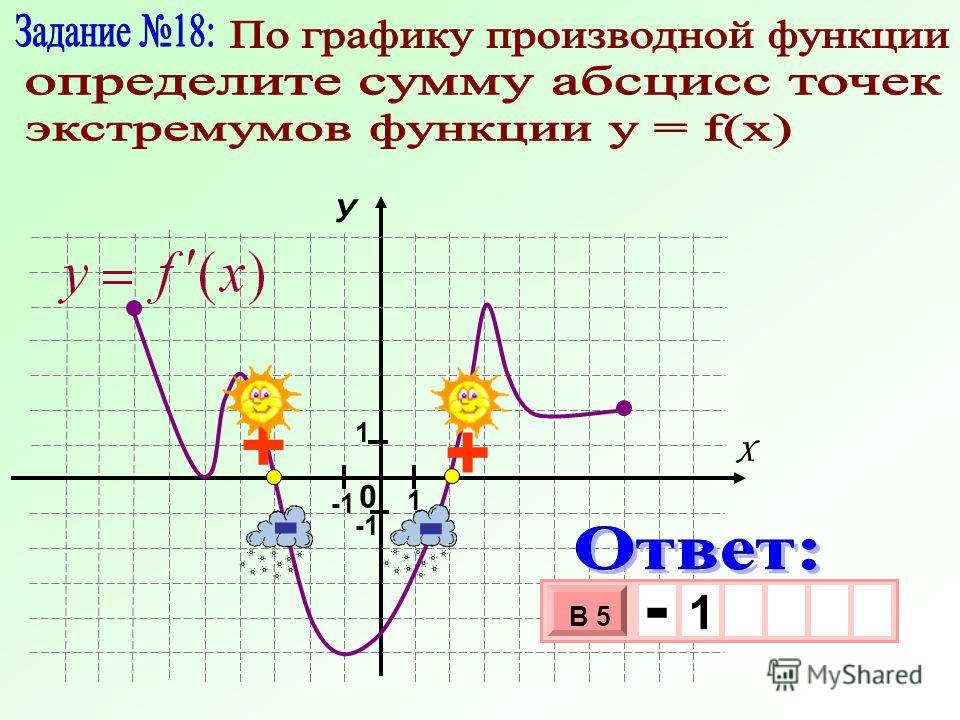

Функция убывает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .

Для убывающей функции большему значению  соответствует меньшее значение . График идет вправо и вниз.

На нашем рисунке функция возрастает на промежутке и убывает на промежутках и .

Определим, что такое точки максимума и минимума функции.

Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.

На нашем рисунке  — точка максимума.

Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».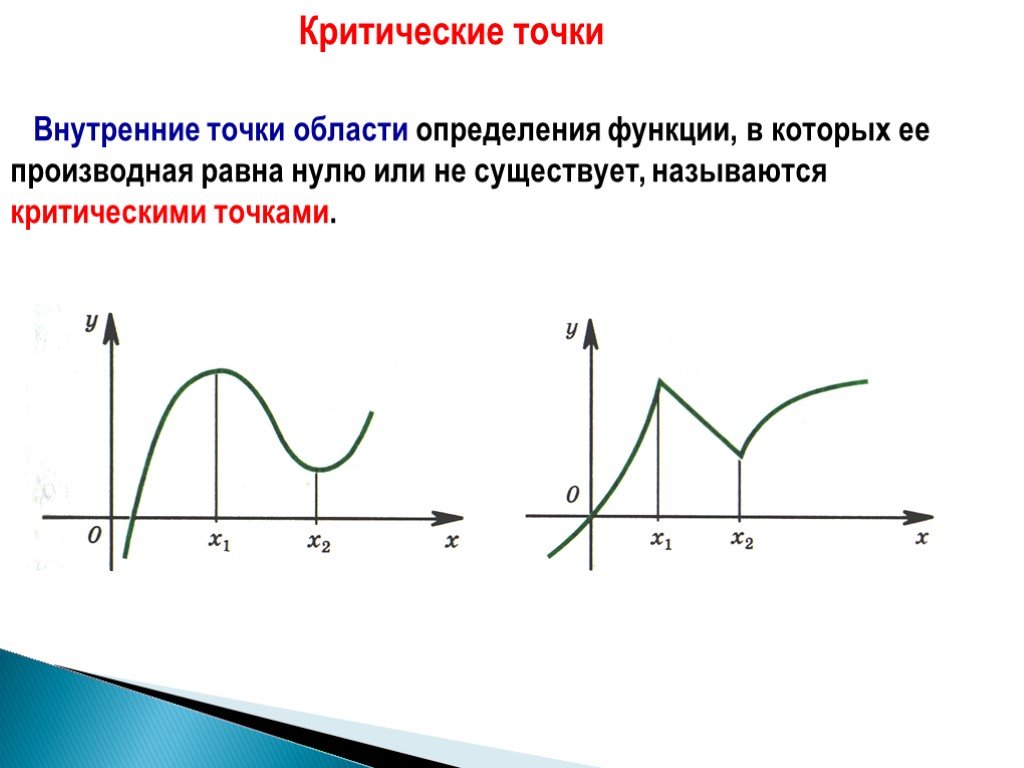

На нашем рисунке  — точка минимума.

Точка  — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и  на нашем графике не может быть точкой минимума.

Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это  и .

А что делать, если нужно найти, например, минимум функции на отрезке ? В данном случае ответ: . Потому что

минимум функции — это ее значение в точке минимума.

Аналогично, максимум нашей функции равен . Он достигается в точке .

Можно сказать, что экстремумы функции равны  и .

Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.

В нашем случае наименьшее значение функции на отрезке равно  и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно . Оно достигается в левом конце отрезка.

В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.

Спасибо за то, что пользуйтесь нашими публикациями. Информация на странице «Исследование графика функции» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена: 09.03.2023

как найти по уравнению, поиск минимума

Содержание:

• Минимум и максимум функции
  • Точка минимума, минимум функции
  • Точка максимума, максимум функции
• Исследование функций на экстремумы
• Примеры задач

Содержание

• Минимум и максимум функции
  • Точка минимума, минимум функции
  • Точка максимума, максимум функции
• Исследование функций на экстремумы
• Примеры задач

Минимум и максимум функции

Минимумом и максимумом функции, другими словами

экстремумами, называют точки, в которых функция меняет характер монотонности (с возрастания на убывание и наоборот). Важно понимать, что экстремумы это не максимальные и минимальные значения функции. Обозначаются следующим образом: 

• \(y_{min}, y_{max}\) — минимум, максимум функции или экстремумы;
• \(x_{min}, x_{max}\) — точки минимума, максимума функции;
• \(y_{наиб}, y_{наим}\) — наибольшее (максимальное), наименьшее (минимальное) значение функции.

Точка минимума, минимум функции

Точка минимума — такая точка \(x_0\), если у неё существует окрестность, для всех точек которой выполняется неравенство \(f(x)\geq f(x_0)\)

Минимум функции — значение функции в точке минимума \(x_0\)

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Простыми словами, точка минимума — это та, где убывание функции меняется на возрастание.

Точка максимума, максимум функции

Точка максимума — такая точка \(x_0\), если у неё существует окрестность, для всех точек которой выполняется неравенство \(f(x)\leq f(x_0)\)

Максимум функции — значение функции в точке максимума \(x_0\)

Простыми словами, точка максимума — это та, где возрастание функции меняется на убывание.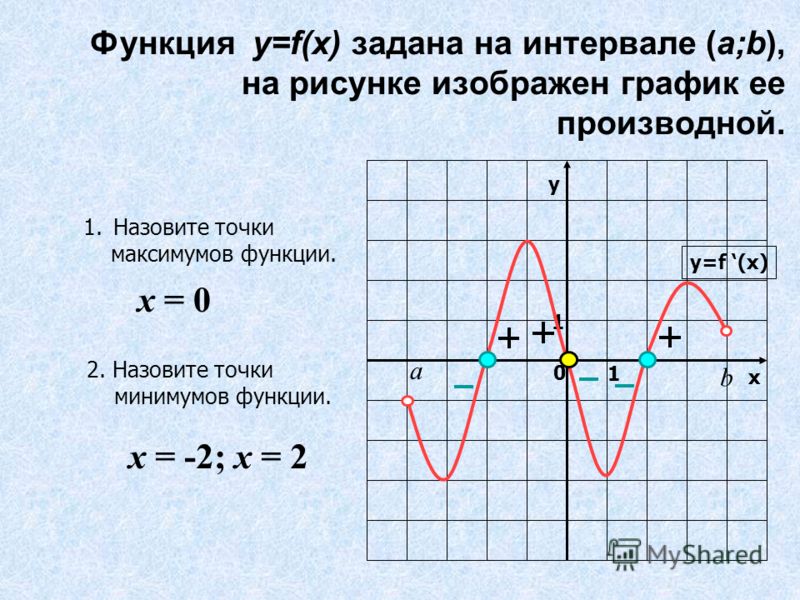 4+6x\)

3) Приравняем f'(x) к 0 и найдем корень: x = 0. Отметим 0 на числовой прямой и определим знак производной на промежутках \((-\infty;0)\) и \((0;+\infty)\). Получим, что производная положительна на обоих промежутках, следовательно функция возрастает на всей числовой прямой.

Утверждение доказано

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 3)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

Максимальные и минимальные значения — Подход к исчислению

Подход

к

C A L C U L U S

Содержание | Дом

10

МЫ ГОВОРИМ, ЧТО ФУНКЦИЯ f ( x ) имеет относительное максимальное значение при x = a ,
, если f ( a ) больше , чем любое предшествующее или предшествующее значение .

Мы называем это «относительным» максимумом, потому что другие значения функции на самом деле могут быть больше.

Мы говорим, что функция

f ( x ) имеет относительное минимальное значение при x = b ,
, если f ( b ) на меньше, чем любое значение, непосредственно предшествующее или следующее за ним.

Опять же, другие значения функции на самом деле могут быть меньше. При таком понимании мы отбросим термин «относительный».

Значение функции, значение y , максимальное или минимальное, называется экстремальным значением.

Теперь, что характеризует график при экстремальном значении?

Касательная к кривой горизонтальна . Мы видим это в точках A и B . Наклон каждой касательной линии — производная при оценке a или b — это 0,

f ‘ ( x ) = 0,

Более того, в точках непосредственно от осталось максимума — в точке C — наклон касательной положителен:   f ‘ ( x ) > 0. справа — в точке D — наклон отрицательный:   f ‘ ( x )

Другими словами, максимум   f ‘ ( x ) меняет знак с + на — .

Как минимум,   f ‘ ( x ) меняет знак с − на + . Мы видим, что в точках E и F ​​ .

Также можно заметить, что в максимуме при A график вогнут вниз. (Тема 14 Precalculus.) Хотя, как минимум, на B он вогнут вверх.

Значение x , при котором функция имеет либо максимум, либо минимум, называется критическим значением. На рисунке —

— критические значения x  = a и x  = b .

Критические значения определяют точки поворота, в которых касательная параллельна оси x . Критические значения — если они есть — будут решений от до f ‘ ( x ) = 0,

Пример 1.   Пусть   f ( x ) = x ² − 6 х + 5.  

Есть ли критические значения — поворотные точки? Если да, то определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума?

Решение . f ‘ ( x ) = 2 x − 6 = 0 означает x = 3. (Урок 9 алгебры.)

x = 3 — единственное критическое значение. Это х -координата точки поворота. Чтобы определить координату y , оцените f при этом критическом значении — оцените f (3):

ф ( х )	=	x 2 − 6 x + 5
f (3)	=	3 2 − 6 · 3 + 5
	=	−4.

Крайнее значение равно −4. Чтобы увидеть, является ли это максимумом или минимумом, в этом случае мы можем просто посмотреть на график.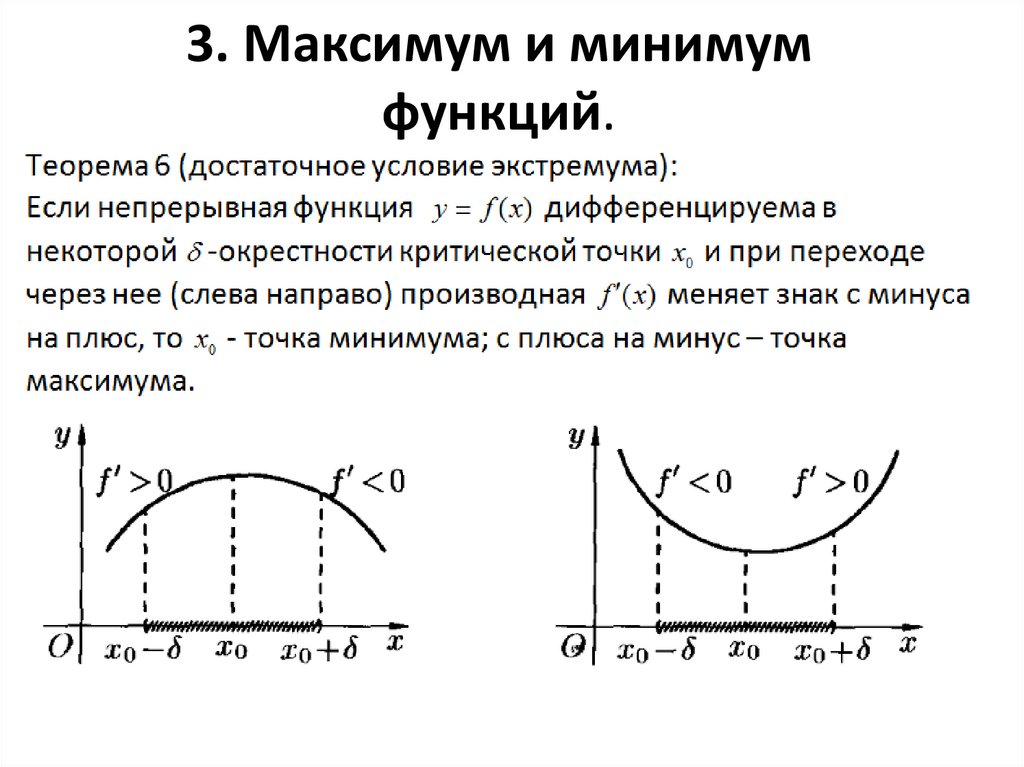

f ( x ) — это парабола, и мы видим, что точка поворота является минимумом.

Найдя значение x , где производная равна 0, то мы обнаружили, что вершина параболы находится в точке (3, −4).

Но не всегда мы сможем посмотреть на график. Алгебраическое условие минимума состоит в том, что f ‘ ( x ) меняет знак с − на + . Это мы видим в точках E , B , F ​​ выше. Значение наклона увеличивается.

Теперь сказать, что наклон увеличивается, значит сказать, что при критическом значении вторая производная (Урок 9) — скорость изменения наклона — плюс .

Опять же, вот f ( x ):

ф ( х )	=	x 2 − 6 x + 5.
f ‘ ( x )	=	2 х − 6,
f » ( x )	=	2.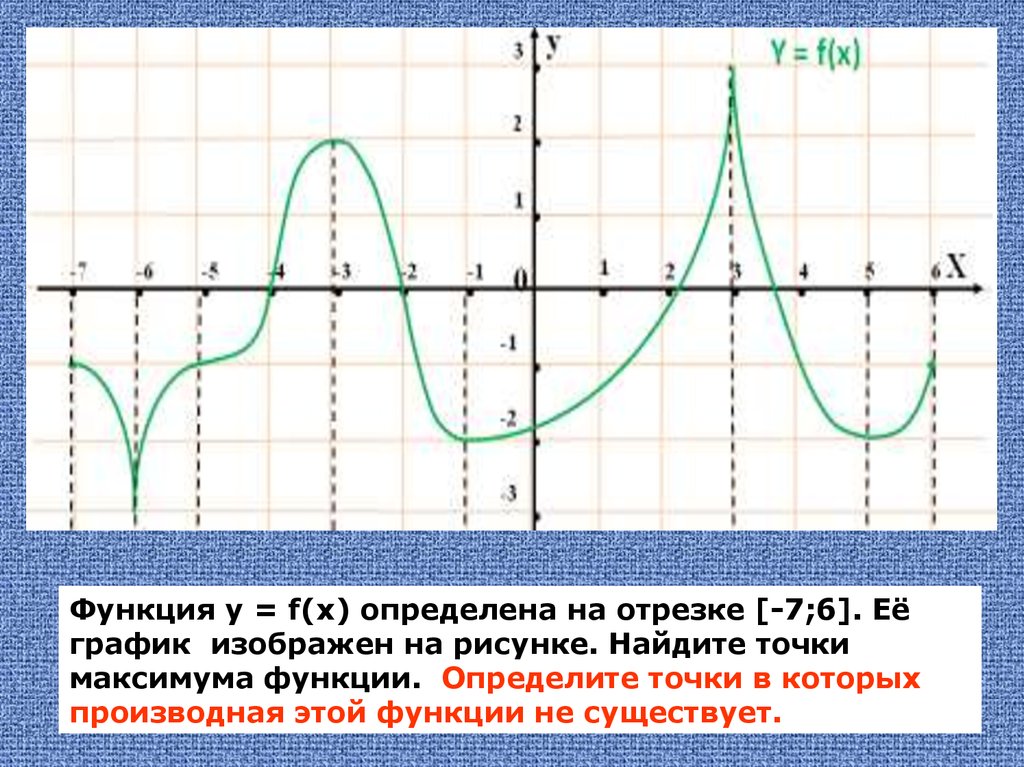

f » оценивается при критическом значении 3 — f» (3) = 2 — положительный. Это говорит нам алгебраически, что критическое значение 3 определяет минимум.

Достаточные условия

Теперь мы можем сформулировать эти достаточные условия для экстремальных значений функции при критическом значении и :

Функция имеет минимальное значение при x  = a  если f ‘ ( a ) = 0
и f » ( a ) = положительное число.

Функция имеет максимальное значение при x  = a  if f ‘ ( a ) = 0
и f » ( a ) = отрицательное число.

В случае максимума наклон касательной равен уменьшается — идет от положительного к отрицательному. Мы видим, что в точках C , A , D .

Пример 2. Пусть f ( x ) = 2 x ³ — 9 x ² + 12 x — 3,

Есть ли экстремальные значения? Во-первых, существуют ли какие-либо критические значения — решения для f ‘ ( x ) = 0 — и определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума? Где поворотные моменты?

Решение .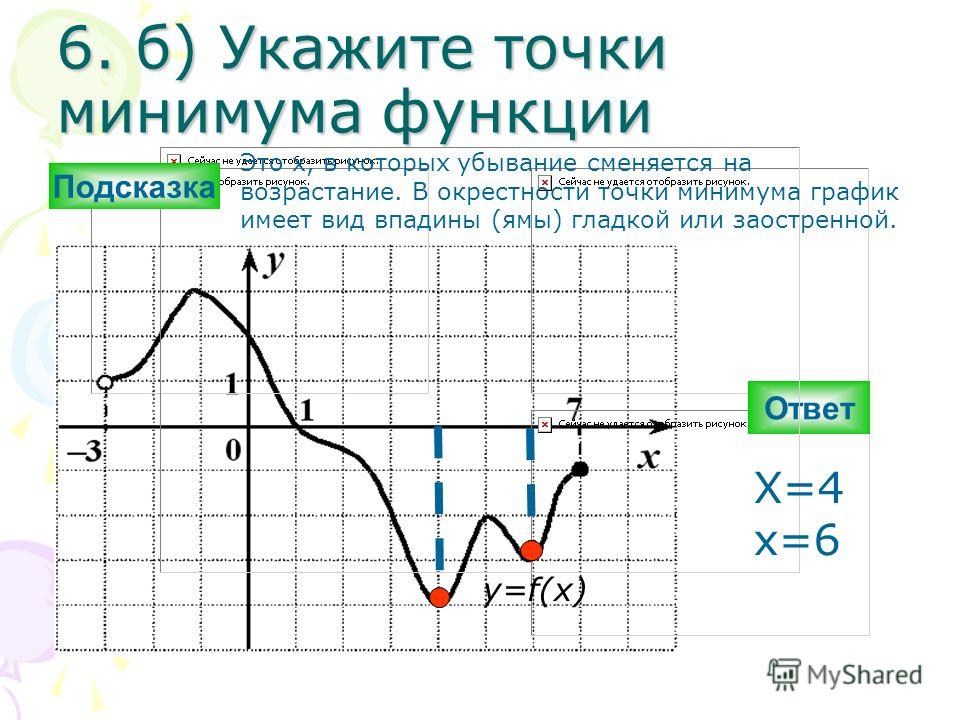 f’ ( х ) = 6 х 2 — 18 х + 12	=	6( х 2 − 3 х + 2)
	=	6( х — 1)( х — 2)
	=	0

подразумевает:

x = 1 или x = 2.

(Урок 37 Алгебры.)

Это критические значения. Каждый из них определяет максимум или он определяет минимум? Чтобы ответить, мы должны оценить вторую производную при каждом значении.

ф’ ( х )	=	6 x 2 − 18 x + 12.
f » ( x )	=	12 x − 18.
ж» (1)	=	12 — 18 = -6.

Вторая производная отрицательна. Таким образом, функция имеет максимум при разрешении x  = 1,

.

Чтобы найти y -координату — экстремальное значение — в этом максимуме мы оцениваем   f (1):

ф ( х )	=	2 x 3 − 9 x 2 + 12 x − 3
f (1)	=	2 − 9 + 12 − 3
	=	2.

Максимум приходится на точку (1, 2).

Далее, определяет ли x = 2 максимум или минимум?

ж» ( х )	=	12 x − 18.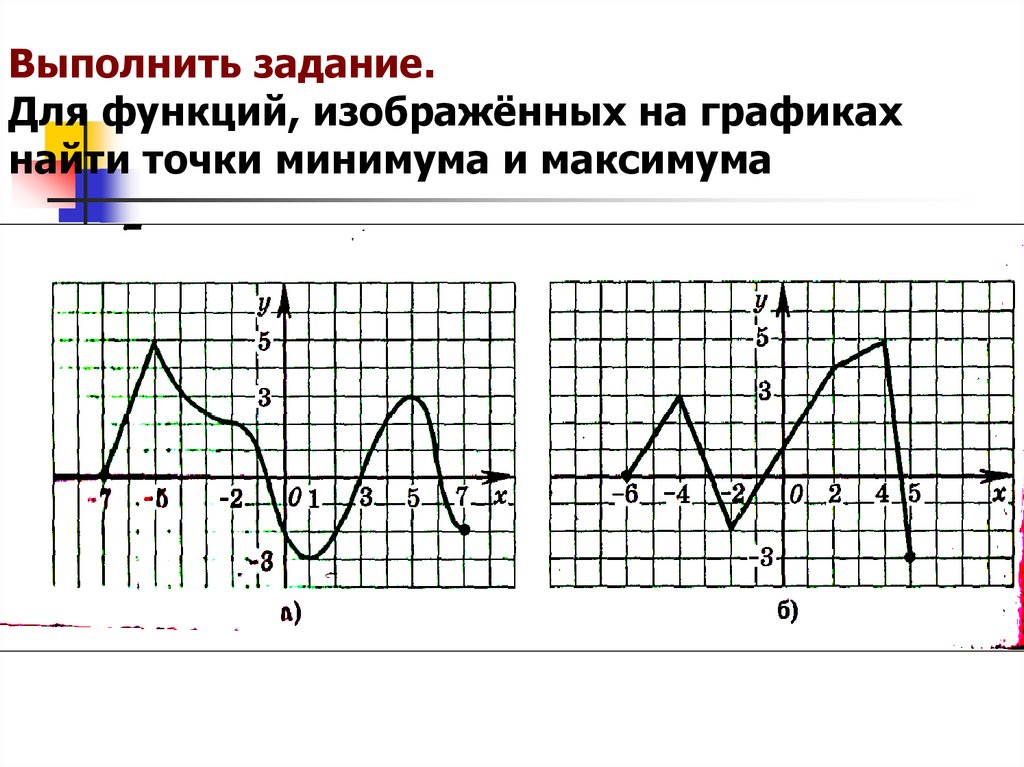
ф» (2)	=	24 — 18 = 6.

Вторая производная положительна. Таким образом, функция имеет минимум при x  = 2,

.

Чтобы найти y -координату — экстремальное значение — при этом минимуме, мы оцениваем ф (2):

ф ( х )	=	2 x 3 − 9 x 2 + 12 x − 3.
f (2)	=	16 − 36 + 24 − 3
	=	1.

Минимум приходится на точку (2, 1).

Вот собственно график f ( x ):

Решения f » ( x ) = 0 указывают точку перегиба в этих решениях, а не максимум или минимум. Пример: y  =  x ³ . г» = 6 x = 0 подразумевает x  = 0. Но x  = 0 является точкой перегиба на графике y  = x ³ , а не максимумом или минимумом.

Другой пример: y = sin x . Решения y » = 0 — это произведения π, которые являются точками перегиба.

Задача 1.   Найти координаты вершины параболы

г = х ² — 8 х + 1.

Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай задачу сам!

у’ = 2 х — 8 = 0,

Отсюда следует, что x = 4. Это x -координата вершины. Чтобы найти координату y , оцените г в х = 4:

y = 4 ² − 8 ·  4 + 1 = −15.

Вершина находится в точке (4, −15).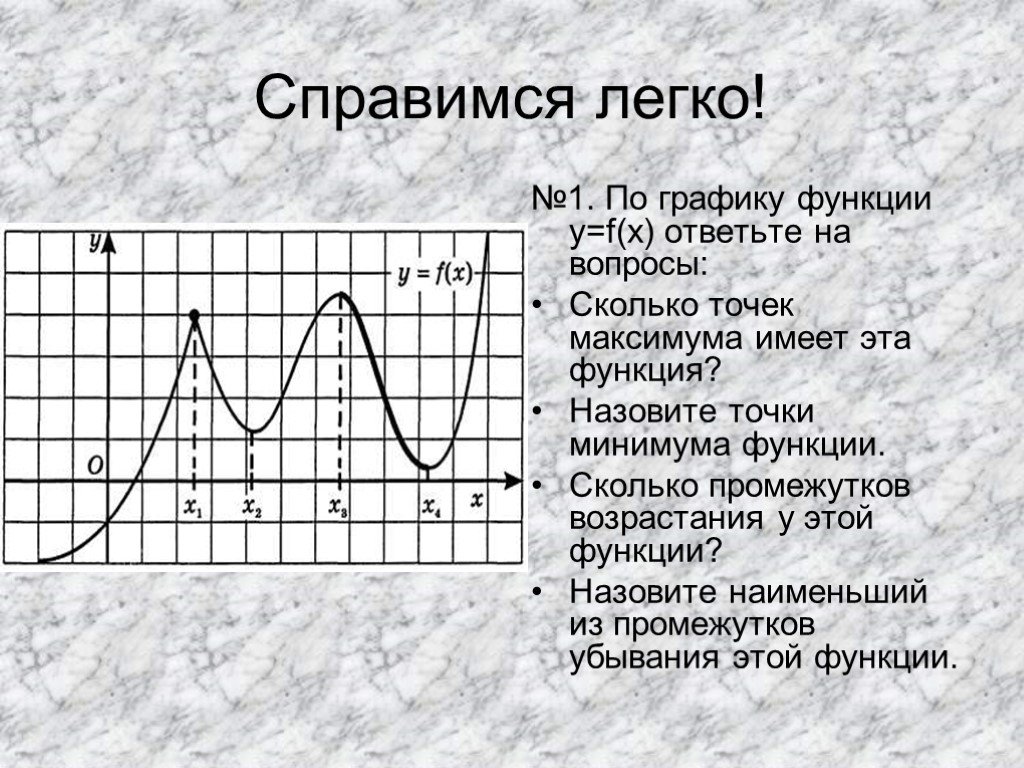

Задача 2.   Исследуйте каждую функцию на наличие максимумов и минимумов.

а)   y = x ³ − 3 x ² + 2,

у’ = 3 х ² — 6 x = 3 x ( x — 2) = 0 подразумевает

x = 0 или x  = 2.

у» ( х ) = 6 х — 6,

г» (0) = -6.

Вторая производная отрицательна. Это означает, что максимальное значение составляет x  = 0. Это максимальное значение равно

.

г (0) = 2.

Далее,

г» (2) = 12 — 6 = 6.

Вторая производная положительна. Это означает, что минимальное значение составляет x  = 2. Это минимальное значение равно

.

y (2) = 2 ³ − 3 ·  2 ² + 2 = 8 − 12 + 2 = −2.

б)   y = −2 x ³ − 3 х ² + 12 х + 10.

При x = 1 максимум y = 17.

При x = -2 есть минимум y = -10.

c)   y = 2 x ³ + 3 x ² + 12 x − 4,

Так как f ‘ ( х ) = 0 не имеет действительных решений, экстремальных значений нет.

d)   y = 3 x ⁴ − 4 x ³ − 12 x ² + 2,

При x = 0 максимум y = 2.

При x = -1 есть минимум y = -3.

При x = 2 минимум г = -30.

Следующий урок: Применение максимальных и минимальных значений

Содержание | Дом

---

Пожалуйста, сделайте пожертвование, чтобы TheMathPage оставался онлайн.
Даже 1 доллар поможет.

---

Copyright © 2021 Лоуренс Спектор

Вопросы или комментарии?

Электронная почта:  teacher@themathpage. com

Нахождение максимума и минимума с помощью производных

Где находится функция в верхней или нижней точке? Расчет может помочь!

Максимум — это верхняя точка, а минимум — нижняя точка:

В плавно изменяющейся функции максимум или минимум всегда находится там, где функция выравнивается   (за исключением седловой точки ).

Где он выравнивается?  Где наклон равен нулю .

Где нулевой наклон?   Производная говорит нам!

Давайте рассмотрим пример:

Пример: Мяч подброшен в воздух. Его высота в любой момент времени t определяется как:

h = 3 + 14t − 5t ²

Какова его максимальная высота?

 

Используя производные, мы можем найти наклон этой функции:

d dt h = 0 + 14 − 5(2t)
= 14 − 10t

(см. ниже этот пример, как мы нашли, что производная. )

Теперь найдите, когда наклон равна нулю :

14 — 10t = 0

10t = 14

t = 14 /10 = 1,4

. Склон — Zero Zero at T = 1.4 секунд

А высота в это время равна:

h = 3 + 14×1,4 − 5×1,4 ²

h = 3 + 19,6 − 9,8 = 12,8

900 А 2 максимум 900 высота 12,8 м (при t = 1,4 с)

 

Краткий обзор производных

Производная в основном находит наклон функции.

В предыдущем примере мы взяли это:

h = 3 + 14t — 5t ²

и получили следующую производную:

d dt 8 h = 0 5 — 24) = 14 − 10t

Что говорит нам о наклоне функции в любой момент времени t

 

Мы использовали следующие производные правила:

• Наклон константы значения (например, 3) равен 0
• Наклон линии например, 2x равно 2, поэтому 14t имеет наклон 14
• Функция квадрата , такая как t ² , имеет наклон 2t, поэтому 5t ² имеет наклон 5(2t)
• А затем мы сложили их: 0 + 14 − 5(2t)

 

Откуда мы знаем, что это максимум (или минимум)?

Мы видели это на графике! Но в остальном.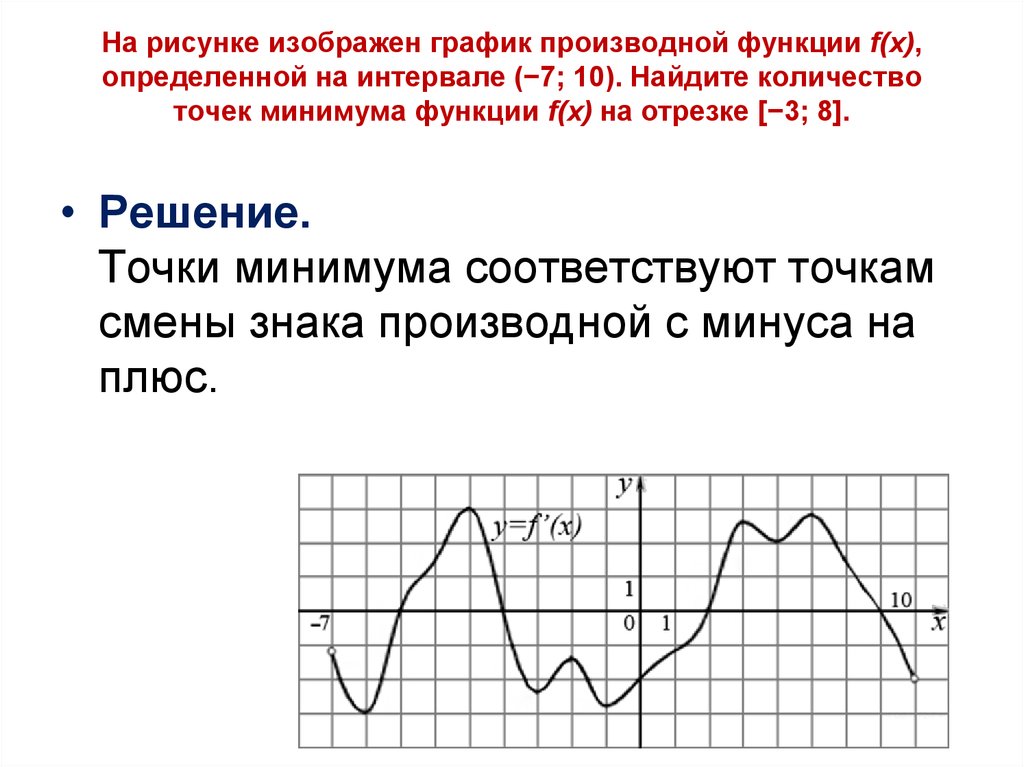 .. на помощь снова приходят производные.

Возьмите производную от наклона (вторая производная исходной функции):

Производная от 14 − 10t равна −10

Это означает, что наклон постоянно уменьшается (-10): при перемещении слева направо наклон начинается с положительного значения (функция возрастает), проходит через ноль (плоская точка), а затем наклон становится отрицательным (функция падает). :

Наклон, который становится меньше (и проходит через 0), означает максимум.

Это называется тестом второй производной

На графике выше я показал наклон до и после, но на практике мы делаем тест в точке, где наклон равен нулю :

Проверка второй производной

Когда наклон функции равен нулю при x , а вторая производная при x :

• меньше 0, это локальный максимум
• больше 0, это локальный минимум
• равно 0, то тест не пройден (хотя могут быть и другие способы узнать)

 

«Вторая производная: меньше 0 — максимум, больше 0 — минимум»

 

Пример: найти максимумы и минимумы для:

Y = 5x ³ + 2x ² — 3x

− 3

Квадратичный с нулями:

• x = −3/5
• х = +1/3

 

Могут ли они быть максимальными или минимальными? (Пока не смотрите на график!)

 

Вторая производная y» = 30x + 4

При x = −3/5:

y» = 30(−3/5) + 4 = −14

меньше чем 0, поэтому −3/5 является локальным максимумом

При x = +1/3:

y» = 30(+1/3) + 4 = +14

больше 0, поэтому + 1/3 — локальный минимум

(Теперь можно посмотреть на график. )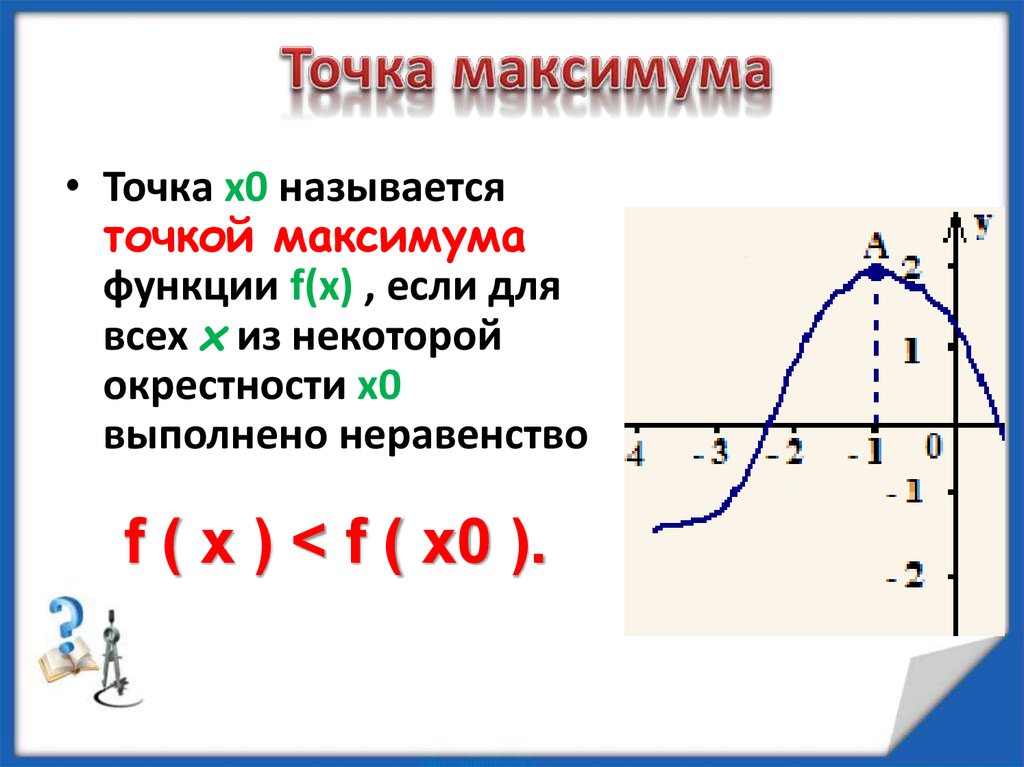

Слов

Высшая точка называется максимум (множественное число максимум ).

Нижняя точка называется минимум (множественное число минимум ).

Общее слово для обозначения максимума или минимума: экстремум (во множественном числе экстремум ).

Мы говорим местное максимальное (или минимальное), когда могут быть более высокие (или более низкие) точки в другом месте, но не поблизости.

Еще один пример

Пример: Найдите максимум и минимум для:

y = x ³ − 6x ² + 12x − 5

Производная:

d dx y = 3x ² − 12x + 12

Что является квадратичным с одним нулем в x = 2

Максимум или максимум?

 

Вторая производная равна y» = 6x − 12

При x = 2:

y» = 6(2) − 12 = 0

это 0, поэтому тест не пройден 3 9000 И вот почему:

Это точка перегиба («седловая точка»)… наклон действительно становится нулевым, но это не максимум и не минимум.