Площадь средней линии треугольника: Средняя линия треугольника и площадь

Средняя линия прямоугольного треугольника – формула

4.2

Средняя оценка: 4.2

Всего получено оценок: 81.

4.2

Средняя оценка: 4.2

Всего получено оценок: 81.

Прямоугольный треугольник стоит особняком от остальных треугольников. Прямой угол делает возможным применение других признаков равенства и подобия. Для углов в прямоугольном треугольнике можно без дополнительных построений использовать геометрические тождества, а любую из сторон можно найти по теореме Пифагора. Но среднюю линию прямоугольного треугольника определить трудно просто потому, что она редко упоминается в задачах, из-за чего мало кто может себе её визуально представить.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики — более 33 лет.

Что такое средняя линия прямоугольного треугольника?

Средняя линия – это отрезок, соединяющий середины сторон в треугольнике. В любом треугольнике можно провести три средних линии. При этом этот отрезок будет равен половине основания – это и считается формулой средней линии прямоугольного треугольника. Основанием считается сторона, с которой средняя линия не пересекается.

Средняя линия в треугольнике отсекает треугольник, подобный большому треугольнику, при этом площадь малого треугольника будет равна ¼ от площади большого, а коэффициент подобия будет равняться ½

Если в треугольнике провести все 3 средних линии, то образуется 4 равных между собой треугольника, которые при этом подобны большому треугольнику с теми же отношениями.

Причем, если средняя линия проводится в прямоугольном треугольнике, то каждый из четырех получившихся треугольников будет являться прямоугольным.

Все эти свойства можно использовать в ряде задач, что позволяет создавать интересные уникальные решения и доказательства.

Задача 1

В прямоугольном треугольнике АВС проведены три средние линии: MN; NP; MP. При этом MN=NP=2.

Рис. 1. Рисунок к задаче

В центре треугольника средними линиями образован малый прямоугольный треугольник, катеты которого известны. Тогда его площадь равна: $S={1\over{2}}*MN*NP={1\over{2}}*2*2=2$.

Так как все 4 малых треугольника равны, то площадь большого будет равна: $S=4*2=8$

Задача 2

В прямоугольном треугольнике АВС проведены три средние линии: MN; NP; MP. В получившемся прямоугольнике MNPA известно, что диагональ MP равна 5, а синус угла между диагоналями равен 0,48. Найти площадь большого прямоугольного треугольника.

Рис. 2. Рисунок к задаче

В прямоугольнике две диагонали между собой равны. Одна из диагоналей MP = 5, значит и вторая диагональ AN равна тоже 5.

Найдем площадь прямоугольника, как произведение диагоналей на синус угла между ними.

$$S=5*5*0,48=12$$

В большом треугольнике 4 малых, а в прямоугольнике 2 малых треугольника. Все малые треугольники между собой равны, значит, чтобы найти площадь прямоугольного треугольника, нужно умножить площадь прямоугольника на 2.

$S=12*2=24$ – ответ получен.

Задача 3

В прямоугольном треугольнике АВС проведены три средние линии: MN; NP; MP.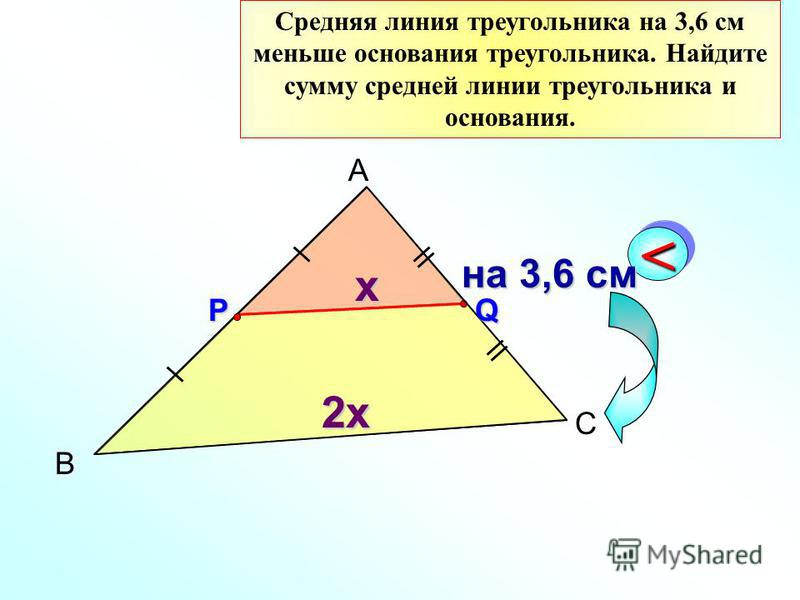 Найти площадь прямоугольника MNPA, если известно, что площадь АВС равна 36.

Рис. 3. Рисунок к задаче

Аналогично с предыдущей задачей, можно вывести утверждение, что площадь треугольника равна двум площадям малого прямоугольника. Подставим в выражение цифры и выразим неизвестное. Площадь треугольника обозначим за S, прямоугольника s.

$$S=2s$$

$$s={S\over2}={36\over2}=18$$

Что мы узнали?

Мы узнали, что такое средняя линия, поговорили о свойствах средней линии и выделили особенности средней линии в прямоугольном треугольнике. Также мы закрепили пройденный материал, подробно изучив алгоритм решения задач на заданную тему.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Оценка статьи

4.2

Средняя оценка: 4.2

Всего получено оценок: 81.

---

А какая ваша оценка?

Основные определения. Линии в треугольнике

Треугольником называется фигура, которая состоит из трехточек, не лежащих на одной прямой, и трех отрезков, соединяющих этиточки попарно.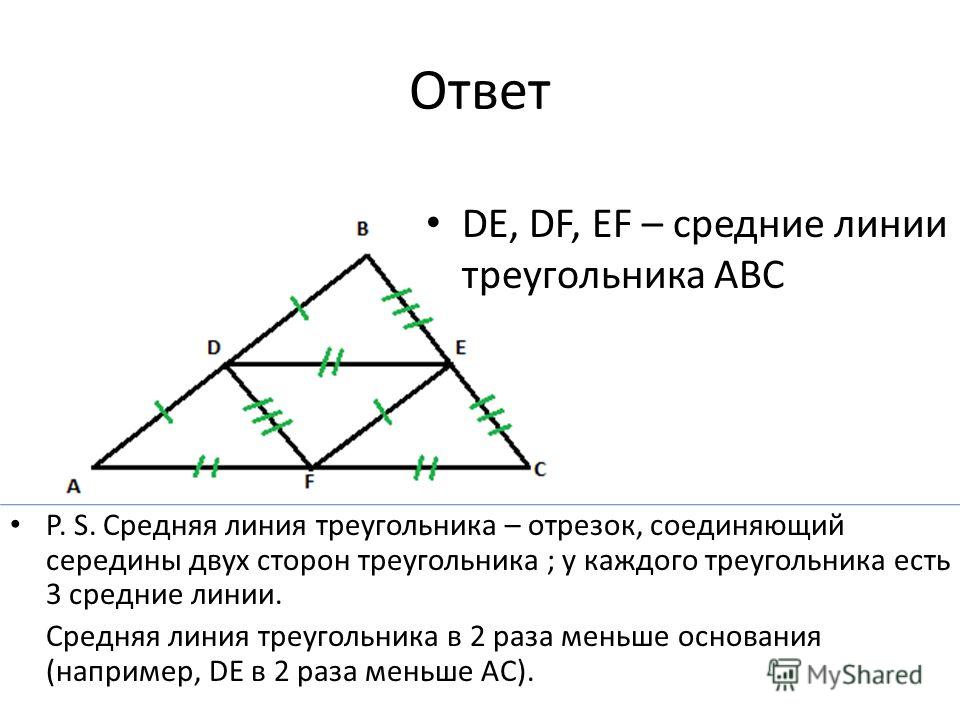 Точки называются вершинами, а отрезки — сторонами треугольника.

Треугольник называется разносторонним, если любые две стороны его не равны друг другу.

Треугольник называется равнобедренным, если у него две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.

Треугольник, все стороны которого равны, называется равносторонним.
Треугольник называется остроугольным, если все его углы острые.
Треугольник называется тупоугольным, если один из его углов тупой.

Внешним углом треугольника на­зывается угол, смежный с каким-нибудь углом этого треугольника.

 

 

Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.

---

Средняя линия треугольника — отрезок, соединяющий середины двух сторон.

1. Средняя линия треугольника параллельна третьей стороне и равна половине этой стороны.
2. Средняя линия отсекает от треугольника треугольник подобный исходному, коэффициент подобия равен 1/2.

---

Медиана треугольника, проведенная из данной вершины, — отрезок прямой, соединяющий данную вершину с серединой противоположной стороны.

1. Во всяком треугольнике медианы пересекаются в одной точке и делятся этой точкой в отношении 2:, считая от вершины.
2. Медиана есть геометрическое место точек, являющихся серединами отрезков прямых, заключенных внутри треугольника и параллельных той стороне, к которой проведена медиана.

Точку пересечения медиан называют центроидом треугольника. Эта точка является центром тяжести (центром масс) треугольника, если:

• система состоит из трех одинаковых точечных масс, сосредоточенных в вершинах треугольника;
• масса системы равномерно распределена по периметру треугольника;
• масса системы равномерно распределена по всему треугольнику.

Центроид является точкой, для которой сумма квадратов расстоянний ее от вершин треугольника принимает наименьшее значение.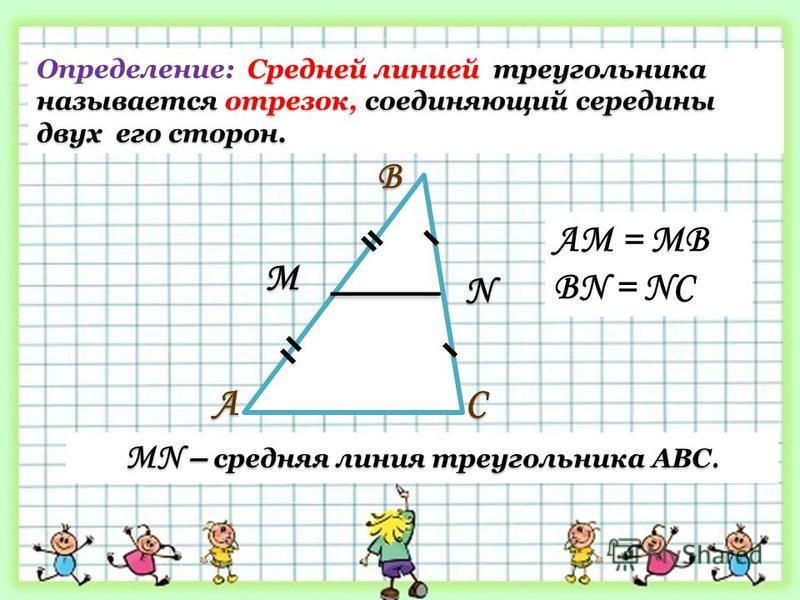

---

Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противоположныю сторону (или ее продолжение).

1. Высоты треугольника пересекаются в одной точке.

 

---

Бисектриса внутреннего угла треугольника — отрезок прямой, делящей данный угол на две равные части, соединяющий вершину угла с точкой на противоположной стороне.

 

1. Бисектриса есть множество точек, равноудаленных от сторон угла.
2. Во всяком треугольнике бисектрисы пересекаются в одной точке, являющейся центром вписанной в треугольник окружности.
3. Бисектриса любого внутреннего ула делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника.
4. Бисектриса лежит между соответствующими медианой и высотой, и ее длина заключена между длиной медианы и длиной высоты h_a< l_a< m_a.
5. Бисектрисы смежных углов перпендикулярны.

---

Срединный перпендикуляр к стороне треугольника — прямая, перпендикулярная стороне треугольника и проходящая через ее середину.

1. Все три срединных перпендикуляра пересекаются в одной точке, являющейся центром описанной вокруг треугольника окружности. Эта точка лежит внутри треугольника, если треугольник остроугольный; на середине гипотенузы, если треугольник прямоугольный; вне треугольника, если треугольник тупоугольный.

---

Трапеция, средняя линия и средний сегмент трапеции и треугольника

Четырехугольник с двумя противоположными параллельными сторонами называется трапецией (трапецией) .

Параллельные стороны трапеции называются основаниями (AB и CD), а те, которые не параллельны, называются катетами (AD и BC).

Если катеты равны по длине, трапеция называется равнобедренной .
DE и CF — это высоты .

Средняя линия трапеции

Линия, соединяющая середины непараллельных сторон, называется средней линией (или средней линией) трапеции.

Линия MN является средней линией ABCD. А отрезок MN является средним отрезком ABCD.

AM = MD
BN = НЗ

Средняя линия трапеции параллельна ее сторонам.
В нашем случае — MN || АБ || ОКРУГ КОЛУМБИЯ.

Теорема 1:

Если прямая, проходящая через середину катета трапеции, параллельна ее основаниям, затем линия проходит через середину другой ноги.

Теорема 2:

Средний сегмент трапеции равен половине длин двух параллельных сторон.

Другими словами:
$\overline{MN} = \frac{\overline{AB} + \overline{DC}}{2}$

Середина треугольника

Отрезок, соединяющий середины двух сторон треугольника, называется серединой треугольника.

Он параллелен третьей стороне и его длина вдвое меньше третьей стороны.

Теорема : Если отрезок пересекает середину одной стороны треугольника и параллелен другой стороне того же треугольника, то этот отрезок делит третью сторону пополам.

$\overline{AM} = \overline{MC}$ и $\overline{BN} = \overline{NC}$ =>

$ млн || AB$
$\overline{MN} = \frac{\overline{AB}}{2}$

Применение свойств средних сегментов

Разделите отрезок на равные отрезки, не измеряя.

Задание: Разделить заданный отрезок $\overline{AB}$ на 5 равных отрезков без измерения.

Решение:

Пусть p — произвольный луч с началом A, не лежащий на AB. Проводим последовательно пять равных отрезков на с.
$\overline{AA_1} = \overline{A_1A_2} = \overline{A_2A_3} = \overline{A_3A_4} = \overline{A_4A_5}$
Соединяем A ₅ с B и проводим линии через A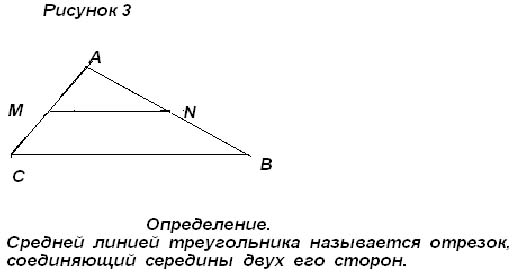

4 , А ₃ , А ₂ и A ₁ , которые параллельны A ₅ B.

Они пересекают АВ в точках B ₄ , B ₃ , B ₂ и B ₁ соответственно. Эти точки делят отрезок $\overline{AB}$ на пять равных отрезков.

Действительно, из трапеции BB ₃ A ₃ A ₅ мы видим, что $\overline{BB_4} = \overline{B_4B_3}$. Таким же образом из трапеции В ₄ В ₂ А ₂ А ₄ , получаем $\overline{B_4B_3} = \overline{B_3B_2}$

А из трапеции B

3 B ₁ A ₁ A ₃ ,
$\overline{B_3B_2} = \overline{B_2B_1}$.
Тогда из B ₂ AA ₂ следует, что $\overline{B_2B_1} = \overline{B_1A}$. В итоге получаем:
$\overline{AB_1} = \overline{B_1B_2} = \overline{B_2B_3} = \overline{B_3B_4} = \overline{B_4B}$

Ясно, что если AB нужно разделить на другое количество равных отрезков, мы должны спроецировать такое же количество равных отрезков на p. Дальше поступаем так же.

Середина треугольника — Cuemath

Замкнутая фигура, состоящая из трех отрезков, образует форму треугольника.

Давайте познакомимся с миром треугольников

Треугольник состоит из множества частей. Например, углы, стороны, медиана, середина, середина и т. Д. Вот занятие для вас. Теперь вы можете визуализировать различные типы треугольников в математике на основе их сторон и углов. Попробуйте изменить положение вершин, чтобы понять связь между сторонами и углами треугольника.

В последней части этой главы мы обсудим середину и средние сегменты треугольника.

Для любых двух точек, скажем, \(A\) и \(C\), середина – это точка \(B\), расположенная посередине между точками \(A\) и \(B\).

Обратите внимание, что точка \(B\) равноудалена от \(A\) и \(C\).

Средняя точка существует только для линейного сегмента.

Линия, соединяющая среднюю точку, называется серединой.

В этом мини-уроке мы исследуем мир середины треугольника, находя ответы на такие вопросы, как что такое середина треугольника, теорема о середине треугольника и доказательство с помощью интерактивных вопросов.

Итак, приступим!

План урока  

1.	Что такое середина треугольника?
2.	Важные замечания о средней линии треугольника
3.	Решенные примеры на средней линии треугольника
4.	Интерактивные вопросы о середине треугольника
5.	Сложный вопрос о средней части треугольника

Что такое середина треугольника ?

Средняя линия треугольника Определение

Средняя линия треугольника — это отрезок, соединяющий середины или центр двух противоположных или смежных сторон треугольника

На приведенном выше рисунке D — это середина AB и E — середина AC.

Здесь DE — средняя линия треугольника ABC.

---

Теорема о середине треугольника

Теорема о середине сегмента утверждает, что отрезок, соединяющий середины любых двух сторон треугольника, параллелен третьей стороне треугольника и составляет ее половину.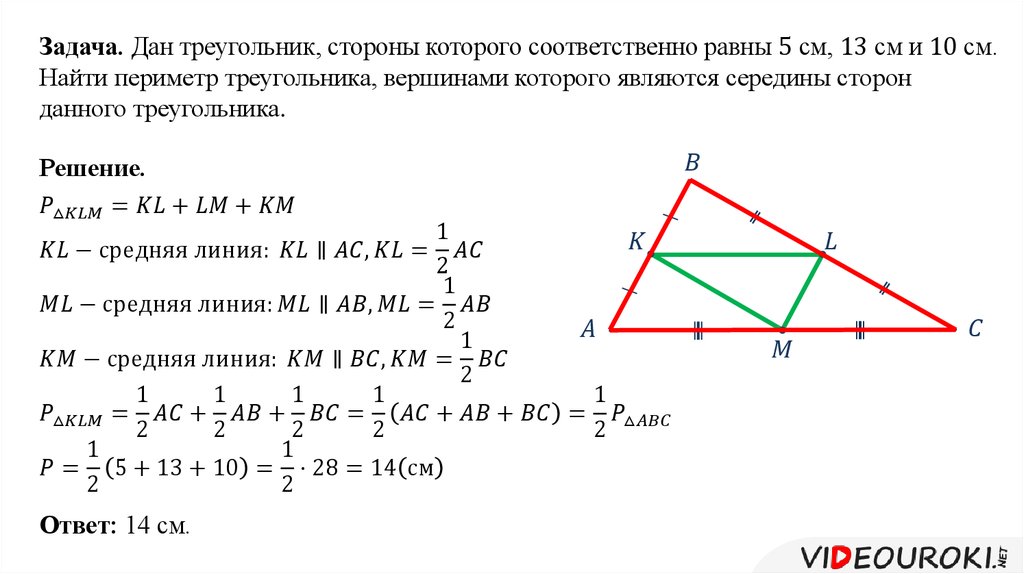

В треугольнике ABC имеем

\(AD=DB\)  и  \(AE=EC\)

Тогда по теореме о средней линии \dfrac{1}{2}\ до н.э.\)

Аналогично,

\(AD=DB\)  и  \(BF=FC\)

Тогда по теореме о срединном отрезке

\(DF∥AC\) и \(DF=\dfrac{1}{2 }\ AC\)

Аналогично,

\(AE=EC\)  и  \(BF=FC\)

Тогда по теореме о середине отрезка

\(EF∥AB\) и \(EF=\dfrac {1}{2}\ AB\)

Доказательство средней линии треугольника

В предыдущем разделе мы видели треугольник \(ABC\) с \(D,\) \(E,\) и \(F\) как три середины.

Чтобы обосновать доказательство теоремы о середине треугольника, нам нужно доказать две вещи:

• \(DE∥BC\)
• \(DE=\dfrac{1}{2}\ до н.э.\)

Дано: D и E — середины отрезков AB и AC

Чтобы доказать, \(DE∥BC\) и \(DE=\dfrac{1}{2}\ BC\), нам нужно нарисуйте линию, параллельную AB, и встретите E, полученную в точке F.

В \(\bigtriangleup{ADE}\) и \(\bigtriangleup{CFE}\)

\(\begin{align} AE &=EC\text{ (E — середина AC)}\\\ \angle{1} &=\angle{2}\text{ (Вертикально противоположные углы)}\\\ \angle{3} &=\angle{4}\text { (Альтернативные углы)}\end{выравнивание}\)

По конгруэнтности треугольника по AAS имеем,

\(\bigtriangleup{ADE} \cong \bigtriangleup{CFE}\)

По CPCT имеем,

\(DE=FE\)

\(AD= CF\)

D — середина AB

\(AD=BD\)

\(BD=CF\)

DBCF — параллелограмм,

\(DF || BC\) и \(DF = BC\)

\(DE || BC\) и \(DF = BC\)

\(DE=\dfrac{1}{2}DF\)

так как, DF = BC

\( DE=\dfrac{1}{2}BC\)

Отсюда доказано

Средняя часть формулы треугольника

Средняя часть \(=\) \(\dfrac{1}{2}\times\) Основание треугольника

---

Что является обратной теоремой о средней линии треугольника?

Теорема, обратная теореме о срединном отрезке, определяется следующим образом: когда отрезок соединяет две середины двух противоположных сторон треугольника и параллелен третьей стороне треугольника и составляет ее половину, то он является средним отрезком треугольника. .

В треугольнике ABC имеем

\(DE∥BC\) и \(DE=\dfrac{1}{2}\ BC\)

Тогда согласно обратной теореме о середине треугольника

\(AD=DB\) и \(AE=EC\)
\(DE\) является средней линией треугольника \(ABC\)

Доказательство обратной теоремы о средней линии треугольника

В предыдущем разделе мы видели \(\bigtriangleup{ABC}\), где \(D ,\) \(E,\) и \(F\) как три середины.

Чтобы обосновать доказательство обратной теоремы о середине треугольника, нам нужно доказать любую из перечисленных ниже вещей:

• \(DE\) является средней частью \(\bigtriangleup{ABC}\)
• \(AD=DB\) и \(AE=EC\)

У нас есть D как середина AB, тогда \(AD = DB\) и \(DE||BC\)

\(AB\) \(=\) \(AD + DB\) \ (=\) \(DB + DB\) \(=\) \(2DB\)

DBCF — параллелограмм.

\(DE||BC\) и \(BD||CF\)

Противоположные стороны параллелограмма равны.

\(BD=CF\)

\(DA=CF\)

В \(\bigtriangleup{ADE}\) и \(\bigtriangleup{CFE}\)

\(\begin{align}\angle{1} &=\angle{2}\text{ (вертикально противоположные углы)}\\\ \angle{3} &=\angle{4}\text{ (альтернативный углов)}\\\ DA &=CF\end{align}\)

По AAS конгруэнтности треугольника мы имеем,

\(\bigtriangleup{ADE} \cong \bigtriangleup{CFE}\)

По CPCT мы have

\(AE=EC\)

E — середина AC и DF.

Следовательно, DE является средней частью \(\bigtriangleup{ABC}\).

 

Важные примечания

а) Отрезок, проходящий через середину, всегда параллелен одной стороне треугольника.
б) Середина \(=\) \(\dfrac{1}{2}\) длина третьей стороны треугольника.
в) Треугольник может иметь не более трех средних сегментов.
г) Середина отрезка теоремы треугольника также известна как теорема о средней точке.

Примеры решения

Чтобы лучше понять среднюю часть треугольника, давайте рассмотрим несколько примеров решения.

Пример 1

 

 

На данном рисунке H и M — середины треугольника EFG. Помогите Джейми доказать \(HM||FG\) для следующих двух случаев.

а) EH = 6, FH = 9, EM = 2 и GM = 3
б) EH = 16, FH = 12, EM = 4 и GM = 3

Решение

а) Имеем EH = 6, FH = 9, EM = 2 и GM = 3

\dfrac{EH}{FH}=\dfrac{6}{9}=\dfrac{2}{3}\)

\(\dfrac{EM}{GM}= \dfrac{EH}{FH}=\dfrac{2}{3}\)

б) Имеем EH = 16, FH = 12, EM = 4, и GM = 3

\(\dfrac{EH}{FH}=\dfrac{16}{12}=\dfrac{4}{3}\)

\(\dfrac{EM}{GM}= \ dfrac{EH}{FH}=\dfrac{4}{3}\)

HM делит EF и EG треугольника EFG в равных отношениях.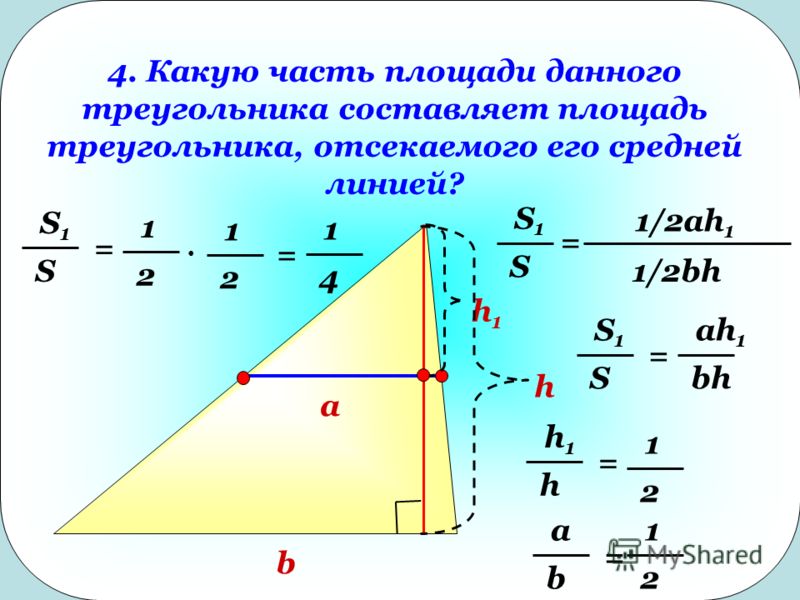

Следовательно, HM — средняя линия треугольника EFG.

\(\следовательно\) \(HM || FG\)

Пример 2

 

 

Помогите Рону найти значение x и значение отрезка AB, учитывая, что A и B являются серединами треугольника PQR.

Решение

У нас есть две середины A и B. 36 &=2(9x)\\\
х &=2\\\
АВ &=18\конец{выравнивание}\)

.

\(\следовательно\) Значение x равно 2 Значение AB равно 18

---

Интерактивные вопросы

Вот несколько упражнений для практики. Выберите/введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.

Вопросы0005

а) Рассмотрим треугольник ABC, и пусть D — любая точка на BC. Пусть X и Y — середины сторон AB и AC. Покажите, что XY делит AD пополам.

б) Рассмотрите параллелограмм ABCD. E и F — середины отрезков AB и CD соответственно. Докажите, что отрезки AF и EC пересекают диагональ BD пополам.

Подведем итоги

Мини-урок был посвящен захватывающему понятию середины треугольника. Математическое путешествие по средней части треугольника начинается с того, что ученик уже знает, и продолжается творческим созданием новой концепции в умах молодых людей. Сделано таким образом, что это не только понятно и легко для понимания, но и останется с ними навсегда. В этом заключается магия Cuemath.

О Cuemath

В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!

Благодаря интерактивному и увлекательному подходу «обучение-преподавание-обучение» учителя изучают тему со всех сторон.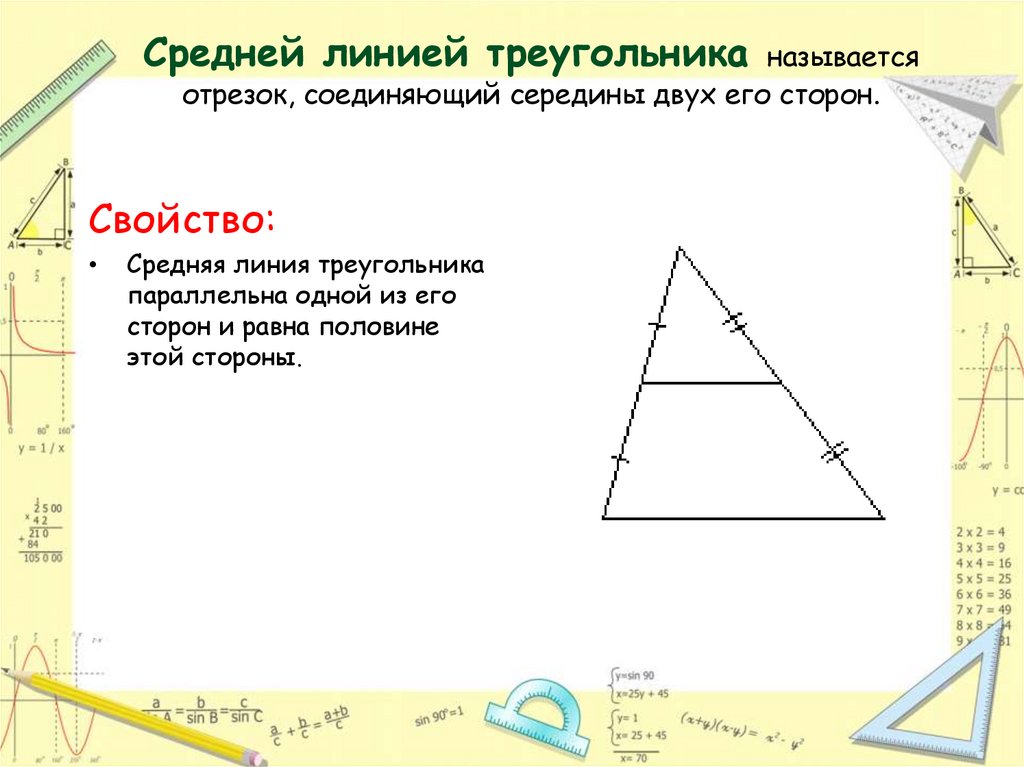

Будь то рабочие листы, онлайн-классы, сеансы сомнений или любая другая форма отношений, мы в Cuemath верим в логическое мышление и разумный подход к обучению.

---

Часто задаваемые вопросы (FAQ)

1. Что такое средняя линия треугольника?

Средняя линия треугольника – это отрезок, соединяющий середины или центры двух противоположных или смежных сторон треугольника.

В треугольнике может быть 3 средних линии.

На приведенном выше рисунке D — это середина AB, E — середина AC, а F — середина BC.

Здесь DE, DF и EF — три средние линии треугольника ABC.

2. Как найти среднюю линию треугольника?

Мы можем найти среднюю часть треугольника, используя формулу средней части треугольника,

Средняя часть \(=\) \(\dfrac{1}{2}\times\) Основание треугольника.

3. Что такое теорема о средней точке?

Теорема о средней точке утверждает , что отрезок прямой, соединяющий середины любых двух сторон треугольника, параллелен третьей стороне и равен половине третьей стороны.