3 задание ЕГЭ по математике профильного уровня 2023: теория и практика

Русский язык Математика (профиль) Математика (база) Обществознание История Биология Физика Химия Английский язык Информатика Литература

Задание 1 Задание 2 Задание 3 Задание 4 Задание 5 Задание 6 Задание 7 Задание 8 Задание 9 Задание 10 Задание 11 Задание 12 Задание 13 Задание 14 Задание 15 Задание 16 Задание 17 Задание 18

За это задание ты можешь получить

1 балл. На решение дается около 3 минут. Уровень сложности: базовый.
Средний процент выполнения: 95%
Ответом к заданию 3 по математике (профильной) может быть целое число или конечная десятичная дробь.

Разбор сложных заданий в тг-канале

Посмотреть

Задачи для практики

Задача 1

Перед началом первого тура чемпионата по спортивным нардам участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует $56$ игроков, среди которых $12$ спортсменов из России, в том числе Евгений Победкин. Найдите вероятность того, что в первом туре Евгений Победкин будет играть с каким-либо игроком из России.

Решение

Будем считать случайным экспериментом выбор соперника Евгения Победкина. Этот эксперимент имеет $56-1 = 55$ равновозможных исходов (сам с собой он играть не может!). При этом $12 — 1 = 11$ исходов благо приятствуют событию «Евгений Победкин будет играть со спортсменом из России» (так как есть $11$ спортсменов из России, не считая самого Евгения Победкина).

По определению искомая вероятность равна ${11}/{55} = 0.2$.

Ответ: 0.2

Показать решение

Бесплатный интенсив

Задача 2

Перед началом первого тура чемпионата по настольному теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует $76$ спортсменов, среди которых $46$ спортсменов из России, в том числе Григорий Соколенко. Найдите вероятность того, что в первом туре Григорий Соколенко будет играть с каким-либо теннисистом из России.

Решение

Будем считать случайным экспериментом выбор соперника Григория Соколенко. Этот эксперимент имеет $76-1=75$ равновозможных исходов (сам с собой он играть не может!). При этом $46-1=45$ исходов благоприятствуют событию «Григорий Соколенко будет играть со спортсменом из России» (так как есть $45$ спортсменов из России, не считая самого Григория Соколенко). По определению, искомая вероятность равна ${45} / {75}=0{,}6$.

Ответ: 0.6

Показать решение

Бесплатный интенсив

Задача 3

Вероятность того, что новая электрическая кофемашина прослужит больше года, равна $0{,}92$. Вероятность того, что она прослужит больше двух лет, равна $0{,}85$. Найдите вероятность того, что она прослужит меньше двух лет, но больше года.

Решение

Заметим, что из событий «кофемашина прослужит меньше года», «кофемашина прослужит от 1 до 2 лет» и «кофемашина прослужит больше двух лет» произойдёт обязательно ровно одно, то есть, говоря математическим языком, они попарно несовместны, а их объединение — достоверное событие. Следовательно, сумма вероятностей этих событий равна 1.

При этом события «кофемашина прослужит меньше года» и «кофемашина прослужит больше года» противоположны, поэтому вероятность события «кофемашина прослужит меньше года» равна 1 — 0.92 = 0.08. Заполним таблицу.

СобытиеПрослужит меньше годаПрослужит от 1 до 2 летПрослужит больше двух лет
Вероятность0. 08?0.85

Отсюда искомая вероятность равна 1 — 0.08 — 0.85 = 0.07.

Ответ: 0.07

Показать решение

Бесплатный интенсив

Задача 4

В некотором городе из $5000$ появившихся на свет младенцев $2075$ мальчиков. Найдите частоту рождения девочек в этом городе. Результат округлите до сотых.

Решение

Из каждых $5000$ появившихся на свет младенцев девочек $5000 — 2075 = 2925$. По определению искомая частота равна ${2925}/{5000} = 0.585 ≈ 0.59$.

Ответ: 0.59

Показать решение

Бесплатный интенсив

Задача 5

На экзамене по физике студент отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Элект-
ричество», равна $0{,}3$. Вероятность того, что это вопрос по теме «Механика», равна $0{,}42$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене студенту достанется вопрос по одной из этих двух тем.

Решение

Из условия следует, что события A = «достанется вопрос по теме Электричество» и B = «достанется вопрос по теме Механика» несовместны. Действительно, нет билетов, относящихся к обоим этим темам одновременно. Событие «достанется вопрос по одной из этих двух тем» — это объединение событий A и B (A $∪$ B). По формуле вероятности объединения несовместных событий получим, что искомая вероятность равна P(A $∪$ B) = P(A) + P(B) = 0.3 + 0.42 = 0.72.

Ответ: 0.72

Показать решение

Бесплатный интенсив

Задача 6

При производстве в среднем на каждые $468$ исправных телефонов приходится $32$ неисправных. Найдите вероятность того, что случайно выбранный телефон окажется неисправным.

Решение

Из условия следует, что в среднем из каждых $468 + 32 = 500$ телефонов $32$ неисправных. По определению искомая вероятность равна ${32}/{500} = 0.064$.

Ответ: 0.064

Показать решение

Бесплатный интенсив

Задача 7

Завод выпускает съёмные жёсткие диски. В среднем $15$ дисков из $300$ имеют скрытые дефекты. Найдите вероятность того, что купленный диск окажется без дефектов.

Решение

По определению вероятность покупки диска с дефектом равна ${15}/{300} = 0.05$. Тогда по формуле вероятности противоположного события вероятность купить диск без дефекта равна $1 — 0.05 = 0.95$.

Ответ: 0.95

Показать решение

Бесплатный интенсив

Задача 8

Фабрика выпускает туфли. В среднем $12$ пар туфель из $200$ пар имеют скрытые дефекты. Найдите вероятность того, что купленная пара туфель окажется без дефектов.

Решение

Из условия следует, что в среднем из каждых $200$ пар $200 — 12 = 188$ не имеют дефектов. Тогда искомая вероятность равна ${188}/{200} = 0.94$.

Ответ: 0.94

Показать решение

Бесплатный интенсив

Задача 9

В чемпионате мира участвуют $16$ команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: $1$, $1$, $1$, $1$, $2$, $2$, $2$, $2$, $3$, $3$, $3$, $3$, $4$, $4$, $4$, $4$. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда «Плутон», участвующая в чемпионате, окажется во второй группе?

Решение

Будем считать, что случайный эксперимент заключается в том, что капитан команды «Плутон» тянет карточку с номером группы. У этого эксперимента $16$ равновозможных исходов (по числу карточек). Событию «Команда „ Плутон“ окажется во второй группе» благоприятствуют $4$ исхода (количество карточек с номером $2$). По определению вероятности искомая вероятность равна ${4} / {16}=0{,}25$.

Ответ: 0.25

Показать решение

Бесплатный интенсив

Задача 10

На конференцию приехали $7$ учёных из Китая, $5$ — из России и $8$ — из Египта. Каждый из них делает на конференции один доклад. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад учёного из России.

Решение

Будем считать, что случайный эксперимент заключается в том, что выбирается учёный, который будет выступать восьмым. Всего существует $20$ равновозможных исходов ($7+5+8=20$ учёных, все имеют равные шансы выступить восьмыми). Событию «Восьмым будет выступать учёный из России» благоприятствуют $5$ исходов. По определению искомая вероятность равна ${5}/{20} = {1}/{4} = 0.25$.

Ответ: 0.25

Показать решение

Бесплатный интенсив

Задача 11

В чемпионате по спортивной гимнастике участвуют $40$ спортсменов: $16$ — из России, $9$ — из Франции, остальные — из Беларуси. Порядок, в котором выступают гимнасты, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется из Беларуси.

Решение

Из Беларуси $40-16-9 = 15$ спортсменов. Будем считать, что случайный эксперимент заключается в том, что выбирается спортсмен, который будет выступать первым. Всего существует $40$ равновозможных исходов ($40$ спортсменов, все имеют равные шансы выступить первыми). Событию Первым будет выступать спортсмен из Беларуси благоприятствуют $15$ исходов. По определению искомая вероятность равна ${15}/{40} = {3}/{8} = 0.375$.

Ответ: 0.375

Показать решение

Бесплатный интенсив

Задача 12

В кармане у Валерия было пять конфет — «Птичье молоко», «Ромашка», «Черноморочка», «Мишка косолапый» и «Ласточка», а также ключи от квартиры. Вынимая ключи, Валерий случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Ромашка».

Решение

Валерий мог с одинаковой вероятностью выронить каждую из пяти конфет, значит, искомая вероятность равна ${1}/{5} = 0.2$.

Ответ: 0.2

Показать решение

Бесплатный интенсив

Задача 13

Света, Марина, Оля и Ксюша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должна будет Света.

Решение

Жребий имеет $4$ равновозможных исхода (все девочки имеют равные шансы начинать игру). Значит, вероятность события «Игру будет начинать Света» равна ${1} / {4}=0{,}25$.

Ответ: 0.25

Показать решение

Бесплатный интенсив

Показать еще

Для доступа к решениям необходимо включить уведомления от группы Турбо в вк — это займет буквально 10 секунд. Никакого спама, только самое важное и полезное для тебя. Ты всегда можешь запретить уведомления.

Включить уведомления

Бесплатный интенсив по математике (профильной)

3 огненных вебинара, домашние задания, беседа курса, личный кабинет, связь с преподавателем и многое другое.


Курс стартует 28 марта. Бесплатный интенсив

ЕГЭ по математике базовый уровень 2022-2023​: подготовка, задания, критерии оценивания

Сдать ЕГЭ по математике базового уровня в 2022-2023 году необходимо для получения аттестата о среднем общем образовании. Какие вопросы ждут выпускников, как проводится экзамен — в материале «КП»

  • Мария Беляева

    Автор КП

  • Елена Щербанова

    Репетитор по математике

  • Алексей Постный

    Заместитель руководителя методического
    отдела Домашней школы «ИнтернетУрок»

ЕГЭ — своеобразный тест на уровень базовой математической грамотности, пройти его должен каждый выпускник. Положительный результат является условием получения аттестата. При этом результаты не дают возможности поступления в технический вуз: для этого нужна профильная аттестация.

Длительность ЕГЭ по математике базового уровня — 180 минут, экзаменационная работа включает 21 задание. Ученики могут пользоваться только обычной (не логарифмической) линейкой, использовать калькулятор нельзя. Справочные материалы есть в составе контрольно-измерительных материалов, но их объем ограничен

Результат базового ЕГЭ по математике — оценка по 5-балльной шкале: именно в таком виде она вносится в аттестат.

Расписание

Досрочно сдать математику в 2022 году можно было 28 марта. В основной период экзамен прошел 3 июня, резервный день был намечен на 24 июня. Ученики, получившие неудовлетворительную оценку за ЕГЭ, могут пересдать предмет осенью.

Задания

ЕГЭ по математике базового уровня состоит из 21 задания, на их решение отводится 3 часа (180 минут). Ответ принимается в краткой форме: подробно описывать решение не нужно. Задачи требуют конкретного ответа, то есть понадобится не просто знание теории, но и умение применять ее на практике.

В тематику базового экзамена включены блоки из школьной программы 5-11 классов. Большинство заданий связаны с математическими вычислениями, решением уравнений и неравенств. Есть отдельный блок по геометрии, а также задачи, связанные с математическим анализом.

Приведем примеры заданий базового уровня по разным тематикам из актуальной демоверсии КИМов (контрольных измерительных материалов) Федерального института педагогических измерений.

Экзамен 2021-2022 года показал, что большинство выпускников хорошо справляются с вычислительными операциями, сложность представляют работа с элементарными математическими моделями и стереометрические задачи. Традиционной ошибкой также является невнимательное чтение условий: на этот момент рекомендуется обратить особое внимание при подготовке.

Критерии оценивания

За каждый правильный ответ выпускнику начисляется 1 первичный балл. Максимальное количество первичных баллов: 21.

В некоторых заданиях правильных ответов может быть несколько. Чтобы ответ был зачтен, необходимо указать хотя бы одно верное значение.

Ответы сверяются с эталонными: значение может быть целым или дробным числом, а также последовательностью цифр. Проверка проводится компьютером, что полностью исключает фактор субъективных ошибок. Если ответ распознан как неверный, результат экзамена можно оспорить.

Читайте также

Апелляция ЕГЭ

Самый главный страх выпускников — получить за ЕГЭ баллы ниже, чем планировалось. Но неправильный ответ — далеко не единственная причина низкой оценки. Разбираемся, в каких случаях стоит подавать на апелляцию и как отстоять свои баллы

Подробнее

Первичные баллы ЕГЭ по математике базового уровня переводятся в оценку по 5-балльной шкале. Шкала перевода для выпускников 2023 года будет опубликована после основного периода сдачи экзамена. Пока можно ориентироваться на данные 2022 года.

Для получения аттестата достаточно дать всего 7 правильных ответов из 20.

Сданный экзамен базового уровня не дает права подавать документы в вузы, где математика заявлена как профильный экзамен для абитуриентов. Зато можно поступать в колледжи: учреждения среднего профобразования набирают учеников на бюджетные места по конкурсу аттестатов.

Пересдача

Пересдача ЕГЭ по математике базового уровня возможна по следующим причинам:

  • выпускник пропустил экзамен по уважительной причине;
  • не набран минимальный пороговый балл;
  • по решению конфликтной комиссии, если была подана апелляция по нарушениям порядка тестирования.

Пересдать экзамен можно в резервные дни основного и дополнительного периода. Если попытки окончились неудачей, получить аттестат можно только в следующем году.

Апелляция возможна в стандартном порядке:

  • если выпускник считает, что были нарушены правила тестирования, подать заявление нужно немедленно, не покидая аудиторию;
  • при несогласии с результатами оценки у выпускника есть два дня после публикации итогового решения на оспаривание результата.

Поскольку правильность ответов оценивается автоматически, в случае неверного распознавания бланка с ответами присутствие ученика на конфликтной комиссии не требуется.

Мнение эксперта

Елена Щербанова, репетитор по математике:

— Базовый ЕГЭ по математике проверяет общую математическую грамотность выпускников, не содержит сложных задач и абстрактных вопросов. С экзаменом легко справляются школьники с гуманитарным типом мышления, поскольку для большинства задач требуется элементарная логика и базовые знания.

На решение одной задачи у школьника есть всего 9 минут. Распределить время на экзамене я рекомендую следующим образом: сначала решить задания, которые кажутся простыми, проверить ответы и перенести значения в бланк работы. Это своеобразная разминка. Оставшееся время можно потратить на внимательное изучение задач, которые показались сложными: для правильного ответа зачастую достаточно внимательно прочитать условия. Нужно учитывать, что в некоторых заданиях может быть более одного правильного ответа. Но приводить все допустимые значения не требуется. Наоборот, я рекомендую этого не делать, поскольку дополнительных баллов это не принесет, а вероятность ошибки повышается.

Практика показывает, что отведенных на тестирование трех часов выпускникам хватает, чтобы справиться со всеми заданиями и несколько раз перепроверить себя. На мой взгляд, базовый ЕГЭ по математике — один из самых легких экзаменов, с которым справляется большинство школьников без каких-либо затруднений.

Алексей Постный, заместитель руководителя методического отдела Домашней школы «ИнтернетУрок»:

— Задания базового уровня в большинстве своем проверяют основные умения: выполнение математических операций с целыми числами, обычными и десятичными дробями, использование формул, применение алгоритмов решения простейших уравнений и неравенств разных типов. Так что при подготовке стоит обратить внимание именно на эти навыки, которые можно отработать решением множества примеров и задач. А вот запоминанию формул и свойств можно уделить меньше внимания: на экзамене вам выдадут справочные материалы, в которых записано большинство необходимых формул и свойств.

Хорошистам и отличникам по математике такая направленность заданий не создает проблем. А вот для остальных она представляет существенные трудности. Ведь зачастую в школах таких учеников ориентируют на минимальные знания по предмету, не уделяя внимание развитию навыков. Для ученика решением проблемы будет отработка этих самых навыков: или самостоятельно (с помощью онлайн-тренажеров), или под руководством репетитора.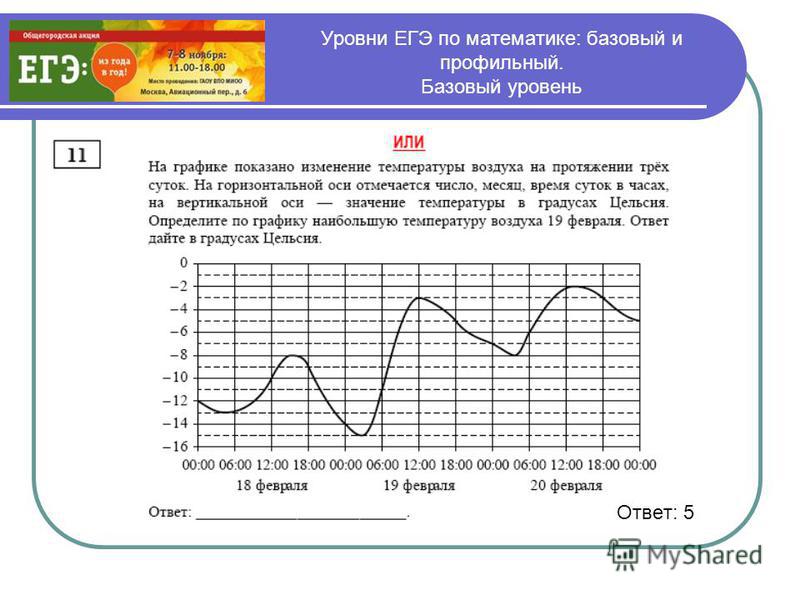 А для учителя это хороший повод изменить подход к обучению.

Читайте также

ЕГЭ по математике

Сдавать ЕГЭ по математике будут все выпускники: экзамен необходим для получения аттестата. В чем различия между базовым и профильным уровнями, какие задания входят в экзамен — в материале «КП»

Подробнее

Фото на обложке: shutterstock.com

Made on

Tilda

Департамент образования штата Орегон: решение задач по математике 3–8 классы: основные навыки: штат Орегон

Перейти к основному содержанию

Официальный сайт штата Орегон. Учиться Откуда ты знаешь » (как определить веб-сайт Oregon.gov) Официальный сайт штата Орегон »

Поиск

Требование к оценке эффективности на местах

Образцы работ более эффективно будут способствовать обучению учащихся, если они будут систематически интегрированы в учебную программу округа, а также станут частью обучения в классе (то есть в обычном, постоянном процессе оценивания и выставления оценок). Например, когда они используются для подведения итогов учебного предмета или расширения представленных понятий, образцы работ могут стать естественной частью занятий в классе и предлагаться много раз в течение учебного года.

Эти примеры рабочих заданий приведены в соответствие с 2011-12 Руководство по подсчету очков для решения математических задач и к Общепринятым государственным стандартам (CCSS).

Местные задания по оценке успеваемости*

* Для 2 класса не требуется оценка успеваемости; задания для 2-го класса предназначены для того, чтобы дать учителям примеры заданий, соответствующих стандартам 2-го класса.

2 класс​

Категория отчетности по баллам (SRC) 1 — ОПЕРАЦИИ И АЛГЕБРАИЧЕСКОЕ МЫШЛЕНИЕ (OA), ЧИСЛА И ДЕЙСТВИЯ В ДЕСЯТИЧНОМ СИСТЕМЕ (NBT)
  • Лимонад
  • Счетчик мармеладок
  • Сумма и разница
  • Чудесная тайна денег
  • Загадай число
SRC 2 — ИЗМЕРЕНИЯ И ДАННЫЕ (MD)
  • Требуют внесения изменений
  • Комбинации монет
  • Деньги Тая
  • 33 цента
  • Продажа мрамора
  • Веселые владельцы ранчо
SRC 3 — ГЕОМЕТРИЯ (G)

Shape House

​​​​

3 класс​

Категория отчетности (SRC) 1 – ОПЕРАЦИИ И АЛГЕБРАИЧЕСКОЕ МЫШЛЕНИЕ (OA), ЧИСЛА И ДЕЙСТВИЯ С СЧИСЛЕНИЕМ С СЧИСЛОМ (NBT) И Дробями (NF)
  • Ферма дедушки
  • Ферма дедушки (оценка)
  • Трейл Микс
  • Дилемма зоопарка
  • Клубника Ольги
  • Клубника Ольги (оценка)
  • Бумажный маршрут
SRC 2 — ИЗМЕРЕНИЯ И ДАННЫЕ (MD)
  • Зеленая и желтая шина
  • Дом Тары и Брэда
  • Дом Тары и Брэда (оценка)
  • Прогулка с собакой
  • Лента реальности
  • Собачья будка Купера
  • Заштрихованная область
  • Прямоугольники в квадрате

SRC 3 — ГЕОМЕТРИЯ (G)

​​​

4 класс​

Категория представления результатов (SRC) 1 – ОПЕРАЦИИ И АЛГЕБРАИЧЕСКОЕ МЫШЛЕНИЕ (OA), ЧИСЛА И ДЕЙСТВИЯ С ДЕСЯТИЧНЫМ ОСНОВАНИЕМ (NBT) И ДРОБЯМИ (NF)

SRC 2 — ИЗМЕРЕНИЯ И ДАННЫЕ (MD)

Kyle’s Corral Caper

SRC 3 — ГЕОМЕТРИЯ (G)

​

5 класс​

Категория отчетности (SRC) 1 – ОПЕРАЦИИ И АЛГЕБРАИЧЕСКОЕ МЫШЛЕНИЕ (OA), ЧИСЛА И ДЕЙСТВИЯ С СОСНОВАНИЕМ ДЕСЯТИЦЫ (NBT) И ДРОБЕЙ (NF)
  • Квадраты
  • Семейная пицца Джонс

SRC 2 — ИЗМЕРЕНИЯ И ДАННЫЕ (MD)

SRC 3 — ГЕОМЕТРИЯ (G)

​​

6 класс​

Категория представления результатов (SRC) 1 – ОТНОШЕНИЯ И ПРОПОРЦИОНАЛЬНЫЕ ОТНОШЕНИЯ (RP), СИСТЕМА ЧИСЛОВ (NS), ВЫРАЖЕНИЯ И УРАВНЕНИЯ (EE)
  • Мальчики и девочки
  • Рисование куба
  • Поездка Даррена
  • Негерметичный кран
  • Шоу Боба и Сэма Шу
  • Уровень воды
  • Размеры коробки
SRC 2 — ГЕОМЕТРИЯ (G)
  • Квадрат ABCD
  • Одеяло
  • Произведение искусства
SRC 3 – СТАТИСТИКА И ВЕРОЯТНОСТЬ (SP)

Балетный класс

​

7 класс​

Категория отчетности (SRC) 1 – ОТНОШЕНИЯ И ПРОПОРЦИОНАЛЬНЫЕ ОТНОШЕНИЯ (RP), СИСТЕМА ЧИСЕЛ (NS), ВЫРАЖЕНИЯ И УРАВНЕНИЯ (EE)
  • Rent a Truck
  • Лифт Экспресс
  • Результаты Карлоса
SRC 2 — ГЕОМЕТРИЯ (G)
  • Tricky Tiles
  • Пазл с квадратной пиццей
  • Смотри вниз!
SRC 3 — СТАТИСТИКА И ВЕРОЯТНОСТЬ (SP)
  • Tetra Dice
  • Tetra Dice (с очками)
  • Желейные бобы
  • Плитка Алекса
  • 3-значный номер

​

8 класс​

Категория отчетности (SRC) 1 – СИСТЕМА ЧИСЛЕНИЙ (NS), ВЫРАЖЕНИЯ И УРАВНЕНИЯ (EE), ФУНКЦИИ (F)
  • Пакеты с попкорном
  • Счетные стулья
  • Телефон Молли
  • Пройдено или не пройдено
  • Взвешивание мрамора
  • Два растения Джека
  • Пончики в изобилии
  • Закон о классах
  • Цены на рубашки
  • Поездка Портленд-Сиэтл

SRC 2 — ГЕОМЕТРИЯ (G)

SRC 3 — СТАТИСТИКА И ВЕРОЯТНОСТЬ (SP)

Увлечение концертами!

​

. gov

Официальные веб-сайты используют домен .gov

Веб-сайт .gov принадлежит официальной правительственной организации США.

Безопасные веб-сайты .gov используют HTTPS

Значок замка ( ) или https:// означает, что вы безопасно подключились к веб-сайту .gov.

TEXAS SUCCESS INITIATIVE ASSESSMENT 2.0 Примеры вопросов по математике

%PDF-1.4 % 1 0 объект /Producer(Adobe PDF Library 15.0)/Title(TEXAS SUCCESS INITIATIVE ASSESSMENT 2.0 Mathematics Sample Questions)/Trapped/Unknown>> эндообъект 2 0 объект /MarkInfo 7 0 R/Метаданные 8 0 R/Имена 9 0 R/OpenAction 275 0 R/Контуры 276 0 R/PageLabels 908 0 R/PageLayout/SinglePage/Pages 13 0 R/StructTreeRoot 871 0 R/Type/Catalog/ViewerPreferences >>> эндообъект 3 0 объект >/Шрифт>>>/Поля[]>> эндообъект 4 0 объект > эндообъект 5 0 объект > эндообъект 6 0 объект > эндообъект 7 0 объект > эндообъект 8 0 объект >поток 3SZfT1uVKS8BEwZpbsDNL32020-08-25T10:44:16+05:302020-09-11T17:24:31+05:302020-09-11T17:24:31+05:30Adobe InDesign CC 13.