Как решать 16 задание в егэ по информатике: ЕГЭ по информатике 2022 — Задание 16 (Рекурсия)

ЕГЭ по информатике 2022 — Задание 16 (Рекурсия)

Шестнадцатое задание из ЕГЭ по информатике 2022 даётся на рекурсию.

Это задание нужно делать с помощью компьютера.

В программировании рекурсией называется процесс, когда функция вызывает сама себя или, когда две функции попарно вызывают друг друга.

Мы будем писать все программы на языке программирования Python.

Что такое Функция в языке программирования Python ?

Функция – это подпрограмма, результатом работы которой может является определенное значение.

Рассмотрим пример функции, которая суммирует два числа!

def F(x, y):
    s = x + y
    return s

a = int(input())
b = int(input())

r = F(a, b)

print(r)

Здесь функция F, которая суммирует два числа.

В главной части программы запрашиваются два числа с клавиатуры: a и b! Эти два числа передаются в функцию F. В функции эти числа кладутся в локальные переменные x и y. Сумма переменных x и y записывается в переменную s. Переменная s возвращается, как результат работы функции F.

Результат работы функции будет помещён в переменную r (в строке r = F(a, b)) в основной части программы.

Таким образом, в переменной r будет сумма двух переменных a и b.

Функции позволяют сократить программный код для однотипных расчётов.

Тренировочные задачи 16 задания из ЕГЭ по информатике 2023

Задача (Стандартная)

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(n) = 1 при n = 1;
F(n) = n + F(n − 1), если n – чётно,
F(n) = 3 × F(n − 2), если n > 1 и при этом n – нечётно.

Чему равно значение функции F(25)?

Решение:

Напишем программу для решения данной задачи. В начале опишем все правила, которые даны в условии задачи для функции. В основной части программы запустим эту функцию.

# Сама функция
def F(n):
    if n==1: return 1
    if n%2==0: return n+F(n-1)
    if n>1 and n%2!=0: return 3*F(n-2)
    
# Основная часть программы
print(F(25))

После запуска рекурсивной функции программа выведет ответ 531441.

Выражение n%2 != 0 (остаток от деления на «2» не равен нулю) обозначает нечётное число. Выражение n%2==0 обозначает чётное число.

Ответ: 531441

Продолжаем тренировку по подготовке к 16 заданию ЕГЭ по информатике 2022.

Задача (Продолжаем подготовку)

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(1) = 1
F(2) = 3
F(n) = F(n–1) * n + F(n–2) * (n – 1) , при n > 2

Чему равно значение функции F(8)? В ответе запишите только натуральное число.

Решение:

# Сама функция
def F(n):
    if n==1: return 1
    if n==2: return 3
    if n>2: return F(n-1)*n + F(n-2)*(n-1)
    
# Основная часть программы
print(F(8))

Ответ получается 148329.

Ответ: 148329

Закрепляющий пример на рекурсию 16 задания из ЕГЭ по информатике 2022.

Задача(Две функции)

Алгоритм вычисления значения функций F(n) и G(n), где n — натуральное число, задан следующими соотношениями:

F(n) = 0, если n F(n) = G(n — 2), если n > 2

G(n) = 0, n G(n) = F(n — 1) + n, если n > 1

Чему равно значение функции F(8)? В ответе запишите только натуральное число.

Решение:

# Сами функции
def F(n):
    if n2: return G(n-2)

def G(n):
    if n1: return F(n-1)+n

# Основная часть программы
print(F(8))

Получается ответ 9.

Ответ: 9

Задача (Количество значений)

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(n) = 2*n*n*n + 1, при n > 25
F(n) = F(n+2) + 2*F(n+3), при n ≤ 25

Определите количество натуральных значений n из отрезка [1; 1000], для которых значение F(n) кратно 11.

Решение:

# Сама функция
def F(n):
    if n>25: return 2*n*n*n + 1
    if n

В начале формируем функцию F. Затем перебираем числа из диапазона от 1 до 1000. Каждое число подставляем в функцию F. Если значение функции F делится на 11, то мы зачитываем такое значение i.

В ответе получается 91.

Ответ: 91

Задача (Используем глобальную переменную)

Решение:

При решении этой задачи можно применить глобальную переменную.

def F(n):
    global s
    s=s+1
    if n>=1:
        s=s+1
        F(n-1)
        F(n-2)
        s=s+1

s=0
F(35)
print(s)

Здесь внутри функции заводим глобальную переменную s, которая будет подсчитывать количество напечатанных звёздочек. Теперь эту переменную видно при любом вызове функции, и при каждом вызове функции она будет одна и та же переменная. Вместо печати звёздочек пишем конструкцию s=s+1.

В основной части программы перед первым запуском функции переменной s присваиваем 0.

Программа может немного медленно работать из-за большой глубины рекурсии, но через минуту выведет число 96631265.

Ответ: 96631265

Новые тенденции

В последнее время мы видим тенденцию в 16 задании из ЕГЭ по информатике 2023, что теперь мало переписать функцию и её запустить. Необходимо подумать, как можно преобразовать то рекурсивное выражение, которое нужно вычислить.

Задача (Новое веяние)

(К. Багдасарян) Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями:

F(n) = 2, если n = 1,
F(n) = 2 · F(n – 1), если n > 1.

Чему равно значение выражения F(1900)/2¹⁸⁹⁰ ?

Решение:

1 Способ (Аналитическое решение)

Если мы просто перепишем функцию и попытаемся вычислить выражение F(1900)/2¹⁸⁹⁰, то получим ошибку RecursionError: maximum recursion depth exceeded. Возникает она из-за слишком большой цепочки вызовов функции.

В подобных задачах нужно попытаться самому упростить выражение, которое пытаемся вычислить. Посмотрим, что из себя представляет функция.

F(1900) = 2*F(1899) = 2*2*F(1898) = … 2 ¹⁹⁰⁰

Тогда

F(1900)/2¹⁸⁹⁰ = 2¹⁹⁰⁰/2¹⁸⁹⁰ = 2¹⁰ = 1024

Получается 1024.

2 Способ (Через lru_cache)

Чтобы уменьшить цепочку вызовов функции, можно использовать инструмент lru_cache.

from functools import lru_cache

@lru_cache(None)
def F(n):
    if n==1: return 2
    if n>1: return 2*F(n-1)

for i in range(2, 1900):
    F(i)

print(F(1900)/2**1890)

В задаче функция опирается на значение функции от n-1 и т.д. За счёт этого происходят длинные вычисления для каждого числа n.

Использовав инструмент lru_cache, мы пробегаемся в цикле по значениям n в возрастающем порядке, и для каждого значения сохраняем результаты функции. Таким образом, вычисляя очередное значение, программа опирается на уже готовый результат, тем самым цепочка вызовов функции будет маленькой.

Ответ: 1024

Задача(Новое веяние, закрепление)

Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:

F(n) = 1 при n ≤ 2;
F(n) = n * F(n-2), если n > 2.

Чему равно значение выражение F(3000)/F(2996) ?

Решение:

1 Способ (Аналитическое решение)

Начнём расписывать F(3000).

F(3000) = 3000*F(2998) = 3000*2998*F(2996)

Получается:

F(3000)/F(2996) = 3000*2998*F(2996)/F(2996) = 3000*2998 = 8994000

2 Способ (Через lru_cache)

from functools import lru_cache

@lru_cache(None)
def F(n):
    if n2: return n*F(n-2)

for i in range(2, 3000):
    F(i)

print(F(3000)/F(2996))

Ответ:

8994000

Задача (Вперёд к победе!)

Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями:

F(n) = 1 при n=1;
F(n) = 2 при n=2;
F(n) = n*(n-1) + F(n-1) + F(n-2), если n > 2.

Чему равно значение функции F(2023) — F(2021) — 2*F(2020) — F(2019)?

Решение:

1 Способ (Аналитическое решение)

F(2023) = 2023*2022 + F(2022) + F(2021) =
= 2023*2022 + 2022*2021 + F(2021) + F(2020) + F(2021) =
=2023*2022 + 2022*2021 + 2021*2020 + F(2020) + F(2019) + F(2020) + F(2021) =
2023*2022 + 2022*2021 + 2021*2020 + 2*F(2020) + F(2019) + F(2021) =
2023*2022 + 2022*2021 + 2021*2020 + F(2021) + 2*F(2020) + F(2019)

Если подставим полученный результат в выражение, которое нужно найти, то получим:

2023*2022 + 2022*2021 + 2021*2020 = 12259388

2 Способ (Через lru_cache)

from functools import lru_cache

@lru_cache(None)
def F(n):
    if n==1: return 1
    if n==2: return 2
    if n>2: return n*(n-1) + F(n-1) + F(n-2)

for i in range(2, 2023):
    F(i)

print(F(2023) - F(2021) -2*F(2020) - F(2019))

Ответ: 12259388

Удачи при решении 16 задания из ЕГЭ по информатике 2022.

ЕГЭ информатика 16 задание разбор, теория, как решать

ЕГЭ информатика 16 задание разбор, теория, как решать.

Рекурсивные алгоритмы, (П) — 1 балл

28.10.2022ЕГЭ Задание 16АдминистраторКомментарии: 0

Алгоритм вычисления значения функции F(n), где n – натуральное число, задан следующими соотношениями: F(n) = 1 при n = 1; F(n) = n × F(n − 1), если n > 1. Чему равно значение выражения F(2023) / F(2020)? Ответ:   Демонстрационный вариант ЕГЭ 2023 г.  – задание №16 

Читать далее

20.04.2022ЕГЭ Задание 16АдминистраторКомментарии: 0

Обозначим частное от деления целочисленного натурального числа a на натуральное число b как a div b, а остаток как a mod b. Например, 13 div 3 = 4, 13 mod 3 = 1. Алгоритм вычисления значения функции F(a, b), где a и b – целые неотрицательные числа, задан следующими соотношениями: F(0, b) = b; F(a, …

Читать далее

22.02.2022ЕГЭ Задание 16АдминистраторКомментарии: 0

Алгоритм вычисления значения функции F(n), где n — натуральное число, задан следующими соотношениями: F(n) = 1 при n = 1; F(n) = 3 × n + F(n — 2), если n > 1 и при этом n нечётно, F(n) = 4 × F(n / 2), если n > 1 и при этом n чётно. Чему …

Читать далее

17.02.2022ЕГЭ Задание 16АдминистраторКомментарии: 0

Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями: F(0) = 0; F(n) = F(n – 1) + 1, если n нечётно; F(n) = F(n/2), если n > 0 и при этом n чётно. Укажите количество таких значений n < 1 000 000 000, для которых F(n) = 2. СтатГрад …

Читать далее

15.12.2021ЕГЭ Задание 16АдминистраторКомментарии: 0

Алгоритм вычисления функции F(n), где n – целое неотрицательное число, задан следующими соотношениями:

F(n) = n + 3, при n ≤ 3 F(n) = F(n – 2) + n, при n > 3 и четном значении F(n-1), F(n) = F(n – 2) + 2· n, при n > 3 и нечетном значении F(n-1)

F(n) = n + 3, при n ≤ 3 F(n) = F(n – 2) + n, при n > 3 и четном значении F(n-1), F(n) = F(n – 2) + 2· n, при n > 3 и нечетном значении F(n-1)

Определите сумму значений, являющихся результатом вызова функции для значений n в диапазоне [40; 50]. Ответ:   Е. Джобс

Читать далее

15.12.2021ЕГЭ Задание 16АдминистраторКомментарии: 0

Алгоритм вычисления функции F(n), где n – целое неотрицательное число, задан следующими соотношениями:

F(0) = 1, F(1) = 3 F(n) = F(n – 1) – F(n – 2) + 3n, при n > 1 и n – четно F(n) = F(n – 2) – F(n – 3) + 2n, при n > 1 и n – нечетно

F(0) = 1, F(1) = 3 F(n) = F(n – 1) – F(n – 2) + 3n, при n > 1 и n – четно F(n) = F(n – 2) – F(n – 3) + 2n, при n > 1 и n – нечетно

Чему равно значение функции F(40)? В ответе запишите только целое число Ответ:   Е. Джобс

Читать далее

18.11.2021ЕГЭ Задание 16АдминистраторКомментарии: 0

Алгоритм вычисления значения функции F(n), где n – целое неотрицательное число, задан следующими соотношениями: F(0) = 0; F(n) = F(n/2), если n > 0 и при этом n чётно; F(n) = 1 + F(n – 1), если n нечётно. Сколько существует таких чисел n, что 1 ≤ n ≤ 500 и F(n) = 8? Ответ: …

Читать далее

10.02.2021ЕГЭ Задание 16АдминистраторКомментарии: 0

Алгоритм вычисления функции F(n) задан следующими соотношениями: F(n) = 1 при n ≤ 1; F(n) = n · F(n – 1) при чётных n > 1; F(n) = n + F(n – 2) при нечётных n > 1; Определите значение F(84). Ответ:   Тренировочный вариант от 16.11.2020 «Евгений Джобс»

Читать далее

28.01.2021ЕГЭ Задание 16АдминистраторКомментарии: 0

Алгоритм вычисления функции F(n) задан следующими соотношениями: F(n) = n · n + 5 · n + 4, при n > 30 F(n) = F(n+1) + 3 · F(n+4), при чётных n ≤ 30 F(n) = 2 · F(n+2) + F(n+5), при нечётных n ≤ 30 Определите количество натуральных значений n из отрезка [1; 1000], …

Читать далее

21.12.2020ЕГЭ Задание 16АдминистраторКомментарии: 0

F(0) = 0; F(n) = n + F(n – 3), если n > 0 и при этом n mod 3 = 0; F(n) = n + F(n – (n mod 3)), если n mod 3 > 0. Чему равно значение функции F(25)? Обозначим через a mod b остаток от деления натурального числа a на натуральное …

Читать далее

Что это на самом деле означает? – Lead by Learning

Голоса учителей и ученых

16 декабря 2019 г. | Соня Спиндт

Непростая задача

Многие из моих учеников жалуются, когда их просят читать техническую литературу, несмотря на мои усилия сделать это интересным и актуальным. Особенно на моем самом продвинутом уроке информатики становится трудно использовать материал, который интересен и актуален для моих учеников, потому что выбор чтения в конечном итоге не зависит от меня. К концу года на экзамене Advanced Placement Computer Science A студенты должны быть в состоянии прочитать и ответить примерно на 8 страницах неясных (а иногда и странных) сценариев, связанных с программированием на Java. В первый раз, когда я попросил своих студентов потренироваться отвечать на один из таких вопросов со свободным ответом (FRQ), каждый пятый студент просто оставил это поле пустым и вздремнул.

Прошли недели практики FRQ, но реакция моих учеников на задание не изменилась. Меня смущали их вялые усилия, а мои студенты были разочарованы тем, что их постоянно просили выполнять «скучные» задания. Однако я знал, что если мои ученики хотят успешно сдать экзамен, им нужно попытаться ответить на эти вопросы и ответить на них правильно. Что еще более важно, благодаря регулярной практике ответов на такие вопросы они начнут развивать навыки критического абстрактного мышления, важность которых выходит далеко за рамки экзамена AP. Просто, верно?

Понимание прочитанного: корень проблемы

Честно говоря, сначала я понятия не имел, как решить эту проблему. Однако при поддержке моих коллег по исследованию Mills Teacher Scholars мы начали замечать, что многие из моих учеников не полностью отвечали на запрос FRQ, даже несмотря на то, что они, казалось, были заняты заданием все время. Я чувствовал, что проблема коренится в понимании прочитанного. Итак, чтобы помочь моим ученикам глубже понять эти технические тексты, я решил сосредоточить свое исследование на создании классных практик, которые развивают навыки аннотирования. Следующие шесть месяцев я провел со своей исследовательской группой, уточняя серию еженедельных заданий, которые включали в себя обведение ключевых словарных терминов, подчеркивание подсказок, наброски идей на полях, а затем попытки ответить на вопросы, которые выпадали из каждого чтения. После того, как учащиеся индивидуально отработали свои навыки аннотирования, они выступали в качестве публичных учеников друг для друга, направляя класс через свои размышления о тексте. К концу моего опроса 86,5% моих учеников естественным образом использовали эти навыки аннотирования для FRQ. Я был рад видеть, что они развивают свои способности к критическому чтению. Однако их фактические результаты никогда не менялись.

Уверенность тоже имеет значение

Я был так сбит с толку! Как мои учащиеся могли реализовать наши стратегии понимания прочитанного и по-прежнему демонстрировать те же реакции, что и в начале года? Почему было так сложно просто взяться за перо и попытаться ответить? Что им было терять? Я рассказал об этих смешанных чувствах своим коллегам-исследователям, которые предположили, что было бы полезно взять интервью у трех фокусных студентов.

После составления протоколов интервью я вернулся к своей группе по расследованию, надеясь, что мои коллеги помогут мне заполнить это белое пятно. Их вопросы бросили вызов моим предположениям, что в конечном итоге позволило мне сосредоточиться на новом виновнике: мои ученики не чувствовали себя достаточно уверенно, чтобы попробовать. Например, один из моих учеников сказал: «Я умею читать. Я просто не знаю, что ответить. Так какой смысл пытаться, если я знаю, что сделаю это неправильно?» Это было действительно удивительно услышать. Я думал, что знаю, что они чувствуют; Я думал, что они были уверены в своих способностях решать проблемы с помощью кода. Моей концентрации на понимании прочитанного было недостаточно. Мне также нужно было понять, как развить их уверенность в том, что они умеют решать проблемы.

Вопрос ведет к новым вопросам

Стремление понять процесс обучения учащихся длится намного дольше одного учебного года. Борьба этого года мотивирует меня искать ответы на связанные вопросы предстоящей осенью. Например, что со временем укрепляет доверие к курсу информатики и что со временем меняет идентичность студентов как учащихся? Я начал обдумывать учебные стратегии, которые уравновешивают «вовлеченность» с тщательным изучением CS. Большую часть времени кажется, что вовлеченность и строгость противоречат друг другу, особенно когда вы начинаете интегрировать понятия «подходящего» CS-образования от некоторых из самых выдающихся умов в этой области. В своем эссе «О жестокости настоящего преподавания информатики» Э. В. Дейкстра написал, что учащиеся должны провести свой первый урок информатики, написав формальные доказательства правильности своих программ. Хотя этот подход может быть академически строгим, я не уверен, что он заинтересует студентов, которым все еще нужно проникнуться идеей компьютерных наук. Мое последнее расследование заставило меня задуматься о том, что уверенность учащегося кроется в тонком пересечении между строгим изучением предмета и увлекательным учебным опытом. Этот многогранный вопрос может показаться пугающим для индивидуального преподавателя. Однако я не одинок. Я знаю, что могу продолжать опираться на будущие циклы исследований, а также на замечательное сообщество инструкторов, которые, как и я, настроены на то, чтобы во всем этом разобраться.

Соня Спиндт последние четыре года работала инструктором информатики в Академии Мэдисон Парк, где преподает веб-разработку, AP CSP и AP CSA. Она постоянно вдохновляется своими учениками и рада продолжать расширять их возможности для изучения областей STEM и карьеры в технологическом секторе. Если вы не можете найти ее в классе, вы обычно можете найти ее в машине — она любит путешествовать со своей сестрой-близнецом, когда может, и считает, что лучший способ познакомиться с новой культурой — это еда!

Полное руководство по новому экзамену AP по принципам компьютерных наук и заданиям для повышения квалификации

Курс AP по основам компьютерных наук — это новый курс AP, который был представлен всего несколько лет назад, осенью 2016 года. Этот курс — один из немногих курсов AP. курсы, которые основаны на собственном опыте и сильных сторонах студентов и подчеркивают важность сотрудничества. Многие, кто привык к более жестко структурированному курсу AP, будут удивлены инновационной, гибкой учебной программой этого класса, которая использует опыт, интересы и сильные стороны студентов для формирования своего пути. Чтобы узнать больше о том, как ваша работа будет оцениваться на экзамене AP Computer Science Principles, ознакомьтесь с разбивкой оценок и советами CollegeVine о том, как лучше всего подготовиться.

 

Хотите узнать, подходит ли вам этот курс? Ознакомьтесь с введением CollegeVine в новый курс AP по информатике .

 

Когда проводится экзамен AP по информатике?

 

Экзамен AP по основам компьютерных наук является одним из заключительных тестов, проводимых Советом колледжей, организацией, которая администрирует AP. Этот экзамен состоится в пятницу, 15 мая, в 8:00. Полный список всех периодов сдачи экзаменов AP (пересмотренный в связи с коронавирусом) см. в нашем посте 9.0043 Расписание экзаменов AP на 2020 год: все, что вам нужно знать .

 

О курсе AP «Основы компьютерных наук»

 

Курс AP «Основы компьютерных наук» развивает навыки вычислительного мышления в контексте творческого решения задач. Основная цель курса — «познакомить студентов с основополагающими концепциями компьютерных наук и побудить их исследовать, как компьютеры и технологии могут повлиять на мир». Курс направлен на расширение участия в компьютерных науках путем привлечения разнообразного студенческого контингента.

 

В этом курсе вы научитесь анализировать и изучать данные, работать с большими наборами данных и делать выводы из тенденций. Хотя набор навыков, который вы развиваете в этом классе, предписывается основной учебной программой курса, точные способы применения ваших знаний будут зависеть от вас. Совет колледжей поощряет учителей поощрять творческий подход учащихся к решению проблем и позволяет учащимся выбирать конкретные, реальные приложения для своей работы.

 

Самостоятельная подготовка к этому экзамену технически очень сложна, хотя и не совсем невозможна. Из-за формата экзамена, который основан на длительной совместной работе в классе для получения 40% баллов, вам понадобится учитель, который поможет сдать вашу работу. Вашему учителю потребуется создать класс AP CSP в цифровом портфолио AP, чтобы вашу работу можно было отправить на оценку. Если класс не предлагается в вашей школе, а координатор AP не желает помогать вам в работе, вы можете записаться на онлайн-курс или попытаться записаться на курс в ближайшей средней школе.

 

Структура курса AP «Основы компьютерных наук»

 

Курс AP «Основы компьютерных наук» посвящен двум конкретным областям: практикам вычислительного мышления и масштабным идеям. Благодаря развитию приобретенных навыков и пониманию изучаемых концепций учащиеся подготовятся не только к успешной сдаче экзамена AP по принципам компьютерных наук, но и к будущим успехам в компьютерных классах колледжа и карьере STEM.

 

Практики вычислительного мышления

 

Участники AP Computer Science Principles должны освоить шесть приемов вычислительного мышления. Это:

 

Практика вычислительного мышления	Описание
Подключение компьютеров	Влияние развития вычислительной техники и связи между людьми и компьютерами
Создание вычислительных артефактов	Творческий аспект вычислений и использование вычислительных технологий для изобретательского решения задач
Абстрагирование	Использовать абстракцию для создания моделей и симуляций и использовать их для прогнозирования
Анализ проблем и артефактов	Разработка и создание вычислительных решений, моделей и артефактов, а также анализ их вычислительной работы и работы других
Связь	Опишите вычисления, а также влияние технологий и вычислений. Объясните свою вычислительную работу и выбор вместе с другими
Сотрудничество	Работайте со студентами с разным опытом, идеями, навыками и точками зрения, чтобы решать сложные проблемы и отвечать на открытые вопросы

 

Большие идеи

 

Большие идеи — это основные понятия, изучаемые в курсе AP Computer Science Principles. Внутри каждой большой идеи есть «основные вопросы», цель которых — побудить к более глубоким размышлениям о конкретной концепции и построить более глубокое ее понимание. Ниже приведены семь основных идей курса AP Computer Science Principles, а также лежащие в их основе важные вопросы и процент разделов с несколькими вариантами ответов экзамена AP Computer Science, которые они составляют.

 

Креативность: Творчески используйте инструменты и методы вычислений для создания актуальных интересных артефактов, которые улучшаются с помощью вычислений.

 

• Как процесс творческой разработки может повлиять на создание вычислительных артефактов?
• Как вычисления и использование вычислительных инструментов могут способствовать творческому самовыражению?
• Как компьютеры могут расширить традиционные формы человеческого самовыражения и опыта?

 

Абстракция: Используйте абстракцию для моделирования мира и общения с людьми и машинами.

 

• Как самые разные виды данных, физических явлений и математических понятий представляются на компьютере?
• Как абстракция помогает нам в написании программ, создании вычислительных артефактов и решении проблем?
• Как вычислительные модели и симуляции могут помочь в создании нового понимания и знаний?

 

Данные и информация: Используйте компьютеры и вычисления, чтобы лучше понять способы преобразования данных в информацию и знания.

 

• Как можно использовать вычисления, чтобы помочь людям обрабатывать данные и информацию, чтобы получить понимание и знания?
• Как можно использовать вычисления для облегчения исследования и открытия при работе с данными?
• Какие соображения и компромиссы возникают при вычислительной обработке данных?
• Какие возможности предоставляют большие наборы данных для решения проблем и создания знаний?

 

Алгоритмы: Разработка и реализация оригинальных алгоритмов, использование алгоритмов на языке и анализ алгоритмов аналитически и эмпирически.

 

• Как реализуются и выполняются алгоритмы на компьютерах и вычислительных устройствах?
• Почему одни языки лучше других при реализации алгоритмов?
• Какие задачи просты, какие сложны, а какие невозможно решить алгоритмически?
• Как оцениваются алгоритмы?

 

Программирование: Изучайте специфику языков программирования, создавайте программы и воплощайте человеческие намерения в вычислительные артефакты.

 

• Как разрабатываются программы, помогающие людям, организациям или обществу решать проблемы?
• Как программы используются для творческого самовыражения, удовлетворения личного любопытства или создания новых знаний?
• Как компьютерные программы реализуют алгоритмы?
• Как абстракция делает возможной разработку компьютерных программ?
• Как люди разрабатывают и тестируют компьютерные программы?
• Какие математические и логические концепции являются фундаментальными для компьютерного программирования?

 

Интернет: Понимать, как работает Интернет, его характеристики и системы, на которых он построен, а также связанные с этим проблемы, такие как кибербезопасность.

 

• Что такое Интернет? Как он построен? Как это работает?
• Какие аспекты дизайна и разработки Интернета помогли ему масштабироваться и процветать?
• Как кибербезопасность влияет на постоянно растущее число пользователей Интернета?

 

Глобальное воздействие: Познакомьтесь с тем, как вычисления способствуют инновациям, и поймите плюсы и минусы использования вычислений в различных контекстах.

 

• Как компьютеры улучшают человеческое общение, взаимодействие и познание?
• Как компьютеры способствуют инновациям?
• Каковы некоторые потенциальные полезные и вредные последствия вычислений?
• Как экономический, социальный и культурный контексты влияют на инновации и использование компьютеров?

 

Большая идея	Приблизительный процент вопросов с несколькими вариантами ответов
Творчество	Н/Д
Абстракция	19%
Данные и информация	18%
Алгоритмы	20%
Программирование	20%
Интернет	13%
Глобальное воздействие	10%

Об экзамене AP по основам информатики

 

Формат оценки AP Computer Science Principles отражает приверженность интересам и сильным сторонам отдельных учащихся. Есть два компонента: исполнительские задания и традиционный итоговый экзамен.

 

Задачи производительности | 40% баллов AP по принципам компьютерных наук

 

Первый компонент оценки AP по принципам компьютерных наук — это оценивание по всему курсу, в ходе которого учащиеся используют время в классе для выполнения двух длительных заданий. Эта часть оценки является новаторской, поскольку она свидетельствует о признании Советом колледжей того, что такие задания на успеваемость «оценивают достижения учащихся более надежными способами, чем те, которые доступны на запланированном по времени экзамене», и существуют цели обучения, которые «более эффективно измеряются в аутентичных, реальная задача производительности». Это первый курс AP за пределами программ студийного искусства и исследований/семинаров, в котором оценка по курсу включена в оценку и окончательную оценку AP.

 

Задание первое: В первом из заданий на эффективность вам предлагается изучить влияние компьютерных инноваций в течение как минимум восьми часов аудиторных занятий, и на его долю приходится 16% общего балла за экзамен.

 

Задание второе: Во втором задании на производительность учащиеся должны создать вычислительный артефакт с помощью программирования в течение не менее 12 часов учебного времени, что составляет 24% от общего балла. Вы должны предоставить видео о работе вашей программы, письменное описание вашей программы и отчет о вашем процессе разработки, а также код программы.

 

Завершающий экзамен

2 часа | ~74 вопроса | 60% баллов

 

Эта часть экзамена проводится как традиционный экзамен AP и длится два часа, что составляет 60% от общего балла. Это тест с несколькими вариантами ответов, состоящий примерно из 74 вопросов, некоторые из которых имеют ответы с одним выбором (только один правильный ответ), а другие — с несколькими вариантами ответов (более одного правильного ответа).

 

Ниже приведен пример вопроса с несколькими вариантами ответа: 

Ответ: C. Источник: College Board.

 

Ниже приведен пример вопроса с множественным выбором: 

Ответы: B, C. Источник: College Board.

 

 

AP Принципы компьютерных наук Распределение баллов за экзамен, средний балл и проходной балл 5 4 3 2 1 AP Принципы информатики 13,8% 21% 37,1% 18,8% 9,3%

    

В 2019 году чуть более 96 000 учащихся сдали экзамен AP по основам компьютерных наук. Результаты экзамена 2019 года показывают высокий проходной балл (3 балла и выше), но сложный уровень мастерства. В то время как 71,9% учащихся, сдававших экзамены, получили оценку 3 и выше, только 13,8% получили наивысшую оценку 5, а 37,1% получили оценку 3.   

 

Имейте в виду, что зачет и продвинутая репутация, основанные на баллах AP, сильно различаются от школы к школе. Дополнительную информацию см. в правилах Совета колледжей относительно того, какие AP имеют право на получение кредитов за курс или углубленное размещение в определенных колледжах.

 

Полное описание курса, которое может помочь вам в обучении и понимании знаний, необходимых для теста, также доступно на сайте College Board.

 

Советы по подготовке к экзамену AP по принципам информатики и контрольным заданиям

 

Шаг 1. Начните с оценки своих навыков

 

Рекомендуется начать обучение с прохождения пробного теста, чтобы получить представление о сильных и слабых сторонах вашей учебной программы. Поскольку курс AP Computer Science Principles является более новым предложением, практические и оценочные материалы ограничены. Вы можете начать оценивать свои навыки, используя практические вопросы, доступные в описании курса. Вы также можете оценить свои навыки, ознакомившись с образцом программы курса или планом курса, приведенным в описании курса. Если вы решите купить коммерческое учебное пособие, вы также можете найти практические тесты во многих из этих книг, но обязательно выберите ту, которая имеет хорошие оценки.

 

После того, как вы получите приблизительное представление о своих существующих навыках и знаниях, составьте список областей контента для обзора. На этом этапе может быть полезно встретиться с вашим учителем или другом, чтобы обсудить каждую большую идею из курса, чтобы убедиться, что ваша самооценка точна. Точная формирующая оценка позволит вам лучше понять, на чем сосредоточить свои усилия в обучении.

 

Шаг 2. Изучите теорию

 

Чтобы понять материал курса AP Computer Science Principles, вам необходимо понять структуру плана курса, которая доступна в описании курса. План объединяет ключевые концепции в семь «больших идей», которые вам нужно будет освоить. Вы должны знать каждое из «постоянных понятий» (подпадающих под каждую большую идею) и иметь примеры необходимых знаний для их поддержки. Чтобы получить лучшее представление об основах учебной программы, просмотрите серию видеороликов Совета колледжей с обзорными модулями для учителей компьютерных наук AP.

 

Как указано выше, основные идеи курса AP Computer Science Principles:

 

• Креативность
• Абстракция
• Данные и информация
• Алгоритмы
• Программирование
• Интернет
• Глобальное воздействие

 

Выше также упоминались шесть практик вычислительного мышления. Это практические навыки, используемые учеными-компьютерщиками ежедневно, и они включают в себя:

 

• Подключение вычислений 
• Создание вычислительных артефактов
• Абстрагирование
• Анализ проблем и артефактов
• Общение
• Сотрудничество

 

Из-за его недавнего введения для курса AP Computer Science Principles существует несколько внешних источников. Тем не менее, на edX есть бесплатный онлайн-курс, который будет полезен для ознакомления с материалами курса. Список рекомендуемых учебников также доступен на странице аудита курса AP «Принципы компьютерных наук».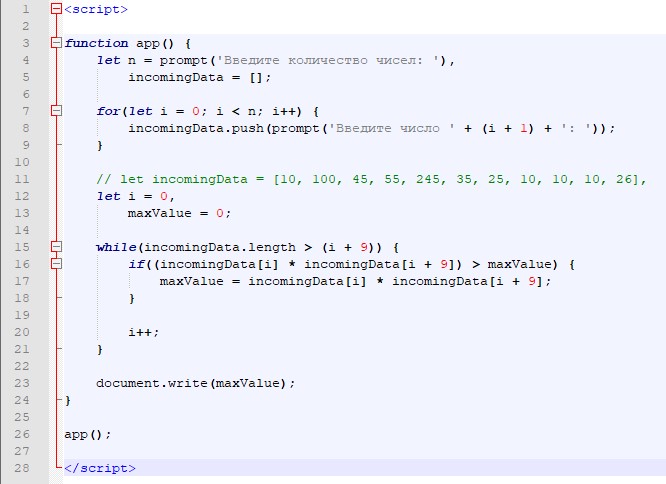 Наконец, вы должны ознакомиться со справочными листами учащихся, доступными в описании курса, начиная со страницы 114.        

 

Шаг 3. Отработка вопросов с несколькими вариантами ответов

 

После того, как вы изучите свою теорию, проверьте ее, отрабатывая вопросы с несколькими вариантами ответов. Вы можете найти их в описании курса, или, если ваш преподаватель зарегистрировался в программе AP Computer Science Principles AP Course Audit, он сможет предоставить вам вопросы с несколькими вариантами ответов из безопасного практического экзамена. Вы также найдете практический тест, включающий вопросы с несколькими вариантами ответов, в ускоренном курсе AP по принципам компьютерных наук: получите более высокий балл за меньшее время.

 

Экзаменационные вопросы с несколькими вариантами ответов оценивают как применение методов вычислительного мышления, так и ваше понимание больших идей. Они могут сопровождаться нетекстовыми материалами, например диаграммами, диаграммами или другими графическими иллюстрациями. Эта часть экзамена посвящена программированию, поэтому убедитесь, что вы понимаете основы того, как и когда применять определенные навыки программирования.

 

Ответив на эти вопросы, постарайтесь отследить, какие области еще сбивают вас с толку, и снова вернитесь к этой теории. Сосредоточьтесь на понимании того, что задает каждый вопрос, и ведите постоянный список любых понятий, которые все еще незнакомы.

 

Шаг 4. Уточните свои задачи на производительность

 

Для прохождения курса AP Computer Science Principles требуется две задачи на производительность. Прежде чем приступить к любому из них, вам необходимо освоить содержание знаний и навыков, необходимых для успеха, выполнить практические задания с учетом отзывов вашего учителя и просмотреть критерии оценки для вашего задания. Вы также можете просмотреть примеры ответов с примерами задач с высокой, средней и низкой оценкой производительности, которые помогут вам понять уровень детализации, ожидаемый от ваших ответов.

 

Наконец, убедитесь, что вы понимаете, когда и как цитировать источник. Вы не получите баллы за задания, в которых не используются соответствующие цитаты. Совет колледжей не диктует определенный формат цитирования, поэтому вы можете выбирать из стилей MLA, APA или IEEE, если вы остаетесь последовательными на протяжении всей своей работы.

 

Первое задание на выступление — это задание на выступление «Изучение — влияние компьютерных инноваций», которое выполняется в течение восьми учебных часов и составляет 16% от вашего итогового балла AP. Вы можете найти полные инструкции для этого задания, начиная со страницы 108 описания курса.

 

В этом упражнении вы должны будете провести исследование вычислительной инновации, которая потенциально может оказать значительное благотворное или вредное воздействие на общество, экономику или культуру. Вы должны выбрать инновацию, которая потребляет, преобразует или производит данные и вызывает хотя бы одну проблему с точки зрения ее безопасности, конфиденциальности или хранения. Вам нужно будет исследовать инновации, попутно оценивая источники на предмет их актуальности, достоверности и доступности. Вы также должны позаботиться о том, чтобы избежать плагиата, надлежащим образом цитируя все использованные источники.

 

Ваше расследование должно не просто собирать факты; вместо этого он должен глубоко вникать в вычислительные инновации, задавая вопросы, предлагая решения и делая продуманные выводы. Это глубокое размышление приведет к созданию вами вычислительного артефакта, который иллюстрирует, представляет или объясняет предполагаемую цель, функцию или эффекты вычислительной инновации.

 

Вам следует стремиться к творческому и привлекательному артефакту, который демонстрирует вашу способность мыслить нестандартно, не ограничиваясь традиционными способами выражения идей. Это может быть анимационное видео, инфографика, песня или что-то еще, что подчеркивает как задачу, так и ваше творчество. Вы отправите свою окончательную задачу производительности Исследовать в виде двух частей: вычислительного артефакта и письменного ответа. См. стр. 109в описании курса для точных требований подачи.

 

Второе задание на выступление — это задание на выступление «Создание приложений из идей», которое выполняется в течение 12 учебных часов и дает 24 % вашего итогового балла AP. Вы можете найти полные инструкции для этого задания, начиная со страницы 111 описания курса.

 

В этом задании вам предлагается создать программу по вашему выбору, которая решает проблему или выражает личный интерес. Вам настоятельно рекомендуется сотрудничать с другим учащимся в вашем классе во время разработки вашей программы, но разработка вашей программы также должна включать значительный объем самостоятельной работы по планированию и разработке частей процесса.

 

Ваша завершенная программа должна демонстрировать ваши навыки программирования. Он должен использовать несколько эффективно интегрированных математических и логических концепций, реализовывать алгоритм, объединяющий другие алгоритмы и математические или логические концепции, а также разрабатывать и использовать абстракции для управления его сложностью.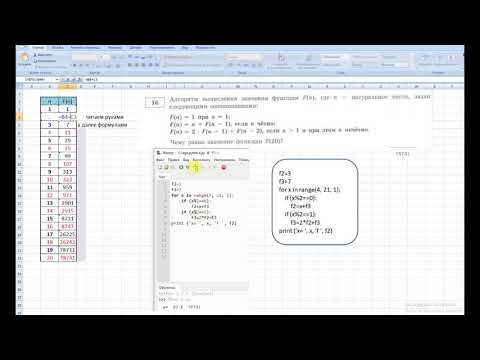

 

Вы составите письменный ответ с описанием вашей программы, процесса ее разработки и кода. Ваша окончательная заявка будет включать видео о работе программы, копию вашего кода и ваш письменный ответ. Полные требования к представлению доступны на странице 112 описания курса.

 

Шаг 5. Повторите свою практику

 

Если у вас есть доступ к другому практическому тесту через вашего учителя, пройдите его, чтобы оценить свой прогресс в вопросах с несколькими вариантами ответов. Просмотрите свои рабочие задания и убедитесь, что вы успешно выполнили хотя бы одно из них при минимальном руководстве со стороны учителя. Помните, что по итоговым заданиям вы не можете отправлять работу, которая была отредактирована или исправлена ​​вашим учителем, и вы не можете обращаться за помощью или отзывами по ответам на вопросы.

 

Шаг 6. Особенности дня экзамена

 

Если вы проходите курс AP, связанный с этим экзаменом, ваш преподаватель расскажет вам, как зарегистрироваться.