При движении прямого проводника в однородном магнитном поле между его … — Учеба и наука

Лучший ответ по мнению автора

E=Blsin(a). т.е. 16 В

03. 10.14
Лучший ответ по мнению автора

Ответ понравился автору вопроса

Михаил Александров
Читать ответы

Андрей Андреевич
Читать ответы

Владимир
Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Физика

Похожие вопросы

При подходе к светофору автомобиль. ..

Велосипедист движется равномерно по окружности…

Решено

задача по физике

Ядро атома гелия, имеющее массу…

эскалатор поднимает стоящего человека за 1 минуту

Пользуйтесь нашим приложением

Электричество и магнетизм

Применим теперь к рассмотренной системе закон сохранения энергии. Пусть — изменение магнитного потока при небольшом перемещении проводника за время . Совершенная работа равна . За счет какого источника совершается эта работа? В окружающем пространстве ничего не изменилось. Единственная доступная энергия черпается из источника тока. Если его ЭДС равна  то за время  источник израсходует энергию . Эта энергия тратится на выделение тепла на сопротивлении

R  и на работу по перемещению проводника

(8. 5)

Разделив обе части на  и перенося слагаемое с потоком в левую часть равенства, получаем

(8.6)

В этом уравнении нетрудно узнать закон Ома: в правой части стоит падение напряжения на сопротивлении, а в левой должна стоять сумма всех действующих в цепи ЭДС. Поэтому уравнение можно переписать в виде

(8.7)

где

                   

(8.8)

Это соотношение есть математическая запись

закона электромагнитной индукции Фарадея (рис. 8.7). 

Видео 8.4. Вихревое электрическое поле.

 

Рис. 8.7. Магнитный поток через замкнутый контур 

В чем же физическая причина возникновения ЭДС индукции в данном случае? Рассмотрим почти такую же систему, но без источника тока и без замкнутой цепи. Пусть отрезок проводника длиной l  движется со скоростью v перпендикулярно вектору магнитной индукции В (рис. 8.8).

Рис. 8.8. Возникновение на концах проводника, движущегося в магнитном поле,

разности потенциалов, равной ЭДС электромагнитной индукции 

Магнитное поле однородно и линии магнитной индукции  перпендикулярны чертежу и направлены от нас. На свободные электроны в проводнике действует сила Лоренца (направление которой определяется правилом буравчика)

                    

(8. 9)

где е — заряд электрона. Под влиянием силы Лоренца произойдет перемещение зарядов и на концах проводника возникнет некоторая разность потенциалов . Возникшее электрическое поле

Е будет препятствовать передвижению зарядов, и их дальнейшее движение прекратится, когда сила со стороны индуцированного электрического поля  будет равна по величине, но противоположна по направлению силе Лоренца .

Таким образом, получаем

откуда

               

(8.10)

Так как , то

              

(8.11)

Скорость проводника равна , а произведение  есть площадь поверхности, заметаемая проводником за время . Получаем, следовательно,

               

(8.12)

Мы пришли к тому же результату, так как разность потенциалов на концах разомкнутого проводника равняется ЭДС индукции. (Напомним, что и для обычного источника тока разность потенциалов на его клеммах при разомкнутой цепи равна ЭДС.) Поскольку сила Лоренца, действующая на отрицательно заряженные электроны, направлена на рис. 8.3 вниз, на нижнем конце проводника скапливается избыток отрицательного заряда, а на верхнем — положительного. Следовательно, потенциал верхнего конца выше потенциала нижнего. Впрочем, о знаке ЭДС индукции мы поговорим особо. 

Напомним, что ранее мы рассмотрели пример (п. 6.7), в котором речь шла о самолете, летящем в вертикальном магнитном поле. Нетрудно заметить, что проблема в том примере идентична только что рассмотренной задаче о движении проводника.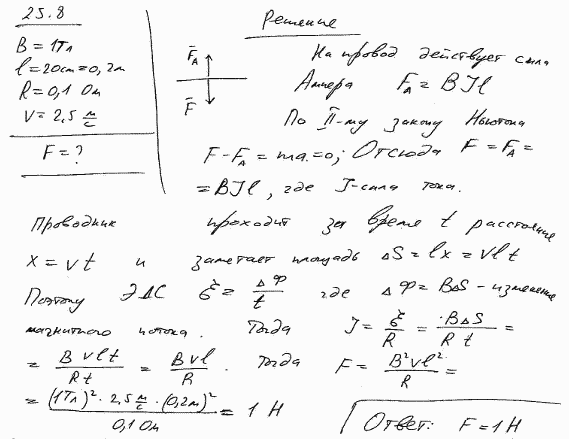 И из преобразований Лоренца мы получили тогда в точности те же результаты, что и сейчас: сравните формулы (8.10) и (6.43). Таким образом, и закон сохранения энергии, и уравнение динамики заряда в магнитном поле, и даже релятивистские преобразования Лоренца для электромагнитного поля приводят к тому же закону Фарадея — в физике (как и вообще в мире) все взаимосвязано. 

Выражение (8.8) для ЭДС электромагнитной индукции имеет очень общий вид: в него не вошли никакие конкретные характеристики движения: скорость проводника, его длина и т. п. Все определяется только скоростью изменения потока вектора магнитной индукции. При этом совершенно неважно, каким путем мы изменяем этот поток. Можно деформировать виток, перемещать его или просто увеличивать магнитную индукцию (рис 8.9, 8.10, 8.11, 8.12, 8.13). Именно последний вариант реализовался в опытах, которые мы обсуждали в начале этой главы. Механизм возникновения ЭДС индукции может бытьразным, но конечный результат будет описываться тем же уравнением (8. 8), которое носит название закона Фарадея. 

Рис. 8.9. Закон Фарадея

 

Рис. 8.10. Возникновение тока в контуре при перемещении провода в  постоянном магнитном поле 

 

Рис. 8.11. Возникновение тока в контуре при подключении батареи  

 

Рис. 8.12. Яркое вспыхивание лампочки при размыкании ключа 

Видео 8.5. Токи замыкания и размыкания. К вопросу: «Можно ли сжечь прибор при его выключении?»

Рис. 8.13. Возникновение переменного тока при вращении контура 

Пример 1. В однородном магнитном поле с индукцией 0,4 Тл в плоскости, перпендикулярной линиям индукции поля, вращается стержень длиной 10 см. Ось вращения проходит через один из концов стержня. Определить разность потенциалов U на концах стержня при частоте вращения 16 .

Решение. За время стержень повернется на угол  и заметет сектор площадью

Разность потенциалов равна скорости изменения потока магнитной индукции

 

Закон Фарадея применим не только к отдельному контуру или витку, но и к катушке, которую можно рассматривать как N  витков, соединенных последовательно. В этом случае суммарная ЭДС будет в N раз больше, чем ЭДС отдельного витка, то есть

(8.13)

где величина

называется потокосцеплением или полным магнитным потоком ( измеряется в тех же единицах, что и , то есть в веберах).

Видео 8.6. Потокосцепление: почему в обмотке чаще всего много витков.

Пример 2. Магнитная индукция поля между полюсами магнита генератора равна 0,8 Тл. Ротор имеет 100 витков площадью 400 см2. Определить частоту вращения якоря, если максимальная ЭДС индукции равна = 200 В (рис. 8.14). 

 

Рис. 8.14. Вращение контура в постоянном магнитном поле 

Решение. Угол между магнитным полем и нормалью к плоскости витков изменяется по закону . Полный магнитный поток через обмотку ротора в момент времени t  равен . Дифференцируямагнитный поток по времени, получаем

Максимальное значение синуса равно единице, следовательно, максимальное значение ЭДС индукции равно

откуда

 

ЭДС индукции возникает не только при перемещении замкнутого контура в магнитном поле или перемещении магнита относительно неподвижного контура. Пусть имеются две катушки с общим железным сердечником, служащим в качестве магнитопровода (рис. 8.15).

Рис. 8.15. Железный сердечник как магнитопровод между двумя катушками 

При разомкнутой цепи магнитный поток в системе равен нулю. При замыкании ключа К через катушку 1 пойдет ток, который создаст магнитное поле, так что катушка 2 будет пронизываться магнитным потоком . Поэтому при замыкании ключа за время нарастания тока до стационарного значения поток через катушку 2, меняется на величину . Соответственно, в ней возникает ЭДС

где N — число витков в катушке 2, и идет индукционный ток, который зарегистрирует гальванометр G.

Когда возрастание тока в катушке 1 прекратится, поток магнитной индукции станет постоянным и ЭДС будет равна нулю. Ток в катушке 2 также перестанет идти, и стрелка гальванометра вернется в исходное положение. Такая же картина будет наблюдаться и при размыкании цепи катушки 1, только стрелка гальванометра отклонится в другую сторону, что свидетельствует об изменении направления тока в катушке 2.

Если через катушку 1 пропустить переменный ток, то по цепи катушки 2 пойдет переменный ток той же частоты. Этот принцип широко используется в трансформаторной технике. 

Пусть контур имеет сопротивление R и пусть магнитный поток через него меняется по какому-то закону. Возникающая в контуре ЭДС электромагнитной индукции

вызывает в контуре ток

                            

(8.14)

Заряд , протекший в контуре за время , связан с током 

Интегрируя, получаем для заряда Q, протекшего по контуру при изменении потока следующее выражение

 

                          

(8. 15)

(мы используем модуль изменения потока, так как направление перетекания заряда нам сейчас не важно). Отсюда, кстати, вытекает связь единицы измерения магнитного потока с зарядом и сопротивлением

Пример 3. Проволочное кольцо радиусом 10 см лежит на столе. Какой заряд протечет по кольцу, если его повернуть с одной стороны на другую. Сопротивление кольца 3 Ом. Вертикальная составляющая индукции магнитного поля Земли равна 50 мкТл.

Решение. Начальный поток магнитной индукции через кольцо равен . После переворачивания кольца величина потока будет той же, но силовые линии входят теперь с другой стороны кольца: . Искомый заряд равен

 

В 1833 г. Э.X. Ленц (рис. 8.16) сформулировал правило (правило Ленца): 

 

Рис. 8.16. Э.Х. Ленц (1804–1865) —  русский физик

Индукционный ток всегда имеет такое направление, что его магнитное поле противодействует изменению магнитного потока, пронизывающего контур.  

Приведем пример использования правила Ленца (рис. 8.17, 8.18).

Рис. 8.17. Иллюстрация правила Ленца

  

Рис. 8.18. Иллюстрация правила Ленца 

Рассматривая рис. 8.8, мы видели, что избыточный положительный заряд накапливался на верхнем конце проводника. Следовательно, в то короткое время, пока движение зарядов в проводнике не прекратилось, индукционный ток тек снизу вверх. По правилу буравчика (поворот ручки от направления тока к направлению поля), сила Ампера была направлена налево, препятствуя движению проводника направо. В опыте, когда постоянный магнит приближается к витку, индуцированный ток также создает противодействующее магнитное поле (рис. 8.19).

Рис. 8.19. При перемещении постоянного магнита в катушке возникает индукционный ток,
поле которого препятствует перемещению магнита 

На рис. 8.20 показан опыт, иллюстрирующий правило Ленца. На концах коромысла, которое может вращаться вокруг вертикальной оси, укреплены два алюминиевых кольца: одно сплошное, а другое — с разрезом. при приближении к первому кольцу постоянного магнита оно отталкивается от него. а при удалении — притягивается, поскольку индукционные токи в соответствии с правилом Ленца препятствуют изменению магнитного потока, охватываемого кольцом. С разрезанным кольцом магнит не взаимодействует.

 

Рис. 8.20. Взаимодействие постоянного магнита с проводящим кольцом

Видео 8.7. Парение колец в магнитном поле.

На рис. 8.21 представлен опыт, в котором демонстрируется взаимодействие проводящего кольца и электромагнита. Кольцо, надетое на выступающий из обмотки конец вертикального сердечника, при включении тока в обмотке взлетает вверх. При горизонтальном расположении сердечника в соответствии с правилом Ленца при включении поля перемещается по сердечнику в сторону от обмотки, а при выключении — обратно к обмотке.  

 

Рис. 8.21. Взаимодействие электромагнита с проводящим кольцом 

Видео 8.8. Электромагнитная пушка.

Математически правило Ленца отображается знаком минус в уравнении (8.8) закона Фарадея. Обсудим подробнее эту связь. Здесь могут возникнуть трудности с определением знака потока вектора магнитной индукции. Когда мы имели дело с замкнутыми поверхностями в электростатике, положительное направление задавалось внешней нормалью. Когда незамкнутая поверхность «натянута» на контур с уже текущим током, направление тока задает положительное направление нормали по правилу буравчика. С этим мы познакомились уже при решении задач онахождении работы по деформированию контура. Но как быть в случае использования закона Фарадея, когда поверхность не замкнута, а направление тока нам не известно и мы только хотим его определить? 

Рассмотрим рис. 8.22. На нем показан контур, пронизываемый силовыми линиями внешнего магнитного поля В.

Рис. 8.22. Иллюстрация применения правила Ленца:
изменение направления обхода контура не меняет знака ЭДС индукции в законе Фарадея 

Выберем положительное направление обхода контура против часовой стрелки (верхний ряд). На рис. 8.22-1 магнитное поле постоянно. При данном выборе положительного направления обхода контура и остром угле между нормалью n к контуру и вектором магнитной индукции В магнитный поток через контур положителен . На рис. 8.22-2 магнитное поле увеличивается. Положительный поток через контур также растет, и потому  Из закона Фарадея следует тогда, что ЭДС индукции и, следовательно, индукционный ток отрицательны. Это значит, что ток течет в обратном направлении по отношению к выбранному пути обхода контура, то есть по часовой стрелке.

Выберем теперь иное положительное направление обхода контура — по часовой стреле (рис. 8.22-3). Поток постоянного магнитного поля здесь отрицателен (угол между n и В тупой, и его косинус отрицателен). При увеличении поля абсолютная величина потока растет, но так как он отрицателен, то (, как показано на рис. 8.22-4). Из закона Фарадея следует тогда, что ЭДС и индукционный ток положительны. Это значит, что направление тока совпадаетс выбранным направлением обхода контура, то есть ток течет по часовой стрелке.

Мы показали, что направление индукционного тока не зависит от выбора положительного направления обхода контура. Так и должно быть, поскольку выбор направления обхода контура делаем мы и притом произвольно, а направление тока — физическая реальность, которая не может зависеть от нашего произвола. С аналогичной ситуацией мы сталкивались при изучении правил Кирхгофа.

Индукционные токи возникают не только в проволочных витках, но и в толще массивных проводников. В этом случае их называют вихревыми токами или токами Фуко. Из–за малого сопротивления проводников они могут достигать большой силы. По правилу Ленца вихревые токи также действуют против причины, их вызывающей. На этом основана идея электромагнитных демпферов, успокаивающих колеблющиеся части приборов (стрелки гальванометров и т. п.). На подвижной части прибора укрепляется металлическая полоска, находящаяся в поле сильного магнита. При движении системы токи Ж. Фуко (рис. 8.23) тормозят ее, но они отсутствуют при покоящейся стрелке и не препятствуют её остановке в нужном месте, согласно значению измеряемой величины (в отличие от сил трения).

Рис. 8.23. Леон Фуко (1819–1868) — французский физик и астроном 

Итогом проведенных рассуждений может быть такая формулировка правила Ленца: индукционный ток всегда направлен так, чтобы препятствовать той причине, которая его породила. Вне зависимости от того, что это за причина.

Например, если проволочное кольцо падает в неоднородном магнитном поле под действием силы тяжести, то в нем течет индукционный ток. Соответственно на кольцо действует сила Ампера. Ничего не вычисляя, можно быть уверенным в том, что эта сила Ампера будет направлена вверх, чтобы — согласно правилу Ленца — мешать силе тяжести, которая является причиной падения кольца, что влечет за собой изменение магнитного потока, а это приводит к появлению индукционного тока, на который действует сила Ампера, тормозящая падение…

Ниже рассматриваются опыты, в которых изучаются свойства токов Фуко.  

На рис. 8.24 показан опыт, демонстрирующий падение тел в неоднородном магнитном поле. Неоднородное магнитное поле тормозит движение проводящих предметов из-за токов Фуко, возникающих в проводниках при изменении магнитного потока через них. Демонстрируется беспрепятственное падение диэлектрического деревянного диска между полюсами сильного электромагнита и медленное падение медного и алюминиевого дисков в магнитном поле, напоминающее движение тел в среде с большой вязкостью.

Рис. 8.24. Падение тел в неоднородном магнитном поле 

Видео 8.9. Электромагнитное торможение: падение медных и алюминиевых дисков  («монет») в магнитном поле.

При падении сильного постоянного магнита внутри вертикальной проводящей трубки в ее стенках возникают токи Фуко, тормозящие это падение. В опыте (рис. 8.25) демонстрируется свободное падение немагнитного алюминиевого цилиндра в разных трубках, а также маленького магнита в стеклянной трубке. Затем показывают замедление падения этого магнита в алюминиевой трубке и его очень медленное падение в толстостенной медной трубке.

 

Рис. 8.25. Падение магнита в трубках 

На рис. 8.26 показано демпфирование колебаний маятника. Толстая сплошная медная пластина, прикрепленная на конце физического маятника, движется при его колебаниях между полюсами сильного электромагнита. Слабо затухающие колебания маятника после включения магнитного поля начинают быстро затухать, превращаясь практически в апериодические колебания. Если на конце маятника закрепить медную пластинку, разрезанную в виде гребенки, то сильное затухание колебаний маятника исчезает, поскольку токи Фуко уже не могут замыкаться в объеме проводника. 

 

Рис. 8.26. Демпфирование колебаний маятника 

Видео 8.10. Электромагнитное торможение: маятник.

В опыте на рис. 8.27 показана левитация сплошного проводящего кольца. Токи Фуко могут возникать не только в проводниках при их перемещении в неоднородном магнитном поле, но и при быстром изменении этого поля. сплошное кольцо из алюминия, надетое на вертикальный сердечник электромагнита, питаемого переменным током частотой 50 Гц, висит в воздухе. в то время как такое же, но разрезанное кольцо свободно падает на обмотку. 

 

Рис. 8.27. Левитация сплошного проводящего кольца 

На рис. 8.28 показано взаимодействие проводника и электромагнита. Толстый медный диск укреплен в подшипниках на оси с ручкой. Вблизи него на такой же оси закреплен электромагнит. Если вращать за ручку включенный электромагнит, то диск начинает вращаться в ту же сторону. Если же, наоборот, вращать за ручку диск вблизи электромагнита, то последний также начинает вращаться. Силы взаимодействия диска и электромагнита, похожие по характеру на силы вязкого трения, обусловлены возникновением токов Фуко в диске.

 

Рис. 8.28. Взаимодействие проводника и электромагнита 

При перемещении сверхпроводника в магнитном поле возникающие в нем незатухающие токи Фуко не позволяют проникать вешнему полю внутрь него. Получается как бы зеркальное отражение магнита, отталкивающее его от сверхпроводника. На рис. 8.29 демонстрируется левитация маленького магнита над большой шайбой из высокотемпературного сверхпроводника (ВТСП-керамики), охлажденной до температуры жидкого азота (77 К), то есть ниже критической температуры перехода ВТСП-керамики в сверхпроводящее состояние. 

 

Рис. 8.29. Левитация маленького магнита над большой шайбой из высокотемпературного сверхпроводника (ВТСП-керамики) 

Видео 8.11. Зависание намагниченного ферромагнетика над сверхпроводником.

Тепловое действие токов Фуко используется в индукционных печах при плавке металла или приготовлении пищи. Такая печь, в сущности, является большой катушкой, питаемой высокочастотным током большой силы. Катушка создает переменный магнитный поток через помещенный в печь образец, а возникающие токи Фуко разогревают последний. 

На рис. 8.30 демонстрируется тепловое действие токов Фуко. Алюминиевое кольцо надевают на сердечник электромагнита, питаемого переменным током частотой 50 Гц, и некоторое время удерживают плоскогубцами в переменном магнитном поле. Затем кольцо опускают в воду, и она закипает, показывая, что кольцо разогрелось индукционными токами до высокой температуры. 

 

Рис. 8.30. Тепловое действие токов Фуко 

Видео 8.12. Кипячение воды индукционным током или основной способ нагрева плазмы в будущем термоядерном реакторе — токамаке.

 

Дополнительная информация

http://www.transformersonline.ru/trans/412/5/index.shtml — трансформаторы;

http://www.electrotrans.org/ — трансформаторы для аппаратуры;

http://principact.ru/content/view/65/108/1/2/ — трансформаторы, принцип работы;

http://electricalschool.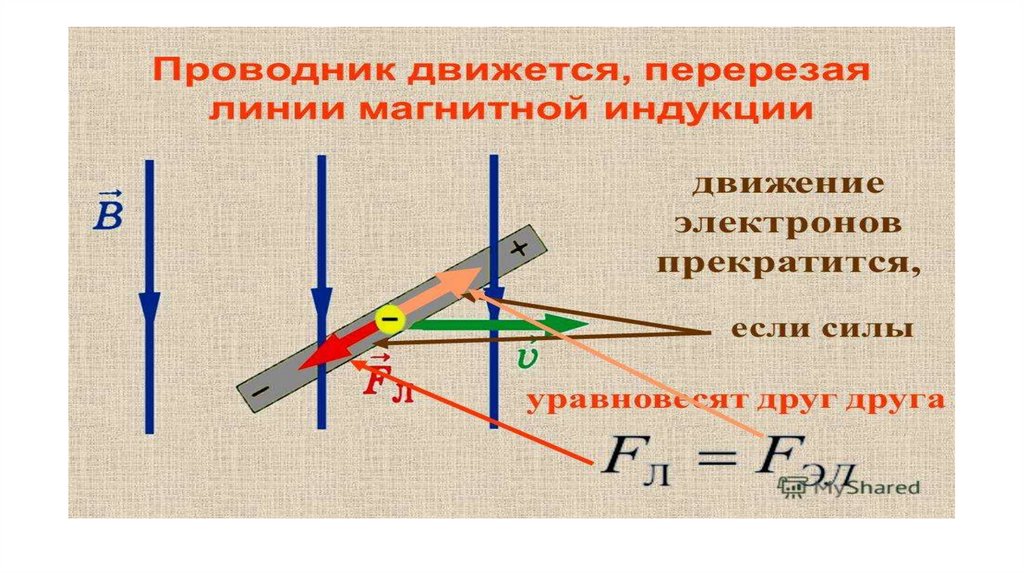 info/main/osnovy/532-vikhrevye-toki.html — вихревые токи;

http://374.ru/index.php?x=2007-10-09-61 — вихревые токи, изобретение микроволновой печи;

http://eletan.ru/index.php?newsid=168 — принцип работы индукционной плиты;

http://electricalschool.info/main/drugoe/235-indukcionnyjj-nagrev-i-indukcionnaja.html — индукционный нагрев, индукционная плавка металлов;

http://www.induction.kaboard.com/induction%20furnace%20-%20page-1.html — индукционные печи, плавка металлов;

http://www.reltec.biz/ru/txt_013.php — индукционные печи;

http://www.superconductors.org/ — сверхпроводники, все о сверхпроводимости;

http://www.chem.msu.su/rus/journals/xr/tretyak.html — химически сверхпроводники;

http://www.americanmagnetics.com/tutorial/supercon.html — сверхпроводимость;

http://www.physics.ubc.ca/~supercon/intro.html — кафедра сверхпроводимости университета UBC;

http://elementy.ru/lib/430825/430831 — сверхпроводимость, применение сверхпроводников;

http://nextbigfuture.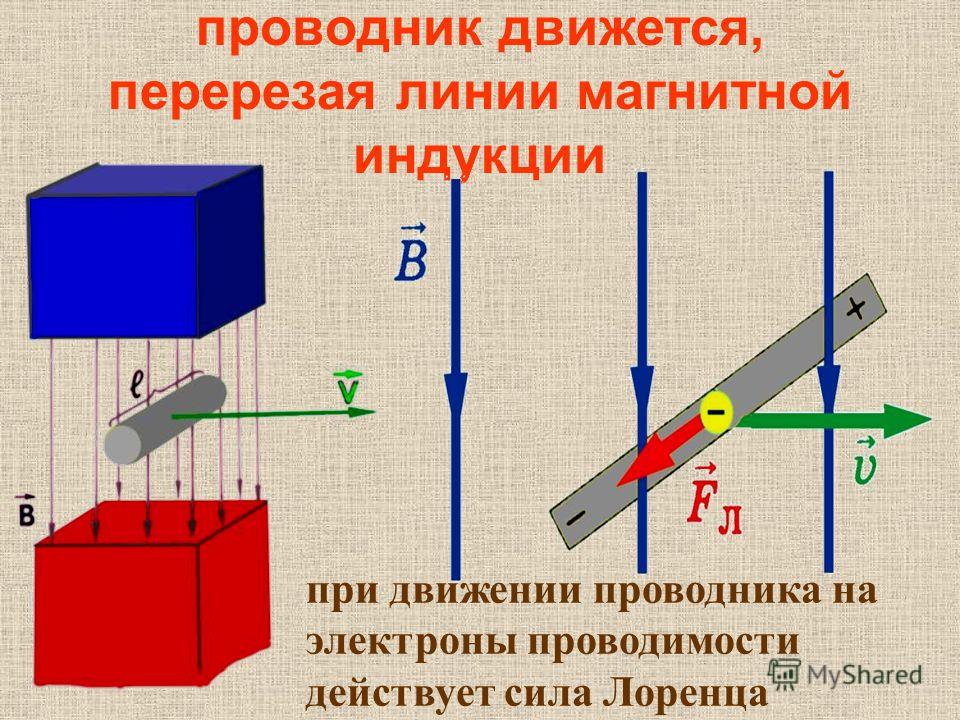 com/2010/03/high-temperature-superconductor-status.html — высокотемпературные сверхпроводники;

http://www.can-superconductors.com/ — ВТСП — керамики.

3/9

Объяснение урока: Движение прямых проводников в однородных магнитных полях

В этом объяснении мы узнаем, как связать разность потенциалов, индуцированную между прямыми проводниками, с их движением в однородных магнитных полях.

Рассмотрим прямой провод, движущийся через однородное магнитное поле, как показано ниже.

Поскольку этот провод является проводником, он содержит электроны, которые могут свободно перемещаться по проводу.

Когда провод движется в поле, на эти электроны действует магнитная сила.

Направление магнитной силы на электронах можно определить, вспомнив правило правой руки для направления магнитной силы на заряды, движущиеся в магнитном поле.

Правой рукой сначала определяем направление 𝑞𝑣, где 𝑞 — заряд рассматриваемой частицы, а 𝑣 — скорость частицы.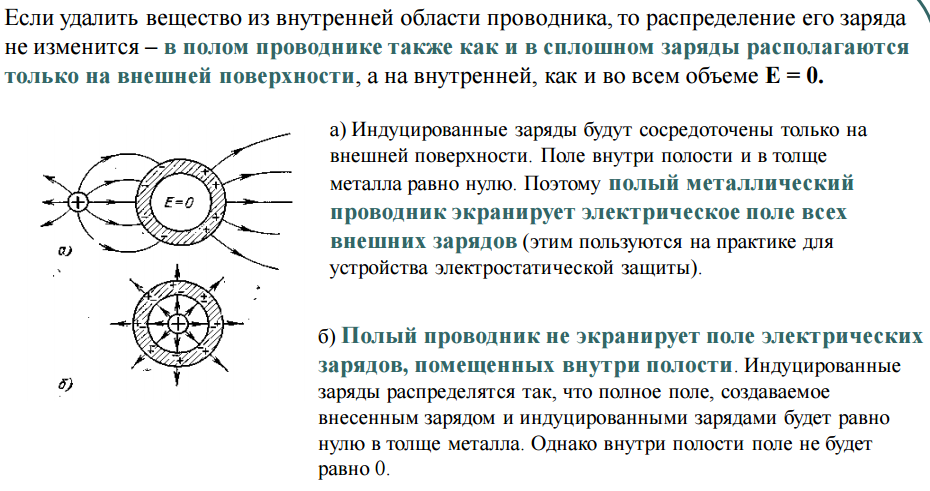

Поскольку электроны имеют отрицательный заряд, 𝑞𝑣 в данном случае указывает направление, противоположное направлению 𝑣. То есть в нашем проводе, который движется вправо, 𝑞𝑣 для электронов указывает налево.

Указываем пальцами правой руки в направлении 𝑞𝑣, как показано на следующем рисунке.

Следующий шаг в использовании правила правой руки — согнуть пальцы в направлении магнитного поля. В данном случае это поле указывает за пределы экрана.

Если наша правая рука сложена таким образом, большой палец будет указывать в направлении магнитной силы, действующей на заряженную частицу, как показано ниже.

Таким образом, электроны в проводе будут отталкиваться к вершине провода.

В целом, по мере движения провода отрицательный заряд будет концентрироваться в его верхней части, а положительный — внизу, как показано ниже.

Электрический потенциал вблизи концентрации отрицательного заряда более отрицателен, чем потенциал вблизи концентрации положительного заряда. Следовательно, на проводе устанавливается разность потенциалов.

Обратите внимание, что в этом сценарии магнитное поле направлено за пределы экрана, а скорость движения провода направлена ​​вправо. Следовательно, угол между этими двумя векторами равен 90∘.

Далее рассмотрим ситуацию, когда провод выходит за пределы экрана, как показано ниже.

Угол между скоростью проволоки и внешним полем теперь равен 0∘. Разность потенциалов на проводе не индуцируется.

Разность потенциалов измеряется в вольтах, как и величина, называемая электродвижущей силой. Эта «сила» представляет собой количество энергии, сообщаемой зарядам. Он обозначается как 𝜖 и математически описывается следующим образом.

Формула: Электродвижущая сила в прямом проводнике, движущемся в однородном магнитном поле

Если прямой проводник длиной 𝑙 движется со скоростью 𝑣 через однородное магнитное поле 𝐵 так, что угол между 𝐵 и 𝑣 равен 𝜃, то электродвижущая сила (𝜖), индуцируемая в проводнике, равна 𝜖=𝑙𝑣𝐵(𝜃). sin

Индуцированная электродвижущая сила (часто для краткости пишется «ЭДС») равна разности потенциалов, индуцированных на проводе, движущемся через однородное магнитное поле.

В этом уравнении 𝑙 — длина проводника, вдоль которого индуцируется ЭДС.

Пример 1. Определение напряженности поля и направления движения прямого проводника, движущегося в однородном магнитном поле

Проводящий стержень длиной 15 см имеет на себе разность потенциалов, как показано на диаграмме. Стержень движется в однородном магнитном поле со скоростью 0,32 м/с. Величина наведенной разности потенциалов составляет 9,6 мВ. Стержень движется в плоскости экрана.

  1. Какова сила магнитного поля?
  2. К какой стороне области, содержащей поле, движется стержень?

Ответ

Часть 1

Разность потенциалов, индуцированная на стержне, по величине равна электродвижущей силе (𝜖) на стержне. Эта «сила» определяется уравнением 𝜖=𝑙𝑣𝐵(𝜃). sin

Здесь 𝑙 — длина стержня, 𝑣 — его скорость, 𝐵 — напряженность магнитного поля, в котором движется стержень, а 𝜃 — угол между 𝑣 и 𝐵.

В этом сценарии мы ищем силу магнитного поля. Напряженность поля 𝐵 можно выделить с одной стороны приведенного выше уравнения, разделив обе части на 𝑙, 𝑣 и sin(𝜃): 𝐵=𝜖𝑙𝑣(𝜃).sin

Величина разности потенциалов, равная электродвижущей силе, составляет 9,6 мВ. Длина стержня 15 см, а его скорость 0,32 м/с. Стержень движется перпендикулярно магнитному полю, то есть 𝜃 равно 90∘.

Прежде чем подставлять эти значения и вычислять 𝐵, мы должны привести их единицы в соответствие друг с другом. Мы можем сделать это, переведя ЭДС из единиц милливольт в единицы вольт и длину из единиц сантиметров в единицы метров.

Мы знаем, что 1‎ ‎000 мВ равно 1 В, поэтому 9,6 мВ равно 0,0096 В.

Аналогично, 100 см равняется одному метру, поэтому 15 см равняется 0,15 м.

Теперь мы можем подставить наши преобразованные значения в уравнение для 𝐵: 𝐵=0,00960,15×0,32/×(90)=0,00960,15×0,32/=0,2. VmmssinVmmsT∘

Этот результат соответствует ответу D.

Часть 2

Направление движения стержня влияет магнитной силы, действующей на заряды в стержне.

Из диаграммы видно, что верхняя часть стержня имеет суммарный положительный заряд, а нижняя часть стержня имеет суммарный отрицательный заряд.

Таким образом, мы знаем, что стержень движется таким образом, что сила, действующая на свободные электроны, направлена ​​к нижней стороне области, содержащей магнитное поле.

Это направление силы задается правилом правой руки. Правило гласит, что если пальцы на правой руке указывают сначала в направлении 𝑞𝑣, где 𝑣 — скорость заряда 𝑞, а затем скручиваются в направлении внешнего магнитного поля 𝐵, большой палец этой руки указывает в направлении 𝑞𝑣. направление магнитной силы на заряд 𝑞.

Учитывая, что в этой ситуации сила на положительные заряды действует в направлении верхней стороны области, содержащей магнитное поле, а магнитное поле направлено за пределы экрана, мы можем использовать правило правой руки, чтобы определить направление движения стержня .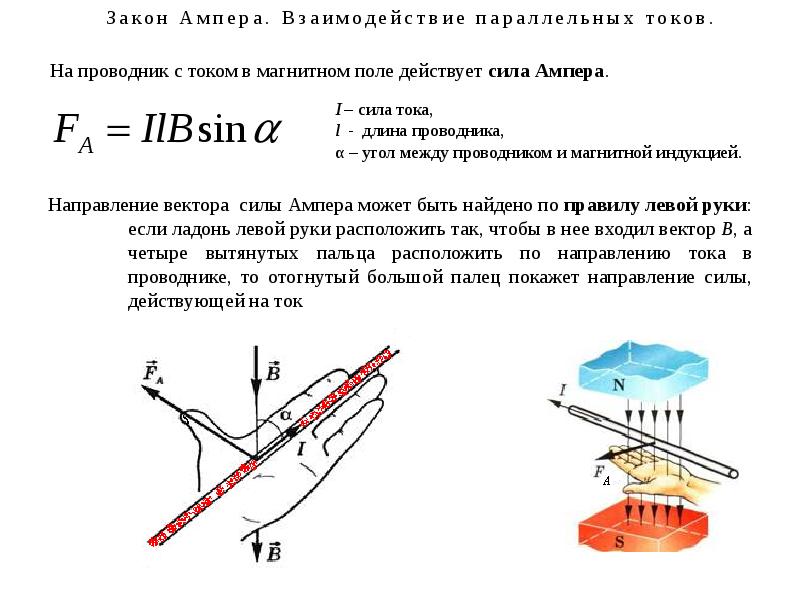

Когда большой палец правой руки направлен вверх, а согнутые пальцы направлены за пределы экрана, как показано на первом изображении ниже, мы видим, что единственное направление, в котором наши пальцы могут указывать, когда они выпрямлены, — это влево, как показано на второе изображение.

Это направление пальца показывает, что для того, чтобы положительные заряды испытывали направленную вверх силу, скорость стержня должна быть слева.

Следовательно, стержень движется к левой стороне области, содержащей поле.

Прямой проводник, движущийся в однородном магнитном поле, может быть частью замкнутой проводящей петли, как показано на следующем рисунке.

В этом сценарии разность потенциалов (или, что то же самое, ЭДС), индуцированная на движущемся проводнике, создает ток в цепи.

Мы видели, что индуцированная разность потенциалов определяется выражением 𝜖=𝑙𝑣𝐵(𝜃).sin

Когда эта разность потенциалов создает ток 𝐼 в цепи сопротивления 𝑅, закон Ома показывает, что 𝜖=𝐼𝑅.

Обратите внимание, что хотя индуцированный ток создает магнитное поле, это индуцированное поле обычно пренебрежимо мало по сравнению с однородным внешним полем 𝐵. Поэтому мы не учитываем его при расчетах 𝜖, 𝐼 или 𝑅.

Пример 2. Решение сопротивления прямого проводника, движущегося в однородном магнитном поле

Токопроводящий стержень движется по токопроводящим рельсам, образующим цепь, содержащую резистор, как показано на схеме. Стержень проходит полное расстояние поперек рельсов за время 36 с, двигаясь с постоянной скоростью. Магнитное поле вокруг контура имеет напряженность 275 мТл. Ток в цепи 32 мкА. Найдите сопротивление стержня с точностью до десятых.

Ответ

При движении стержня через магнитное поле разность потенциалов, определяемая уравнением 𝜖=𝑙𝑣𝐵(𝜃)грех будет индуцироваться через него. Подвижный стержень по существу функционирует как ячейка для показанной электрической цепи. Мы можем связать разность потенциалов 𝜖, ток цепи 𝐼 и полное сопротивление цепи 𝑅, используя закон Ома, следующим образом: 𝜖=𝐼𝑅.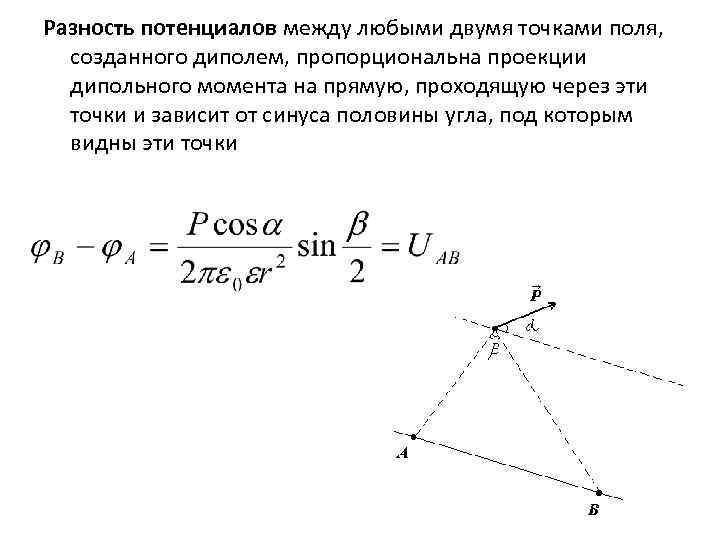

Общее сопротивление цепи 𝑅 состоит из сопротивления резистора (24 Ом) и сопротивления стержня. Обозначив сопротивление стержня 𝑅r, можно написать 𝑅=24+𝑅.Ωr

Следовательно, 𝜖=𝐼×(24+𝑅),Ωr или эквивалентно 𝑙𝑣𝐵(𝜃)=𝐼×(24+𝑅).sinΩr

Начнем решение для 𝑅r с перестановки приведенного выше уравнения так, чтобы 𝑅r было субъектом. Умножение текущего 𝐼 на правую часть уравнения дает нам 𝑙𝑣𝐵(𝜃)=𝐼×24+𝐼𝑅.sinΩr

Вычитая 𝐼×24 Ом с обеих сторон, а затем разделив обе части на 𝐼, находим 𝑅=𝑙𝑣𝐵(𝜃)−𝐼×24𝐼.rsinΩ

Длина стержня 𝑙 задана равной 9,5 см. Это равно 0,095 м.

Скорость стержня 𝑣 определяется выражением 𝑣=𝑑𝑡, где 𝑑 — расстояние, пройденное стержнем, а 𝑡 — время, затраченное на его перемещение. Стержень перемещается на 125 см за 36 с, что означает, что он имеет скорость 125 см за 36 с или 3,472… см/с. В метрах в секунду (м/с) скорость стержня составляет 0,0342… м/с.

Напряженность магнитного поля 𝐵 составляет 275 мТл. Поскольку в 1 Тл содержится 1 000 мТл, это равно 0,275 Тл9. 0003

Что касается угла 𝜃, стержень движется перпендикулярно полю, поэтому 𝜃 равен 90∘. Обратите внимание, что синус 90∘ равен 1.

Ток 𝐼 в цепи равен 32 мкА, или эквивалентно 3,2×10 А.

Подставляя все эти значения в наше уравнение для 𝑅r, мы находим 𝑅=(0,095)×(0,03472…/)×(0,275)×(1)−3,2×10×243,2×10=4,3474….rmmsTAΩAΩ

Округлив до одного десятичного знака, сопротивление стержень 4,3 Ом.

Несмотря на то, что разность потенциалов является скалярной величиной, тем не менее она индуцируется в определенном направлении. Как мы видели, это направление определяется с помощью правила правой руки.

Рассмотрим прямой проводник длиной 𝑙 и квадратным поперечным сечением шириной w, движущийся в однородном магнитном поле, как показано на следующей диаграмме.

Для положительных зарядов 𝑞𝑣 указывает вправо. Магнитное поле 𝐵 указывает на верхнюю часть экрана. По правилу правой руки магнитная сила, действующая на положительные заряды, направлена ​​за пределы экрана.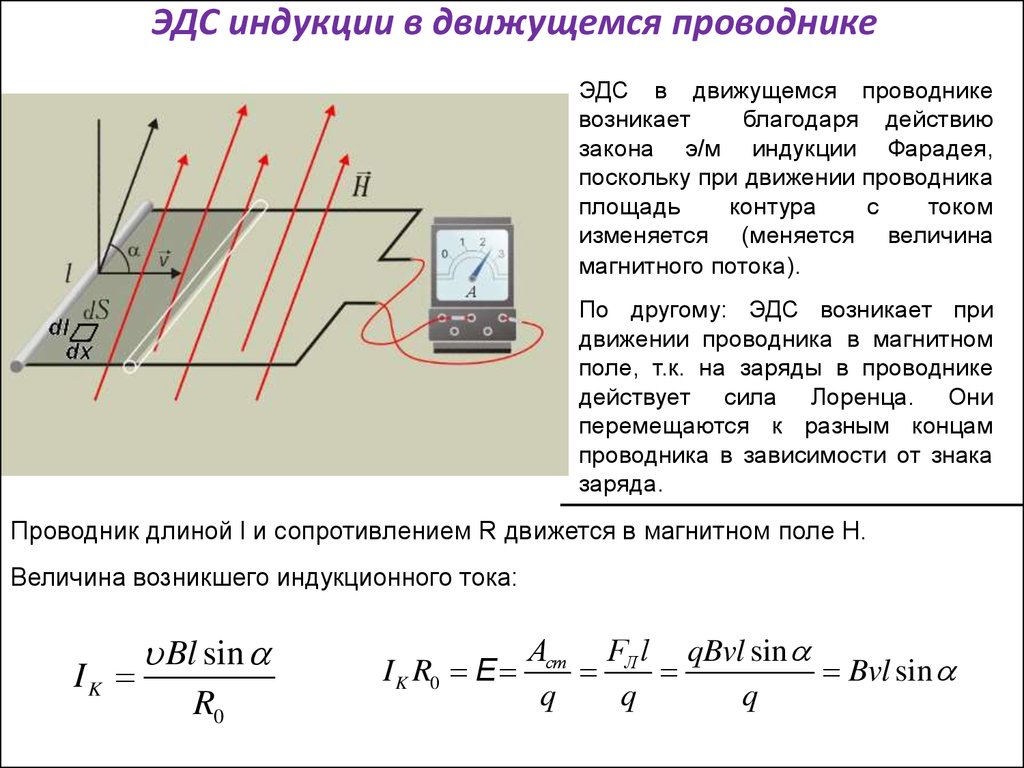

Следовательно, положительный заряд будет накапливаться на лицевой стороне проводника, а отрицательный – на обратной. Это показано на следующей диаграмме, где области чистого положительного заряда окрашены в красный цвет, а области чистого отрицательного заряда окрашены в синий цвет.

Хотя в этом проводнике индуцируется ЭДС, ее величина не равна 𝑙𝑣𝐵(𝜃)sin. Скорее, он равен 𝑤𝑣𝐵(𝜃)sin, где 𝑤 — длина проводника, по которому разделился заряд.

Пример 3. Вращение проводников в однородных магнитных полях

Проводящий стержень вращается, один конец которого неподвижен. Стержень равномерно вращается в однородном магнитном поле, причем направление вращения стержня относительно магнитного поля изменяется, как показано на диаграммах I, II, III и IV. Стержень вращается с одинаковой скоростью на каждой диаграмме.

  1. На какой из диаграмм значение величины разности потенциалов между закрепленным концом стержня и свободным концом стержня изменяется при вращении стержня?
  2. Равна ли величина разности потенциалов между закрепленным концом стержня и свободным концом стержня на схеме I величине разности потенциалов между закрепленным концом стержня и свободным концом стержня? на схеме II?
  3. Является ли величина разности потенциалов, индуцированной между закрепленным концом стержня и свободным концом стержня на диаграмме III, равна величине разности потенциалов, индуцированной между закрепленным концом стержня и свободным концом стержня? на схеме IV?
  4. Равна ли величина разности потенциалов между закрепленным концом стержня и свободным концом стержня на диаграмме I величине разности потенциалов между закрепленным концом стержня и свободным концом стержня? на схеме III?

Ответ

Часть 1

Рассматривая четыре диаграммы, начнем с диаграммы I.

Диаграмма I показывает вращающийся стержень в четыре момента. Мы можем обозначить эти позиции 0∘, 90∘, 180∘ и 270∘, как показано на рисунке ниже.

В каждом положении стержень имеет ненулевую среднюю скорость и движется в однородном магнитном поле вправо.

На следующем рисунке показаны эти средние скорости с соответствующими векторами магнитного поля.

Чтобы определить, индуцируется ли и в каком направлении разность потенциалов в стержне в любом из этих положений, воспользуемся правилом правой руки.

Это правило указывает, что направление действия магнитной силы на заряд 𝑞, движущийся со скоростью 𝑣 через магнитное поле 𝐵, можно определить следующим образом: пальцы правой руки указывают в направлении 𝑞𝑣, затем сгибаются в направление 𝐵. Направление, указанное большим пальцем правой руки, показывает направление магнитной силы, действующей на заряд.

Применяя это правило к четырем положениям стержня на рисунке выше, мы получаем результаты, показанные на следующем рисунке.

Обратите внимание, что во всех четырех положениях магнитная сила на положительный заряд никогда не действует по всей длине проводника. Положительные и отрицательные заряды по длине стержня не разделяются, поэтому разность потенциалов по длине стержня равна нулю.

Теперь рассмотрим стержень под некоторым произвольным углом поворота, отличным от углов, показанных выше. В таком произвольном положении вектор средней скорости стержня можно разделить на горизонтальную и вертикальную составляющие, как показано на рисунке ниже.

Для каждого компонента ЭДС индукции по длине стержня равна нулю. Поскольку угол тета на рисунке произвольный, ЭДС индукции по длине стержня на схеме I равна нулю во всех положениях.

Далее рассмотрим схему II. Обратите внимание, что единственная разница между диаграммой II и диаграммой I заключается в том, что диаграмма II повернута на 90° относительно диаграммы I против часовой стрелки.

Следовательно, на диаграмме II по длине стержня также не индуцируется разность потенциалов.

На диаграмме III магнитное поле указывает на экран. Следовательно, векторы скорости и соответствующие векторы магнитного поля выглядят так, как показано на следующем рисунке.

Опять же, используя правило правой руки для определения направления магнитной силы на положительном заряде в каждой позиции, мы находим результаты ниже, где красные стрелки указывают векторы силы на положительном заряде.

На диаграмме III положительный заряд отталкивается к оси вращения стержня, что означает, что отрицательный заряд отталкивается к свободному концу стержня. Поэтому разделение заряда происходит по длине стержня.

В результате по всей длине стержня индуцируется разность потенциалов.

Вспомним, однако, что нас просят определить диаграммы, где наведенная разность потенциалов вдоль стержня изменяется.

Для сценария, показанного на диаграмме III, индуцированная разность потенциалов вдоль стержня отлична от нуля, но также постоянна — она не меняется при вращении стержня.

Наконец, рассмотрим ситуацию, изображенную на диаграмме IV.

Этот сценарий идентичен сценарию, показанному на диаграмме III, за исключением того, что магнитное поле теперь направлено за пределы экрана, а не внутрь него.

Результатом этой разницы является то, что в сценарии, показанном на диаграмме IV, положительный заряд выталкивается к свободному концу стержня, а отрицательный заряд выталкивается к его закрепленному концу.

По длине стержня индуцируется ненулевая разность потенциалов.

Однако, как и в ситуации, показанной на диаграмме III, эта разность потенциалов не меняется при вращении стержня.

Наш ответ на часть 1 вопроса заключается в том, что ни на одной из диаграмм не показаны сценарии, в которых разность потенциалов, индуцированная по длине стержня, изменяется.

Часть 2

Возвращаясь к нашему анализу в части 1, мы помним, что на диаграммах I и II наведенная разность потенциалов по длине стержня равна нулю. Следовательно, верно, что эти значения равны.

Часть 3

В сценарии, показанном на диаграмме III, положительный заряд накапливается в направлении фиксированного конца стержня, а отрицательный заряд накапливается в направлении его свободного конца, как показано на следующем рисунке.

Величина индуцированной разности потенциалов определяется уравнением 𝜖=𝑙𝑣𝐵(𝜃),грех где 𝑙 — длина проводника, 𝑣 — его скорость, 𝐵 — напряженность магнитного поля, 𝜃 — угол между 𝐵 и 𝑣.

Мы должны сравнить эту величину с величиной ЭДС, индуцированной в сценарии, показанном на диаграмме IV. В этой ситуации положительные и отрицательные заряды накапливаются, как показано ниже.

Полярность индуцированной разности потенциалов противоположна сценарию на диаграмме III. Обратите внимание, однако, что ни одно из значений, влияющих на величину индуцированной разности потенциалов — 𝑙, 𝑣, 𝐵 и 𝜃 — не изменилось.

Следовательно, величина разности потенциалов, индуцированной по длине стержня, одинакова в сценариях, изображенных на диаграммах III и IV.

Часть 4

Мы видели, что на диаграмме I показана ситуация, когда наведенная разность потенциалов между концами стержня равна нулю.

Напротив, на стержне, показанном на диаграмме III, индуцируется ненулевая разность потенциалов. Следовательно, эти величины не равны.

Когда проводник движется в однородном магнитном поле, его движение может быть скорее периодическим, чем постоянным.

Рассмотрим показанный ниже проводник, расположенный в однородном магнитном поле.

Мы можем изменить угол обзора, посмотреть на проводник с одного из его концов и увидеть, что проводник движется по кругу, как показано ниже.

При движении проводника угол между вектором скорости проводника и внешним магнитным полем изменяется.

В местах, отмеченных 1, 2, 3 и 4, этот угол 𝜃, измеренный от вектора магнитного поля до вектора скорости проводника, имеет значения 90°, 0°, 270° и 180°, как показано ниже .

Вспоминая, что электродвижущая сила, индуцируемая в проводнике, определяется выражением 𝜖=𝑙𝑣𝐵(𝜃),грех заметим, что эта величина зависит от синуса угла 𝜃. Следовательно, ЭДС, индуцируемая в этом проводнике, движущемся по кругу, имеет синусоидальный характер, как показано на следующем рисунке.

Пример 4. Изменение разности потенциалов во времени в прямом проводнике, движущемся через однородное магнитное поле перпендикулярно длине стержня на протяжении всего движения. Когда стержень находится в положениях А и С, показанных на схеме, направление кругового движения совпадает с линией направления магнитного поля. Когда стержень находится в положениях B и D, показанных на схеме, направление кругового движения перпендикулярно линии направления магнитного поля. На графике показаны линии четырех разных цветов. Каждая линия может отображать изменение разности потенциалов по длине стержня по мере его перемещения от A к B, затем к C, затем к D и обратно к A. Какой цвет линии правильно отражает изменение разности потенциалов со временем?

  1. Синяя линия
  2. Оранжевая линия
  3. Красная линия
  4. Зеленая линия
  5. Ни один из ответов не является правильным.

Ответ

Изучая схему проводника, движущегося через поле, мы видим, что он движется по окружности в плоскости, параллельной магнитному полю.

Если 𝜃 угол между полем и вектором скорости проводника, 𝜃 постоянно меняется. В частности, в точках, отмеченных A, B, C и D, 𝜃 имеет соответствующие значения 0 ∘, 270 ∘, 180 ∘ и 90∘, как показано ниже.

В общем случае разность потенциалов, индуцируемая в прямом проводнике, движущемся в однородном магнитном поле, описывается уравнением 𝜖=𝑙𝑣𝐵(𝜃).sin

В нашем сценарии 𝜃 меняется, и это уравнение показывает, что это происходит синусоидально.

Мы можем заключить, что индуцированная в проводнике разность потенциалов не является постоянной во времени, а также что индуцированная в проводнике разность потенциалов изменяется в соответствии с формой функции синуса.

Анализируя наши ответы, ответ C — красная кривая — показывает, что разность потенциалов меняется со временем, как это было бы в нашем движущемся проводнике.

Ключевые моменты

  • Для прямого проводника, движущегося в однородном магнитном поле, индуцируется электродвижущая сила (ЭДС), эквивалентная разности потенциалов, согласно уравнению 𝜖=𝑙𝑣𝐵(𝜃)sin, где 𝜖 — ЭДС индукции, 𝑙 — длина проводника, 𝑣 — его скорость, 𝐵 — напряженность внешнего магнитного поля, 𝜃 — угол между 𝑣 и 𝐵.
  • Когда прямой проводник, движущийся в однородном магнитном поле, является частью замкнутой электрической цепи, проводник вызывает протекание заряда по цепи. Разность потенциалов 𝜖, ток цепи 𝐼 и сопротивление цепи 𝑅 связаны законом Ома: 𝜖=𝐼𝑅.
  • Когда проводник периодически движется через однородное магнитное поле, 𝜃 может постоянно изменяться, в результате чего индуцированная ЭДС имеет синусоидальный характер.
Индуцированный потенциал

: значение, пример и формула

Вы когда-нибудь задумывались, как работают динамо-машины и генераторы? Как вы, возможно, уже знаете, моторный эффект вызывает движение провода с током через магнитное поле. Интересно, что это также происходит и наоборот: движение проводящего провода в магнитном поле индуцирует потенциал, который заставляет ток течь по проводу! Узнайте об основах индуцированного потенциала в этой статье.

Прежде чем читать эту статью, мы рекомендуем вам убедиться в том, что вы понимаете эффект двигателя. Это сделает наведенные потенциалы намного проще!

Значение индуцированного потенциала

Когда проводник движется через магнитное поле или когда неподвижный проводник находится в движущемся магнитном поле, проводник видит движущееся магнитное поле. Это вызывает (индуцирует) разность потенциалов между концами проводника.

Индуцированная потенция l (разность) – это разность потенциалов между концами проводника, вызванная движущимся вокруг проводника магнитным полем.

Наведенный потенциал в проводе

Когда провод является проводником и является частью полной электрической цепи, наведенный потенциал вызывает протекание тока по проводу.

Индуцированный ток — это любой ток, возникающий в результате индуцированного потенциала.

Это наиболее распространенный способ получения электричества из других источников энергии: кинетическая энергия магнита вызывает изменяющееся магнитное поле, которое индуцирует ток в проводе. Это основное объяснение того, как работают генераторы и динамо-машины.

Создание индуцированного тока называется генераторным эффектом или ( электромагнитным) индукцией .

Генератор, использующий эффект генератора для индукции тока, Wikimedia Commons CC BY-SA 4.0.

На рисунке выше генератор используется для выработки тока и питания небольшой лампочки. Он состоит из проволочной петли, которая перемещается относительно неподвижного постоянного магнита. В проводящей петле индуцируется разность потенциалов, а значит, и ток. Затем ток используется для питания лампочки.

Принцип индуцированных токов

Индуцированный ток, протекающий по проводнику, создает собственное магнитное поле, которое будет взаимодействовать с первоначальным магнитным полем. Это взаимодействие будет всегда таким, что моторное воздействие на проволоку создаст силу, направленную против движения проволоки.

Наведенный ток всегда имеет такое направление, что моторный эффект уменьшает скорость между проводом и магнитным полем.

Вы можете вспомнить это, думая о кинетической энергии системы, преобразуемой в энергию, переносимую током. Если бы индукционный ток шел в другую сторону, у вас был бы способ получать энергию из ничего, что невозможно.

Факторы, влияющие на индуцированный потенциал

Единственным фактором, влияющим на величину индуцированной разности потенциалов и, следовательно, на индуцированный ток, является количество силовых линий магнитного поля, с которыми сталкивается провод в единицу времени. В свою очередь, факторами, влияющими на это, являются:

  1. напряженность магнитного поля и
  2. скорость движения магнита по сравнению с проводом (или наоборот, помните, что эти ситуации эквивалентны).

Первый фактор приведет к более высокой «плотности» силовых линий магнитного поля, а второй фактор приведет к пересечению магнитных силовых линий с большей скоростью. И то, и другое приведет к тому, что провод столкнется с большим количеством силовых линий магнитного поля.

Формула наведенного потенциала

Хотя это выходит за рамки экзаменов GCSE, мы можем сделать эти утверждения более количественными.

Индуцированный ток через проводящий провод прямо пропорционален количеству силовых линий магнитного поля, которые он встречает в единицу времени, поэтому:

индуцированный ток = постоянная × напряженность магнитного поля × скорость провода.

Это уравнение делает более ясным, что магнит1, который в два раза сильнее, чем магнит2, будет индуцировать ток в два раза больше, чем магнит2, если остальная часть установки такая же. Это также дает понять, что удвоение скорости провода удваивает индукционный ток через него в любой данной ситуации. Обратите внимание, что это сформулированное уравнение говорит нам только о том, насколько велик индукционный ток до константы, поэтому оно ничего не говорит о направлениях вовлеченных величин, и вместо этого мы можем делать только относительные утверждения (удвоение этого значения удваивает это и т. д.) абсолютных утверждений (напряженность магнитного поля той и той скорости будет индуцировать этот ток и т. д.).

Примеры индуцированных потенциалов

Есть несколько очень поучительных примеров индуцированных разностей потенциалов и их индуцированных токов.

Подковообразный магнит и проволока

Простой пример подковообразного магнита и проволоки может быть поучительным. На рисунке ниже показан подковообразный магнит, северный полюс которого находится над южным полюсом, а проводящий провод лежит горизонтально между полюсами магнита. Если мы потянем провод к себе, то возникнет индукционный ток, и провод будет сопротивляться нашему натяжению. Таким образом, двигательный эффект вызывает силу, удаляющуюся от нас. Мы выбираем наше любимое правило руки и заключаем, что индуцированный ток течет слева направо.

Если вытащить провод из этого подковообразного магнита, по проводу будет индуцироваться ток слева направо, Арьян ван Дензен — StudySmarter Originals.

Стержневой магнит и катушка

Стержневой магнит также может индуцировать ток в спиральном проводе, см. рисунок ниже. Вверху мы видим, что мы перемещаем южный полюс ближе к катушке, поэтому катушка хочет остановить это движение и создать южный полюс ближе к магниту. Катушка делает это, производя индуцированный ток, и правило правой руки говорит нам, что амперметр измеряет ток вправо, как показано. Внизу мы видим, что мы отодвигаем северный полюс дальше от катушки, что имеет тот же эффект, что и перемещение южного полюса ближе к катушке: магнитное поле изменяется точно так же. Поэтому измеряем ток в том же направлении, что и сверху.

Движение магнита индуцирует ток в цепи в направлении стрелки, адаптировано из изображения Aaronming CC BY 4.