Тест
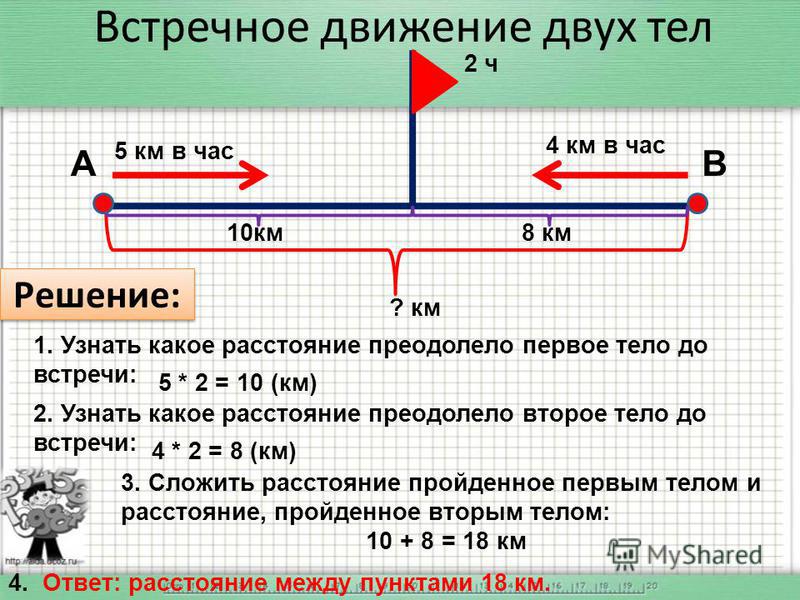
Задача 1.2.1. Два автомобиля движутся по прямому шоссе, направленному с севера на юг. Первый автомобиль движется на юг со скоростью , второй — на север со скоростью . Чему равна скорость второго автомобиля относительно первого?
|
, направлена на юг |
, направлена на север |
|
, направлена на юг |
, направлена на север |
Задача 1.2.2.Скорость лодки в стоячей воде 10 км/ч, скорость течения — 5 км/ч. Во сколько раз время движения между двумя городами, расположенными на берегу реки, вниз по течению меньше времени движения между этими городами вверх по течению?
|
В 2 раза |
В 3 раза |
|
В 4 раза |
В 5 раз |
Задача 1. 2.3.Два тела одновременно начинают равномерно двигаться из одной точки по одной и той же окружности радиусом . Скорости тел направлены противоположно и одна из них в три раза больше другой. На каком расстоянии от начальной точки произойдет первая встреча тел?
2.3.Два тела одновременно начинают равномерно двигаться из одной точки по одной и той же окружности радиусом . Скорости тел направлены противоположно и одна из них в три раза больше другой. На каком расстоянии от начальной точки произойдет первая встреча тел?
Задача 1.2.4.Два тела находятся на расстоянии друг от друга. Тела одновременно начинают двигаться навстречу друг другу с постоянными скоростями и . Через какое время произойдет встреча тел?
Задача 1.2.5.Первый пешеход проходит расстояние между пунктами А и В за время 4 ч, второй — за время 2 ч. Через какое время после выхода встретятся пешеходы, если выйдут одновременно навстречу друг другу из пунктов А и В?
|
4/3 ч |
|
2 ч |
7/3 ч |
Задача 1.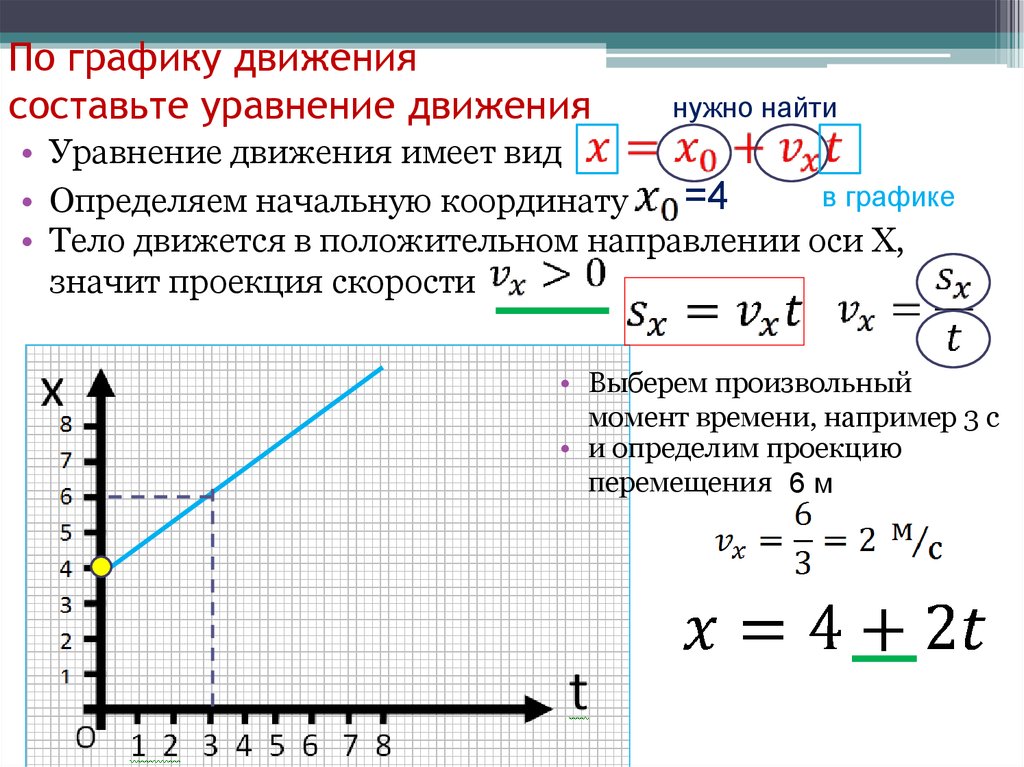 2.6. Вагон длиной движется равномерно со скоростью . Провожающий бежит со скоростью ( > ). На какое расстояние переместится провожающий, пробежав вдоль всего вагона (начальное положение вагона и провожающего показано на рисунке)?
2.6. Вагон длиной движется равномерно со скоростью . Провожающий бежит со скоростью ( > ). На какое расстояние переместится провожающий, пробежав вдоль всего вагона (начальное положение вагона и провожающего показано на рисунке)?
Задача 1.2.7. Автомобиль движется между городами А и В. Первую половину пути автомобиль прошел с постоянной скоростью 40 км/ч, вторую — с постоянной скоростью 60 км/ч. Чему равна средняя скорость автомобиля на всем пути?
|
50 км/ч |
51 км/ч |
48 км/ч |
52 км/ч |
Задача 1.2.8. Поезд едет со скоростью . В поезде перпендикулярно направлению его движения идет человек со скоростью . Чему равна скорость человека относительно земли?
В поезде перпендикулярно направлению его движения идет человек со скоростью . Чему равна скорость человека относительно земли?
Задача 1.2.9. Лодка пересекает реку. Под каким углом к берегу расположена траектория, на переправу по которой затрачи-вается минимальное время (см. рисунок)? Скорость лодки относительно воды и скорость течения равны соответственно и .
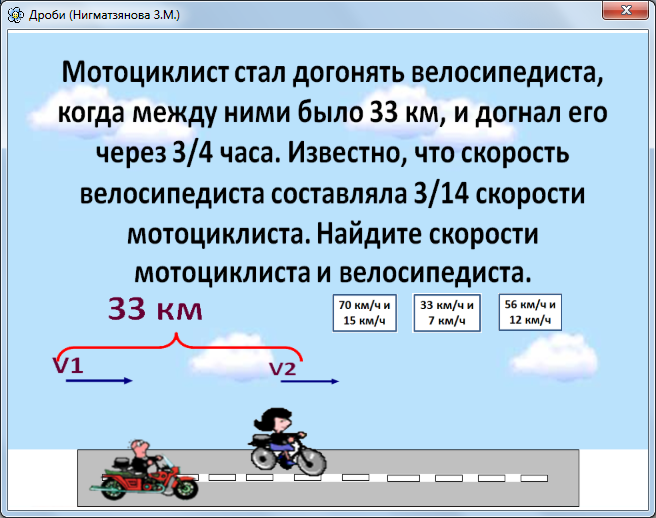
Задача 1.2.10. Два катера, идущие вниз по реке с разными скоростями, одновременно обогнали плывущий по течению плот. Затем через одно и то же время катера повернули назад и поплыли с прежними относительно воды скоростями. Какой из катеров — быстрый или медленный — раньше встретит плот?
Быстрый
Медленный
Одновременно
Мало информации для ответа
Относительность механического движения | СПАДИЛО
Под относительностью понимают зависимость чего-либо от выбора системы отсчета. Так, покой и движение тела, его положение в пространстве всегда относительны. Человек, сидящий внутри движущегося автомобиля, покоится относительно этого автомобиля. Но относительно предметов снаружи он движется с некоторой скоростью.
Так, покой и движение тела, его положение в пространстве всегда относительны. Человек, сидящий внутри движущегося автомобиля, покоится относительно этого автомобиля. Но относительно предметов снаружи он движется с некоторой скоростью.
Относительность перемещения
Пусть движение материальной точки (МТ) описывается относительно двух систем отсчета: подвижной (ПСО) и неподвижной (НСО). Зная, как эта точка движется относительно ПСО, и, как ПСО движется относительно НСО, можно вычислить перемещение точки относительно НСО. В этом заключается правило сложения перемещений:
s′ = s1 + s2
s′ — перемещение МТ относительно НСО, s1— перемещение МТ относительно ПСО, s2 — перемещение ПСО относительно НСО.
Чтобы применять правило сложения перемещений, нужно уметь складывать вектора.
Полезные факты- Если тело движется в направлении движения ПСО, то модуль его перемещения относительно НСО равен сумме модулей перемещения этого тела относительно ПСО и перемещения ПСО относительно НСО:
s′ = s1 + s2
- Если тело движется противоположно движению ПСО, то модуль его перемещения относительно НСО равен разности модулей перемещения этого тела относительно ПСО и перемещения ПСО относительно НСО:
s′ = s1 – s2
- Если тело движется под прямым углом по отношению к направлению движения ПСО, то модуль его перемещения относительно НСО равен корню из суммы квадратов перемещений этого тела относительно ПСО и перемещения ПСО относительно НСО:
s′ = √(s12 + s22)
- Если относительно ПСО тело покоится, то его перемещение относительно НСО равно перемещению ПСО относительно НСО: при s1=0, перемещение s′ = s2
- Если тело движется относительно двух НСО, то его перемещение относительно НСО1 равно перемещению движения относительно НСО2.

Пример №1. Человек прошел в автобусе 2 метра в направлении заднего выхода. За это же время автобус успел переместиться относительно остановки на 10 м. Найти перемещение человека относительно автобусной остановки.
Так как человек двигался в сторону конца автобуса, он двигался противоположно его движению. В этом случае его перемещение будет равно модулю разности перемещений, совершенных человеком относительно автобуса и автобусом относительно остановки:
s′=|s1 – s2|=|10 – 2|=8 (м).
Относительность скорости в ПСО и НСО
Тела и системы отсчета могут двигаться с различной скоростью. Но, зная скорость движения МТ относительно ПСО и скорость движения ПСО относительно НСО, можно вычислить скорость движения МТ относительно НСО. В этом заключается правило сложения скоростей:
В этом заключается правило сложения скоростей:
v′ = v + u
v′ — скорость МТ относительно НСО, v — скорость МТ относительно ПСО, u — скорость движения ПСО относительно НСО.
Складывая векторы скоростей, нужно пользоваться правилами сложения векторов.
Полезные факты- Если тело движется в направлении движения ПСО, то модуль его скорости относительно НСО равен сумме модулей скорости этого тела относительно ПСО и скорости ПСО относительно НСО:
v′ = v + u
- Если тело движется противоположно движению ПСО, то модуль его скорости относительно НСО равен разности модуля скорости этого тела относительно ПСО и скорости ПСО относительно НСО:
v′ = v – u
- Если тело движется под прямым углом по отношению к направлению движения ПСО, то модуль его скорости относительно НСО равен корню из суммы квадратов скорости этого тела относительно ПСО и скорости ПСО относительно НСО:
v′ = √(v2 + u2)
- Если относительно ПСО тело покоится, то его скорость относительно НСО равна скорости ПСО относительно НСО: при v=0, скорость v′ = u
- Если тело движется относительно двух НСО, то его скорость относительно НСО1 равна скорости движения относительно НСО2.
 В этом случае одну из неподвижных систем можно принять за ПСО с нулевой скоростью. При u=0, скорость v′ = u
В этом случае одну из неподвижных систем можно принять за ПСО с нулевой скоростью. При u=0, скорость v′ = u
Пример №2. Моторная лодка должна пересечь реку, скорость течения которой равна 5 км/ч, по кратчайшему пути. Собственная скорость лодки равна 10 км/ч. Определить, под каким углом к берегу должна быть направлена лодка, чтобы она не отклонялась от кратчайшего пути.
Кратчайшим путем между двумя параллельными линиями является отрезок, заключенный между этими линиями при условии, что он лежит на прямой, пересекающей эти линии под прямым углом. На рисунке этот путь отметим отрезком АВ.
Лодка движется прямолинейно. Поэтому направление ее скорости относительно берега совпадает с направлением перемещения:
Векторы скоростей образуют прямоугольный треугольник, и собственная скорость лодки направлена к берегу под некоторым углом α. Косинус этого угла равен отношению прилегающего катета (скорости лодки относительно реки) к гипотенузе (скорости течения реки):
Косинусу 0,5 соответствует угол, равный 60 градусам.
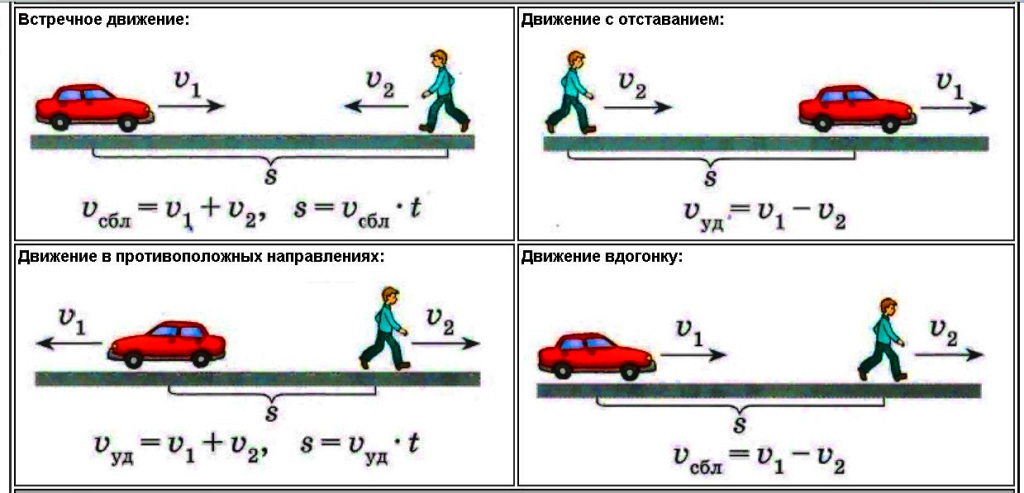
Относительная скорость двух тел
Понятие относительной скорости вводится, когда рассматривается движение двух тел относительно друг друга внутри одной и той же системы отсчета (СО). Примером служат два движущихся автомобиля, в то время как их движение рассматривается относительно неподвижного объекта.
Относительная скорость равна векторной разности скоростей первого и второго тела относительно СО:
vотн = v1– v2
vотн — относительная скорость, или скорость первого тела относительно второго, v1 и v2 — скорость первого и второго тела относительно СО.
Варианты обозначения относительной скорости и их проекций:
- v12 — скорость первого тела относительно второго. Ее проекция равна:
v12x = v1x – v2x
- v21 — скорость второго тела относительно первого.
 Ее проекция равна v21x = v2x – v1x
Ее проекция равна v21x = v2x – v1x
Для вычисления относительной скорости движения тела важно уметь применять правила вычитания векторов.
Полезные факты- Если тела движутся в одном направлении, то относительная скорость равна модулю разности скоростей первого и второго тела:
vотн = |v1 – v2|
- Если тела движутся в противоположных направлениях, то относительная скорость равна сумме скоростей первого и второго тела:
vотн = |v1 + v2|
- Если тела движутся взаимно перпендикулярно, то относительная скорость равна корню из суммы квадратов скоростей первого и второго тела:
vотн = √(v12 + v22)
Пример №3. Два автомобиля движутся противоположно друг другу. Скорость первого автомобиля относительно дороги равна 100 км/ч. Скорость второго автомобиля относительно первого равна 180 км/ч. Найти модуль скорости второго автомобиля относительно дороги.
Скорость первого автомобиля относительно дороги равна 100 км/ч. Скорость второго автомобиля относительно первого равна 180 км/ч. Найти модуль скорости второго автомобиля относительно дороги.
Так как автомобили движутся в противоположном направлении, относительная скорость равна сумме скоростей первого и второго автомобиля. Поэтому скорость второго равна разности относительной скорости и скорости движения второго тела, которым в данном случае является первый автомобиль:
Скорость второго автомобиля относительно дороги равна 80 км/час.
Правила сложения векторов
Эта таблица иллюстрирует правила сложения векторов на примере векторов a и b. Результатом их сложения является вектор c .
| Сложение двух сонаправленных векторов | |
Суммой двух сонаправленных векторов является вектор, направленный в ту же сторону.
Его длина равна сумме длин слагаемых векторов: c = a + b.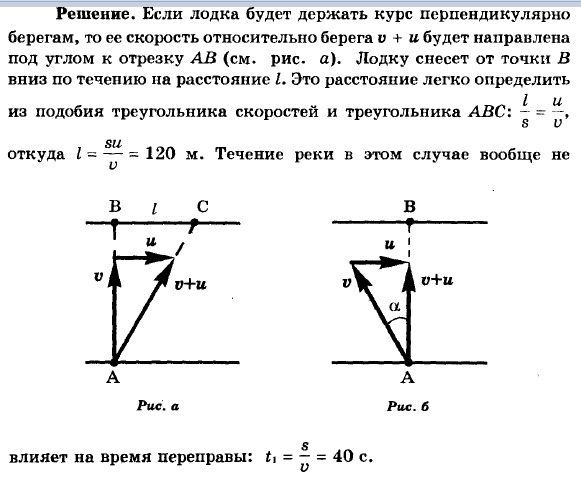 | |
| Сложение двух противоположно направленных векторов | |
| Суммой двух противоположно направленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин слагаемых векторов: c = |a – b|. | |
| Сложение двух векторов, расположенных друг к другу под углом | |
| Суммой двух векторов, расположенных друг к другу под углом является вектор, направление которого определяется графически методом треугольника или параллелограмма. Его длина зависит от величины угла, под которым расположены два слагаемых векторов. | |
| Если слагаемые векторы перпендикулярны, для вычисления длины вектора их суммы используется теорема Пифагора: . | |
Если слагаемые векторы расположены под тупым углом α, для вычисления длины вектора их суммы используется теорема косинусов:
. | |
| Если слагаемые векторы расположены под острым углом α, для вычисления длины вектора их суммы используется теорема косинусов: . | |
Правила вычитания векторов
Эта таблица иллюстрирует правила вычитания векторов на примере векторов Результатом их вычитания является вектор .
| Вычитание двух сонаправленных векторов | |
| Разностью двух сонаправленных векторов является вектор, направленный в сторону большего по модулю вектора. Его длина равна модулю разности длин вычитаемых векторов: c = |a – b|. | |
| Вычитание двух противоположно направленных векторов | |
| Разность двух противоположно направленных векторов есть вектор, направленный в сторону уменьшаемого вектора. Его длина равна сумме длин вычитаемых векторов: c = a + b. | |
| Вычитание двух векторов, расположенных друг к другу под углом | |
Разностью двух векторов, расположенных друг к другу под углом является вектор, являющийся обратным вектору, образующемуся при сложении этих векторов. Его направление определяется графически. Его длина зависит от величины угла, под которым расположены два слагаемых векторов. Его направление определяется графически. Его длина зависит от величины угла, под которым расположены два слагаемых векторов. | |
| Если вычитаемые векторы перпендикулярны, для вычисления длины вектора их разности используется теорема Пифагора: . | |
| Если вычитаемые векторы расположены под углом α, для вычисления длины вектора их разности используется теорема косинусов: . | |
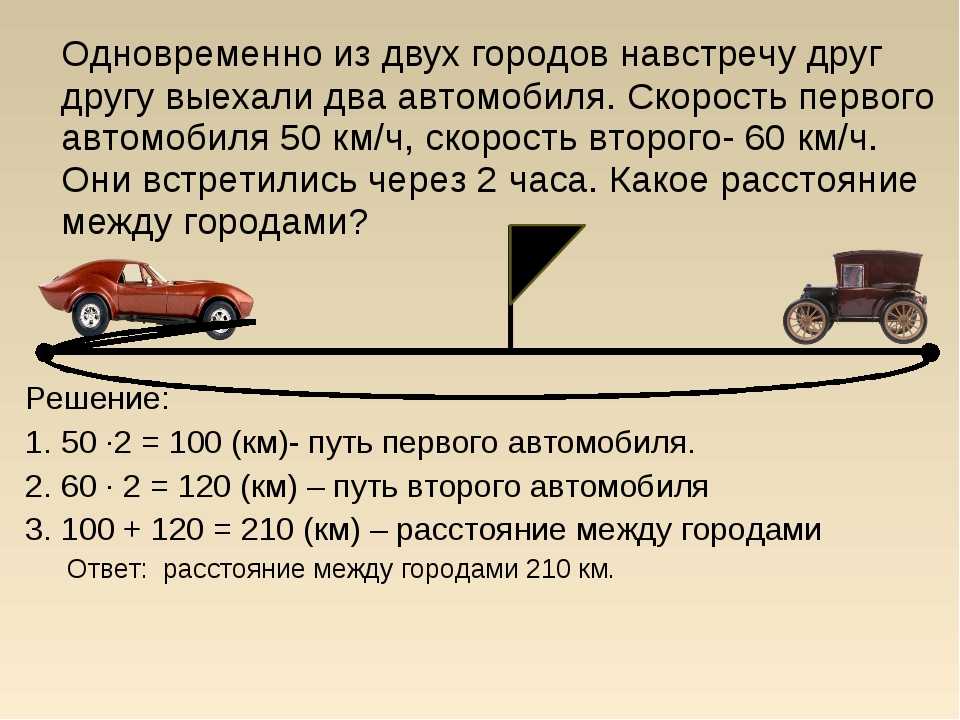
Два автомобиля движутся по прямому шоссе, первый — со скоростью v, второй — со скоростью –4v. Найти скорость второго автомобиля относительно первого.
Алгоритм решения
- Записать данные в определенной системе отсчета.
- Изобразить графическую модель ситуации задачи.
- Записать классический закон сложения скоростей в векторном виде.
- Записать классический закон сложения скоростей в векторном виде применительно к условиям задачи.

- Найти искомую величину.
Решение
Записываем данные относительно Земли:
- Скорость первого автомобиля относительно оси ОХ: v1 = v.
- Скорость второго автомобиля относительно оси ОХ: v2 = –4v.
Изображаем графическую модель ситуации. Так как у второго автомобиля перед вектором скорости стоит знак «–», первый и второй автомобили движутся во взаимно противоположных направлениях.
Записываем закон сложения скоростей в векторном виде:
v′ = v + u
v′ — скорость второго автомобиля относительно оси ОХ (v2), v — скорость второго автомобиля относительно системы отсчета, связанной с первым автомобилем, u — скорость движения первого автомобиля относительно оси ОХ (v1).
Закон сложения скоростей в векторном виде применительно к условиям задачи будет выглядеть так:
v2 = v + v1
Отсюда:
v = v2 — v1 = –4v – v = –5v
Ответ: -5vpазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17518 Два автомобиля движутся в одном направлении. Относительно Земли скорость первого автомобиля 110 км/ч, второго 60 км/ч. Чему равен модуль скорости первого автомобиля в системе отсчёта, связанной со вторым автомобилем?
Относительно Земли скорость первого автомобиля 110 км/ч, второго 60 км/ч. Чему равен модуль скорости первого автомобиля в системе отсчёта, связанной со вторым автомобилем?Алгоритм решения
- Записать данные в определенной системе отсчета.
- Изобразить графическую модель ситуации задачи.
- Записать классический закон сложения скоростей в векторном виде.
- Выбрать систему отсчета.
- Записать классический закон сложения скоростей в скалярном виде.
- Найти искомую величину.
- Скорость первого автомобиля относительно неподвижной системы отсчета: v1 = 110 км/ч;
- Скорость второго автомобиля относительно Земли: v2 = 60 км/ч.
v′ = v + u
v′ — скорость автомобиля относительно земли (v1), v — скорость второго автомобиля относительно системы отсчета, связанной со вторым автомобилем, u — скорость движения второго автомобиля относительно земли (v2). По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:
По условию задачи в качестве системы отсчета нужно выбрать второй автомобиль. Так как система отсчета, связанная со вторым автомобилем, и первый автомобиль движутся в одном направлении, классический закон сложения скоростей в скалярном виде будет выглядеть так:v’ = v + u
Отсюда скорость первого автомобиля в системе отсчёта, связанной со вторым автомобилем:v = v’ – u = v1 – v2 = 110 – 60 = 50 (км/ч).
По условию задачи ответом должен быть модуль этой скорости. Модуль числа 50 есть 50.Ответ: 50pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 7k
Нью-Йорк DMV | Глава 5: перекрестные перекрестки и выводы
Темы:
- Викторина
Примечание. Практические викторины доступны только для тех разделов руководства, которые касаются правил дорожного движения (главы с 4 по 11 и дорожные знаки).
Большинство дорожно-транспортных происшествий происходит на перекрестках, когда водитель поворачивает. Многие из них происходят на больших парковках, открытых для общего пользования, например, в торговых центрах. Чтобы предотвратить аварию такого типа, вы должны понимать правила преимущественного проезда и правильно выполнять повороты.
Право проезда
Дорожные знаки, сигналы и разметка не всегда разрешают дорожные конфликты. Зеленый свет, например, не разрешает конфликт, когда автомобиль поворачивает налево на перекрестке, а приближающийся автомобиль едет через перекресток прямо. Правила преимущественного проезда помогают разрешить эти конфликты. Они говорят вам, кто идет первым, а кто должен ждать в разных условиях.
Вот примеры правил преимущественного проезда:
- Водитель, приближающийся к перекрестку, должен уступить дорогу транспортным средствам, находящимся на перекрестке.
Пример: Вы приближаетесь к перекрестку.
 Светофор горит зеленым, и вы хотите проехать прямо. Другой автомобиль уже находится на перекрестке, поворачивая налево. Вы должны позволить этому транспортному средству завершить свой поворот, прежде чем вы въедете на перекресток.
Светофор горит зеленым, и вы хотите проехать прямо. Другой автомобиль уже находится на перекрестке, поворачивая налево. Вы должны позволить этому транспортному средству завершить свой поворот, прежде чем вы въедете на перекресток. - Если водители, приближающиеся с противоположных направлений, достигают перекрестка примерно в одно и то же время, водитель, поворачивающий налево, должен уступить дорогу транспорту, который движется прямо или поворачивает направо.
Пример: Вы хотите повернуть налево на перекрестке впереди. Транспортное средство подъезжает к перекрестку со встречного направления и движется прямо. Прежде чем повернуть, вы должны дождаться, пока проедет приближающийся транспорт. Вы можете выехать на перекресток, чтобы подготовиться к левому повороту, если горит зеленый свет и никакое другое транспортное средство впереди вас не планирует поворачивать налево (см. «Повороты» далее в этой главе). При въезде на перекресток держитесь правее центральной линии.
 Держите колеса прямо, чтобы не попасть на полосу встречного движения в случае удара сзади. Когда транспортное средство, направляющееся к вам, освобождается или останавливается на красный свет, завершите поворот, когда сможете сделать это безопасно.
Держите колеса прямо, чтобы не попасть на полосу встречного движения в случае удара сзади. Когда транспортное средство, направляющееся к вам, освобождается или останавливается на красный свет, завершите поворот, когда сможете сделать это безопасно.Вы также должны уступить дорогу транспортному средству, направляющемуся к вам, когда вы поворачиваете налево на подъездную дорожку, парковку или другое место, даже если нет никаких знаков или сигналов, регулирующих поворот.
При любом повороте налево закон требует, чтобы вы уступали дорогу любому транспортному средству, движущемуся к вам, которое достаточно близко, чтобы представлять опасность. Решение о том, когда движение слишком близко, требует опыта и здравого смысла. Если у вас есть какие-либо опасения, подождите, пока движение проедет, прежде чем повернуть налево.
- На перекрестках, не регулируемых знаками или сигналами, или когда два или более водителей одновременно останавливаются перед знаками СТОП и они находятся под прямым углом, водитель слева должен уступить право проезда водителю справа.

Пример: Вы остановились у знака остановки и собираетесь проехать перекресток прямо. Водитель на перекрестке остановился у знака «Стоп» справа от вас и тоже собирается ехать прямо. Вы должны уступить дорогу другому водителю.
- Транспортное средство, въезжающее на проезжую часть с проезжей части, переулка, частной дороги или другого места, не являющегося проезжей частью, должно остановиться и уступить дорогу транспортным средствам на проезжей части и пешеходам.
Пример: Вы собираетесь выехать с парковки и повернуть направо, когда выйдете на улицу. Вы выезжаете с парковки и поворачиваете направо, когда въезжаете на улицу. Автомобиль приближается слева от вас. Вы должны остановиться и подождать, пока транспортное средство проедет, прежде чем выйти на улицу. Если бы вы повернули налево, вам пришлось бы уступать транспортным средствам, которые приближаются с обоих направлений. Если бы пешеход перешел съезд с парковки, вам пришлось бы ждать, пока этот человек перейдет дорогу.

- Водители должны уступать дорогу пешеходам, которые на законных основаниях пользуются размеченными или неразмеченными пешеходными переходами. Это означает, что вы должны снизить скорость или остановиться, если это необходимо. В любых ситуациях водители должны соблюдать осторожность, чтобы не столкнуться с пешеходами и велосипедистами.
Пример: Вы остановились на красный свет. Пешеход выходит на пешеходный переход, а затем загорается зеленый свет. Вы должны дождаться, пока пешеход перейдет дорогу. Вы также должны уступать дорогу пешеходам на пешеходных переходах слева или справа перед поворотом.
- Вы не можете въехать на перекресток, если движение с другой стороны затруднено, и вы не можете полностью пересечь перекресток. Подождите, пока движение впереди расчистится, чтобы не заблокировать перекресток.
- Будьте внимательны к перекресткам или смещенным перекресткам, чтобы не вызвать пробки, заблокировав другую улицу.

- Водитель, подъезжающий к круговой развязке или поворотному кругу, должен уступить дорогу водителям, уже находящимся на круге. (Дополнительную информацию о том, как проехать по круговому перекрестку, см. в разделе «Как проехать по кольцевому перекрестку» в главе 8 настоящего руководства.)
Машины скорой помощи
Вы должны уступать дорогу пожарным, машинам скорой помощи, полиции и другим уполномоченным машинам скорой помощи, когда они реагируют на чрезвычайные ситуации. Они будут отображать мигающие красные, красные и синие или красные и белые огни и включать сирену или звуковой сигнал. (Автомобили, которые реагируют на чрезвычайные ситуации для полицейского управления, департамента шерифа или силовых структур штата Нью-Йорк, не всегда обязаны использовать звуковую сирену или звуковой сигнал). сразу к правому краю дороги и остановитесь. Подождите, пока не проедет машина скорой помощи, прежде чем продолжить движение. Если вы находитесь на перекрестке, выезжайте с него, прежде чем остановиться.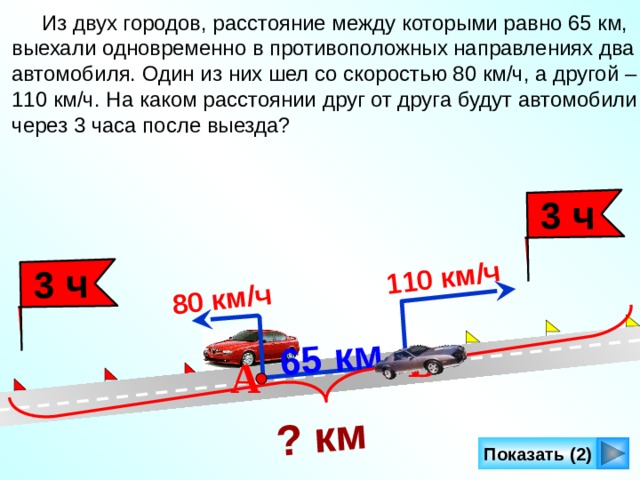
Вы должны съехать на обочину и остановиться перед машиной скорой помощи, даже если она движется к вам по встречной полосе дороги с двусторонним движением.
Если вы слышите звук сирены или гудка поблизости, но не знаете точно, где находится машина скорой помощи, вы должны безопасно съехать к правому краю дороги и остановиться, пока не убедитесь, что она не движется к вам .
Аварийный автомобиль, который использует свет и сирену или звуковой сигнал, может быть непредсказуемым. Водитель может законно превышать ограничение скорости, проезжать красный свет и знаки STOP или YIELD, двигаться не в ту сторону на улицах с односторонним движением и поворачивать в направлениях, которые обычно не разрешены. Хотя водители автомобилей экстренных служб должны быть осторожны, будьте очень осторожны, когда машина скорой помощи движется к вам.
Закон о передвижении
Этот закон требует, чтобы каждый водитель проявлял осторожность, чтобы избежать столкновения с разрешенным аварийным или опасным транспортным средством, которое припарковано, остановлено или стоит на обочине или любом участке шоссе с включенными аварийными огнями или одним или несколькими включены желтые аварийные огни или сочетание одного или нескольких желтых огней и одного или нескольких синих огней.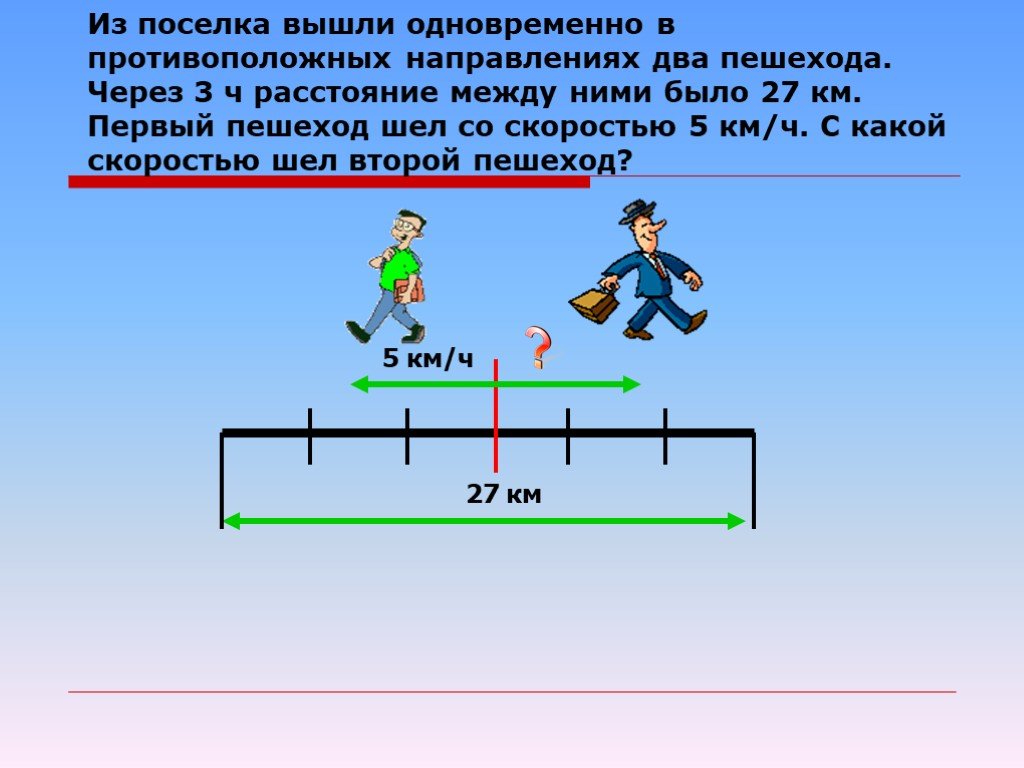 Водители должны снижать скорость на всех дорогах при встрече с такими транспортными средствами, но на бульварах, межштатных автомагистралях и других контролируемых подъездных дорогах с несколькими полосами движения водители также должны двигаться с полосы, примыкающей к аварийному или опасному транспортному средству, если только дорожное движение или другие опасности не мешают этому. безопасно. Водители также обязаны двигаться для транспортных средств с синими и зелеными огнями, которые описаны в следующем разделе. Нарушение этого закона наказывается как нарушение правил перевозки.
Водители должны снижать скорость на всех дорогах при встрече с такими транспортными средствами, но на бульварах, межштатных автомагистралях и других контролируемых подъездных дорогах с несколькими полосами движения водители также должны двигаться с полосы, примыкающей к аварийному или опасному транспортному средству, если только дорожное движение или другие опасности не мешают этому. безопасно. Водители также обязаны двигаться для транспортных средств с синими и зелеными огнями, которые описаны в следующем разделе. Нарушение этого закона наказывается как нарушение правил перевозки.
Синие, зеленые и желтые огни
Личные транспортные средства, которыми управляют пожарные-добровольцы, отвечающие на сигналы тревоги, могут светиться синим светом, а автомобили, которыми управляют добровольцы скорой помощи или члены спасательных отрядов, могут светиться зеленым светом. Желтые огни на транспортных средствах повышенной опасности, таких как снегоочистители и эвакуаторы, или комбинация желтых и синих фонарей на транспортных средствах, предназначенных для буксировки или толкания автомобилей с ограниченными возможностями, предупреждают других водителей о возможных опасностях. Мигающие желтые огни также используются в транспортных средствах доставки почты в сельской местности и школьных автобусах, чтобы предупредить движение об их присутствии. Транспортные средства, которые горят синим, зеленым или желтым светом, не являются разрешенными автомобилями скорой помощи. Их водители должны соблюдать все правила дорожного движения. Хотя вы не обязаны уступать дорогу, вам следует уступить дорогу из вежливости, если вы можете сделать это безопасно.
Мигающие желтые огни также используются в транспортных средствах доставки почты в сельской местности и школьных автобусах, чтобы предупредить движение об их присутствии. Транспортные средства, которые горят синим, зеленым или желтым светом, не являются разрешенными автомобилями скорой помощи. Их водители должны соблюдать все правила дорожного движения. Хотя вы не обязаны уступать дорогу, вам следует уступить дорогу из вежливости, если вы можете сделать это безопасно.
Повороты
Всегда сигнализируйте перед поворотом или перестроением. Важно, чтобы другие участники дорожного движения знали о ваших намерениях. Закон требует, чтобы вы сигнализировали о повороте или смене полосы движения с помощью указателей поворота или ручных сигналов на расстоянии не менее 100 футов (30 м) впереди. Хороший совет по безопасности — по возможности подать сигнал о своем намерении повернуть до того, как вы начнете тормозить или выполнять поворот. Ниже показаны правильные сигналы руками.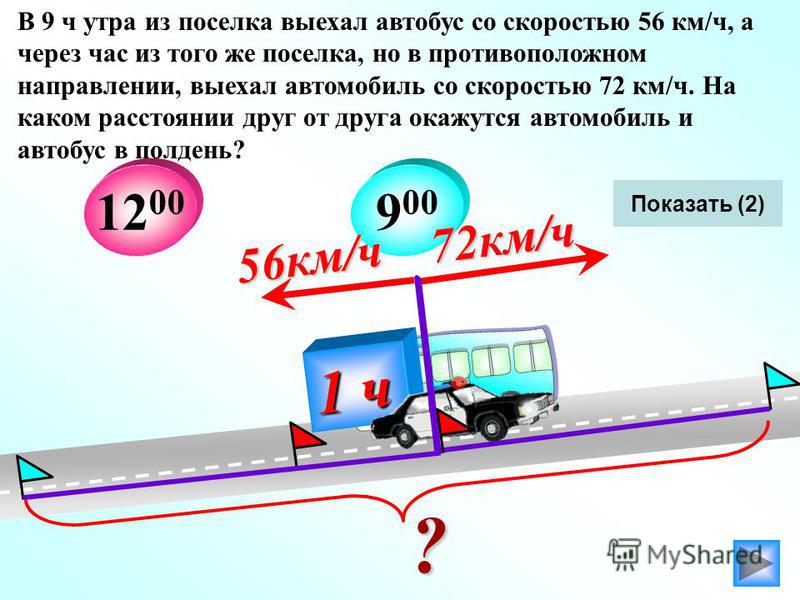
Помните эти другие советы, когда будете готовиться к повороту:
- Сбавьте скорость.
- Будьте внимательны к движению со всех сторон. Будьте особенно осторожны, чтобы проверить наличие мотоциклов. Большинство аварий с участием мотоциклов и других транспортных средств происходит из-за того, что водитель другого транспортного средства не видит мотоцикл.
Держите колеса прямо, пока не начнете поворачивать. Если ваши колеса повернуты и вас ударят сзади, ваш автомобиль может быть выброшен на встречную полосу движения.
- Помните, что ваши задние колеса будут двигаться внутри траектории передних колес, ближе к бордюру (правый поворот) или к транспортному средству, движущемуся к вам (левый поворот).
- Следите за пешеходами, велосипедистами и водителями мопедов, особенно при поворотах направо. Их часто трудно увидеть в пробках.
Будьте особенно внимательны к людям в инвалидных креслах, людям, толкающим коляски, или тем, кто тянет за собой чемодан на колесиках.
 Они могут быть ближе к земле и спрятаны за автомобилем.
Они могут быть ближе к земле и спрятаны за автомобилем.
На следующих рисунках показано правильное положение вашего автомобиля для поворотов. Эти положения являются из требований в законе, а не просто хороший совет.
ПОВОРОТ НАПРАВО:
Готовясь к повороту, двигайтесь вправо как можно дальше. Не делайте широких размашистых поворотов. Если знаки не предписывают вам поступать иначе, поверните на правую полосу дороги, на которую вы въезжаете. См. пример ниже.
ПОВОРОТ НАЛЕВО С ДОРОГИ С ОДНОСТОРОННИМ ДОРОГОЙ НА ДОРОГУ С ОДНОСТОРОННИМ СПОСОБОМ:
Двигайтесь по левой полосе, когда собираетесь повернуть. Если дорога, на которую вы въезжаете, имеет две полосы, вы должны повернуть на ее левую полосу. См. пример ниже.
ПОВОРОТ НА ЛЕВЫЙ С ОДНОСТОРОННЕЙ ДОРОГИ НА ДВУХСТОРОННЮЮ ДОРОГУ:
Подъезжайте к повороту по левой полосе. Проезжая перекресток, выезжайте на дорогу с двусторонним движением справа от ее центральной линии, но как можно ближе к центральной линии.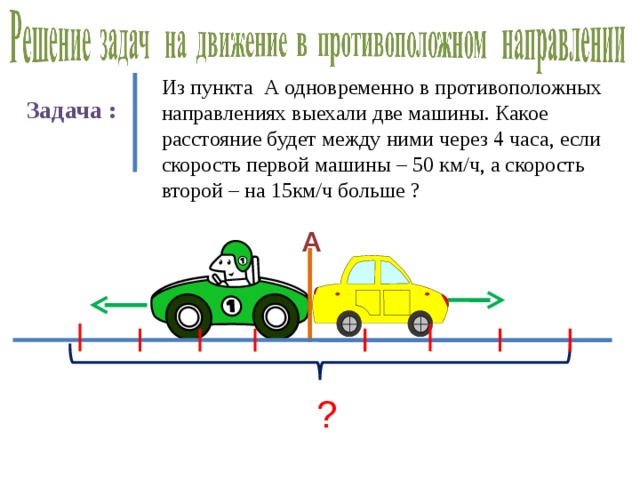 Будьте внимательны к транспортным средствам, приближающимся с дороги слева. Мотоциклы трудно увидеть, и трудно оценить их скорость и расстояние. См. пример ниже.
Будьте внимательны к транспортным средствам, приближающимся с дороги слева. Мотоциклы трудно увидеть, и трудно оценить их скорость и расстояние. См. пример ниже.
ПОВОРОТ НАЛЕВО С ДВУХСТОРОННЕЙ ДОРОГИ НА ДВУХСТОРОННЮЮ ДОРОГУ:
Подъезжайте к повороту с правой половины проезжей части, ближайшей к центру. Старайтесь использовать левую сторону перекрестка, чтобы убедиться, что вы не мешаете движущемуся к вам транспорту, который хочет повернуть налево. Держитесь правее центральной линии дороги, на которую вы въезжаете, но как можно ближе к центральной линии. Будьте внимательны к транспортным средствам, движущимся к вам слева и с полосы, которую вы собираетесь пересечь. Мотоциклы, направляющиеся к вам, трудно увидеть, и трудно оценить их скорость и расстояние до них. Водители часто не видят приближающийся к ним мотоцикл и сбивают его, когда поворачивают на другую сторону полосы движения. См. пример ниже.
ПОВОРОТ НАЛЕВО С ДВУХСТОРОННЕЙ ДОРОГИ НА ДОРОГУ С ОДНОСТОРОННИМ:
Подъезжайте к повороту с правой половины проезжей части, ближайшей к центру. Поверните, не дойдя до центра перекрестка, и поверните на левую полосу дороги, на которую вы въезжаете. См. пример ниже.
Поверните, не дойдя до центра перекрестка, и поверните на левую полосу дороги, на которую вы въезжаете. См. пример ниже.
ПОВОРОТ НАЛЕВО С ДВУХСТОРОННЕЙ ДОРОГИ НА ЧЕТЫРЕХПОЛОСНОЕ ШОССЕ:
Подъезжайте к повороту с правой половины проезжей части, ближайшей к центру. Въезжайте на левую полосу справа от центральной линии. Когда движение позволяет, вы можете выехать из левой полосы. См. пример ниже.
Разворот
Разворот — это любой поворот, который вы делаете, чтобы двигаться в противоположном направлении.
Не пытайтесь развернуться на шоссе без крайней необходимости. Если вам необходимо развернуться, используйте парковку, подъездную дорожку или другое место и, если возможно, выезжайте на проезжую часть по мере движения вперед, а не задним ходом.
Вы можете совершать разворот только с левой части полосы, ближайшей к осевой линии проезжей части, и никогда с правой полосы. Если знаки не говорят вам об обратном, вы можете сделать разворот, когда получите разрешение на движение по сигналу светофора с зеленой стрелкой налево, при условии, что это разрешено, и вы уступаете дорогу другим транспортным средствам.
Вы не можете совершать разворот на вершине холма, на повороте или в любом другом месте, где другие водители не могут видеть ваш автомобиль с расстояния 500 футов ( 150 м ) в любом направлении. Развороты также запрещены в деловых районах Нью-Йорка и там, где нет знаков «Разворот НЕТ». Вы никогда не сможете развернуться на скоростной автомагистрали с ограниченным доступом, даже если пути соединяют вашу сторону скоростной автомагистрали с другой стороной. Кроме того, транспортному средству запрещено делать разворот в школьной зоне.
Если это не запрещено, для разворота на узкой улице с двусторонним движением можно использовать трехточечный поворот. Во время экзамена по вождению вам может потребоваться выполнить трехточечный поворот.
Для трехточечного поворота:
- Подайте сигнал правым указателем поворота, затем сверните направо и остановитесь. Подайте сигнал левым указателем поворота, затем внимательно проверьте движение со всех сторон.

- Поверните налево, перейдите дорогу и остановитесь лицом к левому бордюру или краю дороги.
- Снова проверьте трафик. Поверните руль как можно дальше вправо, затем посмотрите назад, когда будете двигаться задним ходом. Остановитесь, не дойдя до правого бордюра или любого препятствия на правом бордюре или краю дороги.
- Остановитесь, еще раз проверьте наличие других транспортных средств, затем поверните руль до упора влево и тяните вперед, чтобы завершить поворот, когда это будет безопасно.
Вопросы
Прежде чем перейти к главе 6, убедитесь, что вы можете ответить на следующие вопросы:
- Что такое сигнал рукой для остановки? Правый поворот?
- Если два водителя одновременно выезжают на перекресток с противоположных направлений, и один едет прямо, а другой готовится повернуть налево, что должно уступать дорогу?
- Если вы въезжаете на перекресток, чтобы повернуть налево, но встречный транспорт сразу препятствует повороту, что делать?
- Если вы доедете до неконтролируемого перекрестка одновременно с водителем справа от вас, и вы оба собираетесь ехать прямо, кто имеет преимущественное право проезда?
- Что делать, если вы выезжаете на дорогу с проезжей части?
- Вы смотрите на зеленый свет, но движение на другой стороне перекрестка не позволяет вам проехать весь перекресток.
 Вы можете войти на перекресток?
Вы можете войти на перекресток? - Имеет ли транспортное средство, готовое въехать на круговую или поворотную полосу, преимущество перед транспортными средствами, уже находящимися на круге?
- Что делать, если рядом слышишь сирену, но не видишь, где находится машина скорой помощи?
- За какое время до поворота вы должны подать сигнал?
- Когда вы готовитесь к правому повороту, должны ли вы оставаться как можно ближе к центру полосы движения?
- Где вы должны расположить свой автомобиль, когда собираетесь повернуть налево с дороги с двусторонним движением на дорогу с односторонним движением?
Конец главы 5: Викторина по главе 5
< Глава 4 | Содержание | Глава 6 >
Относительная скорость
Относительная скорость
|
Для тех, кто путешествует автостопом по шоссе, две машины, несущиеся по соседним полосам, кажутся размытым пятном. Но если автомобили имеют одинаковую скорость, каждый водитель видит, что другой остается на месте, на расстоянии одной полосы движения. Автостопщик наблюдает скорость примерно 30 м/с, но каждый водитель наблюдает, что скорость другого равна нулю. Ясно, что скорость объекта зависит от наблюдателя, который производит измерение.
Рисунок 3.16 иллюстрирует понятие относительной скорости, показывая пассажира, идущего впереди движущегося поезда. Сидящие в поезде люди видят пассажира, идущего со скоростью +2,0 м/с, где плюс обозначает направление вправо. Предположим, что поезд движется со скоростью +9,0 м/с относительно наблюдателя, стоящего на земле.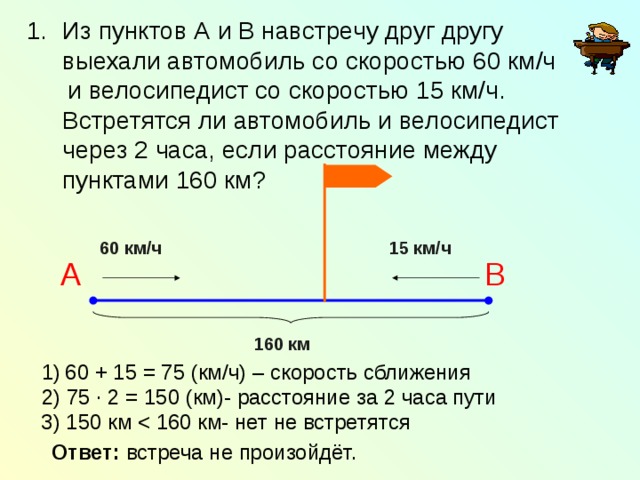 Тогда наземный наблюдатель увидит пассажира, движущегося со скоростью +11 м/с, частично из-за пешеходного движения и частично из-за движения поезда. Чтобы помочь в описании относительной скорости, давайте определим следующие символы:
Тогда наземный наблюдатель увидит пассажира, движущегося со скоростью +11 м/с, частично из-за пешеходного движения и частично из-за движения поезда. Чтобы помочь в описании относительной скорости, давайте определим следующие символы:
In terms of these symbols, the situation in Figure 3.16 can be summarized as follows:
| (3.7) |
or
Согласно уравнению 3.7, v PG представляет собой векторную сумму v PT и v TG , и эта сумма показана на рисунке. Если бы пассажир шел к задней части поезда, а не вперед, скорость относительно наземного наблюдателя была бы .
|
Каждый символ скорости в уравнении 3.7 содержит двухбуквенный нижний индекс. Первая буква в нижнем индексе указывает на тело, которое движется, а вторая буква указывает на объект, относительно которого измеряется скорость. Например, v TG и v PG — скорости поезда и пассажира, измеренные относительно земли. Точно так же v PT — это скорость Пассажира, измеренная наблюдателем, сидящим в Поезде.
Порядок символов нижнего индекса в уравнении 3.7 следует определенной схеме. Первый нижний индекс (P) в левой части уравнения также является первым нижним индексом в правой части уравнения. Точно так же последний нижний индекс (G) с левой стороны также является последним нижним индексом с правой стороны. Третий нижний индекс (T) появляется только в правой части уравнения как два «внутренних» нижних индекса. Цветные прямоугольники ниже подчеркивают расположение символов в нижних индексах:
Третий нижний индекс (T) появляется только в правой части уравнения как два «внутренних» нижних индекса. Цветные прямоугольники ниже подчеркивают расположение символов в нижних индексах:
В других ситуациях нижние индексы не обязательно будут P, G и T, но будут совместимы с именами объектов, участвующих в движении.
| Проверьте свое понимание Три автомобиля A, B и C движутся по прямому участку шоссе. Скорость A относительно B равна v AB , скорость A относительно C равна v AC , а скорость C относительно B равна v CB . Вставьте недостающие скорости в таблицу.
Фон:
Относительные скорости трех (или более) объектов связаны посредством сложения векторов. Рассмотрим, как расположены индексы в этом дополнении. По аналогичным вопросам (в том числе расчетным аналогам) обращайтесь к Тесту для самооценки 3.2. Тест описан в конце этого раздела. | ||||||||||||||||||||||||||||||
|
Уравнение 3.7 было представлено в связи с одномерным движением, но его результат справедлив и для двумерного движения. На рис. 3.17 изображена обычная ситуация, связанная с относительной скоростью в двух измерениях. Часть а рисунка показывает лодку, плывущую по течению реки; двигатель лодки выключен. В части b двигатель был включен, и теперь лодка движется поперек реки по диагонали из-за комбинированного движения, создаваемого течением и двигателем. В списке ниже приведены скорости для этого типа движения и объекты, относительно которых они измеряются:
В списке ниже приведены скорости для этого типа движения и объекты, относительно которых они измеряются:
Скорость v BW лодки относительно воды — это скорость, измеренная наблюдателем, который, например, плывет на внутренней трубе и дрейфует вниз по течению по течению. При выключенном двигателе лодку также сносит вниз по течению, и v BW равно нулю. Однако когда двигатель включен, лодка может двигаться относительно воды, и v BW больше не равно нулю. Скорость v WS воды относительно берега – это скорость течения, измеренная наблюдателем на берегу. Скорость v BS лодки относительно берега обусловлена комбинированным движением лодки относительно воды и движением воды относительно берега. В символах
Порядок индексов в этом уравнении идентичен порядку в уравнении 3. 7, хотя буквы были изменены, чтобы отразить другую физическую ситуацию. Пример 10 иллюстрирует концепцию относительной скорости в двух измерениях.
7, хотя буквы были изменены, чтобы отразить другую физическую ситуацию. Пример 10 иллюстрирует концепцию относительной скорости в двух измерениях.
| Пример 10 Переход через реку |
Двигатель лодки гонит ее по реке шириной 1800 м. Скорость v BW лодки относительно воды 4,0 м/с, направленная перпендикулярно течению, как на рис. 3.18. Скорость v WS воды относительно берега равна 2,0 м/с. а) Какова скорость v BS лодки относительно берега? б) Сколько времени потребуется лодке, чтобы пересечь реку?
Рассуждение
Решение
| |||||||||||||||||
Иногда возникают ситуации, когда два транспортных средства находятся в относительном движении, и полезно знать относительную скорость одного по отношению к другому. Пример 11 рассматривает этот тип относительного движения.
Имитация концепции 3. 3 3 |
| |
| Example 11 Approaching an Intersection |
На рис. 3.19а показаны две машины, приближающиеся к перекрестку по перпендикулярным дорогам. Автомобили имеют следующие скорости: Найдите величину и направление v AB , где
Рассуждение Чтобы найти v AB , мы используем уравнение, индексы которого следуют порядку, указанному ранее. Таким образом, 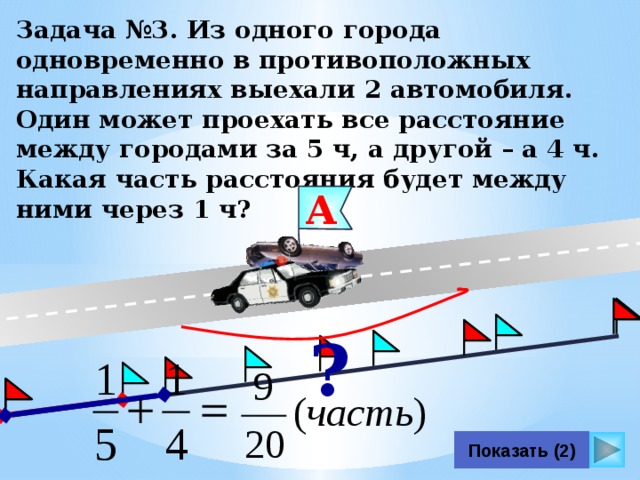 Имея это в виду, на рис. 3.19 показано, как v AG и v GB векторно складываются, чтобы получить v AB . Имея это в виду, на рис. 3.19 показано, как v AG и v GB векторно складываются, чтобы получить v AB .
Решение Из векторного треугольника на рис. 3.19b величина и направление v AB могут быть рассчитаны как | |||||||||||||||||
Во время вождения автомобиля вы когда-нибудь замечали, что заднее стекло иногда остается сухим, даже когда идет дождь? Это явление является следствием относительной скорости, как помогает объяснить рисунок 3.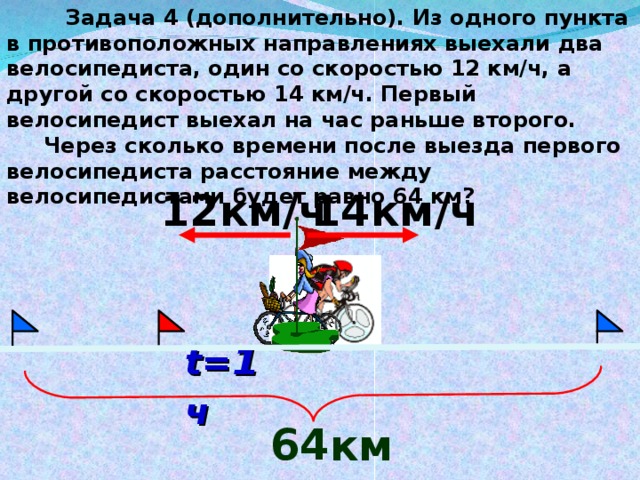 20. Часть а показывает автомобиль, движущийся горизонтально со скоростью v CG и капля дождя, падающая вертикально со скоростью v RG . Обе скорости измеряются относительно земли. Однако, чтобы определить, попадает ли капля дождя в окно, нам нужно учитывать скорость капли относительно автомобиля, а не земли. Эта скорость равна v RC , и мы знаем, что
20. Часть а показывает автомобиль, движущийся горизонтально со скоростью v CG и капля дождя, падающая вертикально со скоростью v RG . Обе скорости измеряются относительно земли. Однако, чтобы определить, попадает ли капля дождя в окно, нам нужно учитывать скорость капли относительно автомобиля, а не земли. Эта скорость равна v RC , и мы знаем, что
В части b рисунка показано расположение «хвост к голове», соответствующее этому сложению векторов, и указано, что направление v RC задается углом q R . Для сравнения, заднее стекло наклонено под углом 90 516 q 90 517 90 335 W 90 336 по отношению к вертикали (см. увеличенное изображение в части а). Когда q R больше, чем q W , капля дождя не попадет в окно. Однако q R определяется скоростью v RG капли дождя и скоростью v CG автомобиля, согласно . При более высоких скоростях автомобиля угол q R становится слишком большим, чтобы капля не попала в окно. Таким образом, на достаточно высокой скорости автомобиль просто выезжает из-под каждой падающей капли
При более высоких скоростях автомобиля угол q R становится слишком большим, чтобы капля не попала в окно. Таким образом, на достаточно высокой скорости автомобиль просто выезжает из-под каждой падающей капли
| ||
Copyright © 2000-2003 John Wiley & Sons, Inc.
|


 В этом случае одну из неподвижных систем можно принять за ПСО с нулевой скоростью. При u=0, скорость v′ = u
В этом случае одну из неподвижных систем можно принять за ПСО с нулевой скоростью. При u=0, скорость v′ = u Ее проекция равна v21x = v2x – v1x
Ее проекция равна v21x = v2x – v1x
 Светофор горит зеленым, и вы хотите проехать прямо. Другой автомобиль уже находится на перекрестке, поворачивая налево. Вы должны позволить этому транспортному средству завершить свой поворот, прежде чем вы въедете на перекресток.
Светофор горит зеленым, и вы хотите проехать прямо. Другой автомобиль уже находится на перекрестке, поворачивая налево. Вы должны позволить этому транспортному средству завершить свой поворот, прежде чем вы въедете на перекресток.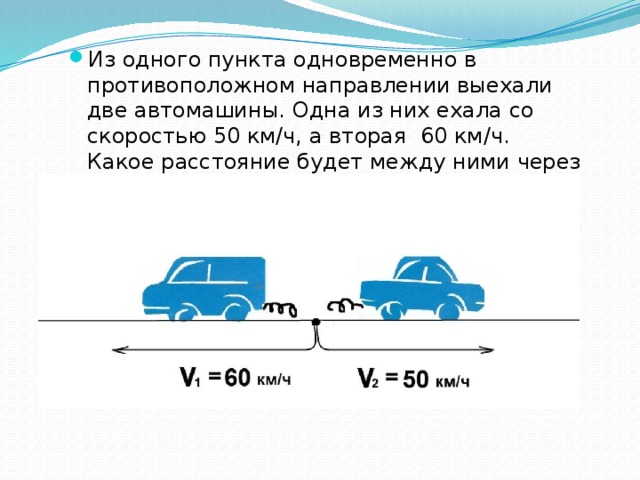 Держите колеса прямо, чтобы не попасть на полосу встречного движения в случае удара сзади. Когда транспортное средство, направляющееся к вам, освобождается или останавливается на красный свет, завершите поворот, когда сможете сделать это безопасно.
Держите колеса прямо, чтобы не попасть на полосу встречного движения в случае удара сзади. Когда транспортное средство, направляющееся к вам, освобождается или останавливается на красный свет, завершите поворот, когда сможете сделать это безопасно.

 Они могут быть ближе к земле и спрятаны за автомобилем.
Они могут быть ближе к земле и спрятаны за автомобилем.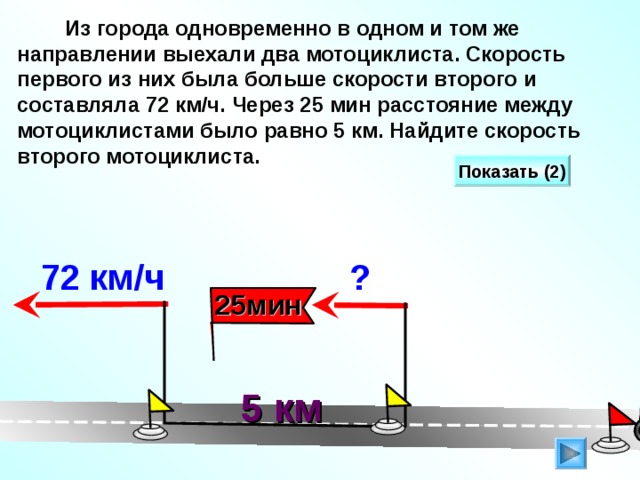
 Вы можете войти на перекресток?
Вы можете войти на перекресток? Для дозаправки нижний самолет выравнивает свою скорость со скоростью заправщика (более крупного самолета) и соединяется с нагнетательной трубой заправщика. Во время дозаправки относительная скорость двух самолетов равна нулю. (© George Hall/Corbis Images)
Для дозаправки нижний самолет выравнивает свою скорость со скоростью заправщика (более крупного самолета) и соединяется с нагнетательной трубой заправщика. Во время дозаправки относительная скорость двух самолетов равна нулю. (© George Hall/Corbis Images)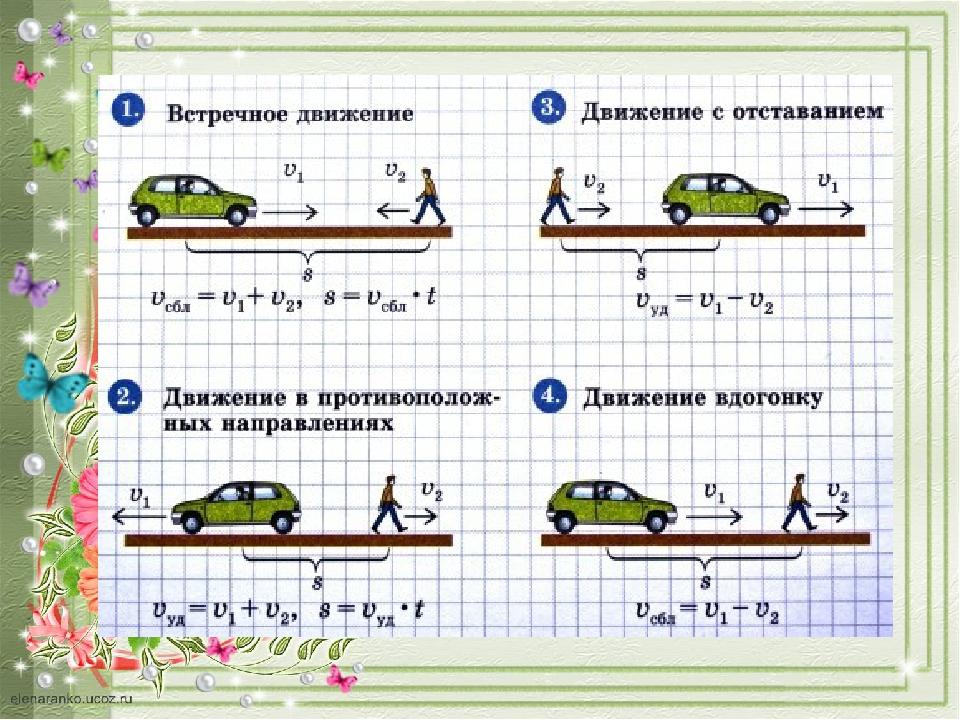 16
Скорость пассажира относительно наземного наблюдателя v PG . Это векторная сумма скорости v PT пассажира относительно поезда и скорости v TG поезда относительно земли: v PG = v PT + v TG .
16
Скорость пассажира относительно наземного наблюдателя v PG . Это векторная сумма скорости v PT пассажира относительно поезда и скорости v TG поезда относительно земли: v PG = v PT + v TG .
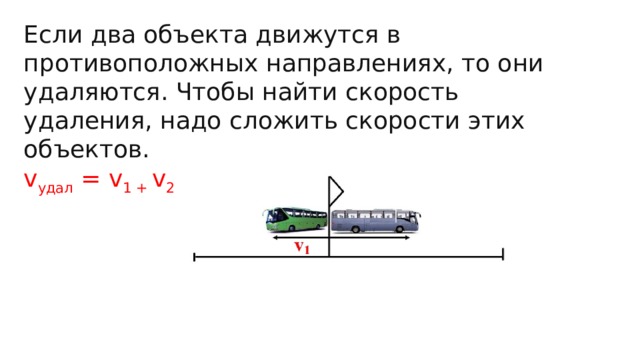
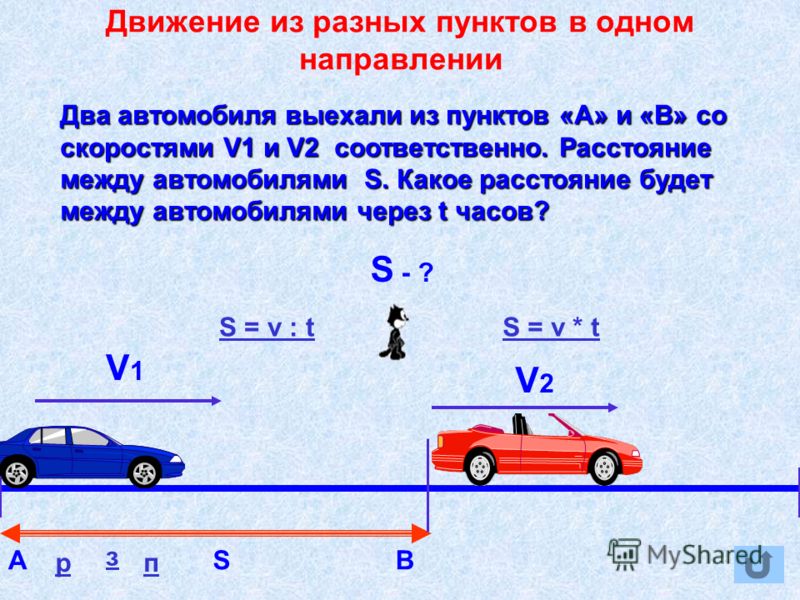 рис. 3.18), величина v BS может быть определена с помощью теоремы Пифагора:
рис. 3.18), величина v BS может быть определена с помощью теоремы Пифагора: 19
Два автомобиля приближаются к перекрестку по перпендикулярным дорогам.
19
Два автомобиля приближаются к перекрестку по перпендикулярным дорогам.
Leave A Comment