Автомобиль движется прямолинейно с постоянным ускорением 2: Автомобиль движется прямолинейно с постоянным ускорением 2 м/с^2, имея в данный момент скорость 10 м/c. Где он был (какой пройден путь) за 4 с до этого? На сколько изменилась скорость автомобиля?

PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3. 2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5. 3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

Прямолинейное движение

Задача 22. (1) Автомобиль движется по прямолинейному участку дороги с постоянной скоростью 90 . Найти перемещение автомобиля за 3,3 мин и его положение в этот же момент времени, если в начальный момент времени автомобиль находился в точке, координата которой равна 12,23 км, а ось Ox направлена 1) вдоль движения автомобиля; 2) против движения автомобиля.

Задача 23. (1) Велосипедист движется по загородной дороге на север со скоростью 12 в течение 8,5 мин, затем он, свернув направо на перекрестке, проехал еще 4,5 км. Найти перемещение велосипедиста за время его движения.

Задача 24. (1) Конькобежец движется прямолинейно с ускорением 2,6 , и за 5,3 с его скорость увеличилась до 18 . Найти начальное значение скорости конькобежца. Какое расстояние пробежит спортсмен за это время?

Задача 25. (1) Автомобиль движется прямолинейно, притормаживая перед знаком ограничения скорости 40 с ускорением 2,3 Сколько времени длилось такое движение, если перед началом торможения скорость автомобиля была равна 70 ? На каком расстоянии от знака водитель начал тормозить?

Задача 26. (1) С каким ускорением движется поезд, если на пути 1200 м его скорость возросла от 10 до 20 ? Сколько времени затратил поезд на этот путь?

Задача 27. (1) Тело, брошенное вертикально вверх, вернулось на землю через 3 с. Какова была начальная скорость тела? На какой максимальной высоте оно побывало?

Задача 28. (2) Тело на веревке поднимают с поверхности земли с ускорением 2,7 м/с² вертикально вверх из состояния покоя. Через 5,8 с веревка оборвалась. Сколько времени двигалось тело до земли после того, как оборвалась веревка? Сопротивлением воздуха пренебречь.

Задача 29. (2) Тело начинает двигаться без начальной скорости с ускорением 2,4 Определить путь, пройденный телом за первые 16 с от начала движения, и путь, пройденный за последующие 16 с. С какой средней скоростью двигалось тело эти 32 с?

Задача 30. (1) Баскетболист бросает мяч в кольцо со скоростью 8,5 под углом 63^о к горизонту. С какой скоростью мяч попал в кольцо, если долетел до него за 0,93 с?

Задача 31. (1) Баскетболист бросает мяч в кольцо. В момент броска мяч находится на высоте 2,05 м, а через 0,88 с падает в кольцо, расположенное на высоте 3,05 м. С какого расстояния от кольца (по горизонтали) произведен бросок, если мяч был брошен под углом 56

о к горизонту?

Задача 32. (2) Мяч брошен горизонтально со скоростью 13 , спустя некоторое время его скорость оказалась равной 18 . Найти перемещение мяча за это время. Сопротивлением воздуха пренебречь.

Задача 33. (2) Тело брошено под некоторым углом к горизонту с начальной скоростью 17 м/с. Найти величину этого угла, если дальность полета тела в 4,3 раза больше максимальной высоты подъема.

Задача 34. (2) Бомбардировщик, пикирующий со скоростью 360 км/ч, сбрасывает бомбу с высоты 430 м, находясь по горизонтали на расстоянии 250 м от цели. Под каким углом должен пикировать бомбардировщик? На какой высоте окажется бомба спустя 2 с от начала падения? Какую скорость она будет иметь в этой точке?

Задача 35. (2) Самолет, летевший на высоте 2940 м со скоростью 410 км/ч, сбросил бомбу. За какое время до прохождения над целью и на каком расстоянии от нее самолет должен сбросить бомбу, чтобы попасть в цель? Найти модуль и направление скорости бомбы спустя 8,5 с от начала ее падения. Сопротивлением воздуха пренебречь.

Задача 36. (2) Снаряд, выпущенный под углом 36,6^о к горизонту, дважды был на одной и той же высоте: спустя 13 и 66 с после вылета. Определить начальную скорость, максимальную высоту подъема и дальность полета снаряда. Сопротивлением воздуха пренебречь.

3.6: Движение с постоянным ускорением (Часть 2)

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

5280

• OpenStax
• OpenStax

Составление уравнений

В следующих примерах мы продолжаем исследовать одномерное движение, но в ситуациях, требующих более сложных алгебраических операций.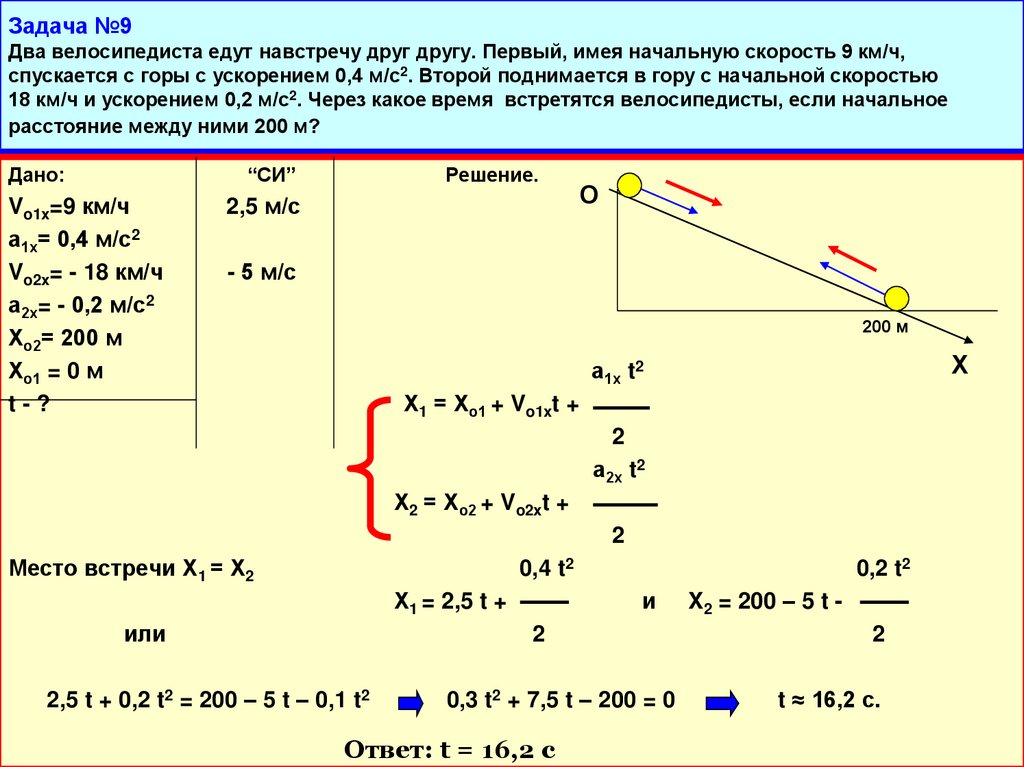 Примеры также дают представление о методах решения проблем. Следующее примечание предназначено для удобства обращения к необходимым уравнениям. Имейте в виду, что эти уравнения не являются независимыми. Во многих ситуациях у нас есть два неизвестных и нужно два уравнения из набора для решения неизвестных. Нам нужно столько уравнений, сколько неизвестных, чтобы решить данную ситуацию. 9{2} + 2a(x — x_{0})\]

Прежде чем мы перейдем к примерам, давайте более внимательно рассмотрим некоторые уравнения, чтобы увидеть поведение ускорения при экстремальных значениях. Переставляя \(v = v_0 + at\), мы имеем

\[a = \frac{v — v_{0}}{t} \ldotp\]

Отсюда мы видим, что за конечное время, если разница между начальной и конечной скоростями мала, ускорение мало, приближаясь к нулю в пределе равенства начальной и конечной скоростей. Наоборот, в пределе t → 0 при конечной разности начальной и конечной скоростей ускорение становится бесконечным. 9{2}}{2(x — x_{0})} \ldotp\]

Таким образом, при конечной разнице между начальной и конечной скоростями ускорение становится бесконечным, в пределе перемещение стремится к нулю.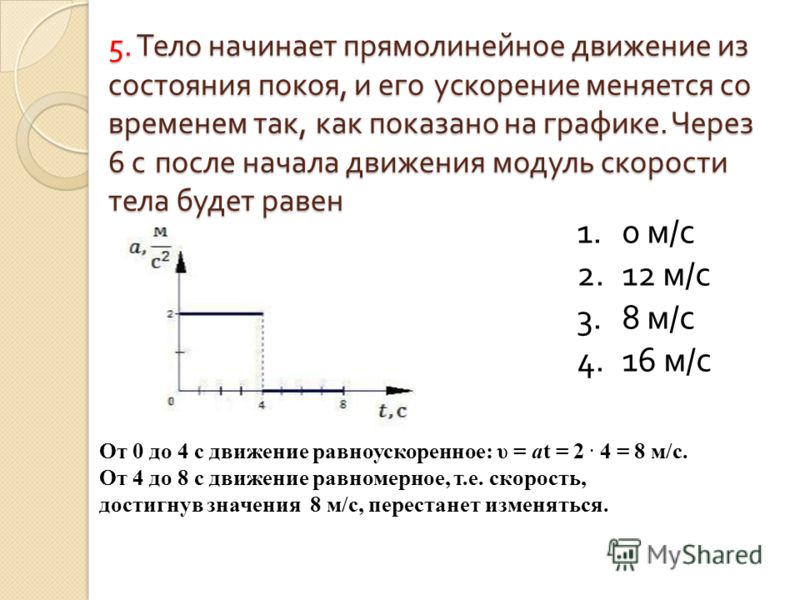 Ускорение стремится к нулю в пределе, когда разность начальной и конечной скоростей стремится к нулю при конечном перемещении.

Пример 3.10: Как далеко едет автомобиль?

На сухом бетоне автомобиль может замедляться со скоростью 7,00 м/с ² , тогда как на мокром бетоне он может замедляться только со скоростью 5,00 м/с

2 . Найдите расстояние, необходимое для остановки автомобиля, движущегося со скоростью 30,0 м/с (около 110 км/ч) по (а) сухому бетону и (б) мокрому бетону. (c) Повторите оба вычисления и найдите перемещение от точки, в которой водитель видит красный сигнал светофора, учитывая время его реакции 0,500 с, чтобы нажать на педаль тормоза.

Стратегия

Сначала нам нужно нарисовать рисунок \(\PageIndex{1}\). Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить.

Рисунок \(\PageIndex{1}\): Пример эскиза для визуализации замедления и тормозного пути автомобиля. {2})} \ldotp$$ Таким образом, $$x = 64,3\; м\; на\; сухой\; бетон \ldotp$$

Эту часть можно решить точно так же, как (а). Единственное отличие состоит в том, что ускорение равно −5,00 м/с ² . Результат: $$x_{мокрый} = 90,0\; м\; на\; влажный\; бетон \ldotp$$

Когда водитель реагирует, тормозной путь такой же, как в (a) и (b) для сухого и мокрого бетона. Итак, чтобы ответить на этот вопрос, нам нужно рассчитать, какое расстояние автомобиль проедет за время реакции, а затем добавить это ко времени остановки. Разумно предположить, что скорость остается постоянной в течение времени реакции водителя. Для этого мы, опять же, идентифицируем известные и то, что мы хотим решить. Мы знаем, что \(\bar{v}\) = 30,0 м/с, t _{реакция} = 0,500 с, а _{реакция} = 0. Примем x _{0-реакцию} равным нулю. Ищем х _{реакцию} . Во-вторых, как и прежде, мы определяем наилучшее уравнение для использования. В этом случае x = x ₀ + \(\bar{v}\)t работает хорошо, потому что единственным неизвестным значением является x, для которого мы и хотим найти. В-третьих, подставляем известные значения для решения уравнения: $$x = 0 + (30,0\; м/с)(0,500\; с) = 15,0\; м \ldotp$$Это означает, что автомобиль проезжает 15,0 м, пока водитель реагирует, что делает общее перемещение в двух случаях с сухим и влажным бетоном на 15,0 м больше, чем если бы он реагировал мгновенно. Наконец, мы прибавляем смещение за время реакции к смещению при торможении (рис. \(\PageIndex{2}\)), $$x_{торможение} + x_{реакция} = x_{общий},$$ и находим (а) быть 64,3 м + 15,0 м = 79.3 м в сухом состоянии и (b) 90,0 м + 15,0 м = 105 м во влажном состоянии.

Рисунок \(\PageIndex{2}\): Расстояние, необходимое для остановки автомобиля, сильно различается в зависимости от дорожных условий и времени реакции водителя. Здесь показаны тормозные пути для сухого и мокрого покрытия, рассчитанные в этом примере для автомобиля, движущегося изначально со скоростью 30,0 м/с. Также показано общее расстояние, пройденное от точки, когда водитель впервые видит красный свет, при условии времени реакции 0,500 с.

Значение

Перемещения, обнаруженные в этом примере, кажутся подходящими для остановки быстро движущегося автомобиля. На мокром асфальте машина останавливается дольше, чем на сухом. Интересно, что к перемещениям существенно добавляет время реакции, но важнее общий подход к решению задач. Мы идентифицируем известные и определяемые величины, затем находим соответствующее уравнение. Если имеется более одного неизвестного, нам нужно столько независимых уравнений, сколько неизвестных для решения. Часто существует более одного способа решения проблемы. Различные части этого примера на самом деле могут быть решены другими методами, но представленные здесь решения являются самыми короткими.

Пример 3.11: Расчет времени

Предположим, что автомобиль въезжает в полосу движения на съезде длиной 200 м. Если его начальная скорость равна 10,0 м/с, а ускорение составляет 2,00 м/с ² , за какое время автомобиль проедет 200 м вверх по пандусу? (Эта информация может быть полезна инженеру по транспорту. )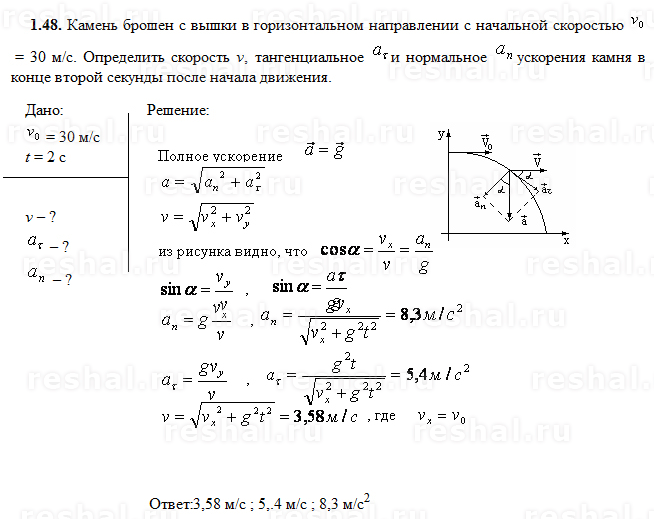

Стратегия

Сначала мы рисуем набросок Рисунок \(\PageIndex{3}\). Нас просят решить за время t. Как и прежде, мы отождествляем известные величины, чтобы выбрать удобное физическое соотношение (то есть уравнение с одним неизвестным, t.)

Рисунок \(\PageIndex{3}\): Эскиз автомобиля, ускоряющегося на съезде с автомагистрали.

Решение

Опять же, мы идентифицируем известные и то, что мы хотим решить. Мы знаем, что x ₀ = 0, v ₀ = 10 м/с, a = 2,00 м/с ² и x = 200 м.

Нам нужно найти t. Уравнение x = x ₀ + v ₀ t + \(\frac{1}{2}\)at ² работает лучше всего, потому что единственной неизвестной в уравнении является переменная t, для которой нам нужно решать. Из этого понимания мы видим, что когда мы вводим известные значения в уравнение, мы получаем квадратное уравнение. 9{2} — 4ac}}{2a},\]

, что дает два решения: t = 10,0 и t = -20,0. Отрицательное значение времени неразумно, так как это означало бы, что событие произошло за 20 с до начала движения. Мы можем отказаться от этого решения. Таким образом,

\[ t = 10,0\; s \ldotp\]

Значение

Всякий раз, когда уравнение содержит неизвестное в квадрате, есть два решения. В некоторых задачах оба решения имеют смысл; в других разумно только одно решение. Ответ 10,0 с кажется разумным для типичного съезда с автострады.

Упражнение 3.5

Пилотируемая ракета разгоняется со скоростью 20 м/с ² во время запуска. За какое время ракета достигнет скорости 400 м/с?

Пример 3.12: Разгон космического корабля

Космический корабль покинул орбиту Земли и направляется к Луне. Он разгоняется со скоростью 20 м/с ² за 2 мин и преодолевает расстояние 1000 км. Каковы начальная и конечная скорости космического корабля?

Стратегия

9{2})(120,0\; с) = 9533,3\; м/с \ldotp\]

Значение

В смещении, времени, скорости и ускорении есть шесть переменных, описывающих движение в одном измерении.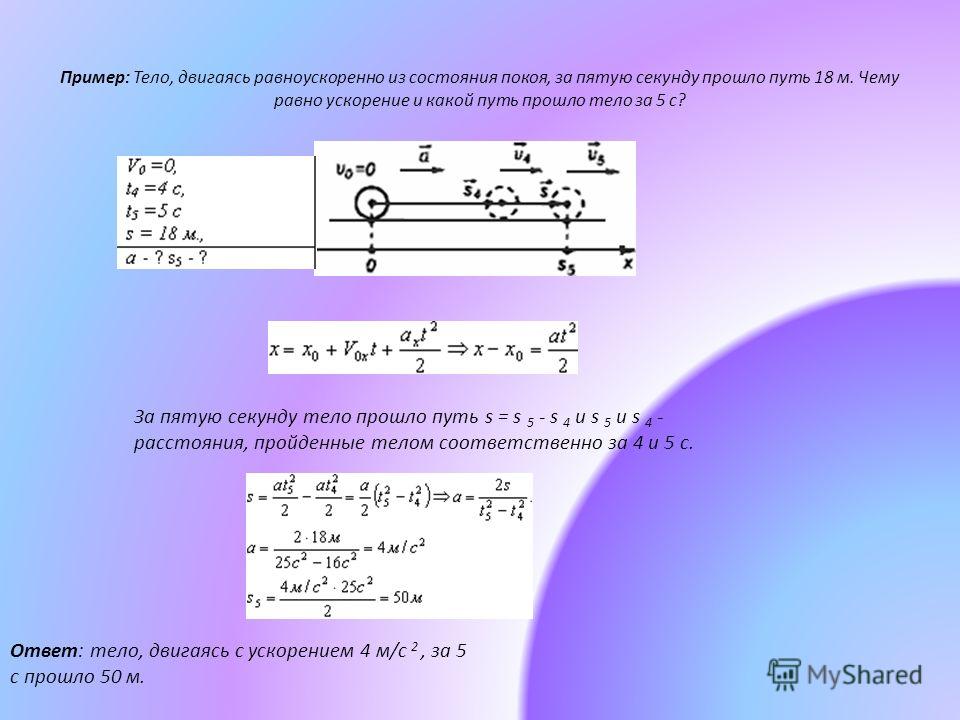 Начальными условиями данной задачи может быть множество комбинаций этих переменных. Из-за этого разнообразия решения могут быть не такими простыми, как простые подстановки в одно из уравнений. Этот пример показывает, что для решения кинематики может потребоваться решение двух одновременных кинематических уравнений.

Познакомившись с основами кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также заметили общий подход к решению задач, который дает как правильные ответы, так и понимание физических взаимосвязей. Следующий уровень сложности наших задач кинематики связан с движением двух взаимосвязанных тел, называемых задачами преследования двух тел .

Задачи преследования двух тел

До этого момента мы рассматривали примеры движения одного тела. Даже для задачи с двумя автомобилями и тормозным путем на мокрой и сухой дороге мы разделили эту задачу на две отдельные задачи, чтобы найти ответы. В задача преследования двух тел , движения объектов связаны, то есть искомое неизвестное зависит от движения обоих объектов. Чтобы решить эти задачи, мы пишем уравнения движения для каждого объекта, а затем решаем их одновременно, чтобы найти неизвестное. Это показано на рисунке \(\PageIndex{4}\).

Рисунок \(\PageIndex{4}\): Сценарий преследования двух тел, в котором автомобиль 2 движется с постоянной скоростью, а автомобиль 1 отстает с постоянным ускорением. Автомобиль 1 догоняет автомобиль 2 позже.

Время и расстояние, необходимые для того, чтобы автомобиль 1 догнал автомобиль 2, зависят от начального расстояния между автомобилем 1 и автомобилем 2, а также от скоростей обоих автомобилей и ускорения автомобиля 1. Кинематические уравнения, описывающие движение обоих автомобилей, должны быть решил найти эти неизвестные.

Рассмотрим следующий пример.

Пример 3.13: Гепард ловит газель

Гепард ждет, прячась за кустом. Гепард замечает газель, пробегающую мимо со скоростью 10 м/с. В момент, когда газель проходит мимо гепарда, гепард ускоряется из состояния покоя со скоростью 4 м/с ² поймать газель. а) Сколько времени потребуется гепарду, чтобы поймать газель? б) Каково водоизмещение газели и гепарда?

Стратегия

Для решения этой задачи используем систему уравнений для постоянного ускорения. Поскольку движутся два объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но что связывает уравнения, так это общий параметр, который имеет одинаковое значение для каждого животного. Если мы внимательно посмотрим на проблему, станет ясно, что общим параметром для каждого животного является их позиция x в более поздний момент времени t. Поскольку они оба начинаются с x ₀ = 0, их перемещения одинаковы в более поздний момент времени t, когда гепард догонит газель. Если мы выберем уравнение движения, которое определяет смещение для каждого животного, мы можем тогда установить уравнения равными друг другу и найти неизвестное, то есть время. {2} — 50\; m \ldotp$$Водоизмещение газели: $$x = \bar{v} t = 10(5) = 50\; m \ldotp$$Мы видим, что оба смещения равны, как и ожидалось.

Значение

Важно проанализировать движение каждого объекта и использовать соответствующие кинематические уравнения для описания движения каждого отдельного объекта. Также важно иметь хорошее визуальное представление о задаче преследования двух тел, чтобы увидеть общий параметр, который связывает движение обоих объектов.

Упражнение 3.6

Велосипед движется с постоянной скоростью 10 м/с. Человек стартует с состояния покоя и начинает бежать, чтобы догнать велосипед через 30 с, когда велосипед находится в том же положении, что и человек. Каково ускорение человека?

---

Эта страница под названием 3.6: Движение с постоянным ускорением (часть 2) распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать оглавление

   нет

2. Теги

   1. источник@https://openstax. org/details/books/university-physics-volume-1
   2. задача преследования двух тел

2. ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ

2. ПРЯМОЛИнейНОЕ ДВИЖЕНИЕ

• ДВИЖЕНИЕ ПО ПРЯМОЙ ЛИНИИ
  • 2.1. Позиция
  • 2.2. Скорость
  • 2.3. Ускорение
  • 2.4. Постоянное ускорение
  • 2.5. Гравитационное ускорение

---

В механике нас интересует попытка понять движение объектов. В этой главе будет обсуждаться движение объектов в 1 измерении. Движение в 1 измерении — это движение по прямой линии.

Положение объекта на прямой линии можно однозначно определить по его расстояние от (выбранного пользователем) источника. (см. рис. 2.1). Примечание : позиция полностью определяется 1 координатой (поэтому это 1-мерное проблема).

Рисунок 2.1. Одномерное положение.

Рисунок 2.2. графики зависимости x от t для различных скоростей.

Для данной задачи начало может быть выбрано в любой точке. удобный. Например, положение объекта в момент времени t = 0 часто выбран в качестве источника. Положение объекта в общем случае будет функцией времени: x(t). Рисунок 2.2. показывает положение в зависимости от времени для объект в состоянии покоя, а также для объектов, движущихся влево и вправо.

Наклон кривой на графике зависимости положения от времени зависит от скорость объекта. См., например, рисунок 2.3. Через 10 секунд гепард преодолел расстояние 310 метров, человек 100 метров, а свинья 50 метров. Очевидно, что гепард имеет наибольшую скорость. Похожий вывод получается, когда мы рассматриваем время, необходимое для покрытия фиксированного расстояние. Гепард преодолевает 300 метров за 10 с, человек за 30 с, а свинья требуется 60 с. Ясно, что более крутой наклон кривой зависимости x от t график соответствует более высокой скорости.

Рисунок 2.3. графики x и t для различных существ.

Объект, который меняет свое положение, имеет ненулевую скорость. В среднем скорость объекта в течение заданного интервала времени определяется как:

Если объект движется вправо, средняя скорость положительна. Ан объект, движущийся влево, имеет отрицательную среднюю скорость. Это ясно из определение средней скорости, которая зависит только от положения объекта в момент времени t = t ₁ и в время t = t ₂ . Это хорошо показано в задаче 2-1 из примера . и 2-2 .

Пример задачи 2-1

Вы едете на потрепанном пикапе по прямой дороге 5,2 мили со скоростью 43 мили в час, в этот момент у вас закончилось топливо. Вы идете на 2 мили дальше, до ближайшего АЗС, за 27 мин (= 0,450 ч). Какова ваша средняя скорость от время, когда вы завели свой грузовик, до того, как вы прибыли на станцию?

Пикап первоначально преодолевает расстояние 5,2 мили со скоростью 43 мили/час. Это занимает 7,3 минуты. После того, как у пикапа закончился газа, вам потребуется 27 минут, чтобы дойти до ближайшей заправки, что составляет 1,2 миль вниз по дороге. Когда вы приедете на заправку, вы покрыли (5.2 + 1,2) = 6,4 мили за период (7,3 + 27) = 34,3 минуты. Ваш средний скорость до этой точки:

Пример задачи 2-2

Предположим, вы затем везете топливо обратно в грузовик, делая туда и обратно за 35 мин. Какова ваша средняя скорость на всем пути от начало вашего движения к вам возвращение к грузовику с топливом ?

Вам потребуется еще 35 минут, чтобы вернуться к своей машине. Когда вы достигнете своего грузовик, вы снова находитесь в 5,2 милях от исходной точки и путешествовали уже (34,4 + 35) = 69,4 минуты. В этот момент ваша средняя скорость равна:

После этого эпизода вы возвращаетесь домой. Вы преодолеваете 5,2 мили снова за 7,3 минуты (скорость 43 мили/час). Когда ты приедешь домой, вы находитесь в 0 милях от исходной точки, и, очевидно, ваша средняя скорость:

Средняя скорость пикапа, оставленного в гараже также 0 миль/час. Поскольку средняя скорость тела зависит только от его начальное и конечное положение и время, а не движение объекта в между, это вообще не полезный параметр. Более полезное количество мгновенная скорость объекта при данной мгновенный. Мгновенная скорость – это значение, при котором средняя скорость приближается по мере того, как интервал времени, в течение которого он измеряется, приближается к нулю:

Например: см. пример задачи 2-5 .

Теперь можно рассчитать скорость объекта при t = 3,5 с:

Скорость объекта определяется с точки зрения изменения положение этого объекта во времени. Величина, используемая для описания изменения скорость тела во времени есть ускорение а. среднее ускорение за интервал времени между t ₁ и t ₂ определяется как:

Обратите внимание на сходство между определением средней скорости и определение среднего ускорения. мгновенный ускорение a определяется как:

Из определения ускорения видно, что ускорение имеет следующие единицы измерения:

Положительное ускорение обычно интерпретируется как означающее увеличение скорости. Однако это неверно. Из определения ускорение, можно сделать вывод, что ускорение положительно, если

Это, очевидно, верно, если скорости положительны, а скорость увеличивается со временем. Однако это верно и для отрицательных скоростей, если скорость становится менее отрицательной с течением времени.

Объекты, падающие под действием силы тяжести, являются одним из примеров объектов движется с постоянным ускорением. Постоянное ускорение означает, что ускорение не зависит от времени:

Интегрируя это уравнение, скорость объекта может быть получено:

где v ₀ — скорость объекта в момент времени t = 0. Из скорость, положение объекта как функцию времени можно рассчитано:

где x ₀ — положение объекта в момент времени t = 0,

Примечание 1 : проверить эти отношения, интегрируя формулы для положение и скорость.

Примечание 2 : уравнения движения лежат в основе большинства задач (см. пример задачи 7).

Пример задачи 2-8

Заметив полицейскую машину, вы тормозите Porsche с 75 км/ч до 45 км/ч. на дистанции 88 м. а) Чему равно ускорение, если считать его постоянным? б) Сколько времени прошло? c) Если вы продолжаете замедляться с ускорение, рассчитанное в (а) выше, сколько времени пройдет, чтобы привести машина отдыхает с 75 км/ч? d) В (c) выше, какое расстояние будет покрытый ? д) Предположим, что при втором испытании с рассчитанным ускорением в (а) выше и с другой начальной скоростью, вы останавливаете свой автомобиль после прохождение 200 м. Каково было общее время торможения?

а) Нашими отправными точками являются уравнения движения:

(1)

(2)

Предоставляется следующая информация:

* v(t = 0) = v ₀ = 75 км/ч = 20,8 м/с

* v(t ₁ ) = 45 км/ч = 12,5 м/с

* x(t = 0) = x ₀ = 0 м (Примечание: начало координат определяется как положение Porsche при t = 0 с)

* х(т ₁ ) = 88 м

* а = константа

Из уравнения (1) получаем:

(3)

Замените (3) в (2):

(4)

Из уравнения (4) мы можем получить ускорение a:

(5)

б) Подставьте уравнение (5) в уравнение (3):

(6)

в) Автомобиль находится в состоянии покоя в момент времени t ₂ :

(7)

Подставив ускорение, рассчитанное с использованием уравнения (5), в уравнение (3):

(8)

d) Подставьте t ₂ (из уравнения (8)) и a (из уравнения (5)) в уравнение (2):

(9)

д) Предоставляется следующая информация:

* v(t ₃ ) = 0 м/с (Примечание: Porsche в состоянии покоя при t = t ₃ )

* x(t = 0) = x ₀ = 0 м (Примечание: начало координат определяется как положение Porsche при t = 0)

* х(т ₃ ) = 200 м

* a = постоянная = — 1,6 м/с ²

^{Уравнение (1) говорит нам:}

(10)

Подставьте уравнение (10) в уравнение (2):

(11)

Теперь можно легко вычислить время t ₃ :

(12)

Частным случаем постоянного ускорения является свободное падение (падение в вакуум). В задачах о свободном падении направление свободного падения определяется вдоль оси Y, и положительное положение вдоль оси Y соответствует восходящему движению. Ускорение свободного падения (g) равно 9,8. м/с ² (по отрицательной оси ординат). Уравнения движения на свободе fall очень похожи на рассмотренные ранее для постоянных ускорение:

где y ₀ и v ₀ — положение и скорость объекта в момент времени t = 0,

Пример

Питчер подбрасывает бейсбольный мяч вертикально вверх с начальной скоростью 25 м/с. (а) Сколько времени нужно, чтобы достичь высшей точки? б) на какой высоте находится мяч подняться выше точки его выброса? в) Через какое время мяч достигнет точка на 25 м выше точки его выброса.

Рисунок 2.4. Вертикальное положение бейсбольного мяча как функция времени.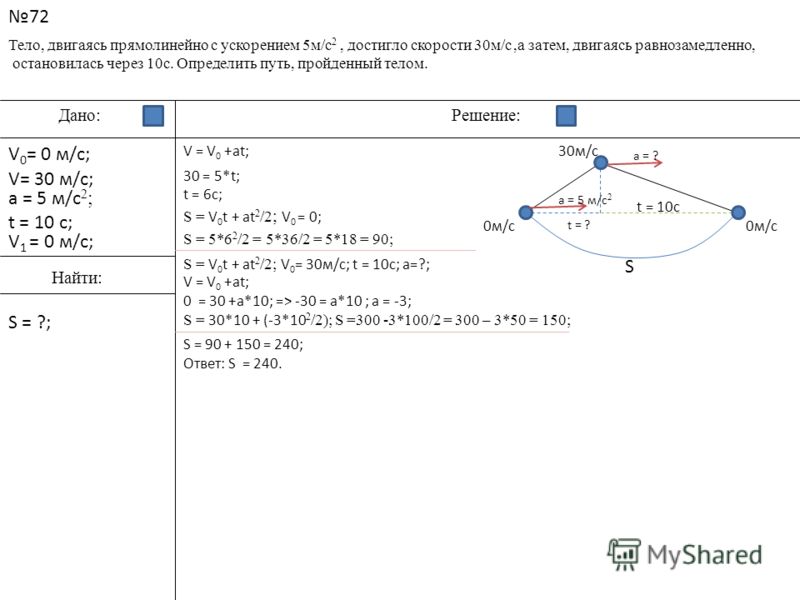

а) Нашими отправными точками являются уравнения движения:

Начальные условия:

* v(t = 0) = v ₀ = 25 м/с (движение вверх)

* y(t = 0) = y ₀ = 0 м (Примечание: начало координат определяется как положение мяча в т = 0)

* г = 90,8 м/с ²

Высшая точка получена в момент времени t = t ₁ . В этот момент скорость равна нулю:

Мяч достигает высшей точки через 2,6 с (см. рис. 2.4).

б) Положение шара в момент t ₁ = 2,6 с легко определить. рассчитано:

c) Уравнение для y(t) можно легко переписать как:

где у — высота мяча в момент времени t. Это уравнение может быть легко решается для t:

Используя начальные условия, указанные в (а), это уравнение можно использовать для расчета времени достижения мячом высоты 25 м (y = 25 м):

t = 1,4 с

t = 3,7 с

Рис.