2

График функции с модулем | Алгебра

Построить график функции с модулем — один из видов задания 23 ОГЭ по математике.

Рассмотрим примеры таких заданий.

1) Постройте график функции

   

и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.

Решение:

Область определения функции D(y): x∈R.

1)Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль:

x-2=0,  x=2.

Найдём значение функции при x=2.

y(2)=5·0-2²+5∙2-3∙0-6=0.

Получили точку (2;0).

2) Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает положительные значения.

Если x-2>0, то есть при x>2, |х-2|=x-2,

y=5|х-2|-x²+5x-6=5(х-2)-x²+5x-6=5х-10-x²+5x-6=-x²+10x-16.

y=-x²+10x-16 — квадратичная функция. График — парабола ветвями вниз (так как a=-1<0).

Координаты вершины параболы

   

   

то есть вершина параболы — точка (5;9). От вершины строим график функции y=-x² (так как a=-1).

3)Ищем промежутки, в которых выражение, стоящее под знаком модуля, принимает отрицательные значения.

Если x-2<0, то есть при x<2, |х-2|=-(x-2),

y=5|х-2|-x²+5x-6=-5(х-2)-x²+5x-6=-5х+10-x²+5x-6=-x²+4.

y=-x²+4 — квадратичная функция. График — парабола ветвями вниз.

Координаты вершины параболы

   

   

то есть вершина параболы — точка (0;4). От вершины строим график функции y=-x².

Прямая x=2 разбивает координатную плоскость на две полуплоскости. Слева от неё, для x<2,  строим параболу y=-x²+4, справа, для x>2 — параболу y=-x²+10x-16:

График функции с модулем можно рассматривать и как график кусочной функции:

   

   

   

Прямая y=m имеет с графиком ровно три общие точки при m=0 и m=4:

Ответ: 0; 4.

2) Постройте график функции

   

и определите, при каких значениях m прямая y=m имеет с графиком ровно три общие точки.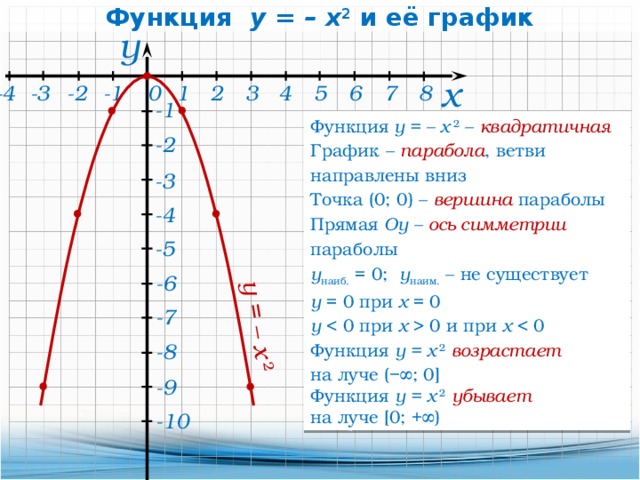

Решение:

Область определения функции D(y): x∈R.

1) Ищем значение, при котором выражение, стоящее под знаком модуля, обращается в нуль:

   

   

   

|6x+1|=6x+1 и y=x²-(6x+1)=x²-6x-1.

y=x²-6x-1 — квадратичная функция. График — парабола ветвями вверх (поскольку a=1>0).

Координаты вершины параболы

   

   

Так как a=1, от вершины (3;-10) строим график y=x².

   

|6x+1|=-(6x+1) и y=x²+(6x+1)=x²+6x+1.

y=x²+6x+1 — квадратичная функция. График — парабола ветвями вверх.

Координаты вершины параболы

   

   

от вершины (-3;-8)  строим график y=x².

Или:

   

   

 

Прямая y=m имеет с графиком ровно три общие точки при m=1/30 и m=-8:

Ответ: -8; 1/36.

3) Постройте график функции

   

и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.

Решение:

Область определения функции D(y): x∈R.

1) Если x=0, y=|0|·0+3·|0|-5·0=0.

2) Если x>0, |x|=x, y=x·x+3·x-5·x=x²-2x.

y=x²-2x — квадратичная функция. График — парабола ветвями вверх (a=1>0).

Координаты вершины параболы

   

   

От вершины (1;-1) строим параболу y=x² (так как a=1).

3) Если x<0, |x|=-x, y=-x·x+3·(-x)-5·x=-x²-8x.

y=-x²-8x — квадратичная функция. График — парабола ветвями вниз (a=-1<0).

Координаты вершины параболы

   

   

От вершины (-4;16) строим параболу y=-x² (так как a=-1).

Таким образом, график данной функции представляет собой комбинацию двух парабол: справа от прямой x=0 (оси Oy) — y=x²-2x, слева — y=-x²-8x:

Альтернативный вариант:

   

   

   

Прямая y=m имеет с графиком ровно две общие точки, когда она проходит через вершины парабол, то есть при m=-1 и m=16:

Ответ: -1; 16.

4) Построить график функции y=|x²+2x-3|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?

Решение:

Область определения функции D(y): x∈R.

Построим график функции y=x²+2x-3.

Эта функция — квадратичная. Её графиком является парабола, ветви которой направлены вверх.

Координаты вершины параболы

   

   

, то есть вершина параболы — точка (-1;-4).

От вершины строим график функции y=x²:

График функции y=|x²+2x-3| может быть получен из графика функции y=x²+2x-3 следующим образом: часть графика, расположенную выше оси Ox, сохраняем. Часть, расположенную ниже оси Ox, отображаем симметрично относительно оси Ox.

Или y=|x²+2x-3|

   

   

Вершина параболы (-1;-4) при этом переходит в точку (-1;4):

Наибольшее число общих точек, которое график данной функции может иметь с прямой, параллельной оси абсцисс, равно 4 (например, прямая y=3 пересекает график в четырёх точках).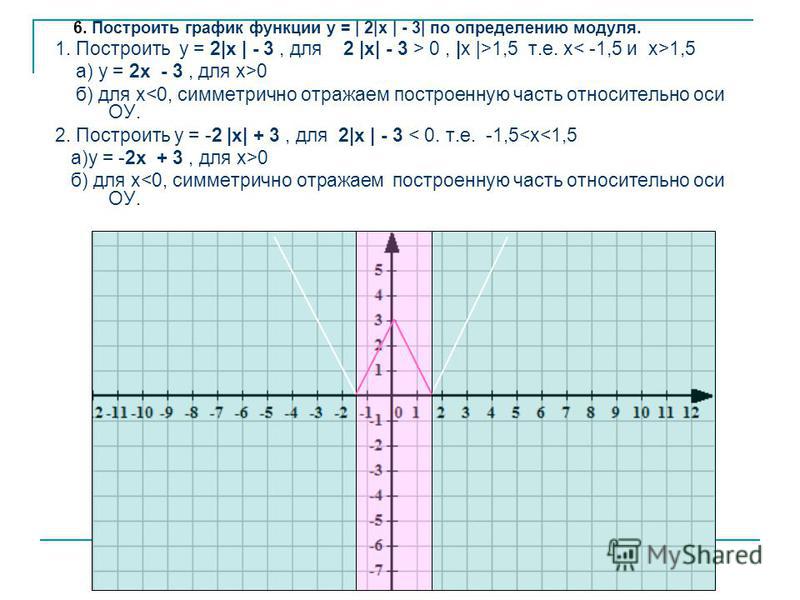

Ответ: 4.

Рубрика: ОГЭ задание 22 | Комментарии        

Функция модуля — формула, график, свойства, примеры

Функция модуля дает величину числа независимо от его знака. Ее также называют функцией абсолютного значения. В математике модуль действительного числа x задается функцией модуля , обозначаемой |x|. Это дает неотрицательное значение x. Модуль или абсолютное значение числа также рассматривается как расстояние числа от начала координат или нуля.

В этой статье мы узнаем об определении функции модуля, вычислении модуля для чисел, переменных и полиномов, а также решенных примерах и вопросах функции модуля.

1. Что такое функция модуля?
2. Формула функции модуля
3. Домен и диапазон функции модуля
4. Применение модульной функции
5. График функции модуля
6.		 Свойства функции модуля
7. Производная и интеграл функции модуля
8. Часто задаваемые вопросы о модульной функции

Что такое функция модуля?

Функция модуля , которая также называется функцией абсолютного значения, дает модуль или абсолютное значение числа независимо от того, является ли число положительным или отрицательным. Он всегда дает неотрицательное значение любого числа или переменной. Функция модуля обозначается как y = |x| или f(x) = |x|, где f: R → (0,∞) и x ∈ R.

|х| — модуль x, где x — действительное число. Если x неотрицательно, то f(x) будет иметь то же значение x. Если x отрицательно, то f(x) будет величиной x, то есть f(x) = -x, если x отрицательно. Подытожим приведенную ниже формулу функции модуля.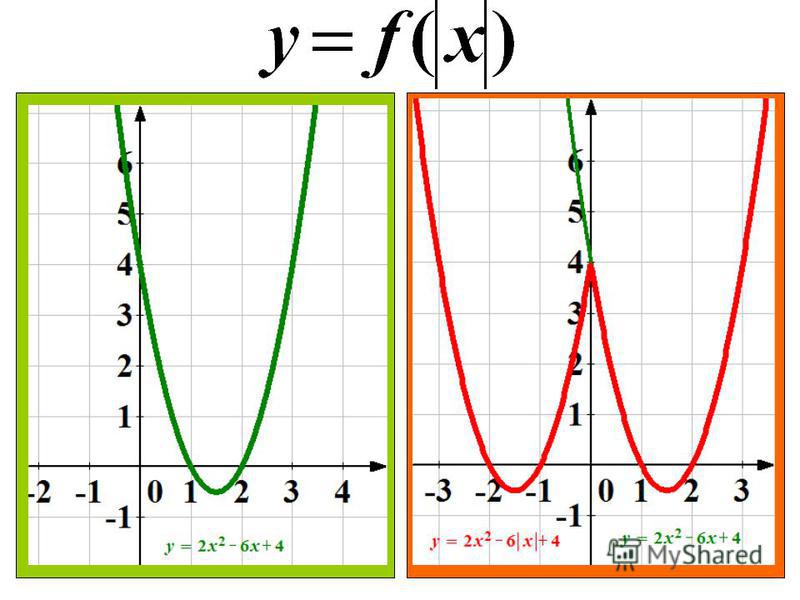

Формула функции модуля

Значение функции модуля всегда неотрицательно. Если f(x) является функцией модуля, то мы имеем:

  • Если x положителен, то f(x) = x
  • Если х = 0, то f(x) = 0
  • Если х < 0, то f(x) = -x

Это означает, что если значение x больше или равно 0, то функция модуля принимает фактическое значение, но если x меньше 0, функция принимает фактическое значение ‘x’ с минусом.

Домен и диапазон функции модуля

Мы можем применить функцию модуля к любому вещественному числу. Диапазон функции модуля — это набор неотрицательных действительных чисел, который обозначается как (0, ∞), а область определения функции модуля — R (где R относится к набору всех действительных чисел). Следовательно, область определения функции модуля равна

R и диапазон (0,∞).

Применение модульной функции

Теперь, когда мы знаем формулу функции модуля, давайте рассмотрим несколько примеров, чтобы понять ее применение. Шаги для вычисления функции модуля приведены ниже:

Пример: Рассмотрим функцию модуля f(x) = |x|.

  • Если x = − 3, то y = f(x) = f(−3) = −(−3) = 3, здесь x меньше 0.
  • Если x = 3, то y = f(x) = f(3) = 3, здесь x больше 0
  • Если x = 0, то y = f(x) = f(0) = 0, здесь x равно 0

Обратите внимание, что здесь f(-3) = f(3). Другими словами, |3| = |-3| = 3.

График функции модуля

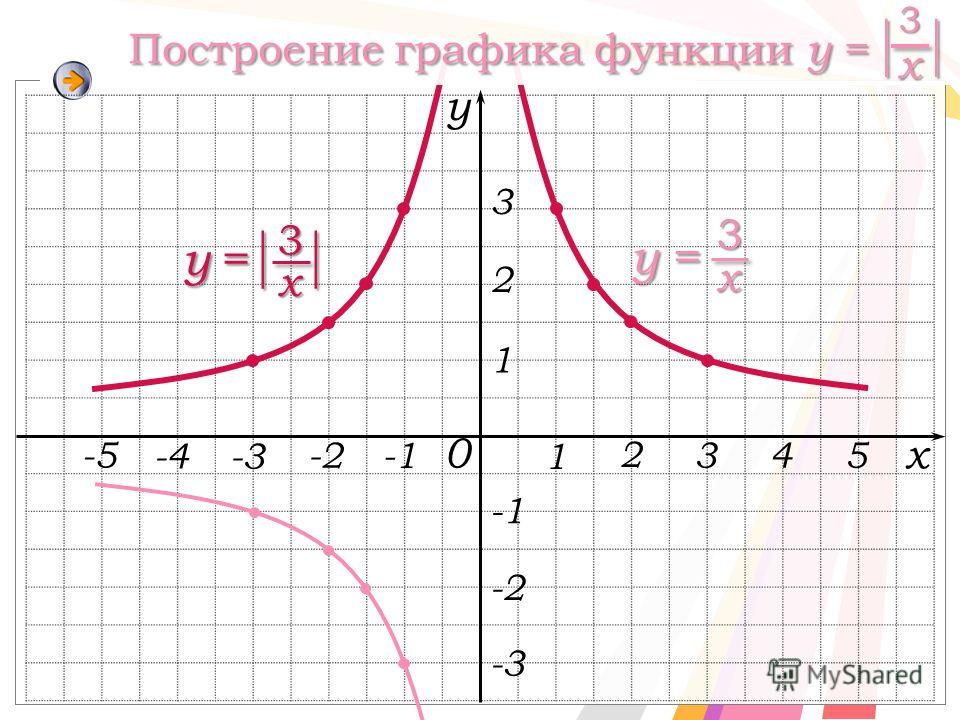
Теперь давайте посмотрим, как построить график для функции модуля. Давайте рассмотрим x как переменную, принимающую значения от -5 до 5. Вычисляя модуль для положительных значений «x», линия на графике представляет собой «y = x», а для отрицательных значений «x» на графике изображена линия «y = -x».

х f(x) = |x|
-5 5
-4 4
-3 3
-2 2
-1 1
0 0
1 1
2 2
3 3
4 4
5 5

Свойства функции модуля

Теперь, когда у нас есть формула для функции модуля и график функции модуля, давайте теперь исследуем свойства функции модуля:

Производная и интеграл функции модуля

Поскольку мы знаем, что функция модуля f(x) = |x| равно x, если x > 0, и -x, если x < 0, поэтому производная функции модуля равна 1, если x > 0, и -1, если x < 0.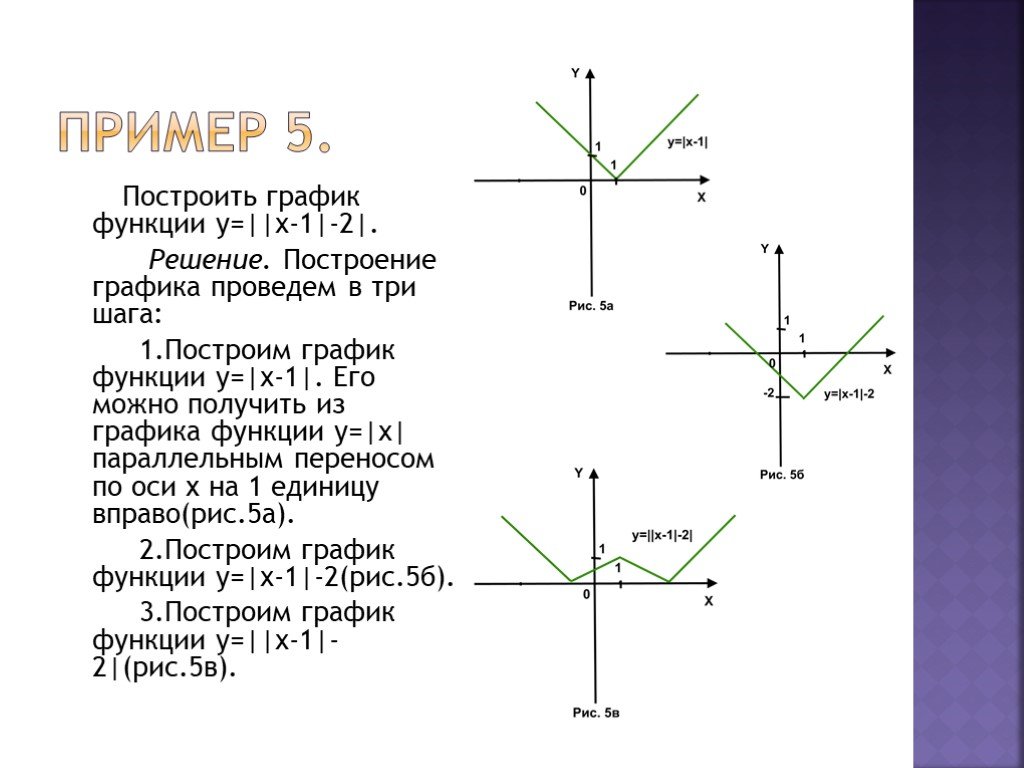 Производная функции модуля не определена для x = 0. Следовательно, производная функции модуля может быть записана как d(|x|)/dx = x/|x| , для всех значений x и x, не равных 0.

Используя формулу функции модуля и формулы интегрирования, интеграл функции модуля равен (1/2)x 2 + C, если x ≥ 0, и его интеграл равен -(1/2)x 2 + C, если x < 0. Таким образом, интегрирование функции модуля может быть выражено как:

  • ∫|x| dx = (1/2)x 2 + C, если x ≥ 0
  • ∫|х| dx = -(1/2)x 2 + C, если x < 0

Важные замечания о функции модуля

  • Функция модуля также называется функцией абсолютного значения и представляет собой абсолютное значение числа. Обозначается |x|.
  • Областью определения модульных функций является множество всех действительных чисел.
  • Диапазон функций модуля — это набор всех действительных чисел, больших или равных 0.
  • Вершина графика модулей y = |x| равно (0,0).
  • Вершина функции модуля y = a |x — h| + k равно (h, k).

Тема, связанная с функцией модуля

  • Модуль комплексного числа
  • Калькулятор абсолютного значения
  • Калькулятор модов

Часто задаваемые вопросы о модульной функции

Что такое функция модуля?

Функция модуля дает модуль или абсолютное значение числа независимо от того, является число положительным или отрицательным. Функция модуля обозначается как y = |x| или f(x) = |x|, где f: R → R и x ∈ R. Это также называется функцией абсолютного значения.

Что такое домен и диапазон функции модуля?

Областью определения функции модуля является R (где R относится к набору всех положительных действительных чисел), а диапазон функции модуля представляет собой набор неотрицательных действительных чисел, который обозначается как (0,∞).

Что такое интегрирование модульной функции?

Интегрирование функции модуля зависит от значения x.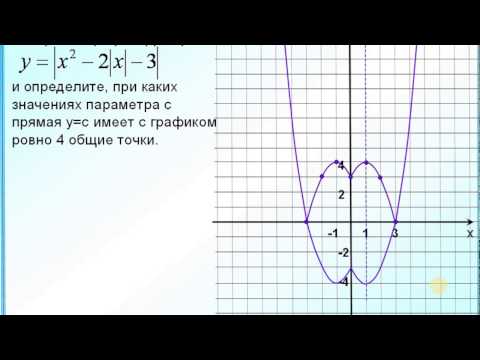 Это:

  • ∫|x| dx = (1/2)x 2 + C, если x ≥ 0
  • ∫|х| dx = -(1/2)x 2 + C, если x < 0

Как дифференцировать функцию модуля?

Имеем f(x) = |x| равно x, если x > 0, и -x, если x < 0, следовательно, производная модульной функции равна 1, если x > 0, и -1, если x < 0. Производная модульной функции не определена для x = 0 Подводя итог, можно сказать, что производная функции модуля |x| равно x/|x|, где x не равно 0.

Всегда ли функция модуля положительна?

Модуль положительного числа положителен. Модуль отрицательного числа получается при игнорировании знака минус. Таким образом, функция модуля всегда положительна.

Почему функция модуля не дифференцируема?

Функция модуля |x| не дифференцируема при x = 0, так как график Mod(x) имеет острую точку при x = 0. Кроме того, левый и правый предел производной не равны при x = 0.

Как вы решаете задачи на модульную функцию?

Задачи модульных функций можно решить, применяя модуль к неотрицательному числу, а отрицательное число всегда дает одно и то же число.

Как построить график функции модуля?

Возьмем несколько положительных и отрицательных значений x. Также возьмем x = 0. Создайте таблицу с двумя столбцами x и y со всеми случайными значениями x, которые мы выбрали. Вычислите модуль каждого числа и заполните столбец y. Затем просто начертите все упорядоченные пары (x, y) и соедините их линиями. Мы получим V-образный график, и это график функции модуля.

Модульные функции: определение, уравнение и правила

Модульные функции (также известные как функции абсолютного значения) обычно представляются как f(x)=|x|. Модуль числа x будет числом той же величины, но положительным.

Но что стоит за этим? Это происходит потому, что он представляет собой расстояние от нуля до числа x на числовой прямой.

Расстояние от нуля до 2 равно 2, и расстояние от нуля до -2 также равно 2, поэтому f(2)=|2|=2 и f(-2)=|-2|=2

Модуль функция на числовой прямой, Марилу Гарсиа Де Тейлор — StudySmarter Originals

Вот почему |x| представляет собой значение числа x независимо от его знака.

Если у вас есть выражение внутри функции модуля, вычислите значение внутри, а затем найдите положительную версию результата.

Если у вас есть функция f(x)=|x-3|+1 findf(-2)

f(-2)=|-2-3|+1

f(-2)=|- 5|+1=5+1=6

Уравнение модульной функции

Уравнение модульной функции обозначается следующим образом:

f(x)=|x|=xifx≥0-xifx<0

Домен модульной функции — это набор всех действительных чисел, а диапазон — это набор всех действительных чисел, больших или равных нулю. Из уравнения мы можем сказать, что если число внутри функции модуля уже положительное, вы оставляете его таким, но если число отрицательное, то результатом будет положительная версия этого числа (как если бы вы умножали отрицательное число на -1).

Свойства модульных функций

Свойства модульных функций:

|4|=4,|-5|=5

|x|=|-x|=x

|4|=|-4 |=4

|axb|=|a|x|b|

|2(-3)|=|2|×|-3||-6|=2×36=6

|ab|=|a||b|

|-93|=|-9||3||-3|=933=3

|a±b|≠|a|±|b|

Сумма:

|1+(-2)|≠|1|+|-2||-1|≠1+21≠3

Вычитание:

|1-(-2) |≠|1|-|-2||3|≠1-23≠-1

Имея в виду, что значение x внутри функции модуля может быть как положительным, так и отрицательным, вам необходимо решить уравнение с учетом обоих случаев, поэтому вы получите два решения.

Для уравнения |3x-2|=4 можно получить 2 возможных решения следующим образом:

1) Решение 1:

3x-2=43x=4+23x=6x=63x=2

2) Решение 2:

-(3x-2)=4-3x+2=4-3x=4-2-3x=2x=-23

Как построить график функций модуля?

Чтобы нарисовать график функции модуля, вам нужно подставить значения x в f(x)=|x|, чтобы получить соответствующие значения y, поскольку y=f(x). Вы получите таблицу значений x и y, которые вам нужно будет нанести на координатную плоскость. We will substitute the values ​​of x from -2 to 2.

x y
-2 2
-1 1
0 0
1 1
2 2

График функции модуля, Марилу Гарсия Де Тейлор — StudySmarter Originals

=ax+b, и отразите часть линии, которая идет ниже оси x, в ось x.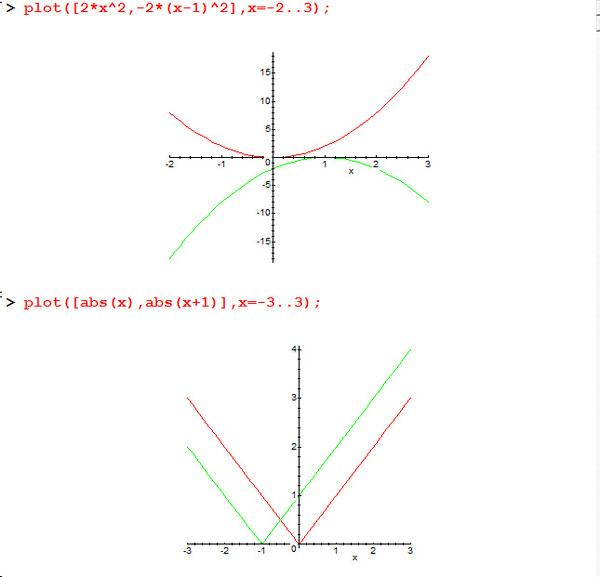

Нарисуйте график для y=|x-1| показывая точки, где они пересекают оси координат.

Не обращая внимания на модуль, нужно нарисовать график y=x-1

  • Когда y=0, x=1

Линия пересекает ось x в точке (1, 0)

  • Когда x=0, ⁣y=-1

Линия пересекает y -ось в точке (0, -1)

Пример графика функции модуля, Марилу Гарсиа Де Тейлор — StudySmarter Originals

  • Для отрицательных значений y отразите по оси x. В этом случае (0, -1) становится (0, 1)

Пример графика модульной функции, Марилу Гарсиа Де Тейлор — StudySmarter Originals

Решение уравнений с использованием модульных функций

Если у вас есть уравнение типа |3x-1|=5, вы можете использовать его график, чтобы найти его решение, выполнив следующие действия:

Решение уравнений с использованием модульных функций, Марилу Гарсия Де Taylor — StudySmarter Originals

  • Определите точки пересечения двух графиков. В этом случае A соответствует точке пересечения между y = 5 и исходным участком графика |3x-1|=3x-1, а B представляет пересечение между y=5 и отраженным участком графика |3x-1|=-(3x-1).

  • Найдите оба решения:

A: 3x -1 = 5

3x = 5+1

3x = 6

x = 63

x = 2

B: -63

x = 2

B: — (3x-1)=5

-3x+1=5

-3x=5-1

-3x=4

x=-43

Решение неравенств с использованием модульных функций

Основываясь на предыдущем примере, теперь мы собираемся решить неравенство |3x-1|>5. Вам нужно действовать так же, как и раньше, чтобы найти значения x в точках пересечения A и B, которые равны x=2 и x=-43.

После того, как у вас есть точки пересечения, вы можете посмотреть на график, чтобы определить значения x, которые удовлетворяют неравенству |3x-1|>5.

Решение неравенств с использованием модульных функций, Марилу Гарсиа Де Тейлор — StudySmarter Originals

Неравенство верно, когда график y=|3x-1| находится выше графика y=5, это происходит при x<-43 или x>2. В записи множества: {x:x<-43}∪{x:x>2}

Обратная функция модуля

обратная функция модуля не является функцией , если вы не ограничите ее область определения так, чтобы она могла быть взаимно однозначной функцией. Чтобы добиться этого, нам нужно ограничить область его применения только половиной графа. Вы можете выбрать любую половину, если она не указана в вопросе.

Найдите обратную функцию f(x)=|x+1|

Обратные функции модуля, Марилу Гарсия Де Тейлор — StudySmarter Originals

Мы ограничим область определения функции только отраженным участком графика (слева от x = -1), который можно обозначить как f(x)=-(x+1) для x≤-1. Теперь мы можем найти обратную, потому что этот участок графика является взаимно однозначной функцией.

Выполните шаги, чтобы найти обратную функцию:

  • Замените f (x) на y

f(x)=-(x+1)

y=-(x+1)

  • Поменяйте местами x и y и найдите y

x=-(y+1)

x=-y-1

y=-x-1

f-1(x)=-x-1 Это функция, обратная f(x)=|x+1|

Область определения обратной функции — это диапазон исходной функции, который равен y≥0. Следовательно, область определения обратной функции f-1(x)=-x-1 равна x≥0.

Как отличить модульную функцию?

Чтобы найти производную функции модуля, нам нужно еще раз взглянуть на уравнение функции модуля:

f(x)=|x|=xifx≥0-xifx<0

Мы знаем, что ddxx=1, поэтому можем сказать следующее:

ddx(|x|)=1ifx>0-1ifx<0Notdefinedifx=0

В общем случае ddx(|x|)=x|x| для всех значений x, кроме x=0

Если мы подставим некоторые значения x в предыдущее уравнение, то увидим, что утверждения в приведенной выше кусочной функции верны:

ddx(|-1|)=-1 |-1|=-11=-1

ddx(|0|)=0|0|=00=undefined

ddx(|1|)=1|1|=11=1

Как интегрировать модульная функция?

Чтобы найти интеграл модульной функции, мы можем действовать следующим образом:

Мы знаем, что модульная функция определяется следующим образом:

f(x)=|x|=xifx≥0-xifx<0

Следовательно, нам нужно вычислить интеграл для x и -x.