Диагональ ас параллелограмма авсд образует с его сторонами углы 35 и 40: Диагональ AC параллелогамма ABCD образует с его сторонами углв, равные 35 грдусам и 40 градусам….

1: Модуль Геометрия. Задание 9

1. B 6 № 89. Найдите больший угол равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной AB углы, равные 30° и 45° соответственно.

Ответ: 105

2. B 6 № 118. В треугольнике ABC угол C прямой, BC = 8 , sin A = 0,4.   Найдите AB.

Ответ: 20

3. B 6 № 141. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.

Ответ: 65

4. B 6 № 144. В треугольнике ABC угол C прямой, AC = 8, cosA = 0,4. Найдите AB.

Ответ: 20

5. B 6 № 193. Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.

Ответ: 80

6. B 6 № 132773. Два острых угла прямоугольного треугольника относятся как 4:5.

Найдите больший острый угол. Ответ дайте в градусах.

Ответ: 50

7. B 6 № 132774. Разность углов, прилежащих к одной стороне параллелограмма, равна 40°. Найдите меньший угол параллелограмма. Ответ дайте в градусах.

Ответ: 70

8. B 6 № 132775. Один угол параллелограмма в два раза больше другого. Найдите меньший угол. Ответ дайте в градусах.

Ответ: 60

9. B 6 № 132776. Сумма двух углов равнобедренной трапеции равна 140°. Найдите больший угол трапеции. Ответ дайте в градусах.

Ответ: 110

10. B 6 № 132777. Сумма двух углов равнобедренной трапеции равна 220°. Найдите меньший угол трапеции. Ответ дайте в градусах.

Ответ: 70

11. B 6 № 132778. Найдите меньший угол равнобедренной трапеции, если два ее угла относятся как 1:2. Ответ дайте в градусах.

Ответ: 60

12. B 6 № 132779. Сумма трех углов выпуклого четырехугольника равна 300°. Найдите четвертый угол. Ответ дайте в градусах.

Ответ: 60

13. B 6 № 132781. В выпуклом четырехугольнике ABCD , , , . Найдите угол A. Ответ дайте в градусах.

Ответ: 95

14. B 6 № 132782. Углы выпуклого четырехугольника относятся как 1:2:3:4. Найдите меньший угол. Ответ дайте в градусах.

Ответ: 36

15. B 6 № 132783. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.

Ответ: 122

16. B 6 № 311320. В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите .

Ответ: 120

17. B 6 № 311343. В равностороннем треугольнике  ABC  медианы  BK  и  AM  пересекаются в точке O. Найдите .

Ответ: 60

18. B 6 № 311355. Биссектрисы углов N и M треугольника  MNP  пересекаются в точке  A. Найдите  , если  , а  

Ответ: 117

19. B 6 № 311365. Биссектрисы углов B и C треугольника  ABC  пересекаются в точке  K.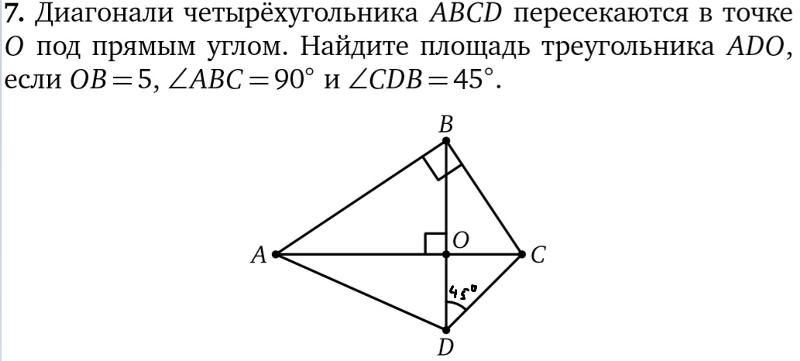

Найдите  , если  , а  

Ответ: 120

20. B 6 № 311412. Углы, отмеченные на рисунке одной дугой, равны. Найдите угол α. Ответ дайте в градусах.

Ответ: 40

21. B 6 № 311455. Найдите угол  ABC  равнобедренной трапеции  ABCD, если диагональ  AC  образует с основанием  AD и боковой стороной  CD  углы, равные 30° и 80° соответственно.

Ответ: 110

22. B 6 № 311456. Найдите угол  ABC  равнобедренной трапеции  ABCD, если диагональ  AC  образует с основанием  AD  и боковой стороной  CD  углы, равные 20° и 100° соответственно.

Ответ: 120

23. B 6 № 311457. Найдите меньший угол равнобедренной трапеции  ABCD, если диагональ  AC  образует с основанием  BC  и боковой стороной  CD  углы, равные 30° и 105° соответственно.

Ответ: 45

24. B 6 № 311458. Диагональ  AC  параллелограмма  ABCD  образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.

Ответ: 105

25. B 6 № 311459. Диагональ  BD  параллелограмма  ABCD  образует с его сторонами углы, равные 50° и 85°. Найдите меньший угол параллелограмма.

Ответ: 45

26. B 6 № 311460. Диагональ  AC  параллелограмма  ABCD  образует с его сторонами углы, равные 45° и 25°. Найдите больший угол параллелограмма.

Ответ: 110

27. B 6 № 311476. Углы, отмеченные на рисунке одной дугой, равны. Найдите угол  . Ответ дайте в градусах.

Ответ: 40

28. B 6 № 311514. На плоскости даны четыре прямые. Известно, что  ,  ,  . Найдите  . Ответ дайте в градусах.

Ответ: 125

29. B 6 № 311680.

В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ABC. Ответ дайте в градусах.

Ответ: 66

30. B 6 № 311759. Четырёхугольник ABCD вписан в окружность.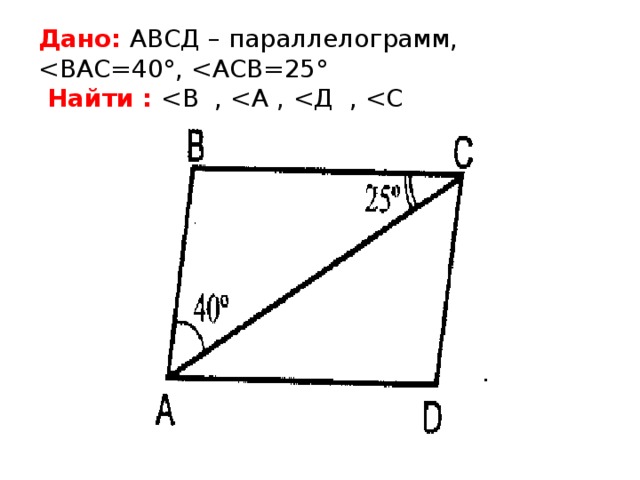 Угол ABC равен 136°, угол CAD равен 82°. Найдите угол ABD. Ответ дайте в градусах.

Ответ: 54

31. B 6 № 311847. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 71°, угол CAD равен 61°. Найдите угол ABC. Ответ дайте в градусах.

Ответ: 132

32. B 6 № 311911.

В параллелограмме ABCD проведена диагональ AC. Угол DAC равен 47°, а угол CAB равен 11°. Найдите больший угол параллелограмма ABCD. Ответ дайте в градусах.

Ответ: 122

33. B 6 № 311955.

Тангенс острого угла прямоугольной трапеции равен   Найдите её большее основание, если меньшее основание равно высоте и равно 15.

Ответ: 33

34. B 6 № 314838. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 25° и 30°. Найдите больший угол параллелограмма.

Ответ: 125

35. B 6 № 314844. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.

Ответ: 65

36. B 6 № 314846. Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.

Ответ: 70

37. B 6 № 314863. Найдите угол АВС равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной CD углы, равные 20° и 100° соответственно.

Ответ: 120

38. B 6 № 314980. Сторона ромба равна 34, а острый угол равен 60° . Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?

Перечислите эти длины в ответе через точку с запятой в порядке возрастания.

Ответ: 17;17

39. B 6 № 315005. Найдите меньший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной CD углы, равные 30° и 105° соответственно.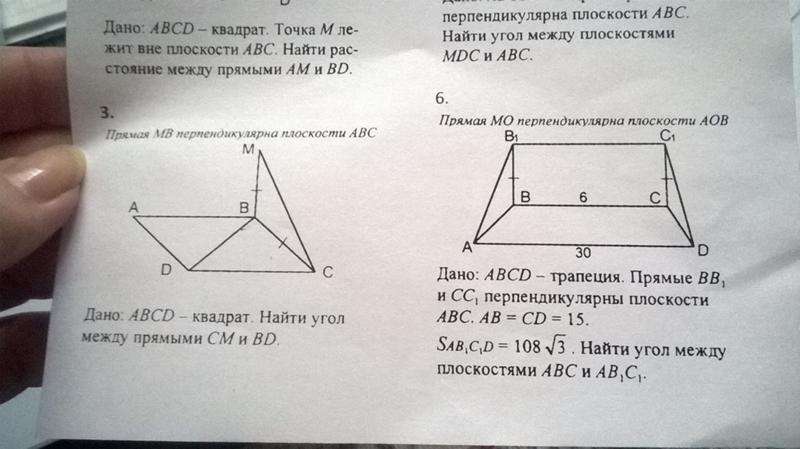

Ответ: 45

40. B 6 № 315026. В треугольнике ABC угол C прямой, BC = 3 , cosB = 0,6. Найдите AB.

Ответ: 5

41. B 6 № 315032. В треугольнике ABC угол C прямой, BC = 9 , sinA = 0,3 . Найдите AB.

Ответ: 30

42. B 6 № 315038. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 60° и 55°. Найдите меньший угол параллелограмма.

Ответ: 65

43. B 6 № 315068. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите больший угол параллелограмма.

Ответ: 115

44. B 6 № 315099. Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.

Ответ: 115

45. B 6 № 315100. В треугольнике ABC угол C прямой, AC = 8 , cosA = 0,4.

Найдите AB.

46. B 6 № 316229. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 19°, угол CAD равен 35°. Найдите угол ABC. Ответ дайте в градусах.

Ответ: 54

47. B 6 № 316256. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 71°, угол CAD равен 61°. Найдите угол ABC. Ответ дайте в градусах.

Ответ: 132

48. B 6 № 316282. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 14°, угол CAD равен 30°. Найдите угол ABC. Ответ дайте в градусах.

Ответ: 44

49. B 6 № 316283. В треугольнике ABC угол C равен 90°, BC = 12 , tgA = 1,5. Найдите AC.

Ответ: 8

50. B 6 № 316319. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 80°, угол CAD равен 54°. Найдите угол ABD. Ответ дайте в градусах.

Ответ: 26

51. B 6 № 316345. На продолжении стороны AD параллелограмма ABCD за точкой D отмечена точка E так, что DC = DE. Найдите больший угол параллелограмма ABCD, если ∠DEC = 53°. Ответ дайте в градусах.

Ответ: 106

52. B 6 № 316371. На продолжении стороны AD параллелограмма ABCD за точкой D отмечена точка E так, что DC = DE. Найдите больший угол параллелограмма ABCD, если ∠DEC = 27°. Ответ дайте в градусах.

Ответ: 126

Параллелограмм в геометрии и свойства параллелограмма

Определение: параллелограмм — это четырехугольник, у которого противолежащие стороны попарно параллельны, является геометрической фигурой.

Высотой параллелограмма называется перпендикуляр, опущенный из его вершины на прямую, содержащую противолежащую ей сторону. В этой статье мы рассмотрим основные свойства параллелограмма и решим задачи, с опорой на эти свойства.

Четырехугольник ABCD — параллелограмм.
BH — высота.

Изучение этой геометрической фигуры начинается в 8 классе, однако знакомство с ней происходит еще в дошкольный период, например, когда мы видим этот четырехугольник в элементах конструктора, а можем сами получить такую фигуру, если прикрепить стороны прямоугольника не крепко и потянуть за одну из них, тогда перпендикулярность сторон нарушится и мы получим тот четырехугольник, который будем сегодня с вами изучать. Этот четырехугольник настолько популярен, что часто встречается в орнаментах и даже есть на флагах некоторых государств, например, на флаге острова Саба — островного государства в Карибском море.

Содержание

Свойства параллелограмма

Свойство 1

Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.

Доказательство.

Рассмотрим параллелограмм ABCD. Докажем, например, что сумма ∠A и ∠B, прилежащих к стороне AB, равна 180°.

Действительно, ∠A и ∠B являются внутренними односторонним углами при параллельных прямых АD, BC и секущей AB. В седьмом классе доказывалось, что если две параллельные прямые пересечены третьей прямой, то внутренние односторонние углы составляют в сумме 180°. Следовательно, сумма ∠А +∠B=180°. Аналогичным образом доказывается, что суммы углов параллелограмма, прилежащих к другим его сторонам, также равны 180°.

Свойство 2

У параллелограмма противоположные стороны равны и противолежащие углы равны.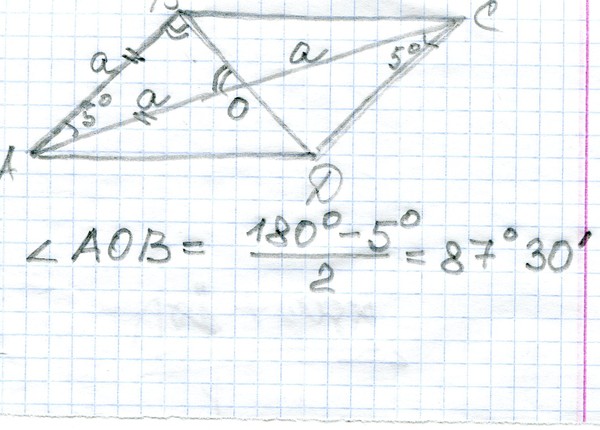

Доказательство.

Рассмотрим параллелограмм ABCD. Диагональ АС разбивает его на два треугольника АВС и CDA. Эти треугольники равны по второму признаку равенства треугольников (AC — общая сторона, ∠1=∠2, ∠3=∠4 как внутренние накрест лежащие углы при двух параллельных прямых и секущей.) Из равенства треугольников следует, что AB=CD, BC=AD и ∠B=∠D. Кроме того, ∠A=∠1+∠3=∠2+∠4=∠C.

Свойство 3

Диагонали параллелограмма в точке пересечения делятся пополам.

Доказательство.

Рассмотрим параллелограмм ABCD. Обозначим O точку пересечения диагоналей AC и BD. Треугольники AOB и COD равны по второму признаку равенства треугольников (AB=CD, ∠1=∠2, ∠3=∠4 как внутренние накрест лежащие углы при двух параллельных прямых и секущей).

Из равенства треугольников следует равенство сторон AO=OC и DO=OB. То есть диагонали точкой пересечения делятся пополам. Что и требовалось доказать.

Неправильно

В геометрии важно не только построение фигур, но и произношение их названий. Так правильно следует говорить «параллелограмм» (с двумя «л» в первом случае и с двумя «м» в конце). Неправильно писать и говорить: паралеллограм, паралелограм, в паралелограми.

Математика требует четкости во всем.

Примеры решения задач

Решим несколько задач

Задача 1

У параллелограмма две стороны равны 30 и 40 см, найдите две другие стороны.

Решение.

По второму свойству стороны данной геометрической фигуры равны, нам даны два разных числа, значит, это не противоположные стороны, а смежные. Смежные стороны четырехугольника — это те стороны, которые прилежат к одной вершине. Таким образом, мы можем сказать, что две другие стороны также будут 30 и 40 см.

Ответ: 30 см, 40 см.

Задача 2

Один из углов параллелограмма равен 45°. Найдите остальные углы параллелограмма?

Решение: Согласно первому свойству углы при одной стороне в сумме дают 180°. А также противоположные углы равны по второму свойству. Таким образом, ∠A= ∠C=45° и ∠B=∠D=180°- 45°=135°.

Ответ: 45°, 135°, 135°.

Задача 3

Диагональ параллелограмма образует с двумя его сторонами углы 15° и 35°. Найдите остальные его углы.

Решение:

Сделаем чертеж. Итак, диагональ AC делит ∠A на две части, по 15 и 35 градусов.

Вместе получается 15+35=50 градусов. Тогда противоположный ∠C тоже будет 50 градусов по второму свойству (о равенстве сторон и противоположных углов). Так как сумма внутренних углов при одной стороне 180°, то найдем: ∠B=180°-∠A=180°-50°=130°.

Таким образом, ∠D = 130°.

Ответ: 50°, 130°, 50°, 130°.

Задача 4

Найдите углы параллелограмма, если известно, что один из его углов больше другого на 20º.

Решение:

Пусть ∠A будет x, тогда ∠B= x+20. Известно, что ∠A и ∠B в сумме дают 180°. Составим уравнение:

x+x+20=180

2x+20=180

2x=180-20

2x=160

x=80

Таким образом, один ∠A= 80°, а ∠B=100°.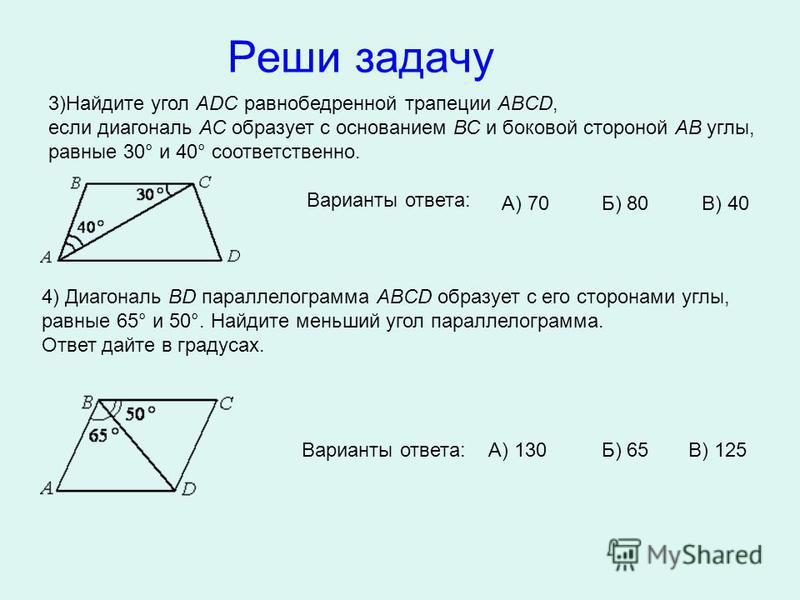 По второму свойству имеет ∠C=80° и ∠D=100°.

Ответ: 80°, 80°, 100°, 100°

Задача 5

Найдите стороны параллелограмма, если его периметр равен 48 см, а одна из его сторон больше другой на 4 см.

Решение:

Пусть одна сторона равна x см, тогда другая сторона x+4. Периметр — это сумма всех сторон, а стороны в данной геометрической фигуре попарно равны по второму свойству. Составим уравнение: 2 (x+x+4)= 48. Решим это уравнение:

2x+4=24

2x=20

x=10

Значит, одна сторона 10 см, а другая сторона будет 10+4=14 см.

Ответ: 10 см и 14 см.

Задача 6

Докажите, что биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.

Доказательство:

Нарисуем параллелограмм ABCD, и проведем биссектрису ∠A. Точку пересечения биссектрисы и стороны BC обозначим N. Требуется доказать, что треугольник ABN равнобедренный.

У равнобедренного треугольника две стороны равны и углы при основании равны. Так как AN биссектриса, то ∠1=∠2 и ∠2=∠3 (как внутренние накрест лежащие углы), отсюда ∠3=∠1. Таким образом, треугольник ABN равнобедренный.

Из того, что треугольник равнобедренный следует, что AB=BN. Это можно будет использовать при решении других подобных задач.

Что и требовалось доказать.

Частный случай параллелограмма

Частным случаем параллелограмма является ромб.

Ромб — это параллелограмм, у которого все стороны равны. Свойства ромба такие же как и свойства параллелограмма. Но есть и особенность — диагонали ромба перпендикулярны и являются биссектрисами его углов.

Изучением ромба мы займемся подробно в следующих статьях, а также докажем это свойство ромба о его диагоналях.

Заключение

В геометрии 8 класса о параллелограмме можно узнать — определение, свойства и по каким признакам определить, что перед вами именно эта геометрическая фигура. Например, нам дана такая задача — определите четырехугольник, если его диагонали пересекаются в точке O, которая делит их пополам и стороны данного четырехугольника попарно параллельны, то понятно о какой фигуре здесь идет речь. О вписанных и описанных окружностях в такой четырехугольник вы узнаете в девятом классе.

Свойства надо выучить, необязательно запоминать их порядок, главное знать содержание, уметь использовать в решении геометрических задач.

косоугольных треугольников

косоугольных треугольников

Наклонный треугольник — это любой треугольник, не являющийся прямоугольным. Это может быть остроугольный треугольник (все три угла треугольника меньше прямых) или тупоугольный треугольник (один из трех углов больше прямого). На самом деле, для целей тригонометрии класс «косоугольных треугольников» мог бы с таким же успехом включать и прямоугольные треугольники. Тогда изучение косоугольных треугольников на самом деле является изучением всех треугольников.

Примем соглашение о обозначении частей косоугольных треугольников, обобщающее правило для прямоугольных треугольников. Пусть углы обозначены А, В, и С, , а противоположные стороны обозначены а, b, и с, соответственно.

Решение косоугольных треугольников

Тригонометрия косоугольных треугольников не так проста, как прямоугольных треугольников, но есть две теоремы геометрии, которые дают полезные законы тригонометрии. Они называются «законом косинусов» и «законом синусов». Есть и другие «законы», которые использовались раньше, но с момента повсеместного использования калькуляторов этих двух законов достаточно.

Закон косинусов

Это просто сформулированное уравнение: С.

Это похоже на теорему Пифагора, за исключением последнего члена, и если C — прямой угол, последний член исчезает (поскольку косинус 90° равен 0), так что закон косинусов на самом деле является обобщением закона косинусов. Теорема Пифагора.

Обратите внимание, что каждый треугольник дает три уравнения закона косинусов, поскольку вы можете переставлять буквы по своему усмотрению. Две другие версии затем A ² = B ² + C ² 2 BC COS A, и B ² = C ^{91329 2} 9 2 2 = C

^{913191329 2} 2 2 2 = C

9 ² = C

² = C

² = C

² = .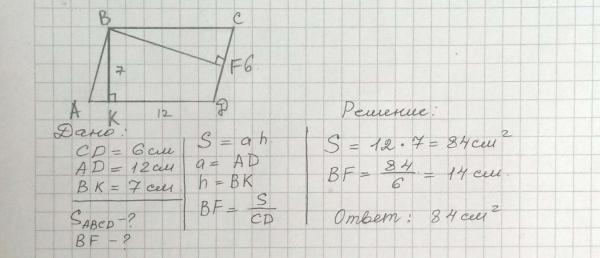 +  a ²   2 ca cos  B.

Закон косинусов связывает три стороны треугольника с одним из углов. Вы можете использовать его несколькими способами.

Во-первых, если вы знаете один угол и две смежные стороны, то вы можете определить противоположную сторону. Например, если угол C = 60°, сторона a = 5, а сторона b = 8, то по закону косинусов c ² = 25 + 64 80 cos 60°. Поскольку косинус угла 60° равен 1/2, это уравнение упрощается до c ²  = 49, поэтому c  = 7.

Во-вторых, если вы знаете все три стороны треугольника, то можете использовать их для нахождения любого угла. Например, если три стороны равны a  = 5, b  = 6 и c  = 7, то закон косинусов говорит: , с помощью калькулятора, C  = 1,3734 радиана = 78,69°.

Примечание: Если треугольник тупоугольный, то cos C отрицателен. Предположим, что три стороны равны a  = 5, b  = 6 и c  = 10. Тогда по закону косинусов 100 = 25 + 36  60 cos C, so cos C  = — 49/60 = — 0,81667. Как видно из графиков на предыдущей странице, косинус тупого угла отрицателен. Это нормально, и ваш калькулятор правильно вычислит арккосинус. Вы получите C  = 2,2556 радиана = 129,237°.

Закон синусов

Закон синусов также представляет собой просто сформулированное уравнение

син А а

=

син Б б

=

син С с

Обратите внимание, что закон синусов гласит, что три отношения равны. Как и закон косинусов, вы можете использовать закон синусов двумя способами.

Во-первых, если известны два угла и сторона, противолежащая одному из них, то можно определить сторону, противолежащую другому из них.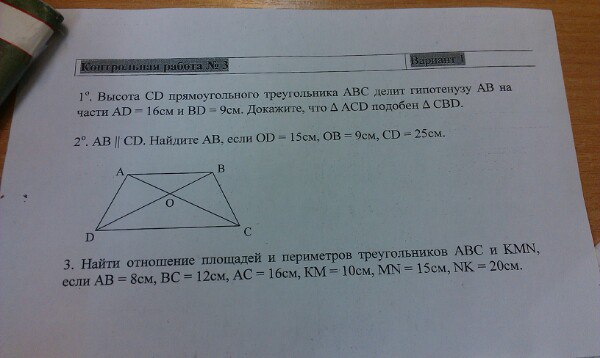 Например, если угол A  = 30°, угол B  = 45°, а сторона a  = 16, то по закону синусов (sin 30°)/16 = (sin 45°)/ b. Решение для b дает b  = 16(sin 45°)/(sin 30°) = 22,6274.

Во-вторых, если вы знаете две стороны и угол, противолежащий одной из них, то вы почти можете определить угол, противолежащий другой из них. Например, если сторона a  = 25, сторона b  = 15, а угол A  = 40°, то по закону синусов (sin 40°)/25 = (sin  В )/15. Нахождение sin B дает sin B = 15 (sin 40°)/25 = 0,38567. Теперь арксинус 0,38567 = 22,686°. Предупреждение: у вас может не быть правильного ответа. Есть два угла между 0 и 180 ° с данным синусоидальным; второй является дополнением первого. Таким образом, в данном случае вторым является тупой угол 180  22,686 = 157,314°. Эта ситуация неопределенная. Зная две стороны и угол, противолежащий одной из них, не всегда достаточно для определения треугольника. В геометрии не существует детерминистской теоремы о конгруэнтности «бок-бок-угол».

Проблемы

553. AB — линия длиной 652 фута на одном берегу ручья, а C — точка на противоположном берегу. A  = 53° 18′ и B  = 48° 36′. Найдите ширину потока от С до АВ.

557. В треугольнике ABC, a  = 700 футов, B  = 73° 48′, и C  = 37° 21′. Если M является средней точкой BC найти длины AM, и углы BAM и MAC.

561. Три окружности радиусов 3, 4 и 5 касаются друг друга снаружи. Найдите углы треугольника, образованного соединением их центров.

563. A и B — точки на противоположных берегах реки. На одном берегу линия AC измеряется 650 футов. Угол A  = 73° 40′, а C  = 52° 38′. Найти АБ.

570. P и Q две недоступные точки. Чтобы найти расстояние между ними, берется точка A в произведенном QP и измеряется линия AB длиной 1200 футов, образующая угол PAB  = 26° 35′. Угол ABP  = 48° 12′ и ABQ  = 106° 42′. Как долго PQ ?

579. Стороны параллелограмма равны AB  = 209.16 и AD = 347,25, а диагональ AC  = 351,47. Найдите углы и другую диагональ.

580. В параллелограмме ABCD, диагональ AC  = 521,16, угол ABC  = 110° 48′ 12″, а BAC  = 27° 19′ 36″. Найдите длины сторон и другой диагонали.

586. Диагонали параллелограмма равны 374,14 и 427,21, а угол между ними равен 70° 12′ 38″. Найдите стороны.

590. Стороны четырехугольника по порядку равны 763,83, 721,75, 547,12 и 593,21, а угол между первыми двумя сторонами равен 53° 13′ 12″. Найдите остальные три угла.

593. A и B — это две точки на противоположных сторонах водоема, и замеры должны производиться по линии AB в точках на одну четверть, половину и три четверти расстояния от A по B. На берегу линия AC измерена длина 1200 футов, а углы BAC = 63° 19′ и ACB  = 78° 43′. Какие углы нужно отклонить от СА на С , чтобы выровнять лодку, с которой производятся замеры, в соответствующих точках на АВ ?

608. На одной стороне линии потока PA  = 586,3 фута, PB  = 751,6 фута являются мерами, угол APB равен 167° 36′. Q — точка на противоположной стороне потока. Угол PAQ  = 63° 18′ и PBQ  = 49° 24′. Найдите ПК.

612. Чтобы найти расстояние между двумя недоступными точками P и Q, откладывается линия AB длиной 763,4 фута так, что AB пересекает PQ внешне [то есть два отрезка линии AB и PQ не пересекаются]. Углы PAB  = 98° 47′, QAB  = 41° 36′, PBA  = 37° 16′ и QBA  = 94° 12′. Найдите длину PQ.

Советы

553. Вы можете использовать закон синусов, чтобы определить любую из длин AB или BC. Задача состоит в том, чтобы найти расстояние от C до AB. Это означает, что вы опускаете перпендикуляр из точки C на эту линию и определяете ее длину. Вы можете использовать угол A и линию AC , чтобы найти его, или вы можете использовать угол B и строку BC , чтобы найти его.

557. Та же подсказка, что и для 553.

561. Окружности касаются друг друга, поэтому линия, проведенная из одного центра в другой, равна сумме радиусов одной окружности и другой. У вас есть треугольник со сторонами 7, 8 и 9. Вы можете использовать закон косинусов, чтобы найти углы.

563. Здесь хорошо работает закон синусов.

570. Нарисуйте фигуру. Чтобы найти PQ, сначала найдите AP и AQ. Вы можете найти AP , используя закон синусов треугольника ABP, , и вы можете найти AQ , используя закон синусов треугольника ABQ.

579. Вы знаете стороны треугольников ABC, и ADC, , поэтому можете определить их углы. В треугольнике ABD вы знаете угол и две смежные стороны, поэтому вы можете найти противоположную сторону BD.

580. Сначала решите треугольник ABC. Далее в треугольнике ABD вы знаете две стороны и легко можете определить угол BAD.

586. «Включенный угол» — это один из двух углов между двумя диагоналями. Другим включенным углом является его дополнение 180&deg  70° 12′ 38″. Пусть P будет точкой пересечения двух диагоналей. Это середина каждой диагонали, так что вы знаете расстояние между P и любой вершиной. Используйте закон косинусов для двух треугольников с вершинами P и две вершины параллелограмма.

590. Вы знаете стороны четырехугольника ABCD и угол при B. Вы можете решить треугольник ABC. Тогда вы знаете все стороны треугольника ACD, и можете найти его углы.

593. Сначала определите расстояние AB по закону синусов. Тогда для каждого из правильных положений лодки P, вы знаете две стороны и угол между ними треугольника PAC, , чтобы можно было определить нужный угол по закону косинусов.

608. Сначала решите треугольник APB. Тогда у вас будет достаточно информации, чтобы решить треугольник AQB.

612. Есть несколько способов решить эту проблему. Вот один из способов. Определить PA по закону синусов для треугольника PAB, и определить QA по закону синусов для треугольника QAB. Затем используйте закон косинусов для треугольника ПАК.

Ответы

553. 345,43 фута.

557. 490,83 фута.

561. 48° 11′ 24″, 58° 24′ 42″, 73° 23′ 54″.

563. 640 футов 10 дюймов.

570. 651,9 футов.

579. 106° 18′ 46″, 73° 41′ 14″, 452,92.

580. 255,93, 372,11, 369,22.

586. 231,94, 328,93.

590,125° 6′ 12″, 70° 57′ 54″, 110° 42′ 42″.

593. 23° 27′, 47° 58, 66° 34′.

608. 854,6 фута.

612. 920,76 футов.

Оглавление. | Вернемся к тригонометрическим функциям. | К тригонометрическим тождествам.

© 1996, 1997.

Дэвид Э. Джойс
Кафедра математики и информатики
Университет Кларка
Вустер, Массачусетс 01610

Электронная почта: [email protected]

Краткий триггерный курс Дэйва находится по адресу http://aleph0.clarku.edu/~djoyce/java/trig.

Калькулятор площади ромба

Автор: Ханна Памула, доктор философии

Рецензию сделали Богна Шик и Стивен Вудинг

Последнее обновление: 10 января 2023 г.0525 Периметр ромба

Как найти площадь ромба?

Является ли квадрат ромбом? Или ромб — это параллелограмм?

Калькулятор площади ромба является отличным инструментом для определения площади ромба , а также его периметра и других характеристик: диагоналей, углов, длины стороны и высоты.

Посмотрите, как можно найти площадь ромба многими способами: по диагоналям ромба, используя основание и высоту, сторону и любой выбранный угол. .. Вы все еще задаетесь вопросом, как найти площадь ромба или периметр ромба ? Проверьте приведенные ниже формулы площади ромба или просто поэкспериментируйте с инструментом.

Ромб и его свойства

Ромб — это простой четырехугольник, у которого все стороны равны (см. калькулятор четырехугольника). Другие названия — равносторонний четырехугольник или ромб (как в игральных картах ♢).

Основные свойства ромба:

• Две диагонали ромба перпендикулярны и делят друг друга пополам;
• Его диагонали делят противоположные углы пополам; и
• Противоположные углы имеют одинаковую меру.

Каждый ромб является параллелограммом и воздушным змеем. Так что, возможно, вам также будет интересен наш калькулятор площади параллелограмма и калькулятор площади воздушного змея.

Формула площади ромба

Существуют три полезные формулы для расчета площади ромба:

1. Зная базу и рост:

   площадь = основание × высота

2. Зная диагонали ромба:

   площадь = (e × f)/2

3. Зная сторону s и любой (!) угол:

   площадь = s² × sin(угол)

Почему мы можем использовать любой угол в последней формуле площади ромба? Потому что мы знаем, что два смежных угла являются дополнительными, и sin(угол) = sin(180° — угол) .

Существуют и другие варианты этих уравнений (например, вычисление площади по высоте и углу), но они представляют собой лишь простые тригонометрические преобразования трех самых популярных формул площади ромба.

Периметр ромба

Нахождение периметра ромба тривиально, если мы знаем длину стороны – это 4 × . Но что, если мы знаем только диагонали ромба? Давайте проверим:

1. Мы знаем, что диагонали перпендикулярны и делят друг друга пополам. Итак, ромб — это не что иное, как четыре конгруэнтных треугольника с катетами, равными e/2 и f/2.

2. Все, что нам нужно сделать, это найти гипотенузу треугольника. Вы можете использовать здесь калькулятор прямоугольного треугольника или калькулятор теоремы Пифагора.

3. Умножьте полученное значение гипотенузы на 4. Это периметр вашего ромба!

Также вы можете использовать эту формулу:

• периметр = 4 × √(e/2)² - (f/2)²)

Или просто введите длины диагоналей в калькулятор площади ромба !

Как найти площадь ромба?

Вы все еще не знаете, как пользоваться калькулятором? Покажем его потенциал на простом примере:

1. Введите первое заданное значение . Предположим, что его сторона = 10 дюймов.

2. Введите второе заданное значение . Например, угол равен 30°.

3. Вау! Калькулятор площади ромба отображает все остальные значения – площадь, высоту, периметр, угол и диагонали . Впечатляет, не правда ли?

Наш инструмент очень гибкий – если можно рассчитать, он это сделает. Обычно достаточно двух заданных значений. Попробуйте!

Является ли квадрат ромбом? Или ромб — это параллелограмм?

Ответ да на оба вопроса. Каждый квадрат является ромбом , что касается ромба, то единственным необходимым условием является то, что все его стороны должны быть одинаковой длины. Как вы прекрасно знаете, у квадрата должны быть равны все стороны и все четыре угла, чтобы он удовлетворял условиям, чтобы быть ромбом.

Точно так же ромб является параллелограммом , так как любая фигура должна иметь две пары параллельных сторон, чтобы быть параллелограммом, а у ромба они есть.