Теория вероятностей | ЕГЭ по математике (профильной)
Вероятностью события $А$ называется отношение числа благоприятных для $А$ исходов к числу всех равновозможных исходов
$P(A)={m}/{n}$, где $n$ – общее количество возможных исходов, а $m$ – количество исходов, благоприятствующих событию $А$.
Вероятность события — это число из отрезка $[0; 1]$
В фирме такси в наличии $50$ легковых автомобилей. $35$ из них чёрные, остальные — жёлтые. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета.
Решение:
Найдем количество желтых автомобилей:
$50-35=15$
Всего имеется $50$ автомобилей, то есть на вызов приедет одна из пятидесяти. Желтых автомобилей $15$, следовательно, вероятность приезда именно желтого автомобиля равна ${15}/{50}={3}/{10}=0,3$
Ответ:$0,3$
Противоположные события
Два события называются противоположными, если в данном испытании они несовместимы и одно из них обязательно
происходит. Вероятности противоположных событий в сумме дают 1.Событие, противоположное событию $А$, записывают
${(А)}↖{-}$.
Вероятности противоположных событий в сумме дают 1.Событие, противоположное событию $А$, записывают
${(А)}↖{-}$.
$Р(А)+Р{(А)}↖{-}=1$
Независимые события
Два события $А$ и $В$ называются независимыми, если вероятность появления каждого из них не зависит от того, появилось другое событие или нет. В противном случае события называются зависимыми.
Вероятность произведения двух независимых событий $A$ и $B$ равна произведению этих вероятностей:
$Р(А·В)=Р(А)·Р(В)$
Иван Иванович купил два различных лотерейных билета. Вероятность того, что выиграет первый лотерейный билет, равна $0,15$. Вероятность того, что выиграет второй лотерейный билет, равна $0,12$. Иван Иванович участвует в обоих розыгрышах. Считая, что розыгрыши проводятся независимо друг от друга, найдите вероятность того, что Иван Иванович выиграет в обоих розыгрышах.
Решения:
Вероятность $Р(А)$ — выиграет первый билет.
Вероятность $Р(В)$ — выиграет второй билет.
События $А$ и $В$ – это независимые события. То есть, чтобы найти вероятность того, что они произойдут оба события, нужно найти произведение вероятностей
$Р(А·В)=Р(А)·Р(В)$
$Р=0,15·0,12=0,018$
Ответ: $0,018$
Несовместные события
Два события $А$ и $В$ называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию $А$, так и событию $В$. (События, которые не могут произойти одновременно)
Вероятность суммы двух несовместных событий $A$ и $B$ равна сумме вероятностей этих событий:
$Р(А+В)=Р(А)+Р(В)$
На экзамене по алгебре школьнику достается один вопрос их всех экзаменационных. Вероятность
того, что это вопрос на тему «Квадратные уравнения», равна $0,3$. Вероятность того, что это вопрос на тему
«Иррациональные уравнения», равна $0,18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите
вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.
Решение:
Данные события называются несовместные, так как школьнику достанется вопрос ЛИБО по теме «Квадратные уравнения», ЛИБО по теме «Иррациональные уравнения». Одновременно темы не могут попасться. Вероятность суммы двух несовместных событий $A$ и $B$ равна сумме вероятностей этих событий:
$Р(А+В)=Р(А)+Р(В)$
$Р = 0,3+0,18=0,48$
Ответ: $0,48$
Совместные события
Два события называются совместными, если появление одного из них не исключает появление другого в одном и том же испытании. В противном случае события называются несовместными.
Вероятность суммы двух совместных событий $A$ и $B$ равна сумме вероятностей этих событий минус вероятность их произведения:
$Р(А+В)=Р(А)+Р(В)-Р(А·В)$
В холле кинотеатра два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится
кофе, равна $0,6$. Вероятность того, что кофе закончится в обоих автоматах, равна $0,32$. Найдите вероятность того,
что к концу дня кофе закончится хотя бы в одном из автоматов.
Решение:
Обозначим события, пусть:
$А$ = кофе закончится в первом автомате,
$В$ = кофе закончится во втором автомате.
Тогда,
$A·B =$ кофе закончится в обоих автоматах,
$A + B =$ кофе закончится хотя бы в одном автомате.
По условию, $P(A) = P(B) = 0,6; P(A·B) = 0,32$.
События $A$ и $B$ совместные, вероятность суммы двух совместных событий равна сумме вероятностей этих событий, уменьшенной на вероятность их произведения:
$P(A + B) = P(A) + P(B) − P(A·B) = 0,6 + 0,6 − 0,32 = 0,88$
Ответ: $0,88$
Практика: решай 4 задание и тренировочные варианты ЕГЭ по математике (профильной)
Треугольник | ЕГЭ по математике (профильной)
Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
На рисунке:
$А,В,С$ — вершины треугольника.
$АВ,ВС$ и $АС$ – стороны треугольника.
Виды треугольников по величине углов:
1. Остроугольный треугольник — такой треугольник, в котором все углы меньше $90°$, т.е. острые.
2. Прямоугольный треугольник — треугольник, имеющий прямой угол.
3. Тупоугольный треугольник — треугольник, содержащий тупой угол, т.е. угол от $90°$ до $180°$.
Виды треугольников по соотношению сторон:
1. Равносторонний (правильный) треугольник – это такой треугольник, у которого все стороны и углы равны.
2. Равнобедренный треугольник — это такой треугольник, у которого две стороны равны. Равные стороны называются боковыми. Третья сторона называется основанием.
3. Разносторонний треугольник – это такой треугольник, у которого длины всех сторон разные.
Медиана, биссектриса, высота
Медиана – это отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Три медианы треугольника пересекаются в одной точке $O$, эта точка делит каждую медиану в отношении $2:1$, считая от вершины.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.
Высота треугольника — это перпендикуляр, опущенный из любой вершины на противоположную сторону (или её продолжение). Эта сторона называется основанием треугольника.
Основные свойства треугольников:
- Сумма всех углов в треугольнике равна $180°$.
- В равнобедренном треугольнике углы при основании равны.
- В равнобедренном треугольнике высота, проведенная к основанию, одновременно является медианой и биссектрисой.
- В равностороннем треугольнике все углы по $60°$.
- Внешний угол треугольника равен сумме двух углов, не смежных с ним.
- Средняя линия треугольника параллельна основанию и равна его половине.
$MN$ — средняя линия, так как соединяет середины соседних сторон.
$MN‖AC, MN={AC}/{2}$
Площадь треугольника:
- $S={a∙h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$.
 {2}√3}/{4}$, где $а$ — длина стороны.
{2}√3}/{4}$, где $а$ — длина стороны. - В прямоугольном треугольнике $S={a∙b}/{2}$, где $а,b$ — катеты.
В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
- Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
- Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
- Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
- Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
- Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$. (Рис.14)
- Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями которых являются катеты данного треугольника.

- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
В треугольнике $АВС$ угол $С$ прямой, гипотенуза равна $39, cosB={5}/{13}$.
Найдите $АС$.
Решение:
Так как нам известен cos угла $В$, то распишем его по определению: косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.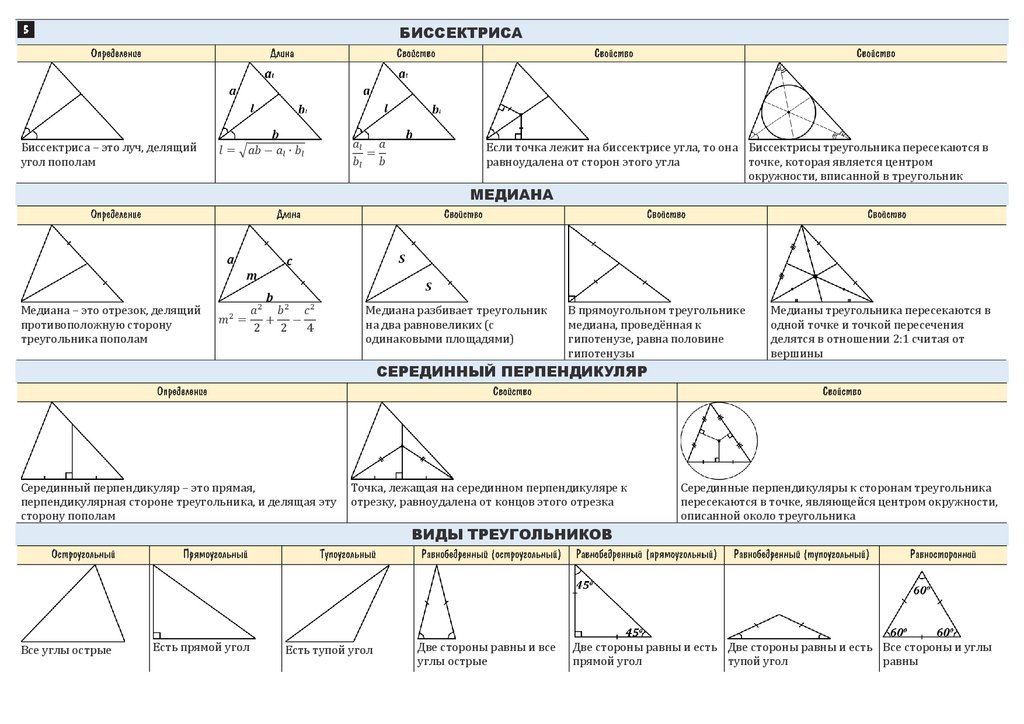 2=(39-15)(39+15)=24∙54=1296$
2=(39-15)(39+15)=24∙54=1296$
$АС=36$
Ответ: $36$
Практика: решай 3 задание и тренировочные варианты ЕГЭ по математике (профильной)
Сэм Нельсон — Теоремы и теории
Два слова, которые часто путают люди, не знакомые с
математика и другие науки суть «теорема» и «теория».
Несмотря на похожее звучание, эти два слова относятся к довольно
различные вещи в математике и других науках.
Путаницу усугубляет тот факт, что, в отличие от «теоремы», которая
проявляется только в математике, слово «теория» имеет обыденное значение.
использование, которое также сильно отличается от значения слова в
наук. В этой статье мы дадим некоторые разъяснения относительно
разное значение этих слов. Сначала рассмотрим математический
термин «теорема» и см. несколько примеров; тогда мы перейдем к научному
значение термина «теория», глядя на то, как это техническое использование
отличается от обычного повседневного использования этого термина. Наконец, мы увидим, как
слово «теория» используется в математике.
Теоремы — вот что такое математика. Теорема – это утверждение, истинность которого доказана особым видом логического аргумент называется строгое доказательство . Строгое доказательство просто надежный дедуктивный аргумент, означающий, что он начинается с утверждений что мы знаем, чтобы быть правдой, а затем делает маленькие шаги, каждый шаг следуя предыдущим шагам, пока не придем к нашему заключению. Одно утверждение следует из другого, если это невозможно для первое утверждение ложно, а второе истинно. Например, утверждение «Сократ смертен» следует из утверждения «Все греки смертны, а Сократ — грек» — это невозможно, ибо «все греки смертен, а Сократ — грек», чтобы быть верным без «Сократ смертен» также быть правдой. Следовательно, если мы начнем с утверждений, которые, как мы знаем, истинны, тогда любое утверждение, которое последует, должно быть точно так же верно.
Как только теорема доказана, мы знаем со 100% уверенностью, что она верна. истинный. Не верить теореме — значит просто неправильно понимать, что эта теорема
говорит. Вот несколько простых примеров.
истинный. Не верить теореме — значит просто неправильно понимать, что эта теорема
говорит. Вот несколько простых примеров.
Теорема: Наибольшего счетного числа не существует.
Доказательство: Предположим, что существует наибольшее счетное число, и назовем его и . Тогда n +1 — счетное число, и оно больше, чем n , поэтому наш выбор n был неправильным. Может n +1 наибольшее счетное число тогда? Нет, потому что снова ( n +1)+1 большее счетное число. Действительно, мы можем применить эту же процедуру к любой кандидат на «наибольшее число», всегда с одним и тем же результатом. Этот показывает, что каждые выбор наибольшего счетного числа неверен, что это значит, что не существует самого большого счетного числа.
Здесь аргумент показывает, что вы можете только не согласиться с выводом
не соглашаясь с нашим значением терминов «самый большой» или «счетное число».
Если вы понимаете, что означают эти термины, вы не можете не согласиться с тем, что
нет счетного числа, которое больше всех остальных.
Другой пример, этот принадлежит Гауссу:
| Теорема: (Гаусс) Сумма счетных чисел от 1 до n равно | . |
Доказательство: Установить x = 1+2+3+…+( n -1)+ n . Затем добавление x+x дает сумма n копий n +1:
| 1 | + | 2 | + | … | + | n -1 | + | n | + |
| + n | + | + n -1 | + | … | + | +2 | + | +1 | = |
| ( n +1) | + | ( n +1) | + | . .. .. | + | ( n +1) | + | ( н +1) | = н ( н +1). |
| х = 1+2+…+ п = | . |
Вы можете сами проверить, что это утверждение верно для любого числа. и , которые вам нравятся. Например, если n =5, то 1+2+3+4+5 =15 а 5 умножить на 6 разделить на 2 30/2 = 15. Есть известная история, которая говорит, что Гаусс думал об этом, когда он был в начальной школе и учителем поручил учащимся сложить числа от 1 до 100 в качестве занятой работы. Маленький Гаусс поразил учителя тем, что закончил всего за несколько минут.
Еще одна известная теорема с хорошим простым доказательством:
Теорема: (Пифагора) Если прямоугольный треугольник имеет короткие стороны с длины a и b , а длинная сторона (гипотенуза) с длиной c , затем
Доказательство: Рассмотрим квадрат ниже. Мы можем вычислить его площадь за два
способами, либо как квадрат длины его стороны ( a + b )
или как сумма площади внутреннего квадрата и четырех треугольников. Мы можем
соедини треугольники так, чтобы получились два прямоугольника с одной стороной длины a и одна сторона длиной b , поэтому общая площадь квадрата
равно c в квадрате плюс дважды a умножить на b . Тогда это должно быть
равно ( a + b ) в квадрате, поскольку обе эти величины равны
описывает площадь квадрата.
Мы можем вычислить его площадь за два
способами, либо как квадрат длины его стороны ( a + b )
или как сумма площади внутреннего квадрата и четырех треугольников. Мы можем
соедини треугольники так, чтобы получились два прямоугольника с одной стороной длины a и одна сторона длиной b , поэтому общая площадь квадрата
равно c в квадрате плюс дважды a умножить на b . Тогда это должно быть
равно ( a + b ) в квадрате, поскольку обе эти величины равны
описывает площадь квадрата.
Несложная алгебра дает нам результат.
Здесь мы могли бы возразить: «А как насчет неевклидовой геометрии?» Это правда
что, изменив то, что мы подразумеваем под «расстоянием», мы можем получить отношения
между сторонами, отличными от той, что указана в теореме. Но опять же, это
требует изменения смысла слов в теореме — с
обычные значения «расстояния» и «прямоугольного треугольника», вывод
теоремы неизбежно.
Математика занимается доказательством теорем. В чистой математике мы изучаем проблемы, которые мы находим интересными сами по себе, отвечая вопросы, начиная с того, что мы знаем и доказывая теоремы. Теоремы иногда называются разными вещами в зависимости от их важности или их связь с другими теоремами. Теорема, которая доказывается прежде всего как шаг к доказательству другой теоремы называется леммой , а теорема, которая следует как простое следствие другой теоремы, называется следствие . Теоремы часто называют предложений , когда они впервые представлены.
Основой современной науки является прикладная математика. В науках,
наблюдения ведут нас к открытию как фактов, так и законов . Закон является наблюдением о закономерности в наблюдаемых фактах, таких как
«предметы падают при падении». Идея, которая может объяснить закон или другой набор
наблюдений называется гипотезой , а гипотезы часто принимают
форма математическая модели , то есть математические системы, чьи
структура должна максимально точно имитировать поведение
изучаемые явления.
Прикладная математика занимается разработкой математических моделей реального мира.
явлений и применяя теоремы мы можем доказать о математических моделях
сделать выводы о соответствующем реальном явлении. Ученые
начните с тщательных наблюдений за миром, затем придумайте математические
модели, которые воспроизводят наблюдения. Можно проверить научную модель,
используя модель для прогнозирования результатов наблюдения, затем делая
фактическое наблюдение и сравнение результатов. Если модель не точно
прогнозировать результат наблюдения, то модель нуждается в уточнении;
если предсказание модели совпадает с наблюдением, то модель соответствует с наблюдением. Согласованность с наблюдением делает
не гарантирует, что модель всегда будет соответствовать явлениям для каждого будущего
наблюдение, но последовательность с достаточно повторяющимися наблюдениями действительно говорит о том, что
модель является разумным кандидатом для объяснения явлений. Над
время модель тестируется и уточняется, а детали дополняются повторяющимися
наблюдения и тесты.
По мере того как математические модели со временем тестируются и уточняются,
уверенность в эффективности нашей общей коллекции математических
модели. То есть со временем текущая версия набора моделей становится
все лучше и лучше описывает реальность. Никогда не бывает
этап, на котором процесс заканчивается, и мы заявляем, что у нас есть 100% точный
описания действительности, так как для этого потребовалось бы сделать все возможное
наблюдение; однако мы можем иметь и имеем математические модели, в которых мы
имеют очень высокий уровень доверия, даже выше, чем уровень
уверенность, которую мы обычно требуем, чтобы назвать утверждение «фактом». 99,9%
уверенность может быть не 100%, но она намного ближе к 100%, чем к 0%.
Обратите внимание, что, напротив, обычным утверждениям часто присваивается статус «факт» после
только одно наблюдение или вывод! Из-за разницы в
уровни тестирования, «факты» повседневной жизни на самом деле гораздо более вероятны
быть неверными, чем наши научные модели.
По мере того, как наши гипотезы проверяются и уточняются, пока наш уровень доверие к ним очень высоко, мы ищем набор принципов, которые дать связное объяснение различным законам и фактам, которые мы собран. Такое подробное объяснение какого-то аспекта реальности, включая все различные хорошо проверенные гипотезы и математические моделей и объяснения различных фактов и законов, которые мы наблюдали, это то, что мы называем научная теория .
Это совсем другой вид вещей, чем то, что можно было бы назвать
«теории» в повседневной жизни. Наше обычное нетехническое значение слова «теория».
гораздо ближе по смыслу к научному термину «гипотеза»,
то есть простая идея, которую можно проверить. Например, детектив может
иметь «теорию» о том, кто совершил убийство, или студент мог
«теория» о том, как лучше всего получить хорошую оценку. Это не «теории»
в научном смысле! Один человек никогда не создает целого
только научная теория, ибо научные теории слишком велики и
сложный. Даже теории, которые связаны с именем человека, такие как
«Общая теория относительности Эйнштейна» или «Теория эволюции Дарвина».
не работа одного человека, а совокупный результат
сотрудничество многих людей с течением времени.
Научная теория представляет собой обширную совокупность знаний, которая
вместе большое количество хорошо проверенных гипотез и математических моделей,
сплетая их в последовательное объяснение фактов и законов, которые мы можем
наблюдать. Повседневная гипотеза является не более научной теорией, чем
одиночный болт — автомобиль.
Даже теории, которые связаны с именем человека, такие как
«Общая теория относительности Эйнштейна» или «Теория эволюции Дарвина».
не работа одного человека, а совокупный результат
сотрудничество многих людей с течением времени.
Научная теория представляет собой обширную совокупность знаний, которая
вместе большое количество хорошо проверенных гипотез и математических моделей,
сплетая их в последовательное объяснение фактов и законов, которые мы можем
наблюдать. Повседневная гипотеза является не более научной теорией, чем
одиночный болт — автомобиль.
Распространенной связанной с этим путаницей является идея о том, что научные теории ждут
быть проверенным и доказанным, прежде чем стать принятым в качестве факта или закона. Это
серьезное недоразумение — идеи, из которых состоит научная теория
уже настолько хорошо протестированы, насколько позволяют современные технологии, прежде чем они
получить статус научной теории. Теоремы доказаны, а не
теории. В математике до того, как теорема доказана, она называется гипотеза . В науках только хорошо проверенные гипотезы
может стать частью теории. Таким образом, термин «научная теория»
выбран очень неудачно, потому что для большей части населения слово «теория»
предполагает слабость и сомнение, когда в научной теории есть только
заслуженное доверие.
В науках только хорошо проверенные гипотезы
может стать частью теории. Таким образом, термин «научная теория»
выбран очень неудачно, потому что для большей части населения слово «теория»
предполагает слабость и сомнение, когда в научной теории есть только
заслуженное доверие.
Другими словами, сказать, что нечто является «научной теорией», значит сказать
что оно подкреплено всеми имеющимися доказательствами и что наша уверенность в его
правильность как описание реальности настолько сильна, насколько это возможно с нашим
Текущая возможность проверить это. теории
не доказываться и не становиться фактами или даже теоремами; если модель или гипотеза
является частью научной теории, то она уже есть настолько «доказанная», насколько это
может когда-нибудь получить. Это правда, что научные теории не
статические и абсолютные; по мере развития технологий мы постоянно находим новые способы
уточнить наши предыдущие идеи. Иногда происходят так называемые «сдвиги парадигмы».
в котором новая теория заменяет старую, но в каждом таком случае новая
теория должна быть в состоянии объяснить, почему старая теория совпадает с наблюдениями
так же как и сделал. Например, относительность смогла заменить только
Ньютоновская механика как общепринятая научная теория гравитации
потому что на малых скоростях и в слабых гравитационных полях относительность
очень похоже на ньютоновскую механику.
Например, относительность смогла заменить только
Ньютоновская механика как общепринятая научная теория гравитации
потому что на малых скоростях и в слабых гравитационных полях относительность
очень похоже на ньютоновскую механику.
Эта путаница между обычным и научным значениями слова «теория», между «простой догадкой, которую нужно проверить» и «обширным набором тщательно проверенные и подтвержденные гипотезы, которые вместе обеспечивают объяснение наблюдаемых фактов и законов», составляет основу для Монти Пайтона эскиз — у персонажа есть «новая теория о бронтозавре», а именно «что все бронтозавры тонкие с одного конца, толстые посередине и тонкие на другом конце.» К сожалению, как и большая часть юмора депутата, эта шутка непонятна необразованным людям.
Более серьезным последствием смешения двух значений является
способность идеологически мотивированных групп использовать эту путаницу,
искажение очень хорошо проверенных и надежных научных теорий как
«только теория».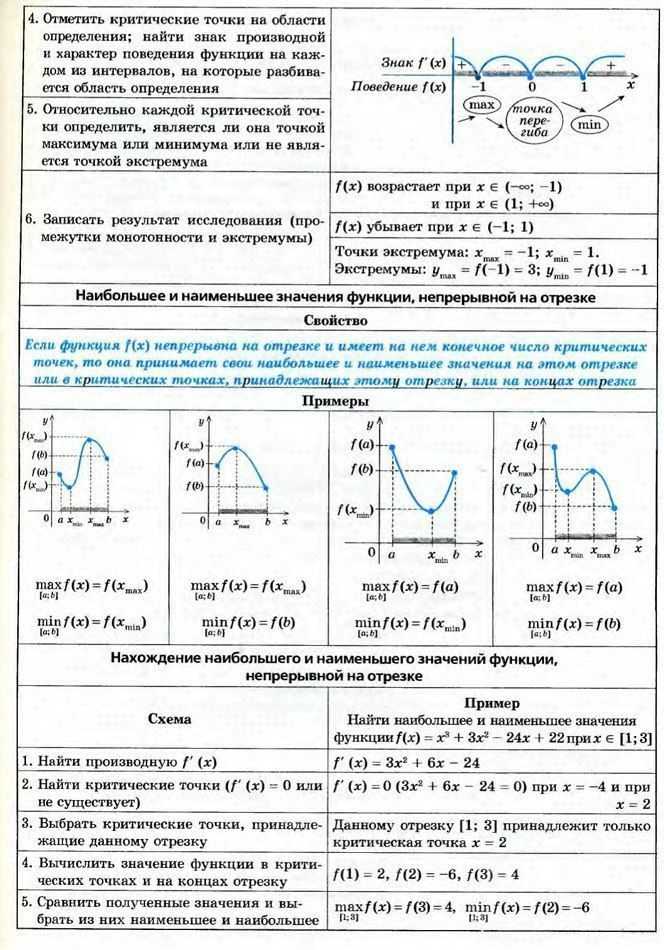 Это создает ложное впечатление, что существуют серьезные
сомнения в теории, когда на самом деле модели и гипотезы,
составляют теорию, как известно, являются точными описаниями реальности с
очень высокий уровень доверия. Примеров множество, но климат
На ум приходят исследования и биология.
Это создает ложное впечатление, что существуют серьезные
сомнения в теории, когда на самом деле модели и гипотезы,
составляют теорию, как известно, являются точными описаниями реальности с
очень высокий уровень доверия. Примеров множество, но климат
На ум приходят исследования и биология.
В частности, попытка критиковать любой аспект науки, говоря «Х — это только теория» — нечестный риторический трюк, использующий тот факт, что слово «теория» имеет два разных значения, чтобы вводить людей в заблуждение. Это похоже на говоря кому-то, что они могут свободно игнорировать решение Верховного суда, поскольку оно только Мнение судей, или как бегун, пытающийся нарушить Закон Сила тяжести.
Наконец, слово «теория» используется в математике таким образом, что
похоже на «научную теорию», что означает что-то вроде «
изучение». Например, «теория узлов» не означает «гипотеза
об узлах», а скорее «математическое изучение узлов» — это действительно
всего лишь краткий способ коллективного обозначения всей совокупности
статьи, теоремы, книги и работы по данной теме. Где
научная теория состоит из хорошо проверенных гипотез и математических
моделей, математическая теория состоит из лемм, теорем и
следствия. Оба всегда неполны, в том смысле, что всегда есть
новые теоремы, которые нужно доказать, и новые гипотезы, которые нужно проверить; оба относятся к
наук, в которых многое известно, но еще больше предстоит узнать
обнаруженный.
Где
научная теория состоит из хорошо проверенных гипотез и математических
моделей, математическая теория состоит из лемм, теорем и
следствия. Оба всегда неполны, в том смысле, что всегда есть
новые теоремы, которые нужно доказать, и новые гипотезы, которые нужно проверить; оба относятся к
наук, в которых многое известно, но еще больше предстоит узнать
обнаруженный.
Исследователь подкрепляет теорию Эйнштейна математикой
Часы работы
Профессор Джорджи рассказывает, как она показала, что черные дыры стабильны, и как открытие, сделанное студенткой Колумбийского университета, определило ее профессиональную «судьбу».
Автор
Кристофер Д. Ши
19 октября 2022 г.
В 1915 году в серии лекций в Берлине Альберт Эйнштейн представил свою общую теорию относительности, используя уравнение для демонстрации того, что энергия и материя влияют на форму пространства-времени, заставляя его искривляться.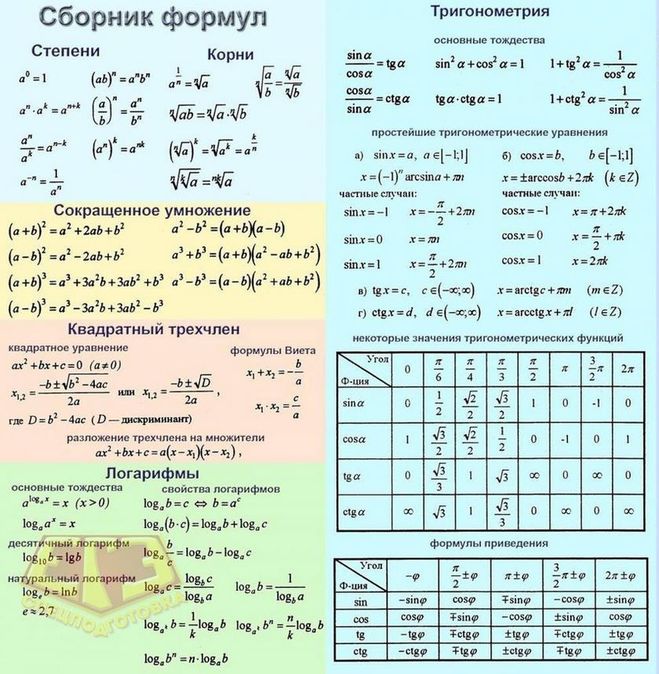 В 1963 году математик Рой Керр решил уравнение, введенное Эйнштейном в 1915 году, с доказательством, описывающим пространство-время вне вращающейся черной дыры. В последующие десятилетия исследователи пытались доказать, что обнаруженные Керром черные дыры стабильны, или, как написал писатель Кевин Хартнетт в статье Quanta 2018 года, что если вы встряхнете одну из них, она «встряхнется, как желе, а затем осядет в стабильная форма, подобная той, с которой он начался».
В 1963 году математик Рой Керр решил уравнение, введенное Эйнштейном в 1915 году, с доказательством, описывающим пространство-время вне вращающейся черной дыры. В последующие десятилетия исследователи пытались доказать, что обнаруженные Керром черные дыры стабильны, или, как написал писатель Кевин Хартнетт в статье Quanta 2018 года, что если вы встряхнете одну из них, она «встряхнется, как желе, а затем осядет в стабильная форма, подобная той, с которой он начался».
Этой весной профессор Елена Гиорги доказала именно это. В статье на 900 с лишним страниц, которую она написала в соавторстве с коллегами-математиками Серджиу Клайнерманом из Принстонского университета и Джереми Сефтелем из Сорбоннского университета, Джорджи продемонстрировала, что черные дыры действительно стабильны. По словам Джорджи, если бы она и ее коллеги-исследователи обнаружили, что черные дыры нестабильны, у физиков возникло бы множество проблем, и они могли бы предположить, что общая теория относительности Эйнштейна неверна.
Джорджи, родом из Италии, получила докторскую степень в Колумбийском университете в 2019 году. Она провела два года в Принстоне в качестве научного сотрудника с докторской степенью, прежде чем присоединиться к Колумбийскому университету в качестве доцента в июле 2021 года. Columbia News связалась с Джорджи, чтобы узнайте больше о ее работе над черными дырами и о том, что ее решение означает для области.
Мы продемонстрировали стабильность этой черной дыры, которую вычислил Керр, когда она медленно вращается. Итак, я математик; мы на математическом факультете. Так почему же мы вообще говорим о черных дырах? Потому что эти объекты на самом деле являются математическим решением уравнения поля Эйнштейна, которое он ввел в 1919 году.15, когда он открыл теорию гравитации. Это то, что позволило Эйнштейну перейти от его специальной теории относительности, где на картинке абсолютно отсутствует материя, к пониманию того, как она будет работать в нашей Вселенной, где есть массивные объекты, такие как звезды. Я изучаю математические свойства черных дыр. Люди, занимающиеся физикой, астрофизическими наблюдениями и т. д., используют эти математические решения для своих вычислений.
Я изучаю математические свойства черных дыр. Люди, занимающиеся физикой, астрофизическими наблюдениями и т. д., используют эти математические решения для своих вычислений.
Возьмем в качестве примера маятник. Точка равновесия маятника — когда он направлен вниз; вы можете колебать его, но он всегда возвращается в это положение.
Но если вы проанализируете маятник с математической точки зрения, у него на самом деле есть две точки равновесия, точки, в которых он остается совершенно неподвижным и не колеблется. Один из них, когда он направлен вниз. Но другой момент, когда он направлен вверх, лицом в противоположном направлении с весом маятника на 180 градусов выше того места, где маятник обычно висит. Если бы вы могли поставить его точно в вертикальное положение, он остался бы там, он бы не двигался. Но, конечно, вы знаете, я никогда не видел маятник в таком положении, и причина, по которой я никогда его не видел, в том, что это неустойчивая точка равновесия.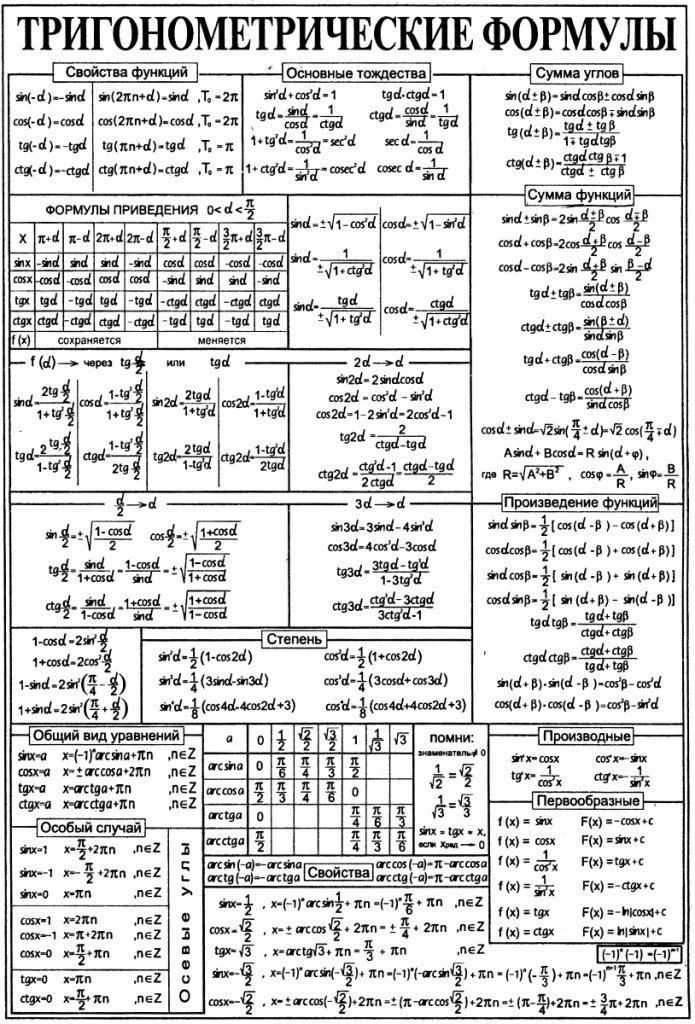 Если вы немного сдвинете его, он упадет и начнет колебаться вокруг своей стабильной, направленной вниз точки равновесия.
Если вы немного сдвинете его, он упадет и начнет колебаться вокруг своей стабильной, направленной вниз точки равновесия.
Авторы и права: Евгений М. Ижикевич/Scholarpedia
Разве он не смог бы оставаться прямо в вертикальном положении, если бы вы использовали свою руку, чтобы перемещать его и поддерживать равновесие?Это другое, потому что тогда вы добавили бы большую динамику маятнику, чтобы удерживать его в равновесии в этом вертикальном положении.
Идея стабильности имеет решающее значение для физических и математических объектов, таких как маятник, потому что разница между стабильностью и нестабильностью — это разница между тем, что возможно, и тем, что невозможно. Невозможно найти маятник в таком восходящем положении. Потому что на самом деле мы никогда не сможем расположить маятник точно в восходящем положении, потому что у нас всегда будет какая-то ошибка в его позиционировании. Его можно представить только в нашем уме как точку равновесия, но не в реальном мире.
Черные дыры являются решениями уравнения Эйнштейна и точкой равновесия уравнения Эйнштейна. Решение Керра появилось в 1963 году, через много лет после того, как уравнение Эйнштейна было записано в 1915 году. Это решение находит точку равновесия с уравнением Эйнштейна, которая не меняется с течением времени. Но тогда возникает вопрос: это маятник, обращенный вниз, или маятник, обращенный вверх? Потому что если это маятник, обращенный вверх, то это хорошее решение, но оно ничего не может представлять в реальном мире.
Физическое сообщество провело анализ стабильности для этих решений черных дыр в некоторых упрощенных условиях и не обнаружило никаких признаков нестабильности, поэтому они сделали вывод, что черные дыры стабильны, не доказывая этого. Но математическому сообществу потребовалось около 60 лет, чтобы догнать и понять, каков реальный механизм этого.
Могли ли мы предположить, что черные дыры стабильны, просто взглянув на них и заметив, что они действительно существуют? Это очень хороший вопрос, но наблюдать за черными дырами не так просто, как, знаете ли, наблюдать за кошкой.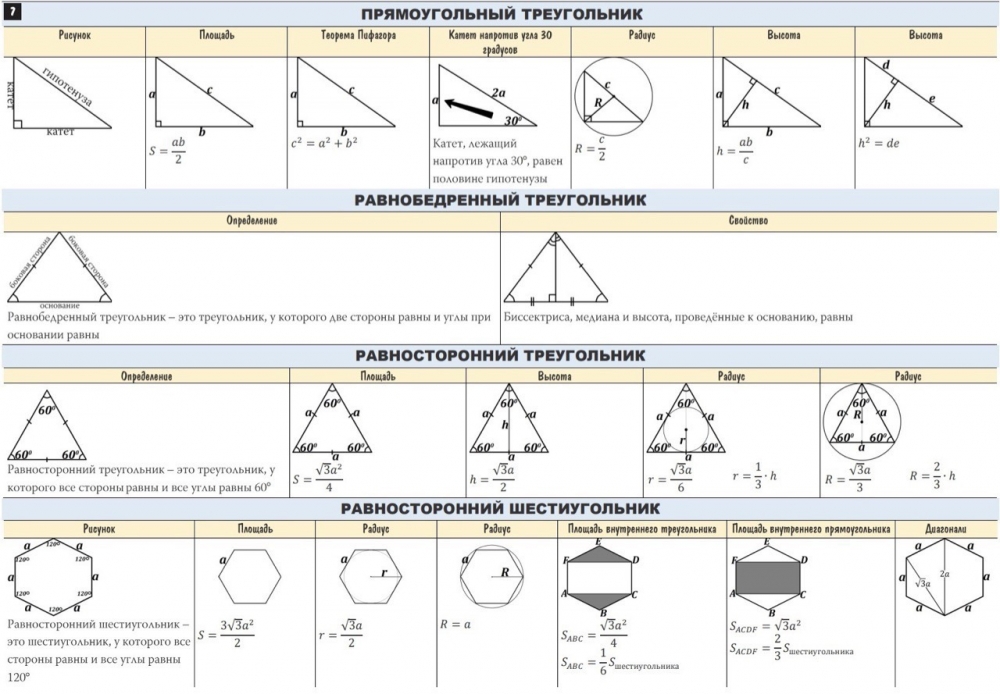 Способ создания изображений черной дыры заключается в том, что есть изображение, полученное телескопами, но есть также план, использующий решение Керра. Как вы интерпретируете данные, которые видите? Сравнивая с вашей моделью. Некоторые вещи выводятся путем наблюдения, а другие предполагаются на основе математики.
Способ создания изображений черной дыры заключается в том, что есть изображение, полученное телескопами, но есть также план, использующий решение Керра. Как вы интерпретируете данные, которые видите? Сравнивая с вашей моделью. Некоторые вещи выводятся путем наблюдения, а другие предполагаются на основе математики.
Я изучал математику на первом курсе, когда был в Пизе в Италии, а затем получил степень магистра математической физики во Франции. Еще со школы или даже раньше мне всегда нравились математика и физика, поэтому я искал что-то, что объединило бы их.
И, конечно же, черные дыры: кто не думает, что они очаровательны?
В сентябре 2015 года, когда я начал работу над докторской диссертацией, произошло первое наблюдение гравитационных волн с помощью LIGO. Об этом было объявлено в феврале 2016 года. [В том же году две обсерватории в Луизиане и Вашингтоне, известные как LIGO, обнаружили гравитационные волны, рябь в пространстве-времени, возникновение которых предсказывала теория Эйнштейна, что доказывает правдивость его предсказаний.]
[В том же году две обсерватории в Луизиане и Вашингтоне, известные как LIGO, обнаружили гравитационные волны, рябь в пространстве-времени, возникновение которых предсказывала теория Эйнштейна, что доказывает правдивость его предсказаний.]
Я был здесь. Я был студентом Колумбийского университета и помню, как ходил в Лернер-холл, они предсказали открытие гравитационных волн в феврале 2016 года. Это было так захватывающе. Может быть, это была своего рода судьба. Это наблюдение значительно расширило поле, заставив его чувствовать себя намного богаче, чем если бы у вас не было этих наблюдений. Некоторые другие области физики, такие как теория струн, не имеют таких волн данных, поступающих из реальных наблюдений.
Что конкретно привело вас в Колумбию? Я получил степень магистра во Франции, так что в определенном смысле я уже был за границей. И мне снова захотелось куда-нибудь поехать. Например, я всегда хотел получить опыт работы в США. Я подал заявку на докторскую степень очень широко. У меня было несколько предложений о поступлении, а потом я посетил Колумбию и был в Нью-Йорке. Было очень трудно сказать «нет», это было так захватывающе. Мне показали кафедру и, находясь в городе, с другими студентами, я очень быстро убедился. Также из-за людей, работающих здесь над дифференциальной геометрией и общей теорией относительности, Колумбия имела большой смысл.
Я подал заявку на докторскую степень очень широко. У меня было несколько предложений о поступлении, а потом я посетил Колумбию и был в Нью-Йорке. Было очень трудно сказать «нет», это было так захватывающе. Мне показали кафедру и, находясь в городе, с другими студентами, я очень быстро убедился. Также из-за людей, работающих здесь над дифференциальной геометрией и общей теорией относительности, Колумбия имела большой смысл.
Не совсем так. На личном уровне мне это, конечно, нравится; Я получаю все информационные бюллетени. Но они не имеют прямого отношения к моей работе. Я не большой звездочет.
Область математики очень мужская. Были ли у вас сильные наставники-женщины в этой области? Считаете ли вы это той ролью, которую вы хотите сыграть для молодых женщин-математиков? В математике действительно преобладают мужчины.

 {2}√3}/{4}$, где $а$ — длина стороны.
{2}√3}/{4}$, где $а$ — длина стороны.
Leave A Comment