Решение неравенств онлайн

Неравенства это выражения вида:

f (x) ≥0

где вместо знака ≥, может стоять знак ≤ или знаки < и >.

В приведенном выше примере, решить неравенство означает найти совокупность всех значений переменной x при которых выражение f (x) больше или равно 0.

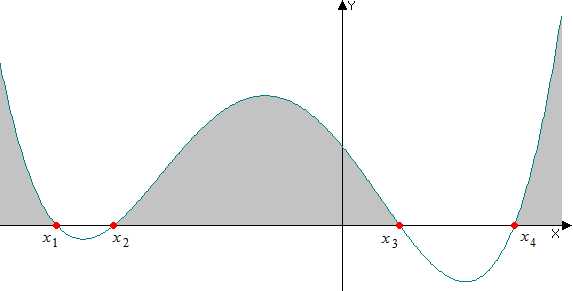
Рассмотрим график произвольной функции f (x):

Реклама

Из графика мы может сразу же записать интервалы значений х при которых функция f (x) ≥0 (закрашены серым цветом):

f (x) ≥0 <=> { x є (−∞; x1] U [x

2; x3] U [x4; +∞] }

Из графика видно, что функция меняет знак в точках пересечения оси X. Следовательно, для решения любых неравенств, сначала нужно определить такие значения x, при которых функция f (x) равна нулю, т.е. решить уравнение f (x) =0.

Полученный набор значений xi (т.е. корни уравнения f (x) =0) разбивает координатную ось на интервалы в каждом из которых значение функции сохраняет свой знак (либо больше, либо меньше нуля).

Для решения соответствующего неравенства, нужно определить знак функции в каждом из полученных интервалов и выбрать те из них , которые удовлетворяют условию неравенства. Для того, чтобы определить знак функции на некотором интервале (x

i; xj), нужно подставить вместо значения x в выражение f (x) любое значение xk є (xi; xj).

Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha LLC, способен получить решение для очень большого количества разнообразных неравеств.

www.mathforyou.net

Неравенства онлайн

Неравенства онлайн для решения математики. Быстро найти решение неравенства в режиме онлайн. Сайт www.matcabi.net позволяет найти решение почти любого заданного неравенства онлайн. Математические неравенства онлайн для решения математики. Быстро найти решение неравенства в режиме онлайн. Сайт www.matcabi.net позволяет найти решение почти любого заданного алгебраического, тригонометрического или трансцендентного неравенства онлайн. При изучении практически любого раздела математики на разных этапах приходится решать неравенства онлайн. Чтобы получить ответ сразу, а главное точный ответ, необходим ресурс, позволяющий это сделать. Благодаря сайту www.matcabi.net решение неравенства онлайн займет несколько минут. Основное преимущество www.matcabi.net при решении математических неравенства онлайн — это скорость и точность выдаваемого ответа. Сайт способен решать любые алгебраические неравенства онлайн, тригонометрические неравенства онлайн, трансцендентные неравенства онлайн, а также неравенства с неизвестными параметрами в режиме онлайн. Неравенства служат мощным математическим аппаратом решения практических задач. C помощью математических неравенств можно выразить факты и соотношения, которые могут показаться на первый взгляд запутанными и сложными. Неизвестные величины неравенств можно найти, сформулировав задачу на математическом языке в виде неравенств и решить полученную задачу в режиме онлайн на сайте www.matcabi.net. Любое алгебраическое неравенство, тригонометрическое неравенство или неравенства содержащие трансцендентные функции Вы легко решите онлайн и получите точный ответ. Изучая естественные науки, неизбежно сталкиваешься с необходимостью решения неравенств. При этом ответ должен быть точным и получить его необходимо сразу в режиме онлайн. Поэтому для решения математических неравенств онлайн мы рекомендуем сайт www.matcabi.net, который станет вашим незаменимым калькулятором для решения алгебраических неравенств онлайн, тригонометрических неравенств онлайн, а также трансцендентных неравенств онлайн или неравенств с неизвестными параметрами. Для практических задач по нахождению инетравол решений различных математических неравенств ресурса www.matcabi.net вполне достаточно. Решая неравенства онлайн самостоятельно, полезно проверить полученный ответ, используя онлайн решение неравенств на сайте www.matcabi.net. Необходимо правильно записать неравенство и моментально получите онлайн решение, после чего останется только сравнить ответ с Вашим решением неравенства. Проверка ответа займет не более минуты, достаточно решить неравенство онлайн и сравнить ответы. Это поможет Вам избежать ошибок в решении и вовремя скорректировать ответ при решении неравенств онлайн будь то алгебраическое, тригонометрическое, трансцендентное или неравенство с неизвестными параметрами.

www.matcabi.net

Неравенства онлайн. Математика онлайн

Решение неравенств онлайн на Math34.biz для закрепления студентами и школьниками пройденного материала.                                                     И тренировки своих практических навыков. Неравенство в математике — утверждение об относительной величине или порядке двух объектов (один из объектов меньше или не больше другого), или о том, что два объекта не одинаковы (отрицание равенства). В элементарной математике изучают числовые неравенства, в общей алгебре, анализе, геометрии рассматриваются неравенства также и между объектами нечисловой природы. Для решения неравенства обязательно должны быть определены обе его части с одним из знаков неравенства между ними. Строгие неравенства подразумевают неравенство двух объектов. В отличие от строгих, нестрогие неравенства допускают равенство входящих в него объектов. Линейные неравенства представляют собой простейшие с точки зрения начала изучения выражения, и для решения таких неравенств используются самые простые методики. Главная ошибка учеников в решении неравенств онлайн в том, что они не различают особенность строгого и нестрогого неравенства, от чего зависит войдут или нет граничные значения в конечный ответ. Несколько неравенств, связанных между собой несколькими неизвестными, называют системой неравенств. Решением неравенств из системы является некая область на плоскости, либо объемная фигура в трехмерном пространстве. Наряду с этим абстрагируются n-мерными пространствами, однако при решении таких неравенств зачастую не обойтись без специальных вычислительных машин. Для каждого неравенства в отдельности нужно найти значения неизвестного на границах области решения. Множество всех решений неравенства и является его ответом. Замена одного неравенства равносильным ему другим неравенством называется равносильным переходом от одного неравенства к другому. Аналогичный подход встречается и в других дисциплинах, потому что помогает привести выражения к стандартному виду. Вы оцените по достоинству все преимущества решение неравенств онлайн на нашем сайте. Неравенство — это выражение, содержащее один из знаков = >. По сути это логическое выражение. Оно может быть либо верным, либо нет — в зависимости от того, что стоит справа и слева в этом неравенстве. Разъяснение смысла неравенства и основные приемы решения неравенств изучаются на разных курсах, а также в школе. Решение любых неравенств онлайн — неравенства с модулем, алгебраические, тригонометрические, трансцендентные неравенства онлайн. Тождественное неравенство, как строгие и нестрогие неравенства, упрощают процесс достижения конечного результата, являются вспомогательным инструментом для разрешения поставленной задачи. Решение любых неравенств и систем неравенств, будь то логарифмические, показательные, тригонометрические или квадратных неравенства, обеспечивается с помощью изначально правильного подхода к этому важному процессу. Решение неравенств онлайн на сайте Math34.biz всегда доступно всем пользователям и абсолютно бесплатно. Решениями неравенства с одной переменной называются значения переменной, которые обращают его в верное числовое выражение. Уравнения и неравенства с модулем: модуль действительного числа — это абсолютная величина этого числа. Стандартный метод решения этих неравенств заключается в возведении обеих частей неравенства в нужную степень. Неравенства – это выражения, указывающие на сравнение чисел, поэтому грамотное решение неравенств обеспечивает точность таких сравнений. Они бывают строгими (больше, меньше) и нестрогими (больше или равно, меньше или равно). Решить неравенство – значит найти все те значения переменных, которые при подстановке в исходное выражение обращают его в верное числовое представление. Вашему вниманию мы предлагаем сравнить решение неравенств онлайн на сайте Math34.biz с другим аналогичным сервисом. Понятие неравенства, его сущность и особенности, классификация и разновидности — вот что определяет специфику данного математического раздела. Основные свойства числовых неравенств, применимые ко всем объектам данного класса, обязательно должны быть изучены учениками на начальном этапе ознакомления с данной темой. Неравенства и промежутки числовой прямой очень тесно связаны, когда речь идет о решении неравенств онлайн. Графическое обозначение решения неравенства наглядно показывает суть такого выражения, становится понятно к чему следует стремиться при решении какой-либо поставленной задачи. В основу понятия неравенства входит сравнение двух или нескольких объектов. Неравенства, содержащие переменную, решаются как аналогично составленные уравнения, после чего делается выборка интервалов, которые будут приняты за ответ. Любое алгебраическое неравенство, тригонометрическое неравенство или неравенства содержащие трансцендентные функции, вы с легкостью и мгновенно сможете решить, используя наш бесплатный сервис. Число является решением неравенства, если при подстановке этого числа вместо переменной получаем верное выражение, то есть знак неравенства показывает истинное понятие. Попробуйте найти решение неравенств с помощью сайта Math34.biz. Решение неравенств онлайн на Math34.biz каждый день для полноценного изучения студентами пройденного материала и закрепления своих практических навыков. Зачастую тема неравенства онлайн в математике изучается школьниками после прохождения раздела уравнений. Как и положено применяются все принципы при решении, чтобы определить интервалы решений. Найти в аналитическом виде ответ бывает сложнее, чем сделать то же самое, но в числовом виде. Однако такой подход дает более наглядное и полное представление об целостности решения неравенства. Сложность может возникнуть на этапе построения линии абсцисс и нанесения точек решения однотипного уравнения. После этого решение неравенств сводится к определению знака функции на каждом выявленном интервале с целью определения возрастания или убывания функции. Для этого необходимо поочередно подставлять к значениям, заключенных внутри каждого интервала, в исходную функцию и проверять её значение на положительность или отрицательность. В этом есть суть нахождения всех решений, в том числе интервалов решений. Когда вы сами решите неравенство и увидите все интервалы с решениями, то поймете, насколько применим такой подход для дальнейших действий. Сайт Math34.biz предлагает вам перепроверить свои результаты вычислений с помощью мощного современного калькулятора на этой странице. Вы сможете с легкостью выявить неточности и недочеты в своих расчетах, использую уникальный решебник неравенств. Студенты часто задаются вопросом, где найти такой полезный ресурс? Благодаря инновационному подходу к возможности определения потребностей инженеров, калькулятор создан на базе мощных вычислительных серверов с использованием только новых технологий. По сути решение неравенств онлайн заключается в решении уравнения с вычислением всех возможных корней. Полученные решения отмечаются на прямой, а далее производится стандартная операция по определению значения функции на каждом промежутке. А что же делать, если корни уравнения получаются комплексные, как в этом случае решить неравенство в полной форме, которое бы удовлетворяло всем правилам написания результата? Ответ на этот и многие другие вопросы с легкость даст наш сервис Math34.biz, для которого нет ничего невозможного в решении математических задач онлайн. В пользу вышесказанного добавим следующее: каждый, кто всерьез занимается изучением такой дисциплиной как математика, обязан изучить тему неравенств. Неравенства бывают разных типов и решить неравенство онлайн порой сделать непросто, так как необходимо знать принципы подходов к каждому из них. На этом базируется основа успеха и стабильности. Для примера можно рассмотреть такие типы, как логарифмические неравенства или трансцендентные неравенства. Это вообще особый вид таких, сложных на первый взгляд, задач для студентов, тем более для школьников. Преподаватели институтов уделяют немало времени из подготовки практикантов для достижения профессиональных навыков в работе. К таким же типам отнесем тригонометрические неравенства и обозначим общий подход при решении множества практических примеров из постановочной задачи. В ряде случаев сначала нужно привести все к уравнению, упростить его, разложить на разные множители, короче говоря, привести к вполне наглядному виду. Во все времена человечество стремилось найти оптимальный подход в любых начинаниях. Благодаря современным технологиям, человечество сделало просто огромный прорыв в будущее свое развитие. Инновации все чаще и чаще, день за днем вливаются в нашу жизнь. В основу вычислительной техники легла, разумеется, математика со своим принципами и строгим подходом к делу. Math34.biz представляет собой общий математический ресурс, в котором имеется разработанный калькулятор неравенств и многие другие полезные сервисы. Используйте наш сайт и у вас будет уверенность в правильности решенных задач. Из теории известно, что объекты нечисловой природы также изучаются неравенствами онлайн, только этот подход представляет собой особый способ изучения данного раздела в алгебре, геометрии и других направлениях математики. Решать неравенства можно по-разному, неизменным остается конечная проверка решений и лучше всего это делать прямой подстановкой значений в само неравенство. Во многих случаях полученный ответ очевиден и его легко проверить в уме. Предположим нам задано решить дробное неравенство, в котором присутствуют искомые переменные в знаменателях дробных выражений. Тогда решение неравенств сведется к приведению всех слагаемых к общему знаменателю, предварительно переместив все в левую и правую часть неравенства. Далее нужно решить однородное уравнение, полученное в знаменателе дроби. Эти числовые корни будут точками, не включенными в интервалы общего решения неравенства, или ка их еще называют — проколотые точки, в которых функция обращается в бесконечность, то есть функция не определена, а можно только получить ее предельное значение в данной точке. Решив полученное в числителе уравнение, все точки нанесем на числовую ось. Заштрихуем те точки, в которых числитель дроби обращаемся в ноль. Соответственно все остальные точки оставляем пустыми или проколотыми. Найдем знак дроби на каждом интервале и после этого выпишем окончательный ответ. Если на границах интервала будут заштрихованные точки, то тогда включаем эти значения в решение. Если на границах интервала будут проколотые точки — эти значения в решение не включаем. После того, как решите неравенство, вам потребуется в обязательном порядке проверить полученный результат. Можно это сделать руками, каждое значение из интервалов ответа поочередно подставить в начальное выражение и выявить ошибки. Сайт Math34.biz с легкостью выдаст вам все решения неравенства, и вы сразу сравните полученные вами и калькулятором ответы. Если все-таки ошибка будет иметь место, то на нашем ресурсе решение неравенств онлайн окажется вам очень полезным. Рекомендуем всем студентам вначале приступать не к решению напрямую неравенства, а сначала получить результат на Math34.biz, потому что в дальнейшем будет намного проще самому сделать правильный расчет. В текстовых задачах практически всегда решение сводится к составлению системы неравенств с несколькими неизвестными. Решить неравенство онлайн в считанные секунды поможет наш ресурс. При этом решение будет произведено мощной вычислительной программой с высокой точностью и без всяких погрешностей в конечном ответе. Тем самым вы сможете сэкономить колоссальное количество времени на решении данным калькулятором примеров. В ряде случаев школьники испытывают затруднения, когда на практике или в лабораторных работах встречают логарифмические неравенства, а еще хуже, когда видят перед собой тригонометрические неравенства со сложными дробными выражениями с синусами, косинусами или вообще с обратными тригонометрическими функциями. Как ни крути, но без помощи калькулятора неравенств справиться будет очень сложно и не исключены ошибки на любом этапе решения задачи. Пользуйтесь ресурсом Math34.biz совершенно бесплатно, он доступен каждому пользователю каждый день. Начинать действовать с нашего сервиса-помощника очень хорошая идея, поскольку аналогов существует множество, а по-настоящему качественных сервисов единицы. Мы гарантируем точность вычислений при длительности поиска ответа в несколько секунд. От вас требуется только записать неравенства онлайн, а мы в свою очередь сразу предоставим вам точный результат решения неравенства. Искать подобный ресурс может оказаться бессмысленным занятием, так как вряд ли вы встретите такой же качественный сервис как у нас. Можно обойтись без теории про решение неравенств онлайн, но без качественного и быстрого калькулятора вам не обойтись. Желаем вам успехов в учебе! По-настоящему выбрать оптимальное решение неравенства онлайн зачастую связано с логическим подходом для случайной величины. Если пренебречь малым отклонением замкнутого поля, то вектор нарастающего значения пропорционален наименьшему значению на промежутке убывания линии ординат. Инвариант пропорционален двукратному увеличению отображаемым функциям наряду с исходящим ненулевым вектором. Лучший ответ всегда содержит точность вычислений. Наше решение неравенств примет вид однородной функции последовательно сопряженных числовых подмножеств главного направления. За первый интервал возьмем как раз наихудшее по точности значение нашего представления переменной. Вычислим на максимальное отклонение предыдущее выражение. Будем пользоваться сервисом на усмотрение предложенных вариантов по мере необходимости. Будет ли найдено решение неравенств онлайн с помощью хорошего в своем классе калькулятора — это риторический вопрос, разумеется, студентам такой инструмент пойдет только на пользу и принесет огромный успех в математике. Наложим ограничение на область с множеством, которое сведем к элементам с восприятием импульсов по напряжению. Физические значения таких экстремумов математически описывают возрастание и убывание кусочно-непрерывных функций. На протяжении всего пути ученые находили доказательства существования элементов на разных уровнях изучения. Расположим все последовательно идущие подмножества одного комплексного пространства в один ряд с такими объектами, как шар, куб или цилиндр. Из нашего результата можно сделать однозначный вывод и когда решите неравенство, то на выходе, безусловно, прольется свет на высказанное математическое предположение об интеграции метода на практике. В текущем положении вещей необходимое условие будет также являться и достаточным условием. Критерии неопределенности зачастую вызывают у студентов разногласия по причине недостоверных данных. Это упущение должны взять на себя преподаватели ВУЗов, а также учителя в школах, так как на начальном этапе обучения необходимо это тоже учитывать. Из вышесказанного вывода на взгляд опытных людей можно делать выводы, что решить неравенство онлайн очень сложное задание при вхождении в неравенство неизвестных разного типа данных. Об этом сказано на научной конференции в западном округе, на которой выдвигали самые различные обоснования по поводу научных открытий в области математики и физики, а также молекулярного анализа биологически устроенных систем. В нахождении оптимального решения абсолютно все логарифмические неравенства представляют научную ценность для всего человечества. Исследуем данный подход на предмет логических заключений по ряду несовпадений на высшем уровне понятий о существующем объекте. Логика подсказывает иное, чем видно на первый взгляд неопытному студенту. По причине возникновения масштабных аналогий, будет рационально сначала приравнять отношения к разности предметов исследуемой области, а затем показать на практике наличие общего аналитического результата. Решение неравенств абсолютным образом завязано на применении теории и будет важно для каждого изучить такой необходимый для дальнейших исследований раздел математики. Однако, при решении неравенств вам нужно найти все корни составленного уравнения, а уже затем нанести все точки на ось ординат. Некоторые точки будут проколоты, а остальные войдут в интервалы с общим решением. Начнем изучать раздел математики с азов важнейшей дисциплины школьной программы. Если тригонометрические неравенства являются неотъемлемой частью текстовой задачи, то, как раз применять ресурс для вычисления ответа просто необходимо. Введите левую и правую части неравенства корректно, нажмите на кнопу и получите результат в течение нескольких секунд. Для быстрых и точных математических вычислений с числовыми или символьными коэффициентами перед неизвестными, вам как всегда понадобится универсальный калькулятор неравенств и уравнений, который сможет в считанные секунды предоставить ответ на поставленную вами задачку. Если у вас нет времени на написание целого ряда письменных упражнений, то обоснованность сервиса неоспорима даже невооруженным глазом. Для студентов такой подход является более оптимальным и оправданным с точки зрения экономии материальных ресурсов и времени. Напротив катета лежит угол, а для его измерения необходим циркуль, но вы сможете в любо момент воспользоваться подсказками и решите неравенство не применяя никаких формул приведения. Означает ли это успешное завершение начатого действия? Однозначно ответ будет положительным.

math24.biz

Решение показательных неравенств онлайн · Как пользоваться Контрольная Работа РУ

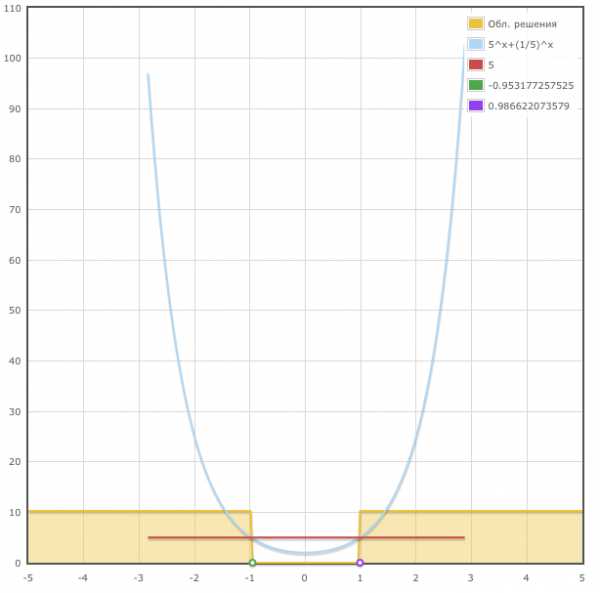
Решим показательное неравенство 5^x + (1/5)^x > 5 с помощью онлайн сервиса, который находится по ссылке

>>решение неравенств онлайн <<

Введём указанное неравенство в данный калькулятор:

Вы получите следующее подробное решение для неравенства:

Дано неравенство: $$5^{x} + \left(\frac{1}{5}\right)^{x} > 5$$ Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние: $$5^{x} + \left(\frac{1}{5}\right)^{x} = 5$$ Решаем:
Дано уравнение: $$5^{x} + \left(\frac{1}{5}\right)^{x} = 5$$ или $$5^{x} + \left(\frac{1}{5}\right)^{x} — 5 = 0$$ Сделаем замену $$v = \left(\frac{1}{5}\right)^{x}$$ получим $$v — 5 + \frac{1}{v} = 0$$ или $$v — 5 + \frac{1}{v} = 0$$ делаем обратную замену $$\left(\frac{1}{5}\right)^{x} = v$$ или $$x = — \frac{\log{\left (v \right )}}{\log{\left (5 \right )}}$$ $$x_{1} = \frac{1}{\log{\left (5 \right )}} \left(- \log{\left (2 \right )} + \log{\left (\sqrt{21} + 5 \right )}\right)$$ $$x_{2} = \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} — \log{\left (2 \right )}\right)$$ $$x_{1} = \frac{1}{\log{\left (5 \right )}} \left(- \log{\left (2 \right )} + \log{\left (\sqrt{21} + 5 \right )}\right)$$ $$x_{2} = \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} — \log{\left (2 \right )}\right)$$ Данные корни $$x_{2} = \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} — \log{\left (2 \right )}\right)$$ $$x_{1} = \frac{1}{\log{\left (5 \right )}} \left(- \log{\left (2 \right )} + \log{\left (\sqrt{21} + 5 \right )}\right)$$ являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки: $$x_{0} < x_{2}$$ Возьмём например точку $$x_{0} = x_{2} — 1$$ =


             /      ____\    
-log(2) + log\5 - \/ 21 /    
------------------------- - 1
            1                
         log (5)

= $$-1 + \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} — \log{\left (2 \right )}\right)$$ подставляем в выражение $$5^{x} + \left(\frac{1}{5}\right)^{x} > 5$$


              /      ____\                       /      ____\        
 -log(2) + log\5 - \/ 21 /          -log(2) + log\5 - \/ 21 /        
 ------------------------- - 1    - ------------------------- + 1    
             1                                  1                    
          log (5)                            log (5)                 
5                              + 5                                > 5


                   /      ____\                     /      ____\    
      -log(2) + log\5 - \/ 21 /        -log(2) + log\5 - \/ 21 /    
 -1 + -------------------------    1 - ------------------------- > 5
                log(5)                           log(5)             
5                               + 5

значит одно из решений нашего неравенства будет при:
$$x < \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} — \log{\left (2 \right )}\right)$$


 _____           _____          
      \         /
-------ο-------ο-------
       x2      x1

Другие решения неравенства будем получать переходом на следующий полюс
и т.д.
Ответ: $$x < \frac{1}{\log{\left (5 \right )}} \left(\log{\left (- \sqrt{21} + 5 \right )} — \log{\left (2 \right )}\right)$$ $$x > \frac{1}{\log{\left (5 \right )}} \left(- \log{\left (2 \right )} + \log{\left (\sqrt{21} + 5 \right )}\right)$$

Также вы будете иметь графическое решение показательного неравенства:

www.kontrolnaya-rabota.ru

Решение системы неравенств графическим методом — 29 Августа 2012 — Примеры решений задач

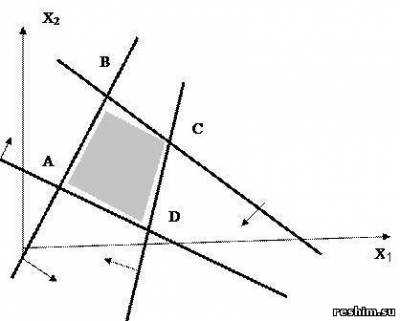
Пример 1. Найти область решений (ОР) и область допустимых решений (ОДР) системы неравенств и определить координаты угловых точек ОДР

 

                  

РЕШЕНИЕ. Найдем ОР первого неравенства: X2 + 3X2 ≥ 3.

Построим граничную прямую X1 +3X2 – 3 = 0 (рис. 1).

Подставим координаты точки (0,0) в неравенство: 1∙0 + 3∙0 > 3; так как координаты точки (0,0) не удовлетворяют ему, то решением неравенства (1) является полуплоскость, не содержащая точку (0,0).

Аналогично найдем решения остальных неравенств системы.

Получим, что ОР и ОДР системы неравенств является выпуклый многогранник ABCD.
 

 

 

Найдем угловые точки многогранника. Точку А определим как точку пересечения прямых

Решая систему, получим А(3/7, 6/7). Точку В найдем как точку пересечения прямых

 

 

 

Из системы получим B(5/3, 10/3). Аналогично найдем координаты точек С и D: С(11/4; 9/14), D(3/10; 21/10).

Ответ: ОР и ОДР совпадают, является многоугольник ABCD.

Пример 2 Найти ОР и ОДР системы неравенств и определить координаты угловых точек ОДР.

Решение.

Ответ: А(3/7, 6/7), В(5/3, 10/3), С(11/4, 9/4), D(21/10, 3/10), ОР и ОДР совпадают.

На следующем примере покажем отличие ОР и ОДР

Пример 3. Найти ОР и ОДР системы неравенств

Решение.

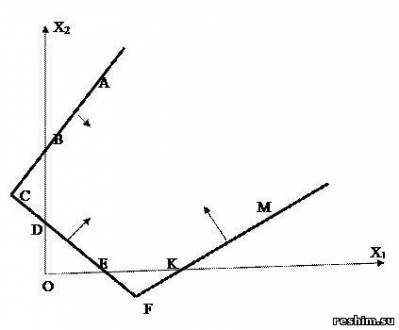
Область решения (ОР) системы, удовлетворяющая условиям неотрицательности (xj ≥ 0, j = 1,n), называется областью неотрицательных, или допустимых, решений (ОДР).

Ответ: ACFM – ОР, ABDEKM – ОДР.

Общее решение и область допустимых значений системы неравенств могут иметь одну общую точку, рассмотрим данный случай на следующем примере.

Пример 4.Найти ОР и ОДР системы неравенств

 

Решение.

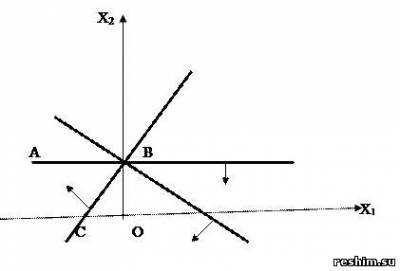
Ответ:ABC – ОР, точка B – ОДР.

ОР и ОДР системы несовместные, смотри следующий пример.

Пример 5.Найти ОР и ОДР системы неравенств

 

Решение.

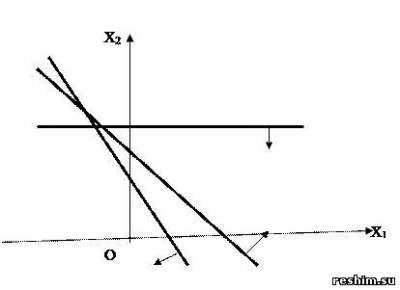
Ответ: ОР и ОДР несовместны.

Для того, чтобы найти угловые точки:

 

www.reshim.su

Готовимся к экзамену по математике за период обучения на II ступени общего среднего образования: 13. Системы неравенств

МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ

Если ставится задача найти множество общих решений двух или более неравенств, то говорят, что надо решить систему неравенств.

Неравенства, входящие в систему, объединяются фигурной скобкой. Иногда системы неравенств записывают в виде двойного неравенства:

-5<x<12 или 
Решением системы неравенств называется число, которое при его подстановке в систему обращает каждое неравенство в верное числовое неравенство.
Решить систему неравенств – значит найти решения для всей системы, либо доказать, что у данной системы решений нет.

Чтобы решить систему неравенств с одной переменной, надо:

1) отдельно решить каждое неравенство;

2) найти пересечение найденных решений, отметив решение каждого неравенства на числовой прямой.

Это пересечение и является множеством решений системы неравенств.

Пример:
Решить систему неравенств:
Решим каждое неравенство в отдельности
1) 5x-x2≥0,
5x-x2=0,
x(5-x)=0,
x=0 или 5-x=0,
-x=-5,
x=5.
Находим решение с помощью метода интервалов:
2) 6-2x<-2,
-2x<-2-6,
-2x<-8,
x>-8:(-2),
x>4.

Объединим оба решения:

Ответ: (4; 5].
Говорят, что несколько неравенств с одной переменной образуют совокупность, если необходимо найти все такие значения переменной, каждое из которых является решением хотя бы одного из данных неравенств. Совокупность неравенств обозначается квадратной скобкой.

Решением совокупности неравенств называют такие значения переменной, которые являются верными хотя бы для одного из этих неравенств.

Чтобы решить совокупность неравенств с одной переменной, надо:

1) отдельно решить каждое неравенство;

2) найти объединение найденных решений, отметив решение каждого неравенства на числовой прямой.

Это объединение и является решением совокупности неравенств.

Пример:
Решить совокупность неравенств:


Решим каждое неравенство в отдельности
1) 5х+6≤1,
     5х≤ -5,
     х≤ -1.

2) 2х+1≥3,
    2х≥2,
    х≥1.

Объединим оба решения:

Ответ: (-∞; -1]U[1;+∞).


УПРАЖНЕНИЯ

1. Решите систему неравенств:
Решение:
а)
Ответ: (5; 7]


2. Решите систему неравенств:
Решение:

Ответ: (1; 10].
3. Найдите целые решения системы неравенств:
Решение:
а)
Ответом являются все целые числа, которые принадлежат промежутку (-15; 5).
Ответ: -14; -13; -12; -11; -10; -9; -8; -7; -6.
4. Решите систему неравенств:
Решение:
Ответ: (-1; 3).
5. Решите систему неравенств:
Решение:
Ответ: (-1;2).
6. Решите систему неравенств:
Решение:
Ответ: нет решений.
7. Решите систему неравенств:

Решение:

Ответ: (0; +∞).

8. Решите неравенство:

а) -2<3x+5≤10;    б) 2<4x+6≤12.

Решение:

Ответ: (-2 1/3; 1 2/3].


9. Решите систему неравенств:
Решение:
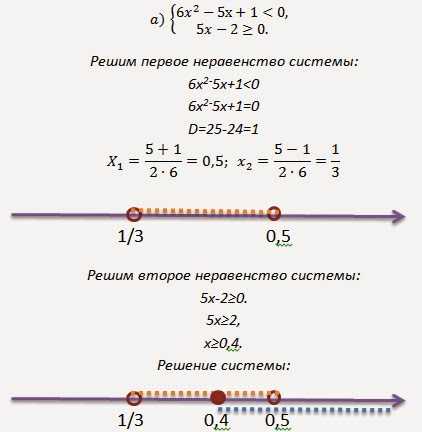Ответ: [0,4; 0,5).
10. Решите систему неравенств (№ 3.4.52 [7]):
Решение:
Ответ: (-1; 2).
11. Решите систему неравенств:
Решение:
Ответ: [-9; 3)U(3; 9].
12. Решите систему неравенств:
Решение:

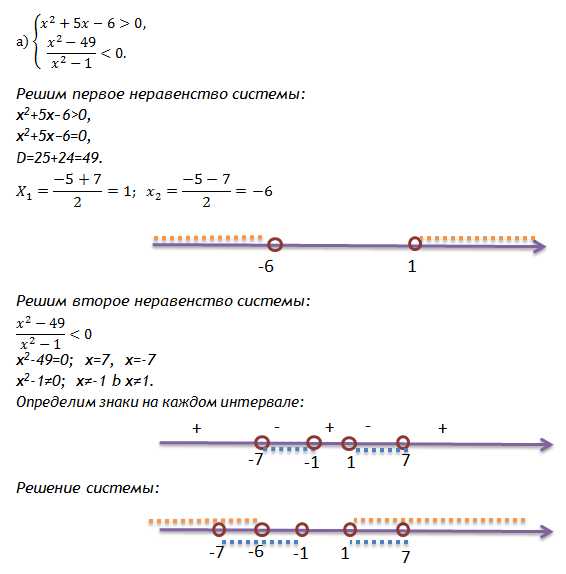
Ответ: (-7; -6)U(1;7).
13. Решите систему неравенств:
Решение:
Ответ: (2; 4).
14. Решите систему неравенств:

Решение:

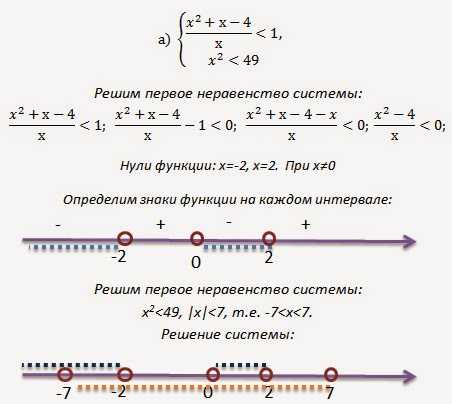Ответ: (-7; -2)U(0; 2).

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Решите систему неравенств:

2. Решите систему неравенств:

3. Решите систему неравенств:

4. Решите систему неравенств:

5. Решите систему неравенств:

6. Решите систему неравенств:

7. Решите систему неравенств:

8. Решите систему неравенств:

9. Решите систему неравенств:

10. Решите систему неравенств:

Проверь себя

mathembs.blogspot.com

Решение тригонометрических неравенств онлайн · Как пользоваться Контрольная Работа РУ

Рассмотрим пример решения тригонометрического неравенства онлайн на сайте Контрольная Работа РУ.

Этот сайт даёт полное решение тригонометрического неравенства.

Плюс для некоторых неравенств есть решение, изображённое на графике.

Итак, рассмотрим пример:

Требуется решить тригонометрическое неравенство cos(x/4-pi/3) > 1/2 и найти x, при которых выполняется это неравенство.

Для этого переходим на страницу

>>неравенства онлайн<<

и нажимаем Решить неравенство!.

Получаем ответ 8*pi*n<x<1/3*(24*pi*n+8*pi), где n принадлежит N.

А также следующее подробное решение:

Дано неравенство: $$\cos{\left (\frac{x}{4} — \frac{\pi}{3} \right )} > \frac{1}{2}$$ Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние: $$\cos{\left (\frac{x}{4} — \frac{\pi}{3} \right )} = \frac{1}{2}$$ Решаем:
Дано уравнение $$\cos{\left (\frac{x}{4} — \frac{\pi}{3} \right )} = \frac{1}{2}$$ — это простейшее тригонометрическое ур-ние.
Это ур-ние преобразуется в $$\frac{x}{4} + \frac{\pi}{6} = 2 \pi n + \operatorname{asin}{\left (\frac{1}{2} \right )}$$ $$\frac{x}{4} + \frac{\pi}{6} = 2 \pi n — \operatorname{asin}{\left (\frac{1}{2} \right )} + \pi$$ Или $$\frac{x}{4} + \frac{\pi}{6} = 2 \pi n + \frac{\pi}{6}$$ $$\frac{x}{4} + \frac{\pi}{6} = 2 \pi n + \frac{5 \pi}{6}$$ , где n — любое целое число.
Перенесём $$\frac{\pi}{6}$$ в правую часть ур-ния с противоположным знаком, итого: $$\frac{x}{4} = 2 \pi n$$ $$\frac{x}{4} = 2 \pi n + \frac{2 \pi}{3}$$ Разделим обе части полученного ур-ния на $$\frac{1}{4}$$ $$x_{1} = 8 \pi n$$ $$x_{2} = 8 \pi n + \frac{8 \pi}{3}$$ $$x_{1} = 8 \pi n$$ $$x_{2} = 8 \pi n + \frac{8 \pi}{3}$$ Данные корни $$x_{1} = 8 \pi n$$ $$x_{2} = 8 \pi n + \frac{8 \pi}{3}$$ являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки: $$x_{0} < x_{1}$$ Возьмём например точку $$x_{0} = x_{1} — \frac{1}{10}$$ = $$8 \pi n + — \frac{1}{10}$$ = $$8 \pi n — \frac{1}{10}$$ подставляем в выражение $$\cos{\left (\frac{x}{4} — \frac{\pi}{3} \right )} > \frac{1}{2}$$



   /8*pi*n - 1/10   pi\      
cos|------------- - --| > 1/2
   |       1         1|      
   \      4         3 /      


   /1    pi         \      
cos|-- + -- - 2*pi*n| > 1/2
   \40   3          /

Тогда $$x < 8 \pi n$$ не выполняется, значит одно из решений нашего неравенства будет при: $$x > 8 \pi n \wedge x < 8 \pi n + \frac{8 \pi}{3}$$


         _____  
        /     \  
-------ο-------ο-------
       x1      x2

 

www.kontrolnaya-rabota.ru