Задания №13 и №16 базового уровня с кубом
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Практикум №1 по решению стереометрических задач (базовый уровень)
Задания №13 и №16базового уровня
с кубом
3. Содержание
• Задача №1• Задача №2
• Задача №3
• Задача №4
• Задача №5
• Задача №6
• Задача №7
• Задача №8
• Задача №9
• Задача №10
• Задача №11
• Задача №12
• Задача №13
• Задача №14
4.
 ВСПОМНИМ• Куб – прямоугольный параллелепипед, все грани
ВСПОМНИМ• Куб – прямоугольный параллелепипед, все граникоторого – квадраты.
• Все грани куба равные квадраты.
• Sп.пов. = 6а²;
Sосн. = а²
• V = a³
• Все диагонали куба равны, пересекаются в одной точке
и делятся этой точкой пополам.
• Боковые рёбра перпендикулярны его основаниям
• d² = 3·a²
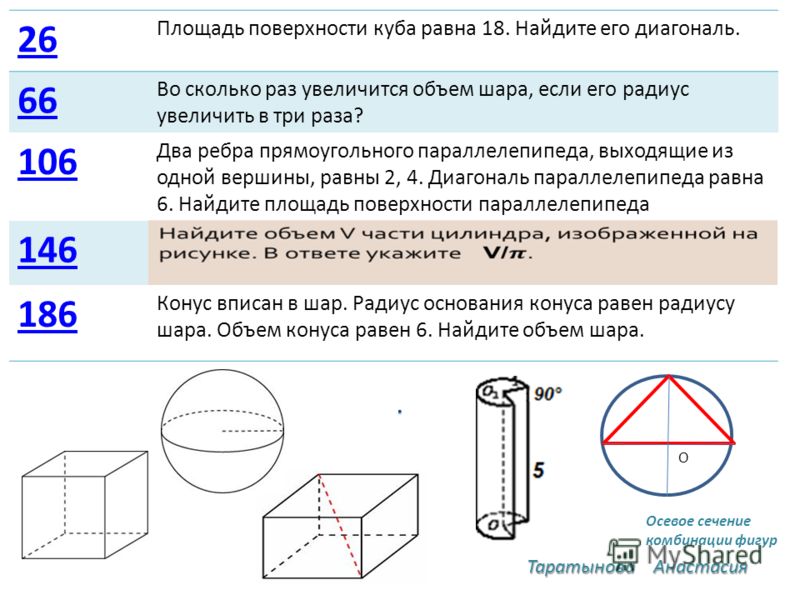
5. Задача №1
Площадь поверхности куба равна 18. Найдите егодиагональ.
Решение.
Пусть ребро куба равно а, тогда площадь
поверхности куба S=6a², а диагональ куба
d = a√3. Тогда
Ответ: 3.
6. Задача №2
Объем куба равен 8. Найдите площадь егоповерхности.
Решение.
Площадь поверхности куба выражается через
его ребро а как S=6a², а объем — как V=a³.
Отсюда видно, что площадь поверхности куба
выражается через его объем как
.
Отсюда находим, что
7. Задача №3
Если каждое ребро куба увеличить на 1, то егоплощадь поверхности увеличится на 54. Найдите
ребро куба.
Решение.
Площадь поверхности куба выражается через его ребро a
как S=6a², поэтому при увеличении длины ребра на 1
площадь увеличится на
Отсюда находим, что ребро
8. Задача №4
Во сколько раз увеличится объем куба, если егоребра увеличить в три раза?
Решение.
Объем куба с ребром а равен V=a³. Если ребра
увеличить в 3 раза, то объем куба увеличится
в 3³=27 раз.
Ответ: 27
9. Задача №5
Объем куба равен 24√3 . Найдите его диагональ.Решение.
Пусть ребро куба равно а, тогда площадь
поверхности куба S=6a², а диагональ
куба d = a√3. Тогда
Значит d = 6.
Можно решить и через….
10. Задача №6
Если каждое ребро куба увеличить на 1, то его объемувеличится на 19. Найдите ребро куба.
Решение.
Объем куба с ребром а равен V=a³. Увеличение объема равно
19:
Решим уравнение: a² + a — 6 = 0 => a=2; a= -3(не подходит)
Ответ: 2.
11. Задача №7
Во сколько раз увеличится площадь поверхностикуба, если его ребро увеличить в три раза?
Решение.

Площади подобных тел относятся как квадрат
коэффициента подобия, поэтому при увеличении
ребра в 3 раза, площадь поверхности увеличится
в 9 раз.
12. Задача №8
Диагональ куба равна 1. Найдите площадь егоповерхности.
Решение.
Знаем, что d = a√3. => а = d:√3 = 1/√3 , тогда
13. Задача №9
Площадь поверхности куба равна 24. Найдите его объем.Решение.
Объем куба с ребром а равен V=a³, а S=6a². => а²=S/6
Т.е. а=√S/6, тогда
14. Задача №10
Объем одного куба в 8 раз больше объема другого куба.Во сколько раз площадь поверхности первого куба
больше площади поверхности второго куба?
Решение.
Объемы подобных тел относятся как куб коэффициента
подобия, поэтому один из кубов в 2 раза больше
другого.
Площади поверхностей подобных тел относятся как
квадрат коэффициента подобия, поэтому их отношение
равно 4.
15. Задача №11
От деревянного кубика отпилили все его вершины (см.рис).
 Сколько граней у получившегося многогранника
Сколько граней у получившегося многогранника(невидимые ребра на рисунке не обозначены)?
Решение.
У кубика 6 граней. В результате
отпиливания 8 вершин появились 8
граней. Всего 14 граней.
16. Задача №12
Плоскость, проходящая через три точки A, B и С,разбивает куб на два многогранника. Сколько граней у
многогранника, у которого больше рёбер?
Решение.
В
сечении
получается
четырёхугольник.
У одной отсечённой фигуры 15 рёбер
и 7 граней, у второй — 9 рёбер и 5
граней.
Ответ: 7 граней.
17. Задача №13
Ящик, имеющий форму куба с ребром 10 см без однойграни, нужно покрасить со всех сторон снаружи.
Найдите площадь поверхности, которую необходимо
покрасить. Ответ дайте в квадратных сантиметрах.
Решение.
Площадь одной грани равна 10 · 10 = 100 см². В кубе
шесть граней, но нам надо найти только площадь пяти
граней, следовательно 100 · 5 = 500 см².
Ответ: 500
18. Задача №14
Диагональ куба равна √12 . Найдите его объем.
Найдите его объем.Решение.
Диагональ куба d = a√3 , т.е. в √3 раз
больше его ребра. Получим, что ребро равно
Тогда V=a³ = 2³ = 8
Задачи
для самостоятельного
решения
20. Задача №1 Решите самостоятельно
1) Площадь поверхности куба равна 2592. Найдитеего диагональ.
Ответ: 36
2) Площадь поверхности куба равна 1568. Найдите
его диагональ.
3) Площадь поверхности куба равна 18. Найдите
его диагональ.
21. Задача №2 Решите самостоятельно
1) Объем куба равен 8. Найдите площадь егоповерхности.
2) Объем куба равен 343. Найдите площадь его
поверхности.
3) Объем куба равен 216. Найдите площадь его
поверхности.
4) Объем куба равен 125. Найдите площадь его
поверхности.
22. Задача №3 Решите самостоятельно
1) Если каждое ребро куба увеличить на 5, то егоплощадь поверхности увеличится на 390.
Найдите ребро куба.
Ответ: 4
2) Если каждое ребро куба увеличить на 2, то его
площадь поверхности увеличится на 144.

Найдите ребро куба.
3) Если каждое ребро куба увеличить на 4, то его
площадь поверхности увеличится на 240.
Найдите ребро куба.
23. Задача №4 Решите самостоятельно
1) Во сколько раз увеличится объем куба, если егоребра увеличить в пятнадцать раз?
2) Во сколько раз увеличится объем куба, если его
ребра увеличить в шесть раз?
3) Во сколько раз увеличится объем куба, если его
ребра увеличить в 12 раз?
4) Во сколько раз увеличится объем куба, если его
ребра увеличить в 10 раз?
24. Задача №5 Решите самостоятельно
Задача №51)
2)
3)
4)
5)
6)
Решите самостоятельно
Объем куба равен 0,003√3. Найдите его диагональ.
Объем куба равен 1536√3. Найдите его диагональ.
Объем куба равен 3000√3. Найдите его диагональ.
Объем куба равен 81√3. Найдите его диагональ.
Объем куба равен 192√3. Найдите его диагональ.
Объем куба равен 2187√3. Найдите его диагональ.
25. Задача №6 Решите самостоятельно
1) Если каждое ребро куба увеличить на 2, то его объемувеличится на 728.
 Найдите ребро куба.
Найдите ребро куба.2) Если каждое ребро куба увеличить на 3, то его объем
увеличится на 819. Найдите ребро куба.
3) Если каждое ребро куба увеличить на 3, то его объем
увеличится на 1413. Найдите ребро куба.
4) Если каждое ребро куба увеличить на 1, то его объем
увеличится на 721. Найдите ребро куба.
26. Задача №7 Решите самостоятельно
1) Во сколько раз увеличится площадьповерхности куба, если его ребро увеличить в 2
раза?
2) Во сколько раз увеличится площадь
поверхности куба, если его ребро увеличить в 24
раза?
3) Во сколько раз увеличится площадь
поверхности куба, если его ребро увеличить в 33
раза?
27. Задача №8 Решите самостоятельно
1) Диагональ куба равна 6. Найдите площадь егоповерхности.
2) Диагональ куба равна 34. Найдите площадь его
поверхности.
3) Диагональ куба равна 41. Найдите площадь его
поверхности.
4) Диагональ куба равна 9. Найдите площадь его
поверхности.
28.
 Задача №9 Решите самостоятельно1) Площадь поверхности куба равна 864. Найдите его
Задача №9 Решите самостоятельно1) Площадь поверхности куба равна 864. Найдите егообъем.
2) Площадь поверхности куба равна 54. Найдите его
объем.
3) Площадь поверхности куба равна 216. Найдите его
объем.
4) Площадь поверхности куба равна 96. Найдите его
объем.
29. Задача №10 Решите самостоятельно
1) Объем одного куба в 125 раз больше объема другогокуба. Во сколько раз площадь поверхности первого куба
больше площади поверхности второго куба?
2) Объем одного куба в 64 раз больше объема другого
куба. Во сколько раз площадь поверхности первого куба
больше площади поверхности второго куба?
3) Объем одного куба в 729 раз больше объема другого
куба. Во сколько раз площадь поверхности первого куба
больше площади поверхности второго куба?
30. Задача №13 Решите самостоятельно
1) Ящик, имеющий форму куба с ребром 30 см безодной грани, нужно покрасить со всех сторон
снаружи. Найдите площадь поверхности,
которую необходимо покрасить.
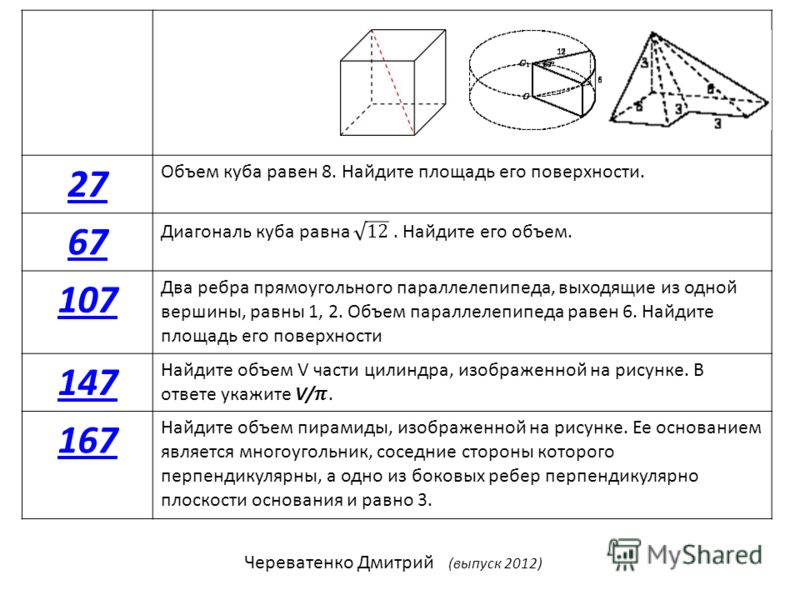 Ответ дайте в
Ответ дайте вквадратных сантиметрах. Ответ: 4500
31. Задача №14 Решите самостоятельно
1)2)
3)
4)
5)
6)
Диагональ куба равна √243 . Найдите его объем.
Диагональ куба равна √588 . Найдите его объем.
Диагональ куба равна √48 . Найдите его объем.
Диагональ куба равна √300 . Найдите его объем.
Диагональ куба равна √27 . Найдите его объем.
Диагональ куба равна √675 . Найдите его объем.
32. Интернет ресурсы
• Шаблон подготовила учитель русского языка и литературыТихонова Надежда Андреевна
• «Решу ЕГЭ» Образовательный портал для подготовки к ЕГЭ и ОГЭ. Режим доступа:
http://mathb.reshuege.ru
http://sch-53.ru/files/director/GIA/2016/%D0%95%D0%93%D0%AD%202016.jpg
http://a550.phobos.apple.com/us/r30/Purple/v4/0c/91/17/0c9117c4-c866-54fc68ce-0e5aa31f5929/mzl.dfcpkqki.png
English Русский Правила
Диагональ куба равна корню
Не откладывайте! ЗАГОВОРИТЕ на Английском!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2014-02-05
Для вас следующая статья с кубами и прямоугольными параллелепипедами. Посмотрите предыдущую, там перечислены используемые формулы (вдруг позабылись). Задачи здесь представлены несложные, они очень похожи друг на друга. Думаю, будет полезно.
Посмотрите предыдущую, там перечислены используемые формулы (вдруг позабылись). Задачи здесь представлены несложные, они очень похожи друг на друга. Думаю, будет полезно.
Рассмотрим задания:
Диагональ куба равна корню из трёхсот. Найдите его объем.
Обозначим ребро куба как a.
Объём куба вычисляется по формуле:
То есть для нахождения объёма куба необходимо найти его ребро.
Диагональ куба находится по формуле:
Значит
Таким образом:
Ответ: 1000
Объём куба равен 81√3. Найдите его диагональ.
Это задача обратная предыдущей.
Диагональ куба находится по формуле:
Выразим ребро куба из формулы объёма подставим:
*Если вы хотите вспомнить как работать со степенями и корнями, тогда вам сюда.
Ответ: 9
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 72 и 18. Диагональ параллелепипеда равна 78.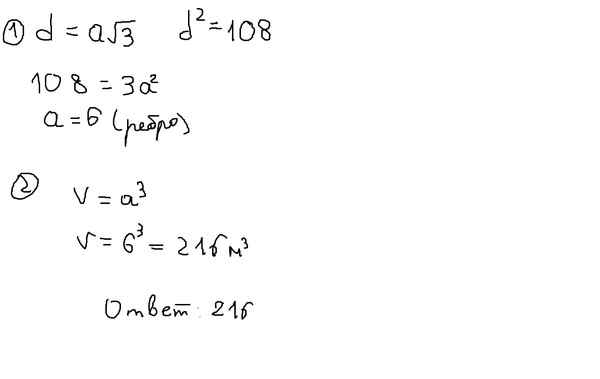 Найдите объем параллелепипеда.
Найдите объем параллелепипеда.
Пусть рёбра параллелепипеда равны a, b и с.
Для нахождения объёма нам необходимо знать его третье ребро. Как его найти?
Мы можем воспользоваться формулой диагонали параллелепипеда:
Получается:
Вычислим неизвестное ребро:
Таким образом, объём параллелепипеда равен:
*При разности квадратов используйте формулу, решение упрощается.
Ответ: 31104
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 12 и 6. Объем параллелепипеда равен 864. Найдите его диагональ.
Задача обратная предыдущей. Для того, чтобы найти диагональ, необходимо знать чему равно третье ребро. Мы можем вычислить его воспользовавшись формулой объёма:
Диагональ параллелепипеда равна:
Ответ: 18
Диагональ куба равна 41. Найдите площадь его поверхности.
Площадь поверхности куба равна:
Формула длины диагонали куба:
Выразим ребро и подставим полученное выражение в формулу площади поверхности:
Тогда площадь поверхности куба:
Ответ: 3362
Площадь поверхности куба равна 216. Найдите его объем.
Найдите его объем.
Площадь поверхности куба со стороной равна S = 6 a2.
Найдём ребро куба:
Объем куба равен:
Ответ: 216
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.
Для того, чтобы вычислить площадь поверхности необходимо знать третье ребро:
Используем формулу длины диагонали:
Получается:
Таким образом:
Ответ: 64
27128. Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите его площадь поверхности. Ответ: 22.
27146. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1 и 2 Объем параллелепипеда равен 6. Найдите площадь его поверхности. Ответ: 22
27098. Диагональ куба равна корню из двенадцати. Найдите его объем.
Посмотреть решение
27101. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.
Посмотреть решение
27139. Диагональ куба равна 1. Найдите площадь его поверхности.
Посмотреть решение
27141. Площадь поверхности куба равна 24. Найдите его объем.
Посмотреть решение
Вот ещё задачи с кубами и параллелепипедами, но они чуть посложнее, не пропустите!
На этом всё! Успеха вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Стереометрия ПРИЗМЫ | ЕГЭ-№2
НЕ ОТКЛАДЫВАЙ! Заговори на английском!
ДОЛОЙ обидные ошибки на ЕГЭ!!
Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Кубический корень из 243 — Как найти кубический корень из 243? [Решено]
Значение кубического корня из 243, округленное до 6 знаков после запятой, равно 6,240251. Это действительное решение уравнения x 3 = 243. Кубический корень из 243 выражается как ∛243 или 3 ∛9 в радикальной форме и как (243) ⅓ или (243) 0,33 в радикальной форме. показательная форма. Разложение числа 243 на простые множители равно 3 × 3 × 3 × 3 × 3, следовательно, кубический корень из 243 в его низшей радикальной форме выражается как 3 ∛9.
Это действительное решение уравнения x 3 = 243. Кубический корень из 243 выражается как ∛243 или 3 ∛9 в радикальной форме и как (243) ⅓ или (243) 0,33 в радикальной форме. показательная форма. Разложение числа 243 на простые множители равно 3 × 3 × 3 × 3 × 3, следовательно, кубический корень из 243 в его низшей радикальной форме выражается как 3 ∛9.
- Кубический корень из 243:
- Кубический корень из 243 в экспоненциальной форме: (243) ⅓
- Кубический корень из 243 в радикальной форме: ∛243 или 3 ∛9
| 1. | Что такое кубический корень из 243? |
| 2. | Как вычислить кубический корень из 243? |
| 3. | Является ли кубический корень из числа 243 иррациональным? |
4. | Часто задаваемые вопросы о кубическом корне из 243 |
Что такое кубический корень из 243?
Кубический корень из 243 — это число, которое при трехкратном умножении само на себя дает произведение 243. Поскольку 243 можно выразить как 3 × 3 × 3 × 3 × 3. Следовательно, кубический корень из 243 = ∛(3 × 3 × 3 × 3 × 3) = 6,2403.
☛ Проверка: Калькулятор кубического корня
Как вычислить значение кубического корня из 243?
Кубический корень из 243 по методу Галлея
Его формула: ∛a ≈ x ((x 3 + 2a)/(2x 3 + a))
где,
a = число, для которого вычисляется кубический корень
x = целочисленное предположение его кубического корня.
Здесь а = 243
Предположим, что x равен 6
.
[∵ 6 3 = 216, а 216 — ближайший совершенный куб, меньший 243]
Следовательно,
∛243 = 6 (6 3 + 2 × 243)/(2 × 6 3 + 243)) = 6,24
⇒ ∛243 ≈ 6,24
Таким образом, кубический корень из 243 приблизительно равен 6,24.

Является ли кубический корень из числа 243 иррациональным?
Да, потому что ∛243 = ∛(3 × 3 × 3 × 3 × 3) = 3 ∛9 и его нельзя выразить в виде p/q, где q ≠ 0. Следовательно, значение кубического корня из 243 — иррациональное число.
☛ Также проверьте:
- Кубический корень из 125
- Кубический корень из 3000
- Кубический корень из 432
- Кубический корень из 23
- Кубический корень из 192
- Кубический корень из 189
- Кубический корень из 19
Кубический корень из 243 решенных примеров
Пример 1: Дан объем куба 243 в 3 . Найдите длину стороны куба.
Решение:
Объем куба = 243 в 3 = a 3
⇒ а 3 = 243
Укоренение куба с обеих сторон,
⇒ а = ∛243 в
Поскольку кубический корень из 243 равен 6,24, следовательно, длина стороны куба равна 6,24 дюйма.
Пример 2. Найдите действительный корень уравнения x
Решение:
x 3 − 243 = 0, то есть x 3 = 243
Решение для x дает нам
x = ∛243, x = ∛243 × (-1 + √3i))/2 и x = ∛243 × (-1 — √3i))/2
где я называется мнимой единицей и равен √-1.
Игнорирование мнимых корней,
х = ∛243
Следовательно, действительный корень уравнения x 3 − 243 = 0 равен x = ∛243 = 6,2403.Пример 3: Каково значение ∛243 ÷ ∛(-243)?
Решение:
Кубический корень из -243 равен минусу кубического корня из 243.
⇒ ∛-243 = -∛243Следовательно,
⇒ ∛243/∛(-243) = ∛243/(-∛243) = -1
перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем.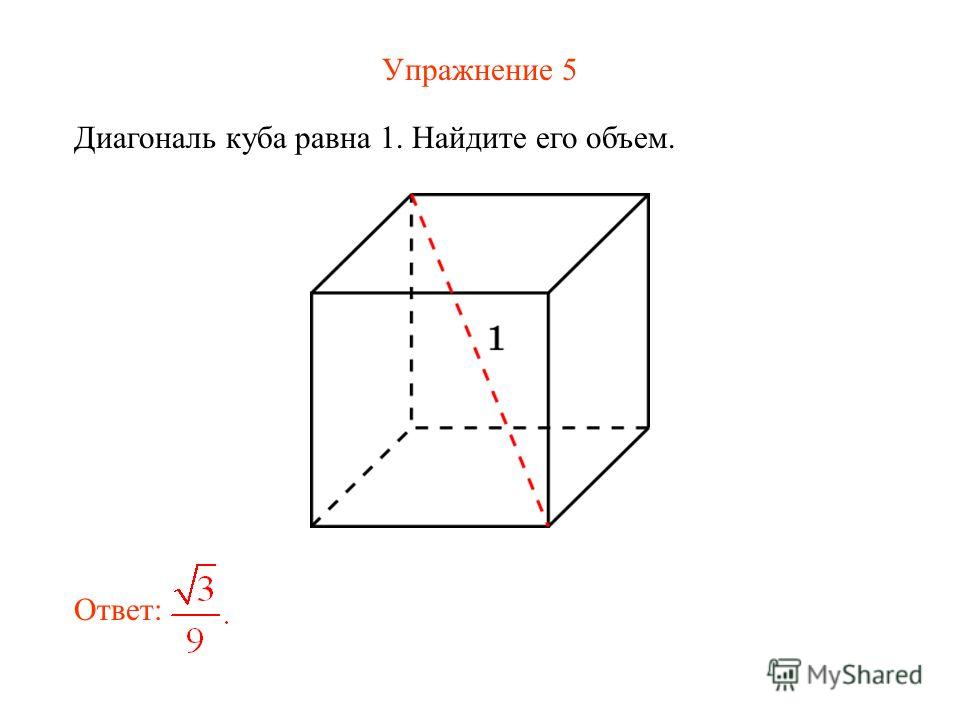 Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Запишитесь на бесплатный пробный урок
Часто задаваемые вопросы о кубическом корне из 243
Каково значение кубического корня из 243?
Мы можем выразить 243 как 3 × 3 × 3 × 3 × 3, то есть ∛243 = ∛(3 × 3 × 3 × 3 × 3) = 6,24025. Следовательно, значение кубического корня из 243 равно 6,24025.
Что такое куб кубического корня из 243?
Куб кубического корня из 243 есть само число 243, т. е. (∛243) 3 = (243 1/3 ) 3 = 243.
Почему значение кубического корня из 243 Иррациональный?
Значение кубического корня из 243 не может быть выражено в виде p/q, где q ≠ 0. Следовательно, число ∛243 иррационально.
Каково значение 12 плюс 18 кубический корень 243?
Значение ∛243 равно 6,24. Итак, 12 + 18 × ∛243 = 12 + 18 × 6,24 = 124,32000000000001. Следовательно, значение 12 плюс 18 кубический корень 243 равно 124,32000000000001.
Если кубический корень числа 243 равен 6,24, найдите значение ∛0,243.
Представим ∛0,243 в виде p/q, т.е. ∛(243/1000) = 6,24/10 = 0,62. Следовательно, значение ∛0,243 = 0,62.
Что такое кубический корень из -243?
Кубический корень из -243 равен отрицательному значению кубического корня из 243. Следовательно, ∛-243 = -(∛243) = -(6,24) = -6,24.
Как найти диагональ куба
Все ресурсы по промежуточной геометрии
8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Learn by Concept
Intermediate Geometry Help » Твердая геометрия » Кубики » Как найти диагональ куба
Найдите диагональ куба со стороной .
Возможные ответы:
Правильный ответ:
Объяснение:
Диагональ куба просто определяется как:
Где это длина стороны куба.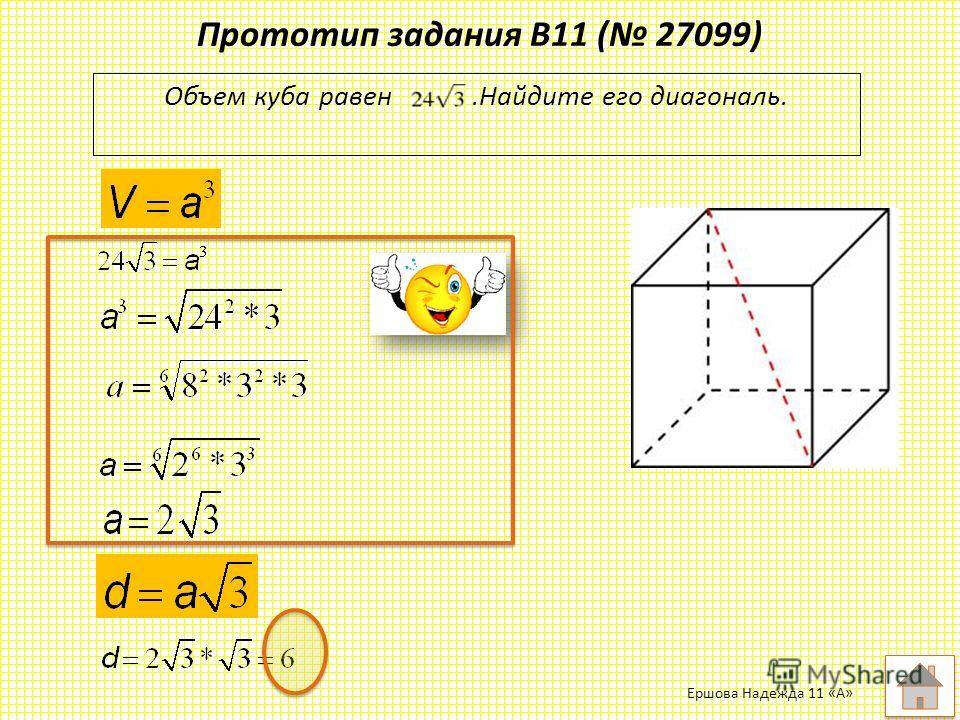
Итак, поскольку наш
Сообщить об ошибке
Если объем куба равен одной восьмой, какова диагональ куба?
Возможные ответы:
Пояснение:
Запишите объем куба и подставьте данный объем, чтобы найти длину стороны.
Напишите формулу диагонали куба и подставьте длину стороны.
Сообщить об ошибке
Найдите длину диагонали куба объемом
Возможные ответы:
Правильный ответ:
Пояснение:
Существует формула для длины диагонали куба через длину стороны. Однако мы можем не помнить эту формулу, поскольку она менее распространена.
Но сначала нам нужно найти длину стороны. Мы знаем, что объем равен 64. Наша формула для объема:
Подстановка дает
Получение кубического корня дает нам длину стороны 4. Теперь давайте посмотрим на наш куб.
Начнем с того, что найдем длину диагонали нижней грани нашего куба (зеленый отрезок). Это можно сделать либо с помощью теоремы Пифагора, либо поняв, что прямоугольный треугольник на самом деле является треугольником 45-45-90. В любом случае, мы понимаем, что наша диагональ (гипотенуза) равна .
Теперь попробуем найти диагональ куба (синий сегмент). Мы делаем это, глядя на образованный им прямоугольный треугольник, левое вертикальное ребро и только что найденную диагональ грани. На этот раз нам остается только воспользоваться теоремой Пифагора.
В общем, формула для диагонали куба с длиной стороны – это
. Какова длина диагонали?
Какова длина диагонали?
Возможные ответы:
Правильный ответ:
Пояснение:
Напишите уравнение объема куба. Подставьте объем, чтобы найти длину стороны, .
Напишите уравнение для нахождения диагоналей куба по длине ребра.
Подставьте длину стороны, чтобы найти длину диагонали.
Ответ .
Сообщить об ошибке
Если объем куба равен , то какова длина диагонали?
Возможные ответы:
Правильный ответ:
Объяснение:
Напишите уравнение для нахождения объема куба и подставьте в него объем.
Напишите диагональное уравнение для кубов и подставьте в него заданную длину.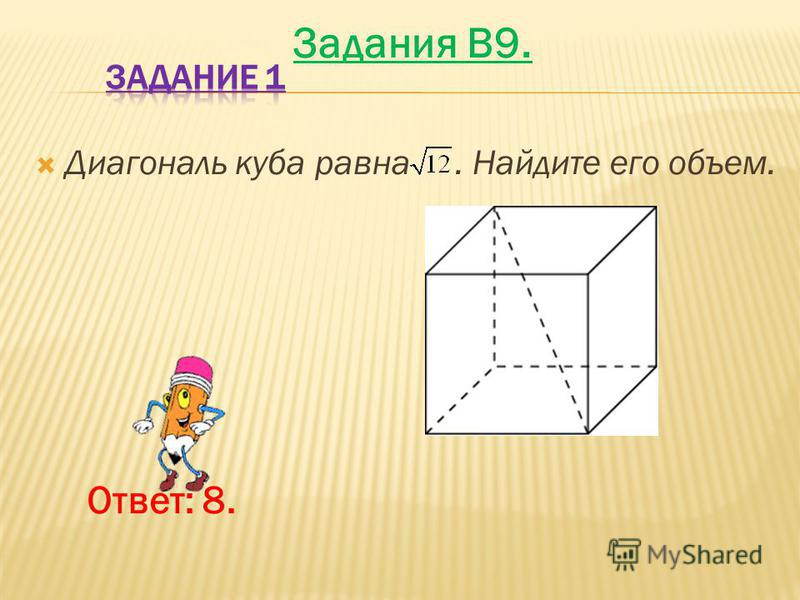
Сообщить об ошибке
Если площадь поверхности куба равна , какова длина диагонали?
Возможные ответы:
Правильный ответ:
Объяснение:
Напишите формулу площади поверхности для кубов и подставьте заданную площадь.
Напишите формулу диагонали куба и подставьте длину стороны.
Отчет о ошибке
Найдите расстояние от точки A до точки B в кубе ниже (оставьте ответ в самой простой радикальной форме):
Возможные ответы:
Правильный ответ:
9003 . Объяснение: При вычислении диагонали куба, точка А в точку Б. Сначала мы должны найти диагональ основания куба. Основание куба представляет собой квадрат, все стороны которого равны 8. Диагональ этого квадрата находится либо по теореме Пифагора, либо по тому, что мы знаем о 45-45-90 треугольниках, чтобы получить диагональ основания ниже : Диагональ основания будет проходить от точки A до точки C на чертеже. Мы видим, что диагональ основания и сторона BC куба образуют две стороны прямоугольного треугольника, что позволит нам найти трехмерную диагональ всего куба. Используйте теорему Пифагора с BC и диагональю основания. Извлеките квадратный корень из обеих сторон. После упрощения всего получаем окончательный ответ для Диагонали Куба (AB). Сообщить об ошибке Куб имеет длину стороны 6 метров. Какова длина его диагонали, проходящей через одну из граней? Возможные ответы: метра Ни один из этих метров метра метра Правильный ответ: метры 4
Пояснение: Так как все стороны куба равны и все стороны образуют прямые углы, мы используем теорему Пифагора, чтобы найти длину диагонали.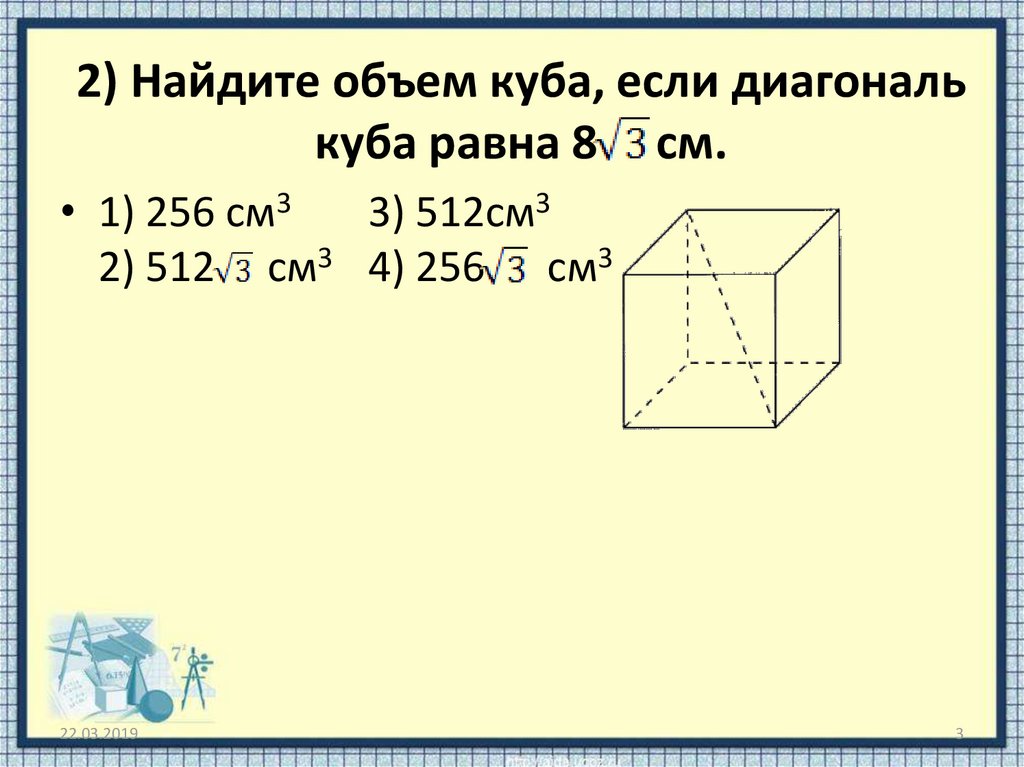



Leave A Comment