10 класс. Геометрия. Многогранники. Призма. — Многогранники. Призма. Задачи на призму.
Комментарии преподавателяНа этом занятии мы повторим основные сведения о многогранниках. Особенное внимание уделим определению призмы. Вспомним теорему о площади боковой поверхности прямой призмы.
На рисунке 1 изображена призма ABCDFA1B1C1D1F1, ее основания ABCDF и A1B1C1D1F1. Пятиугольники ABCDF и A1B1C1D1F1 равны и лежат в параллельных плоскостях.
Рис. 1
Призма – это многогранник, в основаниях которого лежат равные многоугольники, а боковые грани – параллелограммы.
Основания призмы – это две грани, являющиеся равными многоугольниками, которые лежат в параллельных плоскостях.
Боковыми гранями являются все грани призмы, кроме оснований. Каждая боковая грань является параллелограммом.
Общие стороны боковых граней называются боковыми ребрами.
Вернемся к рисунку 1. В пятиугольнике ABCDFA1B1C1D1F1:
ABCDF
Боковыми гранями являются грани АА1В1В, ВВ1С1С, CC1D1D, DD1F1F, FF1A1A. А боковыми ребрами – АА1, ВВ1, СС1, DD1, FF1.
Определение. Если боковое ребро призмы перпендикулярно плоскости ее основания, то такая призма называется прямой.
Рассмотрим пятиугольную призму ABCDFA1B1C1D1F1 (рис. 2).
Пусть боковое ребро AA1 перпендикулярно плоскости основания. Значит, данная призма – прямая. Так как ребро 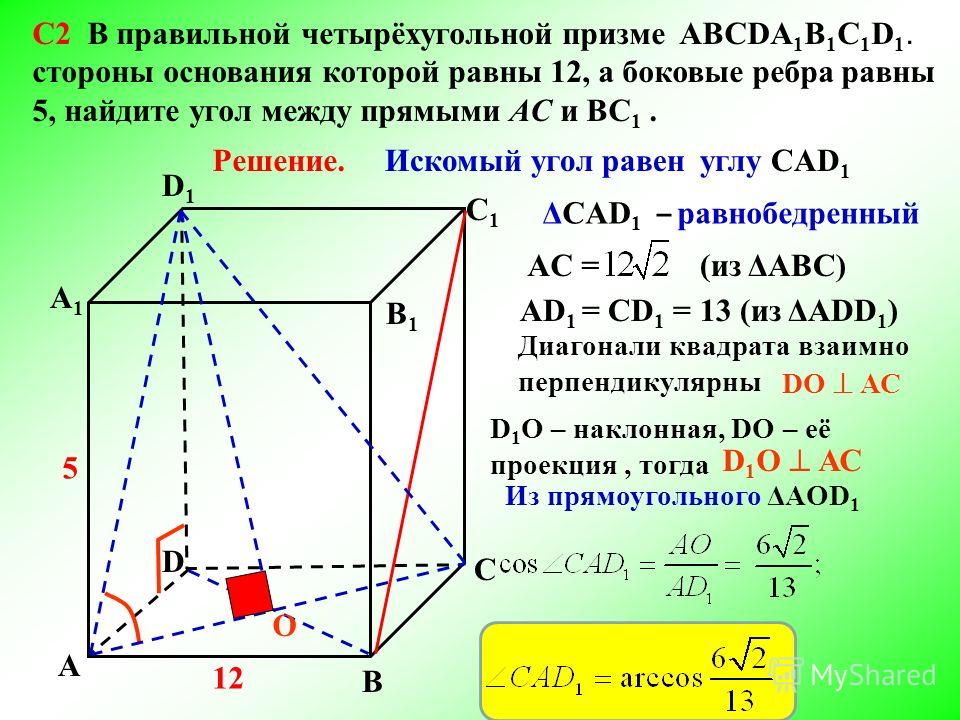 Значит, боковая грань является прямоугольником.
Значит, боковая грань является прямоугольником.
Рис. 2
Рассмотрим параллелепипед ABCDA1B1C1D1 (рис. 3) – частный случай призмы. В основаниях призмы лежат параллелограммы ABCD и A1B1C1D1.
Рис. 3
Если боковое ребро перпендикулярно плоскости основания, то такой параллелепипед будет называться прямым параллелепипедом.
Рис. 4
Рассмотрим параллелепипед ABCDA1B1C1D1
Если в основании прямого параллелепипеда лежит прямоугольник, то такой параллелепипед называется прямоугольным. Обозначение: ABCDA1B1C1D1 или кратко AC1.
Определение. Правильной n-угольной призмой называется такая прямая призма, у которой в основаниях лежит правильный n-угольник.
Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
Рассмотрим эту теорему на примере треугольной прямой призмы ABCA1B1C1
Дано: АВСА1В1С1 – прямая призма, т. е. АА1 ⊥ АВС.
АА1 = h.
Доказать: Sбок = Росн ∙ h.
Рис. 5
Доказательство.
Треугольная призма АВСА1В1С1 – прямая, значит, боковые грани АА1В1В, АА1С1С, ВВ1С1С – прямоугольники. А все боковые ребра призмы равны высоте призмы.
Найдем площадь боковой поверхности как сумму площадей прямоугольников АА1В1В, АА1С1С, ВВ1С1С:
Sбок = АВ∙ АА1 + ВС∙ ВВ1 + СА∙ СС1 = АВ∙ h + ВС∙ h + СА∙ h = (AB + ВС + CА) ∙ h = Pосн ∙ h.
Получаем, Sбок = Росн ∙ h, что и требовалось доказать.
В правильной n-угольной призме сторона основания равна a и высота равна h. Вычислить площадь боковой и полной поверхности призмы, если n = 3, h = 15 см, a = 10 см. См. рис. 6.
Вычислить площадь боковой и полной поверхности призмы, если n = 3, h = 15 см, a = 10 см. См. рис. 6.
Дано: АВСА1В1С1 – призма,
АА1 ⊥ АВС,
h = АА1 = 15см,
АВ = BC = CA = a = 10 см.
Найти: Sбок , Sполн.
Рис. 6
Решение:
По условию призма прямая. Значит, ребро АА1 перпендикулярно плоскости основания и равно высоте призмы.
Площадь боковой поверхности прямой призмы равна произведению периметра основания призмы на высоту. Найдем площадь боковой поверхности.
Sбок = Pосн ∙ h = PАВС ∙ АА1 = 3 ∙ АВ ∙ h = 3∙ 10 ∙ 15 = 450 (см2).
В основании призмы лежит правильный треугольник АВС. Найдем его площадь.
(см2)
Площадь полной поверхности призмы – это площадь всех ее граней, то есть площадь боковой поверхности плюс площади двух оснований. Значит:
(см2).
Ответ: (см2).
Боковое ребро наклонной четырехугольной призмы равно 12 см. Перпендикулярным сечением является ромб со стороной 5 см. Найти площадь боковой поверхности.
Дано: призма ABCDA1B1C1D1 (рис. 7),
АА1 = 12 см,
перпендикулярное сечение – ромб со стороной 5 см.
Найти: Sбок
Рис. 7
Решение:
Мы доказали на прошлом уроке, что площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на боковое ребро.
По условию, перпендикулярным сечением является ромб со стороной 5 см. Все стороны ромба равны. Значит, периметр перпендикулярного сечения равен см.
Теперь вычислим площадь боковой поверхности:
(см2).
Ответ: 240 см2.
Основанием прямой призмы является равнобедренная трапеция с основаниями 25 см и 9 см и высотой 8 см. Найдите двугранные углы при боковых рёбрах призмы. См. рис. 8.
Дано: ABCDA1B1C1D1 – призма,
AA1 ⊥ ABC,
AB ∥ CD, CB = AD,
AB = 9 см, CD = 25 см,
hтрап= 8 см.
Найти: двугранные углы при боковых рёбрах призмы.
Рис. 8
Решение:
Вспомним, что такое двугранный угол. Пусть у нас есть две полуплоскости α и β, которые пересекаются по прямой СC1 (рис. 9). Тогда они образовывают двугранный угол с ребром СC1. Двугранный угол измеряется своим линейным углом.
Как строится линейный угол? Берется произвольная точка M на ребре, и проводятся два перпендикуляра: один перпендикуляр в плоскости β – перпендикуляр b, второй перпендикуляр в плоскости α – перпендикуляр a. Тогда угол между прямыми a и b и будет линейным углом двугранного угла.
Рис. 9
Найдем линейный угол при ребре СС1
Аналогичным образом, получаем, что линейные угол при ребре АА1 – это угол ВAD, при ребре DD1 – ∠ADC, при ребре BB1 – ∠ABC. Все эти углы являются углами трапеции ABCD. Найдем их градусную меру.
Рассмотрим трапецию ABCD (рис. 10). Проведем высоты АН и КВ. По условию, высота трапеции равна 8 см. Значит,
Рис. 10
Найдем НК. Прямые АН и КВ перпендикулярны одной и той же прямой DC. Значит, прямые АН и КВ параллельны. Так как АН = КВ, то АНКВ – параллелограмм. Значит, НК = АВ = 9 см.
Прямые АН и КВ перпендикулярны одной и той же прямой DC. Значит, прямые АН и КВ параллельны. Так как АН = КВ, то АНКВ – параллелограмм. Значит, НК = АВ = 9 см.
Так как трапеция ABCD равнобедренная, то см.
Рассмотрим треугольник DHA. Он прямоугольный, так как АН ⊥ DC и равнобедренный, так как АН = DH. Значит, ∠HAD = ∠HDA
Так как трапеция ABCD равнобедренная, то ∠DCB = ∠СDA = 45°, ∠DAB = ∠ABC = 180° — 45° = 135°.
Ответ: 45°, 45°, 135°, 135°.
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/10-klass/mnogogranniki/mnogogranniki-prizma-zadachi-na-prizmu
http://www.youtube.com/watch?v=IkmNyC8d8RM
http://lusana.ru/files/4353/presentation.zip
http://profmeter.com.ua/communication/learning/course/course7/chapter0539/?LESSON_PATH=456.523.539
http://profmeter.com.ua/communication/learning/course/course7/lesson205/?LESSON_PATH=456.523.539.205http://www.youtube.com/watch?v=l0a3EtZySKI
Правильная четырехугольная призма. Задача № 14 ЕГЭ Профиль
В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания АВ равна 2√3, а боковое ребро АА1 равно 3. На рёбрах A1D1 и DD1 отмечены соответственно точки К и М так, что А1К = KD1, a DM:MD1=2:1.а) Докажите, что прямые МК и ВК перпендикулярны.
б) Найдите угол между плоскостями BMK и BCC1.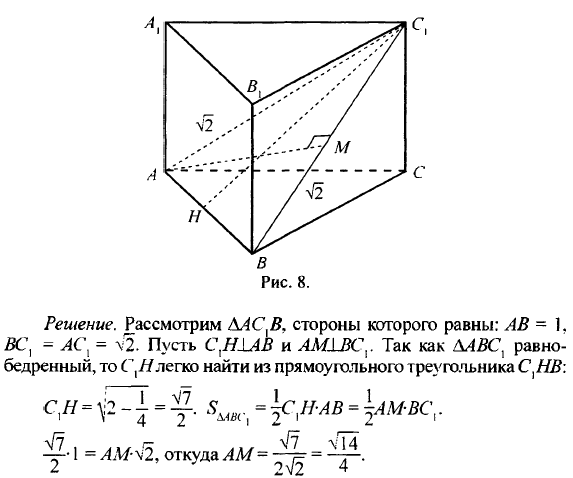
Решение:
Правильная четырехугольная призма — это прямая призма, основанием которой служит квадрат.
Прямая призма — призма, у которой боковые рёбра перпендикулярны основаниям.
а) Так как D1M:MD = 1:2, то D1M = 1; MD = 2.
Так как A1K = KD1, то A1K = KD1 = √3.
△BDC:BD² = BC² + CD²
«D² = (2√3)²+(2√3)²
«D² = 24
△A1B1B: A1B² = A1B1² + B1B²
A1B² = (2√3)²+3²
A1B² = 21
△KD1M: KM² = KD1² + D1M²
KM² = (√3)²+1²
KM² = 4
△BMD:BM² = BD² + MD²
«M² = 24+2²
«M² = 28
△A1KB: BK² = A1K² + A1B²
«K² = (√3)²+21
«K² = 24
Заметим, что для △KBM: BM² = KM² + BK².
Значит △KBM — прямоугольный. Тогда BM — гипотенуза и KM⊥BK.
б) Плоскости (BCC1) и (ADD1) параллельны, то есть (BCC1) || (ADD1). Тогда ∠(BMK; BCC1) = ∠(BMK; ADD1).
Угол между плоскостями — это угол между перпендикулярами, проведёнными к линии пересечения плоскостей.
Линия пересечения плоскостей (BMK) и (ADD1) -отрезок KM.
«K ⊥ KM. Пусть LK ⊥ KM. Тогда∠(BMK;ADD1) = ∠LKB = α
Заметим, что в △KD1M: KM = 2·D1M. Тогда ∠MKD1 = 30° и ∠KMD1 = 60°.
△A1KL:∠A1KL = 180°-∠LKM-∠MKD1 = 180° — 90° — 30° = 60°. Тогда∠KA1L = 30°.
tg∠A1KL = tg60° = A1L/A1K → A1L = A1K·tg60° = √3·√3 = 3 → L = A и∠(BMK;ADD1) = ∠AKB = α
AK² = AA1²+A1K² = 3²+(√3)² = 12 = (2√3)²
△KAB — прямоугольный: tgα = AB/AK = (2√3)/(2√3) = 1.
Тогда∠(BMK;BCC1) =∠(BMK;ADD1) = α = 45°
Ответ: б) 45°
В правильной четырёхугольной призме ABCDA1B1C1D1… — Задание 14 ЕГЭ по математике (Стереометрическая задача)
Задание:
В правильной четырёхугольной призме ABCDA1B1C1D1 на ребре СС1 взята точка К так, что СК : КС1 = 1 : 2.
а) Постройте сечение призмы плоскостью, проходящей через точки D и К параллельно диагонали основания АС.
б) Найдите угол между плоскостью сечения и плоскостью основания, если CC1 = 4,5√2, АВ = 3.
Решение:
а) Так как призма ABCDA1B1C1D1 правильная, то ABCD — квадрат и боковые грани — равные прямоугольники.
Построим сечение призмы плоскостью, проходящей через точки D и K параллельно AC. Линия пересечения плоскости сечения и плоскости AA1C1 проходит через точку K и параллельна AC.
В плоскости ACC1 через точку K проведём отрезок KF параллельно диагонали AC.
Так как грани A1ADD1 и B1BCC1 призмы параллельны, то по свойству параллельных плоскостей линии пересечения плоскости сечения и этих граней параллельны. Проведём PK || FD. Четырёхугольник FPKD — искомое сечение.
б) Найдём угол между плоскостью сечения и плоскостью основания. Пусть плоскость сечения пересекает плоскость основания по некоторой прямой p, проходящей через точку D. AC || FK, следовательно, AC || p (если плоскость проходит через прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна этой прямой). Так как диагонали квадрата взаимно перпендикулярны, то BD ⊥ AC, а значит,
BD ⊥ p. BD — проекция PD на плоскость ABC, поэтому PD ⊥ p по теореме о трёх перпендикулярах. Следовательно, ∠PDB — линейный угол двугранного угла между плоскостью сечения и плоскостью основания.
FK || p, значит, FK ⊥ PD. В четырёхугольнике FPKD имеем FD || PK и KD || FP, значит, FPKD — параллелограмм, а так как прямоугольные треугольники FAD и KCD равны по двум катетам (AD = DC как стороны квадрата, FA = KC как расстояния между параллельными прямыми AC и F K), то FPKD — ромб. Отсюда PD = 2OD.
По условию CK : KC1 = 1 : 2, тогда KC = 1/3*CC1 = 4,5√2 / 3 = 1,5√2.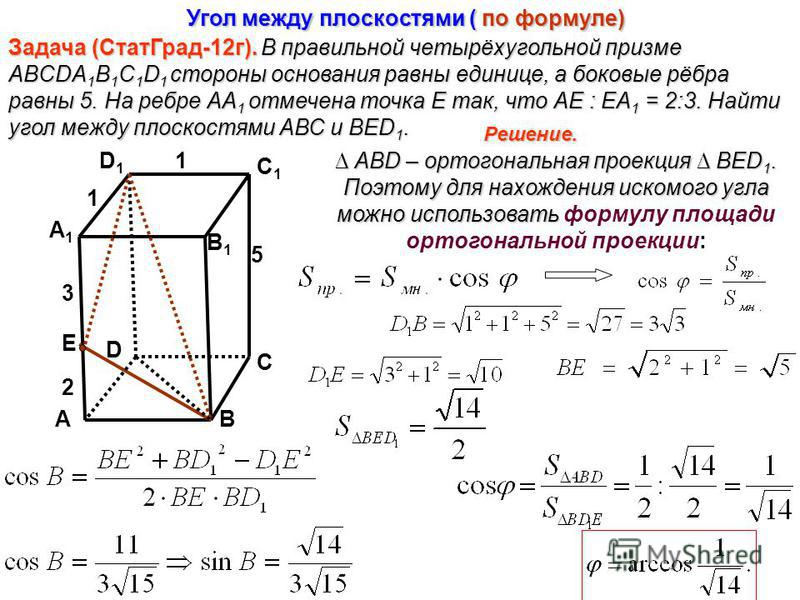
В ΔDKC по теореме Пифагора KD2 = DC2 + KC2 , KD = =
√13,5.
AC = 3√2 как диагональ квадрата, OK = EC = 1/2*AC, OK = 1,5√2.
В ΔKOD по теореме Пифагора OD2 = KD2 − OK2,
OD = = 3. PD = 2OD = 6.
В прямоугольном треугольнике PDB cos ∠PDB = BD / PD = 3√2 / 6 = √2 / 2 , следовательно, ∠PDB = 45◦ .
Ответ: 45◦ .
Задача 14 из реального ЕГЭ 2018 (профиль).
Задача 14 из реального ЕГЭ 2018 от 30.03.2018 (профиль). Здравствуйте, ребята! Посмотрите задачу по стереометрии, она из досрочного варианта экзамена от 30.03.2018. Вынес её отдельно. Решение указанного варианта на 80 баллов можете посмотреть здесь. Если на ЕГЭ решить ещё и данную задачу, то это ещё плюс 4 тестовых балла. Ещё раз отмечу, что такие баллы можно получить без экономики, параметров и свойств чисел.
Решение довольно развёрнутое, в символьной записи всё будет намного компактнее. Задача довольно простая и не требует применения каких-то глубоких знаний.
Дана правильная четырехугольная призма ABCDA1B1C1D1. На ребре AA1 отмечена точка K так, что AK:KA1=1:3. Плоскость альфа проходит через точки В и К параллельно прямой АС. Эта плоскость пересекает DD1 в точке М.
1. Докажите, что точка М середина ребра DD1
2. Найдите площадь сечения призмы плоскостью альфа, если АВ=5, AA1=4
Решение. Построим призму. Отметим точку К:
Известно, что прямая параллельна плоскости: если она не имеет с ней общей точки или, говоря иным языком, если она параллельна любой прямой в этой плоскости.
В условии сказано, что плоскость альфа проходит через точки В и К параллельно АС. Нам понятно, что альфа пересекает диагональную плоскость АА1С1С при чём линия их пересечения проходит через точку К.
Следовательно прямая АС будет параллельна плоскости альфа тогда когда она будет параллельна прямой проходящей через точку К.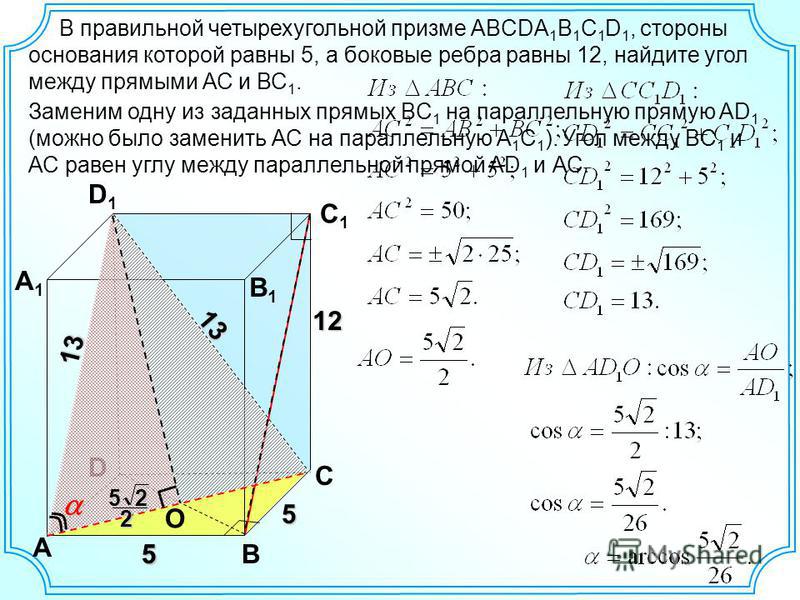
Таким образом, построив такую прямую мы получим точку пересечения плоскости альфа и ребра СС1. Строим КL так что KL||AC:
Известно, что если плоскость пересекает две параллельные плоскости, то прямые пересечения плоскостей параллельны.
Значит отрезки по которым плоскость альфа пересекает параллельные грани АА1В1В и DD1С1С параллельны. Проведём отрезок LM||BK, затем соединим точки К и М:
Сечение построено. LM будет параллельно KB по тому же свойству.
Докажем, что точка М середина ребра DD1.
Построим LF||CD. Отметим, что AK=LC=DF (по построению это противолежащие стороны прямоугольников). Все они составляют четверть от высоты призмы.
Рассмотрим треугольники AKB и FML. Они равны по катету и строму углу:
Значит AK=FM, то есть FM от высоты призмы составляет также четвертую часть. Следовательно:
То есть точка М середина ребра DD1
*Комментарий. Как ещё можно доказать, что точка М середина указанного ребра? Посмотрите, если посмотреть на призму со второны ребра АА1, то построи таую проекцию мы увидим два подобных прямоугольных треугольника с коэффициентом подобия 2. Также если посмотреть на призму со стороны ребра ВВ1, то мы увидим, что сечение спроецируется в ромб.
Вычислим площадь сечения.
Воспользуемся следующим свойством: известно, что площадь фигуры и площадь проекции этой фигуры связана формулой. Обозначим площадь фигуры как S1, площадь проекции как S2, пусть угол между плоскостями в которых лежат фигуры равен альфа, тогда:
В нашем случае основание ABCD является проекцией сечения KBLM.
Площадь основания равна 25. Остаётся вычислить угол между плоскостями. Мы уже интуитивно понимаем, что это угол DBM. Докажем это.
Углом между плоскостями является угол между перпендикулярами проведёнными к линии пересечения плоскостей.
Или! Если плоскости альфа и бэтта пересекаются и их пересекает третья плоскость перпендикулярно линии их пересечения, то образованный двугранный угол является углом между плоскостями альфа и бэтта.
Построим линию пересечения плоскостей. Это означает, что нам необходимо найти общие точки для прямых лежащих в указанных плоскостях, мы можем построить ещё две точки (одна уже имеется это В).
Прямые МК и DA пересекутся в точке (обозначим её Р), то есть МК∩DA=P. Прямые МL и DC пересекутся в точке (обозначим её R), то есть МL∩DC=R.
Треугольник PDR равнобедренный прямоугольный (∆PDM=∆RDM по катету и острому углу, то есть PD=RD).
Прямая PR перпендикулярна DB, так как DB является биссектрисой, а значит и высотой в треугольнике PDR. DB является проекцией наклонной МВ, значит по теореме трёх перпендикулярах PR перпендикулярен МВ.
Следовательно ∠DBM это угол между сечением и основанием призмы. Таким образом:
Вычислим площадь сечения:
Ответ: 15√3
*В ответ можно записать как 5√27 так и 15√3.
Образцы задач ЕГЭ В 11 по теме «Правильные призмы» | |
Правильная треугольная призма | |
1. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 27 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 3 раза больше, чем у первого? Ответ выразите в сантиметрах. | 1. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 18 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 3 раза больше, чем у первого? Ответ выразите в сантиметрах. |
2. В сосуд, имеющий форму правильной
треугольной призмы, налили 1100 см3 воды и полностью в нее погрузили
деталь. | 2. В сосуд, имеющий форму правильной треугольной призмы, налили 1300 см3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 28 см. Чему равен объем детали? Ответ выразите в см3. |
3. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен , а высота равна 4. | 3. Найдите площадь боковой поверхности правильной треугольной призмы, вписанной в цилиндр, радиус основания которого равен 6, а высота равна 3. |
4. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна 1. | 4. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна 1. |
Правильная четырёхугольная призма | |
1. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 7. Найдите площадь боковой поверхности призмы. | 1. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 5,5. Найдите площадь боковой поверхности призмы. |
2. Правильная
четырехугольная призма описана около
цилиндра, радиус основания которого
равен 1. | 2. Правильная четырехугольная призма описана около цилиндра, радиус основания которого равен 4. Площадь боковой поверхности призмы равна 32. Найдите высоту цилиндра. |
Правильная шестиугольная призма | |
1. Найдите объем правильной шестиугольной призмы, стороны основания которой равны 6, а боковые ребра равны . | 1. Найдите объем правильной шестиугольной призмы, стороны основания которой равны 4, а боковые ребра равны . |
2. Найдите объем правильной шестиугольной призмы, все ребра которой равны 3. | 2. Найдите объем правильной шестиугольной призмы, все ребра которой равны 4. |
3. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна 3. | 3. Найдите площадь боковой поверхности правильной шестиугольной призмы, описанной около цилиндра, радиус основания которого равен , а высота равна 1. |
4. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 7, а боковые ребра равны и наклонены к плоскости основания под углом 300. | 4. Найдите объем призмы, в основаниях
которой лежат правильные шестиугольники
со сторонами 7, а боковые ребра равны
4 и наклонены к плоскости основания
под углом 300. |
Подготовка школьников к ЕГЭ (Справочник по математике — Стереометрия
Призма, вписанная в сферу. Свойства призмы, вписанной в сферу
Определение 1. Призмой, вписанной в сферу, называют такую призму, все вершины которой лежат на сфере (рис. 1).
Определение 2. Если призма вписана в сферу, то сферу называют описанной около призмы.
Рис.1
Теорема. Около призмы можно описать сферу тогда и только тогда, когда выполнены следующие два условия:
- Призма является прямой призмой;
- Около оснований призмы можно описать окружности.
Доказательство. Докажем сначала, что если n – угольная призма A1A2 … AnA’1A’2 … A’n вписана в сферу, то оба условия теоремы выполнены.
Для этого заметим, что плоскость каждого из оснований призмы пересекает сферу по окружности, на которой лежат вершины этого основания. Таким образом, многоугольники, являющиеся основаниями призмы, оказываются вписанными в окружности (рис. 1), то есть второе условие теоремы выполнено.
Каждая из боковых граней призмы также вписана в окружность (рис. 2).
Рис.2
В разделе «Призмы» доказано, что каждая из боковых граней призмы – параллелограмм. Но около параллелограмма можно описать окружность тогда и только тогда, когда этот параллелограмм – прямоугольник. Следовательно, все боковые грани призмы являются прямоугольниками.
Рассмотрим какое-нибудь боковое ребро призмы, например, A2A’2. Поскольку это ребро перпендикулярно к ребрам основания A1A2 и A2A3, то в силу признака перпендикулярности прямой и плоскости заключаем, что боковое ребро A2A’2 перпендикулярно к плоскости основания призмы, то есть призма является прямой призмой.
Таким образом, мы доказали, что, если призма вписана в сферу, то оба условия теоремы выполнены.
Теперь рассмотрим прямую n – угольную призму A1A2 … AnA’1A’2 … A’n высоты h, около оснований которой можно описать окружности, и докажем, что около такой призмы можно описать сферу.
Для этого обозначим символом O1 центр окружности радиуса r, описанной около нижнего основания призмы, а символом O’1 обозначим центр окружности, описанной около верхнего основания призмы (рис. 3).
Рис.3
Поскольку многоугольники, лежащие в основаниях призмы равны, то и радиусы описанных около них окружностей будут равны.
Согласно утверждению 1 из раздела «Призмы, вписанные в цилиндры» отрезок O1O’1, соединяющий центры окружностей, описанных около нижнего и верхнего оснований призмы, параллелен и равен боковому ребру призмы. Так как рассматриваемая призма прямая, то ее боковые ребра перпендикулярны плоскости основания и равны высоте призмы h. Значит, и отрезок O1O’1 перпендикулярен плоскости основания призмы и равен h.
Обозначим буквой O середину отрезка O1O’1 и докажем, что все вершины призмы будут находиться на одном и том же расстояниии от точки O (рис. 4).
Рис.4
C помощью теоремы Пифагора из равных прямоугольных треугольников OA1O1, OA2O1, … OAnO1, OA’1O’1, OA’2O’1, . .. OA’nO’1 получаем, что точка O находится на расстоянии
.. OA’nO’1 получаем, что точка O находится на расстоянии
| (1) |
от всех вершин призмы. Отсюда следует, что точка O является центром сферы радиуса R , описанной около призмы.
Теорема доказана.
Следствие 1. Около любой прямой треугольной призмы можно вписать сферу.
Справедливость следствия 1 вытекает из того, что около любого треугольника можно описать окружность.
Следствие 2. Около любого прямоугольного параллелепипеда (в частности, около куба прямоугольного параллелепипеда (в частности, около куба) можно описать сферу.
Справедливость следствия 2 вытекает из того, что около любого прямоугольника можно описать окружность.
Следствие 3. Около любой правильной призмы можно описать сферу.
Для доказательства следствия 3 достаточно заметить, что правильная n – угольная призма – это прямая призма, основания которой являются правильными n – угольниками, а около любого правильного n – угольника можно описать окружность.
Радиус сферы, описанной около правильной n — угольной призмы
Задача 1. Найти радиус сферы, описанной около правильной n — угольной призмы с высотой h и ребром основания a.
Решение. Поскольку радиус описанной около правильного n — угольника окружности выражается через сторону этого многоугольникарадиус описанной около правильного n — угольника окружности выражается через сторону этого многоугольника по формуле
то из формулы (1) получаем выражение для радиуса описанной сферы
| (2) |
Ответ.
Следствие 4. Радиус сферы, описанной около правильной треугольной призмы правильной треугольной призмы с высотой h и ребром основания a равен
Радиус сферы, описанной около правильной треугольной призмы правильной треугольной призмы с высотой h и ребром основания a равен
Следствие 5. Радиус сферы, описанной около правильной четырехугольной призмы правильной четырехугольной призмы с высотой h и ребром основания a равен
Следствие 6. Радиус сферы, описанной около около правильной шестиугольной призмы с высотой h и ребром основания a равен
Отношение объема правильной n — угольной призмы к объему шара, ограниченного описанной около призмы сферой
Задача 2. Около правильной n — угольной призмы с высотой h и ребром основания a описана сфера. Найти отношение объемов призмы и шара, ограниченного сферой, описанной около данной призмы.
Решение. Объем шара выражается через его радиус по формуле
Воспользовавшись формулой (2), выразим объем шара, ограниченного описанной около призмы сферой, через высоту и ребро основания призмы:
Объем правильной n — угольной призмы найдем по формулеОбъем правильной n — угольной призмы найдем по формуле:
Таким образом,
Ответ.
Следствие 7. Отношение объема правильной треугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно
Следствие 8. Отношение объема правильной четырехугольной призмы правильной четырехугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно
Следствие 9. Отношение объема правильной шестиугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно
Отношение объема правильной шестиугольной призмы с высотой h и ребром основания a к объему шара, ограниченного сферой, описанной около данной призмы, равно
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
2 $ за точки в открытом подмножестве каждой грани, но как насчет ребер?Чтобы проиллюстрировать мою точку зрения, возьмем куб. Отрежьте угол и вставьте его обратно, чтобы куб восстановился, за исключением «линии», которую мы «нарисовали» вокруг одного угла. Это одна линия или три на поверхности куба? Если это три линии, то эти линии образуют края треугольника в кубе. Как определить углы этого треугольника? Это больше похоже на треугольную пирамиду с удаленным основанием. Для наглядности назовем ребра образованного таким образом треугольника сторонами, а ребра исходного куба назовем ребрами.Вернемся к «треугольнику». Мы также измеряем углы в поверхности? Т.е. вместо того, чтобы принимать угол между двумя сторонами в качестве угла между двумя плоскостями, в которых лежат эти стороны, измеряем ли мы сначала угол между стороной треугольника и краем куба и делаем это также для другой стороны, а затем суммировать углы?
Это немного похоже на метрику такси. Вместо использования гипотенузы в качестве меры расстояния используется сумма длин сторон (содержащих прямой угол).2 $, но потом я понял, что эти грани должны быть открытыми, и поэтому края будут опущены. Следующий атлас, который я придумал, заключался в том, чтобы обернуть кубик вокруг четырех сторон, как суши, точно так же, как рисование цилиндра. За исключением того, что потребовалось бы три обертывания в разных направлениях, чтобы покрыть края, и даже тогда я не уверен, исправлены ли углы.
Моя дифференциальная геометрия и топология довольно просты; Буду признателен за доступные объяснения.
Еще вопросы:
(i) Является ли куб поверхностью без границ, как сфера? Я знаю, что он закрыт.
(ii) Мешают ли острые края быть гладким коллектором?
Поперечное сечение правильной четырехугольной призмы. Раздел правильного четырехугольного приза в правильном четырехугольном призе ABCDA1B1C1D1
В правильной призме с четырьмя спусковыми крючками ABCDA 1 B 1 C 1 D 1 стороны основания равны 2, а боковые ребра равны 5. На ребре AA 1 отмечена точка E, что AE: EA 1 = 3: 2. Найдите угол между плоскостями ABC и Bed 1.
Решение. Пусть прямая D 1 E пересекает прямую AD в точке K. Тогда плоскости ABC и Bed 1 будут сброшены в прямую линию KB.
Из точки E опускаем перпендикуляр EH в прямой Kb, тогда отрезок AH (проекция Eh) будет перпендикулярен прямому Kb (теорема о трех перпендикулярах).
Угол AHE — это линейный угол соединенного угла, образованный плоскостями ABC и Bed 1.
Поскольку AE: EA 1 = 3: 2, получаем:.
Из подобия треугольников A 1 D 1 E и AKE получаем:.
В прямоугольном треугольнике АКБ с прямым углом A: AU = 2, AK = 3,; Где высота от
.
Из прямоугольного треугольника AHE с прямым углом A получаем: и ∠ ahe = arctg (√13 / 2).
Ответ: arctg (√13 / 2).
Задачи для самостоятельного решения
1. Б. прямоугольный параллелепипед ABCDA 1 B 1 C 1 D 1 AB 1 = 2, AD = AA 1 = 1. Найдите угол между прямой AV и плоскостью ABC 1.
2.В прямой шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 1 Все углы равны 1. Найдите расстояние от точки до плоскости DEA 1.
3. В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 AB = 1, AA 1 = 2. Найдите угол между прямой AV 1 и плоскостью ABC 1.
Рассмотрим следующую двухуровневую стереометрическую задачу по обучению ким.
Задача. Справа один четырехугольный приз
ABCDA 1 B 1 C 1 D 1 Сторона AB основания 5, а боковая кромка AA 1 равна квадратному корню из пяти.На краях солнышко и C 1 D 1 ответили точки K и L соответственно, причем SK = 2, а C 1 L = 1. Плоскость g. параллельно прямой Б.Д. и содержит точки на andL.
Плоскость g. параллельно прямой Б.Д. и содержит точки на andL.
a) Докажите, что прямая a 1 с перпендикулярной плоскостьюg ..
б) Найдите объем пирамиды, вершиной которой является точка A 1, а основанием — поперечное сечение плоскости этой призмы.
Решение. а) внимательно выполните чертеж и проанализируйте данные. Поскольку ABCDA 1 B 1 C 1 D 1 — правая четырехугольная призма, значит базис Abcd.- Квадрат со стороной 5. Боковые края перпендикулярны основанию. Поскольку самолет. проходит через точку и параллельно прямой D. тогда линия пересечения плоскостей g. а плоскость ABC параллельна прямой D. ( Если другая плоскость прямо параллельна этой плоскости, то линия пересечения этих плоскостей будет параллельна этой прямой ).
Через точку провести прямую параллельную inD. до пересечения S.CD В точке M. означает км, перпендикулярный AS (, потому что диагональ Квадрат BD. и перпендикулярные динамики ).
Треугольники bcd. и SCM подобны (как прямоугольные, так и равные), значит CM = COP = 2. Согласно теореме Пифагора о треугольнике SCM находим, что KM = 2√2, а из треугольника BCD BD = 5 √ 2. Диагональ квадрата равна, значит оба = 5 √2.
Теперь через точку L. проводим прямую параллель inD. до пересечения С.B 1 C 1 В точке T. по сечению TL Плоскость km l пересекает верхнее основание ( Если две параллельные плоскости пересекают третью плоскость, то линии пересечения будут параллельны ). Итак, T.C 1 = C 1 L = 1. Из треугольника T.LC 1. Согласно теореме Пифагора TL = √2.
В уравнительной трапеции КТЛ. M точка n — среднее верхнее основание, точка N. — середина нижнего основания, что означает N. — Высота трапеции, нН. перпендикулярно км. Таким образом, CM перпендикулярна плоскости AA 1 C, включая прямую A 1 S.
Рассмотрим диагональное сечение прямоугольника призмы AA 1 C 1 C. От точки n вниз перпендикулярно AU. Тогда N E = EU = H C 1 = 0,5 √2. Не = С 1 = √5.
Не = С 1 = √5.
В треугольниках AA 1 C и N. RS Угол Rs — Общие. Касательный угол AA 1 C равен 5√2: √5 = √10 Касательный угол H n E от треугольника nN E равен √5: 0,5 √2 = √10. Итак, углы AA 1 C и NN. E равно. Но тогда оставшиеся углы 1 заклинание = N RS = 90 ⁰.У нас есть 1 с перпендикуляром directN. и км, это означает 1 с перпендикуляром к плоскости трапеции KT. М. Что требовалось доказать.
Чтобы найти объем пирамиды A 1 CTL. М, вам нужно найти квадрат трапеции КТ L. М и высотой А 1 р. Из треугольника nN. E по теореме Пифагора nN 2. = 5.5. КТ трапеции квадрат L m равен n * (T L + км) / 2 = √5,5 * (√2 + 2 √2) / 2 = 1,5 √11.
Задача.
В правильной четырехугольной призме ABCDA 1 B 1 C 1 D 1 стороны основания равны 3, а боковые ребра равны 4.Край Aa 1 отмечается точкой E так, чтобы AE: Ea 1 = 1: 3.
a) Постройте прямое пересечение плоскостей ABC и Bed 1.
б) Найдите угол между плоскостями ABC и Bed 1.
Решение:
a) Постройте прямое пересечение плоскостей ABC I. Слой 1. .
Строим плоскость BED 1. Точки E и D 1 лежат в одной плоскости, поэтому проведем прямой ED 1.
Точки E и B лежат в одной плоскости, поэтому мы проведем прямую эв.Чтобы грань правильной четырехугольной призмы параллельна, проводим в границах BB 1 C 1 с прямым BF параллельно прямому ED 1. Точки F и D 1 лежат в одной плоскости, поэтому будем проводить прямые FD 1. Получил желаемый самолет Кровать 1.
.Поскольку прямая ED 1 и прямая AD лежат в одной плоскости сложения 1, то они пересекаются в точке K, лежащей в плоскости ABC. Точки to и B лежат в плоскостях ABC и BED 1, поэтому плоскости ABC и BED 1 пересекаются по прямой.Желаемое прямое пересечение плоскостей ABC и Bed 1 построено.
б) Найдите угол между плоскостями ABC I. Слой 1.
Отрезок AE перпендикулярен плоскости ABC за пределами точки E, чтобы опустить EH перпендикулярно прямой четверти. Точка H лежит в плоскости ABC, тогда AH — проекция EH на плоскость ABC. Через точку H проходит прямая, перпендикулярная наклонной Eh, затем по теореме о трех перпендикулярных участках AH, перпендикулярных прямой четверти.
Точка H лежит в плоскости ABC, тогда AH — проекция EH на плоскость ABC. Через точку H проходит прямая, перпендикулярная наклонной Eh, затем по теореме о трех перпендикулярных участках AH, перпендикулярных прямой четверти.
Угол eha — это линейный угол соединенного угла, образованный плоскостями ABC и Bed 1. Угол eha — это искомый угол между плоскостями ABC и BED 1. Находим величину этого угла.
Рассмотрим прямоугольный треугольник EHA (∠A = 90˚):
По условию AE: Ea 1 = 1: 3, тогда AE: AA 1 = 1: 4.
Треугольники AKE и A 1 D 1 E похожи, тогда
A 1 D 1 = 3, AE = 1, A 1 E = AA 1 — AE = 3
Рассмотрим прямоугольный треугольник АКБ (∠A = 90˚).
Конспект по плоской геометрии
Синопсис по твердой геометрии В.В. ПРАСОЛОВ, И.Ф. ШАРЫГИН 3
Классификация задач по тематике, способам решения и уровню сложности.
ГЛАВА 1. ЛИНИИ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ
1. Углы и расстояния между косыми линиями 1.1. Дан куб ABCDA1B1C1D1 со стороной a. Найдите угол и расстояние
между прямыми A1B и AC1.
1.2. Данный куб со стороной 1.Найдите угол и расстояние между диагоналями двух соседних граней.
1.3. Пусть K, L и M — середины ребер AD, A1B1 и CC1 куба ABCDA1B1C1D1. Докажите, что треугольник KLM равносторонний, а его центр совпадает с центром куба.
1.4. Для куба ABCDA1B1C1D1 со стороной 1 пусть K будет средней точкой edgeDD1. Найдите угол и расстояние между прямыми CK и A1D.
1.5. Ребро CD тетраэдра ABCD перпендикулярно плоскости ABC; M — середина DB, N — середина AB, а точка K делит ребро CD в отношении CK: KD = 1: 2.Докажите, что прямая CN равноудалена от прямых AM и BK.
1.6. Найдите расстояние между двумя скошенными медианами граней правильного тетраэдра с ребром 1. (Исследуйте все возможные положения медиан.)
2. Углы между прямыми и плоскостями 1.7. Плоскость задается уравнением
ax + by + cz + d = 0.
Докажите, что вектор (a, b, c) перпендикулярен этой плоскости.
1.8. Найдите косинус угла между векторами с координатами (a1, b1, c1) и (a2, b2, c2).
1.9. В прямоугольном параллелепипеде ABCDA1B1C1D1 длины ребер известны: AB = a, AD = b, AA1 = c.
а) Найдите угол между плоскостями BB1D и ABC1.
б) Найдите угол между плоскостями AB1D1 и A1C1D.
c) Найдите угол между прямой BD1 и плоскостью A1BD.
1.10. Основание правильной треугольной призмы — треугольник ABC со стороной a. На боковых кромках точки А1, В1 и С1 взяты так, чтобы расстояния от них до плоскости основания были равны 12а, а и
32а соответственно.Найдите угол
между плоскостями ABC и A1B1C1.
Набор AMS-TEX
1
2 ГЛАВА 1. ЛИНИИ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ
3. Линии, образующие равные углы с прямыми и с плоскостями 1.11. Прямая l составляет равные углы с двумя пересекающимися прямыми l1 и l2 и находится на
не перпендикулярно плоскости, содержащей эти прямые. Докажите, что проекция l на плоскость также составляет равные углы с прямыми l1 и l2.1.12. Докажите, что прямая l образует равные углы с двумя пересекающимися прямыми тогда и только тогда, когда
перпендикулярна одной из двух биссектрис углов между этими прямыми.1.13. Даны две косые прямые l1 и l2; точки O1 и A1 взяты на l1; точки O2
и A2 взяты на l2, так что O1O2 является общим перпендикуляром к прямым l1 и l2, а прямая A1A2 образует равные углы с линиями l1 и l2. Докажите, что O1A1 = O2A2.1.14. Точки A1 и A2 принадлежат плоскостям 1 и 2 соответственно, а прямая l — это
, линия пересечения 1 и 2. Докажите, что прямая A1A2 образует равные углы с плоскостями 1 и 2 тогда и только тогда, когда точки A1 и A2 равноудалены от прямой. л.1.15. Докажите, что прямая, образующая попарно равные углы с тремя попарно пересекающимися линиями
, лежащими в плоскости, перпендикулярна .1.16. Даны три прямые, не параллельные одной плоскости, докажите, что существует прямая
, образующая с ними равные углы; причем через любую точку можно провести ровно четыре таких линии.
4. Косые линии 1.17. Для данных двух наклонных линий докажите, что существует единственный отрезок, перпендикулярный им и концам на этих линиях.1.18. В пространстве даны две косые прямые l1 и l2 и точка O не на любых
из них. Всегда ли существует линия, проходящая через точку O и пересекающая обе данные линии? Может ли быть две такие строки? 1.19. В пространстве даны три попарные косые линии. Докажите, что существует
единственного параллелепипеда, три ребра которого лежат на этих прямых. 1.20. На общем перпендикуляре к наклонным прямым p и q берется точка A.
Вдоль линии p точка M движется, а N — проекция точки M на точку q.Докажите, что все самолеты АМН имеют общую линию.
5. Теорема Пифагораса в пространстве 1.21. Линия l представляет собой углы, а с тремя попарно перпендикулярными линиями
. Докажите, что cos2 + cos2 + cos2 = 1.
1.22. Плоские углы при вершине D тетраэдра ABCD прямые. Докажите, что сумма квадратов площадей трех прямоугольных граней тетраэдра равна квадрату площади грани ABC. 1.23. Внутри шара радиуса R рассмотрим точку A на расстоянии a от центра шара
.Через A проходят три попарно перпендикулярные хорды. A) Найдите сумму квадратов длин этих хорд. B) Найдите сумму квадратов длин отрезков хорд, на которые точка A
делит их. 1.24. Докажите, что сумма квадратов длин выступов
ребер куба на любую плоскость равна 8a2, где a — длина ребра куба. 1.25. Рассмотрим правильный тетраэдр. Докажите, что сумма квадратов длин
проекций ребер тетраэдра на любую плоскость равна 4a2, где a — длина ребра тетраэдра.
ПРОБЛЕМЫ ДЛЯ НЕЗАВИСИМОГО ИССЛЕДОВАНИЯ 3
1.26. Дан правильный тетраэдр с ребром a. Докажите, что сумма квадратов длин проекций (на любую плоскость) отрезков, соединяющих центр тетраэдра с его вершинами, равна a2.
6. Координатный метод 1.27. Докажите, что расстояние от точки с координатами (x0, y0, z0) до плоскости
, заданное уравнением ax + by + cz + d = 0, равно
| ax0 + by0 + cz0 + d | a2 + b2 + c2
.
1.28. Для двух точек A и B и положительного числа k 6 = 1 найдите геометрическое место точек M такое, что AM: BM = k.1.29. Найдите геометрическое место точек X, такое что
pAX2 + qBX2 + rCX2 = d,
, где A, B и C — заданные точки, p, q, r и d — заданные числа, такие что p + q + r = 0,1.30. Даны два конуса с равными углами между осью и образующей.
Пусть их оси параллельны. Докажите, что все точки пересечения поверхностей этих конусов лежат в одной плоскости.1.31. Для куба ABCDA1B1C1D1 с ребром a докажите, что расстояние от
долюбой точки пространства до одной из прямых AA1, B1C1, CD не короче, чем a2.
1.32. На трех взаимно перпендикулярных прямых, пересекающихся в точке O, зафиксированы точки A, B и C, равноудаленные от O. Пусть l — произвольная прямая, проходящая через О. Пусть точки A1, B1 и C1 симметричны через l относительно A, B и C. Плоскости, проходящие через точки A1, B1 и C1 перпендикулярно прямым OA, OB и OC соответственно, пересекаются в точке M.Найдите геометрическое место точек M.
Задачи для самостоятельного изучения
1.33. Параллельные прямые l1 и l2 лежат в двух плоскостях, пересекающихся по прямой l. Проверять, l1 l.1.34. Даны три попарные косые прямые. Докажите, что существует бесконечно много
прямых, каждая из которых пересекает все три из этих прямых. 1.35. Треугольники ABC и A1B1C1 не лежат в одной плоскости, а прямые AB и
A1B1, AC и A1C1, BC и B1C1 попарно скошены. A) Докажите, что точки пересечения указанных прямых лежат на одной прямой.б) Докажите, что прямые AA1, BB1 и CC1 либо пересекаются в одной точке, либо параллельны
. 1.36. Дано несколько линий в пространстве так, чтобы любые две из них пересекались. Докажите, что
либо все они лежат в одной плоскости, либо все они проходят через одну точку. 1.37. В прямоугольном параллелепипеде ABCDA1B1C1D1 диагональ AC1 перпендикулярна плоскости A1BD на
. Докажите, что этот параллелепипед — куб. 1.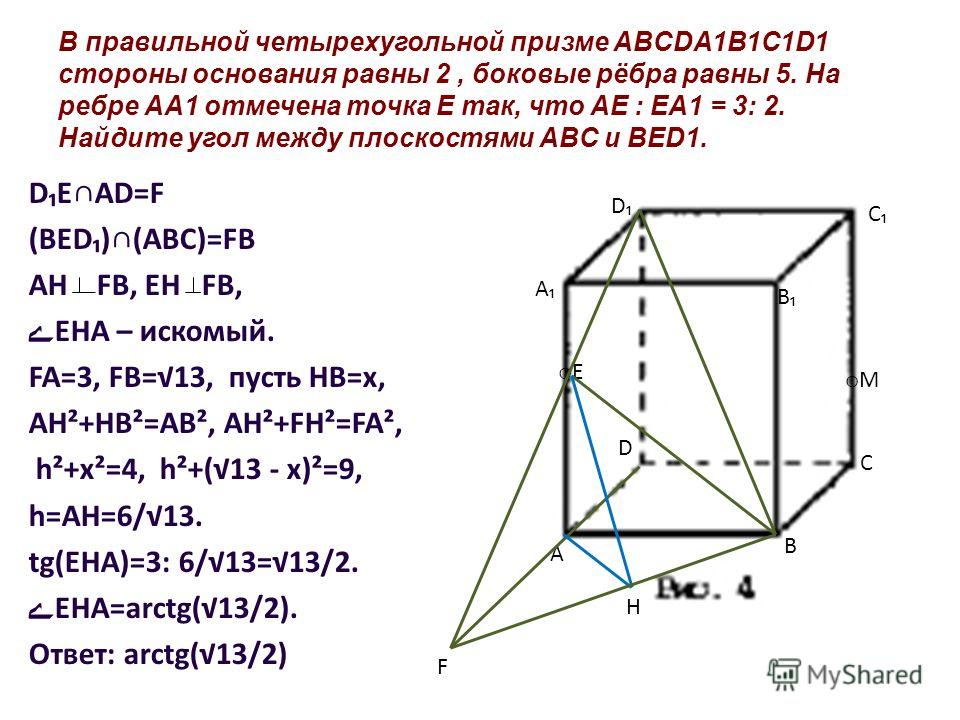 38. При каком расположении двугранного угла и пересекающей его плоскости
38. При каком расположении двугранного угла и пересекающей его плоскости
мы получаем в качестве сечения угол, пересекаемый по своей биссектрисе биссектрисой двугранного угла? 1.39. Докажите, что сумма углов, которые образует линия с двумя перпендикулярными плоскостями
, не превышает 90.
4 ГЛАВА 1. ЛИНИИ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ
1.40. В правильной четырехугольной пирамиде угол между боковым ребром и плоскостью ее основания равен углу между боковым ребром и плоскостью боковой грани, не содержащей этого ребра. Найдите этот угол. 1.41. Через ребро AA1 куба ABCDA1B1C1D1 проведена плоскость, которая образует равные
углов с прямыми BC и B1D.Найдите эти углы.
Решения
1.1. Легко проверить, что треугольник A1BD равносторонний. Более того, точка A равноудалена от своих вершин. Следовательно, его проекция — центр треугольника. Точно так же проекция отображает точку C1 в центр треугольника A1BD. Следовательно, прямые A1B и AC1 перпендикулярны, и расстояние между ними равно расстоянию от центра треугольника A1BD до его стороны. Поскольку все стороны этого треугольника равны
2, рассматриваемое расстояние равно
a6.
1.2. Рассмотрим диагонали AB1 и BD куба ABCDA1B1C1D1. Поскольку B1D1 BD, угол между диагоналями AB1 и BD равен AB1D1. Баттреугольник AB1D1 — равносторонний, поэтому AB1D1 = 60
. Легко проверить, что прямая BD перпендикулярна плоскости ACA1C1; следовательно, проекция
на плоскость отображает BD в среднюю точку M сегмента AC. Точно так же точка B1 отображается под этой проекцией в среднюю точку N сегмента A1C1, поэтому расстояние между линиями AB1 и BD равно расстоянию от точки M до линии AN.
Если катеты прямоугольного треугольника равны a и b, а его гипотенуза равна c, то расстояние от вершины прямого угла до гипотенузы равно abc. В прямоугольном треугольнике катеты AMN равны 1 и
12; следовательно, его гипотенуза
равна
32, а рассматриваемое расстояние равно
13.
1.3. Пусть O — центр куба. Тогда 2 {OK} = {C1D}, 2 {OL} = {DA1} и 2 {OM} = {A1C1}. Поскольку треугольник C1DA1 равносторонний, треугольник KLM также равносторонний, а O — его центр.1.4. Сначала рассчитаем значение угла. Пусть M будет mi
теория и практика представления космических объектов в …
Acta Didactica Universitatis Comenianae Ma the matics, Выпуск 8, 2008 ТЕОРИЯ И ПРАКТИКА ПРЕДСТАВЛЕНИЯ КОСМИЧЕСКИХ ОБЪЕКТОВ В ШКОЛЕ МАТЕМАТИКА 1 МАРТА ПЕМОВА Аннотация. В документе представлены — помимо истории профессиональных фундаментальных < strong> the orem of наклонная аксонометрия ( the orem Полке) — гениальный элементарный pro of обобщенного высказывания в молодого студента Польке, Х.А. Шварц (1864). Основная цель этой статьи — выявить тесную связь между / strong> метод косой аксонометрии и «свободной» параллельной проекции, используемый в школьной практике с в обучении в стереометрии.Одна из важных проблем в школьной стереометрии — это решение в g стереометрических задач. на самолетах изображения космических объектов . Более подробно в документе рассматривается проблема полноты наклонного изображения геометрической фигуры (рассмотрите в g проблемы геометрия положения, а также проблемы в volv в g перпендикулярности и метрических проблем. ) В заключение это примечания о возможных направлениях исследования в < / strong> это поле. Резюме. L’objet pr in cipal de cet article, à part de quelques remarques Historiques, касающегося демонстрации фундаментальной теории косой аксонометрии Польке, акцентирующей внимание на связи между этим методом и целевой проекцией. свободный параллелизм в использовании в искусстве создания геометрии в пространстве .Une des questions les plus important qu’on y rencontre est la résolution des problèmes en utilisant les images de figure géométriques. Ceci mene à la nécessité de la formula exacte d’un problème de la géométrie dans l’e space — образ сложного наклонного изображения фигуры по отношению к разрешению Prodlèmes de position ou de mesures. Nous in diquons aussi les возможные направления de notre future recherche dans ce doma in e.Zusammenfassung. Das Ziel dieser Arbeit liegt dar in , nebst der Historischen Bemerkungen zum Beweis des Pohlkeschen Fundamentalsatzes der schiefen Axonometrie auch auf e in en engen Zusammenhang dieser Abbildungsmethode mit der Methode der sog. freien Parallelprojektion h in zuweisen, die in der Schulpraxis im Unterricht der Stereometrie angew и t wird. Die Lösung der Aufgaben an den Bildfiguren geometrischer Objekte in der freien Parallelprojektion ist e in e von den wichtigsten Problemen im Unterricht / Aneignen stereometrische Kenntnis.Damit ist auch e in Problem der richtigen Angabe e in er stereometrischen Aufgabe verbunden, nähmlich das Problem der Vollständigkeit e in es geometrischen Gebilde 1 Эта статья был поддержан Европейским социальным фондом JPD 3 BA-2005 / 1-063 и VEGA n.
) В заключение это примечания о возможных направлениях исследования в < / strong> это поле. Резюме. L’objet pr in cipal de cet article, à part de quelques remarques Historiques, касающегося демонстрации фундаментальной теории косой аксонометрии Польке, акцентирующей внимание на связи между этим методом и целевой проекцией. свободный параллелизм в использовании в искусстве создания геометрии в пространстве .Une des questions les plus important qu’on y rencontre est la résolution des problèmes en utilisant les images de figure géométriques. Ceci mene à la nécessité de la formula exacte d’un problème de la géométrie dans l’e space — образ сложного наклонного изображения фигуры по отношению к разрешению Prodlèmes de position ou de mesures. Nous in diquons aussi les возможные направления de notre future recherche dans ce doma in e.Zusammenfassung. Das Ziel dieser Arbeit liegt dar in , nebst der Historischen Bemerkungen zum Beweis des Pohlkeschen Fundamentalsatzes der schiefen Axonometrie auch auf e in en engen Zusammenhang dieser Abbildungsmethode mit der Methode der sog. freien Parallelprojektion h in zuweisen, die in der Schulpraxis im Unterricht der Stereometrie angew и t wird. Die Lösung der Aufgaben an den Bildfiguren geometrischer Objekte in der freien Parallelprojektion ist e in e von den wichtigsten Problemen im Unterricht / Aneignen stereometrische Kenntnis.Damit ist auch e in Problem der richtigen Angabe e in er stereometrischen Aufgabe verbunden, nähmlich das Problem der Vollständigkeit e in es geometrischen Gebilde 1 Эта статья был поддержан Европейским социальным фондом JPD 3 BA-2005 / 1-063 и VEGA n. 1/3024/06
1/3024/06
Определите расстояние от точки m до плоскости. Расстояние от точки до самолета онлайн. Вывод формулы для координатного метода нахождения расстояния от точки до плоскости в пространстве
Рассмотрим в пространстве некоторую плоскость π и произвольную точку M 0.Выберем для плоскости единичный вектор нормали n с началом в некоторой точке М 1 ∈ π, и пусть p (М 0, π) будет расстоянием от точки М 0 до плоскости π. Тогда (рис. 5.5)
p (М 0, π) = | пр n M 1 M 0 | = | нМ 1 M 0 |, (5,8)
с | п | = 1.
Если плоскость π задана в прямоугольной системе координат своим общим уравнением Ax + By + Cz + D = 0, то ее вектор нормали представляет собой вектор с координатами (A; B; C) и как единичную нормаль вектор можно выбрать
Пусть (x 0; y 0; z 0) и (x 1; y 1; z 1) координаты точек M 0 и M 1.Тогда выполняется равенство Ax 1 + By 1 + Cz 1 + D = 0, так как точка M 1 принадлежит плоскости, и мы можем найти координаты вектора M 1 M 0: M 1 M 0 = (x 0 -x 1; y 0 -y 1; z 0 -z 1). Записав скалярное произведение nM 1 M 0 в координатной форме и преобразовав (5.8), получим
, т.к. Ax 1 + By 1 + Cz 1 = — D. Итак, для расчета расстояния от точки до плоскости нужно подставить координаты точки в общее уравнение плоскости, а затем разделить абсолютное значение результата с помощью нормирующего множителя, равного длине соответствующего вектора нормали.
- Плоскость в пространстве задается уравнением 3x-4y + 2z + 5 = 0, найдите расстояние от нее до точки M (3; -2; 6).
Дано:
$$ x_0 = 3, \ quad y_0 = -2, \ quad z_0 = 6 $$
$$ A = 3, \ quad B = -4, \ quad C = 2, \ quad D = 5 $$
Решение:Для решения задачи воспользуемся формулой для нахождения расстояния от точки до плоскости, равного длине перпендикуляра, опущенного из этой точки на плоскость:
$$ p = (| A \ cdot x_0 + B \ cdot y_0 + C \ cdot z_0 + D |) \ over \ sqrt ((A ^ 2 + B ^ 2 + C ^ 2))
$где A, B, C, D — коэффициенты уравнения плоскости, а x0, y0, z0 — координаты точки.
 2))) $$ Для самолета $$ 4 x-6y-4z + 7 = 0 $$,
2))) $$ Для самолета $$ 4 x-6y-4z + 7 = 0 $$,$$ A = 4, $$
Ответ:
$$ B = -6, $$
$$ C = -4, $$
$$ D = 7.2))) = 0,85 $$
В этой статье рассказывается об определении расстояния от точки до плоскости. разберем метод координат, который позволит нам найти расстояние от заданной точки в трехмерном пространстве. Для закрепления рассмотрим примеры нескольких задач.
Расстояние от точки до плоскости находится посредством известного расстояния от точки до точки, где одна из них задана, а другая является проекцией на данную плоскость.
Когда точка M 1 с плоскостью χ задана в пространстве, через точку можно провести прямую, перпендикулярную плоскости. H 1 — общая точка их пересечения. Отсюда получаем, что отрезок M 1 H 1 является перпендикуляром, проведенным из точки M 1 в плоскость χ, где точка H 1 является основанием перпендикуляра.
Определение 1
Вызывается расстояние от заданной точки до основания перпендикуляра, который был проведен из заданной точки в заданную плоскость.
Определение можно записать в разных формулировках.
Определение 2
Расстояние от точки до плоскости называется длиной перпендикуляра, который был проведен из данной точки в данную плоскость.
Расстояние от точки M 1 до плоскости χ определяется следующим образом: расстояние от точки M 1 до плоскости χ будет наименьшим от данной точки до любой точки на плоскости. Если точка Н 2 расположена в плоскости χ и не равна точке Н 2, то получится прямоугольный треугольник вида М 2 H 1 H 2 , прямоугольной формы, где есть ножка M 2 H 1, M 2 H 2 — гипотенуза.Отсюда следует, что M 1 H 1 считается наклонной, которая проводится от точки M 1 к плоскости χ. У нас есть, что перпендикуляр, проведенный из данной точки к плоскости, имеет меньший наклон, чем перпендикуляр, проведенный из точки в данную плоскость. Рассмотрим этот случай на рисунке ниже.
Расстояние от точки до плоскости — теория, примеры, решения
Существует ряд геометрических задач, решения которых должны содержать расстояние от точки до плоскости. Способ обнаружить это может быть разным.Для разрешения используйте теорему Пифагора или подобие треугольников. Когда по условию необходимо вычислить расстояние от точки до плоскости, заданное в прямоугольной системе координат трехмерного пространства, это решается методом координат. В этом разделе обсуждается этот метод.
По условию задачи имеем, что задана точка трехмерного пространства с координатами M 1 (x 1, y 1, z 1) с плоскостью χ, необходимо определить расстояние от M 1 до плоскость χ.Есть несколько способов решить эту проблему.
Первый путь
Этот метод основан на нахождении расстояния от точки до плоскости с использованием координат точки H 1, которые являются основанием перпендикуляра от точки M 1 к плоскости χ. Далее необходимо рассчитать расстояние между M 1 и H 1.
Для решения задачи вторым способом используется нормальное уравнение данной плоскости.
Второй путь
По условию имеем, что H 1 является основанием перпендикуляра, опущенного из точки M 1 в плоскость χ.Затем определяем координаты (x 2, y 2, z 2) точки H 1. Требуемое расстояние от М 1 до плоскости χ находится по формуле M 1 H 1 = (x 2 — x 1) 2 + (y 2 — y 1) 2 + (z 2 — z 1) 2, где M 1 (x 1, y 1, z 1) и H 1 (x 2, y 2, z 2). Для ее решения необходимо знать координаты точки H 1.
Имеем, что H 1 — это точка пересечения плоскости χ с прямой a, проходящей через точку M 1, расположенную перпендикулярно плоскости χ. Отсюда следует, что необходимо составить уравнение прямой, проходящей через данную точку перпендикулярно данной плоскости.Именно тогда мы можем определить координаты точки H 1. Необходимо вычислить координаты точки пересечения прямой и плоскости.
Алгоритм нахождения расстояния от точки с координатами M 1 (x 1, y 1, z 1) до плоскости χ:
Определение 3
- составьте уравнение прямой a, проходящей через точку M 1 и одновременно
- перпендикулярно плоскости χ;
- найти и вычислить координаты (x 2, y 2, z 2) точки H 1, которые являются точками
- пересечение прямой a с плоскостью χ;
- рассчитайте расстояние от M 1 до χ по формуле M 1 H 1 = (x 2 — x 1) 2 + (y 2 — y 1) 2 + z 2 — z 1 2.
Третий путь
В данной прямоугольной системе координат O xyz существует плоскость χ, то получаем нормальное уравнение плоскости вида cos α x + cos β y + cos γ z — p = 0. Отсюда получаем, что расстояние M 1 H 1 с точкой M 1 (x 1, y 1, z 1), проведенной к плоскости χ, рассчитывается по формуле M 1 H 1 = cos α x + cos β y + cos γ z — p. Эта формула верна, поскольку она установлена теоремой.
Теорема
Если задана точка M 1 (x 1, y 1, z 1) в трехмерном пространстве, имеющая нормальное уравнение плоскости χ в виде cos α x + cos β y + cos γ z — p = 0, то расчет расстояния от точки до плоскости M 1 H 1 производится по формуле M 1 H 1 = cos α x + cos β y + cos γ z — p, поскольку x = х 1, у = у 1, z = z 1.
Свидетельства
Доказательство теоремы сводится к нахождению расстояния от точки до линии. Следовательно, мы находим, что расстояние от M 1 до плоскости χ является модулем разности численной проекции радиус-вектора M 1 на расстояние от начала координат до плоскости χ. Тогда получаем выражение M 1 H 1 = n p n → O M → — p. Вектор нормали к плоскости χ имеет вид n → = cos α, cos β, cos γ, а его длина равна единице, npn → OM → — числовая проекция вектора OM → = (x 1, y 1, z 1) в направлении, определяемом вектором n →.
Применим формулу для вычисления скалярных векторов. Тогда получаем выражение для нахождения вектора вида n →, OM → = n → npn → OM → = 1 npn → OM → = npn → OM →, так как n → = cos α, cos β, cos γ z и OM → = (x 1, y 1, z 1). Обозначение координат примет вид n →, OM → = cos α x 1 + cos β y 1 + cos γ z 1, тогда M 1 H 1 = npn → OM → — p = cos α x 1 + cos β Y 1 + cos γ z 1 — п. Теорема доказана.
Отсюда получаем, что расстояние от точки M 1 (x 1, y 1, z 1) до плоскости χ вычисляется путем подстановки в левую часть нормального уравнения плоскости cos α x + cos β y + cos γ z — p = 0 вместо координат x, y, z x 1, y 1 и z 1 , относящихся к точке M 1, принимая абсолютное значение полученного значения.
Рассмотрим примеры определения расстояния от точки с координатами до заданной плоскости.
Пример 1
Вычислить расстояние от точки с координатами M 1 (5, — 3, 10) до плоскости 2 x — y + 5 z — 3 = 0.
Решение
Решим проблему двумя способами.
Первый метод начинается с вычисления вектора направления прямой a. По условию имеем, что данное уравнение 2 x — y + 5 z — 3 = 0 является уравнением плоскости общего вида, а n → = (2, — 1, 5) — вектор нормали плоскости данный самолет.Он используется как вектор направления прямой линии a, перпендикулярной данной плоскости. Вы должны написать каноническое уравнение прямой в пространстве, проходящей через M 1 (5, — 3, 10) с вектором направления с координатами 2, — 1, 5.
Уравнение примет вид x — 5 2 = y — (- 3) — 1 = z — 10 5 ⇔ x — 5 2 = y + 3 — 1 = z — 10 5.
Необходимо определить точки пересечения. Для этого можно аккуратно объединить уравнения в систему для перехода от канонических к уравнениям двух пересекающихся прямых.Мы возьмем эту точку как H 1. Получаем
.x — 5 2 = y + 3-1 = z — 10 5 ⇔ — 1 (x — 5) = 2 (y + 3) 5 (x — 5) = 2 (z — 10) 5 y + 3) = — 1 (z — 10) ⇔ ⇔ x + 2 y + 1 = 0 5 x — 2 z — 5 = 0 5 y + z + 5 = 0 ⇔ x + 2 y + 1 \ u003d 0 5 x — 2 z — 5 = 0
Тогда нужно разрешить систему
x + 2 y + 1 = 0 5 x — 2 z — 5 = 0 2 x — y + 5 z — 3 = 0 ⇔ x + 2 y = 1 5 x — 2 z = 5 2 x — у + 5 z = 3
Обратимся к правилу решения системы по Гауссу:
1 2 0 — 1 5 0 — 2 5 2 — 1 5 3 ~ 1 2 0 — 1 0 — 10 — 2 10 0 — 5 5 5 ~ 1 2 0 — 1 0 — 10 — 2 10 0 0 6 0 ⇒ ⇒ z = 0 6 = 0, y = — 1 10 10 + 2 z = — 1, x = — 1-2 y = 1
Получаем H 1 (1, — 1, 0).
Считаем расстояние от заданной точки до плоскости. Берем точки M 1 (5, — 3, 10) и H 1 (1, — 1, 0) и получаем
M 1 H 1 = (1-5) 2 + (- 1 — (- 3)) 2 + (0-10) 2 = 2 30
Второе решение — сначала привести данное уравнение 2 x — y + 5 z — 3 = 0 к его нормальной форме. Определите нормирующий коэффициент и получите 1 2 2 + (- 1) 2 + 5 2 = 1 30. Отсюда выводим уравнение плоскости 2 30 x — 1 30 y + 5 30 z — 3 30 = 0. Расчет левой части уравнения выполняется путем замены x = 5, y = — 3, z = 10, причем расстояние нужно взять от M 1 (5, — 3, 10) до 2 x — y + 5 z — 3 = 0 по модулю.Получаем выражение:
M 1 H 1 = 2 30 5-1 30-3 + 5 30 10-3 30 = 60 30 = 2 30
Ответ: 2 30.
Если плоскость χ задается одним из методов задания плоскости, то сначала нужно получить уравнение плоскости χ и вычислить желаемое расстояние любым методом.
Пример 2
Точки с координатами M 1 (5, — 3, 10), A (0, 2, 1), B (2, 6, 1), C (4, 0, — 1) указаны в трехмерное пространство.Рассчитайте расстояние от M 1 до плоскости A B C.
Решение
Сначала нужно записать уравнение плоскости, проходящей через заданные три точки с координатами M 1 (5, — 3, 10), A (0, 2, 1), B (2, 6, 1), С (4, 0, — 1).
x — 0 y — 2 z — 1 2 — 0 6 — 2 1 — 1 4 — 0 0 — 2 — 1 — 1 = 0 ⇔ xy — 2 z — 1 2 4 0 4 — 2 — 2 = 0 ⇔ ⇔ — 8 х + 4 y — 20 z + 12 = 0 ⇔ 2 x — y + 5 z — 3 = 0
Следовательно, проблема имеет решение, аналогичное предыдущему.Это означает, что расстояние от точки M 1 до плоскости A B C имеет значение 2 30.
Ответ: 2 30.
Найти расстояние от заданной точки на плоскости или до плоскости, которой они параллельны, удобнее, применяя формулу M 1 H 1 = cos α x 1 + cos β y 1 + cos γ z 1 — p. Отсюда получаем, что нормальные уравнения плоскостей получаются за несколько действий.
Пример 3
Найдите расстояние от заданной точки с координатами M 1 (- 3, 2, — 7) до координатной плоскости O x y z и плоскости, заданной уравнением 2 y — 5 = 0.
Решение
Координатная плоскость O y z соответствует уравнению вида x = 0. Для плоскости O y z она нормальна. Поэтому необходимо подставить в левую часть выражения значение x = — 3 и взять модуль значения расстояния от точки с координатами M 1 (- 3, 2, — 7) до плоскости. Получаем значение, равное — 3 = 3.
После преобразования нормальное уравнение плоскости 2 y — 5 = 0 приобретет вид y — 5 2 = 0.Затем можно найти необходимое расстояние от точки с координатами M 1 (- 3, 2, — 7) до плоскости 2 y — 5 = 0. Подставляя и вычисляя, получаем 2 — 5 2 = 5 2 — 2
Ответ: Требуемое расстояние от M 1 (- 3, 2, — 7) до O y z имеет значение 3, а до 2 y - 5 = 0 имеет значение 5 2 — 2.
Если вы заметили ошибку в тексте, выделите ее и нажмите Ctrl + Enter
Пусть будет плоскость … Проведем нормаль
через начало координат O.Пусть
— углы, образованные нормалью с осями координат.
… Пусть будет — длина нормального отрезка
до пересечения с плоскостью. Предполагая, что направляющие косинусы нормали известны, мы выводим уравнение плоскости.
Пусть будет
) Это произвольная точка плоскости. Единичный вектор нормали имеет координаты. Найдите проекцию вектора
на нормаль.
Так как точка M принадлежит плоскости, то
.
Это уравнение данной плоскости, называемое нормальное .
Расстояние от точки до плоскости
Пусть дана плоскость, M *
— точка в пространстве, d — его расстояние от плоскости.
Определение. Отклонение точек M * от плоскости называется цифрой ( + д ) , если M * лежит на другой стороне плоскости, где положительное направление нормали указывает, и число (- d ), если точка расположена на другой стороне плоскости:
.
Теорема . Пусть плоскость с единичной нормалью задается уравнением нормали:
Пусть будет M *
— точка в пространстве Отклонение t. M * с плоскости определяется выражением
Evidence. Проекция т.
* нормалью обозначим Q . Точечное отклонение M * от плоскости составляет
.
Правило. Найти отклонение т. M * от плоскости нужно подставить координаты m в нормальное уравнение плоскости. M * … Расстояние от точки до плоскости.
Приведение общего уравнения плоскости к нормальной форме
Пусть одна и та же плоскость задана двумя уравнениями:
Общее уравнение,
Нормальное уравнение.
Поскольку оба уравнения определяют одну и ту же плоскость, их коэффициенты пропорциональны:
Возводим в квадрат первые три равенства и складываем:
Отсюда находим — нормализующий коэффициент:
.(10)
Умножив общее уравнение плоскости на нормирующий множитель, получим нормальное уравнение плоскости:
Примеры задач по теме «Самолет».
Пример 1. Плоскость уравнения, проходящая через заданную точку
(2,1, -1) и параллельная плоскости.
Решение … Нормаль к плоскости:
… Поскольку плоскости параллельны, нормаль также является нормалью к желаемой плоскости … Используя уравнение плоскости, проходящей через заданную точку (3), получаем для плоскости уравнение:
Ответ:
Пример 2. Основание перпендикуляра, опущенного из начала координат на плоскость, — это точка
… Найдите уравнение плоскости.
Решение … Вектор
перпендикулярен плоскости … Точка M 0 принадлежит самолету. Вы можете использовать уравнение плоскости, проходящей через заданную точку (3):
Ответ:
Пример 3. Постройте плоскость, проходящую через точки
и перпендикулярную плоскости:.
Следовательно, для какой-то точки M ( x , y , z ) принадлежало плоскости, необходимо, чтобы три вектора
были копланарными:
= 0.
Осталось выявить определитель и привести полученное выражение к виду общего уравнения (1).
Пример 4. Плоскость, заданная общим уравнением:
Найдите отклонение точки
от заданной плоскости.
Решение … Приведем уравнение плоскости к нормальному виду.
,
.
Подставим в получившееся нормальное уравнение координаты точки M * .
.
Ответ:
.
Пример 5. Пересекает ли прямая плоскость.
Решение … Чтобы отрезок AB пересек плоскость, отклонения и от плоскости должны иметь разные знаки:
.
Пример 6. Пересечение трех плоскостей в одной точке.
.
Система имеет уникальное решение, поэтому три плоскости имеют одну общую точку.
Пример 7. Нахождение биссектрис двугранного угла, образованного двумя заданными плоскостями.
Пусть будет и — отклонение некоторой точки
от первой и второй плоскостей.
На одной из биссектральных плоскостей (соответствующей углу, под которым лежит начало координат) эти отклонения равны по величине и знаку, а на другой — равны по величине и противоположны по знаку.
Это уравнение первой биссектральной плоскости.
Это уравнение второй биссектральной плоскости.
Пример 8. Расположение двух заданных точек относительно двугранных углов, образованных этими плоскостями.
Пусть будет
… Определите, есть ли точки в одном, соседних или вертикальных углах и.
и). Если a и лежат по одну сторону от и от, то они лежат в одном двугранном углу.
б). Если a и лежат на одной стороне и отличны от, то они лежат в соседних углах.
дюйма). Если a и лежат по разные стороны от и, то они лежат в вертикальных углах.
Системы координат 3
Линии на плоскости 8
Линии первого порядка. Прямые на плоскости. десять
Угол между прямыми 12
Общее уравнение прямой 13
Неполное уравнение первой степени 14
Уравнение прямой «отрезками» 14
Совместное исследование уравнений двух прямых 15
Нормаль к прямой 15
Угол между двумя прямыми 16
Каноническое уравнение прямой 16
Параметрические уравнения прямой 17
Нормальное (нормализованное) уравнение прямой 18
Расстояние от точки до прямой 19
Уравнение пучка прямых 20
Примеры задач по теме «линия на плоскости» 22
Векторное произведение векторов 24
Свойства перекрестного произведения 24
Геометрические свойства 24
Алгебраические свойства 25
Выражение перекрестного произведения через координаты факторов 26
Смешанное произведение трех векторов 28
Геом трёхмерный смысл смешанного произведения 28
Выражение смешанного произведения через векторные координаты 29
Примеры решения задач
, г. Конкурс «Презентация к уроку».
Класс: 11
Презентация урока
Назад вперед
Внимание! Предварительный просмотр слайда используется только в информационных целях и может не отображать все параметры презентации.Если вам интересна эта работа, пожалуйста, скачайте полную версию.
Задачи:
- обобщение и систематизация знаний и умений студентов;
- развитие умений анализировать, сравнивать, делать выводы.
Оборудование:
- проектор мультимедийный;
- компьютер;
- листов с текстами задач
ПРОЦЕСС УРОКА
I. Организационный момент
II.Этап обновления знаний (слайд 2)
Повторяем, как определяется расстояние от точки до плоскости
III. Лекция (слайды 3-15)
В этом уроке мы рассмотрим различные способы определения расстояния от точки до плоскости.
Первый метод: пошаговое вычисление
Расстояние от точки M до плоскости α:
— равно расстоянию до плоскости α от произвольной точки P, лежащей на прямой a, проходящей через точку M и параллельной плоскости α;
— равно расстоянию до плоскости α от произвольной точки P, лежащей на плоскости β, которая проходит через точку M и параллельна плоскости α.
Решим следующие задачи:
№1. В кубе A … D 1 найти расстояние от точки C 1 до плоскости AB 1 C.
Осталось вычислить значение длины отрезка O 1 N.
№2. В правильной шестиугольной призме A … F 1, все ребра которой равны 1, найти расстояние от точки A до плоскости DEA 1.
Следующий метод: объемный метод .
Если объем пирамиды ABCM равен V, то расстояние от точки M до плоскости α, содержащей ∆ABS, рассчитывается по формуле ρ (M; α) = ρ (M; ABC) =
При решении задач, мы используем равенство объемов одной фигуры, выраженное двумя разными способами.
Решим следующую задачу:
№3. Ребро AD пирамиды DABC перпендикулярно плоскости основания ABC. Найти расстояние от A до плоскости, проходящей через середины ребер AB, AC и AD, если.
При решении задачи координатным методом расстояние от точки M до плоскости α можно вычислить по формуле ρ (M; α) =, где M (x 0; y 0; z 0), а плоскость задается формулой уравнение ax + by + cz + d = 0
Решим следующую задачу:
№4. В единичном кубе A … D 1 найти расстояние от точки A1 до плоскости BDC 1.
Мы вводим систему координат с началом в точке A, ось y будет проходить вдоль кромки AB, ось x — вдоль кромки AD, а ось z — вдоль кромки AA 1.Затем координаты точек В (0; 1; 0) D (1; 0; 0;) C 1 (1; 1; 1)
Составим уравнение плоскости, проходящей через точки B, D, C 1.
Тогда — dx — dy + dz + d = 0 x + y — z — 1 = 0. Следовательно, ρ =
Следующий метод, который можно использовать при решении задач этого типа — метод поддержки задач.
Применение этого метода состоит в применении известных опорных задач, которые формулируются в виде теорем.
Решим следующую задачу:
№5. В единичном кубе A … D 1 найти расстояние от точки D 1 до плоскости AB 1 C.
Рассмотрим приложение векторного метода.
№6. В единичном кубе A … D 1 найти расстояние от точки A 1 до плоскости BDC 1.
Итак, мы рассмотрели различные методы, которые можно использовать для решения этого типа проблем. Выбор того или иного метода зависит от конкретной задачи и ваших предпочтений.
IV. Работа в группах
Попробуйте решить проблему разными способами.
№1. Ребро куба A … D 1 равно. Найти расстояние от вершины C до плоскости BDC 1.
№2. Найти расстояние от точки A до плоскости BDC в правильном тетраэдре ABCD с ребром
№3. В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 1, найти расстояние от A до плоскости BCA 1.
№4. В правильной прямоугольной пирамиде SABCD со всеми краями, равными 1, найдите расстояние от A до плоскости SCD.
V. Краткое содержание урока, домашнее задание, размышление
Страна мам. Здоровье. Дети. Косметические средства. Мысли вслух
Страна мам. Здоровье. Дети. Косметические средства. Мысли вслух- Биография Альберта Эйнштейна
- Раздутые туфельки Раздутые туфли
- Мелилот медонос желтый или белый
- О Шотландии и Шотландии
- Музыканты всего мира помнят Честера Беннингтона
- Как летописец относится к князю Всеволодовичу Мстеволоду Хроника
- Природные условия Урала Как называется восточный склон Уральских гор
- Инструкция, цена и отзывы
- Манометры, термометры, термоманометры
- Черты характера: примеры
- Человеческие черты и их проявление
- Как правильно питаться при диагнозе холецистит?
- Выбор наиболее эффективного средства от ячменя
- Причина — неотъемлемая часть
- Трава горца горца — полезные и лечебные свойства, противопоказания, отзывы
- Год казни Жанны д’Арк.Загадка Жанны д’Арк. Самозванец или воскресший из мертвых
- Основы ухода — Обуховец T
- Какие страны были основными кредиторами СССР Ввиду сложной экономической ситуации
- Черный рыцарь, уничтоженный иллюминатами
- Сколько женщин было у Казановы Сколько женщины были у Казановы
- Малоизвестные подвиги Великой Отечественной войны
- История трех покушений на Леонида Брежнева
- Бехтерев Владимир Михайлович
- Как побороть страх у взрослых
- Концентрированная тренировка
- В.Бехтерев работает. Вклад В. Бехтерева в становлении и развитии русской психологии. Рекомендации по развитию мозга
- Какие джинсы были в ссср
- Анкилозирующий спондилит. Вклад В. Бехтерева в становлении и развитии русской психологии. Эксперименты с животными
- Мусульманские батальоны ГРУ
- Как советский офицер спас мир от ядерной войны & nbsp
- «Доброе утро!» С. Есенин. «Золотые звезды задремали, Зеркало заводи дрогнуло, На заводях реки рассветает и краснеет сетка неба.Сонные березки улыбнулись
- Как спланировать время, чтобы все успеть Правильно спланировать действия
- Как поступить с тем, кто постоянно опаздывает
- Иван Бунин «Мамы» Презентация к уроку чтения (2 класс) на тему Верень Ангел
- Скины без регистрации. Скины. Скачать скины для Майнкрафт
- Мифические существа, которые человечество еще помнит
- Анализ стихотворения «Двенадцать»
- Энциклопедия мифических животных
- Мифологические существа.Мифические существа. Мифические существа и духи
- Презентация на тему: «Язык — это исповедь людей
- СПИД — самая большая мистификация ХХ века
- ROSA FRESH R10 Системные требования KDE
- Аудиоверсия выступления Plastinki80 на PDJTV One Hits 80-х виниловая пластинка
- Истерия: причины, признаки и лечение этого заболевания
- Лагерное мероприятие «Зачетная книжка лагеря»
- Что такое электризация тел?
- Как правильно уменьшить объем желудка — 2 лучших способа для заядлых обжор и для тех, кто переедать только изредка
- Сложный приговор
- Греческий салат с китайской капустой
- Выращивание ежевики Размножение и обрезка ежевики
- Секреты выращивания ежевики без колючек Размножение и обрезка ежевики уход за собой
- Барсучий жир: применение, от которого он помогает, лечебные свойства , формы выпуска
- Использование нефтяной пирамиды для сел f-actualization
- Лечебные свойства барсучьего жира — применение от кашля и противопоказания для детей
- Игорь манн как стать doin
- Двоеточие: где, когда и зачем нужно ставить толстую кишку
- Вагин Игорь Олегович.Вагин Игорь. Книги онлайн Тренинги вагина
- Белая ноша. Джозеф Редьярд Киплинг. Человеческое бремя. Бремя белой расы
- К чему снится Танцевать с мужчиной?
- «К чему снится алкоголик?
- Из чьей руки смертельный поводок
- Пропавший герой забрал девушку домой 2
- Как долго длится беременность у женщин
- Как алкоголь и фертильность связаны у мужчин?
- Удаление пищевода при онкологических последствиях
- Диета и питание при раке прямой кишки
- Газообразование в кишечнике: причины и лечение, питание, препараты
- Жидкое стекло для автомобилей отзывы цена где купить «В час, когда нарциссы» напиться… »
- Как подготовиться к зачатию ребенка?
- Измена во сне: обоснованные подозрения или неуверенность в себе
- К чему снится кататься на мотоцикле
- Ромашковое полоскание десен: как заварить, лечить воспаление
- Почему душица считается женщиной-целительницей?
- Вадим Куркин о секретах счастливых отношений: подробности
- Я верю, город поверю, что сад зацветет
- Индивидуально-психологические особенности человека
- Гибкая водопроводная линия
- Какие плоды могут беременные женщины едят?
- К чему снится бледный брат в гробу?
- Как разложить на множитель трехчлен в квадрате
- Как разложить на множитель трехчлен в квадрате
- Внутренний конфликт: чувства против разума — композиция
- Основные причины развития
- Выращивание плодоносящей хурмы из косточки в домашних условиях
- Третье соборное послание апостола Иоанна Богослова
- L inear функция.Теория. Анализ задач Сбор и использование личной информации
- Альфред Теннисон, «Улисс»: Анализ и история Теннисона Улисс
- Список препаратов и разжижителей крови
- Тразодон — инструкция, применение, по показаниям, противопоказаниям, действию, побочным эффектам, аналоги, состав, дозировка Тразодон
- Горец лекарственное растение для водоемов
- Александр Невский как олицетворение русской армии
- Листья лопуха: польза и вред, когда собирать и как использовать
- Древнейшие цивилизации мира
- Влияние легкой атлетики на человеческий организм
- Какая самая древняя цивилизация на Земле?
- Самая большая звезда в нашей галактике
- Самая большая звезда в галактике Млечный Путь
- Тайны космоса: как называется самая большая звезда
- Винчестерский туннель или туннель?
- Что такое туннель Винчестера?
- Тибетская медицина об очищении организма
- Каланхоэ degremona лечебные свойства Каланхоэ degremona лечебные свойства
- Лучшие пляжные курорты Таиланда
- Выпускник Май Богатырев Павел 1964
- Как операционные системы получили свои названия?
- Кто принадлежит к славянской группе народов
- Славяне (происхождение славян)
- Чем закончилась жизнь Александра Македонского
- Съедобные насекомые для выживания в экстремальных ситуациях, ловли и готовки
- Microsoft Windows: история и интересное Факты Интересные факты о windows 7
- Гимнастические упражнения при коксартрозе для восстановления подвижности
- Как операционные системы получили свои названия?
- Картофельные чипсы домашние
- «Проклятие Тутанхамона»: мифы и правда Почему гробницу Тутанхамона считают проклятой
- Маринованные помидоры при беременности
- Упражнения при боли в бедре
- Высшее командование Орджоникидзевская школа им. Род неотклоняющихся существительных
- Лечебные свойства пырея, использование в медицине и противопоказания
- English School of Science and Information Technology
- Делитель делитель неполный остаток от деления
- Полезные советы, как лечить артроз коленного сустава в домашних условиях
- Когда собирать корни пырей
- Белки — их роль в организме человека и насколько они важны в спорте
- Листья крапивы (Urticae folia)
- Уродливый толстый садист пощекотал плену, пощекотал историю пыток
- Значение середины Эпохи в истории человечества Значение средневековья is
- Заброшенные туннели расскажут историю ушедшей цивилизации
- На каком языке чаще всего говорят на МКС?
- Нервная система человека: как побаловать и от чего уберечь
- Типы трубных центраторов
- Внешний центратор для труб: виды, характеристики
- Странные, но правдивые истории, случившиеся с беременными женщинами
- Ким Чен Ир Годы жизни.Ким Чен Ир. Ким Чен Ир — лидер Северной Кореи
- Внутренняя политика Николая I: кратко об основных направлениях
- Свойства параллельных линий
- Nise инструкция по применению в ампулах
- Devine RPG 1.7 10 новая версия
- К чему снится кружево в сонник Видеть во сне платье из тонкого кружева
- К чему вы чувствуете усталость после поедания сладкого?
- Что значит, если снится рыба
- Видеоурок «Электроскоп.Электрическое поле. Электроскоп. Электрическое поле Презентация электроскопа проводники и диэлектрики электрическое поле
- Что будет, если вам приснится свадьба
- Решение нестандартных математических задач в начальной школе
- Как гликемический индекс продуктов влияет на желание спать
- Есть красная рыбка по соннику
- К чему снится красная рыба
- Образец медицинской справки о бесплодии, Справка о бесплодии женщины образца Справка о бесплодии мужчины образца
- Тысячелистник в народной медицине, о пользе и вреде
- Цикорий: необычные свойства и применение
- Тысячелистник — польза, вред, народная медицина
- Целебная сила незаметного цикория: советы по использованию и выращиванию растения
- Сонник: К чему снится женщине
- Викторианская эпоха века.О викторианской эпохе. Уважаемые дамы и господа
- Если болит голова и давит на глаза — как это связано и как лечить?
- Эхинацея: состав, препарат, лечебные свойства, применение и противопоказания
- Причины белых выделений при беременности
- Основные занятия жителей Финикии
- Лимон польза и вред для организма
- Что такое глутамат натрия — вредно или нет, его влияние на тело
- Квадратные штаны Губка Боб раскраски
- Задачи из коллекции Кузнецова L
- Задачи из коллекции Кузнецова L
- Интересные факты о России
- Был ли Яков Джугашвили в плену?
- История династии Романовых
- Одышка — одышка, лечение народными средствами Лечение одышки
- Страны, появившиеся в XXI веке Как жили шумеры
- Интересные факты о растительных гормонах
- Кто был Ленин в 1917 г.Владимир Ильич Ленин. Биография. Дорога к революции
- На что способен Tegra K1?
- «Русские не сдаются» — история крылатой фразы
- СССР — союз советских социалистических республик
- Герб Челябинской области В чем сходство символики городов Челябинска
- Граница войска НКВД СССР в начале Великой войны
- Как проявили себя советские пограничники в первые дни войны
- Все книги о: «книгах о военных моряках…
- Мировой опыт: удачные и неудачные примеры отказа от кириллицы в пользу латинского алфавита
- Unidox Solutab: применение и побочные эффекты препарата
- Geisha art — первыми были мужчины
- Крымская война: wiki: Факты о России Факты о Крымской войне 1853 1856
- Скачать моды супер оружия 1
- интересные факты о числах
- Луи Пастер и его открытия: интересные факты и видео
- Интересные факты о словах
- Откуда взялось выражение «курилка» жить «откуда?»
- Как ускорить роды в домашних условиях
- Выращивание инжира на открытом воздухе
- Почему Пушкин все делает для всех и откуда добралось выражение «до ручки»
- Тот же ефрейтор Альфред Лисков
- «К чему снится балкон?
- К чему снится, что вы умираете?
- Последствия избытка йода в организме: выявление и устранение
- Йод в организме человека
- К чему снится метеорит, падающий на землю
- Увидеть стадо овец в сон
- «Греческий огонь» — секретное оружие Византийской империи. Какой смесью византийцы жгли лодки Руси
- Причины, особенности и лечение боли в спине при кашле
- «Греческий огонь» — секретное оружие Византийская империя Какой смесью византийцы сожгли лодки Руси
- Богатое пианино до и после.Богатая Пиана. Жизнь и смерть легенды бодибилдинга. Смерть Рича Пианы
- Постинор — все плюсы и минусы дедушкиной посткоитальной контрацепции
- Самые нелепые запатентованные изобретения в истории
- Боль в левом боку внизу живота — основные причины и способы избавления от симптомов
- Выделения из полового члена: паника или успокоение?
- Чем полезен эстрагон, в лечебных целях
- История покорения Южного полюса Земли
- На что указывает боль в спине между лопатками при кашле?
- Категории зависимых крестьян Древней Руси: кто такие смерды, рабы, покупатели, рядовичи, их сравнительная характеристика
- Трава эстрагона: описание, свойства, посадка и уход
- Отхаркивающие травы от сухого и влажного кашля
- Как правильно лечить используйте отхаркивающие травы
- Rapten® Rapid — быстродействующий нестероидный противовоспалительный препарат Диклофенак калия или натрия
- Как рассчитать плавучесть (плавучесть)
- Что сказать маме, чтобы она не ходила в школу
- Причины увеличения печени и лечение народными средствами
- Скачать на android alien shooter 2 full
- Четырехугольная призма: высота, диагональ, площадь
- Причины, симптомы и лечение заболеваний ушей у человека
- Белор — партизан.Армейский дзен. Белорусский партизан (1 фото). Посмотрите, что такое «Белорусский партизан» в других словарях
- Что такое пирамида потребностей Авраама Маслоу
- «Драйв времени: Как успеть жить и работать» — Глеб Архангельский
- Ласточкины гнезда китай. Съедобные птичьи гнезда. БАД: искусственные заменители продукта
- Ложь и правда о Второй мировой войне Другая правда о Второй мировой войне Гарин
- Что такое смерд — этимология слова и история его использования
- Иллюзия обмана: Гарри Гудини и всемирно известных фокусников
- Перелом костей пальца ноги: симптомы, признаки, лечение, выздоровление Человек без пальца ноги
- Софья Ивановна Блюштейн, или «Соня-золотая ручка»
- Можно ли не ходить в школу ?
- Лирика — наркотик или обычные таблетки с романтическим названием?
- Правда о штрафных батальонах: штрафные части СССР и Германии
- Новые уроки сводки — новый подход к изучению грамматики Обзор 1 готовое домашнее задание
- Полезные свойства и противопоказания березового сока
- Патриция Томпсон — американская дочь великого русского поэта
- Открытое новогоднее мероприятие «Зимняя сказка» Зимняя сказка про клевер новогодней елки
- Психология дети добрые и его друзья читают
- Паук во сне или к чему снятся пауки?
- Ключевые особенности iMazing
- Сонник: к чему снится рыба
- Почему нельзя употреблять алкоголь?
- Что вышло из строя на станции
- Причастия совершенного вида
- Гауляйтеры в нацистской Германии — это кто?
- Восстановление после лучевой терапии рака шейки матки
- РПК74: детали и механизмы ручного пулемета, их назначение; задержки стрельбы, их причины и способы устранения
- Школа отчаяния Сезон 3 Все герои
- Сельское хозяйство и животноводство: возникновение, разделение Что привело к появлению сельского хозяйства и животноводства
- Пространственно-ориентированные культурные коды в индоевропейских традициях — файл №1
- Индометацин: формы выпуска, показания и противопоказания
- Как научиться общаться с людьми?
- Александр Пушкин — Медсестра: Стихи
- Непристойные стихи Маяковского
- Как возникает привязанность к человеку
- Чем отличается девиантное поведение от делинквентного
- Чем резиновая девочка лучше живой?
- Как научиться общаться с людьми: секреты общения
- Психологическая помощь Актуальность психологического консультирования
- Пластика лица: хирургические и безоперационные методы
- История «Молодой гвардии»
- Полезные медицинские слова на английском языке
- Консультация психолога
- Польза и вред ботвы моркови для организма
- Жирная пища: виды, польза и вред, суточное потребление в рационе
- Сочувствие и неумение сопереживать
- Миндаль, что ценится, как употреблять отличить горькое от сладкого
- Барная стойка своими руками: виды, этапы создания и рекомендации
- Сорта и виды хлорофитума для комнатного выращивания
- «Полосатый полет» во сне… Толкование снов с тиграми для женщин
- Анализ сока простаты: показания, особенности и толкование результатов
- «Божественные отношения» доктора Сытина
- Просроченное пиво или кефир: что будет, если выпить?
- Я все еще томлюсь тоской по желаниям … (сборник) Текст
- Причины появления и лечение жжения в ногах
- Каменное масло: инструкция по применению и тонкости применения при различных заболеваниях
- Основное лечение саркомы
- Возвращение легендарного Сэма к серьезному Сэму Скачать Serious Sam 2 для android
- Поэма «Дед Мазай и зайцы»
- Сечение в обычной четырехугольной призме
- Матрица Эйзенхауэра: простой инструмент для распределения проблем
- Меню для сушки тела принципы и рецепты питания
- Дельфин Спасенный Поэт 5
- Что взять с собой в поездку: список необходимых вещей и сборов
- В какой круг отправить ребенка
- Вильгельм Райх и проект Феникс
- Тестовая анкета локуса J шкалы контроля
- Что брать архитектору-проектировщику
- Раздел в обычном четырехугольная призма Основание правильной четырехугольной призмы abcda1b1c1d1
- Сказки студентов
- Restore Point Creator Создание точек восстановления системы Windows Restore Point Creator на русском языке
- Полный список вещей, которые можно взять с собой в отпуск
- Сказки, написанные студентами
- Первые симптомы туберкулеза у женщин
- Лакто-вегетарианское меню на неделю
- Польза и вред вибромассажеров и виброплатформ для похудения Влияние вибрационных машин для похудения
- Как можно использовать красный перец для похудения ?
- От чего помогает Метеоспазмил?
- 0 специфическое нарушение речевой артикуляции
- Нарушение артикуляции у детей и взрослых
- Грибы шиитаке: фото, отзывы и свойства
- Грибы шиитаке — полезные свойства полисахаридов лечебных грибов
- Насосные станции для частного дома или дачи: как правильно выбрать и установить
- Рейтинг фильтров для воды для мытья: рейтинг лучших моделей и руководство по выбору
- Вибротренажер для похудения живота и боков: преимущества и противопоказания Вибротренажер для похудения в домашних условиях
- Инструкция, цена и отзывы
- Главный фильтр для очистки воды в квартире — как выбрать подходящий
- Какие бывают системы очистки воды для квартиры?
- Фильтры для водопроводной воды
- Паровая сирена.Редьярд Киплинг. Серые глаза — рассвет. Анализ стихотворения Киплинга «Четыре цвета глаз»
- Мифы о GIA: экзамен по русскому языку не так страшен, как его рисуют
- Аккаунт Google Play Market — вход, регистрация и восстановление
- Как создать аккаунт в телефоне: пошаговая инструкция
- Как войти в «Аккаунт Google» на Android — пошаговая инструкция
- Что такое панический страх, его симптомы и как от него избавиться
- Что означает выражение «сизифов труд» иметь в виду?
- Происхождение и значение фразеологизма «Манна небесная»
- «Вавилонское столпотворение» — значение фразеологизма
- Значение словосочетания «Содом и гоморра»
- Что такое «яблоко раздора»?
- Показать, где впадают в спячку раки
- Застрявший, как банный лист, значение фразеологизма
- Бойтесь данцев, которые приносят подарки (троянский конь)
- Что означает фразеологизм «проливать крокодиловы слезы»
- Что означает выражение «вообще не видно»?
- Что означает ли выражение «казанская сирота»?
- Манна небесная, происхождение, значение
- «гомеровский смех» — значение и происхождение фразеологизмов с примерами?
- Ведущий за нос: значение фразеологизма в одном слово
- Почему мы говорим в одиночку, как палец
- Сохранение ценности в секрете
- Сложение натуральных чисел по столбцам, примеры, решения 90 169 Почему появилось выражение «высунуть язык»?
- Голос в пустыне
- Фразеологизмы на английском и русском языках
- Фразеологизмы со словом «голова» и их значение (с примерами)
- Фразеологизмы со словом «голова» и их значение (с примерами)
- Для мытья кости значение
- Что означает выражение «сшитые белой нитью»?
- Значение слова попасть в беду
- Откуда взялось выражение «облажаться»
- Фразеологизмы в русском языке
- Две вершины от горшка и одна от смерти
- Что означает выражение «собака на сене» » иметь в виду?
- Значение выражения «бросать бусы перед свиньями»
- Что значит фразеологизм, как снег на голове
- Съешь пуд соли, выше мед ценит
- Для обеих щек значение фразеологизма
- «Нить Ариадны»: значение фразеологизма, происхождение, примеры
- Что ждет тигренка в год
- Телец по гороскопу Змея.Быки — Дева
- Телец кабан прогноз на год
- год: прогноз по знакам зодиака на год Огненной Обезьяны
- Змея, которая ждет гороскоп на май
- Основы крепких семейных уз
- Неблагоприятные дни в июне Дева
- Что ждет Козерога в августе
- Прогноз карьеры и финансового положения
- Модные тенденции осень-зима — имиджевые идеи, обновки, модные фасоны
- Любовный гороскоп Скорпиона
- Что не надеть на новогодний корпоратив
- Что есть аспекты планет, о которых вы узнаете в прогнозе
- Мода на открытый живот: стильные откровения
- Любовный гороскоп на январь
- Гороскоп Скорпион Свинья на год
- Встречаем год Красного Огненного Петуха — что надеть?
- Гороскоп для мужчин Весы на сегодня
- Основные черты лучших моделей из нашего каталога купальных костюмов
- Предсказание для женщины-Тельца
- Женские пижамы в интернет-магазине DreamValley
- Короткие пижамы.Женские пижамы. Фланелевая пижама для капризной межсезонья
- Джинсовое платье с кружевом: актуальная, практичная вещь
- С чем носить блузки, чтобы быть самой модной?
- Как и с чем носить белые туфли
- Функциональные вязаные шапки
- Модные длинные юбки тенденции модных стилей фото
- Вечерние платья звезд: самые лучшие, эффектные и даже откровенные образы
- Как правильно одеться на пикник весной?
- Короткие юбки Пышные модели в мини-юбках
- Модели с завышенной талией
- Какие челки идут на удлиненное лицо
- Как обновить гардероб дешево, бесплатно, если нет денег или сделай сам
- Большой китайский гороскоп для свиньи
- Модные расцветки платьев Платье в маленький цветок
- Как самому увеличить грудь: самые эффективные средства
- Что модно весной для девочек
- Гороскоп на 10.4 рака от глоба. Гороскоп от Василисы Володиной
- Модные тенденции осень-зима
- Летние сарафаны: новинки и тренды сезона
- Летние сарафаны: новинки и тренды сезона
- Летние сарафаны: новинки и тренды сезона
- Летние сарафаны: новинки и тренды сезона
- Одежда из одного материала
- С чем носить джинсы, чтобы выглядеть ярко и нарядно
- Модные ботинки на шнуровке
- Какие модные цвета в одежде будут в тренде
- Модные цвета платьев Платье в маленький цветок
- Длинное платье с длинными рукавами — это невероятно красиво!
- Гороскоп для семьи и отношений
- Короткий торс и высокая талия — что надеть?
- Оригинальная форма каблука
- Классические туфли-лодочки на шпильке фото
- Предсказания Третьей мировой войны, которых вы не знали
- Халаты женские
- Жалкий трус Игорь Гиркин (Стрелков)
- Модные цвета одежды на весну
- Почему «убитые боевики ИГИЛ» продолжают убивать российских военных
- Летние женские футболки (50 фото)
- Лучшие платья на Новый год
- Модные тенденции от известных модельеров
- Женственное замшевое платье: советы по выбору и завершает 15 осенне-зимних модных тенденций
- ДНР объявила о возобновлении полномасштабных боевых действий
- Русский не по национальности
- Вечер для двоих: как устроить незабываемый романтический ужин
- Витамин В 12 отвечает.Витамин B12. Что о нем полезно знать. Какие анализы подтверждают нехватку витамина
- Как жить дальше после измены жены?
- Скупой — психология мужской жадности
- Принесите им бутылку боярышника: россиянам на примерах объяснили, почему украинцы не горюют по своему самолету
- Что такое бездетный, а кто бездетный и бездетный
- Педофил в контакте. Педофилы «на связи. Что ждет жертв педофила «ВКонтакте»
- Демушкин: Мизантропическая дивизия — это просто паблик »ВКонтакте Мизантропическая дивизия
- Сводки ополченцев Новороссии 5
- Слова Путина о ядерной войне вызвали общественный резонанс
- в Palmyra жест презрения Кремля к Западу — наблюдатели
- «О чем на самом деле молились верующие вне парламента?»
- Убийство Гиви: как погиб один из лидеров ДНР.Где сейчас Гиви?
- Путин поддержал идею «закона о русской нации»
- Славянский ген, пробуждения которого евреи очень боятся
- Россияне рассказали о своем отношении к Навале
- «Бешеный пес» станет соперником Шойгу: Трамп определился с главой Пентагона
- Почему «русские расисты» не отправляют черных в космос?
- Мода для полных женщин года
- О чем России договариваться с Кубой?
- Саудовская Аравия борется с колдунами, геями и алкоголиками
- Черное вечернее платье — для настоящих дам!
- Адмирал Колчак предатель
- Либеральный тоталитаризм: основы концептуального синтеза
- Почему русские воюют с русскими на Донбассе
- Почему Россия не присоединяется к Донбассу
- Как прошла четырехчасовая битва между российскими наемниками и американскими спецназ Сирия
- Нашли руины Содома (7 фото)
- Вежливые люди wiki.Вежливые люди. Кто такие «вежливые люди»
- Вооруженные силы Саудовской Аравии
- Таким образом, Сирия — территория современной войны
- Проблемы языковой безопасности
- «Я не говорил, что убивал русских солдат»
- «Земля была дорога нас с древних времен », h
- Вассерман обвиняет российских экономистов в непрофессионализме
- Платье Чикаго — с чем носить
- Зимние женские сапоги — модные тенденции
- Черная куртка — это совершенно скучная мода!
- Модная мужская одежда — тенденции, фото, стильные идеи гардероба
- Бархатное платье: где купить и с чем надеть?
- Синие брюки: уроки стиля и сочетания
- Черное пальто: красивые женские образы
- Джинсовые шорты — с чем носить
- Модные летние платья для женщин
- Брюки цвета хаки для женщин: модные образы на каждый день
- Как и с с чем носить джинсовые шорты — фото
- С чем носить кожаную юбку
- Модные брюки года.Модные фасоны и расцветки. Брюки широкие с карманами
- Красное платье в пол — самые модные и красивые вечерние и повседневные наряды
- Ботинки-чулки: фото стильных образов
- С чем носить джинсы женщинам-бойфрендам: фото модных сочетаний
- Спортивные брюки и угги. С чем носить угги зимой? С чем носить короткие угги? С чем носить блестящие угги зимой
- С чем носить бойфренда зимой
- Для кого подходят джинсы-бойфренды?
- Выбор блузки по телосложению
- Пышная юбка, уличная мода и индивидуальный стиль
- Красное пальто: фасоны, цветовые сочетания и шарфы
- С чем носить слипоны: модно комфортно
- Кому и к чему подходит носить с этим сезоном расклешенные джинсы?
- Самцы второй свежести, или самцы тоже имеют срок годности
- Музыка и развлечения: все как в прошлом
- Мы его окружили, и игра началась Сильвио
- Что носить с водолазкой: сочетания цветов и моделей
- Что модно зимой.Пальто из овечьей шерсти
- Модные головные уборы на осень, зиму и весну: снуд, федора, шапка, берет
- Кожаные леггинсы: как выбрать и с чем носить
- С кем носить джинсы скинни
- Всегда актуально и женственно !
- Всегда актуально и женственно!
- Элегантные пальто от Chanel
- Красивые, стильные и элитные шубы
- С чем носить юбку миди — самые гармоничные сочетания
- Пижамный стиль — как выглядеть женственно каждый день?
- Выпускные образы: что надеть, чтобы быть самой красивой?
- Девушка в норковой шубе зимой
- Что надеть зимой: модные луки на холодное время года
- Как защитить волосы на пляже: платок
- Стильные платья — яркая личность
- Чуваки в клетчатых рубашках
- В каменные джунгли: Гардероб в стиле сафари
- Вечернее платье-футляр
- Бархатные платья модные года
- Что носить осенью: модная осенняя одежда — фото идеи
- Бежевая юбка: фото и стильные сочетания
- Что можно надеть на вечеринку
- Идеи тематической вечеринки: обзор праздничных тем
- Модный французский стиль — удобство и элегантность
- Как одеваться, чтобы выглядеть выше и стройнее?
- Базовый гардероб от Эвелины Хромченко
- Что такое одежда унисекс
В правильной четырехугольной призме abcda1b1c1d1.Сечение в правильной четырехугольной призме
Задача.
В правильной четырехугольной призме ABCDA 1 B 1 C 1 D 1 стороны основания равны 3, а боковые ребра — 4. На ребре AA 1 отмечается точка E так, чтобы AE: EA 1 = 1: 3.
а) Постройте линию пересечения плоскостей ABC и BED 1.
б) Найдите угол между плоскостями ABC и BED 1.
Решение:
а) Постройте прямую линию пересечения плоскостей ABC и BED 1 .
Построим плоскость BED 1. Точки E и D 1 лежат в одной плоскости, поэтому проведем линию ED 1.
Точки E и B лежат в одной плоскости, поэтому проведем линию EB. Итак, грани правильной четырехугольной призмы параллельны, проведем на грани BB 1 C 1 C прямую BF, параллельную прямой ED 1. Точки F и D 1 лежат в одной плоскости, поэтому проведем линию FD 1. Получили желаемое. самолет BED 1.
Поскольку прямая ED 1 и прямая AD лежат в одной плоскости ADD 1, они пересекаются в точке K, лежащей в плоскости ABC.Точки K и B лежат в плоскостях ABC и BED 1, следовательно, плоскости ABC и BED 1 пересекаются по прямой KB. Построена искомая линия пересечения плоскостей ABC и BED 1.
б) Найдите угол между плоскостями ABC и BED 1
Отрезок AE перпендикулярен плоскости ABC, из точки E опускаем перпендикуляр EH до линии KB. Точка H лежит в плоскости ABC, тогда AH — проекция EH на плоскость ABC. Прямая, перпендикулярная наклонной EH, проходит через точку H, тогда по теореме о трех перпендикулярах отрезок AH перпендикулярен прямой KB.
Угол ∠EHA — это линейный угол двугранного угла, образованного плоскостями ABC и BED 1. Угол ∠EHA — искомый угол между плоскостями ABC и BED 1. Найдем значение этого угла.
Рассмотрим прямоугольный треугольник EHA (∠A = 90˚):
По условию AE: EA 1 = 1: 3, тогда AE: AA 1 = 1: 4.
Треугольники AKE и A 1 D 1 E похожи, тогда
A 1 D 1 = 3, AE = 1, A 1 E = AA 1 — AE = 3
Рассмотрим прямоугольный треугольник АКБ (∠A = 90˚).
Рассмотрим еще одну двухточечную стереометрическую задачу из обучения КИМ.
Задача. В правильной четырехугольной призме ABCDA 1 B 1 C 1 D 1 сторона AB основания равна 5, а боковая грань AA 1 равна корню квадратному из пяти. На краях самолета C 1 и D 1 обозначены точки K и L соответственно, при этом CK = 2 и C 1 L = 1. Плоскость g параллельна линии BD и содержит точки K и L.
а) Докажите, что прямая А 1 С перпендикулярна плоскости g.
б) Найдите объем пирамиды, вершиной которой является точка A1, а основанием — сечение данной призмы плоскостью g.
Решение. a) Тщательно выполните рисунок и проанализируйте данные. Потому что ABCDA 1 B 1 C 1 D 1 — правильная четырехугольная призма, что означает основание, ABCD — квадрат со стороной 5. Боковые ребра перпендикулярны основаниям. Поскольку плоскость g проходит через точку K и параллельна прямой BD, то линия пересечения плоскости g и плоскости ABC параллельна прямой BD ( Если другая плоскость проведена через прямую, параллельную этой плоскости, то прямая пересечения этих плоскостей будет параллельно этой прямой ().
Проведите прямую линию, параллельную B, через точку KD до пересечения CD в точке M. Таким образом, KM перпендикулярна AS (, потому что диагоналей квадрата BD , и AC перпендикулярны ).
Треугольники BCD и SCM подобны (как прямоугольные, так и равнобедренные), следовательно CM = KS = 2. По теореме Пифагора из треугольника CKM находим, что KM = 2√2, а из треугольника BCD BD = 5 √2… Диагонали квадрата равны, поэтому AC = 5 √2.
Теперь через точку L проведем прямую параллельную BD перед пересечением B 1 C 1 в точке T. Вдоль сегмента TL плоскость KM L пересечет верхнее основание ( Если две параллельные плоскости пересекаются третьей плоскостью, то линии пересечения будут быть параллельным ). Итак, TC 1 = C 1 L = 1. Из треугольника TLC 1 по теореме Пифагора TL = √2.
У равнобедренной трапеции CTL M точка H — середина верхнего основания, pointN — середина нижнего основания, затем HN — высота трапеции, NN перпендикулярно CM.Итак, КМ перпендикулярна плоскости AA 1 C, включая прямую A 1 C.
Рассмотрим диагональное сечение прямоугольной призмы AA 1 C 1 C. Из точки H опустим перпендикуляр к AC. Тогда N E = EC = H C 1 = 0,5 √2. НЕ = С С 1 = √5.
В треугольниках AA 1 C и N PC угол PCA — общий. Тангенс угла AA 1 C равен 5√2: √5 = √10 Тангенс угла HNE от треугольника HN E равен √5: 0,5 √2 = √10 … Значит, углы AA 1 C и HN E равны.Но тогда оставшиеся углы A 1 AC = N РС = 90 ⁰ … Имеем A 1 C перпендикулярно прямым HN и KM, поэтому A 1 C перпендикулярно плоскости трапеции KTL M. Что требовалось, чтобы доказывать.
Чтобы найти объем пирамиды A 1 CTL M, нужно найти площадь трапеции CTL M и высоту A 1 R. Из треугольника HN E по теореме Пифагора HN 2 = 5.5. Площадь трапеции CT L M равна H N * (T L + KM) / 2 = √5,5 * (√2 + 2 √2) / 2 = 1.5 √11.
В правильной четырехугольной призме ABCDA 1 B 1 C 1 D 1 стороны основания равны 2, а боковые грани — 5. На ребре AA 1 отмечается точка E так, чтобы AE: EA 1 = 3 : 2. Найти угол между плоскостями ABC и BED 1 …
Решение. Пусть прямая D 1 E пересекает прямую AD в точке K. Тогда плоскости ABC и BED 1 пересекаются по линии KB.
Из точки E опускаем перпендикуляр EH на линию KB, тогда отрезок AH (проекция EH) будет перпендикулярен прямой KB (теорема о трех перпендикулярах).
Угол AHE — это линейный угол двугранного угла, образованного плоскостями ABC и BED 1.
Поскольку AE: EA 1 = 3: 2, получаем :.
Из подобия треугольников А 1 D 1 E и AKE получаем:.
В прямоугольном треугольнике АКБ с прямым углом А: АВ = 2, АК = 3,; где высота
.
Из прямоугольного треугольника AHE с прямым углом A получаем: и ∠ AHE = arctan (√13 / 2).
Ответ: arctg (√13 / 2).
Задания самопомощи
1.

 При этом уровень жидкости в
сосуде поднялся с отметки 25 см до
отметки 29 см. Чему равен объем детали?
Ответ выразите в см3.
При этом уровень жидкости в
сосуде поднялся с отметки 25 см до
отметки 29 см. Чему равен объем детали?
Ответ выразите в см3. Площадь боковой поверхности
призмы равна 24. Найдите высоту цилиндра.
Площадь боковой поверхности
призмы равна 24. Найдите высоту цилиндра.
 2))) $$ Для самолета $$ 4 x-6y-4z + 7 = 0 $$,
2))) $$ Для самолета $$ 4 x-6y-4z + 7 = 0 $$,
Leave A Comment