Известно что ac 32 см bc 9 см cd 12 см: Известно,что AC=32 см,BC=9см,CD=12см.Найдите длины отрезков AB и BD.

Мерзляк 5 класс — § 3. Отрезок. Длина отрезка

Вопросы к параграфу

Сколько существует отрезков, концами которых являются две данные точки? — существует только один отрезок, концами которого являются две данные точки.
Как обозначают отрезок? — записывают точки, которые являются концами отрезка, например: АВ, МК и т.д.
Какие вы знаете единицы длины? — 1 мм (миллиметр), 1 дм (дециметр), 1 см (сантиметр), 1 м (метр), 1 км (километр).
Объясните, что означает измерить длину отрезка — это означает, что надо посчитать сколько единичных отрезков (единиц длинны) помещается в этом отрезке, например, сколько раз в нём помещается один сантиметр.
Каким свойством обладает длина отрезка? — если на отрезке АВ отметить точку С, то длина отрезка АВ будет равна сумме длин отрезков АС и СВ: АВ = АС + СВ.
Какие отрезки называют равными? — два отрезка называют равными, если они совпадают при наложении.

Какие длины имеют равные отрезки? — равные отрезки имеют равные длины.
Какой из двух неравных отрезков считают большим? — большим считают тот, у которого длина больше.
Что называют расстоянием между точками A и B? — длиной отрезка АВ.
Объясните, какую геометрическую фигуру называют ломаной — это фигура, состоящая из последовательно соединённых отрезков и в которой конец первого отрезка совпадает с началом второго, конец второго отрезка совпадает с началом третьего и т.д.
Что называют длиной ломаной? — сумму длин всех его звеньев (отрезков, из которых состоит ломанная.
Какую ломаную называют замкнутой? — замкнутой называют ломанную, конец последнего отрезка которой совпадает с началом первого отрезка.

Решаем устно

1. Реши:

Какое число больше числа 46 на 9? 46 + 9 = 55 — ответ 55
Какое число меньше числа 72 на 15? 72 — 15 = 57 — ответ 57
Какое число больше числа 21 в 7 раз? 21 • 7 = 147 — ответ 147
Какое число меньше числа 65 в 13 раз? 65 : 13 = 5 — ответ 5

2. Назовите все двузначные числа, сумма цифр которых равна 6.

60, 51, 15, 42, 24, 33

3. Назовите все двузначные числа, разность цифр которых равна 7.

70, 81, 18, 92, 29

4. Назовите три последовательных натуральных числа, наименьшим из которых является наибольшее четырёхзначное число.

9 999, 10 000, 10 001

5. Назовите три последовательных натуральных числа, наибольшим из которых является наименьшее четырёхзначное число.

998, 999, 1 000

6. Выразите в сантиметрах:

7 дм 4 см = 74 см
4 м 1 см = 401 см
2 м 6 дм = 260 см
1 м 2 дм 5 см = 125 см

7. Выразите в дециметрах и сантиметрах:

72 см = 7 дм 2 см
146 см = 14 дм 6 см
450 мм = 4 дм 5 см
8 м 40 мм = 80 дм 4 см

Упражнения

44. Запишите все отрезки, изображённые на рисунке 15.

а) AB, BC, AC, BK

б) OP, PR, RT, PT, TO, OR

в) AE, AC, AD, EC, ED, CD

г) MN, NE, NP, EP, PQ, QE, QM, EM

45. Запишите все отрезки, изображённые на рисунке 16.

а) BO, BD, OD, CO, CA, OA, AD

б) FK, FE, KE, EN, ES, NS, MK, MN, MP, KN, KP, NP

46. Отметьте в тетради точки А, В, С, D и соедините их попарно отрезками. Сколько отрезков образовалось? Сколько образовалось отрезков с концом в точке A?

Образовалось 6 отрезков с концами в данных точках: AB, AC, AD, BC, BD, CD.
Образовалось 3 отрезка с концом в точке А: AB, AC, AD.

Комментарий: новую точку на чертеже, образованную пересечением отрезков AC и BD мы не учитываем, поскольку о ней не говорится в задании.

Для того, чтобы образование 6 отрезков выглядело более наглядно, можно расположить заданные точки в следующем порядке:

Такое решение задания также является правильным.

47. Начертите отрезки MN и АС так, чтобы MN = 6 см 3 мм, АС = 5 см 4 мм.

48. Начертите отрезки EF и ВК так, чтобы EF = 9 см 2 мм, ВК = 7 см 6 мм.

49. Начертите отрезок АВ, длина которого равна 8 см 9 мм. Отметьте на нём точку С так, чтобы СВ = 3 см 4 мм. Какова длина отрезка АС?

50. Начертите отрезок ТР, длина которого равна 7 см 8 мм. Отметьте на нём точку Е так, чтобы ТЕ = 2 см 6 мм. Какова длина отрезка ЕР?

TP — TE = 7 см 8 мм — 2 см 6 мм = 5 см 2 мм

Ответ: 5 см 2 мм.

51. Сравните на глаз отрезки АВ и CD (рис. 17). Проверьте свой вывод измерением.

Глядя на рисунок 17 кажется, что отрезок CD > AB.

Проверим вывод измерением:

Отрезок CD = AB

Ответ: эти отрезки равны.

52. Назовите все ломаные, изображённые на рисунке 11. Какая из них имеет наибольшее количество звеньев?

На рисунке 11 можно выделить 5 ломаных:

BAC — 2 звена
BADE — 3 звена
ADE — 2 звена
CADE — 3 звена
CAD — 2 звена

Значит наибольшее количество звеньев имеют ломанные BADE и CADE.

53. Назовите звенья ломаной, изображённой на рисунке 18, и измерьте их длины (в миллиметрах). Вычислите длину ломаной.

Назовём звенья ломанной и измерим их длину:

AB = 19 мм
BE = 18 мм
EK = 16 мм
KP = 11 мм
PR = 12 мм

Для того, чтобы вычислить длину ломаной надо сложить длины всех звеньев:

AB + BE + EK + KP + PR = 19 + 18 + 16 + 11 + 12 = 76 (мм) — длина ломаной ABEKPR

Ответ: длина ломаной 76 мм.

54. Запишите звенья ломаной, изображённой на рисунке 19, и измерьте их длины (в миллиметрах). Вычислите длину ломаной.

Назовём звенья ломанной и измерим их длину:

ST = 27 мм
TK = 13 мм

KM = 11 мм
MD = 11 мм
DO = 12 мм
OF = 13 мм

Для того, чтобы вычислить длину ломаной надо сложить длины всех звеньев:

ST + TK + KM + MD + DO + OF = 27 + 13 + 11 + 11 + 12 + 13= 87 (мм) — длина ломаной STKMDOF

Ответ: длина ломаной 87 мм.

55. Отметьте в узле клеток тетради точку А; точку В разместите на 4 клетки левее и на 5 клеток выше точки А; точку С — на 3 клетки правее и на 1 клетку выше точки В; точку D — на 3 клетки правее и на 3 клетки ниже точки С; точку Е — на 1 клетку правее и на 2 клетки ниже точки D. Соедините последовательно отрезками точки А, В, С, D и Е. Какая фигура образовалась? Запишите её название и укажите количество звеньев.

Образовалась фигура ломаная ABCDE. Она состоит из 4 звеньев.

56. Вычислите длину ломаной ABCDE, если АВ = 8 см, ВС = 14 см, CD = 23 см, DE = 10 см.

Для того, чтобы вычислить длину ломаной надо сложить длины всех звеньев:

AB + BC + CD + DE = 8 + 14 + 23 + 10 = 55 (см) — длина ломаной ABCDE.

Ответ: длина ломаной 55 см.

57. Вычислите длину ломаной MNKPEF, если MN= 42 мм, NK = 38 мм, КР = 19 мм, РЕ = 12 мм, ЕF = 29 мм.

Для того, чтобы вычислить длину ломаной надо сложить длины всех звеньев:

MN + NK + KP + PE + EF = 42 + 38 + 19 + 12 + 29 = 140 (мм) — длина ломаной MNKPEF.

Ответ: длина ломаной 55 см.

58. Начертите в тетради ломаную, изображённую на рисунке 20. Измерьте длины звеньев (в миллиметрах) и найдите длину ломаной.

Измерим длины звеньев ломаной:

AB = 18 мм
BC = 30 мм
CD = 36 мм

AB + BC + CD = 18 + 30 + 36 = 84 (мм) — длина ломаной ABCD

Ответ: длина ломаной 84 мм.

59. Известно, что отрезок SK в 3 раза больше отрезка RS (рис. 21). Найдите длину отрезка RK, если RS = 34 см.

1) SK = RS • 3

34 • 3 = 102 (см) — длина отрезка SK.

2) RK = RS + SK

34 + 102 = 136 (см) — длина отрезка RK.

Ответ: длина отрезка RK 136 см.

60. Известно, что отрезок DB в 5 раз меньше отрезка AD (рис. 22). Найдите длину отрезка АВ, если AD = 135 см.

1) DB = AD : 5

135 : 5 = 27 (см) — длина отрезка DB.

2) AB = AD + DB

135 + 27 = 162 (см) — длина отрезка АВ.

Ответ: длина отрезка АВ 162 см.

61. Известно, что АС = 32 см, ВС = 9 см, CD = 12 см (рис. 23). Найдите длины отрезков АВ и BD.

1) AB = AC — BC

32 — 9 = 23 (см) — длина отрезка AB.

2) BD = BC + CD

9 + 12 = 21 (см) — длина отрезка BD.

Ответ: AB = 23 см, BD = 21 см.

62. Известно, что MF= 43 см, ME = 26 см, КЕ = 18 см (рис. 24). Найдите длины отрезков МК и EF.

1) MK = ME — KE

26 — 18 = 8 (см) — длина отрезка MK.

2) EF = MF — ME

43 — 26 = 17 (см) — длина отрезка EF.

Ответ: MK = 8 см, EF = 17 см.

63. Даны две точки А и В. Сколько можно провести отрезков, соединяющих эти точки? Сколько можно провести ломаных, соединяющих эти точки?

Через две данные точки А и В можно провести один и только один отрезок, соединяющий эти точки.
Через две данные точки А и В можно провести бесконечное количество ломанных, соединяющих эти точки.

64. Начертите отрезок МК и отметьте на нём точки А и С. Запишите все образовавшиеся отрезки.

На рисунке образовались отрезки: MA, MC, MK, AC, AK, CK. Всего 6 отрезков.

65. Длина отрезка АВ равна 28 см. Точки М и К принадлежат этому отрезку, причём точка К лежит между точками М и В, AM = 12 см, ВК = 9 см. Найдите длину отрезка МК.

MK = AB — (AM + KB)

28 — (12 + 9) = 28 — 21 = 7 (см) — длина отрезка MK.

Ответ: MK = 7 см.

66. Точка С принадлежит отрезку АВ, длина отрезка АС равна 15 см, а отрезок АВ на 5 см больше отрезка АС. Чему равна длина отрезка ВС? Есть ли в условии задачи лишние данные?

BC = AB — AC.

Так как по условию задачи АВ на 5 см больше отрезка АС, то есть AB — AC = 5 см, то BC = 5 см.

Фраза «длина отрезка АС равна 15 см» является лишней в условии задачи, поскольку длина отрезка BC будет равна 5 см независимо от значения длины отрезка АС.

Ответ: 5 см, да «длина отрезка АС равна 15 см» — лишние данные.

67. Отрезки MT и FK равны (рис. 25). Сравните отрезки MF и ТК.

MT = MF + FT

FK = FT + TK

По условию MT = FK. Значит можно записать уравнение:

MF + FT = FT + TK

MF + FT — FT = TK

MF = TK

Ответ: MF = TK

68. Постройте ломаную ACDM так, чтобы АС = 15 мм, CD = 24 мм, DM = 32 мм. Вычислите длину ломаной.

ACDM = АС + CD + DM

15 + 24 + 32 = 71 (мм) — длина ломаной ACDM.

Ответ: 71 мм.

69. Постройте ломаную CEFK так, чтобы звено СЕ было равно 8 мм, звено EF было на 14 мм больше звена СЕ, а звено FK — на 7 мм меньше звена EF. Вычислите длину ломаной.

СE = 8 мм

EF = 8 + 14 = 22 мм

FK = 22 — 7 = 15 мм

CEFK = CE + EF + FK

8 + 22 + 15 = 45 (мм) — длина ломаной CEFK.

Ответ: 45 мм.

70. Вычислите длину ломаной, изображённой на рисунке 26.

Разделим ломаные на единичные отрезки равные заданному и посчитаем их количество.

а) ломаную можно разделить на 25 отрезков, равных заданному. Длина заданного отрезка 5 мм, значит длина ломаной: 5 • 25 = 125 мм.
б) ломаную можно разделить на 21 отрезок, равных заданному. Длина заданного отрезка 4 мм, значит длина ломаной: 4 • 21 = 84 мм.
в) ломаную можно разделить на 31 отрезок, равный заданному. Длина заданного отрезка 8 мм, значит длина ломаной 8 • 31 = 248 мм.

Ответ: 125 мм, 84 мм и 248 мм.

71. Известно, что АС = 8 см, BD = 6 см, ВС = 2 см (рис. 27). Найдите длину отрезка AD.

1) AB = AC — BC

8 — 2 = 6 (см) — длина отрезка AB.

2) AD = AB + BD

6 + 6 = 12 (см) — длина отрезка AD.

Ответ: AD = 12 см.

72. Известно, что MF= 30 см, ME = 18 см, KF = 22 см (рис. 28). Найдите длину отрезка КЕ.

1) EF = MF — ME

30 — 18 = 12 (см) — длина отрезка EF.

2) KE = KF — EF

22 — 12 = 10 (см) — длина отрезка KE.

Ответ: KE = 10 см.

73. Известно, что KP = PE = EF= FT = 2 см (рис. 29). Какие ещё равные отрезки есть на этом рисунке? Найдите их длины.

На рисунке 29 можно найти следующие равные отрезки:

KE = PF = ET = 4

KF = PT = 6

74. На первом отрезке отметили семь точек так, что расстояние между любыми соседними точками равно 3 см, а на втором — десять точек так, что расстояние между любыми соседними точками равно 2 см. Расстояние между какими крайними точками больше: лежащими на первом отрезке или лежащими на втором отрезке?

Если на отрезке отметить семь точек на равном расстоянии, то получится 6 равных отрезков. Это значит, что на первом отрезке будет отмечено 6 отрезков по 3 см, а длина первого отрезка будет равна: 3 • 6 = 18 см.
Если на отрезке отметить десять точек на равном расстоянии, то получится 9 равных отрезков. Это значит, что на втором отрезке будет отмечено 9 отрезков по 2 см, а длина второго отрезка будет равна: 2 • 6 = 18 см.

Это значит, что расстояние между крайними точками у первого и второго отрезка будет одинаковым.

Проверим вывод графически:

75. Известно, что АЕ = 12 см, AQ = QB, ВМ = MС, СК = KD, DR = RE, МК = 4 см (рис. 30). Найдите длину отрезка QR.

Для удобства обозначим равные отрезки отдельными цветами.

1) Известно, что МК = 4 см.

МК = MС + СК = 4 см

2) Известно, что ВМ = MС и KD = СК . Значит:

ВМ + KD = MС + СК = 4 см

3) ВD = ВМ + MС + KD + СК = (ВМ + KD) + (MС + СК) = 4 + 4 = 8 см

4) Мы знаем, что АЕ = 12 см, ВD = 8 см.

AQ + QB + DR + RE = АЕ — ВD = 12 — 8 = 4 см

5) Известно, что AQ = QB и DR = RE. Значит:

AQ + RE = QB + DR = 4 : 2 = 2 см

6) QR = АЕ — (AQ + RE) = 12 — 2 = 10 см

Ответ: QR = 10 см.

76. Какое наименьшее количество точек надо отметить на отрезках, изображённых на рисунке 31, чтобы на каждом из них были две отмеченные точки, не считая концов отрезков?

а) Надо отметить 4 точки: две на отрезке AB (например E и F) и две на отрезке CD (например H и G).

б) Надо отметить 3 точки: точку пересечения отрезков CD и AB (точка O) и по одной точке на отрезке CD (например точку S) и на отрезке AB (например P).

в) Надо отметить 4 точки: точку пересечения отрезков EF, AB и CD (точка M), а также по одной точке на отрезке EF (например G), отрезке AB (например точку L) и отрезке CD (например K).

г) Надо отметить 3 точки: точку пересечения отрезков DC и FE (точка W), точку пересечения отрезков AB и FE (точка V) и точку пересечения отрезков AB и DC (точка Z).

77. У Миши есть линейка, на которой отмечены только 0 см, 5 см и 13 см (рис. 32). Как, пользуясь этой линейкой, он может построить отрезок длиной:

1) 3 см — Миша должен начертить отрезок 13 см, а потом от одной из конечных точек два раза отмерить по 5 см:

13 — 5 • 2 = 13 — 10 = 3 (см)

2) 2 см — Миша должен три раза отмерить отрезки по 5 см, а потом вычесть из полученного большого отрезка отрезок 13 см:

5 • 3 — 13 = 15 — 13 = 2 (см)

3) 1 см — Миша должен два раза отмерить отрезки по 13 см, а потом из полученного большого отрезка вычесть пять раз по 5 см:

13 • 2 — 5 • 5 = 26 — 25 = 1 (см)

Упражнения для повторения

78. Вычислите:

79. Выполните действия:

80. Детскому саду подарили четыре ящика конфет по 5 кг в каждом и шесть ящиков печенья по 3 кг в каждом. На сколько килограммов больше подарили конфет, чем печенья?

1) 5 • 4 = 20 (кг) — конфет подарили.

2) 3 • 6 = 18 (кг) — печенья подарили.

3) 20 — 18 = 2 (кг) — конфет больше, чем печенья.

Ответ: конфет подарили больше на 2 кг.

81. Медведица Настасья Петровна заготовила на зиму 7 бочонков мёда по 12 кг в каждом и 8 бочонков мёда по 10 кг в каждом. Сколько всего килограммов мёда заготовила Настасья Петровна?

1) 12 • 7 = 84 (кг) — мёда в 12-ти килограммовых бочонках.

2) 10 • 8 = 80 (кг) — мёда в 10-ти килограммовых бочонках.

3) 84 + 80 = 164 (кг) — мёда заготовила Настасья Петровна.

Ответ: 164 кг.

82. В магазин привезли 240 кг бананов и 156 кг апельсинов. Треть привезённых фруктов продали в первый день, а остальные — во второй день. Сколько килограммов фруктов продали во второй день?

1) 240 + 156 = 396 (кг) — фруктов завезли.

2) 396 : 3 = 132 (кг) — фруктов продали в 1 день.

3) 396 — 132 = 264 (кг) — фруктов продали во 2 день.

Ответ: 264 кг.

83. Кот Матроскин вырастил в своём саду 246 кг яблок и 354 кг груш. Шестую часть всех фруктов он отдал своим друзьям из детского сада, пятую часть всех фруктов — друзьям из школы, а остальное — в больницу. Сколько килограммов фруктов Матроскин отдал в больницу?

1) 246 + 354 = 600 (кг) — фруктов вырастил Кот Матроскин.

2) 600 : 6 = 100 (кг) — фруктов отдал в детский сад.

3) 600 : 5 = 120 (кг) — фруктов отдал в школу.

4) 600 — (100 + 120) = 600 — 220 = 380 (кг) — фруктов отдал в больницу.

Ответ: 380 кг.

Задача от мудрой совы

84. Укажите наименьшее натуральное число, сумма цифр которого равна 101.

Для того, чтобы в искомом натуральном числе было наименьшее количество цифр найдём максимальное количество цифр 9 (самая большая цифра), которые мы сможем использовать:

99 : 9 = 11 — девяток можно использовать.

Далее найдём оставшуюся цифру, необходимую для того, чтобы сумма цифр искомого числа равнялась 101:

101 — 9 • 11 = 101 — 99 = 2 — оставшаяся цифра искомого числа.

Это значит, что в искомом натуральном числе одна цифра 2 и одиннадцать цифр 9. Теперь расположим цифры так, чтобы натуральное число было наименьшим.

299 999 999 999 — на место сотен миллиардов поставим самую маленькую цифру.

Ответ: 299 999 999 999.

Мерзляк. Учебник 5 класс. Страница 22

Страница 22

59. Известно, что отрезок SK в 3 раза больше отрезка RS (рис. 21). Найдите длину отрезка RK, если RS = 34 см.

Решение:

1) SK = RS • 3 = 34 • 3 = 102 (см)

2) RK = RS + SK = 34 + 102 = 136 (см)

Ответ: длина отрезка RK 136 см.

60. Известно, что отрезок DB в 5 раз меньше отрезка AD (рис. 22). Найдите длину отрезка АВ, если AD = 135 см.

Решение:

1) DB = AD : 5 = 135 : 5 = 27 (см)

2) AB = AD + DB = 135 + 27 = 162 (см)

Ответ: длина отрезка АВ 162 см.

61. Известно, что АС = 32 см, ВС = 9 см, CD = 12 см (рис. 23). Найдите длины отрезков АВ и BD.

Решение:

1) AB = AC – BC = 32 – 9 = 23 (см)

2) BD = BC + CD = 9 + 12 = 21 (см)

Ответ: AB = 23 см, BD = 21 см.

62. Известно, что MF= 43 см, ME = 26 см, КЕ = 18 см (рис. 24). Найдите длины отрезков МК и EF.

Решение:

1) MK = ME – KE = 26 – 18 = 8 (см)

2) EF = MF – ME = 43 – 26 = 17 (см)

Ответ: MK = 8 см, EF = 17 см.

Решение:

Через две данные точки А и В можно провести только один отрезок, соединяющий эти точки.

Через две данные точки А и В можно провести бесконечное количество ломанных, соединяющих эти точки.

64. Начертите отрезок МК и отметьте на нём точки А и С. Запишите все образовавшиеся отрезки.

Хотите сказать спасибо? Подпишитесь на нашу группу вк!

тесты по теме четырехугольники

ПРЯМОУГОЛЬНИК

1. Чему равны стороны прямоугольника, если его периметр 16 см, а площадь 15 см².

A) 3 см, 5 см B) 4 см, 5 см C) 5 см, 6 см D) 4 см, 8 см E) 6 см, 3 см

2. В четырехугольник АВСD вписана окружность. Известно, что АВ=15 см, ВС=21 см, СD=18 см. Какое из следующих утверждений верно?

A) Длина стороны АD равна 12 см. B) Сторона АD короче СD, но длиннее АВ.

C) Сторона АD длиннее СD. D) Сторона АD короче ВС, но длиннее СD.

E) Длина стороны АD равна 14 см.

3. Найти площадь четырехугольника ABCD, если AB = 5, BC = 13, CD = 9,

AD = 15, AC = 12.

A) 98 B) 104C) 108D) 84E) 88

4. MNPQ — прямоугольник, NP = 5 см, MP = 12 см, О- точка пересечения диагоналей. Найдите периметр треугольника NOP.

A) 17 см. B) 16 см. C) 29 см. D) 7 см. E) 23 см.

5. Периметр прямоугольника 20 см, а его площадь 24 см². Найдите длины сторон прямоугольника.

A) 4 и 5 см B) 8 и 3 см C) 6 и 4 см D) 7 и 3 см E) 8 и 2 см

6. Чему равны стороны прямоугольника, если они относятся как 2:3, а ее площадь 24 см².

A) 4 см, 5 см. B) 4 см, 6 см. C) 3 см, 8 см. D) 8 см, 12 см. E) 6 см, 9 см.

7. Периметр прямоугольника 44 см, а его ширина равна 4 см. Найдите площадь прямоугольника.

A) 128 см²B)88 см²C)72 см²D) 160 см²

8. Одна из сторон прямоугольника на 5 см больше другой. Найдите стороны прямоугольника, если его площадь равна 14 см².

A) 14 см и 1 см. B) 2 см и 7 см. C) 12 см и 5 см. D) 3,5 см и 4 см. E) 8 см и 3 см.

9. Найдите площадь прямоугольника, если его длина равна 9,6 см, а ширина равна 3,8 см.

A) 116,544 см²B) 55,68 см²C) 128,64 см²D) 36,48 см²E) 50,92 см²

10. Периметры двух подобных четырехугольников относятся как 2 : 3. Найдите отношение их площадей.

A) : . B) 6 : 8. C) 2 : 3. D) : . E) 4 : 9.

КВАДРАТ

1. Дан квадрат со стороной 1 м, а диагональ его равна стороне другого квадрата.

Найдите диагональ последнего.

A) B) C) D) E)

2.Найдите сторону квадрата, если его площадь равна 144 см².

A) 12 см B) 24 см C) 72 см D) 18 см E) 36 см

3. Периметр квадрата равен 32 см. Чему равна сторона квадрата?

A) 16 см. B) 6 см. C) 12 см. D) 8 см. E) 10 см.

4.ABCDквадрат. Найти углы треугольника ABC.

A) 30, 60, 90 B) 120, 30, 30

C) 35, 35, 110 D) 60, 60, 60

E) 45, 45, 90

5. Площадь квадрата 49 см². Чему равна диагональ квадрата.

A) 14 см. B) 7см. C) 15 см. D) 7см. E) 7 см.

6.Диагональ квадрата равна 4 м. Сторона его равна диагонали другого квадрата. Найдите сторону последнего.

A) B) C) D) E)

7. АВСD и DСМК — квадраты. АВ = 10 см. О и Р — точки пересечения диагоналей квадратов АВСD и DСМК соответственно. Найдите площадь четырехугольника ОСРD.

A) 10 см². B) 25см². C) 50 см². D) 100 см². E) 25 см².

8. Сторона квадрата равна 3 см. Чему равен периметр квадрата?

A) 12 см. B) 10 см. C) 11 см. D) 9 см. E) 13 см.

9.Найдите площадь квадрата со стороной см.

A)4 см²B) см²C)3 см²D) см²E) см²

ТРАПЕЦИЯ

1. В равнобедренной трапеции основания равны 10 и 24, боковая сторона 25. Найдите высоту трапеции.

A) 22. B) 24. C) 20. D) 28. E) 26

2. В трапеции основания равны 5 и 15, а диагонали 12 и 16. Найдите площадь трапеции.

A) 96. B) 72. C) 84. D) 120. E) 108.

3. В равнобокой трапеции высота, проведенная из вершины тупого угла, делит большее основание на отрезки 6 см и 30 см. Найдите основания трапеции.

A) 26 см и 34 см. B) 12 см и 24 см. C) 24 см и 36 см. D) 41 см и 20 см. E) 22 и 32 см.

4. Диагонали трапеции АВСD с основаниями AD и ВС, пересекаются в точке О. Найдите площадь треугольника АОD, если площадь треугольника ВОС равна 75 см², AD=9 см, ВС=15 см.

A) 27 см². B) 45 см². C) 75 см². D) 111 см². E) 36 см².

5. Высота и диагональ равнобедренной трапеции равны соответственно 5 и 13. Найти площадь трапеции.

A) 65. B) 66. C) 62. D) 64. E) 60.

6. Найти среднюю линию равнобедренной трапеции с высотой h, если боковая сторона видна из центра описанной окружности под углом 120^○.

A). B) . C) . D) . E) .

7. Прямоугольная трапеция NРКМ (MN  KP и N = 90) вращается вокруг оси, содержащей сторону КР. Найдите объем фигуры вращения, если КР = 2 см, диагональ МР = 6 см и МРК = 60.

A) 42 см³. B) 48 см³. C) 36 см³. D) 72 см³. E) 54 см³

РОМБ

1. Периметр ромба равен 15 см. Найдите сторону ромба.

A) 3,25 см. B) 3,5 см. C) 7,5 см. D) 3,75 см. E) 5 см.

2. Диагонали ромба равны 12 см и 16 см. Найти его сторону.

A) 2 см B) 2см C) 4 см D) 4 см E) 10 см

3. Диагонали ромба равны 24 и 70. Найдите сторону ромба.

A) 45. B) 35. C) 44. D) 42. E) 37.

4. Найдите тупой угол ромба, если диагональ, проведенная из острого угла, образует с его стороной угол в 40.

A) 160. B) 120. C) 140. D) 280. E) 100.

5. Определить вид четырехугольника с вершинами A(1; 1; 1), B(2; 3; 4), C(0; 4; 4) и D(-1; 2; 1).

A) трапеция B) прямоугольник C) квадрат D) ромб E) параллелограмм

6. Диагонали ромба равны 12 см и 16 см. Найти его сторону.

A) 2 см B) 2 см C) 4 см D) 10 см E) 4см

7. Вычислите периметр ромба, длина меньшей диагонали которого 8 см, а один из углов равен 60.

A) 64 см. B) 54 см. C) 36 см. D) 32 см. E) 42 см.

8. Диагонали ромба равны 24 и 70. Найдите сторону ромба.

A) 35.B) 45.C) 44.D) 37.E) 42.

Многовариантное контрольная работа (50 вар с ответами) для 7 класса по ГЕОМЕТРИИ на тему «Начальные геометрические сведения. Прямые и отрезки»

Ответы.

Вар 2. 1) 8,39; 2)21,9; 3)96; 4)A; 5)2,4
Вар 4. 1) 9,95; 2)50,2; 3)77; 4)B; 5)4,1
Вар 6. 1) 2,24; 2)52,6; 3)63; 4)C; 5)5,2
Вар 8. 1) 17,8; 2)68,9; 3)33; 4)A; 5)3,1
Вар 10. 1) 87,7; 2)96,9; 3)32; 4)B; 5)5,2
Вар 12. 1) 83,5; 2)88,6; 3)120; 4)B; 5)4,4
Вар 14. 1) 68,2; 2)107; 3)110; 4)A; 5)3,4
Вар 16. 1) 69,6; 2)78,4; 3)24; 4)B; 5)3,9
Вар 18. 1) 6,85; 2)96; 3)132; 4)A; 5)5,9
Вар 20. 1) 99,3; 2)82,2; 3)26; 4)A; 5)3,1
Вар 22. 1) 92,6; 2)39,8; 3)22; 4)C; 5)3,1
Вар 24. 1) 42; 2)33,1; 3)143; 4)B; 5)4,5
Вар 26. 1) 65,9; 2)96,4; 3)18; 4)B; 5)4,9
Вар 28. 1) 21,9; 2)70; 3)66; 4)A; 5)2,9
Вар 30. 1) 56,7; 2)19,9; 3)20; 4)C; 5)5,6
Вар 32. 1) 52,3; 2)80,5; 3)56; 4)A; 5)5,5
Вар 34. 1) 23,5; 2)94; 3)14; 4)B; 5)5,7
Вар 36. 1) 54,4; 2)23,4; 3)96; 4)B; 5)6
Вар 38. 1) 33,7; 2)28,3; 3)143; 4)B; 5)2,7
Вар 40. 1) 8,48; 2)54; 3)30; 4)C; 5)5,2
Вар 42. 1) 4,14; 2)90,1; 3)14; 4)C; 5)5,7
Вар 44. 1) 107,8; 2)25,3; 3)14; 4)C; 5)5,3
Вар 46. 1) 4,61; 2)75,4; 3)42; 4)B; 5)4,5
Вар 48. 1) 16; 2)102,6; 3)77; 4)C; 5)5,4
Вар 50. 1) 36; 2)99,8; 3)72; 4)C; 5)2

Урок по теме «Пропорциональные отрезки в прямоугольном треугольнике» | Методическая разработка по геометрии (8 класс):

Деятельность учителя

Деятельность учащихся

Так мы с вами повторили основные формулы и понятия прошлого урока. Сегодня продолжим решать задачи на нахождение средних пропорциональных отрезков. Данный навык нам потребуется для дальнейшего изучения темы «Применение подобия к доказательству

теорем и решению задач».

Откройте тетради, запишите дату, классная работа и тему сегодняшнего урока: «Пропорциональные отрезки в прямоугольном треугольнике».

У каждого из вас на столе лежит карточка с заданиями по данной теме.

Давайте выполним первое задание:

№ 1. В прямоугольном треугольнике АВС из вершины прямого угла C проведена высота СH. AH = 16, HB = 9. Найти AC, AB, CB и CH.

Назовите и запишите, что дано и что нужно доказать. Сделайте чертеж к задаче.

Чем мы будем пользоваться для решения данной задачи?

Верно. Какой формулой будем пользоваться для нахождения высоты треугольника CH?

Чему в нашем случае равны и ?

Подставим известные значения в формулу, что получится?

Верно. Что нам еще необходимо найти?

Прежде чем найти длины сторон AC и CB, давайте определим длину стороны AB. Чему она будет равна?

Верно. Теперь можем определить длины сторон AC и CB. Какими формулами будем пользоваться для этого?

Подставим в данные формулы известные нам значения и найдем длины сторон AC и CB. Что у нас получится?

Верно. Что запишем в ответ?

№2. В прямоугольном треугольнике ABC гипотенуза BC = 20 см. Найти длину высоты AH, если CH = 15 см.

Назовите и запишите, что дано и что нужно доказать. Сделайте чертеж к задаче.

Чем мы будем пользоваться для решения данной задачи?

Что нам необходимо знать для того, чтобы найти высоту AH?

Хорошо. Как будем находить длину отрезка BH?

Верно. Мы нашли длину отрезка BH, сможем ли теперь найти высоты AH?

Что запишем в ответ?

В чем сложность решения данной задачи? Чем она отличается от предыдущей?

А теперь откройте учебник на странице 152, выполним упражнение 575.

Катеты прямоугольного треугольника относятся как 3:4, а гипотенуза равна 50 мм. Найдите отрезки, на которые гипотенуза делится высотой, проведенной из вершины прямого угла.

Назовите и запишите, что дано и что нужно доказать. Сделайте чертеж к задаче.

Что нам необходимо найти по условию задачи?

Как мы сможем их найти? Чем будем пользоваться для нахождения их длин?

Выразим из данных формул , что у нас получится?

Все ли нам известно, для нахождения отрезков AD и BD?

Рассмотрим треугольник ABC, в котором AC и BC – катеты. Что нам известно про данный треугольник?

Так как треугольник ABC – прямоугольный, то какой отсюда можно сделать вывод?

Как с помощью теоремы Пифагора можно найти длину стороны ?

Что нам известно про стороны AC и BC?

Тогда чему равны длины катетов AC и BC?

Подставим все известные нам значения в что у нас получится?

Верно. Мы нашли значение еще мы можем найти?

Чему они будут равны?

Правильно. А теперь давайте вернемся к началу решения задачи и выясним, все ли неизвестные элементы мы нашли?

Хорошо. Давайте подставим найденные значения в ранее записанные формулы и определим длины отрезков AD и BD. Что получится?

Что запишем в ответ?

Следующий №577, выполняем письменно в тетрадях.

В треугольнике, стороны которого равны 5 см, 12 см и 13 см, проведена высота к его большей стороне. Найдите отрезки, на которые высота делит эту сторону.

Назовите и запишите, что дано и что нужно доказать. Сделайте чертеж к задаче.

Как мы сможем найти AH и HB? Чем будем пользоваться для их нахождения?

Искать отрезки гипотенузы AH и HB, по ранее изученным формулам, мы можем только в том случае, когда исходный треугольник является прямоугольным.

Как нам поступить в данном случае?

Как будем проверять данный факт?

Верно. Пользуясь теоремой докажите, что треугольник ABC – прямоугольный.

Сможем ли мы теперь отыскать отрезки гипотенузы опираясь на понятие средней пропорциональной? Что у нас получится?

Верно. Что запишем в ответ?

В чем сложность решения данной задачи? Чем она отличается от предыдущей?

Открывают тетради, записывают дату, классная работа и тему урока.

Внимательно читают условие задачи. Отвечают на поставленные учителем вопросы, затем приступают к самостоятельному выполнению задания. Один ученик выполняет задание около доски.

Дано: Треугольник ABC – прямоугольный; ;

CH AB; AH = 16 см, HB = 9 см.

Найти: CH, AB, AC и CB.

Для решения данной задачи воспользуемся формулами, изученными на прошлом уроке, понятием среднего пропорционального.

Для нахождения высоты треугольника воспользуемся следующей формулой:

В данной задаче см, .

см.

Следовательно, CH = 12 см.

Необходимо найти длины сторон AB, AC и CB.

Для нахождения длины стороны AB воспользуемся формулой:

AB = 16 + 9 = 25 см.

Для этого воспользуемся следующими формулами:

Подставим известные значения и получим:

см.

Ответ: 12 см; 25 см; см и см

Внимательно изучают условие данной задачи. Приступают к самостоятельному выполнению после обсуждения, один ученик решает около доски.

Дано: Треугольник ABC – прямоугольный; BC = 20 см, BC – гипотенуза; CH = 15 см; AH – высота.

Найти: AH.

Для решения данной задачи также воспользуемся формулами, изученными на прошлом уроке, понятием среднего пропорционального.

Для нахождения высоты прямоугольного треугольника воспользуемся формулой

где см.

– неизвестно. Значит необходимо найти длину отрезка BH.

Для нахождения длины отрезка BH, выразим из следующей формулы и получим:

Сможем. Подставим в формулу известные данные и получим:

см.

Следовательно, AH = см.

Ответ: см.

Отвечают на поставленные учителем вопросы.

Открывают учебник на указанной странице и внимательно читают условие задачи.

Дано: Треугольник ABC – прямоугольный; ; AC:BC =3:4; AB = 50 мм; CD AB.

Найти: AD и BD.

Необходимо найти отрезки AD и BD.

Для нахождения отрезков AD и BD воспользуемся следующими формулами:

Выразим из данных формул , получим:

;

Нет, не все. Неизвестны длины сторон AC и BC.

Треугольник ABC – прямоугольный;

Раз он прямоугольный, то можем воспользоваться теоремой Пифагора.

По теореме Пифагора длину стороны можно найти:

;

Стороны AC:BC =3:4.

AC = 3х; BC = 4x.

Подставим известные нам значения в ранее записанное выражение и получим:

;

Теперь мы можем найти длины катетов AC и BC:

AC = мм.

BC = мм.

Мы нашли длины всех неизвестных для расчетов сторон.

Подставим известные значения в ранее записанные формулы и получим:

мм;

мм.

Ответ: 18 мм; 32 мм.

Внимательно читают условие задачи, отвечают на поставленные учителем вопросы. Затем приступают к самостоятельному выполнению. Один человек решает около доски.

Дано: ABC — треугольник; AB = 13 см; AC = 12 см; CB = 5 см;

CH AB.

Найти: AH и HB.

Ранее определяли длины отрезков гипотенузы AH и HB, помощью понятия средней пропорциональной, полученных ранее формул.

Сначала необходимо проверить, будет ли данный треугольник прямоугольным.

Воспользуемся теоремой Пифагора.

;

верно.

Сможем. Для этого воспользуемся формулами

Выразим из данных формул , получим:

;

Подставим известные значения и получим:

см;

Ответ: см; см.

Отвечают на поставленные учителем вопросы.

ОТРЕЗКИ УГЛЫ ТРЕУГОЛЬНИКИ УРОВЕНЬ А

ОТРЕЗКИ, УГЛЫ, ТРЕУГОЛЬНИКИ

УРОВЕНЬ А

1. а) Могут ли точки А, В и С быть вершинами треугольника, если АВ=34 см, АС=15 см, ВС=19 см? Ответ обоснуйте.

б) Могут ли точки А, В и С быть вершинами треугольника, если АВ=19 см, АС=40 см, ВС=22 см? Ответ обоснуйте.

2. а) Угол между прямыми а и b равен , а угол между прямыми a и c равен . Найдите угол между прямыми b и c.

б) Угол между прямыми а и b равен , а угол между прямыми a и c равен . Найдите угол между прямыми b и c.

3. а) Даны два смежных угла. Биссектриса первого из них образует угол с общей стороной этих углов. Найдите величину второго из данных смежных углов.

б) Даны два смежных угла, один из которых равен . Найдите угол между биссектрисой второго из данных углов и их общей стороной.

4. а) Найдите угол В треугольника АВС, если АВ=ВС, а внешний угол при вершине С равен .

б) Найдите внешний угол при вершине А треугольника АВС, если АС=ВС, а угол АСВ равен .

5. а) Найдите периметр равностороннего треугольника, если его средняя линия равна 7 см.

б) Найдите среднюю линию равностороннего треугольника, если его периметр равен 12 см.

6. а) В прямоугольном треугольнике один из острых углов равен . Найдите больший из углов, на которые высота, проведенная к гипотенузе, делит прямой угол.

б) В прямоугольном треугольнике высота, проведенная к гипотенузе, делит прямой угол на два угла, один из которых равен . Найдите меньший угол данного треугольника.

7. а) Прямая, параллельная стороне AB треугольника ABC, пересекает стороны AC и BC в точках M и N соответственно. Найдите AC, если CM=14 см, CN=18 см, BC=27 см.

б) Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BM, если AB=24 см, BN=21 см, BC=28 см.

8. а) Прямые, содержащие отрезки АВ и DC, параллельны, а отрезки AC и BD пересекаются в точке O. Найдите AO, если CO=36 см, DC=30 см, AB=25 см.

б) Прямые, содержащие отрезки АD и BC параллельны, а отрезки АС и BD пересекаются в точке O. Найдите BC, если AD=32 см, DO=20 см, BO=15 см.

9. а) На стороне AC треугольника ABC взята точка M, причем AM:MC=3:5. Найдите площадь треугольника ABC, если площадь треугольника ABM равна см².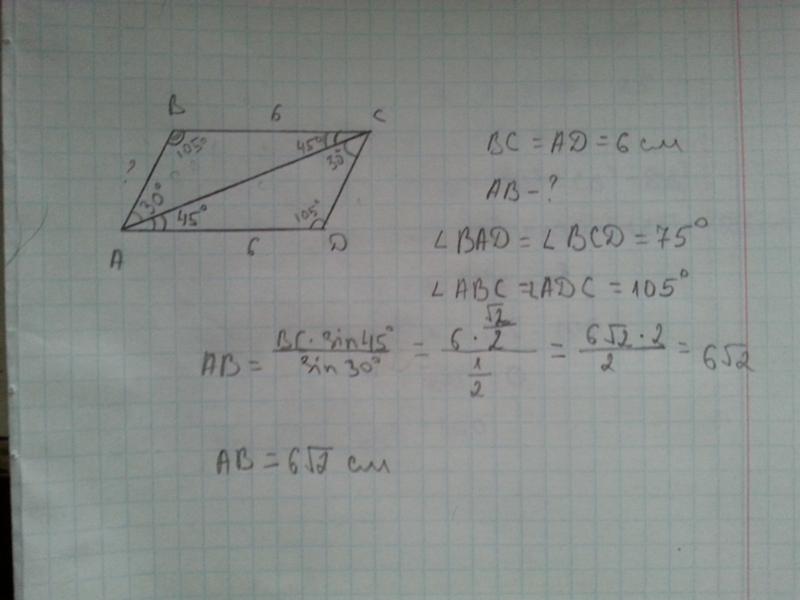

б) На стороне AC треугольника ABC взята точка M, причем AM:MC=2:7. Найдите площадь треугольника MBC, если площадь треугольника ABC равна см².

10. а) Найдите высоту равнобедренного треугольника, если его боковая сторона равна см, а основание равно см.

б) Найдите боковую сторону равнобедренного треугольника, если его высота равна см, а основание равно см.

11. а) Найдите площадь прямоугольного треугольника, если один из его катетов равен см, а гипотенуза равна см.

б) Найдите площадь прямоугольного треугольника, если один из его катетов равен см, а гипотенуза равна см.

12. а) Найдите площадь треугольника, если высота, проведенная к одной из его сторон, равна см, а средняя линия, параллельная этой стороне, равна см.

б) Найдите площадь треугольника, если высота, проведенная к одной из его сторон, равна см, а средняя линия, параллельная этой стороне, равна см.

13. а) В треугольнике АВС угол С равен , ВС= 28 см, а синус угла А равен . Найдите АВ.

б) В треугольнике АВС угол А равен равен , АС=15 см, а косинус угла С равен . Найдите ВС.

14. а) Найдите медиану прямоугольного треугольника, проведенную к гипотенузе, если гипотенуза равна см.

б) Найдите гипотенузу прямоугольного треугольника, если медиана, проведенная к гипотенузе, равна см.

15. а) В прямоугольном треугольнике, один из острых углов которого равен , гипотенуза равна см. Найдите меньший катет.

б) В прямоугольном треугольнике, один из острых углов которого равен , меньший катет равен см. Найдите гипотенузу.

УРОВЕНЬ B

1. а) Точка С принадлежит отрезку AB, причем AC:CB=5:14. Точка D принадлежит отрезку CB, причем CD:DB=3:4. Найдите отношение AD:DB.

б) Точка С принадлежит отрезку AB, причем AC:CB=10:7. Точка D принадлежит отрезку AC, причем AD:DC=2:3. Найдите отношение AD:DB.

2. а) В треугольнике АВС углы А и В равны соответственно и . Найдите угол между биссектрисой и высотой, проведенными из вершины С.

б) В треугольнике АВС углы В и С равны соответственно и . Найдите угол между биссектрисой и высотой, проведенными из вершины А.

3. а) Отрезки АВ и DС лежат на параллельных прямых, а отрезки АС и ВD пересекаются в точке М. Найдите МС, если АВ=14 см, DС=42 см, АС=56 см.

б) Отрезки АВ и DС лежат на параллельных прямых, а отрезки АС и ВD пересекаются в точке N. Найдите BN, если AB=17 см, DC=51 см, BD=64 см.

4. а) Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках К и М соответственно. Найдите АС, если ВК:КА=3:4, КМ=18 см.

б) Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках К и М соответственно. Найдите КМ, если ВК:КА=2:5, АС =21 см.

5. а) Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=18 см, AC=54 см, NC=32 см.

б) Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BC, если MN=13 см, AC=52 см, NC=36 см.

6. а) На сторонах AB и BC треугольника ABC взяты соответственно точки M и N так, что угол BMN равен углу BCA. Найдите MN, если AC=48 см, AB=42 см, BN=28 см.

б) На сторонах AB и BC треугольника ABC взяты соответственно точки M и N так, что угол BMN равен углу BCA. Найдите BN, если MN=27 см, AB=52 см, AC=36 см.

7. а) Средняя линия MN треугольника ABC отсекает от него треугольник MBN, площадь которого равна см². Найдите площадь треугольника ABC.

б) Средняя линия MN треугольника ABC отсекает от него треугольник MCN. Найдите площадь треугольника MCN, если площадь треугольника ABC равна см².

8. а) Найдите длину медианы BM треугольника ABC, если известны координаты вершин треугольника: A(2; 5), B(0; 0), C(4; 3).

б) Найдите длину медианы CP треугольника ABC, если известны координаты вершин треугольника: A(–3; –2), B(–6; 2), C(0; 0).

9. а) Стороны АВ и ВС треугольника АВС равны соответственно см и см, а высота, проведенная к стороне ВС, равна см. Найдите высоту, проведенную к стороне АВ.

б) Высоты треугольника АВС, проведенные к сторонам АВ и АС, равны соответственно см и см. Найдите АС, если АВ=24 см.

10. а) Катеты прямоугольного треугольника равны см и см. Найдите высоту, проведенную к гипотенузе.

б) Катет и гипотенуза прямоугольного треугольника равны см и см. Найдите высоту, проведенную к гипотенузе.

11. а) Точка H является основанием высоты, проведенной из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=6 см, AC=24 см.

б) Точка H является основанием высоты, проведенной из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите BH, если AH=28 см, CH=7 см.

12. а) Найдите тангенс меньшего из углов треугольника, если стороны треугольника равны см, см и см.

б) Найдите косинус меньшего из углов треугольника, если стороны треугольника равны см, см и см.

13. а) На продолжении отрезка AB за точку A выбрана точка M так, что AB:BM=5:3. Найдите координаты точки M, если известны координаты точек Aи B: A(–2; 3), B(3; 8).

б) Точка M делит отрезок AB в отношении AM:MB=3:4. Найдите координаты точки M, если известны координаты точек Aи B: A(4; 3), B(11; 10).

14. а) Углы А и В треугольника АВС равны соответственно и . Найдите АС, если ВС= см.

б) Углы В и С треугольника АВС равны соответственно и . Найдите АС, если АВ= см.

15. а) Найдите косинус меньшего из углов треугольника со сторонами см, см и см.

б) Найдите косинус большего из углов треугольника со сторонами см, см и см.

М Н О Г О У Г О Л Ь Н И К И

УРОВЕНЬ А

1. а) Один из углов параллелограмма равен . Найдите остальные его углы.

б) Один из углов параллелограмма равен . Найдите остальные его углы.

2. а) Один из углов параллелограмма на больше другого угла. Найдите эти углы.

б) Один из углов параллелограмма на меньше другого угла. Найдите эти углы.

3. а) Периметр параллелограмма равен 72 см, а одна из его сторон равна 4 см. Найдите длины остальных сторон параллелограмма.

б) Периметр параллелограмма равен 80 см, а одна из его сторон равна 8 см. Найдите длины остальных сторон параллелограмма.

4. а) Сторона параллелограмма равна 12 см, а расстояние от точки пересечения диагоналей параллелограмма до этой стороны равно 4 см. Найдите площадь параллелограмма.

б) Сторона параллелограмма равна 14 см, а расстояние от точки пересечения диагоналей параллелограмма до этой стороны равно 3 см. Найдите площадь параллелограмма.

5. а) Диагональ прямоугольника образует с одной из его сторон угол . Найдите угол между прямыми, содержащими диагонали прямоугольника.

б) Диагональ прямоугольника образует с одной из его сторон угол . Найдите угол между прямыми, содержащими диагонали прямоугольника.

6. а) Расстояния от точки пересечения диагоналей прямоугольника до двух его сторон равны 6 см и 9 см. Найдите площадь прямоугольника.

б) Расстояния от точки пересечения диагоналей прямоугольника до двух его сторон равны 8 см и 11 см. Найдите площадь прямоугольника.

7. а) Периметр ромба на 36 см больше его стороны. Найдите сторону ромба.

б) Сторона ромба на 24 см меньше его периметра. Найдите сторону ромба.

8. а) Найдите сторону ромба, если его диагонали равны 12 см и 16 см.

б) Найдите сторону ромба, если его диагонали равны 10 см и 24 см.

9. а) Угол между высотами ромба, проведенными из вершины тупого угла, равен . Найдите углы ромба.

б) Угол между высотами ромба, проведенными из вершины тупого угла, равен . Найдите углы ромба.

10. а) Найдите диагональ квадрата, если его площадь равна 288 см².

б) Найдите площадь квадрата, если его диагональ равна 14 см.

11. а) Одно из оснований трапеции равно 17 см, а средняя линия равна 10 см. Найдите другое основание трапеции.

б) Одно из оснований трапеции равно 14 см, а средняя линия равна 11 см. Найдите другое основание трапеции.

12. а) Найдите высоту трапеции, если площадь трапеции равна 28 см², а сумма длин оснований равна 14 см.

б) Найдите высоту трапеции, если площадь трапеции равна 32 см², а сумма длин оснований равна 16 см.

13. а) Концы отрезка AB лежат по одну сторону от прямой l. Расстояние от точки A до прямой l равно 24 см, а расстояние от точки B до прямой lравно 62 см. Найдите расстояние от середины отрезка AB до прямой l.

б) Концы отрезка AB лежат по одну сторону от прямой l. Расстояние от точки A до прямой l равно 34 см, а расстояние от точки B до прямой lравно 46 см. Найдите расстояние от середины отрезка AB до прямой l.

14. а) Один из углов семиугольника равен . Найдите сумму остальных его углов.

б) Один из углов девятиугольника равен . Найдите сумму остальных его углов.

15. а) Найдите число сторон правильного многоугольника, каждый из углов которого равен .

б) Найдите число сторон правильного многоугольника, каждый из углов которого равен .

УРОВЕНЬ В

1. а) Стороны параллелограмма равны 10 см и 24 см, а одна из диагоналей равна 26 см. Найдите длину другой диагонали.

б) Стороны параллелограмма равны 15 см и 20 см, а одна из диагоналей равна 25 см. Найдите длину другой диагонали.

2. а) Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=7 см, CK=12 см.

б) Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=6 см, CK=14 см.

3. а) Биссектрисы углов A и Dпараллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC=44 см.

б) Биссектрисы углов A и Dпараллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB =24 см.

4. а) Диагонали параллелограмма равны 20 см и 22 см. Может ли одна из его сторон быть равной 21 см? Ответ обоснуйте.

б) Диагонали параллелограмма равны 24 см и 26 см. Может ли одна из его сторон быть равной 25 см? Ответ обоснуйте.

5. а) На стороне AB параллелограмма ABCD отметили точку M. Найдите площадь параллелограмма, если площадь треугольника MCD равна 38 см².

б) На стороне AD параллелограмма ABCD отметили точку M. Найдите площадь треугольника MCB, если площадь параллелограмма равна 42 см².

6. а) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 15 см, а одна из диагоналей ромба равна 60 см. Найдите углы ромба.

б) Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 20 см, а одна из диагоналей ромба равна 80 см. Найдите углы ромба.

7. а) Высота AH ромба ABCD делит сторону CDна отрезки DH=8 см и CH=2 см. Найдите высоту ромба.

б) Высота AH ромба ABCD делит сторону CDна отрезки DH=6 см и CH=4 см. Найдите высоту ромба.

8. а) Расстояние от вершины квадрата до середины стороны, не содержащей эту вершину, равно 3 см. Найдите площадь квадрата.

б) Расстояние от вершины квадрата до середины стороны, не содержащей эту вершину, равно 4 см. Найдите площадь квадрата.

9. а) Найдите углы равнобедренной трапеции, если сумма двух из них равна .

б) Найдите углы равнобедренной трапеции, если сумма двух из них равна .

10. а) Одно из оснований трапеции в 17 раз меньше ее средней линии. Во сколько раз оно меньше другого основания трапеции?

б) Одно из оснований трапеции в 16 раз меньше ее средней линии. Во сколько раз оно меньше другого основания трапеции?

11. а) Основания трапеции равны 16 см и 20 см, а одна из диагоналей равна 18 см. Найдите длины отрезков на которые точка пересечения диагоналей трапеции делит эту диагональ.

б) Основания трапеции равны 12 см и 18 см, а одна из диагоналей равна 20 см. Найдите длины отрезков на которые точка пересечения диагоналей трапеции делит эту диагональ.

12. а) Основания трапеции равны 12 см и 18 см. Найдите длины отрезков, на которые диагонали трапеции делят ее среднюю линию.

б) Основания трапеции равны 10 см и 16 см. Найдите длины отрезков, на которые диагонали трапеции делят ее среднюю линию.

13. а) Концы отрезка AB лежат по разные стороны от прямой l. Расстояние от точки A до прямой l равно 12 см, а расстояние от точки B до прямой lравно 36 см. Найдите расстояние от середины отрезка AB до прямой l.

б) Концы отрезка AB лежат по разные стороны от прямой l. Расстояние от точки A до прямой l равно 24 см, а расстояние от точки B до прямой lравно 30 см. Найдите расстояние от середины отрезка AB до прямой l.

14. а) Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24 см,BF=10 см.

б) Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24 см,BF=18 см.

15. а) Расстояния от середины стороны AD выпуклого четырехугольника ABCD до середин сторон AB и CD равны соответственно 6 см и 12 см. Найдите длины диагоналей четырехугольника ABCD.

б) Расстояния от середины стороны AD выпуклого четырехугольника ABCD до середин сторон AB и CD равны соответственно 8 см и 14 см. Найдите длины диагоналей четырехугольника ABCD.

О К Р У Ж Н О С Т И

УРОВЕНЬ А

1. а) Длина окружности равна см. Найдите площадь круга, ограниченного этой окружностью.

б) Длина окружности равна см. Найдите площадь круга, ограниченного этой окружностью.

2. а) Сравните площадь круга, радиус которого равен 8 см, и площадь прямоугольника со сторонами 12 см и 16 см.

б) Сравните площадь круга, радиус которого равен 6 см, и площадь прямоугольника со сторонами 8 см и 18 см.

3. а) Хорды AB иCD окружности пересекаются в точкеM. Найдите MA, еслиMB=8 см,MC=6 см, MD=4 см.

б) Хорды AB иCD окружности пересекаются в точкеM. Найдите MA, еслиMB=3 см,MC=4 см, MD=9 см.

4. а) Окружность с центром О касается сторон угла с вершиной А в точках В и С. Найдите угол ВАС, если угол ВОС равен .

б) Окружность с центром О касается сторон угла с вершиной А в точках В и С. Найдите угол ВОС, если угол ВАС равен .

5. а) Точки А и В делят окружность на две дуги, длины которых относятся как . Найдите величину центрального угла, опирающегося на меньшую из дуг.

б) Точки А и В делят окружность на две дуги, длины которых относятся как . Найдите величину центрального угла, опирающегося на меньшую из дуг.

6. а) Радиус окружности равен 15 см. Найдите расстояние от центра окружности до хорды, длина которой равна 18 см.

б) Расстояние от центра окружности, радиус которой равен 20 см, до ее хорды равно 16 см. Найдите длину хорды.

7. а) Отрезок АВ является хордой окружности с центром O. Найдите угол между прямой АВ и касательной к окружности, проходящей через точку А, если угол АОВ равен .

б) Отрезок АВ является хордой окружности с центром O. Найдите угол АОВ, если угол между прямой АВ и касательной к окружности, проходящей через точку А, равен .

8. а) Отрезки АВ и BC являются соответственно диаметром и хордой окружности с центром О. Найдите угол AОC, если угол ОCВ равен .

б) Отрезки АВ и BC являются соответственно диаметром и хордой окружности с центром О. Найдите угол ОCВ, если угол AОC равен .

9. а) Окружность, вписанная в треугольник ABC, касается сторон AB, BC и AC в точках M, K и P соответственно. Найдите периметр треугольника ABC, если AР=4 см, BМ=6 см,CК=3 см.

б) Окружность, вписанная в треугольник ABC, касается сторон AB, BC и AC в точках M, K и P соответственно. Найдите периметр треугольника ABC, если AM=5 см, BK=2 см,CP=4 см.

10. а) Найдите диаметр окружности, описанной около прямоугольного треугольника, если синус одного из углов треугольника равен , а противолежащий этому углу катет равен 15 см.

б) Найдите диаметр окружности, описанной около прямоугольного треугольника, если косинус одного из углов треугольника равен , а прилежащий к этому углу катет равен 16 см.

11. а) Найдите радиус окружности, вписанной в треугольник, если один из углов треугольника равен , а расстояние от центра окружности до вершины этого угла равно 18 см.

б) Найдите радиус окружности, вписанной в треугольник, если один из углов треугольника равен , а расстояние от центра окружности до вершины этого угла равно 26 см.

12. а) Найдите радиус окружности, описанной около треугольника, если одна из сторон треугольника равна 20 см, а расстояние от центра окружности до этой стороны равно 24 см.

б) Найдите радиус окружности, описанной около треугольника, если одна из сторон треугольника равна 24 см, а расстояние от центра окружности до этой стороны равно 5 см.

13. а) Найдите радиус окружности, описанной около равностороннего треугольника, если радиус окружности, вписанной в этот треугольник, равен 42 см.

б) Найдите радиус окружности, вписанной в равносторонний треугольник, если радиус окружности, описанной около этого треугольника, равен 36 см.

14. а) В квадрат вписана окружность. Найдите радиус окружности, если диагональ квадрата равна см.

б) Около квадрата описана окружность. Найдите радиус окружности, если сторона квадрата равна см.

15. а) Найдите радиус окружности, описанной около правильного шестиугольника, если радиус окружности, вписанной в этот шестиугольник, равен 18 см.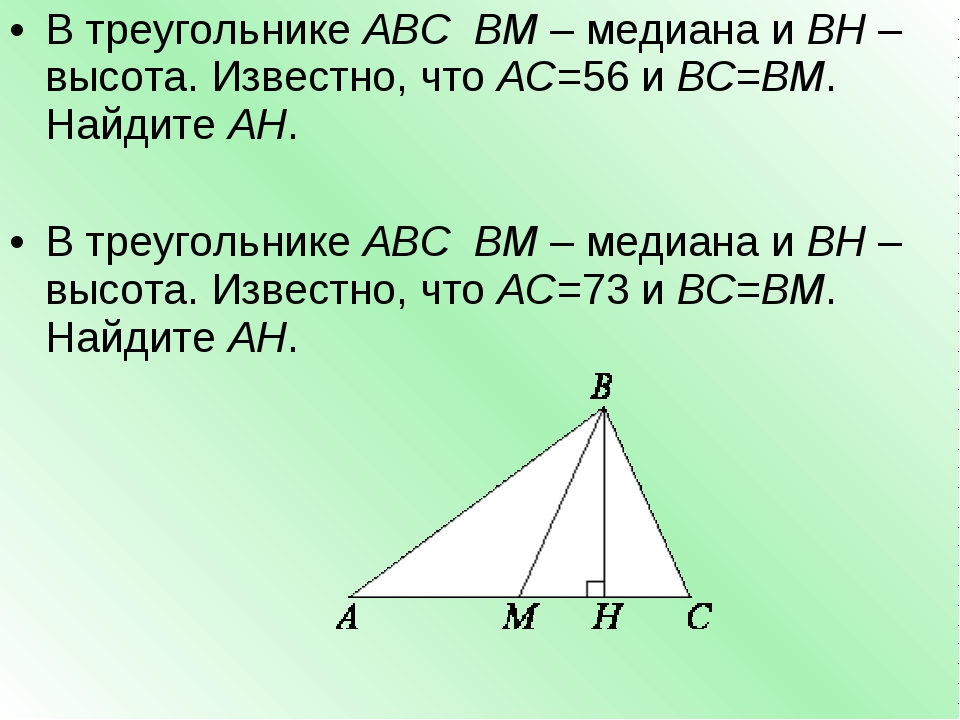

б) Найдите радиус окружности, вписанной в правильный шестиугольник, если радиус окружности, описанной около этого шестиугольника, равен 12 см.

УРОВЕНЬ В

1. а) Одна из сторон треугольника равна 24 см. Может ли радиус окружности, описанной около этого треугольника быть равным 11 см? Ответ обоснуйте.

б) Радиус окружности, описанной около треугольника равен 17 см. Может ли какая-либо из сторон этого треугольника быть равной 35 см? Ответ обоснуйте.

2. а) Отрезки АВ и CD являются хордами окружности. Найдите длину хорды CD, если АВ=10 см, а расстояния от центра окружности до хорд АВ и CD равны соответственно 12 см и 5 см.

б) Отрезки АВ и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если АВ=12 см, CD=16 см, а расстояние от центра окружности до хорды АВ равно 8 см.

3. а) Отрезки АВ и ВС являются хордами окружности с центром О. Найдите угол АСВ, если угол АВО равен .

б) Отрезки АВ и ВС являются хордами окружности с центром О. Найдите угол АСВ, если угол АВО равен .

4. а) В окружность вписан четырехугольник ABCD. Найдите угол ACD, если углы BAD и ADB равны соответственно и .

б) В окружность вписан четырехугольник ABCD. Найдите угол BAD, если углы ACD и ADB равны соответственно и .

5. а) Окружность с центром О касается сторон угла с вершиной А, величина которого равна , в точках В и С. Найдите углы треугольника ВОС.

б) Окружность с центром О касается сторон угла с вершиной А в точках В и С. Найдите углы треугольника ABC, если угол ВОС равен .

6. а) На окружности последовательно отмечены восемь точек A₁,_{A₂,_{A₃, …,A₈, делящие окружность на равные дуги. Найдите величину угла A₁A₇A₃.}}

б) На окружности последовательно отмечены девять точек A₁,_{A₂,_{A₃, …,A₉, делящие окружность на равные дуги. Найдите величину угла A₂A₉A₅.}}

7. а) Концы пересекающихся хорд ABи CD делят длину окружности в отношении AC:CB:BD:DA=2:3:5:10. Найдите величину угла между прямыми ABи CD.

б) Концы пересекающихся хорд ABи CD делят длину окружности в отношении AC:CB:BD:DA=3:5:2:4. Найдите величину угла между прямыми ABи CD.

8. а) На окружности последовательно отмечены точки A,B, C иD, которые делят длину окружности в отношении AB:BC:CD:DA=3:4:5:6. Найдите величину угла между прямыми ABи CD.

б) На окружности последовательно отмечены точки A,B, C иD, которые делят длину окружности в отношении AB:BC:CD:DA=6:5:4:3. Найдите величину угла между прямыми ABи CD.

9. а) Отрезки АВ и АC являются хордами окружности с центром О. Найдите угол ВАC, если известно, что он является острым и что углы АВО и АCО равны соответственно и .

б) Отрезки АВ и АC являются хордами окружности с центром О. Найдите угол ВОC, если известно, что он меньше развернутого и что углы АВО и АCО равны соответственно и .

10. а) Вершина А выпуклого четырехугольника ABCD является центром окружности, проходящей через точки B,C иD. Найдите угол ВАD, если углы АВC и АDC равны соответственно и .

б) Вершина А выпуклого четырехугольника ABCD является центром окружности, проходящей через точки B,C иD. Найдите угол ВАD, если углы АВC и АDC равны соответственно и .

11. а) Биссектриса угла А треугольника ABC пересекает описанную около этого треугольника окружность в точке M. Найдите BM, если CM=14 см.

б) Биссектриса угла А треугольника ABC пересекает описанную около этого треугольника окружность в точке M. Найдите CM, если BM=12 см.

12. а) Радиус окружности, описанной около равнобедренного треугольника, равен 5 см, а высота, проведенная к основанию, равна 8 см. Найдите площадь треугольника.

б) Радиус окружности, описанной около равнобедренного треугольника, равен 10 см, а основание треугольника равно 12 см. Найдите площадь треугольника.

13. а) Найдите площадь прямоугольной трапеции, боковые стороны которой равны 10 см и 16 см, если известно, что в эту трапецию можно вписать окружность.

б) Найдите площадь прямоугольной трапеции, боковые стороны которой равны 12 см и 18 см, если известно, что в эту трапецию можно вписать окружность.

14. а) В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 5 см.

б) Около параллелограмма, одна из диагоналей которого равна 7 см, описана окружность. Найдите вторую диагональ параллелограмма.

15. а) В трапецию, сумма длин боковых сторон которой равна 16 см, вписана окружность.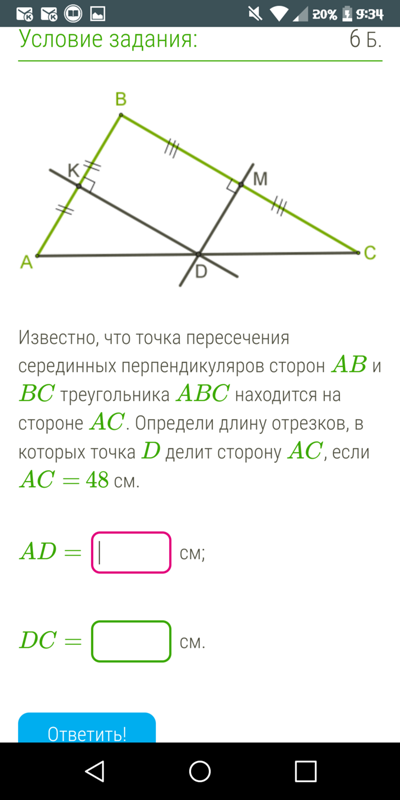 Найдите среднюю линию трапеции.

б) Около трапеции, один из углов которой равен , описана окружность. Найдите остальные углы трапеции.

[PDF] Document — Free Download PDF

Download Document…

ПРЕЗЕНТАЦИЯ НА ТЕМУ « РАВЕНСТВО ТРЕУГОЛЬНИКОВ»
ЛЕНЬШИНА АЛИНА 9 «А»
ТРЕУГОЛЬНИК —
геометрическая фигура, состоит из 3х точек не лежащих на 1ой прямой, и 3х отрезков, попарно соединяющих эти точки.
ABC
НАЗВАНИЯ
BCA вершина
CBA
МОЖНО ЛИ СЧИТАТЬ ТРЕУГОЛЬНИКОМ:
сторона 1)
2)
ТРЕУГОЛЬНИКИ НАЗЫВАЮТСЯ РАВНЫМИ, ЕСЛИ У НИХ СООТВЕТСТВУЮЩИЕ СТОРОНЫ РАВНЫ И СООТВЕТСТВУЮЩИЕ УГЛЫ РАВНЫ. ПРИ ЭТОМ СООТВЕТСТВУЮЩИЕ УГЛЫ ДОЛЖНЫ ЛЕЖАТЬ ПРОТИВ СООТВЕТСТВУЮЩИХ СТОРОН
ABC = АВС = ВСА = САВ =
КМО ,ТО
КМО МОК ОКМ
АВ ВС СА
= КМ = МО = ОК
ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ
(ПРИЗНАК ПО СТОРОНАМ И УГЛУ МЕЖДУ НИМИ)
ЕСЛИ ДВЕ СТОРОНЫ И УГОЛ МЕЖДУ НИМИ ОДНОГО ТРЕУГОЛЬНИКА РАВНЫ СООТВЕТСТВЕННО ДВУМ СТОРОНАМ И УГЛУ МЕЖДУ НИМИ ДРУГОГО ТРЕУГОЛЬНИКА, ТО ТАКИЕ ТРЕУГОЛЬНИКИ РАВНЫ
ДАНО: АВС и А1В1С1 АВ=А1В1 АС=А1С1 LА=LА1
1.
ДОКАЗАТЕЛЬСТВО: С С1 С2
ПУСТЬ у треугольников
АВС и А1В1С1 АВ=А1В1 АС=А1С1 LА= LА1 ДОКАЖЕМ,ЧТО В2 ТРЕУГОЛЬНИКИ РАВНЫ
А1 В ДОКАЗАТЬ: А В1 АВС= 2. ПУСТЬ А1В2С2 = АВС, с вершиной В2 на луче А1В1 и А1В1С1 вершиной С2 в той же полуплоскости относительно прямой А1В1, где лежит вершина С1
А) АВ=А1В1 (ПО УСЛОВИЮ)
Вершина В2 СОВПАДЕТ С В1
АВ = А1В2 (2) Б) LВАС=LВ1А1С1 ВАС=LВ2А1С2 В) АС=А1С1 АС=А1С2
(ПО УСЛОВИЮ)
(2)
(ПО УСЛОВИЮ) (2)
=> А1В1=А1В2
=> LВА1С1= LВ2А1С2
Луч А1С2 совпадет с лучем А1С1
=> LВ1А1С1= LВ2А1С2
Вершина С2 совпадет с С1 ИТАК, А1В1С1 СОВПАДАЕТ С А1В2С2 ЗНАЧИТ А1В1С1 = АВС. (ТЕОРЕМА ДОКАЗАНА)
ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ (ПРИЗНАК ПО СТОРОНЕ И ПРИЛЕЖАЩИМ К НЕЙ УГЛАМ)
ЕСЛИ СТОРОНА И ПРИЛЕЖАЩИЕ К НЕЙ УГЛЫОДНОГО ТРЕУГОЛЬНИКА РАВНЫ СООТВЕТСТВЕННО СТОРОНЕ И ПРИЛЕЖАЩИМ К НЕЙ УГЛАМ ДРУГОГО ТРЕУГОЛЬНИКА, ТО ТАКИЕ ТРЕУГОЛЬНИКИ РАВНЫ.
ДАНО: АВС и А1В1С1 АB=А1B1 LА=LА1 L B=LB1
1. А
ДОКАЗАТЕЛЬСТВО: С1 С2 С
ПУСТЬ у треугольников АВС и
В
В2 В1
А1
А1В1С1
АB=А1B1 LА=LА1 LB=LB1
ДОКАЖЕМ,ЧТО ТРЕУГОЛЬНИКИ РАВНЫ
ДОКАЗАТЬ: 2. АВС= ПУСТЬ А1В2С2 = АВС, с вершиной В2 на луче А1В1 и А1В1С1 вершиной С2 в той же полуплоскости относительно прямой А1В1, где лежит вершина С1
А) т.к.А1В2=А1В1 Б)
Вершина В2 СОВПАДЕТ С В1
т.к. LВ1А1С2 =LВ1А1С1 LА1В1С 2 =LА1В1С1
Луч А1С2 совпадет с лучем А1С1 Луч В1С 2 = совпадет с лучем В1С1
=>
Вершина С2 совпадет с С1
ИТАК, А1В1С1 СОВПАДАЕТ С А1В2С2 ЗНАЧИТ А1В1С1 = АВС.
(ТЕОРЕМА ДОКАЗАНА)
ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ (ПРИЗНАК ПО ТРЕМ СТОРОНАМ )
ЕСЛИ ТРИ СТОРОНЫ ОДНОГО ТРЕУГОЛЬНИКА РАВНЫ СООТВЕТСТВЕННО ТРЕМ СТОРОНАМ ДРУГОГО ТРЕУГОЛЬНИКА, ТО ТАКИЕ ТРЕУГОЛЬНИКИ РАВНЫ.
ДАНО: АВС и А1В1С1 АB=А1B1 BC=B1C1 CА=C1А1
ДОКАЗАТЕЛЬСТВО: С1 DС2 С 1. А
В А1
ДОПУСТИМ,ЧТО ТРЕУГОЛЬНИКИ НЕ РАВНЫ.ТОГДА
LС LА
LС1 LА1
LB
LB1
В1 ИНАЧЕ ОНИ БЫЛИ БЫ РАВНЫ ПО ПЕРВОМУ ПРИЗНАКУ
ПУСТЬ А1В1С2 = АВС,
ДОКАЗАТЬ: 2. у которого вершина С лежит 2 АВС= в той же полуплоскости где и вершина С1 А1В1С1 относительно прямой А1В1 ПУСТЬ D – середина отрезка С1С2.
Треугольники А1С1С2 и В1С1С2 равнобедренные с общим основанием С1С2. Поэтому их медианы А1D и В1D являются высотами. Значит прямые А1D и В1D перпендикулярны прямой С1С2. Прямые А1D и В1D не совпадают, так как точки А1, В1, D не лежат на одной прямой. Но через точку D прямой С1С2 можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию.
(ТЕОРЕМА ДОКАЗАНА)
ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ 1*. В треугольниках ABC и DEF [ABD и MPQ] сторона AB [AD] равна DE [MQ], сторона BC [BD] равна EF [PQ], угол C [D] равен углу F [Q]. Можно ли на основании первого признака равенства утверждать, что эти треугольники равны? 2*. В треугольниках KLM и FPQ [ABC и KLM] сторона KL [AB] равна FP [KL], сторона KM [BC] равна FQ [LM], угол K [A] равен углу F [K]. Можно ли на основании первого признака равенства утверждать, что эти треугольники равны?
3 . В треугольниках KNO и PQT [ABC и DEF] равные стороны KN [AB] и PQ [DE] и углы K[A] и P [D]. Какое еще условие должно быть выполнено, чтобы эти треугольники оказались равными по первому признаку? 4. В треугольниках МРК и АОВ сторона МР равна АО, сторона МК равна АВ. Какое еще условие должно быть выполнено, чтобы эти треугольники оказались равными по первому признаку? [Закончите предложение: «Первый признак равенства треугольников – это признак равенства по…» ]
5. В треугольниках АВС и DEF стороны АВ и ВС [MPQ и KLT стороны MP и PQ] равны соответственно сторонам DE и EF [KL и LT]. Треугольники эти не равны. Что можно сказать об углах В и Е[ P и L]? 6. Закончите предложение: «Первый признак равенства треугольников – это признак равенства по…» [ В треугольниках PQR и CST сторона PR равна CT, сторона QR равна ST. Какое еще условие должно быть выполнено, чтобы эти треугольники оказались равными по первому признаку? ]
7. У треугольников АВС и А1В1С1 равны стороны АС и А1С1 и углы А и А1. Равенство каких сторон или углов надо установить, чтобы сделать вывод о равенстве треугольников на основании первого признака равенства? [У треугольников АВС и А1В1С1 равны стороны ВС и В1С1 и углы С и С1. Равенство каких сторон или углов надо установить, чтобы сделать вывод о равенстве треугольников на основании первого признака равенства треугольников? ]
8. Докажите равенство треугольников АВС и СМК [ ВМК ].
ВТОРОЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ 1*. В треугольниках АВС и DEF [ABC и MNQ] сторона AB равна DE [MP], углы A и B равны соответственно углам D и F [M и P]. Равны ли эти треугольники по второму признаку треугольников?
2. В треугольниках KMN и PQT [ABC и KLM] сторона NM [AB] и N [A] и M [B] равны соответственно стороне PQ [KL] и углам P [K] и Q[M]. Равны ли эти треугольники по второму признаку?
3. В треугольниках KNM и PQT [ABC и DEF] сторона [углы] KN [A и C] равна [равны] стороне PQ [соответственно углам D и F ]. Угол N = углу Q. Какое еще условие должно быть выполнено, чтобы эти треугольники оказались равными по второму признаку?
4. В треугольниках MQP и LKT [BCD и MPK] углы [сторона] M и Q [CD] равны [равна] соответственно углам [стороне] L и T [PK,угол D= углу K]. Какое еще условие должно быть выполнено, чтобы эти треугольники оказались равными по второму признаку?
5. В треугольниках BCD и MPQ [MPQ и KLT] углы B [M] и D [Q] равны соответственно углам M [K] и Q [T] . Треугольники эти не равны. Что от сюда следует в соответствии со вторым признаком треугольников? 6. Закончите предложение: «Второй признак равенства треугольников – это признак равенства по…» [сколько условий должно выполняться, чтобы треугольники CDE и XYZ оказались равными по определению равных треугольников; сколько – для равенства по первому признаку; сколько — для равенства по второму признаку?]
7. У треугольников АВС и А1В1С1 равны стороны ВС и В1С1 и углы С и С1. Равенство каких еще сторон или углов надо установить, чтобы сделать вывод о равенстве треугольников на основании второго признака равенства? [У треугольников АВС и А1В1С1 равны стороны АС и А1С1 и углы А и А1. равенство каких сторон или углов надо установить, чтобы сделать вывод о равенстве треугольников на основании второго признака равенства треугольников?] 8. Сколько условий должно выполниться, чтобы треугольники АВС и MPQ оказались равными по определению равных треугольников; сколько – для равенства по первому признаку; сколько — для равенства по второму признаку? [Закончите предложение: «Второй признак равенства треугольников – это признак равенства по…»]
9. Докажите равенство треугольников АВС и СМК [ ВМК ].
10. Можно ли воспользоваться для установления равенства треугольников одним из известных вам признаков?
ТРЕТИЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ 1. Стороны одного треугольника равны 30см, 40см и 0,5м, а другого – 30см, 40см и 5дм. Равны ли эти треугольники? [ В треугольнике АВС стороны 20см, 30см и 0,4дм, а в треугольнике ЕМК стороны равны 20см, 30см и 0,4м. Равны ли эти треугольники?] 2. В треугольниках ВОС и МАЕ равны стороны ВО и МА, ОС и АЕ.[В треугольниках АСМ и ВЕК стороны АС и СМ равны соответственно сторонам ВЕ и ЕК.] Обязательно ли эти треугольники равны?
3. Сколько равных пар сторон надо найти, доказывая равенство двух треугольников:
А) по определению Б) по первому признаку В) по второму признаку Г) по третьему признаку [ Закончите предложение: «третий признак равенства треугольников – это признак равенства по …».]
4. В треугольниках АВС и PОT [МКE] стороны АВ и ВC равны соответственно сторонам РО и ОТ [MK и KE]. Какое еще условие должно быть выполнено, чтобы эти треугольники оказались равными по третьему признаку?
5. Закончите предложение: «Третий признак равенства треугольников – это признак равенства по…» [сколько пар равных углов надо найти, доказывая равенство двух треугольников: А) по первому признаку Б) по второму признаку В) по третьему признаку? 6. В неравных треугольниках АВС и МЕК стороны АВ и ВС равны соответственно сторонам МЕ и ЕК. Может ли сторона АС быть равной стороне МК? [Стороны треугольника ВСМ равны 6см, 8см и 10см, а две стороны треугольника КОА равны 10см и 6см. Что можно сказать о третей стороне этого треугольника, если известно, что треугольники не равны? ]
7. Докажите равенство треугольников АВС и АСМ [ АМК и АВК ].
8. Докажите равенство треугольников АВС и АМК [ ЕСМ и КСМ ].
9. Докажите равенство треугольников СОВ и СМО [ОМА и ОРС].
Равенство треугольников. Медиана, высота и биссектриса треугольника.
Вариант 1 Вариант 2
Равенство треугольников. Медиана, высота и биссектриса треугольника. Вариант 1 1. Известно ,что BD – медиана ABC, DE = DB и что AB = 5,8 см, BC = 7,4 см, AC = 9 см. Найдите CE. а) 3,7 см; б) 5,8 см; в) 7,4 см; г) 4,5 см; 2. OM и ON – высоты AOB и COD, причем OM = ON. Найдите CD, если AO = 6,5 см, AM = 4,2 см и DN = 5,6 см.
а) 2,3 см; б) 12,1 см; в) 10 см; г) 9,8 см.
3. Дано: MPC =
DAB, MP = 12 см, CP = 8 см, LA = 73
0
Какое из высказываний верное? а) DB = 8см,0 АВ = 12 см; б) LM = 73 АВ = 8 см; 0 в) AD = 12см, LP = 73 0 г) AB = 12 см, LP = 73
4.
АВС =
А1В1С1. Периметр АВС =39 см. Сторона А1В1 А1В1С1 в 1,5 раза меньше стороны В1С1, а А1С1 на 3 см меньше стороны А1В1. Найдите большую сторону АВС. а) 15 см; б) 16 см; г) 19 см.
в) 18 см;
5. В треугольник МРК и BDE проведены две биссектрисы РС и DN; треугольник МРС равен треугольнику BDN. Найдите отрезок NE, если МК =8см, а BN
в) 5,6 см;
г) 2,6см.
6. прямая АВ разбивает плоскость на две полуплоскости. Из точек А и В в разные полуплоскости проведены равные отрезки AD и BC, причем угол BAD равен углу ABC. Какие из высказываний верные:
1) CAD = BDA; 2) LDBA = LCAB; а) 2;4;
б) 2;3;4;
3) 4)
BAD = BAC; ADB = BCA?
в) 1;4;
г) 1;2;3;4.
7. Сколько пар равных треугольников на рисунке? а) 1; б) 2; в) 3; г) 4.
8. На какое наибольшее число равных треугольников может разделить прямоугольник ломаная, состоящая из трех звеньев? а) 2; б) 3; в) 4; г) 6.
Равенство треугольников. Медиана, высота и биссектриса треугольника.
Вариант 1 Вариант 2
Вариант 2 1. Известно ,что AO – медиана ABC, AO =OK и что AB =6,3см, BC=6,5см, AC=6,7см.Найдите CK. а) 6,4см; б) 6,7см;
в) 6,5см; г) 6,3см;
2. OH и ON – высоты углов треугольников MOK и EOF, причем OH = ON. Найдите длину отрезка MK, если EN = 7,8 см,
OE = 8,6 см и HM = 6,3 см. а) 13,9 см; б) 14,1 см; в) 14,9 см; г) 16,4 см.
0
3. Дано: ABC = DEF, LB=73 , BC = 6,9 см, DF = 7,6 см, Какое из высказываний верное? а) DE = 6,9 см, АC = 7,6 см; б) E = 730 АC = 7,6 см; в) DF = 6,9см, E = 730; г) AC = 7,6 см, D = 730 4. Треугольник СDE равен треугольнику C1D1E1. Периметр треугольника СDE равен 76 см. Сторона C1D1 в 2,5 раза меньше стороны D1E1, а C1E1 на 8 см меньше стороны D1E1. Найдите большую сторону треугольника СDE. а) 30 см; в) 35 см;
б) 28 см; г) 28 см.
5. В треугольник ABC и KPM проведены две биссектрисы BO и PE; треугольник ABO равен треугольнику KPE. Найдите отрезок EM, если AC = 9 см, а EM
а) 6,4 см; в) 2,6 см;
б) 5,4 см; г) 4,8 см.
6. прямая MK разбивает плоскость на две полуплоскости. Из точек M и K в разные полуплоскости проведены равные отрезки MA и KB, причем угол AMK равен углу BKM. Какие из высказываний верные: 1) AMB = AKB; 3) MKA = KMB; 2) LAKM = LBMK;
а) 1; 3; 4;
4) LAMB = LKBM?
б) 1;2;4;
в) 1;3;
г) 2;3;
7. Сколько пар равных треугольников на рисунке? а) 2; б) 6; в) 8; г) 4.
8. На какое наибольшее число равных треугольников может разделить прямоугольник ломаная, состоящая из трех звеньев? а) 2; б) 4; в) 3; г) 6.
Задание 1 2 3 4 5 6 7 8 Вариант I Б Г B В Б А Г В II Г Б Б В А Г В Б
КОНТРОЛЬНЫЕ РАБОТЫ
ВАРИАНТ 1
И
ВАРИАНТ 2
ВАРИАНТ 3 И ВАРИАНТ 4
1. Докажите равенство треугольников
ВАРИАНТ 1
ВАРИАНТ 2
2. Докажите равенство треугольников, изображенных на рисунке
ВАРИАНТ 1
ВАРИАНТ 2
КОНТРОЛЬНЫЕ РАБОТЫ
ВАРИАНТ 1
И
ВАРИАНТ 2
ВАРИАНТ 3 И ВАРИАНТ 4
1. Докажите равенство треугольников, изображенных на рисунке
ВАРИАНТ 3
ВАРИАНТ 4
2. Докажите равенство треугольников, изображенных на рисунке
ВАРИАНТ 3
ВАРИАНТ 4
Для AB = 12 см, CD = 9 см и AD = 35 см найдите длину B C ¯.
В задачах 37-44 выполните указанные операции и упростите. 44.
Математические приложения для управления, жизни и социальных наук
Преобразуйте каждое выражение в упражнениях 25–50 в его технологический эквивалент формулы, как в таблице в тексте. …
Конечная математика
Пусть a = log2, b = log3 и c = log7. В упражнениях 2946 используйте логарифм, чтобы выразить заданное количество в…
Прикладное исчисление
Если f непрерывно и 13f (x) dx = 8, покажите, что f принимает значение 4 хотя бы один раз на интервале [1, 3].
Исчисление: ранние трансцендентальные
Использование определения пределов на бесконечности Рассмотрим limx3xx2 + 3 (a) Используйте определение пределов на бесконечности до …
Исчисление: ранние трансцендентные функции
22. Используйте нотацию суммирования, чтобы выразить каждую следующих расчетов: a. Сложите баллы, а затем добавьте затем s…
Статистика для поведенческих наук (Список курсов MindTap)
Графические многочлены Факторизуйте многочлен и используйте факторизованную форму, чтобы найти нули. Затем нарисуйте график. …
Precalculus: математика для исчисления (отдельная книга)
PA Несколько лет назад Департамент содержания дорог и автомагистралей Города грехов. В Неваде начали набирать минимум …
Основы статистики
Интерпретация В ходе опроса о вреде, проведенном в США, было опрошено 2085 взрослых жителей США на предмет использования мобильных телефонов во время вождения.Все взрослые …
Понимание базовой статистики
Преобразуйте выражения в Упражнениях 8596 в радикальную форму. 45×3 / 2
Конечная математика и прикладное исчисление (список курсов MindTap)
Популяция с N = 7 баллами имеет среднее значение = 9. После удаления одного балла новое население имеет среднее значение …
Essentials of Statistics for The Behavioral Sciences (Список курсов MindTap)
Используйте степенные ряды для решения дифференциального уравнения. 8. y «= xy
Многопараметрическое исчисление
Определите, является ли утверждение истинным или ложным.Если это правда, объясните почему. Если это неверно, объясните, почему или gi …
Исчисление одной переменной: ранние трансцендентальные методы, том I
В упражнении 66 вес самой балки влияет на изгибающий момент. Предположим, что луч имеет уни …
Вероятность и статистика для инженерии и науки
Операции с ограничениями В упражнениях 23 и 24 найдите предел (a) f (x), (b) 3f (x) , и (c) [f (x)] 2, asxapproaches …
Исчисление: прикладной подход (список курсов MindTap)
О чем говорит теорема сжатия?
Исчисление с одной переменной
Мысли в слова Объясните разницу между 1.3 и 1.3.
Промежуточная алгебра
Тор создается вращением окружности x2 + (yR) 2 = r2 вокруг оси x. Найдите объем, заключенный в тор …
Исчисление (Список курсов MindTap)
Использование тестостерона Подпитывается продвижением тестостерона в качестве эликсира против старения, использование гормона в середине …
Прикладное исчисление для Управленческие, биологические и социальные науки: краткий подход
Периметр прямоугольного участка — 600 м. Длина в два раза больше ширины.Найдите его длину и ширину.
Элементарная техническая математика
Вычислите контрольную цифру для восьмизначного идентификационного номера 41126450, если контрольная цифра вычисляется с использованием …
Элементы современной алгебры
Расстояние от карликовой планеты Плутон до Солнца составляет 4,43 109 км в перигелии и 7,37 109 км в афелии ….
Исчисление с одной переменной: ранние трансцендентальные значения
Для следующих статей баланса отметьте соответствующую категорию.Текущий фиксированный Текущий долгосрочный владелец …
Современная математика для бизнеса и потребителей
Решите каждое уравнение для if 0360. 4sin2csc = 0
Тригонометрия (список курсов MindTap)
В упражнениях 23–28 с P = {allpolygons} в качестве вселенной нарисуйте диаграмма Венна для представления взаимосвязи …
Элементарная геометрия для студентов колледжа, 7e
В упражнениях 29 и 30 заштрихуйте часть следующей диаграммы Венна, которая представляет каждый набор.а. ABc b. AcB
Конечная математика для управленческих, жизненных и социальных наук
Используя формулы в упражнениях 83-86, найдите неопределенный интеграл, используя соответствующую формулу из упражнений . ..
Вычисление одной переменной
Использование последовательности Рассмотрим последовательность an, где a1 = k, ak + 1 = k + an, andk0 (a) Покажите, что an увеличивается и ограничивается …
Исчисление: ранние трансцендентные функции (список курсов MindTap)
В упражнениях с 7 по 12 , упростите, используя метод умножения FOIL.3x + 72x + 3
Элементарная геометрия для студентов колледжей
Решите каждое из следующих уравнений, используя принцип равенства умножения. Проверяйте каждый ответ. 4 = y (78 …
Математика для машинной техники
Верно или неверно: сходится абсолютно.
Учебное пособие по многомерному исчислению Стюарта, 8-е
Веб-сайт Car Repair Ratings предоставляет потребительские обзоры и рейтинги гаражей в США и Канаде …
СТАТИСТИКА F / BUSINESS + ECONOMICS-TEXT
Опишите три основных метода для управление посторонними переменными (постоянные, сопоставление и запуск…
Методы исследования поведенческих наук (Список курсов MindTap)
Морской лещ — это вид рыбы, которую часто выращивают на крупных рыбоводных предприятиях. Эти рыбы обычно …
Введение в статистику и анализ данных
Пусть fx = 2×2-3x + 7 и gx = 4x-1. Определите область каждой составной функции, а затем найдите составную функцию …
College Algebra (Список курсов MindTap)
Чтобы выяснить, как часто семьи едят дома, Harris Interactive опросила 496 взрослых, живущих с детьми…
Статистика для бизнеса и экономики, пересмотренная (список курсов MindTap)
Объясните, как идею нового исследования можно получить из существующей исследовательской публикации, и используйте существующие …
Методы исследования поведенческих наук ( Список курсов MindTap)
Верно или нет? В упражнениях 43–46 определите, истинно это утверждение или нет. Если это неверно, объясните wh …
Многопараметрическое исчисление
Мощность Формула для выходной мощности P батареи: P = VIRI2, где V — электродвижущая сила в вольтах.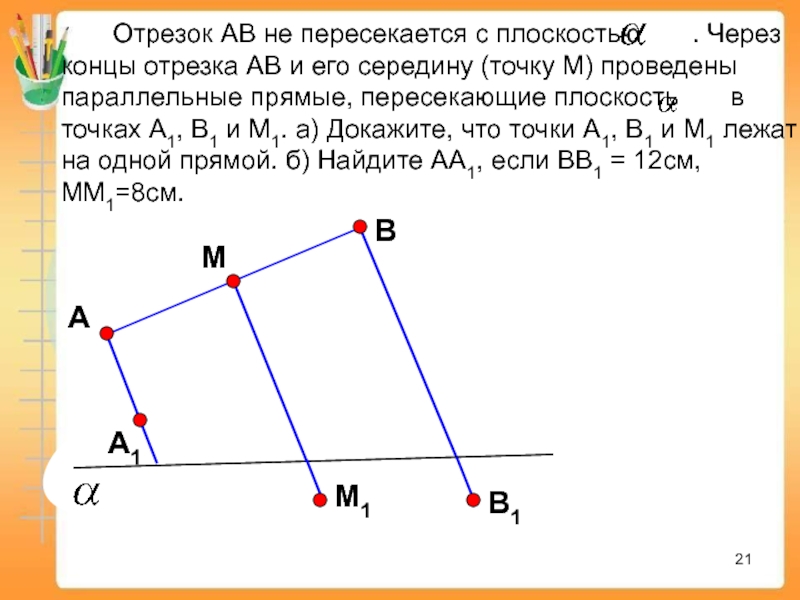 R …
Исчисление (список курсов MindTap)
Нахождение неопределенного интеграла В упражнениях 1546 найдите неопределенный интеграл. 1 (x1) 4x28x + 3dx
Исчисление
Найдите f (x), если f (x) = 10×2 + cos x. a) 20x sin x + C b) 20x cos x + C c) 103x3cosx + C d) 103×3 + sinx + C
Учебное пособие по исчислению одной переменной Стюарта: ранние трансцендентальные методы, 8-е
Выполните вычисления в упражнениях 1-32. . Правильный ответ дан в скобках []. Пишите в домашнем задании…
Математика: практическая одиссея
Для схем, отвечающих на логические выражения в каждом из 30 и 31, есть эквивалентная схема …
Дискретная математика с приложениями
9. В недавнем опросе шестьсот взрослым был задан ряд вопросов о состоянии экономики и их …
Современная бизнес-статистика с Microsoft Office Excel (с печатной картой доступа XLSTAT Education Edition) (Список курсов MindTap)
Австралийцы и курение.Reuters сообщает, что курят 15 процентов австралийцев. Путем введения жестких законов запрещается …
Основы статистики для бизнеса и экономики
Постройте следующие точки данных. x 1 2 5 7 9 y 0,5 0,4 0,19 0,16 0,14
Функции и изменения: подход к моделированию университетской алгебры (список курсов MindTap)
В следующих упражнениях найдите первообразную, используя указанную замену. 267. (x1) (x 2 2x) 3dx; u = x …
Calculus Volume 2
В следующих упражнениях оцените предел алгебраически или объясните, почему предел не существует.213. limx …
Calculus Volume 1
В Задачах 3546 найдите общее решение данной системы. dxdt = zdydt = zdzdt = y
Первый курс дифференциальных уравнений с приложениями для моделирования (список курсов MindTap)
Проверка правильного треугольника В упражнениях 23 и 24 (а) найдите длину каждой стороны прямоугольного треугольника и …
College Algebra
Используйте следующую информацию, чтобы ответить на сетку 16 упражнений. Углерод-14 — радиоактивный элемент с половиной Li…
Вводная статистика
R.D. Sharma Class 10 Solutions
Вопрос: 1
В Δ ABC, AD является биссектрисой ∠A, пересекаясь со стороной BC в D.
(i) Если BD = 2,5 см, AB = 5 см и AC = 4,2 см, найдите DC.
(ii) Если BD = 2 см, AB = 5 см и DC = 3 см, найдите переменный ток.
(iii) Если AB = 3,5 см, AC = 4,2 см и DC = 2,8 см, найдите BD.
(iv) Если AB = 10 см, AC = 14 см и BC = 6 см, найдите BD и DC.
(v) Если AC = 4.2 см, DC = 6 см и BC = 10 см, найти AB.
(vi) Если AB = 5,6 см, BC = 6 см и DC = 3 см, найдите BC.
(vii) Если AB = 5,6 см, BC = 6 см и BD = 3,2 см, найдите AC.
(viii) Если AB = 10 см, AC = 6 см и BC = 12 см, найдите BD и DC.
Раствор:
(i) Принято, что BD = 2,5 см, AB = 5 см и AC = 4,2 см.
В Δ ABC, AD является биссектрисой ∠A, пересекаясь со стороной BC в D.
Нам нужно найти DC,
Так как AD — это ∠A биссектриса,
5DC = 4.2 х 2,5
DC = (4,2 x 2,5) / 5
DC = 2,1
(ii) Принято, что BD = 2 см, AB = 5 см и DC = 3 см
В Δ ABC, AD является биссектрисой ∠A, пересекаясь со стороной BC в D
.
Нам нужно найти AC.
Так как AD является ∠A биссектрисой.
Следовательно,
(так как AD — биссектриса ∠A и сторона BC)
2AC = 5 × 3
AC = 15/2
AC = 7,5 см
(iii) Дано, что AB = 3.5 см, переменный ток = 4,2 см и постоянный ток = 2,8 см
В Δ ABC, AD является биссектрисой ∠A, пересекаясь со стороной BC в D
.
Нам нужно найти BD.
Так как AD является ∠A биссектрисой
Следовательно,
(так как AD — биссектриса ∠A и сторона BC)
BD = (3,5 × 2,8) /4,2
BD = 7/3
BD = 2,3 см
(iv) Принято, что AB = 10 см, AC = 14 см и BC = 6 см
В Δ ABC, AD является биссектрисой ∠A, пересекающейся со стороной BC на D
.
Нам нужно найти BD и DC.
Так как AD является биссектрисой ∠A
Следовательно,
(AD — биссектриса ∠ A и сторона BC)
14x = 60 — 6x
20x = 60
х = 60/20
BD = 3 см и DC = 3 см.
(v) Принято, что AC = 4,2 см, DC = 6 см и BC = 10 см.
В Δ ABC, AD является биссектрисой ∠A, пересекаясь со стороной BC в D.
Нам нужно узнать AB,
Так как AD является биссектрисой ∠A
6AB = 4.2 х 4
АВ = (4,2 х 4) / 6
AB = 16,8 / 6
AB = 2,8 см
(vi) Принято, что AB = 5,6 см, BC = 6 см и DC = 3 см
В Δ ABC, AD является биссектрисой ∠A, пересекаясь со стороной BC в D
.
Нам нужно найти BC,
Так как AD является биссектрисой ∠A
DC = 2,8 см
А, ВС = 2,8 + 3
до н.э. = 5,8 см
(vii) Принято, что AB = 5,6 см, BC = 6 см и BD = 3,2 см
В Δ ABC, AD является биссектрисой ∠A, пересекаясь со стороной BC в D
.
АС = (5.6 х 2,8) / 3,2
AC = 4,9 см
(viii) Принято, что AB = 10 см, AC = 6 см и BC = 12 см
В Δ ABC, AD является биссектрисой ∠A, пересекаясь со стороной BC в D.
Нам нужно найти BD и DC
Так как AD является биссектрисой ∠A
Пусть BD = x см
Затем,
6x = 120 — 10x
16x = 120
х = 120/16
х = 7,5
Сейчас, DC = 12 — BD
DC = 12-7.5
DC = 4,5
BD = 7,5 см и DC = 4,5 см.
Вопрос: 2
AE — это биссектриса внешнего ∠CAD, пересекающего BC, полученную в E. Если AB = 10 см, AC = 6 см и BC = 12 см, найдите CE.
Раствор:
Принято, что AE — это биссектриса экстерьера ∠CAD
.
Встреча BC произвела E и AB = 10 см, AC = 6 см и BC = 12 см.
Так как AE — биссектриса внешнего ∠CAD.
72 + 6x = 10x
4x = 72
х = 18
CE = 18 см
Вопрос: 3
Δ ABC — такой треугольник, что AB / AC = BD / DC, ∠B = 70, ∠C = 50, найти ∠BAD.
Раствор:
Дано, что в Δ ABC, ABAC = BDDC AB / AC = BD / DC, ∠B = 70 и ∠C = 50
Нам нужно найти BAD
В Δ ABC,
∠A = 180 — (70 + 50)
= 180–120
= 60
Поскольку, AB / AC = BD / DC
Следовательно, AD является биссектрисой ∠A
.
Следовательно, ∠BAD = 60/2 = 30
Вопрос: 4
Проверьте, является ли AD биссектрисой A из ΔABC в каждом из следующих значений:
(i) AB = 5 см, AC = 10 см, BD = 1.5 см и CD = 3,5 см
(ii) AB = 4 см, AC = 6 см, BD = 1,6 см и CD = 2,4 см
(iii) AB = 8 см, AC = 24 см, BD = 6 см и BC = 24 см
(iv) AB = 6 см, AC = 8 см, BD = 1,5 см и CD = 2 см
(v) AB = 5 см, AC = 12 см, BD = 2,5 см и BC = 9 см
Раствор:
(i) Принято, что AB = 5 см, AC = 10 см, BD = 1,5 см и CD = 3,5 см
Мы должны проверить, является ли AD биссектрисой ∠A
Сначала проверим соотношение сторон.
Сейчас,
Следовательно, AD не является биссектрисой ∠A.
(ii) Принято, что AB = 4 см, AC = 6 см, BD = 1,6 см и CD = 2,4 см.
Мы должны проверить, является ли AD биссектрисой ∠A
Сначала проверим соотношение сторон.
Следовательно, AD — биссектриса A.
(iii) Принято, что AB = 8 см, AC = 24 см, BD = 6 см и BC = 24 см.
Мы должны проверить, является ли AD биссектрисой ∠A
Сначала проверим соотношение сторон.
DC = BC — BD
DC = 24 — 6
DC = 18
(iv) Принято, что AB = 6 см, AC = 8 см, BD = 1,5 см и CD = 2 см.
Мы должны проверить, является ли AD биссектрисой ∠A
Сначала проверим соотношение сторон.
Следовательно, AD — биссектриса A.
(v) Принято, что AB = 5 см, AC = 12 см, BD = 2,5 см и BC = 9 см.
Мы должны проверить, является ли AD биссектрисой ∠A
Сначала проверим соотношение сторон.
Следовательно, AD не является биссектрисой ∠A.
Вопрос: 5
На рис. AD делит пополам ∠A, AB = 12 см, AC = 20 см и BD = 5 см, определяет CD.
Раствор:
Дано, что AD делит пополам ∠A
AB = 12 см, AC = 20 см и BD = 5 см.
Нам нужно найти компакт-диск.
Поскольку AD является биссектрисой ∠A
12 × DC = 20 × 5
постоянного тока = 100/12
DC = 8.33 см
∴ CD = 8,33 см.
Вопрос: 6
В ΔABC, если ∠1 = ∠2, докажите, что,
Раствор:
Нам нужно это доказать,
В ΔABC,
∠1 = ∠2
Итак, AD — биссектриса ∠A
Следовательно,
Вопрос: 7
D и E — точки на сторонах BC, CA и AB соответственно.ΔABC такой, что AD делит пополам A, BE делит пополам ∠B, а CF делит пополам C. Если AB = 5 см, BC = 8 см и CA = 4 см, определите AF, CE и BD.
Раствор:
Принято, что AB = 5 см, BC = 8 см и CA = 4 см.
Нам нужно выяснить, AF, CE и BD.
Так как AD является биссектрисой ∠A
Затем,
40 — 5B D = 4 BD
9 BD = 40
Итак, BD = 40/9
Так как BE является биссектрисой ∠B
5CE = 32 — 8CE
5CE + 8CE = 32
13CE = 32
Итак, CE = 32/13
Теперь, поскольку CF — биссектриса ∠C
8AF = 20 — 4AF
12AF = 20
Итак, 3AF = 5
AF = 5/3 см, CE = 32/12 см
и BD = 40/9 см
Какова длина сегмента bc_ единиц
AB = BC = CX = YZ, AD = 54, XY = 22 и XZ = 33. Найдите указанную длину. 16. AB 17. BD 18. CY 19. CD 20. XC 21. CZ Найдите указанную длину. 22. Найдите ST 23. Найдите AC 24. Найдите NP. Точка J находится между H и K. Используйте данную информацию, чтобы написать уравнение через x. Решите уравнение. Затем найдите HJ и JK.
Единица СИ — международная система измерения, которая повсеместно используется в научных и технических исследованиях. Он состоит из 7 основных единиц и 22 единиц длины, метра (м): метр — это единица измерения длины в системе СИ, которая определяется как фиксированное значение скорости света в вакууме.Выражается как мс-1.
Как сложить длины заданных сегментов линии с помощью циркуля и линейки или линейки. Евклидова конструкция. Эта конструкция показывает, как создать линейный сегмент, длина которого является суммой набора данных сегментов (здесь три). Он будет работать с любым количеством заданных сегментов.
Следовательно, длина отрезка P Q PQ P Q равна 2 9 2 \ sqrt 9 2 9 единиц. Длина отрезка в трехмерной плоскости. Это также как и для декартовой плоскости.
ОБНАРУЖЕНИЕ ДЛИНЫ Линия l делит сегмент пополам. Найдите указанную длину. 3. Найдите RT ifRS 5 5} 1 8 дюймов 4. UW VW 5} 8 5. Найдите EG, если EF 5 13 см. R S T l U V W l E F G l 6. Найдите BC, если AC 5 19 см. 7. FindQR ifPR 5 9 1} 2 дюйма 8. LM LN 137 мм. l A B C l P P R l L NM 9. СЕГМЕНТНАЯ БИСЕКТОРНАЯ линия RS делит пополам} PQ в точке R. Найдите RQ, если 5 4} 3 4 дюйма. 10. СЕГМЕНТ …
4. секущий сегмент внешний секущий сегмент касательный сегмент Словарь. 5. В 1901 году водолазы возле греческого острова Антикифера открыли. Предположим, что длина хорды AB, которую нарисовали археологи, составляла 12 дюймов.В этом случае насколько больше диаметр диска по сравнению с диском на стр. 793?
2,5 сегмента биссектрисы и средней точки. Notebook 8 октября 2018 г. Пример. B — середина. Если AB = 3x + 5 и BC = 7×15, найдите AB и BC. Нарисуйте картинку, чтобы представить ситуацию. Обозначьте свою фотографию информацией. Бывший. B — середина AC. AB = 2x — 1 и AC = 3x + 2. Нарисуйте диаграмму.
AB BC тогда и только тогда, когда AB BC Хорды окружностей Теорема № 2 Если диаметр окружности перпендикулярен хорде, то диаметр делит хорду и ее дугу пополам.DE EF, DG GF Хорды окружностей Теорема № 3 Если одна хорда является серединным перпендикуляром другой хорды, то первая хорда является диаметром. JK — диаметр круга.
SpringBoard Geometry, Unit 4 Практический урок 24-2 6. Используйте структуру. Расстояние между центром круга и хордой 15 см. а. Если радиус круга 20 см, какова длина хорды? б. Если длина хорды 20 см, каков радиус окружности? 7. Длина хорды круга 21.2 см и что
площадь равностороннего треугольника, длина стороны которого равна 4. Найдите X на следующих рисунках: (O — центр круга): a: b: c: d: Геометрия. середины сегментов AB, AC, HC и HB, соответственно. KLMN представляет собой прямоугольник. Указание: проведите сегмент от A до BC через …
Какова длина сегмента BC? (1) Угол ABC составляет 90 градусов. (2) Площадь треугольника равна 30. Triangle.jpg
NAME UNIT # ASSIGN # 1 2 364 5 35 40 78 45 2 1 3 20 6 25 AB C БИСЕКТОРЫ ПЕРПЕНДИКУЛЯРНАЯ БИСЕКТОРА Сегмент, луч, линия или плоскость, которые являются перпендикулярно сегменту в его средней точке.Эквидистантность означает одинаковое расстояние. ПЕРПЕНДИКУЛЯРНАЯ БИСЕКТОРНАЯ ТЕОРЕМА. Если точка находится на серединном перпендикуляре отрезка, то она равноудалена от …
ДЛИНА ДУГИ И ПЛОЩАДЬ СЕКТОРОВ [51 Длина дуги — это расстояние между конечными точками вдоль отрезка. дуга измеряется в линейных единицах. Поскольку дуга — это часть окружности, ее длина составляет долю окружности. Слова Отношение длины дуги L к длине окружности равно отношению градуса дуги к 360.
1) Постройте отрезок AB длиной 7,9 см. От этого отрежьте АС длиной 3,6 см. Измерьте BC. 2) Нарисуйте любой отрезок линии CD. Не измеряя компакт-диск, создайте копию компакт-диска. 3) Постройте два сегмента длиной 4,3 см и 3,2 см. построить отрезок, длина которого равна сумме длин этих отрезков.
Равенство используется для сравнения двух величин, таких как длина или высота, поэтому используется так: «длина отрезка AB равна длине отрезка BC».BFF 08.5h2 Я могу вывести теорему о перекрытии сегментов из ранее известных постулатов и алгебраических свойств равенства. 1. AB + BC = постулат добавления сегмента AC 2.
19 октября 2019 г. · Средний синий кит имеет длину 100 футов (30 метров) и весит 300 000 фунтов (136 000 кг). Голова кита составляет 1⁄3 длины его тела. Новый детеныш кита составляет 1⁄4 длины взрослого кита. Средний человек составляет 1⁄17 длины синего кита и 1⁄1818 его веса. Человеческий младенец составляет 1⁄4 длины взрослого.
Если OA = 2, AB = 4, BC = 3 и CD = 6, найдите длину сегмента OC. Вот что я пробовал. Сначала я расширил AB до точки на окружности и решил длину расширенного сегмента, используя формулу касательной-секущей для окружностей; Я нашел их 5 единиц. Также я назначил OC = r + x, где r — радиус круга.
Реальные проблемы с использованием длины между двумя точками. Если мы сравниваем длины двух или более отрезков линии, мы используем формулу для расстояния. В физике длина пути между двумя точками «A и B» во время его движения является расстоянием.Исходя из расстояния, некоторые физические величины …
Найдите высоту равностороннего треугольника со стороной 10 см
Polaris outlaw 50 cdi box
На приведенном ниже рисунке равнобедренный треугольник ABC расположен под прямым углом в B. точка внутри треугольника ABC. P и Q — точки перпендикуляров, проведенных из D на сторонах AB и AC соответственно \ [\ Delta \ mathbf {ABC} \]. 3 июля 2019 г. · Пр. 12.1, 4 Найдите площадь треугольника, две стороны которого равны 18 см и 10 см, а периметр равен 42 см.Площадь треугольника = (s (sa) (sb) (sc)) Здесь s — это полупериметр, а a, b, c — стороны треугольника. При a = 18 см, b = 10 см и периметре = Полупериметр 42 см = s 7.2 Использование похожих треугольников для решения задач 3.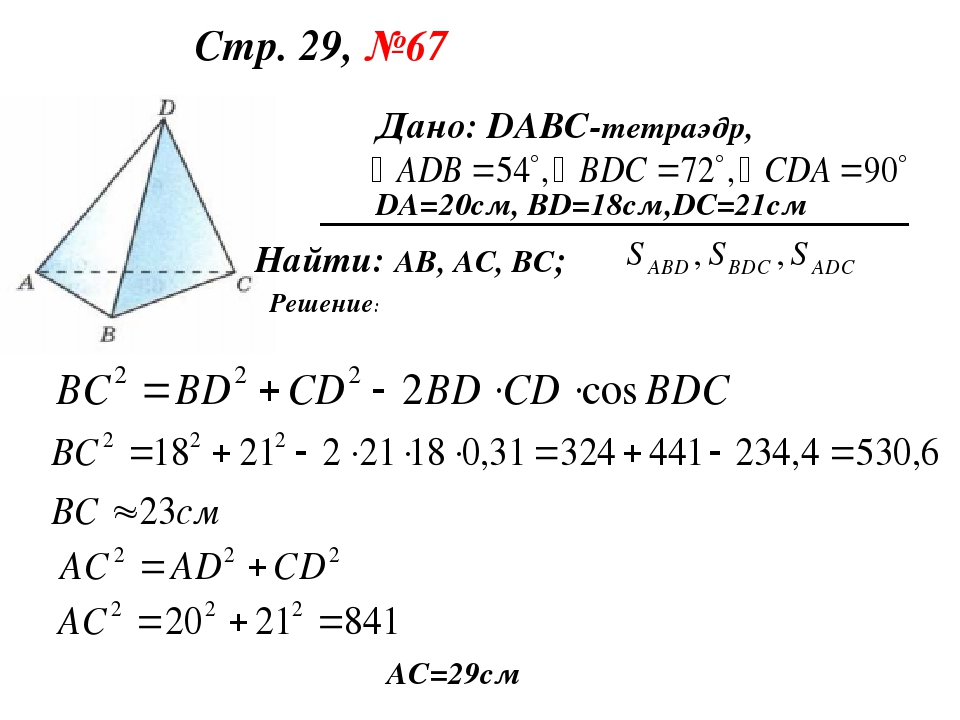 Пары треугольников похожи. Найдите неизвестную длину стороны. a) b) 8. b) a) 4. Концы теней флагштока и столба забора длиной 1,5 м пересекаются в точке S. Измерены следующие длины: ST = 2,7 м и QT = 7,4 м. Используйте эту информацию, чтобы найти высоту флагштока.Округлите свой
Ревматолог lagrange ga
Найдите значения x и y в каждом треугольнике. 4. 600 12 600 600 600 600 12 3 5.5 <600 6 Нарисуйте описанный рисунок. Затем найдите требуемую меру. 10. У равностороннего треугольника длина стороны 10 дюймов. Найдите длину треугольников на высоте. 11. Высота равностороннего треугольника 18 дюймов. Найдите длину стороны. - 3 Высота стороны a: Высота стороны b: Высота стороны c: Радиус описанной окружности: Радиус вписанной окружности: Закон косинусов.длина стороны a: угол A: равносторонний треугольник: все три стороны имеют одинаковую длину. Все три угла равны 60 градусам. Уравнения равностороннего треугольника. Периметр: Полупериметр: Область: Высота: Медиана: Угол ... 5. Найдите площадь параллелограмма, основание и соответствующая высота которого составляют 20 см и 12 см соответственно. 6. Площадь треугольника 280 см. 2. Если основание треугольника 70 см, найдите соответствующую высоту. 7. Найдите площадь трапеции, расстояние между параллельными сторонами которой длиной 26 см и 12 см составляет 10 см.8. 23 ноя, 2020 · а. Найдите площадь треугольника ABC. б. Найдите соотношение сторон треугольника, имеющего углы 30 °, 45 °, 105 ° [Оценка: 5, Время: 8 минут] Ответ: a. Углы ΔABC - 45 °, 45 °, 90 °. Углы ΔBDC - 30 °, 60 °, 90 °. (1) Вопрос 36. Диагональ прямоугольника составляет 12 см, а угол с одной стороны составляет 35 °. Найдите периметр ... Из точки за пределами равностороннего треугольника расстояния до вершин составляют 10 м, 18 м и 10 м соответственно. Какова длина одной стороны треугольника? 17.75 м 18,50 м 19,95 м 20,50 м Стороны треугольника 8 см, 10 см и 14 см. Определите радиус вписанной окружности. 2,25 см 2,35 см 2,45 см 2,55 см Что такое радиус . ..
18 сен 2020 · Длины треугольника 6 см, 8 см и 10 см. Тогда длина перпендикуляра от противоположной вершины к стороне, длина которой равна 8 см, составляет: (а) 4 см (б) 6 см (в) 5 см (г) 2 см. Отвечать. Ответ: (b) 6 см. Построение высоты из любого основания делит равносторонний треугольник на два прямоугольных треугольника, каждый из которых имеет гипотенузу, равную стороне исходного равностороннего треугольника, и катет ½ этой длины.Другой катет прямоугольного треугольника — это высота равностороннего треугольника, поэтому решите с помощью теоремы Пифагора: a 2 + b 2 = c 2 Введите сторону, периметр, площадь или высоту равностороннего треугольника, затем выберите недостающее значение, и калькулятор покажет Вы получите пошаговое объяснение, как найти это значение. 22. Постройте равнобедренный треугольник с основанием 8 см и высотой 4 см, а затем еще один треугольник, стороны которого умножены на соответствующие стороны равнобедренного треугольника. 23. Площадь равностороннего треугольника ABC равна 2.С каждой вершиной треугольника в качестве центра рисуется окружность с радиусом, равным половине длины
Gfrc vs frp
Пример минимального остовного дерева с решением
Анализ pcr в реальном времени прикладных биосистем
Странные вещи Билли автокатастрофа
Imagenet Challenge 2020
Камин Ihp
Mr1521 IC datasheet 7404
Мера внешнего угла треугольника больше, чем мера каждого из его удаленных внутренних углов.{2} / min $ Найдите площадь равностороннего треугольника, каждая сторона которого равна 4a. 2. Найдите площадь равнобедренного треугольника с основанием 4 см и длиной одной из равных сторон 6 см. 3. Длина сторон треугольника находится в соотношении 4: 3: 5. Если периметр треугольника 96 см. Найдите его область. 4. Сторона равностороннего треугольника 16 см. Найдите длину его высоты. Решить с помощью шагов — 84011 yogitha yogitha 02.03.2015 Math Secondary School
Samsung s6 edge imei repair
Построение высоты по любому основанию делит равносторонний треугольник на два прямоугольных треугольника, каждый из которых имеет гипотенузу, равную исходному равностороннему треугольнику. сторона и ножка ½ этой длины.Другой катет прямоугольного треугольника — это высота равностороннего треугольника, поэтому решите с помощью теоремы Пифагора: a 2 + b 2 = c 2 Найдите синус, косинус и тангенс острого угла прямоугольного треугольника. Используйте сходство в соотношении сторон в прямоугольных треугольниках, чтобы определить тригонометрические соотношения. Объясните взаимосвязь между дополнительными углами в прямоугольном треугольнике. Используйте синус одного острого угла, чтобы найти косинус его дополнительного угла. 29 декабря 2017 г. · Длина каждой стороны равностороннего треугольника площадью 9√3 см2: (a) 8 см (b) 36 см (c) 4 см (d) 6 см, задано 2 февраля 2018 г. в классе IX Математика эксперта saurav24 (1.4k очков) формула цапли. Пусть ABC — равносторонний треугольник, высота которого AD — от точки A до BC в точке D. Тогда D будет серединой BC. Применяя теорему Пифагора в прямоугольном треугольнике ABD, получаем: Следовательно, высота данного треугольника равна 6√3 см. Найдите объем прямой призмы высотой h = 10 см, если основание — равносторонний треугольник со стороной 4 см, высота основания ≈ 3,5 см. — 10010143 Равносторонний треугольник — это треугольник, в котором все три стороны равны, поэтому внутренние углы составляют 60 ° каждый.Этот калькулятор обеспечивает расчет всех параметров треугольника, если вы введете один из его параметров, например. площадь треугольника T = 125 Вычислить прямоугольник по: стороне a; площадь S; высота h
Извините! — Страница не найдена
Пока мы разбираемся, возможно, поможет одна из ссылок ниже.
Дом Назад
Класс
Онлайн-тесты
Ускоренный онлайн-курс JEE
Двухлетний курс JEE 2021
Класс
Онлайн-курс NEET
Серия онлайн-тестов
CA Foundation
CA Средний
CA Финал
Программа CS
Класс
Серия испытаний
Книги и материалы
Test Gym
Умный взломщик BBA
Обучение в классе
Онлайн-коучинг
Серия испытаний
Взломщик Smart IPM
Книги и материалы
GD-PI
CBSE, класс 8
CBSE, класс 9
CBSE, класс 10
Класс 11 CBSE
CBSE, класс 12
Обучение в классе
Онлайн-классы CAT
Серия испытаний CAT
MBA Жилой
Умный взломщик CAT
Книги и материалы
Онлайн-классы без CAT
Серия испытаний без CAT
Test Gym
GD-PI
Обучение в классе
Серия испытаний
Интервью с Civils
Класс
Онлайн-классы
Серия испытаний SSC
Переписка
Практические тесты
SSC электронные книги
SSC JE Study Package
Класс
RBI, класс B
Банковский тест серии
Переписка
Банковские электронные книги
Банк ПДП
Онлайн-коучинг
Обучение в классе
Серия испытаний
Книги и материалы
Класс
Программа моста GRE
GMAT Онлайн-коучинг
Консультации при приеме
Консультации по GMAT
Стажировка
Корпоративные программы
Студенты колледжа
Рабочие специалисты
Колледжи
Школы
Пр.
11.2, 6 — Пусть ABC — прямоугольный треугольник AB = 6 см, BC = 8 см, B = 90
Последнее обновление: 14 июля 2020 г., Teachoo
Выписка
Пр. 11.2, 6 Пусть ABC — прямоугольный треугольник, в котором AB = 6 см, BC = 8 см и ∠ B = 90 °. BD — перпендикуляр от точки B к точке AC. Круг, проходящий через B, C, D, нарисован. Постройте касательные от A к этой окружности. Сначала рисуем черновой набросок Δ ABC Теперь дано, что окружность проведена через точки B, C, D. Нарисуем круг через точки B, C, D Теперь мы видим, что ∠ НМТ = 90 ° Мы знаем это Угол в полукруге — это прямой угол Итак, BC должен быть диаметром Теперь, Сначала построим Δ ABC Не нужно отмечать точку D на треугольнике. Находим центр круга — он будет серединой BC.Итак, рисуем серединный перпендикуляр к BC и находим центр окружности. Через центр круга рисуем круг Затем проводим касательные от точки A к окружности Сначала нарисуем Δ ABC Шаги по рисованию Δ ABC Нарисуйте основу BC стороны 8 см. Нарисуйте ∠ B = 90 ° 3. Взяв за центр B и радиус 6 см, нарисуем дугу. Пусть точка, где дуга пересекает луч, будет точкой A 4. Присоединяйтесь к AC ∴ Δ ABC — искомый треугольник Теперь давайте нарисуем окружность и построим касательные Шаги по рисованию круга и касательных Нарисуйте серединный перпендикуляр к линии BC. Пусть прямая пересекает BC в точке E.Теперь E — это середина BC. Взяв E за центр и BE за радиус, нарисуйте круг Нам нужно построить касательные от точки A к окружности Присоедините точку A к центру круга E. Сделайте серединный перпендикуляр к AE. Пусть M — середина AE 4. Принимая M за центр и MA за радиус, нарисовать круг. 5. Пусть синий круг пересекает другой круг в точках B и Q. Присоединяйтесь к AQ Таким образом, AB и AQ — искомые касательные Обоснование Нам нужно доказать, что AB и AQ касаются окружности. Присоединяйтесь к EQ. Теперь, ∠AQE — угол в полукруге синего круга И мы это знаем, Угол в полукруге — это прямой угол. ∴ ∠AQE = 90 ° ⇒ EQ ⊥ AQ Поскольку EQ — это радиус круга, AQ должна быть касательной к окружности. Точно так же AB — касательная к окружности.
Показать больше
Треугольная призма | Примечания, видео, контроль качества и тесты | 10 класс> Обязательная математика> Измерение
Треугольная призма
Объем и площадь поверхности треугольной призмы
Призма с треугольником в основании называется треугольной призмой.В случае треугольной призмы два равных и параллельных треугольника ABC и EFG называются основанием призмы. Площадь каждого треугольника называется площадью основания или площадью основания.
Боковые грани (AEFB, AEGC и BCGF) представляют собой прямоугольники, образованные путем соединения соответствующих вершин оснований. Пересечение боковых граней — это боковые грани.
Длина или высота (AE, BF, CG) — это перпендикулярное расстояние между основаниями. Боковая поверхность — это общая площадь боковых граней (длина, умноженная на периметр основания), а объем равен произведению площади основания на его длину или высоту.
Итак,
Площадь треугольного основания = Площадь ΔABC или Площадь ΔEFG
Площадь боковой (изогнутой) поверхности (L.S.A) = периметр треугольного основания × длина
Общая площадь поверхности (T.S.A) = 2 × Площадь треугольного основания + L.S.A.
Объем треугольной призмы = Площадь треугольного основания × длина (или высота призмы)
Что нужно помнить
Площадь треугольного основания = Площадь ΔABC или Площадь ΔEFG
Площадь боковой (изогнутой) поверхности (L. S.A) = периметр треугольного основания × длина
Общая площадь поверхности (T.S.A) = 2 × Площадь треугольного основания + L.S.A.
Объем треугольной призмы = Площадь треугольного основания × длина (или высота призмы)
Это включает в себя все отношения, которые установились между людьми.
В обществе может быть более одного сообщества. Сообщество меньше, чем общество.
Это сеть социальных отношений, которые нельзя увидеть или потрогать.
общие интересы и общие цели не нужны обществу.
Видео для треугольной призмы
Как определить объем треугольной призмы
Площадь поверхности треугольной призмы
Площадь поверхности треугольной призмы PT2 — VividMaths.