Из 16 в 8 систему: 500 Internal Server Error

8-ная и 16-ная системы счисления | Практическая информатика

При наладке аппаратных средств ЭВМ или создании новой программы возникает необходимость «заглянуть внутрь» памяти машины, чтобы оценить ее текущее состояние. Но там все заполнено длинными последовательностями нулей и единиц двоичных чисел. Эти последовательности очень неудобны для восприятия человеком, привыкшим к более короткой записи десятичных чисел. Кроме того, естественные возможности человеческого мышления не позволяют оценить быстро и точно величину числа, представленного, например, комбинацией из 16 нулей и единиц.

Для облегчения восприятия двоичного числа решили разбивать его на группы разрядов, например, по три или четыре разряда. Эта идея оказалась очень удачной, так как последовательность из трех бит имеет 8 комбинаций, а последовательность из 4 бит — 16. Числа 8 и 16 являются степенями двойки, поэтому легко находить соответствие с двоичными числами. Развивая эту идею, пришли к выводу, что группы разрядов можно закодировать, сократив при этом длину последовательности знаков. Для кодировки трех битов требуется восемь цифр, поэтому взяли цифры от 0 до 7 десятичной системы. Для кодировки же четырех битов необходимо шестнадцать знаков; для этого взяли 10 цифр десятичной системы и 6 букв латинского алфавита: A, B, C, D, E, F. Полученные системы, имеющие основания 8 и 16, назвали соответственно восьмеричной и шестнадцатеричной.

В восьмеричной (octal) системе счисления используются восемь различных цифр 0, 1, 2, 3, 4, 5, 6, 7. Основание системы — 8. При записи отрицательных чисел перед последовательностью цифр ставят знак минус. Сложение, вычитание, умножение и деление чисел, представленных в восьмеричной системе, выполняются весьма просто подобно тому, как это делают в общеизвестной десятичной системе счисления. В различных языках программирования запись восьмеричных чисел начинается с 0, например, запись 011 означает число 9.

В шестнадцатеричной (hexadecimal) системе счисления применяется десять различных цифр и шесть первых букв латинского алфавита. При записи отрицательных чисел слева от последовательности цифр ставят знак минус. Для того чтобы при написании компьютерных программ отличить числа, записанные в шестнадцатеричной системе, от других, перед числом ставят 0x. То есть 0x11 и 11 — это разные числа. В других случаях можно указать основание системы счисления нижним индексом.

Шестнадцатеричная система счисления широко используется при задании различных оттенков цвета при кодировании графической информации (модель RGB). Так, в редакторе гипертекста Netscape Composer можно задавать цвета для фона или текста как в десятичной, так и шестнадцатеричной системах счисления.

Перевод из одной системы счисления в другую

Для перевода чисел из одной системы счисления в другую необходимо владеть основными сведениями о системах счисления и форме представления чисел в них.

Количество s различных цифр, употребляемых в системе счисления, называется основанием, или базой системы счисления. В общем случае положительное число

X в позиционной системе с основанием s может быть представлено в виде полинома:

где s — база системы счисления, — цифры, допустимые в данной системе счисления . Последовательность образует целую часть X, а последовательность — дробную часть X.

В вычислительной технике наибольшее применение нашли двоичная (BIN — binary), и двоично кодированные системы счисления: восьмеричная (OCT — octal), шестнадцатеричная (HEX — hexadecimal) и двоично-кодированная десятичная (BCD — binary coded decimal).

В дальнейшем для обозначения используемой системы счисления число будет заключаться в скобки, а в индексе указано основание системы. Число X по основанию s будет обозначено .

Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.

Основанием системы счисления служит число 2 (s = 2) и для записи чисел используются только две цифры: 0 и 1. Чтобы представить любой разряд двоичного числа, достаточно иметь физический элемент с двумя чётко различными устойчивыми состояниями, одно из которых изображает 1, а другое 0.

Прежде чем заняться переводом из любой системы счисления в двоичную, нужно внимательно изучить пример записи числа в двоичной системе счисления:

Эти системы счисления относятся к двоично-кодированным, в которых основание системы счисления представляет собой целую степень двойки: — для восьмеричной и — для шестнадцатеричной.

В восьмеричной системе счисления(s = 8) используются 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7.

Прежде чем заняться переводом из любой системы счисления в восьмеричную, нужно внимательно изучить пример записи числа в восьмеричной системе:

В шестнадцатеричной системе счисления (s = 16) используются 16 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.

Пример записи числа в шестнадцатеричной системе:

Широкое применение восьмеричной и шестнадцатеричной систем счисления обусловлено двумя факторами.

Во-первых, эти системы позволяют заменить запись двоичного числа более компактным представлением (запись числа в восьмеричной и шестнадцатеричной системах будет соответственно в 3 и 4 раза короче двоичной записи этого числа). Во-вторых, взаимное преобразование чисел между двоичной системой с одной стороны и восьмеричной и шестнадцатиречной — с другой осуществляется сравнительно просто.

Действительно, поскольку для восьмеричного числа каждый разряд представляется группой из трёх двоичных разрядов (триад), а для шестнадцатеричного — группой из четырёх двоичных разрядов (тетрад), то для преобразования двоичного числа достаточно объединить его цифры в группы по 3 или 4 разряда соответственно, продвигаясь от разделительной запятой вправо и влево. При этом, в случае необходимости, добавляют нули слева от целой части и/или справа от дробной части и каждую такую группу — триаду или тетраду — заменяют эвивалентной восьмеричной или шестнадцатеричной цифрой (см. таблицу).

Соответствие между цифрами в различных системах счисления

DEC	BIN	OCT	HEX	BCD
0	0000	0	0	0000
1	0001	1	1	0001
2	0010	2	2	0010
3	0011	3	3	0011
4	0100	4	4	0100
5	0101	5	5	0101
6	0110	6	6	0110
7	0111	7	7	0111
8	1000	10	8	1000
9	1001	11	9	1001
10	1010	12	A	0001 0000
11	1011	13	B	0001 0001
12	1100	14	C	0001 0010
13	1101	15	D	0001 0011
14	1110	16	E	0001 0100
15	1111	17	F	0001 0101

Для обратного перевода каждая OCT или HEX цифра заменяется соответственно триадой или тетрадой двоичных цифр, причём незначащие нули слева и справа отбрасываются.

Для рассмотренных ранее примеров это выглядит следующим образом:

В двоично-десятичной системе вес каждого разряда равен степени 10, как в десятичной системе, а каждая десятичная цифра кодируется четырьмя двоичными цифрами. Для записи десятичного числа в BCD-системе достаточно заменить каждую десятичную цифру эквивалентной четырёхразрядной двоичной комбинацией:

Любое десятичное число можно представить в двоично-десятичной записи, но следует помнить, что это не двоичный эквивалент числа. Это видно из следующего примера:

Пусть X — число в системе счисления с основанием s, которое требуется представить в системе с основанием h. Удобно различать два случая.

В первом случае и, следовательно, при переходе к основанию h можно использовать арифметику этой системы. Метод преобразования состоит в представлении числа в виде многочлена по степеням s, а также в вычислении этого многочлена по правилам арифметики системы счисления с основанием h. Так, например, удобно переходить от двоичной или восьмеричной системы счисления к десятичной. Описанный приём иллюстрируют следующие примеры:

В обоих случаях арифметические действия выполняются по правилам системы счисления с основанием 10.

Во втором случае () удобнее пользоваться арифметикой по основанию s. Здесь следует учитывать, что перевод целых чисел и правильных дробей производится по различным правилам. При переводе смешанных дробей целая и дробная части переводятся каждая по своим правилам, после чего полученные числа записываются через запятую.

Перевод целых чисел

Правила перевода целых чисел становится ясным из общей формулы записи числа в произвольной позиционной системе. Пусть число в исходной системе счисления s имеет вид . Требуется получить запись числа в системе счисления с основанием h:

Для нахождения значений разделим этот многочлен на h:

Как видно, младший разряд , то есть , равен первому остатку. Следующий значащий разряд определяется делением частного на h:

Остальные также вычисляются путём деления частных до тех пор, пока не станет равным нулю.

Для перевода целого числа из s-ичной системы счисления в h-ичную необходимо последовательно делить это число и получаемые частные на h (по правилам системы счисления с основанием h) до тех пор, пока частное не станет равным нулю. Старшей цифрой в записи числа с основанием h служит последний остаток, а следующие за ней цифры образуют остатки от предшествующих делений, выписываемые в последовательности, обратной их получению.

Пример 1. Перевести число 75 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы.

Решение:

Перевод правильных дробей

Правильную дробь , имеющую в системе с основанием s вид , можно выразить в системе счисления с основанием h как многочлен вида

Старшая цифра может быть найдена умножением этого многочлена на h, т.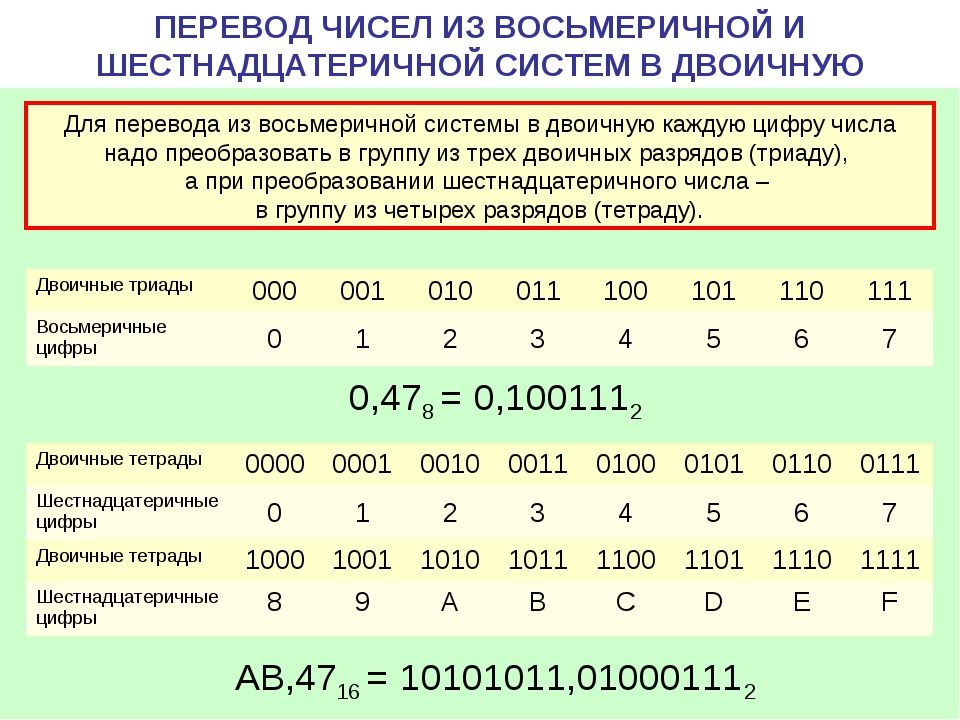 е.

Если это произведение меньше 1, то цифра равна 0, если же оно больше или равно 1, то цифра равна целой части произведения. Следующая цифра справа определяется путём умножения дробной части указанного выше произведения на h и выделения его целой части и т.д. Процесс может оказаться бесконечным, т.к. не всегда можно представить дробь по основанию h конечным набором цифр.

Для перевода правильной дроби из системы счисления с основанием s в систему счисления с основанием h нужно умножать исходную дробь и дробные части получающихся произведений на основание h (по правилам «старой» s-системы счисления). Целые части полученных произведений дают последовательность цифр дроби в h-системе счисления.

Описанная процедура продолжается до тех пор, пока дробная часть очередного произведения не станет равной нулю либо не будет достигнута требуемая точность изображения числа X в h-ичной системе счисления. Представлением дробной части числа X в новой системе счисления будет последовательности целых частей полученных произведений, записанных в порядке их получения и изображённых h-ичной цифрой. Абсолютная погрешность перевода числа X при p знаков после запятой равняется .

Пример 2. Перевести правильную дробь 0,453 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.

* В двоичную систему:

Ответ:

** В восьмеричную систему:

Ответ:

*** В шестнадцатеричную систему:

Ответ: так как , то

Поделиться с друзьями

Быстрый переход между двоичной, 8-ичной и 16-ичной системами

Быстрый переход между двоичной, восьмеричной и шестнадцатеричной системами

Как перевести число из одной недесятичной системы в другую недесятичную? Можно, например, сначала перевести его в десятичную, а потом из десятичной в нужную систему.

Но в случае, если перевод осуществляется между двоичной, восьмеричной и шестнадцатеричной системами, всё оказывается гораздо проще.

Чтобы быстро перейти от двоичной системы к восьмеричной, необходимо разбить двоичное число на так называемые триады – группы по три цифры, начиная от младших разрядов и заканчивая старшими. В случае, если при этом последняя триада из старших цифр оказывается неполной (содержит одну или две цифры), нужно дополнить ее до трех цифр, приписав нужное количество нулей. Например, разбив на триады число 1101110₂, получим

001 101 110

Теперь нужно просто воспользоваться таблицей соответствия двоичных триад восьмеричным цифрам:

000₂ = 0₈
001₂ = 1₈
010₂ = 2₈
011₂ = 3₈
100₂ = 4₈
101₂ = 5₈
110₂ = 6₈
111₂ = 7₈

Исходя из таблицы, наше число равно 156₈. По той же таблице можно совершать обратный переход из восьмеричной системы в двоичную.

Аналогично можно переводить числа из двоичной системы в 16-ичную и обратно. Для этого нужно разбить двоичное число на группы по 4 цифры (эти группы называются «тетрадами») и воспользоваться таблицей соответствия шестнадцатеричных цифр двоичным тетрадам.

Замечание. Данный способ применим только к двоичной, четверичной, восьмеричной и шестнадцатеричной системам, то есть, к системам с основанием 2ⁿ, где n – целое число.

Онлайн калькулятор
для перевода чисел в двоичную, восьмеричную и шестнадцатеричную системы

Для получения пошагового объяснения перевода чисел в двоичную, восьмеричную и шестнадцатеричную системы вы можете воспользоваться калькулятором вверху страницы. Введите число, которое вы собираетесь перевести из одной системы в другую, а также выберите соответствующие системы счисления (из какой и в какую будете переводить).

Шестнадцатеричная система счисления

☰

Шестнадцатеричная система счисления, так же как восьмеричная, широко используется в компьютерной науке из-за простоты перевода в нее двоичных чисел. В случае шестнадцатеричной записи числа получаются более компактными.

В качестве алфавита шестнадцатеричной системы счисления используются цифры от 0 до 9 и шесть первых латинских букв – A, B, C, D, E, F. При переводе в десятичную систему буквы заменяются числами 10, 11, 12, 13, 14, 15 соответственно.

При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не кратно четырем, первая четверка дописывается нулями впереди. Каждой четверке соответствует одноразрядное число шестнадцатеричной системы счисления.

Пример:

10001100101 = 0100 1100 0101 = 4 C 5 = 4C5

В случае обратного перевода шестнадцатеричные цифры заменяются соответствующими четырехразрядными двоичными числами.

Перевод из шестнадцатеричной системы счисления в десятичную выполняется аналогично переводу из двоичной и восьмеричной. Только здесь в качестве основания степени выступает число 16, а цифры от A до F заменяются десятичными числами от 10 до 15.

4C5 = 4 * 16² + 12 * 16¹ + 5 * 16⁰ = 4 * 256 + 192 + 5 = 1221

Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи, – это число FF.

FF₁₆ = 15 * 16¹ + 15 * 16⁰ = 240 + 15 = 255₁₀

В двоичном представлении FF будет выглядеть как восьмиразрядное число 11111111. Наименьшей рабочей ячейкой компьютерной памяти является байт, который состоит из 8-ми битов. Каждый бит может быть в двух состояниях – «включено» и «выключено». Одному из них сопоставляют ноль, другому – единицу.

Следовательно, в одном байте можно сохранить любое двоичное число в диапазоне от 00000000 до 11111111. В десятичном представлении это числа от 0 до 255. В шестнадцатеричном – от 0 до FF. С помощью шестнадцатеричной системы счисления удобно кратко, с помощью двух цифр-знаков, записывать значения байтов. Например, 0E или F5.

Несмотря на то, что 255₁₀ – это максимальное значение, которое можно сохранить в байте, состояний у 8-ми битного байта 256, так как одно из них отводится под хранение нуля. Количество возможных состояний ячейки памяти вычисляется по формуле 2ⁿ, где n – количество составляющих ее бит. В случае восьми бит получаем:

2⁸ = 256

Как перевести отрицательное число в шестнадцатеричную систему

Способы представления чисел

Алгоритм перевода чисел из одной системы счисления в другую

Пример №1 .

Перевод из 2 в 8 в 16 системы счисления.
Эти системы кратны двум, следовательно, перевод осуществляется с использованием таблицы соответствия (см. ниже).

Для перевода числа из двоичной системы счисления в восьмиричную (шестнадцатиричную) необходимо от запятой вправо и влево разбить двоичное число на группы по три (четыре – для шестнадцатиричной) разряда, дополняя при необходимости нулями крайние группы. Каждую группу заменяют соответствующей восьмиричной или шестнадцатиричной цифрой.

Пример №2 . 1010111010,1011 = 1.010.111.010,101.1 = 1272,51₈
здесь 001=1; 010=2; 111=7; 010=2; 101=5; 001=1

При переводе в шестнадцатеричную систему необходимо делить число на части, по четыре цифры, соблюдая те же правила.
Пример №3 . 1010111010,1011 = 10.1011.1010,1011 = 2B12,13_HEX
здесь 0010=2; 1011=B; 1010=12; 1011=13

Перевод чисел из 2 , 8 и 16 в десятичную систему исчисления производят путем разбивания числа на отдельные и умножения его на основание системы (из которой переводится число) возведенное в степень соответствующую его порядковому номеру в переводимом числе. При этом числа нумеруются влево от запятой (первое число имеет номер 0) с возрастанием, а в правую сторону с убыванием (т.е. с отрицательным знаком). Полученные результаты складываются.

Пример №4 .
Пример перевода из двоичной в десятичную систему счисления. Пример перевода из восьмеричной в десятичную систему счисления. Пример перевода из шестнадцатеричной в десятичную систему счисления.

Еще раз повторим алгоритм перевода чисел из одной системы счисления в другую ПСС

Из десятичной системы счисления:
разделить число на основание переводимой системы счисления;
найти остаток от деления целой части числа;
записать все остатки от деления в обратном порядке;
Из двоичной системы счисления
Для перевода в десятичную систему счисления необходимо найти сумму произведений основания 2 на соответствующую степень разряда;
Для перевода числа в восьмеричную необходимо разбить число на триады.
Например, 1000110 = 1 000 110 = 106₈
Для перевода числа из двоичной системы счисления в шестнадцатеричную необходимо разбить число на группы по 4 разряда.
Например, 1000110 = 100 0110 = 46₁₆

Позиционной называется система, для которой значимость или вес цифры зависит от ее места расположения в числе. Соотношение между системами выражается таблицей.
Таблица соответствия систем счисления:

Двоичная СС	Шестнадцатеричная СС
0000	0
0001	1
0010	2
0011	3
0100	4
0101	5
0110	6
0111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

Таблица для перевода в восьмеричную систему счисления

Двоичная СС	Восьмеричная СС
000	0
001	1
010	2
011	3
100	4
101	5
110	6
111	7

Пример №2 .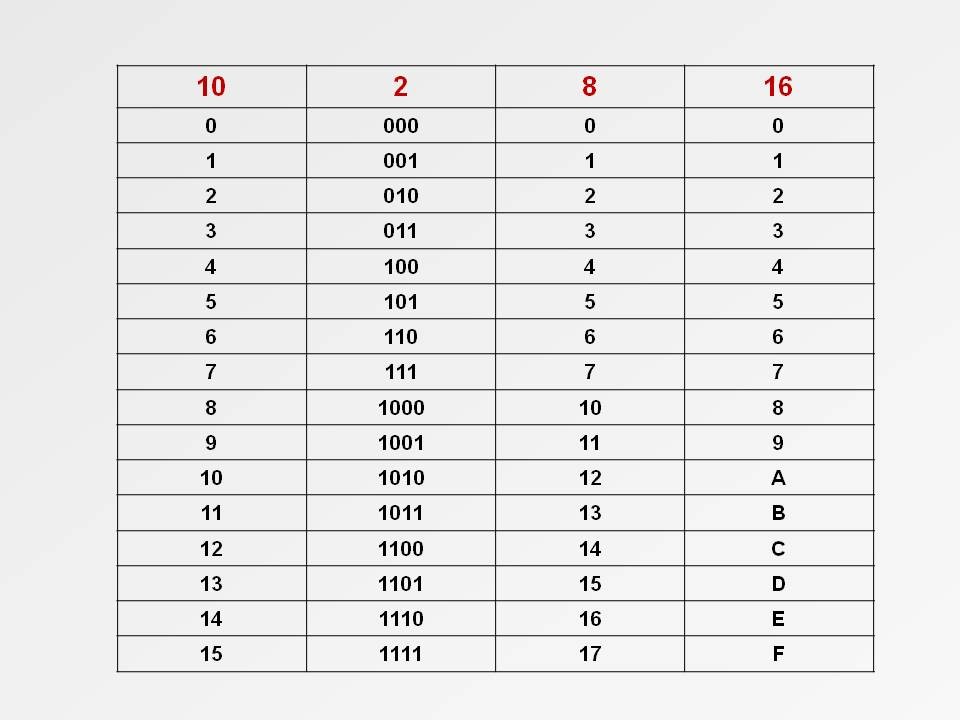 Перевести число 100,12 из десятичной системы счисления в восьмеричную систему счисления и обратно. Пояснить причины расхождений.
Решение.
1 Этап. Перевод числа из десятичной системы счисления в восьмеричную систему счисления.

Целая часть от деления	Остаток от деления
100 div 8 = 12	100 mod 8 = 4
12 div 8 = 1	12 mod 8 = 4	1 div 8 = 0	1 mod 8 = 1

Остаток от деления записываем в обратном порядке. Получаем число в 8-ой системе счисления: 144
100 = 144₈

Для перевода дробной части числа последовательно умножаем дробную часть на основание 8. В результате каждый раз записываем целую часть произведения.
0.12*8 = 0.96 (целая часть 0)
0.96*8 = 7.68 (целая часть 7)
0.68*8 = 5.44 (целая часть 5)
0.44*8 = 3.52 (целая часть 3)
Получаем число в 8-ой системе счисления: 0753.
0.12 = 0.753₈

2 Этап. Перевод числа из десятичной системы счисления в восьмеричную систему счисления.
Обратный перевод из восьмеричной системы счислений в десятичную.

Для перевода целой части необходимо умножить разряд числа на соответствующую ему степень разряда.
144 = 8 2 *1 + 8 1 *4 + 8 0 *4 = 64 + 32 + 4 = 100

Для перевода дробной части необходимо разделить разряд числа на соответствующую ему степень разряда
0753 = 8 -1 *0 + 8 -2 *7 + 8 -3 *5 + 8 -4 *3 = 0.119873046875 = 0.1199

144,0753₈ = 100,96₁₀
Разница в 0,0001 (100,12 – 100,1199) объясняется погрешностью округлений при переводе в восьмеричную систему счислений. Эту погрешность можно уменьшить, если взять большее число разрядов (например, не 4, а 8).

Сдающим ЕГЭ и не только…

Странно, что в школах на уроках информатики обычно показывают ученикам самый сложный и неудобный способ перевода чисел из одной системы в другую. Это способ заключается в последовательном делении исходного числа на основание и сборе остатков от деления в обратном порядке.

Например, нужно перевести число 810₁₀ в двоичную систему:

Результат записываем в обратном порядке снизу вверх. Получается 81010 = 11001010102

Если нужно переводить в двоичную систему довольно большие числа, то лестница делений приобретает размер многоэтажного дома. И как тут собрать все единички с нулями и ни одной не пропустить?

В программу ЕГЭ по информатике входят несколько задач, связанных с переводом чисел из одной системы в другую. Как правило, это преобразование между 8- и 16-ричными системами и двоичной. Это разделы А1, В11. Но есть и задачи с другими системами счисления, как например, в разделе B7.

Для начала напомним две таблицы, которые хорошо бы знать наизусть тем, кто выбирает информатику своей дальнейшей профессией.

Таблица степеней числа 2:

2 1	2 2	2 3	2 4	2 5	2 6	2 7	2 8	2 9	2 10
2	4	8	16	32	64	128	256	512	1024

Она легко получается умножением предыдущего числа на 2. Так, что если помните не все эти числа, остальные нетрудно получить в уме из тех, которые помните.

Таблица двоичных чисел от 0 до 15 c 16-ричным представлением:

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0000	0001	0010	0011	0100	0101	0110	0111	1000	1001	1010	1011	1100	1101	1110	1111
0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F

Недостающие значения тоже нетрудно вычислить, прибавляя по 1 к известным значениям.

Перевод целых чисел

Итак, начнем с перевода сразу в двоичную систему. Возьмём то же число 810₁₀. Нам нужно разложить это число на слагаемые, равные степеням двойки.

Ищем ближайшую к 810 степень двойки, не превосходящую его. Это 2 9 = 512.
Вычитаем 512 из 810, получаем 298.
Повторим шаги 1 и 2, пока не останется 1 или 0.
У нас получилось так: 810 = 512 + 256 + 32 + 8 + 2 = 2 9 + 2 8 + 2 5 + 2 3 + 2 1 .

Далее есть два способа, можно использовать любой из них. Как легко увидеть, что в любой системе счисления её основание всегда 10. Квадрат основания всегда будет 100, куб 1000. То есть степень основания системы счисления — это 1 (единица), и за ней столько нулей, какова степень.

Способ 1: Расставить 1 по тем разрядам, какие получились показатели у слагаемых. В нашем примере это 9, 8, 5, 3 и 1. В остальных местах будут стоять нули. Итак, мы получили двоичное представление числа 810₁₀ = 1100101010₂ . Единицы стоят на 9-м, 8-м, 5-м, 3-м и 1-м местах, считая справа налево с нуля.

Способ 2: Распишем слагаемые как степени двойки друг под другом, начиная с большего.

810 =

2 9 =	1000000000	(1 и девять нулей) +
2 8 =	100000000	(1 и восемь нулей) +
2 5 =	100000	(1 и пять нулей) +
2 3 =	1000	(1 и три нуля) +
2 1 =	10	(1 и один ноль)

А теперь сложим эти ступеньки вместе, как складывают веер: 1100101010 .

Вот и всё. Попутно также просто решается задача «сколько единиц в двоичной записи числа 810?».

Ответ — столько, сколько слагаемых (степеней двойки) в таком его представлении. У 810 их 5.

Теперь пример попроще.

Переведём число 63 в 5-ричную систему счисления. Ближайшая к 63 степень числа 5 — это 25 (квадрат 5). Куб (125) будет уже много. То есть 63 лежит между квадратом 5 и кубом. Тогда подберем коэффициент для 5 2 . Это 2.

Получаем 63₁₀ = 50 + 13 = 50 + 10 + 3 = 2 * 5 2 + 2 * 5 + 3 = 223₅ .

Ну и, наконец, совсем лёгкие переводы между 8- и 16-ричными системами. Так как их основанием является степень двойки, то перевод делается автоматически, просто заменой цифр на их двоичное представление. Для 8-ричной системы каждая цифра заменяется тремя двоичными разрядами, а для 16-ричной четырьмя. При этом все ведущие нули обязательны, кроме самого старшего разряда.

Переведем в двоичную систему число 547₈.

Ещё одно, например 7D6A₁₆.

7D6A₁₆=	(0)111	1101	0110	1010
7	D	6	A

Переведем в 16-ричную систему число 7368. Сначала цифры запишем тройками, а потом поделим их на четверки с конца: 736₈ = 111 011 110 = 1 1101 1110 = 1DE₁₆ . Переведем в 8-ричную систему число C25₁₆. Сначала цифры запишем четвёрками, а потом поделим их на тройки с конца: C25₁₆ = 1100 0010 0101 = 110 000 100 101 = 6045₈ . Теперь рассмотрим перевод обратно в десятичную. Он труда не представляет, главное не ошибиться в расчётах. Раскладываем число на многочлен со степенями основания и коэффициентами при них. Потом всё умножаем и складываем. E68₁₆ = 14 * 16 2 + 6 * 16 + 8 = 3688 . 732₈ = 7 * 8 2 + 3*8 + 2 = 474 .

Перевод отрицательных чисел

Здесь нужно учесть, что число будет представлено в дополнительном коде. Для перевода числа в дополнительный код нужно знать конечный размер числа, то есть во что мы хотим его вписать — в байт, в два байта, в четыре. Старший разряд числа означает знак. Если там 0, то число положительное, если 1, то отрицательное. Слева число дополняется знаковым разрядом. Беззнаковые (unsigned) числа мы не рассматриваем, они всегда положительные, а старший разряд в них используется как информационный.

Для перевода отрицательного числа в двоичный дополнительный код нужно перевести положительное число в двоичную систему, потом поменять нули на единицы и единицы на нули. Затем прибавить к результату 1.

Итак, переведем число -79 в двоичную систему. Число займёт у нас один байт.

Переводим 79 в двоичную систему, 79 = 1001111. Дополним слева нулями до размера байта, 8 разрядов, получаем 01001111. Меняем 1 на 0 и 0 на 1. Получаем 10110000. К результату прибавляем 1, получаем ответ 10110001 . Попутно отвечаем на вопрос ЕГЭ «сколько единиц в двоичном представлении числа -79?». Ответ — 4.

Прибавление 1 к инверсии числа позволяет устранить разницу между представлениями +0 = 00000000 и -0 = 11111111. В дополнительном коде они будут записаны одинаково 00000000.

Перевод дробных чисел

Дробные числа переводятся способом, обратным делению целых чисел на основание, который мы рассмотрели в самом начале. То есть при помощи последовательного умножения на новое основание с собиранием целых частей. Полученные при умножении целые части собираются, но не участвуют в следующих операциях. Умножаются только дробные. Если исходное число больше 1, то целая и дробная части переводятся отдельно, потом склеиваются.

Переведем число 0,6752 в двоичную систему.

0	,6752
*2
1	,3504
*2
0	,7008
*2
1	,4016
*2
0	,8032
*2
1	,6064
*2
1	,2128

Процесс можно продолжать долго, пока не получим все нули в дробной части или будет достигнута требуемая точность. Остановимся пока на 6-м знаке.

Получается 0,6752 = 0,101011 .

Если число было 5,6752, то в двоичном виде оно будет 101,101011 .

Введение

В повседневной деятельности мы привыкли к счету с применением цифр 1, 2, 3 и т. д. Вследствие технических особенностей, компьютер применяет другой метод счета, в котором используется всего две цифры 0 и 1. Например, до пяти компьютер считает так: 1, 10, 11, 100, 101. Числа 10, 11, 100 . являются двоичными, они базируются на системе счисления, состоящей из двух цифр. Десятичная система состоит из десяти цифр 0 . 9.

Одно и тоже число можно записать в разных системах счисления. Например: двоичное число 10 соответствует десятичному 2.

Компьютер может оперировать только двоичными числами. Но программисту очень неудобно использовать длинные цепочки нулей и единиц, отображающих разные числовые значения. Поэтому, для написания программ был придуман другой, более компактный способ записи чисел – шестнадцатеричная система счисления.

Изучение шестнадцатеричной системы счисления мы начнем в специальной программе – DEBUG.EXE, которая входит в состав операционной системы Windows.

Debug

Название Debug произошло от слова “Bugs” (насекомые) – так программисты именуют ошибки в программе.

Используя Debug можно проверить работу программы в пошаговом режиме. Это позволяет найти и исправить возможные ошибки. Данный процесс называется отладка “debugging”, отсюда и произошло название программы.

Термин “debugging” (обезжучивание) имеет глубокие корни – он появился в тот день, когда перестал работать компьютер Гарвардского университета Марк 1. После долгих поисков техники обнаружили небольшую моль, попавшую между контактами реле. Они удалили моль и внесли запись в сменный журнал о процессе под названием “debugging”, произведенном над Марком.

Наиболее удобной средой для изучения Debug является файл-менеджер FAR. Для запуска Debug необходимо в командной строке FAR-а набрать команду “debug” и нажать [Enter]:

Дефис означает, что Debug ждет команды. Чтобы покинуть программу наберите команду “Q” (Quit – выход) и нажмите ввод:

Для сложение и вычитание двух шестнадцатеричных чисел используем команду “H” (Hex – шестнадцатеричный), например:

Debug печатает сумму 3 + 2 = 5 и разность 3 – 2 = 1. С числами от 0 до 9 Debug ведет себя как с десятичными числами. Сходство между шестнадцатеричной и десятичной системами заканчивается при получении результата больше девяти, например 9 + 1:

A – это шестнадцатеричное число, аналог десятичного числа 10. Выполните вычисления: 9 + 2, 9 + 3, 9 + 4, 9 + 5, 9 + 6. В результате получатся остальные числа: B, C, D, E, F. Такой способ записи чисел является очень компактным и удобным с точки зрения представления информации в компьютере.

Debug работает только с шестнадцатеричными числами. Некоторые операции с такими числами могут давать не совсем обычные результаты. Например, сложите 8 + 8:

10 – это шестнадцатеричное число, аналог десятичного числа 16. Теперь найдите разность между числами 2 и 3:

Разность чисел FFFF – это шестнадцатеричное число, соответствующее единице со знаком минус “-1”. Попробуйте получить -2, -3 и другие отрицательные числа.

Перевод шестнадцатеричных чисел в десятичную форму

Название “шестнадцатеричный” произошло от числа 16. Цифры 0 . 9 одинаковы и для шестнадцатеричной, и для десятичной систем счисления. Шестнадцатеричные цифры от A до F соответствуют десятичным числам от 10 до 15. Соответствие между десятичными числами (Decimal) и шестнадцатеричными (Hexadecimal) можно представить в виде таблицы:

dec	hex
0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10	A
11	B
12	C
13	D
14	E
15	F
16	10
17	11
18	12
19	13
20	14

Обычно шестнадцатеричные числа помечают специальным символом “h”: 12h, F8h, 10h и др. Это позволяет избегать путаницы между десятичными и шестнадцатеричными числами, не содержащими букв: 12 – десятичное, 12h – шестнадцатеричное.

Для перевода чисел из hex- в dec- форму используется очень простой алгоритм.
Например, переведем A7h в десятичную форму:

1	переводим обе цифры в десятичную форму	A => 10 7 => 7
2	умножаем каждое число на коэффициент, соответствующий разряду числа (весовой коэффициент)	10 * 16 1 = 160 7 * 16 0 = 7
3	складываем полученные числа	160 + 7 = 167

Шестнадцатеричное число A7h соответствует десятичному числу 167.
Данный пример можно записать более компактно:

A => 10 * 16 1 = 160
7 => 7 * 16 0 = 7 перевод числа A7h в десятичную форму
A7h = 160 + 7 = 167

Примеры перевода чисел из одной системы счисления в другую:

Перевод 2E8h в десятичную форму:

Перевод AF1Ch в десятичную форму:

2 => 2 * 16 2 = 512
E => 14 * 16 1 = 224
8 => 8 * 16 0 = 8
2E8h = 512 + 224 + 8 = 744

A => 10 * 16 3 = 40960
F => 15 * 16 2 = 3840
1 => 1 * 16 1 = 16
C => 12 * 16 0 = 12
AF1Ch = 40960 + 3840 + 16 + 12 = 44828

Весовые коэффициенты:Перевод 3B8D2h в десятичную форму:16 46553516 3409616 225616 11616 01

3 => 3 * 16 4 = 196608
B => 11 * 16 3 = 45056
8 => 8 * 16 2 = 2048
D => 13 * 16 1 = 208
2 => 2 * 16 0 = 2
3B8D2h = 196608 + . + 2 = 243922

Переведите следующие шестнадцатеричные числа в десятичную форму:

Сложение и вычитание шестнадцатеричных чисел

Сложение и вычитание шестнадцатеричных чисел проходит аналогично действиям над десятичными числами.
Приведем несколько простых примеров:

Рассмотрим, как получается 1Eh в результате сложения F + F. Запишем результат операции в десятичном виде: F + F = 15 + 15 = 30.

Проверим, сколько шестнадцатеричных десятков содержится в числе 30: 30 / 16 = 1 (один десяток). Шестнадцатеричный десяток 10h соответствует десятичному числу 16. Проводим вычитание 30 – 16 и получаем остаток 14, откуда: 14 + 16 = Eh + 10h = 1Eh.

Числа с большим числом разрядов можно складывать “столбиком”:

Вычислите “столбиком” следующие примеры, а результаты проверьте в Debug:

Пятизначные шестнадцатеричные числа

Что произойдет, если в сложении использовать пятизначное шестнадцатеричное число? Вычислим сумму следующих чисел:

Debug сообщил об ошибке. Команда “h” не может обрабатывать числа, длина которых больше четырех разрядов. Шестнадцатеричное число, состоящее из четырех разрядов называют так: “СЛОВО” или “WORD”.

Если сложить два “слова”, например C000h и D000h, то вместо действительного результата 19000h получится “урезанный” до четырех разрядов результат 9000h:

Debug сохраняет четыре младших цифры ответа, а единицу из старшего разряда заносит в специальную ячейку, которая будет рассмотрена позже.

Подумайте, какое значение имеет старший (пятый) разряд при сложении четырехразрядных шестнадцатеричных чисел?

Перевод десятичных чисел в шестнадцатеричную форму

Перевод десятичного числа в шестнадцатеричную форму выполняется делением исходного числа на 16. Например, переведем 300 в шестнадцатеричную форму:

Примеры перевода чисел 1000 и 60000 в шестнадцатеричную форму:

Переведите следующие числа в шестнадцатеричную форму:

Шестнадцатеричный результат переведите обратно в десятичную форму – это позволит проверить корректность ваших действий.

Отрицательные числа

Ранее было отмечено, что FFFFh фактически равно -1. Однако если перевести число FFFFh в десятичную форму, то получится 65535. Почему так происходит? Действительно ли FFFFh ведет себя как отрицательное число?

Пусть так, тогда если сложить FFFFh и 5, то должно получиться 4:

Похоже, Debug действительно обращается с FFFFh, как с -1. Рассмотрим механизм сложения чисел 5 и FFFFh, при суммировании “столбиком”:

Если игнорировать единицу в старшем разряде, то получается правильный ответ 5 + (-1) = 4. Debug сохраняет четыре младшие цифры результата. Старший (пятый) разряд запоминается в специальной ячейке памяти и называется – “ПЕРЕПОЛНЕНИЕ”.

FFFF	-1
FFFE	-2
FFFD	-3
FFFC	-4
FFFB	-5
FFFA	-6
FFF9	-7
FFF8	-8
FFF7	-9
FFF6	-A
FFF5	-B
FFF4	-C
FFF3	-D
FFF2	-E
FFF1	-F
FFF0	-10

Сложение чисел, больших чем 8000h дает переполнение. Такие числа ведут себя аналогично отрицательным числам:

В последнем примере установлено соответствие чисел 8FEFh и -7011h. Как проверить справедливость этого утверждения? Ранее отмечалось, что FFFFh это (-1), значит FFFEh это (-2) и т.д. В приведенной таблице представлен ряд отрицательных чисел. Если ряд продолжить, то при достижении числа 8FEFh мы увидим его отрицательный эквивалент: -7011h

Любой язык программирования позволяет оперировать двумя типами чисел: знаковыми и беззнаковыми. Представление числа зависит от конкретной ситуации. Например: FFFAh можно рассматривать как число без знака, и как отрицательное число -6. Если в программе нужны отрицательные числа, то диапазон 0 . FFFFh делится на две части:

Отрицательный аналог числа 8FEFh называется его дополнительным кодом, и выражается числом -7011h.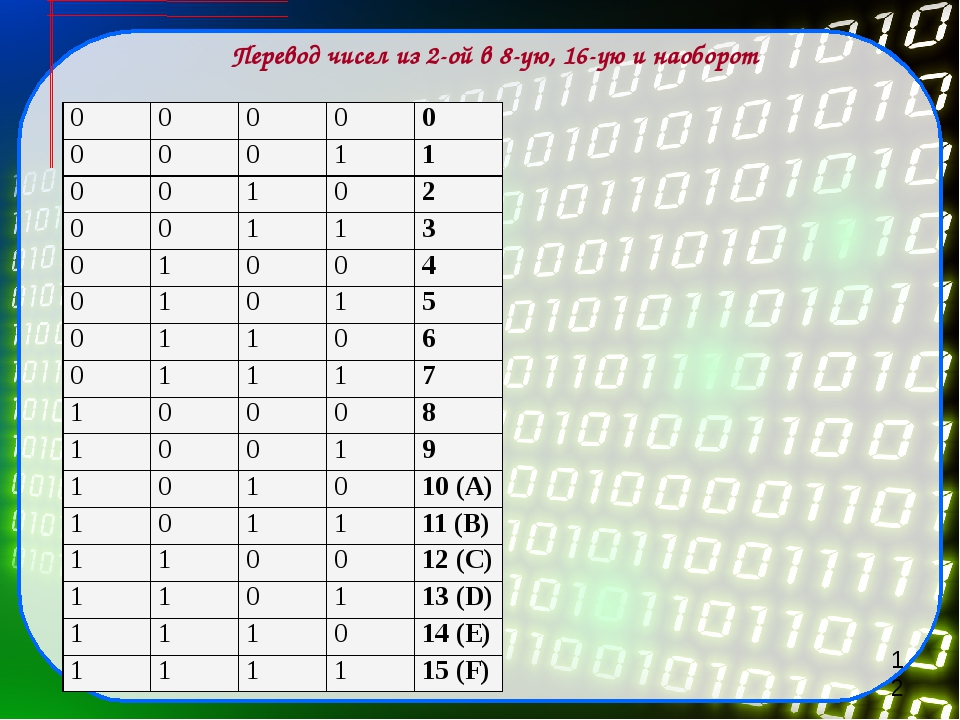 Рассмотрим алгоритм нахождения дополнительного кода:

Инвертировать исходное число, т.е. заменить все цифры числа на противоположные:
F => 0, E => 1, D => 2, C => 3, B => 4 и т.д. После инверсии 8FEFh выглядит так: 7010h
К инверсному числу добавить единицу: 7010h + 1 = 7011h – получилось искомое число.

Если в программе используются только положительные числа, то область числовых значений ограничивается диапазоном:

Если в вычислениях требуются отрицательные числа, то предыдущий диапазон смещается в отрицательную область:

Деление чисел на два типа весьма условно, и определяется в основном потребностями программиста. При этом микропроцессору совершенно безразлично, к каким типам мы относим те или иные числа.

Вычислите дополнительный код следующих чисел:

Двоичная система счисления

Микропроцессор, будучи устройством электронным, воспринимает цифры, как комбинации электрических сигналов. Например, число может быть представлено так:

При этом вероятность возникновения ошибки (например, из-за колебаний напряжения) очень велика. Наиболее надежным способом представления чисел в электронном устройстве, является двоичная система счисления:

Такая разница между уровнями сигналов (соответствующих “0” и “1”) практически исключает ошибки связанные с колебаниями напряжения и другими искажениями сигнала. Кроме того, значительно упрощается компонентная база компьютера.

Таким образом, двоичная система счисления стала единым стандартом представления чисел в любом “думающем” электронном устройстве.

Двоичная система оптимальна для разработки микропроцессорных систем, но очень неудобна для написания программ. Чтобы упростить процесс общения с микропроцессором, были разработаны программы, транслирующие шестнадцатеричные числа в двоичный код, и выполняющие обратное преобразование. Одной из таких программ является Debug.

Для вывода на экран чисел в шестнадцатеричном формате, Debug использует небольшую подпрограмму, которая переводит двоичные числа (обрабатываемые микропроцессором), в шестнадцатеричную форму.

Двоичные числа мы будем помечать индексом “b” (binary – двоичный), например: 10010111b

Рассмотрим число 1101b. Все разряды числа характеризуются весовыми коэффициентами, которые получаются возведением основания системы счисления (два) в степень, соответствующую номеру разряда. Нумерация разрядов начинается с нуля.

Для перевода числа из двоичной системы в десятичную, необходимо выбрать весовые коэффициенты тех разрядов, где есть единица (в случае числа 1101b, это: 2 3 , 2 2 и 2 0 ). Далее нужно сложить эти числа: 2 3 + 2 2 + 2 0 = 13

Номера разрядов	3	2	1	0
Весовые коэффициенты	2 3	2 2	2 1	2 0
Число	1	1	0	1

Перевод числа 11010010b в десятичную форму:

2 7	2 6	2 5	2 4	2 3	2 2	2 1	2 0
1	1	0	1	0	0	1	0
2 7 + 2 6 + 2 4 + 2 1 = 210

Переведите следующие двоичные числа в десятичный формат:

По размеру двоичные числа делятся на следующие:

Графически это разделение можно показать так:

bin	hex	dec
0000	0	0
0001	1	1
0010	2	2
0011	3	3
0100	4	4
0101	5	5
0110	6	6
0111	7	7
1000	8	8
1001	9	9
1010	A	10
1011	B	11
1100	C	12
1101	D	13
1110	E	14
1111	F	15

Рассмотрим таблицу, в которой отражено соответствие двоичных, шестнадцатеричных и десятичных чисел.

Из таблицы видно, что двоичная и шестнадцатеричная системы кратны между собой. Данную пропорциональность в размерности чисел можно сформулировать так:

Благодаря кратности, преобразования чисел из двоичной системы в шестнадцатеричную, выполняются очень просто. Двоичное число разбивается на декады (четырехбитные фрагметны):

Каждая декада переводится в шестнадцатеричный формат, аналогично преобразованию чисел из двоичной системы счисления в десятичную:

Переведите следующие числа в шестнадцатеричную форму:

Арифметические действия с двоичными числами выполняются аналогично действиям с десятичными числами. Например, сложение одноразрядных двоичных чисел выглядит так:

Сложение четырехразрядных и восьмиразрядных двоичных чисел:

Выполните следующие действия:

(проверку результатов выполните в шестнадцатеричной системе счисления)

Дополнительный код

0000 0000 0000 0000	0000h
.	.
0111 1111 1111 1111	7FFFh
1000 0000 0000 0000	8000h
.	.
1111 1111 1111 1111	FFFFh

Раннее отмечалось, что в некоторых случаях числа 8000h . FFFFh ведут себя как отрицательные.
Рассмотрим числа 0 . FFFFh в двоичной системе счисления. Данный ряд делится на две равные части. Cтарший бит, в двоичном представлении чисел, выделен жирным шрифтом. Начиная с числа 8000h, старший бит устанавливается в единицу.

Старший бит является признаком отрицательного числа. По его состоянию микропроцессор определяет знак числа. Но если в программе используются команды для чисел без знака, то микропроцессор игнорирует знаковый бит, и воспринимает диапазон [0 . FFFFh] как ряд положительных чисел.

Числа, в которых старший бит используется для хранения знака, известны как двоичное дополнение положительных чисел или дополнительный код.

Ранее мы находили дополнительный код шестнадцатеричных чисел (вспомните инверсию шестнадцатеричного числа с добавлением единицы). Дополнительный код двоичного числа определяется аналогично. Например, найдем дополнительный код числа 1101011010001001:

Вычитание двоичных чисел, например A – B, сводится к их сложению A + (-B). При этом: A не меняется, B преобразуется в дополнительный код. Далее числа складываются. Например, надо произвести вычитание 1101b – 1010b:

“>

суть, правила, плюсы и минусы, эффективность интервального похудения

Intermittent fasting (IF), интермиттент-фастинг, прерывистый пост или интервальное голодание – это относительно новая схема питания, при которой разрешено употреблять пищу только конкретный промежуток времени. К примеру, 4 или 8 часов. А в остальное время можно налегать разве что на воду или фрукто-овощные соки (в мягком варианте подобного питания).

Одним из самых популярных разновидностей такого цикличного голодания является диета 8 на 16 – она же 16/8. В некоторых странах бум на неё начался еще в 2017-м, а в Украину этот тренд пришел совсем недавно, в первую очередь, затронув звезд и инфлюенсеров. Сторонники диеты утверждают, что это простой, удобный и эффективный способ похудеть и улучшить общее состояние здоровья. Также, поговаривают, она способствует омоложению и хорошему настроению.

В ТЕМУ: Как похудеть на 5 кг с пользой для организма: меню на пять дней от диетолога

Питание по принципу 8:16 подходит для тех, кто не знает, как похудеть быстро и сбросить пару лишних кило без насилия над организмом. Некоторые люди настолько привыкают к подобному режиму питания, что придерживаются его годами. На первый взгляд идея питаться лишь в определенное время может показаться абсурдной, но в ней есть рациональное зерно, о котором и поговорим дальше.

В чем суть диеты 16/8?

16/8 – это не дроби, как тебе могло показаться. Цифра 16 означает период поста, то есть время, когда организм должен голодать, а 8 в свою очередь – часовой промежуток, в который разрешено употреблять пищу. В сумме обе цифры дают 24 – то есть, количество часов в сутках, о чем ты уже могла догадаться.

Самое главное, что тебе нужно знать об этой диете – в период 8-часового окна ты можешь есть всё, что хочешь, и в таком количестве, сколько душа пожелает. Но по окончанию времени – ни крошки в рот! Да, тебе не показалось: в течение 8 часов можно свободно потреблять столько калорий, сколько хочешь, кушая при этом любые продукты (да, даже булочку и шоколадку) – это не помешает потере веса. Такой режим питания очень хорошо ускоряет метаболизм.

Правила диеты 8/16

Как ты уже поняла из сути такого питания, потреблять калории можно только в определенное время суток (на протяжении 8 часов) и разрешается есть любые продукты без ограничений, а в остальной промежуток времени (оставшиеся 16 часов) организм будет усиленно сжигать калории.

Цикличный способ голодания достаточно либерален: худеющий может сам определять свои временные рамки приема пищи, зависящие от собственных биоритмов и ежедневных обстоятельств. Если ты жаворонок, тебе будет проще питаться, к примеру, с 08:00 до 16:00 или же с 09:00 до 17:00 вечера. Совам же вполне подойдет время с 12:00 до 20:00.

Есть можно разрешенные продукты (о них поговорим чуть позже), а для повышения эффективности и запуска обменных процессов, рекомендуется включить в свой график питания тренировки. Не пугайся: достаточно посвятить 8-10 минут времени по утрам активным физическим упражнениям и кардио. На первый взгляд всё просто, но минусы и подводные камни в таком похудении всё же есть. О них узнаешь дальше.

Продуктовая корзина

Несмотря на то, что при такой диете можно есть всё, что угодно, есть ряд продуктов, которые рекомендуется включить в свой рацион при системе питания 8/16, чтобы получить не только ушедшие объемы, но и улучшить здоровье. Делятся они на две категории.

Жиросжигающие:

постное, нежирное мясо (курица, индейка, кролик) и яйца;
орехи (миндаль и грецкие), а также сырые тыквенные семечки;
бобовые: фасоль, нут, горох;
молочная продукция с низким содержанием жиров (например, йогурт без добавок).

Оздоровительные:

синие и красные ягоды: вишня, смородина, ежевика;
источники клетчатки и антиоксидантов: цитрусовые, яблоки и т.д.;
овощи зеленого цвета и зелень: все виды капусты, огурцы, шпинат и пр.;
каротиноиды- и ликопин-содержащие овощи: помидоры, морковь, сладкий перец.

В каждый из приемов пищи рекомендуется включать хотя бы по одному продукту из обеих групп. Количество потребляемых углеводов нужно минимизировать либо вовсе отказаться. Но если ты не можешь без них обойтись, хитри: сочетай пасту с нежирным сыром и овощами, хлопья с молоком и фруктами, а хлеб добавляй к постному мясу и салату. Алкоголь стоит ограничить, а вот воды нужно пить много, особенно в голодающее окно.

Польза диеты 8/16

Обувь на картинке от интернет магазина Бестеп.

Эксперты по питанию говорят, что интервальное голодание способствует разгону метаболизма, что и приводит к достаточно быстрой потере килограммов. Также, по мнению американских ученых, диета 8:16 позволяет снизить не только вес, но и артериальное давление, продлить молодость и пребывать в хорошем настроении.

При этом на ней позволено питаться именно тем, чего желает человек (разумеется, в ограниченный период). А во время поста о еде необходимо забыть, но именно в этом интервале организм будет сжигать калории, а ты – терять вес.

Главное – настрой. И в моменты, когда тебе будет казаться, что придерживаться такого режима очень сложно, помни, что есть еще одна версия интервального голодания – диета 20/4, а она гораздо суровее 🙂

Недостатки диеты 8/16

Конечно, как и в любом другом методе похудения с помощью диет и специальных систем питания, здесь также есть свои подводные камни. Их всего несколько, но тебе стоит об этом знать.

Во-первых, стоит помнить об индивидуальном факторе: люди, критикующие эту диету, нарекают, что план питания работает не у всех. И это правда. Эксперты британской диетической ассоциации (BDA) говорят, что концепция этой системы будет работать только у тех, у кого нет нарушений обмена веществ и расстройства пищевого поведения или эмоционального переедания.

Во-вторых, по утверждениям диетологов, эффект после этой диеты может длится недолго, а в некоторых случаях он мимолетен, но многие превращают эту систему питания в свой сбалансированный образ жизни, что и позволяет им удерживать вес.

Если ты не готова на такие подвиги, смотри трезво на ситуацию и устанавливай для себя более реалистичные цели. Минус 5-10% медленной, но неуклонной потери веса при здоровом и сбалансированном питании, подкрепленном физической активностью (например, утренние привычки по типу вакуума и планки + получасовая тренировка вечером) приведут тебя к желаемому и, главное, устойчивому результату.

Интервальное голодание 16/8 — расписание, правила и отзывы

Интервальное голодание — это система питания, подразумевающая регулярный отказ от употребления пищи на определенный промежуток времени. Одним из наиболее популярных режимов является график 16/8 — прием пищи запрещен на 16 часов, после которых следуют 8 часов, когда можно есть.

Правила диеты 16/8 подразумевают отказ от завтрака, плотный обед, полдник и ранний ужин — по сути, еда допустима исключительно с полудня до 8 часов вечера. Плюсом интервального голодания является нормализация обмена веществ. Согласно отзывам, данная диета особенно эффективна для женщин.

// Диета 16/8 — что это такое?

Диета 16/8 — это система питания, подразумевающая ежедневное голодание в течение 16 часов. Поскольку большая часть этого времени приходится на ночь, подобную диету достаточно просто соблюдать. Кроме этого, хотя сокращение калорийности рациона желательно, но не обязательно.

Польза интервального голодания строится на том, что периодический отказ от еды является методом нормализации реакций организма на углеводы. В частности, речь идет о нормализации уровня глюкозы и улучшении процессов выработки инсулина¹. Также диета 16/8 способна оптимизировать выработку гормона голода лептина².

Исследования на животных показывают, что интервальное голодание — эффективный способ продления срока их жизни и повышения иммунитета³. Однако отметим, что в этом случае польза достигается не только за счет соблюдения системы интервального голодания 16/8, но и за счет ограничения калорийности.

// Читать дальше:

В чем принцип работы?

Употребление углеводных продуктов приводит к повышению уровня глюкозы в крови. Если энергия этой глюкозы избыточна, она отправляется в жировые запасы. Отказ от углеводов (или от питания в принципе) понижает уровень глюкозы, заставляя тело использовать резервы — на этом принципе строится работа безуглеводной кето диеты.

Прежде всего, диета 16/8 помогают бороться с синдромом инсулинорезистентности и связанными с ним болезнями —ожирением и повышенным давлением. Исследования показывают, что интервальное голодание уменьшает количество микровоспалений в организме и снижает уровень гормона стресса кортизола³.

Кроме этого, отдельное значение имеют упомянутые выше гормональные изменения — низкий инсулин и высокий гормон роста провоцируют выброс в кровь мощного жиросжигающего гормона норадреналина. В среднем, интервальное голодание повышает скорость метаболизма на цифру от 3.6 до 14%.

// Читать дальше:

Интервальное голодание 16/8 — отзывы

Интервальное голодание и диета 16/8 — действенный метод борьбы с зависимость от сладкого. Зачастую чувство голода — это вовсе не настоящий голод, а лишь сигнал организма о низком уровне глюкозы в крови. То есть, желание перекусить часто связано с привычкой регулярно употреблять в пищу углеводы с высоким гликемическим индексом.

При этом полноценный переход тела в режим голодовки требует порядка 30-40 часов отказа от пищи. Лишь после этого времени включатся механизмы настоящего голода, характеризующиеся резким повышением уровней стрессового гормона кортизола и гормона голода лептина, заставляющего мозг думать исключительно о еде.

Другими словами, интервальное голодание оптимизирует метаболизм (в первую очередь, реакцию на простые углеводы) без запуска негативных процессов, связанных с полным отказом от еды.

// Читать дальше:

Отзывы читательниц Фитсевен

Зинаида:

Мне 60, и спортом не занималась никогда. Сейчас не работаю, постоянно дома. Начала интервальное голодание неделю назад, три умеренных приема пищи в день: в 10 , 14 и 18. В 17 часов — апельсин или яблоко. В 9 утра гимнастика под музыку 20-25 минут. После каждого приема пищи хожу активно по квартире 30 минут под любую музыку. Тело подтянулось, объём постепенно уходит. Вечером есть совершенно не хочется. Настроение прекрасное! Очень рекомендую!

Николь:

Очень помогает, если придерживаться этой диеты, то она станет как режим дня. Я ем в 10-12 (в 10 — кофе или чай, в 13 – обед, в 15-16 — полдник перекус), никакие изнурительные диеты не нужны, а результат отличный. Похудеете, и даже если перестанете соблюдать эту диету, быстро не наберёте свой вес.

// Читать дальше:

Интервальное голодание для женщин

Система интервального голодания особенно полезна для женщин. При соблюдении диеты 16/8 сокращение суточной калорийности питания на 15-20% и отказ от быстрых углеводов помогает быстро избавиться как от навязчивого чувства голода, так и от лишнего веса — даже при отсутствии жиросжигающих тренировок.

При этом важно помнить, что интервальное голодание заставляет организм использовать жировые резервы вовсе не за счет ограничения питания, а за счет оптимизации секреции инсулина и снижения чувствительности к углеводам с высоким гликемическим индексом.

// Читать дальше:

Противопоказания

Интервальное голодание подходит далеко не всем. Во-первых, оно не рекомендуется беременным и кормящим женщинам. Во-вторых, диета 16/8 может усугубить хронические заболевания. Плюс, в конечном итоге, влияние на здоровье будет определяться составом рациона.

Другими словами, время употребления пищи (или отказа от нее) всегда играет вторичную роль по сравнению с общей калорийностью и балансом БЖУ. При этом резкое сокращение калорийности питания (более, чем на 20% от нормы) само по себе может нести опасность для здоровья.

Правила сушки на диете 16/8

Интервальное голодание меняет работу обмена веществ — вместо переработки пищи организм переключается на использование имеющихся запасов. В результате меняется гормональный уровень, а клетки начинают избавляться от накопившегося “мусора” — данный процесс носит название аутофагия.

Исследования говорят о том, что при интервальном голодании уровень выработки гормона роста (напомним, что он ответственен за набор мышечной массы и сжигание жира) увеличивается примерно в 5 раз. Одновременно с этим снижается уровень инсулина — помогая телу быстрее извлекать энергию из жировых запасов.

Отзывы спортсменов

Изначально система интервального голодания и диета 16/8 применялась спортсменами как способ набора сухой мышечной массы без жира. Ключевыми правилами тренировок при соблюдении этой диеты являются увеличение отдыха между подходами и обязательное использование страховки при выполнении упражнений.

В случае использования диеты 16/8 для похудения, в утренний период рекомендуется проводить низкоинтенсивную и продолжительную жиросжигающую тренировку. Это может быть как кручение педалей велотренажера на протяжении не меньше 40 минут, так и прогулка быстрым шагом.

Кирилл:

Тренируюсь на пустой желудок уже 3 мес. Честно, чувствую себя гораздо лучше, чем на “сырых” тренировках. По силовым нет никаких проблем. 16 часов голода для организма не срок. Ужинаю примерно в 20:00 тренируюсь на след день в 10-11 утра. Рекомендую. Жир горит силовые растут.

Андрей:

Отличная система. Один раз пробовал – результат был хороший. Кстати ученые проверяли опытным путём, что даже спортсмены при правильном раскладе не теряют мышечную массу используя данный метод похудения.

Практические советы

При соблюдении диеты 16/8 наиболее эффективным временем для тренировки станет утро, когда уровень глюкозы в крови минимален. Отметим, что в первое время тренировки на пустой желудок могут показаться тяжелыми (особенно людям с низким уровнем физической подготовки), однако постепенно организм приспособится.

В частности, улучшатся механизмы запасания энергии из углеводов именно в гликоген (топливо для мышц), а не в жировые запасы. Упомянем и то, что тренировки при интервальном голодании допускают употребления аминокислот BCAA — они останавливают катаболические процессы и снижают аппетит.

// Читать дальше:

***

Диета 16/8 — это схема интервального голодания, изначально использовавшейся спортсменами для сушки. Данный режим питания помогает нормализовать реакцию организма на быстрые углеводы — что нормализует уровень сахара в крови и помогает похудеть (за счет снижения аппетита).

Научные источники:

Effects of Intermittent Fasting on Health, Aging, and Disease, source
Intermittent fasting: the science of going without, source
Intermittent fasting: Surprising update, source

В продолжение темы

Дата последнего обновления материала — 15 марта 2021

Система прерывистого голодания 16/8: что и почему?

Столкнувшись с болезнью, воспалением и / или увеличением веса, большинство людей начинают планировать, что они собираются есть, чтобы достичь большего здоровья. Но не менее важно знать не только , что есть , но и , когда есть . Прерывистое голодание — это стратегия планирования времени приема пищи.

Когда люди спрашивают, почему поститься? Зачем сознательно морить себя голодом? Во-первых, я говорю им, что периоды приема пищи и голодания естественны для человеческого тела, так же как периоды активности и отдыха. Тело функционирует лучше, если сбалансировано и то, и другое.

Я также люблю говорить им, что голодание не означает чрезмерный голод или «голодание». Люди, практикующие прерывистое голодание, быстро понимают, что умеренное чувство голода — это нормально, и проходят.Чем дольше вы соблюдаете периодическое голодание, тем более адаптированным вы становитесь, а чувство голода проявляется мягкими волнами. Люди, которые постятся, учатся верить, что волна пройдет, и они могут продержаться еще час или два, иногда дольше, до своего окна приема пищи или когда у них есть время поесть.

И последнее, что я хотел бы сказать: вы спрашиваете бегуна или бегуна, почему они бегают, если за ними никто не гонится? Нет, вы не стали бы спрашивать их об этом, потому что очевидно, что бегун использует свои действия как стратегию для здоровья.То же самое и с постом. Пост — это стратегия здоровья.

Польза для здоровья

Когда вы голодаете, вы становитесь более «чувствительными к инсулину». Это потому, что вы не злоупотребляете все время инсулином, чтобы постоянно проталкивать сахар в клетки. Ваше тело, ваша поджелудочная железа, ваши клетки получают перерыв. Если вы постоянно используете инсулин в хронической форме, ваше тело больше не реагирует — это десенсибилизация. Поскольку инсулин — это гормон, предполагается, что он будет пульсирующим, а не непрерывным.Непрерывное / хроническое производство инсулина является причиной высокого уровня сахара в крови. Инсулин больше не может проталкивать сахар в клетки.

Сам по себе инсулин также оказывает токсическое действие при хроническом применении и приводит к воспалению. Опять же, это потому, что инсулин является гормоном и должен быть пульсирующим. Поэтому, когда производство инсулина хронически продолжается в течение многих лет, адаптивный механизм организма должен стать инсулинорезистентным. Организм сопротивляется перегрузке.

Время имеет значение

Время является важным компонентом, потому что вы становитесь диабетиком и воспаляетесь только из-за хронической выработки и воздействия инсулина с течением времени.Вот почему для проявления преддиабетического состояния требуется около 13 лет.

По мере того, как время идет и воздействие продолжается, инсулин организма перестает продвигать сахар (глюкозу) в клетки, сахар выливается в кровоток и в ткани. Со временем у диабетиков появляются незаживающие раны и хронические инфекции. Это потому, что сахар заполняет все лишние места. Он ищет место, куда можно пойти, потому что больше не помещается в камеры.

Прерывистое голодание — это причудливый способ сказать: «Я стратегически планирую время, когда я ем.Простой способ понять это — знать, что когда вы голодаете, уровень инсулина низкий. Когда вы не голодаете, уровень инсулина высок (пока вы едите углеводы, но об этом позже).

Вот почему ваш врач просит вас голодать, когда вы делаете анализ сахара в крови. Они хотят увидеть, остается ли сахар в кровотоке через много часов (8–12 часов). Если уровень сахара высокий, это означает, что инсулин не может выполнять свою работу, потому что клетка организма больше не принимает глюкозу.Рецепторы на клетках не работают, потому что клетка уже переполнена, как чемодан, наполненный слишком большим количеством одежды. Чемодан максимально вместителен. Защелки сломаны, одежда вываливается на пол.

Преимущества голодания выходят за рамки здорового инсулинового ответа
Помимо уравновешивания инсулиновой реакции, голодание помогает при воспалениях и аутоиммунных заболеваниях. В голодном состоянии организм усиливает все клеточное «хозяйство».Он очищает от мусора, восстанавливает клетки и «сбрасывает» иммунную систему. Люди, которые голодают, живут дольше, у них меньше рака, риска сердечно-сосудистых заболеваний и слабоумия.
С чего начать: Метод 16-8
Есть много способов поститься. Вы можете голодать часами, днями или неделями. Но самый простой способ начать пост — это придерживаться принципа 16: 8. Это когда вы выбираете 8-часовое «окно приема пищи», а в остальное время (16 часов) вы поститесь.
Примеры окон для приема пищи:
с 11 до 19
с 12 до 20 часов
10: 00–17: 00
Выбранное вами окно может отличаться в зависимости от того, что подходит вашему расписанию. Я прошу людей оставлять 3 часа между сном и ужином. Итак, если вы заканчиваете ужин в 19:00, вы спите к 22:00, а на следующий день вы не ешьте до 11:00. Вы голодали 16 часов.

Вода, чай и кофе разрешены за пределами столовой.Сахар и сливки / сливки и т. Д. Не допускаются. Если вам абсолютно необходимо что-то в кофе, в первые дни голодания вы можете использовать источник жира, например цельные сливки (не ½ и ½, а цельные сливки, содержащие весь жир) или масло. Если вы используете цельные сливки или масло, это не «настоящий» пост, но он все равно поможет вам перейти в режим сжигания жира, потому что не вызовет большого скачка инсулина. Однако по мере того, как вы привыкните к голоданию, вы перейдете на черный чай или кофе в качестве утреннего напитка, чтобы получить все преимущества настоящего голодания.

Пост способствует более гибкому питанию
Пост — инструмент, и он гибкий. Поскольку вы проводите больше времени в состоянии сжигания жира (с низким уровнем инсулина), вы можете быть более гибкими в своем окне приема пищи. Тем не менее, для людей с сильным воспалением, увеличением веса, диабетом или преддиабетом вам, вероятно, придется придерживаться относительно низкоуглеводной или кето-диеты в своем окне приема пищи.
Пост можно использовать как стратегию «откладывать, не отрицай».Я действительно рекомендую людям как можно больше придерживаться здоровой пищи в свой период приема пищи. Тем не менее, голодание — удобный инструмент после уик-энда, посвященного социальным сборищам, где еды, возможно, было слишком много!
Пост — это не ограничение калорий

Диеты с ограничением калорий кратковременно помогают похудеть, потому что на какое-то время вы снижаете потребление энергии. Проблема в том, что организм приспосабливается и замедляет метаболизм, чтобы компенсировать это.Это может повредить ваш метаболизм, если делать это хронически, и люди в конечном итоге набирают больше веса, даже если они продолжают «диету» (ограничение калорий) и упражнения.

Пост не повредит вашему метаболизму, потому что вы не ограничиваете количество калорий, вы просто стратегически рассчитываете время приема пищи. Вы намеренно проводите более длительный период времени с низким уровнем инсулина. Вы не будете беспокоиться о калориях и не будете отслеживать их во время голодания.

Большинство людей придерживаются низкоуглеводной или кето-диеты. Вы сосредоточитесь на получении большого количества полезных жиров и белков.Это будет ваш основной источник топлива.
Кузов работает на гибридном двигателе
Человеческая физиология очень разумна. Он разработал систему с двумя двигателями, в которой тело может сжигать два типа источников топлива — сахар или жир. Вот почему вы не погибнете посреди ночи, если не съедите банан. Снижается уровень глюкозы, инсулина и повышается уровень другого гормона, называемого глюкагоном. Начинается сжигание жира.

Инсулин и глюкагон — противоположности, инь и янь.Две стороны качелей. Когда инсулин натощак низкий, глюкагон высокий. Глюкагон = сжигание жира. Люди начинают худеть. Если вы соблюдаете очень ограниченную углеводную диету с периодическим голоданием, вы впадете в кетоз. Это когда тело полностью погружается в режим сжигания жира, а мозг начинает использовать кетоны в качестве топлива. Голод также подавляется.
Пост нормальный
Тело было построено очень быстро. На протяжении тысячелетий мы развивались во времена пира или голода.Мы храним энергию эффективно и рационально. В наше время мы редко сталкиваемся с голодом или даже временами года. Зима обычно была временем, когда еды было мало, и мы жили за счет жировых запасов, которые увеличивались во время летнего и осеннего сбора урожая.
Но польза от нашей способности поститься выходит за рамки простого поддержания жизни. Когда мы сжигаем жировые запасы, мы производим меньше окислительного стресса, клетки восстанавливаются, и мы находимся в улучшенном психическом состоянии. Было высказано предположение, что некоторая когнитивная резкость, возникающая во время голодания, является биологической адаптацией.Чтобы охотиться на добычу, нужно быть ясным, проницательным и быстрым. Вы часто будете охотиться на добычу, когда голодны (голодны).

Большинство людей делают 8:16
Охотники-собиратели определенно сжигали жир. Им не нужно было перекусывать каждые 2-4 часа, чтобы «поддерживать стабильный уровень сахара в крови». Это было бы вредно для выживания. Только последние 40 лет мы сделали упор на завтраки с высоким содержанием углеводов (хлопья, тосты), постоянные перекусы и углеводы при каждом приеме пищи.Повальное увлечение низким содержанием жиров 80-х и 90-х годов углубило эту привычку.

Большинство людей делают 8:16. Они голодают 8 часов и едят 16. Нам просто нужно начать с изменения этих временных рамок.
Получение «Hangry»
Собиратели Hunter не зависели от глюкозы. Они не упали в кустах через 3 часа в приступе голода или «низкого уровня сахара в крови» и нуждаются в батончике для сникерса, чтобы они могли продержаться до конца своей охоты.Они поддерживали ясность ума и энергию только за счет собственных жировых запасов.
Глюкозозависимость — это когда ваше тело настолько привыкло к системе инсулин-глюкозного двигателя, что не может переключиться на двигатель, сжигающий глюкагон-жир, очень быстро или эффективно (пока). Результатом этой неэффективности является то, что когда уровень сахара в крови падает, человек становится капризным, шатким, тошнотворным и очень голодным. Это явление поддерживает зависимость некоторых людей от глюкозы, потому что они тянутся к еде в момент, когда ощущают эти симптомы.
Ирония заключается в том, что если бы они протолкнулись, выпили немного воды с электролитом (конечно, без сахара) и съели больше жира и белка во время основного приема пищи, в течение пары недель они бы легко переключились на сжигание жира и перестали бы. дольше испытывать эти экстремальные провалы.
Для здоровых людей, желающих похудеть
Это зависит от того, сколько веса вы хотите сбросить. Если вы все еще зависимы от глюкозы и не занимаетесь кето, разумно начинать с 16: 8, 3-7 дней в неделю.Через 2 недели вы можете уменьшить окно приема пищи до 18: 6 или даже 20: 4. Некоторые люди могут легко перейти на 22: 2. Когда вы сокращаете свое окно, вы можете перейти на 3 дня в неделю и делать 16: 8 в остальную часть недели.
Убедитесь, что вы съели достаточно в течение вашего периода приема пищи. Опять же, это не ограничение калорий и не подсчет калорий!
Для тех, кто хочет похудеть, а также страдает диабетом или другими видами воспалений (аутоиммунитет и т. Д.).)
Прежде всего, вы должны находиться под наблюдением опытного врача, который обучен диетическому лечению вашего конкретного заболевания.
Во-вторых, все люди разные и имеют разные потребности, даже те, у кого одинаковый диагноз или расстройство. Вы должны находиться под наблюдением врача, который провел полный анализ ваших систем. Желательно, чтобы команда врачей, которые хорошо играли друг с другом, и координировали ваше лечение .
Тем не менее, большинство людей будут следовать указанным выше рекомендациям, но вы будете чаще консультироваться со своим врачом. Этим людям обычно необходимо придерживаться той или иной версии низкоуглеводного образа жизни. Я также рекомендую следить за уровнем глюкозы в крови, проверяя его утром и через 90-120 минут после еды.
Нет, не всем следует поститься
Некоторым людям не следует поститься. Сюда входят беременные и / или кормящие женщины, люди старше 70 лет (есть исключения) и люди с определенными хроническими заболеваниями.Всегда, без исключения, проконсультируйтесь с врачом, имеющим опыт использования голодания в качестве стратегии, прежде чем переходить к такому образу жизни. Это эффективно, но, как и все меры по изменению образа жизни, вы должны знать, как делать это правильно и безопасно, чтобы получить полную пользу!
Если у вас есть какие-либо вопросы о прерывистом голодании, запишитесь на бесплатную консультацию сегодня!
Связанные
— — — Продукция — GeoVision
О компании
Профиль компании
Премия
Связи с инвесторами
Продукты
IP-камера
Система наблюдения
Программное обеспечение для управления видео
Контроль доступа
Распознавание номерных знаков
IP-декодер / HD-видеокодер
Цифровые вывески
Решение PoE
Принадлежности
Поддержка
FAQ
Демо-видео
Список поддерживаемых IP-камер
Калькулятор пропускной способности
Партнер
IP-камера
Марка сетевого видеорегистратора
Скачать
Брошюра
Рекомендуемые товары
Общие
Свяжитесь с нами
Деловое сотрудничество
Гарантия
УСЛОВИЯ ИСПОЛЬЗОВАНИЯ
Конфиденциальность
Пиратство
GDPR
Кибербезопасность
© GeoVision Inc.Все права защищены.
Simple English Wikipedia, бесплатная энциклопедия
Шестнадцатеричная система счисления , часто сокращаемая до «шестнадцатеричная» , представляет собой систему счисления, состоящую из 16 символов (основание 16). Стандартная система счисления называется десятичной (основание 10) и использует десять символов: 0,1,2,3,4,5,6,7,8,9. В шестнадцатеричном формате используются десятичные числа и шесть дополнительных символов. Числовых символов, представляющих значения больше девяти, нет, поэтому используются буквы английского алфавита, в частности A, B, C, D, E и F.Шестнадцатеричный A = десятичный 10 и шестнадцатеричный F = десятичный 15.
Люди в основном используют десятичную систему счисления. Вероятно, это потому, что у людей на руках десять пальцев. Однако у компьютеров есть только включение и выключение, называемое двоичной цифрой (или для краткости битом). Двоичное число — это просто строка из нулей и единиц: например, 11011011. Для удобства инженеры, работающие с компьютерами, обычно группируют биты вместе. Раньше, например, в 1960-е, они группировали по 3 бита за раз (подобно тому, как большие десятичные числа сгруппированы по тройкам, например, 123 456 789).Три бита, каждый из которых включен или выключен, могут представлять восемь чисел от 0 до 7: 000 = 0; 001 = 1; 010 = 2; 011 = 3; 100 = 4; 101 = 5; 110 = 6 и 111 = 7. Это называется восьмеричным.
По мере того, как компьютеры становились больше, было удобнее группировать биты по четыре вместо трех. Это удваивает числа, которые будет представлять символ; он может иметь 16 значений вместо восьми. Hex = 6 и Decimal = 10, поэтому он называется шестнадцатеричным. На компьютерном жаргоне четыре бита составляют полубайт (иногда пишется полубайт ).Полубайт — это одна шестнадцатеричная цифра, записанная с использованием символа 0-9 или A-F. Два полубайта составляют байт (8 бит). В большинстве компьютерных операций используется байт или кратное байту (16 бит, 24, 32, 64 и т. Д.). Шестнадцатеричный код упрощает запись этих больших двоичных чисел.
Чтобы избежать путаницы с десятичной, восьмеричной или другими системами счисления, шестнадцатеричные числа иногда записываются с буквой «h» после или «0x» перед числом. Например, 63h и 0x63 означают 63 в шестнадцатеричном формате.
Шестнадцатеричная система счисления похожа на восьмеричную систему счисления (основание 8), потому что каждую из них можно легко сравнить с двоичной системой счисления.В шестнадцатеричном формате используется четырехбитное двоичное кодирование. Это означает, что каждая цифра в шестнадцатеричном формате совпадает с четырьмя цифрами в двоичном формате. Octal использует трехбитную двоичную систему.
В десятичной системе первая цифра — это разряда , следующая цифра слева — это разряда десятков, следующая — разряда сотен и т. Д. В шестнадцатеричном формате каждая цифра может иметь 16 значений. , а не 10. Это означает, что цифры соответствуют , — шестнадцати — , а следующая — 256 — .Таким образом, 1h = 1 десятичный, 10h = 16 десятичный и 100h = 256 в десятичном.
Примеры значений шестнадцатеричных чисел, преобразованных в двоичные, восьмеричные и десятичные.
шестигранник двоичный восьмеричное десятичный
0 0 0 0
1 1 1 1
2 10 2 2
3 11 3 3
4 100 4 4
5 101 5 5
6 110 6 6
7 111 7 7
8 1000 10 8
9 1001 11 9
А 1010 12 10
B 1011 13 11
С 1100 14 12
D 1101 15 13
E 1110 16 14
Ф 1111 17 15
10 1 0000 20 16
11 1 0001 21 17
24 10 0100 44 36
5E 101 1110 136 94
100 1 0000 0000 400 256
3E8 11 1110 1000 1750 1000
1000 1 0000 0000 0000 10000 4096
ЛИЦО 1111 1010 1100 1110 175316 64206
Двоичное в шестнадцатеричное [изменить | изменить источник]
Для изменения числа с двоичного на шестнадцатеричный используется метод группировки.Двоичное число разделено на группы по четыре цифры, начиная справа. Затем эти группы преобразуются в шестнадцатеричные числа, как показано на приведенной выше диаграмме для шестнадцатеричных чисел от 0 до F. Для перехода с шестнадцатеричного числа выполняется обратное. Каждая шестнадцатеричная цифра заменяется двоичной, и группировка обычно удаляется.
Двоичный Группы шестигранник
01100101 0110 0101 65
010010110110 0100 1011 0110 4B6
1101011101011010 1101 0111 0101 1010 D75A
Когда количество битов в двоичном числе не кратно 4, оно дополняется нулями, чтобы сделать это так.Примеры:
двоичный 110 = 0110, что составляет 6 Hex.
в двоичном формате 010010 = 00010010, что составляет 12 шестнадцатеричных чисел.
Шестнадцатеричное в десятичное [изменить | изменить источник]
Существует два распространенных способа преобразования числа из шестнадцатеричного в десятичное.
Первый метод чаще всего выполняется при ручном преобразовании:
Используйте десятичное значение для каждой шестнадцатеричной цифры. Для 0–9 это то же самое, но A = 10, B = 11, C = 12, D = 13, E = 14 и F = 15.
Сохраняйте сумму преобразованных чисел на каждом шаге ниже.
Начать с младшей шестнадцатеричной цифры. Это цифра на правом конце. Это будет первый предмет в сумме.
Возьмем вторую наименьшую значащую цифру. Это рядом с цифрой на правом конце. Умножьте десятичное значение цифры на 16. Добавьте это к сумме.
Сделайте то же самое для третьей младшей значащей цифры, но умножьте ее на 16 ² (то есть на 16 в квадрате или 256).Добавьте это к сумме.
Продолжайте для каждой цифры, умножая каждое место на другую степень 16. (4096, 65536 и т. Д.)
Местоположение
6 5 4 3 2 1
Значение 1048576 (16 ⁵) 65536 (16 ⁴) 4096 (16 ³) 256 (16 ²) 16 (16 ¹) 1 (16 ⁰)

Следующий метод чаще используется при программном преобразовании числа.Ему не нужно знать, сколько цифр имеет число до его начала, и оно никогда не умножается более чем на 16, но на бумаге оно выглядит длиннее.
Используйте десятичное значение для каждой шестнадцатеричной цифры. Для 0–9 это то же самое, но A = 10, B = 11, C = 12, D = 13, E = 14 и F = 15.
Сохраняйте сумму преобразованных чисел на каждом шаге ниже.
Начните со старшей цифры (цифра в крайнем левом углу). Это первая позиция в сумме.
Если существует другая цифра, умножьте сумму на 16 и добавьте десятичное значение следующей цифры.
Повторяйте вышеуказанный шаг, пока не кончатся цифры.

Пример: 5Fh и 3425h в десятичном формате, метод 1
5Fh в десятичной системе
шестигранник десятичный
5Fh = (5 x 16) + (15 х 1)
= 80 + 15
5Fh = 95
3425h в десятичной системе
шестигранник десятичный
3425h = (3 x 4096) + (4 х 256) + (2 х 16) + (5 х 1)
= 12288 + 1024 + 32 + 5
3425h = 13349
Пример: 5Fh и 3425h в десятичной системе, метод 2
5Fh в десятичной системе
шестигранник десятичный
сумма = 5
= (5 х 16) + 15
сумма = 80 + 15 (больше цифр)
5Fh = 95
3425h в десятичной системе
шестигранник десятичный
сумма = 3
= (3 х 16) + 4 = 52
сумма = (52 х 16) + 2 = 834
сумма = (834 х 16) + 5 = 13349
3425h = 13349
г.2021: Как преобразовать основание 2, 4, 8, 16 в десятичное основание 10 Системные уроки
Обновлено: 28 августа, 2020
URL страницы указывает дату исходной публикации; Между тем времена меняются, а обновления продолжаются.
Двоичное основание 2, четвертичное основание 4, восьмеричное основание 8, шестнадцатеричное основание 16; Включает таблицы
Система счисления в десятичной системе счисления 10 уроков
(HAL говорит привет)

Введение и начало учебного курса по системам счисления
В этих четырех уроках по базовой системе нумерации используется одна и та же методика обучения.Таким образом, когда вы выучите один, вы выучите их все. Также присутствует некоторая повторяемость, цель которой — уменьшить ненужную прокрутку. Также могут оказаться полезными сравнения различных систем счисления.
Если вы понимаете повседневную десятичную систему счисления с основанием 10, которую мы все используем; затем вы уже понимаете основание 2, основание 4, основание 8 и основание 16 системы нумерации. Вы просто еще не знаете, что знаете.
Как вы знаете, в повседневной жизни мы используем десятичную систему счисления с основанием 10.Десятичная система с основанием 10 состоит из десяти чисел (0-9) и порядков величины, которые являются временем десять. Число наименьшего порядка представляет собой умноженное на единицу. Следующий порядок число представляет собой умноженное на десять. Следующий номер заказа представляет умножить на 10 x 10 или сам умножить на 100. Следующий порядковый номер представляет сам раз 10 х 10 х 10 или сам раз 1000. И так далее.
Примером десятичной системы счисления может быть число 7824. Это число означает, что есть:
Четыре единицы,
две десятки,
восемь сотен,
и семь тысяч.
Что представляет собой 4 + 20 + 800 + 7000; всего 7824.
Учебное пособие продолжается ниже для урока по базовой системе нумерации по вашему выбору. Это большой файл, ваш выбор может занять несколько секунд, чтобы отобразить правильный раздел.
Содержание
Существуют также отдельные руководства для Base 5 Quinary и Base 12 Duodecimal .
Уроки и примеры следуют или выбираются из содержания.

Комбинации 0 и 1
Как выполнить преобразование двоичной системы счисления с основанием 2.
Включает примеры.

Двоичный код — основа всех цифровых технологий; строки 1 и 0. Различные комбинации единиц и нулей определяют, как технология говорит сама себе, что делать.
Вот все, что вам нужно знать о том, как преобразовать двоичный код с основанием 2 в десятичный. И для преобразование из десятичной системы в двоичное.
Как было сказано ранее: если вы понимаете десятичную (основание 10) систему счисления, которую используете каждый день, то вы уже понимаете двоичную (основание 2) систему счисления.
А для тех, кто ввел поисковую фразу: , что да в двоичном формате? Ответ:
1 это да или означает истинный в двоичном формате.
0 — это нет или означает ложный в двоичном формате.

Как сделать двоичную систему нумерации с основанием 2
Согласно введению, основание 10 состоит из десяти чисел (0–9) и порядков величины, равных времени десять. Порядки: l, 10, 100 (10×10), 1000 (10x10x10) и т. Д.
Примером может служить число 497. Это число означает, что есть:
Семь единиц,
девять десятков,
и четыре сотни.
Что представляет собой 7 +90 +400; всего 497.
В двоичной системе счисления с основанием 2 (нули и единицы) используется та же структура, единственная разница заключается в порядке величины. База 2 состоит из двух чисел (0-1) и порядков, умноженных на два. В число наименьшего порядка представляет собой умноженное на единицу. Следующий номер заказа умножается на два.Следующий порядковый номер представляет себя умноженным на 2×2 или сам умноженным на 4. Следующий порядковый номер представляет себя умноженный на 2x2x2 или сам умноженный на 8. Следующий порядковый номер представляет себя как 2x2x2x2 или сам умноженный на 16, и так далее.
Порядки величин в Базе 2
1 · 2 · 4 · 8 · 16 · 32 · 64 · 128 · 256 · 512 · 1024 · 2448 · 4096 · 8192
Позиционный
8192 · 4096 · 2048 · 1024 · 512 · 256 · 128 · 64 · 32 · 16 · 8 · 4 · 2 · 1 Базовым первым примером двоичного числа будет число 11111 с основанием 2.Это будет означать, что есть:
one 1,
один 2,
один 4,
одна 8,
и один 16.
Что представляет собой 1 + 2 + 4 + 8 + 16; всего 31 в десятичной системе счисления.
Другой пример с основанием 2 — это двоичное число 101. Это число означает, что есть:
одна единица,
№ 2’s,
и одна четверка.
Что представляет собой 1 + 0 + 4; итого 5 в десятичной системе.
Другой пример с основанием 2 — это двоичное число 10110.Это число означает, что есть:
№ 1,
one 2’s,
одна четверка,
№ 8,
и один 16.
Что представляет собой 0 + 2 + 4 + 0 + 16; итого 22 в десятичной системе счисления.
Порядки величин в Базе 2
1 · 2 · 4 · 8 · 16 · 32 · 64 · 128 · 256 · 512 · 1024 · 2448 · 4096 · 8192
Позиционный
8192 · 4096 · 2048 · 1024 · 512 · 256 · 128 · 64 · 32 · 16 · 8 · 4 · 2 · 1
Таблица: Примеры преобразования двоичного (основание 2) в десятичное (основание 10)
Заголовки столбцов в следующей таблице — это просто удобный список соответствующих порядков величин, применяемых к каждому столбцу.Не имеет значения, где заканчивается один столбец и начинается следующий.
——————————
——————————
———————————
8 · 4 · 2 · 1
16 · 8 · 4 · 2 · 1
64 · 32 · 16 · 8 · 4 · 2 · 1

0 1 2 3
Как выполнить преобразование четвертичной системы счисления с основанием 4.
Включает примеры.

База 4, также известная как четвертичная система счисления, преимущественно используется в генотипировании ДНК, некоторых приложениях электроники и т. Д. [Обновление за 2019 год. Ученые добавили в алфавит ДНК еще четыре буквы, поэтому основание 8 также может иметь значение.]
Этот урок дает вам все, что вам нужно знать для преобразования из четвертичного, известного как основание 4, в десятичное и для преобразования из десятичного, известного как основание 10, в четвертичное. Если вы понимаете десятичную систему счисления или двоичную (базовую 2) систему счисления, если на то пошло, то вы уже понимаете четвертичную (базовую 4) систему счисления.
Согласно введению, основание 10 состоит из десяти чисел (0–9) и порядков величины, равных времени десять. Порядки величин: l, 10, 100 (10×10), 1000 (10x10x10) и т. Д.
Примером может быть число 7112. Это число означает, что есть:
две единицы,
, одна десятка,
одна сотня
и семь тысяч.
Что представляет собой 2 + 100 + 100 + 7000; всего 7112 шт.
Как использовать четвертичную систему нумерации по основанию 4

База 4 использует ту же структуру базы 10, единственная разница — порядки величины.База 4 состоит из четырех чисел (0–3) и порядков, умноженных на четыре. Число наименьшего порядка представляет собой умноженное на единицу. В номер следующего порядка представляет себя умноженным на четыре. Следующий порядковый номер представляет себя умноженный на 4×4 или сам умноженный на 16. Следующий порядковый номер представляет себя умноженный на 4x4x4 или сам умноженный на 64. Следующий порядковый номер представляет себя умноженный на 4x4x4x4 или сам умноженный на 256. И так далее.
Порядки величин в Базе 4
1 · 4 · 16 · 64 · 256 · 1024 · 4096 · 16384
Позиционный
16384 · 4096 · 1024 · 256 · 64 · 16 · 4 · 1
Базовым, первым примером четвертичного числа будет число 11111 с основанием 4.Это будет означать, что есть:
one 1,
один 4,
один 16,
одна 64,
и один 256.
Что представляет собой 1 + 4 + 16 + 64 + 256; всего 341 в десятичной системе счисления.
Другой пример с основанием 4 — это четверное число 321. Это число означает, что есть:
одна единица,
две четверки,
и три 16-х.
Что представляет собой 1 + 8 + 48; итого 57 в десятичной системе.
Другой пример с основанием 4 — это четверное число 3023. Это число означает, что есть:
три единицы,
две четверки,
№ 16,
и три 64-х.
Что представляет собой 3 + 8 + 0 + 192; итого 203 в десятичной системе.
Порядки величин в Базе 4
1 · 4 · 16 · 64 · 256 · 1024 · 4096 · 16384
Позиционный
16384 · 4096 · 1024 · 256 · 64 · 16 · 4 · 1
Таблица: Примеры преобразования четвертичного (основание 4) в десятичное (основание 10)
Заголовки столбцов в следующей таблице — это просто удобный список соответствующих порядков величин, применяемых к каждому столбцу.
——————————
——————————
——————————
4 · 1
16 · 4 · 1
64 · 16 · 4 · 1

0 1 2 3 4 5 6 7
Как преобразовать восьмеричную систему счисления с основанием 8.
Включает примеры.

База 8, также известная как восьмеричная система счисления, в основном используется в электронике, некоторых приложениях для анализа ДНК и т. Д.
Вот все, что вам нужно знать о том, как преобразовать восьмеричную систему счисления в десятичную. И для преобразование из десятичной системы в восьмеричное.
Как ранее было сказано: если вы понимаете десятичную (основание 10) систему счисления пользуешься каждый день, значит уже разбираешься в восьмеричном (основание 8) система нумерации.
Согласно введению, основание 10 состоит из десяти чисел (0–9) и порядков величины, равных времени десять. Порядки величины: l, 10, 100 (10×10), 1000 (10x10x10) и т. Д.
Примером может быть число 2375. Это число означает, что есть:
пять единиц,
семь десятков,
три 100
и две 1000-х.
Что представляет собой 5 + 70 + 300 + 2000; в общей сложности 2375.
Как сделать восьмеричную систему нумерации с основанием 8

База 8 использует ту же структуру базы 10, с той лишь разницей, что это порядки величины.База 8 состоит из восьми чисел (0-7) и порядков величины, равных времени 8. Число наименьшего порядка представляет собой умноженное на единицу. В число следующего порядка представляет собой умноженное на восемь. Следующий порядковый номер представляет себя умноженный на 8×8 или сам умноженный на 64. Следующий порядковый номер представляет себя умноженный на 8x8x8 или сам умноженный на 512. И так далее.
Порядки величин в Базе 8
1 · 8 · 64 · 512 · 4096 · 32768 · 262144
Позиционный
262144 · 32768 · 4096 · 512 · 64 · 8 · 1
Базовым первым примером восьмеричного числа будет число 11111 с основанием 8.Это будет означать, что есть:
one 1,
одна 8,
одна 64,
одна 512,
и один 4096.
Что представляет собой 1 + 8 + 64 + 512 + 4096; в общей сложности 4681 в десятичной системе счисления.
Другой пример с основанием 8 — восьмеричное число 321. Это число означает, что есть:
одна единица,
две восьмерки,
и три 64-х.
Что представляет собой 1 + 16 + 192; итого 209 в десятичной системе счисления.
Другой пример с основанием 8 — восьмеричное число 4075. Это число означает, что есть:
пять единиц,
семь восьмерок,
№ 64’s,
и четыре 512.
Что представляет собой 5 + 56 + 0 + 2048; итого 2109 в десятичной системе счисления.
Порядки величин в Базе 8
1 · 8 · 64 · 512 · 4096 · 32768 · 262144
Позиционный
262144 · 32768 · 4096 · 512 · 64 · 8 · 1
Таблица: Примеры преобразования восьмеричного (основание 8) в десятичное (основание 10)
Заголовки столбцов в следующей таблице — это просто удобный список соответствующих порядков величин, применяемых к каждому столбцу.
——————————
——————————
——————————
8 · 1
8 · 1
512 · 64 · 8 · 1

Шестнадцатеричный: 0-9, A a, B b, C c, D d, E e, F f
Как преобразовать шестнадцатеричную систему счисления с основанием 16.
Включает примеры.

Шестнадцатеричная система счисления (основание 16) — это основная система счисления, используемая компьютерными программистами. Шестнадцатеричный код используется во всем, от дампов ядра до цветовых кодов и всего, что между ними.
Согласно введению, основание 10 состоит из десяти чисел (0-9) и порядков, которые десять. Порядки величины: l, 10, 100 (10×10), 1000 (10x10x10) и т. Д.
Примером может быть число 5681. Это число означает, что есть:
одна единица,
восемь десятков,
шесть сотен,
и пять тысяч.
Что представляет собой 1 + 80 + 600 + 5000; всего 5681.
Base 16 использует ту же структуру base 10, с той лишь разницей, что это порядки величины.
Как сделать шестнадцатеричную систему нумерации с основанием 16

Остерегайтесь просчетов
Порядки умножены на шестнадцать. Число наименьшего порядка представляет собой умноженное на единицу. Число следующего порядка представляет себя умноженным на шестнадцать.Следующий порядковый номер представляет себя умноженный на 16×16 или сам умноженный на 256. Следующий порядковый номер представляет себя умноженный на 16x16x16 или сам умноженный на 4096. И так далее.
Шестнадцатеричный порядок величины:
1 · 16 · 256 · 4096 · 65536 · 1048576
Позиционный:
1048576 · 65536 · 4096 · 256 · 16 · 1
База 16, также известная как шестнадцатеричная, состоит из шестнадцати чисел (0-F). Первые десять чисел — это обычные от 0 до 9. Следующие шесть чисел — A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Всего имеем:
0 = 0, 1 = 1, 2 = 2, 3 = 3, 4 = 4, 5 = 5, 6 = 6, 7 = 7, 8 = 8, 9 = 9,
A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Базовым первым примером шестнадцатеричного числа будет число 11111 с основанием 16. Это будет означать, что существует:
один 1,
один 16,
одна 256,
один 4096,
и один 65536.
Что представляет собой 1 + 16 + 256 + 4096 + 65536; итого 69905 в десятичной системе счисления.
Другой пример с основанием 16 — это шестнадцатеричное число 5C7F. Это число означает:
пятнадцать единиц,
семь 16,
двенадцать 256,
и пять 4096.
Что представляет собой 15 +112 +3072 + 20480; итого 23679 в десятичной системе.
Другой пример с основанием 16 — это шестнадцатеричное число D24A. Это число означает:
десять единиц,
четыре 16,
два 256,
и тринадцать 4096.
Что представляет собой 10 +64 +512 + 53248; итого 53834 в десятичной системе.
Шестнадцатеричные порядки величины
1 · 16 · 256 · 4096 · 65536 · 1048576
Позиционный
1048576 · 65536 · 4096 · 256 · 16 · 1
Таблица: Примеры преобразования шестнадцатеричного (основание 16) в десятичное (основание 10)
Заголовки столбцов в следующей таблице — это просто удобный список соответствующих порядков величин, применяемых к каждому столбцу. Не имеет значения, где заканчивается один столбец и начинается следующий.
A = 10, B = 11, C = 12, D = 13, E = 14, F = 15
—————————
—————————
————————————
16 · 1
256 · 16 · 1
65536 · 4096 · 256 · 16 · 1

Просто последовательный список шестнадцатеричных чисел
Таблица создана по формуле Microsoft Excel: «= DEC2HEX (здесь адрес ячейки)».
1 2 3 4 5 6 7 8 9 ABCDEF 10 11 12 13 14 15 16 17 18 19 1A 1B 1C 1D 1E 1F 20 21 22 23 24 25 26 27 28 29 2A 2B 2C 2D 2E 2F 30 31 32 33 34 35 36 37 38 39 3A 3B 3C 3D 3E 3F 40 41 42 43 44 45 46 47 48 49 4A 4B 4C 4D 4E 4F 50 51 52 53 54 55 56 57 58 59 5A 5B 5C 5D 5E 5F 60 61 62 63 64 65 66 67 68 69 6A 6B 6C 6D 6E 6F 70 71 72 73 74 75 76 77 78 79 7A 7B 7C 7D 7E 7F 80 81 82 83 84 85 86 87 88 89 8A 8B 8C 8D 8E 8F 90 91 92 93 94 95 96 97 98 99 9A 9B 9C 9D 9E 9F A0 A1 A2 A3 A4 A5 A6 A7 A8 A9 AA AB AC AD AE AF B0 B1 B2 B3 B4 B5 B6 B7 B8 B9 BA BB BC BD BE BF C0 C1 C2 C3 C4 C5 C6 C7 C8 C9 CA CB CC CD CE CF D0 D1 D2 D3 D4 D5 D6 D7 D8 D9 DA DB DC DD DE DF E0 E1 E2 E3 E4 E5 E6 E7 E8 E9 EA EB EC ED EE EF F0 F1 F2 F3 F4 F5 F6 F7 F8 F9 FA FB FC FD FE FF 100 101102103104105106107108109 10A 10B 10C 10D 10E 10F 110111112113115116117118119 11A 11B 11C 11D 11E 11F 120 121122 123 124 125 126 127 128 129 12A 12B 12C 12D 12E 12F 130 131 132 133 134 135 136 137 138 139 13A 13B 13C 13D 13E 13F 140 141 142 143 144 145 146 147 148 149 14A 14B 14C 14D 14E 14F 150 151152 153 154 155 156 157 158 159 15A 15B 15C 15D 15E 15F 160161162 163 164 165 166 167 168 169 16A 16B 16C 16D 16E 16F 170 171 172 173 174 175 176 177 178 179 17A 17B 17C 17D 17E 17F 180 181 182 183 184 185 186 187 188 189 18A 18B 18C 18D 18E 18F 190 1 193 194 195 196 197 198 199 19A 19B 19C 19D 19E 19F 1A0 1A1 1A2 1A3 1A4 1A5 1A6 1A7 1A8 1A9 1AA 1AB 1AC 1AD 1AE 1AF 1B0 1B1 1B2 1B3 1B4 1B5 1B6 1B7 1B8 1B9 1BA 1BCEB 1BC 1BD 1BE 1C1C 1C0 1C0 1C0 1C5 1C0C 1C0 1C0 1C0 1C0 1C0C1C0 1C0 1C0 1C0 1C0C0 1D1 1D2 1D3 1D4 1D5 1D6 1D7 1D8 1D9 1DA 1DB 1DC 1DD 1DE 1DF 1E0 1E1 1E2 1E3 1E4 1E5 1E6 1E7 1E8 1E9 1EA 1EB 1EC 1ED 1EE 1EF 1F0 1FFF1 1F4 200D 1F7 1F7 1F7 1F7 1F5 1F7 1F7 1F7 1F7 1F7 1F7 1F7 1F7 1F7 900 201202203204205206207208209 20A 20B 20C 20D 20E 20F 210 211212 213214 215 216217 218 219 21A 21B 21C 21D 21E 21F 220 2212222232224 225 226 227 228 229 22A 22B 22C 22D 22E 22F 230 23 1 232 233234 235 236 237 238 239 23A 23B 23C 23D 23E 23F 240 24124 244 245 246 247 248 249 24A 24B 24C 24D 24E 24F 250 251 252 253 254 255 256 257 258 259 25A 25B 25C 25D 25E 25F 260 261262 263264 265 266 267 268 269 26A 26B 26C 26D 26E 26F 270 271272273274 275 276 277 278 279 27A 27B 27C 27D 27E 27F 280 281282283284 285 286 287 288 289 28A 28B 28C 28D 28E 28F 290 294 292 29329 295 296 297 298 299 29A 29B 29C 29D 29E 29F 2A0 2A1 2A2 2A3 2A4 2A5 2A6 2A7 2A8 2A9 2AA 2AB 2AC 2AD 2AE 2AF 2B0 2B1 2B2 2B3 2B3 2B4 2B5 2B6 2B7 2BDC2 2BDC4 2BD2 2BD 2BC4 2BD2B2 2BD 2BC4 2BD 2BC2 2C7 2C8 2C9 2CA 2CB 2CC 2CD 2CE 2CF 2D0 2D1 2D2 2D3 2D4 2D5 2D6 2D7 2D8 2D9 2DA 2DB 2DC 2DD 2DE 2DF 2E0 2E1 2E2 2E3 2E4 2E5 2E6 2E7 2E8 2E9 2EAF7 2EF2 2F2F 2F2F2 2F2F2 2F2F 2F2 2F2F 2F2F 2F2 2F2F 2F2 2F2F2 2FF2 2FF2 2F2F2 2F2F2 2FF 2F2F2 2F9 2FA 2FB 2FC 2FD 2FE 2FF 300 301 302 303 304 305 306 307 308 309 30A 30B 30C 30D 30E 30F 310 311 312 313 314 315 316 317 318 319 31A 31B 31C 31D 31E 31F 320 321 322 323 324 325 326 327 328 329 32A 32B 32C 32D 32E 32F 330 331 332 333 334 335 336 337 338 339 33A 33B 33C 33D 33E 33F 340 341 342 343 344 345 346 347 348 349 34A 34B 34C 34D 34E 34F 350 351 352 353 354 355 356 357 358 359 35A 35B 35C 35D 35E 35F 360 3613623634365 366 367 368 369 36A 36B 36C 36D 36E 36F 370 3713723734375 376 377 378 379 37A 37B 37C 37D 37E 37F 380 381 382 383 384 385 386 387 388 389 38A 38B 38C 38D 38E 38F 390 391 392 393 394 395 396 397 398 399 39A 39B 39C 39D 39E 39F 3A0 3A1 3A2 3A3 3A4 3A5 3A6 3A7 3A8 3A9 3AA 3AB 3AC 3AD 3AD 3AE 3AF 3B0 3B1 3B6B9 3B3B3 3BE 3BF 3C0 3C1 3C2 3C3 3C4 3C5 3C6 3C7 3C8 3C9 3CA 3CB 3CC 3CD 3CE 3CF 3D0 3D1 3D2 3D3 3D4 3D5 3D6 3D7 3D8 3D9 3DA 3DB 3DC 3DD 3DE 3DF 3E0 3E1 3E2 3E9 3E5 3E3E0 3E1 3E2 3E3E3 3F0 3F1 3F2 3F3 3F4 3F5 3F6 3F7 3F8 3F9 3FA 3FB 3FC 3FD 3FE 3FF 400 401 402 403 404 405 406 407 408 409 40A 40B 40C 40D 40E 40F 410 411 412 413 414 418 419 41C 41C 41C 41C 41C 41C 41 E 41F 420 42142 423 424 425 426 427 428 429 42A 42B 42C 42D 42E 42F 430 43143 243 434 435 436 437 438 439 43A 43B 43C 43D 43E 43F 440 44144 444 444 445 446 447 448 449 44A 44B 44C 44D 44E 450 451 452 453 454 455 456 457 458 459 45A 45B 45C 45D 45E 45F 460 461462463464 465 466 467 468 469 46A 46B 46C 46D 46E 46F 470 4714724734744475 476 477 478 479 47A 47B 47C 47D 47E 47F 482 483 484 485 486 487 488 489 48A 48B 48C 48D 48E 48F 490 491 492 493 494 495 496 497 498 499 49A 49B 49C 49D 49E 49F 4A0 4A1 4A2 4A3 4A4 4A5 4A6 4A7 4A8 4A9 4A1 4BA 4A2 4AB 4A 4A 4A 4A 4A 2A 4A 2A 4A 4A 2A 4A 4A 4A 2A 4A 2A 4A 4A 2A 4A 4A 4A 4A 2A 4A 2A 4A 2A 4B4 4B5 4B6 4B7 4B8 4B9 4BA 4BB 4BC 4BD 4BE 4BF 4C0 4C1 4C2 4C3 4C4 4C5 4C6 4C7 4C8 4C9 4CA 4CB 4CC 4CD 4CE 4CF 4D0 4D1 4D2 4D3 4D8D 4DE 4DE 4DE 4DE 4DE 4DE 4DE 4DE 4DE 4DE 4DE 4DE 4DE 4DE 4DE 4DE 4DE 4D6 4E6 4E7 4E8 4E9 4EA 4EB 4EC 4ED 4EE 4EF 4F0 4F1 4F2 4F3 4F4 4F5 4F6 4F7 4F8 4F9 4FA 4FB 4FC 4FD 4FE 4FF 500 501 502 503 504 505 506 507 508 5010 501 502 503 504 505 506 507 508 5010 511 501 5014 511 501 501 501 5014 501 501 5014 515 516 517 518 519 51A 51B 51C 51D 51E 51F 520 521522523524 525 526527528529 52A 52B 52C 52D 52E 52F 530 531 532 533 534 535 536 537 538 539 53A 53B 53C 53D 53E 53F 540 541545 546 544 547 548 549 54A 54B 54C 54D 54E 54F 550 551 552 553 554 555
— Конец статьи —
Re: Используете мобильный телефон?
Home : вступление к сайту и избранные статьи / ресурсы.
Просмотр веб-версии : отображает категории статей в главном меню (будут расположены ниже), дополнительную информацию о сайте (внизу и сбоку), функцию поиска.

ФРС — Письмо CA 16-8 по делам потребителей о единой межведомственной системе оценки соответствия потребителей
CA 16-8:
Единая межведомственная система оценки соответствия потребителей
СОВЕТ УПРАВЛЯЮЩИХ
ФЕДЕРАЛЬНОЙ РЕЗЕРВНОЙ СИСТЕМЫ
ВАШИНГТОН, Д.С. 20551
ОТДЕЛЕНИЕ ПО ПОТРЕБИТЕЛЬСКИМ И ОБЩЕСТВЕННЫМ ВОПРОСАМ
CA 16-8
22 ноября 2016 г. ДОЛЖНЫМ ЛИЦАМ И МЕНЕДЖЕРАМ ПО ПОТРЕБИТЕЛЬСКИМ ВОПРОСАМ РАЗДЕЛЫ

ТЕМА:
Единая межведомственная система оценки соответствия потребителей
Применимость к общественным банковским организациям: Это руководство применимо ко всем учреждениям, находящимся под надзором Федеральной резервной системы, включая те, чьи общие консолидированные активы составляют 10 миллиардов долларов или меньше.
Федеральный экзаменационный совет финансовых учреждений (FFIEC) недавно объявил о выпуске обновленной Единой межведомственной рейтинговой системы соответствия потребителей (CC Rating System). ^[1] Рейтинговая система CC — это надзорная политика для оценки соблюдения финансовыми учреждениями требований потребителей. ^[2] Эксперты Федеральной резервной системы будут применять рейтинговую систему CC ко всем проверкам соответствия потребителей, которые начинаются 31 марта 2017 г. или позднее.
Новая рейтинговая система CC разработана, чтобы лучше отражать текущие подходы надзора за соблюдением требований потребителей и более полно согласовывать рейтинговую систему CC с текущими основанными на рисках и адаптированными процессами проверки. Поправки к рейтинговой системе CC не были разработаны для того, чтобы установить новые или более высокие ожидания надзорных органов для финансовых учреждений, и их принятие не повлечет за собой дополнительной регулятивной нагрузки.
Рейтинговая система CC обеспечивает общую основу для оценки факторов оценки соответствия с целью присвоения рейтинга соответствия потребителям каждому финансовому учреждению, регулируемому на федеральном уровне.Основная цель рейтинговой системы CC — обеспечить всестороннюю и последовательную оценку регулируемых финансовых учреждений и надлежащую ориентацию надзорных ресурсов на области, демонстрирующие риск причинения вреда потребителям, и на учреждения, требующие повышенного внимания со стороны надзорных органов. В пересмотренной системе рейтингов CC подчеркивается важность систем управления соответствием (CMS) организаций с упором на методы управления рисками соответствия, предназначенные для управления риском соблюдения требований потребителей, поддержки соблюдения требований и предотвращения причинения вреда потребителям.
Рейтинговая система CC состоит из руководств и определений. Руководство дает экспертам указания относительно того, как использовать определения при присвоении учреждению рейтинга соответствия потребителя. Определения состоят из качественных описаний для каждой рейтинговой категории и включают элементы CMS, отражающие процессы контроля рисков, предназначенные для управления риском соблюдения требований потребителей, и соображения, касающиеся нарушений законов, причинения вреда потребителям, а также размера, сложности и профиля риска учреждения.
Рейтинговая система CC основана на шкале от 1 до 5 в порядке возрастания степени обеспокоенности надзорных органов. Таким образом, 1 представляет наивысший рейтинг и, следовательно, самый низкий уровень надзорного беспокойства, а 5 — самый низкий рейтинг и, следовательно, наиболее критически недостаточный уровень эффективности и наивысший уровень надзорного беспокойства. Рейтинг соблюдения требований потребителей отражает эффективность CMS учреждения для обеспечения соблюдения законов и постановлений о защите прав потребителей и снижения риска причинения вреда потребителям.
Если у вас есть какие-либо вопросы, свяжитесь с Ланетт Мейстер, старшим надзорным аналитиком потребительских финансовых услуг, по телефону (202) 452-2705, или Тимом Робертсоном, менеджером, по телефону (202) 452-2565. Кроме того, вопросы можно отправлять через общедоступный веб-сайт Совета. ^[3]
подписано
Эрик С.Бельский
Директор
Подразделение Потребителя
и общественные дела
Заменяет:
CA 80-15 «Письмо о передаче межведомственной рейтинговой системы соответствия» (11 декабря 1980 г.)
Система фильтров LEE SW150 Mark II, специально разработанная для ряда популярных сверхширокоугольных объективов.
Адаптер для каждого объектива
SW150 Mark II устанавливается через адаптер объектива, который был специально разработан для этого объектива (адаптер приобретается отдельно от держателя фильтра).
Каждый адаптер состоит переднего кольцо, компрессионное кольцо и стопорное кольцо. При установке эти формы воротник, который постоянно остается на линзе.
Мы часто добавляем новые адаптеры, подходящие для других объективов, поэтому, если вы не видите свой в списке, повторите попытку.
Систему SW150 Mark II можно использовать со следующими объективами:
Nikon AF-S Nikkor 14-24mm f / 2.8G ED
Nikon 14 мм f2.8 D AF ED
Nikon PC NIKKOR 19mm f / 4E ED Tilt-Shift
Адаптеры
доступны для систем SW150 и 100 мм. Адаптер 100 мм не позволяет полностью перемещать объектив без виньетирования.
Canon EF 14 мм f2.8 L II USM
Canon EF 11-24 мм f4L USM
Обратите внимание, что из-за физических размеров этого объектива и чрезвычайно широкого угла Держатель фильтра SW150 будет винить при самых широких углах обзора.Чтобы избежать этого, мы при использовании держателя фильтра рекомендуется использовать минимальное фокусное расстояние 13,5 мм. с двумя прорезями для фильтров и 12,5 мм при использовании держателя с одной прорезью для фильтра.
Canon TS-E 17 мм
Этот адаптер позволяет фотографам использовать весь диапазон функций наклона и сдвига объектива.
Fujifilm XF 8-16 мм f2.8
Olympus 7-14 мм Pro f2.8
Адаптеры
доступны для систем SW150 и 100 мм.
Pentax FA 15-30 мм f2.8 ED SDM WR
У этого объектива нет собственного адаптера, но адаптер Tamron 15-30 мм подходит идеально.
Samyang 14mm f / 2.8 ED AS IF UMC
Sigma 12-24 мм f4.5-5.6 DG HSM II
Sigma 12-24mm f4 Art DG HSM
Обратите внимание, что из-за физических размеров этого объектива и чрезвычайно широкого угла Держатель фильтра SW150 будет винить при самых широких углах обзора. Чтобы избежать этого, мы рекомендуем использовать минимальное фокусное расстояние 15 мм при использовании держателя фильтра с двумя прорезями для фильтров и 13.5 мм при использовании держателя с одним отверстием для фильтра.
Sigma 14-24mm f2.8 Art
Обратите внимание, что виньетирование может происходить на близких расстояниях фокусировки при конфигурации с двумя слотами.
Sigma 14 мм f1.8 DG Art
Sigma 20mm f1.4 HSM Art
Tamron 15-30 мм f2.8 SP Di VC
долларов США
Tokina AT-X 16-28 мм f / 2.8 PRO FX
PowerLab (DAQ) Аппаратное устройство сбора данных для исследований
Целостность данных
PowerLab — это устройство сбора данных (DAQ), разработанное для точного, последовательного и надежного сбора данных.
PowerLab, разработанный в 1985 году, стал надежным продуктом для целого поколения ученых и преподавателей, предлагая простое и гибкое решение. практически для всех типов сбора физиологических данных.
PowerLabs способны непрерывно записывать на диск (совокупно) со скоростью до 400000 выборок в секунду и совместимы с приборами, формирователи сигналов и преобразователи, поставляемые ADInstruments и многими другими ведущими брендами.
Наши исследовательские лаборатории PowerLab созданы для обеспечения точности и предназначены для предоставления вам высококачественных, воспроизводимых данных при соблюдении самых строгих требований. международные стандарты безопасности.
Research PowerLabs обеспечивает 16-битное разрешение во всех диапазонах усиления для высокого разрешения даже для самых маленьких сигналов. Каждый канал имеет индивидуальный фильтры и схема шумоподавления для минимизации перекрестных помех канала и шума сигнала.Все исследовательские PowerLabs имеют 2 аналоговых выхода, триггерный вход. и предлагаем 5-летнюю гарантию на продукт.
Высокофункциональный и адаптируемый даже для самых требовательных приложений, PowerLab для исследований может удовлетворить ваши требования.
×
checkmark Товар успешно добавлен в ваш запрос предложения.
С 16 аналоговыми входными каналами (4 из которых можно использовать в дифференциальном режиме), 8 цифровыми входами, 8 цифровыми выходами и АЦП 400kS / s, обеспечивающим максимальная частота дискретизации на канал 200 kS / s — 16/35 research PowerLab — наша самая мощная система сбора данных.
×
checkmark Товар успешно добавлен в ваш запрос предложения.
Наша самая популярная модель, 8/35 PowerLab, предназначена для исследователей, которым требуется расширенный набор функций. 8 аналоговых входных каналов (4 из которых могут быть используется в дифференциальном режиме), 8 цифровых входов, 8 цифровых выходов и максимальная частота дискретизации 200 kS / s на канал.
×
checkmark Товар успешно добавлен в ваш запрос предложения.
Наша система сбора данных исследовательского уровня начального уровня, 4/26 имеет 4 аналоговых входных канала и максимальную частоту дискретизации 100 кГц на канал.Независимые АЦП для каждого канала для идеальной синхронизации данных.
×
checkmark Товар успешно добавлен в ваш запрос предложения.
Для тех, кому требуется минимум каналов, 2/26 — идеальный вариант входа.Максимальная частота дискретизации 100 кГц на канал. Независимые АЦП для каждого канал для идеальной синхронизации данных.
«Другие системы не соответствуют PowerLab. Это отличный продукт.»
Д-р Кенгатхаран , президент и главный операционный директор, Armetheon, Inc.
Идеальное решение для сбора данных для экспериментов в классе медико-биологических наук.PowerLab поддерживает увлекательное практическое обучение с простой настройкой и высококачественными данными. Справится с многократным и интенсивным использованием студентами и сохранит точность и надежность данных.
PowerLab серии T — это недорогой высококачественный DAQ-блок со встроенным полностью изолированным двухканальным биоусилителем, изолированным стимулятором, отдельными неизолированными аналоговыми входами и дифференциальным аналоговым выходом.
×
checkmark Товар успешно добавлен в ваш запрос предложения.
Встроенная функция записи данных с двойным биоусилителем, изолированным стимулятором, триггерный вход, 4 аналоговых входа, 8 цифровых входов и 8 цифровых входов. выходы. Независимые АЦП для каждого канала для идеальной синхронизации данных.
×
checkmark Товар успешно добавлен в ваш запрос предложения.
Встроенная система записи данных начального уровня с двойным биоусилителем, изолированным стимулятором и 2 аналоговыми входами. Независимые АЦП для каждого канала хранить данные в полной синхронизации.
«PowerLab просто РАБОТАЕТ. Он никогда не выходит из строя, его не нужно перезагружать, он на 100% надежен ».
Др.Джованни Касотти , профессор биологии Западно-Честерского университета
Простота использования
PowerLabs — это портативные USB-устройства сбора данных (DAQ). Просто установите PowerLab на рабочем месте, подключите его и начните использовать с LabChart. программного обеспечения.
Надежная работа
Долговечность с использованием высококачественных и прочных материалов с гарантией на оборудование до 5 лет
Высокая скорость дискретизации практически любого аналогового сигнала
Полное разрешение во всех диапазонах усиления для высокоточной записи даже самых слабых сигналов
Максимальная частота дискретизации 200 кГц на канал (серия 35)
Превосходное подавление внешнего шума, низкий внутренний шум и входы с высоким CMRR
Гибкий
Работает с платформами Mac и ПК
Обнаруживает широкий спектр сигналов одновременно через несколько устройств и преобразователей с регулируемой частотой дискретизации
Аналоговые выходы для управления внешними устройствами или протоколов стимуляции
Разъемы DIN для предварительно откалиброванных преобразователей и недорогих усилителей
Цифровые входные и выходные разъемы для передачи сигналов от внешних устройств
Возможность адаптации к различным исследованиям и программам обучения
Различные модели для различных исследований и образовательных потребностей
Надежный
Надежный сбор данных в биологических науках — более 30 лет
Сертифицирован на соответствие самым строгим международным стандартам безопасности для людей и животных, включая ISO и знак CE
Цитируется более чем 20000 научных статей в рецензируемых журналах
Изготовлено в Австралии из высококачественных и долговечных материалов
Надежный
«Оборудование ADInstruments работает великолепно! Согласно нашему предыдущему опыту и опыту других, фактические измерения газов в конце прилива и вентиляция была практически невозможна выше 4000 м.Мы провели почти 2 недели на высоте 5050 м и практически превратили ADInstruments оборудование было включено, когда мы приехали, и оно работало почти непрерывно во время экспериментов, которые проводились во сне днем и ночью. время.»
Д-р Эйнсли
Кафедра канадских исследований в области физиологии сосудов головного мозга.
Письмо по поводу исследовательской экспедиции на Эверест.
Экономичное подключение
«Если у вас есть система PowerLab, добавление дополнительных функций обойдется относительно недорого.Например, когда наши преподаватели хотели больше ЭКГ аппараты для экспериментов ЭКГ в 12 отведениях, мы рассмотрели наши варианты. Мы могли бы получить новые аппараты ЭКГ по цене около 6000 долларов за штуку или блоки ЭКГ с распределительными коробками для использовать с системами PowerLab по цене менее 1000 долларов каждая. Выбор модулей ЭКГ в качестве дополнения к имеющимся у нас тренажерам спас школе многие тысячи долларов »
Г-жа Келли Риджес
Операционный менеджер Института здравоохранения и медицинских исследований Иллаварры, Университет Вуллонгонга.
Прочный и портативный
«Размер PowerLab был идеальным, поскольку он помещался в мой рюкзак! Это также было одно из немногих устройств, которое хорошо работало с генератор в базовом лагере. Многие другие части оборудования потребляли слишком много энергии, что приводило к короткому замыканию генераторов »
Д-р Эйнсли
Кафедра канадских исследований в области физиологии сосудов головного мозга.
Письмо по поводу исследовательской экспедиции на Эверест.
Коды товаров
PL3516 PowerLab 16/35
PL3508 PowerLab 8/35
PL2604 PowerLab 4/26
PL2602 PowerLab 2/26
PL26T04 PowerLab 26T (LTS)
PL15T02 PowerLab 15T (LTS)
Системные требования
PowerLab требует интерфейса USB 2 или 3 для подключения к вашему компьютеру.
PowerLabs предназначены для работы с программным обеспечением LabChart 8 или LabChart Lightning для исследований или с программным обеспечением LabStation, Lt или LabChart for Education при обучении. В большинстве обстоятельства, любой ПК или Mac настольный или портативный компьютер с новейшим процессором Intel или AMD и 2 ГБ или более системной памяти будет достаточный. Пожалуйста, смотрите системные требования для LabChart для более подробной информации.
Технические характеристики и сравнение характеристик
ИССЛЕДОВАНИЯ ОБРАЗОВАНИЕ
16/35 8/35 26 апреля 26/2 26 т 15 т
Включенное программное обеспечение LabChart LabChart LabChart LabChart Нет, LabChart, LabStation или Lt приобретаются отдельно Нет, LabChart, LabStation или Lt приобретаются отдельно
Передача данных USB 2.0 USB 2.0 USB 2.0 USB 2.0 USB 2.0 USB 2.0
Триггерный вход Есть Есть Есть Есть Есть №
Каналы аналогового ввода 16 8 4 2 4 2
Несимметричные входы 16 8 4 2 4 2
Дифференциальные входы 4 4 4 2 4 2
Диапазон входного напряжения от ± 2 мВ до ± 10 В от ± 2 мВ до ± 10 В от ± 20 мВ до ± 10 В от ± 20 мВ до ± 10 В от ± 20 мВ до ± 10 В от ± 20 мВ до ± 10 В
Разрешение данных 16 бит 16 бит 16 бит 16 бит 16 бит 16 бит
Мин. Частота дискретизации 1 с / 10 мин 1 с / 10 мин 1 с / 10 мин 1 с / 10 мин 1 с / 10 мин 1 с / 10 мин
Макс.частота дискретизации на канал 200 kS / s (макс. 400kS / s в совокупности) 200 kS / s (макс. 400kS / s в совокупности) 100 кСм / с 100 кСм / с 100 кСм / с 100 кСм / с
Перекрестные помехи на входе 75 дБ (мин) 75 дБ (мин) > 90 дБ > 90 дБ > 90 дБ > 90 дБ
Амплитудно-частотная характеристика -3 дБ (25 кГц, 10 В) -3 дБ (25 кГц, 10 В) -3 дБ (37 кГц, 10 В) -3 дБ (37 кГц, 10 В) -3 дБ (37 кГц, 10 В) -3 дБ (37 кГц, 10 В)
CMRR > 100 дБ при 100 Гц, 2-100 мВ > 100 дБ при 100 Гц, 2-100 мВ > 95 дБ при 100 Гц, 20-100 мВ > 95 дБ при 100 Гц, 20-100 мВ > 95 дБ при 100 Гц, 20-100 мВ > 95 дБ при 100 Гц, 20-100 мВ
Входное сопротивление 1 МОм при 100 пФ 1 МОм при 100 пФ 1 МОм при 150 пФ 1 МОм при 150 пФ 1 МОм при 150-200 пФ 1 МОм при 150 пФ
Выходной усилитель Есть Есть Есть Есть Есть Есть
Выходные каналы 2 2 1 1 1 1
Выходное разрешение 16 бит 16 бит 16 бит 16 бит 16 бит 16 бит
Диапазоны выходного напряжения от ± 200 мВ до ± 10 В от ± 200 мВ до ± 10 В от ± 200 мВ до ± 10 В от ± 200 мВ до ± 10 В от ± 200 мВ до ± 10 В от ± 200 мВ до ± 10 В
Цифровые выходные каналы 8 8 0 0 8 0
Каналы цифрового ввода 8 8 0 0 8 0
Встроенный биоусилитель № № № № Есть Есть
Рейтинг безопасности IEC60601-1 IEC60601-1 IEC60601-1 IEC60601-1 IEC60601-1 IEC60601-1
Каналы биоусилителя – – – – 2 2
Диапазон усиления – – – – от ± 200 мкВ до ± 20 мВ от ± 200 мкВ до ± 20 мВ
Биоусилитель CMRR – – – – 110 дБ 110 дБ
Изолированный стимулятор № № № № Есть Есть
Диапазон тока изолированного стимулятора – – – – 0-20 мА 0-20 мА
Длительность импульса – – – – 50-200 мкс 50-200 мкс
Частота пульса – – – – Выбирается программно Выбирается программно
Загрузки
Самая мощная система сбора данных ADInstruments с 16 аналоговыми входными каналами, 4 из которых могут использоваться в дифференциальном режиме.
×
checkmark Товар успешно добавлен в ваш запрос предложения.
8 аналоговых входных каналов, 4 из которых могут использоваться в дифференциальном режиме.
×
checkmark Товар успешно добавлен в ваш запрос предложения.
Недорогой 4-канальный сбор данных с 4 аналоговыми входами.
×
checkmark Товар успешно добавлен в ваш запрос предложения.
2-канальный сбор данных начального уровня с 2 аналоговыми входами.
×
checkmark Товар успешно добавлен в ваш запрос предложения.
Встроенная функция записи данных с двойным биоусилителем, изолированным стимулятором, триггерный вход, 4 аналоговых входа, 8 цифровых входов и 8 цифровых входов. выходы.26T включает программное обеспечение LabChart.
×
checkmark Товар успешно добавлен в ваш запрос предложения.
Встроенная система записи данных начального уровня с двойным биоусилителем, изолированным стимулятором и 2 аналоговыми входами.
×
checkmark Товар успешно добавлен в ваш запрос предложения.
×
Запросить демо
Благодарим вас за интерес к PowerLab . Пожалуйста, заполните и отправьте форму ниже, и представитель ADInstruments свяжется с вами в течение одного рабочего дня.Если вы хотите с кем-то поговорить немедленно, контактная информация офиса доступна на странице контактов. ×
Задать вопрос
Благодарим вас за интерес к PowerLab . Пожалуйста, заполните и отправьте форму ниже, и представитель ADInstruments свяжется с вами в течение одного рабочего дня. Если вы хотите с кем-то поговорить немедленно, контактная информация офиса доступна на странице контактов. ×
.

Из 16 в 8 систему: 500 Internal Server Error

8-ная и 16-ная системы счисления | Практическая информатика

Перевод из одной системы счисления в другую

Быстрый переход между двоичной, 8-ичной и 16-ичной системами

Шестнадцатеричная система счисления

Как перевести отрицательное число в шестнадцатеричную систему

Способы представления чисел

Алгоритм перевода чисел из одной системы счисления в другую

Contents

Введение

Debug

Перевод шестнадцатеричных чисел в десятичную форму

Сложение и вычитание шестнадцатеричных чисел

Пятизначные шестнадцатеричные числа

Перевод десятичных чисел в шестнадцатеричную форму

Отрицательные числа

Двоичная система счисления

Дополнительный код

суть, правила, плюсы и минусы, эффективность интервального похудения

В чем суть диеты 16/8?

Правила диеты 8/16

Продуктовая корзина

Польза диеты 8/16

Недостатки диеты 8/16

Интервальное голодание 16/8 — расписание, правила и отзывы

// Диета 16/8 — что это такое?

В чем принцип работы?

Интервальное голодание 16/8 — отзывы

Отзывы читательниц Фитсевен

Интервальное голодание для женщин

Противопоказания

Правила сушки на диете 16/8

Отзывы спортсменов

Практические советы

***

В продолжение темы

Система прерывистого голодания 16/8: что и почему?

Система прерывистого голодания 16/8: что и почему?

— — — Продукция — GeoVision

Simple English Wikipedia, бесплатная энциклопедия

Двоичное в шестнадцатеричное [изменить | изменить источник]

Шестнадцатеричное в десятичное [изменить | изменить источник]

г.2021: Как преобразовать основание 2, 4, 8, 16 в десятичное основание 10 Системные уроки

Двоичное основание 2, четвертичное основание 4, восьмеричное основание 8, шестнадцатеричное основание 16; Включает таблицы

Система счисления в десятичной системе счисления 10 уроков

Введение и начало учебного курса по системам счисления

Содержание

Как сделать двоичную систему нумерации с основанием 2

Порядки величин в Базе 2

Позиционный

Порядки величин в Базе 2

Позиционный

Таблица: Примеры преобразования двоичного (основание 2) в десятичное (основание 10)

Как использовать четвертичную систему нумерации по основанию 4

Порядки величин в Базе 4

Позиционный

Порядки величин в Базе 4

Позиционный

Таблица: Примеры преобразования четвертичного (основание 4) в десятичное (основание 10)

Как сделать восьмеричную систему нумерации с основанием 8

Порядки величин в Базе 8

Позиционный

Порядки величин в Базе 8

Позиционный

Таблица: Примеры преобразования восьмеричного (основание 8) в десятичное (основание 10)

Как сделать шестнадцатеричную систему нумерации с основанием 16

Шестнадцатеричный порядок величины:

Позиционный:

Шестнадцатеричные порядки величины

Позиционный

Таблица: Примеры преобразования шестнадцатеричного (основание 16) в десятичное (основание 10)

Просто последовательный список шестнадцатеричных чисел

ФРС — Письмо CA 16-8 по делам потребителей о единой межведомственной системе оценки соответствия потребителей

CA 16-8:

Система фильтров LEE SW150 Mark II, специально разработанная для ряда популярных сверхширокоугольных объективов.

Адаптер для каждого объектива

PowerLab (DAQ) Аппаратное устройство сбора данных для исследований

Целостность данных

PowerLab — это устройство сбора данных (DAQ), разработанное для точного, последовательного и надежного сбора данных.

Простота использования