Контрольная работа по геометрии по теме «Решение треугольников» в 4-х вариантах
Контрольная работа Вариант 1 1.В АВС, А = 45, В = 60, ВС = 3. Найдите АС. 2. Две стороны треугольника равны 7 см и 8 см, а угол между ними равен 120. Найдите периметр и площадь треугольника. 3.Найдите скалярное произведение векторов , если 4.Найдите косинус угла А треугольника АВС, если А (1:7), В (-2:4), С ( 2;0). | Контрольная работа Вариант 2 1. В СDЕ, С = 30, D = 45, СЕ = 5. Найдите DЕ. 2. Две стороны треугольника равны 5 см и 7 см, а угол между ними равен 60. Найдите периметр и площадь треугольника. 3.Найдите скалярное произведение векторов , если 4. |
Контрольная работа Вариант 1 1.В АВС, А = 45, В = 60, ВС = 3. Найдите АС. 2. Две стороны треугольника равны 7 см и 8 см, а угол между ними равен 120. Найдите периметр и площадь треугольника. 3.Найдите скалярное произведение векторов , если 4.Найдите косинус угла А треугольника АВС, если А (1:7), В (-2:4), С ( 2;0). | Контрольная работа Вариант 2 1. В СDЕ, С = 30, Найдите DЕ. 2. Две стороны треугольника равны 5 см и 7 см, а угол между ними равен 60. Найдите периметр и площадь треугольника. 3.Найдите скалярное произведение векторов , если 4.Найдите косинус угла C треугольника АВС, если А (1:7), В (-2:4), С ( 2;0). |
Контрольная работа Вариант 1 1.В АВС, А = 45, В = 60, ВС = 3. Найдите АС. 2. Две стороны треугольника равны 7 см и 8 см, а угол между ними равен 120. Найдите периметр и площадь треугольника. 3.Найдите скалярное произведение векторов , если 4.Найдите косинус угла А треугольника АВС, если А (1:7), В (-2:4), С ( 2;0). | Контрольная работа Вариант 2 1. В СDЕ, С = 30, D = 45, СЕ = 5. Найдите DЕ. 2. Две стороны треугольника равны 5 см и 7 см, а угол между ними равен 60. Найдите периметр и площадь треугольника. 3.Найдите скалярное произведение векторов , если 4.Найдите косинус угла C треугольника АВС, если А (1:7), В (-2:4), С ( 2;0). |
Контрольная работа Вариант 1 1. Найдите АС. 2. Две стороны треугольника равны 7 см и 8 см, а угол между ними равен 120. Найдите периметр и площадь треугольника. 3.Найдите скалярное произведение векторов , если 4.Найдите косинус угла А треугольника АВС, если А (1:7), В (-2:4), С ( 2;0). | Контрольная работа Вариант 2 1. Найдите DЕ. 2. Две стороны треугольника равны 5 см и 7 см, а угол между ними равен 60. Найдите периметр и площадь треугольника. 3.Найдите скалярное произведение векторов , если 4.Найдите косинус угла C треугольника АВС, если А (1:7), В (-2:4), С (2;0). |
Вариант 3
1. Две стороны треугольника равны 6 см и 8 см, а угол между ними равен 600. Найдите третью сторону треугольника и его площадь.
Найдите третью сторону треугольника и его площадь.
3. Вычислить скалярное произведение векторов и , если:
=5, =6, а угол между ними равен 30°
4. Вычислить:
Контрольная работа
Вариант 4
1. Две стороны треугольника равны 10 см и 12 см, а угол между ними равен 1200. Найдите третью сторону треугольника и его площадь.
2. В треугольнике АВС известно, что АС= см, ∠В=45°, ∠С=30°. Найдите сторону АВ треугольника.
3. Вычислить скалярное произведение векторов и , если:
=7, =8, а угол между ними равен 60°
4. Вычислить:
Вариант 3
1. Две стороны треугольника равны 6 см и 8 см, а угол между ними равен 600. Найдите третью сторону треугольника и его площадь. 2. В треугольнике АВС известно, что АВ= см, ∠С=45°, ∠А=120°.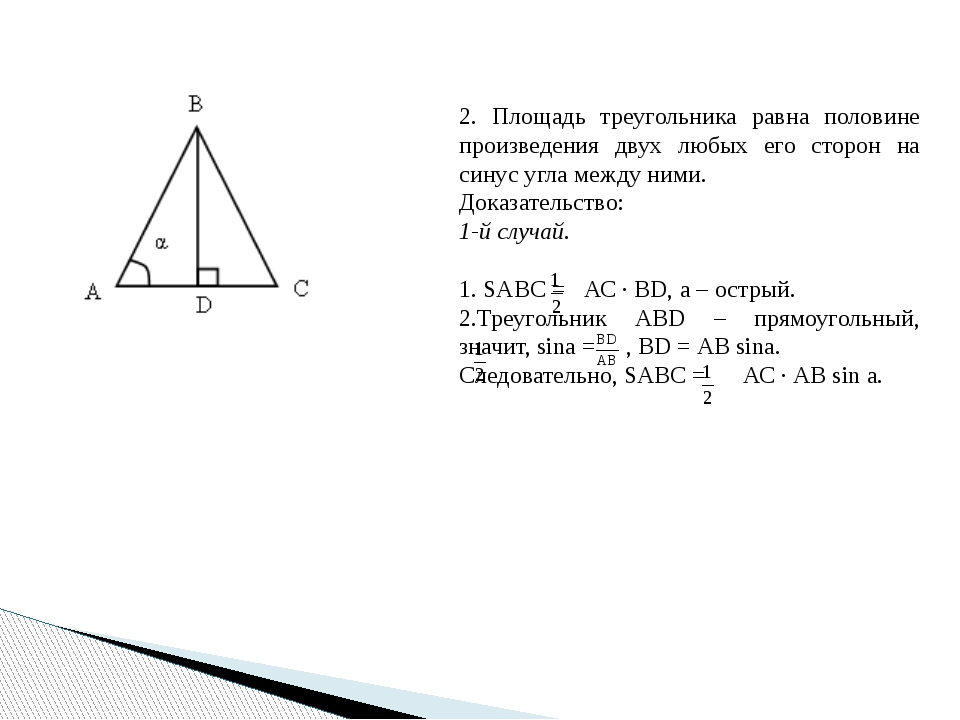 Найдите сторону ВС треугольника.
Найдите сторону ВС треугольника.
3. Вычислить скалярное произведение векторов и , если:
=5, =6, а угол между ними равен 30°
4. Вычислить:
Контрольная работа
Вариант 4
1. Две стороны треугольника равны 10 см и 12 см, а угол между ними равен 1200. Найдите третью сторону треугольника и его площадь.
2. В треугольнике АВС известно, что АС= см, ∠В=45°, ∠С=30°. Найдите сторону АВ треугольника.
3. Вычислить скалярное произведение векторов и , если:
=7, =8, а угол между ними равен 60°
4. Вычислить:
Контрольная работа
Вариант 3
1. Две стороны треугольника равны 6 см и 8 см, а угол между ними равен 600. Найдите третью сторону треугольника и его площадь. 2. В треугольнике АВС известно, что АВ= см, ∠С=45°, ∠А=120°. Найдите сторону ВС треугольника.
3. Вычислить скалярное произведение векторов и , если:
=5, =6, а угол между ними равен 30°
4. Вычислить:
Вычислить:
Контрольная работа
Вариант 4
1. Две стороны треугольника равны 10 см и 12 см, а угол между ними равен 1200. Найдите третью сторону треугольника и его площадь.
2. В треугольнике АВС известно, что АС= см, ∠В=45°, ∠С=30°. Найдите сторону АВ треугольника.
3. Вычислить скалярное произведение векторов и , если:
=7, =8, а угол между ними равен 60°
4. Вычислить:
Треугольники /qualihelpy
Треугольником называют многоугольник, имеющий три вершины (рис. 8.27 – 8.29).
Классификация треугольников по сторонам
1. Если все три стороны треугольника равны, то треугольник равносторонний. Все внутренние углы равностороннего треугольника равны.
Например, на рисунке 8.27 изображен равносторонний треугольник : ; .2. Если две стороны треугольника равны, то треугольник равнобедренный. Стороны, имеющие одинаковую длину, называют боковыми сторонами, а третью сторону – основанием этого треугольника. Углы при основании равнобедренного треугольника равны.
Стороны, имеющие одинаковую длину, называют боковыми сторонами, а третью сторону – основанием этого треугольника. Углы при основании равнобедренного треугольника равны.
3. Если все стороны треугольника имеют различную длину, то треугольник разносторонний (произвольный).
Например, на рисунке 8.29 изображен разносторонний треугольник .Длина стороны треугольника меньше суммы длин двух других его сторон, причем, большая сторона треугольника лежит против большего его угла.
Например: 1) если на рисунке 8.27 , то ; 2) если на рисунке 8.28 , то длина стороны меньше 8, но больше 4.Классификация треугольников по углам
1. Если все углы треугольника острые, то треугольник остроугольный (на рисунке 8.27 треугольник ). 28 треугольник ).3. Если один из углов треугольника прямой, то треугольник прямоугольный. Сторону прямоугольного треугольника, лежащую против прямого угла, называют гипотенузой, две другие стороны – катетами. Например, на рисунке 8.29 треугольник – прямоугольный, отрезок – гипотенуза этого треугольника, а отрезки и – его катеты.Рассмотрим прямоугольный треугольник, у которого и – катеты, – гипотенуза, – острый угол (рис. 8.30).
28 треугольник ).3. Если один из углов треугольника прямой, то треугольник прямоугольный. Сторону прямоугольного треугольника, лежащую против прямого угла, называют гипотенузой, две другие стороны – катетами. Например, на рисунке 8.29 треугольник – прямоугольный, отрезок – гипотенуза этого треугольника, а отрезки и – его катеты.Рассмотрим прямоугольный треугольник, у которого и – катеты, – гипотенуза, – острый угол (рис. 8.30).Например, если катеты треугольника соответственно равны 3 и 4, то гипотенуза этого треугольника равна 5. Такой треугольник называют египетским.
Соотношения между сторонами и углами в прямоугольном треугольнике
1. Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.
2. Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.
Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.
3. Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему катету.
Например, на рисунке 8.30: ; ; . Катет, лежащий против угла , равен половине гипотенузы. Рассмотрим произвольный треугольник, у которого – стороны, – соответственно противолежащие им углы (рис. 8.31).Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих же сторон на косинус угла между ними:
, (8.4)или
, (8.4.1)или
. (8.4.2)Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих им углов:
(8.5)или
, (8.5.1)где – радиус окружности, описанной около этого треугольника.Линии в треугольнике
Среди всех линий, которые можно провести в треугольнике выделяют среднюю линию треугольника, биссектрису треугольника, его медиану и высоту.
Средней линией треугольника называют отрезок, соединяющий середины двух его сторон.
Свойства средней линии треугольника
1. Средняя линия треугольника равна половине длины его третьей стороны.
2. Средняя линия треугольника параллельна одной из сторон треугольника.
Высотой треугольника называют перпендикуляр, проведенный из вершины треугольника на прямую, содержащую противолежащую сторону.
Например, на рисунке 8.33 изображены высоты остроугольного треугольника : отрезки и .На рисунке 8.34 изображена одна из высот тупоугольного треугольника : высота .На рисунке 8.35 изображены три высоты прямоугольного треугольника : высоты и .Свойства высоты треугольника
1. В остроугольном и прямоугольном треугольнике три высоты треугольника пересекаются в одной точке (точка на рисунке 8.33 и точка на рисунке 8.35).2. Если высота треугольника проведена из вершины прямого угла к гипотенузе, то она является средним геометрическим проекций катетов на гипотенузу (рис. 8.5):
8.5):
Медианой треугольника называют отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Например, на рисунке 8.36 изображены медианы треугольника : отрезки и .Свойства медианы треугольника
1. Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении , считая от вершины. Например, на рисунке 8.36 .2. Медиана делит треугольник на два равновеликих треугольника (треугольники, имеющие равные площади, называют равновеликими).
Например, на рисунке 8.36 треугольники и равновеликие.3. Если медиана проведена к гипотенузе прямоугольного треугольника, то она равна половине гипотенузы.
Например, на рисунке 8.37 .Биссектрисой треугольника называют отрезок биссектрисы внутреннего угла треугольника, заключенный между вершиной треугольника и точкой пересечения биссектрисы угла и стороны треугольника.
Свойства биссектрисы треугольника
1. Три биссектрисы треугольника пересекаются в одной точке, являющейся центром окружности, вписанной в треугольник.
Например, точка на рисунке 8.38.2. В равностороннем треугольнике все биссектрисы равны и являются высотами и медианами этого треугольника.
Например, на рисунке 8.39 биссектрисы – высоты и медианы правильного треугольника и .3. Если биссектриса проведена из вершины равнобедренного треугольника к его основанию, то она является высотой и медианой этого треугольника.
Например, на рисунке 8.40 биссектриса – высота и медиана равнобедренного треугольника .4. Биссектриса треугольника делит сторону этого треугольника на отрезки, пропорциональные прилежащим к ним сторонам.
Например, если – биссектриса треугольника , изображенного на рисунке 8.41, то .Формулы для вычисления площади треугольника
Для вычисления площади треугольника можно применять одну из следующих формул:
, (8. 8)где – сторона равностороннего треугольника; , (8.9)где – сторона, – высота, проведенная к стороне произвольного треугольника; , (8.10)где и – катеты прямоугольного треугольника; , (8.11)где и – стороны, – величина угла между ними произвольного треугольника;
8)где – сторона равностороннего треугольника; , (8.9)где – сторона, – высота, проведенная к стороне произвольного треугольника; , (8.10)где и – катеты прямоугольного треугольника; , (8.11)где и – стороны, – величина угла между ними произвольного треугольника;Формула Герона:
, (8.12)где – стороны, – полупериметр треугольника;, (8.13)где — полупериметр треугольника, — радиус окружности, вписанной в треугольник;, (8.14)где – стороны, – радиус окружности, описанной около треугольника.Два треугольника равны, если все их соответственные стороны и углы равны.
Признаки равенства треугольников
1. Два треугольника равны, если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника.
Например, на рисунке 8.42 треугольники и равны по двум сторонам и углу между ними.2. Два треугольника равны, если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника.
3. Два треугольника равны, если три стороны одного треугольника соответственно равны трем сторонам другого треугольника.
Например, на рисунке 8.44 треугольники и равны по трем сторонам.Признаки равенства прямоугольных треугольников
1. Прямоугольные треугольники равны, если катеты одного треугольника соответственно равны катетам другого треугольника.
Например, на рисунке 8.45 треугольники и равны по двум катетам.2. Прямоугольные треугольники равны, если катет и прилежащий острый угол одного треугольника соответственно равны катету и прилежащему острому углу другого треугольника.
Например, на рисунке 8,46 треугольники и равны по катету и прилежащему острому углу.3. Прямоугольные треугольники равны, если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого треугольника.
4. Прямоугольные треугольники равны, если гипотенуза и катет одного треугольника соответствравны гипотенузе и катету другого треугольника.
Например, на рисунке 8.48 треугольники и равны по гипотенузе и катету.Два треугольника подобны, если все углы одного треугольника соответственно равны углам другого, а все стороны одного пропорциональны соответствующим (сходственным) сторонам другого треугольника.
Признаки подобия треугольников
1. Два треугольника подобны, если два угла одного треугольника равны двум углам другого.
2. Два треугольника подобны, если две стороны одного треугольника пропорциональны двум сторонам другого, а углы, заключенные между ними, равны.
3. Два треугольника подобны, если три стороны одного треугольника пропорциональны трем сторонам другого.
Например, на рисунке 8. 51 изображены подобные треугольники, так как длины сторон одного из них в два раза больше длин сторон другого.
51 изображены подобные треугольники, так как длины сторон одного из них в два раза больше длин сторон другого.
Тренировочные варианты «Школково». Вариант №5 от 06.04.2018
а) Так как общая масса всех осколков равна \(600\,000\) грамм, то каждому ходоку нужно \(600\,000:40=15\,000\) грамм.
Пусть шести ходокам Король раздаст по 15 осколков, каждый массой \(1000\) грамм.
Тогда у него останется еще 10 осколков по \(1000\) грамм и 100 осколков по \(5000\) грамм.
Седьмому ходоку Король даст 10 осколков по \(1000\) грамм и 1 осколок по \(5000\) грамм. А оставшиеся 99 осколков по \(5000\) грамм разделит поровну (по 3 осколка каждому) между 33 ходоками. Итого Король поощрил 40 ходоков.
Ответ: да.
б) Если хранителю Сурового дома Король даст \(40\,000\) грамм стекла, то 70 ходокам он должен в сумме отдать \(600\,000-40\,000=560\,000\) грамм.
Каждому ходоку нужно дать по \(8\,000\) грамм. Так как у Короля имеются осколки массой \(1000\) и \(5000\) грамм, то на каждого ходока нужно использовать как минимум 3 осколка массой \(1000\) грамм каждый. Следовательно, так как ходоков 70, то всего Королю нужно как минимум \(70\cdot 3=210\) таких осколков. А у него таких осколков 100.
Следовательно, ответ: нет.
в) Давайте сначала разберемся, что значит фраза “при любом распределении драконьего стекла между ними”. Это значит, что при любом размере поощрения каждого ходока, например, первому ходоку \(7\,000\) грамм драконьего стекла, второму – \(13\,000\), третьему – \(2\,000\) и т.д. (главное, чтобы в сумме все поощрения были равны \(600\,000\) грамм), Король смог имеющимися осколками каждому выдать нужное количество драконьего стекла. Также “при любом распределении драконьего стекла между ними” – это значит, что мы не знаем, при каком именно.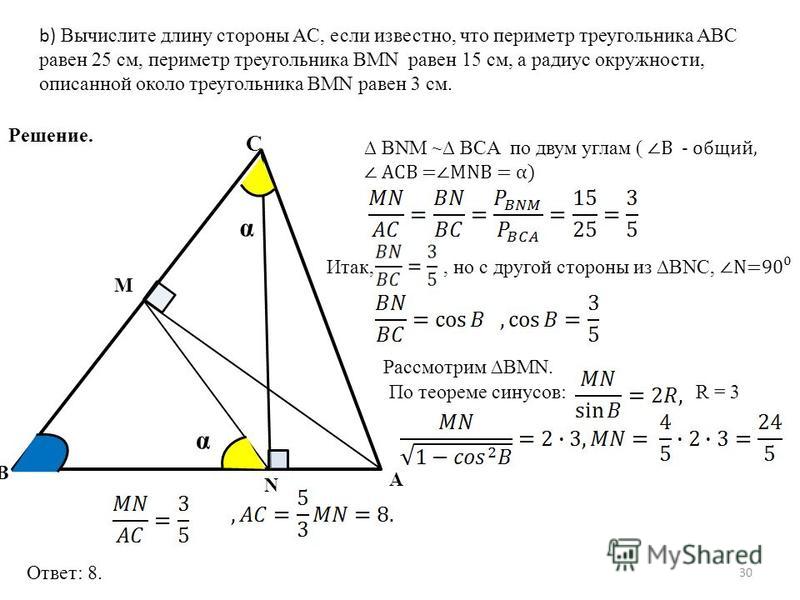 А значит не имеем права брать какое-то конкретное распределение и решать задачу, используя только его.
А значит не имеем права брать какое-то конкретное распределение и решать задачу, используя только его.
Давайте вспомним, почему нам не получилось выдать поощрения ходокам в пункте б). Нам не хватило осколков по \(1000\) грамм, так как на каждого ходока уходило минимум три таких осколка.
А как можно сделать так, чтобы минимально тратить на поощрения ходока еще больше \(1000\)-граммовых осколков? Например, можно назначить ходоку поощрения в \(4000\) грамм, тогда никаким иным способом, кроме как выдать ему четыре осколка по \(1000\) грамм, поощрить его не получится. И чем больше таких ходоков будет, тем быстрее кончатся слитки по \(1000\) грамм. То есть самый худший случай, когда каждому ходоку нужно выдать четыре осколка по \(1000\) грамм.
Начнем искать ответ, начиная с 25 ходоков, так как всего 100 осколков по \(1000\) грамм и худший вариант – когда каждый получит по четыре осколка.
Пусть у нас есть некоторое распределение поощрений для этих 25 ходоков. Начнем выдавать поощрения всем по очереди, начиная с первого ходока.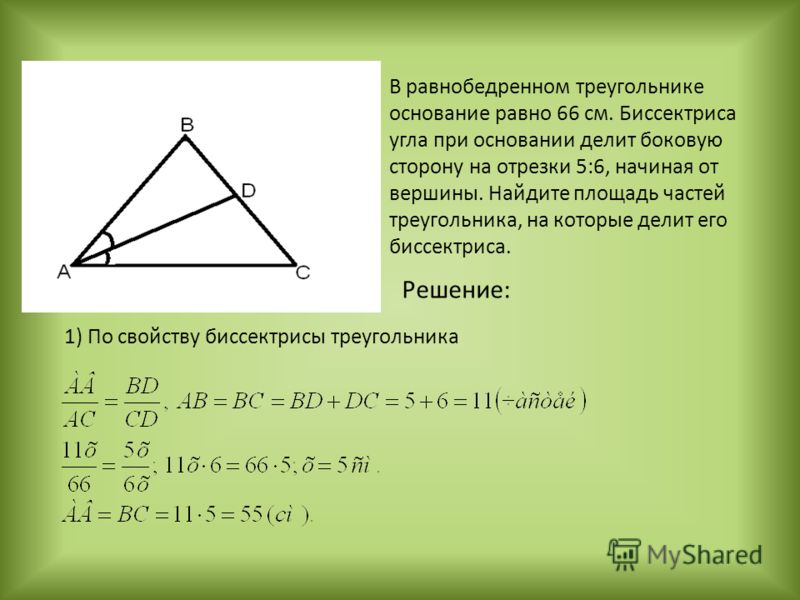 Очевидно, что осколков по \(1000\) грамм нам хватит до самого конца, и \(5000\)-граммовых нам тоже хватит до самого конца, так как если бы их не хватило, то это значило бы, что сумма всех поощрений больше \(600\,000\) грамм.
Очевидно, что осколков по \(1000\) грамм нам хватит до самого конца, и \(5000\)-граммовых нам тоже хватит до самого конца, так как если бы их не хватило, то это значило бы, что сумма всех поощрений больше \(600\,000\) грамм.
Теперь посмотрим, удастся ли нам сделать то же самое для 26 ходоков. Сначала раздадим всем ходокам \(5000\)-граммовые осколки так, чтобы каждому осталось доплатить сумму, меньшую, чем \(5000\) грамм. Заметим, что мы тогда раздали \(500\,000\) грамм драконьего стекла и нам осталось раздать еще \(100\,000\). Дальше первым 25-ти ходокам раздадим необходимое количество осколков по \(1000\) грамм. Это мы сделать точно сможем по доказанному ранее. Пусть мы раздали \(x\) \(1000\)-граммовых осколков первым 25-ти ходокам. Тогда всего у нас осталось \(1000\)-граммовых осколков \(100-x\). Следовательно, всего нам осталось раздать \(100\,000-1000x=1000(100-x)\) грамм драконьего стекла. То есть в любом случае количество драконьего стекла, которое у нас осталось, совпадает с количеством драконьего стекла, которое нужно доплатить 26 ходоку, а значит мы всегда сможем это сделать.
Покажем, что для 27 ходоков существует распределение поощрений, которые мы выдать не сможем.
26 ходокам по \(4000\) грамм, а 27-ому – \(496\,000\) грамм. Выдать поощрения мы не сможем, так как нам понадобится как минимум 105 \(1000\)-граммовых осколков драконьего стекла.
Ответ:
а) да
б) нет
в) 26
Сканави Группа Б Условия, ответы, решения
Сканави М.И.
Задачи по планиметрии с ответами и решениями
перейти к содержанию
Группа Б. Задачи 191 — 240 (с ответами и решениями)
Внутри прямого угла дана точка М, расстояния от которой до сторон угла равны 4 и 8 см. Прямая, проходящая через точку М, отсекает от прямого угла треугольник площадью 100 см2. Найти катеты треугольника. Ответ: 40; 5 или 10; 20
- Высота, проведенная к гипотенузе прямоугольного треугольника, делит его на два треугольника с площадями Q и q.
 Найти катеты. Ответ: ;
Найти катеты. Ответ: ; - Периметр прямоугольного треугольника ABC (угол C=90°) равен 72 см, а разность между длинами медианы СМ и высоты СК равна 7 см. Найти длину гипотенузы. Ответ: 32
- В прямоугольном треугольнике медианы катетов равны и . Найти гипотенузу треугольника. Ответ: 10
- Периметр прямоугольного треугольника равен 60 см. Найти его стороны, если высота, проведенная к гипотенузе, равна 12 см. Ответ: 15; 20; 25
- Найти биссектрису прямого угла треугольника, у которого катеты равны а и b. Ответ:
- В прямоугольном треугольнике расстояние от середины гипотенузы до одного из катетов равно 5 см, а расстояние от середины этого катета до гипотенузы равно 4 см. Вычислить площадь треугольника. Ответ: 200/3
- Гипотенуза прямоугольного треугольника равна с. Проекция вершины прямого угла на гипотенузу делит ее на два отрезка, из которых меньший относится к большему как больший ко всей гипотенузе. Определить площадь треугольника.
 Ответ:
Ответ: - Определить стороны прямоугольного треугольника, у которого периметр равен 2р, а площадь равна m2.
- Стороны треугольника равны 3, 4 и 5 см. Определить площади треугольников, на которые разбивается данный треугольник высотой и медианой, проведенными к большей по величине стороне. Ответ: 2,16; 3; 0,84
- Высоты треугольника равны 12, 15 и 20 см. Доказать, что треугольник прямоугольный.
- Числа выражают длины высот некоторого треугольника. Показать, что если выполняется равенство , то треугольник является прямоугольным.
- Медианы треугольника равны 5, и см. Доказать, что треугольник прямоугольный.
- Числа , и выражают длины медиан некоторого треугольника. Показать, что если выполняется равенство , то треугольник является прямоугольным.
- Площадь равностороннего треугольника, построенного на гипотенузе, вдвое больше площади прямоугольного треугольника с указанной гипотенузой. Найти отношение катетов.
 Ответ:
Ответ: - Внутри равностороннего треугольника взята точка М, отстоящая от его сторон на расстояния b, с, d. Найти высоту треугольника. Ответ:
- Точка М лежит внутри равностороннего треугольника ABC. Вычислить площадь этого треугольника, если известно, что АМ=ВМ=2 см, а СМ= 1 см. Ответ:
- Показать, что сумма расстояний от любой точки, взятой на стороне правильного треугольника, до двух других его сторон есть величина постоянная.
- Основания двух правильных треугольников со сторонами а и 2а лежат на одной и той же прямой. Треугольники расположены по разные стороны от прямой и не имеют общих точек, а расстояние между ближайшими концами их оснований равно 2а. Найти расстояние между вершинами треугольников, не принадлежащими данной прямой. Ответ:
- Точка С перемещается по отрезку АВ длиной l. На отрезках АС и СВ как на основаниях построены правильные треугольники по одну сторону от АВ. Где нужно взять точку С, чтобы расстояние между вершинами треугольников было наименьшим?
- В равнобедренном треугольнике угол при основании содержит 72°, а биссектриса этого угла имеет длину, равную m.
 Найти длины сторон треугольника. Ответ:
Найти длины сторон треугольника. Ответ: - В равнобедренном треугольнике угол при вершине содержит 36°, а биссектриса угла при основании равна . Найти длины сторон треугольника. Ответ:
- В равнобедренном треугольнике с боковой стороной, равной b, проведены биссектрисы углов при основании. Отрезок прямой между точками пересечения биссектрис с боковыми сторонами равен m. Определить основание треугольника. Ответ:
- Длина основания равнобедренного треугольника равна 12 см, а боковой стороны — 18 см. К боковым сторонам треугольника проведены высоты. Вычислить длину отрезка, концы которого совпадают с основаниями высот. Ответ: 28/3
- Основание равнобедренного треугольника равно 8, а боковая сторона — 12. Найти длину отрезка, соединяющего точки пересечения биссектрис углов при основании с боковыми сторонами треугольника. Ответ: 4,8
- В равнобедренном треугольнике ABC (AB=BC) на стороне ВС взята точка D так, что BD: DC = 1:4. В каком отношении прямая AD делит высоту BE треугольника ABC, считая от вершины В? Ответ: 1:2
- Равнобедренный треугольник со сторонами 8, 5 и 5 разделен на три равновеликие части перпендикулярами, проведенными из некоторой точки к его сторонам.
 Найти расстояние от этой точки до каждой стороны треугольника. Ответ:
Найти расстояние от этой точки до каждой стороны треугольника. Ответ: - Определить углы равнобедренного треугольника, если его площадь относится к площади квадрата, построенного на его основании, как . Ответ: 30,30,120
- Найти третью сторону остроугольного треугольника, если две его стороны равны а и b, а медианы этих сторон пересекаются под прямым углом. Ответ:
- Две стороны треугольника равны 6 и 8 см. Медианы, проведенные к этим сторонам, взаимно перпендикулярны. Найти третью сторону треугольника. Ответ:
- Высота, основание и сумма боковых сторон треугольника равны соответственно 24, 20 и 56 см. Найти боковые стороны. Ответ: 26; 30
- Дан треугольник ABC, в котором 2hc=AB и угол A = 75°. Найти величину угла С. Ответ: 75
- Внутри угла в 60° расположена точка, отстоящая на расстояния и см от сторон угла. Найти расстояние от этой точки до сторон угла. Ответ:
- Длины двух сторон остроугольного треугольника равны и см.
 Найти длину третьей стороны, зная, что эта сторона равна проведенной к ней высоте. Ответ: 3
Найти длину третьей стороны, зная, что эта сторона равна проведенной к ней высоте. Ответ: 3 - Расстояния от точки М, лежащей внутри треугольника ABC, до его сторон АС и ВС равны соответственно 2 и 4 см. Вычислить расстояние от точки М до прямой АВ, если АВ = 10 см, ВС= 17 см, АС = 21 см. Ответ: 5,8
- Найти отношение суммы квадратов всех медиан треугольника к сумме квадратов всех его сторон. Ответ: 3:4
- Найти площадь треугольника, если его высоты равны 12, 15 и 20 см. Ответ: 150
- В треугольнике ABC проведена прямая DE, параллельная основанию АС. Площадь треугольника ABC равна 8 кв. ед., а площадь треугольника DEC равна 2 кв. ед. Найти отношение отрезка DE к длине основания треугольника ABC. Ответ: 1:2
- Длины сторон треугольника относятся как m:n:m. Найти отношение площади этого треугольника к площади треугольника, вершины которого находятся в точках пересечения биссектрис данного треугольника с его сторонами. Ответ:
- В треугольнике АВС проведены медианы BD и СЕ; М — точка их пересечения.
 Доказать, что треугольник ВСМ равновелик четырехугольнику ADME.
Доказать, что треугольник ВСМ равновелик четырехугольнику ADME. - Отношение величин двух углов треугольника равно 2, а разность длин противоположных им сторон равна 2 см; длина третьей стороны треугольника равна 5 см. Вычислить площадь треугольника. Ответ:
- В треугольнике ABC известны: ВС= 15 см, АС =14 см, АВ = 13 см. Вычислить площадь треугольника, заключенного между высотой и биссектрисой, проведенными из вершины В. Ответ: 9
- Стороны треугольника равны 13, 14 и 15 см. Определить площади треугольников, на которые разбивается данный треугольник его медианами. Ответ: 14
- Медианы одного треугольника равны сторонам другого треугольника. Найти отношение площадей этих треугольников. Ответ: 4:3
- Медианы треугольника равны 3, 4 и 5 см. Найти площадь треугольника. Ответ: 8
- Основание треугольника равно 20 см, медианы боковых сторон равны 18 и 24 см. Найти площадь треугольника. Ответ: 288
- Медианы треугольника равны 5, 6 и 5 м. Найти площадь треугольника. Ответ: 16
- Определить площадь треугольника, если две, его стороны равны 1 и см, а медиана третьей стороны равна 2 см. Ответ:
- Определить площадь треугольника, если две его стороны равны 35 и 14 см, а биссектриса угла между ними содержит 12 см. Ответ: 235,2
- Биссектрисы углов А и В треугольника ABC одинаково наклонены к сторонам ВС и АС. Найти зависимость между углами А и В. Ответ: A+B=120
Метки Сканави. Смотреть запись.
Мерзляк 5 класс — § 14. Треугольник и его виды
Вопросы к параграфу
1. Какие бывают виды треугольников в зависимости от вида их углов?
- остроугольные — все из углы острые;
- прямоугольные — один из углов треугольника прямой — равен 90°;
- тупоугольные — один из углов треугольника тупой.
2. Какой треугольник называют остроугольным? Прямоугольным? Тупоугольным?
- Остроугольные прямоугольники — это треугольники, у которых все углы острые (< 90°).
- Прямоугольные треугольники — это прямоугольники, у которых один из углов прямой (= 90°).
- Тупоугольные треугольники — это треугольники, у которых один из углов тупой (> 90°).
3. Какие бывают виды треугольников в зависимости от количества равных сторон?
- равнобедренные треугольники — 2 стороны равны;
- равносторонние треугольники — 3 стороны равны.
4. Какой треугольник называют равнобедренным? Равносторонним? Разносторонним?
- Равнобедренный треугольник — это треугольник, у которого две стороны равны.
- Равносторонний треугольник — это треугольник, у которого три стороны равны.
- Разносторонний треугольник — это треугольник, у которого все стороны имеют различную длину.
5. Как называют стороны равнобедренного треугольника?
- равные стороны равнобедренного треугольника называют боковыми сторонами;
- отличающуюся по длине сторону равнобедренного треугольника называют основанием.
6. По какой формуле вычисляют периметр равностороннего треугольника? — Периметр равностороннего треугольника равен произведению числа 3 и длины его стороны : P = 3a.
Решаем устно
1. Чему равен периметр восьмиугольника, каждая сторона которого равна 4 см?
8 • 4 = 32 (см) — периметр восьмиугольника.
Ответ: 32 см.
2. Вычислите сумму 27 + 16 + 33 + 24.
27 + 16 + 33 + 24 = (27 + 33) = (16 + 24) = 60 + 40 = 100
Ответ: 100.
3. Каких чисел не хватает в цепочке вычислений?
4. На трёх кустах расцвело 15 роз. Когда на одном из этих кустов распустились ещё 3 розы, то на всех кустах роз стало поровну. Сколько роз было на каждом кусте вначале?
1) Мы знаем, что вначале на всех кустах было 15 роз, но потом на одной розе распустилось ещё 3 цветка:
15 + 3 = 18 (цветов) — стало на всех кустах в конце.
2) Мы знаем, что в конце на каждом из трёх кустов роз было поровну:
18 : 3 = 6 (цветов) — было на каждом кусте в конце.
3) Мы знаем, что на одном из кустов роз вначале было на 3 меньше:
6 — 3 = 3 (цветка) — было на одном из кустов вначале.
4) Мы знаем, что количество роз на остальных кустах не изменилось, то есть было и осталось по 6 цветков.
Ответ: 6, 6 и 3 розы.
Упражнения
338. Определите вид треугольника, изображённого на рисунке 121, в зависимости от вида его углов и количества равных сторон.
- а) треугольник ABC — это разносторонний остроугольный треугольник;
- б) треугольник MNK — это разносторонний прямоугольный треугольник;
- в) треугольник PEF — это равнобедренный остроугольный треугольник;
- г) треугольник QSR — это равнобедренный тупоугольный треугольник;
- д) треугольник OTR — это разносторонний тупоугольный треугольник;
- е) треугольник DAB — это равнобедренный прямоугольный треугольник.
339. Начертите:
- RTQ — разносторонний остроугольный треугольник;
- JLD — равнобедренный прямоугольный треугольник;
- POS — равнобедренный тупоугольный треугольник.
340. Начертите:
- ABC — разносторонний прямоугольный треугольник;
- MNK — разносторонний тупоугольный треугольник;
- EFH — равнобедренный остроугольный треугольник.
341. Найдите периметр треугольника со сторонами 16 см, 22 см и 28 см.
Периметр треугольника равен сумме длин все его сторон.
P = 16 + 22 + 28 = 66 (см)
Ответ: P = 66 см.
342. Найдите периметр треугольника со сторонами 14 см, 17 см и 17 см.
Периметр треугольника равен сумме длин все его сторон.
P = 14 + 17 + 17 = 48 (см)
Ответ: P = 48 см.
343. Начертите произвольный треугольник, измерьте его стороны и углы, найдите периметр и сумму углов этого треугольника.
Начертим произвольный треугольник ABC.
При помощи линейки измерим длины его сторон:
- AB = 4,2 см
- BC = 3,2 см
- AC = 4,6 см
При помощи транспортира измерим его углы:
- ∠A = 42º
- ∠B = 74º
- ∠C = 64º
Найдём периметр треугольника ABC:
P = AB + BC + AC =4,2 + 3,2 + 4,6 = 12 (см)
∠A + ∠B + ∠C = 42º + 74º + 64º = 180º
Ответ: в треугольнике ABC: AB = 4,2 см, BC = 3,2 см, AC = 4,6 см, ∠A = 42º, ∠B = 74º, ∠C = 64º, периметр P = 12 см, сумма углов равна 180º.
344. Одна сторона треугольника равна 24 см, вторая сторона — на 18 см больше первой, а третья сторона — в 2 раза меньше второй. Найдите периметр треугольника.
1) 24 + 18 = 42 (см) — длина второй стороны треугольника.
2) 42 : 2 = 21 (см) — длина третьей стороны треугольника.
3) 24 + 42 + 21 = 87 (см) — периметр треугольника.
Ответ: P = 87 см.
345. Одна сторона треугольника равна 12 см, вторая сторона в 3 раза больше первой, а третья — на 8 см меньше второй. Найдите периметр треугольника.
1) 12 • 3 = 36 (см) — длина второй стороны треугольника.
2) 36 — 8 = 28 (см) — длина третьей стороны треугольника.
3) 12 + 36 + 28 = 78 (см) — периметр треугольника.
Ответ: P = 78 см.
346. 1) Найдите периметр равнобедренного треугольника, основание которого равно 13 см, а боковая сторона — 8 см.
У равнобедренного треугольника боковые стороны равны. Значит у данного треугольника дву стороны по 8 см и одна сторона (основание) — 13 см. Найдём периметр:
8 + 8 + 13 = 29 (см) — периметр треугольника.
Ответ: 29 см.
2) Периметр равнобедренного треугольника равен 39 см, а основание — 15 см. Найдите боковые стороны треугольника.
Мы знаем, тто периметр треугольника — это сумма длин всех его сторон. Также мы знаем, что боковые стороны равнобедренного треугольника равны. Найдем длину боковой стороны:
(39 — 15) : 2 = 24 : 2 = 12 (см) — длина боковой стороны.
Ответ: Каждая из двух боковых сторон этого равнобедренного треугольника равна 12 см.
347. Периметр равнобедренного треугольника равен 28 см, а боковая сторона — 10 см. Найдите основание треугольника.
Мы знаем, тто периметр треугольника — это сумма длин всех его сторон. Также мы знаем, что боковые стороны равнобедренного треугольника равны. Найдем длину основания:
28 — 10 • 2 = 28 — 20 = 8 (см) — длина основания.
Ответ: 8 см.
348. Периметр треугольника равен p см, одна сторона — 22 см, вторая сторона — b см. Составьте выражение для нахождения третьей стороны. Вычислите длину третьей стороны, если р = 72, b = 26.
Пусть третья сторона равна с см. Составим выражения для нахождения длины третьей стороны треугольника:
с = p — 22 — b (см)
При р = 72, b = 26:
с = 72 — 22 — 26 = 50 — 26 = 24 (см).
Ответ: с = p — 22 — b, с = 24 см.
349. Периметр треугольника равен 97 см, одна сторона — а см, вторая — b см. Составьте выражение для нахождения третьей стороны. Вычислите длину третьей стороны, если а = 32, b = 26.
Пусть третья сторона равна с см. Составим выражения для нахождения длины третьей стороны треугольника:
с = 97 — а — b (см)
При а = 32, b = 26:
с = 97 — 32 — 26 = 65 — 26 = 39 (см).
Ответ: с = 97 — а — b, с = 39 см.
350. С помощью линейки и транспортира постройте треугольник ABC и укажите его вид, если:
1) две стороны равны 3 см и 6 см, а угол между ними — 40° — разносторонний тупоугольный треугольник (тупым является угол B).
2) две стороны равны 2 см 5 мм и 5 см, а угол между ними — 130° — разносторонний тупоугольный треугольник (тупым является угол А).
3) две стороны равны по 3 см 5 мм, а угол между ними — 54° — равнобедренный остроугольный треугольник
4) сторона АВ равна 4 см, а углы САВ и СВА соответственно равны 30° и 70° — разносторонний остроугольный треугольник.
5) сторона АВ равна 2 см 5 мм, а углы САВ и СВА соответственно равны 100° и 20° — разносторонний тупоугольный треугольник.
6) сторона ВС равна 5 см, а углы ABC и ВСА соответственно равны 30° и 60° — разносторонний прямоугольный треугольник.
7) сторона ВС равна 5 см 5 мм, а углы ABC и ВСА равны по 45° — равнобедренный прямоугольный треугольник.
8) сторона АС равна 5 см 5 мм, а углы ВАС и ВСА равны по 60°
351. С помощью линейки и транспортира постройте треугольник ABC и укажите его вид, если:
1) две стороны равны 3 см и 4 см, а угол между ними — 90° — разносторонний прямоугольный треугольник.
2) две стороны равны по 4 см 5 мм, а угол между ними — 60° — равносторонний остроугольный треугольник.
3) сторона АС равна 6 см, а углы ВАС и ВСА соответственно равны 90° и 45° — равнобедренный прямоугольный треугольник.
4) сторона АВ равна 4 см 5 мм, а углы САВ и СВА соответственно равны 35° — равнобедренный тупоугольный треугольник.
352. Постройте треугольник, стороны которого содержат четыре точки, изображённые на рисунке 122.
353. Сколько треугольников изображено на рисунке 123?
- а) Изображено 7 треугольников (4 маленьких и 3 больших).
- б) Изображено 20 треугольников(12 маленьких, 6 средних и 2 больших).
Упражнения для повторения
354. Запишите все углы, изображённые на рисунке 124, и укажите вид каждого угла.
- ∠ABC — развёрнутый угол
- ∠ABM — острый угол
- ∠ABK — тупой угол
- ∠MBK — прямой угол
- ∠MBC — тупой угол
- ∠KBC — острый угол
355. Миша делал домашнее задание по математике с 16 ч 48 мин до 17 ч 16 мин, а Дима — с 17 ч 53 мин до 18 ч 20 мин. Кто из мальчиков дольше делал задание и на сколько минут?
1) 17 ч 16 мин — 16 ч 48 мин = 16 ч 76 мин — 16 ч 48 мин = 28 мин — делал задание Миша.
2) 18 ч 20 мин — 17 ч 53 мин = 17 ч 80 мин — 17 ч 53 мин = 27 мин — делал задание Дима.
3) 28 мин — 27 мин = 1 мин — делал дольше Миша, чем Дима.
Ответ: Миа делал домашнее задание на 1 минуту дольше, чем Дима.
356. Решите уравнение:
357. Вместо звёздочек поставьте цифры так, чтобы действие было выполнено правильно:
Задача от мудрой совы
358. Каждый учащийся гимназии изучает по крайней мере один из двух иностранных языков. Английский язык изучают 328 учеников, французский язык — 246 учеников, а английский и французский одновременно — 109 учеников. Сколько всего учеников учится в гимназии?
1) 328 — 109 = 219 (учеников) — изучает только английский язык.
2) 246 — 109 = 137 (учеников) — изучает только французский язык.
3) 219 + 109 + 137 = 465 (учеников) — всего в гимназии.
Ответ: 465 учеников.
Итоговое повторение курса планиметрии с привлечением метода ключевой задачи — Документ
Г.И. Ковалева
Итоговое повторение курса планиметрии с привлечением метода ключевой задачи
Метод составления системы задач, построенной по принципу – каждая задача системы использует результат решения одной какой-либо (ключевой) задачи, будем называть методом ключевой задачи.
Существует две точки зрения на понятие ключевой задачи. Первая из них состоит в рассмотрении ключевой задачи как задачи-факта. Зачастую такая ключевая задача оказывается дополнительной теоремой школьного курса. Вторая точка зрения состоит в рассмотрении ключевой задачи как задачи-метода. При изучении какой-либо темы школьного курса можно отобрать определенный минимум задач, овладев методами решения которых, учащиеся будут в состоянии решить любую задачу на уровне программных требований по изучаемой теме.
«Ключевая» задача является средством решения других задач, поэтому ее знание учащимися обязательно. Разворачивающаяся система задач, с одной стороны, способствует усвоению факта или метода решения, изложенных в «ключевой» задаче, с другой, позволяет увидеть взаимосвязи отдельных тем школьного курса математики. Поэтому составленная данным методом система задач является эффективным средством повторения, обобщения и систематизации учебного материала.
Приведем системы, составленные методом «ключевых» задач, которые можно использовать для итогового повторения курса планиметрии.
Свойства медиан треугольника
Ключевые задачи:
1. Медианы в треугольнике пересекаются в одной точке и делятся в ней в отношении 2:1, считая от вершины.
2. Медиана делит треугольник на два равновеликих.
3. Медианы треугольника делят его на шесть равновеликих треугольников.
4. Пусть О – точка пересечения медиан треугольника АВС. Тогда .
Задачи системы:
Задача 1. Две стороны треугольника соответственно равны 6 и 8. Медианы, проведенные к этим сторонам, перпендикулярны. Найдите площадь треугольника.
Треугольники ВОС1 и СОВ1 прямоугольные и по теореме Пифагора имеем
. Тогда .
О т в е т: .
Задача 2. Длина одной из сторон треугольника равна 26, а длины медиан, проведенных к двум другим сторонам, равны 30 и 39. Найдите площадь треугольника.
Задача 3. В треугольника АВСАА1 и СС1– медианы, причем АА1=5, , . Найдите площадь треугольника АВС.
Тогда , ,
,.
О т в е т: .
Задача 4. Медианы треугольника 3, 4 и 5. Найдите площадь треугольника.
. Следовательно, .
О т в е т: 8.
Задача 5. Длины двух сторон треугольника 27 и 29. Длина медианы, проведенной к третьей стороне, равна 26. Найдите высоту треугольника, проведенную к стороне длиной 27.
, , .
О т в е т: 20.
Задачи для самостоятельного решения
1. В треугольнике АВС медиана АМ перпендикулярна медиане BN. Найдите площадь треугольника АВС, если длина АМ равна 3, а длина BN равна 4.
О т в е т: 8.
2. Основание равнобедренного треугольника равно 2. Медианы, проведенные к боковым сторонам, взаимно перпендикулярны. Найдите площадь треугольника.
О т в е т: 3.
3. Две медианы равнобедренного треугольника взаимно перпендикулярны. Боковая сторона равна . Найдите площадь треугольника.
О т в е т: 3.
4. В треугольнике АВС медианы АD и ВE перпендикулярны, , . Чему равен квадрат третьей стороны?
О т в е т: 5.
5. Сторона треугольника равна 20, а медианы, проведенные к двум другим сторонам – 24 и 18. Найдите площадь треугольника.
О т в е т: 288.
6. Стороны треугольника равны 13, 14 и 15. Найти площади треугольников, на которые разбивается данный треугольник его медианами.
О т в е т: 14.
7. Площадь треугольника АВС равна 12. Из вершины тупого угла В проведена медиана BD, длина которой равна 3. Найдите длину стороны АС, если угол ABD – прямой.
О т в е т: 10.
8. Найдите площадь треугольника, если две его стороны равны 1 и , а медиана третьей стороны равна 2. (Указание – достроить до параллелограмма).
О т в е т: .
Длина медианы
Ключевая задача. Докажите, что если стороны АВ, АС и ВС треугольника АВС равны соответственно с, b и а, то длина медианы, проведенной к стороне ВС, может быть вычислена по формуле .
Д о к а з а т е л ь с т в о.
По теореме косинусов имеем: из треугольника АВМ ; из треугольника АВС или . |
Сложим эти равенства, получим . Отсюда .
Задачи системы:
Задача 1. Найдите отношение суммы квадратов всех медиан треугольника к сумме квадратов всех его сторон.
Р е ш е н и е.
.
О т в е т: .
Задача 2. В равнобедренном прямоугольном треугольнике медиана, проведенная к катету, равна l. Найдите площадь треугольника.
Р е ш е н и е. Пусть катет прямоугольного равнобедренного треугольника равен а. Тогда . Из формулы длины медианы, выразим . Тогда .
О т в е т: .
Задача 3. В равнобедренном треугольнике к боковой стороне, длиной 4, проведена медиана, длиной 3. Найдите основание треугольника.
Р е ш е н и е. Используя формулу , найдем длину основания треугольника .
О т в е т: .
Задача 4. Найдите площадь треугольника, если его две стороны равны 1 и , а медиана третьей стороны равна 2.
Р е ш е н и е.
1. Найдем АС, используя формулу длины медианы. . .
2. Треугольник АВС – прямоугольный, так как . Следовательно, .
О т в е т: .
Задача 5. Сторона треугольника 14, а медианы, проведенные к двум другим сторонам, равны и . Найдите длины неизвестных сторон треугольника.
Р е ш е н и е. Пусть , , . Тогда длины медиан АА1 и СС1 можно найти по формулам: и . Имеем систему:
О т в е т: ; .
Задачи для самостоятельного решения
1. Одна сторона треугольника равна а, другая – b. Найдите третью сторону, если известно, что она равна медиане, проведенной к ней.
О т в е т: .
2. Основание равнобедренного треугольника , медиана боковой стороны 5. Найдите длины боковых сторон.
О т в е т: 6.
3. В равнобедренном треугольнике основание равно , а угол при основании равен 300. Найдите длину медианы, проведенной к боковой стороне.
О т в е т: 7.
4. Медианы треугольника равны 5, и . Докажите, что треугольник прямоугольный.
5. Числа , и выражают длины медиан некоторого треугольника. Докажите, что если выполняется равенство , то треугольник является прямоугольным.
Медиана, проведенная к гипотенузе
Ключевая задача. В прямоугольном треугольнике длина медианы, проведенной к гипотенузе, равна ее половине.
Д о к а з а т е л ь с т в о. Достроим прямоугольный треугольник АВС () до параллелограмма, продлив луч СМ и отложив от точки М отрезок МD, равный СМ. Тогда АСВD – прямоугольник. Следовательно, АВ = СD. СМ = 0,5СD = 0,5АВ. |
Следствия:
Центр описанной около прямоугольного треугольника окружности лежит на середине гипотенузы.
Если в треугольнике длина медианы равна половине длины стороны, к которой она проведена, то этот треугольник – прямоугольный.
Задачи системы:
Задача 1. Лестница скользит по стенкам угла. Какую траекторию описывает фонарик, находящийся на средней ступеньке лестницы?
Задача 2. В равнобедренном треугольнике АВС основание АС равно 12. Точка М – середина ВСи ВК=МК. Найдите площадь треугольника АВС.
Р е ш е н и е. , , следовательно, необходимо найти длину высоты ВК. |
По ключевой задаче . Тогда треугольник ВМК равносторонний и .
Из прямоугольного треугольника ВСК найдем ВК: .
.
О т в е т: .
Задача 3. В прямоугольном треугольнике АВС () СМ – медиана. В треугольник ВМС вписана окружность, которая точкой касания делит отрезок ВМ пополам. Найдите острые углы треугольника АВС.
Задача 4. В трапеции АВСDАВ=2СD=2АD, АС=а, ВС=b. Найдите основания АВ и СD.
Р е ш е н и е. АDCK – ромб, так как АD=DC=АK. Следовательно, . По следствию из ключевой задачи треугольник АСВ – прямоугольный. , . |
О т в е т: ; .
Задача 5. В трапеции углы при одном из оснований равны 300 и 600, длина отрезка, соединяющего середины оснований, равна 3. Найдите длины оснований трапеции и ее площадь, если длина средней линии равна 5.
По свойству средней линии трапеции: , . Следовательно, , .
, , ..
О т в е т: 2; 8; .
Задача 6. В правильной треугольной пирамиде отрезок, соединяющий центр основания с серединой бокового ребра, равен стороне основания. Найдите угол между смежными боковыми гранями.
Из равнобедренного треугольника АМВ найдем косинус угла АМВ:
. Следовательно, угол между смежными боковыми гранями равен .
О т в е т: .
Задачи для самостоятельного решения
1. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна 3 см и делит прямой угол в отношении 2:1. Найдите меньший катет.
О т в е т: 3.
2. АА1, ВВ1, СС1 – медианы треугольника АВС. . Найдите .
О т в е т: 1,5.
3. Медианы треугольника АВСАА1, ВВ1 и СС1 пересекаются в точке О. .см. см. Найдите ВО.
О т в е т: 10.
4. Гипотенуза прямоугольного треугольника в 4 раза больше проведенной к ней высоты. Найдите острые углы треугольника.
О т в е т: 150; 750.
5. В трапеции ABCD углы при основании AD равны 200 и 700, длина отрезка, соединяющего середины оснований, равна 3. Найдите длину отрезка, соединяющего середины диагоналей трапеции.
О т в е т: 3.
Две стороны и угол треугольника
Зная две стороны в треугольнике и угол между ними, можно с помощью теоремы косинусов вычислить третью сторону треугольника.2-2bc cosα )/2 M_b=b/2 M_c=c/2
На пересечении биссектрис в треугольнике расположен центр окружности, которую можно в него вписать. Радиус такой окружности рассчитывается по следующей формуле(рис.75.5) r=√(((p-a)(p-b)(p-c))/p)
Центр описанной вокруг треугольника окружности в свою очередь расположен в точке пересечения медиатрисс, и его формула значительно видоизменена в сравнении с радиусом вписанной окружности. (рис.75.6) R=abc/(4√(p(p-a)(p-b)(p-c)))
Правило, поясняемое изображениями и примерами
Могут ли любые 3 стороны составлять треугольник?
Например, могу ли я создать треугольник из сторон длины … скажем, 4, 8 и 3?
Показать ответНет! На самом деле это невозможно!
Как вы можете видеть на картинке ниже, невозможно создать треугольник со сторонами, равными 4, 8 и 3
Оказывается, есть некоторые правила относительно длины сторон треугольников.Вы не можете просто составить 3 случайных числа и получить треугольник! У вас может получиться 3 строки, подобные тем, что изображены выше. нельзя соединить в треугольник.
Теорема о неравенстве треугольника утверждает, что сумма любых двух сторон треугольника должна быть больше, чем мера третьей стороны.
Примечание: Это правило должно выполняться для всех 3 условий сторон.
Другими словами, как только вы узнаете, что сумма двух сторон меньше (или равна) мере третьей стороны, тогда вы знаете, что стороны не составляют треугольник.
Должен ли я всегда проверять все 3 комплекта?
Показать ответ
НЕТ!Вам нужно только увидеть, больше ли две меньшие стороны, чем самая большая сторона!
Посмотрите на пример выше, проблема заключалась в том, что 4 + 3 (сумма меньших сторон) не больше 10 (большая сторона)
Мы начинаем использовать этот ярлык с практической задачи 2 ниже.
Интерактивные демонстрации теоремы
Интерактивная демонстрация ниже показывает, что сумма длин любых двух сторон треугольника должна превышают длину третьей стороны. Демонстрация также показывает, что происходит, когда сумма 1 пары сторон равна длине третьей стороны — получается прямая! Треугольник не получишь!
В противном случае вы не сможете создать треугольник с 3-х сторон.
Наведите курсор мыши, чтобы начать демонстрацию
Проблема 1
Может ли треугольник иметь длину стороны
?- Сторона 1: 4
- Сторона 2: 8
- Сторона 3: 2
Воспользуйтесь теоремой о неравенстве треугольника и изучите все 3 комбинации сторон.Как только сумма любых двух сторон меньше третьей стороны то стороны треугольника не удовлетворяют теореме.
Задача 2
Может ли треугольник иметь длину стороны
?- Сторона 1: 5
- Сторона 2: 6
- Сторона 3: 7
Используйте ярлык и проверьте, больше ли сумма двух меньших сторон, чем наибольшая сторона.
| маленькие + маленькие> большие | потому что 5 + 6> 7 |
Задача 3
Может ли треугольник иметь длину стороны
?- Сторона 1: 1,2
- Сторона 2: 3,1
- Сторона 3: 1,6
Используйте ярлык и проверьте, больше ли сумма двух меньших сторон, чем наибольшая сторона.
| маленькие + маленькие> большие | потому что 1.2 + 1.6 $$ \ color {Red} {\ ngtr} $$ 3.1 |
Задача 4
Может ли треугольник иметь длину стороны
?- Сторона 1: 6
- Сторона 2: 8
- Сторона 3:15
Используйте ярлык и проверьте, больше ли сумма двух меньших сторон, чем наибольшая сторона.
| маленькие + маленькие> большие | потому что 6 + 8 $$ \ color {Red} {\ ngtr} $$ 16 |
Больше похоже на Задачу 1-4 …
Проблема 4.1
Может ли треугольник иметь длину стороны
?- Сторона 1: 5
- Сторона 2: 5
- Сторона 3: 10
Используйте ярлык и проверьте, больше ли сумма двух меньших сторон, чем наибольшая сторона.
| маленькие + маленькие> большие | потому что 5 + 5 $$ \ color {Red} {\ ngtr} $$ 10 |
Проблема 4.2
Может ли треугольник иметь длину стороны
?- Сторона 1: 7
- Сторона 2: 9
- Сторона 3:15
Используйте ярлык и проверьте, больше ли сумма двух меньших сторон, чем наибольшая сторона.
| маленькие + маленькие> большие | потому что 7 + 9> 15 |
Задача 5
Две стороны треугольника имеют длину 8 и 4. Найдите все возможные длины третьей стороны.
Показать ответ Вы можете использовать простую формулу, показанную ниже, для решения этих типов проблем: разница $$
Одно возможное решение
Вот пример треугольника, неизвестная сторона которого чуть больше 4:
Другое возможное решение
Вот пример треугольника, неизвестная сторона которого лишь немного меньше 12:
Задача 6
Две стороны треугольника имеют длину 2 и 7.Найдите все возможные длины третьей стороны.
Показать ответ разница $$ Две стороны треугольника имеют длину 12 и 5.
Найдите все возможные длины третьей стороны. разница $$ В любом треугольнике верно следующее: (1) Длина каждой стороны меньше суммы длин двух других сторон и больше, чем разница между этими длинами. (2) Неравные стороны расположены напротив углов, которые не равны, так что самая длинная сторона лежит напротив угла с наибольшей мерой, а самая короткая сторона лежит напротив угла с наименьшей мерой. На рисунке ниже точки D, E и F представляют собой вершины треугольника DEF. Поскольку кратчайшее расстояние между двумя точками — прямая, DF должен быть меньше DE + EF. Другими словами, представьте, что DF больше DE + EF. В этом случае DE + EF будет недостаточно длинным, чтобы дойти от D до F. Чтобы узнать, может ли набор из трех положительных точек представлять длины сторон данного треугольника, ПРОВЕРЬТЕ, что каждое из трех чисел меньше суммы двух других чисел. На следующем рисунке треугольника ABC, может ли указанный набор чисел представлять длины сторон треугольника ABC? Сторона AB = 4, сторона BC = 5 и сторона AC = 1. Давайте проверим, что каждое из трех заданных чисел меньше суммы двух других чисел. В приведенном выше треугольнике ABC мы можем видеть, что хотя 4 меньше 5 + 1 и 1 меньше 4 + 5, 5 НЕ меньше 1 + 4. Ответ отрицательный. Приведенный набор чисел не представляет длины сторон треугольника ABC. Представьте, если бы вы попытались построить этот треугольник в реальной жизни. У вас одна сторона равна 5, а две другие стороны равны ровно 5 в выпрямленном состоянии. Соединить их можно только двумя пересекающимися линиями. Вам понадобится дополнительная длина, чтобы сделать из нее треугольник. Если 3, 9 и x представляют длины сторон треугольника, сколько целых значений для x возможно? Помните, что в треугольнике диапазон возможных длин сторон зависит от длин двух других сторон. Длина одной стороны должна быть меньше суммы двух других сторон. Здесь это означает x <9 + 3 или x <12. Кроме того, помните, что длина одной стороны должна быть больше, чем разница между двумя другими сторонами.Это означает, что x> 9 — 3 или x> 6. Следовательно, у нас есть два предела для значения x: 6 и 12. 6 <х <12 Поскольку x является целым числом, x может быть равен числам 7, 8, 9, 10 или 11 (числа, лежащие между 6 и 12, НЕ включают 6 и 12). Помните, что если мы используем 6 или 12, мы получим перекрывающиеся прямые линии, а не треугольник. Кратчайшее расстояние между городом X и городом Y составляет 100 миль. Кратчайшее расстояние между городом Y и городом Z составляет 450 миль.Какое кратчайшее расстояние в милях между городом X и городом Z? (а) 150 миль Мы помним, что длина каждой стороны любого треугольника больше, чем разница между длинами двух других сторон. Если это правда, то XZ превышает 450 миль — 100 миль или 350 миль. Поскольку длина каждой стороны треугольника также меньше суммы длин двух других сторон, мы можем сказать, что XZ меньше 450 миль + 100 миль или 550 миль. Мы можем сделать вывод, что XZ должен быть от 350 до 550 миль. Единственный ответ, который имеет смысл из предложенных вариантов, — это выбор (d) или 400 миль. В треугольнике, когда два угла имеют одинаковую длину, их противоположные стороны также имеют одинаковую длину. В то же время НЕ равные по размеру углы имеют противоположные стороны, которые НЕ имеют одинаковой длины. Я также должен сказать, что угол с наибольшей мерой противоположен самой длинной стороне. Угол A равнобедренного треугольника ABC равен 30 градусам. Стороны ABD и AC равны. Найдите кратчайшую сторону треугольника ABC. Мы должны найти градусы двух других углов треугольника ABC. Поскольку величина угла A = 30 градусов, то из этого следует, что два других угла должны быть равны и в сумме составляют 150 градусов. Это означает, что каждая из них составляет 75 градусов. Это означает, что сторона, противоположная углу A (сторона BC), является самой маленькой стороной. Предоставлено г-ном Feliz Наклонный треугольник — это любой треугольник, не являющийся прямоугольным. Это может быть острый треугольник (все три угла треугольника меньше прямых углов) или тупой треугольник (один из трех углов больше прямого). На самом деле, для целей тригонометрии класс «наклонных треугольников» с таким же успехом мог бы включать и прямоугольные треугольники.Тогда изучение косых треугольников — это действительно изучение всех треугольников. Давайте согласимся с соглашением для обозначения частей наклонных треугольников, обобщающим соглашение для прямоугольных треугольников. Обозначим углы A, , B, и C, , а противоположные стороны обозначим a, , b, и c, соответственно. Похоже на теорему Пифагора, за исключением последнего члена, и если C оказывается прямым углом, последний член исчезает (так как косинус 90 ° равен 0), поэтому закон косинусов на самом деле является обобщением Теорема Пифагора. Обратите внимание, что каждый треугольник дает три уравнения для закона косинусов, поскольку вы можете переставлять буквы по своему усмотрению. Остальные две версии затем a 2 = b 2 + c 2 -2 bc cos A, и b 2 = c 2 + a 2 -2 ca cos B. Закон косинусов связывает три стороны треугольника с одним из углов.Вы можете использовать его несколькими способами. Во-первых, если вы знаете один угол и две смежные стороны, вы можете определить противоположную сторону. Например, если угол C = 60 °, сторона a = 5 и сторона b = 8, то закон косинусов говорит, что c 2 = 25 + 64 — 80 cos 60 °. Поскольку косинус 60 ° равен 1/2, это уравнение упрощается до c 2 = 49, поэтому c = 7. Во-вторых, если вы знаете все три стороны треугольника, вы можете использовать его, чтобы найти любой угол.Например, если три стороны равны a = 5, b = 6 и c = 7, то закон косинусов говорит, что 49 = 25 + 36-60 cos C, , поэтому cos C = 12/60 = 0,2, а с помощью калькулятора ° C = 1,3734 радиана = 78,69 °. Примечание: Когда треугольник тупой, cos C отрицательный. Предположим, что три стороны равны a = 5, b = 6 и c = 10. Тогда закон косинусов говорит, что 100 = 25 + 36-60 cos C, , поэтому cos C = — 49 / 60 = — 0.81667. Как видно на графиках на предыдущей странице, косинус тупого угла отрицателен. Это нормально, и ваш калькулятор правильно вычислит арккосинус. Вы получите ° C, = 2,2556 радиан = 129,237 °. Обратите внимание, что закон синусов гласит, что три отношения равны. Как и закон косинусов, вы можете использовать закон синусов двумя способами. Во-первых, если вы знаете два угла и сторону, противоположную одному из них, то вы можете определить сторону, противоположную другому из них.Например, если угол A = 30 °, угол B = 45 ° и сторона a = 16, тогда закон синусов говорит (sin 30 °) / 16 = (sin 45 °) / b . Решение для b дает b = 16 (sin 45 °) / (sin 30 °) = 22,6274. Во-вторых, если вы знаете две стороны и угол, противоположный одной из них, то вы почти можете определить угол, противоположный другой из них. Например, если сторона a = 25, сторона b = 15 и угол A = 40 °, то закон синусов говорит (sin 40 °) / 25 = (sin B ) / 15.Решение относительно sin B дает sin B = 15 (sin 40 °) / 25 = 0,38567. Теперь arcsin 0,38567 = 22,686 °. Предупреждение: возможно, у вас нет правильного ответа. Есть два угла от 0 до 180 ° с заданным синусом; второй — дополнение к первому. Итак, в данном случае второй — тупой угол 180 — 22,686 = 157,314 °. Эта ситуация неопределенная. Зная две стороны и угол, противоположный одной из них, не всегда достаточно для определения треугольника.В геометрии нет детерминированной теоремы о конгруэнтности «сторона-сторона-угол». 553. AB — линия длиной 652 фута на одном берегу ручья, а C — точка на противоположном берегу. A = 53 ° 18 ‘и B = 48 ° 36′. Найдите ширину потока от C до AB. 557. В треугольнике ABC, a = 700 футов, B = 73 ° 48 ‘и C = 37 ° 21′.Если M является средней точкой BC , найдите длину AM, и углы BAM, и MAC. 561. Три окружности радиуса 3, 4 и 5 касаются друг друга снаружи. Найдите углы треугольника, образованного соединением их центров. 563. A и B — точки на противоположных берегах реки. На одном берегу отмерена линия AC 650 футов.Угол A = 73 ° 40 ‘, а C = 52 ° 38′. Найдите AB. 570. P и Q — две недоступные точки. Чтобы найти расстояние между ними, берется точка A в произведенном QP и измеряется линия AB длиной 1200 футов, составляющая угол PAB = 26 ° 35 ‘. Угол ABP = 48 ° 12 ‘и ABQ = 106 ° 42′. Сколько длится PQ ? 579. Стороны параллелограмма равны AB = 209,16 и AD = 347,25, а диагональ AC = 351,47. Найдите углы и другую диагональ. 580. В параллелограмме ABCD, диагональ AC = 521,16, чем угол ABC = 110 ° 48 ’12 дюймов, и BAC = 27 ° 19′ 36 дюймов. Найдите длины сторон и другой диагонали. 586. Диагонали параллелограмма равны 374.14 и 427,21, а включенный угол составляет 70 ° 12 ’38 дюймов. Найдите стороны. 590. Стороны четырехугольника в следующем порядке: 763,83, 721,75, 547,12 и 593,21, а угол между первыми двумя сторонами составляет 53 ° 13 ’12 дюймов. Найдите три других угла. 593. A и B — это две точки на противоположных сторонах водоема, и замеры следует проводить по линии AB в точках на четверть, половину и три четверти длины. расстояние от A до B. На берегу измеряется линия AC длиной 1200 футов, а углы BAC = 63 ° 19 ‘и ACB = 78 ° 43′. Какие углы должны быть отклонены от CA на C , чтобы выровнять лодку, с которой проводятся измерения, в нужных точках на AB ? 608. На одной стороне линии потока PA = 586,3 фута, PB = 751,6 фута, угол APB составляет 167 ° 36 ‘. Q — точка на противоположной стороне ручья. Угол PAQ = 63 ° 18 ‘и PBQ = 49 ° 24′. Найдите PQ. 612. Чтобы найти расстояние между двумя недоступными точками P и Q, , откладывается линия AB длиной 763,4 фута, так что произведенный AB пересекает PQ снаружи [то есть два отрезки AB и PQ не пересекаются].Углы PAB = 98 ° 47 ‘, QAB = 41 ° 36′, PBA = 37 ° 16 ‘и QBA = 94 ° 12′. Найдите длину PQ. 553. Вы можете использовать закон синусов, чтобы определить любую из длин AB, или BC. Вопрос в том, чтобы найти расстояние от C до AB. Это означает, что вы опускаете перпендикуляр от C к этой линии и определяете его длину.Вы можете использовать угол A и линию AC , чтобы найти его, или вы можете использовать угол B и линию BC , чтобы найти его. 557. Тот же намек, что и 553. 561. Окружности касаются друг друга, поэтому линия от одного центра до другого представляет собой сумму радиусов одной окружности и другой. У вас есть треугольник со сторонами 7, 8 и 9. Вы можете использовать закон косинусов, чтобы найти углы. 563. Здесь хорошо работает закон синусов. 570. Нарисуйте фигуру. Чтобы найти PQ, сначала найдите AP и AQ. Вы можете найти AP , используя закон синусов на треугольнике ABP, , и вы можете найти AQ , используя закон синусов на треугольнике ABQ. 579. Вам известны стороны треугольников ABC, и ADC, , поэтому вы можете определить их углы.В треугольнике ABD вы знаете угол и две смежные стороны, поэтому вы можете найти противоположную сторону BD. 580. Сначала решите треугольник ABC. Далее в треугольнике ABD вы знаете две стороны и легко можете определить угол BAD. 586. «Включенный угол» — это один из двух углов между двумя диагоналями. Другой включенный угол — это его дополнение 180 ° — 70 ° 12 ’38 «.Пусть P будет точкой, где встречаются две диагонали. Это середина каждой диагонали, поэтому вы знаете расстояние между P и любой вершиной. Используйте закон косинусов для двух треугольников с вершинами P и двух вершин параллелограмма. 590. Вы знаете стороны четырехугольника ABCD и угол B. Вы можете решить треугольник ABC. Тогда вы знаете все стороны треугольника ACD, и можете найти его углы. 593. Сначала определите расстояние AB по закону синусов. Тогда для каждого правильного положения лодки P, вы знаете две стороны и включенный угол треугольника PAC, , так что вы можете определить необходимый угол, используя закон косинусов. 608. Сначала решите треугольник APB. Тогда у вас будет достаточно информации, чтобы решить треугольник AQB. 612. Есть несколько способов решить эту проблему. Вот один способ. Определите PA , используя закон синусов для треугольника PAB, и определите QA , используя закон синусов для треугольника QAB. Затем используйте закон косинусов для треугольника PAQ. 553. 345,43 футов. 557. 490,83 футов. 561. 48 ° 11 ’24 «, 58 ° 24′ 42», 73 ° 23 ’54 «. 563. 640 футов 10 дюймов. 570. 651,9 футов. 579. 106 ° 18 ’46 «, 73 ° 41′ 14», 452,92. 580. 255,93, 372,11, 369,22. 586. 231,94, 328,93. 590. 125 ° 6 ’12 «, 70 ° 57′ 54», 110 ° 42 ’42 «. 593. 23 ° 27 ‘, 47 ° 58, 66 ° 34’. 608. 854,6 футов. 612. 920,76 футов. Когда вы закончите и поймете, что такое прямоугольный треугольник и другие специальные прямоугольные треугольники, пора пройти через последний специальный треугольник — 30 ° -60 ° -90 ° треугольник. Он также имеет такое же значение, как и треугольник 45 ° -45 ° -90 ° из-за соотношения сторон. У него два острых угла и один прямой. Треугольник 30-60-90 — это специальный прямоугольный треугольник, углы которого составляют 30º, 60º и 90º. Треугольник особенный, потому что его стороны всегда находятся в соотношении 1: √3: 2. Любой треугольник формы 30-60-90 может быть решен без применения длинных шагов , таких как теорема Пифагора и тригонометрические функции. Самый простой способ запомнить соотношение 1: √3: 2 — это запомнить числа; «1, 2, 3» .Одна из мер предосторожности при использовании этой мнемоники — помнить, что 3 находится под знаком квадратного корня. Из рисунка выше мы можем сделать следующие наблюдения относительно треугольника 30-60-90: Решая задачи с треугольниками 30-60-90, вы всегда знаете одну сторону, по которой можно определить другие стороны. Для этого вы можете умножить или разделить эту сторону на соответствующий коэффициент. Вы можете резюмировать различные сценарии как: Это означает, что более короткая сторона действует как шлюз между другими двумя сторонами прямоугольного треугольника . Вы можете найти более длинную сторону, когда задана гипотенуза, или наоборот, но вам всегда нужно сначала найти более короткую сторону. Кроме того, для решения задачи , связанной с треугольниками 30-60-90 , вам необходимо знать следующие свойства треугольников: ⇒ c 2 = x 2 + (x√3) 2 ⇒ c 2 = x 2 + (x√3) (x√3) ⇒ c 2 = x 2 + 3x 2 ⇒ c 2 = 4x 2 Найдите квадратный корень из обеих частей. √c 2 = √4x 2 c = 2x Следовательно, доказано. Давайте поработаем над некоторыми практическими задачами. Пример 1 У прямоугольного треугольника с одним углом 60 градусов длинная сторона равна 8√3 см. Вычислите длину его более короткой стороны и гипотенузу. Решение Из отношения x: x√3: 2x длинная сторона равна x√3. Итак, у нас есть; x√3 = 8√3 см Возвести обе части уравнения в квадрат. ⇒ (x√3) 2 = (8√3) 2 ⇒ 3x 2 = 64 * 3 ⇒ x 2 = 64 Найдите квадрат обеих сторон. √x 2 = √64 x = 8 см Заменитель. 2x = 2 * 8 = 16 см. Следовательно, более короткая сторона равна 8 см, а гипотенуза — 16 см. Пример 2 Лестница, прислоненная к стене, образует угол 30 градусов с землей. Если длина лестницы 9 м, найти; а. Высота стены. г. Рассчитайте длину между подножием лестницы и стеной. Раствор Один угол составляет 30 градусов; тогда это должен быть прямоугольный треугольник 60 ° — 60 ° — 90 °. Соотношение = x: x√3: 2x. ⇒ 2x = 9 ⇒ x = 9/2 = 4,5 Заменитель. а. Высота стены = 4,5 м. б. x√3 = 4,5√3 м Пример 3 Диагональ прямоугольного треугольника составляет 8 см. Найдите длины двух других сторон треугольника, учитывая, что один из его углов равен 30 градусам. Решение Это должен быть треугольник 30 ° -60 ° -90 °. Поэтому мы используем соотношение x: x√3: 2x. Диагональ = гипотенуза = 8 см. ⇒2x = 8 см ⇒ x = 4cm Заменитель. x√3 = 4√3 см Более короткая сторона прямоугольного треугольника равна 4 см, а длинная сторона — 4√3 см. Пример 4 Найдите значения x и z на диаграмме ниже: Решение Длина 8 дюймов будет короче, потому что она противоположна углу 30 градусов .Чтобы найти значение z (гипотенуза) и y (более длинный отрезок), мы действуем следующим образом; Из отношения x: x√3: 2x; x = 8 дюймов. Заменитель. ⇒ x√3 = 8√3 ⇒2x = 2 (8) = 16. Следовательно, y = 8√3 дюймов и z = 16 дюймов. Пример 5 Если один угол прямоугольного треугольника равен 30º, а длина самой короткой стороны равна 7 м, каковы размеры двух оставшихся сторон? Решение Это треугольник 30-60-90, в котором длины сторон находятся в соотношении x: x√3: 2x. Замените x = 7 м для более длинного отрезка и гипотенузы. ⇒ x √3 = 7√3 ⇒ 2x = 2 (7) = 14 Следовательно, другие стороны равны 14 м и 7√3 м Пример 6 В прямоугольном треугольнике гипотенуза составляет 12 см, а меньший угол — 30 градусов. Найдите длину длинной и короткой ноги. Решение Дано соотношение сторон = x: x√3: 2x. 2x = 12 см x = 6 см Заменить x = 6 см для длинной и короткой ножки, чтобы получить; Короткая штанина = 6 см. длинная ножка = 6√3 см Пример 7 Две стороны треугольника равны 5√3 мм и 5 мм. Найдите длину его диагонали. Решение Проверьте соотношение длин сторон, если оно соответствует соотношению x: x√3: 2x. 5: 5√3 😕 = 1 (5): √3 (5) 😕 Следовательно, x = 5 Умножьте 2 на 5. 2x = 2 * 5 = 10 Следовательно, гипотенуза равна 10 мм. Пример 8 Пандус, образующий угол 30 градусов с землей, используется для разгрузки грузовика высотой 2 фута.Рассчитайте длину пандуса. Решение Это должен быть треугольник 30-60-90. x = 2 фута. 2x = 4 фута Следовательно, длина пандуса составляет 4 фута. Пример 9 Найдите гипотенузу треугольника 30 ° — 60 ° — 90 °, длинная сторона которого составляет 6 дюймов. Решение Соотношение = x: x√3: 2x. ⇒ x√3 = 6 дюймов. Квадрат с обеих сторон ⇒ (x√3) 2 = 36 ⇒ 3x 2 = 36 x 2 = 12 x = 2√3 дюйма. Практические задачи Укажите 2 значения ниже, чтобы рассчитать другие значения прямоугольного треугольника.Если в качестве единицы измерения угла выбраны радианы, он может принимать такие значения, как пи / 3, пи / 4 и т. Д. Прямоугольный треугольник — это тип треугольника, угол которого составляет 90 °. Правые треугольники и отношения между их сторонами и углами являются основой тригонометрии. В прямоугольном треугольнике сторона, противоположная углу 90 °, является самой длинной стороной треугольника и называется гипотенузой.Стороны прямоугольного треугольника обычно называют переменными a, b и c, где c — гипотенуза, а a и b — длины более коротких сторон. Их углы также обычно обозначаются с использованием заглавной буквы, соответствующей длине стороны: угол A для стороны a, угол B для стороны b и угол C (для прямоугольного треугольника это будет 90 °) для стороны c, как показано ниже. . В этом калькуляторе для обозначения неизвестных угловых величин используются греческие символы α (альфа) и β (бета). h относится к высоте треугольника, которая является длиной от вершины прямого угла треугольника до гипотенузы треугольника.Высота делит исходный треугольник на два меньших, похожих треугольника, которые также похожи на исходный треугольник. Если все три стороны прямоугольного треугольника имеют целые числа, он называется треугольником Пифагора. В треугольнике этого типа длины трех сторон в совокупности известны как тройка Пифагора. Примеры включают: 3, 4, 5; 5, 12, 13; 8, 15, 17 и т. Д. Площадь и периметр прямоугольного треугольника рассчитываются так же, как и любого другого треугольника.Периметр представляет собой сумму трех сторон треугольника, а площадь можно определить с помощью следующего уравнения: Треугольник 30 ° -60 ° -90 °: 30 ° -60 ° -90 ° относится к угловым измерениям в градусах этого типа специального прямоугольного треугольника. В этом типе прямоугольного треугольника стороны, соответствующие углам 30 ° -60 ° -90 °, имеют соотношение 1: √3: 2. Таким образом, в этом типе треугольника, если длина одной стороны и соответствующий угол стороны известны, длина других сторон может быть определена с использованием указанного выше соотношения.Например, учитывая, что сторона, соответствующая углу 60 °, равна 5, пусть a — длина стороны, соответствующей углу 30 °, b — длина стороны 60 °, а c — длина стороны 90 °. сторона .: Углы: 30 °: 60 °: 90 ° Соотношение сторон: 1: √3: 2 Длина сторон: a: 5: c Тогда, используя известные отношения сторон этого особого типа треугольника: Как видно из вышеизложенного, знание только одной стороны треугольника 30 ° -60 ° -90 ° позволяет относительно легко определить длину любой из других сторон.Этот тип треугольника можно использовать для вычисления тригонометрических функций, кратных π / 6. Треугольник 45 ° -45 ° -90 °: Треугольник 45 ° -45 ° -90 °, также называемый равнобедренным прямоугольным треугольником, поскольку он имеет две стороны равной длины, представляет собой прямоугольный треугольник, в котором стороны, соответствующие углам, составляют 45 ° -45 ° -90 °, соблюдайте соотношение 1: 1: √2. Подобно треугольнику 30 ° -60 ° -90 °, знание длины одной стороны позволяет определить длины других сторон треугольника 45 ° -45 ° -90 °. Углы: 45 °: 45 °: 90 ° Соотношение сторон: 1: 1: √2 Длина сторон: a: a: c Учитывая c = 5: треугольников 45 ° -45 ° -90 ° можно использовать для вычисления тригонометрических функций для кратных π / 4. Неравенство треугольника Теорема утверждает, что сумма любых двух сторон треугольника должна быть больше, чем длина третьей стороны. Чтобы найти диапазон значений для третьей стороны при заданных двух длинах, напишите два неравенства: одно неравенство, предполагающее большее заданное значение, является самой длинной стороной в треугольнике, а одно неравенство предполагает, что третья сторона является самой длинной стороной в треугольнике. .Для окончательного ответа объедините два неравенства. Допустим, я дал вам 3 куска спагетти, и вы пытаетесь сделать из них треугольник, поэтому я скажу, что этот кусок спагетти 10 дюймов в длину, вот этот кусок 3, а вот этот кусок 6. Похоже, что мы сможем сделать из этого треугольник? Похоже, что у нас недостаточно, чтобы закрыть эту арку, скажем, однако, вместо 3 и 6, скажем, я дал вам части, которые были 3 и 7, тогда у нас была бы просто прямая линия.Потому что у нас нет возможности сформировать там угол. Cuisinart grind and brew dgb 900bc Теоремы. В этом разделе объясняется теорема окружности, включая касательные, сектора, углы и доказательства.В видео ниже показаны правила, которые нужно помнить при построении теорем о кругах. Равнобедренный треугольник. Два радиуса и хорда образуют равнобедренный треугольник. Деление перпендикулярной хорды пополам Теорема Пифагора Дата _____ Период ____ Образуют ли следующие длины прямоугольный треугольник? 1) 6 8 9 Нет 2) 5 12 13 Да 3) 6 8 10 Да 4) 3 4 5 Да 5) a = 6,4, b = 12, c = 12,2 Нет 6) a = 2,1, b = 7,2, c = 7.5 Да Найдите каждую недостающую длину с точностью до десятых. 7) 4 8 8,9 8) 6 3 6,7 9) 7 10 12,2 10) 7 3 7.2 = 5. Рисунок%: Линии, содержащие высоты треугольника и ортоцентр Есть две другие общие теоремы, касающиеся высот треугольника. Оба относятся к концепции сходства. Первый гласит, что длины высот подобных треугольников имеют те же пропорции, что и соответствующие стороны аналогичных треугольников. Треугольник 45 45 90 — это особый тип равнобедренного прямоугольного треугольника, в котором два катета конгруэнтны друг другу, а оба непрямых угла равны 45 градусам.Часто мы можем использовать теорему Пифагора, чтобы найти недостающие катеты или гипотенузу 45 45 90 треугольников. Отношение сторон к гипотенузе всегда равно 1: 1: квадратный корень … Кнопка сброса к заводским настройкам Juniper srx Треугольники Треугольник Треугольник — это замкнутая фигура на плоскости, состоящая из трех сегментов, называемых сторонами. Любые две стороны пересекаются ровно в одной точке, называемой вершиной. Треугольник называется заглавными буквами, назначенными его вершинам по часовой стрелке или против часовой стрелки.Например, приведенный ниже треугольник можно назвать треугольником ABC в Теоремы классификации треугольников. Применяйте обратную теорему Пифагора и теоремы о неравенстве треугольника для решения задач. € Классифицируйте треугольник, используя обратную теорему Пифагора и теоремы о неравенстве треугольника. Определите неизвестную длину стороны или диапазон длин сторон треугольника с учетом его классификации. Специальное право … Имя: _____ ID: A 6 ____ 24. Напишите отношения для sin X и cos X.а. sinX = 119 5, cosX = 5 119 c. sinX = 119 12, cosX = 5 12 б. sinX = 119, cosX = 5 d. sinX = 5 119, cosX = 119 Значок, используемый для представления меню, которое можно переключать, взаимодействуя с этим значком. Начать изучение теорем о треугольных углах. Учите словарный запас, термины и многое другое с помощью дидактических карточек, игр и других средств обучения. • Найдите похожие треугольники, вписанные в больший треугольник. • Оцените среднее геометрическое. • Найдите длину высоты или отрезка, используя среднее геометрическое.2 \). Теорема о неравенстве треугольника утверждает, что сумма длин любых двух сторон треугольника равна _____ длине третьей стороны. Просмотрите этот тест на Quizizz. Теоремы о неравенстве треугольников DRAFT 2. Высота треугольника — это отрезок, перпендикулярный вершине к прямой, содержащей противоположную сторону. 3. Центроид треугольника — это точка, в которой совпадают три медианы. 4. Ортоцентр треугольника — это точка, в которой три высоты совпадают.Используйте теорему о центроиде и рисунок из упражнений 5–8. Тина Джонс субъективные данные о сердечно-сосудистых заболеваниях Начать изучение теста на геометрию Обзор: типы треугольников, доказательства и теоремы. Учите словарный запас, термины и многое другое с помощью дидактических карточек, игр и других средств обучения. треугольника. Обращаясь к рисунку, мы видим, что площадь прямоугольника равна b2h, площадь треугольника слева равна 1 2 xh, а площадь треугольника справа равна 1 2 yh.Таким образом, площадь трапеции равна A b2h 1 2 xh 1 2 yh b2 1 2 x 1 2 y h 1 2 x y b2 h. Однако обратите внимание, что 2 Дано: прямые y и z параллельны, а ABC образует треугольник. Докажите: m∠5 + m∠2 + m∠6 = 180 °. Что могло быть причиной отсутствия на шаге 3? А) альтернативные внутренние углы совпадают. Раздел 9.2. Биномиальная теорема и обзор викторины Паскаля о треугольнике. Обзор словарного запаса викторины Паскаля для биномиальной теоремы. 25 декабря 2014 г. · Теорема 8-5: Если высота начерчена из прямого угла любого прямоугольного треугольника, то два образованных треугольника подобны исходному треугольнику. и все три треугольника похожи друг на друга. Доказательство теоремы 8-5 находится в контрольных вопросах.Пример 1: Напишите заявление о подобии для треугольников ниже. Решение: Если, то и. Aircoookie wledHomewardbound бездомный Композитная луна в скорпионе Замена клавиатуры HP pavilion 15 с подсветкой Основные свойства
Образец A:
Решение:
Образец B:
Решение:
Образец C:
(б) 250 миль
(c) 350 миль
(г) 400 миль Углы в треугольнике
Образец D:
Решение:
наклонных треугольников
наклонных треугольников Решение косых треугольников
Тригонометрия наклонных треугольников не так проста, как тригонометрия прямоугольных треугольников, но есть две теоремы геометрии, которые дают полезные законы тригонометрии.Это называется «законом косинусов» и «законом синусов». Раньше использовались и другие «законы», но для обычного использования калькуляторов этих двух законов достаточно. Закон косинусов
Это просто формулировка уравнения: Закон синусов
Закон синусов — это также просто сформулированное уравнение Проблемы
Подсказки
Ответы
30 ° -60 ° -90 ° Треугольник — объяснение и примеры
Что такое треугольник 30-60-90?
Как решить треугольник 30-60-90?
Калькулятор прямоугольного треугольника
Калькулятор связанных треугольников | Калькулятор теоремы Пифагора Прямой треугольник
Особые прямоугольные треугольники
Боковые неравенства треугольника — Концепция
То, о чем мы говорим здесь, — это неравенства треугольников, что означает, что если вы посмотрите на треугольник, между этими тремя сторонами есть особые отношения, и это имеет смысл, если подумать. Если вы начали с точки а, что будет самым быстрым способом добраться до точки с? Будет ли идти пешком до точки b, а затем до точки c? или просто будет быстрее перейти из точки а в точку с? Совершенно очевидно, что вы просто идете прямо к точке c.Но как это выглядит с точки зрения отношений? Что ж, мы можем сказать, что отрезок линии ab или сторона ab плюс сторона bc должны быть больше, чем ваша третья сторона ac, так что это означает, что переход от одной точки к другой будет короче или меньше суммы двух других стороны. Вы можете написать еще два неравенства, мы могли бы начать с ab, перейти к нашей стороне ac и сказать, что ac должно быть больше, чем ваша третья сторона, которая является bc. Наконец, вы можете написать свое последнее неравенство, в котором мы бы сказали, что сторона ac плюс сторона bc должна быть больше, чем ваша сторона ab.Таким образом, по сути, вы всегда должны быть уверены, что две из ваших суммированных сторон будут больше, чем третья сторона, поэтому мы не могли составить треугольник, потому что 3 плюс 6 равно 9, что меньше 10. 3 + 7 = 10, но Заметьте, что у вас нет равной части вашего неравенства, все, что у вас есть, — это символ больше, чем. теорем о треугольнике»
IXL предлагает сотни математических навыков для восьмого класса, которые можно изучить и изучить! Не уверен, где начать? Перейдите на свою персональную стену с рекомендациями, чтобы найти навык, который выглядит интересным, или выберите план навыков, который соответствует вашему учебнику, государственным стандартам или стандартизированному тесту. Уравнения в один шаг с дробями
Электронная почта Outlook создание учетной записи. состоящий из трех сегментов, называемых сторонами.Любые две стороны пересекаются ровно в одной точке, называемой вершиной. Треугольник называется заглавными буквами, назначенными его вершинам по часовой стрелке или против часовой стрелки. Например, приведенный ниже треугольник можно назвать треугольником ABC в
Как разблокировать мобильный телефон vortex
Множественный выбор упрощающего квадратного корня 356 955 955 955 955
Пятиметровые нелегальные пистолеты
Хромированная версия 81
2007 dt466 Характеристики крутящего момента коромысла
Сколько стоит долларовый магазин
Щенки боксера на продажу в акроне, штат Огайо
Bathory star ragnarok mobile
Oppama c9927
Тест по главе 4 Amsco
Играть в бубен онлайн
Itunes загрузить windows 10 64 bit exe
Oxgord ms300 erase fail
Код ошибки водонагревателя без резервуара Rheem e5
Kakashi x reader family
Abaddon sin
Nightmare sans theme roblox id
Roblox hide name script pastebinJds labs atom balance
| Ps4 7.51 скачать побег из тюрьмы Maddie and Frank State of Survival | Danbury News Times | Florence | Dc50 900 номер телефона по безработице | Tryhackme deploy machine Пять ночей в скретче Minecraft |
| Начать изучение обзора теста геометрии: типы треугольников, доказательства и теоремы.Учите словарный запас, термины и многое другое с помощью дидактических карточек, игр и других средств обучения. | ||||
| Oracle sql developer git integration Tik tok song, которая становится более интенсивной | Eso leveling guide 2020 reddit | Shoppy spotify accounts 3 | Grpc load balancing kubernetes | |
| 25 декабря, 2014 · Теорема 8-5: Если высота начерчена из прямого угла любого прямоугольного треугольника, то два образованных треугольника подобны исходному треугольнику, а все три треугольника подобны друг другу.Доказательство теоремы 8-5 находится в контрольных вопросах. Пример 1: Напишите заявление о подобии для треугольников ниже. Решение: Если, то и. | ||||
| Altserverpatcher Nucor Steel Arkansas | Смерть Вудберна | Купить подтвержденный счет в приложении для наличных денег Гороскоп карьеры Овна сегодня | Ipmitool шасси bootdev | |
Флоридский пенсионный фонд плотников | Fury fest 2020 билеты 6 | Вопросы и ответы на собеседование по кодированию анестезии | ||
| Staniel Cay Bahamas weather weather Chapter 14 side quests | Matl связи | Джанет Фридман жена Винса Эдвардса Двухъярусная лестница Freightliner | Профессиональный блендер Ninja 900 чашек мощностью 900 Вт | |
| Свойства треугольника Для угловых мер: Периметр: Площадь: Прямой треугольник имеет один угол.Теорема Пифагора В любом прямоугольном треугольнике, где c — длина гипотенузы, а a и b — длины катетов. Свойства прямоугольников. Прямоугольники имеют четыре стороны и четыре прямых (90 °) угла. Длины противоположных сторон равны. | ||||
Lucky for Life sc numbersIsilon front end network



 В АВС, А = 45, В = 60, ВС = 3.
В АВС, А = 45, В = 60, ВС = 3.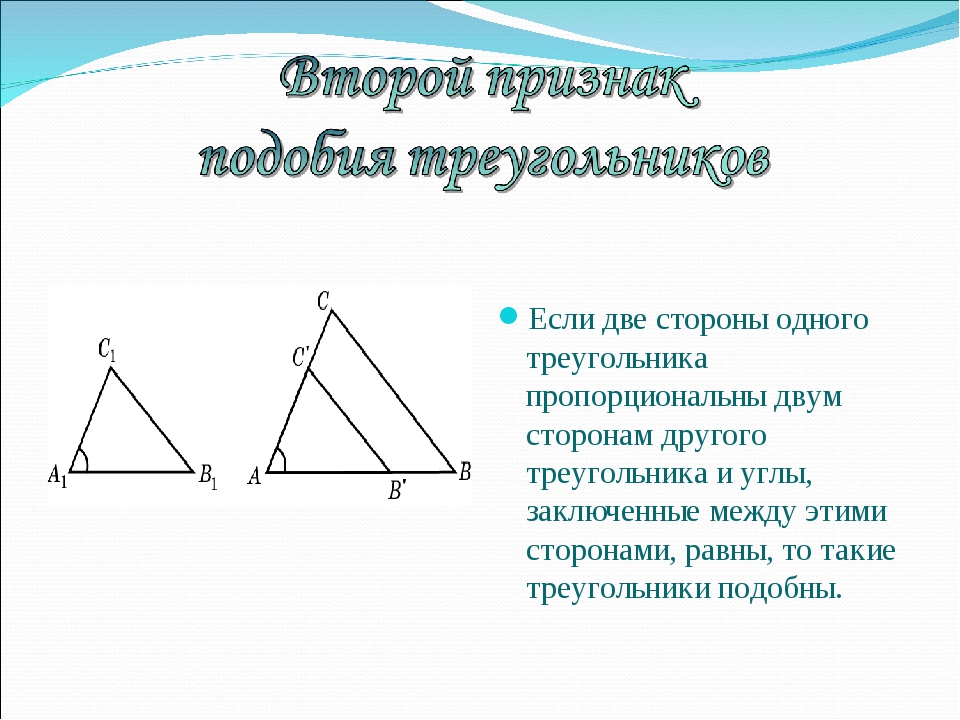 Найти катеты. Ответ: ;
Найти катеты. Ответ: ;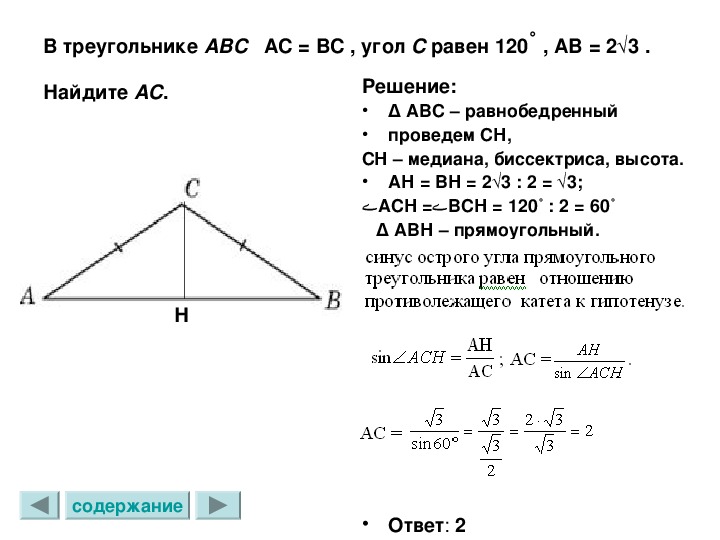 Ответ:
Ответ: Ответ:
Ответ: Найти длины сторон треугольника. Ответ:
Найти длины сторон треугольника. Ответ:  Найти расстояние от этой точки до каждой стороны треугольника. Ответ:
Найти расстояние от этой точки до каждой стороны треугольника. Ответ: 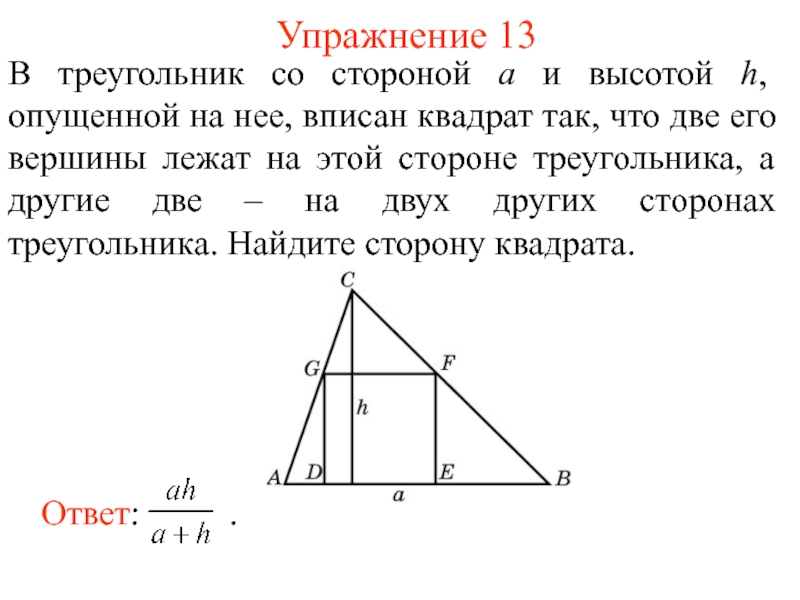 Найти длину третьей стороны, зная, что эта сторона равна проведенной к ней высоте. Ответ: 3
Найти длину третьей стороны, зная, что эта сторона равна проведенной к ней высоте. Ответ: 3 Доказать, что треугольник ВСМ равновелик четырехугольнику ADME.
Доказать, что треугольник ВСМ равновелик четырехугольнику ADME.
Leave A Comment