3.3. Преобразование алгебраических выражений
Определение 3.8. Алгебраическим выражением называется выражение, составленное из чисел и переменных, знаков действия над ними (сложения, вычитания, умножения, деления, возведения в степень с рациональным показателем, извлечения арифметического корня) и скобок.
Два выражения называют тождественно равными, если при всех допустимых для них значениях переменных соответственные значения этих выражений равны. Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием выражения.
Различают целые рациональные, дробные рациональные и иррациональные выражения. К целым рациональным выражениям относят одночлены и многочлены. Способы их преобразования были рассмотрены в пункте 3.2.
При тождественных преобразованиях дробных рациональных выражений (то есть содержащих деление на выражение с переменной) используются следующие основные приемы.
1. Сокращение
дробей, основанное на свойстве дроби:  .
Например,
.
Например,
,
( ).
).
2. Приведение к общему знаменателю – для этого необходимо:
1) разложить знаменатель каждой дроби на множители;
2) составить наименьший общий знаменатель;
3) домножив числитель и знаменатель каждой дроби на дополнительные множители, привести их к общему знаменателю.
Напомним, что действия над алгебраическими дробями осуществляются следующим образом
 ,
,  ,
, .
.
Пример 3.12. Упростить выражение
.
Решение.
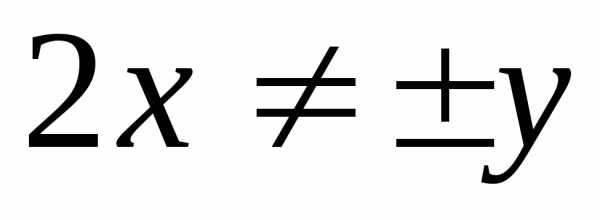 ).
). Ответ:  , (
, ( ).
).
Пример 3.13. Упростить выражение
.
Решение.
,
(, ).
).
Ответ:  ,
,
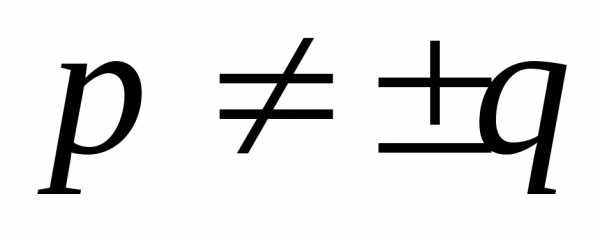 ).
).Рассмотрим далее преобразование иррациональных выражений. Выражение называется иррациональным, если оно содержит извлечение корня из переменной или возведение переменной в дробную степень. Как правило, тождественные преобразования выполняются на множестве неотрицательных чисел. При решении примеров мы будем это подразумевать и специально не оговаривать.
Пример 3.14. Упростить выражение .
Решение.

.
Ответ:  .
.
Пример 3.15. Упростить выражение .
Решение.
 .
.
Избавимся от
иррациональности в знаменателе. Для этого домножим числитель и знаменатель
на выражение, сопряженной к знаменателю,
то есть на сумму  .
Получим
.
Получим

 .
.
Ответ:  .
.
Пример 3.16. Упростить выражение
.
Решение. Избавимся от иррациональности в знаменателе каждой из дробей в первой скобке:
,
.
Подстановка полученных выражений дает
.
Ответ: 
Пример 3.17. Упростить выражение
.
Решение. Сделаем замену переменной . Тогда исходное выражение примет вид
.
Рассмотрим далее пример, содержащий произведение корней с различными показателями.
Ответ:  .
.
Пример 3.18. Упростить выражение .
Решение.
Ответ:  .
.
Пример 3.19. Вычислить .
Решение. Заметим, что
, тогда
=.
Ответ: 6.
Пример 3.20. Вычислить .
Решение. Так как , то
=.
Ответ: 6.
Пример 3.21. Вычислить .
Решение.
.
Ответ:  .
.
Пример 3.22. Найти
значение выражения при  .
.
Решение. Упростим предварительно заданное выражение
,
тогда при  получим .
получим .
Ответ: 9.
Пример 3.22. Найти значение выражения a) ,
б) , в) .
Решение. а) Представим оба подкоренных выражения в виде полных квадратов: и , тогда
.
б) Действуя аналогично пункту а), получаем
=
.
в) .
Ответ: a)  ;
б) 4; в) 3.
;
б) 4; в) 3.
Пример 3.23. Упростить
выражение 
Решение. Проведем преобразования в ОДЗ
().
Ответ: 
Пример 3.24. Упростить
выражение 
Решение. Проведем преобразования в ОДЗ ().
.
Ответ:  , .
, .
Пример 3.25.
.
Решение. Воспользуемся равенством:
.
Тогда
.
Раскрывая скобки и приведя подобные, получаем
.
Ответ:  .
.
studfiles.net
Тема № 2 преобразование алгебраических выражений i теоретический материал
Тема № 2.
Преобразование алгебраических выражений
I. Теоретический материал
Основные понятия
Алгебраическое выражение: целое, дробное, рациональное, иррациональное.
Область определения, допустимые значения выражения.
Значение алгебраического выражения.
Одночлен, многочлен.
Формулы сокращенного умножения.
Разложение на множители, вынесение за скобки общего множителя.
Основное свойство дроби.
Степень, свойства степени.
Корtym, свойства корней.
Преобразование рационального и иррационального выражений.
Выражение, составленное из чисел и переменных с помощью знаков сложения, вычитания, умножения, деления, возведения в рациональную степень, извлечения корня и с помощью скобок называется алгебраическим.
Например: ;  ;
;  ;
;
 ;
;  ;
;  ;
;  .
.
Если алгебраическое выражение не содержит деления на переменные и извлечения корня из переменных (в частности, возведения в степень с дробным показателем), то оно называется целым.
Например: ;  ;
;  .
.
Если алгебраическое выражение составлено из чисел и переменных с помощью действий сложения, вычитания, умножения, возведения в степень с натуральным показателем и деления, причем используется деление на выражения с переменными, то оно называется дробным.
Например:  ;
;  .
.
Целые и дробные выражения называются рациональными выражениями.
Например: ; ;
.
Если в алгебраическом выражении используется извлечение корня из переменных (или возведение переменных в дробную степень), то такое алгебраическое выражение называется иррациональным.
Например:  ;
;  .
.
Значения переменных, при которых алгебраическое выражение имеет смысл, называются допустимыми значениями переменных.
Множество всех допустимых значений переменных называется областью определения.
Областью определения целого алгебраического выражения является множество действительных чисел.
Областью определения дробного алгебраического выражения является множество всех действительных чисел, кроме тех, которые обращают знаменатель в нуль.
Например:  имеет смысл при
имеет смысл при  ;
;
 имеет смысл при , то есть при
имеет смысл при , то есть при  .
.
Областью определения иррационального алгебраического выражения является множество всех действительных чисел, кроме тех, которые обращают в отрицательное число выражение, стоящее под знаком корня четной степени или под знаком возведения в дробную степень.
Например: имеет смысл при  ;
;
 имеет смысл при , то есть при
имеет смысл при , то есть при  .
.
Числовое значение, полученное при подстановке в алгебраическое выражение допустимых значений переменных, называется значением алгебраического выражения.
Например: выражение  при
при  ,
,  принимает значение .
принимает значение .
Алгебраическое выражение, содержащее только числа, натуральные степени переменных и их произведения, называется одночленом.
Например: ;  ;
;  .
.
Одночлен, записанный в виде произведения числового множителя, стоящего на первом месте, и степеней различных переменных, приведен к стандартному виду.
Например:  ;
; 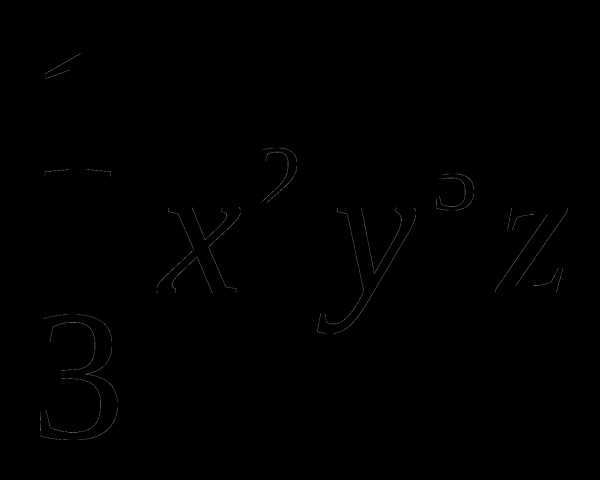 .
.
Числовой множитель стандартной записи одночлена называется коэффициентом одночлена. Сумма показателей степеней всех переменных называется степенью одночлена.
При умножении одночлена на одночлен и при возведении одночлена в натуральную степень получаем одночлен, который нужно привести к стандартному виду.
Сумма одночленов называется многочленом.
Например: ; ;  .
.
Если все члены многочлена записаны в стандартном виде и выполнено приведение подобных членов, то полученный многочлен стандартного вида.
Например: .
Если в многочлене только одна переменная, то наибольший показатель степени этой переменной называется степенью многочлена.
Например: многочлен имеет пятую степень.
Значение переменной, при которой значение многочлена равно нулю, называется корнем многочлена.
Например: корнями многочлена являются числа 1,5 и 2.
Формулы сокращенного умножения
Разность квадратов: .
Квадрат суммы: .
Квадрат разности: .
Сумма кубов: .
Разность кубов: .
Куб суммы: .
Куб разности: .
Частные случаи использования формул сокращенного умножения
Разность квадратов: или
.
Квадрат суммы: или
.
Квадрат разности: или
.
Сумма кубов: или
.
Разность кубов: или
.
Куб суммы: или
.
Куб разности: или
.
Преобразование многочлена в произведение нескольких сомножителей (многочленов или одночленов) называется разложением многочлена на множители.
Например:.
Способы разложения многочлена на множители
Применение распределительного закона в виде: называется вынесением общего множителя за скобки. При вынесении общего множителя за скобки каждую переменную, входящую во все члены многочлена, выносят с наименьшим показателем, который есть в данном многочлене. Если все коэффициенты многочлена – целые числа, то в качестве коэффициента общего множителя берут наибольший по модулю общий делитель всех коэффициентов многочлена.
Например: .
Использование формул сокращенного умножения.
Например: .
Способ группировки. Переместительный и сочетательный законы позволяют группировать члены многочлена различными способами. Один из способов приводит к тому, что в скобках получается одинаковое выражение, которое в свою очередь выносится за скобки.
Например:.
Любое дробное алгебраическое выражение можно записать в виде частного двух рациональных выражений с переменной в знаменателе.
Например: .
Дробь, у которой числитель и знаменатель являются рациональными выражениями и в знаменателе есть переменная, называется рациональной дробью.
Например:  ;
;  ;
;  .
.
Если числитель и знаменатель рациональной дроби умножить или разделить на одно и то же отличное от нуля число, одночлен или многочлен, то значение дроби не изменится. Данное выражение называется основным свойством дроби:
 .
.
Действие деления числителя и знаменателя дроби на одно и то же число, называется сокращением дроби:
 .
.
Например:  ; .
; .
Произведение n множителей, каждый из которых равен а, где а – произвольное алгебраическое выражение или действительное число, а n – натуральное число, называется степенью а:
.
Алгебраическое выражение а называется основанием степени, число
n – показателем.
Например: .
Полагают по определению, что для любого а, не равного нулю:
 и
и  .
.
Если , то 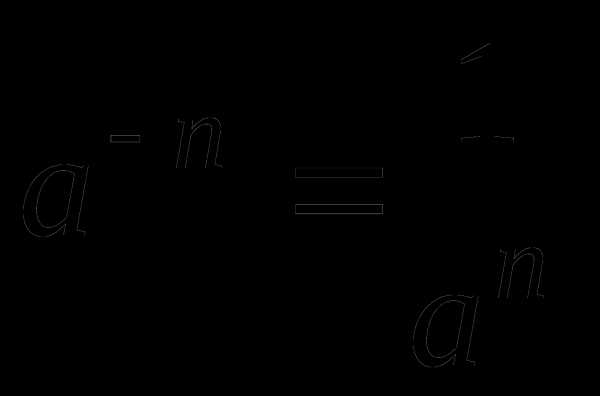 .
.
Свойства степени
1. .
2. .
3. .
4. .
5.  .
.
Если ,  , то выражение, n-я степень которого равна а, называется корнем n-й степени из а. Его принято обозначать
, то выражение, n-я степень которого равна а, называется корнем n-й степени из а. Его принято обозначать  . При этом а называется подкоренным выражением, n называется показателем корня.
. При этом а называется подкоренным выражением, n называется показателем корня.
Например: 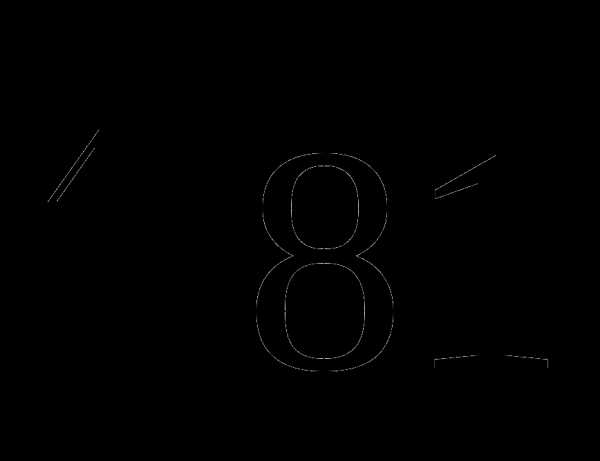 ;
;  ;
; 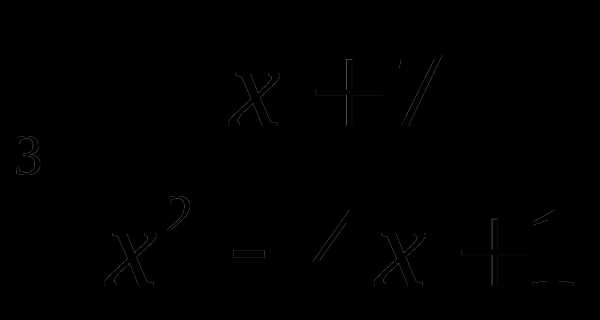 .
.
Свойства корня n-й степени из а
1. .
2. 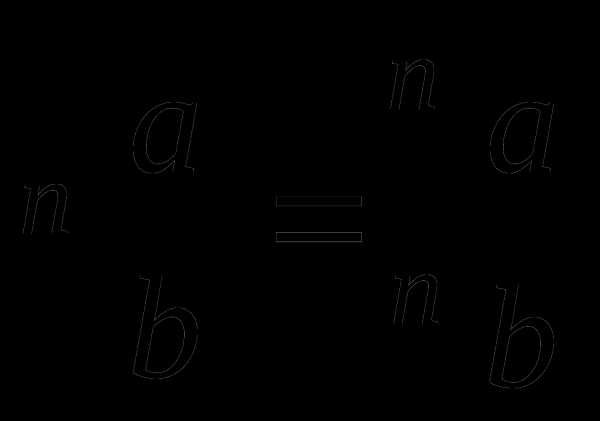 ,
,  .
.
3. .
4.  .
.
5. .
Обобщая понятие степени и корня, получают понятие степени с рациональным показателем:
 .
.
В частности,  .
.
Действия, производимые с корнями
Если подкоренное выражение можно представить в виде произведения множителей, и хотя бы из одного из них можно извлечь корень, то можно провести вынесение множителя из-под знака корня. Например: .
Обратное действие – внесение множителя под знак корня.
Например: .
II. Практический материал
Примеры выполнения заданий
Пример 1. Найдите значение дроби  .
.
Решение.
.
Ответ:  .
.
Пример 2. Упростите выражение .
Решение.
Преобразуем выражение в первых скобках:
 , если
, если  .
.
Преобразуем выражение во вторых скобках:
 .
.
Разделим результат из первой скобки на результат из второй скобки:
.
Ответ: 
Пример 3. Упростите выражение:
.
Решение.


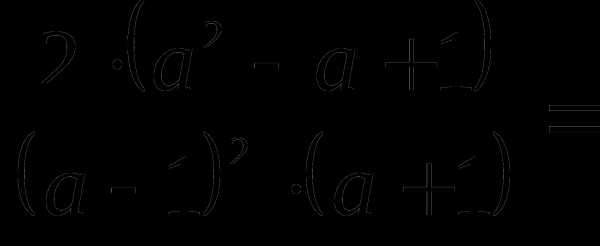
 .
.
Ответ: .
Пример 4. Упростите выражение .
Решение.
Преобразуем первую дробь:
.
Преобразуем вторую дробь:
.
В результате получим:  .
.
Ответ: 0.
Пример 5. Упростите выражение 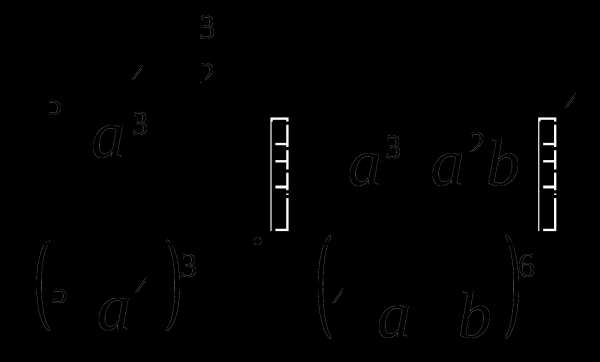 .
.
Решение. Выполним решение по действиям:
1) ;
2)  ;
;
3)  ;
;
4) ;
5) ;
6) ;
7) .
Ответ: 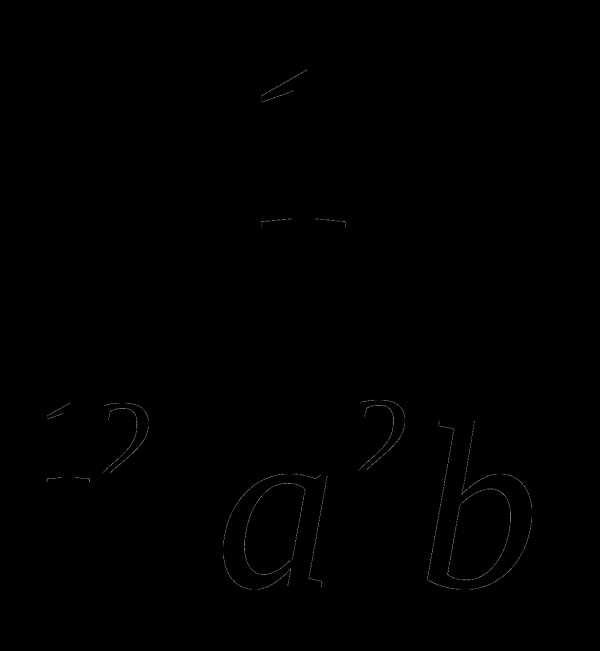 .
.
Пример 6. Докажите тождество .
Решение. Выполняем по действиям:
1) ;
2) ;
3) .
Ответ: .
Пример 7. Упростите выражение:
.
Решение. Выполняем по действиям:
1)
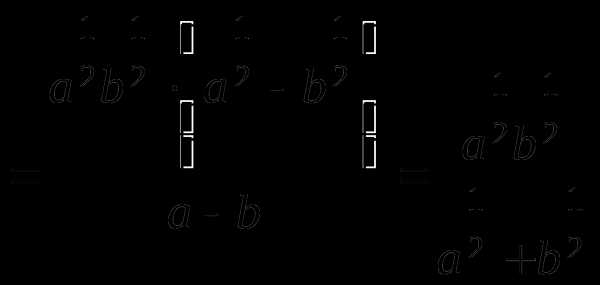 ;
;
2)  .
.
Ответ: 1.
Пример 8. Докажите тождество .
Решение. Выполняем по действиям:
1) ;
2)
 ;
;
3) .
Задания для самостоятельной работы
1. Упростите выражение:
а) ;
б) ;
в) ;
г) ;
д) .
2. Разложите на множители:
а) ;
б)  ;
;
в)  ;
;
г)  .
.
3. Упростите выражение:
а)  ; б)
; б)  ;
;
в)  ; г)
; г) 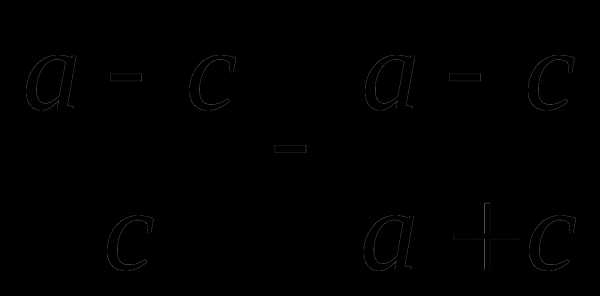 ;
;
д) 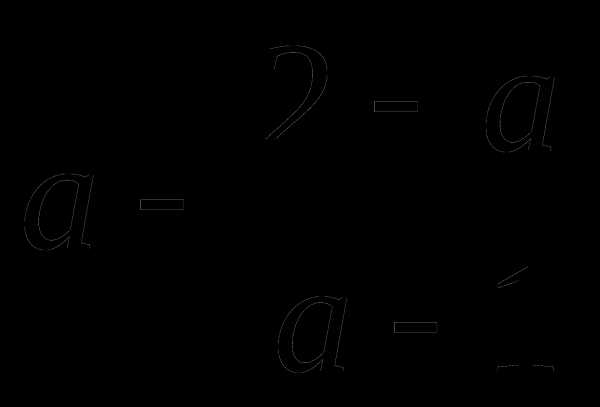 ; е)
; е) 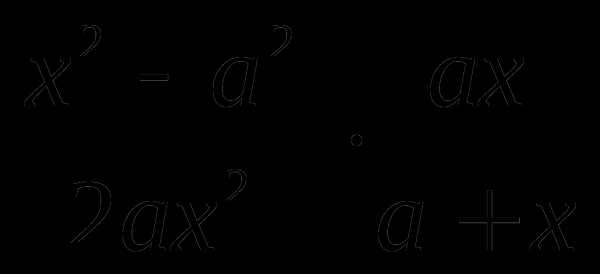 ;
;
ж)  ;
;  ;
;
з) .
4. Упростите выражение:
а) ; б)  ;
;
в) 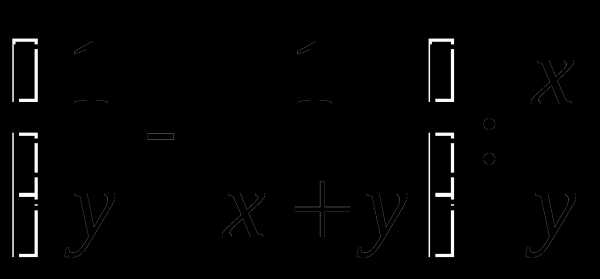 ; г) .
; г) .
5. Сократите дробь:
а)  ; б)
; б) 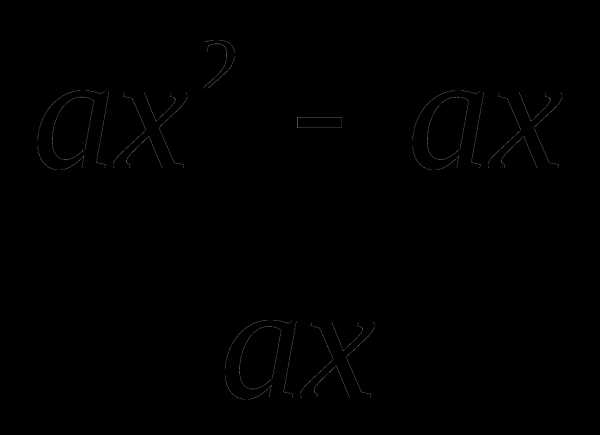 ;
;
в)  ; г)
; г) 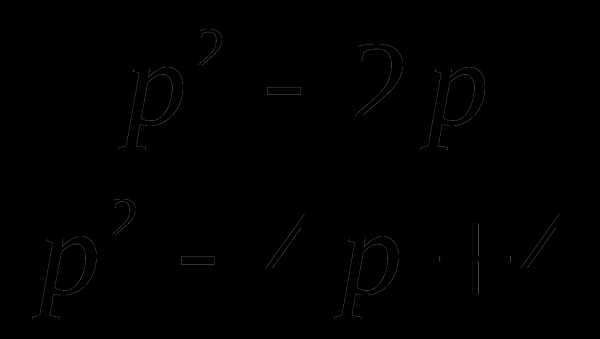 .
.
6. Найдите область определения дроби:
а) 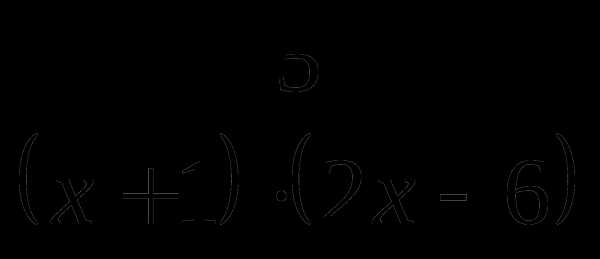 ; б)
; б)  .
.
7. Упростите выражение:
а) ; б) ; в)  .
.
8. Найдите значение дроби:
а)  ; б)
; б)  ;
;
в)  ; г)
; г)  .
.
9. Упростите выражение:
.
Ответ:  , если
, если
10. Докажите, что  .
.
11. Упростите выражение  .
.
Ответ: 1.
12. Упростите выражение:
,
где  ;
;  ;
;  .
.
Ответ:  .
.
textarchive.ru
Рациональные выражения. Задачи В11 ЕГЭ по математике
Часть 1.
Здесь смотрим части 2, 3, 4, 5
Разбор Задач №9 ЕГЭ по математике из открытого банка заданий
I. Преобразование числовых рациональных выражений
Задание 1.
Найдите значение выражения .
Решение: + показать Ответ: 18.
Задание 2.
Найдите значение выражения .
Решение: + показать Ответ: 0,1.
Задание 3.
Найдите значение выражения .
Решение: + показать
Задание 4.
Найдите значение выражения: .
Решение: + показать Ответ: -24,32.
II. Преобразование буквенных рациональных выражений
Задание 1.
Найдите значение выражения .
Решение: + показать
Задание 2.
Найдите значение выражения .
Решение: + показать
Задание 3.
Найдите значение выражения .
Решение: + показать Раскладываем числитель на множители, пользуясь формулой разности квадратов: Ответ: -2.
Задание 4.
Найдите значение выражения .
Решение: + показать Раскладываем числитель и знаменатель на множители путем вынесения общего множителя за скобку: Ответ: 17.
Задание 5.
Найдите значение выражения .
Решение: + показать
Задание 6.
Найдите значение выражения .
Решение: + показать Не выполняя действие во вторых скобках, сразу производим раскрытие скобок: Ответ: -8.
Задание 7.
Найдите , если при .
Решение: + показать Ответ: 1.
Задание 8.
Найдите , если при .
Решение: + показать Ответ: 0.
Задание 9.
Найдите , если .
Решение: + показать => Делим обе части равенства на : Ответ: -0,2.
Задание 10.
Найдите , если .
Решение: + показать => Тогда Ответ: 2.
Задание 11.
Найдите значение выражения , если , .
Решение: + показать
🙂 За улыбкой сюда –>+ показать
Надеюсь, вам было также интересно…

Вы можете пройти тест по заданиям 9 «Преобразования рациональных выражений».
egemaximum.ru
Преобразования алгебраических выражений — Повышенный уровень — Сборник задач
Глава II. Сборник задач
§ 2. Повышенный уровень (часть 2)
2.1. Преобразования алгебраических выражений
Упростите выражение (22—61):
Найдите сумму иррациональных чисел (62—63):
64. Между какими соседними натуральными числами заключено значение выражения
65. Найдите значение выражения
Упростите выражение (66—67):
Сократите дробь (68-71):
Упростите выражение (72—85):
86. Докажите тождество
Упростите выражение (87—95):
96. Разложите многочлены mn2 — n2 + mn — n на линейные множители.
97. Сократите дробь при х ≠ ±3.
98. Разложите на множители при ху ≠ 0.
99. Разложите на множители при ху ≠ 0.
100. Найдите наименьшее значение выражения (2х2 + 3у + х + 5)2 + (у + 3 — 2х)2 и значения х и у, при которых оно достигается.
101. Найдите наименьшее значение выражения (7х — 3у + 11)2 + (2х + 6у — 14)2 — 5 и значения х и у, при которых оно достигается.
102. Найдите наименьшее значение выражения (17 — 4х — 5у)2 + (3х — у — 4,2)2 + 3 и значения х и у, при которых оно достигается.
103. Найдите все пары чисел (х0; у0), при которых верно равенство
104. Найдите все пары чисел (а; b), при которых равны значения выражений
compendium.su
АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ – Репетитор по математике
АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ, НЕРАВЕНСТВА И СИСТЕМЫ
Разложение многочлена на множители методом неопределенных коэффициентов
В этой статье мы рассмотрим решение уравнения четвертой степени с помощью разложения на множители методом неопределенных коэффициентов.
Решить уравнение:
Решение. показать
Перед нами уравнение четвертой степени.
Чтобы решить это уравнение, разложим левую часть уравнения на множители.
Многочлен четвертой степени можно разложить на произведение двух многочленов второй степени.
Воспользуемся методом неопределенных коэффициентов.
Пусть выполняется равенство:
Здесь -целые числа.
Перемножим две скобки справа и приведем подобные члены. Получим:
Два многочлена равны тогда и только тогда, когда равны их коэффициенты.
Приравняем коэффициенты при одинаковых степенях и получим систему уравнений:
Без ограничения общности можем считать, что
, тогда пусть
, отсюда или .
Рассмотрим два случая:
- ,
Получим систему уравнений:
Из второго и третьего уравнений получаем — что не удовлетворяет третьему уравнению. Система не имеет решений.
2. ,
Из второго и третьего уравнений получаем — и эти значения удовлетворяет третьему уравнению.
Получили:
Тогда наше разложение имеет вид:
Осталось приравнять квадратные трехчлены в скобках к нулю и найти корни:
Ответ: ,
И.В. Фельдман, репетитор по математике
ege-ok.ru
Математика. Тождественные преобразования алгебраических выражений. Тренировка № 15. Задание + решение.
Математика. Тождественные преобразования алгебраических выражений. Тренировка № 15. Задание + решение.
Выражение, составленное из конечного числа букв и чисел, соединенных знаками действий сложения, вычитания, умножения, деления, возведения в целую степень, извлечение корня, называется алгебраическим выражением.
Буквы, входящие в алгебраическое выражение, могут принимать значения из некоторого числового множества, которое называется множеством его допустимых значений или областью определения.
Примеры.
1. — целое алгебраическое выражение, множеством допустимых значений которого являются любые числа.
2. 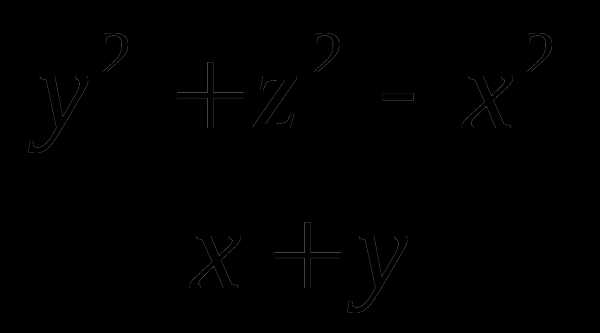 — дробно-рациональное алгебраическое выражение. Так как на нуль делить нельзя, то множеством допустимых значений этого выражения являются все значения
— дробно-рациональное алгебраическое выражение. Так как на нуль делить нельзя, то множеством допустимых значений этого выражения являются все значения  и
и  , удовлетворяющие условию
, удовлетворяющие условию  или
или .
.
3.  — иррациональное алгебраическое выражение. Множество допустимых значений этого алгебраическое выражение состоит из всех значений
— иррациональное алгебраическое выражение. Множество допустимых значений этого алгебраическое выражение состоит из всех значений  и
и  , таких что аb, b0 и а>0 . Т.к. выражение, стоящее под знаком корня четной степени должно быть, по определению арифметического корня, неотрицательным.
, таких что аb, b0 и а>0 . Т.к. выражение, стоящее под знаком корня четной степени должно быть, по определению арифметического корня, неотрицательным.
Замечание. В общем случае допустимыми значениями для
целых алгебраических выражений являются любые числа;
дробно-рациональных алгебраических выражений все числа, которые не обращают в нуль знаменатель дробей, входящих в это выражение;
иррациональных выражений только те значения букв, при которых выражения, стоящие под знаком корня четной степени принимают неотрицательные значения.
Тождеством называется равенство двух алгебраических выражений справедливое для любых допустимых значений, входящих в него букв.
Тождественным преобразованием алгебраического выражения называется замена одного алгебраического выражения другим тождественно ему равным, но отличным по форме.
Целью тождественного преобразования может быть придание выражению вида, более удобного для численных расчетов или дальнейших преобразований.
Перечислим основные тождественные преобразования алгебраических вражений:
приведение подобных членов;
раскрытие скобок;
разложение на множители;
приведение алгебраических дробей к общему знаменателю;
избавление от иррациональности в знаменателе и т.п.
Для успешного осуществления тождественных преобразований алгебраических выражений нужно помнить:
формулы сокращенного умножения;
свойства степени с целым показателем;
формулы корней квадратного трехчлена ax2 + bx + c;
теорему Виета;
разложение квадратного трехчлена ax2 + bx + c на множители;
определение арифметического корня n-ой степени;
определение модуля числа;
свойства арифметического корня;
Рассмотрим примеры тождественных преобразований алгебраических выражений.
Задача 1. Разложить многочлен на множители
Решение.
Для решения задачи необходимо сгруппировать слагаемые так, чтобы они имели общий множитель, который можно будет, затем вынести за скобки, перейдя от суммы к произведению.
Объединим первое и третье слагаемые в одну группу, второе и четвертое в другую:
2) Вынесем за скобки в первой группе  , во второй – общий множитель
, во второй – общий множитель  , получим:
, получим:
3) Вынесем за скобки общий множитель первого и второго слагаемого  :
:
Полученное выражение есть произведение двух сомножителей, а значит первоначальный многочлен разложен на множители.
Ответ:
Задача 2. Разложить на множители многочлен
Решение.
Заметим, что как бы мы не группировали слагаемые получить группы слагаемых, имеющие одинаковые множители невозможно. Поэтому, сначала преобразуем сами слагаемые.
–7а2 = –3а2 – 4а2; 7а = 12а – 5а
3) Сгруппируем слагаемые попарно, и из каждой скобки вынесем общий множитель:
(a3 – 3а2) +( – 4а2 +12а) + (– 5а +15) = а2 (а – 3) – 4а (а – 3) – 5(а – 3)
4) В полученном выражении все слагаемые имеют общий множитель (а – 3), который и выносим за скобки.= (а – 3)(а2 – 4а – 5)
5) Мы получили уже произведение двух множителей, но второй множитель в свою очередь, может быть разложен на множители. Для этого, используя теорему Виета, разложим трехчлен (а2 – 4а – 5) на множители.
По теореме Виета корнями трехчлена (а2 – 4а – 5) являются а1=5 и а2= –1.
Тогда имеем (а2 – 4а – 5) = (а – 5)(а +1), следовательно
= (а – 3)(а – 5)(а + 1)
Ответ: a3 – 7а2 + 7а +15 = (а – 3)(а – 5)(а + 1).
Рассмотрим примеры тождественных преобразований дробно-рациональных выражений. При выполнении тождественных преобразований таких выражений необходимо указывать их множество допустимых значений. Некоторые преобразования могут приводить к расширению области допустимых значений выражения. Поэтому, выполнив преобразования выражения, нужно всегда уметь ответить на вопрос, на каком множестве оно тождественно равно полученному.
Задача 3. Сократить дробь
Решение.
Чтобы сократить дробь нужно представить числитель и знаменатель дроби в виде произведения сомножителей. Таким образом, задача сводится к разложению многочленов на множители.
1)
2)
3)
Заметим, что выражение при любом  , следовательно дробь можно сократить на это выражение:
, следовательно дробь можно сократить на это выражение:

Ответ: 
multiurok.ru
Алгебраические выражения
Алгебраические выражения. В этой статье рассмотрим с вами примеры входящие в состав экзамена по математике, при решении которых у ребят возникают проблемы. Многие таких вообще не видели и в школьном курсе их не касались. Будем преобразовывать алгебраические выражения. Задания есть довольно простые, где достаточно знать формулы сокращённого умножения, свойства степеней, уметь «работать» с дробями. Вот типичные несложные примеры, можете решить и проверить себя:
Далее мы рассмотрим примеры, решения которых просты, но сами условия могут несколько отпугнуть вас, так как подобные задания в курсе школьной программы встречаются редко. Посмотрев процесс решения, уверен, вы всё поймёте без проблем. Есть примеры для самостоятельного решения, практикуйтесь, затем сверьте с решением представленным на блоге.
Найдите p (b)/(p (1/b)), если
Сначала необходимо найти
То есть, вместо b в исходное выражение мы подставили 1/b. Итак:
Ответ: 1
Посмотреть аналогичный пример
Найдите 49a – 41b – 14, если
В подобных примерах не раздумывайте над тем, как данное выражение можно найти, выполните преобразование выражения:
Для того, чтобы найти чему равно данное выражение, необходимо вычесть 34 из обеих частей уравнения:
Ответ: –34
Посмотреть аналогичный пример
Найдите
Так как a/b=3, значит a=3b. Тогда можем преобразовать:
Ответ: 2
Найдите значение выражения 3p (a) – 6a +7, если p (a)=2a–3.
В данном случае просто подставляем p (a) и решаем:
3p (a) – 6a +7 = 3 (2a – 3) – 6a +7 = 6a – 9 – 6a +7 = –2
Ответ: –2
Найдите значение выражения 7x+2y+6z, если 7x+y = 7, 6z + y = 5.
В подобных задачах ищите сумму или разность уравнений под условием «если», результат как правило, будет сведён нахождению значения данного выражения, найдём сумму уравнений:
7x+y+6z+y= 7+5
7x+2y+6z = 12
В других примерах, возможно потребуется разделить или умножить обе части уравнения на какое-либо число.
Ответ: 12
Посмотреть аналогичный пример
Найдите значение выражения q (b–7)–q (b+7), если q (b)=–6b.
Если q (b)=–6b, то q (b–7)=–6 (b–7) и q (b+7)=–6 (b+7).
То есть мы подставляем аргумент в формулу задающую функцию, значит:
q (b–7)–q (b+7)=–6 (b–7)–(–6)(b+7)=–6b+42+6b+42=84
Ответ: 84
Посмотреть аналогичный пример
Найдите значение выражения 5 (p (2x)–2p (x+5)), если p (x)= x–10.
Если p (x)= x–10, то p (2x) =2x–10 и p (x+5) =x+5–10.
Получаем:
5 (p (2x) –2p (x+5)) = 5 (2x–10–2 (x+5–10)) = 5 (2x–2x–10–10+20)=0
Ответ: 0
Найдите p (x–7)+p (13–x), если p (x)=2x+1.
Подставляем аргумент в формулу задающую функцию.
Если p (x)=2x+1, то p (x–7)=2 (x–7)+1 и p (13–x) =2 (13–x)+1.
Находим сумму:
p (x–7)+ p (13–x)=2 (x–7)+1+2 (13–x)+1=2x–14+1+26–2x+1=14
Ответ: 14
Найдите 2p (x+5)–p (2x), если p (x)=2x–6.
Если p (x)=2x–6, то p (x+5)=2 (x+5)–6 и p (2x)=2 (2x)–6.
Находим разность:
2p (x+5)–p (2x)=2 (2 (x+5)–6)–(2 (2x)–6)=2 (2x+4)–4x+6=14
Ответ: 14
Посмотреть аналогичный пример
Найдите p (x) + p (12 –x), если
Если
То
Найдём сумму:
Ответ: 0
В будущем продолжим рассмотрение заданий с выражениями, не пропустите! На этом закончим. Время стремительно бежит, помните об этом. Практикуйтесь, отрабатывайте навыки.
Всего доброго!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru

Leave A Comment