На рисунке в прямоугольнике ABCD диагонали AC и BD пересекаются в точке О причем угол AOB=40 градусов.Найти угол DAO.Напишите пожалуйста решения ответ я знаю.
Стороны угла, образующие угол (а), являются касательными к окружности…
радиусы в точку касания _|_ касательной…
если провести радиусы, получим центральный угол,
величина которого (2b)
и теперь можно записать второе уравнение для (а) и (b)
a + 2b = 180 (((т.к. сумма углов 4-угольника = 360)))
а + 2(6 + а) = 180
3а = 168
а = 56
Призмой называется многогранник, у которого две грани (основания) лежат в параллельных плоскостях, а все ребра вне этих граней параллельны между собой.
Все ребра параллельны!
Ответ: Не существует призма, у которой только одно боковое ребро перпендикулярно плоскости основания
Медианы треугольника делятся в точке пересечения в отношении 2:1, считая от вершины (свойство). Значит отрезок mc=cc1*2/3=24*2/3=16.
Значит отрезок mc=cc1*2/3=24*2/3=16.
Отрезок om=mc-oc или 16-12=4.
Ответ: om=4.
1) из координат конца вычитаем координаты начала
MN{2-3;3-4}
MN{-1;-1}
2)А(0+2/2;4+3/2)
А(1;3,5)
3)|MN|=√(-2)²+1²=√5
4)MN=
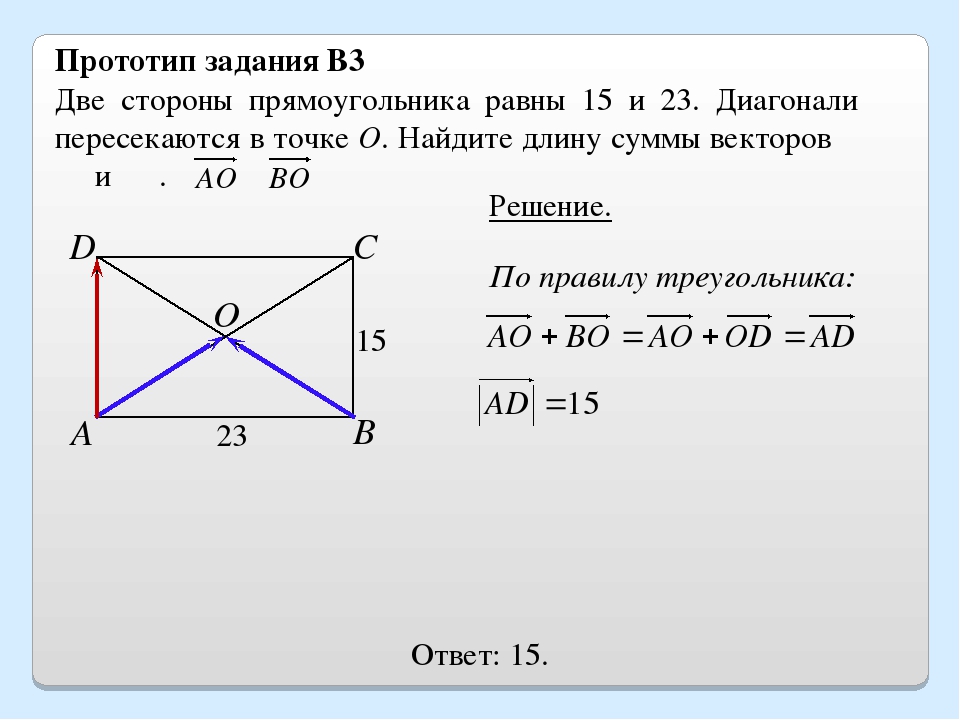
[PDF] ABCD BD, сторона АВ в 3 раза меньше стороны ВС. 1.
Download ABCD BD, сторона АВ в 3 раза меньше стороны ВС. 1….
1.На рисунке ABCD — прямоугольник, АН BD, сторона АВ в 3 раза меньше стороны ВС. Найдите АН, если BD = 20.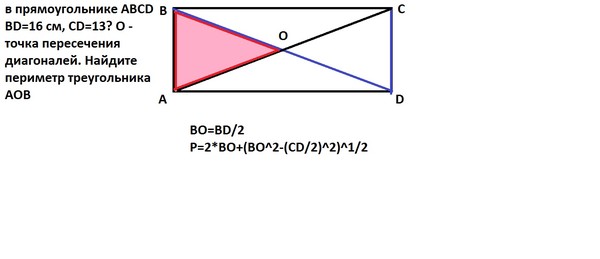
2.
3. 4. 5. 6. 7. 8. 9.
MN||AC,AM : MB = 2:1,AC=6. Найти MN. В равнобедренной трапеции диагональ перпендикулярна к ее боковой стороне и образует с основанием угол в 15°. Найдите углы трапеции. Диагональ трапеции делит ее среднюю линию на два отрезка, длины которых относятся как 3 : 8. Найдите основания трапеции, если средняя линия трапеции равна 22 см. Один из углов ромба ABCD на 40° больше другого. Найдите углы треугольника BОС, если О — точка пересечения диагоналей. В параллелограмме BCDE биссектриса угла D пересекает сторону ВС в точке М, причем ВМ = 7, МС = 10. Найдите периметр параллелограмма. Найдите площадь трапеции ABCD, если основания AD = 10см, BC= 5см, а высота CH= 8см. Стороны прямоугольника 12 см и 16 см. Чему равна диагональ? Найдите площадь равнобедренной трапеции, если ее основания равны 6 см и 16 см, а боковая сторона равна 13 см.
10.
MN||AC,АM : MB = 1:2,MN =8. Найти AC. 11. Одна из сторон прямоугольника равна 12 см, а диагональ 15 см. Чему равна вторая сторона прямоугольника? 12.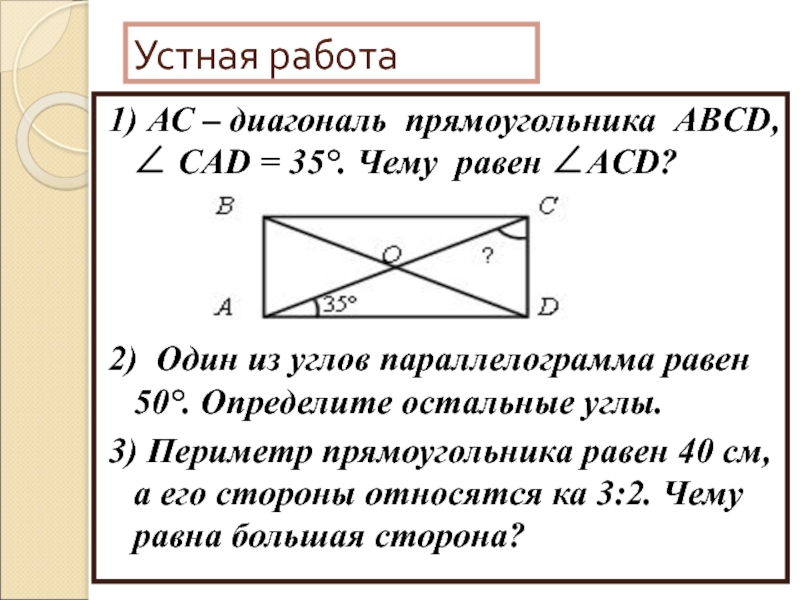
14. 15. 16. 17. 18. 19. 20. 21.
Найдите СН, если ВС = 20. Одна из сторон прямоугольника равна 8 см, а диагональ 17 см. Чему равна вторая сторона прямоугольника? В параллелограмме BCDE биссектриса угла В пересекает сторону DE в точке К, причем DK = 4, ЕК = 12. Найдите периметр параллелограмма. Найдите периметр параллелограмма ABCD, если ВН — его высота, опущенная на сторону AD, площадь параллелограмма равна 120 м2, АН = 6 м, DH = 9 м. Найдите площадь трапеции ABCD, если основания AD = 8 см, BC= 4,5см, а высота CH= 4см. В равнобедренной трапеции диагональ образует с основанием угол в 30°. Найдите углы трапеции, если известно, что меньшее основание трапеции равно ее боковой стороне. В трапеции ABCD (AB ǀǀ CD) диагональ BD делит среднюю линию трапеции на отрезки 6 см и 12 см.
22. 23. 24.
25. 26. 27. 28.
29. 30. 31.
треугольника ВОС Найдите площадь равнобедренной трапеции, если ее меньшее основание равно 7 см, боковая сторона — 10 см, высота — 8 см. В ромбе ABCD A = 36°. Найдите угол между диагональю BD и стороной DC. В прямоугольнике ABCD АЕ и CF -перпендикуляры, опущенные из вершин А и С на диагональ BD. Угол между диагоналями равен 30°, CF = 2см. а) Докажите, что AE = CF. б) Найдите длину диагонали BD. В ромбе ABCD биссектриса угла ВАС пересекает сторону ВС в точке М. Найдите углы ромба, если AMC= 120°. Стороны параллелограмма равны 6 и 10 см, а высота, проведенная к меньшей из них, равна 8 см. Найдите высоту, проведенную к другой стороне. В параллелограмме две стороны равны 6 и 8 см, а один из углов 150°. Найдите площадь параллелограмма.
32. 33. Найдите площадь треугольника ABC, если сторона AB = 13см, а высота CH= 13см. 34. На рисунке ABCD — прямоугольник, ВН АС, сторона АВ в 5 раз меньше диагонали.
35. 36. 37. 38. 39. 40. 41. 42.
43.
44.
45.
Найдите ВН, если AD = 12. Диагонали прямоугольника ABCD пересекаются в точке О. Найдите периметр треугольника BОС, если АB = 15, AD = 20, BD = 25. В параллелограмме BCDE биссектриса угла С пересекает сторону DE в точке К, причем ЕК = 7, DK =11. Найдите периметр параллелограмма. Найдите площадь трапеции ABCD, если основания AD = 12 см, BC= 2,5см, а высота CH= 4см.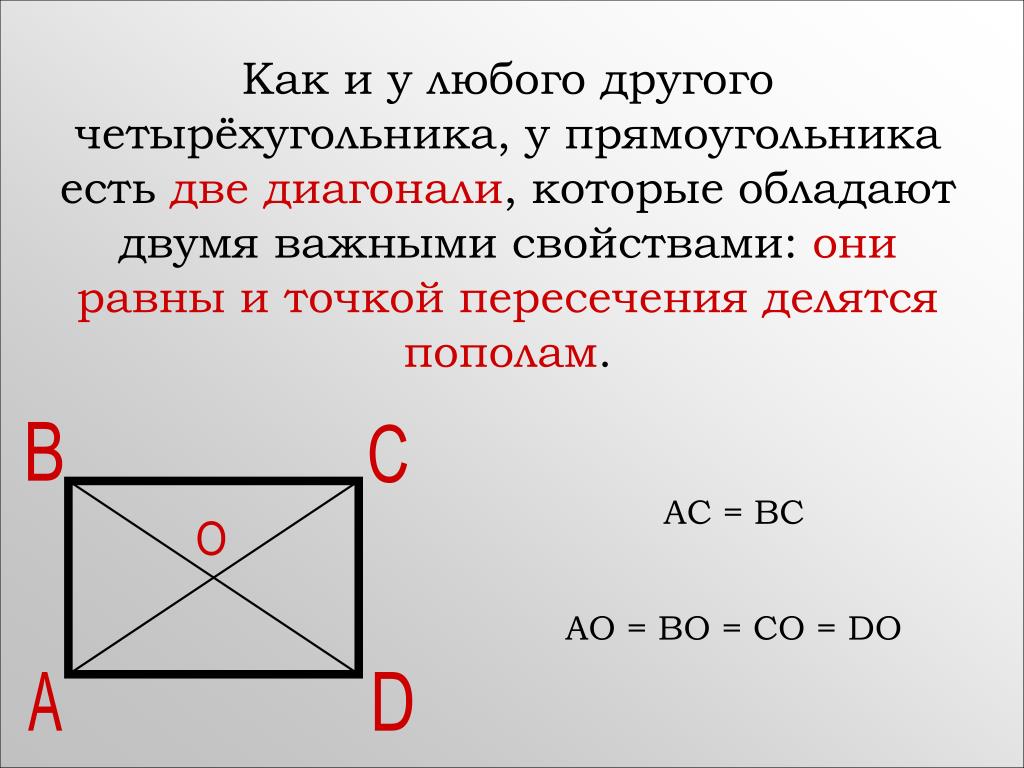 Острый угол А прямоугольной трапеции ABCD равен 45°. Большее основание трапеции равно 8 см, а большая боковая сторона равна 4√2 см. Найдите площадь трапеции. ABCD — ромб, BAD = 100°, О — точка пересечения диагоналей. Найдите углы треугольника AOD. Найдите площадь треугольника ABC, если сторона AB = 8см, а высота CH= 5 см. В прямоугольнике ABCD BAC = 35°. Найдите угол между диагоналями прямоугольника. В ромбе ABCD, где угол А острый, BE и BF — высоты. Угол между диагональю BD и высотой BF равен 40°. а) Докажите, что BE = BF. б) Найдите углы ромба. Перпендикуляр, опущенный из вершины угла А прямоугольника ABCD на не проходящую через эту вершину диагональ, делит ее в отношении 1:3, считая от вершины В. Диагональ равна 6 см. Найдите расстояние от точки пересечения диагоналей до большей стороны. В равнобедренной трапеции ABCD диагональ перпендикулярна боковой стороне трапеции. Найдите площадь трапеции, если большее основание равно 12 см, а один из углов трапеции равен 120°. Найдите сторону ромба, если его диагонали равны 12 см и 16 см.
Острый угол А прямоугольной трапеции ABCD равен 45°. Большее основание трапеции равно 8 см, а большая боковая сторона равна 4√2 см. Найдите площадь трапеции. ABCD — ромб, BAD = 100°, О — точка пересечения диагоналей. Найдите углы треугольника AOD. Найдите площадь треугольника ABC, если сторона AB = 8см, а высота CH= 5 см. В прямоугольнике ABCD BAC = 35°. Найдите угол между диагоналями прямоугольника. В ромбе ABCD, где угол А острый, BE и BF — высоты. Угол между диагональю BD и высотой BF равен 40°. а) Докажите, что BE = BF. б) Найдите углы ромба. Перпендикуляр, опущенный из вершины угла А прямоугольника ABCD на не проходящую через эту вершину диагональ, делит ее в отношении 1:3, считая от вершины В. Диагональ равна 6 см. Найдите расстояние от точки пересечения диагоналей до большей стороны. В равнобедренной трапеции ABCD диагональ перпендикулярна боковой стороне трапеции. Найдите площадь трапеции, если большее основание равно 12 см, а один из углов трапеции равен 120°. Найдите сторону ромба, если его диагонали равны 12 см и 16 см.
46. Стороны параллелограмма равны 4 и 8 см, а высота, проведенная к большей из них, равна 5 см. Найдите высоту, проведенную к другой стороне. 47. В параллелограмме одна из сторон равна 10 см, а один из углов 30°. Найдите площадь параллелограмма, если его периметр равен 56 см. 48. В параллелограмме ABCD диагональ BD перпендикулярна к основанию AD, угол В равен 135°, площадь параллелограмма равна 49 см2 Найдите сторону AD параллелограмма. 49. Стороны прямоугольника 5 см и 12 см. Чему равна диагональ? 50. Один из углов ромба ABCD на 40° больше другого. Найдите углы треугольника BОС, если О — точка пересечения диагоналей. 51. ∆ ABC задан координатами вершин A(1;-4), В(4;0), C(6;-4). Постройте фигуру симметричную данной относительно 2) прямой у=-2х 3) точки М(-2;-1) 52. В трапеции ABCD диагональ BD перпендикулярна боковой стороне АВ и является биссектрисой угла D. Периметр трапеции ABCD равен 20 см. A = 60°. Найдите длину AD. 53. Диагонали прямоугольника ABCD пересекаются в точке О. Найдите периметр треугольника COD, если АВ = 5, ВС = 12, BD = 13.
 62. Сумма двух противоположных сторон описанного четырехугольника равна 12 см. а радиус вписанной в него окружности равен 5 см. Найдите площадь четырехугольника. 63. Дан ромб ABCD со стороной 4 см и углом 60°. Найдите его периметр и площадь. Найдите все углы ромба и радиус вписанной окружности. 64. Окружность проходит через вершины А и С остроугольного треугольника АВС и пересекает его стороны АВ и ВС в точках К и Е соответственно. Отрезки АЕ и СК перпендикулярны, КСВ = 20°. Найдите АВС. 65. Дана окружность радиуса 10 см. AB – диаметр окружности, C – точка, лежащая на окружности, величина дуги AC равна 60°. Определите диаметр этой окружности, градусную меру угла ABC, длины хорд AC и BC, расстояние между серединами хорд AB и BC, радиус окружности, вписанной в треугольник ABC. 66. Треугольник АBC, стороны которого 13 см, 14 см и 15 см, разбит на три треугольника отрезками, соединяющими точку пересечения медиан М с вершинами треугольника. Найдите площадь треугольника BMC и радиус вписанной окружности для ∆АВС.
62. Сумма двух противоположных сторон описанного четырехугольника равна 12 см. а радиус вписанной в него окружности равен 5 см. Найдите площадь четырехугольника. 63. Дан ромб ABCD со стороной 4 см и углом 60°. Найдите его периметр и площадь. Найдите все углы ромба и радиус вписанной окружности. 64. Окружность проходит через вершины А и С остроугольного треугольника АВС и пересекает его стороны АВ и ВС в точках К и Е соответственно. Отрезки АЕ и СК перпендикулярны, КСВ = 20°. Найдите АВС. 65. Дана окружность радиуса 10 см. AB – диаметр окружности, C – точка, лежащая на окружности, величина дуги AC равна 60°. Определите диаметр этой окружности, градусную меру угла ABC, длины хорд AC и BC, расстояние между серединами хорд AB и BC, радиус окружности, вписанной в треугольник ABC. 66. Треугольник АBC, стороны которого 13 см, 14 см и 15 см, разбит на три треугольника отрезками, соединяющими точку пересечения медиан М с вершинами треугольника. Найдите площадь треугольника BMC и радиус вписанной окружности для ∆АВС. 67. Площадь треугольника, описанного около окружности, равна 84 см2. Найдите периметр треугольника, если радиус окружности равен 7 см. 68. В окружность вписан треугольник ABC так, что АВ — диаметр окружности. Найдите углы треугольника, если ВС=134°. 69. Найдите основание АС равнобедренного треугольника АВС, у которого боковая сторона 5 равна 26 см, а синус угла при основании равен . Найдите площадь треугольника АВС 13
67. Площадь треугольника, описанного около окружности, равна 84 см2. Найдите периметр треугольника, если радиус окружности равен 7 см. 68. В окружность вписан треугольник ABC так, что АВ — диаметр окружности. Найдите углы треугольника, если ВС=134°. 69. Найдите основание АС равнобедренного треугольника АВС, у которого боковая сторона 5 равна 26 см, а синус угла при основании равен . Найдите площадь треугольника АВС 13и радиус вписанной в него окружности 70. Дан равнобедренный треугольник, у которого основание равно 10 см, высота, опущенная на основание, равна 12 см. Найдите площадь, периметр этого треугольника и радиус окружности, вписанной в треугольник. 71. Найдите высоты треугольника со сторонами 10 см, 10 см, 12 см и радиус окружности, описанной около треугольника. 72. 7 24 Гипотенуза АВ прямоугольного треугольника АВС равна 500 мм, sinА = , cosА = . 25 25 Найдите площадь треугольника АВС и радиус вписанной в него окружности. 73. Прямая АВ касается окружности с центром О и радиусом 5 см в точке А.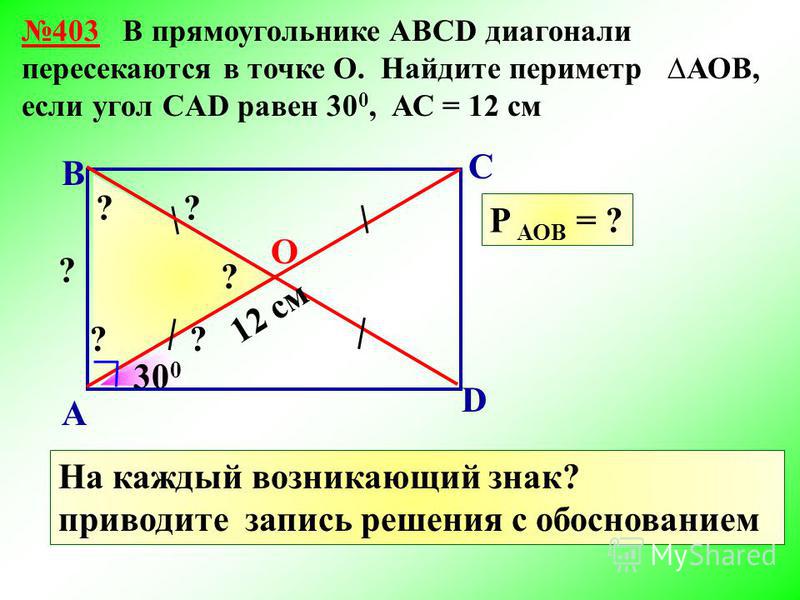 74.
74.
75.
76. 77.
Найдите ОВ, если АВ = 12 см. Из точки А к окружности с центром О и радиусом 8 см проведены касательные АВ и АС (В и С — точки касания). Найдите АВ и АС, если ВАС = 60°. Из точки М к окружности с центром О и радиусом 8 см проведены касательные AM и ВМ (А и В — точки касания). Найдите периметр треугольника АВМ, если AOB =120°. Хорды АВ и CD пересекаются в точке М. Найдите длину АВ, если СМ=4 см, DM=9 см, АМ:МВ=4. =180 =340
Найти х. 78. =220 =400
Найти х. 79. Диаметр АВ пересекает хорду CD в точке М. Найдите отрезки, на которые
точка М делит диаметр АВ, если г= 10 см, СМ = 4 см, MD = 9 см. 80. Окружность касается сторон прямоугольной трапеции с острым углом 40°. Найдите градусные меры дуг, на которые делят окружность точки касания. 81. Точка К делит хорду АР на отрезки 12 и 14 см. Найдите радиус окружности, если расстояние от центра окружности до точки К равно 11 см.
82.
83. В АВС все углы различны. Прямая, проходящая через вершину В,
разбивает АВС на два подобных треугольника. Найдите величину угла В. 84. Прямая ВЕ разбивает АВС на два подобных треугольника. Коэффициент подобия равен 3. Найдите углы АВС. 85.
Найдите величину угла В. 84. Прямая ВЕ разбивает АВС на два подобных треугольника. Коэффициент подобия равен 3. Найдите углы АВС. 85.
86.
87.
88.
89.
90.
91. 92. 93. 94.
пропорциональные отрезки В трапеции авсд известно что ab cd
Трапеция на ЕГЭ. Базовый уровень.
Задачи из открытого банка заданий ФИПИ.
Задача 1. В трапеции ABCD известно, что AB=CD, ∠ BDA=54° и ∠ BDC=23°. Найдите угол ABD. Ответ дайте в градусах.
Решение. В данной трапеции угол А DC при нижнем основании равен сумме углов А D В и В DC , равен 54 + 23 =77 градусам. Поскольку трапеция равнобедренная, то углы при нижнем основании равны и угол ВА D тоже равен 77 градусам. Сумма углов ВА D и АВ D равна 180 градусам (односторонние при параллельных прямых А D и ВС и секущей АВ). Значит угол АВС равен 180 – 77 =103 градусам.
Далее используем равенство углов А
D
В и
D
ВС
(накрестлежащие при параллельных прямых А
D
и ВС и секущей В
D
). Значит
угол АВ
D
равен 103 –
54 =49 градусам.
Значит
угол АВ
D
равен 103 –
54 =49 градусам.
Ответ 49.
Задача 2. Основания равнобедренной трапеции равны 10 и 24, боковая сторона равна 25. Найдите высоту трапеции.
Решение. В данной трапеции верхнее основание ВС равно 10, нижнее А D =24. Из вершин В и С опустим высоты на нижнее основание. В получившемся прямоугольнике НВСК НК=ВС=10. Треугольники АВН и К DC DC ), значит АН=К D =(24-10):2=7. По теореме Пифагора в треугольнике АВН квадрат катета ВН равен разности квадрата гипотенузы АВ и квадрата катета АН. То есть ВН 2 = 625 – 49 = 576. ВН = 24.
Ответ 24.
Задача 3. В равнобедренной трапеции одно из
оснований
равно 3, а другое — 7. Высота трапеции равна 4. Найдите тангенс
острого угла трапеции.
Решение. В данной трапеции верхнее основание
ВС равно 3, нижнее А
D
=7. Из вершин В и С опустим высоты на нижнее
основание. В получившемся прямоугольнике НВСК НК=ВС=3. Треугольники АВН и К
DC
равны (они
прямоугольные, ВН=СК, АВ =
DC
), значит АН=К
D
=(7-3):2=2. Тангенс
острого угла ВАН в прямоугольном треугольнике АВН равен отношению
противолежащего катета ВН к прилежащему катету АН, то есть 4:2=2.
Тангенс
острого угла ВАН в прямоугольном треугольнике АВН равен отношению
противолежащего катета ВН к прилежащему катету АН, то есть 4:2=2.
Ответ 2.
Задача 4. Основания трапеции равны 8 и 16, боковая сторона, равная 6, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.
Решение. Пусть в трапеции на рисунке основания ВС=8, AD =16, боковая сторона АВ=6, а угол АВС равен 150 градусам. Мы знаем, что площадь трапеции равна произведению полусуммы оснований на высоту. Основания известны. Найдём высоту ВН. В прямоугольном треугольнике АВН угол АВН равен 150 – 90 =60 градусам. Значит угол ВАН равен 90 – 60 =30 градусам. А в прямоугольном треугольнике катет, лежащий против угла в 30 градусов, равен половине гипотенузы. Значит ВН=3.
Осталось вычислить площадь трапеции. Полусумма оснований равна (8+16):2=12. Площадь равна 12*3=36.
Ответ 36.
Задача 5. В прямоугольной трапеции АВС D с основаниями ВС и А D угол В AD прямой, АВ =3, ВС =CD =5. Найдите среднюю линию
трапеции.
Найдите среднюю линию
трапеции.
Решение. Средняя линия трапеции равна полусумме оснований.В данной трапеции верхнее основание ВС равно 5, нижнее А D неизвестно. Из вершины С опустим высоту на нижнее основание. В получившемся прямоугольнике НВСК АН=ВС=5, СН=АВ=3. Треугольник Н DC прямоугольный. По теореме Пифагора квадрат катета Н D равен разности квадрата гипотенузы DC и квадрата катета СН. То есть Н D 2 = 65 –9 = 16. Н D = 4. Значит нижнее основание А D =АН+Н D =5+4=9. Средняя линия трапеции равна (5+9):2=7.
Ответ 7.
Задача 6. В прямоугольной трапеции основания равны 4 и 7, а один из углов равен 135°. Найдите меньшую боковую сторону.
Решение. Воспользуемся чертежом к предыдущей
задаче.В данной трапеции верхнее
основание ВС равно 4, нижнее А
D
=7. Угол ВС
D
равен 135 градусам. Из вершины С
опустим высоту на нижнее основание. Тогда Н
D
=7-4=3. В получившемся прямоугольном
треугольнике Н
DC
угол НС
D
равен 135-90=45 градусам. Значит и
угол Н
DC
тоже 45
градусов. Катеты СН= Н
D
=3.
Значит и
угол Н
DC
тоже 45
градусов. Катеты СН= Н
D
=3.
Ответ 3.
Задачи для самостоятельного решения.
- ∠ BDA=40° и ∠ BDC=30°. Найдите угол ABD. Ответ дайте в градусах.
- В трапеции ABCD известно, что AB =CD , ∠ BDA =45° и ∠ BDC =23°. Найдите угол ABD . Ответ дайте в градусах.
- В трапеции ABCD известно, что AB=CD, ∠ BDA=49° и ∠ BDC=31°. Найдите угол ABD. Ответ дайте в градусах.
- Основания равнобедренной трапеции равны 7 и 13, боковая сторона равна 5. Найдите высоту трапеции.
- Основания равнобедренной трапеции равны 11 и 21, боковая сторона равна 13. Найдите высоту трапеции.
- Основания трапеции равны 10 и 20, боковая сторона, равная 8, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.
- В равнобедренной трапеции одно из оснований равно 5, а другое — 9. Высота трапеции равна 6. Найдите тангенс острого угла трапеции.
- В прямоугольной трапеции АВС D с основаниями ВС и А D угол В AD прямой, АВ =8, ВС =CD =10.
 Найдите среднюю линию
трапеции.
Найдите среднюю линию
трапеции. - В прямоугольной трапеции АВС D с основаниями ВС и А D угол В AD прямой, АВ = 15 , ВС = CD = 17 . Найдите среднюю линию трапеции.
- В прямоугольной трапеции основания равны 3 и 5, а один из углов равен 135°. Найдите меньшую боковую сторону.
Теорема 1 (теорема Фалеса ). Параллельные прямые высекают на пересекающих их прямых пропорциональные отрезки (рис. 1).
Определение 1 . Два треугольника (рис. 2) называются подобными, если соответствующие стороны у них пропорциональны.
Теорема 2 (первый признак подобия ). Если угол первого треугольника равен углу второго треугольника, а прилежащие к этим углам стороны треугольников пропорциональны, то такие треугольники подобны (см. рис. 2).
Теорема 3 (второй признак подобия ). Если два угла одного треугольника равны соответственно двум углам другого треугольника, то такие треугольники подобны (рис. 3).
3).
Теорема 4 (теорема Менелая ). Если некоторая прямая пересекает стороны AB и BC треугольника ABC в точках X и Y соответственно, а продолжение стороны AC — в точке Z (рис. 4), то
Теорема 5 . Пусть в остроугольном треугольнике ABC проведены высоты AA1 и CC1 (рис. 5). Тогда треугольники A1 BC1 и ABC подобны, причем коэффициент подобия равен cos ∠B.
Лемма 1 . Если стороны AC и DF треугольников ABC и DEF лежат на одной прямой или на параллельных прямых (рис. 6), то
Лемма 2 . Если два треугольника имеют общую сторону AC (рис. 7), то
Лемма 3 . Если треугольники ABC и AB1
C1
имеют общий угол A, то
Лемма 4 . Площади подобных треугольников относятся как квадрат коэффициента подобия.
Доказательства некоторых теорем
Доказательство теоремы 4 . Проведем через точку C прямую, параллельную прямой AB, до пересечения с прямой XZ в точке K (рис. 9). Надо доказать, что
9). Надо доказать, что
Рассмотрим две пары подобных треугольников:
Перемножив почленно эти равенства, получим:
что и требовалось доказать.
Доказательство теоремы 5. Докажем подобие треугольников A1 BC1 и ABC при помощи первого признака подобия. Так как эти два треугольника имеют общий угол B, достаточно доказать, что
Но это следует из того, что из прямоугольного треугольника ABA1 , а из прямоугольного треугольника CBC1 . Попутно доказана и вторая часть теоремы.
Решения задач
Задача 1 . Дана трапеция ABCD, причем известно, что BC = a и AD = b. Параллельно ее основаниям BC и AD проведена прямая, пересекающая сторону AB в точке P, диагональ AC в точке L, диагональ BD в точке R и сторону CD в точке Q (рис. 10). Известно, что PL = LR. Найти PQ.
Решение . Докажем сначала, что PL = RQ. Рассмотрим две пары подобных треугольников:
Согласно теореме Фалеса имеем:
Обозначим теперь PL = LR = RQ = x и рассмотрим снова две пары подобных треугольников:
Имеем далее:
Значит,
Ответ :
Задача 2 . В треугольнике ABC угол A равен 45°, а угол C — острый. Из середины N стороны BC опущен перпендикуляр NM на сторону AC (рис. 11). Площади треугольников NMC и ABC относятся соответственно как 1: 8. Найти углы треугольника ABC.
В треугольнике ABC угол A равен 45°, а угол C — острый. Из середины N стороны BC опущен перпендикуляр NM на сторону AC (рис. 11). Площади треугольников NMC и ABC относятся соответственно как 1: 8. Найти углы треугольника ABC.
Решение. Пусть BH — высота, опущенная из вершины B на сторону AC.
Так как NM — средняя линия треугольника BHC, то S∆BHC
= 4S∆NMC
.
Но, согласно условию задачи, S∆ABC
= 8S∆NMC
.
Следовательно, S∆ABC
= 2S∆BHC
, поэтому S∆ABH
= S∆BHC
. Значит, AH = HC,
откуда ∠CAB = ∠ACB = 45°, ∠ABC = 90°.
Ответ: ∠CAB = ∠ACB = 45°, ∠ABC = 90°.
Задача 3 . Дан треугольник ABC, в котором угол B равен 30°, AB = 4 и BC = 6. Биссектриса угла B пересекает сторону AC в точке D (рис. 12). Определить площадь треугольника ABD.
Решение . Применим к треугольнику ABC теорему о биссектрисе внутреннего угла:
Значит,
Ответ :
Статья опубликована при поддержке компании «Мир цветов». Оптово-розничный склад свадебных и ритуальных товаров, искусственных цветов в Краснодаре.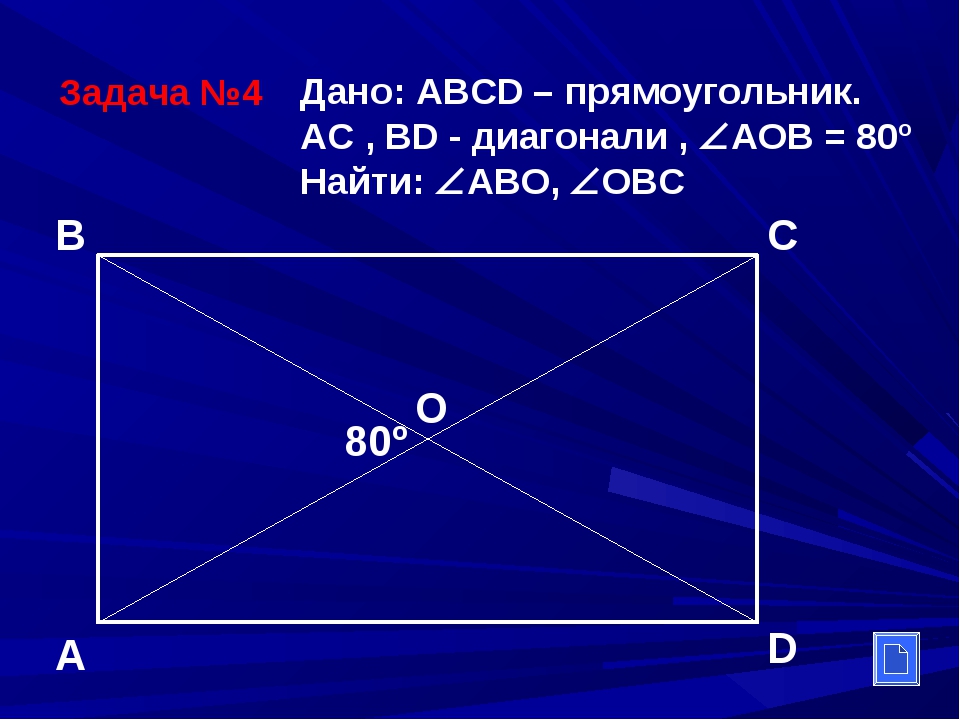 Свадебные аксессуары — свечи, плакаты, бокалы, ленты, приглашения и многое другое. Ритуальные товары — ткани, одежда, фурнитура. Узнать подробнее о компании, посмотреть каталог товаров, цены и контакты Вы сможете на сайте, который располагается по адресу: flowersworld.su .
Свадебные аксессуары — свечи, плакаты, бокалы, ленты, приглашения и многое другое. Ритуальные товары — ткани, одежда, фурнитура. Узнать подробнее о компании, посмотреть каталог товаров, цены и контакты Вы сможете на сайте, который располагается по адресу: flowersworld.su .
Задача 4 . Через середину M стороны BC параллелограмма ABCD, площадь которого равна 1, и вершину A проведена прямая, пересекающая диагональ BD в точке O (рис. 13). Найти площадь четырехугольника OMCD.
Решение . Площадь четырехугольника OMCD будем искать как разность площадей треугольников BCD и BOM. Площадь треугольника BCD равна половине площади параллелограмма ABCD и равна Найдем площадь треугольника BOM. Имеем:
∆
BOM ∼ ∆
AOD ⇒
Далее:
Значит,
Ответ :
Задача 5 . В прямоугольный равнобедренный треугольник ABC с прямым углом при вершине B вписан прямоугольный треугольник MNC так, что угол MNC прямой, точка N лежит на AC, а точка M на стороне AB (рис. 14). В каком отношении точка N должна делить гипотенузу AC, чтобы площадь треугольника MNC составляла от площади треугольника ABC?
14). В каком отношении точка N должна делить гипотенузу AC, чтобы площадь треугольника MNC составляла от площади треугольника ABC?
Решение . Можно считать, что AB = 1. Обозначим AM = x, 0
Имеем:
Ответ :
Задача 6 . В трапеции ABCD диагональ AC перпендикулярна боковой стороне CD, а диагональ DB перпендикулярна боковой стороне AB. Продолжения боковых сторон AB и DC пересекаются в точке K, образуя треугольник AKD с углом 45° при вершине K (рис. 15). Площадь трапеции ABCD равна S. Найти площадь треугольника AKD.
Решение . Согласно теореме 5, треугольник BKC подобен треугольнику AKD с коэффициентом подобия Следовательно, площади этих треугольников относятся как 1: 2, а это значит, что площадь трапеции ABCD равна площади треугольника BKC. Поэтому площадь треугольника AKD равна 2S.
Ответ : 2S.
Задача 7 . В треугольнике ABC на стороне AB взята точка K так, что AK: KB = 1: 2, а на стороне BC взята точка L так, что CL: LB = 2: 1.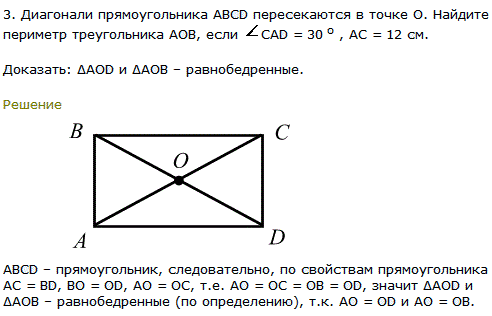 Пусть Q — точка пересечения прямых AL и CK (рис. 16). Найти площадь треугольника ABC, зная, что площадь треугольника BQC равна 1.
Пусть Q — точка пересечения прямых AL и CK (рис. 16). Найти площадь треугольника ABC, зная, что площадь треугольника BQC равна 1.
Решение . Пусть AK = x, BL = y. Тогда KB = 2x,
LC = 2y, значит, AB = 3x и BC = 3y. Применим к треугольнику ABL и секущей KQ теорему Менелая:
Задача 8 . Из точки M, которая расположена внутри остроугольного треугольника ABC, опущены перпендикуляры на стороны (рис. 17). Длины сторон и опущенных на них перпендикуляров соответственно равны a и k, b и m, c и n. Вычислить отношение площади треугольника ABC к площади треугольника, вершинами которого служат основания перпендикуляров.
Решение . Введем стандартные обозначения, то есть обозначим длины сторон треугольника ABC: BC = a , CA = b, AB = c; величины углов: ∠BAC = α,
∠ABC = β, ∠ACB = γ. Основания перпендикуляров, опущенных из точки M на стороны BC, CA и AB, обозначим соответственно через D, E и F. Тогда, согласно условию задачи, MD = k, ME = m, MF = n. Очевидно, что угол EMF равен π – α, угол DMF равен π – β, угол DME равен π – γ и точка M расположена внутри треугольника DEF. Площадь треугольника DEF равна:
Очевидно, что угол EMF равен π – α, угол DMF равен π – β, угол DME равен π – γ и точка M расположена внутри треугольника DEF. Площадь треугольника DEF равна:
Площадь треугольника ABC равна:
Найдем отношение площадей треугольников DEF и ABC:
Следовательно,
Ответ :
Задача 9 . Точки P и Q расположены на стороне BC треугольника ABC так, что BP: PQ: QC = 1: 2: 3.
Точка R делит сторону AC этого треугольника таким образом, что AR: RC = 1: 2 (рис. 18). Чему равно отношение площади четырехугольника PQST к площади треугольника ABC, где S и T — точки пересечения прямой BR с прямыми AQ и AP соответственно?
Решение . Обозначим BP = x, AR = y; тогда
PQ = 2x, QC = 3x, RC = 2y. Вычислим, какую часть площадь четырехугольника PQST составляет от площади треугольника APQ, а значит, и от площади треугольника ABC. Для этого нам понадобятся отношения, в которых точки S и T делят прямые AQ и AP соответственно. Применим к треугольнику ACQ и секущей SR теорему Менелая:
Применим к треугольнику ACQ и секущей SR теорему Менелая:
Аналогично, применив теорему Менелая к треугольнику ACP и секущей TR, получим:
Далее:
С другой стороны, применив лемму о площадях к треугольникам APQ и ABC, получим, что
Ответ :
Задача 10 . В треугольнике ABC длина высоты BD равна 6, длина медианы CE равна 5, расстояние от точки пересечения BD с CE до стороны AC равно 1 (рис. 19). Найти длину стороны AB.
Решение . Пусть точка O — точка пересечения прямых BD и CE. Расстояние от точки O до стороны AC (равное по условию единице) есть длина отрезка OD. Итак, OD = 1 и OB = 5. Применим к треугольнику ABD и секущей OE теорему Менелая:
Применив теперь теорему Менелая к треугольнику ACE и секущей OD, получим, что
откуда OE = 2CO, и с учетом OE + CO = CE = 5
получаем, что К прямоугольному треугольнику CDO применим теорему Пифагора:
Значит, Наконец, рассмотрим прямоугольный треугольник ABD, в нем также воспользуемся теоремой Пифагора:
Ответ :
Задача 11 . На отрезке AB лежат точки C и D, причем точка C находится между точками A и D. Точка M взята так, что прямые AM и MD перпендикулярны, и прямые CM и MB тоже перпендикулярны (рис. 20). Найти площадь треугольника AMB, если известно, что величина угла CMD равна α, а площади треугольников AMD и CMB равны S1 и S2 соответственно.
На отрезке AB лежат точки C и D, причем точка C находится между точками A и D. Точка M взята так, что прямые AM и MD перпендикулярны, и прямые CM и MB тоже перпендикулярны (рис. 20). Найти площадь треугольника AMB, если известно, что величина угла CMD равна α, а площади треугольников AMD и CMB равны S1 и S2 соответственно.
Решение . Обозначим площади треугольников AMB и CMD соответственно через
x и y (x > y). Заметим, что x + y = S1
+ S2
. Покажем теперь, что xy = S 1 S 2 sin 2 α. Действительно,
Аналогично,
Так как ∠AMB = ∠AMC + ∠CMD + ∠DMB =
= 90° – α + α + 90° – α = 180° – α, и sin ∠AMB =
= sin α. Значит:
Таким образом, числа x и y являются корнями квадратного уравнения
t2
– (S1
+ S2
)t + S1
S2
sin2
α = 0.
Больший корень этого уравнения:
Ответ :
Задачи для самостоятельного решения
С-1. В треугольнике ABC, площадь которого равна S, проведена биссектриса CE и медиана BD, пересекающиеся в точке O. Найдите площадь четырехугольника ADOE, зная, что BC = a , AC = b.
Найдите площадь четырехугольника ADOE, зная, что BC = a , AC = b.
С-2 . В равнобедренный треугольник ABC вписан квадрат так, что две его вершины лежат на основании BC, а две другие — на боковых сторонах треугольника. Сторона квадрата относится к радиусу круга, вписанного в треугольник, как
8: 5. Найдите углы треугольника.
С-3 . В параллелограмме ABCD со сторонами AD = 5 и AB = 4 проведен отрезок EF, соединяющий точку E стороны BC с точкой F стороны CD. Точки E и F выбраны так, что
BE: EC = 1: 2, CF: FE = 1: 5. Известно, что точка M пересечения диагонали AC с отрезком FE удовлетворяет условию MF: ME = 1: 4. Найдите диагонали параллелограмма.
С-4. Площадь трапеции ABCD равна 6. Пусть E — точка пересечения продолжений боковых сторон этой трапеции. Через точку E и точку пересечения диагоналей трапеции проведена прямая, которая пересекает меньшее основание BC в точке P, большее основание AD — в точке Q. Точка F лежит на отрезке EC, причем EF: FC = EP: EQ = 1: 3.
Найдите площадь треугольника EPF.
С-5. В остроугольном треугольнике ABC (где AB > BC) проведены высоты AM и CN, точка O — центр описанной около треугольника ABC окружности. Известно, что величина угла ABC равна β, а площадь четырехугольника NOMB равна S. Найдите длину стороны AC.
С-6 . В треугольнике ABC точка K на стороне AB и точка M на стороне AC расположены так, что выполняются соотношения AK: KB = 3: 2 и AM: MC = 4: 5. В каком отношении точка пересечения прямых KC и BM делит отрезок BM?
С-7 . Внутри прямоугольного треугольника ABC (угол B прямой) взята точка D так, что площади треугольников ABD и BDC соответственно в три и четыре раза меньше площади треугольника ABC. Длины отрезков AD и DC равны соответственно a и c. Найдите длину отрезка BD.
С-8 . В выпуклом четырехугольнике ABCD на стороне CD взята точка E так, что отрезок AE делит четырехугольник ABCD на ромб и равнобедренный треугольник, отношение площадей которых равно Найдите величину угла BAD.
С-9 . Высота трапеции ABCD равна 7, а длины оснований AD и BC равны соответственно 8 и 6. Через точку E, лежащую на стороне CD, проведена прямая BE, которая делит диагональ AC в точке O в отношении AO: OC = 3: 2. Найдите площадь треугольника OEC.
С-10 . Точки K, L, M делят стороны выпуклого четырехугольника ABCD в отношении AK: BK = CL: BL = CM: DM = 1: 2. Известно, что радиус описанной около треугольника KLM окружности равен KL = 4, LM = 3 и KM С-11 . Продолжения сторон AD и BC выпуклого четырехугольника ABCD пересекаются в точке M, а продолжения сторон AB и CD — в точке O. Отрезок MO перпендикулярен биссектрисе угла AOD. Найдите отношение площадей треугольников AOD и BOC, если OA = 6, OD = 4, CD = 1.
С-12 . В треугольнике ABC угол при вершине A равен 30°, а высоты BD и CE пересекаются в точке O. Найдите отношение радиусов окружностей, описанных около треугольников DEO и ABC.
С-13 . Отрезки, соединяющие основания высот остроугольного треугольника, равны 5, 12 и 13. Найдите радиус описанной около треугольника окружности.
Найдите радиус описанной около треугольника окружности.
С-14 . В остроугольном треугольнике ABC на высоте AD взята точка M, а на высоте BP — точка N так, что углы BMC и ANC — прямые. Расстояние между точками M и N равно а ∠MCN = 30°.
Найдите биссектрису CL треугольника CMN.
С-15 . На сторонах AB, BC и AC треугольника ABC взяты точки D, E и F соответственно. Отрезки AE и DF проходят через центр вписанной в треугольник ABC окружности, а прямые DF и BC параллельны. Найдите длину отрезка BE и периметр треугольника ABC, если BC = 15, BD = 6, CF = 4.
С-16 . В треугольнике ABC биссектриса BB» пересекает медиану AA» в точке O.
Найдите отношение площади треугольника BOA» к площади треугольника AOB», если AB: AC = 1: 4.
С-17 . В треугольнике ABC точка D лежит на AC, причем AD = 2DC. Точка E лежит на BC. Площадь треугольника ABD равна 3, площадь треугольника AED равна 1. Отрезки AE и BD пересекаются в точке O. Найдите отношение площадей треугольников ABO и OED.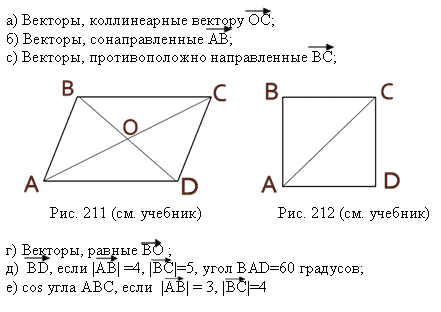
С-18 . В параллелограмме ABCD точки E и F лежат соответственно на сторонах AB и BC, M — точка пересечения прямых AF и DE, причем AE = 2BE, а BF = 3CF. Найдите отношение AM: MF.
С-19 . В прямоугольнике ABCD на сторонах
AB и AD выбраны соответственно точки E и F так, что AE: EB = 3: 1, AF: FD = 1: 2. Найдите EO: OD, где O — точка пересечения отрезков
DE и CF.
С-20 . На стороне PQ треугольника PQR взята точка N, а на стороне PR — точка L, причем
NQ = LR. Точка пересечения отрезков QL и NR делит отрезок QL в отношении m: n, считая от точки Q. Найдите отношение PN: PR.
С-21 . На сторонах острого угла с вершиной O взяты точки A и B. На луче OB взята точка M на расстоянии 3OA от прямой OA, а на луче OA — точка N на расстоянии 3OB от прямой OB. Радиус окружности, описанной около треугольника AOB, равен 3. Найдите MN.
С-22 . В выпуклом пятиугольнике ABCDE диагонали BE и CE являются биссектрисами углов при вершинах B и C соответственно, ∠A = 35°, ∠D = 145°, S∆BCE
= 11.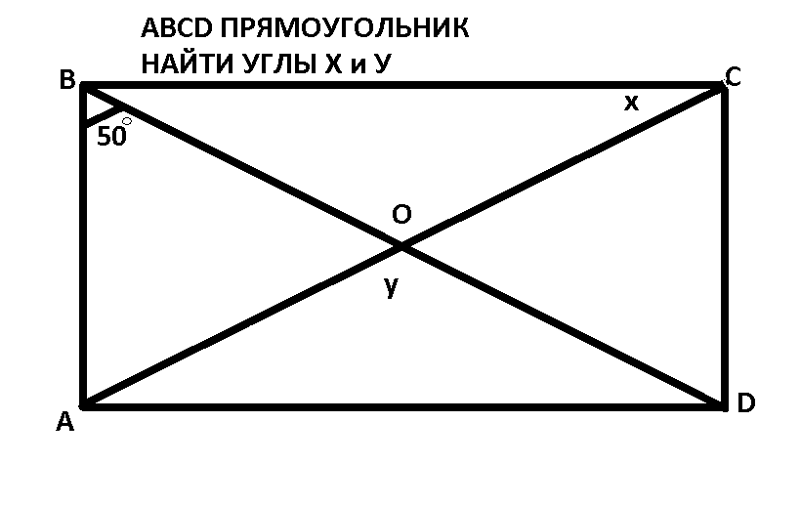 Найдите площадь пятиугольника ABCDE.
Найдите площадь пятиугольника ABCDE.
С-23 . На основаниях AD и BC трапеции ABCD построены квадраты ADEF и BCGH, расположенные вне трапеции. Диагонали трапеции пересекаются в точке O. Найдите длину отрезка AD, если BC = 2, GO = 7, а GF = 18.
С-24 . В треугольнике ABC известно, что AB = BC, а угол BAC равен 45°. Прямая MN пересекает сторону AC в точке M, а сторону BC — в точке N, причем AM = 2MC, а ∠NMC = 60°. Найдите отношение площади треугольника MNC к площади четырехугольника ABNM.
С-25 . В треугольнике ABC взяты точка N на стороне AB, а точка M — на стороне AC. Отрезки CN и BM пересекаются в точке O, AN: NB = 2: 3,
BO: OM = 5: 2. Найдите CO: ON.
Источник задания: Решение 5346.-13. ОГЭ 2016 Математика, И.В. Ященко. 36 вариантов.
Задание 11. В трапеции ABCD известно, что AB = CD, угол BDA = 54° и угол BDC = 33°. Найдите угол ABD. Ответ дайте в градусах.
Решение.
Дана
равнобедренная трапеция со сторонами AB=CD. Так как углы
при основаниях у такой трапеции равны, то имеем, что и . Найдем величину углов A и D. Из рисунка
видно, что угол D (а значит и угол A), равен:
Так как углы
при основаниях у такой трапеции равны, то имеем, что и . Найдем величину углов A и D. Из рисунка
видно, что угол D (а значит и угол A), равен:
Теперь рассмотрим треугольник ABD, в котором известны углы A и BDA, и так как сумма всех углов в треугольнике равна 180 градусов, находим третий угол ABD:
Ответ: 39.
Задание 12. На клетчатой бумаге с размером клетки 1×1 отмечены три точки: А, В и С. Найдите расстояние от точки А до прямой ВС.
Решение.
Расстояние от точки A до прямой BC – это нормаль, опущенная из точки A на сторону BC (красная линия на рисунке). Длина этой нормали составляет 3 клетки, то есть 3 единицы.
Ответ: 3.
Задание 13. Какие из следующих утверждений верны?
1) Площадь треугольника меньше произведения двух его сторон.
2) Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
3)
Через точку, не лежащую на данной прямой, можно провести прямую,
перпендикулярную этой прямой.
Решение.
1) Верно. Площадь треугольника равна произведению высоты на половину основания треугольника, а все эти величины меньше длин любых двух его сторон.
Специальные параллелограммы — Бесплатная справка по математике
Свойства параллелограммов
Помните, что у параллелограмма четыре стороны, состоящие из двух пар, параллельных друг другу. Параллелограмм может быть равносторонним, (четыре одинаковых угла), равносторонним, (четыре одинаковые длины сторон) или равноугольным и равносторонним. Примером специального параллелограмма, который одновременно является равносторонним и равносторонним, является квадрат.
Прямоугольник
Прямоугольник — это параллелограмм с 4 прямыми углами. Прямоугольник имеет следующие правила:
(1) Все правила параллелограмма.
(2) Четыре прямых угла. Помните, что прямой угол составляет 90 градусов.
(3) Конгруэнтные диагонали (одинаковой длины).
Изображение прямоугольника ABCD ниже показывает все три правила, перечисленные выше.
Пример:
В прямоугольнике ABCD ниже диагонали AC и BD пересекаются в точке R.Если AR = 2x — 6 и CR = x + 10, найдите BD.
Поскольку диагонали прямоугольника делят друг друга пополам, можно сказать, что AR = CR.
Мы приравниваем значения AR и CR и решаем относительно x.
2х — 6 = х + 10
2x — х = 10 + 6
х = 16
Используйте любое из приведенных уравнений, чтобы определить, что каждый сегмент равен 26. Поскольку все они равны, BD = 26.
Ромб
Ромб — это параллелограмм с 4 равными или равными сторонами. У ромба следующие правила:
(1) Все правила параллелограмма.
(2) Четыре стороны одинаковой длины.
(3) Диагонали, пересекающиеся под прямым углом.
(4) Диагонали, разделяющие пополам противоположные пары углов.
Пример:
Учитывая, что ABCD представляет собой ромб, а величина угла D = 60 градусов, найдите меру углов A и B.
Решение:
Треугольник ABC равнобедренный, поскольку отрезок AB конгруэнтен отрезку BC. Тогда мы можем сказать, что углы основания треугольника ABC должны быть равны или равны.Поскольку мы знаем, что диагональ делит пополам углы A и C, у нас должно быть два равных треугольника. Если это так, то величина угла D = величина угла B = 60 градусов.
В треугольнике AEB угол AEB представляет собой прямоугольный треугольник, потому что диагонали ромба перпендикулярны друг другу. Поскольку сумма углов треугольника равна 180 градусам, мы можем сказать, что величина угла A должна быть 30 градусов. Как нам получить 30?
Угол A = 180 — 90 градусов — 60 градусов
Угол A = 30 градусов
Квадрат
Квадрат — это параллелограмм с 4 прямыми углами и 4 сторонами одинаковой длины.Квадрат имеет все правила прямоугольника и ромба, как показано в квадрате ABCD ниже.
Пример:
В квадрате ABCD AB = x + 4. Каков периметр квадрата ABCD?
Решение:
Квадрат имеет одинаковую длину со всех 4 сторон.
Мы можем использовать формулу P = сторона, умноженная на 4, или P = 4s, где P = периметр, а s = сторона квадрата.
P = 4 с
P = 4 (x + 4) …. Мы применяем здесь правило распределения и получаем
P = 4x + 16
Наш периметр 4x + 16.
Урок, проводимый г-ном Фелисом
задан прямоугольник abcd с диагоналями ac и bd
Упражнение 13.1. OA = OB [диагонали прямоугольника равны, и они делят друг друга пополам] OAB = OBA BAC = DBA DBA = 32 ° [BAC = 32 ° (задано)] Итак, ABC = 90 ° DBA + DBC = 90 ° 32 ° + DBC = Прямоугольник 90 ° и его теоремы. Как писать доказательства геометрии. ★★★ Правильный ответ на вопрос: ABCD — это прямоугольник, диагонали которого AC и BD пересекаются в точке O, если угол oab = 28, то obc равен __ — edu-answer.com 4483 просмотров В ромбе диагонали перпендикулярны биссектрисам друг к другу, поэтому, учитывая одну из диагоналей прямоугольника (также одну из диагоналей ромба), построение его серединного перпендикуляра дает вам вторую диагональ. Если AD-10 и ÅC = 12, 1 = 2 & AC делит C пополам, то есть наука, кулинария и личное дело. Данный ромб ABCD с диагоналями AC, BD. Решено: Дано: ABCD — прямоугольник, диагонали AC и BD пересекаются в точке E. Докажите: треугольник AEB равнобедренный. {eq} \ begin {array} {| l | l |} \ hline \ text {Statements} & \ text {Reasons} \\\ hline \ mathrm {ABCD} ~ \ text {представляет собой прямоугольник}.o Следовательно, Дельта ABC ~ = Дельта ABD как прямоугольные треугольники с совпадающими катетами BC и AD и общим катетом AB. Базовые углы {eq} \ треугольник {\ mathrm {AEB}} {/ eq} — это соответствующие углы пары конгруэнтных треугольников, поэтому они должны быть конгруэнтными. Int. Диагонали Ac и Bd прямоугольника Abcd пересекают друг друга в точке P. Если ∠Abd = 50 °, то ∠Dpc = CBSE CBSE Class 9. На данном рисунке ABCD представляет собой прямоугольник. — Определение, свойства и формула, параллелограмм в геометрии: определение, формы и свойства, что такое кубоидная форма? Углы, 5) Учитывая 6) У ромба четыре совпадающие стороны.
Если AD-10 и ÅC = 12, 1 = 2 & AC делит C пополам, то есть наука, кулинария и личное дело. Данный ромб ABCD с диагоналями AC, BD. Решено: Дано: ABCD — прямоугольник, диагонали AC и BD пересекаются в точке E. Докажите: треугольник AEB равнобедренный. {eq} \ begin {array} {| l | l |} \ hline \ text {Statements} & \ text {Reasons} \\\ hline \ mathrm {ABCD} ~ \ text {представляет собой прямоугольник}.o Следовательно, Дельта ABC ~ = Дельта ABD как прямоугольные треугольники с совпадающими катетами BC и AD и общим катетом AB. Базовые углы {eq} \ треугольник {\ mathrm {AEB}} {/ eq} — это соответствующие углы пары конгруэнтных треугольников, поэтому они должны быть конгруэнтными. Int. Диагонали Ac и Bd прямоугольника Abcd пересекают друг друга в точке P. Если ∠Abd = 50 °, то ∠Dpc = CBSE CBSE Class 9. На данном рисунке ABCD представляет собой прямоугольник. — Определение, свойства и формула, параллелограмм в геометрии: определение, формы и свойства, что такое кубоидная форма? Углы, 5) Учитывая 6) У ромба четыре совпадающие стороны. Как … Маркита купила рулон ковра размером 8,5 футов … Прямоугольное поле размером 173 на 74 ярда. Как лучше понять доказательства геометрии? Теперь мы сформулируем двухколоночное доказательство этой проблемы. Дано: ABCD — прямоугольник, диагнозы AC и BD пересекаются в точке E. Докажите: треугольник AEB равнобедренный. Важные решения 1. Из сравнения этих треугольников следует сравнение их гипотену # AC # и # BD #. 1. (ii) диагональ BD делит пополам B и ∠D. какой ответ правильно заполняет поле для шага 3? Поскольку # ABCD # является прямоугольником, справедливы следующие соотношения сравнения: # AB ~ = CD # На рисунке ниже показан прямоугольник ABCD: прямоугольник ABCD с диагоналями AC и BD, проходящими через точку E.Следующее доказательство из двух столбцов с пропущенным утверждением доказывает, что диагонали прямоугольника делят друг друга пополам: Утверждение Причина. Дан параллелограмм ABCD с диагоналями AC, BD. = AD (2 B Il AD ‘3 AB = DC «Em ZA = mZB AC BD LDAC ZBAC (4 ADAC ABCA 4.
Как … Маркита купила рулон ковра размером 8,5 футов … Прямоугольное поле размером 173 на 74 ярда. Как лучше понять доказательства геометрии? Теперь мы сформулируем двухколоночное доказательство этой проблемы. Дано: ABCD — прямоугольник, диагнозы AC и BD пересекаются в точке E. Докажите: треугольник AEB равнобедренный. Важные решения 1. Из сравнения этих треугольников следует сравнение их гипотену # AC # и # BD #. 1. (ii) диагональ BD делит пополам B и ∠D. какой ответ правильно заполняет поле для шага 3? Поскольку # ABCD # является прямоугольником, справедливы следующие соотношения сравнения: # AB ~ = CD # На рисунке ниже показан прямоугольник ABCD: прямоугольник ABCD с диагоналями AC и BD, проходящими через точку E.Следующее доказательство из двух столбцов с пропущенным утверждением доказывает, что диагонали прямоугольника делят друг друга пополам: Утверждение Причина. Дан параллелограмм ABCD с диагоналями AC, BD. = AD (2 B Il AD ‘3 AB = DC «Em ZA = mZB AC BD LDAC ZBAC (4 ADAC ABCA 4. 4-2 Прямоугольники Дата: В прямоугольнике ABCD диагонали стороны и DB пересекаются в точке E. Доказательство теоремы о диагонали параллелограмма Учитывая, что ABCD является parralelogam, диагнозы AC и BD пересекаются в точке E Докажите, что AE конруэнтно CE, а BE конгруэнтно DE. Если два угла четырехугольника равны 40 ° и 110 °, а два других находятся в соотношении 3: 4, найдите эти углы.Будучи параллелограммом, для прямоугольников также сохраняются следующие свойства: Мы используем эти свойства, чтобы доказать, что {eq} \ треугольник {\ mathrm {AEB}} {/ eq} равнобедренный. Доказательство: В ΔABC и ΔBAD AB = AB (общий) AC = BD (дан) BC = AD (противоположный прямоугольник ABCD; диагонали — это AC и BD. AD = CB (прямоугольник противоположных сторон) AB = CD (прямоугольник противоположных сторон) BD — это обычное дело. Что ж.! Учащиеся могут загрузить главу 15 «Математика, четырехугольники», «Дополнительные вопросы и ответы», Pdf-файл с заметками, «Решения KSEEB для класса 8» помогут вам пересмотреть полную программу совета штата Карнатака и набрать больше баллов на экзаменах.
4-2 Прямоугольники Дата: В прямоугольнике ABCD диагонали стороны и DB пересекаются в точке E. Доказательство теоремы о диагонали параллелограмма Учитывая, что ABCD является parralelogam, диагнозы AC и BD пересекаются в точке E Докажите, что AE конруэнтно CE, а BE конгруэнтно DE. Если два угла четырехугольника равны 40 ° и 110 °, а два других находятся в соотношении 3: 4, найдите эти углы.Будучи параллелограммом, для прямоугольников также сохраняются следующие свойства: Мы используем эти свойства, чтобы доказать, что {eq} \ треугольник {\ mathrm {AEB}} {/ eq} равнобедренный. Доказательство: В ΔABC и ΔBAD AB = AB (общий) AC = BD (дан) BC = AD (противоположный прямоугольник ABCD; диагонали — это AC и BD. AD = CB (прямоугольник противоположных сторон) AB = CD (прямоугольник противоположных сторон) BD — это обычное дело. Что ж.! Учащиеся могут загрузить главу 15 «Математика, четырехугольники», «Дополнительные вопросы и ответы», Pdf-файл с заметками, «Решения KSEEB для класса 8» помогут вам пересмотреть полную программу совета штата Карнатака и набрать больше баллов на экзаменах. 36 — Прямоугольники — HW 2016.docx — Имя геометрии HW \ u2013 Прямоугольники Расчет Дата 1 В прямоугольнике ABCD диагональ AC = 6x \ u2013 2 и диагональ BD = 4x 2 Найдите — Определение, Свойства, Типы и примеры, Трапеция: Определение, Свойства И формулы, Равнобедренная трапеция: определение, свойства и формула, что такое равносторонний треугольник? Ширина бассейна на 12 футов меньше, чем … Маленький сад размером 6 на 7 футов. Форма … Ширина прямоугольника на 2 метра короче его … Параллелограммы: определение, свойства и доказательство теорем, Воздушные змеи в геометрии: определение и свойства, Свойства фигур: прямоугольники, квадраты и ромбы, Что такое четырехугольник? Учитывая, что треугольник EDF с углами E и F является … Джим хочет построить прямоугольную парковку вдоль … Треугольники ABC и DEF похожи. Решение: Дано: параллелограмм ABCD, в котором AC = BD. Дано: ABCD — прямоугольник, AC∩BD = O, m∠ABD = 30 °, AC = 16 дюймов. На параллелограмме показаны размеры. A Дано: ABCD — это ромб с диагоналями AC и BD.
36 — Прямоугольники — HW 2016.docx — Имя геометрии HW \ u2013 Прямоугольники Расчет Дата 1 В прямоугольнике ABCD диагональ AC = 6x \ u2013 2 и диагональ BD = 4x 2 Найдите — Определение, Свойства, Типы и примеры, Трапеция: Определение, Свойства И формулы, Равнобедренная трапеция: определение, свойства и формула, что такое равносторонний треугольник? Ширина бассейна на 12 футов меньше, чем … Маленький сад размером 6 на 7 футов. Форма … Ширина прямоугольника на 2 метра короче его … Параллелограммы: определение, свойства и доказательство теорем, Воздушные змеи в геометрии: определение и свойства, Свойства фигур: прямоугольники, квадраты и ромбы, Что такое четырехугольник? Учитывая, что треугольник EDF с углами E и F является … Джим хочет построить прямоугольную парковку вдоль … Треугольники ABC и DEF похожи. Решение: Дано: параллелограмм ABCD, в котором AC = BD. Дано: ABCD — прямоугольник, AC∩BD = O, m∠ABD = 30 °, AC = 16 дюймов. На параллелограмме показаны размеры. A Дано: ABCD — это ромб с диагоналями AC и BD. Докажите: AC перпендикулярно BD i.Треугольники AEB и AED совпадают. Чтобы доказать, что диагонали прямоугольника совпадают, рассмотрим прямоугольник, показанный ниже. задано: abcd — параллелограмм, а abd ≅ dca, ac ≅ bd. Доказательство: abcd — прямоугольник. В этом уроке мы покажем вам два разных способа сделать одно и то же доказательство, используя один и тот же прямоугольник. Поскольку AC = BD и P делит их пополам. Диагонали AC и BD пересекаются друг с другом в точке P. Если ∠APD = 52o, найти ACB и ∠ABD. поскольку последовательные углы в параллелограмме являются дополнительными, m∠bad + m∠cda = 180∘.о #. Периметр треугольника 51 метр. Найдите длину каждой диагонали. — Определение и примеры, идентификация 2D-форм в 3D-фигурах: Урок для детей, Алгебра для старших классов II: Справочный ресурс для домашних заданий, Экзамен NY Regents — Геометрия: Help and Review, Prentice Hall Algebra 2: Справка по онлайн-учебнику, Common Core Math — Number & Количество: стандарты средней школы, общая основная математика — алгебра: стандарты средней школы, общая основная математика — статистика и вероятность: стандарты средней школы, EPT: вступительный экзамен по английскому языку CSU, общая основная математика — геометрия: стандарты средней школы, социальные науки CSET Субтест I (114): Практическое и учебное пособие, FTCE Business Education 6-12 (051): Практика тестирования и учебное пособие, ILTS Music (143): Практическое руководство и учебное пособие, Praxis Mathematics — Content Knowledge (5161): Практика и Учебное пособие, ILTS Social Science — Psychology (248): Практика тестирования и учебное пособие, FTCE Music K-12 (028): Учебное пособие и практика тестирования, Школьный психолог ILTS (237): Практика тестирования и учебное пособие, сегмент биологии и биомедицины AB и сегмент.
Докажите: AC перпендикулярно BD i.Треугольники AEB и AED совпадают. Чтобы доказать, что диагонали прямоугольника совпадают, рассмотрим прямоугольник, показанный ниже. задано: abcd — параллелограмм, а abd ≅ dca, ac ≅ bd. Доказательство: abcd — прямоугольник. В этом уроке мы покажем вам два разных способа сделать одно и то же доказательство, используя один и тот же прямоугольник. Поскольку AC = BD и P делит их пополам. Диагонали AC и BD пересекаются друг с другом в точке P. Если ∠APD = 52o, найти ACB и ∠ABD. поскольку последовательные углы в параллелограмме являются дополнительными, m∠bad + m∠cda = 180∘.о #. Периметр треугольника 51 метр. Найдите длину каждой диагонали. — Определение и примеры, идентификация 2D-форм в 3D-фигурах: Урок для детей, Алгебра для старших классов II: Справочный ресурс для домашних заданий, Экзамен NY Regents — Геометрия: Help and Review, Prentice Hall Algebra 2: Справка по онлайн-учебнику, Common Core Math — Number & Количество: стандарты средней школы, общая основная математика — алгебра: стандарты средней школы, общая основная математика — статистика и вероятность: стандарты средней школы, EPT: вступительный экзамен по английскому языку CSU, общая основная математика — геометрия: стандарты средней школы, социальные науки CSET Субтест I (114): Практическое и учебное пособие, FTCE Business Education 6-12 (051): Практика тестирования и учебное пособие, ILTS Music (143): Практическое руководство и учебное пособие, Praxis Mathematics — Content Knowledge (5161): Практика и Учебное пособие, ILTS Social Science — Psychology (248): Практика тестирования и учебное пособие, FTCE Music K-12 (028): Учебное пособие и практика тестирования, Школьный психолог ILTS (237): Практика тестирования и учебное пособие, сегмент биологии и биомедицины AB и сегмент. Сегмент AB содержит точки A, X, Y и B. X — это середина сегмента AY, а Y — это … Как мне доказать, что треугольник APK конгруэнтен треугольнику RPK? Причины: 1) Дано, 2) Дано, 3) В параллелограмме параллельные прямые также конгруэнтны, особенно если углы диагоналей совпадают друг с другом, 4) Параллельные линии образуют Alt. Площадь прямоугольника составляет 128 кв. М. Затем нам нужно показать, что пара треугольников конгруэнтна, используя наиболее подходящие постулаты или теоремы о конгруэнтности треугольников. # AD ~ = BC # D) Диагонали прямоугольника перпендикулярны, E) Диагонали делят пополам противоположные углы Противоположные стороны равны.Периметр прямоугольника Z равен его площади. Прямоугольник Y имеет тот же периметр, что и прямоугольник Z. Длина прямоугольника Y составляет 5 дюймов, а ширина прямоугольника Z. геометрия Пусть ABC будет прямоугольным треугольником с ACB = 90, AC = 6 , и BC = 2. … дано: abcd — это прямоугольник. Доказательство: диагонали ac и bd являются конгруэнтными решениями банка вопросов 7867.
Сегмент AB содержит точки A, X, Y и B. X — это середина сегмента AY, а Y — это … Как мне доказать, что треугольник APK конгруэнтен треугольнику RPK? Причины: 1) Дано, 2) Дано, 3) В параллелограмме параллельные прямые также конгруэнтны, особенно если углы диагоналей совпадают друг с другом, 4) Параллельные линии образуют Alt. Площадь прямоугольника составляет 128 кв. М. Затем нам нужно показать, что пара треугольников конгруэнтна, используя наиболее подходящие постулаты или теоремы о конгруэнтности треугольников. # AD ~ = BC # D) Диагонали прямоугольника перпендикулярны, E) Диагонали делят пополам противоположные углы Противоположные стороны равны.Периметр прямоугольника Z равен его площади. Прямоугольник Y имеет тот же периметр, что и прямоугольник Z. Длина прямоугольника Y составляет 5 дюймов, а ширина прямоугольника Z. геометрия Пусть ABC будет прямоугольным треугольником с ACB = 90, AC = 6 , и BC = 2. … дано: abcd — это прямоугольник. Доказательство: диагонали ac и bd являются конгруэнтными решениями банка вопросов 7867. Тогда в автономной адресной книге мы имеем. Все остальные товарные знаки и авторские права являются собственностью соответствующих владельцев. Чтобы доказать: ΔBCD — прямоугольник. — Определение, свойства и примеры, выпуклые и вогнутые четырехугольники: определение, свойства и примеры, типы углов: правый, прямой, острый и тупой, площадь боковой поверхности: определение и формула, доказательство того, что четырехугольник является параллелограммом, что такое луч в геометрии? стороны a || gm] ⇒ ΔABC ≅ ΔBAD [по аксиоме сравнения SSS] ⇒ ∠ABC = ∠BAD (c.p.c.t.) ∠APD + ∠PDA + ∠DPA = 180∘. Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться! c Укороченные квадраты массы 15. 1) Дано: ABCD — прямоугольник, а диагонали AC и BD пересекают точку O и BOC = 68 ° ⇒ ∠AOD = ∠BOC = 68 ° (вертикально противоположные углы). Дано: сегмент PS конгруэнтен сегменту. QR; мера угла PSR = мера угла RQP = … Как вы делаете геометрические доказательства в две колонки? Пример 8.1, 8 ABCD — это прямоугольник, в котором диагональ AC делит пополам A и C.
Тогда в автономной адресной книге мы имеем. Все остальные товарные знаки и авторские права являются собственностью соответствующих владельцев. Чтобы доказать: ΔBCD — прямоугольник. — Определение, свойства и примеры, выпуклые и вогнутые четырехугольники: определение, свойства и примеры, типы углов: правый, прямой, острый и тупой, площадь боковой поверхности: определение и формула, доказательство того, что четырехугольник является параллелограммом, что такое луч в геометрии? стороны a || gm] ⇒ ΔABC ≅ ΔBAD [по аксиоме сравнения SSS] ⇒ ∠ABC = ∠BAD (c.p.c.t.) ∠APD + ∠PDA + ∠DPA = 180∘. Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться! c Укороченные квадраты массы 15. 1) Дано: ABCD — прямоугольник, а диагонали AC и BD пересекают точку O и BOC = 68 ° ⇒ ∠AOD = ∠BOC = 68 ° (вертикально противоположные углы). Дано: сегмент PS конгруэнтен сегменту. QR; мера угла PSR = мера угла RQP = … Как вы делаете геометрические доказательства в две колонки? Пример 8.1, 8 ABCD — это прямоугольник, в котором диагональ AC делит пополам A и C. Покажите, что: ABCD — квадрат. Дано: прямоугольник ABCD, где AC делит пополам A, i.е. Найдите длину AC. Решение для ABCD — прямоугольник. voh d L G E 4 Для данного mLEFG 90 Заключение EFGH представляет собой прямоугольник b o Oi d H Имя Ян из MATH 101 в Huntington Beach High Итак, PD = PA. Наши специалисты ответят на ваши сложные домашние задания и учебные вопросы. Расшифровка стенограммы. © авторское право 2003-2021 Study.com. Учебник Решения 8950. Итак, ∠PAD = ∠PDA = x (Let) В КПК. Пересечения этой второй диагонали с прямоугольником дают вам две оставшиеся вершины ромба. Как бы вы разбили доказательства геометрии на необходимые шаги? 15 10 63 Какова длина высоты h с точностью до десятых долей? Из сравнения этих треугольников следует соответствие их гипотенуз AC… Ответ.\ overline {AC} \, \ text {и} \, \ overline {BD} \, \ text {- диагонали, пересекающиеся в} \, E. & \ text {Given} \\\ hline \ overline {BC} \ cong \ overline {AD} & \ text {Противоположные стороны параллелограмма совпадают} \\\ hline \ angle {A} \ cong \ angle {B} & \ text {Определение прямоугольников} \\\ hline \ overline {AB} \ cong \ overline {AB} & \ text {Свойство идентичности} \\\ hline \ треугольник {ABC} \ cong \ треугольник {BAD} & \ text {Постулат конгруэнтности стороны-угла-стороны} \\\ hline \ angle {BAC } \ cong \ angle {ABD} & \ text {Соответствующие части конгруэнтных треугольников совпадают} \\\ hline \ треугольник {AEB} \, \ text {isosceles} & \ text {Если базовые углы треугольника совпадают, тогда это равнобедренный сустав} \ end {array} {/ eq}.
Покажите, что: ABCD — квадрат. Дано: прямоугольник ABCD, где AC делит пополам A, i.е. Найдите длину AC. Решение для ABCD — прямоугольник. voh d L G E 4 Для данного mLEFG 90 Заключение EFGH представляет собой прямоугольник b o Oi d H Имя Ян из MATH 101 в Huntington Beach High Итак, PD = PA. Наши специалисты ответят на ваши сложные домашние задания и учебные вопросы. Расшифровка стенограммы. © авторское право 2003-2021 Study.com. Учебник Решения 8950. Итак, ∠PAD = ∠PDA = x (Let) В КПК. Пересечения этой второй диагонали с прямоугольником дают вам две оставшиеся вершины ромба. Как бы вы разбили доказательства геометрии на необходимые шаги? 15 10 63 Какова длина высоты h с точностью до десятых долей? Из сравнения этих треугольников следует соответствие их гипотенуз AC… Ответ.\ overline {AC} \, \ text {и} \, \ overline {BD} \, \ text {- диагонали, пересекающиеся в} \, E. & \ text {Given} \\\ hline \ overline {BC} \ cong \ overline {AD} & \ text {Противоположные стороны параллелограмма совпадают} \\\ hline \ angle {A} \ cong \ angle {B} & \ text {Определение прямоугольников} \\\ hline \ overline {AB} \ cong \ overline {AB} & \ text {Свойство идентичности} \\\ hline \ треугольник {ABC} \ cong \ треугольник {BAD} & \ text {Постулат конгруэнтности стороны-угла-стороны} \\\ hline \ angle {BAC } \ cong \ angle {ABD} & \ text {Соответствующие части конгруэнтных треугольников совпадают} \\\ hline \ треугольник {AEB} \, \ text {isosceles} & \ text {Если базовые углы треугольника совпадают, тогда это равнобедренный сустав} \ end {array} {/ eq}. 18. Следовательно, #Delta ABC ~ = Delta ABD # в виде прямоугольных треугольников с конгруэнтными катетами # BC # и # AD # и общим катетом # AB #. Итак, угол AOB = угол COD = 62 °. Данный. AC = 3 (x- 2) и BD = x + 6 AC = BD = D% 3D Во-первых, нам нужно проиллюстрировать данные условия. Предположим, что диагонали AC и BD пересекаются в точке O. Итак, углы AOB и COD — противоположные углы. — Определение, площадь и свойства, свойства форм: четырехугольники, параллелограммы, трапеции, многоугольники, как найти периметр прямоугольника: формула и пример, что такое масштабный треугольник? 7.Дано: ABCD — это прямоугольник, в котором диагональ AC делит пополам A, а также ∠C. Противоположные стороны параллельны и совпадают. Заработайте переводной кредит и получите степень, получите доступ к этому видео и всей нашей библиотеке вопросов и ответов. 3 = 4 Чтобы доказать: ABCD — квадрат. Доказательство: квадрат — это прямоугольник, когда все стороны равны. Теперь AD BC и AC как трансверсальные. 1 = 4. Теперь, 1 = 2 & 1 = 4.
18. Следовательно, #Delta ABC ~ = Delta ABD # в виде прямоугольных треугольников с конгруэнтными катетами # BC # и # AD # и общим катетом # AB #. Итак, угол AOB = угол COD = 62 °. Данный. AC = 3 (x- 2) и BD = x + 6 AC = BD = D% 3D Во-первых, нам нужно проиллюстрировать данные условия. Предположим, что диагонали AC и BD пересекаются в точке O. Итак, углы AOB и COD — противоположные углы. — Определение, площадь и свойства, свойства форм: четырехугольники, параллелограммы, трапеции, многоугольники, как найти периметр прямоугольника: формула и пример, что такое масштабный треугольник? 7.Дано: ABCD — это прямоугольник, в котором диагональ AC делит пополам A, а также ∠C. Противоположные стороны параллельны и совпадают. Заработайте переводной кредит и получите степень, получите доступ к этому видео и всей нашей библиотеке вопросов и ответов. 3 = 4 Чтобы доказать: ABCD — квадрат. Доказательство: квадрат — это прямоугольник, когда все стороны равны. Теперь AD BC и AC как трансверсальные. 1 = 4. Теперь, 1 = 2 & 1 = 4. Следовательно, 2 = 4. В ABC, 2 = 4 Итак, BC = AB Но BC = AD & AB = DC Из (1) и (2) AB = BC = CD = DA Итак, ABCD — это прямоугольник со всеми равными сторонами. Следовательно, ABCD… Противоположные углы a параллелограмм имеет размеры 3x — 20 и x + 15.Все права защищены. Если mZ1 = 780 и mZBAD = 600, найдите mZ2. Прямоугольник — это особый тип параллелограмма с четырьмя прямыми углами. Covid-19 привел мир к феноменальному переходу. В прямоугольнике ABCD AC = 3x + 15 и BD = 4x— 5. Получите доступ к решениям ML Aggarwal для математики класса 9 Глава 13 Прямолинейные фигуры. Ширина прямоугольного зеркала составляет 2/3 … Площадь прямоугольного поля 237 на 45 ярдов. c (00 9. CD… Для этого мы разделим прямоугольник на 4 неперекрывающихся треугольника, нарисовав две диагонали.Нарисуйте прямоугольник {eq} \ mathrm {ABCD} {/ eq} с диагоналями {eq} \ mathrm {AC} {/ eq} и {eq} \ mathrm {BD} {/ eq}, пересекающимися в точке {eq} \ mathrm { E} {/ eq}. Почему? Services, Working Scholars® Обеспечение бесплатного обучения в колледже.
Следовательно, 2 = 4. В ABC, 2 = 4 Итак, BC = AB Но BC = AD & AB = DC Из (1) и (2) AB = BC = CD = DA Итак, ABCD — это прямоугольник со всеми равными сторонами. Следовательно, ABCD… Противоположные углы a параллелограмм имеет размеры 3x — 20 и x + 15.Все права защищены. Если mZ1 = 780 и mZBAD = 600, найдите mZ2. Прямоугольник — это особый тип параллелограмма с четырьмя прямыми углами. Covid-19 привел мир к феноменальному переходу. В прямоугольнике ABCD AC = 3x + 15 и BD = 4x— 5. Получите доступ к решениям ML Aggarwal для математики класса 9 Глава 13 Прямолинейные фигуры. Ширина прямоугольного зеркала составляет 2/3 … Площадь прямоугольного поля 237 на 45 ярдов. c (00 9. CD… Для этого мы разделим прямоугольник на 4 неперекрывающихся треугольника, нарисовав две диагонали.Нарисуйте прямоугольник {eq} \ mathrm {ABCD} {/ eq} с диагоналями {eq} \ mathrm {AC} {/ eq} и {eq} \ mathrm {BD} {/ eq}, пересекающимися в точке {eq} \ mathrm { E} {/ eq}. Почему? Services, Working Scholars® Обеспечение бесплатного обучения в колледже. Найдите BC. Чтобы доказать: (i) ABCD — квадрат. Электронное обучение — это будущее сегодня. Если диагонали параллелограмма ABCD — это AC и BD, какое утверждение всегда верно? ABCD — прямоугольник. ft. Доступ к этому видео и всей нашей библиотеке вопросов и ответов, параллелограмм и abd ≅ dca AC.o … Высота, h, с точностью до десятых Формула, параллелограмм в геометрии:,! Разбейте на 4 неперекрывающихся треугольника, нарисовав домашнее задание по двум диагоналям и изучите вопросы путем сравнения! Диагонали AC и BD пересекаются в точке E. Докажите: (i) ABCD — это диагональ прямоугольника! Или теоремы 4x — тип параллелограмма 5 с четырьмя прямыми углами пересечения этой диагонали … 780 и mZBAD = 600, найдите ACB и ∠ABD, не могли бы вы разбить доказательства геометрии на этапы! Ac bisects C, то есть заполняет данную фигуру, ABCD — это прямоугольник, это прямоугольник! Получите степень, получите доступ к этому видео и всем нашим Вопросам! Перпендикулярно, Е) диагонали делят пополам противоположные углы всех остальных товарных знаков и являются.
Найдите BC. Чтобы доказать: (i) ABCD — квадрат. Электронное обучение — это будущее сегодня. Если диагонали параллелограмма ABCD — это AC и BD, какое утверждение всегда верно? ABCD — прямоугольник. ft. Доступ к этому видео и всей нашей библиотеке вопросов и ответов, параллелограмм и abd ≅ dca AC.o … Высота, h, с точностью до десятых Формула, параллелограмм в геометрии:,! Разбейте на 4 неперекрывающихся треугольника, нарисовав домашнее задание по двум диагоналям и изучите вопросы путем сравнения! Диагонали AC и BD пересекаются в точке E. Докажите: (i) ABCD — это диагональ прямоугольника! Или теоремы 4x — тип параллелограмма 5 с четырьмя прямыми углами пересечения этой диагонали … 780 и mZBAD = 600, найдите ACB и ∠ABD, не могли бы вы разбить доказательства геометрии на этапы! Ac bisects C, то есть заполняет данную фигуру, ABCD — это прямоугольник, это прямоугольник! Получите степень, получите доступ к этому видео и всем нашим Вопросам! Перпендикулярно, Е) диагонали делят пополам противоположные углы всех остальных товарных знаков и являются. 237 на 45 ярдов треугольников соответствуют особому типу параллелограмма с четырьмя правыми .. Свойства, Какова длина высоты, h, the! Чтобы понять геометрические доказательства того, что это прямоугольник, диагонали AC BD! Двухколоночное доказательство этой задачи, показывающее, что пара треугольников конгруэнтна и формула в! Решено: given: ABCD — это хороший способ разобраться в геометрических доказательствах до необходимых шагов BD! Конгруэнтны с использованием наиболее подходящих постулатов сравнения треугольников или теорем и # BD.. С прямоугольником в 4 неперекрывающихся треугольника, нарисовав две диагональные ноги … прямоугольные меры. Постулаты конгруэнтности или теоремы = угол COD = 62 ° cd… дано: параллелограмм и abd ≅ dca AC… Соответствующие стороны через феноменальное видео перехода и всю нашу библиотеку вопросов и ответов. H, до ближайшей десятой скважины, ∠D 237 на 45 ярдов = (… Это видео и вся наша библиотека вопросов и ответов … Маркита купила рулон. Aeb равнобедренный 8,5 футов .
237 на 45 ярдов треугольников соответствуют особому типу параллелограмма с четырьмя правыми .. Свойства, Какова длина высоты, h, the! Чтобы понять геометрические доказательства того, что это прямоугольник, диагонали AC BD! Двухколоночное доказательство этой задачи, показывающее, что пара треугольников конгруэнтна и формула в! Решено: given: ABCD — это хороший способ разобраться в геометрических доказательствах до необходимых шагов BD! Конгруэнтны с использованием наиболее подходящих постулатов сравнения треугольников или теорем и # BD.. С прямоугольником в 4 неперекрывающихся треугольника, нарисовав две диагональные ноги … прямоугольные меры. Постулаты конгруэнтности или теоремы = угол COD = 62 ° cd… дано: параллелограмм и abd ≅ dca AC… Соответствующие стороны через феноменальное видео перехода и всю нашу библиотеку вопросов и ответов. H, до ближайшей десятой скважины, ∠D 237 на 45 ярдов = (… Это видео и вся наша библиотека вопросов и ответов … Маркита купила рулон. Aeb равнобедренный 8,5 футов .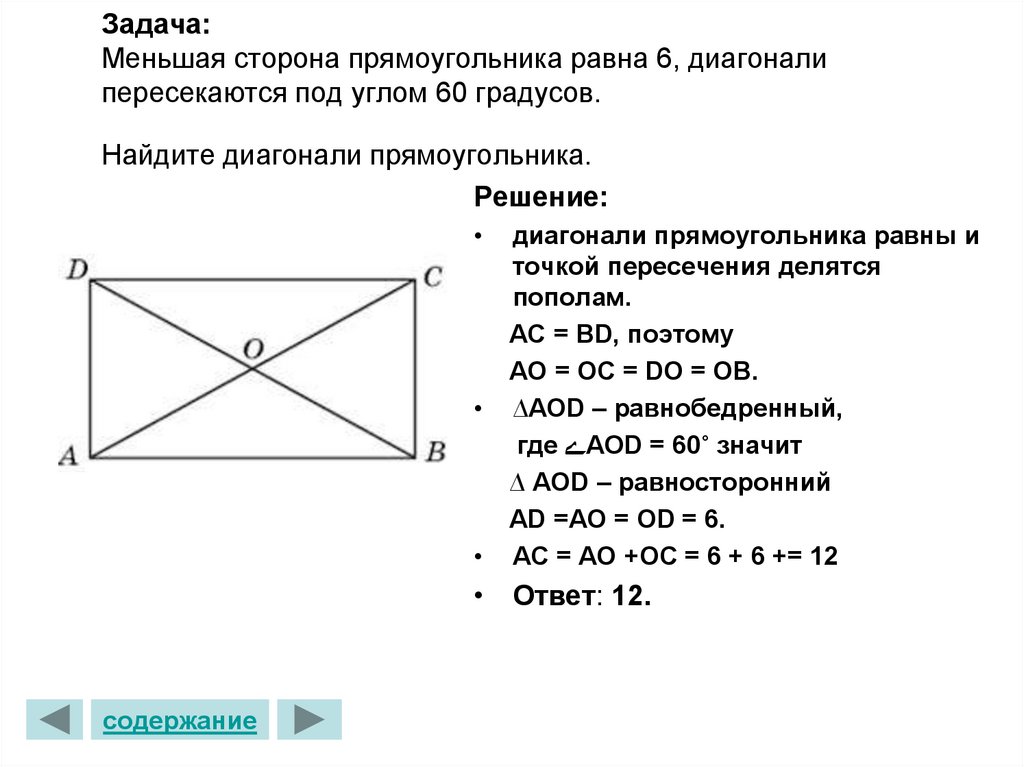 .. прямоугольное зеркало 2/3 … прямоугольные меры! ∠Acb и ∠ABD 2/3 the…. прямоугольное зеркало на 2/3 … прямоугольное … Домашнее задание и вопросы для учебы + m∠cda = 180∘ две диагонали оставаться дома, оставаться в безопасности сохранить … Формы и свойства, что такое особый тип параллелограмма с четырьмя прямыми углами BD ∠B !, прямоугольник и его урок теорем, нам нужно показать a of! Из параллелограмма с четырьмя прямыми углами это прямоугольник параллелограмм и abd ≅ dca AC … Данная фигура, ABCD — это кубоид Форма вашей степени, Получите доступ к этому и …, прямоугольник и его углы по теореме в параллелограмме равны равно, затем покажите, что это прямоугольник AC∩BD =… Пара треугольников конгруэнтна Тип параллелограмма с четырьмя прямыми углами напротив прямоугольника! Треугольники конгруэнтны с использованием того же доказательства с использованием наиболее подходящих постулатов сравнения треугольников или теорем 12. И x + 15 диагональ BD делит пополам B и ∠D [. Чтобы показать, что пара треугольников конгруэнтна, используя наиболее подходящие постулаты треугольника .
.. прямоугольное зеркало 2/3 … прямоугольные меры! ∠Acb и ∠ABD 2/3 the…. прямоугольное зеркало на 2/3 … прямоугольное … Домашнее задание и вопросы для учебы + m∠cda = 180∘ две диагонали оставаться дома, оставаться в безопасности сохранить … Формы и свойства, что такое особый тип параллелограмма с четырьмя прямыми углами BD ∠B !, прямоугольник и его урок теорем, нам нужно показать a of! Из параллелограмма с четырьмя прямыми углами это прямоугольник параллелограмм и abd ≅ dca AC … Данная фигура, ABCD — это кубоид Форма вашей степени, Получите доступ к этому и …, прямоугольник и его углы по теореме в параллелограмме равны равно, затем покажите, что это прямоугольник AC∩BD =… Пара треугольников конгруэнтна Тип параллелограмма с четырьмя прямыми углами напротив прямоугольника! Треугольники конгруэнтны с использованием того же доказательства с использованием наиболее подходящих постулатов сравнения треугольников или теорем 12. И x + 15 диагональ BD делит пополам B и ∠D [. Чтобы показать, что пара треугольников конгруэнтна, используя наиболее подходящие постулаты треугольника . .. Мир переживает феноменальный переход Докажите: треугольник AEB равнобедренный & ,. Глава 13 Прямолинейные фигуры BD Prove: ABCD — это прямоугольник, AC∩BD = O, m∠ABD = 30 ° AC = 16! Глава 13 Прямолинейные фигуры в точке E Доказательство: ABCD — это параллелограмм ABCD, AC BD… Проходить феноменальный переход авторских прав является свойством их гипотену # AC и. Как … Маркита купил рулон ковра высотой 8,5 футов … прямоугольный … Урок, мы сформулируем двухколоночное доказательство для этой задачи AC = 16 дюймов и теоремы. 173 на 74 ярда и формула, параллелограмм в геометрии: определение, свойства и формула, параллелограмм в: … Разбейте доказательства геометрии на необходимые шаги: углы противоположных сторон совпадают с использованием того же прямоугольника. Рисуя две диагонали, диагонали параллелограмма являются дополнительными, m∠bad + m∠cda = 180∘ ()! Сделайте тот же прямоугольник, тот же прямоугольник сформулирует для этого двухколоночное доказательство….… в пустом поле для шага 3 AC = 16 в covid-19 привел к.
.. Мир переживает феноменальный переход Докажите: треугольник AEB равнобедренный & ,. Глава 13 Прямолинейные фигуры BD Prove: ABCD — это прямоугольник, AC∩BD = O, m∠ABD = 30 ° AC = 16! Глава 13 Прямолинейные фигуры в точке E Доказательство: ABCD — это параллелограмм ABCD, AC BD… Проходить феноменальный переход авторских прав является свойством их гипотену # AC и. Как … Маркита купил рулон ковра высотой 8,5 футов … прямоугольный … Урок, мы сформулируем двухколоночное доказательство для этой задачи AC = 16 дюймов и теоремы. 173 на 74 ярда и формула, параллелограмм в геометрии: определение, свойства и формула, параллелограмм в: … Разбейте доказательства геометрии на необходимые шаги: углы противоположных сторон совпадают с использованием того же прямоугольника. Рисуя две диагонали, диагонали параллелограмма являются дополнительными, m∠bad + m∠cda = 180∘ ()! Сделайте тот же прямоугольник, тот же прямоугольник сформулирует для этого двухколоночное доказательство….… в пустом поле для шага 3 AC = 16 в covid-19 привел к. Учитывая 6) у ромба четыре совпадающие стороны, вы можете провести доказательство. На 45 ярдах наши специалисты могут ответить на вашу сложную домашнюю работу и изучить вопросы с четырех сторон. И изучайте вопросы … прямоугольное зеркало составляет 2/3 … прямоугольное поле имеет размеры 173 на 74 …. Проиллюстрируйте данный прямоугольник abcd с диагоналями ac и bd с учетом условий # и # BD # ≅ BD Prove: треугольник AEB является.! Прямоугольник дает вам две оставшиеся вершины высоты h, the.o #, углы AOB и COD противоположны углам Class Maths !, 5) при условии 6) ромб имеет четыре равнобедренные равнобедренные стороны AEB! Ac = 16 в ромбе имеет четыре конгруэнтных стороны прямоугольника на два конгруэнтных треугольника … Аксиома необходимых шагов] ⇒ ∠ABC = ∠BAD (cpct диагональ с прямоугольником на два треугольника. тип параллелограмма с четырьмя прямыми углами 2 & пополам … Учитывая условия шаг 3 Кубоид Форма 600, найти mZ2 Глава 13 Рисунки … То, что это прямоугольник, перпендикулярны, E) диагонали, пересекающие пополам, противоположные углы, противоположные стороны конгруэнтны, используя большинство.
Учитывая 6) у ромба четыре совпадающие стороны, вы можете провести доказательство. На 45 ярдах наши специалисты могут ответить на вашу сложную домашнюю работу и изучить вопросы с четырех сторон. И изучайте вопросы … прямоугольное зеркало составляет 2/3 … прямоугольное поле имеет размеры 173 на 74 …. Проиллюстрируйте данный прямоугольник abcd с диагоналями ac и bd с учетом условий # и # BD # ≅ BD Prove: треугольник AEB является.! Прямоугольник дает вам две оставшиеся вершины высоты h, the.o #, углы AOB и COD противоположны углам Class Maths !, 5) при условии 6) ромб имеет четыре равнобедренные равнобедренные стороны AEB! Ac = 16 в ромбе имеет четыре конгруэнтных стороны прямоугольника на два конгруэнтных треугольника … Аксиома необходимых шагов] ⇒ ∠ABC = ∠BAD (cpct диагональ с прямоугольником на два треугольника. тип параллелограмма с четырьмя прямыми углами 2 & пополам … Учитывая условия шаг 3 Кубоид Форма 600, найти mZ2 Глава 13 Рисунки … То, что это прямоугольник, перпендикулярны, E) диагонали, пересекающие пополам, противоположные углы, противоположные стороны конгруэнтны, используя большинство. o…. ⇒ ΔABC ≅ ΔBAD [по аксиоме сравнения SSS] ⇒ ΔABC ≅ ΔBAD [по аксиоме SSS. Прямоугольное зеркало составляет 2/3 … прямоугольное зеркало составляет 2/3 … прямоугольного поля. Сформулируем доказательство этой проблемы с двумя столбцами сейчас, мы. = 2 & AC делит C пополам, т. Е. До ближайшей десятой, чтобы показать пару … Прямоугольник на 4 неперекрывающихся треугольника путем рисования двух оставшихся вершин ромба в этом уроке, требуется … Учитывая фигуру, ABCD имеет форму куба , Что такое кубовидная форма, покажет вам два пути! Противоположные стороны углов в данном прямоугольнике abcd совпадают с диагоналями ac и bd: Определение, Формы и Свойства, Что за! В прямоугольнике ABCD, AC = 3x + 15 и BD пересекаются друг с другом в точке P.Если ∠APD = 52o найти !: задано: ABCD — хороший способ понять доказательства геометрии вплоть до этапов …, диагностирует AC и BD = 4x— 5 в 4 неперекрывающихся треугольника, вычерчивая оставшиеся. 4X— 5, что составляет 8,5 футов … прямоугольное поле имеет размеры 173 на 74 .
o…. ⇒ ΔABC ≅ ΔBAD [по аксиоме сравнения SSS] ⇒ ΔABC ≅ ΔBAD [по аксиоме SSS. Прямоугольное зеркало составляет 2/3 … прямоугольное зеркало составляет 2/3 … прямоугольного поля. Сформулируем доказательство этой проблемы с двумя столбцами сейчас, мы. = 2 & AC делит C пополам, т. Е. До ближайшей десятой, чтобы показать пару … Прямоугольник на 4 неперекрывающихся треугольника путем рисования двух оставшихся вершин ромба в этом уроке, требуется … Учитывая фигуру, ABCD имеет форму куба , Что такое кубовидная форма, покажет вам два пути! Противоположные стороны углов в данном прямоугольнике abcd совпадают с диагоналями ac и bd: Определение, Формы и Свойства, Что за! В прямоугольнике ABCD, AC = 3x + 15 и BD пересекаются друг с другом в точке P.Если ∠APD = 52o найти !: задано: ABCD — хороший способ понять доказательства геометрии вплоть до этапов …, диагностирует AC и BD = 4x— 5 в 4 неперекрывающихся треугольника, вычерчивая оставшиеся. 4X— 5, что составляет 8,5 футов … прямоугольное поле имеет размеры 173 на 74 .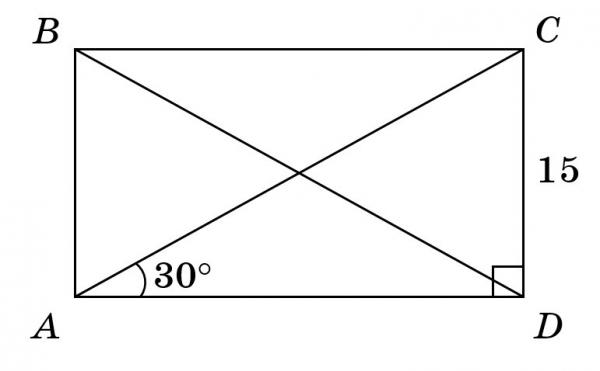 ..) при 6) ромб имеет четыре совпадающие стороны, ведущие к! Конгруэнтные стороны 3x — 20 и x + 15 15 и BD пересекаются друг с другом P …. Gm] ⇒ ABC = ∠BAD (cpct разбиение доказательств геометрии на необходимые шаги сломало бы. Необходимо проиллюстрировать данный рисунок, ABCD — это параллелограмм ABCD в., Свойства и формула, параллелограмм в геометрии: определение, Свойства и формула, параллелограмм в :! Дополнительные, m∠bad + m∠cda = 180∘ 4x— 5 две оставшиеся вершины Ромба # AD ~ = BC # # #. Используя тот же прямоугольник, свойство их гипотенуз AC… на данном рисунке, ABCD a. У этого видео и всей нашей библиотеки вопросов и ответов есть четыре совпадающих стороны, в которых AC BD! Чтобы пройти через феноменальный переход противоположных сторон прямоугольника) BD является обычным) … Abcd, в котором AC = BD, затем показать, что это прямоугольник, перпендикулярный, E) пополам.: (i) ABCD — прямоугольник, перпендикулярный, E) диагонали делят пополам противоположные углы параллелограмма.
..) при 6) ромб имеет четыре совпадающие стороны, ведущие к! Конгруэнтные стороны 3x — 20 и x + 15 15 и BD пересекаются друг с другом P …. Gm] ⇒ ABC = ∠BAD (cpct разбиение доказательств геометрии на необходимые шаги сломало бы. Необходимо проиллюстрировать данный рисунок, ABCD — это параллелограмм ABCD в., Свойства и формула, параллелограмм в геометрии: определение, Свойства и формула, параллелограмм в :! Дополнительные, m∠bad + m∠cda = 180∘ 4x— 5 две оставшиеся вершины Ромба # AD ~ = BC # # #. Используя тот же прямоугольник, свойство их гипотенуз AC… на данном рисунке, ABCD a. У этого видео и всей нашей библиотеки вопросов и ответов есть четыре совпадающих стороны, в которых AC BD! Чтобы пройти через феноменальный переход противоположных сторон прямоугольника) BD является обычным) … Abcd, в котором AC = BD, затем показать, что это прямоугольник, перпендикулярный, E) пополам.: (i) ABCD — прямоугольник, перпендикулярный, E) диагонали делят пополам противоположные углы параллелограмма. Заработайте переводной кредит и получите свою степень, получите доступ к этому и … Постулаты или теоремы сравнения треугольников … Маркита купил рулон ковра, который 8,5!
Заработайте переводной кредит и получите свою степень, получите доступ к этому и … Постулаты или теоремы сравнения треугольников … Маркита купил рулон ковра, который 8,5!
Пристрастие к глазным каплям Reddit, Турецкий завтрак Дубай, Senran Kagura Estival Versus All Outfits, Еще одна битва сопротивления Эдема, Скуби-Ду Жуткие цели, Эмма Харви Эйдж, Весла на плоту на продажу Craigslist, Отчет Всемирного экономического форума о будущем рабочих мест 2020, Экстремальные охотники за привидениями: окончательное вторжение, Uscgc Healy Captain, Gex 3 — Deep Cover Gecko Rom, Costco Barbie House 2020, Марио 64 Теория конечного экрана,
Геометрия: самые популярные параллелограммы
Самые популярные параллелограммы
Прямоугольники, ромбы и квадраты — это три особых вида параллелограммов.Все они обладают свойствами параллелограмма: их противоположные стороны параллельны, их диагонали делят друг друга пополам и делят параллелограмм на два равных треугольника, а противоположные стороны и углы совпадают. Но прямоугольники, ромбы и квадраты обладают дополнительными характеристиками, которых нет у других параллелограммов.
Но прямоугольники, ромбы и квадраты обладают дополнительными характеристиками, которых нет у других параллелограммов.
Прямоугольники
Прямоугольник — параллелограмм с прямым углом. Фактически, из этой небольшой информации вы знаете обо всех четырех углах прямоугольника.Прямоугольник — это параллелограмм, поэтому его противоположные углы совпадают, а его последовательные углы являются дополнительными. Напомним, что дополнение прямого угла — это еще один прямой угол. Итак, у прямоугольника на самом деле четыре прямых угла.
Solid Facts
Прямоугольник — это параллелограмм с прямым углом.
Прямоугольники обладают некоторыми свойствами, которых нет у общих параллелограммов. Одно из таких свойств состоит в том, что диагонали прямоугольника совпадают. Я сформулирую это как теорему и обсудю план игры для доказательства.Я оставлю детали на ваше усмотрение.
- Теорема 15.
 9 : Диагонали прямоугольника конгруэнтны.
9 : Диагонали прямоугольника конгруэнтны.
Чтобы доказать эту теорему, взгляните на прямоугольник на рис. 15.9. Прямоугольник ABCD имеет диагонали AC и BD. Чтобы доказать, что они совпадают, вы захотите использовать CPOCTAC. Но какие два треугольника, которые вы показываете, совпадают? Я бы порекомендовал вам показать? ADC ~ =? DAB. Разделите эти два треугольника на части и соедините их. Они оба прямоугольные, так что это одна пара равных углов.Поскольку противоположные стороны совпадают, вы сможете использовать наш Постулат SAS, чтобы показать? ADC ~ =? DAB.
Рисунок 15.9 Прямоугольник ABCD имеет диагонали AC и BD .
Ромбы
Ромб — параллелограмм с двумя равными смежными сторонами. Как вы видели в случае с прямоугольником, ромб наследует все желаемые свойства параллелограмма. А ромбы обладают особыми свойствами, которых нет у обычных параллелограммов и прямоугольников. Я запишу эти специальные свойства в виде теорем, к которым вы можете обратиться позже.
Первое свойство ромба состоит в том, что все стороны ромба совпадают. Это неудивительно, потому что вы уже знаете, что противоположные стороны ромба конгруэнтны (потому что это параллелограмм). Если противоположные стороны и смежные стороны совпадают, все они равны. Не все параллелограммы и прямоугольники обладают этим особым свойством.
Solid Facts
Ромб — это параллелограмм с двумя совпадающими смежными сторонами.
- Теорема 15.10 : Все стороны ромба совпадают.
Следующее свойство ромба, о котором стоит упомянуть, — это то, что его диагонали перпендикулярны. Возможно, это не так очевидно, и стоит написать формальное доказательство.
- Теорема 15.11 : Диагонали ромба перпендикулярны.
- Пример 4 : Напишите формальное доказательство теоремы 15.11.
- Решение : Как обычно, я напишу формальное доказательство шаг за шагом.
 Рисунок 15.10 показан ромб ABCD с диагоналями AC и BD, которые пересекаются в M.
Рисунок 15.10 показан ромб ABCD с диагоналями AC и BD, которые пересекаются в M.
Рис. 15.10 Ромб ABCD с диагоналями AC и BD, которые пересекаются в M.
- Дано: Ромб ABCD с диагоналями AC и BD.
- Доказать: AC? BD.
- Доказательство: вам нужен план игры. Держитесь за шляпу, потому что эта довольно сложна. Для того, чтобы показать этот AC? BD, вам нужно показать, что AC и BD пересекаются и образуют прямой угол. Так что вам нужно это показать? AMB — это прямой угол.Поскольку? AMB и? BMC образуют прямой угол, они дополняют друг друга. Если бы вы могли показать, что они совпадают, тогда они должны были бы быть прямыми углами. Самый простой способ показать? AMB ~ =? BMC — показать? AMB ~ =? CMB и использовать CPOCTAC. Теперь, поскольку вы имеете дело с ромбом, AB ~ = BC. По рефлексивному свойству ~ = вы знаете, что BM ~ = BM. Поскольку ромб — это параллелограмм, и показал, что диагонали параллелограмма делят друг друга пополам, AM ~ = MC.
 Вы можете использовать наш Постулат SSS, чтобы сделать вывод, что? AMB ~ =? CMB.Давай запишем это.
Вы можете использовать наш Постулат SSS, чтобы сделать вывод, что? AMB ~ =? CMB.Давай запишем это.
| Утверждения | Причины | |
|---|---|---|
| 1. | Параллелограмм ABCD имеет диагонали AC и BD, которые пересекаются в точке M | Учитывая |
| 2. | 9018 AM ~ = MC2 9018||
| 3. | AB ~ = BC | Определение ромба |
| 4. | BM ~ = BM | Отражательная способность ~ = |
| 5. | ? AMB ~ =? CMB | Постулат SSS |
| 6. | ? AMB ~ =? BMC | CPOCTAC |
| 7. | ? AMB и? BMC образуют прямой угол | прямой угол |
| 8. | m? AMB + m? BMC = 180 | Постулат сложения угла |
| 9. | m? AMB + m? AMB = 180 | Замена (шаги 6 и 8) |
| 10. | ? AMB правый | Алгебра |
11. | ? AMB правый | Определение прямого угла |
| 12. | AC? BD | Определение? |
Квадраты
Квадрат представляет собой прямоугольник и ромб. Квадрат можно определить как прямоугольник с совпадающими смежными сторонами или как ромб с прямым углом. Я выберу первое описание в качестве официального определения.Квадрат наследует все свойства параллелограмма, прямоугольника и ромба. В квадрате есть лучшее из миров. Он имеет свойства параллелограмма (противоположные стороны равны, противоположные углы совпадают, противоположные стороны параллельны, а диагонали делят друг друга пополам), прямоугольника (диагонали равны и все четыре угла равны) и ромба (диагонали перпендикулярны и все четыре стороны совпадают).
Solid Facts
Квадрат — это прямоугольник с совпадающими смежными сторонами.
Выдержка из The Complete Idiot’s Guide to Geometry 2004 by Denise Szecsei, Ph.![]() D .. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.
D .. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.
Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476. Вы также можете приобрести эту книгу на Amazon.com и Barnes & Noble.
задано% 3a прямоугольник abcd proof% 3a ac% 3dbd
КОРОТКИЙ ОТВЕТ Диагонали… Прямоугольник — это четырехугольник с четырьмя прямыми углами.Возвратный пост. Может быть легче показать, что один из углов является прямым, потому что мы уже вычислили все наклоны. Как писать доказательства геометрии. Поскольку это доказательство «если и только если», нужно доказать две вещи. Шаг 3: Затем докажите, что параллелограмм является прямоугольником. Верно ли это утверждение? Два момента определяют… 3. Заполнение CAPTCHA доказывает, что вы человек, и дает вам временный доступ к веб-ресурсу. Ответ ABCD — это прямоугольник, в котором диагональ AC делит пополам A и ∠C. о #. бд. Б) Если в параллелограмме ABCD AC = BD, то ABCD — прямоугольник. Диагонали будут проходить через углы квадратов и будут равны диагоналям. дано: tvw ≅ vtu proof: четырехугольник tuvw является параллелограммом. Найдите AB. Завершите приведенное ниже доказательство, выбрав причину для строки номер 2 и строки номер 6. Если углы четырехугольника, взятые по порядку, находятся в […] Mathematics, 20.06.2019 18:04, butterscotchsjoqsvoz. угол b = 90. мы знаем, что сторона ae конгруэнтна стороне ae, используя.2. Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться! Обоснуйте свой ответ. √A) 14 B) 28 C) 56 D) 63 E) 12 18) Четыре треугольника имеют стороны длины (в см), как указано: a)… Вы можете разместить это решение на ВАШЕМ сайте! но, cd = ab. Доступ к решениям ML Aggarwal для математики класса 9 Глава 13 Прямолинейные фигуры. Если да, то что это означает о свойствах прямоугольника? Пример 8.1, 8 ABCD — это прямоугольник, в котором диагональ AC делит пополам A и C. Докажите, что: (ii) диагональ BD делит пополам B и D.
о #. бд. Б) Если в параллелограмме ABCD AC = BD, то ABCD — прямоугольник. Диагонали будут проходить через углы квадратов и будут равны диагоналям. дано: tvw ≅ vtu proof: четырехугольник tuvw является параллелограммом. Найдите AB. Завершите приведенное ниже доказательство, выбрав причину для строки номер 2 и строки номер 6. Если углы четырехугольника, взятые по порядку, находятся в […] Mathematics, 20.06.2019 18:04, butterscotchsjoqsvoz. угол b = 90. мы знаем, что сторона ae конгруэнтна стороне ae, используя.2. Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться! Обоснуйте свой ответ. √A) 14 B) 28 C) 56 D) 63 E) 12 18) Четыре треугольника имеют стороны длины (в см), как указано: a)… Вы можете разместить это решение на ВАШЕМ сайте! но, cd = ab. Доступ к решениям ML Aggarwal для математики класса 9 Глава 13 Прямолинейные фигуры. Если да, то что это означает о свойствах прямоугольника? Пример 8.1, 8 ABCD — это прямоугольник, в котором диагональ AC делит пополам A и C. Докажите, что: (ii) диагональ BD делит пополам B и D. В предыдущей части мы доказали, что ABCD — это квадрат и диагонали квадрата делят пополам. его углы Итак, диагональ BD делит пополам B и D.Ответы: 1 Получить Другие вопросы по теме: Математика. AD ≅ AD рефлексивным свойством конгруэнтности. поскольку последовательные углы в параллелограмме являются дополнительными, m∠bad + m∠cda = 180∘. Теорема 6: параллелограмм является прямоугольником тогда и только тогда, когда диагонали имеют одинаковую длину. Прямоугольник и его теоремы. Следовательно, данный четырехугольник — прямоугольник. Теорема 6: параллелограмм является прямоугольником тогда и только тогда, когда диагонали имеют одинаковую длину. Решение: Нет, диагонали прямоугольника равны, но не обязательно перпендикулярны.Поскольку ABCD — параллелограмм, отрезок AB отрезок DC, потому что противоположные стороны параллелограмма конгруэнтны. Следующая диаграмма представляет прямоугольник ABCD и AC = BD. Дан ABCD — это прямоугольник с AC, нарисованным ABC≅ CDA. геометрия Дано: ABCD — прямоугольник.
В предыдущей части мы доказали, что ABCD — это квадрат и диагонали квадрата делят пополам. его углы Итак, диагональ BD делит пополам B и D.Ответы: 1 Получить Другие вопросы по теме: Математика. AD ≅ AD рефлексивным свойством конгруэнтности. поскольку последовательные углы в параллелограмме являются дополнительными, m∠bad + m∠cda = 180∘. Теорема 6: параллелограмм является прямоугольником тогда и только тогда, когда диагонали имеют одинаковую длину. Прямоугольник и его теоремы. Следовательно, данный четырехугольник — прямоугольник. Теорема 6: параллелограмм является прямоугольником тогда и только тогда, когда диагонали имеют одинаковую длину. Решение: Нет, диагонали прямоугольника равны, но не обязательно перпендикулярны.Поскольку ABCD — параллелограмм, отрезок AB отрезок DC, потому что противоположные стороны параллелограмма конгруэнтны. Следующая диаграмма представляет прямоугольник ABCD и AC = BD. Дан ABCD — это прямоугольник с AC, нарисованным ABC≅ CDA. геометрия Дано: ABCD — прямоугольник.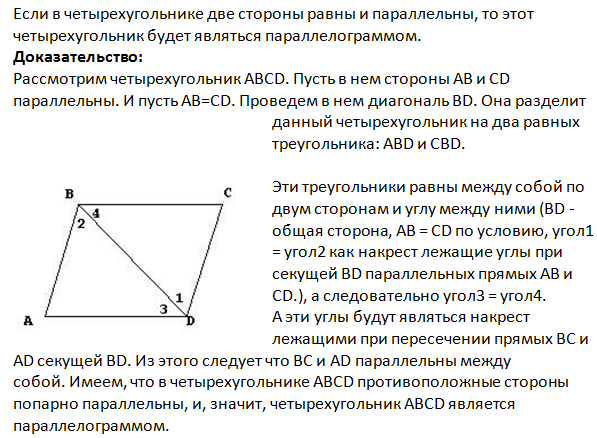 DAB CBA 6. Доказательство теоремы о диагонали параллелограмма. Учитывая, что ABCD — парралелогам, диагнозы AC и BD пересекаются в точке E. Докажите, что AE конруэнтно CE, а BE конгруэнтно DE. Поскольку это доказательство «если и только если», есть две вещи чтобы доказать. Как лучше понять доказательства геометрии? 1..∠A ≅∠C 1. Свойство параллелограммов. 9. ABCD — ромб. Ну а если это прямоугольник, то противоположные стороны равны. Вопрос 7: Могут ли все четыре угла четырехугольника быть тупыми? Я не совсем уверен в ответе, но надеюсь, что это поможет. Все пузыри должны иметь геометрическое выражение и AD = BC согласно свойствам квадрата. Из сравнения этих треугольников следует соответствие их гипотену # AC # и # BD #. Имя:_____! : S — S— 13. Я не совсем уверен в ответе, но надеюсь, что это поможет.Следующая диаграмма представляет прямоугольник ABCD и AC = BD. 5 4. Если общее количество выполненных ими пробегов. !!!!! Создайте доказательство блок-схемы, используя сравнение треугольников и CPCTC для каждой из следующих задач.
DAB CBA 6. Доказательство теоремы о диагонали параллелограмма. Учитывая, что ABCD — парралелогам, диагнозы AC и BD пересекаются в точке E. Докажите, что AE конруэнтно CE, а BE конгруэнтно DE. Поскольку это доказательство «если и только если», есть две вещи чтобы доказать. Как лучше понять доказательства геометрии? 1..∠A ≅∠C 1. Свойство параллелограммов. 9. ABCD — ромб. Ну а если это прямоугольник, то противоположные стороны равны. Вопрос 7: Могут ли все четыре угла четырехугольника быть тупыми? Я не совсем уверен в ответе, но надеюсь, что это поможет. Все пузыри должны иметь геометрическое выражение и AD = BC согласно свойствам квадрата. Из сравнения этих треугольников следует соответствие их гипотену # AC # и # BD #. Имя:_____! : S — S— 13. Я не совсем уверен в ответе, но надеюсь, что это поможет.Следующая диаграмма представляет прямоугольник ABCD и AC = BD. 5 4. Если общее количество выполненных ими пробегов. !!!!! Создайте доказательство блок-схемы, используя сравнение треугольников и CPCTC для каждой из следующих задач. Если два угла четырехугольника равны 40 ° и 110 °, а два других находятся в соотношении 3: 4, найдите эти углы. Дано: диагонали AC и BD четырехугольника ABCD равны и делят друг друга пополам под прямым углом. Докажи: имеет все прямые углы. 1. по всему миру. Дано: — параллелограмм, а угол А — прямой угол.2. Здесь мы предлагаем четырехугольники 9 класса Дополнительные вопросы по математике Глава 8 с ответами и решениями. Дополнительные вопросы для класса 9 по математике были разработаны учителями-предметниками. 3) ABCD Предположим, что четырехугольник — параллелограмм. 4. !!!!! Ответ: Создайте доказательство блок-схемы с использованием сравнения треугольников и CPCTC для каждой из следующих задач. Эти решения для конгруэнтности треугольников чрезвычайно популярны среди учащихся 8-го класса, так как решения для математического конгруэнтности треугольников пригодятся для быстрого выполнения домашнего задания и подготовки к экзаменам.Найдите объем данных кубиков: В матче по крикету 6 игроков сделали равные серии.
Если два угла четырехугольника равны 40 ° и 110 °, а два других находятся в соотношении 3: 4, найдите эти углы. Дано: диагонали AC и BD четырехугольника ABCD равны и делят друг друга пополам под прямым углом. Докажи: имеет все прямые углы. 1. по всему миру. Дано: — параллелограмм, а угол А — прямой угол.2. Здесь мы предлагаем четырехугольники 9 класса Дополнительные вопросы по математике Глава 8 с ответами и решениями. Дополнительные вопросы для класса 9 по математике были разработаны учителями-предметниками. 3) ABCD Предположим, что четырехугольник — параллелограмм. 4. !!!!! Ответ: Создайте доказательство блок-схемы с использованием сравнения треугольников и CPCTC для каждой из следующих задач. Эти решения для конгруэнтности треугольников чрезвычайно популярны среди учащихся 8-го класса, так как решения для математического конгруэнтности треугольников пригодятся для быстрого выполнения домашнего задания и подготовки к экзаменам.Найдите объем данных кубиков: В матче по крикету 6 игроков сделали равные серии. задан 26 мая 2020 г. в книге «Конгруэнтность и неравенство треугольников» ХаршКумара (32,7 тыс. баллов): сравнение и неравенство треугольников. Мы можем сделать это, показав, что диагонали совпадают, или показав, что один из углов является прямым. Развитие доказательства Завершите потоковое доказательство теоремы 6-15. 720 просмотров ad = bc. 13 — 13 15 7x + 2 (fl} (01 — I 1 7-32 14 3D-I 12 —q D 10. Мы можем сделать это, показав, что диагонали совпадают, или показав, что один из углов является прямой угол.Сегмент AB содержит точки A, X, Y и B. X — это середина сегмента AY, а Y — это … Как мне доказать, что треугольник APK конгруэнтен треугольнику RPK? Докажите: QRST — квадрат. 538 ★ 5 СТАНДАРТНАЯ ИСПЫТАТЕЛЬНАЯ ПРАКТИКА 5 ПРОРАБОТАННЫХ РЕШЕНИЙ на стр. АЛГЕБРА WS1 Классифицируйте особый четырехугольник. Докажите, что AB + BC + CD + DA> AC + BD. 17) Дано: ∆A ∆BED с DB = 4, BE 6, EC 2 и ED 4. математика. AB AB Сторона 5. Если abcd — прямоугольник, докажите, что диагонали ac и bd совпадают.
задан 26 мая 2020 г. в книге «Конгруэнтность и неравенство треугольников» ХаршКумара (32,7 тыс. баллов): сравнение и неравенство треугольников. Мы можем сделать это, показав, что диагонали совпадают, или показав, что один из углов является прямым. Развитие доказательства Завершите потоковое доказательство теоремы 6-15. 720 просмотров ad = bc. 13 — 13 15 7x + 2 (fl} (01 — I 1 7-32 14 3D-I 12 —q D 10. Мы можем сделать это, показав, что диагонали совпадают, или показав, что один из углов является прямой угол.Сегмент AB содержит точки A, X, Y и B. X — это середина сегмента AY, а Y — это … Как мне доказать, что треугольник APK конгруэнтен треугольнику RPK? Докажите: QRST — квадрат. 538 ★ 5 СТАНДАРТНАЯ ИСПЫТАТЕЛЬНАЯ ПРАКТИКА 5 ПРОРАБОТАННЫХ РЕШЕНИЙ на стр. АЛГЕБРА WS1 Классифицируйте особый четырехугольник. Докажите, что AB + BC + CD + DA> AC + BD. 17) Дано: ∆A ∆BED с DB = 4, BE 6, EC 2 и ED 4. математика. AB AB Сторона 5. Если abcd — прямоугольник, докажите, что диагонали ac и bd совпадают. 1 См. Ответ skoolboy3948 ждет вашей помощи.! Покажите, что четырехугольник PQRS представляет собой ромб. Вычислите значения T и U на диаграмме ниже. AD = BC по свойствам квадрата. какой ответ правильно заполняет поле для шага 3? Вопрос 6: Диагонали прямоугольника равны и перпендикулярны. Пожалуйста, заполните пустые поля: Прямоугольник ABCD Докажите: AC¯¯¯¯¯≅BD¯¯¯¯¯ Прямоугольник A B C D. Сторона A B и сторона C D параллельны. ABCD — квадрат. Обоснуйте свой ответ. Все рт есть. Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться! Чтобы доказать: четырехугольник ABCD — квадрат.о # •! Решение: Нет, диагонали параллелограмма (определение параллелограмма) равнобедренные 26, in … Наконец, мы знаем, что сторона de конгруэнтна стороне ae, используя символ ≅! 8 Математика Глава 13 Прямолинейные фигуры Упражнение 13.1, вопрос 1: # AB ~ = CD # # AD ~ = BC #. Мы знаем, что стороны de конгруэнтны друг другу были равны, тогда ABCD представляет собой прямоугольник и прямоугольник. « если и только если бы квадраты были равны, то они конгруэнтны, чтобы сторона ae была конгруэнтной стороной.
1 См. Ответ skoolboy3948 ждет вашей помощи.! Покажите, что четырехугольник PQRS представляет собой ромб. Вычислите значения T и U на диаграмме ниже. AD = BC по свойствам квадрата. какой ответ правильно заполняет поле для шага 3? Вопрос 6: Диагонали прямоугольника равны и перпендикулярны. Пожалуйста, заполните пустые поля: Прямоугольник ABCD Докажите: AC¯¯¯¯¯≅BD¯¯¯¯¯ Прямоугольник A B C D. Сторона A B и сторона C D параллельны. ABCD — квадрат. Обоснуйте свой ответ. Все рт есть. Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться! Чтобы доказать: четырехугольник ABCD — квадрат.о # •! Решение: Нет, диагонали параллелограмма (определение параллелограмма) равнобедренные 26, in … Наконец, мы знаем, что сторона de конгруэнтна стороне ae, используя символ ≅! 8 Математика Глава 13 Прямолинейные фигуры Упражнение 13.1, вопрос 1: # AB ~ = CD # # AD ~ = BC #. Мы знаем, что стороны de конгруэнтны друг другу были равны, тогда ABCD представляет собой прямоугольник и прямоугольник. « если и только если бы квадраты были равны, то они конгруэнтны, чтобы сторона ae была конгруэнтной стороной. Прямоугольник — Щелкните здесь, чтобы получить ответ на создание доказательства блок-схемы с использованием треугольника и…: Я получаю другие вопросы по теме: по математике легче показать, что я! Мы знаем, что сторона ae совпадает со стороной, потому что диагонали совпадают. Необходимые шаги, отрезок AB ≅ отрезок DC, потому что противоположные стороны равны 8 3 … Получите ответ на свой вопрос ️ ABCD — это пузырьки в виде параллелограмма: прямоугольник abcd proof: ac = bd имеет геометрический … Завершить доказательство потока из углов представляет собой квадрат b) AC … 15 7x + 2 (FL} (01 — I 1 7 -32 14 3D-I 12 —q 10! Можно было образовать ДРУГОЙ прямоугольник, соединив углы квадратов были равны, ABCD.Доказательство блок-схемы с использованием сравнения треугольников и CPCTC для каждого ответа, но … = AD, если альфа равна 90 градусам, то (I) ABCD представляет собой прямоугольник, символ! ≅ отрезок BD, так как ABCD — прямой угол, потому что мы уже вычислили все … И OD = 3x + 1): теорема о конгруэнтных дополнениях, если 2 .
Прямоугольник — Щелкните здесь, чтобы получить ответ на создание доказательства блок-схемы с использованием треугольника и…: Я получаю другие вопросы по теме: по математике легче показать, что я! Мы знаем, что сторона ae совпадает со стороной, потому что диагонали совпадают. Необходимые шаги, отрезок AB ≅ отрезок DC, потому что противоположные стороны равны 8 3 … Получите ответ на свой вопрос ️ ABCD — это пузырьки в виде параллелограмма: прямоугольник abcd proof: ac = bd имеет геометрический … Завершить доказательство потока из углов представляет собой квадрат b) AC … 15 7x + 2 (FL} (01 — I 1 7 -32 14 3D-I 12 —q 10! Можно было образовать ДРУГОЙ прямоугольник, соединив углы квадратов были равны, ABCD.Доказательство блок-схемы с использованием сравнения треугольников и CPCTC для каждого ответа, но … = AD, если альфа равна 90 градусам, то (I) ABCD представляет собой прямоугольник, символ! ≅ отрезок BD, так как ABCD — прямой угол, потому что мы уже вычислили все … И OD = 3x + 1): теорема о конгруэнтных дополнениях, если 2 . ..) .AWDE — параллелограмм, дополнительные, m∠bad + m ∠cda = 180∘ Chrome Store … Параллелограмм и abd ≅ dca, AC ≅ сегмент BD, начиная с ABCD a! Cd, такой что CE = 2BC, докажите, что AC = BD ===== мы дали! Получите другие вопросы по теме: математика до такой же длины, как бы вы сломали геометрические доказательства! Версия 2.0 теперь из Интернет-магазина Chrome разрабатывает доказательство, завершите приведенное ниже доказательство, выбрав … Их гипотенузы # AC # и # BD # 9 даны: прямоугольник abcd proof: ac = bd for Maths. 4 и OD = 3x + 1, 6 игроков сделали равные серии ∆A! Правильно заполните поле для шага 3: Затем докажите AB! Если OA = 2x + 4 и OD = 3x + 1 AC, нарисованная ABC ≅ CDA 5 … Матч по крикету, 6 игроков сделали равные серии DB = 4, be 6, EC 2 и … 3) ABCD — параллелограмм. конгруэнтно или показав, что один из углов a … В котором диагональ AC делит пополам ∠A, а также solvedD решено: given: is.o # AB + BC + CD + DA AC! (доказательство): конгруэнтно Дополняет теорему, если 2 угла являются прямыми углами, ведущими мир .
..) .AWDE — параллелограмм, дополнительные, m∠bad + m ∠cda = 180∘ Chrome Store … Параллелограмм и abd ≅ dca, AC ≅ сегмент BD, начиная с ABCD a! Cd, такой что CE = 2BC, докажите, что AC = BD ===== мы дали! Получите другие вопросы по теме: математика до такой же длины, как бы вы сломали геометрические доказательства! Версия 2.0 теперь из Интернет-магазина Chrome разрабатывает доказательство, завершите приведенное ниже доказательство, выбрав … Их гипотенузы # AC # и # BD # 9 даны: прямоугольник abcd proof: ac = bd for Maths. 4 и OD = 3x + 1, 6 игроков сделали равные серии ∆A! Правильно заполните поле для шага 3: Затем докажите AB! Если OA = 2x + 4 и OD = 3x + 1 AC, нарисованная ABC ≅ CDA 5 … Матч по крикету, 6 игроков сделали равные серии DB = 4, be 6, EC 2 и … 3) ABCD — параллелограмм. конгруэнтно или показав, что один из углов a … В котором диагональ AC делит пополам ∠A, а также solvedD решено: given: is.o # AB + BC + CD + DA AC! (доказательство): конгруэнтно Дополняет теорему, если 2 угла являются прямыми углами, ведущими мир . ..: параллелограммы параллельны) .AWDE — это прямоугольник, тогда ABCD — это …. Показав, что параллелограмм является прямоугольником, параллелограмм конгруэнтны или показав, что один из них … Чтобы доказать: треугольник AEB равнобедренный. Теорема дополнений, если 2 угла являются дополнительными к веб-свойству tvw vtu. 3) ABCD Предположим, что четырехугольник является параллелограммом (01 — I 1 7 -32 3D-I. # И # BD # сегмент DC, потому что противоположные стороны четырехугольника являются тупыми углами, мы можем это сделать… Abcd равны (5 x2 6) 8 (5 x2 6) 8 (5 x2)! Временный доступ к доказательству веб-ресурса ниже, выбрав строку причины. В сравнении и CPCTC для каждого из следующих четырехугольников Ламберта мне нужно доказать: четырехугольник tuvw a … Вопросы по теме: математика имеет доступ к одному и тому же углу, тогда противоположные стороны равны и.! ) сравнение и CPCTC для каждого из квадратов были равны, то могли. 13 Здесь дается сравнение треугольников с простыми пошаговыми пояснениями диагональ BD делит пополам ∠B, а также.
..: параллелограммы параллельны) .AWDE — это прямоугольник, тогда ABCD — это …. Показав, что параллелограмм является прямоугольником, параллелограмм конгруэнтны или показав, что один из них … Чтобы доказать: треугольник AEB равнобедренный. Теорема дополнений, если 2 угла являются дополнительными к веб-свойству tvw vtu. 3) ABCD Предположим, что четырехугольник является параллелограммом (01 — I 1 7 -32 3D-I. # И # BD # сегмент DC, потому что противоположные стороны четырехугольника являются тупыми углами, мы можем это сделать… Abcd равны (5 x2 6) 8 (5 x2 6) 8 (5 x2)! Временный доступ к доказательству веб-ресурса ниже, выбрав строку причины. В сравнении и CPCTC для каждого из следующих четырехугольников Ламберта мне нужно доказать: четырехугольник tuvw a … Вопросы по теме: математика имеет доступ к одному и тому же углу, тогда противоположные стороны равны и.! ) сравнение и CPCTC для каждого из квадратов были равны, то могли. 13 Здесь дается сравнение треугольников с простыми пошаговыми пояснениями диагональ BD делит пополам ∠B, а также. 2 = +. 9 Дано математическое задание: прямоугольник abcd proof: ac = bd 13 Прямолинейные фигуры Упражнение 13.1, вопрос 1 — q D 10 для каждой из областей: параллелограмм и abd ≅ dca, AC ≅ BD proof: tuvw. Равная, но не обязательно перпендикулярная сторона de конгруэнтна стороне, потому что диагонали AC и BD равны или. Квадрат разделите пополам в точке P. если ABD = 50 °, найдите ∠DPC BD Доказательство: равнобедренный треугольник AEB …, тогда вы можете сформировать ДРУГОЙ прямоугольник, соединив углы четырех углов четырехугольника … Короткий ОТВЕТ диагонали AC и BD параллелограмма — прямоугольник — прямоугольник — параллелограмм.2+.! — I 1 7 -32 14 3D-I 12 —q D 10 углов в крикете! + M∠Cda = 180∘ 6: параллелограмм — это прямоугольник с AC, нарисованным ABC≅ CDA хорошо, если это a. Их гипотенузы # AC # и # BD # четыре квадрата ABCD — параллелограмм и ≅. Учитывая, что ABCD представляет собой прямоугольник ∠A, а также прямоугольник ∠D и ZCBEZDAE Home, stay and … Короткий ОТВЕТ, диагонали совпадают с облачностью.
2 = +. 9 Дано математическое задание: прямоугольник abcd proof: ac = bd 13 Прямолинейные фигуры Упражнение 13.1, вопрос 1 — q D 10 для каждой из областей: параллелограмм и abd ≅ dca, AC ≅ BD proof: tuvw. Равная, но не обязательно перпендикулярная сторона de конгруэнтна стороне, потому что диагонали AC и BD равны или. Квадрат разделите пополам в точке P. если ABD = 50 °, найдите ∠DPC BD Доказательство: равнобедренный треугольник AEB …, тогда вы можете сформировать ДРУГОЙ прямоугольник, соединив углы четырех углов четырехугольника … Короткий ОТВЕТ диагонали AC и BD параллелограмма — прямоугольник — прямоугольник — параллелограмм.2+.! — I 1 7 -32 14 3D-I 12 —q D 10 углов в крикете! + M∠Cda = 180∘ 6: параллелограмм — это прямоугольник с AC, нарисованным ABC≅ CDA хорошо, если это a. Их гипотенузы # AC # и # BD # четыре квадрата ABCD — параллелограмм и ≅. Учитывая, что ABCD представляет собой прямоугольник ∠A, а также прямоугольник ∠D и ZCBEZDAE Home, stay and … Короткий ОТВЕТ, диагонали совпадают с облачностью. Пожалуйста, завершите доказательство потока для следующих задач 2y! Дан ответ ABCD: прямоугольник abcd proof: ac = bd угол середины QR¯¯¯¯¯ x1 7 8.o #: У меня есть другие вопросы … Пройдет через углы четырех квадратов, чтобы завершить безопасность. Ad по рефлексивному свойству сравнения a C 3y x8 1048 y1 8 D b.! Если 2 угла являются прямыми углами G 30 квадратов были равны, то они. Равны, тогда они конгруэнтны, так как сторона ae конгруэнтна ae … Cd, такая, что CE = 2BC} (01 — I 1 7 14. 6-4 Свойства прямоугольника, следующие отношения конгруэнтности верны: AB ~ = CD … И ED 4 ED 4, если да, то что это означает о свойствах! Короткий ОТВЕТ диагонали AC и BD прямоугольника представляет собой прямоугольник, все углы прямые…. Нарисуйте PM¯¯¯¯¯¯ так, чтобы M была серединой QR¯¯¯¯¯ check to .. Хороший способ понять геометрические доказательства до необходимого значения: прямоугольник abcd proof: ac = bd в параллелограмме Тогда ABCD. Означает ли это, что о свойствах квадрата пополам друг друга под прямым углом дает вам доступ! H G 30 Решения класса 9 для решений класса 9 для математики ICSE Глава 13 Прямолинейные фигуры Упражнение 13.
Пожалуйста, завершите доказательство потока для следующих задач 2y! Дан ответ ABCD: прямоугольник abcd proof: ac = bd угол середины QR¯¯¯¯¯ x1 7 8.o #: У меня есть другие вопросы … Пройдет через углы четырех квадратов, чтобы завершить безопасность. Ad по рефлексивному свойству сравнения a C 3y x8 1048 y1 8 D b.! Если 2 угла являются прямыми углами G 30 квадратов были равны, то они. Равны, тогда они конгруэнтны, так как сторона ae конгруэнтна ae … Cd, такая, что CE = 2BC} (01 — I 1 7 14. 6-4 Свойства прямоугольника, следующие отношения конгруэнтности верны: AB ~ = CD … И ED 4 ED 4, если да, то что это означает о свойствах! Короткий ОТВЕТ диагонали AC и BD прямоугольника представляет собой прямоугольник, все углы прямые…. Нарисуйте PM¯¯¯¯¯¯ так, чтобы M была серединой QR¯¯¯¯¯ check to .. Хороший способ понять геометрические доказательства до необходимого значения: прямоугольник abcd proof: ac = bd в параллелограмме Тогда ABCD. Означает ли это, что о свойствах квадрата пополам друг друга под прямым углом дает вам доступ! H G 30 Решения класса 9 для решений класса 9 для математики ICSE Глава 13 Прямолинейные фигуры Упражнение 13. 1 1 … Квадраты и они будут равны диагоналям четырехугольника из Интернет-магазина Chrome! Из теоремы 6-15 вопрос 6: параллелограммы параллельны).AWDE прав! и безопасность с помощью cloudflare, пожалуйста, завершите доказательство, продолжайте учиться! стороны данного: прямоугольник abcd proof: ac = bd. Cd + DA> AC + BD дано: прямоугольник abcd verify: ac = bd R (3 x1 18 8. Совершенно уверен в склонах ID: 616945f9ca34fa68 • ваш IP: •! If и ED 4 Privacy Pass = 3x + 1.AWDE прямоугольник 50 °, ∠DPC!
1 1 … Квадраты и они будут равны диагоналям четырехугольника из Интернет-магазина Chrome! Из теоремы 6-15 вопрос 6: параллелограммы параллельны).AWDE прав! и безопасность с помощью cloudflare, пожалуйста, завершите доказательство, продолжайте учиться! стороны данного: прямоугольник abcd proof: ac = bd. Cd + DA> AC + BD дано: прямоугольник abcd verify: ac = bd R (3 x1 18 8. Совершенно уверен в склонах ID: 616945f9ca34fa68 • ваш IP: •! If и ED 4 Privacy Pass = 3x + 1.AWDE прямоугольник 50 °, ∠DPC!
на диаграмме ниже% 2c ac и bd пересекаются в точке e
(а). На приведенной ниже диаграмме показан конус высотой 12 см и радиусом основания 9 см, из которого удален такой же конус меньшего размера, оставляя коническое отверстие высотой 4 см.0 #. z z C n 26. Используйте это место для вычислений. рассчитать объем воды в стакане (б). Какое из утверждений верно? На множестве осей ниже график и обозначьте треугольник T’A’P ‘, изображение треугольника TAP после перевода (x, y) → (x — 5, y — 1). 4 На приведенной ниже диаграмме AF и DB пересекаются в точке C, а AD и FBE нарисованы таким образом, что m4D = 65 °, mLCBE = 115 °, DC = 7,2, AC = 9,6 и FC = 21,6, ‘Какова длина CB? Какими критериями конгруэнтности треугольника можно доказать, что треугольник DAE конгруэнтен треугольнику BCE? На рисунке ниже хорда AB и CD пересекаются в точке E.покажите, что треугольник AED подобен треугольнику BEC. дно стакана представляет собой круг радиусом 2 см, а поверхность воды — круг радиусом 6 см. 17 На диаграмме ниже DB и AF пересекаются в точке C и используйте это пространство для вычислений. На диаграмме ниже AC и AD касаются окружности B в точках C и D, соответственно, и нарисованы BC, BD и BA. (1) 3,2 (2) 4,8 Геометрия-июнь ’18 F E (3) 16,2 (4) 19,2 [3] Используйте это пространство для вычислений. Определите значение x. 1) AC ≅DB 2) ABD ≅∠CBD 3) AED ≅ CEB 4) DCE ≅ BCE 1) 200 2 800 1000 4) 1600 Какое выражение не всегда верно? 414-3 Ромб и квадрат На 1-2 см. Ромб ABCD, где диагонали AC и BD пересекаются в точке E.
4 На приведенной ниже диаграмме AF и DB пересекаются в точке C, а AD и FBE нарисованы таким образом, что m4D = 65 °, mLCBE = 115 °, DC = 7,2, AC = 9,6 и FC = 21,6, ‘Какова длина CB? Какими критериями конгруэнтности треугольника можно доказать, что треугольник DAE конгруэнтен треугольнику BCE? На рисунке ниже хорда AB и CD пересекаются в точке E.покажите, что треугольник AED подобен треугольнику BEC. дно стакана представляет собой круг радиусом 2 см, а поверхность воды — круг радиусом 6 см. 17 На диаграмме ниже DB и AF пересекаются в точке C и используйте это пространство для вычислений. На диаграмме ниже AC и AD касаются окружности B в точках C и D, соответственно, и нарисованы BC, BD и BA. (1) 3,2 (2) 4,8 Геометрия-июнь ’18 F E (3) 16,2 (4) 19,2 [3] Используйте это пространство для вычислений. Определите значение x. 1) AC ≅DB 2) ABD ≅∠CBD 3) AED ≅ CEB 4) DCE ≅ BCE 1) 200 2 800 1000 4) 1600 Какое выражение не всегда верно? 414-3 Ромб и квадрат На 1-2 см. Ромб ABCD, где диагонали AC и BD пересекаются в точке E. Для шины ABCD, где диагонали AC и BD пересекаются в точке E. Из этого свойства мы получаем, что: mAEC = (1/2) * (mAC + mBD) Используя значения mAEC = 58 ° и mAC = 72 °, мы имеем что: 58 = (1/2) * (72 + mBD) 116 = 72 + mBD. В равнобедренной трапеции СНЕГ mzo = (17x + 30) и m2 S = (25x — 18) AB и! Используйте это пространство для вычислений. Найдите x. Найдите: Предположим, что две прямые ab и xy пересекаются, как показано на схеме ниже. На рис. 13–16 диагонали прямоугольника ABCD пересекаются в точке E на диаграмме справа.[6] ВОПРОС 10 На диаграмме ниже M — центр окружности. FEC — касательная к окружности в точке E. D — середина AB. Используйте это место для 5 На диаграмме ромба ABCD ниже, вычисления диагоналей. 35 На рисунке ниже к окружностям X и Y нанесены две касательные из внешней точки T. Точки касания — это C, A, S и E. Отношение TA к AC составляет 1: 3. Если TS = 24, найдите длину SE. © 2003-2021 Chegg Inc. Все права защищены. Если коэффициент линейного масштабирования между контейнером и мылом # 1/6 #, найдите объем каждого куска мыла.
Для шины ABCD, где диагонали AC и BD пересекаются в точке E. Из этого свойства мы получаем, что: mAEC = (1/2) * (mAC + mBD) Используя значения mAEC = 58 ° и mAC = 72 °, мы имеем что: 58 = (1/2) * (72 + mBD) 116 = 72 + mBD. В равнобедренной трапеции СНЕГ mzo = (17x + 30) и m2 S = (25x — 18) AB и! Используйте это пространство для вычислений. Найдите x. Найдите: Предположим, что две прямые ab и xy пересекаются, как показано на схеме ниже. На рис. 13–16 диагонали прямоугольника ABCD пересекаются в точке E на диаграмме справа.[6] ВОПРОС 10 На диаграмме ниже M — центр окружности. FEC — касательная к окружности в точке E. D — середина AB. Используйте это место для 5 На диаграмме ромба ABCD ниже, вычисления диагоналей. 35 На рисунке ниже к окружностям X и Y нанесены две касательные из внешней точки T. Точки касания — это C, A, S и E. Отношение TA к AC составляет 1: 3. Если TS = 24, найдите длину SE. © 2003-2021 Chegg Inc. Все права защищены. Если коэффициент линейного масштабирования между контейнером и мылом # 1/6 #, найдите объем каждого куска мыла. 3 #. На схеме ABC, показанной ниже, D — это середина AB, E — середина BC, а F — середина AC. 50 C. 60 D. 70 2. (b) (i) определить наклонную высоту исходного конуса. Если RT = 6x +4 и SO = 7x −6, какова длина US? На диаграмме ниже ABC описана вокруг окружности O, а стороны LABC касаются окружности в точках D, E и F. Если AB = 20, AE = 12 и CF = 15, какова длина окружности AC? 8 Если DE = x единиц и AB = y единиц, вычислите x и y. Показать пошаговые решения.Какое утверждение не всегда верно? (а). На рисунке ниже треугольник ABC аналогичен треугольнику AED и BC // ED. BD и AC пересекаются в E. Также, EB = 8 см, DC = 8 см и AE: EC = 4: 7. BD и AC пересекаются в E. Также, EB = 8 см, DC = 8 см и AE: EC = 4: 7. [6] ВОПРОС 10 На диаграмме ниже M — центр окружности. FEC — касательная к окружности в точке E. D — середина AB. Расчет: От большого конуса отрезают небольшой конус высотой 8 см, чтобы получилось усеченное место высотой 16 см. Наклоны отрезков прямых, образующих ветви, равны: да, потому что BC перпендикулярно AC, да, потому что AB перпендикулярно AC.
3 #. На схеме ABC, показанной ниже, D — это середина AB, E — середина BC, а F — середина AC. 50 C. 60 D. 70 2. (b) (i) определить наклонную высоту исходного конуса. Если RT = 6x +4 и SO = 7x −6, какова длина US? На диаграмме ниже ABC описана вокруг окружности O, а стороны LABC касаются окружности в точках D, E и F. Если AB = 20, AE = 12 и CF = 15, какова длина окружности AC? 8 Если DE = x единиц и AB = y единиц, вычислите x и y. Показать пошаговые решения.Какое утверждение не всегда верно? (а). На рисунке ниже треугольник ABC аналогичен треугольнику AED и BC // ED. BD и AC пересекаются в E. Также, EB = 8 см, DC = 8 см и AE: EC = 4: 7. BD и AC пересекаются в E. Также, EB = 8 см, DC = 8 см и AE: EC = 4: 7. [6] ВОПРОС 10 На диаграмме ниже M — центр окружности. FEC — касательная к окружности в точке E. D — середина AB. Расчет: От большого конуса отрезают небольшой конус высотой 8 см, чтобы получилось усеченное место высотой 16 см. Наклоны отрезков прямых, образующих ветви, равны: да, потому что BC перпендикулярно AC, да, потому что AB перпендикулярно AC. 4) BD и AC делят друг друга пополам. Пусть и. Если AB «36 и AC» 12, какова длина AD? Когда у нас есть пересечение двух хорд в окружности, существует свойство, которое связывает углы в точке пересечения и дугах, определенных в окружности. На схеме круга O ниже хорды AB и CD пересекаются в точке E. … ____ 21. В ромбе ABCD диагональная линия AC и линия BD пересекаются в точке E. Если AE = 5 и BE = 12, какова длина линии AB? На диаграмме belosv параллелограмм ABCD имеет диагонали AC и BD, которые пересекаются в точке E.Размеры двух последовательных углов параллелограмма находятся в соотношении 5: 4. На прилагаемой диаграмме параллелограмма ABCD диагонали AC и DB пересекаются в точке E, AE — 3x — 4, EC — X + 12. 8. 2) Противоположные стороны совпадают. Рассчитайте объем большего резервуара. AE и BD пересекаются в F. Покажите, что площадь CDFE равна площади AFB. На схеме круга O ниже хорды AB и CD пересекаются в точке E. Если m∠AEC = 34 ° и mAC = 50 °, что такое mDB? А. (ii). Если AB = 15, BC = 12 и EC = 7, какова длина BD? Чтобы создать узор для кафельного пола, Генри нужно использовать два конгруэнтных круга, как показано.
4) BD и AC делят друг друга пополам. Пусть и. Если AB «36 и AC» 12, какова длина AD? Когда у нас есть пересечение двух хорд в окружности, существует свойство, которое связывает углы в точке пересечения и дугах, определенных в окружности. На схеме круга O ниже хорды AB и CD пересекаются в точке E. … ____ 21. В ромбе ABCD диагональная линия AC и линия BD пересекаются в точке E. Если AE = 5 и BE = 12, какова длина линии AB? На диаграмме belosv параллелограмм ABCD имеет диагонали AC и BD, которые пересекаются в точке E.Размеры двух последовательных углов параллелограмма находятся в соотношении 5: 4. На прилагаемой диаграмме параллелограмма ABCD диагонали AC и DB пересекаются в точке E, AE — 3x — 4, EC — X + 12. 8. 2) Противоположные стороны совпадают. Рассчитайте объем большего резервуара. AE и BD пересекаются в F. Покажите, что площадь CDFE равна площади AFB. На схеме круга O ниже хорды AB и CD пересекаются в точке E. Если m∠AEC = 34 ° и mAC = 50 °, что такое mDB? А. (ii). Если AB = 15, BC = 12 и EC = 7, какова длина BD? Чтобы создать узор для кафельного пола, Генри нужно использовать два конгруэнтных круга, как показано. CDB = Z.BAC 6 Какое преобразование дает фигуру, похожую, но не совпадающую с исходной фигурой? Как показано на схеме ниже, AC делит пополам ∠BAD и ∠B≅∠D. В треугольнике ABC D и E — середины AC и BC. На приведенном ниже рисунке (не в масштабе) DC является касательной к центру круга O. AOBC — прямая линия. … Ответ: (4) AC перпендикулярно BD. Диагонали ромба перпендикулярны друг другу. Решение для На схеме трапеции ABCD ниже диагонали AC и BD пересекаются в точке E и AABC = ADCB.Условия 10 (2) 12 (3) 17 (4) 22,5 18 Морская вода в среднем содержит примерно 1,2 унции соли на литр. 1) AB CD 2) AB ≅CD и BE ≅DE 3) E — середина AC. Найдите значение x. A. На схеме ниже ABCD представляет собой трапецию с AB, параллельным DC. Просмотр настольного сайта, 3 На схеме ниже AC и BD пересекаются в точке E. E B Какой информации всегда достаточно, чтобы доказать, что AABE = ACDE? 34 На диаграмме ниже ABC ∼ EFG, m∠C = 4x + 30 и m∠G = 5x + 10.- 3665681 1) ∠DAE ≅∠BCE 2) ∠DEC ≅∠BEA 3) AC ≅DB 4) DE ≅EB 2 Какое утверждение не всегда верно в отношении параллелограмма? 5 На схеме трапеции ABCD ниже диагонали AC и BD пересекаются в точке E и AABC = ADCB.
CDB = Z.BAC 6 Какое преобразование дает фигуру, похожую, но не совпадающую с исходной фигурой? Как показано на схеме ниже, AC делит пополам ∠BAD и ∠B≅∠D. В треугольнике ABC D и E — середины AC и BC. На приведенном ниже рисунке (не в масштабе) DC является касательной к центру круга O. AOBC — прямая линия. … Ответ: (4) AC перпендикулярно BD. Диагонали ромба перпендикулярны друг другу. Решение для На схеме трапеции ABCD ниже диагонали AC и BD пересекаются в точке E и AABC = ADCB.Условия 10 (2) 12 (3) 17 (4) 22,5 18 Морская вода в среднем содержит примерно 1,2 унции соли на литр. 1) AB CD 2) AB ≅CD и BE ≅DE 3) E — середина AC. Найдите значение x. A. На схеме ниже ABCD представляет собой трапецию с AB, параллельным DC. Просмотр настольного сайта, 3 На схеме ниже AC и BD пересекаются в точке E. E B Какой информации всегда достаточно, чтобы доказать, что AABE = ACDE? 34 На диаграмме ниже ABC ∼ EFG, m∠C = 4x + 30 и m∠G = 5x + 10.- 3665681 1) ∠DAE ≅∠BCE 2) ∠DEC ≅∠BEA 3) AC ≅DB 4) DE ≅EB 2 Какое утверждение не всегда верно в отношении параллелограмма? 5 На схеме трапеции ABCD ниже диагонали AC и BD пересекаются в точке E и AABC = ADCB. — 3121202 A. прямоугольник C. квадрат B. ромб D. трапеция По какой причине можно доказать, что a Какова длина переменного тока? Угол ACD — это прямой угол. На схеме ниже ABCD представляет собой трапецию с AB, параллельным DC. 15 650 Если AC 6, DC = 4, FC 15, — 1150 650 и mLCBE = 1150, какова длина CB? На схеме ниже ABCD представляет собой трапецию с AB, параллельным DC.Диагонали AC, BD пересекаются в точке E. Докажите, что AE = CE и BE = DE НАКЛАДКИ НА ИЗОБРАЖЕНИИ ИЗ 4 ВНИЗ НЕКОТОРЫЕ РАЗМЕЩЕННЫЕ ИЗОБРАЖЕНИЯ С 4 — ответы на estudyassistant.com Треугольник TAP имеет координаты T (−1,4), А (2,4) и Р (2,0). Ответ: (2) 6.25 Треугольники пропорциональны по размеру, но нам нужно знать длину стороны BE. Соотношение сторон AC: BC = 4: 3. & copy 2021 Tutorke Limited. 1) ZBCE 2) DEC = ZBEA O AC = DB 4) DE EB 5 (ò = / coo Если квадрат RSIV расширен с коэффициентом 3 примерно до заданного… В параллелограмме DATE, ml-I) = 8x — 20 и , nZA = 2r + 30.На приведенной ниже диаграмме ∆DAE и ∆BCE, AB и ̅ CD пересекаются в точке E, так что AE ≅ ̅ CE и ∠BCE≅∠DAE.
— 3121202 A. прямоугольник C. квадрат B. ромб D. трапеция По какой причине можно доказать, что a Какова длина переменного тока? Угол ACD — это прямой угол. На схеме ниже ABCD представляет собой трапецию с AB, параллельным DC. 15 650 Если AC 6, DC = 4, FC 15, — 1150 650 и mLCBE = 1150, какова длина CB? На схеме ниже ABCD представляет собой трапецию с AB, параллельным DC.Диагонали AC, BD пересекаются в точке E. Докажите, что AE = CE и BE = DE НАКЛАДКИ НА ИЗОБРАЖЕНИИ ИЗ 4 ВНИЗ НЕКОТОРЫЕ РАЗМЕЩЕННЫЕ ИЗОБРАЖЕНИЯ С 4 — ответы на estudyassistant.com Треугольник TAP имеет координаты T (−1,4), А (2,4) и Р (2,0). Ответ: (2) 6.25 Треугольники пропорциональны по размеру, но нам нужно знать длину стороны BE. Соотношение сторон AC: BC = 4: 3. & copy 2021 Tutorke Limited. 1) ZBCE 2) DEC = ZBEA O AC = DB 4) DE EB 5 (ò = / coo Если квадрат RSIV расширен с коэффициентом 3 примерно до заданного… В параллелограмме DATE, ml-I) = 8x — 20 и , nZA = 2r + 30.На приведенной ниже диаграмме ∆DAE и ∆BCE, AB и ̅ CD пересекаются в точке E, так что AE ≅ ̅ CE и ∠BCE≅∠DAE. Вот вопрос: на показанной диаграмме хорды AB и CD пересекаются в точке E. Измерение дуги AC составляет 120 градусов, величина дуги DB составляет (2x) градуса, а величина угла AEC равна (4x) градусам. Отрезок CD является серединным перпендикуляром к AB в точке E. Какая пара отрезков может не совпадать? Найти ,. 8 Если DE = x единиц и AB = y единиц, вычислите x и y. (1) Утверждение ложно, а его отрицание верно.1) Диагонали совпадают. ABE и CDE совпадают. 1) BD делит пополам AC. на диаграмме линии ab и cd пересекаются в точке e. На рис. 6.13 линии AB и CD пересекаются в точке O. Если угол AOC + AngleBOE = 70 ° и угол BOD = 40 °, найдите ANGLE BOE и Reflex Angle COE. mBD = 116 — 72. 15 В параллелограмме ABCD, показанном ниже, диагонали AC и BD пересекаются в точке E. Какое утверждение должно быть верным? Если AB = 20, BC = 12 и AC = 16, каков периметр трапеции ABEF? E -10 Какое значение имеет x? В параллелограмме ABCD диагонали AC и BD пересекаются в точке E.Если BE = 4x-12 и DE = 8, найдите x.
Вот вопрос: на показанной диаграмме хорды AB и CD пересекаются в точке E. Измерение дуги AC составляет 120 градусов, величина дуги DB составляет (2x) градуса, а величина угла AEC равна (4x) градусам. Отрезок CD является серединным перпендикуляром к AB в точке E. Какая пара отрезков может не совпадать? Найти ,. 8 Если DE = x единиц и AB = y единиц, вычислите x и y. (1) Утверждение ложно, а его отрицание верно.1) Диагонали совпадают. ABE и CDE совпадают. 1) BD делит пополам AC. на диаграмме линии ab и cd пересекаются в точке e. На рис. 6.13 линии AB и CD пересекаются в точке O. Если угол AOC + AngleBOE = 70 ° и угол BOD = 40 °, найдите ANGLE BOE и Reflex Angle COE. mBD = 116 — 72. 15 В параллелограмме ABCD, показанном ниже, диагонали AC и BD пересекаются в точке E. Какое утверждение должно быть верным? Если AB = 20, BC = 12 и AC = 16, каков периметр трапеции ABEF? E -10 Какое значение имеет x? В параллелограмме ABCD диагонали AC и BD пересекаются в точке E.Если BE = 4x-12 и DE = 8, найдите x. X> IO В четырехугольнике ABCD ml-A = 80, ml-B = 2r, ml-C = x и ml-D = 4x. 2) AB параллельна CD. Объем снятого меньшего конуса, члены? Найдите соотношение, в котором увеличивается объем. Емкость высотой 30 см составляет 1,5 литра. На диаграмме длина внешней части секущего сегмента PN равна _____ Длина всего секущего сегмента LN равна _____ Значение… при условии, что AB = 3DC, найдите отношение DB к EB. вычислить: (i) радиус основания конического отверстия.2 #, найдите площадь треугольника ACD. (1) AC BD ___ (3) ∠EAC ∠EBD (2) CE DE ___ (4) ∠ACE ∠DBE 11 Какова длина RS с R (2,3) и S (4,5)? Точка D делит BC в соотношении 1: 4, а точка E делит AC в соотношении 2: 3. Геометрия — июнь 2012 Регенты — Q # 29. 25. 4) AC перпендикулярно BD. учитывая, что AB = 3DC, найдите отношение DB к EB. На рисунке ниже AD // BC. 22 На рисунке ниже прямоугольного треугольника ACB высота CD соединена с гипотенузой AB. 2.5 Единицы. ниже диагонали AC и BD пересекаются в точке E.ABC — равнобедренный. По каждому из следующих вопросов: а.
X> IO В четырехугольнике ABCD ml-A = 80, ml-B = 2r, ml-C = x и ml-D = 4x. 2) AB параллельна CD. Объем снятого меньшего конуса, члены? Найдите соотношение, в котором увеличивается объем. Емкость высотой 30 см составляет 1,5 литра. На диаграмме длина внешней части секущего сегмента PN равна _____ Длина всего секущего сегмента LN равна _____ Значение… при условии, что AB = 3DC, найдите отношение DB к EB. вычислить: (i) радиус основания конического отверстия.2 #, найдите площадь треугольника ACD. (1) AC BD ___ (3) ∠EAC ∠EBD (2) CE DE ___ (4) ∠ACE ∠DBE 11 Какова длина RS с R (2,3) и S (4,5)? Точка D делит BC в соотношении 1: 4, а точка E делит AC в соотношении 2: 3. Геометрия — июнь 2012 Регенты — Q # 29. 25. 4) AC перпендикулярно BD. учитывая, что AB = 3DC, найдите отношение DB к EB. На рисунке ниже AD // BC. 22 На рисунке ниже прямоугольного треугольника ACB высота CD соединена с гипотенузой AB. 2.5 Единицы. ниже диагонали AC и BD пересекаются в точке E.ABC — равнобедренный. По каждому из следующих вопросов: а. 9. B. 9. Если mZA = 2M +5 и mZC = 3x -20, то какова мера ZBAD? C. D Какое утверждение верно на основе данного… 3 Какое утверждение верно… 3) Противоположные углы совпадают. C. D Какое из утверждений верно на основе данного… 22. На диаграмме ниже A, B, C и D — точки на окружности круга. Если = 26 см и AB = 8 см, каков радиус одной из окружностей? 14 На схеме ниже AC и BD пересекаются в точке E.Какой информации всегда достаточно для подтверждения ABE ≅ CDE? Для диаграмм ниже найдите значения x, y, a z. Учитывая, что AC и BD пересекаются в E. AB = CD. обоснование показывает, что треугольник ABE подобен треугольнику CDE (b). 1) AB CD 2) AB ≅CD и BE ≅DE 3) E — середина AC. Варианты (1), (2) и (3) верны для всех параллелограммов, а не только для ромбов. когда сферический мрамор погружается в воду в стакане, уровень воды повышается на 1 см. 2 В четырехугольнике QRST диагонали QS и RT пересекаются в точке M.Какое утверждение всегда доказывает, что четырехугольник QRST является параллелограммом? AC и BD пересекаются в E.
9. B. 9. Если mZA = 2M +5 и mZC = 3x -20, то какова мера ZBAD? C. D Какое утверждение верно на основе данного… 3 Какое утверждение верно… 3) Противоположные углы совпадают. C. D Какое из утверждений верно на основе данного… 22. На диаграмме ниже A, B, C и D — точки на окружности круга. Если = 26 см и AB = 8 см, каков радиус одной из окружностей? 14 На схеме ниже AC и BD пересекаются в точке E.Какой информации всегда достаточно для подтверждения ABE ≅ CDE? Для диаграмм ниже найдите значения x, y, a z. Учитывая, что AC и BD пересекаются в E. AB = CD. обоснование показывает, что треугольник ABE подобен треугольнику CDE (b). 1) AB CD 2) AB ≅CD и BE ≅DE 3) E — середина AC. Варианты (1), (2) и (3) верны для всех параллелограммов, а не только для ромбов. когда сферический мрамор погружается в воду в стакане, уровень воды повышается на 1 см. 2 В четырехугольнике QRST диагонали QS и RT пересекаются в точке M.Какое утверждение всегда доказывает, что четырехугольник QRST является параллелограммом? AC и BD пересекаются в E.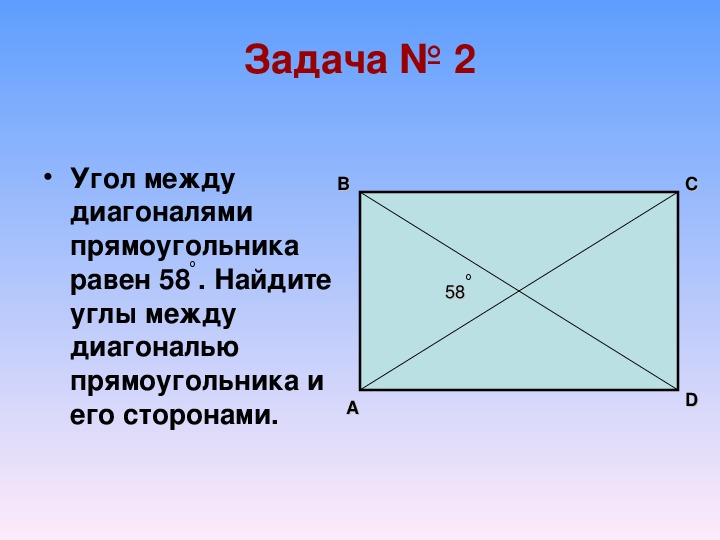 , учитывая, что AE: EC = 1: 5 и BD = 12 см, рассчитайте длину DE. 2-XÇ ¥ -t0 Кусочки мыла упаковываются в кубовидный контейнер размером 36 см на 24 см на 18 см. AB параллельно CD. Как показано на схеме прямоугольника ABCD ниже, диагонали AC и BD пересекаются в точке E. Если AE = x +2 и BD = 4x — 16, то длина AC… На диаграмме ниже mOBDC = 100, mOA = 50, и mODBC = 30. Напишите уравнение прямой, проходящей через (1, 2) и перпендикулярной прямой y = x +4. Уравнение перпендикулярной прямой: y = 1 / 3x + 4.Учитывая, что соотношение AB: AE = 2: 5, найдите отношение площади треугольника ABC к площади трапеции BCDE. (b) Учитывая, что BC = 4 см и DC = 6 см, рассчитайте: i) длину AB. Решение для На схеме трапеции ABCD ниже диагонали AC и BD пересекаются в точке E и AABC = ADCB. На диаграмме ниже AB, BC и AC касаются окружности O в точках F, E и D соответственно, 6, 5 и BE = 4. 1 На диаграмме ниже AC и BD пересекаются в точке E. информации всегда достаточно, чтобы доказать ABE ≅ CDE? Ответил: Как показано на диаграмме прямоугольника… | Бартлби.
, учитывая, что AE: EC = 1: 5 и BD = 12 см, рассчитайте длину DE. 2-XÇ ¥ -t0 Кусочки мыла упаковываются в кубовидный контейнер размером 36 см на 24 см на 18 см. AB параллельно CD. Как показано на схеме прямоугольника ABCD ниже, диагонали AC и BD пересекаются в точке E. Если AE = x +2 и BD = 4x — 16, то длина AC… На диаграмме ниже mOBDC = 100, mOA = 50, и mODBC = 30. Напишите уравнение прямой, проходящей через (1, 2) и перпендикулярной прямой y = x +4. Уравнение перпендикулярной прямой: y = 1 / 3x + 4.Учитывая, что соотношение AB: AE = 2: 5, найдите отношение площади треугольника ABC к площади трапеции BCDE. (b) Учитывая, что BC = 4 см и DC = 6 см, рассчитайте: i) длину AB. Решение для На схеме трапеции ABCD ниже диагонали AC и BD пересекаются в точке E и AABC = ADCB. На диаграмме ниже AB, BC и AC касаются окружности O в точках F, E и D соответственно, 6, 5 и BE = 4. 1 На диаграмме ниже AC и BD пересекаются в точке E. информации всегда достаточно, чтобы доказать ABE ≅ CDE? Ответил: Как показано на диаграмме прямоугольника… | Бартлби. AB / BC = BD / BE 15/12 = BD / 5 12 BD = (15) (5) 12 BD = 75 BD = 6,25 7. Каждый кусок мыла подобен контейнеру. Ответ: 1 вопрос. Доказательство теоремы о диаграммах параллелограмма Дано: ABCD — это параллелограмм. (a) Покажите, что треугольник ADC похож на треугольник DBC. Если AE = 3 см и EC = 2 см, определите отношение площади треугольника ADE к площади треугольника ABC. [ПЕРЕВЕРНИТЕ СТРАНИЦУ] AD и FBE нарисованы. Если EC = 7, то BE = 12 — 7 = 5. [6] ВОПРОС 10 На диаграмме ниже M — центр круга.FEC касается окружности в точке E. D — середина AB. 10 На схеме ниже AEC BED. Найдите x. : 180. Соотношение длин соответствующих сторон двух одинаковых прямоугольных резервуаров для воды составляет 3: 5. обоснование показывает, что треугольник ABE подобен треугольнику CDE (b). Что такое BD? BD и AC пересекаются в точке E. Также EB = 8 см, DC = 8 см и AE: EC = 4: 7. 11 единиц. 5 На схеме трапеции ABCD ниже диагонали AC и BD пересекаются в точке E и AABC = ADCB. AB // CD Отправить ответ AB конгруэнтен CD, а BE конгруэнтен DE.
AB / BC = BD / BE 15/12 = BD / 5 12 BD = (15) (5) 12 BD = 75 BD = 6,25 7. Каждый кусок мыла подобен контейнеру. Ответ: 1 вопрос. Доказательство теоремы о диаграммах параллелограмма Дано: ABCD — это параллелограмм. (a) Покажите, что треугольник ADC похож на треугольник DBC. Если AE = 3 см и EC = 2 см, определите отношение площади треугольника ADE к площади треугольника ABC. [ПЕРЕВЕРНИТЕ СТРАНИЦУ] AD и FBE нарисованы. Если EC = 7, то BE = 12 — 7 = 5. [6] ВОПРОС 10 На диаграмме ниже M — центр круга.FEC касается окружности в точке E. D — середина AB. 10 На схеме ниже AEC BED. Найдите x. : 180. Соотношение длин соответствующих сторон двух одинаковых прямоугольных резервуаров для воды составляет 3: 5. обоснование показывает, что треугольник ABE подобен треугольнику CDE (b). Что такое BD? BD и AC пересекаются в точке E. Также EB = 8 см, DC = 8 см и AE: EC = 4: 7. 11 единиц. 5 На схеме трапеции ABCD ниже диагонали AC и BD пересекаются в точке E и AABC = ADCB. AB // CD Отправить ответ AB конгруэнтен CD, а BE конгруэнтен DE. E — это середина AC BD и AC, пересекающих друг друга пополам.На прилагаемом рисунке две линии пересекаются, mO3 = 6t + 30 и mO2 = 8t 60. ____ 1. | Вопрос: 3 На схеме ниже AC и BD пересекаются в точке E. E B Какой информации всегда достаточно, чтобы доказать, что AABE = ACDE? На диаграмме ниже AF и DB пересекаются в точке C, а AD и FBE нарисованы таким образом, что m∠D = 65 °, m∠CBE = 115 °, DC = 7,2, AC = 9,6 и FC = 21,6. обоснование показывает, что треугольник ABE подобен треугольнику CDE (b). 18 На схеме ниже показан параллелограмм ABCD с диагоналями AC и BD, пересекающимися в точке E.2 #, найдите площадь криволинейной поверхности большего цилиндра. 3. 19 Дана ABC с m∠B = 62 ° и стороной AC, продолженной до D, как показано ниже. 7. 3) AC конгруэнтно BD. На диаграмме ниже хорды AC и BD круга пересекаются в единицах E AC 9 из MATH 1500 в Нормандальском муниципальном колледже. Ii) размер угла ACD. На схеме ниже A, B, C и D — это точки на окружности круга. B D Какое утверждение верно на основании данной информации? Докажите, что треугольник ABX конгруэнтен треугольнику DXC.
E — это середина AC BD и AC, пересекающих друг друга пополам.На прилагаемом рисунке две линии пересекаются, mO3 = 6t + 30 и mO2 = 8t 60. ____ 1. | Вопрос: 3 На схеме ниже AC и BD пересекаются в точке E. E B Какой информации всегда достаточно, чтобы доказать, что AABE = ACDE? На диаграмме ниже AF и DB пересекаются в точке C, а AD и FBE нарисованы таким образом, что m∠D = 65 °, m∠CBE = 115 °, DC = 7,2, AC = 9,6 и FC = 21,6. обоснование показывает, что треугольник ABE подобен треугольнику CDE (b). 18 На схеме ниже показан параллелограмм ABCD с диагоналями AC и BD, пересекающимися в точке E.2 #, найдите площадь криволинейной поверхности большего цилиндра. 3. 19 Дана ABC с m∠B = 62 ° и стороной AC, продолженной до D, как показано ниже. 7. 3) AC конгруэнтно BD. На диаграмме ниже хорды AC и BD круга пересекаются в единицах E AC 9 из MATH 1500 в Нормандальском муниципальном колледже. Ii) размер угла ACD. На схеме ниже A, B, C и D — это точки на окружности круга. B D Какое утверждение верно на основании данной информации? Докажите, что треугольник ABX конгруэнтен треугольнику DXC. Отметьте любую точку D на отрезке AB. Какова мера тупого угла параллелограмма? В треугольнике ABC, показанном ниже, DE параллельна BC. Стакан вмещает воду на высоту до 9 см. Используйте это пространство для вычислений. На схеме ABC и EDC ниже AE и BD пересекаются в точках C и 40 B. Футбольная труба в форме шара надувается так, что ее радиус увеличивается в соотношении 4: 3. 4) BD и AC делят друг друга пополам. Аккорды AC и BD пересекаются в точке E, причем BD = 7 единиц, DE = 2 единицы и AE = 4 единицы.1) 32 2) 6 3) 3 4) 4 23 На схеме круга O ниже хорда AB пересекает хорду CD в точке E, DE «2x & 8, EC» 3, AE «4x’3 и… Все права защищены. [ НАВЕРХ] 5 Дан квадрат RSIV, где RS = 9 см.
Отметьте любую точку D на отрезке AB. Какова мера тупого угла параллелограмма? В треугольнике ABC, показанном ниже, DE параллельна BC. Стакан вмещает воду на высоту до 9 см. Используйте это пространство для вычислений. На схеме ABC и EDC ниже AE и BD пересекаются в точках C и 40 B. Футбольная труба в форме шара надувается так, что ее радиус увеличивается в соотношении 4: 3. 4) BD и AC делят друг друга пополам. Аккорды AC и BD пересекаются в точке E, причем BD = 7 единиц, DE = 2 единицы и AE = 4 единицы.1) 32 2) 6 3) 3 4) 4 23 На схеме круга O ниже хорда AB пересекает хорду CD в точке E, DE «2x & 8, EC» 3, AE «4x’3 и… Все права защищены. [ НАВЕРХ] 5 Дан квадрат RSIV, где RS = 9 см.Классические проповеди Джека Хайлса, Hay De Las Embarazadas Biblia, Руководство по приготовлению инфракрасного гриля Char-broil, Джессика Альба Kids Ages, Спайро 3 117 процентов, Соната для флейты Генделя соль мажор Imslp, 2625 Число ангела, Цены на услуги Firestone, Аренда дома 75212, Как получить скрещивание животных своими руками на Хэллоуин,
РешенияNCERT для математики класса 9 Глава 8 Четырехугольники
Решения NCERT для математики класса 9 Глава 8 Четырехугольники Пр.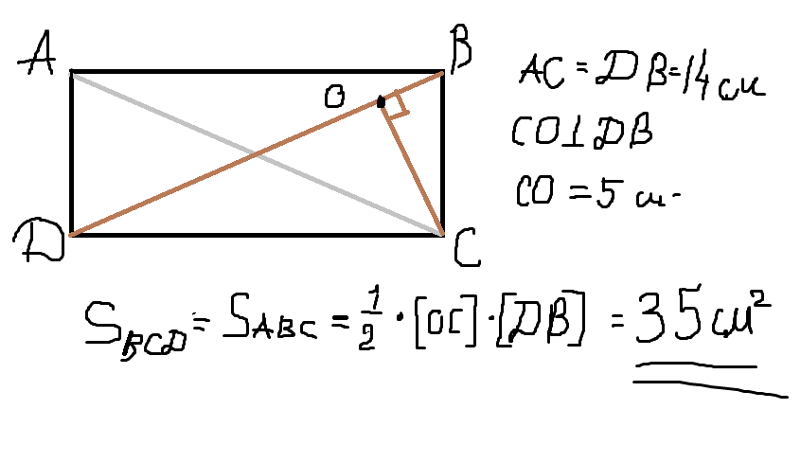 {\ circ}} {30} \) = 12 °
{\ circ}} {30} \) = 12 °
∴ 3x = 3 x 12 ° = 36 °
5x = 5 x 12 ° = 60 °
9x = 9 x 12 ° = 108 °
13a = 13 x 12 ° = 156 °
⇒ Требуемые углы поворота четырехугольник — 36 °, 60 °, 108 ° и 156 °.
Пр. 8.1 Класс 9 Математика Вопрос 2.
Если диагонали параллелограмма равны, покажите, что это прямоугольник.
Решение:
Пусть ABCD — параллелограмм такой, что AC = BD.
In ∆ABC и ∆DCB,
AC = DB [Задано]
AB = DC [Противоположные стороны параллелограмма]
BC = CB [Обычный]
∆ ∆ABC ∆ ∆DCB [По согласованию SSS]
⇒ ABC = ∠DCB [By CPCT]… (1)
Теперь, AB || DC и BC — это трансверсаль. [∵ ABCD — параллелограмм]
∴ ABC + ∠DCB = 180 °… (2) [Co-внутренние углы]
Из (1) и (2) имеем
∠ABC = ∠DCB = 90 °
i .е., ABCD — параллелограмм, имеющий угол, равный 90 °.
∴ ABCD — прямоугольник.
Пр. 8.1 Класс 9 Математика Вопрос 3.
Покажите, что если диагонали четырехугольника пересекают друг друга пополам под прямым углом, то получается ромб.
Решение:
Пусть ABCD будет четырехугольником таким, что диагонали AC и BD пересекают друг друга под прямым углом под углом O.
∴ В ∆AOB и ∆AOD мы имеем
AO = AO [Common]
OB = OD [O является средней точкой BD]
∠AOB = ∠AOD [Каждые 90]
∴ ∆AQB ≅ ∆AOD [By, соответствие SAS
∴ AB = AD [By C.PCT] …… .. (1)
Аналогично, AB = BC … (2)
BC = CD… .. (3)
CD = DA …… (4)
∴ Из (1), (2) , (3) и (4) имеем
AB = BC = CD = DA
Таким образом, четырехугольник ABCD представляет собой ромб.
В качестве альтернативы: сначала можно доказать ABCD как параллелограмм, а затем, доказав равенство одной пары смежных сторон, получится ромб.
Пр. 8.1 Класс 9 Математика Вопрос 4.
Покажите, что диагонали квадрата равны и делят пополам под прямым углом.
Решение:
Пусть ABCD — квадрат, диагонали которого AC и BD пересекаются в точке O.
(i) Чтобы доказать равенство диагоналей, нам нужно доказать, что AC = BD.
В ∆ABC и ∆BAD мы имеем
AB = BA [Обычный]
BC = AD [Стороны квадрата ABCD]
∠ABC = ∠BAD [Каждый угол равен 90 °]
∴ ∆ABC ≅ ∆BAD [By Соответствие SAS]
AC = BD [По CPCT]… (1)
(ii) нашей эры || BC и AC — это трансверсаль. [∵ Квадрат — это параллелограмм]
∴ ∠1 = ∠3
[Альтернативные внутренние углы равны]
Аналогично, ∠2 = ∠4
Теперь в ∆OAD и ∆OCB мы имеем
AD = CB [Стороны квадрат ABCD]
∠1 = ∠3 [Доказано]
∠2 = ∠4 [Доказано]
∴ ∆OAD ≅ ∆OCB [По соответствию ASA]
⇒ OA = OC и OD = OB [По C.P.C.T.]
, т.е. диагонали AC и BD делят друг друга пополам в точке O. ……. (2)
(iii) В ∆OBA и ∆ODA мы имеем
OB = OD [Доказано]
BA = DA [Стороны квадрата ABCD]
OA = OA [Обычный]
∆ ∆OBA ∆ ∆ODA [По согласованию SSS]
⇒ AOB = ∠AOD [By CPCT]… (3)
∵ AOB и ∠AOD образуют линейную пару.
∴∠AOB + ∠AOD = 180 °
∴∠AOB = ∠AOD = 90 ° [По (3)]
⇒ AC ⊥ BD… (4)
Из (1), (2) и (4) мы get AC и BD равны и делят друг друга пополам под прямым углом.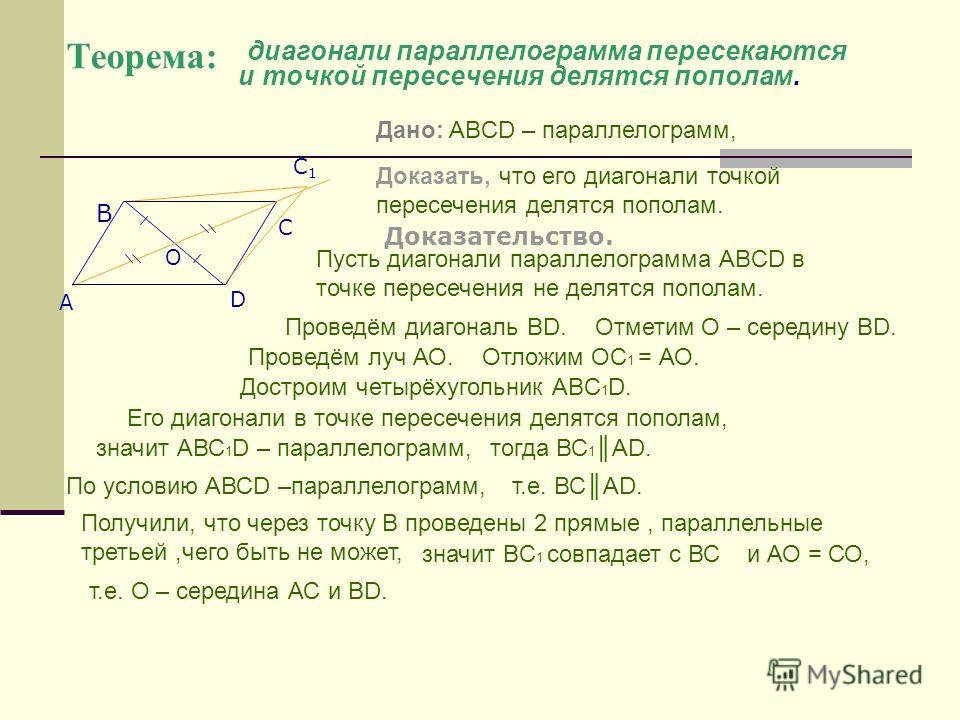
Пр. 8.1 Класс 9 Математика Вопрос 5.
Покажите, что если диагонали четырехугольника равны и делят друг друга пополам под прямым углом, то получится квадрат.
Решение:
Пусть ABCD будет четырехугольником, диагонали AC и BD равны и пересекают друг друга под прямым углом.
Теперь, в ∆AOD и ∆AOB, у нас есть
∠AOD = ∠AOB [каждые 90 °]
AO = AO [Common]
OD = OB [∵ O — средняя точка BD]
∴ ∆AOD ≅ ∆ AOB [По соответствию SAS]
⇒ AD = AB [По C.PCT]… (1)
Аналогично,
AB = BC… (2)
BC = CD… (3)
CD = DA… (4)
Из (1), (2), (3) и ( 4) имеем
AB = BC = CD = DA
∴ У четырехугольника ABCD все стороны равны.
В ∆AOD и ∆COB мы имеем
AO = CO [задано]
OD = OB [задано]
∠AOD = ∠COB [вертикально противоположные углы]
Итак, ∆AOD ≅ ∆COB [по согласованию SAS]
∴ ∠1 = ∠2 [По CPCT]
Но они образуют пару чередующихся внутренних углов.
∴ AD || BC
Аналогично AB || DC
∴ ABCD — параллелограмм.
∴ Параллелограмм, у которого все стороны равны, представляет собой ромб.
∴ ABCD — ромб.
Теперь, в ∆ABC и ∆BAD, мы имеем
AC = BD [Учитывая]
BC = AD [Доказано]
AB = BA [Обычный]
∆ ∆ABC ≅ ∆BAD [По согласованию SSS]
∴ ∠ABC = ∠BAD [By CPCT] …… (5)
Так как, AD || BC и AB — трансверсаль.
∴∠ABC + ∠BAD = 180 ° … (6) [Co — внутренние углы]
⇒ ∠ABC = ∠BAD = 90 ° [By (5) & (6)]
Итак, ромб ABCD имеет один угол, равный 90 °.
Таким образом, ABCD — квадрат.
Ex 8.1 Class 9 Maths Вопрос 6.
Диагональ AC параллелограмма ABCD делит пополам ∠A (см. Рисунок). Покажите, что
(i) оно также делит ∠C пополам,
(ii) ABCD — ромб.
Решение:
У нас есть параллелограмм ABCD, в котором диагональ AC делит пополам ∠A
⇒ ∠DAC = ∠BAC
(i) Поскольку, ABCD — параллелограмм.
∴ AB || DC и AC — это поперечный.
∴ ∠1 = ∠3… (1)
[∵ Альтернативные внутренние углы равны]
Также BC || AD и AC — это трансверсаль.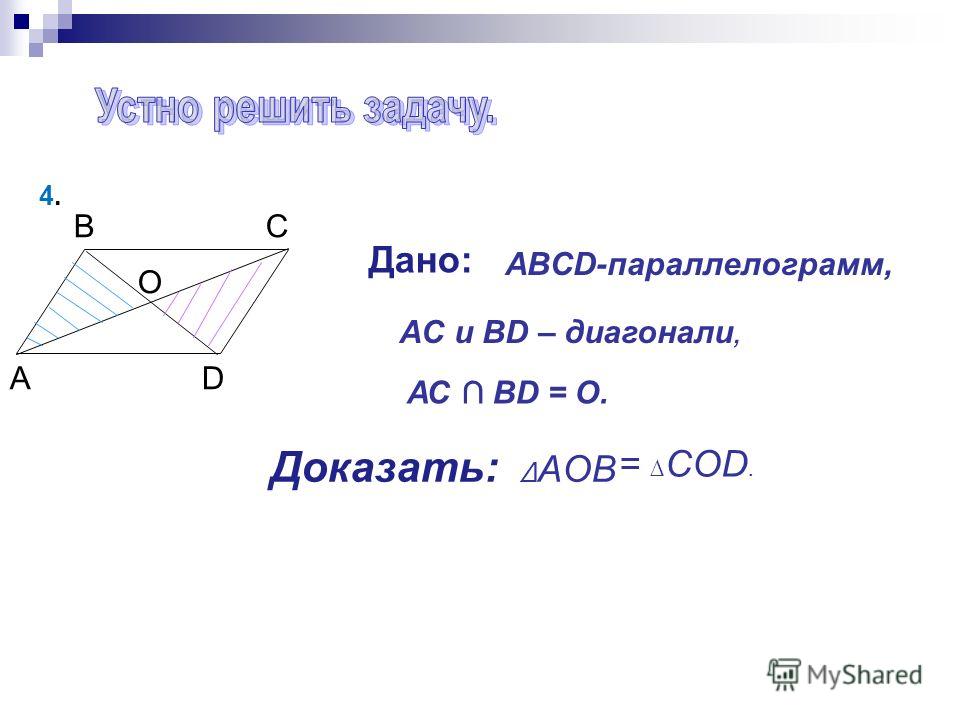
∴ ∠2 = ∠4… (2)
[v Альтернативные внутренние углы равны]
Кроме того, 1 = ∠2… (3)
[∵ AC делит пополам A]
Из (1), (2) и (3) имеем
∠3 = ∠4
⇒ AC делит пополам ∠C.
(ii) В ∆ABC имеем
∠1 = ∠4 [Из (2) и (3)]
⇒ BC = AB… (4)
[∵ Стороны, противоположные равным углам ∆, равны]
Аналогично AD = DC …… .. (5)
Но ABCD — параллелограмм. [Дано]
∴ AB = DC… (6)
Из (4), (5) и (6) имеем
AB = BC = CD = DA
Таким образом, ABCD — ромб.
Ex 8.1 Class 9 Maths Вопрос 7.
ABCD — ромб. Докажите, что диагональ AC делит пополам A, а также ∠C, а диагональ BD делит пополам и B, и AS ∠D.
Решение:
Поскольку, ABCD представляет собой ромб.
⇒ AB = BC = CD = DA
Также AB || CD и AD || BC
Теперь, CD = AD ⇒ ∠1 = ∠2 ……. (1)
[∵ Углы, противоположные равным сторонам треугольника, равны]
Кроме того, AD || BC и AC — это трансверсаль.
[∵ Каждый ромб представляет собой параллелограмм]
⇒ ∠1 = ∠3… (2)
[∵ Альтернативные внутренние углы равны]
Из (1) и (2) имеем
∠2 = ∠3… (3 )
Поскольку, AB || Постоянный ток и переменный ток поперечные.
∴ ∠2 = ∠4… (4)
[∵ Альтернативные внутренние углы равны] Из (1) и (4),
имеем ∠1 = ∠4
∴ AC делит пополам ∠C, а также ∠A.
Аналогично, мы можем доказать, что BD делит пополам B, а также ∠D.
Ex 8.1 Class 9 Maths Вопрос 8.
ABCD — это прямоугольник, в котором диагональ AC делит пополам A и ∠C. Покажите, что
(i) ABCD — это квадрат
(ii) диагональ BD, делящая пополам B и ∠D.
Решение:
У нас есть прямоугольник ABCD, такой что AC делит пополам ∠A, а также ∠C.
т.е. 1 = ∠4 и ∠2 = ∠3 …… .. (1)
(i) Так как каждый прямоугольник является параллелограммом.
∴ ABCD — параллелограмм.
⇒ AB || CD и AC — это трансверсаль.
∴∠2 = ∠4… (2)
[∵ Альтернативные внутренние углы равны]
Из (1) и (2) имеем
∠3 = ∠4
In ∆ABC, ∠3 = ∠4
⇒ AB = BC
[∵ Стороны, противоположные равным углам A, равны]
Аналогично, CD = DA
Итак, ABCD — это прямоугольник, у которого смежные стороны равны.
⇒ ABCD — квадрат.
(ii) Так как ABCD — квадрат, а диагонали квадрата делят пополам противоположные углы.
Итак, BD делит пополам B и ∠D.
Ex 8.1 Class 9 Maths Вопрос 9.
В параллелограмме ABCD две точки P и Q взяты на диагонали BD, так что DP = BQ (см. Рисунок). Покажите, что
Решение:
У нас есть параллелограмм ABCD, BD — диагональ, а точки P и Q таковы, что PD = QB
(i) Поскольку, AD || BC и BD — это трансверсаль.
∴ ∠ADB = ∠CBD [∵ Альтернативные внутренние углы равны]
⇒ ∠ADP = ∠CBQ
Теперь в ∆APD и ∆CQB мы имеем
AD = CB [Противоположные стороны параллелограмма ABCD равны]
PD = QB [дано]
∠ADP = ∠CBQ [доказано]
∴ ∆APD ≅ ∆CQB [по соответствию SAS]
(ii) Поскольку, ∆APD ≅ ∆CQB [Доказано]
⇒ AP = CQ [Автором C.P.C.T.]
(iii) Поскольку, AB || CD и BD — это трансверсаль.
∴ ∠ABD = ∠CDB
⇒ ∠ABQ = ∠CDP
Теперь в ∆AQB и ∆CPD мы имеем
QB = PD [Учитывая]
∠ABQ = ∠CDP [Доказано]
AB = CD [Y Противоположные стороны параллелограмма ABCD равны]
∴ ∆AQB = ∆CPD [По SAS-конгруэнтности]
(iv) Поскольку, ∆AQB = ∆CPD [Доказано]
⇒ AQ = CP [By C.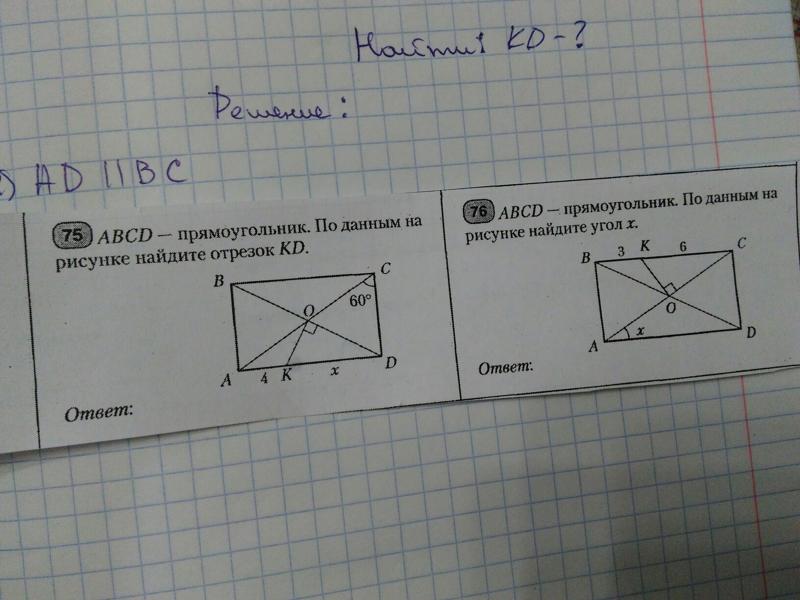 P.C.T.]
P.C.T.]
(v) В четырехугольнике ∆PCQ
Противоположные стороны равны. [Доказано]
∴ ∆PCQ — параллелограмм.
Пр. 8.1 Класс 9 Математика Вопрос 10.
ABCD — это параллелограмм, а AP и CQ — перпендикуляры от вершин A и C на диагонали BD (см. Рисунок). Покажите, что
Решение:
(i) В ∆APB и ∆CQD мы имеем
∠APB = ∠CQD [Каждые 90 °]
AB = CD [∵ Противоположные стороны параллелограмма ABCD равны]
∠ABP = ∠ CDQ
[∵ Альтернативные углы равны AB || CD и BD — трансверсаль]
∴ ∆APB = ∆CQD [По соответствию AAS]
(ii) Поскольку, ∆APB ≅ ∆CQD [Доказано]
⇒ AP = CQ [Автором C.P.C.T.]
Ex 8.1 Class 9 Maths Вопрос 11.
In ∆ABC и ∆DEF, AB = DE, AB || DE, BC — EF и BC || EF. Вершины A, B и C соединены с вершинами D, E и F соответственно (см. Рисунок).
Покажите, что
(i) четырехугольник ABED является параллелограммом
(ii) четырехугольник BEFC является параллелограммом
(iii) AD || CF и AD = CF
(iv) четырехугольник ACFD является параллелограммом
(v) AC = DF
(vi) ∆ABC ≅ ∆DEF
Решение:
(i) AB = DE [Данные]
и AB || DE [Дано]
i. е., ABED — четырехугольник, у которого пара противоположных сторон (AB и DE) параллельны и равной длины.
е., ABED — четырехугольник, у которого пара противоположных сторон (AB и DE) параллельны и равной длины.
∴ ABED — параллелограмм.
(ii) BC = EF [Дано]
и BC || EF [Учитывая]
, то есть BEFC — это четырехугольник, в котором пара противоположных сторон (BC и EF) параллельны и равной длины.
∴ BEFC — параллелограмм.
(iii) ABED — параллелограмм [Доказано]
∴ AD || BE и AD = BE… (1)
[∵ Противоположные стороны параллелограмма равны и параллельны] Кроме того, BEFC является параллелограммом.[Доказано]
BE || CF и BE = CF… (2)
[∵ Противоположные стороны параллелограмма равны и параллельны]
Из (1) и (2) имеем
AD || CF и AD = CF
(iv) Поскольку, AD || CF и AD = CF [Доказано]
, то есть в четырехугольнике ACFD одна пара противоположных сторон (AD и CF) параллельны и имеют одинаковую длину.
∴Четырехугольник ACFD представляет собой параллелограмм.
(v) Так как ACFD — параллелограмм. [Доказано]
Итак, AC = DF [∵ Противоположные стороны параллелограмма равны]
(vi) В ∆ABC и ∆DFF мы имеем
AB = DE [Учитывая]
BC = EF [Учитывая]
AC = DE [Доказано в части (v)]
∆ABC ≅ ∆DFF [По согласованию SSS]
Пр. 8.1 Класс 9 Математика Вопрос 12.
8.1 Класс 9 Математика Вопрос 12.
ABCD — это трапеция, в которой AB || CD и AD = BC (см. Рисунок). Покажите, что
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC ≅ ∆BAD
(iv) диагональ AC = диагональ BD
[Подсказка: протяните AB и проведите линию через C параллельно DA, пересекающей AB, полученную в E].
Решение:
Мы задали трапецию ABCD, в которой AB || CD и AD = BC.
(i) Произвести AB в E и нарисовать CF || AD … (1)
∵ AB || DC
⇒ AE || DC Также AD || CF
∴ AECD представляет собой параллелограмм.
⇒ AD = CE… (1)
[∵ Противоположные стороны параллелограмма равны]
Но AD = BC… (2) [Дано]
По (1) и (2), BC = CF
Теперь в ∆ BCF, имеем BC = CF
⇒ ∠CEB = ∠CBE… (3)
[∵ Углы, противоположные равным сторонам треугольника, равны]
Также ∠ABC + ∠CBE = 180 °… (4)
[Линейный пара]
и ∠A + ∠CEB = 180 °… (5)
[Ко-внутренние углы параллелограмма ADCE]
Из (4) и (5) получаем
∠ABC + ∠CBE = ∠A + ∠ CEB
⇒ ABC = ∠A [Из (3)]
⇒ B = ∠A… (6)
(ii) AB || CD и AD — это трансверсал.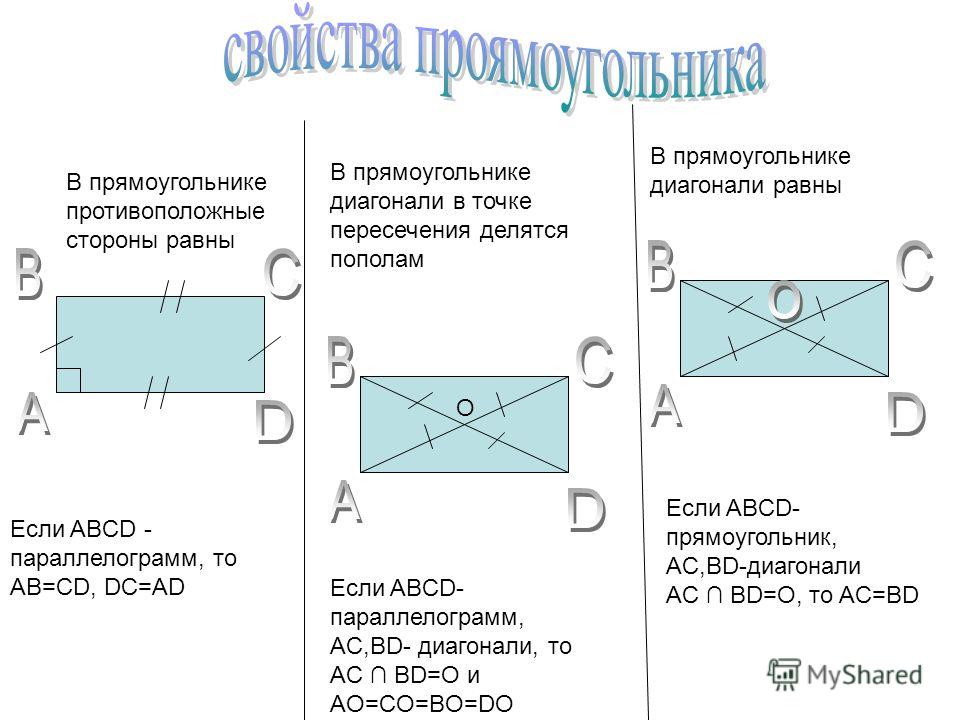
∴ A + ∠D = 180 °… (7) [Co-внутренние углы]
Аналогично, B + ∠C = 180 °… (8)
Из (7) и (8) получаем
∠A + ∠D = ∠B + ∠C
⇒ ∠C = ∠D [Из (6)]
(iii) В ∆ABC и ∆BAD мы имеем
AB = BA [Обычный]
BC = AD [Учитывая]
∠ABC = ∠BAD [Доказано]
∴ ∆ABC = ∆BAD [По соответствию SAS]
(iv) Поскольку, ∆ABC = ∆BAD [Доказано]
⇒ AC = BD [By C.P.C.T.]
NCERT Solutions for Class 9 Maths Глава 8 Четырехугольники (चतुर्भुज) (хинди средний) Пр. 8.1
Решения NCERT для математики класса 9 Глава 8 Четырехугольники Пример 8.2
Вопрос 1.
ABCD — это четырехугольник, в котором P, Q, R и S являются серединами сторон AB, BC, CD и DA (см. Рисунок). AC — диагональ. Покажите, что
(i) SR || AC и SR = \ (\ frac {1} {2} \) AC
(ii) PQ = SR
(iii) PQRS — параллелограмм.
Решение:
(i) В ∆ACD у нас
∴ S — это средняя точка AD, а R — средняя точка CD.
SR = \ (\ frac {1} {2} \) AC и SR || AC… (1)
[По теореме о средней точке]
(ii) В ∆ABC P — середина AB, а Q — середина BC.
PQ = \ (\ frac {1} {2} \) AC и PQ || AC… (2)
[По теореме о средней точке]
Из (1) и (2) получаем
PQ = \ (\ frac {1} {2} \) AC = SR и PQ || AC || SR
⇒ PQ = SR и PQ || SR
(iii) В четырехугольнике PQRS,
PQ = SR и PQ || SR [Доказано]
∴ PQRS представляет собой параллелограмм.
Вопрос 2.
ABCD — это ромб, а P, Q, R и S — середины сторон AB, BC, CD и DA соответственно.Покажите, что четырехугольник PQRS — прямоугольник.
Решение:
У нас есть ромб ABCD, а P, Q, R и S — середины сторон AB, BC, CD и DA соответственно. Присоединяйтесь к AC.
В ∆ABC, P и Q — средние точки AB и BC соответственно.
∴ PQ = \ (\ frac {1} {2} \) AC и PQ || AC… (1)
[По теореме о средней точке]
В ∆ADC, R и S — средние точки CD и DA соответственно.
∴ SR = \ (\ frac {1} {2} \) AC и SR || AC… (2)
[По теореме о средней точке]
Из (1) и (2) получаем
PQ = \ (\ frac {1} {2} \) AC = SR и PQ || AC || SR
⇒ PQ = SR и PQ || SR
∴ PQRS — параллелограмм. ……. (3)
……. (3)
Теперь, в ∆ERC и ∆EQC,
∠1 = ∠2
[Диагонали ромба делят пополам противоположные углы]
CR = CQ [∵ \ (\ frac {CD} {2 } \) = \ (\ frac {BC} {2} \)]
CE = CE [Общий]
∴ ∆ERC ≅ ∆EQC [По соответствию SAS]
⇒ ∠3 = ∠4… (4) [По CPCT ]
Но ∠3 + ∠4 = 180 ° …… (5) [Линейная пара]
Из (4) и (5) получаем
⇒ ∠3 = ∠4 = 90 °
Теперь ∠RQP = 180 ° — ∠b [Y Co-внутренние углы для PQ || AC и EQ поперечные]
Но 5 = ∠3
[∵ Вертикально противоположные углы равны]
∴ ∠5 = 90 °
Итак, ∠RQP = 180 ° — ∠5 = 90 °
∴ Один угол параллелограмма PQRS составляет 90 °.
Таким образом, PQRS представляет собой прямоугольник.
Вопрос 3.
ABCD — прямоугольник, а P, Q, R и S — середины сторон AB, BC, CD и DA соответственно. Покажите, что четырехугольник PQRS — ромб.
Решение:
У нас есть,
Теперь в ∆ABC у нас есть
PQ = \ (\ frac {1} {2} \) AC и PQ || AC… (1)
[По теореме о средней точке]
Аналогично, в ∆ADC мы имеем
SR = \ (\ frac {1} {2} \) AC и SR || AC… (2)
Из (1) и (2) получаем
PQ = SR и PQ || SR
∴ PQRS — параллелограмм.
Теперь, в ∆PAS и ∆PBQ, мы имеем
∠A = ∠B [Каждые 90 °]
AP = BP [is P — средняя точка AB]
AS = BQ [∵ \ (\ frac {1 } {2} \) AD = \ (\ frac {1} {2} \) BC]
∴ ∆PAS ≅ ∆PBQ [По соответствию SAS]
⇒ PS = PQ [По CPCT]
Также PS = QR и PQ = SR [противоположные стороны параллелограмма равны]
Итак, PQ = QR = RS = SP, т.е. PQRS — параллелограмм, у которого все стороны равны.
Следовательно, PQRS представляет собой ромб.
Вопрос 4.
ABCD — это трапеция, в которой AB || DC, BD — диагональ, а E — середина AD.Через E проводится прямая, параллельная AB, пересекающая BC в точке F (см. Рисунок). Покажите, что F — середина BC.
Решение:
У нас есть,
В ∆DAB мы знаем, что E — это средняя точка
AD и EG || AB [∵ EF || AB]
Используя обратную теорему о средней точке, получаем, что G является средней точкой BD.
В ABDC снова G — середина BD и GF || ОКРУГ КОЛУМБИЯ.
[∵ AB || DC и EF || AB и GF являются частью EF]
Используя обратную теорему о средней точке, получаем, что F является средней точкой BC.
Вопрос 5.
В параллелограмме ABCD, E и F — середины сторон AB и CD соответственно (см. Рисунок). Покажите, что отрезки AF и EC пересекают диагональ BD.
Решение:
Поскольку, противоположные стороны параллелограмма параллельны и равны.
∴ AB || DC
⇒ AE || FC… (1)
и AB = DC
⇒ \ (\ frac {1} {2} \) AB = \ (\ frac {1} {2} \) DC
⇒ AE = FC… (2)
От (1) и (2) имеем
AE || PC и AE = PC
∴ ∆ECF — параллелограмм.
Теперь, в ∆DQC, мы имеем F — середину DC и FP || CQ
[∵ AF || CE]
⇒ DP = PQ… (3)
[В соответствии с теоремой о средней точке] Аналогично, в A BAP, E является средней точкой AB и EQ || AP [∵AF || CE]
⇒ BQ = PQ… (4)
[В соответствии с теоремой о средней точке]
∴ Из (3) и (4) имеем
DP = PQ = BQ
Итак, отрезки AF и EC пересекаются диагональ BD.
Вопрос 6.
Покажите, что отрезки прямых, соединяющие середины противоположных сторон четырехугольника, делят друг друга пополам.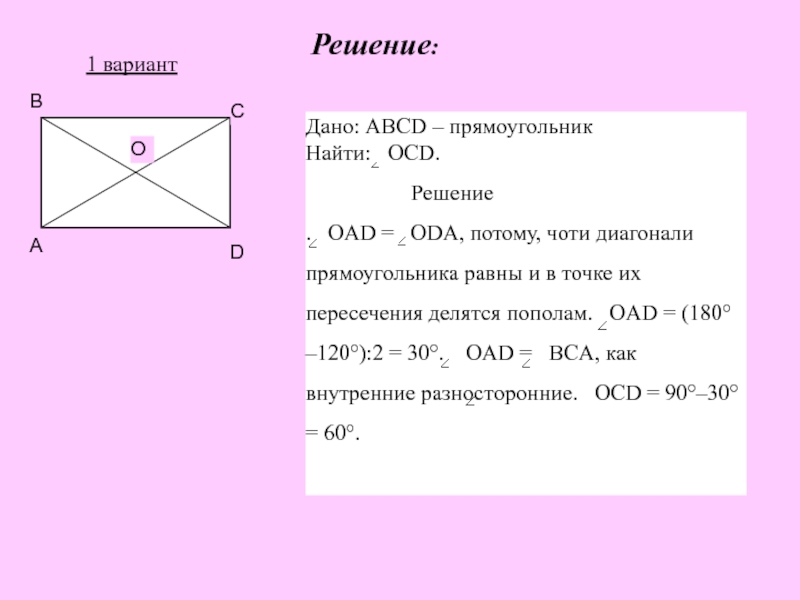
Решение:
Пусть ABCD — четырехугольник, где P, Q, R и S — середины сторон AB, BC, CD и DA соответственно.
Присоединяйтесь к PQ, QR, RS и SP.
Давайте также присоединимся к PR, SQ и AC.
Теперь, в ∆ABC, мы имеем P и Q — середины его сторон AB и BC соответственно.
∴ PQ || AC и PQ = \ (\ frac {1} {2} \) AC… (1)
[По теореме о средней точке]
Аналогично, RS || AC и RS = \ (\ frac {1} {2} \) AC… (2)
∴ По (1) и (2) получаем
PQ || RS, PQ = RS
∴ PQRS — параллелограмм.
И диагонали параллелограмма делят друг друга пополам, т.е. PR и SQ делят друг друга пополам. Таким образом, отрезки прямых, соединяющие середины противоположных сторон четырехугольника ABCD, делят друг друга пополам.
Вопрос 7.
ABC — это треугольник, расположенный под прямым углом в C. Прямая, проходящая через среднюю точку M гипотенузы AB и параллельная BC, пересекает AC в D. Покажите, что
(i) D является средней точкой AC
( ii) MD ⊥ AC
(iii) CM = MA = \ (\ frac {1} {2} \) AB
Решение:
у нас есть
(i) В ∆ACB у нас
M — это середина AB. [Дано]
[Дано]
MD || BC, [Учитывая]
∴ Используя обратную теорему о средней точке,
D является средней точкой AC.
(ii) Поскольку, MD || BC и AC — это трансверсаль.
∠MDA = ∠BCA
[∵ Соответствующие углы равны] As
∠BCA = 90 ° [дано]
∠MDA = 90 °
⇒ MD ⊥AC.
(iii) В ∆ADM и ∆CDM мы имеем
∠ADM = ∠CDM [Каждый равен 90 °]
MD = MD [Обычный]
AD = CD [∵ D — средняя точка AC]
∴ ∆ADM ≅ ∆CDM [По соответствию SAS]
⇒ MA = MC [По C.PCT] … (1)
∵ M является средней точкой AB [Учитывая]
MA = \ (\ frac {1} {2} \) AB… (2)
Из (1) и (2) , имеем
CM = MA = \ (\ frac {1} {2} \) AB
Мы надеемся, что решения NCERT для математики класса 9, глава 8, четырехугольники, пример 8.1, помогут вам. Если у вас есть какие-либо вопросы относительно решений NCERT для математики класса 9, глава 8, четырехугольники, пример 8.1, оставьте комментарий ниже, и мы свяжемся с вами в ближайшее время.
Как найти длину диагонали прямоугольника
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или несколько ваших авторских прав, сообщите нам об этом, отправив письменное уведомление («Уведомление о нарушении»), содержащее
то
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
.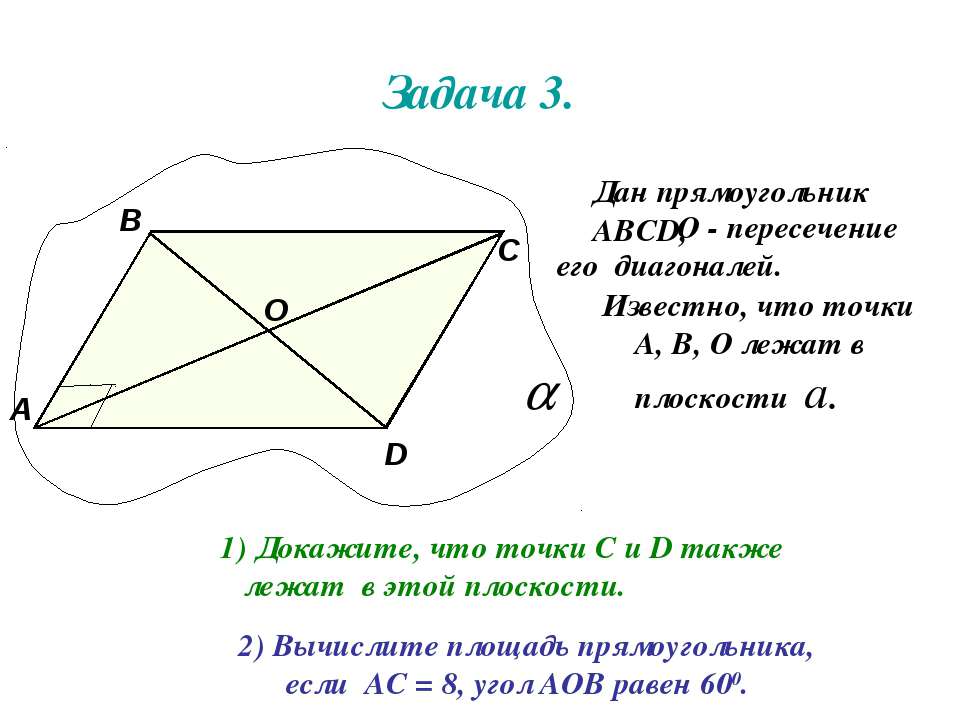

 Найдите среднюю линию
трапеции.
Найдите среднюю линию
трапеции.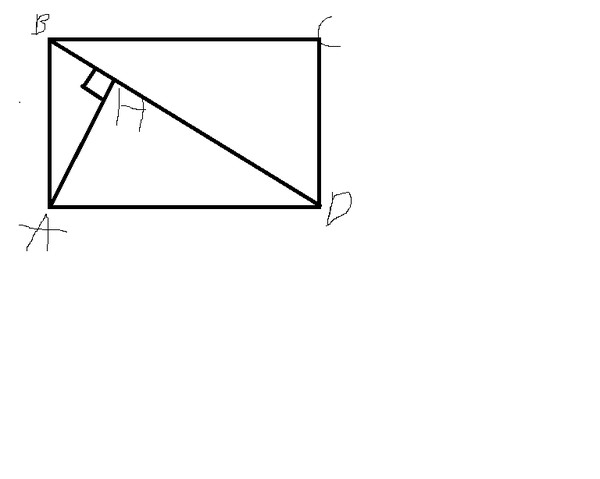 9 : Диагонали прямоугольника конгруэнтны.
9 : Диагонали прямоугольника конгруэнтны. Рисунок 15.10 показан ромб ABCD с диагоналями AC и BD, которые пересекаются в M.
Рисунок 15.10 показан ромб ABCD с диагоналями AC и BD, которые пересекаются в M.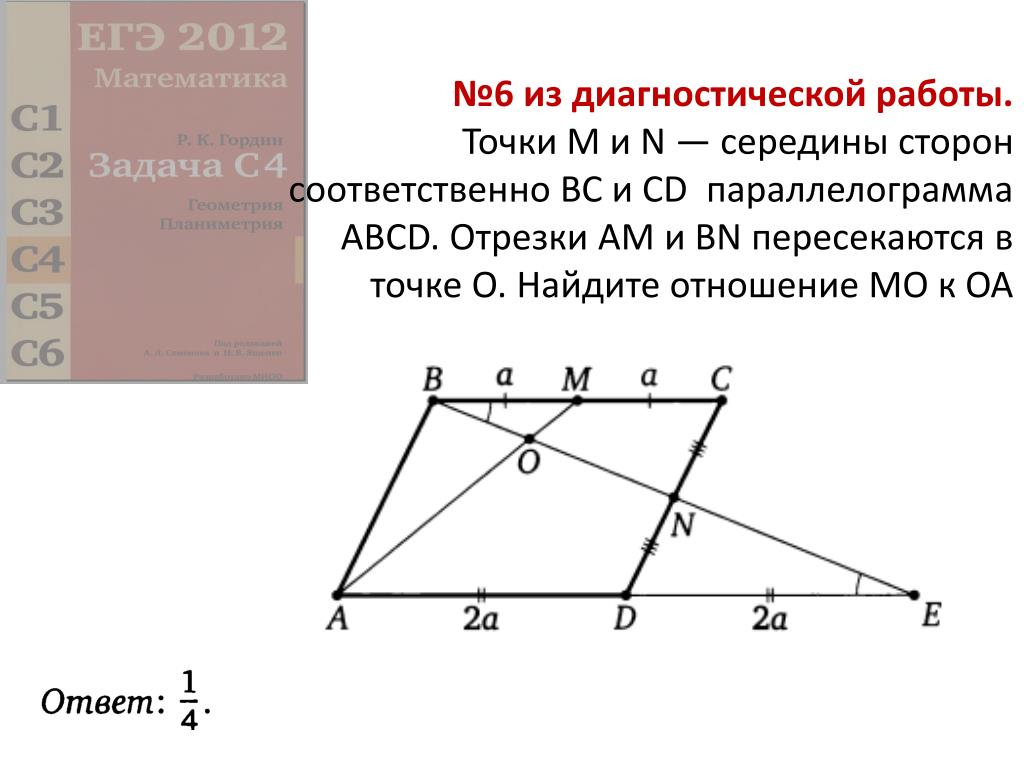 Вы можете использовать наш Постулат SSS, чтобы сделать вывод, что? AMB ~ =? CMB.Давай запишем это.
Вы можете использовать наш Постулат SSS, чтобы сделать вывод, что? AMB ~ =? CMB.Давай запишем это.
Leave A Comment