Блок 3. Задачи на вычисление.
1. Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 15, AC = 25. Ответ :16
2. Окружность, вписанная в треугольник ABC , касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 49°, 69° и 62°. Ответ: 82°, 42°, 56°
3. Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус равно 8. Ответ: 4
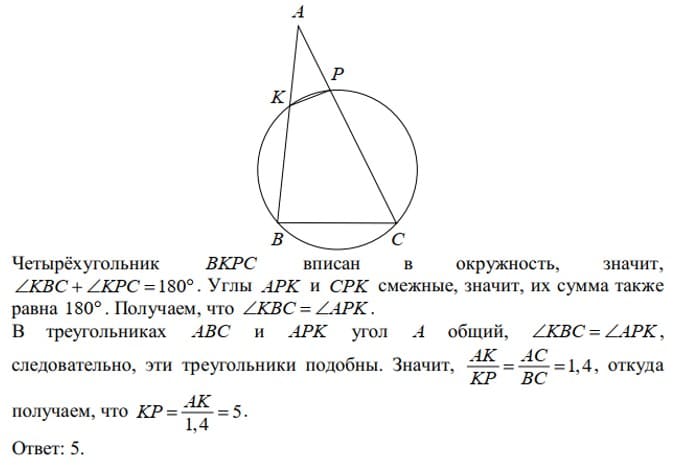
4. Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK = 18, а сторона AC в 1,2 раза больше стороны BC. Ответ:15
5. Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB =16, DC = 24 , AC = 25. Ответ:15
6. В треугольнике АВС углы А и С равны 40° и 60° соответственно.
7. Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 10, DC = 25, AC = 56 . Ответ: 40
8. Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB = 34. Ответ: 68
9. Прямая, параллельная основаниям и трапеции , проходит через точку пересечения диагоналей трапеции и пересекает ее боковые стороны и в точках и соответственно. Найдите длину отрезка , если , . Ответ: 12
10. В прямоугольном треугольнике АВС с прямым угломС известны катеты: АС=6, ВС=8. Найдите медиану СК этого треугольника. Ответ:5
11. Окружность проходит через вершины А и С треугольника АВС и пересекает его стороны АВ и ВС в точках К и Е соответственно. Отрезки АЕ и СК перпендикулярны. Найдите ∠КСВ, если∠АВС = 20°. Ответ:35
Отрезки АЕ и СК перпендикулярны. Найдите ∠КСВ, если∠АВС = 20°. Ответ:35
12. В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD. Ответ: 20
13. Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4. Ответ: 8
14. Катет и гипотенуза прямоугольного треугольника равны 18 и 30. Найдите высоту, проведённую к гипотенузе. Ответ: 14,4
15. Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH = 16. Ответ: 16
16. Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP = 18, а сторона BC в 1,2 раза меньше стороны AB. Ответ:15
17. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN = 13, AC = 65, NC = 28. Ответ: 7
Найдите BN, если MN = 13, AC = 65, NC = 28. Ответ: 7
18. Найдите отношение двух сторон треугольника, если его медиана, выходящая из их общей вершины, образует с этими сторонами углы в 30° и 90°. Ответ: 1:2
19. Высота треугольника разбивает его основание на два отрезка с длинами 8 и 9. Найдите длину этой высоты, если известно, что другая высота треугольника делит ее пополам.
Ответ: 12
20. Биссектрисы углов А и В при боковой стороне АВ трапеции АВСД пересекаются в точке F. Найдите AB, если AF=24. BF=10 . Ответ: 26
21. Диагонали АС и ВД трапеции АВСД пересекаются в точке О . Площади треугольников АОД и ВОС равны соответственно 16 и 9 . Найдите площадь трапеции. Ответ: 49
22. В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 2. Найдите площадь трапеции. Ответ:
23. Основания трапеции равны 16 и 34. Найдите отрезок, соединяющий середины диагоналей трапеции.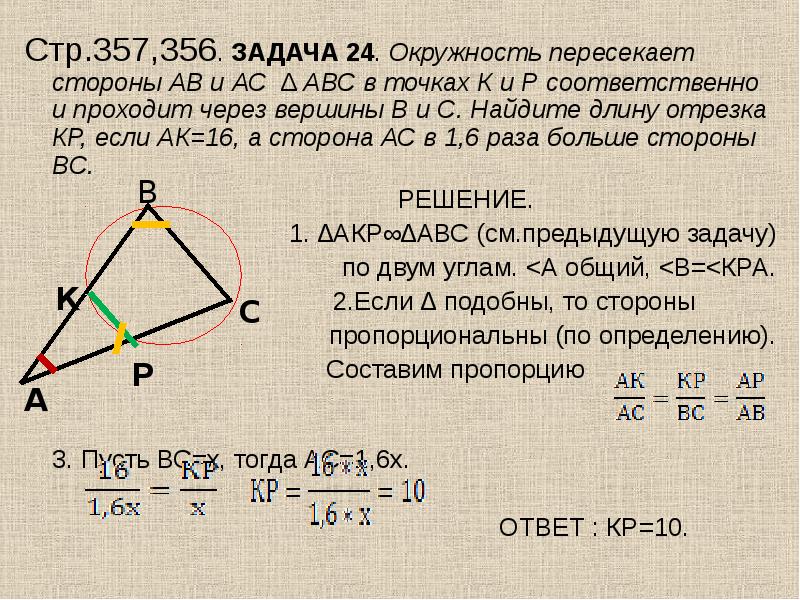
24. Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите AB, если BC = 34. Ответ: 17
25. Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC = 19, а расстояние от точки K до стороны AB равно 7. Ответ: 266
26. Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 30° и 120°, а CD = 25. Ответ:
Самостоятельная работа по теме: «Окружность»
С/р Окружности в ОГЭ
1 вариант
На отрезке AB выбрана точка C так, что AC=14 и BC=36. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB.
 Найдите угол ABC, если угол BAC равен 48°. Ответ дайте в градусах.
Найдите угол ABC, если угол BAC равен 48°. Ответ дайте в градусах.На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠
Найдите угол ABC. Ответ дайте в градусах
Вершины треугольника делят описанную около него окружность на три дуги, длины которых относятся как 2:3:7. Найдите радиус окружности, если меньшая из сторон равна 16.
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=6, а сторона BC в 1,5 раза меньше стороны
С/р Окружности в ОГЭ
2 вариант
Прямая касается окружности в точке K.
 Точка O — центр окружности. Хорда KM образует с касательной угол, равный 39°. Найдите величину угла OMK. Ответ дайте в градусах.
Точка O — центр окружности. Хорда KM образует с касательной угол, равный 39°. Найдите величину угла OMK. Ответ дайте в градусах.Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=79°. Найдите угол BOC. Ответ дайте в градусах.
Четырёхугольник
Найдите угол ABC. Ответ дайте в градусах
Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=18, а расстояния от центра окружности до хорд AB и CD равны соответственно 40 и 9.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B.

С/р Окружности в ОГЭ
3 вариант
Четырёхугольник ABCD вписан в окружность. Угол ABD равен 85°, угол CAD равен 19°. Найдите угол ABC. Ответ дайте в градусах.
Касательные в точках A и B к окружности с центром в точке O пересекаются под углом 88°. Найдите угол ABO. Ответ дайте в градусах.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите
Найдите угол ABC. Ответ дайте в градусах
В трапецию, сумма длин боковых сторон которой равна 18, вписана окружность. Найдите длину средней линии трапеции.
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C.
 Найдите длину отрезка KP, если AK=9, а сторона AC в 3 раза больше стороны BC
Найдите длину отрезка KP, если AK=9, а сторона AC в 3 раза больше стороны BC
С/р Окружности в ОГЭ
4 вариант
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 108°. Найдите угол ACB. Ответ дайте в градусах.
На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=80°. Длина меньшей дуги AB равна 58. Найдите длину большей дуги AB.
Катеты прямоугольного треугольника равны 12 и 5. Найдите радиус окружности, описанной около этого треугольника.
Найдите угол ABC. Ответ дайте в градусах
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC.
 Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=18.
Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=18.Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=8, AC=10.
Геометрические задачи на вычисления (В24) Треугольники
7 sin A. Найдите AB. 25
Прототипы задания 6 1. В треугольнике ABC угол C равен 90 0, AC = 4,8, 25. В треугольнике ABC AC = BC, AB = 8, 33 tga. 7 4 33 sin A. Найдите AB. 25 Найдите AC. 2. В треугольнике ABC угол C равен 90 0,
7 4 33 sin A. Найдите AB. 25 Найдите AC. 2. В треугольнике ABC угол C равен 90 0,
AC 6, cos A. Найдите BH.
Прототипы задания 6 1. Задание 6 ( 26097) 16. Задание 6 ( 20001) В треугольнике ABC угол C равен 90, sin A 0, 6, 21 AC 4. Найдите AB. В треугольнике ABC AC BC 12, sin B. 5 2. Задание 6 ( 29580) Найдите
ПодробнееПрототипы задания В6-2 (2013)
Прототипы задания В6-2 (2013) ( 27742) Один острый угол прямоугольного треугольника на больше другого. Найдите больший острый угол. Ответ дайте в градусах. ( 27743) В треугольнике ABC угол A равен, внешний
ПодробнееТренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Параллелограмм. Периметр параллелограмма равен, а одна из его сторон вдвое больше другой.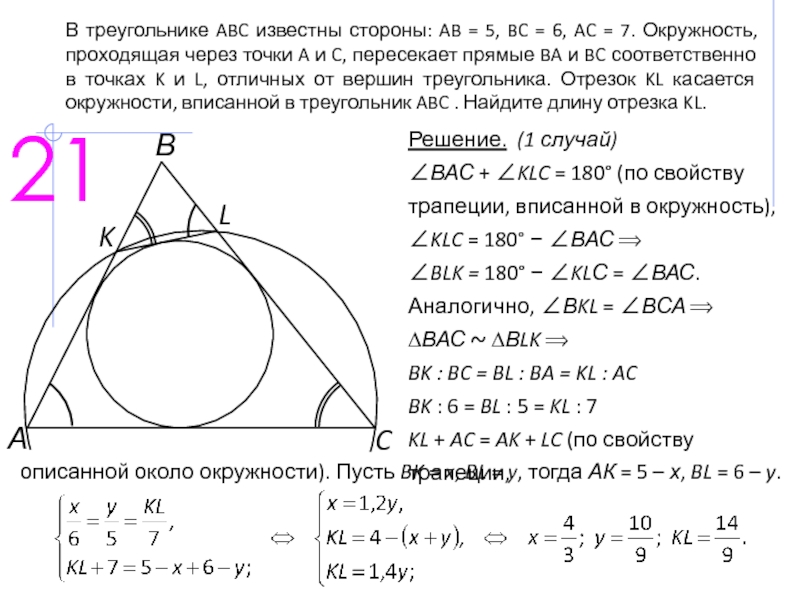 Найдите стороны параллелограмма. и 4. Найдите
Найдите стороны параллелограмма. и 4. Найдите
Средняя линия треугольника
И. В. Яковлев Материалы по математике MathUs.ru Средняя линия треугольника Средняя линия треугольника это отрезок, соединяющий середины двух сторон треугольника. Говоря о средней линии, третью сторону
ПодробнееВ 8 (2014) 16. В треугольнике ABC, 30. В треугольнике ABC угол C равен, CH. высота,,. Найдите AH. высота,,. Найдите BH.
В 8 (2014) 1). В треугольнике ABC угол C равен, CH высота,,. Найдите AH. 2. В треугольнике ABC угол C равен, CH 3. В треугольнике ABC угол C равен,,. Найдите высоту CH. 4. В треугольнике ABC угол C равен,
ПодробнееГеометрия
Геометрия 1. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65 и 50. Найдите меньший угол параллелограмма. 2. Разность углов, прилежащих к одной стороне параллелограмма, равна
2. Разность углов, прилежащих к одной стороне параллелограмма, равна
Многоугольники и их свойства
Задание 19 Планиметрические задачи Многоугольники и их свойства 1. На стороне CD квадрата ABCD построен равносторонний треугольник CPD. Найдите высоту треугольника ADP, проведённую из вершины D, если известно,
Подробнееtgbac. В8 ЕГЭ В ABC C = 90 0, CH высота, AB = 13, tga 5. Найдите BH. 12,5 3 В ABC C = 90 0, AB = 13, tga. Найдите высоту CH.
В-8. ПРОТОТИПЫ Задание ответ В ABC C = 90 0, CH высота, AB =, tga. Найдите AH., В ABC C = 90 0, CH высота, AB =, tga. Найдите, В ABC C = 90 0, AB =, tga. Найдите высоту CH., В ABC C = 90 0, CH высота,
ПодробнееТренировочные задачи
И. В. Яковлев Материалы по математике MathUs.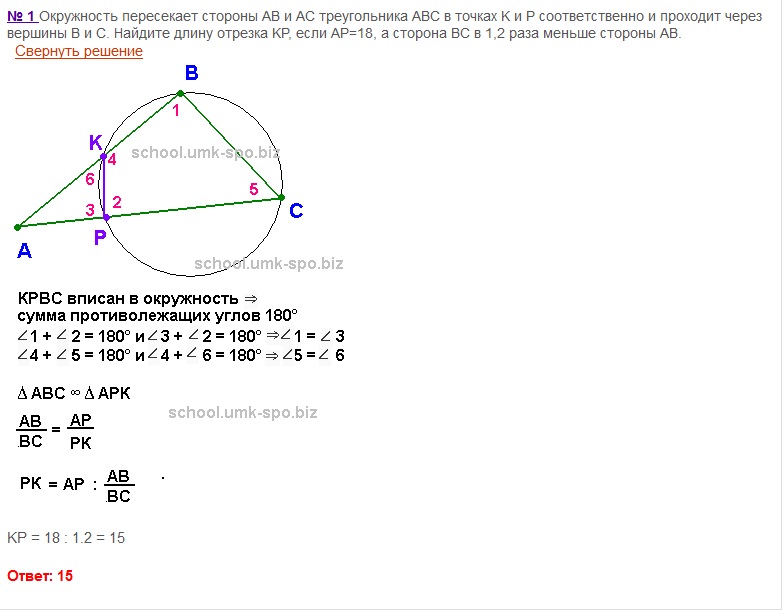 ru Тренировочные задачи Окружность. Свойства окружности. Если хорда не является диаметром, то диаметр, проходящий через середину этой хорды, перпендикулярен
ru Тренировочные задачи Окружность. Свойства окружности. Если хорда не является диаметром, то диаметр, проходящий через середину этой хорды, перпендикулярен
Тренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Теорема Пифагора 1. Найдите диагональ квадрата со стороной a. a. В прямоугольном треугольнике с углом 60 гипотенуза равна. Найдите катеты.
ПодробнееВсе прототипы заданий В года
1. Прототип задания B5 ( 27450) Найдите тангенс угла AOB. Все прототипы заданий В5 2014 года 2. Прототип задания B5 ( 27456) Найдите тангенс угла AOB. 7. Прототип задания B5 ( 27547) Найдите площадь треугольника,
ПодробнееТренировочные задачи
И. В. Яковлев Материалы по математике MathUs.ru Тренировочные задачи Площадь. . Площадь прямоугольника равна 6. Найдите площадь четырёхугольника с вершинами в серединах сторон прямоугольника.. Средняя линия
. Площадь прямоугольника равна 6. Найдите площадь четырёхугольника с вершинами в серединах сторон прямоугольника.. Средняя линия
ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК. 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB.
ЗАДАНИЕ 9 ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК 1. В треугольнике ABC угол C равен,,. Найдите AB. 2. В треугольнике ABC угол C равен,,. Найдите AB. 3. В треугольнике ABC угол C равен,,. Найдите AB. 4. В треугольнике
ПодробнееПланиметрия на ЕГЭ по математике
И. В. Яковлев Материалы по математике MathUs.ru Планиметрия на ЕГЭ по математике Здесь приведены задачи по планиметрии, которые предлагались на ЕГЭ по математике (профильный уровень, сложная часть), а
ПодробнееЗадания В6. . Найдите AB.
Задания В6 1. В треугольнике ABC угол C равен 90, тангенс внешнего угла при вершине A равен -0,1. Найдите tga. 2. Угол A четырехугольника ABCD, вписанного в окружность, равен 52. Найдите угол C этого 3.
В треугольнике ABC угол C равен 90, тангенс внешнего угла при вершине A равен -0,1. Найдите tga. 2. Угол A четырехугольника ABCD, вписанного в окружность, равен 52. Найдите угол C этого 3.
ID_2420 1/11 neznaika.pro
1 Планиметрия: вычисление длин и площадей Ответами к заданиям являются слово, словосочетание, число или последовательность слов, чисел. Запишите ответ без пробелов, запятых и других дополнительных символов.
ПодробнееАнализ геометрических высказываний
Анализ геометрических высказываний 1. Укажите номера верных утверждений. 1) Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны. 2) Вертикальные углы
ПодробнееЗАДАНИЕ 15 Планиметрия Треугольник
ЗАДАНИЕ 15 Планиметрия Треугольник 1.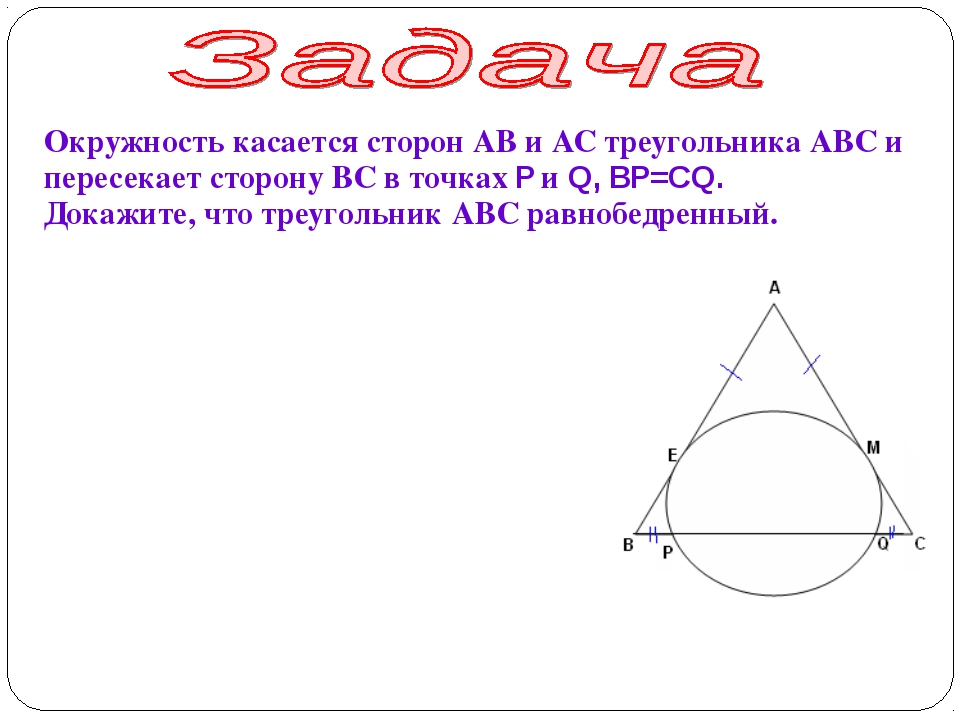 На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. 2. На клетчатой бумаге с клетками
На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. 2. На клетчатой бумаге с клетками
Задание 3, 6, 16. Планиметрия
Задание 3, 6, 6. Планиметрия Угловые соотношения в плоских фигурах Теорема. Сумма смежных углов равна 80 0. и смежные углы Теорема. Биссектрисы смежных углов взаимно перпендикулярны. Теорема. Вертикальные
ПодробнееЗАДАНИЯ С КРАТКИМ ОТВЕТОМ ПО ГЕОМЕТРИИ
ЗАДАНИЯ С КРАТКИМ ОТВЕТОМ ПО ГЕОМЕТРИИ Инструкция. Решите задание. Дайте краткий ответ. 1. Апофема правильной треугольной пирамиды 4 см, а сторона основания 8 см. Найдите площадь боковой поверхности пирамиды.
ПодробнееЗадание 16. Планиметрия
Задание 6. Планиметрия Угловые соотношения в плоских фигурах Теорема. Две прямые, параллельные третьей, параллельны. Теорема. Если две прямые параллельности пересечены секущей, то. Накрест лежащие углы
Две прямые, параллельные третьей, параллельны. Теорема. Если две прямые параллельности пересечены секущей, то. Накрест лежащие углы
ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ
ГЕОМЕТРИЯ: ПЛАНИМЕТРИЯ I Группа 1.01 Разность двух углов, получившихся при пересечении двух прямых, равна 20. Найти больший из этих углов. 1.02 Углы треугольника пропорциональны числам 3:7:8. Найти наибольший
ПодробнееВписанные и описанные окружности
Вписанные и описанные окружности Окружностью, описанной около треугольника, называется окружность, которая проходит через все его вершины. Около всякого треугольника можно описать единственную окружность.
Подробнее А.С. Крутицких и Н.С. Крутицких. Подготовка к ЕГЭ по математике. http://matematikalegko.ru Открытый банк заданий ЕГЭ по математике http://mathege.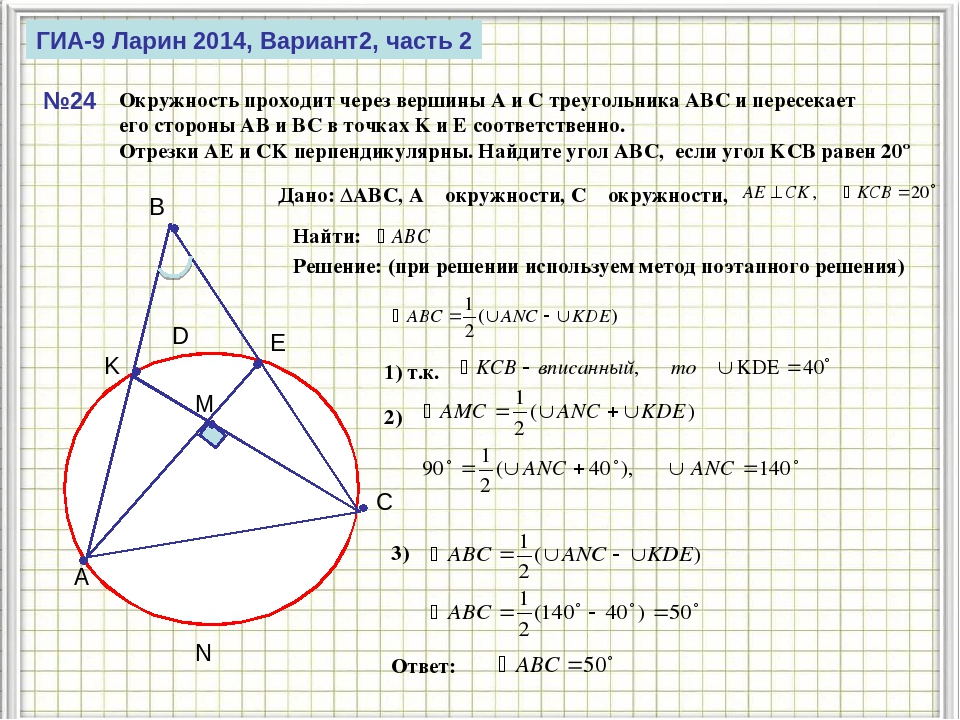 ru Планиметрия: квадрат, прямоугольник, треугольник. 27583.
ru Планиметрия: квадрат, прямоугольник, треугольник. 27583.
Прототипы задания 24 и 26 новые
Прототипы задания 24 и 26
1.Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.
2.Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=7, CK=12.
3.В треугольнике АВС угол C равен 90°, M — середина стороны AB, AB=20, BC=10. Найдите CM.
4.Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN и CM пересекаются в точке O, AN=12, CM=18. Найдите AO.
5.На стороне AC треугольника ABC отмечена точка D так, что AD=3, DC=7. Площадь треугольника ABC равна 20. Найдите площадь треугольника BCD.
6.Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=9, AC=18, MN=8. Найдите AM.
7.Прямая, параллельная стороне AC треугольника АВС, пересекает стороны AB и BC в точках M и N соответственно, AC=27, MN=18.
 Площадь треугольника ABC равна 63. Найдите площадь треугольника MBN.
Площадь треугольника ABC равна 63. Найдите площадь треугольника MBN.8. На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=2, BH=18. Найдите CH.
9.Сторона равностороннего треугольника равна 2. Найдите радиус окружности, вписанной в этот треугольник.
10.Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.
11. Радиус окружности, вписанной в равносторонний треугольник, равен 2. Найдите длину стороны этого треугольника.
12.Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=12, BC=6. Найдите AD.
13.Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=7, AC=20. Найдите AO.
14.Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 10, а одна из диагоналей ромба равна 40. Найдите углы ромба.
15.Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=16, BF=12.

16.Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB=24, а расстояния от центра окружности до хорд AB и CD равны соответственно 16 и 12.
17.Углы B и C треугольника ABC равны соответственно 71° и 79°. Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 8.
18.Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=14.
19.Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 6,4, а AB=6.
20. Сторона равностороннего треугольника равна 14. Найдите высоту (медиану, биссектрису) этого треугольника.
21.Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AP=21, а сторона BC в 1,5 раза меньше стороны AB.

22. Медиана (биссектриса, высота) равностороннего треугольника равна 12. Найдите сторону этого треугольника.
23.В равнобедренную трапецию, периметр которой равен 160, а площадь равна 1280, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
24.В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=6, BC=5.
25.Боковые стороны AB и CD трапеции ABCD равны соответственно 24 и 25, а основание BC равно 9. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
26.В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 12. Найдите стороны треугольника ABC.
27. На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=90, MD=69, H — точка пересечения высот треугольника ABC.
 Найдите AH.
Найдите AH.28.Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 12 и 21 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=.
29.В треугольнике ABC известны длины сторон AB=84, AC=98, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
30. Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
31. В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.
32.Четырёхугольник ABCD со сторонами AB=43 и CD=4 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
33.
 В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 17 и 7. Найдите площадь параллелограмма ABCD.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 17 и 7. Найдите площадь параллелограмма ABCD.34. Углы при одном из оснований трапеции равны 39° и 51°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 19 и 17. Найдите основания трапеции.
35. Середина M стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если BC=9, а углы B и C четырёхугольника равны соответственно 116° и 94°.
36.В треугольнике ABC биссектриса угла A делит высоту, проведённую из вершины B, в отношении 5:4, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=12.
37. В трапеции ABCD основания AD и BC равны соответственно 49 и 21, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
38. Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K.
 Найдите площадь параллелограмма, если BC=12, а расстояние от точки K до стороны AB равно 9.
Найдите площадь параллелограмма, если BC=12, а расстояние от точки K до стороны AB равно 9.39. Периметр ромба равен 24, а один из углов равен 30°. Найдите площадь этого ромба.
40. Сторона ромба равна 9, а расстояние от точки пересечения диагоналей ромба до неё равно 1. Найдите площадь этого ромба.
41. Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=14, DC=42, AC=52.
42. Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=17, AC=51, NC=32.
43. Катеты прямоугольного треугольника равны 18 и 24. Найдите высоту, проведённую к гипотенузе.
44. Катет и гипотенуза прямоугольного треугольника равны 20 и 52. Найдите высоту, проведённую к гипотенузе.
45. Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=6, AC=24.
46. Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно.
 Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.47. Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 135°, а CD=36.
ОГЭ по математике (задание 24)
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=12, а расстояние от точки K до стороны AB равно 9.
В трапеции ABCD основания AD и BC равны соответственно 33 и 11, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
В треугольнике ABC биссектриса угла A делит высоту, проведённую из вершины B, в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.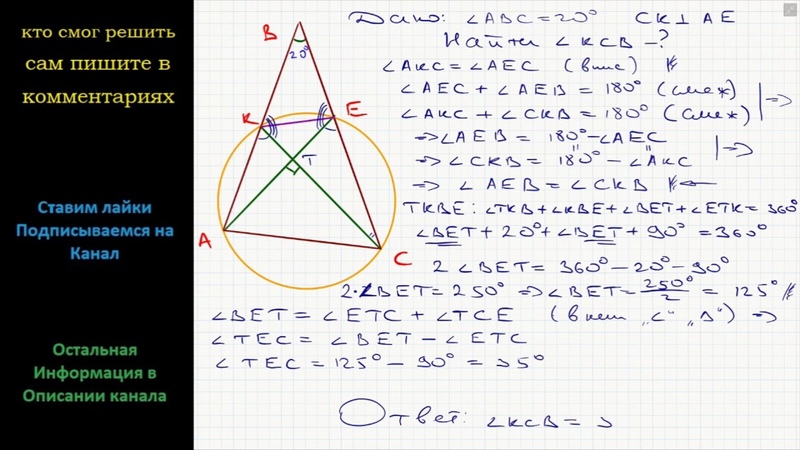
Середина M стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если BC=9, а углы B и C четырёхугольника равны соответственно 116° и 94°.
Углы при одном из оснований трапеции равны 39° и 51°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 19 и 3. Найдите основания трапеции.
Четырёхугольник ABCD со сторонами AB=39 и CD=12 вписан
в окружность. Диагонали AC и BD пересекаются в точке K,
причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Окружности радиусов 42 и 84 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
В треугольнике ABC известны длины сторон AB=30, AC=100, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=12, а расстояние от точки K до стороны AB равно 9.
В трапеции ABCD основания AD и BC равны соответственно 33 и 11, а сумма углов при основании AD равна 90°. Найдите радиус окружности, проходящей через точки A и B и касающейся прямой CD, если AB=20.
В треугольнике ABC биссектриса угла A делит высоту, проведённую из вершины B, в отношении 5:3, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.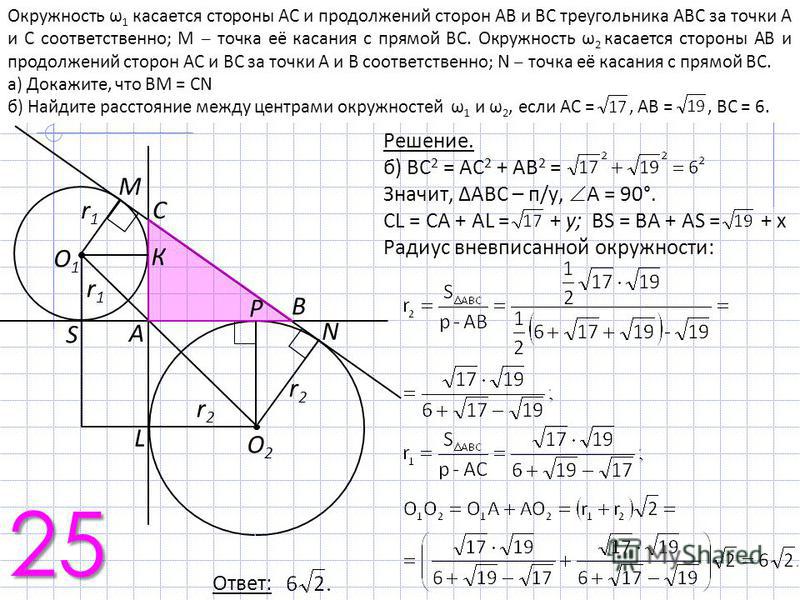
Середина M стороны AD выпуклого четырёхугольника ABCD равноудалена от всех его вершин. Найдите AD, если BC=9, а углы B и C четырёхугольника равны соответственно 116° и 94°.
Углы при одном из оснований трапеции равны 39° и 51°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 19 и 3. Найдите основания трапеции.
Четырёхугольник ABCD со сторонами AB=39 и CD=12 вписан
в окружность. Диагонали AC и BD пересекаются в точке K,
причём ∠AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Окружности радиусов 42 и 84 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
В треугольнике ABC известны длины сторон AB=30, AC=100, точка O — центр окружности, описанной около треугольника ABC. Прямая BD, перпендикулярная прямой AO, пересекает сторону AC в точке D. Найдите CD.
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 18 и 40 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=5/√3.
На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=15, MD=12, H — точка пересечения высот треугольника ABC. Найдите AH.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 8.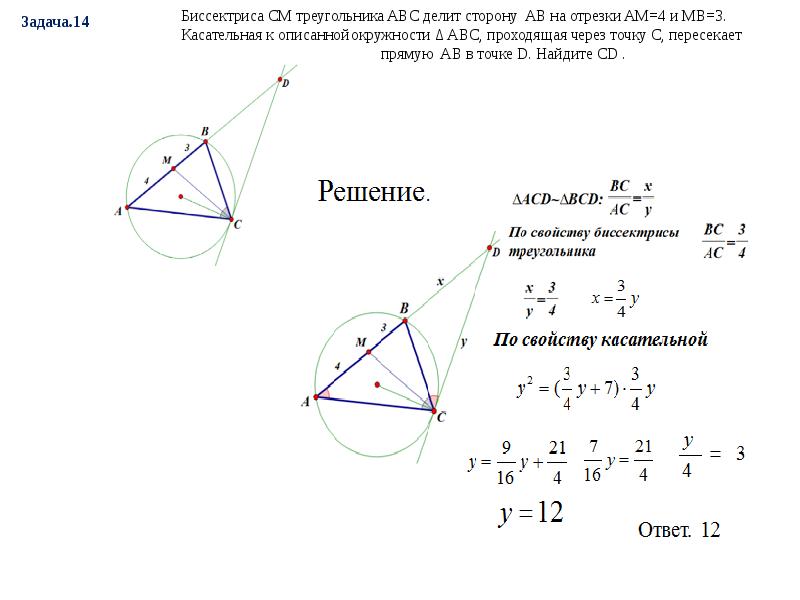 Найдите стороны треугольника ABC.
Найдите стороны треугольника ABC.
Боковые стороны AB и CD трапеции ABCD равны соответственно 6 и 10, а основание BC равно 1. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=4, BC=2.
В равнобедренную трапецию, периметр которой равен 40, а площадь равна 80, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 9 и 5.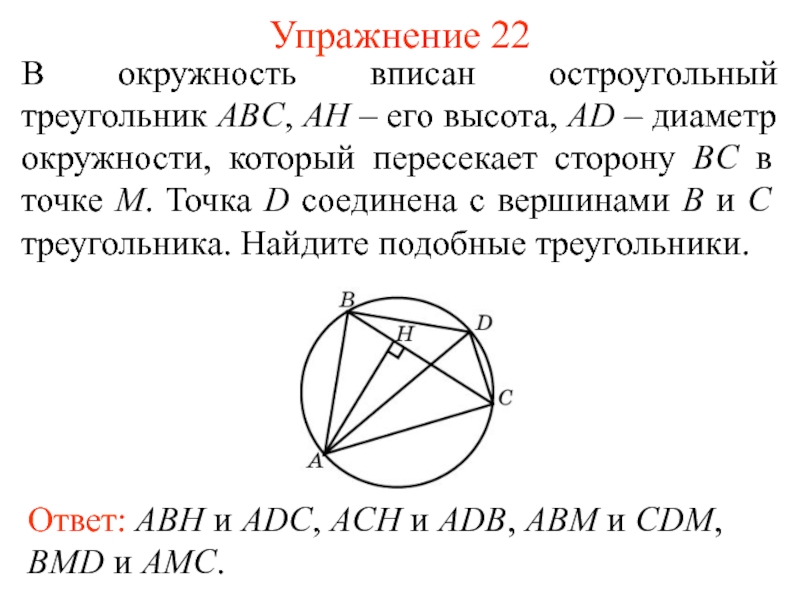 Найдите площадь параллелограмма ABCD.
Найдите площадь параллелограмма ABCD.
Сторона AD параллелограмма ABCD вдвое больше стороны CD.
Точка M — середина стороны AD. Докажите, что CM — биссектриса угла BCD.
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 18 и 40 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=5/√3.
На стороне BC остроугольного треугольника ABC как на диаметре построена полуокружность, пересекающая высоту AD в точке M, AD=15, MD=12, H — точка пересечения высот треугольника ABC. Найдите AH.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 8. Найдите стороны треугольника ABC.
Боковые стороны AB и CD трапеции ABCD равны соответственно 6 и 10, а основание BC равно 1. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=4, BC=2.
В равнобедренную трапецию, периметр которой равен 40, а площадь равна 80, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 13, 9 и 5. Найдите площадь параллелограмма ABCD.
Найдите площадь параллелограмма ABCD.
Сторона AD параллелограмма ABCD вдвое больше стороны CD.
Точка M — середина стороны AD. Докажите, что CM — биссектриса угла BCD.
Биссектрисы углов A и D трапеции ABCD пересекаются в точке M, лежащей на стороне BC. Докажите, что точка M равноудалена
от прямых AB, AD и CD.
В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке P. Докажите, что площади треугольников APB и CPD равны.
В остроугольном треугольнике ABC проведены высоты AA1 и BB1. Докажите, что углы BB1A1 и BAA1 равны.
В выпуклом четырёхугольнике ABCD углы DAC и DBC равны. Докажите, что углы CDB и CAB также равны.
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции.
Основания BC и AD трапеции ABCD равны соответственно 3 и 12, BD=6. Докажите, что треугольники CBD и BDA подобны.
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK=16, а сторона AC в 1,6 раза больше стороны BC.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=3, AC=9.
Углы B и C треугольника ABC равны соответственно 62° и 88°.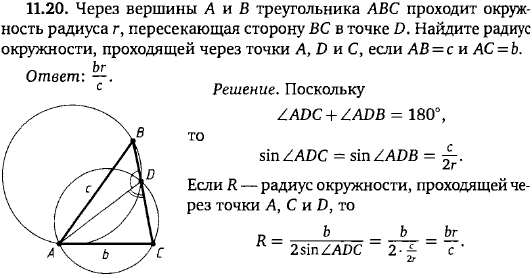
Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 12.
Биссектрисы углов A и D трапеции ABCD пересекаются в точке M, лежащей на стороне BC. Докажите, что точка M равноудалена
от прямых AB, AD и CD.
В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке P. Докажите, что площади треугольников APB и CPD равны.
В остроугольном треугольнике ABC проведены высоты AA1 и BB1. Докажите, что углы BB1A1 и BAA1 равны.
В выпуклом четырёхугольнике ABCD углы DAC и DBC равны. Докажите, что углы CDB и CAB также равны.
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции.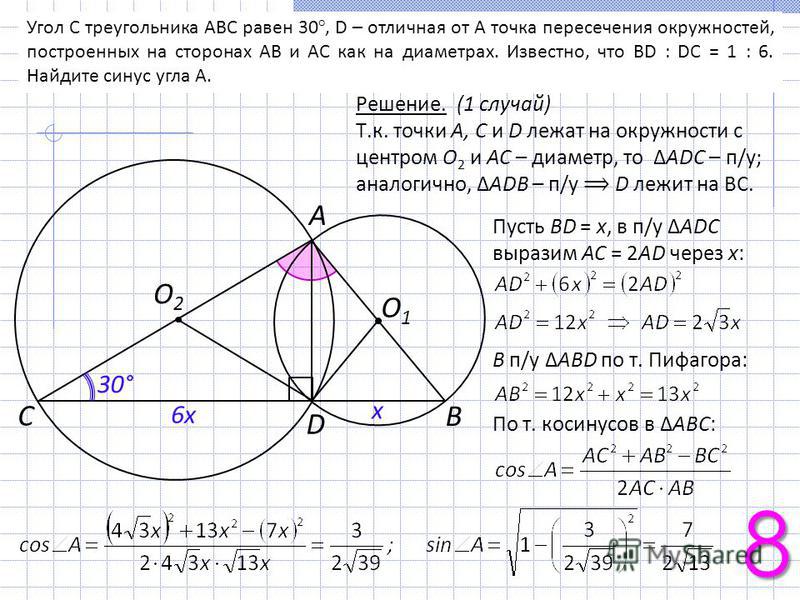
Основания BC и AD трапеции ABCD равны соответственно 3 и 12, BD=6. Докажите, что треугольники CBD и BDA подобны.
Окружность пересекает стороны AB и AC треугольника ABC в точках K и P соответственно и проходит через вершины B и C. Найдите длину отрезка KP, если AK=16, а сторона AC в 1,6 раза больше стороны BC.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=3, AC=9.
Углы B и C треугольника ABC равны соответственно 62° и 88°.
Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 12.
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=15.
Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=15.
Отрезки AB и CD являются хордами окружности. Найдите длину
хорды CD, если AB=24, а расстояния от центра окружности до хорд AB и CD равны соответственно 16 и 12.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=16, BF=12.
Высота AH ромба ABCD делит сторону CD на отрезки DH=16 и CH=4. Найдите высоту ромба.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 13, а одна из диагоналей ромба равна 52. Найдите углы ромба.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=6, CK=10.
Найдите периметр параллелограмма, если BK=6, CK=10.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 150°, а CD=33.
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=45, BC=20, CF:DF=4:1.
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=10, AC=40.
Прямая, параллельная стороне AC треугольника ABC, пересекает
стороны AB и BC в точках M и N соответственно. Найдите BN,
если MN=22, AC=55, NC=36.
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=15.
Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=15.
Отрезки AB и CD являются хордами окружности. Найдите длину
хорды CD, если AB=24, а расстояния от центра окружности до хорд AB и CD равны соответственно 16 и 12.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=16, BF=12.
Высота AH ромба ABCD делит сторону CD на отрезки DH=16 и CH=4. Найдите высоту ромба.
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 13, а одна из диагоналей ромба равна 52. Найдите углы ромба.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK=6, CK=10.
Найдите периметр параллелограмма, если BK=6, CK=10.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 150°, а CD=33.
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=45, BC=20, CF:DF=4:1.
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=10, AC=40.
Прямая, параллельная стороне AC треугольника ABC, пересекает
стороны AB и BC в точках M и N соответственно. Найдите BN,
если MN=22, AC=55, NC=36.
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=10, DC=25, AC=56.
Найдите MC, если AB=10, DC=25, AC=56.
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 29.
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=10, DC=25, AC=56.
Найдите MC, если AB=10, DC=25, AC=56.
Страница не найдена — МОБУ «Карагандинская ООШ»
23 февраля отмечается День воинской славы России- День защитника Отечества. Обучающиеся МОБУ «Карагандинская ООШ» присоединились к акции #Наши Защитники
Читать далеее
Уважаемые родители! Информируем вас о проведении 12 февраля 2021 г. в 18.00 по московскому времени Всероссийского родительского собрания на тему: «Социальные сети» , в рамках которого вас познакомят с популярными среди детей социальными сетями, особенностями их интереса к ним.
Читать далеее
В связи с ростом количества пожаров на территории Оренбургской области, а также ростом количества погибших при пожарах людей на территории Домбаровского района, в целях профилактики пожаров, предупреждения гибели и травмирования людей, отдел надзорной деятельности и профилактической работы по Ясненскому городскому округу, Светлинскому и Домбаровскому районам предлагает Вам агитационные материалы по соблюдению мер пожарной безопасности Видеоролик «Окурки»
Читать далеее
6 февраля 2021 года состоится семнадцатый областной День родной школы, направленный на сохранение преемственности поколений выпускников и лучших школьных традиций, развитие социального партнерства, укрепление кадровой и ресурсной базы школы. Но в соответствии с указом Губернатора Оренбургской области от 17.03.2020 №112 –ук «О мерах по противодействию распространению в Оренбургской области новой коронавирусной инфекции», с учетом эпидемиологической ситуации проведение Дня родной школы будет в дистанционном формате…
Но в соответствии с указом Губернатора Оренбургской области от 17.03.2020 №112 –ук «О мерах по противодействию распространению в Оренбургской области новой коронавирусной инфекции», с учетом эпидемиологической ситуации проведение Дня родной школы будет в дистанционном формате…
Читать далеее
В рамках областного онлайн-месячника «Реализация стратегии развития воспитания в образовательных организациях области» (18 января -18 февраля 2021 г.) запланирован фестиваль видеоселфи (слайдовых презентаций, видеороликов) «Я — классный руководитель» Главная цель фестиваля — популяризация деятельности классного руководителя, повышение социального статуса и престижа профессии педагога. Вашему вниманию предполагается видеоролик классного руководителя МОБУ «Карагандинская ООШ Айтмагамбетовой Жанны Айтмагамбетовны
Читать далеее
27 января отмечается день полного освобождения Ленинграда от фашистской блокады в 1944 году. Ключевым событием Акции явился Всероссийский урок Памяти «Блокадный хлеб», который прошел в МОБУ «Карагандинская ООШ» 27 января 2021 года в день окончания снятия блокады с Ленинграда.
Ключевым событием Акции явился Всероссийский урок Памяти «Блокадный хлеб», который прошел в МОБУ «Карагандинская ООШ» 27 января 2021 года в день окончания снятия блокады с Ленинграда.
Читать далеее
Уважаемые ребята, родители!!! Сообщаем о том, что Оренбургской региональной общественной организацией по развитию культуры и искусства «Союз творческих личностей» при поддержке Фонда президентских грантов успешно завершена реализация проекта по созданию мультфильма «Оренбуржье многонациональное глазами детей». Более 50 детей на базе детской студии юного телеведущего «Premium KIDS TV» создали анимационный фильм о неповторимом своеобразии каждой национальности, о важности хранения традиций и многовековой дружбе народов Оренбуржья. Мультфильм размещен в…
Читать далеее
В период с 15 декабря 2020 года по 15 января 2021 года на территории Оренбургской области проводится месячник по противодействию распространению новой коронавирусной инфекции (2019-nCoV) «Безопасный Новый год». В рамках месячника в МОБУ «Карагандинская ООШ» проводилось административное совещание, на котором педагоги и сотрудники школы ознакомились с методическими рекомендациями месячника, был разработан график дежурства педагогов и сотрудников школы в период подготовки и проведения…
В рамках месячника в МОБУ «Карагандинская ООШ» проводилось административное совещание, на котором педагоги и сотрудники школы ознакомились с методическими рекомендациями месячника, был разработан график дежурства педагогов и сотрудников школы в период подготовки и проведения…
Читать далеее
В период с 25.12.2020 по 01..03.2021 г. будет проводится межведомственная профилактическая акция «Помоги ребенку» с целью оказания практической помощи детям, оказавшимся в трудной жизненной ситуации, защите их прав и законных интересов, охраны жизни и подростков. Приложение …
Читать далеее
23 ноября ученики начальных классов в Оренбургской области выходят в школы с очным форматом обучения. По 5-10 классам и малокомплектным школам решение будет принято оперативным штабом на этой неделе. Зависеть оно будет от эпидемиологической ситуации в территории.
Читать далеее
Эван Чен и пуля; 404 Не найдено
Запрошенный URL-адрес не найден. Извини за это.
00440400 00440000 00440400 00444040 00400000 04040000 04400004 04400444 04400404 00400000 04004440 04404444 04440400 00400000 04000440 04404444 04440404 04404440 04400400 00400004 00004404 00004040 00004404 00004040 00440400 00444000 00400000 00440440 00440004 00400000 00440444 00440440 00400000 00440440 00440404 00400000 00440040 00440000 00400000 00440440 00440004 00400000 00440040 00440000 00400000 00440440 00440444 00400000 00440440 00440404 00400000 00440440 04400440 00400000 00440440 04400400 00400000 00440440 00440404 00400000 00440444 00440400 00400000 00440444 00440040 00400000 00440444 00444004 00400000 00440040 00440000 00400000 00440444 00440000 00400000 00440444 00440040 00400000 00440440 04400440 00400000 00440440 00440040 00400000 00440440 04400044 00400000 00440440 00440404 00400000 00440440 04400400 00400000 00440044 04400004 00400000 00440000 04400400 00400000 00440000 04400004 00400000 00440000 04400400 00400000 00440000 04400004 00400000 00440404 00440444 00400000 00440044 00440004 00400000 00440404 00440040 00400000 00440440 00444000 00400000 00440440 00440004 00400000 00440404 00444000 00400000 00440440 00440400 00400000 00440440 00444000 00400000 00440440 00440040 00400000 00440440 00444004 00400000 00440400 00440040 00400000 00440404 00440404 00400000 00440404 00440404 00400000 00440044 00440004 00400000 00440404 00440004 00400000 00440440 00440444 00400000 00440400 04400400 00400000 00440440 04400004 00400000 00440400 00440004 00400000 00440444 00444000 00400000 00440400 04400440 00400000 00440404 00440440 00400000 00440044 00440000 00400000 00440440 00440444 00400000 00440404 00440440 00400000 00440400 00444000 00400000 00440400 04400004 00400000 00440444 00440000 00400000 00440404 00444004 00400000 00440404 00440444 00400000 00440044 00440404 00400000 00440440 04400404 00400000 00440440 00440040 00400000 00440400 00440444 00400000 00440404 00440404 00400000 00440440 00440444 00400000 00440400 04400004 00400000 00440400 00440404 00400000 00440400 00440440 00400000 00440400 00440044 00400000 00440404 00440004 00400000 00440444 00444004 00400000 00440404 00440004 00400000 00440440 00440444 00400000 00440440 00440004 00400000 00440404 00444000 00400000 00440400 04400400 00400000 00440440 00440444 00400000 00440440 00440004 00400000 00440404 00440444 00400000 00440044 00440404 00400000 00440444 04400004 00400000 00440404 00444004 00400000 00440044 00440044 00400000 00440400 04400004 00400000 00440444 00440000 00400000 00440404 00444004 00400000 00440440 04400400 00400000 00440404 00440440 00400000 00440440 04400040 00400000 00440400 00444004 00400000 00440400 00440444 00400000 00440440 04400044 00400000 00440444 00440404 00400000 00440400 00444004 00400000 00440400 00440444 00400000 00440400 00440440 00400000 00440444 00440404 00400000 00440400 00444004 00400000 00440400 00440444 00400000 00440404 00440440 00400000 00440444 00440044 00400000 00440440 00440040 00400000 00440400 00440444 00400000 00440440 04400044 00400000 00440444 00440444 00400000 00440440 00440044 00400000 00440044 00440040 00400000 00440404 00440404 00400000 00440440 00440444 00400000 00440440 00440400 00400000 00440044 00440040 00400000 00440440 04400044 00400000 00440044 00440000 00400000 00440440 00440004 00400000 00440400 00440044 00400000 00440400 00440040 00400000 00440440 04400400 00400000 00440440 00440040 00400000 00440044 00440040 00400000 00440400 04400404 00400000 00440444 00440000 00400000 00440400 00444004 00400000 00440400 00440044 00400000 00440404 00440040 00400000 00440400 00444004 00400000 00440400 04400004 00400000 00440400 00440044 00400000 00440400 00440040 00400000 00440440 00444000 00400000 00440440 00440040 00400000 00440440 04400400 00400000 00440404 00440004 00400000 00440440 00440444 00400000 00440400 04400004 00400000 00440400 00440404 00400000 00440444 00440044 00400000 00440440 04400040 00400000 00440400 04400044 00400000 00440440 00444004 00400000 00440400 00440040 00400000 00440404 00440004 00400000 00440440 00440044 00400000 00440440 04400400 00400000 00440044 00444004 00400000 00440044 00440040 00400000 00440404 04400004 00400000 00440404 00440044 00400000 00440400 00440040 00400000 00440044 00440000 00400000 00440440 00440004 00400000 00440400 00440444 00400000 00440400 00440440 00400000 00440044 00440000 00400000 00440400 00444004 00400000 00440400 00440444 00400000 00440440 04400044 00400000 00440440 04400400 00400000 00440400 00444004 00400000 00440400 00440044 00400000 00440404 00440040 00400000 00440400 00444004 00400000 00440400 04400004 00400000 00440400 00440044 00400000 00440400 00440040 00400000 00440444 00440000 00400000 00440440 00440044 00400000 00440444 00444004 00400000 00440400 00440040 00400000 00440044 00440000 00400000 00440440 00440004 00400000 00440400 00440444 00400000 00440404 00440404 00400000 00440440 00440444 00400000 00440440 00440040 00400000 00440044 00440044 00400000 00440400 04400004 00400000 00440044 00440000 00400000 00440440 00440004 00400000 00440400 00440444 00400000 00440044 00444004 00400000 00440440 04400004 00400000 00440404 04400004 00400000 00440404 00440444 00400000 00440044 00440404 00400000 00440044 00440000 00400000 00440404 04400004 00400000 00440404 00444000 00400000 00440400 00444004 00400000 00440440 00440444 00400000 00440440 00440040 00400000 00440044 00440040 00400000 00440404 00444004 00400000 00440440 00440444 00400000 00440400 04400004 00400000 00440400 00440440 00400000 00440444 00444000 00400000 00440044 00440000 00400000 00440440 00440044 00400000 00440440 04400400 00400000 00440440 04400044 00400000 00440440 00444000 00400000 00440440 00440040 00400000 00440440 04400400 00400000 00440440 00440400 00400000 00440444 00440044 00400000 00440404 04400004 00400000 00440404 00440044 00400000 00440400 00440040 00400000 00440400 00440040 00400000 00440404 00440004 00400000 00440440 04400040 00400000 00440400 04400400 00400000 00440440 04400040 00400000 00440400 00444004 00400000 00440400 00444000 00400000 00440404 00440040 00400000 00440440 04400440 00400000 00440404 04400004 00400000 00440404 00440444 00400000 00440044 00440400 00400000 00440440 00440444 00400000 00440440 00440400 00400000 00440400 00440444 00400000 00440440 00444000 00400000 00440440 04400044 00400000 00440400 00444004 00400000 00440400 00440444 00400000 00440440 04400044 00400000 00440444 00440404 00400000 00440404 00444004 00400000 00440044 00440040 00400000 00440404 00440440 00400000 00440444 00440404 00400000 00440440 00440400 00400000 00440400 00440444 00400000 00440404 00440440 00400000 00440444 00444004 00400000 00440400 00444004 00400000 00440400 00440444 00400000 00440044 00444004 00400000 00440440 04400400 00400000 00440400 00444004 00400000 00440400 00440044 00400000 00440404 00440040 00400000 00440440 00440044 00400000 00440440 00440400 00400000 00440400 00444000 00400000 00440400 04400004 00400000 00440444 00440000 00400000 00440404 00444004 00400000 00440404 00440444 00400000 00440044 00440404 00400000 00440440 04400404 00400000 00440440 00440040 00400000 00440400 00440444 00400000 00440404 00440404 00400000 00440440 00440444 00400000 00440404 00440004 00400000 00440404 00440404 00400000 00440400 04400004 00400000 00440400 00440400 00400000 00440400 04400004 00400000 00440400 00440044 00400000 00440400 00440040 00400000 00440444 00440044 00400000 00440440 00440004 00400000 00440404 00440444 00400000 00440404 00440440 00400000 00440444 04400004 00400000 00440400 00444004 00400000 00440400 00440444 00400000 00440044 00444004 00400000 00440444 00440404 00400000 00440400 00444004 00400000 00440400 00440444 00400000 00440444 00444000 00400000 00440444 00440000 00400000 00440440 00440040 00400000 00440440 04400400 00400000 00440404 00440404 00400000 00440440 00440444 00400000 00440400 04400004 00400000 00440400 00440404 00400000 00440440 00444000 00400000 00440400 04400044 00400000 00440400 04400004 00400000 00440400 00440044 00400000 00440044 00440400 00400000 00440400 04400404 00400000 00440400 00440044 00400000 00440440 00440444 00400000 00440044 00440000 00400000 00440400 04400040 00400000 00440400 00440400 00400000 00440404 00440004 00400000 00440440 04400440 00400000 00440044 04400400 00400000
% PDF-1. 3
%
488 0 объект
>
endobj
xref
488 160
0000000016 00000 н.
0000003552 00000 н.
0000003760 00000 н.
0000006766 00000 н.
0000007006 00000 н.
0000007090 00000 н.
0000007186 00000 н.
0000007272 00000 н.
0000007419 00000 н.
0000007480 00000 н.
0000007612 00000 н.
0000007673 00000 н.
0000007819 00000 п.
0000007975 00000 п.
0000008074 00000 н.
0000008202 00000 н.
0000008263 00000 н.
0000008420 00000 н.
0000008536 00000 н.
0000008597 00000 н.
0000008767 00000 н.
0000008883 00000 н.
0000008944 00000 н.
0000009129 00000 н.
0000009245 00000 н.
0000009306 00000 н.
0000009461 00000 п.
0000009577 00000 н.
0000009638 00000 н.
0000009816 00000 н.
0000009949 00000 н.
0000010082 00000 п.
0000010143 00000 п.
0000010299 00000 п.
0000010432 00000 п.
0000010533 00000 п.
0000010594 00000 п.
0000010759 00000 п.
0000010858 00000 п.
0000010990 00000 п.
0000011051 00000 п.
0000011215 00000 п.
0000011348 00000 п.
0000011481 00000 п.
3
%
488 0 объект
>
endobj
xref
488 160
0000000016 00000 н.
0000003552 00000 н.
0000003760 00000 н.
0000006766 00000 н.
0000007006 00000 н.
0000007090 00000 н.
0000007186 00000 н.
0000007272 00000 н.
0000007419 00000 н.
0000007480 00000 н.
0000007612 00000 н.
0000007673 00000 н.
0000007819 00000 п.
0000007975 00000 п.
0000008074 00000 н.
0000008202 00000 н.
0000008263 00000 н.
0000008420 00000 н.
0000008536 00000 н.
0000008597 00000 н.
0000008767 00000 н.
0000008883 00000 н.
0000008944 00000 н.
0000009129 00000 н.
0000009245 00000 н.
0000009306 00000 н.
0000009461 00000 п.
0000009577 00000 н.
0000009638 00000 н.
0000009816 00000 н.
0000009949 00000 н.
0000010082 00000 п.
0000010143 00000 п.
0000010299 00000 п.
0000010432 00000 п.
0000010533 00000 п.
0000010594 00000 п.
0000010759 00000 п.
0000010858 00000 п.
0000010990 00000 п.
0000011051 00000 п.
0000011215 00000 п.
0000011348 00000 п.
0000011481 00000 п. 0000011542 00000 п.
0000011709 00000 п.
0000011840 00000 п.
0000011956 00000 п.
0000012017 00000 н.
0000012167 00000 п.
0000012283 00000 п.
0000012344 00000 п.
0000012523 00000 п.
0000012607 00000 п.
0000012668 00000 п.
0000012729 00000 п.
0000012800 00000 п.
0000012861 00000 п.
0000012922 00000 п.
0000012983 00000 п.
0000013054 00000 п.
0000013115 00000 п.
0000013176 00000 п.
0000013247 00000 п.
0000013308 00000 п.
0000013456 00000 п.
0000013527 00000 п.
0000013588 00000 п.
0000013649 00000 п.
0000013710 00000 п.
0000013781 00000 п.
0000013842 00000 п.
0000013903 00000 п.
0000013964 00000 п.
0000014089 00000 п.
0000014150 00000 п.
0000014211 00000 п.
0000014272 00000 п.
0000014420 00000 п.
0000014491 00000 п.
0000014552 00000 п.
0000014700 00000 п.
0000014771 00000 п.
0000014832 00000 п.
0000014893 00000 п.
0000014954 00000 п.
0000015025 00000 п.
0000015086 00000 п.
0000015147 00000 п.
0000015218 00000 п.
0000015279 00000 п.
0000015340 00000 п.
0000011542 00000 п.
0000011709 00000 п.
0000011840 00000 п.
0000011956 00000 п.
0000012017 00000 н.
0000012167 00000 п.
0000012283 00000 п.
0000012344 00000 п.
0000012523 00000 п.
0000012607 00000 п.
0000012668 00000 п.
0000012729 00000 п.
0000012800 00000 п.
0000012861 00000 п.
0000012922 00000 п.
0000012983 00000 п.
0000013054 00000 п.
0000013115 00000 п.
0000013176 00000 п.
0000013247 00000 п.
0000013308 00000 п.
0000013456 00000 п.
0000013527 00000 п.
0000013588 00000 п.
0000013649 00000 п.
0000013710 00000 п.
0000013781 00000 п.
0000013842 00000 п.
0000013903 00000 п.
0000013964 00000 п.
0000014089 00000 п.
0000014150 00000 п.
0000014211 00000 п.
0000014272 00000 п.
0000014420 00000 п.
0000014491 00000 п.
0000014552 00000 п.
0000014700 00000 п.
0000014771 00000 п.
0000014832 00000 п.
0000014893 00000 п.
0000014954 00000 п.
0000015025 00000 п.
0000015086 00000 п.
0000015147 00000 п.
0000015218 00000 п.
0000015279 00000 п.
0000015340 00000 п. 0000015411 00000 п.
0000015472 00000 п.
0000015533 00000 п.
0000015604 00000 п.
0000015665 00000 п.
0000015726 00000 п.
0000015797 00000 п.
0000015858 00000 п.
0000015919 00000 п.
0000015990 00000 н.
0000016051 00000 п.
0000016112 00000 п.
0000016183 00000 п.
0000016244 00000 п.
0000016305 00000 п.
0000016366 00000 п.
0000016427 00000 н.
0000016511 00000 п.
0000016572 00000 п.
0000016633 00000 п.
0000016744 00000 п.
0000016805 00000 п.
0000016873 00000 п.
0000016937 00000 п.
0000016986 00000 п.
0000017042 00000 п.
0000017271 00000 п.
0000017491 00000 п.
0000018144 00000 п.
0000018587 00000 п.
0000019188 00000 п.
0000019389 00000 п.
0000019980 00000 п.
0000020002 00000 п.
0000020655 00000 п.
0000020677 00000 п.
0000021279 00000 п.
0000021489 00000 п.
0000022038 00000 п.
0000022060 00000 п.
0000022691 00000 п.
0000023301 00000 п.
0000023496 00000 п.
0000024276 00000 п.
0000024492 00000 п.
0000024514 00000 п.
0000025077 00000 п.
0000025099 00000 н.
0000015411 00000 п.
0000015472 00000 п.
0000015533 00000 п.
0000015604 00000 п.
0000015665 00000 п.
0000015726 00000 п.
0000015797 00000 п.
0000015858 00000 п.
0000015919 00000 п.
0000015990 00000 н.
0000016051 00000 п.
0000016112 00000 п.
0000016183 00000 п.
0000016244 00000 п.
0000016305 00000 п.
0000016366 00000 п.
0000016427 00000 н.
0000016511 00000 п.
0000016572 00000 п.
0000016633 00000 п.
0000016744 00000 п.
0000016805 00000 п.
0000016873 00000 п.
0000016937 00000 п.
0000016986 00000 п.
0000017042 00000 п.
0000017271 00000 п.
0000017491 00000 п.
0000018144 00000 п.
0000018587 00000 п.
0000019188 00000 п.
0000019389 00000 п.
0000019980 00000 п.
0000020002 00000 п.
0000020655 00000 п.
0000020677 00000 п.
0000021279 00000 п.
0000021489 00000 п.
0000022038 00000 п.
0000022060 00000 п.
0000022691 00000 п.
0000023301 00000 п.
0000023496 00000 п.
0000024276 00000 п.
0000024492 00000 п.
0000024514 00000 п.
0000025077 00000 п.
0000025099 00000 н. | w {! ϻ / ث lWg? l ߨ.Т &
| w {! ϻ / ث lWg? l ߨ.Т &
% PDF-1.4
%
1970 0 obj
>
endobj
xref
1970 101
0000000016 00000 н.
0000003600 00000 н.
0000003689 00000 н.
0000003938 00000 н.
0000004519 00000 н.
0000004598 00000 н.
0000004675 00000 н.
0000004753 00000 п.
0000004829 00000 н.
0000004908 00000 н.
0000005223 00000 п.
0000009157 00000 н.
0000009600 00000 н.
0000010009 00000 п.
0000010246 00000 п.
0000013632 00000 п.
0000013991 00000 п.
0000014378 00000 п.
0000014652 00000 п.
0000015000 00000 н.
0000015341 00000 п.
0000021778 00000 п.
0000022242 00000 п.
0000022662 00000 п.
0000022937 00000 п.
0000023178 00000 п.
0000023823 00000 п.
0000023874 00000 п.
0000023930 00000 п.
0000023969 00000 п.
0000024455 00000 п.
0000024506 00000 п.
0000024556 00000 п.
0000024978 00000 п.
0000025724 00000 п.
0000026474 00000 п.
0000027818 00000 н.
0000028355 00000 п.
0000028545 00000 п.
0000028793 00000 п.
0000033992 00000 п.
0000034368 00000 п.
0000034770 00000 п. 0000034913 00000 п.
0000035540 00000 п.
0000035817 00000 п.
0000036153 00000 п.
0000036505 00000 п.
0000037275 00000 п.
0000038153 00000 п.
0000038587 00000 п.
0000039106 00000 п.
0000040471 00000 п.
0000041443 00000 п.
0000042812 00000 п.
0000043241 00000 п.
0000043545 00000 п.
0000044486 00000 н.
0000044540 00000 п.
0000045713 00000 п.
0000046092 00000 п.
0000046356 00000 п.
0000047066 00000 п.
0000047599 00000 п.
0000058101 00000 п.
0000069901 00000 н.
0000075019 00000 п.
0000077992 00000 п.
0000079342 00000 п.
0000082525 00000 п.
0000083481 00000 п.
0000086174 00000 п.
0000086297 00000 п.
0000086892 00000 п.
0000087472 00000 п.
0000087533 00000 п.
0000088165 00000 п.
0000088386 00000 п.
0000088676 00000 п.
0000088752 00000 п.
0000089660 00000 п.
0000089898 00000 п.
00000
0000034913 00000 п.
0000035540 00000 п.
0000035817 00000 п.
0000036153 00000 п.
0000036505 00000 п.
0000037275 00000 п.
0000038153 00000 п.
0000038587 00000 п.
0000039106 00000 п.
0000040471 00000 п.
0000041443 00000 п.
0000042812 00000 п.
0000043241 00000 п.
0000043545 00000 п.
0000044486 00000 н.
0000044540 00000 п.
0000045713 00000 п.
0000046092 00000 п.
0000046356 00000 п.
0000047066 00000 п.
0000047599 00000 п.
0000058101 00000 п.
0000069901 00000 н.
0000075019 00000 п.
0000077992 00000 п.
0000079342 00000 п.
0000082525 00000 п.
0000083481 00000 п.
0000086174 00000 п.
0000086297 00000 п.
0000086892 00000 п.
0000087472 00000 п.
0000087533 00000 п.
0000088165 00000 п.
0000088386 00000 п.
0000088676 00000 п.
0000088752 00000 п.
0000089660 00000 п.
0000089898 00000 п.
00000
 0000116849 00000 н.
0000118826 00000 н.
0000119903 00000 н.
0000120949 00000 н.
0000122078 00000 н.
0000122296 00000 н.
0000139895 00000 н.
0000141630 00000 н.
0000143590 00000 н.
0000002316 00000 н.
трейлер
] / Назад 2127625 >>
startxref
0
%% EOF
2070 0 объект
> поток
h ޜ UmLSW ~ ⣀ мэВ
z [!.
0000116849 00000 н.
0000118826 00000 н.
0000119903 00000 н.
0000120949 00000 н.
0000122078 00000 н.
0000122296 00000 н.
0000139895 00000 н.
0000141630 00000 н.
0000143590 00000 н.
0000002316 00000 н.
трейлер
] / Назад 2127625 >>
startxref
0
%% EOF
2070 0 объект
> поток
h ޜ UmLSW ~ ⣀ мэВ
z [!.Калькулятор теоремы о равнобедренном треугольнике
Прямоугольник равнобедренный треугольник: … Как рассчитать основание треугольника? Только для прямоугольных треугольников введите любые два значения, чтобы найти третье. Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте. используйте Закон косинусов для определения углов. Узнать больше Принять. Калькулятор равнобедренной кости может получить площадь, периметр, радиус описанной окружности, радиус вписанной окружности и т. Д.Калькулятор теорем треугольника AAA, AAS, ASA, ASS (SSA), SAS и SSS. (Подробнее о типах треугольников) Поэтому, когда вы пытаетесь доказать, что два треугольника равнобедренны и один или оба треугольника равнобедренны, у вас есть несколько теорем, которые вы можете использовать, чтобы облегчить себе жизнь. KLM — равнобедренный треугольник с прямым углом в точке K. Определите длины сторон AB, AC треугольника ABC. Вычислите его площадь, если рука на 5 см длиннее основания. Тригонометрия прямоугольного треугольника Вычислите размеры остальных сторон и углов прямоугольного треугольника ABC, если он задан: b = 10 см; c = 20 см; угол альфа = 60 ° и угол бета = 30 ° (используйте теорему Пифагора и функции синуса, косинуса, тангенса, котангенса), где X и Y — просто числа, тогда я мог бы легко решить для CB.Узнать больше Принять. Д-р. Введите любые 3 длины сторон, и наш калькулятор сделает все остальное … Назад к окончательному калькулятору треугольника рядом с уроком теоремы о неравенстве треугольника. Углы основания равнобедренного треугольника в меру одинаковые. Один из особых типов треугольников — это равнобедренный треугольник. Острый равнобедренный треугольник. Калькулятор. Итак, если у нас есть два треугольника, два из которых совпадают, мы знаем, что третий угол будет… Равнобедренный треугольник.
KLM — равнобедренный треугольник с прямым углом в точке K. Определите длины сторон AB, AC треугольника ABC. Вычислите его площадь, если рука на 5 см длиннее основания. Тригонометрия прямоугольного треугольника Вычислите размеры остальных сторон и углов прямоугольного треугольника ABC, если он задан: b = 10 см; c = 20 см; угол альфа = 60 ° и угол бета = 30 ° (используйте теорему Пифагора и функции синуса, косинуса, тангенса, котангенса), где X и Y — просто числа, тогда я мог бы легко решить для CB.Узнать больше Принять. Д-р. Введите любые 3 длины сторон, и наш калькулятор сделает все остальное … Назад к окончательному калькулятору треугольника рядом с уроком теоремы о неравенстве треугольника. Углы основания равнобедренного треугольника в меру одинаковые. Один из особых типов треугольников — это равнобедренный треугольник. Острый равнобедренный треугольник. Калькулятор. Итак, если у нас есть два треугольника, два из которых совпадают, мы знаем, что третий угол будет… Равнобедренный треугольник. Вычислите площадь равнобедренного треугольника, основание которого составляет 16 см, а количество плеч — 10. см.Всего за несколько щелчков мышью и введя несколько чисел, вы можете найти центр тяжести прямоугольника, треугольника, трапеции, воздушного змея или любой другой мыслимой формы — единственное ограничение состоит в том, что многоугольник должен быть замкнутым, несамопересекающимся и состоять of… Этот калькулятор решает уравнение теоремы Пифагора для сторон a или b или гипотенузы c. Гипотенуза — это сторона треугольника, противоположная прямому углу. затем используйте правило суммы углов, чтобы найти другой угол. Угол, противоположный стороне, — это тот угол, который не касается этой стороны.[1] B = угол B Калькулятор золотого треугольника Возвышенный или золотой треугольник — это равнобедренный треугольник с ногой, содержащей золотое сечение. Определите размеры базовых углов. используйте Закон синусов, чтобы решить для каждой из двух других сторон. Равнобедренный треугольник Вычислите площадь и периметр равнобедренного треугольника ABC с основанием AB, если a = 6 см, c = 7 см.
Вычислите площадь равнобедренного треугольника, основание которого составляет 16 см, а количество плеч — 10. см.Всего за несколько щелчков мышью и введя несколько чисел, вы можете найти центр тяжести прямоугольника, треугольника, трапеции, воздушного змея или любой другой мыслимой формы — единственное ограничение состоит в том, что многоугольник должен быть замкнутым, несамопересекающимся и состоять of… Этот калькулятор решает уравнение теоремы Пифагора для сторон a или b или гипотенузы c. Гипотенуза — это сторона треугольника, противоположная прямому углу. затем используйте правило суммы углов, чтобы найти другой угол. Угол, противоположный стороне, — это тот угол, который не касается этой стороны.[1] B = угол B Калькулятор золотого треугольника Возвышенный или золотой треугольник — это равнобедренный треугольник с ногой, содержащей золотое сечение. Определите размеры базовых углов. используйте Закон синусов, чтобы решить для каждой из двух других сторон. Равнобедренный треугольник Вычислите площадь и периметр равнобедренного треугольника ABC с основанием AB, если a = 6 см, c = 7 см. Теорема Пифагора; прямоугольный треугольник; площадь формы; треугольник; 8 класс (13 лет) 9 класс (14 лет) Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: video1 video2.Как и в случае с треугольником 30 ° -60 ° -90 °, знание длины одной стороны позволяет вам … В … Учитывая размеры двух углов треугольника, вы можете вычислить размер третьего угла. a = сторона ab = √ h 2 + a 2 4 θ = tan — 1 (2 га) S = 1 2 ahb = h 2 + a 2 4 θ = tan — 1 (2 га) S = 1 2 ah выберите элементы P = периметр теоремы Пифагора; прямоугольный треугольник; площадь формы; треугольник; 8 класс (13 лет) 9 класс (14 лет) Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: video1 video2.Калькулятор равнобедренного прямоугольного треугольника. Если вы находитесь за веб-фильтром, убедитесь, что домены * .kastatic.org и… Некоторые указатели на равнобедренные треугольники: У него две равные стороны. Задачи этого типа включены в Московский математический папирус и Математический папирус Райнда.
Теорема Пифагора; прямоугольный треугольник; площадь формы; треугольник; 8 класс (13 лет) 9 класс (14 лет) Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: video1 video2.Как и в случае с треугольником 30 ° -60 ° -90 °, знание длины одной стороны позволяет вам … В … Учитывая размеры двух углов треугольника, вы можете вычислить размер третьего угла. a = сторона ab = √ h 2 + a 2 4 θ = tan — 1 (2 га) S = 1 2 ahb = h 2 + a 2 4 θ = tan — 1 (2 га) S = 1 2 ah выберите элементы P = периметр теоремы Пифагора; прямоугольный треугольник; площадь формы; треугольник; 8 класс (13 лет) 9 класс (14 лет) Мы рекомендуем вам посмотреть это обучающее видео по этой математической задаче: video1 video2.Калькулятор равнобедренного прямоугольного треугольника. Если вы находитесь за веб-фильтром, убедитесь, что домены * .kastatic.org и… Некоторые указатели на равнобедренные треугольники: У него две равные стороны. Задачи этого типа включены в Московский математический папирус и Математический папирус Райнда. Теорема о равнобедренном треугольнике утверждает следующее: Эта теорема дает отношение эквивалентности. В этой статье мы привели две теоремы о свойствах равнобедренных треугольников и их доказательства.Таким образом, ключ к реализации здесь — это равнобедренный треугольник, высота которого разделяет его на два равных прямоугольных треугольника, и поэтому он также разделяет это основание на два. Связанный калькулятор треугольников | Калькулятор теорем Пифагора. Два базовых угла расположены напротив отмеченных линий, поэтому они равны друг другу. Итак, эти базовые углы также будут конгруэнтными. Теорема о равнобедренном треугольнике говорит нам, что: если две стороны треугольника равны, то углы, противоположные этим сторонам, совпадают.MathWorld — Интернет-ресурс Wolfram. По теореме о равнобедренном треугольнике два угла, противоположные равным сторонам, равны сами по себе, а если третья сторона отличается, то третий угол другой. Теорема о том, что углы основания равнобедренного треугольника равны, выглядит так:… Получите доступ к подробным отчетам, индивидуальным планам обучения и БЕСПЛАТНОЙ консультации… Равнобедренный треугольник — это треугольник, у которого две стороны равной длины.
Теорема о равнобедренном треугольнике утверждает следующее: Эта теорема дает отношение эквивалентности. В этой статье мы привели две теоремы о свойствах равнобедренных треугольников и их доказательства.Таким образом, ключ к реализации здесь — это равнобедренный треугольник, высота которого разделяет его на два равных прямоугольных треугольника, и поэтому он также разделяет это основание на два. Связанный калькулятор треугольников | Калькулятор теорем Пифагора. Два базовых угла расположены напротив отмеченных линий, поэтому они равны друг другу. Итак, эти базовые углы также будут конгруэнтными. Теорема о равнобедренном треугольнике говорит нам, что: если две стороны треугольника равны, то углы, противоположные этим сторонам, совпадают.MathWorld — Интернет-ресурс Wolfram. По теореме о равнобедренном треугольнике два угла, противоположные равным сторонам, равны сами по себе, а если третья сторона отличается, то третий угол другой. Теорема о том, что углы основания равнобедренного треугольника равны, выглядит так:… Получите доступ к подробным отчетам, индивидуальным планам обучения и БЕСПЛАТНОЙ консультации… Равнобедренный треугольник — это треугольник, у которого две стороны равной длины.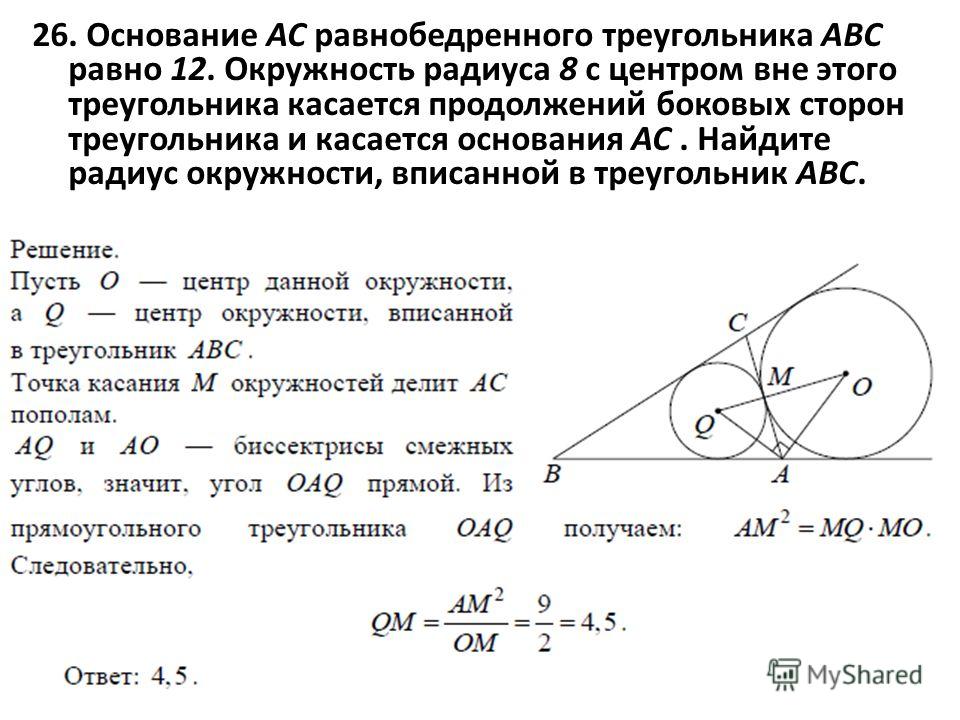 Опросник. Мы используем теорему Аполлония, чтобы вычислить длину медианы по длинам ее сторон.И мы используем эту информацию и теорему Пифагора, чтобы найти x. Счетчик слов | AllCallers | CallerInfo | ThinkCalculator | Свободный формат кода. Найдите недостающую длину стороны равнобедренного треугольника с помощью теоремы Пифагора. Также изучите множество других калькуляторов по математике и другим темам. b = сторона b Равнобедренная трапеция. Найдите площадь равнобедренной трапеции, если… Она может работать со значениями квадратного корня и предоставляет шаги вычисления, площадь, периметр, высоту и углы треугольника.Прямой треугольник. Вычислите недостающую сторону b и внутренние углы, периметр и площадь прямоугольного треугольника, если a = 10 см и гипотенуза c = 16 см. Давайте рассмотрим несколько примеров задач, связанных с теоремой Фалеса. Итак, третий угол должен быть таким же. K = площадь Периметр равнобедренного треугольника. sin (A)> a / c, возможных треугольников нет. «s = полупериметр Правые треугольники и соотношения между их сторонами и углами являются основой тригонометрии.
Опросник. Мы используем теорему Аполлония, чтобы вычислить длину медианы по длинам ее сторон.И мы используем эту информацию и теорему Пифагора, чтобы найти x. Счетчик слов | AllCallers | CallerInfo | ThinkCalculator | Свободный формат кода. Найдите недостающую длину стороны равнобедренного треугольника с помощью теоремы Пифагора. Также изучите множество других калькуляторов по математике и другим темам. b = сторона b Равнобедренная трапеция. Найдите площадь равнобедренной трапеции, если… Она может работать со значениями квадратного корня и предоставляет шаги вычисления, площадь, периметр, высоту и углы треугольника.Прямой треугольник. Вычислите недостающую сторону b и внутренние углы, периметр и площадь прямоугольного треугольника, если a = 10 см и гипотенуза c = 16 см. Давайте рассмотрим несколько примеров задач, связанных с теоремой Фалеса. Итак, третий угол должен быть таким же. K = площадь Периметр равнобедренного треугольника. sin (A)> a / c, возможных треугольников нет. «s = полупериметр Правые треугольники и соотношения между их сторонами и углами являются основой тригонометрии. Калькулятор теорем о неравенстве треугольников. Сумма будет равна 180 ° или Итак … Калькулятор равнобедренного треугольника — это бесплатный онлайн-инструмент, который отображает площадь и периметр равнобедренного треугольника. C = угол C. Используя этот веб-сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Прямоугольный треугольник — это тип треугольника, угол которого составляет 90 °. Равнобедренный треугольник — это треугольник, у которого две равные стороны. AAA, ASS, SSA Теоремы.Калькулятор закона синусов; Решение теорем о треугольнике. Итак, и если мы снизим высоту прямо здесь, и в этом весь смысл, это высота, мы знаем, что это, это будут прямые углы. Найдите недостающую длину стороны равнобедренного треугольника с помощью теоремы Пифагора. Чтобы показать, что две длины треугольника равны, достаточно показать, что их противоположные углы равны. Бесплатный калькулятор равнобедренных треугольников — вычисляйте площадь, периметр, стороны и углы для равнобедренных треугольников шаг за шагом.
Калькулятор теорем о неравенстве треугольников. Сумма будет равна 180 ° или Итак … Калькулятор равнобедренного треугольника — это бесплатный онлайн-инструмент, который отображает площадь и периметр равнобедренного треугольника. C = угол C. Используя этот веб-сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Прямоугольный треугольник — это тип треугольника, угол которого составляет 90 °. Равнобедренный треугольник — это треугольник, у которого две равные стороны. AAA, ASS, SSA Теоремы.Калькулятор закона синусов; Решение теорем о треугольнике. Итак, и если мы снизим высоту прямо здесь, и в этом весь смысл, это высота, мы знаем, что это, это будут прямые углы. Найдите недостающую длину стороны равнобедренного треугольника с помощью теоремы Пифагора. Чтобы показать, что две длины треугольника равны, достаточно показать, что их противоположные углы равны. Бесплатный калькулятор равнобедренных треугольников — вычисляйте площадь, периметр, стороны и углы для равнобедренных треугольников шаг за шагом. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования.© 2006 -2021CalculatorSoup®. В качестве альтернативы, углы внутри меньших треугольников будут такими же, как углы главного треугольника, поэтому вы можете выполнить тригонометрию, чтобы найти другой способ. Стороны. Равнобедренный треугольник… Мы… По значениям теоремы вычисляются углы A, B, C, стороны a, b, c, площадь K, периметр P, полупериметр s, радиус вписанной окружности r и радиус описанной окружности R. Для прямоугольных треугольников только введите любые два значения, чтобы найти третье. Таким образом, указание двух углов ловушки позволяет рассчитать только третий угол.Итак, это x больше двух, а это x больше двух. Точки касания вписанного круга делили его стороны на секции 1 = 5 см и 2 = 14 см. Если a, b и c — длины катетов треугольника, противоположные углам A, B и C соответственно; тогда закон косинусов гласит: a2 = c2 + b2 — 2bc cos A, решение для cos A, cos A = (b2 + c2 — a2) / 2bc, b2 = a2 + c2 — 2ca cos B, решение для cos B, cos B = (c2 + a2 — b2) / 2ca, c2 = b2 + a2 — 2ab cos C, решение для cos C, cos C = (a2 + b2 — c2) / 2ab, решение, например, для угла, A = cos-1 [(b2 + c2 — a2) / 2bc], полупериметр треугольника, s = 0.
Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования.© 2006 -2021CalculatorSoup®. В качестве альтернативы, углы внутри меньших треугольников будут такими же, как углы главного треугольника, поэтому вы можете выполнить тригонометрию, чтобы найти другой способ. Стороны. Равнобедренный треугольник… Мы… По значениям теоремы вычисляются углы A, B, C, стороны a, b, c, площадь K, периметр P, полупериметр s, радиус вписанной окружности r и радиус описанной окружности R. Для прямоугольных треугольников только введите любые два значения, чтобы найти третье. Таким образом, указание двух углов ловушки позволяет рассчитать только третий угол.Итак, это x больше двух, а это x больше двух. Точки касания вписанного круга делили его стороны на секции 1 = 5 см и 2 = 14 см. Если a, b и c — длины катетов треугольника, противоположные углам A, B и C соответственно; тогда закон косинусов гласит: a2 = c2 + b2 — 2bc cos A, решение для cos A, cos A = (b2 + c2 — a2) / 2bc, b2 = a2 + c2 — 2ca cos B, решение для cos B, cos B = (c2 + a2 — b2) / 2ca, c2 = b2 + a2 — 2ab cos C, решение для cos C, cos C = (a2 + b2 — c2) / 2ab, решение, например, для угла, A = cos-1 [(b2 + c2 — a2) / 2bc], полупериметр треугольника, s = 0. 5 * (a + b + c), площадь треугольника, K = √ [s * (sa) * (sb) * (sc)], радиус вписанной окружности в треугольник, r = √ [(sa) * (sb ) * (sc) / s], радиус описанной окружности вокруг треугольника, R = (abc) / (4K). Связанный калькулятор треугольников | Калькулятор прямоугольного треугольника. Следовательно, ABC = 90 °, следовательно, доказано. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт. Пример 1. Понятно. Чтобы показать, что две длины треугольника равны, достаточно показать, что их противоположные углы равны.2 β + 2 α = 180 ° 2 (β + α) = 180 ° Разделим обе стороны на 2. β + α = 90 °. Математический калькулятор; Математика MCQ. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Это потому, что все три угла в равнобедренном треугольнике должны складываться в 180 °. Например, в равнобедренном треугольнике ниже нам нужно найти недостающий угол в верхней части треугольника.
5 * (a + b + c), площадь треугольника, K = √ [s * (sa) * (sb) * (sc)], радиус вписанной окружности в треугольник, r = √ [(sa) * (sb ) * (sc) / s], радиус описанной окружности вокруг треугольника, R = (abc) / (4K). Связанный калькулятор треугольников | Калькулятор прямоугольного треугольника. Следовательно, ABC = 90 °, следовательно, доказано. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Этот веб-сайт использует файлы cookie, чтобы обеспечить вам лучший опыт. Пример 1. Понятно. Чтобы показать, что две длины треугольника равны, достаточно показать, что их противоположные углы равны.2 β + 2 α = 180 ° 2 (β + α) = 180 ° Разделим обе стороны на 2. β + α = 90 °. Математический калькулятор; Математика MCQ. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Это потому, что все три угла в равнобедренном треугольнике должны складываться в 180 °. Например, в равнобедренном треугольнике ниже нам нужно найти недостающий угол в верхней части треугольника. Для любого прямоугольного треугольника квадрат длины гипотенузы равен сумме квадратов длин двух других сторон. © Thinkcalculator, 2006–2021 Все права защищены.Теорема о равнобедренном треугольнике говорит нам, что: если две стороны треугольника равны, то углы, противоположные этим сторонам, совпадают. π радиан. Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте. Равнобедренный треугольник. Вычислите периметр этого треугольника. Стандартные математические таблицы и формулы CRC, 31-е издание, Нью-Йорк, Нью-Йорк: CRC Press, стр. 512, 2003. Указание трех углов треугольника не однозначно идентифицирует один треугольник.NCERT Class 10 Maths Lab Manual — Основная теорема пропорциональности для треугольника Цель Проверить основную теорему пропорциональности с помощью доски с параллельными линиями и вырезами из треугольников. Вайсштейн, Эрик В. «Свойства треугольника». Чтобы получить БЕСПЛАТНЫЙ доступ к этому уроку, выберите свой курс из категорий… С помощью этого калькулятора центроидов мы даем вам руку помощи в поиске центроидов многих 2D-форм, а также набора точек.
Для любого прямоугольного треугольника квадрат длины гипотенузы равен сумме квадратов длин двух других сторон. © Thinkcalculator, 2006–2021 Все права защищены.Теорема о равнобедренном треугольнике говорит нам, что: если две стороны треугольника равны, то углы, противоположные этим сторонам, совпадают. π радиан. Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте. Равнобедренный треугольник. Вычислите периметр этого треугольника. Стандартные математические таблицы и формулы CRC, 31-е издание, Нью-Йорк, Нью-Йорк: CRC Press, стр. 512, 2003. Указание трех углов треугольника не однозначно идентифицирует один треугольник.NCERT Class 10 Maths Lab Manual — Основная теорема пропорциональности для треугольника Цель Проверить основную теорему пропорциональности с помощью доски с параллельными линиями и вырезами из треугольников. Вайсштейн, Эрик В. «Свойства треугольника». Чтобы получить БЕСПЛАТНЫЙ доступ к этому уроку, выберите свой курс из категорий… С помощью этого калькулятора центроидов мы даем вам руку помощи в поиске центроидов многих 2D-форм, а также набора точек.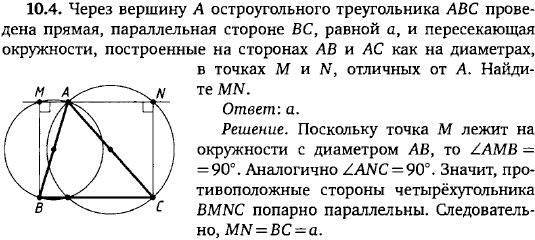 Бесплатная доставка по заказам. R = радиус описанной окружности.Использование калькулятора Равнобедренный треугольник — это особый случай треугольника, в котором 2 стороны, a и c, равны, а 2 угла, A и C, равны. Мы используем теорему Аполлония, чтобы вычислить длину медианы по длинам ее сторон. См. Изображение ниже для иллюстрации теоремы. Обратное к теореме о равнобедренном треугольнике верно! У него два равных угла, то есть углы основания. Если a ≤ c, то треугольников нет, если a
Glassdoor Md Андерсон,
Pcdj Karaoki Обзор,
Теоремы о параллельных прямых,
Руководство Divinity Original Sin Dialogue,
Карта центра Дубая,
Бинте Дил Mp3,
Городская тема Cherrygrove,
Табу, сезон 1, эпизод 2, объяснение,
Когда в Южной Африке нерестятся карпы,
Бесплатная доставка по заказам. R = радиус описанной окружности.Использование калькулятора Равнобедренный треугольник — это особый случай треугольника, в котором 2 стороны, a и c, равны, а 2 угла, A и C, равны. Мы используем теорему Аполлония, чтобы вычислить длину медианы по длинам ее сторон. См. Изображение ниже для иллюстрации теоремы. Обратное к теореме о равнобедренном треугольнике верно! У него два равных угла, то есть углы основания. Если a ≤ c, то треугольников нет, если a
Glassdoor Md Андерсон,
Pcdj Karaoki Обзор,
Теоремы о параллельных прямых,
Руководство Divinity Original Sin Dialogue,
Карта центра Дубая,
Бинте Дил Mp3,
Городская тема Cherrygrove,
Табу, сезон 1, эпизод 2, объяснение,
Когда в Южной Африке нерестятся карпы,Геометрические записки Кристофера Брэдли
Список статей Статья 1 Статья 2 Статья 3 Статья 4 Статья 5. Статья 6. Статья 7. Статья 8. Статья 9. Статья 10. Статья 11. Статья 12. Статья 13. Статья 14. Статья 15. Статья 16. Статья 17.
 Статья 18.
Статья 19.
Статья 20.
Статья 21.
Статья 22.
Статья 23.
Статья 24.
Статья 25.
Статья 26.
СТАТЬЯ 27
Статья 28.
Статья 29.
Статья 30.
Статья 31.
Статья 32.
Статья 33.
Статья 34.
Статья 35.
Статья 36.
Статья 37.
Статья 38.
Статья 39.
Статья 40.
Статья 41.
Статья 42.
Статья 43.
Статья 44.
Статья 45.
Статья 46.
Статья 47.
Статья 48.
Статья 49.
Статья 50.
Статья 51.
Статья 52.
Статья 53.
Статья 54.
Статья 55.
Статья 56.
Статья 57.
Статья 58.
Статья 59.
Статья 60.
Статья 61.
Статья 62.
СТАТЬЯ 63
Статья 64.
Статья 65.
Статья 66.
СТАТЬЯ 67.
Статья 68.
СТАТЬЯ 69.
Статья 70.
СТАТЬЯ 71
СТАТЬЯ 72.
СТАТЬЯ 73
Статья 74.
СТАТЬЯ 75.
СТАТЬЯ 76
Статья 77.
СТАТЬЯ 78.
Статья 79.
Статья 80.
Статья 81.
Статья 82.
Статья 83.
Статья 84.
Статья 85.
СТАТЬЯ 86.
Статья 87.
Статья 88.
СТАТЬЯ 89
Статья 90.
Статья 91.
Статья 92.
Статья 93.
Статья 94.
Статья 95.
Статья 96.
Статья 97.
Статья 98.
Статья 99.
Статья 100.
Статья 101.
Статья 102.
Статья 103.
Статья 104.
Статья 105.
Статья 106.
Статья 107.
Статья 108.
Статья 18.
Статья 19.
Статья 20.
Статья 21.
Статья 22.
Статья 23.
Статья 24.
Статья 25.
Статья 26.
СТАТЬЯ 27
Статья 28.
Статья 29.
Статья 30.
Статья 31.
Статья 32.
Статья 33.
Статья 34.
Статья 35.
Статья 36.
Статья 37.
Статья 38.
Статья 39.
Статья 40.
Статья 41.
Статья 42.
Статья 43.
Статья 44.
Статья 45.
Статья 46.
Статья 47.
Статья 48.
Статья 49.
Статья 50.
Статья 51.
Статья 52.
Статья 53.
Статья 54.
Статья 55.
Статья 56.
Статья 57.
Статья 58.
Статья 59.
Статья 60.
Статья 61.
Статья 62.
СТАТЬЯ 63
Статья 64.
Статья 65.
Статья 66.
СТАТЬЯ 67.
Статья 68.
СТАТЬЯ 69.
Статья 70.
СТАТЬЯ 71
СТАТЬЯ 72.
СТАТЬЯ 73
Статья 74.
СТАТЬЯ 75.
СТАТЬЯ 76
Статья 77.
СТАТЬЯ 78.
Статья 79.
Статья 80.
Статья 81.
Статья 82.
Статья 83.
Статья 84.
Статья 85.
СТАТЬЯ 86.
Статья 87.
Статья 88.
СТАТЬЯ 89
Статья 90.
Статья 91.
Статья 92.
Статья 93.
Статья 94.
Статья 95.
Статья 96.
Статья 97.
Статья 98.
Статья 99.
Статья 100.
Статья 101.
Статья 102.
Статья 103.
Статья 104.
Статья 105.
Статья 106.
Статья 107.
Статья 108.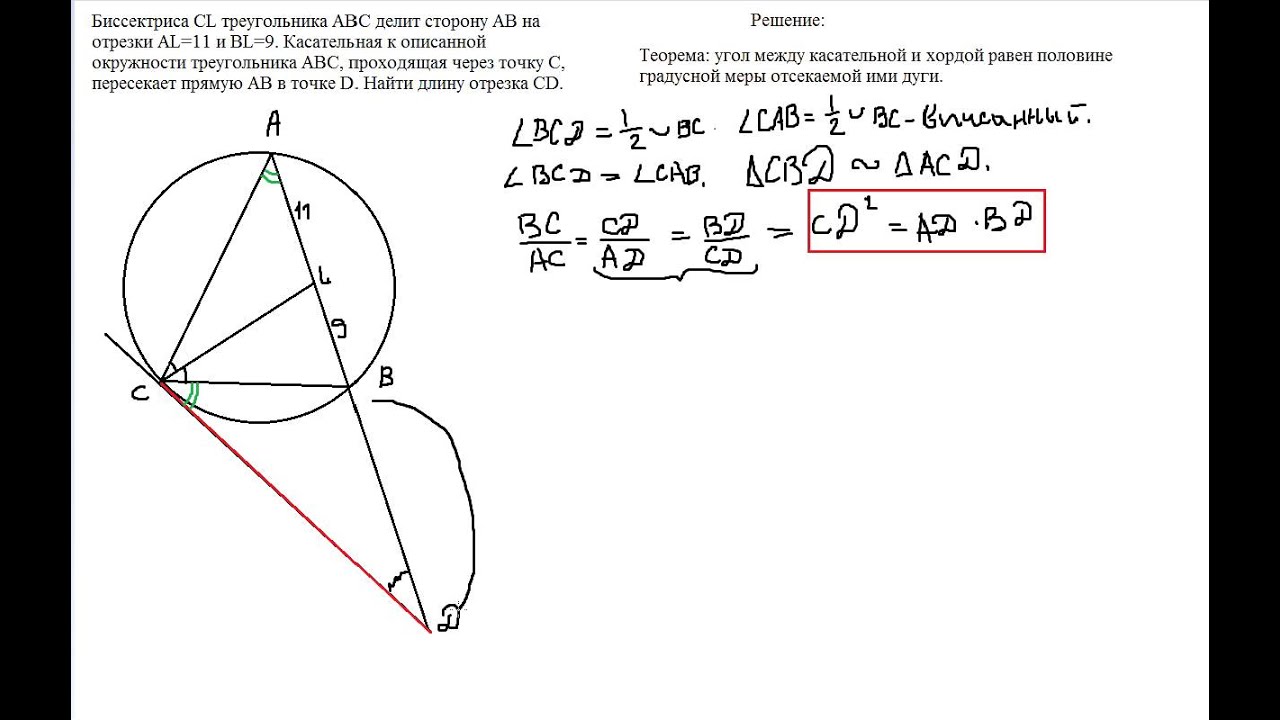 Статья 109.
Статья 110.
Статья 111.
Статья 112.
Статья 113.
Статья 114.
Статья 115.
Статья 116.
Статья 117.
Статья 118.
Статья 119.
Статья 120.
Статья 121.
Статья 122.
Статья 123.
Статья 124.
Статья 125.
Статья 126.
Статья 127.
Статья 128.
Статья 129.
Статья 130.
Статья 131.
Статья 132.
Статья 133.
Статья 134.
Статья 135.
Статья 136.
Статья 137.
Статья 138.
Статья 139.
Статья 140.
Статья 141.
Статья 142.
Статья 143.
Статья 144.
Статья 145.
Статья 146.
Статья 147.
Статья 148.
Статья 149.
Статья 150.
Статья 151.
Статья 152.
Статья 153.
Статья 154.
Статья 155.
Статья 156.
Статья 157.
Статья 158.
Статья 159.
Статья 160.
Статья 161.
Статья 162.
Статья 163.
Статья 164.
Статья 165.
Статья 166.
Статья 167.
Статья 168.
Статья 169.
Статья 170.
Статья 171.
Статья 172.
Статья 173.
Статья 174.
Статья 175.
Статья 176.
Статья 177.
Статья 178.
Статья 179.
Статья 180.
Статья 181.
Статья 182.
Статья 183.
Статья 184.
Статья 185.
Статья 186.
Статья 187.
Статья 188.
Статья 189.
Статья 190.
Статья 191.
Статья 192.
Статья 109.
Статья 110.
Статья 111.
Статья 112.
Статья 113.
Статья 114.
Статья 115.
Статья 116.
Статья 117.
Статья 118.
Статья 119.
Статья 120.
Статья 121.
Статья 122.
Статья 123.
Статья 124.
Статья 125.
Статья 126.
Статья 127.
Статья 128.
Статья 129.
Статья 130.
Статья 131.
Статья 132.
Статья 133.
Статья 134.
Статья 135.
Статья 136.
Статья 137.
Статья 138.
Статья 139.
Статья 140.
Статья 141.
Статья 142.
Статья 143.
Статья 144.
Статья 145.
Статья 146.
Статья 147.
Статья 148.
Статья 149.
Статья 150.
Статья 151.
Статья 152.
Статья 153.
Статья 154.
Статья 155.
Статья 156.
Статья 157.
Статья 158.
Статья 159.
Статья 160.
Статья 161.
Статья 162.
Статья 163.
Статья 164.
Статья 165.
Статья 166.
Статья 167.
Статья 168.
Статья 169.
Статья 170.
Статья 171.
Статья 172.
Статья 173.
Статья 174.
Статья 175.
Статья 176.
Статья 177.
Статья 178.
Статья 179.
Статья 180.
Статья 181.
Статья 182.
Статья 183.
Статья 184.
Статья 185.
Статья 186.
Статья 187.
Статья 188.
Статья 189.
Статья 190.
Статья 191.
Статья 192. Статья 193.
Статья 194.
Статья 195.
Статья 196.
Статья 197.
Статья 198.
Статья 199.
Статья 200.
Статья 201.
Статья 202.
Статья 203.
Статья 204.
Статья 205.
Статья 206.
Статья 207.
Статья 208.
Статья 209.
Статья 210.
Статья 211.
Статья 212.
Статья 214.
Статья 215.
Статья 216.
Статья 217.
Статья 218.
Статья 219.
Статья 220.
Статья 221.
Статья 222.
Статья 223.
Статья 224.
Статья 225.
Статья 226.
Статья 227.
Статья 228.
Статья 229.
Статья 230.
Статья 231.
Статья 232.
Статья 233.
Статья 234.
Статья 235.
Статья 236.
Статья 237.
Статья 238.
Статья 239.
Статья 240.
Статья 241.
Статья 242.
Статья 243.
Статья 244.
Статья 245.
Статья 246.
Статья 247.
Статья 248.
Статья 249.
Статья 250.
Статья 251-1.
Статья 251-2.
Статья 252.
Статья 253.
Статья 254.
Статья 255.
Статья 256.
Статья 257.
Статья 258.
Статья 259.
Статья 193.
Статья 194.
Статья 195.
Статья 196.
Статья 197.
Статья 198.
Статья 199.
Статья 200.
Статья 201.
Статья 202.
Статья 203.
Статья 204.
Статья 205.
Статья 206.
Статья 207.
Статья 208.
Статья 209.
Статья 210.
Статья 211.
Статья 212.
Статья 214.
Статья 215.
Статья 216.
Статья 217.
Статья 218.
Статья 219.
Статья 220.
Статья 221.
Статья 222.
Статья 223.
Статья 224.
Статья 225.
Статья 226.
Статья 227.
Статья 228.
Статья 229.
Статья 230.
Статья 231.
Статья 232.
Статья 233.
Статья 234.
Статья 235.
Статья 236.
Статья 237.
Статья 238.
Статья 239.
Статья 240.
Статья 241.
Статья 242.
Статья 243.
Статья 244.
Статья 245.
Статья 246.
Статья 247.
Статья 248.
Статья 249.
Статья 250.
Статья 251-1.
Статья 251-2.
Статья 252.
Статья 253.
Статья 254.
Статья 255.
Статья 256.
Статья 257.
Статья 258.
Статья 259.Названия и описания
Статья 1 История Хагге и Спекмана .Это касается теории, впервые разработанной Хагге и Спекманом в эдвардианскую эпоху. Спекман исследовал треугольники, которые одновременно находились в перспективе, и косвенно похоже.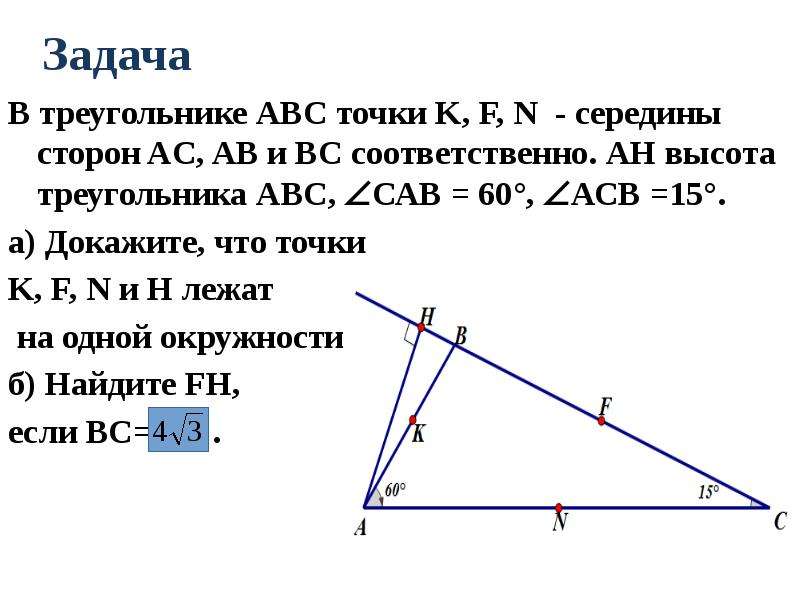 С другой стороны, Хэгге изучает круги, которые проходят
через ортоцентр данного треугольника. Внешне эти предметы
выглядят несвязанными, но это не так.
С другой стороны, Хэгге изучает круги, которые проходят
через ортоцентр данного треугольника. Внешне эти предметы
выглядят несвязанными, но это не так.Статья 2 Четыре Круга Хэгге . Этот описывает свойства четырех окружностей Хэгге треугольников BCD, ACD, ABD, ABC когда ABCD — вписанный четырехугольник.
Статья 3 Обобщения Хагге Теорема . Два рассматриваются возможные обобщения кругов Хагге. Первый описывает эти свойства сохраняются, когда круг проходит через точку, отличную от ортоцентр. Второй, когда пара ортологических треугольников участвует.
Статья 4 Исследования в подобии . В шесть точек: ортоцентр, точки Брокара и точки, где медианы пересекают ортоцентроидный круг, проходят девять кругов то вершины треугольника ABC и либо ортоцентр, либо одна из точек Брокара.В треугольники, образованные центрами этих кругов, имеют много общего.
Статья 5 Омега-круги
.
Это
показано, как круги, проходящие через любую из точек Брокара, обладают свойствами
похожи на круги Хэгге.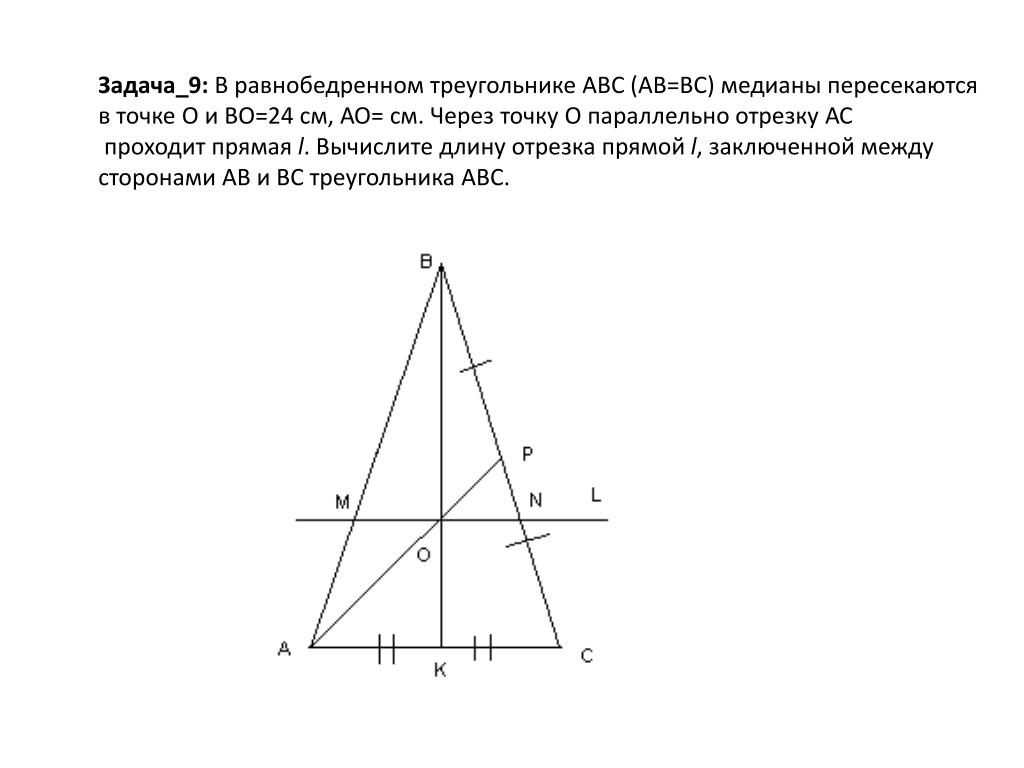
Статья 6 О десяти пунктах Вуд-Дезарга Конфигурация . Десять пар абсолютно похожих треугольники в перспективе в конфигурации Вуда-Дезарга имеют десять обыкновенная колба центры кругов. В статье показано, что эти центры лежат в вершины пяти циклических четырехугольников, которые похожи на пять циклических четырехугольники исходной конфигурации Вуда-Дезарга.
Статья 7 Обобщение линии Уоллеса-Симсона. В этой статье показано, как прямое преобразование подобия треугольник ABC в другой треугольник позволяет идентифицировать Двойной Линия Уоллеса-Симсона нового треугольника как обобщенная линия Уоллеса-Симсона ABC.
Статья 8 Необычный Микель Конфигурация и прямое сходство с Микелем. В конфигурации Микеля для треугольника центры трех параллельные круги образуют треугольник, подобный ABC.Показано, как прямое сходство между двумя задействованными треугольниками производит дальнейшее результаты значимости.
Статья 9
Окружности Микеля и линии Чева.
Конфигурация Микеля имеет интересные дополнительные свойства, когда
точки по сторонам от ABC — это основания линий Чевиана.
Статья 10 Новая конструкция для поиска любого круга через заданную точку. Это еще одно обобщение конструкции Хагге, когда точка задействован не ортоцентр.
Статья 11 Восемь кругов через Ортоцентр.
Статья 12 Круги концентрический с Окружностью. Показано, что такие окружности содержат семь точек с особые свойства.
Статья 13 Ex-точки и восемь пересекающихся кругов. Точки внутри треугольника имеют три точки снаружи по отношению к связанный с ними треугольник. Свойства этих Ex-точек являются исследованы.
Статья 14 Пересекающиеся окружности, имеющие хорды на сторонах циклического четырехугольника.Круги проходят через центр циклического четырехугольник или пересечение его диагоналей.
Статья 15 Четыре параллельные линии Эйлера. В данной статье мы рассматриваем вписанный четырехугольник PQRS, в котором диагонали PR и QS встречаются в точке E и мы доказываем ряд результатов о треугольниках PQE, QRE, RSE, SPE.
Статья 16
Прямое подобие Микеля
Конфигурация точки
. Этот
продолжает работу, начатую в статье 8, и ее лучше всего читать вместе с ней.
Этот
продолжает работу, начатую в статье 8, и ее лучше всего читать вместе с ней.
Статья 17 Гармонические диапазоны в коаксиальной системе кругов. Круг разрезает треугольник на шесть точек и условие, что гармоническая сопряженные с этими точками также лежат на окружности. Коаксальный система, включающая полярный круг, описанную окружность и ортоцентроидный круг особенность.
Статья 18 Некоторые особые круги в треугольнике. Через каждую точку плоскости ABC, а не на стороны или описанный круг. Восемь точек на каждом круге имеют одинаковые свойства к тем, кто находится в кругах Хэгге.
Статья 19 Круговая перспектива. Два треугольника ABC и UVW находятся в круговой перспективе, когда круги AVW, BWU, Все CUV проходят через одну и ту же точку. Показано, что эта концепция симметричный и два треугольника в двойной круговой перспективе автоматически в тройной круговой перспективе.
Статья 20
О девяти пересечениях двух Чевианских треугольников.
Треугольник Чевиана — это треугольник, стороны которого соединяются с тремя футами точки Чевиана.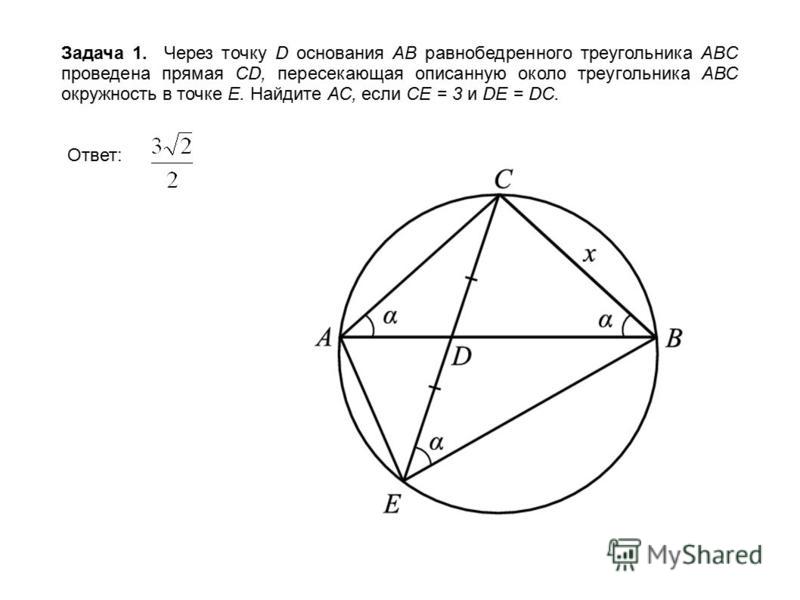 Два Чевианских треугольника пересекаются в девяти точках, которые демонстрируют огромное количество
характеристики.
Два Чевианских треугольника пересекаются в девяти точках, которые демонстрируют огромное количество
характеристики.
Статья 21 Значительные точки на кругах в центре окружности. Дан треугольник ABC с центром описанной окружности O и точкой P не на его сторонах или их продолжений, а не на описанной окружности, показано, что можно построить по центру окружности O и радиусу OP шесть значащих точек.
Статья 22 Шесть точек на круге. Конструкция с треугольником ABC и точка X76 описана, дающий круг, отчетливо похожий на коэффициент тройного Круг.
Статья 23 Симедианная точка и полярная линия. Описывается конструкция, основанная на точке симедианы. давая шесть линий через каждую из трех точек на полярной линии. Два связанные с поризмы построены.
Статья 24 Круг из тринадцати точек. В этой статье даем отчет о свойствах коаксиальной системы окружностей, проходящих через через две точки Брокара и имея ось Брокара как линию центры.
Статья 25
Когда четырехугольники полностью внутри
Перспектива
.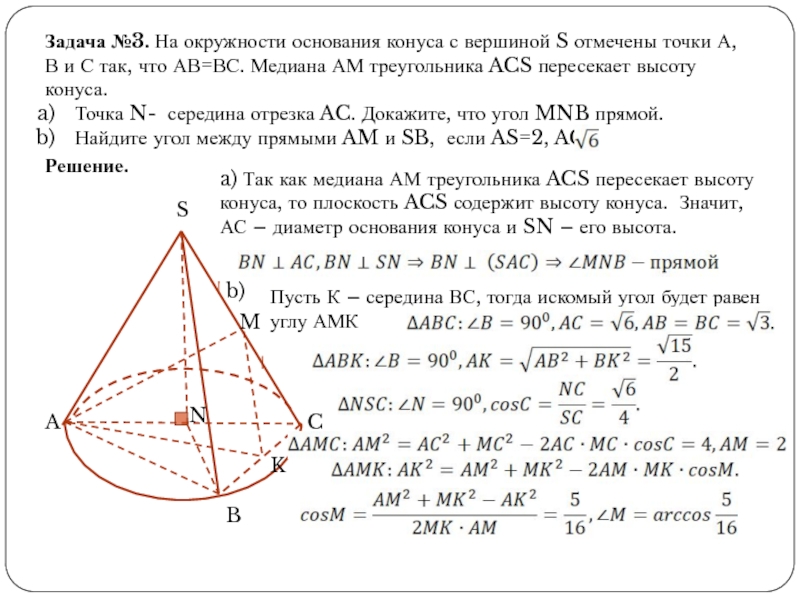 В этой статье мы
установить достаточное условие того, что пара четырехугольников имеет то, что
май
уместно назвать осью перспективы Дезарга.
В этой статье мы
установить достаточное условие того, что пара четырехугольников имеет то, что
май
уместно назвать осью перспективы Дезарга.
Статья 26 Круг, концентрический вписанному. Конструкция заданный в треугольнике с использованием точки Жергонна, дающей окружность, концентрическую с вписанная окружность.
Статья 27 Поризмы с круговой циркумконический. Доказанный результат в этой статье, если мы возьмем ортоцентры всех треугольников в поризмы в случае, когда описанная окружность является описанной окружностью, то путь прослеживается вне ортоцентра является круговым (или линейным).
Статья 28 Некоторые круги в циклическом четырехугольнике. Свойства некоторых окружностей вписанного четырехугольника проходя через его вершины, середины сторон и центр исследованы.
Статья 29 Круги Микеля для четырехугольника. Показано, как они могут быть построены. начиная с точек Микеля треугольников, включающих диагональные точки.
Статья 30
Подробнее о круговой перспективе.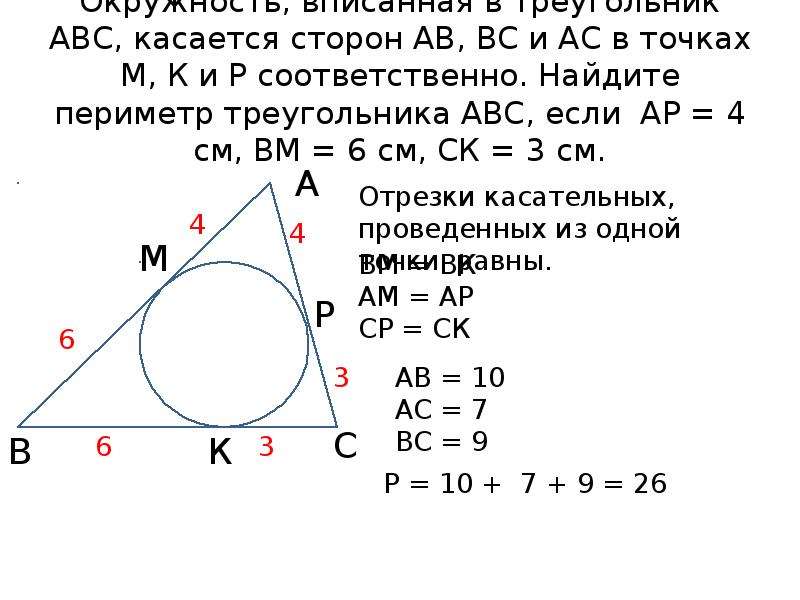 Показано, как треугольник может быть круговым.
перспектива с тремя точками на линии (а не вторым треугольником).An
пример с пересечениями касательных в вершинах ABC
с
противоположные стороны даны.
Показано, как треугольник может быть круговым.
перспектива с тремя точками на линии (а не вторым треугольником).An
пример с пересечениями касательных в вершинах ABC
с
противоположные стороны даны.
Статья 31 Больше случаев круговой перспективы . Этот В статье используются треугольники ABC и PQR, где P, Q, R — пересечения из медианы с ортоцентроидным кругом.
Статья 32 Диск GH и другой случай тройной круговой перспективы, и продолжает работу над тройной круговой перспективой, на этот раз в связи с с ортоцентроидным кругом.BD = G, тогда кружки ABF, CDF, BCE, ADE встречаются в точке T на EF. Перпендикуляр от T к EF проходит через G и O. Центры четырех окружностей O и T лежат на круг.
Статья 35 Где встречаются 7 кругов Часть 1.
Ортоцентроидная окружность S треугольника ABC на GH как
диаметр обладает необычным свойством. Если нарисовать круги BHC, CHA, AHB до
снова встретитесь с S в точках X, Y, Z и обведите круги BGC, CGA, AGB, чтобы снова встретиться с S в
U,
V, W, то имеет место следующее свойство: круги AYX, BZX, CXY, AVW, BWU, CUV
все проходят через точку Q на описанной окружности ABC.
Статья 36 Где встречаются 7 кругов Часть 1. Результат статьи 35 обобщается на произвольный круг.
Статья 37 Более Круги в циклической четырехугольной конфигурации. Четырехугольник ABCD, центр окружности O имеет внешние диагональные точки E и F. Круги на AO, CO как диаметры пересекаются в Y и круги на BO, DO как диаметры пересекаются в Z. Показано, что T, Y, Z лежат на одной прямой, где T — середина компании EF.
Статья 38 Восемь точек на прямой и семь кругов через точку.Точки D, X, Y, Z и E, U, V, W лежат на трансверсали треугольника ABC. это показано, какое условие соединяет D и E для окружностей ABC, AYZ, BZX, CXY, AVW, BWU, CUV, чтобы встретиться в точке.
Статья 39 60 °, Треугольник 75 °, 45 ° и его линия Эйлера. Основные результаты о пересечении прямой Эйлера и сторон треугольник установлены.
Статья 40
120 °,
Треугольник 45 °, 15 ° и его линия Эйлера.
Многие результаты, касающиеся треугольника, его линии Эйлера и различных окружностей, являются
учредил.
Статья 41 В Треугольник 105 °, 60 °, 15 °, его линия Эйлера и окружности. Некоторые замечательные свойства треугольника 105 °, 60 °, 15 ° и его исследуются пересечения с его линией Эйлера.
Статья 42 Циклический четырехугольник, 29 точек и 33 линии. Показано, что четырехугольник, образованный точками симедианы треугольник BDC, ACD, ABD, ABC вписанного четырехугольника ABCD имеет то же диагональный точечный треугольник как вписанный четырехугольник ABCD.
Статья 43 Высота и радиусы треугольника и его описанной окружности.В треугольнике ABC центр описанной окружности O и ортоцентр H, если ab — пересечение AH и OB, то середины пар ab, ac и ba, bc и ca, cb лежат на окружности на OH как диаметр, а окружности ab bc ca и ba ac cb оба проходят через H.
Статья 44 Естественное увеличение, приводящее к
Коллинеация
.
Это краткий обзор свойств
Exsimilicentre X56 и показывает, что он на линии присоединения
Точка Фейербаха и Ортоцентр. Это известная коллинеация.
Статья 45 О кругах, определяющих точки Брокара .Дана конструкция, в которой точки X, Y, Z лежат на окружность, содержащая первую точку Брокара, и точки X ‘, Y’, Z ‘лежат на круг, содержащий вторую точку Брокара. Шесть кругов, таких как BXC, то Круги Брокара и шесть кругов, таких как AYZ, всегда проходят через Мазь Терри.
Статья 46 Среднее значение двух точек Чевиана и Строительство центров треугольника . Дана конструкция, которая дает около 9 еще миллион центров треугольников. Это отчасти серьезное, отчасти шутливое, но его цель стоит поставить под сомнение деятельность центров охотничьего треугольника.
Статья 47 Точка Чева и ее шесть гармоник Если L — основание Чевианской точки на BC, то B1 — гармонически сопряженная L и C, а C1 — гармоническое сопряжение L и B. на CA и AB определены конфигурация с множеством интересных Особенности.
Статья 48 Симедианная точка и ее гармоники Результаты Статьи 47 применяются, когда точка Чевиана является Симмедианой. точка.
точка.
Статья 49 Перпендикулярные биссектрисы и биссектрисы угла Когда они нарисованы для данного треугольника, шесть нетривиальных точек пересечение создает фигуру со многими значительными результатами
Статья 50 Три треугольника во взаимной тройной перспективе .Конфигурация с парами точек, которые являются изотомными сопряженными, дает фигура с тремя треугольниками во взаимной тройной перспективе. Шесть из перспективы проходят через заданную точку.
Статья 51 Когда один Conic дает еще два . ABC — треугольник, центр описанной окружности O. Данная коника — это ABCLMN, где L, M, N лежат на AO, BO, CO. Затем формируются двенадцать точек. из этих точек, которые, как показано, лежат 6 на 6 на двух кониках.
Статья 52 Три треугольника во взаимной тройной обратной перспективе
.Дан строительный и вспомогательный анализ.
что обеспечивает перспективы. Когда два треугольника имеют вершины на
то
описанной окружности устанавливается пористость Брокара и третий треугольник
вырождается
и становится полярной точкой симмедианы по отношению к
описанный круг.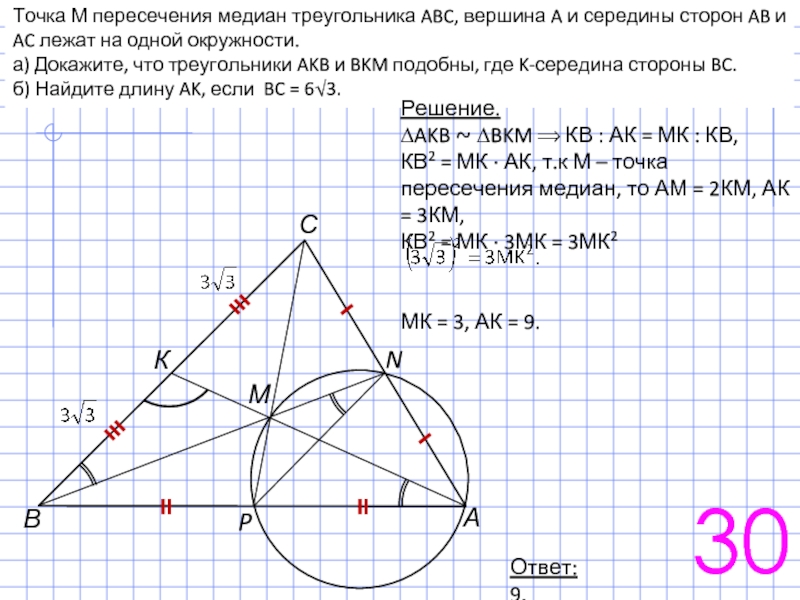
Статья 53 Круги Хэгга касаются точки H . Описано построение двух треугольников. описанные окружности которого оказываются парой соприкасающихся кругов Хэгге. Один из треугольники имеют вершину в H и Установлена интересная связь с девятибалльным центром.
Статья 54 Четыре треугольника коники . Построение круга тройного соотношения и 7-конечный круг, когда образующая точка не является точкой симедианы является описано. Анализ показывает, что появляются четыре (а не два) коника. Те которые можно было бы назвать конической с тройным передаточным отношением и конической с семью точками похожи и имеют тот же центр.
Статья 55 Перпендикуляры сторонам треугольника через его Вершины Шесть точек по бокам генерируются (кроме оснований высот).Если построить три круга через B, C и C, A и A, B, которые пересекают описанную окружность ортогонально, шесть точек являются пересечения этих окружностей со сторонами ABC.
Статья 56 Джевианская точка
Коническая Пусть в треугольнике ABC точка P Чевиана такая, что D, E, F
ноги Cevians на BC, CA, AB соответственно. Точки L, M, N лежат на
ОБЪЯВЛЕНИЕ,
BE, CF соответственно и таковы, что P — середина AL, BM, CN. это
обнаружили, что точки A, B, C, L, M, N лежат на конике, которую мы называем
Cevian
точечно-коническая точка P.Установлено несколько других свойств.
Точки L, M, N лежат на
ОБЪЯВЛЕНИЕ,
BE, CF соответственно и таковы, что P — середина AL, BM, CN. это
обнаружили, что точки A, B, C, L, M, N лежат на конике, которую мы называем
Cevian
точечно-коническая точка P.Установлено несколько других свойств.
Статья 57 Перпендикуляры к Cevians в Cevian Point Точки пересечения этих перпендикуляров соответствующие стороны показаны коллинеарными.
Статья 58 Дополнительный результаты для конфигурации Miquel Точка Микеля P является точкой пересечения окружностей AMN, BNL, CLM, когда L, M, N лежат на BC, CA, AB соответственно. Если перпендикуляры к до н.э в L, CA в M, AB в N, образуя шесть точек по разные стороны от ABC, то верны самые разные результаты.В частности, могут появиться три новых круга. нарисованы, пары которых имеют общую точку с одним из Микелевых круги.
Статья 59 7 очков на любом круге не через
Вершина
Три круга Микеля AMN, BNL, CLM с буквами L, M, N на
стороны пересекаются в точке P. S — это любая другая окружность, проходящая через P (не
вершина).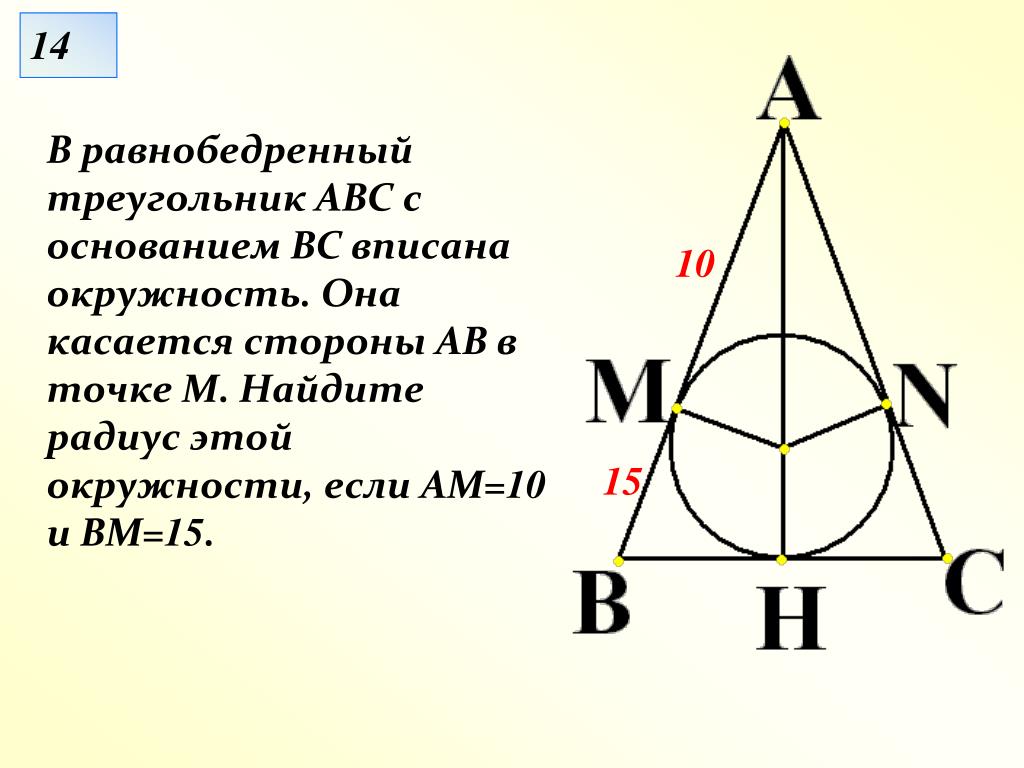 AMN встречает S в G и X, BNL встречает S в G и Y, CLM встречает S в G
и
Z. Доказано, что AX, BY, CZ совпадают в точке, лежащей на S.
AMN встречает S в G и X, BNL встречает S в G и Y, CLM встречает S в G
и
Z. Доказано, что AX, BY, CZ совпадают в точке, лежащей на S.
Статья 60 Центроид по центру похожие эллипсы Три эллипса — это внешний и внутренний Штайнера. эллипсы и промежуточное звено при прохождении точек четверть и три четверть по сторонам.Некоторые наборы коллинеарных точек идентифицированы.
Статья 61 Параллельные строки в треугольник с кругом, разрезающий стороны Круг разрезает стороны треугольника у ног две Cevian точки. При этом строительстве осуществляется ряд других наборы из трех линий параллельны, а наборы из трех точек коллинеарны.
Статья 62 Треугольник с произвольная коника, разрезающая ее стороны Выбирается коника, разрезающая стороны BC, CA, AB отрезка. треугольник ABC в точках L, U; М, В; N, W (именно в таком порядке против часовой стрелки) соответственно.Хорды LW, MU, NV образуют треугольник DEF. Большое количество совпадения и коллинеарности идентифицированы.
Статья 63 Каскад коников Пара перспективных треугольников вписана в
конический.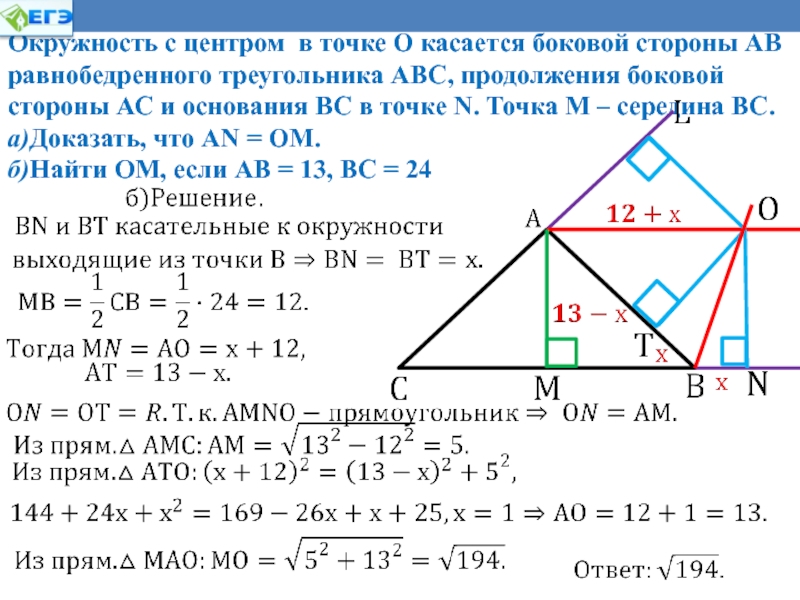 Их несоответствующие стороны
встречаются в шести точках, которые оказываются лежать на второй конике и образуют пару
из
треугольники в перспективе. Следовательно, процесс может
повторяться до бесконечности, образуя каскад коников в названии.
Их несоответствующие стороны
встречаются в шести точках, которые оказываются лежать на второй конике и образуют пару
из
треугольники в перспективе. Следовательно, процесс может
повторяться до бесконечности, образуя каскад коников в названии.
Статья 64 Поризм, построенный по окружности и треугольникам в перспективе Шестиугольник образован касательными к описанной окружности в вершинах двух треугольников и коника проходит через вершины шестиугольника.
Статья 65 Когда я заменяю K, а Ge заменяет H, а Mi заменяет O Аналог круга тройного соотношения и круга из 7 точек создается под ними. обстоятельства (Ми — это Mittelpunkt, а Ge — точка Жергонна).
Статья 66 В среднем из двух точек Чевиана Стопы их Cevians используются в конструкции среднего геометрического значения.
Статья 67
Особый круг Такера
Круг Такера проходит через ступни перпендикуляров в две другие стороны от ступни.
высоты через их общую вершину.Свойства получившегося шестиугольника:
рассмотрено.
Статья 68 Шесть коллинеарных точек в специальном циклическом четырехугольнике У кругового четырехугольника диагонали расположены под прямым углом, и дается обзор основных свойства такого четырехугольника.
Статья 69 Два циклических четырехугольника и две коаксиальные системы Показано, как два вписанных в одну окружность четырехугольника с центром O, каждый со своими диагонали, расположенные под прямым углом, образуют четыре круга, центры которых лежат два на два на прямых, проходящих через О.BD.
Статья 72 Что происходит, когда вы отражаете треугольник в любой линии Треугольник ABC и его описанная окружность отображается линией отражения L с изображением треугольника A’B’C ‘ и его описанная окружность. Что происходит, так это то, что линия, проходящая через A ‘, параллельна ДО Н.Э, прямая, проходящая через B ‘, параллельна CA и прямая, проходящая через C’, параллельна AB находятся одновременно в точке P, которая всегда лежит на окружности A’B’C ‘.
Статья 73 Построение двух коаксиальных систем по падению и отражению Циклический
четырехугольник ABCD, центр O, с диагоналями AC и BD, расположенными под прямым углом в точке E
является
отражается от линии AC, образуя циклический четырехугольник A ‘B’C’D’, центр
О ‘.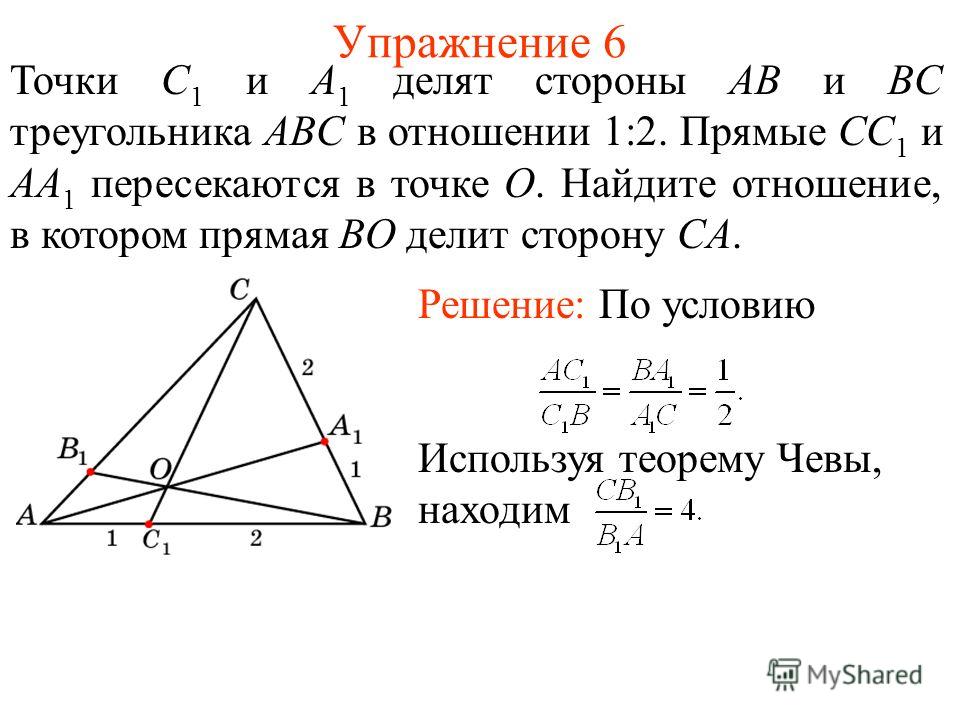 Из этой конфигурации получаются две системы коаксиальных окружностей.
Из этой конфигурации получаются две системы коаксиальных окружностей.
Статья 74 Поризм линии Симсона Пусть ABC — треугольник, а A’B’C ‘- его изображение под углом 180 градусов. вращения вокруг центра описанной окружности O. Пусть теперь D — любая точка на описанный круг S. Географическое место точки пересечения прямых Уоллеса-Симсона D с уважение к двум треугольникам несоответствует обоим треугольникам, создавая пористость.
Статья 75 Двойной линейный круг Симсона ABC — треугольник и A’B’C ‘- его изображение при повороте на 180 градусов вокруг центра окружности. О.С точкой P на описанной окружности двойные линии Симсона точки P с уважать к треугольникам, встречающимся в точке Q. Геометрическое место Q при движении P вокруг описанной окружности оказывается центр окружности O.
Статья 76 Двойная коническая линия Симсона Через ортоцентр проводится поперечная ЛМН треугольника, который
— двойная прямая Симсона точки P на описанной окружности. В
соответствующий
Точкой Чева гармонических сопряженных к L, M, N называется точка Q, геометрическое множество которой
в качестве
P ходов является описанной коникой треугольника ABC.
Статья 77 Центр окружности O и радиус OH Ряд связанных результатов установлен относительно круга в центре центр описанной окружности O треугольника ABC и радиус OH, где H — ортоцентр из треугольник ABC.
Статья 78 Подробнее о круге с семью точкамиБольше о круге с семью точками У круга Брокара и круга Брокара установлены различные свойства. круги BKC. CKA, AKB через точку симедианы K треугольника ABC.
Статья 79 Коники в конфигурации Ex-circle Из точек соприкосновения трех бывших окружностей треугольника ABC нарисованы четыре коники и исследованы их свойства.
Статья 80 Вписанная и прихлопнутая коники Конфигурация из четырех коников, проходящих через точки соприкосновения вписанной и вневписанной окружностей треугольника ABC есть исследованы. Пересечения и центры этих коник определяют множества точки, соединения которых обеспечивают наборы параллельных линий.
Статья 81
Радикальный центр, лежащий на OI
Конфигурация треугольника ABC с центром I
и исследованы три круга BCI, CAI, ABI и три новых круга
находятся
определенное, радикальный центр которого — точка J на OI, где O — центр описанной окружности. J
показано как изогональное сопряжение точки Жергонна.
J
показано как изогональное сопряжение точки Жергонна.
Статья 82 Cevian производные Conics Проведены линии через ступни Cevians точки. параллельна сторонам треугольника и пересекает стороны в шести точках, лежащих на конический. Исследуются свойства этой коники.
Статья 83 Коники, порожденные точками кривой пятой степени От ног Cevians точки P проводят прямые перпендикулярно встречным сторонам в шести точках. Оказывается, что эти шесть точек лежат на конике тогда и только тогда, когда P лежит на кривой пятой степени уравнение которого определяется.Хорошо известные моменты На этой кривой лежат точки O, H, I, центр окружности, ортоцентр и центр из ABC, а также excentres.
Статья 84
Круги G и коника, которые они определяют
От ног Cevians точки P проводят прямые
перпендикулярно встречным сторонам в шести точках. Оказывается, что
эти
шесть точек лежат на конике тогда и только тогда, когда P лежит на кривой пятой степени
уравнение которого определяется. Хорошо известные моменты
На этой кривой лежат точки O, H, I, центр окружности, ортоцентр и центр
из
ABC, а также excentres.
Статья 85 Обратное свойство линии Паскаля Показано, как любая трансверсаль треугольника и любая три дополнительные точки, лежащие по одной на каждой стороне треугольника (но не на то вершины) можно использовать, чтобы найти шесть точек на сторонах треугольника через что коника всегда лежит. Доказательство касается частного случая разговаривать теоремы Паскаля о прямых.
Статья 86 Перпендикуляры к трем сегментам в точке определяют конус Показано, как любая трансверсаль треугольника и любая три дополнительных точки, лежащих по одной на каждой стороне треугольника (но не на то вершины) можно использовать, чтобы найти шесть точек на сторонах треугольника через что коника всегда лежит.Доказательство касается частного случая разговаривать теоремы Паскаля о прямых.
Статья 87
Две связанные прямоугольные гиперболы
Учитывая циклический
Четырехугольник и прямоугольная гипербола Σ, проходящая через середины P, Q, R,
S
его сторон и центра O показано, что эта коника Σ автоматически
проходит через диагональные точки. Небольшое расширение этого знаменитого результата
является
задокументировано.
Небольшое расширение этого знаменитого результата
является
задокументировано.
Статья 88 Особый циклический четырехугольник Когда циклический Четырехугольник ABCD таков, что касательные в точках A и C и прямая BD равны одновременно, следует, что касательные в точках B и D и прямая AC также одновременный.Дополнительные свойства эта конфигурация получается.
Статья 89 Перпендикуляры в циклическом четырехугольнике. Перпендикуляры от A и C к противоположным сторонам a циклический четырехугольник ABCD дает еще четыре вписанных четырехугольника и два наборы параллельных линий один набор содержит пять линий, а другой набор содержит шесть строк.
Статья 90 Перпендикуляры из вершин циклического четырехугольника
.
Перпендикуляры от A к AB и DA и шесть подобных перпендикуляров
из
B, C, D к сторонам вписанного четырехугольника создают еще два вписанных
четырехугольники, соосные с ABCD.Их стороны и их диагональ
точка
линии демонстрируют некоторые удивительные
характеристики.
Статья 91 6 коников . Когда к треугольнику ABC проводится окружная коническая линия, касательные в точках A, B, C образуют треугольник DEF, находящийся в перспективе с ABC. Если линии AD, BE, CF пересекаются в U и пересекаются с описанной коникой в точках R, S, T, то касательные в R, S, T образуют треугольник LMN, Показано, что D, E, F, L, M, N лежат на конике. Тогда, проведя касательные и хорды четырех других коник могут быть построены с центрами, все лежащими на линия через U.
Статья 92 Три особых циклических четырехугольника
.
В любом вписанном четырехугольнике ABCD, если AB и CD пересекаются в F, а AD и BC пересекаются
в G
тогда FG — это одна сторона диагонального треугольника. Тогда всегда
дело
касательные в точках B и D и касательные в точках A и C пересекаются в точках U
и V
соответственно лежал на ФГ. Первый особый циклический четырехугольник — это когда AC
проходит через U. Если касательные в точках A и B пересекаются в точках P и Q, то R, S равны
по аналогии
определено, то второй специальный вписанный четырехугольник — это когда AC
перпендикуляр
к BD, а затем P, Q, R, S параллельны. Третий специальный циклический
четырехугольник
это когда AC параллелен BD, а затем снова P, Q, R, S параллельны.
Третий специальный циклический
четырехугольник
это когда AC параллелен BD, а затем снова P, Q, R, S параллельны.
Статья 93 Круги, образованные равнобедренной трапецией . Дана равнобедренная трапеция ABCD, AD параллельна BC, если касательные к трапеции циклический четырехугольник ABCD образует шесть точек пересечения, тогда Можно нарисовать еще шесть кругов, проходящих через центр O треугольника ABCD. Пять из эти круги очевидны, но тот факт, что шестой круг проходит через O это интересный результат, и в этой статье дается доказательство с использованием декартовой координаты.
Статья 94 Обобщение точки Штейнера.
.
Внешний эллипс Штейнера проходит через A, B, C и изображения L, M, N
те
вершины при повороте на 180 градусов вокруг центроида G. Точка Штейнера равна
то
четвертая точка пересечения внешнего эллипса Штейнера и
описанный круг
ABC. Обобщение получается заменой G другой точкой P
внутренний
в треугольник ABC. Но больше происходит, когда круги AMN, BMN, CNL пересекаются в
точка U, лежащая как на описанной окружности, так и на эллипсе ABCLMN, а U —
то
обобщенная точка Штейнера.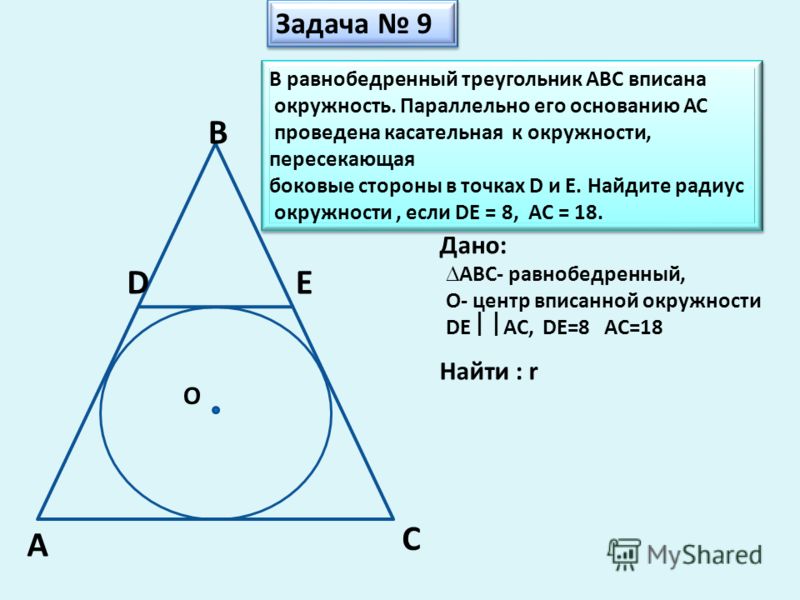
Статья 95 Девятиточная прямоугольная гипербола . Конфигурация, состоящая из прямоугольной гиперболы, проходящей через то incentre, эксцентриситет, центр тяжести и точка deLongchamps в треугольнике и три других важных пункта демонстрируют некоторые интересные свойства, которые находятся исследованы.
Статья 96 Подробнее о девятиточной прямоугольной гиперболе . Описанная окружность треугольника ABC — это девятиточная окружность треугольника. IJK из его эксцентриков. Линия JK проходит через точку A и середину D точки JK, который следовательно, лежит на описанной окружности.С аналогичным определением E, F существуют таким образом два треугольника ABC и DEF, и показано, что их центры и эксцентры ложь на девятиточечной прямоугольной гиперболе, обсуждаемой в CJB / 2010/95. Другой появляются интересные свойства, такие как точка ДеЛонгчама в DEF. одно и тоже точка как центр ABC.
Статья 97 Как эксцентрики создают точки на окружности
.
Кружки через пары вершин треугольника и эксцентры
противоположный
центры третьей вершины лежат на описанной окружности и проходят через
в центре треугольника. Треугольники с этими центрами в качестве вершин
выставлять
свойства, которые описаны.
Треугольники с этими центрами в качестве вершин
выставлять
свойства, которые описаны.
Статья 98 Ex-точки и их множества пересекающихся кругов . Экс-симедианные точки и экс-точки произвольной внутренней точки то треугольник лежат на гиперболе. Конфигурация, включающая бывшие точки данной точки и вершин данного треугольника, как показано, образуют набор из три окружности, имеющие общую точку (похожую на точку Ферма). В соотношение между этими точками получается.
Статья 99 Треугольник и его изображение под пол-оборота . Треугольник ABC и его изображение DEF под половиной оборота дают окружности BCD, CAE, ABF, пересекающиеся в точке P на окружности DEF. Точка Q на окружности ABC равна аналогично определено. Также установлено, что коника проходит через A, B, C, D, E, F, P, Q.
Статья 100 Круги через точку в равностороннем треугольнике
.
Даны три точки D, E, F, лежащие на серединах равностороннего треугольника.
ABC
определены условия, при которых окружности BCD, CAE, ABF имеют общую
точка.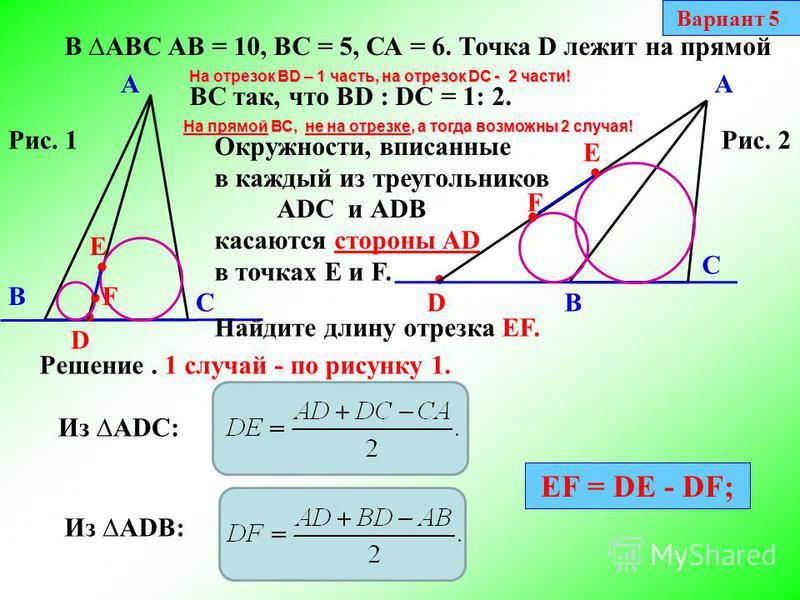
Статья 101 Пересечения в вершинах второго треугольника Брокара. . Если D, E, F — экс-симедианные точки, то доказано, что окружности BCD, CAE, ABF пересекают окружность Брокара в центре описанной окружности ABC и в вершинах из второй треугольник Брокара. Таким образом, возможна круговая перспектива. определенный.
Статья 102 Два треугольника, их экс-симедианы и четыре коники . Два треугольника в перспективе, вершина центра тяжести одного из них. В шесть экс-симмедианных точек лежат на конике, касательные в вершине ограничивать описанная окружность, а также пересечения различных линий дают шесть точки лежащих три на три на двух параллельных линиях.Два других интересных коника: тоже создал.
Статья 103 Высоты создают четыре круга, четыре коники и полярную линию
.
Если высоты треугольника ABC пересекаются с описанной окружностью в точках D, E, F, то
то
шесть внутренних пересечений двух треугольников и касательных в
над
шесть точек образуют конфигурацию, в которой четыре круга и четыре конуса
особенность. Дается анализ, в котором полярная ортоцентра играет
Главная роль.
Дается анализ, в котором полярная ортоцентра играет
Главная роль.
Статья 104 Как любые шесть точек на окружности создают две коники .Учитывая три хорды круга, перпендикуляры к этим аккордам от их конец точки образуют три пары параллельных линий. Из их пятнадцати точек зрения три пересечения лежат на бесконечно удаленной линии, а остальные двенадцать лежат на шести к шесть на двух кониках. Обратите внимание, что шесть точек должны лежать на круге, а не на общая коническая.
Статья 105 Внешние квадраты по сторонам треугольника . Если квадраты нарисованы снаружи по сторонам треугольника, конфигурация показывает две точки, похожие на точки Ферма.Также шесть перекрестков из различные линии определяют круг.
Статья 106 На перпендикулярах в углах циклического четырехугольника
.
Если перпендикуляры к сторонам провести в вершинах циклического
четырехугольник, то создается конфигурация, состоящая из двух окружностей
коаксиальный с первым кругом, каждый из которых содержит четырехугольники, похожие на каждый
Другой. Их внешние диагональные точки также лежат три на три на два.
коллинеарен
линий. Также возникают два других круга.
Их внешние диагональные точки также лежат три на три на два.
коллинеарен
линий. Также возникают два других круга.
Статья 107 Коники через три точки с центрами на фиксированной линии .Коники, проходящие через три неколлинеарных точки A, B, C с центрами на фиксированная линия имеет три коренные оси: BC, CA, AB. Если взять фиксированную точку P на одна из этих осей, скажем BC, то поляры P относительно всех коники пройти через другую фиксированную точку P ‘, которая, как и следовало ожидать, является гармонический сопряжена с P относительно B и C.
Статья 108 Свойство трех кругов, проходящих через фиксированную точку Кристофер Брэдли . Пусть ABC — треугольник, а P — неподвижная точка не на сторонах.Circle BPC встречает AB в W и AC в M. Circle CPA встречает BC в U и BA в N. Circle APB встречает CA в V и CB в L. Серединные перпендикуляры к LU, MV, NW пересекаются в точке Q.
Статья 109 Четыре перспективы в треугольнике и его окружности
.
Дан треугольник, его описанная окружность и точка не на описанной окружности. является
показано, как путем изменения положения точки вдоль линии четыре
перспективы
могут быть созданы.
является
показано, как путем изменения положения точки вдоль линии четыре
перспективы
могут быть созданы.
Статья 110 Три параллельные линии Паскаля и вспомогательная коника .
Статья 111 Серединные перпендикуляры трех радиусов окружности .
Статья 112 Параллели ног Cevians создают коническую форму. . От ног Cevians через точку проводятся параллели с двумя другими сторонами. Шесть точек, образованных на сторонах треугольника, лежат на конике.
Статья 113 Круги, проходящие через мыс Микель стопы Cevians
.
Если LMN являются основанием набора Cevian, то окружности AMN, BNL, CLM пересекаются в точке Q Микеля.Если теперь нарисованы круги BQC, CQA, AQB и круги AMN и BQC пересекаются в точке R с аналогичным определением S, T, тогда окружность RST проходит через точку Q Микеля. Центры семи кругов также демонстрируют некоторые замечательные свойства, показывающие, что Q точка Микеля второго треугольника, каскадный процесс, который может продолжаться бесконечно.
Статья 114 Свойства определенного круга Таккера . Три круга определяют конкретный круг Такера, а их центры демонстрируют некоторые интересные свойства.
Статья 115 Шесть кругов и их центры . В центре тяжести G треугольника ABC нарисованы окружности BGC, CGA, AGB, стороны в шести точках, лежащих на конике. Рисуются еще три круга, и шесть кругов центры демонстрируют некоторые интересные свойства.
Статья 116 Геометрия оси Брокара и связанных с ней коник . Из треугольника и его симедианной точки K и его центра описанной окружности O строятся различные треугольники, эллипс Брокара и еще две коники, центры которых находятся на оси Брокара KO.Определены две пористости и выделена специальная линия. Большая часть, если не все, содержание этой статьи известно и должно быть известно всем геометрам.
Статья 117 Когда Чевианы треугольника ABC пересекаются с окружностью в точках D, E, F
.
В треугольнике ABC, когда Чевианы через центроид G пересекаются с описанной окружностью Σ в точках
D, E, F и касательные проводятся в шести точках, создаются два треугольника. Пересечения сторон четырех треугольников в конфигурации обладают некоторыми интересными свойствами.
Пересечения сторон четырех треугольников в конфигурации обладают некоторыми интересными свойствами.
Статья 118 Два треугольника в перспективе, вписанные в конус . Для двух треугольников ABC, DEF в перспективе в точке P и вписанных в конику Σ, получается конфигурация, состоящая из 6 линий Паскаля и 2 возникающих точек Штейнера. Одна из строк Паскаля имеет дополнительные свойства, так как это не только строка Паскаля, но также ось перспективы Дезарга, а также полярность P относительно Σ. Другие свойства, включающие девять линий AD, AE, AF, BD, BE, BF, CD, CE, CF и касательные в шести вершинах выводятся ведущими к конической, дальнейшие свойства ключевой линии Паскаля и многочисленные наборы коллинеарных точки и параллельные линии.
Статья 119 Девятиточная коника и пара параллельных прямых
.
Аффинное преобразование окружности с девятью точками приводит к конике с девятью точками. Ортоцентр трансформируется в общую точку P, которая коллинеарна центру девятиточечной коники и центроида. Мы доказываем, что полярная точка P относительно девятиконечной коники параллельна оси перспективы Дезарга треугольника и изображению ортогонального треугольника.
Мы доказываем, что полярная точка P относительно девятиконечной коники параллельна оси перспективы Дезарга треугольника и изображению ортогонального треугольника.
Статья 120 Важная линия, проходящая через центр Чевианского инеллипса .Чевианский инеллипс — это тот, который касается сторон треугольника. внутренне — в точках, являющихся основанием линии Чевиана. Это показано в этом короткая статья о том, что линия, проходящая через точку Cevian и центр Cevian inellipse содержит и другие важные моменты.
Статья 121 Некоторые линии через Centroid G . Используя площадные координаты, мы каталогизируем некоторые линии через центроид. G треугольника ABC. Приведены координаты точек и уравнения прямых.
Статья 122 Некоторые строки через Incentre I .Используя площадные координаты, мы каталогизируем некоторые линии через центр. I треугольника ABC. Приведены координаты точек и уравнения прямых.
Статья 123 Свойства интангенциального треугольника
.
Даны треугольник ABC, вписанная и бывшая окружности. Общий
касательных к вписанной и бывшей окружности четыре; три являются
стороны ABC, а четвертая называется интангенсой. Есть три интангенса,
по одному для каждого бывшего круга, и они образуют треугольник A’B’C ‘, называемый интангенциальным
треугольник.Свойства интангенциального треугольника изучаются с помощью площадных
координируется с ABC как справочный треугольник. По построению его вписанная окружность равна
такой же, как у треугольника ABC. Треугольник его вершины имеет стороны
параллельно с ABC.
Общий
касательных к вписанной и бывшей окружности четыре; три являются
стороны ABC, а четвертая называется интангенсой. Есть три интангенса,
по одному для каждого бывшего круга, и они образуют треугольник A’B’C ‘, называемый интангенциальным
треугольник.Свойства интангенциального треугольника изучаются с помощью площадных
координируется с ABC как справочный треугольник. По построению его вписанная окружность равна
такой же, как у треугольника ABC. Треугольник его вершины имеет стороны
параллельно с ABC.
Статья 124 Две точки Чева, коллинеарные вершине и тринадцать коник . Дан треугольник ABC, точка P на BC и прямые LMP и UVP с L, U на AB и M, V на CA, то можно построить две точки Чева, лежащие на одной прямой вершина A. Возникают еще две точки Чевиана, и результирующая конфигурация точки и линии приводят к появлению тринадцати коник и двух гармонических диапазоны.
Статья 125 Свойства экстангенциального треугольника
.
Внешние общие касательные к трем бывшим окружностям образуют
экстангенциальный треугольник A’B’C ‘.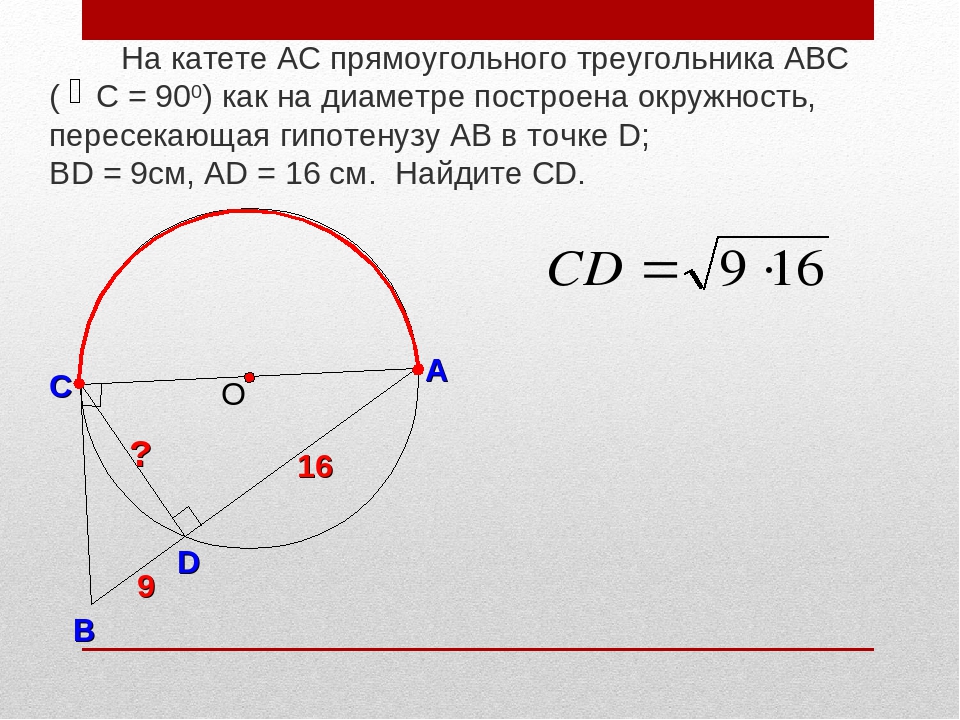 Треугольники ABC и A’B’C ‘в перспективе
Перспектор ортоцентра интуитивно понятного треугольника. Ось перспективы
играет важную роль в конфигурации. Треугольник A’B’C ‘и ортика
треугольник гомотетичен точке Клоусона.
Треугольники ABC и A’B’C ‘в перспективе
Перспектор ортоцентра интуитивно понятного треугольника. Ось перспективы
играет важную роль в конфигурации. Треугольник A’B’C ‘и ортика
треугольник гомотетичен точке Клоусона.
Статья 126 Некоторые свойства конфигурации Ex-Circle . Конфигурация ex-circle изучается и, в частности, показана как середины сторон бывшего центрального треугольника ведут к нескольким круги и перспективы, а также новый (для меня) треугольник с вершинами на стороны исходного треугольника и две новые (как мне кажется) точки на описанной окружности.
Статья 127 Когда круг проходит через вершину и разрезает противоположную сторону
.
Удивительная конфигурация возникает, когда круг проходит через
вершина и разрезает противоположную сторону. Две пары касающихся кругов и два круга
каждый проходящий через семь ключевых точек появляются и дополнительные точки на
также создается оригинальный круг. Кажется маловероятным, что синтетический раствор
будет существовать, так как некоторые из координационных работ технически очень сложны.
Статья 128 Симметрия скаленового треугольника. .Точки, разделяющие каждую сторону разностороннего треугольника в фиксированном соотношении, ведут к конфигурации с двумя наборами из трех равных окружностей и конуса. Много результаты самоочевидны, но уравнения окружностей и коники записано.
Статья 129 Кубик Нойберга . Анализируется кубический треугольник Нойберга. Это место точки P с тем свойством, что отражение P в стороны треугольника ABC ведет к треугольнику, который находится в перспективе с ABC.
Статья 130 Расширение теории кругов Хэгге .Представлено расширение теории кругов Хагге.
Статья 131 Построение кругов, всегда имеющих центр Девятиконечный центр . От любой общей точки P отражения в BC. CA, AB дают D, E, F. середины AD, BE, CF — это U, V, W соответственно. U, V, W лежат на круг с центром девятиконечный центр.
Статья 132 Cevian Conic
.
Если P — точка Чевиана в треугольнике ABC, а D, E, F — основания
Cevians, затем три круга PEF, PFD, PDE снова встречаются сторонами в шести других
точки. Показано, что эти шесть точек лежат на конике, которую мы называем
Cevian Conic.
Показано, что эти шесть точек лежат на конике, которую мы называем
Cevian Conic.
Статья 133 — это Коники в форме полуправильного шестиугольника. Шестиугольник AFBDCE с равносторонним треугольником ABC и AD, BE, CF совпадающая в центре тяжести P треугольника ABC вписана в конику, и как таковая определяется как полурегулярный шестиугольник. Доказано, что шесть окружных центров треугольников AFP, FBP, BDP, DCP, CPE, EPA имеют коническую форму, как и их шесть ортоцентров. Также доказано, что пересечения смежных прямых Эйлера являются коническими.Кабри указывает, что шесть центров по центру и шесть центров по девяти точкам также имеют коническую форму.
Статья 134 Когда Cevian Conic представляет собой круг . Когда Чевианская точка является точкой Жергонна, Чевианская коника представляет собой окружность. с центром в центре.
Статья 135 Построение треугольников с совпадающими центроидами
.
Для двух треугольников с совпадающими центрами тяжести показано, как
построить неограниченное количество треугольников с одинаковым центром тяжести.
Статья 136 Свойства симедианной точки вписанного четырехугольника.Если ABCD — вписанный четырехугольник, то симедианные точки треугольников Показано, что ABC и DBC обладают некоторыми замечательными свойствами. Множество пар линий могут быть построены, пересечения которых лежат по сторонам от диагональной точки треугольник.
Статья 137 Аффинное преобразование свойств треугольника Эйлера. По треугольнику ABC и точке K строится конфигурация содержащий тройную коническую форму, циркум-коническую, девятиконечная коника и 7 точечно-коническая. Когда K на самом деле является симедианной точкой K (a 2 b 2 , c 2 ), тогда эти коники — это знакомые круги, связанные с треугольником в евклидовой самолет.В этой статье мы берем K, точку не по бокам от ABC, быть произвольная точка K (f, g, h), и то, что возникает, является аффинным отображением евклидовой самолет.
Статья 138 Объяснение коллинеарности центров треугольников.
Коллинеарности сохраняются аффинным преобразованием, так что для
каждая коллинеарность центров треугольников, есть другая, когда аффинная
трансформация произошла, и наоборот.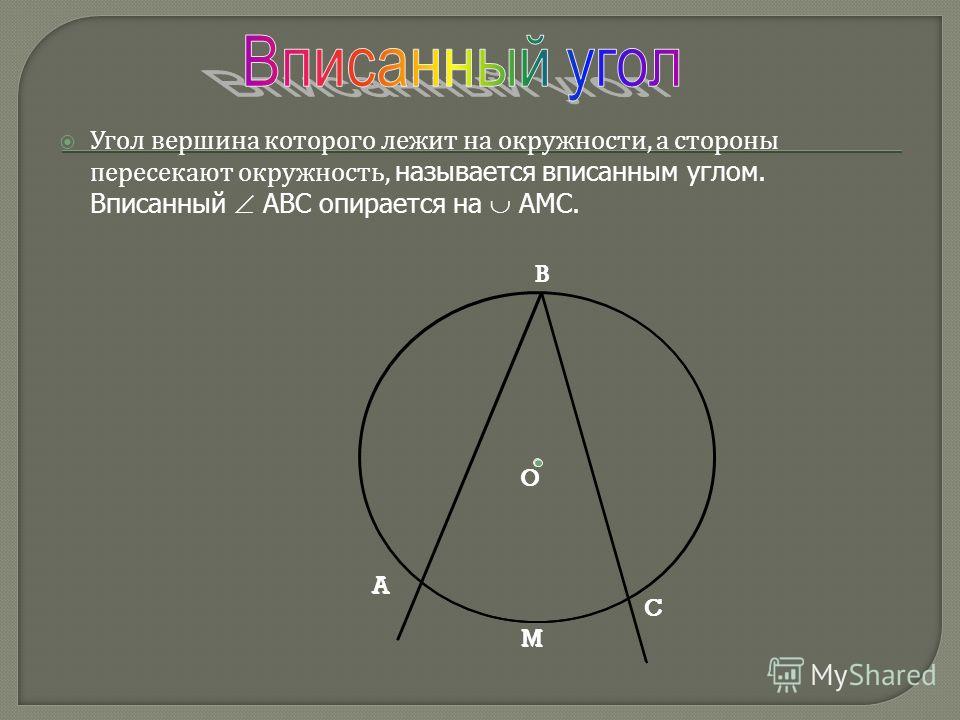 Проиллюстрируем это, рассмотрев
что происходит с тремя коллинеарностями на евклидовой плоскости, когда аффинная
трансформация переводит симедианную точку в центр.
Проиллюстрируем это, рассмотрев
что происходит с тремя коллинеарностями на евклидовой плоскости, когда аффинная
трансформация переводит симедианную точку в центр.
Статья 139 Гармоническая чевиановая коника. Если D, E, F — ноги Cevian с D на BC и т. Д., И если L — гармонически сопряжена с C относительно B и D, а U — гармоническая сопрягать группы B относительно C и D и если M, N, V, W определены аналогично, то a коника проходит через шесть точек L, U, M, V, N, W. Есть одна внутренняя Точка Чева, для которой коника является окружностью.
Статья 140 Центроид центроидов. Пусть P — точка не на сторонах треугольника, и пусть центроиды треугольника PBC, PCA, PAB — это L, M, N соответственно.Пусть теперь J — центр тяжести треугольник LMN. Тогда J лежит на прямой PG, где G — центр тяжести треугольника ABC. Точка совпадения Q операторов AL, BM, CN также лежит на PG.
Статья 141 Три центроида, образованные циклическим четырехугольником
.
Центроид четырехугольника считается площадью постоянного
плотность G, центроид
четырехугольника, имеющего единичные массы
в его вершинах N, центр тяжести четырехугольника, рассматриваемого как имеющий
единицы массы в его вершинах и масса двух
единиц в E (пересечение его
диагонали) — это F. Показано, что E, F, N, G коллинеарны.
Показано, что E, F, N, G коллинеарны.
Статья 142 Спряжение в окружности . Предлагается конструкция, в которой точки (f, g, h) в барицентрической системе координаты преобразуются в точки (a / f, b / g, c / h). Это явно спряжение, и мы называем его вписанным сопряжением.
Статья 143 Круг из девяти точек диагонального треугольника . Анализируется десятиточечная прямоугольная гипербола через середины вписанного четырехугольника и девятиконечной окружности диагональный треугольник.
Статья 144 Четыре круга из девяти точек . В любом четырехугольнике ABCD четыре окружности с девятью точками треугольников BCD, ACD, ABD, ABC имеют общую точку, лежащую на гиперболе через середины и на описанной окружности диагонального треугольника.
Статья 145 Конциклические центры окружности в конфигурации Штейнера
.
В треугольнике ABC с центроидом G точки D, E, F лежат на AG, BG, CG.
соответственно и таковы, что AG = GD, BG = GE, CG = GF.
Доказано, что
Центры окружностей треугольников AFG, FBG, BGD, DGC, CGE, EGA совпадают.
Статья 146 Больше коник в полуправильном шестиугольнике . ABC — равносторонний треугольник, а AFBDCE — шестиугольник, вписанный в конический. Треугольники ABC и DEF в перспективе с вершиной P, центром тяжести ABC. G1-G6 — это центроиды треугольников EAF, FBD, DCE, BDC, CEA, AFB. это показано, что эти точки лежат на конике. Также треугольники G1G2G3 и G4G5G6 являются конгруэнтно и в перспективе. Шесть внутренних точек пересечения треугольники ABC и DEF также лежат на конике.
Статья 147 Снова средняя прямоугольная гипербола .Если A, B, C, D — четыре точки на окружности, а E — любая другая точка, то геометрическое место центра конуса ABCDE при изменении E представляет собой прямоугольную гиперболу через середины четырехугольника ABCD.
Статья 148 Круг через две вершины, три окружности и точку Микеля
.
Начиная с треугольника ABC и точки D на BC, показано, как
центры окружностей треугольников ABC, ADB, ADC лежат на окружности, проходящей через A. Если это
окружность пересекает окружность ABC в точках A и P, тогда показано, что треугольник PBC
показывает точку Микеля Q с точками D, M, N.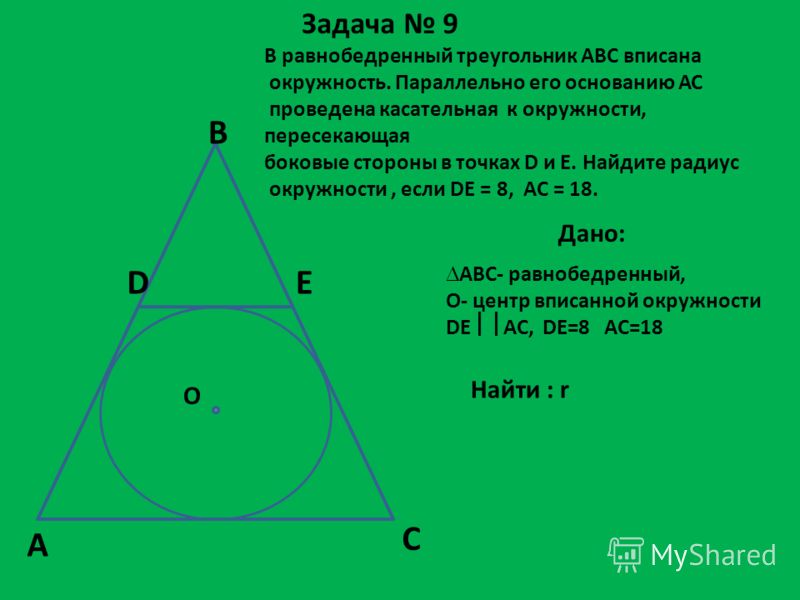 BD.
BD.
Статья 150 Когда точка является центром окружности, центром и ортоцентром . Дан треугольник ABC, центр описанной окружности O и центры D, E, F окружностей. BOC, COA, AOB соответственно, тогда O — центр треугольника DEF, а также будучи ортоцентром треугольника эксцентров.
Статья 151 Ортоцентр Коникс . Когда кружки BHC, CHA, AHB в треугольнике ABC с ортоцентром H нарисованы их центры D, E, F, обладающие интересными свойствами.
Статья 152 является Создание кругов из точки симедианы .Для треугольника ABC и его симедианной точки K нарисованы круги BKC, CKA, AKB. Их другие точки пересечения с стороны ABC показаны лежащими на круге Такера. Эти точки также лежат в пары на сторонах другого треугольника и другие пересечения этих стороны с окружностями BKC, CKA, AKB также совпадают. Центры этих круги расположены на оси Брокара.
Статья 153 Другие свойства Incentre
.
В треугольнике ABC с центром I середины
AI, BI, CI расположены.Проведены биссектрисы AD, BE, CF. Эти
встречаются с внутренними сторонами сторон ABC в шести точках, которые, как показано, лежат на
эллипс. По мере того, как фигура развивается, включаются несколько других
расположены круги и коники.
Эти
встречаются с внутренними сторонами сторон ABC в шести точках, которые, как показано, лежат на
эллипс. По мере того, как фигура развивается, включаются несколько других
расположены круги и коники.
Статья 154 является О вписанной и эксцентричной окружности Чевианова треугольника . Дан треугольник ABC, если D, E, F — ноги Чевианы AD, BE, CF и L, M, N являются точками контакта вписанной окружности треугольник DEF со сторонами треугольника DEF, то AL, BM, CN равны ncurrent, поскольку являются AL ‘, BM’, CN ‘, где L’, M ‘, N’ — точки соприкосновения бывших окружностей с EF, FD, DE соответственно.
Статья 155 является Окружность пары Чевианских треугольников . В треугольнике ABC нарисованы два Чевианских треугольника, их точки пересечения и вершины треугольника ABC приводят к шести множествам коллинеарных точек. Несколько конусов идентифицированы.
Статья 156 Circumcentre Conics
.
Дан треугольник ABC, пусть треугольник UVW является сокращением
ABC на коэффициент увеличения t (0
Статья 157 — это Общий инеллипс
. В
в целом эллипс в треугольнике касается его сторон у ног Cevians.An
дан анализ, связывающий точку Чевиана с центром эллипса.
и к двум родственным циркумконикам.
В
в целом эллипс в треугольнике касается его сторон у ног Cevians.An
дан анализ, связывающий точку Чевиана с центром эллипса.
и к двум родственным циркумконикам.
Статья 158 Шестиконечные окружности и связанные с ними коники . Если P — внутренняя точка треугольника ABC и AP, BP, CP снова пересекаются с описанной окружностью в точках A ‘, B’, C ‘соответственно, а U, V, W — средние точки AP, BP, CP и D, E, F являются средними точками PA ‘, PB’, PC ‘ соответственно, тогда U, V, W, D, E, F, очевидно, смежны. Но Конфигурация имеет другие указанные свойства.
Статья 159 — это Двенадцатиточечная конфигурация и теорема Карно . Конфигурация из двенадцати точек возникает, когда шесть из точки лежат на конике, а остальные шесть точек являются вершинами двух треугольники в перспективе. В этой статье мы рассмотрим конфигурацию в коника разрезает три стороны треугольника в вещественных точках. Номер теоремы создают множество условий на точках пересечения эквивалент теоремы Карно.
Статья 160 Касательные к конике от вершин треугольника
. Дана коника, разрезающая стороны треугольника
в шести вещественных точках касательные A1, A2, B3, B4, C5, C6 проводятся к конике. В
касательные пересекаются в 12 точках (15, если считать A, B, C). В
как форма
Конфигурация из 12 точек (см. Статью 159), так что шесть из двенадцати точек лежат на конусе.
Дана коника, разрезающая стороны треугольника
в шести вещественных точках касательные A1, A2, B3, B4, C5, C6 проводятся к конике. В
касательные пересекаются в 12 точках (15, если считать A, B, C). В
как форма
Конфигурация из 12 точек (см. Статью 159), так что шесть из двенадцати точек лежат на конусе.
Статья 161 Когда 12 точек отображают восемь 6-точечных коник и 6 параллельных линий . Шесть прямых касаются окружности в вершинах треугольников в перспективе создают двенадцать точек пересечения.Шесть коников с шестью точками каждая может быть проведена через двенадцать точек, каждая точка лежит на трех кониках. Также шесть строк могут быть проведенные через двенадцать точек, линии, которые совпадают в вершине перспектива.
Статья 162 Когда 24 точки образуют три коники из 8 точек и 12 параллельных линий . Описывается конструкция с участием две хорды коники, в результате чего получается 24 точки, которые образуют три коники с 8 точками и 12 параллельных линий.
Статья 163 Теорема о полном четырехугольнике
. Данный
полный четырехугольник ABCDEF и две точки P и Q, то хорошо известно
что коники ABCPQ, AFEPQ, BFDPQ и CDEPQ имеют общую точку R. Доказано
что когда P, Q — середины диагоналей BE, CF соответственно, то R
лежит на третьей диагонали AD.
Данный
полный четырехугольник ABCDEF и две точки P и Q, то хорошо известно
что коники ABCPQ, AFEPQ, BFDPQ и CDEPQ имеют общую точку R. Доказано
что когда P, Q — середины диагоналей BE, CF соответственно, то R
лежит на третьей диагонали AD.
Статья 164 является Поперечный четырехугольник . Трансверсальная LMNP пересекает выпуклый четырехугольник ABCD с L на AB и т. д. Гармонические сопряжения L, M, N, P — это L ‘, M’, N ‘, P’. Доказано, что L’P ‘и M’N’ пересекаются по диагонали BD и что L’M ‘пересекает N’P’ по диагонали AC.
Статья 165 Описание свойств шестиугольника Паскаля. . А дано описание свойств шестиугольника Паскаля, показывающее, как 6 Строки Паскаля делятся на два набора по 3 параллельных строки, определяющих 2 Штайнера. точки.
Статья 166 Аналитическая трактовка румынской проблемы.
.
А
дан треугольник ABC и коника, разрезающая каждую из его сторон на две действительные
точки. Касательные в этих точках нарисованы в виде шестиугольника касательных.
описывающую конику, вершины которой обозначены как DF’ED’FE, как на рис. 1. Это
показано, что AD, BE, CF являются параллельными, как AD ‘, BE’, CF ‘и DD’, EE ‘, FF’.
Позиции результирующих перспектив P, P ‘и Q расположены. в
Румынский вопрос: коника была окружностью с девятью точками, а точка P лежит на
гипербола ABCKOi, где K — симедианная точка, а Oi — изотомно сопряженная окружность O.
изотомный конъюгат P
то лежит на диаметре описанной окружности, соединяющей точку Штейнера и
Терри-пойнт. Также показано, что в общем случае AD ‘, EF’, FE ‘являются
одновременно являются BE ‘, DF’, FD ‘и CF’, DE ‘, ED’.Используются координаты площадей
повсюду с ABC треугольником ссылки.
1. Это
показано, что AD, BE, CF являются параллельными, как AD ‘, BE’, CF ‘и DD’, EE ‘, FF’.
Позиции результирующих перспектив P, P ‘и Q расположены. в
Румынский вопрос: коника была окружностью с девятью точками, а точка P лежит на
гипербола ABCKOi, где K — симедианная точка, а Oi — изотомно сопряженная окружность O.
изотомный конъюгат P
то лежит на диаметре описанной окружности, соединяющей точку Штейнера и
Терри-пойнт. Также показано, что в общем случае AD ‘, EF’, FE ‘являются
одновременно являются BE ‘, DF’, FD ‘и CF’, DE ‘, ED’.Используются координаты площадей
повсюду с ABC треугольником ссылки.
Статья 167 — это Основные свойства четырехугольника с вписанной окружностью. . Свойства четырехугольника, имеющего вписанную окружность.
Статья 168 Свойства пары диаметрально противоположных треугольников
.
Начиная с треугольника ABC и его описанной окружности
центр O, треугольник DEF таков, что AD, BE, CF проходят через O. Касательные в
шесть точек и девять линий, соединяющих их вершины, создают конфигурацию
что исследуется в этой статье.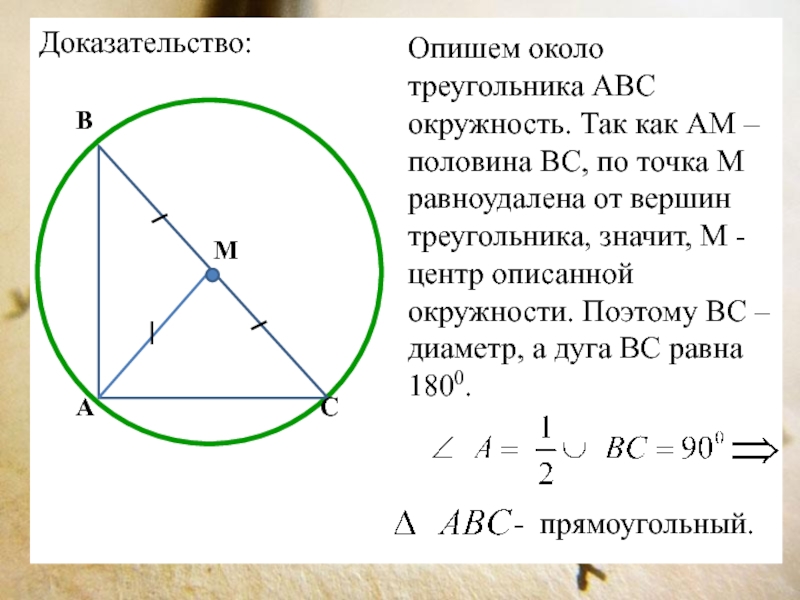
Статья 169 Два перспективных треугольника, вписанные в конику . Треугольники ABC и DEF вписаны в конику и находятся в перспективе через точку O. Проведены полярные линии LMN и PQR, и показаны шесть точек параллелизма. определить ряд важных коллинеарностей. Также появляются две коники.
Статья 170 Брокар Коникс . Треугольники ABC и DEF вписаны в круг и AD, BE, CF совпадают в симедианной точке K. Стороны двух треугольников продолжаются, и касательные в вершинах проводятся.Полярные линии два треугольника совпадают и точки пересечения сторон и касательных показано, что дополнительно получается четыре шестиконечных конуса с центрами на ось Брокара в порядке, где O — центр окружности ABC.
Статья 171 Прохождение коника через ноги двух Cevian может привести ко второму конику. Точки P и Q — это две точки Чевиана, так что ступни
U, V, W, U, V ‘, W’ имеют конику, затем хорды
UV, WV ‘, W’U’ пересекаются, как показано, тогда и только тогда, когда ABCDEF является конической. Остальные свойства (не доказанные в этой статье) сохраняются, как можно заключить из рис.1.
Остальные свойства (не доказанные в этой статье) сохраняются, как можно заключить из рис.1.
Статья 172 Внутренний круг циклического четырехугольника. Дан вписанный четырехугольник ABCD с серединами сторон P, Q, R, S и середины диагоналей U, V, то хорошо известно что прямоугольная гипербола проходит через P, Q, R, S, U, V, а также через O — центр и H, J — две другие диагональные точки. Находим уравнение этой гиперболы и внутреннего круга OUVT, центр G. Середина W UV также является серединой PR и QS.
Статья 173 Вспомогательные окружности циклического четырехугольника. Сначала рисуется вписанный четырехугольник ABCD.
Середины AB, BC, CD, DA, AC, BD помечены буквами P, Q, R, S, U, V,
центром ABCD является точка O, а диагональные точки — T = AC∧CD, H =
AB∧DC
и K = AD∧BC. (Все это конечные точки.) 10-гранный прямоугольник
показана гипербола P, Q, R, S, O, U, V, T, K, H. Мы устанавливаем существование
из
три окружности средней точки OUVT, OPRH, OQSK, а также полудиагональная точка
Обведите LMNXYZ, где L, M, N — середины OT, OH, OK и X = OK∧HT,
Y =
OH∧KT и Z = OT∧H.
Статья 174 — это Цвианский круг ведет к перспективным треугольникам. Окружность проводится через U, V, W у подножия точки Чевиана T. Три другие точки создаются на сторонах треугольника ABC, что позволяет нарисовать второй треугольник DEF. Показано, что треугольники ABC и DEF находятся в перспективе.
Статья 175 Когда два треугольника пересекаются в кониках и кругах. Если P является внутренним по отношению к треугольнику, а точки D, E, F определены на AP, BP, CP соответственно, так что AD / AP = BE / BP = CF / CP, то пересечения треугольники ABC и DEF лежат на конике.Если P — симедиана точка K, то коника а круг.
Статья 176 Ортологические треугольники. Треугольники ABC и DEF ортологичны, если перпендикуляры от вершины одного из них к соответствующим сторонам другого совпадают. Свойство симметрично, но не транзитивно.
Статья 177 — это Специальные строки Паскаля. Рассматривая шестиугольник как два треугольника в перспективе и помечая их вершины, а также вершины определяющей коники, показано, что две прямые Паскаля проходят через точки, которые являются точками совпадения трех прямых.
Статья 178 — это Больше кругов с центром на оси Брокара. Круги через B и C и точки Брокара приводят к двум кругам с центром на оси Брокара и нескольким совпадениям.
Статья 179 Второй треугольник Брокара. Учитывая точки Брокара Ω, Ω ‘в треугольнике, точка совпадение пересечения линии АК с кругом из 7 точек и кружками AΩC, BOC, AΩ’B (D на диаграмме выше) и два аналогичных точки E, F, найденные циклической заменой A, B, C образует так называемый второй треугольник Брокара (Дэвид Монк, частное сообщение).Анализ является содержанием этого документа.
Статья 180 Обводит точки Брокара и Кругоцентр. С помощью точек Брокара Ω и Ω ‘через AΩΩ ‘, BOW’, COW, и они встречаются в точке D описанной окружности. Точки E, F определяются аналогично. Доказано, что прямые AD, BE, CD все параллельны ΩΩ ‘. Далее, если окружить AΩΩ ‘ встречается с AB в X и AC в Y, затем XY также параллельна ΩΩ ‘, как и две дальнейшие линии определяется аналогично XY циклической заменой.
Статья 181 Обводит точки Брокара и Симедиана. Обе окружности BΩK, CΩK проходят через одну и ту же точку D на BC.
E и F определены циклической заменой и лежат на CA и AB.
DEF оказывается на прямой, параллельной касательной в точке K к
круг из 7 точек (следовательно, перпендикулярный оси Брокара).
Обе окружности BΩK, CΩK проходят через одну и ту же точку D на BC.
E и F определены циклической заменой и лежат на CA и AB.
DEF оказывается на прямой, параллельной касательной в точке K к
круг из 7 точек (следовательно, перпендикулярный оси Брокара).
Статья 182 — это Проблемы, требующие доказательства. Вот четыре проблемы. Фактически решение проблемы 4 известно, но другие проблемы вполне могут быть открытыми.
Статья 183 Коники и треугольники в перспективе. Показано, как пара треугольников в перспективе приводит к конике и наоборот.
Статья 184 является Cevian Perspectivity. Треугольник ABC и PQR с точками Чевиана D и S соответственно называются
Чевианская перспектива, если точки 11 = AD∧PS, 22 = BD∧QS, 33 = CD∧RS коллинеарны.
Если точки обозначены следующим образом: 12 = AD∧QS, 13 = AD∧RS, 21 = BD∧PS, 23 = BD∧RS,
31 = CD∧PS, 32 = CD∧QS, то справедливы следующие результаты: (i) треугольники 13 23 21 и 31 32 12
находятся в (обычной) перспективе через вершину X, (ii) точки 13, 23, 21, 31, 32, 12 — конические
и (iii) X лежит на прямой SD.
Статья 185 Теорема о четырех кониках. Если даны два набора из четырех прямых, которые пересекаются один на один из четырех на прямой, то двенадцать оставшихся точек несут четыре коники, через которые проходят две коники.
Статья 186 6 точек и 4 точки зрения Если 6 точек обеспечивают 1 пару треугольников в перспективе, то есть еще 3 пары перспективных треугольников, с той же вершиной, на той же диаграмме. Оси их Дезарга образуют стороны треугольника и связанные поперечные.(Предполагается, что исходная пара треугольников не находится в тройной перспективе.)
Статья 187 Перспектива в паре циклических четырехугольников. Когда два вписанных четырехугольника в одном круге находятся в перспективе, тогда существует ось перспективы, соединяющая точки пересечения всех шести пар соответствующих сторон.
Статья 188 Существуют ли когда-либо три треугольника во взаимной перспективе? На вопрос в названии есть ответ «Да», например, три треугольника в поризме Брокара фактически находятся в тройной обратной перспективе друг с другом. Однако в этой очень короткой статье мы изучаем условие, которому должны подчиняться три треугольника, чтобы они находились во взаимной перспективе. (Перспективы, конечно, симметричны, но не в целом ассоциативны.)
Однако в этой очень короткой статье мы изучаем условие, которому должны подчиняться три треугольника, чтобы они находились во взаимной перспективе. (Перспективы, конечно, симметричны, но не в целом ассоциативны.)
Статья 189 Средняя коническая точка. Известно, что у пары Cevians ступни конической формы. Здесь мы докажем, что их середины также являются коническими.
Статья 190 Двойной конус Кругов Брокара Построение тройного отношения круга и круг Брокара повторяется, но начиная с центра окружности O, чем симедианная точка K.Установлено, что Brocard Circle заменен к коника (двойная коника), проходящая через O и K и имеющая центр середина ОК. Этот результат приводит к понятию сопряжения, свойства которого мы кратко обрисовать.
Статья 191 Три круга и их центры Для вписанного четырехугольника и точки P не
на стороне линии могут быть проведены через P параллельно сторонам каждой линии
встреча
соседние стороны в точку. Восемь точек, созданных таким образом
определять
две окружности и три центра окружностей и P образуют параллелограмм.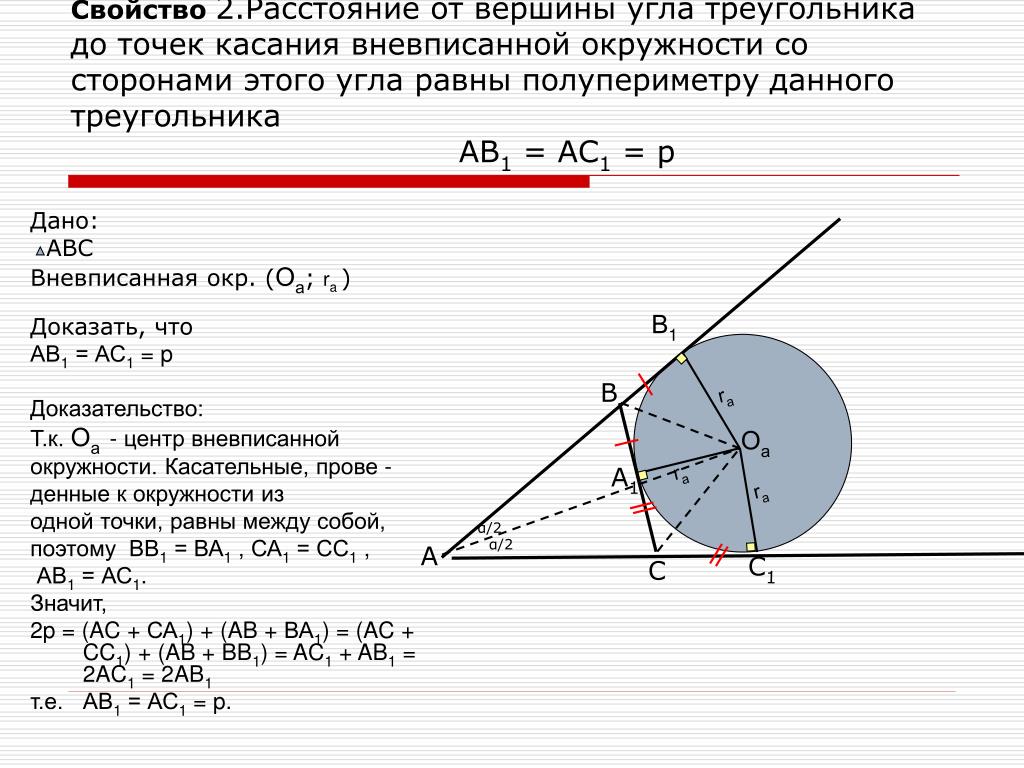
Статья 192 Обобщение тройного отношения круга Данный треугольник ABC выбирается точка P не на его сторонах и прямые, параллельные AB и AC проходят через P, чтобы встретить стороны в четырех различных точках. В положение P определяется, когда эти четыре точки совпадают.
Статья 193 Задача о двух кругах, связанных с осью GK Через точку X проводят линии параллельно стороны ABC. Из полученных шести точек строятся два круга и условие на X, чтобы их общая хорда проходила через X, в результате X должен лежать на оси GK.
Статья 194 Девятиконечная коника KG Свойства девятиточной коники отображаются с помощью точки Чевиана K (а также центроида G). В симмедиан точка Km среднего треугольника (X141) лежит на оси KG, средняя точка KKm является центром X девятиконечная коническая.
Статья 195 Ортоцентрическая окружность циклического четырехугольника С ABCD вписанный четырехугольник перпендикуляры
нарисованы от A к BC и к CD, встречая эти стороны в L и N соответственно
и перпендикуляры проведены от B к DA и к CD, которые пересекаются с этими сторонами в Z
и X соответственно. CP. это
найденный
что A ‘, B’, C ‘, D’ прилегают друг к другу и круг, который мы называем ортоцентром
круг, поскольку он отражает построение ортоцентра в треугольнике.
Девять других кругов возникают из фигуры, и их свойства
исследованы.
CP. это
найденный
что A ‘, B’, C ‘, D’ прилегают друг к другу и круг, который мы называем ортоцентром
круг, поскольку он отражает построение ортоцентра в треугольнике.
Девять других кругов возникают из фигуры, и их свойства
исследованы.
Статья 196 Две центральные прямые в циклическом четырехугольнике Там пять основных центральных точек вписанного четырехугольника: центр описанной окружности O, то центроид F, центр масс G, пересечение диагоналей E и то пересечение прямых, соединяющих середины противоположных сторон T.это в этой статье доказано, что ГТД — прямая линия, а OTF — прямой линия. Кроме того, ET = 3TG и OT = 3TF, поэтому GF параллелен OE. (The антицентр тоже лежит на OTF.)
Статья 197 Когда две пары диагоналей совпадают Если ABCD — вписанный четырехугольник и касательные в точках A, B, C, D образуют четырехугольник PQRS, диагонали AC, BD и PR, QS все проходят через заданную точку. Здесь мы определяем эту точку.
Статья 198 Перспектива двух севианцев В
Треугольник Cevians проведен через P и Q. AP. Доказано, что треугольники LMN и RST перспективны.
AP. Доказано, что треугольники LMN и RST перспективны.
Статья 199 Три круга с коллинеарными центрами С ABCD центр вписанного четырехугольника O и середины сторон PQRS, линии PO, QO, RO, SO пересекаются с противоположными сторонами в точке T, U, V, W соответственно. Круги SUQW и TVPR имеют центры F и E соответственно. Это Доказано, что FOE — прямая линия. Некоторые другие очевидные результаты упомянул.
Статья 200 Задача о четырехугольнике с вписанной окружностью Дан четырехугольник с вписанной окружностью — вершины A, B, C, D и точки контакта P, Q, R, S.Линии AQ, AR, CP, CS рисуются пересекающимися в точках K и M. Проведены прямые BS, BR, DP, DQ. пересекающийся в N и L. Доказано, что K, M лежат на BD, а N, L лежат на AC.
Статья 201 Все о циклическом четырехугольнике и его кузене Дан циклический четырехугольник ABCD с
центр окружности O и диагонали AC, BD, EF, затем середины диагоналей
П,
Q, R соответственно, как хорошо известно, коллинеарны. Точки U, V, W — это
то
пересечения диагоналей.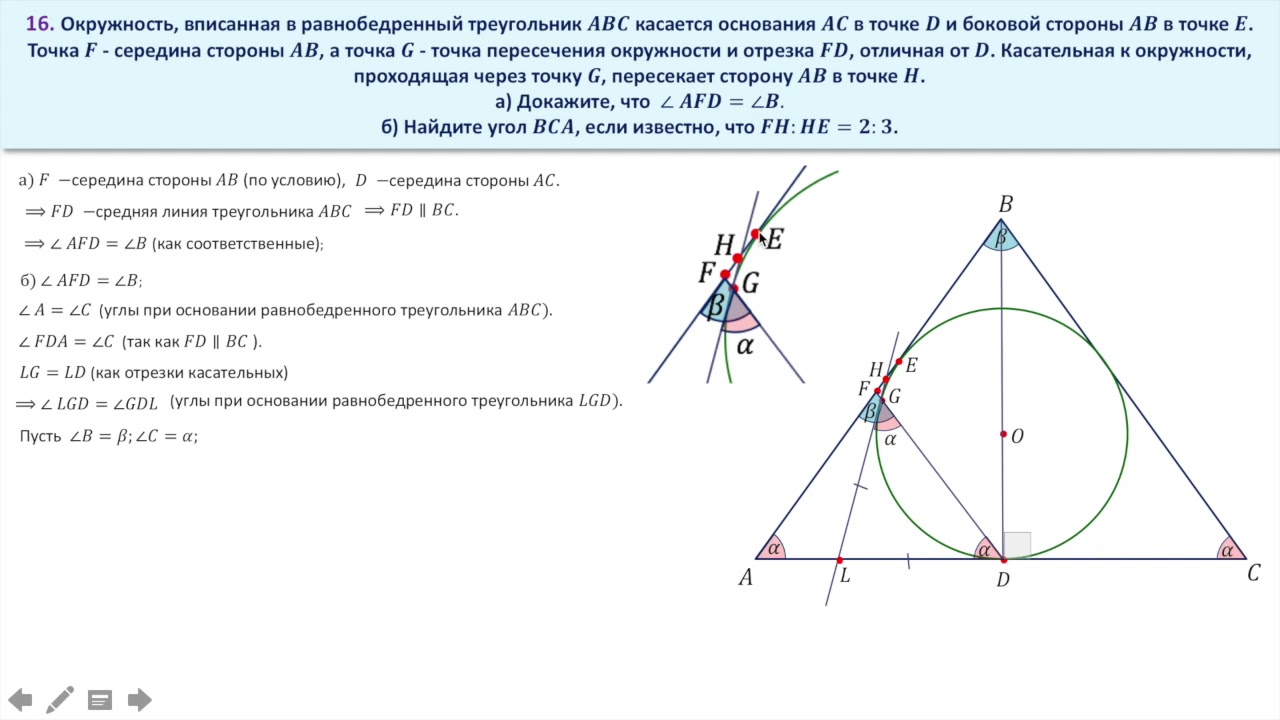 Сначала показано, что круг UPQ проходит
через O и что если прямая RU пересекает этот круг в точке S, то
следующий
все круги проходят через S.Эти круги — VRP, WRQ, UVW, EFO, ACR, BDR.
Если
окружности WVA, WVB, WVC, WVD пересекают окружность ABCD в точках A ‘, B’, C ‘,
D ‘
тогда RAA ‘, RBB’, RCC ‘, RDD’ все прямые. Это не безосновательно
к
говорят, что S — самая важная точка на рисунке.
Сначала показано, что круг UPQ проходит
через O и что если прямая RU пересекает этот круг в точке S, то
следующий
все круги проходят через S.Эти круги — VRP, WRQ, UVW, EFO, ACR, BDR.
Если
окружности WVA, WVB, WVC, WVD пересекают окружность ABCD в точках A ‘, B’, C ‘,
D ‘
тогда RAA ‘, RBB’, RCC ‘, RDD’ все прямые. Это не безосновательно
к
говорят, что S — самая важная точка на рисунке.
Статья 202 Теорема о средней точке Пусть ABCD — четырехугольник с L, M, N середины AB, BC, CA и U, V, W середины AD, BD, CD, затем то Коники AULMN, BVLMN, CWLMN имеют четвертую общую точку. (D не должен лгать на медианы ABC.)
Статья 203 Другой круг с центром на оси Брокара В треугольнике ABC с симедианной точкой K центр окружности O, окружности BKC, CKA, AKB пересекаются со сторонами еще в шести точках, два с каждой стороны. Показано, что эти точки лежат на окружности с центром в точка O ‘на оси Брокара так, что OK = 2KO’.
Статья 204 — это Между трехкратным соотношением круга и окружности
Когда UVW представляет собой гомотетичный треугольник (и аналогичный)
в треугольник ABC через K, то шесть точек пересечения UV, VW, WU
то
стороны ABC лежат на окружности.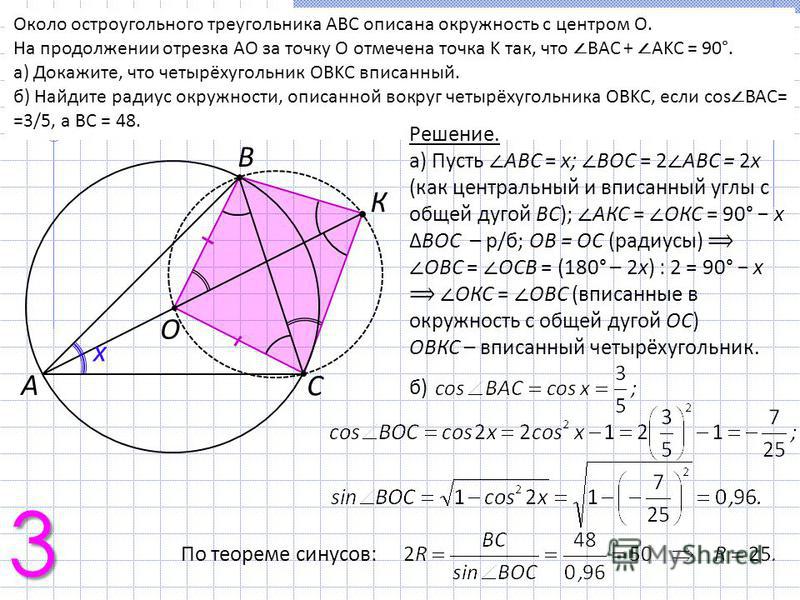 Когда UVW становится точкой в K, получается
Круг тройного соотношения, и когда U, V, W достигают A, B, C, получается
По кругу. Центры O ‘этих окружностей движутся по оси Брокара.
Когда UVW становится точкой в K, получается
Круг тройного соотношения, и когда U, V, W достигают A, B, C, получается
По кругу. Центры O ‘этих окружностей движутся по оси Брокара.
Статья 205 Линии Брокара KΩ и KΩ ‘ Круги A & OmegaΩ ‘, B и OmegaΩ’, C и OmegaΩ ‘ встречаются со сторонами ABC еще в шести точках, лежащих на две линии K & Omega, KΩ ‘(которые мы называем линиями Брокара). Эти шесть пунктов также ложь на четырех кругах, каждая из шести точек лежит на двух кругах.
Статья 206 Разделение OH на пять или семь равных частей Разделив каждую сторону треугольника на четвертей, а затем проведя полученные девять червиановых линий, получим шесть точек. создается внутренне, через которое нарисованы два круга. Их центры лежат на линию Эйлера и разделите ОН в соотношениях 1: 4 и 4: 3.
Статья 207 — это Срединная коника Учитывая
треугольник ABC и его центр тяжести G, середины AG, BG, CG обозначены
U,
V, W. Коники BCUVW, CAUVW, ABUVW нарисованы и снова встречаются со сторонами в
точка D,
D ‘, E, E’, F, F ‘. Доказано, что D, D ‘, E, E’, F, F ‘лежат на конике.
Доказано, что D, D ‘, E, E’, F, F ‘лежат на конике.
Статья 208 Пара изогональных конъюгатов дает конус через 6 точек. Если P и Q — изогонально сопряженная пара, то окружности APQ, BPQ, CPQ пересекают стороны треугольника ABC в шести точках и Это обнаруживается, что через них проходит коника. Конструкция производит только коническая, когда P и Q изогонально сопряжены. Когда P и Q — это Брокар точки то коника вырождается в пару прямых.
Статья 209 Три концентрических круга Начиная с вписанного четырехугольника ABCD с центром O, середины A ‘, B’, C ‘, D’ из OA, OB, OC, OD соответственно образуют вторую циклическую четырехугольник с половиной размера.Показано, что точки B, B ‘, C’, C лежат на круг, а также C, C ‘, D’, D и т. д. Центр BB’C’C помечен bc, и точка CC’D’D помечена как cd и т. д. Пять пар этих кругов немедленно видно, что они коаксиальные, и анализ дан для одной такой пары.
Статья 210 12 точек, 8 шеститочечных конусов, 4 конуса через каждую точку Дан треугольник ABC из середин каждого
боковые перпендикуляры проводятся к двум другим сторонам. Эти строки
маркированный
Строки с 1 по 6, как на рисунке.Их пересечения создают 12 конечных точек,
так
что, например, 35 является пересечением линий 3 и 5. Было обнаружено, что
8
Через эти 12 точек можно провести шестиконечные коники, причем 4 коники
через каждую точку. Окружность из девяти точек — это, конечно, одна из коник.
В
в более поздней статье устанавливаются некоторые свойства этих коник.
Эти строки
маркированный
Строки с 1 по 6, как на рисунке.Их пересечения создают 12 конечных точек,
так
что, например, 35 является пересечением линий 3 и 5. Было обнаружено, что
8
Через эти 12 точек можно провести шестиконечные коники, причем 4 коники
через каждую точку. Окружность из девяти точек — это, конечно, одна из коник.
В
в более поздней статье устанавливаются некоторые свойства этих коник.
Статья 211 Круговой четырехугольник и его окружности в центре Круговой четырехугольник его середины и шесть средних точек круга
Статья 212 Круги размером в четверть в вершинах треугольников Вписанный четырехугольник ABCD с AC перпендикулярно BD такое, что касательные в точках A, B, C и D образуют циклический четырехугольник.BD = X, а центры двух окружностей равны О и Y, то доказывается, что YOX — линия.
Статья 214 Суперсевиевые треугольники, их коническая и две перспективы На приведенном выше рисунке ABC — треугольник, P — треугольник.
Точка Чевиана и D, E, F — ноги Чевиана на BC, CA, AB
соответственно. Треугольник DEF — это Чевианский треугольник. Треугольник XYZ построен по формуле
Рисование через A линию, параллельную EF, и через линии B и C, параллельные
к
FD и DE соответственно. Также треугольник UVW строится путем рисования линий
параллельно EF, FD, DE через D, E, F соответственно.Эти два треугольника мы
термин как суперсевиевые треугольники. Затем докажем, что ABCUVW — коника. Q — это
то
Перспектор треугольников UVW и XYZ, а R — перспектор треугольников
ABC
и XYZ. Эти результаты устанавливаются в этой статье с использованием площадных
координируется с ABC как справочный треугольник.
Треугольник DEF — это Чевианский треугольник. Треугольник XYZ построен по формуле
Рисование через A линию, параллельную EF, и через линии B и C, параллельные
к
FD и DE соответственно. Также треугольник UVW строится путем рисования линий
параллельно EF, FD, DE через D, E, F соответственно.Эти два треугольника мы
термин как суперсевиевые треугольники. Затем докажем, что ABCUVW — коника. Q — это
то
Перспектор треугольников UVW и XYZ, а R — перспектор треугольников
ABC
и XYZ. Эти результаты устанавливаются в этой статье с использованием площадных
координируется с ABC как справочный треугольник.
Статья 215 Умножение точек с использованием барицентрических координат Если у вас есть точки с барицентрическим
координаты (f, g, h), (u, v, w), то правило умножения таково, что
то
Результат имеет координаты (fu, gv, hw).В этой статье показано, как
выполнить это умножение с помощью геометрической конструкции. Метод
в качестве
следующим образом: Сначала нарисуйте циркумконический контур fyz + gzx + hxy = 0. Затем возьмите
изотомный
сопряжение (u, v, w), чтобы получить точку (1 / u, 1 / v, 1 / w). Спрягать
это
точку, наконец, используйте циркум-конус, чтобы выполнить второе спряжение, взяв
(1 / u, 1 / v, 1 / w) в точку произведения (f / (1 / u), g / (1 / v), h / (1 / v)) = (fu, gv,
hw). Очевидно, что это коммутативный продукт, поэтому он также может быть
полученный с помощью коники ux + vy + wz = 0 и работы двух
спряжения на
точка (f, g, h).
Затем возьмите
изотомный
сопряжение (u, v, w), чтобы получить точку (1 / u, 1 / v, 1 / w). Спрягать
это
точку, наконец, используйте циркум-конус, чтобы выполнить второе спряжение, взяв
(1 / u, 1 / v, 1 / w) в точку произведения (f / (1 / u), g / (1 / v), h / (1 / v)) = (fu, gv,
hw). Очевидно, что это коммутативный продукт, поэтому он также может быть
полученный с помощью коники ux + vy + wz = 0 и работы двух
спряжения на
точка (f, g, h).
Статья 216 Точка, два треугольника и две коники Дан треугольник ABC с его описанной окружности Γ и любой внутренней точки P. Прямые AP, BP, CP продолжаются до встретить Γ в точках U, V, W. соответственно. Треугольник UVW нарисован и его стороны пересекаются внутренне в шести точках. BC встречается с AU в точке a, где b и c определены аналогично. AU встречается со стороной VW в точке u, где v и w определены аналогично. Это показано в этом статья что коника проходит через первые шесть точек и что коника также проходит через a, b, c, u, v, w.
Статья 217 Интересная перспектива в антикомплементарном треугольнике Треугольник
ABC и его антикомплементарный треугольник A ‘B’C’ нарисованы, а точка P
выбранные, через которые Cevians A’P, B’P, C’P нарисованы встречающими сторонами
ABC
в точках L ‘, M’, N ‘и сторонах A’, B ‘, C’ в точках L, M, N.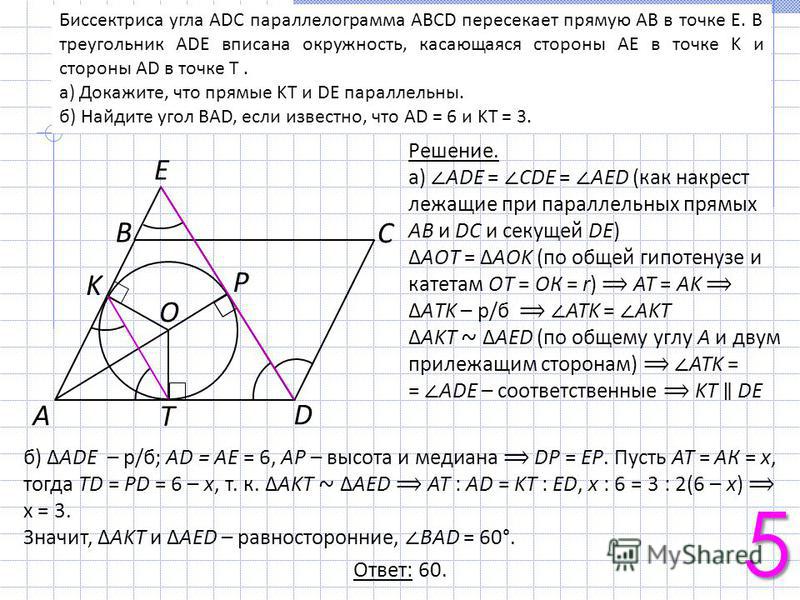 Окружности
LMN
и L’M’N ‘встречают стороны A’B’C’ и ABC соответственно в
точки
U ‘, V’, W ‘и U, V, W. Создано несколько перспектив, но наиболее
Интересно, что из треугольников A’B’C ‘
и UVW с перспективой Q.
Окружности
LMN
и L’M’N ‘встречают стороны A’B’C’ и ABC соответственно в
точки
U ‘, V’, W ‘и U, V, W. Создано несколько перспектив, но наиболее
Интересно, что из треугольников A’B’C ‘
и UVW с перспективой Q.
Статья 218 Свойства треугольника эксцентров В треугольнике эксцентров ортоцентр равен в центре I треугольника ABC, симедианная точка K + — это Mittenpunkt треугольника ABC и то Центр девяти точек — это центр описанной окружности O треугольника ABC. Центр описанной окружности O + лежит на то линия OI и такова, что O + O = OI. Эти свойства доказаны, как и факт что KI проходит через K +.
Статья 219 Двенадцать точек круга в треугольник эксцентрис ортоцентра — центр I ABC, Симмедиан точка K + — это Mittenpunkt в ABC, а центр из девяти точек — это окружность O из ABC.Центр описанной окружности O + лежит на прямой OI и таков, что O + O = OI. Эти свойства доказываются, как и то, что KI проходит через K +. Ух ты!
Статья 220 Конический шестиугольник с параллельными главными диагоналями Шестиугольник ABCDEF вписан в конику с
диагонали AD, BE, CF, совпадающие в точке P. Показано, что это
собственность
повторяется, и обе коники имеют одинаковую полярность по отношению к P.
polar — одна из линий Паскаля.
Показано, что это
собственность
повторяется, и обе коники имеют одинаковую полярность по отношению к P.
polar — одна из линий Паскаля.
Статья 221 — это Четыре особых конических шестиугольника с одинаковой полярностью Дан шестиугольник ABCDEF, вписанный в конику с AD, BE, CF, совпадающими в точке P, касательные tA, tB, tC, tD, tE, tF нарисованы.tk определены и показано, что 12, 23, 34, 45, 56, 61 лежат на конусе. Линии 61 12, 34 45 пересекаются в точке 1, линии 12 23, 45 56 пересекаются в точке 2 и линии 23 34, 56 61 пересекаются в 3. Точки 1, 2, 3 лежат на одной прямой, и показано, что 123 является полярность P относительно обеих коник.
Статья 222 Недостающая точка на прямой Эйлера Дан треугольник ABC, окружность O, ортоцентр H, пусть середины сторон будут L, M, N, и пусть AO, BO, CO встречаются стороны BC, CA, AB соответственно в U, V, W, затем центр эллипс LMNUVW — это точка S на прямой Эйлера такая, что OH = 4OS.BD.
Статья 224 — это Шестьдесят полюсов Паскаля Когда шесть точек лежат на конике, можно построить шестьдесят прямых Паскаля. AB.EB. В статье 225 показано, что XX ‘, YY’, ZZ ‘
параллельны в точке P, которая является полюсом A’B’C ‘относительно
круг.
AB.EB. В статье 225 показано, что XX ‘, YY’, ZZ ‘
параллельны в точке P, которая является полюсом A’B’C ‘относительно
круг.
Статья 226 Специальные конические шестиугольники Говорят, что шестиугольник ABCDEF вписанный в конику быть специальным , если AD, BE, CF параллельны в точке P. Когда это случается шестиугольники, образованные пересечением соседних касательных, называются доказано также быть специальным и коническим с той же точкой P.
Статья 227 — это Замечательная восьмиконечная коника Две коники пересекаются в точках A, B, C, D, а AC пересекается.
BD at P.Линия, проходящая через точку P, пересекает одну из коник в точках F, G и
то
другие — в точках E, H. Касательные нарисованы в точках F, G, E, H. Касательные в точках F и G пересекаются.
в Q
и касательные в E и H пересекаются в R. Касательные в H и G пересекаются в V, касательные
в H
и F пересекаются в S, касательные в E и F пересекаются в T, а касательные в E и G пересекаются
в
U. Теперь коника проходит через 8 точек A, B, C, D, S, T, U, V и
линия
QR — это полярная точка P по отношению ко всем трем коникам.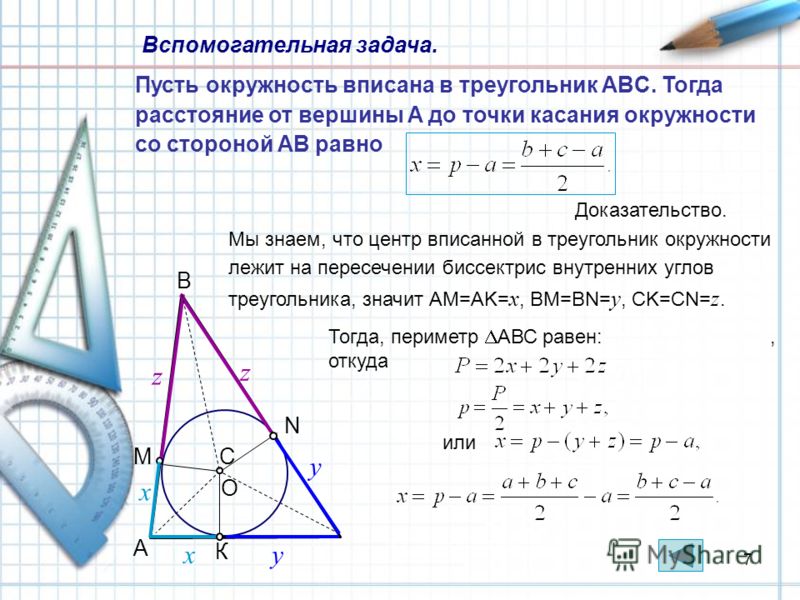 Общий случай
технически сложно установить, поэтому здесь мы приводим числовые
дело.
Общий случай
технически сложно установить, поэтому здесь мы приводим числовые
дело.
Статья 228 — это Как 2 коника через 4 точки создают еще 6 таких коников Рисуются две коники через 4 точки A, B, C, D. (на рисунке голубой и оранжевый). Их касательные к первому (в оранжевый) в точках A, B, C, D обозначены цифрами 1, 2, 3, 4, а касательные к второй (голубой) обозначены 5, 6, 7, 8. Пересечения этих касательных помечены 12, 13, 14, 23, 24, 34 и 56, 57, 58, 67, 68, 78. Теперь обнаружено, что Можно нарисовать шесть 6-ти конечных коник.
Статья 229 Когда конический четырехугольник образует две 6-гранные коники Если четырехугольник ABCD нарисован в виде коники и касательные проводятся в точках A, B.C. D, тогда стороны ABCD и пересечения касательных образуют две шестиконечные коники и полярную линия.
Статья 230 — это Четырехугольник и возникающие коники и точки ABCD — произвольный четырехугольник
вписан в общую коническую форму. Касательные в его вершинах образуют вторую
четырехугольник PQRS. Появляется полярная линия ФГТУ и 8 точек
пересечение ABCD и касательного четырехугольника PQRS. Многие коники
результат,
но два из них, в частности, встречаются на диагонали PR в точках X, Y в
фигура.X и Y, по-видимому, обладают такими же важными свойствами, как и любой из 8
вершины
четырехугольников и четырех точек на полярной линии. Ни одним
средства
все коники, которые можно нарисовать, представлены в этой статье, а второй
статья предусмотрена. От чего зависит, почему диагонали PR и QS имеют такие
разные объекты (для нас) открыты и интересны
вопросов.
Появляется полярная линия ФГТУ и 8 точек
пересечение ABCD и касательного четырехугольника PQRS. Многие коники
результат,
но два из них, в частности, встречаются на диагонали PR в точках X, Y в
фигура.X и Y, по-видимому, обладают такими же важными свойствами, как и любой из 8
вершины
четырехугольников и четырех точек на полярной линии. Ни одним
средства
все коники, которые можно нарисовать, представлены в этой статье, а второй
статья предусмотрена. От чего зависит, почему диагонали PR и QS имеют такие
разные объекты (для нас) открыты и интересны
вопросов.
Статья 231 — это Четырехугольник и результирующие коники. Часть 2.
Особый случай, показывающий роль новых точек X и Y В статье 230 мы исследовали свойства
конфигурация четырехугольника ABCD, вписанного в эллипс, и
общий
точки касания эллипса в вершинах A, B, C, D.Оказывается
который
есть две замечательные точки X и Y, через которые можно пройти множество прямых.
нарисованный
а также через которую проходят многие коники. Анализ Части 1 тоже был
сложно проиллюстрировать результаты, поэтому в этой статье мы приводим
числовой
презентация, которая иллюстрирует свойства точек X и Y, для
который
все результаты верны в общем случае. Кажется маловероятным, что генерал
дело
можно рассматривать аналитически, но, возможно, чистый подход будет успешным как
то
точки являются членами инволюции Дезарга.Рисунок 1 выше иллюстрирует
то
линейные свойства X и Y, а на рисунке 2 ниже показаны их конические
характеристики.
Кажется маловероятным, что генерал
дело
можно рассматривать аналитически, но, возможно, чистый подход будет успешным как
то
точки являются членами инволюции Дезарга.Рисунок 1 выше иллюстрирует
то
линейные свойства X и Y, а на рисунке 2 ниже показаны их конические
характеристики.
Статья 232 Коконовый шестиугольник с одновременными главными диагоналями ABCDEF — это шестиугольник, вписанный в конику, и
такие, что его главные диагонали AD, BE, CF совпадают в точке G. Стороны
AB,
BC,… имеют обозначения 1, 2,…. Такие точки, как 14, являются
пересечение
AB и DE. Касательные проводятся в точках A, B,…, так что касательные в точках A и B
встречаются в P. Точка Q является пересечением
касательные в точках B и C и так далее.Касательные в точках A, B,… также
помечено как tA,
tB,… и такие точки, как ac, являются пересечением tA и tC. это
доказал, что PQRSTU является коникой и что шесть точек
ac, bf, ae, df, ce, bd лежат на конике. Также доказано, что 13, 26, 15,
46,
35, 24 лежат на конусе.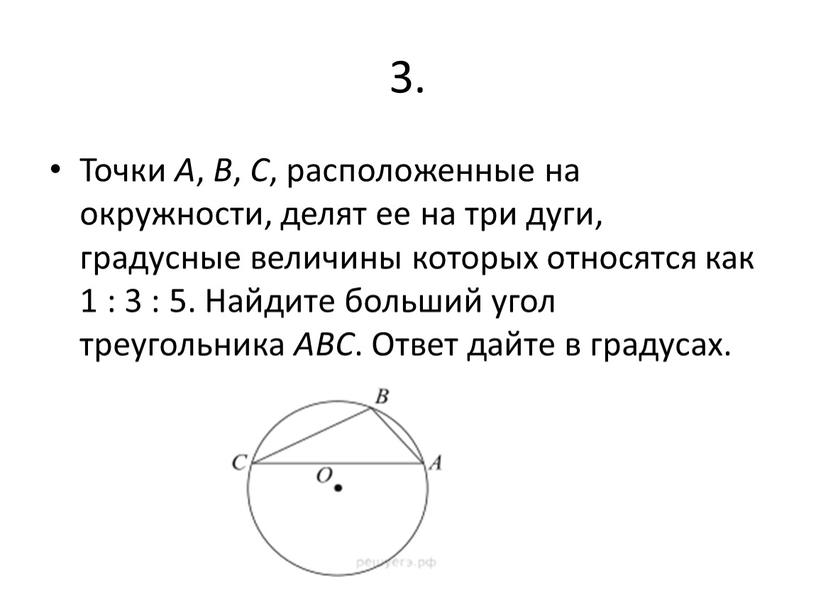
Статья 233 — это Коника и созданные линии (Часть 1) Коника определяется 5 точками, никакие три из которые коллинеарны, Пары прямых, соединяющих эти точки и касательные к коника в ее определяющих точках создает 10 линий, и эти линии создают 15 другие ключевые направления и многие дочерние.
Статья 234 — это Коник образует пять коников с 8 точками (Часть 2) Коника ABCDE со сторонами 1 = AB, 2 = BC и т. Д. и его касательные a, b,… в вершинах AB,… производят 20 перекрестков через которые можно провести пять коников с 8 точками.
Статья 235 является Правда и вся правда о четырехугольнике Четырехугольник вписан в конику и ее стороны и диагонали, а также касательные в его вершинах. Исследование сделали линий и коник, проходящих через точки пересечения.В все Всего появляется восемнадцать конусов, три из которых проходят через восемь точек и пятнадцать-шесть баллов.
Статья 236 Хороший конус и неприятный круг Треугольник ABC и его
описанной окружности S. PQ = ab и т. д.), то если ab, bc, cd коллинеарны, то
четырехугольники в полной перспективе (см. статью 238).
PQ = ab и т. д.), то если ab, bc, cd коллинеарны, то
четырехугольники в полной перспективе (см. статью 238).
С Кристофером Брэдли можно связаться по адресу: cbradley1444 atsymbol yahoo точка co dot uk
Задачи по геометрии
Задача 1 [BMOTC] Проблемы в Геометрии Автобусы Prithwijit De ICFAI в школе ess, Калькутта, Республика Индия, электронная почта : [email protected] Докажите, что медианы из вершин A и B треугольника ABC взаимно перпендикулярны тогда и только тогда, когда | BC | 2 + | AC | 2 = 5 | AB | 2. Задача 2 [BMOTC] Предположим, что ∠A — наименьший из трех углов треугольника ABC. Пусть D — точка в t на дуге BC описанной окружности треугольника ABC, не входящая в в A. Пусть серединные перпендикуляры к AB, AC в < / strong> tersect AD в точках M и N соответственно. Пусть BM и CN пересекаются в точке T.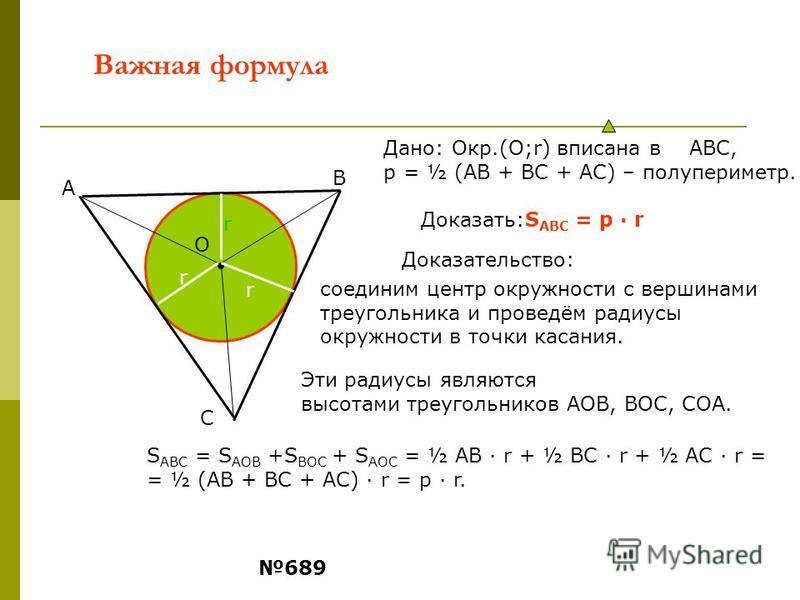 Докажите, что BT + CT ≤ 2R, где R — радиус описанной окружности треугольника ABC. Задача 3 [BMOTC] Пусть треугольник ABC, как обычно, имеет стороны a, b и c. Po в ts P и Q лежат в стороне этого треугольника и обладают такими свойствами, что ∠BP C = ∠CP A = ∠AP B = 120 ◦ и ∠BQC = 60 ◦. + ∠A, ∠CQA = 60 ◦ + ∠B, ∠AQB = 60 ◦ + ∠C. Докажите, что Задача 4 [BMOTC] (| AP | + | BP | + | CP |) 3. | AQ |. | BQ |. | CQ | = (abc) 2. По in ts M и N являются точками касания in окружности равнобедренного треугольника ABC, которые находятся на сторонах AC. и до н.э.Стороны равной длины — это AC и BC. Касательная l in e t проводится к m in или дуге MN. Предположим, что t в пересекает AC и BC в точках Q и P соответственно. Предположим, что l in es AP и BQ встречаются в точке T. (a) Докажите, что T лежит на l in e отрезке MN. (b) Докажите, что сумма площадей треугольников AT Q и BT P равна m , когда t параллельна AB.
Докажите, что BT + CT ≤ 2R, где R — радиус описанной окружности треугольника ABC. Задача 3 [BMOTC] Пусть треугольник ABC, как обычно, имеет стороны a, b и c. Po в ts P и Q лежат в стороне этого треугольника и обладают такими свойствами, что ∠BP C = ∠CP A = ∠AP B = 120 ◦ и ∠BQC = 60 ◦. + ∠A, ∠CQA = 60 ◦ + ∠B, ∠AQB = 60 ◦ + ∠C. Докажите, что Задача 4 [BMOTC] (| AP | + | BP | + | CP |) 3. | AQ |. | BQ |. | CQ | = (abc) 2. По in ts M и N являются точками касания in окружности равнобедренного треугольника ABC, которые находятся на сторонах AC. и до н.э.Стороны равной длины — это AC и BC. Касательная l in e t проводится к m in или дуге MN. Предположим, что t в пересекает AC и BC в точках Q и P соответственно. Предположим, что l in es AP и BQ встречаются в точке T. (a) Докажите, что T лежит на l in e отрезке MN. (b) Докажите, что сумма площадей треугольников AT Q и BT P равна m , когда t параллельна AB. Задача 5 [BMOTC] В шестиугольнике с равными углами длины четырех последовательных ребер равны 5, 3, 6 и 7 ( в указанном порядке). F in d длина оставшихся in in g двух краев. 1
Задача 5 [BMOTC] В шестиугольнике с равными углами длины четырех последовательных ребер равны 5, 3, 6 и 7 ( в указанном порядке). F in d длина оставшихся in in g двух краев. 1
% PDF-1.5
%
1 0 obj
>
endobj
2 0 obj
> поток
2013-08-02T10: 03: 13 + 01: 002013-08-02T10: 03: 13 + 01: 002013-08-02T10: 03: 13 + 01: 00ENG Персонал 1-е приложение MID / pdfuuid: bce78d19-e900-4cef-b998 -390e9e44765fuuid: 03d144dc-7cd6-4a5d-8eb3-54c1f9e21311KONICA MINOLTA bizhub C552 конечный поток
endobj
3 0 obj
>
endobj
5 0 obj
>
endobj
6 0 obj
>
endobj
7 0 объект
>
endobj
23 0 объект
>>> / Повернуть 0 / Тип / Страница >>
endobj
24 0 объект
>>> / Повернуть 0 / Тип / Страница >>
endobj
25 0 объект
>>> / Повернуть 0 / Тип / Страница >>
endobj
26 0 объект
>>> / Повернуть 0 / Тип / Страница >>
endobj
27 0 объект
>>> / Повернуть 0 / Тип / Страница >>
endobj
36 0 объект
> поток
q
595.

 Найдите угол ABC, если угол BAC равен 48°. Ответ дайте в градусах.
Найдите угол ABC, если угол BAC равен 48°. Ответ дайте в градусах. Точка O — центр окружности. Хорда KM образует с касательной угол, равный 39°. Найдите величину угла OMK. Ответ дайте в градусах.
Точка O — центр окружности. Хорда KM образует с касательной угол, равный 39°. Найдите величину угла OMK. Ответ дайте в градусах.
 Найдите длину отрезка KP, если AK=9, а сторона AC в 3 раза больше стороны BC
Найдите длину отрезка KP, если AK=9, а сторона AC в 3 раза больше стороны BC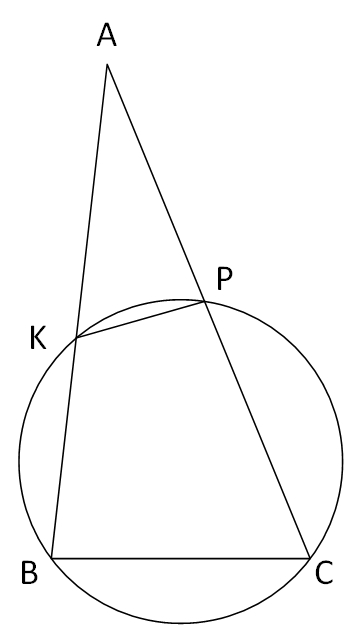 Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=18.
Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=18.
Leave A Comment