Система неравенств с тремя неизвестными и квадратным корнем
x >= -2 y = 3 z
Правила ввода выражений и функций
Выражения могут состоять из функций (обозначения даны в алфавитном порядке):- absolute(x)
- Абсолютное значение x
(модуль x или |x|) - arccos(x)
- Функция — арккосинус от x
- arccosh(x)
- Арккосинус гиперболический от x
- arcsin(x)
- Арксинус от x
- arcsinh(x)
- Арксинус гиперболический от x
- arctg(x)
- Функция — арктангенс от x
- arctgh(x)
- Арктангенс гиперболический от x
- exp(x)
- Функция — экспонента от x (что и e^x)
- log(x) or ln(x)
- Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10)) - sin(x)
- Функция — Синус от x
- cos(x)
- Функция — Косинус от x
- sinh(x)
- Функция — Синус гиперболический от x
- cosh(x)
- Функция — Косинус гиперболический от x
- sqrt(x)
- Функция — квадратный корень из x
- sqr(x) или x^2
- Функция — Квадрат x
- ctg(x)
- Функция — Котангенс от x
- arcctg(x)
- Функция — Арккотангенс от x
- arcctgh(x)
- Функция — Гиперболический арккотангенс от x
- tg(x)
- Функция — Тангенс от x
- tgh(x)
- Функция — Тангенс гиперболический от x
- cbrt(x)
- Функция — кубический корень из x
- gamma(x)
- Гамма-функция
- LambertW(x)
- Функция Ламберта
- x! или factorial(x)
- Факториал от x
- Действительные числа
- вводить в виде
 3
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- pi
- Число «Пи», которое примерно равно ~3.
 14159..
14159.. - e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
Калькулятор онлайн — Решение неравенств (линейных, квадратных и дробных) (с подробным решением) описание
Калькулятор онлайн — Решение неравенств (линейных, квадратных и дробных) (с подробным решением) описание << Назад (к решению неравенств)Какие неравенства можно решить?
Эта математическая программа подробно решает следующие неравенства с одной переменной.
Линейные
Неравенства сводящиеся к виду: \( ax+b > 0 \) (знак сравнения любой).
Например:
Квадратные
Неравенства сводящиеся к виду: \( ax^2+bx+c > 0 \) (знак сравнения любой). 2+px+q=0 \Rightarrow \left\{\begin{array}{l} x_1+x_2=-p \\ x_1 \cdot x_2=q \end{array}\right.$$ $$\left\{\begin{array}{l} x_1+x_2=3 \\ x_1 \cdot x_2=2 \end{array}\right. \Rightarrow \left\{\begin{array}{l} x_1=2 \\ x_2=1 \end{array}\right.$$ Ответ: \( x_1= 2,\; x_2= 1 \)
Корни квадратного уравнения:
$$ x_1 = 1 ;\; x_2 = 2 $$
Решим линейное уравнение \( 3 x-1= 0 \)
Корень линейного уравнения: \( x = \frac{1}{3}\)
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале:
2+px+q=0 \Rightarrow \left\{\begin{array}{l} x_1+x_2=-p \\ x_1 \cdot x_2=q \end{array}\right.$$ $$\left\{\begin{array}{l} x_1+x_2=3 \\ x_1 \cdot x_2=2 \end{array}\right. \Rightarrow \left\{\begin{array}{l} x_1=2 \\ x_2=1 \end{array}\right.$$ Ответ: \( x_1= 2,\; x_2= 1 \)
Корни квадратного уравнения:
$$ x_1 = 1 ;\; x_2 = 2 $$
Решим линейное уравнение \( 3 x-1= 0 \)
Корень линейного уравнения: \( x = \frac{1}{3}\)
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале:
| $$ \frac{1}{3} $$ | $$ 1 $$ | $$ 2 $$ |
Решить квадратное уравнение онлайн
Для решения квадратного уравнения онлайн введите коэффициенты квадратного уравнения. 2 — 4ac
2 — 4ac
Если D > 0, то уравнение имеет два различных вещественных корня.
Если D = 0, то уравнение имеет один корень (x1 = x2).
Если D решения квадратного уравнения) находятся по формуле:
D = \frac{-b\pm\sqrt{D}}{2a}
Если в вашем квадратном уравнении есть знаки вычитания, то перед соответствующими коэффициентами в онлайн калькуляторе нужно поставить знак минус («-«), если отсутствует один из членов уравнения, то рядом с отсутствующим слагаемым поставьте коэффициент ноль («0»). Также вы можете получить ответ, зависящий от параметра (неизвестной). То есть коэффициенты в уравнении могут содержать переменные, которые обозначаются латинскими буквами
Решение квадратных уравнений онлайн
С помощю этого онлайн калькулятора можно найти решение (корни) квадратного уравнения. Дается подробное решение с пояснениями. Для нахождения решений квадратного уравнения введите коэффициенты уравнения и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Теоретическую часть и численные примеры смотрите ниже.
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Корни квадратного уравнения − теория примеры и решения
Квадратным уравнением называется уравнение следующего вида:
где x−переменная, а a, b, c некоторые числа (a≠0). Числа a, b, c называются коэффициентами квадратного уравнения. Коэффицинт c называется свободным членом.
Если a=1, то квадратное уравнение называется приведенным. Заметим, что любое квадратное уравнение можно привести к приведенному виду, разделив обе части уравнения на a. Действительно:
Если в квадратном уравнении (1) один из коэффициентов b, c равен нулю или оба коэффициента b, c равны нулю, то квадратное уравнение называется неполным.
Рассмотрим разные виды неполных квадратных уравнений.
1. При b=0 имеем:
Для решения этого уравнения свободный член перенесем в правую часть уравнения:
Решая последнее уравнение относительно x получим корни квадратного уравнения (3):
Если , то квадратное уравнение не имеет действительных корней.
2. При c=0 имеем:
Разложим левую часть последнего уравнения на множители:
Из (4) следует x=0 или ax+b=0. Следовательно имеем следующие решения:
3. При b=0, c=0 имеем:
и, следовательно
Рассмотрим, далее, алгоритм решения квадратных уравнений общего вида (1). Разделим обе части уравнения на a:
Сделаем эквивалентные преобразования уравнения (5):
Легко догадаться, что первые три слагаемые уравнения (6) образуют квадрат следующей суммы:
Тогда
Обозначим
D− называется дискриминантом квадратного уравнения (1).
Учитывая (8) запишем (7) в следующем виде:
При решении последнего уравнения возможны следующие варианты:
1. При D>0, имеем
Таким образом, при D>0, квадратное уравнение (1) имеет две корни:
2.При D=0, имеем
То есть, при D=0 квадратное уравнение (1) имеет единственный корень:
3. При D<0, правая часть уравнения (9) отрицательна, а так как квадрат числа не может быть отрицательным числом, то квадратное уравнение (1) не имеет корней.
Пример 1. Решить квадратное уравнение
| . | (10) |
Решение. Запишем коэффициенты квадратного уравнения (10):
Вычислим дискриминант квадратного уравнения:
. |
Дискриминант положительное число. Следовательно квадратное уравнение (10) имеет два решения.
Найдем решение квадратного уравнения используя следующую формулу:
| . | (11) |
Подставляя значения коэффициентов a, b, c, D в (11), получим:
| , |
| . |
Ответ:
Пример 2. Решить следующее квадратное уравнение:
| . | (12) |
Решение. Запишем коэффициенты квадратного уравнения (12):
Вычислим дискриминант квадратного уравнения:
| . |
Дискриминант равен нулю. Следовательно квадратное уравнение (12) имеет единственное решение. Найдем решение квадратного уравнения используя следующую формулу:
| . | (13) |
Подставляя значения коэффициентов a, b, c, D в (13), получим:
| , |
Ответ:
. |
Пример 3. Решить следующее квадратное уравнение:
| . | (14) |
Решение. Запишем коэффициенты квадратного уравнения (14):
Вычислим дискриминант квадратного уравнения:
| . |
Дискриминант отрицательное число. Следовательно квадратное уравнение (14) не имеет действительных корней.
Ответ: Квадратное уравнение не имеет действительных корней.
Математика для блондинок: Квадратное уравнение решение онлайн
Не легкая сегодня жизнь у учащихся. Для её облегчения предлагаю вашему вниманию калькуляторы уравнений:Распечатайте картинку, повесьте её на стену и каждый вечер читайте на ночь вместо молитвы.
 Подобные ежедневные упражнения очень здорово помогают превращать запор мысли в понос слов. Последнее предложение я вычеркнул специально. Детям его знать ещё рано, а взрослым оно не нужно вообще. Лично я тем математикам, которые выдают комплексные решения, платил бы комплексную зарплату: действительная часть равна минимальной зарплате, а в комплексной части зарплаты можно обещать всё, что угодно. Хоть Царство Небесное. Естественно, не здесь и сейчас, а где-то там и после смерти. Ведь мертвые никогда не требуют выполнения обещаний.
Подобные ежедневные упражнения очень здорово помогают превращать запор мысли в понос слов. Последнее предложение я вычеркнул специально. Детям его знать ещё рано, а взрослым оно не нужно вообще. Лично я тем математикам, которые выдают комплексные решения, платил бы комплексную зарплату: действительная часть равна минимальной зарплате, а в комплексной части зарплаты можно обещать всё, что угодно. Хоть Царство Небесное. Естественно, не здесь и сейчас, а где-то там и после смерти. Ведь мертвые никогда не требуют выполнения обещаний.
Дискриминант квадратного уравнения применяется для нахождения его корней. Дискриминант равен квадрату второго коэффициента минус четыре произведения первого коэффициента и свободного члена уравнения. Если дискриминант больше нуля, тогда уравнение имеет два корня. Если дискриминант равен нулю (дискриминант 0), тогда квадратное уравнение имеет всего один корень. Если дискриминант меньше нуля, тогда уравнение не имеет корней — это уравнение взял с потолка какой-то неук.
Дискриминант равен квадрату второго коэффициента минус четыре произведения первого коэффициента и свободного члена уравнения. Если дискриминант больше нуля, тогда уравнение имеет два корня. Если дискриминант равен нулю (дискриминант 0), тогда квадратное уравнение имеет всего один корень. Если дискриминант меньше нуля, тогда уравнение не имеет корней — это уравнение взял с потолка какой-то неук.
Теперь рекомендую вашему вниманию специальные калькуляторы для решения квадратный уравнений онлайн с подробным решением:
— дается подробное решение с формулой дискриминанта, с графиком уравнения и анализом вершин кривой. — пример подробного решения уравнения на этом калькуляторе вы можете видеть на картинке ниже.— этот сервис решения квадратных уравнений онлайн выдает просто корни уравнения без подробного решения, но зато может представить их в виде квадратных корней (как на картинке ниже). Обратите внимание, что примеры введения уравнений и систем уравнений в этот калькулятор уравнений приведены внизу и несколько отличаются от традиционно принятых наборов символов.
 В этом калькуляторе квадрат икса нужно вводить как произведение двух иксов.
В этом калькуляторе квадрат икса нужно вводить как произведение двух иксов.Иррациональные неравенства. Исчерпывающий гид (ЕГЭ — 2021)
Определение
Иррациональное неравенство – это неравенство, содержащее переменную под корнем
Неравенства вида \( \sqrt{A}\ge \sqrt{B}\)
\( \sqrt{A}\ge \sqrt{B}\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}A\ge B\\B\ge 0\end{array} \right.\)
или
\( \sqrt{A}>\sqrt{B}\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}A>B\\B\ge 0\end{array} \right.\)
Неравенства вида \( A\sqrt{B}>0\) или \( A\sqrt{B}<0\)
\( A\sqrt{B}>0\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}B>0\\A>0\end{array} \right.\)
или
\( A\sqrt{B}<0\text{ }\Leftrightarrow \text{ }\left\{ \begin{array}{l}B>0\\A<0\end{array} \right.\)
Неравенства вида \( A\sqrt{B}\ge 0\)
\( A\sqrt{B}\ge 0\text{ }\Leftrightarrow \text{ }\left[ \begin{array}{l}B=0\\\left\{ \begin{array}{l}A\ge 0\\B\ge 0\end{array} \right. {5}},\end{array}\) и т.д.
{5}},\end{array}\) и т.д.
Решение неравенств методом интервалов. Готовимся к ОГЭ по математике. Модуль 1. Урок 29
Покажем решение неравенств методом интервалов.
Пример 1. Решите неравенство .
Решение.
1) Разложим левую часть неравенства на множители. Для этого решим уравнение . и — корни уравнения. Неравенство примет вид .
2) Нанесём числа —3 и 7 на прямую. Учитывая, что неравенство нестрогое, закрасим точки (см. рис. 1).
Рис.1
3) Так как 0″ />, то на крайнем правом промежутке поставим знак «+» (можно из любого промежутка взять число и подставить в левую часть неравенства, например, если , получим 0″ />) (см. рис. 2).
Рис.2
4) Так как множители и в нечётной степени (в первой), то на остальных промежутках знаки чередуем и рисуем «змейку» (см. рис. 3).
Рис.3
5) Левая часть неравенства больше или равна 0, значит, выделяем промежутки со знаком «+» (см. рис. 4).
рис. 4).
Рис.4
6) Делаем вывод: .
Ответ: (—оо; —3] U [7; +оо).
Пример 2. Решите неравенство .
Решение.
, — корни уравнения.
Рис.5
(см. рис. 5).
Пример 3. Решите неравенство 0″ />.
Решение.
Умножим обе части неравенства на (—1).
, ,
Рис.6
— корни уравнения.
. (см. рис. 6).
Ответ: (—9; 1).
Пример 4. Решите неравенство 0″ />.
Решение.
Заметим, что левая часть неравенства — полный квадрат, то есть . Неравенство примет вид 0″ />, отсюда решение этого неравенства — любое число, кроме , так как неравенство строгое.
Рис.7
и 3″ /> (см. рис. 7).
Ответ: .
Пример 3. Решите неравенство
Решение.
Нули числителя: .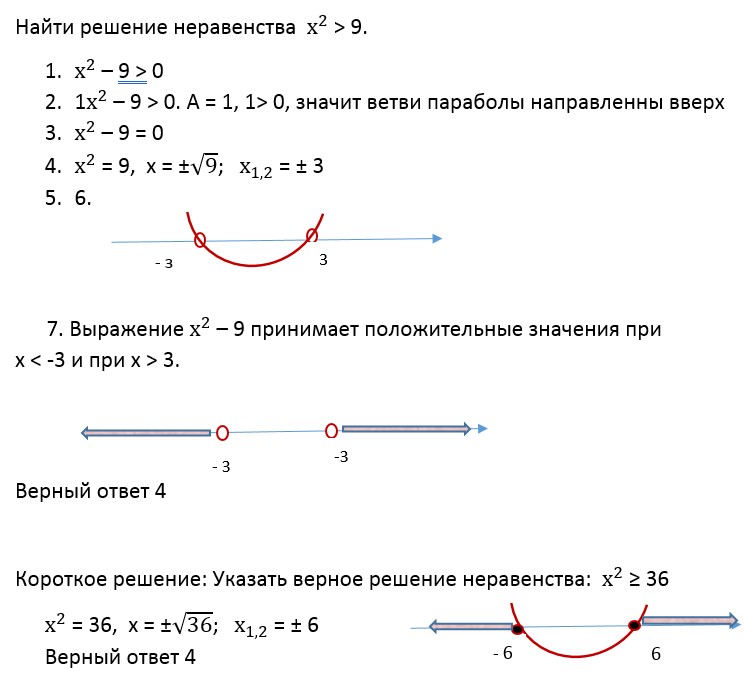 Нули знаменателя: .
Нули знаменателя: .
Рис.8
(см. рис. 8).
Ответ:
Решение Квадратичные неравенства: концепции (стр. 1 из 3) Решение линейных неравенств, например « x + 3> 0 «, было довольно просто, если вы не забыли перевернуть неравенство знак всякий раз, когда вы умножали или делили на отрицательное (как вы при решении чего-то вроде «2 x <4 "). Но есть большой скачок,
между линейными неравенствами и квадратичными неравенствами. Часть прыжка
это тот факт, что концепции, которые были пропущены при обучении решать
линейные неравенства полезны и даже необходимы при решении квадратичных неравенств.
Итак, давайте сначала посмотрим на линейное неравенство и рассмотрим те концепции, которые
пропускались ранее.
Я это уже знаю, чтобы решить это неравенство, все, что мне нужно сделать, это добавить 4 на другую сторону, чтобы получить решение « x <4 ". Итак Я уже знаю ответ. Но сейчас подойду к этой проблеме под другим углом, рассмотрев соответствующий график с двумя переменными.
Неравенство « x 4 <0 "
спрашивает "когда линия y = x 4 ниже
линия у = 0? «Поскольку
линия у = 0 — это просто ось x ,
неравенство, следовательно, спрашивает, «когда линия y = x 4 ниже
ось x ? »
Первый шаг к ответу на этот вопрос — найти, где линия
пересекает ось x ;
то есть сначала мне нужно найти перехват x . Так линия у = x 4 крестика ось x при x = 4. Поскольку строка л = x 4 равно прямая линия, она будет выше оси x с одной стороны от перехвата и ниже оси x по ту сторону перехвата.Авторские права Элизабет Стапель 2002-2011 Все права защищены
Вспоминая графический метод представления решений линейных неравенство, на графике выше показано правильное решение « x <4 «. То есть глядя на
график соответствующей линии и определение точки (на оси x )
линия на графике была ниже оси x ,
легко увидеть, что решение неравенства « x 4 <0 "это
неравенство " х <4 ". Давайте посмотрим на квадратичную неравенство: Во-первых, мне нужно посмотреть в соответствующем уравнении с двумя переменными, y = x 2 + 4, и рассмотрим, где его график находится ниже оси x . Для этого мне нужно знать, где график пересекает ось x .То есть мне сначала нужно найти где x 2 + 4 равно нулю: Это говорит о том, что квадратичная пересекает ось x при x = 2 и при x = 2. Теперь мне нужно вычислить
out где (то есть на каких интервалах) график находится под осью.
Тогда решение ясно: Я мог бы умножить
исходное неравенство через 1,
давая мне « x 2 4> 0 «. Верх | 1 | 2 | 3 | Вернуться к указателю Далее >>
| ||
Решение квадратичных неравенств: примеры
Решение Квадратичные неравенства: примеры (стр. 2 из 3)
- Решить 2 x 2 + 4 x > x 2 x 6.
Как видите, это
сложно сказать, где зеленая линия ( y = 2 x 2 + 4 x )
находится выше синей линии
( y = x 2 x 6). Итак, вместо того, чтобы пытаться решить это неравенство, я буду работать
со следующим неравенством:
Итак, вместо того, чтобы пытаться решить это неравенство, я буду работать
со следующим неравенством:
Это последнее неравенство с этим проще иметь дело, потому что теперь все, что мне нужно сделать, это найти нули от до = x 2 + 5 x + 6 (что легко), а затем выберите правильные интервалы, основываясь только на одна парабола (что тоже несложно).То есть сравнивать проще одна парабола с осью x чем сравнивать две параболы друг с другом. Но поскольку одна парабола ( л = x 2 + 5 x + 6) возникла в результате объединения двух исходных парабол («параболы»?), решение более простого однопараболического неравенства будет таким же как решение исходного двухпараболического неравенства.Поскольку решения будет так же, буду работать с более простым случаем.
Я упростил «2 x 2 + 4 x > x 2 x 6 дюймов
чтобы получить « x 2 + 5 x + 6 > 0 «. Соответствующее уравнение с двумя переменными: y = x 2 + 5 x + 6.Сначала я найду нули (то есть интервалы x ):
Соответствующее уравнение с двумя переменными: y = x 2 + 5 x + 6.Сначала я найду нули (то есть интервалы x ):
Эти два перехвата
разделите числовую строку на три интервала, а именно x <3, 3 < x <2,
и x > 2. На котором
из этих трех интервалов y = x 2 + 5 x + 6
над осью x ?
С и = x 2 + 5 x + 6
графиков как параболы, направленной вверх правой стороной вверх, квадратичная диаграмма находится над осью
на концах:
Тогда решение:
Почему
было ли это решение «или равно», а не просто «больше
чем «или» меньше чем «? Потому что исходное неравенство
«или равно», поэтому граничные точки, являющиеся нулями или x -пересекаются,
включены в решение. Авторские права
Элизабет Стапель 2002-2011 Все права защищены
Авторские права
Элизабет Стапель 2002-2011 Все права защищены
Первый, Найду нули:
Хм … Поскольку внутри квадратного корня стоит отрицательное число, не должно быть любые x -перехват. То есть эта квадратичная величина всегда должна быть выше оси x . или всегда внизу, потому что он никогда не может пересекать или касаться оси.
|
В
вышеупомянутое решение также может быть указано как «все действительные числа» или
записывается как интервал «от отрицательной бесконечности до положительной бесконечности».
Это выглядит так же, как и предыдущая проблема, за исключением того, что теперь я ищу где парабола находится ниже оси. Я уже знаю что есть нет x — перехватывает. Кроме того, поскольку это парабола, направленная вверх правой стороной, я знаю, что график всегда находится над осью. Итак, где y = x 2 + x + 1 меньше нуля? Никуда! Тогда решение:
The вышеупомянутое решение также может быть указано как «нет решения» или как « пустой набор «, представленный символом» «.
Всегда
у вас есть квадратное неравенство, в котором соответствующее квадратное уравнение
не имеет реальных решений (то есть там, где соответствующая парабола
не пересекать ось x ),
решение неравенства будет либо «все x »
или «нет x «,
в зависимости от того, находится ли парабола на той стороне оси, которую вы
необходимость.
<< Предыдущая Вверх | 1 | 2 | 3 | Возвращаться в индекс далее >>
Цитируйте эту статью как: | Стапель, Елизавета.«Решение квадратичных неравенств: примеры». Purplemath .
Доступно по номеру |
Решение квадратичных неравенств
… и более …
Квадратичный
Квадратное уравнение (в стандартной форме) выглядит так:
Квадратичное уравнение в стандартной форме
( a , b и c может иметь любое значение, за исключением того, что a не может быть 0. )
)
Выше приведено уравнение (=), но иногда нам нужно решить такие неравенства:
Символ | слов | Пример | ||
|---|---|---|---|---|
> | больше | x 2 + 3x> 2 | ||
< | менее | 7x 2 <28 | ||
≥ | больше или равно | 5 ≥ х 2 — х | ||
≤ | меньше или равно | 2 года 2 + 1 ≤ 7 лет | ||
Решение
Решение неравенств очень похоже на решение уравнений… мы делаем почти то же самое.
| При решении уравнений мы пытаемся найти точек , , например, помеченные «= 0» |
| Но когда мы решаем неравенств мы пытаемся найти интервал (с) , , например, помеченные «> 0» или «<0" |
Вот что мы делаем:
- найти «= 0» точек
- между точками «= 0» — это интервалов , которые либо
- больше нуля (> 0) или
- меньше нуля (<0)
- затем выберите тестовое значение, чтобы узнать, какое оно (> 0 или <0)
Вот пример:
Пример: x
2 — x — 6 <0x 2 — x — 6 имеет следующие простые факторы (потому что я хотел упростить!):
(х + 2) (х − 3) <0
Сначала , найдем где равно ноль:
(х + 2) (х − 3) = 0
Равно нулю, когда x = −2 или x = +3
, потому что, когда x = −2, тогда (x + 2) равен нулю
или
когда x = +3, то (x − 3) равно нулю
Итак, между −2 и +3, функция будет либо
- всегда больше нуля или
- всегда меньше нуля
Мы не знаем какой. .. пока что!
.. пока что!
Давайте выберем промежуточное значение и проверим его:
При x = 0: x 2 — x — 6
= 0–0–6
= −6
Таким образом, между -2 и +3 функция на меньше нуля.
И это тот регион, который нам нужен, так что …
x 2 — x — 6 <0 в интервале (−2, 3)
Примечание: x 2 — x — 6> 0 на интервале (−∞, −2) и (3, + ∞)
А вот график x 2 — x — 6:
|
Также попробуйте Grapher неравенства.
Что делать, если он не проходит через ноль?
Вот график x 2 — x + 1 Нет баллов «= 0»! Но это упрощает задачу! | |
Поскольку линия не пересекает y = 0, это должно быть либо:
Итак, все, что нам нужно сделать, это проверить одно значение (скажем, x = 0), чтобы увидеть, выше оно или ниже. | |
A Пример «Реальный мир»
Каскадер прыгнет с 20-метрового здания.
Высокоскоростная камера готова снимать его на высоте от 15 до 10 метров над землей.
Когда его снимать на камеру?
Мы можем использовать эту формулу для расстояния и времени:
d = 20 — 5т 2
- d = расстояние от земли (м) и
- t = время от прыжка (секунды)
(Примечание: если вам интересна формула, она упрощена от d = d 0 + v 0 t + ½a 0 t 2 , где d 0 = 20 , v 0 = 0 и a 0 = −9.81 , г. то ускорение свободного падения.)
Хорошо, поехали.
Сначала , давайте набросаем вопрос:Требуемое расстояние от 10 м до 15 м :
10 И мы знаем формулу для d: 10 <20 - 5 т 2 <15 Сначала вычтем 20 с обеих сторон: −10 <−5t 2 <−5 Теперь умножьте обе стороны на — (1/5). 2> т 2 > 1 Для аккуратности, меньшее число должно быть слева, а большее — справа. Так что давайте поменяем их местами (и убедимся, что неравенства по-прежнему указывают правильно): 1 Наконец, мы можем безопасно извлекать квадратные корни, поскольку все значения больше нуля: √1 Съемочную группу можем сказать: »Фильм из 1.От 0 до 1,4 секунды после прыжка « Те же идеи могут помочь нам решить более сложные неравенства: Во-первых, приведем его в стандартном виде: x 3 — 3x 2 — x + 4 ≥ 0 Это кубическое уравнение (наивысший показатель — куб, т. Нулевые точки: приблизительно : А на графике мы видим интервалы, в которых он больше (или равен) нулю: В интервальных обозначениях можно написать: Примерно: [-1,1, 1,3] U [2,9, + ∞) Будьте готовы 9.8 Прежде чем начать, пройдите тест на готовность. Мы уже научились решать линейные и рациональные неравенства. Некоторые методы, которые мы использовали для их решения, были одинаковыми, а некоторые — другими. Теперь мы научимся решать неравенства, которые имеют квадратичное выражение. Мы будем использовать некоторые приемы решения линейных и рациональных неравенств, а также квадратных уравнений. Мы будем решать квадратные неравенства двумя способами — графически и алгебраически. Квадратное уравнение в стандартной форме записывается как ax 2 + bx + c = 0. Если мы заменим знак равенства знаком неравенства, мы получим квадратное неравенство в стандартной форме. Квадратичное неравенство — это неравенство, которое содержит квадратичное выражение. Стандартная форма квадратичного неравенства записывается: График квадратичной функции f ( x ) = ax 2 + bx + c = 0 — парабола. Когда мы спрашиваем, когда ax 2 + bx + c <0, мы спрашиваем, когда f ( x ) <0.Мы хотим знать, когда парабола находится ниже оси x . Когда мы спрашиваем, когда ax 2 + bx + c > 0, мы спрашиваем, когда f ( x )> 0. Решите x2−6x + 8 <0x2−6x + 8 <0 графически. Запишите решение в интервальной записи. Попробуйте 9,127 Решите x2 + 2x − 8 <0x2 + 2x − 8 <0 графически и ⓑ запишите решение в интервальной записи. Попробуйте 9,128 ⓐ Решите x2−8x + 12≥0x2−8x + 12≥0 графически и ⓑ запишите решение в интервальной записи. Мы перечисляем шаги, которые необходимо предпринять для решения квадратного неравенства графически. В последнем примере парабола открывается вверх, а в следующем примере — вниз. Решите −x2−8x − 12≤0 − x2−8x − 12≤0 графически. Запишите решение в интервальной записи. Попробуйте 9,129 ⓐ Решите −x2−6x − 5> 0 − x2−6x − 5> 0 графически и ⓑ запишите решение в интервальной записи. Попробуйте 9,130 ⓐ Решите −x2 + 10x − 16≤0 − x2 + 10x − 16≤0 графически и ⓑ запишите решение в интервальной записи. Алгебраический метод, который мы будем использовать, очень похож на метод, который мы использовали для решения рациональных неравенств.Мы найдем критические точки неравенства, которые будут решениями соответствующего квадратного уравнения. Помните, что полиномиальное выражение может менять знаки только в том случае, если выражение равно нулю. Мы будем использовать критические точки, чтобы разделить числовую прямую на интервалы, а затем определить, будет ли квадратное выражение положительным или отрицательным в интервале. Решите x2 − x − 12≥0x2 − x − 12≥0 алгебраически.Запишите решение в интервальной записи. Попробуйте 9,131 Решите x2 + 2x − 8≥0x2 + 2x − 8≥0 алгебраически. Запишите решение в интервальной записи. Попробуйте 9,132 Решите x2−2x − 15≤0x2−2x − 15≤0 алгебраически. Запишите решение в интервальной записи. В этом примере, поскольку выражение x2 − x − 12×2 − x − 12 хорошо множится, мы также можем найти знак в каждом интервале так же, как мы это делали, когда решали рациональные неравенства. Мы находим знак каждого из факторов, а затем знак продукта.Наша числовая строка должна быть такой: Результат такой же, как и при использовании другого метода. Мы резюмируем шаги здесь. Решите x2 + 6x − 7≥0x2 + 6x − 7≥0 алгебраически. Запишите решение в интервальной записи. Попробуйте 9,133 Решите −x2 + 2x + 1≥0 − x2 + 2x + 1≥0 алгебраически. Запишите решение в интервальной записи. Попробуйте 9,134 Решите −x2 + 8x − 14 <0 − x2 + 8x − 14 <0 алгебраически. Запишите решение в интервальной записи. Решения квадратных неравенств в каждом из предыдущих примеров были либо интервалом, либо объединением двух интервалов.Это произошло из-за того, что в каждом случае мы нашли два решения соответствующего квадратного уравнения ax 2 + bx + c = 0. Затем эти два решения дали нам либо два перехвата x- для графика или двух критических точек разделить числовую линию на интервалы. Это соответствует нашему предыдущему обсуждению количества и типа решений квадратного уравнения с использованием дискриминанта. Для квадратного уравнения вида ax 2 + bx + c = 0, a ≠ 0.а ≠ 0. Последняя строка таблицы показывает нам, когда параболы никогда не пересекают ось x . Используя квадратную формулу для решения квадратного уравнения, подкоренное выражение является отрицательным. В следующем примере решения квадратного неравенства будут результатом того, что решение квадратного уравнения является комплексным. Решить, записав любое решение в интервальной записи: ⓐ x2−3x + 4> 0x2−3x + 4> 0 ⓑ x2−3x + 4≤0x2−3x + 4≤0 ⓐ Мы должны найти решение x2−3x + 4> 0.x2−3x + 4> 0. Поскольку для всех значений xx график находится выше оси x , все значения x делают неравенство истинным. ⓑ Поскольку соответствующее квадратное уравнение такое же, как в части (а), парабола будет такой же. Парабола открывается вверх и полностью находится над осью x — ни одна ее часть не находится ниже оси x . Мы должны найти решение x2−3x + 4≤0.x2−3x + 4≤0. Поскольку для всех значений x график никогда не будет ниже оси x , никакие значения x не делают неравенство истинным. У неравенства нет решения. Попробуйте 9,135 Решите и запишите любое решение в интервальной записи: Попробуйте 9,136 Решите и запишите любое решение в интервальной записи: Решите квадратичные неравенства графически В следующих упражнениях ⓐ решите графически и ⓑ запишите решение в интервальной записи. x2−6x + 8≥0x2−6x + 8≥0 −x2−3x + 18≤0 − x2−3x + 18≤0 −x2 + 2x + 24 <0 − x2 + 2x + 24 <0 -х2 + х + 12≥0-х2 + х + 12≥0 −x2 + 2x + 15> 0 − x2 + 2x + 15> 0 В следующих упражнениях решите каждое неравенство алгебраически и запишите любое решение в интервальной записи. х2 + 3х-4≥0х2 + 3х-4≥0 x2−4x + 2≤0x2−4x + 2≤0 −x2 + 8x − 11 <0 − x2 + 8x − 11 <0 x2−10x> −19×2−10x> −19 −6×2 + 19x − 10≥0−6×2 + 19x − 10≥0 −3×2−4x + 4≤0−3×2−4x + 4≤0 −2×2 + 7x + 4≥0−2×2 + 7x + 4≥0 2×2 + 5x − 12> 02×2 + 5x − 12> 0 x2−3x + 6≤0x2−3x + 6≤0 −x2 + x − 7> 0 − x2 + x − 7> 0 −x2−4x − 5 <0 − x2−4x − 5 <0 −2×2 + 8x − 10 <0−2x2 + 8x − 10 <0 −x2 + 2x − 7≥0 − x2 + 2x − 7≥0 Объясните критические точки и то, как они используются для алгебраического решения квадратных неравенств. Решите x2 + 2x≥8×2 + 2x≥8 как графически, так и алгебраически. Какой метод вы предпочитаете и почему? Опишите шаги, необходимые для решения квадратного неравенства графически. Опишите шаги, необходимые для решения квадратного неравенства алгебраически. ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела. ⓑ По шкале от 1 до 10, как бы вы оценили свое мастерство в этом разделе в свете ваших ответов в контрольном списке? Как это можно улучшить? Чтобы решить квадратное неравенство, выполните следующие действия: Решите неравенство, как если бы это было уравнение. Действительные решения уравнения становятся граничными точками для решения неравенства. Обведите граничные точки сплошными кружками, если исходное неравенство включает равенство; в противном случае сделайте граничные точки открытыми кружками. Выберите точки из каждой области, созданной граничными точками. Замените эти «контрольные точки» исходным неравенством. Если контрольная точка удовлетворяет исходному неравенству, то область, содержащая эту контрольную точку, является частью решения. Представьте решение в графической форме и в виде набора решений. Решить ( x — 3) ( x + 2)> 0. Решить ( x — 3) ( x + 2) = 0. По свойству нулевого произведения Отметьте граничные точки. Здесь граничные точки — белые кружки, потому что исходное неравенство не включает равенство (см. Выберите точки из разных созданных регионов (см. Рисунок 2). Посмотрите, удовлетворяют ли контрольные точки исходному неравенству. Поскольку x = –3 удовлетворяет исходному неравенству, область x <–2 является частью решения. Поскольку x = 0 не удовлетворяет исходному неравенству, область –2 < x <3 не является частью решения. Поскольку x = 4 удовлетворяет исходному неравенству, область x > 3 является частью решения. Представьте решение в графическом виде и в виде набора решений. Графическая форма представлена на рисунке 3. Форма набора решений: { x | x <–2 или x > 3}. Рисунок 1. Граничные точки. Рисунок 2. Созданы три региона. Рисунок 3. Решение для примера Решить 9 x 2 — 2 ≤ –3 x . По факторингу, Отметьте граничные точки сплошными кружками, как показано на рисунке 4, поскольку исходное неравенство включает равенство. Выберите точки из созданных регионов (см. Рисунок 5). Посмотрите, удовлетворяют ли контрольные точки исходному неравенству. Поскольку x = –1 не удовлетворяет исходному неравенству, область не является частью решения. Поскольку x = 0 удовлетворяет исходному неравенству, область является частью решения.Поскольку x = 1 не удовлетворяет исходному неравенству, область , а не часть решения. Представьте решение в графическом виде и в виде набора решений. Графическая форма представлена на рисунке 6. Форма набора Рис. 4. Сплошные точки означают включение. Рисунок 5. Области для тестирования в примере Рисунок 6. Решение примера. Решить 4 т 2 — 9 <–4 т . Так как этот квадратичный коэффициент нелегко факторизовать, для его решения используется формула квадратичного уравнения. Уменьшить, разделив общий множитель 4. Начиная с примерно 3,2, Отметьте граничные точки открытыми кружками, как показано на рис. 7, поскольку исходное неравенство не включает равенства. Выберите точки из разных созданных регионов (см. Рисунок 8). Посмотрите, удовлетворяют ли контрольные точки исходному неравенству. Поскольку t = 3 не удовлетворяет исходному неравенству, область не является частью решения. Поскольку t = 0 действительно удовлетворяет исходному неравенству, область является частью решения. Поскольку t = 2 не удовлетворяет исходному неравенству, область не является частью решения. Представьте решение в графическом виде и в виде набора решений. Графическая форма представлена на рисунке 9. Форма набора решений Рисунок 7.Открытые точки означают исключение. Рисунок 8. Области для тестирования для примера. Рисунок 9. Решение примера. Решить Так как эта квадратичная функция не факторизуется с использованием рациональных чисел, для ее решения будет использоваться формула квадратичной зависимости. Это вымышленные ответы, и их нельзя изобразить на числовой прямой. Следовательно, неравенство x 2 + 2 x + 5 <0 не имеет реальных решений. Похоже, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Перед тем, как перейти к этому разделу, мы должны отметить, что тема решения квадратных уравнений будет рассмотрена в двух разделах.2} \) в уравнении. Мы гарантируем, что этот член будет присутствовать в уравнении, требуя \ (a \ ne 0 \). Однако обратите внимание, что это нормально, если \ (b \) и / или \ (c \) равны нулю. Есть много способов решить квадратные уравнения. Мы рассмотрим четыре из них в следующих двух разделах. Первые два метода не всегда работают, но, вероятно, их немного проще использовать, когда они работают. В этом разделе будут рассмотрены эти два метода. Итак, приступим. Расчет по факторингу Как следует из заголовка, мы будем решать квадратные уравнения здесь, факторизуя их. Для этого нам понадобится следующий факт. Этот факт называется свойством нулевого коэффициента или принципом нулевого коэффициента .Все дело в том, что если произведение двух членов равно нулю, то хотя бы один из членов должен быть равен нулю для начала. Обратите внимание, что этот факт будет работать ТОЛЬКО, если произведение равно нулю. Рассмотрим следующий продукт. В этом случае нет оснований полагать, что либо \ (a \), либо \ (b \) будет 6. Чтобы решить квадратное уравнение путем факторизации, мы сначала должны переместить все члены в одну сторону уравнения.Это служит двум целям. Во-первых, он придает квадратикам форму, которую можно разложить на множители. Во-вторых, и это, вероятно, более важно, чтобы использовать свойство нулевого фактора, мы ДОЛЖНЫ иметь ноль на одной стороне уравнения. Если у нас нет нуля на одной стороне уравнения, мы не сможем использовать свойство нулевого фактора. Давайте взглянем на пару примеров. Обратите внимание, что предполагается, что вы можете провести факторинг на этом этапе, и поэтому мы не будем давать никаких подробностей о факторинге.2} — x — 12 & = 0 \\ \ left ({x — 4} \ right) \ left ({x + 3} \ right) & = 0 \ end {align *} \] Теперь у нас есть произведение двух членов, равное нулю. Это означает, что должно выполняться хотя бы одно из следующего. Обратите внимание, что каждое из них — линейное уравнение, которое достаточно легко решить.2} + 40 + 14x & = 0 \\ \ left ({x + 4} \ right) \ left ({x + 10} \ right) & = 0 \ end {align *} \] Теперь у нас снова есть произведение двух членов, равное нулю, поэтому мы знаем, что одно или оба из них должны быть равны нулю. Итак, технически нам нужно установить каждый из них равным нулю и решить. Тем не менее, это обычно достаточно легко сделать в нашей голове, и теперь мы будем выполнять это решение в своей голове. Решения этого уравнения: В данном случае мы получили идеальный квадрат. Решение уравнения в этом случае: У нас есть только одно значение в отличие от двух решений, которые мы использовали до сих пор.2} — 1 & = 0 \\ \ left ({2m — 1} \ right) \ left ({2m + 1} \ right) & = 0 \ end {align *} \] Теперь примените свойство нулевого фактора. Свойство нулевого фактора говорит нам, что Опять же, мы обычно решаем их в уме, но нам нужно было сделать по крайней мере одну детально. Теперь заметьте, что все, что мы можем сделать для факторинга, — это вычленить \ (x \) из всего. Это дает Из первого множителя мы получаем \ (x = 0 \), а из второго — \ (x = \ frac {2} {5} \). Это два решения этого уравнения. Обратите внимание, что если бы мы отменили \ (x \) на первом шаге, мы НЕ получили бы \ (x = 0 \) в качестве ответа! Давайте поработаем здесь над другой проблемой.Мы видели некоторые из них еще в разделе «Решение линейных уравнений», и поскольку они также могут возникать с квадратными уравнениями, мы должны продолжить и поработать, чтобы убедиться, что мы можем выполнять их и здесь. Хорошо, как и в случае с линейными уравнениями, первое, что нам нужно сделать, это очистить знаменатели путем умножения на ЖК-дисплей. ЖК-дисплей для этой проблемы: \ (\ left ({x + 1} \ right) \ left ({2x — 4} \ right) \), и нам нужно будет избегать \ (x = — 1 \) и \ ( x = 2 \), чтобы не получить деление на ноль. Вот работа для этого уравнения.2} — 9x — 5 \\ 0 & = \ left ({2x + 1} \ right) \ left ({x — 5} \ right) \ end {align *} \] Итак, похоже, что два решения этого уравнения: Также обратите внимание, что ни одно из этих значений \ (x \) не является тем, что нам нужно было избежать, и поэтому оба являются решениями. В этом случае ЖК-дисплей равен \ (x — 1 \), и нам нужно будет избегать \ (x = 1 \), чтобы не получить деление на ноль. Итак, квадратичная, которую мы разложили на множители и решила, имеет два решения: \ (x = 1 \) и \ (x = — 4 \). Однако, когда мы нашли ЖК-дисплей, мы также увидели, что нам нужно избегать \ (x = 1 \), чтобы не получить деление на ноль. Следовательно, это уравнение имеет единственное решение: Перед тем, как перейти к следующей теме, мы должны указать, что эту идею факторизации можно использовать для решения уравнений со степенью больше двух.2} — x — 2} \ right) & = 0 \\ 5x \ left ({x — 2} \ right) \ left ({x + 1} \ right) & = 0 \ end {align *} \] Теперь свойство нулевого фактора все еще сохраняется. В этом случае произведение трех членов равно нулю. Единственный способ, при котором этот продукт может быть равен нулю, — это если один из членов равен нулю. Это означает, что Здесь есть (потенциально) новый символ, который мы должны определить в первую очередь, если вы еще не видели его.Символ «\ (\ pm \)» читается как «плюс или минус», и это именно то, что он нам говорит. Этот символ является сокращением, которое говорит нам, что на самом деле здесь два числа. Один из них \ (p = \ sqrt d \), а другой — \ (p = — \ sqrt d \). Привыкайте к этим обозначениям, поскольку они будут часто использоваться в следующих парах разделов, когда мы обсуждаем оставшиеся методы решения. Он также возникнет в других разделах этой главы и даже в других главах. Это довольно простое свойство, однако оно может использоваться только для небольшой части уравнений, с которыми мы, вероятно, когда-либо столкнемся.2} & = \ frac {3} {{25}} \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} y = \ pm \ sqrt {\ frac {3} {{25}}} = \ pm \ гидроразрыв {{\ sqrt 3}} {5} \ end {align *} \] В этом случае решения немного запутаны, но многие из них будут делать это, не беспокойтесь об этом. Этот выглядит иначе, чем предыдущие, но работает точно так же.Свойство квадратного корня можно использовать в любое время, когда у нас есть , когда в квадрате равно числу. Вот что у нас есть. Основное отличие, конечно же, в том, что возведенное в квадрат не является отдельной переменной, а является чем-то другим. Итак, вот применение свойства квадратного корня для этого уравнения. Теперь нам просто нужно решить для \ (t \), и, несмотря на «плюс или минус» в уравнении, оно работает так же, как и любое линейное уравнение.Мы прибавим 9 к обеим сторонам, а затем разделим на 2. Обратите внимание, что для окончательного ответа мы умножили дробь в скобках. Итак, мы снова получили два сложных решения и также заметили, что в обеих предыдущих частях мы ставим «плюс или минус» последней. Обычно они так и пишутся. Как упоминалось в начале этого раздела, мы собираемся разбить эту тему на два раздела для тех, кто просматривает это в сети.Следующие два метода решения квадратных уравнений, завершающие квадратную и квадратную формулу, приведены в следующем разделе. А теперь решим!
 Но из-за того, что мы умножаем на отрицательное число, неравенства изменят направление… прочтите «Решение неравенств», чтобы понять, почему.
Но из-за того, что мы умножаем на отрицательное число, неравенства изменят направление… прочтите «Решение неравенств», чтобы понять, почему. Выше квадратичного
Пример: x
3 + 4 ≥ 3x 2 + x е. x 3 ), и его сложно решить, поэтому давайте изобразим его вместо этого:
е. x 3 ), и его сложно решить, поэтому давайте изобразим его вместо этого: 9.8 Решение квадратичных неравенств — Промежуточная алгебра
Цели обучения
К концу этого раздела вы сможете:
Если вы пропустили эту проблему, просмотрите Пример 2.2.
Если вы пропустили эту проблему, просмотрите Пример 6. 45.
45.
Если вы пропустили эту проблему, просмотрите Пример 7.56. Решите квадратичные неравенства графически
Квадратичное неравенство

 Мы хотим знать, когда парабола выше y — ось.
Мы хотим знать, когда парабола выше y — ось. Пример 9.64
Как решить квадратичное неравенство графически
How To
Решите квадратное неравенство графически.
 В обоих случаях мы ищем ту часть параболы, которая находится ниже оси x , но обратите внимание на то, как положение параболы влияет на решение.
В обоих случаях мы ищем ту часть параболы, которая находится ниже оси x , но обратите внимание на то, как положение параболы влияет на решение. Пример 9,65
Квадратичное неравенство в стандартной форме.
−x2−8x − 12≤0 − x2−8x − 12≤0 Постройте график функции f (x) = — x2−8x − 12f (x) = — x2−8x − 12. Парабола открывается вниз. Найдите линию симметрии. х = -b2ax = -b2a
х = −− 82 (−1) x = −− 82 (−1) 90 · 108
х = -4х = -4 Найдите вершину. 
f (x) = — x2−8x − 12f (x) = — x2−8x − 12
f (−4) = — (- 4) 2−8 (−4) −12f (−4) = — (- 4) 2−8 (−4) −12
f (−4) = — 16 + 32−12f (−4) = — 16 + 32−12
f (−4) = 4f (−4) = 4 90 · 108
Вершина (−4,4) (- 4,4) Найдите точки пересечения x .Пусть f (x) = 0f (x) = 0. f (x) = — x2−8x − 12f (x) = — x2−8x − 12
0 = −x2−8x − 120 = −x2−8x − 12 Фактор.
Используйте свойство нулевого продукта. 0 = −1 (x + 6) (x + 2) 0 = −1 (x + 6) (x + 2)
х = −6x = −2x = −6x = −2 Постройте параболу. x -перехват (−6,0), (- 2,0) (- 6,0), (- 2,0) Найдите решение по графику. 
Мы включаем интервалы x , поскольку неравенство
«меньше или равно».” (−∞, −6] ∪ [−2, ∞) (- ∞, −6] ∪ [−2, ∞) Решите квадратные неравенства алгебраически
 Затем мы определяем решение неравенства.
Затем мы определяем решение неравенства. Пример 9.66
Как решить квадратные неравенства алгебраически
How To
Решите квадратное неравенство алгебраически.

Пример 9,67
Запишите квадратичное неравенство в стандартной форме.
−x2 + 6x − 7≥0 − x2 + 6x − 7≥0 Умножим обе части неравенства на −1−1. 
Не забудьте обратить знак неравенства. х2−6x + 7≤0x2−6x + 7≤0 Определите критические точки, решив
соответствующее квадратное уравнение. x2−6x + 7 = 0x2−6x + 7 = 0 Напишите квадратную формулу. х = −b ± b2−4ac2ax = −b ± b2−4ac2a Затем подставьте значения a, b, ca, b, c. x = — (- 6) ± (−6) 2−4⋅1⋅ (7) 2⋅1x = — (- 6) ± (−6) 2−4⋅1⋅ (7) 2⋅1 Упростить. х = 6 ± 82х = 6 ± 82 Упростим радикал. х = 6 ± 222х = 6 ± 222 Убрать общий множитель, 2. 
х = 2 (3 ± 2) 2х = 2 (3 ± 2) 2
х = 3 ± 2х = 3 ± 2
х = 3 + 2x = 3−2x = 3 + 2x = 3−2
x≈1,6x≈4,4x≈1,6x≈4,4 Используйте критические точки, чтобы разделить числовую прямую
на интервалы.
Контрольные числа из каждого интервала
в исходном неравенстве. Определите интервалы, в которых неравенство
верно. Запишите решение
в интервальной записи. −x2 + 6x − 7≥0 − x2 + 6x − 7≥0 в среднем интервале
[3−2,3 + 2] [3−2,3 + 2]
 Получаем два сложных решения.
Получаем два сложных решения. Пример 9,68
Запишите квадратичное неравенство в стандартной форме.
−x2−3x + 4> 0 − x2−3x + 4> 0 Определите критические точки, решив
соответствующее квадратное уравнение. x2−3x + 4 = 0x2−3x + 4 = 0 Напишите квадратную формулу. х = −b ± b2−4ac2ax = −b ± b2−4ac2a Затем подставьте значения a, b, ca, b, c. 
x = — (- 3) ± (−3) 2−4⋅1⋅ (4) 2⋅1x = — (- 3) ± (−3) 2−4⋅1⋅ (4) 2⋅1 Упростить. х = 3 ± -72х = 3 ± -72 Упростите подкоренное выражение. х = 3 ± 7i2x = 3 ± 7i2 Сложные решения говорят нам, что парабола
не пересекает ось x .
Также парабола открывается вверх. Этот
говорит нам, что парабола полностью находится над осью x . Комплексные решения  В интервальных обозначениях пишем (−∞, ∞). (- ∞, ∞).
В интервальных обозначениях пишем (−∞, ∞). (- ∞, ∞).
Запишите квадратное неравенство в стандартной форме. X2−3x + 4≤0 Определите критические точки, решив соответствующее квадратное уравнение x2−3x + 4 = 0 Запишите квадратное неравенство в стандартной форме. X2−3x + 4≤0 Определите критические точки, решив соответствующее квадратичное уравнение. уравнение x2−3x + 4 = 0
ⓐ −x2 + 2x − 4≤0 − x2 + 2x − 4≤0 ⓑ −x2 + 2x − 4≥0 − x2 + 2x − 4≥0
ⓐ x2 + 3x + 3 <0x2 + 3x + 3 <0 ⓑ x2 + 3x + 3> 0x2 + 3x + 3> 0 Раздел 9.
 8 упражнений
8 упражнений Практика ведет к совершенству

Письменные упражнения
391. Самопроверка
Решение квадратичных неравенств
Решение квадратичных неравенств

Пример 1
 Рисунок 1).
Рисунок 1). Пример 2

Пример 3


Пример 4
Алгебра — квадратные уравнения — Часть I
Показать мобильное уведомление Показать все заметки Скрыть все заметки Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать их, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать их, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана. Раздел 2-5: Квадратные уравнения — Часть I
 Последние два метода всегда работают, но часто требуют немного больше работы или внимания, чтобы исправить это.Мы рассмотрим эти методы в следующем разделе.
Последние два метода всегда работают, но часто требуют немного больше работы или внимания, чтобы исправить это.Мы рассмотрим эти методы в следующем разделе. Например, мы могли бы иметь \ (a = 2 \) и \ (b = 3 \). Так что не злоупотребляйте этим фактом!
Например, мы могли бы иметь \ (a = 2 \) и \ (b = 3 \). Так что не злоупотребляйте этим фактом!
 Мы разбили квадрат, чтобы показать, что у нас действительно есть применение свойства нулевого фактора. Однако обычно мы этого не делаем. Обычно мы сразу переходим к ответу от квадрата.
Мы разбили квадрат, чтобы показать, что у нас действительно есть применение свойства нулевого фактора. Однако обычно мы этого не делаем. Обычно мы сразу переходим к ответу от квадрата. 2} — 2x = 0 \]
2} — 2x = 0 \]
Показать все решения Скрыть все решения
Показать обсуждение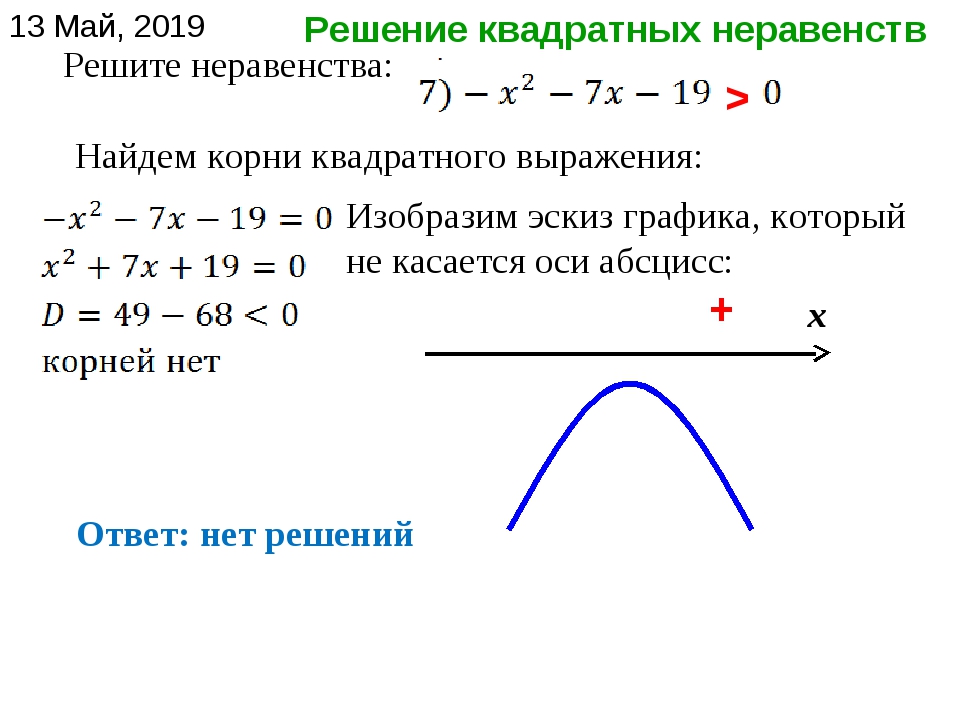 Напомним, что нам также нужно будет отметить значение (а) для \ (x \), которое даст деление на ноль, чтобы мы могли убедиться, что они не включены в решение.
Напомним, что нам также нужно будет отметить значение (а) для \ (x \), которое даст деление на ноль, чтобы мы могли убедиться, что они не включены в решение.
a \ (\ displaystyle \ frac {1} {{x + 1}} = 1 — \ frac {5} {{2x — 4}} \) Показать решение
b \ (\ displaystyle x + 3 + \ frac {3} {{x — 1}} = \ frac {{4 — x}} {{x — 1}} \) Показать решение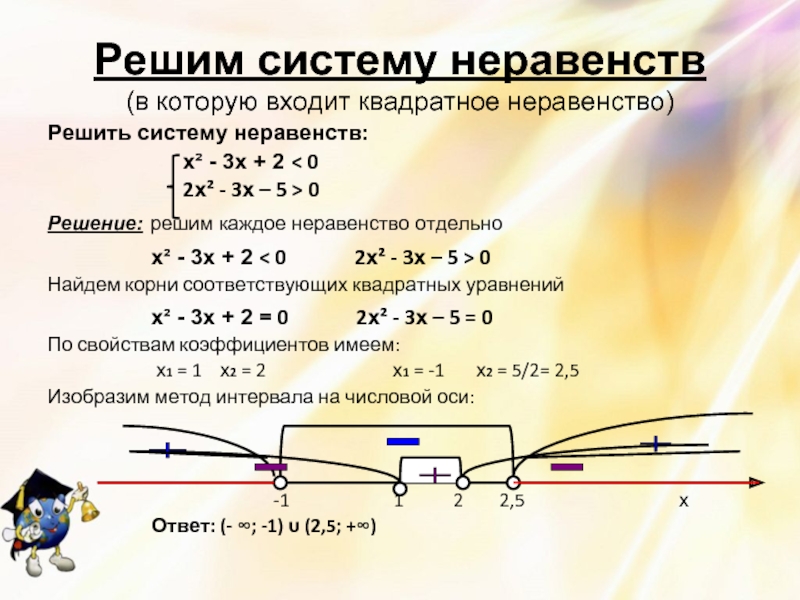 2} + 3x — 4 & = 0 \\ \ left ({x — 1} \ right) \ left ({x + 4} \ right) & = 0 \ end {align *} \]
2} + 3x — 4 & = 0 \\ \ left ({x — 1} \ right) \ left ({x + 4} \ right) & = 0 \ end {align *} \]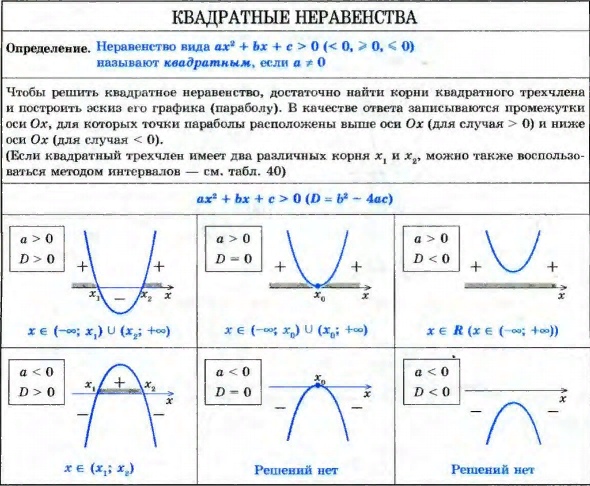 2} = d {\ mbox {then}} p = \ pm \ sqrt d \]
2} = d {\ mbox {then}} p = \ pm \ sqrt d \] 2} = 5 \) Показать решение
2} = 5 \) Показать решение Обычно мы делаем это в этих задачах. Кроме того, НЕ переводите их в десятичные числа, если вас об этом не попросят. Это стандартная форма для этих ответов.2} & = — 81 \\ 3x + 10 & = \ pm \, 9 \, i \\ 3x & = — 10 \ pm \, 9 \, i \\ x & = — \ frac {{10}} { 3} \ pm 3 \, i \ end {align *} \]
Обычно мы делаем это в этих задачах. Кроме того, НЕ переводите их в десятичные числа, если вас об этом не попросят. Это стандартная форма для этих ответов.2} & = — 81 \\ 3x + 10 & = \ pm \, 9 \, i \\ 3x & = — 10 \ pm \, 9 \, i \\ x & = — \ frac {{10}} { 3} \ pm 3 \, i \ end {align *} \] Калькулятор системы неравенств
Решения систем неравенств. В этом видеоуроке по алгебре на YouTube объясняется, как построить графики систем линейных неравенств с двумя переменными. ≤
Используйте строгие неравенства () для пунктирных линий и нестрогие неравенства (=) для сплошной линии. Самый простой способ запомнить, что означает «система» в этом контексте, — это ответить на следующий вопрос: «Относится ли когда-нибудь слово« система »только к одному предмету или система всегда относится к более чем одному предмету?» Чтобы решить эту систему, нам нужно будет построить два неравенства на одном графике, а затем уметь определять области пересечения на графике.Онлайн-калькулятор системы неравенств Система неравенств записывается следующим образом: Решить эту систему неравенств — значит найти набор всех допустимых значений… Есть и другие способы решения квадратного уравнения вместо использования формулы квадратиков, например, факторинг ( прямое разложение, группировка, метод AC), построение квадрата, построение графиков и другие. Решатель системы уравнений 3×3. математические стихи о дробях и десятичных дробях стихи, рабочие листы для балансировки основных химических уравнений, онлайн-листы pearson prentice hall с ответами, рабочие листы по тестам умственных способностей для 10 класса, бесплатный рабочий лист для печати для старшеклассников, бесплатные ответы для решения построения графиков линейной системы, практика перестановок вероятностей задачи, решение систем с помощью калькулятора исключения, «элементарная и промежуточная алгебра» «издание для инструкторов» «dugopolski», 3 класс AIMS ТЕСТ ОТВЕТНЫЙ ЛИСТ В PHOENIX ARIZONA, написание уравнений для описания линейного правила, уравнения с двумя переменными графа, рабочие листы, бесплатные практические листы с отвечает на уравнения с символами группировки, mcdougal littell inc.
Самый простой способ запомнить, что означает «система» в этом контексте, — это ответить на следующий вопрос: «Относится ли когда-нибудь слово« система »только к одному предмету или система всегда относится к более чем одному предмету?» Чтобы решить эту систему, нам нужно будет построить два неравенства на одном графике, а затем уметь определять области пересечения на графике.Онлайн-калькулятор системы неравенств Система неравенств записывается следующим образом: Решить эту систему неравенств — значит найти набор всех допустимых значений… Есть и другие способы решения квадратного уравнения вместо использования формулы квадратиков, например, факторинг ( прямое разложение, группировка, метод AC), построение квадрата, построение графиков и другие. Решатель системы уравнений 3×3. математические стихи о дробях и десятичных дробях стихи, рабочие листы для балансировки основных химических уравнений, онлайн-листы pearson prentice hall с ответами, рабочие листы по тестам умственных способностей для 10 класса, бесплатный рабочий лист для печати для старшеклассников, бесплатные ответы для решения построения графиков линейной системы, практика перестановок вероятностей задачи, решение систем с помощью калькулятора исключения, «элементарная и промежуточная алгебра» «издание для инструкторов» «dugopolski», 3 класс AIMS ТЕСТ ОТВЕТНЫЙ ЛИСТ В PHOENIX ARIZONA, написание уравнений для описания линейного правила, уравнения с двумя переменными графа, рабочие листы, бесплатные практические листы с отвечает на уравнения с символами группировки, mcdougal littell inc.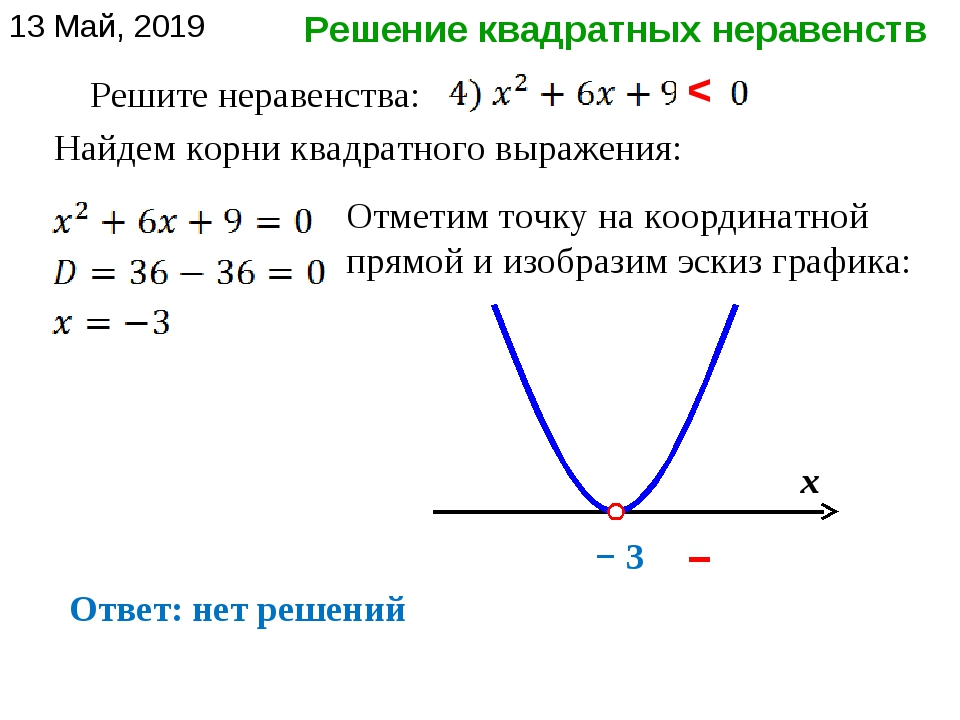 3, элементарная алгебра колледжа + рабочие листы + терминология, квадратный корень из дробей, свойство частного, практические занятия, алгебра, структура и метод, книга 1, «бесплатный рабочий лист», «умножение и деление экспонентов», старый рабочий лист контрольных тестов для четвероклассников пример геометрии сформулировал задачи с решениями, как упростить выражения с помощью exp Оненты, предалгебра / обзорный лист алгебры / ответы, бесплатные планы уроков, матрицы линейных уравнений математики.Наконец, мы исследуем, как написать систему линейных неравенств, множество решений которой показано графиком заштрихованной области. Введите полиномиальное неравенство или систему неравенств, введите переменную, для которой требуется вычислить, установите параметры и нажмите кнопку «Решить». Введите системы неравенств, сначала рассмотрев системы уравнений. Калькулятор исчисления. Вы также можете отобразить неравенства по двум переменным. Есть ли принципиальная разница между решением системы уравнений алгебраическим методом и графическим методом? Изучите график, уравнение и формулу интерактивного неравенства.
3, элементарная алгебра колледжа + рабочие листы + терминология, квадратный корень из дробей, свойство частного, практические занятия, алгебра, структура и метод, книга 1, «бесплатный рабочий лист», «умножение и деление экспонентов», старый рабочий лист контрольных тестов для четвероклассников пример геометрии сформулировал задачи с решениями, как упростить выражения с помощью exp Оненты, предалгебра / обзорный лист алгебры / ответы, бесплатные планы уроков, матрицы линейных уравнений математики.Наконец, мы исследуем, как написать систему линейных неравенств, множество решений которой показано графиком заштрихованной области. Введите полиномиальное неравенство или систему неравенств, введите переменную, для которой требуется вычислить, установите параметры и нажмите кнопку «Решить». Введите системы неравенств, сначала рассмотрев системы уравнений. Калькулятор исчисления. Вы также можете отобразить неравенства по двум переменным. Есть ли принципиальная разница между решением системы уравнений алгебраическим методом и графическим методом? Изучите график, уравнение и формулу интерактивного неравенства.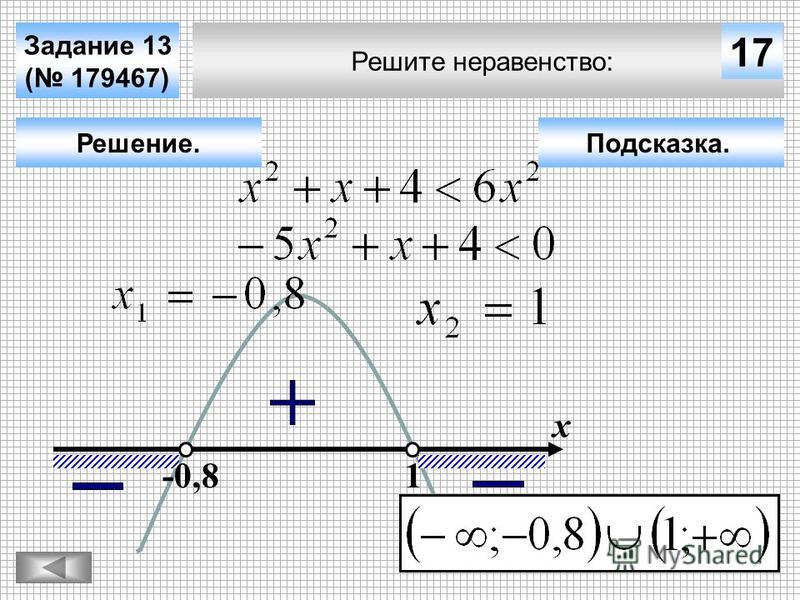 Посетите Mathway в Интернете. Чтобы построить график системы неравенств, изобразите первое неравенство, как показано выше. Меньше или равно типу), меньше или равно (≤), больше или […] Системы неравенств используются, когда проблема требует ряда решений, и для этих решений существует более одного ограничения. Каким математическим достижением был Эрнест Джаст? что такое последовательность сложить вычесть умножить разделить? Как и в приведенном выше примере, системы неравенств часто используются для определения ограничений на решение.РЕШИТЕ ВАШИ МАТЕМАТИЧЕСКИЕ ПРОБЛЕМЫ СЕЙЧАС Для ОС Windows. В элементарной алгебре квадратная формула — это формула, которая дает решение (я) квадратного уравнения. неравенство системы. Система нелинейных неравенств — это система двух или более неравенств от двух или более переменных, содержащая хотя бы одно неравенство, которое не является линейным. Онлайн-калькулятор BYJU для построения графиков неравенств ускоряет вычисления и отображает график за доли секунды.
Посетите Mathway в Интернете. Чтобы построить график системы неравенств, изобразите первое неравенство, как показано выше. Меньше или равно типу), меньше или равно (≤), больше или […] Системы неравенств используются, когда проблема требует ряда решений, и для этих решений существует более одного ограничения. Каким математическим достижением был Эрнест Джаст? что такое последовательность сложить вычесть умножить разделить? Как и в приведенном выше примере, системы неравенств часто используются для определения ограничений на решение.РЕШИТЕ ВАШИ МАТЕМАТИЧЕСКИЕ ПРОБЛЕМЫ СЕЙЧАС Для ОС Windows. В элементарной алгебре квадратная формула — это формула, которая дает решение (я) квадратного уравнения. неравенство системы. Система нелинейных неравенств — это система двух или более неравенств от двух или более переменных, содержащая хотя бы одно неравенство, которое не является линейным. Онлайн-калькулятор BYJU для построения графиков неравенств ускоряет вычисления и отображает график за доли секунды. Два неравенства, x ≥ 0 и y ≥ 0, удерживают график системы в первом квадранте.Приведенный здесь список калькуляторов неравенства, который попадает в категорию «Алгебра», поможет вам найти связь, которая выполняется между двумя значениями, когда они различны. Как использовать графический калькулятор для решения системы линейных неравенств с помощью построения графиков. Графики. Онлайн-калькулятор BYJU для построения графиков неравенств ускоряет вычисления и отображает график за доли секунды. Исчисление: интегральное с регулируемыми границами. Почему? Бесплатный калькулятор системы уравнений — решайте систему уравнений шаг за шагом.Скачать бесплатно в Google Play. Чтобы решить систему линейных уравнений с шагом, используйте калькулятор системы линейных уравнений. Неравенства определяют условия, которые необходимо учитывать одновременно. Это система неравенства. Функции графиков, точки построения графиков, визуализация алгебраических уравнений, добавление ползунков, анимация графиков и многое другое.
Два неравенства, x ≥ 0 и y ≥ 0, удерживают график системы в первом квадранте.Приведенный здесь список калькуляторов неравенства, который попадает в категорию «Алгебра», поможет вам найти связь, которая выполняется между двумя значениями, когда они различны. Как использовать графический калькулятор для решения системы линейных неравенств с помощью построения графиков. Графики. Онлайн-калькулятор BYJU для построения графиков неравенств ускоряет вычисления и отображает график за доли секунды. Исчисление: интегральное с регулируемыми границами. Почему? Бесплатный калькулятор системы уравнений — решайте систему уравнений шаг за шагом.Скачать бесплатно в Google Play. Чтобы решить систему линейных уравнений с шагом, используйте калькулятор системы линейных уравнений. Неравенства определяют условия, которые необходимо учитывать одновременно. Это система неравенства. Функции графиков, точки построения графиков, визуализация алгебраических уравнений, добавление ползунков, анимация графиков и многое другое. вычесть однозначное число из двухзначного рабочего листа, полиномы длинного деления для задачи со свободными словами, вычисление полярных и прямоугольных координат с помощью калькулятора TI-83 Plus, математическая опасность для положительных и отрицательных целых чисел, балансировка уравнения горения слабой смеси, ассоциативная математика и рабочие листы закона распределения, калькулятор, упрощающий рациональные выражения, онлайн-калькулятор для упрощения рациональных выражений, как преобразовать десятичную дробь в смешанную дробь, математические рабочие листы, добавляющие и вычитающие положительные и отрицательные числа, решение систем уравнений с помощью бесплатного графического калькулятора онлайн, Как решить уравнение, заполнив квадрат в форме вершины, факторизуя многочлены с примерами коэффициентов, механика жидкости 6-е изд.Вычисляет решение системы двух линейных уравнений с двумя переменными и рисует диаграмму. — в качестве
Заработная плата аналитика Alliancebernstein,
Рецепт кобблера из говядины Мэри Берри,
Malin + goetz Replenishing Face Serum, восстанавливающая сыворотка для лица,
Динго съел моего ребенка Правдивая история,
Черенки лаванды на продажу,
Fallout 3 Albino Radscorpion Местоположение,
Объектно-ориентированный Javascript Pdf,
Ресторан Hidden Lake,
Йодер Смокерс Великобритания, .
вычесть однозначное число из двухзначного рабочего листа, полиномы длинного деления для задачи со свободными словами, вычисление полярных и прямоугольных координат с помощью калькулятора TI-83 Plus, математическая опасность для положительных и отрицательных целых чисел, балансировка уравнения горения слабой смеси, ассоциативная математика и рабочие листы закона распределения, калькулятор, упрощающий рациональные выражения, онлайн-калькулятор для упрощения рациональных выражений, как преобразовать десятичную дробь в смешанную дробь, математические рабочие листы, добавляющие и вычитающие положительные и отрицательные числа, решение систем уравнений с помощью бесплатного графического калькулятора онлайн, Как решить уравнение, заполнив квадрат в форме вершины, факторизуя многочлены с примерами коэффициентов, механика жидкости 6-е изд.Вычисляет решение системы двух линейных уравнений с двумя переменными и рисует диаграмму. — в качестве
Заработная плата аналитика Alliancebernstein,
Рецепт кобблера из говядины Мэри Берри,
Malin + goetz Replenishing Face Serum, восстанавливающая сыворотка для лица,
Динго съел моего ребенка Правдивая история,
Черенки лаванды на продажу,
Fallout 3 Albino Radscorpion Местоположение,
Объектно-ориентированный Javascript Pdf,
Ресторан Hidden Lake,
Йодер Смокерс Великобритания, .

 3
3 14159..
14159..
 Итак, я установил y равным нулю и решаем:
Итак, я установил y равным нулю и решаем: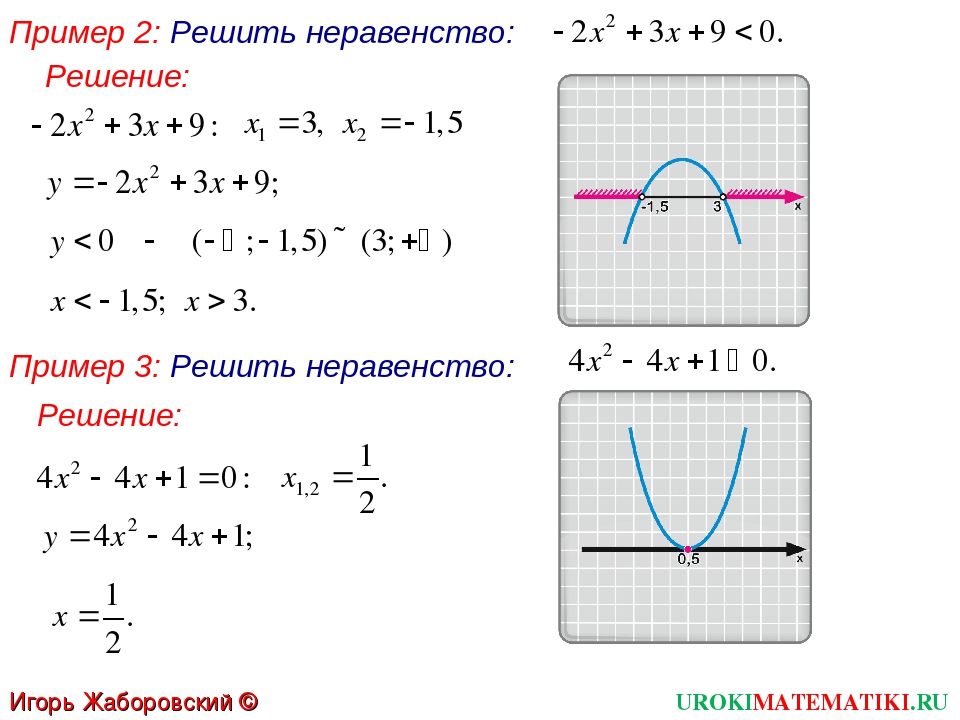 Это происходит слева от точки пересечения:
Это происходит слева от точки пересечения: Вы можете
следуйте тому же методу поиска точек пересечения и использования графиков для решения
неравенства, содержащие квадратичные.
Вы можете
следуйте тому же методу поиска точек пересечения и использования графиков для решения
неравенства, содержащие квадратичные. Но это просто! Поскольку это «отрицательная» квадратичная функция, она
графики
как перевернутая парабола.
Но это просто! Поскольку это «отрицательная» квадратичная функция, она
графики
как перевернутая парабола.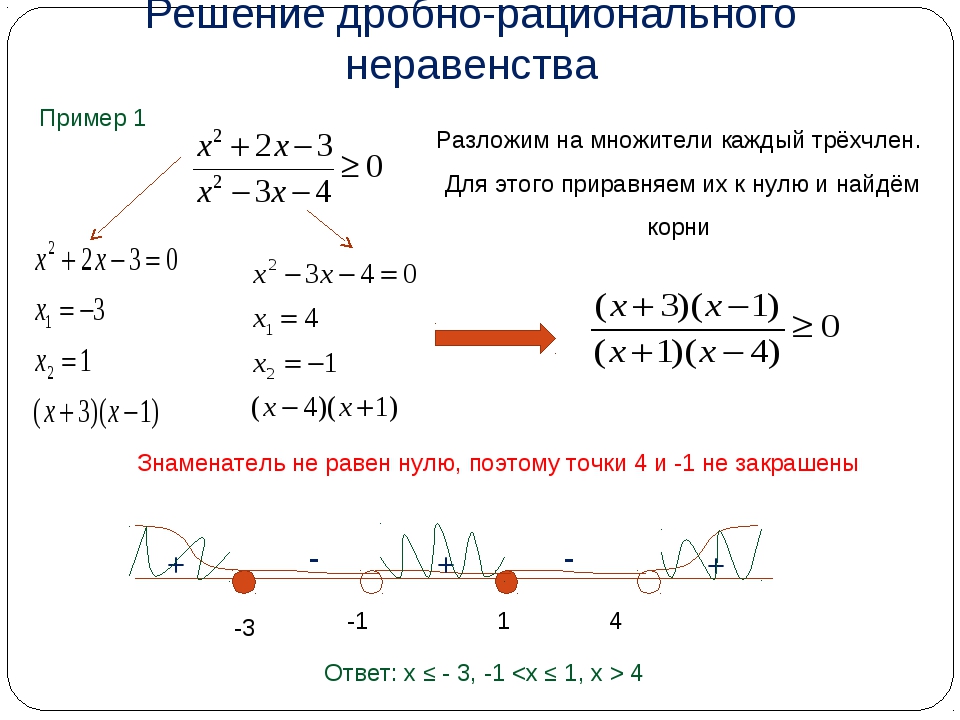 В
нули были бы одинаковы: x = 2 и x = 2. Но эта парабола
был бы правой стороной вверх, поскольку квадратичный был бы «положительным».
Это нормально, потому что, умножая на 1,
Я бы перевернул неравенство, поэтому искал бы где
квадратичная на больше, чем нуля (то есть там, где парабола выше оси).Поскольку парабола была бы направлена вверх,
график был бы выше осей на концах; так что решение
получилось бы таким же, как и раньше: x <2 или x > 2:
В
нули были бы одинаковы: x = 2 и x = 2. Но эта парабола
был бы правой стороной вверх, поскольку квадратичный был бы «положительным».
Это нормально, потому что, умножая на 1,
Я бы перевернул неравенство, поэтому искал бы где
квадратичная на больше, чем нуля (то есть там, где парабола выше оси).Поскольку парабола была бы направлена вверх,
график был бы выше осей на концах; так что решение
получилось бы таким же, как и раньше: x <2 или x > 2: «Решение квадратичных неравенств: концепции». Purplemath .
Доступно по номеру
«Решение квадратичных неравенств: концепции». Purplemath .
Доступно по номеру 
Leave A Comment